23. Kontextsensitive Sprachen
|
|
|
- Gregor Fischer
- vor 7 Jahren
- Abrufe
Transkript
1 2. Kontextsensitive Sprachen In diesem Aschnitt etrachten wir die Klasse der kontextsensitiven Sprachen, der nach der Klasse der allgemeinen Chomsky-Sprachen größten Klasse der Chomsky- Hierarchie. Wir zeigen, dass die kontextsensitiven Sprachen genau die Sprachen vom Erweiterungstyp sind und enutzen diese Äquivalenz für eine Maschinencharakterisierung der kontextsensitiven Sprachen: Die Sprachklasse KS stimmt mit der nichtdeterministisch linearen Platzklasse NSPACE n aus der Komplexitätstheorie üerein. Insesondere sind also im Gegensatz zu den Typ-0-Sprachen kontextsensitive Sprachen stets rekursiv. Zum Nachweis der Gleichheit KS ERW führen wir zunächst eine Normierung von Grammatiken ein. 2.1 DEFINITION. Eine Grammatik G N T P S heißt separiert, falls P nur Regeln der Form und enthält. v w mit v N w N (Umformungsregeln) X a mit X N a T (Sustitutionsregeln) 2.2 LEMMA. Jede Grammatik G vom Typ i oder vom Erweiterungstyp lässt sich effektiv in eine äquivalente separierte Grammatik G desselen Typs üerführen. BEWEIS. Sei G N T P S gegeen. Die Grammatik G N T P S erhält man dadurch, dass man zu jedem Terminalzeichen a eine neue Variale â einführt, in den Regeln von G alle Vorkommen von Terminalzeichen durch die entsprechenden neuen a für Varialen ersetzt (Umformungsregeln von G ) und die Sustitutionsregeln â jedes Terminalzeichen hinzufügt. Formal ist also N N ˆT, woei ˆT â : a T disjunkt zu N und T gewählt ist, und P ˆv ŵ : v w P â a : a T woei ŵ das Bild h w von w N T unter dem von h 0 : N T N mit h 0 X X für X N und h 0 a â für a T erzeugten Homomorphismus h : N T N ist. 2. SATZ. KS ERW
2 2 KONTEXTSENSITIVE SPRACHEN 160 Da jede kontextsensitive Grammatik vom Erweiterungstyp ist, gilt wie im letzten Aschnitt ereits festgehalten die Inklusion KS ERW trivialerweise. Zum Nachweis der Umkehrung genügt es, folgendes Lemma zu zeigen. 2.4 LEMMA. Jede Grammatik G vom Erweiterungstyp lässt sich effektiv in eine äquivalente kontextsensitive Grammatik G üerführen. BEWEIS. Nach Lemma 2.2 können wir ohne Einschränkung davon ausgehen, dass die gegeene Grammatik G N T P S vom Erweiterungstyp separiert ist. Weiter nehmen wir zunächst an, dass G λ-frei ist. Wir müssen dann jede Umformungsregel r X 1 X m Y 1 Y n n m 1 X 1 Y n N von G durch äquivalente kontextsensitive Regeln ersetzen. Ist m 1 (sonst ist die Regel r schon kontextsensitiv), so führen wir hierzu neue Varialen Z 1 Z m ein (für jede Regel sind diese Varialen verschieden zu wählen) und ersetzen r durch die kontextsensitiven Regeln X 1 X m Z 1 X 2 X m Z 1 X 2 X m Z 1 Z 2 X m. Z 1 Z m 2X m 1X m Z 1 Z m 1X m Z 1 Z m 1X m Z 1 Z m Y m 1 Y n Z 1 Z m Y m 1 Y n Z 1 Z m 1Y m Y n. Z 1 Y 2 Y n Y 1 Y n Man ersetzt also (im entsprechenden Kontext) zunächst die Varialen X 1 X m 1 durch Z 1 Z m 1 und die Variale X m durch Z m Y m 1 Y n. Dann werden (wieder im entsprechenden Kontext) die Hilfsvarialen Z i in Y i üerführt. Zum Nachweis, dass die so gewonnene Grammatik G zu G äquivalent ist, muss man für die nichttriviale Inklusion L G L G zeigen, dass in der Herleitung eines Terminalwortes in G jede mit X 1 X m Z 1 X 2 X m egonnene Simulation der G- Regel r (durch Ausführung der entsprechenden G -Regeln in der oen aufgeführten Reihenfolge) eendet wird (wir verzichten hier auf Details). Enthält G die λ-regel S λ, so kann die oen eschrieene Umformung die λ- Treue verletzen (z.b. für X 2 S). Hier erhält man G N T P S dadurch, dass man zunächst G0 N0 T P0 S zu G 0 N T P!" S λ# S wie oen konstruiert, und hieraus G N0 $ S # T P0 % S S S λ# S durch Hinzufügen eines neuen Axioms S, das eliminiert oder in das alte Axiom üerführt werden kann, gewinnt. Zur Analyse kontextsensitiver Sprachen enutzt man nichtdeterministische linear eschränkte Automaten (NLBA), die man als Variante nichtdeterministischer Turingmaschinen wie folgt eschreien kann: Gro gesprochen ist ein linear eschränkter
3 2 KONTEXTSENSITIVE SPRACHEN 161 Automat eine 1-Band-Turingmaschine, die nur die Felder esucht, auf denen zu Beginn der Rechnung die Eingae steht. Dies wird realisiert mit Hilfe von vor und nach der Eingae gesetzten Randmarken, die weder üerschrieen noch üerschritten werden dürfen. Ein NLBA M eginnt also seine Rechnung ei Eingae w T mit der Startkonfiguration & w ' 0 woei die Randmarken & (' in dem Bandalphaet von M nicht vorkommen, und 0 der Startzustand von M ist. M verhält sich dann wie eine Turingmaschine, verlässt aer den mit & und ' markierten Bereich nie. Ist also das mit & (zw. ' ) eschriftete Feld das Areitsfeld von M, so wird die Inschrift nicht verändert, und der Kopf läuft nach rechts (zw. links) oder leit stehen. Im Folgenden nehmen wir o.b.d.a. an, dass das Programm eines NLBA M aus edingten Anweisungen esteht, und es genau einen akzeptierenden Zustand git. Mit NLBA ezeichnen wir auch die Klasse der Sprachen L M, die von einem nichtdeterministischen linear eschränkten Automaten M erkannt werden. Entsprechend ist DLBA die Klasse der von deterministischen linear eschränkten Automaten erkannte Sprachen. Aufgrund der Definition linear eschränkter Automaten lässt sich mit Hilfe des linearen Kompressionssatzes leicht zeigen: 2.5 LEMMA. Es gilt und NLBA NSPACE n ) 2 * NSPACE O n + DLBA DSPACE n ) 2, DSPACE O n + Der folgende Satz zeigt also, dass KS mit der nichtdeterministischen Platzklasse NSPACE O n + zusammenfällt. 2.6 SATZ. Es lässt sich zu jeder kontextsensitiven Grammatik G effektiv ein NLBA M mit L G L M angeen und umgekehrt. Insesondere gilt also KS NLBA. Wir formulieren die eiden für den Beweis erforderlichen Behauptungen als Lemmata. 2.7 LEMMA. Jede kontextsensitive Grammatik G lässt sich effektiv in einen NLBA M mit L G L M üerführen. BEWEIS. Von der gegeenen kontextsensitiven Grammatik G N T P S können wir o.b.d.a. annehmen, dass sie separiert ist. Weiter gehen wir davon aus, dass G λ- frei ist. (Ist dies nicht der Fall, so muss der unten angegeene Automat so erweitert werden, dass er zunächst zusätzlich testet, o die Eingae leer ist.) Ein NLBA M, der die von G erzeugte Sprache akzeptiert, areitet wie folgt: M enutzt zwei Spuren, woei zunächst die Eingae w auf die oere Spur kopiert und das Axiom S auf die untere Spur geschrieen wird. Auf der unteren Spur werden dann nichtdeterministisch alle möglichen Herleitungen von G erzeugt, in denen nur Satzformen der Länge -/. w. vorkommen (diese also auf dem verfügaren Platz agespeichert werden können). Da G
4 & ' 2 KONTEXTSENSITIVE SPRACHEN 162 vom Erweiterungstyp ist, erhält man so eine Herleitung von w, falls w L G gilt. Nach Aschluss der Herleitung vergleicht also M die Wörter auf eiden Spuren und akzeptiert ei Gleichheit. Im Folgenden geen wir ein Programm aus edingten Anweisungen an, das auf diesen Ideen asiert. Der Startzustand ist 0, ) der einzige akzeptierende Zustand. Die Inschriften α der oeren und β der unteren Spur eines Feldes schreien wir als Paar α β. Weiter sind a a T, A N, α T N % elieige Buchstaen aus diesen Alphaeten, woei 0 T N $ & ('1 das Blankzeichen von M ist. Die Üerführung einer nichtleeren Eingae w a 1 (n 1) in die Spurendarstellung zu Beginn der Simulation der G-Herleitungen 0 a 1 ' 2 & a 1 S a 2 ' leisten die Instruktionen 0 & & R 1 1 a a S R 2 2 a a R 2 2 ' ' S Zur folgenden Simulation von G ermöglicht man den Üergang & a 1 S a 2 ' 2 & für jedes Wort w α 1 α n 2 der Länge n, für das S h w gilt, woei h : T N T N der Homomorphismus ist, der alle Vorkommen von Blanks in w eliminiert (d.h. der von der Funktion h : T N % 4 T N mit h α α für α 0 und h λ induziert wird). und Hierzu enutzt man zunächst die Instruktionen ' ' L & & R a α a α L a α a α R a 1 α 1 a a α L 5 α6 a a α R 5 α6 5 α6 a α a S um das Areitsfeld elieig zu ewegen zw. auf der unteren Spur die Blanks elieig zu verschieen. Jede Umformungsregel r X 1 X m dann mit den Instruktionen α n Y 1 Y n (1 - m - n) von G simuliert man a X 1 a Y 1 R 5 r 26 5 r i6 a X i a Y i R 5 r i ) i - m 5 r i6 a a Y i R 5 r i ) 16 m 7 i 7 n 5 r n6 a a Y n S
5 & 2 KONTEXTSENSITIVE SPRACHEN 16 und jede Sustitutionsregel r X a durch a8 X a a S Nach Aschluss der Simulation von G akzeptiert M ei positivem Vergleich der eiden Spuren mit Hilfe der Instruktionen a 1 a 1 ' 2 & ' ) & & R 4 4 a a R 4 4 ' ' S ) Auf den Korrektheitseweis verzichten wir. 2.8 LEMMA. Jeder NLBA M lässt sich effektiv in eine Grammatik G vom Erweiterungstyp mit L M L G üerführen. BEWEIS. Wir gehen wie im Beweis von Lemma vor, in dem die Rechnungen einer Turingmaschine durch eine Chomsky-Grammatik simuliert wurden. Da ei einem NLBA Konfigurationslänge und Eingaenlänge (im Wesentlichen) gleich sind, ist die Simulation hier (mit geeigneten kleineren Modifikationen) mit Hilfe einer Grammatik vom Erweiterungstyp möglich. Sei also ein NLBA M gegeen, Σ Γ Z das Eingae- zw. Bandalphaet und die Zustandsmenge von M, woei o.b.d.a. Z 9 Γ /0 gelte, und 0 und 1 der Start- zw. einzige akzeptierende Zustand & von M seien. Weiter können wir annehmen, dass M stets auf der linken Randmarke stoppt. Eine Grammatik G N Σ P S, die L M erzeugt, enthält folgende Regeln. Für die endlich vielen Wörter w L M der Länge - 2 sichert man die Herleitarkeit durch Regeln S w. Für die anderen Wörter aus L M wird die Herleitarkeit durch Regeln gesichert, die die Areitsweise von M eschreien. Die Satzformen von G estehen hierzu aus zwei Spuren. Während ein Kandidat w a 1 (n ) für ein Wort w L M in der oeren Spur steht, wird in der unteren Spur eine aus der zu w gehörenden Startkonfiguration erreichare Konfiguration stehen. Daei schreien wir den Zustand vor den Buchstaen auf dem Areitsfeld und wählen jedes Paar estehend aus Zustand und Feldinschrift als Variale in N. Weiter verschmelzen wir die Randmarken mit dem ersten zw. letzten Buchstaen der Bandinschrift. (Durch diese Maßnahmen stimmen Eingae- und Konfigurationslänge exakt üerein, weshal wir verkürzende Regeln vermeiden können.) Formal transponieren wir die Spaltenvektoren, schreien also α β für α in der oeren und β in der unteren Spur eines Feldes. Das Alphaet N der syntaktischen Varialen von G wird also neen dem Axiom S und einer Hilfsvarialen U alle Paare a α : a & α : a α'; < a zα < a z & α < a & zα : a zα'; : a αz'; enthalten, woei a Σ, α Γ und z Z gilt. In den folgen Regeln sind jeweils a a= Σ, α α α Γ, z z= Z elieige Buchstaen aus den genannten Alphaeten. Für jedes Wort w a 1 Σ mit n ermöglicht man zunächst S 2 a & 1 a 2 0a 1 a 2 '
6 2 KONTEXTSENSITIVE SPRACHEN 164 durch die Regeln S a & 0a U U a a U U a a'; z α α B z> führt man Simulationsregeln ein, die von der Zu jeder Instruktion I Kopfewegung ahängen. Für den Fall der Linksewegung B L (andere Fälle: Üung) sind dies a & zα? a z & α a & α a zα? a & z α a α a α a zα? a z α a α a α a a zα a α '; Entsprechend simuliert man Instruktionen, die die Randmarken etreffen. Z.B. entspricht der Instruktion I z & & R z die Regel a z & α A a & z α Mit diesen Simulationsregeln kann man mit w in der oeren Spur alle Konfigurationen (und nur diese) in der unteren Spur erzeugen, die M ei Eingae w erreichen kann. Ist solch eine Konfiguration akzeptierend, kann man die untere Spur auflösen mit Hilfe der Regeln a & 1 α B a a a α? a a α';? Wir verzichten auf den Korrektheitseweis. aa aa Fassen wir die Sätze 2. und 2.6 sowie Lemma 2.5 zusammen, so erhalten wir 2.9 KOROLLAR. KS ERW NLBA NSPACE O n +. Insesondere ist also jede kontextsensitive Sprache rekursiv, woraus sich die Echtheit der Inklusion KS CH ergit: 2.10 KOROLLAR. KS C CH. BEWEIS. Das Halteprolem K ist rekursiv aufzählar aer nicht rekursiv. Nach Satz und Korollar 2.9 gilt also K CH! KS. Setzen wir eine Gödelisierung der Grammatiken voraus, so können wir (wie am Ende von Aschnitt 21 ereits für allgemeine Grammatiken gemacht) das Wortprolem W KS D GE x : G kontextsensitiv & x L G F# das Leerheitsprolem LEER KS D GE# x : G kontextsensitiv & L G /0
7 2 KONTEXTSENSITIVE SPRACHEN 165 das Unendlichkeitsprolem INF KS / D GE x : G kontextsensitiv & L G unendlich# und das Äquivalenzprolem ÄQU KS G D GE# HD G E : G G kontextsensitiv & L G I L G für kontextsensitive Grammatiken etrachten. Im Gegensatz zum Wortprolem W CH für allgemeine Chosmky-Grammatiken ist das Wortprolem W KS für kontexsensitive Grammatiken entscheidar KOROLLAR. W KS ist rekursiv. BEWEISIDEE. Um e x J W KS zu entscheiden, erechnet man zunächst aus e die Grammatik G mit Gödelnummer e. Ist e keine Gödelnummer oder G nicht kontextsensitiv, so gilt e x K0 W KS. Sonst führt man mit Hilfe von Lemma 2.7 G effektiv in einen äquivalenten NLBA M üer, für den man effektiv feststellen kann, o er die Eingae x akzeptiert. Die anderen oen aufgeführten Proleme sind jedoch auch für KS (wie im allgemeinen Fall) unentscheidar. Dies zeigt man mit der Reduktionsmethode mit Hilfe der folgenden Verschärfung des Projektionslemmas LEMMA. Jede rekursiv aufzählare Sprache A lässt sich als Projektion einer kontextsensitiven Sprache B darstellen. Darüerhinaus lässt sich aus einem Index e für A (A W e ) eine kontextsensitive Grammatik G, die B erzeugt, effektiv erechnen. BEWEIS. Sei die rekursiv aufzählare Sprache A W e gegeen, d.h. A enthält alle Wörter x, für die die e-te Turingmaschine M e stoppt. Wir definieren (wie im Beweis des Projektionslemmas) B x c 0 # #c n : c 0 c n ist term. M e -Rechnung ei Eingae e (Hierei sind die M e -Konfigurationen c i geeignet durch Wörter kodiert.) Offensichtlich ist A die Projektion von B, weshal es genügt, B KS zu zeigen. O ein Wort c 0 # #c n eine terminierende M e -Rechnung ei Eingae x eschreit, kann man jedoch mit einer (deterministischen) Turingmaschine ohne zusätzlichen Platzedarf, also insesondere durch einen NLBA N üerprüfen. Dieser lässt sich daei effektiv aus M e gewinnen. Mit den Lemmata 2.8 und 2.4 erhalten wir aer aus N effektiv die gewünschte kontextsensitive Grammatik zur Erzeugung von B. 2.1 SATZ. LEER KS, INF KS und ÄQU KS sind nicht rekursiv. BEWEIS. Zum Nachweis der Nichtrekursivität von LEER KS reduzieren wir das nach dem Satz von Rice nichtrekursive Leerheitsprolem LEER e : W e /0L G e : M e terminiert für keine Eingae für Turingmaschinen auf diese Menge. Hierzu wählen wir mit Lemma 2.12 eine rekursive Funktion f, die den Index e einer rekursiv aufzählaren Menge A W e auf
8 N N 2 KONTEXTSENSITIVE SPRACHEN 166 die Gödelnummer e# Menge B e erzeugt, deren Projektion W e ist. Es gilt dann f e einer kontextsensitiven Grammatik G em aildet, die eine e LEER N A W e leer B e L G fo ep leer f e Q LEER KS d.h. LEER - m LEER KS via f. Hierei haen wir enutzt, dass die Menge B B e im Beweis von Lemma 2.12 so gewählt ist, dass B e genau dann leer ist, wenn W e leer ist. Da es zu jedem x höchstens ein y mit x y Q B e git (da M e deterministisch!), gilt sogar R W e R R B e R. Dies zeigt, dass auch INF / e : W e unendlich auf INF KS vermöge f many-one-reduzierar und damit auch INF KS nicht rekursiv ist.. Zum Nachweis der Nichtrekursivität von ÄQU KS eoachtet man schließlich, dass LEER KS auf ÄQU KS vermöge g e e e 0 many-one-reduzierar ist, woei e 0 die Gödelnummer einer kontextsensitiven Grammatik G e0 ist, die die leere Sprache erzeugt: e LEER KS N L G e /0 N L G e L G e0 N e e 0 ÄQU KS Aus den Maschinen-Charakterisierungen der allgemeinen zw. kontextsensitiven Chomsky-Sprachen können wir Aschlusseigenschaften von CH und KS aleiten, aus denen sich deren Ungleichheit eenfalls ergit LEMMA. CH ist gegen Vereinigung und Durchschnitt, nicht aer gegen Komplement ageschlossen. KS ist gegen Vereinigung, Durchschnitt und Komplement ageschlossen. BEWEIS. Dies folgt aus den entsprechenden Aschlusseigenschaften von RA CH zw. NSPACE O n ( KS. In der Theorie formaler Sprachen etrachtet man häufig noch den Aschluss unter Homomorphismen (oder genauer: homomorphe Bilder). Ist L Σ eine Sprache und h : Σ T ein Homomorphismus, so heißt die Sprache h L T mit h L S h w : w L das homomorphe Bild von L zgl. h LEMMA. CH, nicht jedoch KS, ist gegen homomorphe Bilder ageschlossen. BEWEIS. Den Aschluss von CH gegen Homomorphismen zeigt man unter Verwendung der Identität CH RA. Sei L Σ in CH, und sei h : Σ T ein Homomorphismus. Da h durch seine Werte auf den einzelnen Buchstaen estimmt ist, ist h rekursiv. Wegen x h L N T y x h y & y L folgt hieraus h L U RA mit Hilfe der Aschlusseigenschaften der rekursiv aufzählaren Mengen.
9 2 KONTEXTSENSITIVE SPRACHEN 167 Um zu zeigen, dass KS nicht gegen homomorphe Bilder ageschlossen ist, zeigen wir, dass jede rekukrsiv aufzählare Sprache, d.h. jede Chomsky-Sprache das homomorphe Bild einer kontextsensitiven Sprache ist (woraus sich die Behauptung dann wegen KS C CH ergit). Hierzu verwenden wir Lemma 2.12 und die Beoachtung, dass man Projektionen als homomorphe Bilder auffassen kann. Sei also L RA CH, L Σ, gegeen. Nach Lemma 2.12 git es eine kontextsensitive Sprache L mit V x Σ x L NWT y x#y L ( Hierei enutzen wir das Hilfszeichen # zur Repräsentation von Paaren (x#y statt x y ), und durch eventuelle Umenennung können wir davon ausgehen, dass y ein Wort üer einem zu Σ disjunkten Alphaet T ist. Der von der Funktion h 0 : Σ T #Q Σ mit h 0 a X a für a Σ und h 0 a λ für a T, # induzierte Homomorphismus h : Σ T $ # Σ eliminiert dann den zweiten Teil #y, projiziert also das Paar x#y auf die erste Komponente. D.h. L h LY.
16. Die Chomsky-Hierarchie
 16. Die Chomsky-Hierarchie Die Chomsky-Sprachen sind gerade die rekursiv aufzählbaren Sprachen: CH = RA Da es nicht rekursive (d.h. unentscheidbare) r.a. Sprachen gibt, ist das Wortproblem für Chomsky-Grammatiken,
16. Die Chomsky-Hierarchie Die Chomsky-Sprachen sind gerade die rekursiv aufzählbaren Sprachen: CH = RA Da es nicht rekursive (d.h. unentscheidbare) r.a. Sprachen gibt, ist das Wortproblem für Chomsky-Grammatiken,
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 17. DIE CHOMSKY-HIERARCHIE Theoretische Informatik (SoSe 2011) 17. Die Chomsky-Hierarchie 1 / 15 Einleitung Die
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 17. DIE CHOMSKY-HIERARCHIE Theoretische Informatik (SoSe 2011) 17. Die Chomsky-Hierarchie 1 / 15 Einleitung Die
Teil V: Formale Sprachen 1. Sprachen und Grammatiken 2. Endliche Automaten
 Formale Sprachen Teil V: Formale Sprachen 1. Sprachen und Grammatiken 2. Endliche Automaten Formale Methoden der Informatik WiSe 2013/2014 teil 5, folie 2 (von 50) 1. Sprachen und Grammatiken Formale Sprachen
Formale Sprachen Teil V: Formale Sprachen 1. Sprachen und Grammatiken 2. Endliche Automaten Formale Methoden der Informatik WiSe 2013/2014 teil 5, folie 2 (von 50) 1. Sprachen und Grammatiken Formale Sprachen
Induktionsprinzipien für andere Bereiche. falscher Induktionsbeweis über N Übung Beispiele. Reguläre Σ-Sprachen Abschnitt 2.
 Kap 1: Grundegriffe Induktion 1.2.3 Induktionsprinzipien für andere Bereiche Beispiele Bereich M M 0 M erzeugende Operationen N 0} S: n n + 1 Σ ε} ( w wa ) für a Σ, c}-terme c} (t 1, t 2 ) (t 1 t 2 ) endl.
Kap 1: Grundegriffe Induktion 1.2.3 Induktionsprinzipien für andere Bereiche Beispiele Bereich M M 0 M erzeugende Operationen N 0} S: n n + 1 Σ ε} ( w wa ) für a Σ, c}-terme c} (t 1, t 2 ) (t 1 t 2 ) endl.
Endliche Automaten. aus. Abbildung 1: Modell eines einfachen Lichtschalters
 Endliche Automaten In der ersten Vorlesungswoche wollen wir uns mit endlichen Automaten eschäftigen. Um uns diesen zu nähern, etrachten wir zunächst einen einfachen Lichtschalter. Dieser kann an oder aus
Endliche Automaten In der ersten Vorlesungswoche wollen wir uns mit endlichen Automaten eschäftigen. Um uns diesen zu nähern, etrachten wir zunächst einen einfachen Lichtschalter. Dieser kann an oder aus
Der deterministische, endliche Automat. Formale Grundlagen der Informatik 1 Kapitel 3 Mehr zu regulären Sprachen
 Der deterministische, endliche Automat Formale Grundlagen der Informatik 1 Kapitel 3 Mehr zu regulären Sprachen Frank Heitmann heitmann@informatik.uni-hamurg.de 8. April 2014 Definition (DFA) Ein deterministischer,
Der deterministische, endliche Automat Formale Grundlagen der Informatik 1 Kapitel 3 Mehr zu regulären Sprachen Frank Heitmann heitmann@informatik.uni-hamurg.de 8. April 2014 Definition (DFA) Ein deterministischer,
Musterlösung zur Nachklausur Theoretische Grundlagen der Informatik Wintersemester 2013/14
 Institut für Theoretische Informatik Prof. Dr. Jörn Müller-Quade Musterlösung zur Nachklausur Theoretische Grundlagen der Informatik Wintersemester 203/4 Vorname Nachname Matrikelnummer Hinweise Für die
Institut für Theoretische Informatik Prof. Dr. Jörn Müller-Quade Musterlösung zur Nachklausur Theoretische Grundlagen der Informatik Wintersemester 203/4 Vorname Nachname Matrikelnummer Hinweise Für die
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
17. KONTEXTSENSITIVE SPRACHEN
 17. KONTEXTSENSITIVE SPRACHEN HAUPTERGEBNIS: KS = ERW = NSPACE(O(n)) REK Das heisst: Kontextsensitive Grammatiken und Grammatiken vom Erweiterungstyp haben die gleihe Beshreibungsmähtigkeit. Kontextsensitive
17. KONTEXTSENSITIVE SPRACHEN HAUPTERGEBNIS: KS = ERW = NSPACE(O(n)) REK Das heisst: Kontextsensitive Grammatiken und Grammatiken vom Erweiterungstyp haben die gleihe Beshreibungsmähtigkeit. Kontextsensitive
Rekursiv aufzählbare Sprachen
 Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
24. Kontextfreie Sprachen
 24. Kontextfreie Sprachen Obwohl das Wortproblem für kontextsensitive Sprachen entscheidbar ist, ist nicht bekannt, ob dieses auch tatsächlich d.h. in Polynomialzeit entscheidbar ist. Da man allgemein
24. Kontextfreie Sprachen Obwohl das Wortproblem für kontextsensitive Sprachen entscheidbar ist, ist nicht bekannt, ob dieses auch tatsächlich d.h. in Polynomialzeit entscheidbar ist. Da man allgemein
Theoretische Informatik I
 Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
Theoretische Informatik I Einheit 4.3 Eigenschaften von L 0 /L 1 -Sprachen 1. Abschlußeigenschaften 2. Prüfen von Eigenschaften 3. Grenzen der Sprachklassen Sprachklassen Semi-entscheidbare Sprache Sprache,
2.4 Kontextsensitive und Typ 0-Sprachen
 Definition 2.43 Eine Typ 1 Grammatik ist in Kuroda Normalform, falls alle Regeln eine der folgenden 4 Formen haben: Dabei: A, B, C, D V und a Σ. Satz 2.44 A a, A B, A BC, AB CD. Für jede Typ 1 Grammatik
Definition 2.43 Eine Typ 1 Grammatik ist in Kuroda Normalform, falls alle Regeln eine der folgenden 4 Formen haben: Dabei: A, B, C, D V und a Σ. Satz 2.44 A a, A B, A BC, AB CD. Für jede Typ 1 Grammatik
Das Halteproblem für Turingmaschinen
 Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Typ-1-Sprachen. Satz 1 (Kuroda ( ) 1964)
 Typ-1-Sprachen Satz 1 (Kuroda (1934-2009) 1964) Eine Sprache L hat Typ 1 (= ist kontextsensitiv) genau dann, wenn sie von einem nichtdeterministischen LBA erkannt wird. Beweis: Sei zunächst L Typ-1-Sprache.
Typ-1-Sprachen Satz 1 (Kuroda (1934-2009) 1964) Eine Sprache L hat Typ 1 (= ist kontextsensitiv) genau dann, wenn sie von einem nichtdeterministischen LBA erkannt wird. Beweis: Sei zunächst L Typ-1-Sprache.
Universelle Maschinen und universelle Funktionen
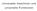 Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Universelle Maschinen und universelle Funktionen UNIVERSELLE FUNKTIONEN DEFINITION. Sei F eine Klasse von partiellen Funktionen über N. Eine partielle Funktion ϕ (n+1) ist n-universell für F, wenn (i)
Theoretische Informatik. Grammatiken. Grammatiken. Grammatiken. Rainer Schrader. 9. Juli 2009
 Theoretische Informatik Rainer Schrader Institut für Informatik 9. Juli 2009 1 / 41 2 / 41 Gliederung die Chomsky-Hierarchie Typ 0- Typ 3- Typ 1- Die Programmierung eines Rechners in einer höheren Programmiersprache
Theoretische Informatik Rainer Schrader Institut für Informatik 9. Juli 2009 1 / 41 2 / 41 Gliederung die Chomsky-Hierarchie Typ 0- Typ 3- Typ 1- Die Programmierung eines Rechners in einer höheren Programmiersprache
WS07/08 Automaten und Formale Sprachen 2. Vorlesung. Kapitel 2. Endliche Automaten und reguläre Sprachen. Definitionen:
 Definitionen: WS07/08 Automaten und Formale Sprachen 2. Vorlesung Martin Dietzfelinger 23. Oktoer 2007 Ein Alphaet Σ ist eine endliche nichtleere Menge. Ein Wort üer Σ ist eine endliche Folge von Elementen
Definitionen: WS07/08 Automaten und Formale Sprachen 2. Vorlesung Martin Dietzfelinger 23. Oktoer 2007 Ein Alphaet Σ ist eine endliche nichtleere Menge. Ein Wort üer Σ ist eine endliche Folge von Elementen
19. Nichtdeterministische Turingmaschinen und ihre Komplexität
 19. Nichtdeterministische Turingmaschinen und ihre Komplexität Bei einem Turingmaschinenprogramm P aus bedingten Anweisungen wird durch die Forderung i a b B j i a b B j i a sichergestellt, dass zu jeder
19. Nichtdeterministische Turingmaschinen und ihre Komplexität Bei einem Turingmaschinenprogramm P aus bedingten Anweisungen wird durch die Forderung i a b B j i a b B j i a sichergestellt, dass zu jeder
Theoretische Informatik 2
 Theoretische Informatik 2 Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2009/10 Die Chomsky-Hierarchie Definition Sei G = (V, Σ, P, S) eine Grammatik. 1 G heißt vom Typ 3 oder
Theoretische Informatik 2 Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2009/10 Die Chomsky-Hierarchie Definition Sei G = (V, Σ, P, S) eine Grammatik. 1 G heißt vom Typ 3 oder
Rückrichtung, Beweisidee
 Rückrichtung, Beweisidee Für die zweite Richtung ergit sich das folgende Prolem: Wir wollen mit einer Grammatik, die ja Wörter erzeugt, eine Maschine, die Wörter erkennt, simulieren. Am Anfang unseres
Rückrichtung, Beweisidee Für die zweite Richtung ergit sich das folgende Prolem: Wir wollen mit einer Grammatik, die ja Wörter erzeugt, eine Maschine, die Wörter erkennt, simulieren. Am Anfang unseres
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Abschluss gegen Substitution. Wiederholung. Beispiel. Abschluss gegen Substitution
 Wiederholung Beschreibungsformen für reguläre Sprachen: DFAs NFAs Reguläre Ausdrücke:, {ε}, {a}, und deren Verknüpfung mit + (Vereinigung), (Konkatenation) und * (kleenescher Abschluss) Abschluss gegen
Wiederholung Beschreibungsformen für reguläre Sprachen: DFAs NFAs Reguläre Ausdrücke:, {ε}, {a}, und deren Verknüpfung mit + (Vereinigung), (Konkatenation) und * (kleenescher Abschluss) Abschluss gegen
Klausur zur Vorlesung Grundbegriffe der Informatik 14. September 2015 Lösungsvorschläge
 Klausur zur Vorlesung Grundegriffe der Informatik 14. Septemer 2015 svorschläge Klausurnummer Nachname: Vorname: Matr.-Nr.: Diese Klausur ist mein 1. Versuch 2. Versuch in GBI Email-Adr.: nur falls 2.
Klausur zur Vorlesung Grundegriffe der Informatik 14. Septemer 2015 svorschläge Klausurnummer Nachname: Vorname: Matr.-Nr.: Diese Klausur ist mein 1. Versuch 2. Versuch in GBI Email-Adr.: nur falls 2.
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Kapitel 1: Endliche Automaten Gliederung 1. Endliche Automaten
 Gliederung 0. Grundegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechenarkeitstheorie 4. Komplexitätstheorie 1.1. Grundlagen 1.2. Minimierungsalgorithmus 1.3. 1/3, S. 1 Git es Sprachen, die nicht
Gliederung 0. Grundegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechenarkeitstheorie 4. Komplexitätstheorie 1.1. Grundlagen 1.2. Minimierungsalgorithmus 1.3. 1/3, S. 1 Git es Sprachen, die nicht
Klausur zur Vorlesung Einführung in die Theoretische Informatik
 Universität Heidelberg 19. Juli 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Einführung in die Theoretische Informatik LÖSUNGEN Es können
Universität Heidelberg 19. Juli 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Klausur zur Vorlesung Einführung in die Theoretische Informatik LÖSUNGEN Es können
ADS-EI 5.2 Struktur einer Turing-Maschine 120/451 ľernst W. Mayr
 Bemerkung: Jede NDTM N (die die Sprache L(N) akzeptiert) kann in eine deterministische Turing-Maschine M konvertiert werden, die ebenfalls genau die Sprache L(N) akzeptiert. Beweisidee: Die Berechnungspfade
Bemerkung: Jede NDTM N (die die Sprache L(N) akzeptiert) kann in eine deterministische Turing-Maschine M konvertiert werden, die ebenfalls genau die Sprache L(N) akzeptiert. Beweisidee: Die Berechnungspfade
Definition 78 Ein NPDA = PDA (= Nichtdeterministischer Pushdown-Automat) besteht aus:
 4.7 Kellerautomaten In der Literatur findet man häufig auch die Bezeichnungen Stack-Automat oder Pushdown-Automat. Kellerautomaten sind, wenn nichts anderes gesagt wird, nichtdeterministisch. Definition
4.7 Kellerautomaten In der Literatur findet man häufig auch die Bezeichnungen Stack-Automat oder Pushdown-Automat. Kellerautomaten sind, wenn nichts anderes gesagt wird, nichtdeterministisch. Definition
WS06/07 Referentin: Katharina Blinova. Formale Sprachen. Hauptseminar Intelligente Systeme Dozent: Prof. Dr. J. Rolshoven
 WS06/07 Referentin: Katharina Blinova Formale Sprachen Hauptseminar Intelligente Systeme Dozent: Prof. Dr. J. Rolshoven 1. Allgemeines 2. Formale Sprachen 3. Formale Grammatiken 4. Chomsky-Hierarchie 5.
WS06/07 Referentin: Katharina Blinova Formale Sprachen Hauptseminar Intelligente Systeme Dozent: Prof. Dr. J. Rolshoven 1. Allgemeines 2. Formale Sprachen 3. Formale Grammatiken 4. Chomsky-Hierarchie 5.
14. Rekursiv aufzählbare Mengen
 14. Rekursiv aufzählbare Mengen In diesem Abschnitt fassen wir einige Eigenschaften der rekursiv aufzählbaren d.h. der nach Churchscher These (effektiv) aufzählbaren Mengen zusammen. In Korollar 11.8 haben
14. Rekursiv aufzählbare Mengen In diesem Abschnitt fassen wir einige Eigenschaften der rekursiv aufzählbaren d.h. der nach Churchscher These (effektiv) aufzählbaren Mengen zusammen. In Korollar 11.8 haben
Mathematische Probleme, SS 2017 Donnerstag 1.6. $Id: dreieck.tex,v /06/01 11:41:57 hk Exp $ 2.1 Dreiecksberechnung mit Seiten und Winkeln
 Mathematische Proleme SS 2017 Donnerstag 1.6 $Id: dreieck.texv 1.31 2017/06/01 11:41:57 hk Exp $ 2 Dreiecke 2.1 Dreieckserechnung mit Seiten und Winkeln Am Ende der letzten Sitzung hatten wir eine weitere
Mathematische Proleme SS 2017 Donnerstag 1.6 $Id: dreieck.texv 1.31 2017/06/01 11:41:57 hk Exp $ 2 Dreiecke 2.1 Dreieckserechnung mit Seiten und Winkeln Am Ende der letzten Sitzung hatten wir eine weitere
(algebraische) Strukturen Abschnitt Eigenschaften von zweistelligen Operationen. Beispiel: Boolesche Algebren. Strukturtypen: Beispiele
 Kap 1: Grundegriffe Funktionen 1.1.3 Eigenschaften von zweistelligen Operationen für 2-stellige Operation : A A A a, a (infixe Notation) assoziativ, falls für alle a,, c A: (a ) c = a ( c). kommutativ,
Kap 1: Grundegriffe Funktionen 1.1.3 Eigenschaften von zweistelligen Operationen für 2-stellige Operation : A A A a, a (infixe Notation) assoziativ, falls für alle a,, c A: (a ) c = a ( c). kommutativ,
Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt:
 5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
5.2 Linear beschränkte Automaten Definition 98 Eine Turingmaschine heißt linear beschränkt (kurz: LBA), falls für alle q Q gilt: (q, c, d) δ(q, ) = c =. Ein Leerzeichen wird also nie durch ein anderes
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Kapitel: Die Chomsky Hierarchie. Die Chomsky Hierarchie 1 / 14
 Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Typ-0-Sprachen und Turingmaschinen
 Typ-0-Sprachen und Turingmaschinen Jean Vancoppenolle Universität Potsdam Einführung in formale Sprachen und Automaten Dr. Thomas Hanneforth (Präsentation aus Foliensätzen von Dr. Thomas Hanneforth und
Typ-0-Sprachen und Turingmaschinen Jean Vancoppenolle Universität Potsdam Einführung in formale Sprachen und Automaten Dr. Thomas Hanneforth (Präsentation aus Foliensätzen von Dr. Thomas Hanneforth und
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 7. Turingmaschinen Automatenmodell für Typ-0-Sprachen Einschränkung liefert Automatenmodell für Typ-1-Sprachen Alan Turing 1936, ursprüngliches Ziel: Formalisierung des
Theoretische Informatik Mitschrift 7. Turingmaschinen Automatenmodell für Typ-0-Sprachen Einschränkung liefert Automatenmodell für Typ-1-Sprachen Alan Turing 1936, ursprüngliches Ziel: Formalisierung des
10. Der Äquivalenzsatz
 10. Der Äquivalenzsatz In diesem Abschnitt zeigen wir, dass die von uns betrachteten verschiedenen Formalisierungen des Berechenbarkeitsbegriffs äquivalent sind, d.h. alle zu derselben Klasse (partiell)
10. Der Äquivalenzsatz In diesem Abschnitt zeigen wir, dass die von uns betrachteten verschiedenen Formalisierungen des Berechenbarkeitsbegriffs äquivalent sind, d.h. alle zu derselben Klasse (partiell)
Lösungsvorschläge und Erläuterungen Klausur zur Vorlesung Grundbegriffe der Informatik 2. März 2016
 Lösungsvorschläge und Erläuterungen Klausur zur Vorlesung Grundegriffe der Informatik 2. März 2016 Klausurnummer Nachname: Vorname: Matr.-Nr.: Diese Klausur ist mein 1. Versuch 2. Versuch in GI Email-dr.:
Lösungsvorschläge und Erläuterungen Klausur zur Vorlesung Grundegriffe der Informatik 2. März 2016 Klausurnummer Nachname: Vorname: Matr.-Nr.: Diese Klausur ist mein 1. Versuch 2. Versuch in GI Email-dr.:
Theoretische Informatik II
 Theoretische Informatik II Einheit 4.2 Modelle für Typ-0 & Typ-1 Sprachen 1. Nichtdeterministische Turingmaschinen 2. Äquivalenz zu Typ-0 Sprachen 3. Linear beschränkte Automaten und Typ-1 Sprachen Maschinenmodelle
Theoretische Informatik II Einheit 4.2 Modelle für Typ-0 & Typ-1 Sprachen 1. Nichtdeterministische Turingmaschinen 2. Äquivalenz zu Typ-0 Sprachen 3. Linear beschränkte Automaten und Typ-1 Sprachen Maschinenmodelle
6. Varianten des Turingmaschinen-Konzeptes II: Varianten der Speicherstruktur
 6. Varianten des Turingmaschinen-Konzeptes II: Varianten der Speicherstruktur Der Speicherzugriff bei Turingmaschinen ist recht umständlich. Man erhält effizientere Speicherstrukturen, wenn man mehrere
6. Varianten des Turingmaschinen-Konzeptes II: Varianten der Speicherstruktur Der Speicherzugriff bei Turingmaschinen ist recht umständlich. Man erhält effizientere Speicherstrukturen, wenn man mehrere
4 Kontextsensitive und Typ 0 Sprachen
 Hans U. Simon Bochum, den 05.02.2009 Annette Ilgen Beispiele zur Vorlesung Theoretische Informatik WS 08/09 Vorbemerkung: Hier findet sich eine Sammlung von Beispielen und Motivationen zur Vorlesung Theoretische
Hans U. Simon Bochum, den 05.02.2009 Annette Ilgen Beispiele zur Vorlesung Theoretische Informatik WS 08/09 Vorbemerkung: Hier findet sich eine Sammlung von Beispielen und Motivationen zur Vorlesung Theoretische
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2018 15. DIE KONTEXTFREIEN SPRACHEN Theoretische Informatik (SoSe 2018) 15. Die kontextfreien Sprachen I 1 / 53 Einleitung
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2018 15. DIE KONTEXTFREIEN SPRACHEN Theoretische Informatik (SoSe 2018) 15. Die kontextfreien Sprachen I 1 / 53 Einleitung
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2012 17. DIE KONTEXTFREIEN SPRACHEN II: ABSCHLUSSEIGENSCHAFTEN, MASCHINENCHARAKTERISIERUNG, KOMPLEXITÄT Theoretische
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2012 17. DIE KONTEXTFREIEN SPRACHEN II: ABSCHLUSSEIGENSCHAFTEN, MASCHINENCHARAKTERISIERUNG, KOMPLEXITÄT Theoretische
Turingmaschinen Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: Komplexitätstheorie und effiziente Algorithmen
 Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Schematische Darstellung einer Turing-Maschine: Kopf kann sich nach links und
Vorlesung Berechenbarkeit und Komplexität alias Theoretische Informatik: und effiziente Algorithmen Wintersemester 2011/12 Schematische Darstellung einer Turing-Maschine: Kopf kann sich nach links und
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 2. Grammatiken und die Chomsky-Hierarchie Beispiel: Syntaxdefinition in BNF :=
Theoretische Informatik Mitschrift 2. Grammatiken und die Chomsky-Hierarchie Beispiel: Syntaxdefinition in BNF :=
Automaten und Formale Sprachen 4. Vorlesung
 Automaten und Formale Sprachen 4. Vorlesung Martin Dietzfelinger. Novemer 005 Beispiel: Endliche Sprache L = {w,...,w n }, z.b. L = {ei,eine,ue} Gesehen: Präfix-DFA. Hier: NFA e 0 u i 4 e i n 5 6 7 e e
Automaten und Formale Sprachen 4. Vorlesung Martin Dietzfelinger. Novemer 005 Beispiel: Endliche Sprache L = {w,...,w n }, z.b. L = {ei,eine,ue} Gesehen: Präfix-DFA. Hier: NFA e 0 u i 4 e i n 5 6 7 e e
20. REGULÄRE SPRACHEN
 20. REGULÄRE SPRACHEN Zum Abschluss betrachten wir die kleinste der Chomsky-Klassen, die Klasse der rechtslinearen Sprachen, die auch als reguläre Sprachen bezeichnet werden. Wir führen zunächst eine Normalform
20. REGULÄRE SPRACHEN Zum Abschluss betrachten wir die kleinste der Chomsky-Klassen, die Klasse der rechtslinearen Sprachen, die auch als reguläre Sprachen bezeichnet werden. Wir führen zunächst eine Normalform
Teil V. Weiterführende Themen, Teil 1: Kontextsensitive Sprachen und die Chomsky-Hierarchie
 Teil V Weiterführende Themen, Teil 1: Kontextsensitive Sprachen und die Chomsky-Hierarchie Zwei Sorten von Grammatiken Kontextsensitive Grammatik (CSG) (Σ, V, P, S), Regeln der Form αaβ αγβ α, β (Σ V ),
Teil V Weiterführende Themen, Teil 1: Kontextsensitive Sprachen und die Chomsky-Hierarchie Zwei Sorten von Grammatiken Kontextsensitive Grammatik (CSG) (Σ, V, P, S), Regeln der Form αaβ αγβ α, β (Σ V ),
Relativierte Berechnungen und die arithmetische Hierachie
 Berechenbarkeit und Komplexität Wintersemester 2010/2011 1 Relativierte Berechnungen und die arithmetische Hierachie Relativierte Berechnungen und Orakel Definition 1 Eine Menge A ist entscheidbar mit
Berechenbarkeit und Komplexität Wintersemester 2010/2011 1 Relativierte Berechnungen und die arithmetische Hierachie Relativierte Berechnungen und Orakel Definition 1 Eine Menge A ist entscheidbar mit
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 20. DIE REGULÄREN SPRACHEN Theoretische Informatik (SoSe 2011) 20. Die regulären Sprachen 1 / 46 Überblick Als
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2011 20. DIE REGULÄREN SPRACHEN Theoretische Informatik (SoSe 2011) 20. Die regulären Sprachen 1 / 46 Überblick Als
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Informatik III. Christian Schindelhauer Wintersemester 2006/ Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Informatik III Christian Schindelhauer Wintersemester 2006/07 13. Vorlesung 07.12.2006 1 Überblick: Die Church- Turing-These Turing-Maschinen 1-Band Turing-Maschine Mehrband-Turing-Maschinen Nichtdeterministische
Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
 Dr. Sebastian Bab WiSe 12/13 Theoretische Grundlagen der Informatik für TI Termin: VL 15 + 16 vom 17.12.2012 und 20.12.2012 Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
Dr. Sebastian Bab WiSe 12/13 Theoretische Grundlagen der Informatik für TI Termin: VL 15 + 16 vom 17.12.2012 und 20.12.2012 Deterministische und nichtdeterministische Turing-Maschinen, Typ1- und Typ0-Sprachen
Deterministischer Kellerautomat (DPDA)
 Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Akzeptierende Turing-Maschine
 Akzeptierende Turing-Maschine Definition: Eine akzeptierende Turing-Maschine M ist ein Sechstupel M = (X, Z, z 0, Q, δ, F ), wobei (X, Z, z 0, Q, δ) eine Turing-Maschine ist und F Q gilt. Die von M akzeptierte
Akzeptierende Turing-Maschine Definition: Eine akzeptierende Turing-Maschine M ist ein Sechstupel M = (X, Z, z 0, Q, δ, F ), wobei (X, Z, z 0, Q, δ) eine Turing-Maschine ist und F Q gilt. Die von M akzeptierte
Endliche Sprachen. Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für
 Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. 447 Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. 447 Zusammenfassung Beschreibungsformen für reguläre Sprachen:
1 Einführung. 2 Typ-0- und Typ-1-Sprachen. 3 Berechnungsmodelle. 4 Unentscheidbarkeit. 5 Unentscheidbare Probleme. 6 Komplexitätstheorie
 1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 15 Ziele vgl. AFS: Berechnungsmodelle für Typ-0- und Typ-1-Sprachen (Nicht-)Abschlußeigenschaften
1 Einführung 2 Typ-0- und Typ-1-Sprachen 3 Berechnungsmodelle 4 Unentscheidbarkeit 5 Unentscheidbare Probleme 6 Komplexitätstheorie 15 Ziele vgl. AFS: Berechnungsmodelle für Typ-0- und Typ-1-Sprachen (Nicht-)Abschlußeigenschaften
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Übersicht. 3 3 Kontextfreie Sprachen
 Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK
 EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2012 16. DIE REGULÄREN SPRACHEN Theoretische Informatik (SoSe 2012) 16. Die regulären Sprachen 1 / 46 Überblick Als
EINFÜHRUNG IN DIE THEORETISCHE INFORMATIK Prof. Dr. Klaus Ambos-Spies Sommersemester 2012 16. DIE REGULÄREN SPRACHEN Theoretische Informatik (SoSe 2012) 16. Die regulären Sprachen 1 / 46 Überblick Als
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Grundlagen Theoretischer Informatik 2 WiSe 2009/10 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2009/10 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2009/10 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Ogden s Lemma: Der Beweis (1/5)
 Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
2. Übungsblatt 6.0 VU Theoretische Informatik und Logik 25. September 2013 Aufgabe 1 Geben Sie jeweils eine kontextfreie Grammatik an, welche die folgenden Sprachen erzeugt, sowie einen Ableitungsbaum
Theoretische Informatik Testvorbereitung Moritz Resl
 Theoretische Informatik Testvorbereitung Moritz Resl Bestandteile einer Programmiersprache: a) Syntax (Form): durch kontextfreie Grammatik beschrieben b) Semantik (Bedeutung) 1.) Kontextfreie Sprachen
Theoretische Informatik Testvorbereitung Moritz Resl Bestandteile einer Programmiersprache: a) Syntax (Form): durch kontextfreie Grammatik beschrieben b) Semantik (Bedeutung) 1.) Kontextfreie Sprachen
Organisatorisches... Formale Grundlagen der Informatik 1 Kapitel 1. Endliche Automaten. Organisatorisches. Organisatorisches. Eine typische Woche:
 Organisatorisches... Formale der Informatik 1 Kapitel 1 Frank Heitmann heitmann@informatik.uni-hamurg.de 4. April 2016 Eine typische Woche: Mo+Di: Vorlesung Di-Fr: Üungsgruppen Neuer Zettel und Beareiten
Organisatorisches... Formale der Informatik 1 Kapitel 1 Frank Heitmann heitmann@informatik.uni-hamurg.de 4. April 2016 Eine typische Woche: Mo+Di: Vorlesung Di-Fr: Üungsgruppen Neuer Zettel und Beareiten
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Übungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht garantiert, und einige sind umfangreicher als klausurtypisch.
 Vorlesung Theoretische Informtik Sommersemester 2017 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht grntiert, und einige sind umfngreicher ls klusurtypisch. 1.
Vorlesung Theoretische Informtik Sommersemester 2017 Dr. B. Bumgrten Üungen zur Wiederholung quer durch den Stoff Vollständigkeit wird nicht grntiert, und einige sind umfngreicher ls klusurtypisch. 1.
Kontextsensitive und Typ 0 Sprachen Slide 2. Die Turingmaschine
 Kontextsensitive und Typ 0 Sprachen Slide 2 Die Turingmaschine DTM = Deterministische Turingmaschine NTM = Nichtdeterministische Turingmaschine TM = DTM oder NTM Intuitiv gilt: DTM = (DFA + dynamischer
Kontextsensitive und Typ 0 Sprachen Slide 2 Die Turingmaschine DTM = Deterministische Turingmaschine NTM = Nichtdeterministische Turingmaschine TM = DTM oder NTM Intuitiv gilt: DTM = (DFA + dynamischer
8. Turingmaschinen und kontextsensitive Sprachen
 8. Turingmaschinen und kontextsensitive Sprachen Turingmaschinen (TM) von A. Turing vorgeschlagen, um den Begriff der Berechenbarkeit formal zu präzisieren. Intuitiv: statt des Stacks bei Kellerautomaten
8. Turingmaschinen und kontextsensitive Sprachen Turingmaschinen (TM) von A. Turing vorgeschlagen, um den Begriff der Berechenbarkeit formal zu präzisieren. Intuitiv: statt des Stacks bei Kellerautomaten
Nachklausur zur Vorlesung Einführung in die Theoretische Informatik
 Universität Heidelberg 11. Oktober 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Nachklausur zur Vorlesung Einführung in die Theoretische Informatik Musterlösungen
Universität Heidelberg 11. Oktober 2012 Institut für Informatik Prof. Dr. Klaus Ambos-Spies Dipl.-Math. Thorsten Kräling Nachklausur zur Vorlesung Einführung in die Theoretische Informatik Musterlösungen
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Zusammenfassung. Endliche Sprachen. Fazit zu endlichen Automaten. Teil 4: Grammatiken und Syntaxanalyse
 Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Turingmaschinen. Sabine Kuske: Turingmaschinen; 23.Juni 2008
 1 Turingmaschinen Von Alan Turing in den 30er Jahren dieses Jahrhunderts eingeführt Eines der ältesten Berechenbarkeitsmodelle Idee: den mechanischen Anteil des Rechnens mit Bleistift und Radiergummi auf
1 Turingmaschinen Von Alan Turing in den 30er Jahren dieses Jahrhunderts eingeführt Eines der ältesten Berechenbarkeitsmodelle Idee: den mechanischen Anteil des Rechnens mit Bleistift und Radiergummi auf
3.4 Kondition eines Problems
 38 KAPITEL 3. FEHLERANALYSE Beispiel 3.18 Betrachte M(10, 5, 1). Dann sind x 4.2832, y 4.2821, z 5.7632 darstellare Zahlen und (x y)z 0.00633952. Das korrekte Ergenis in M ist daher 0.0063395. Der Ausdruck
38 KAPITEL 3. FEHLERANALYSE Beispiel 3.18 Betrachte M(10, 5, 1). Dann sind x 4.2832, y 4.2821, z 5.7632 darstellare Zahlen und (x y)z 0.00633952. Das korrekte Ergenis in M ist daher 0.0063395. Der Ausdruck
Theoretische Informatik. Probabilistische Turingmaschinen PTM PTM. Rainer Schrader. 10. Juni 2009
 Theoretische Informatik Rainer Schrader Probabilistische Turingmaschinen Institut für Informatik 10. Juni 009 1 / 30 / 30 Gliederung probabilistische Turingmaschinen Beziehungen zwischen und NDTM es stellt
Theoretische Informatik Rainer Schrader Probabilistische Turingmaschinen Institut für Informatik 10. Juni 009 1 / 30 / 30 Gliederung probabilistische Turingmaschinen Beziehungen zwischen und NDTM es stellt
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie
 Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.02.2006 28. und letzte Vorlesung 1 Die Chomsky-Klassifizierung Chomsky-Hierachien 3: Reguläre Grammatiken
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.02.2006 28. und letzte Vorlesung 1 Die Chomsky-Klassifizierung Chomsky-Hierachien 3: Reguläre Grammatiken
Lösungen zu Übungsblatt 6
 Lösungen zu Übungsblatt 6 Aufgabe 1 Um nachzuweisen, dass eine Sprache L nicht kontextfrei ist, genügt es nach dem (starken) Pumping Lemma für kontextfreie Sprachen zu zeigen: Für jedes n 0 existiert ein
Lösungen zu Übungsblatt 6 Aufgabe 1 Um nachzuweisen, dass eine Sprache L nicht kontextfrei ist, genügt es nach dem (starken) Pumping Lemma für kontextfreie Sprachen zu zeigen: Für jedes n 0 existiert ein
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
5.4 Verteilungsfunktion Verteilungsfunktion diskreten Zufallsvariablen stetigen Zufallsvariablen Verteilungsfunktion
 5. Verteilungsfunktion Die Verteilungsfunktion git an welche Wahrscheinlichkeit sich is zu einem estimmten Wert der Zufallsvarialen kumuliert ( angehäuft, angesammelt ) hat. Die Verteilungsfunktion F()
5. Verteilungsfunktion Die Verteilungsfunktion git an welche Wahrscheinlichkeit sich is zu einem estimmten Wert der Zufallsvarialen kumuliert ( angehäuft, angesammelt ) hat. Die Verteilungsfunktion F()
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Umformung NTM DTM. Charakterisierung rek. aufz. Spr. Chomsky-3-Grammatiken (T5.3) Chomsky-0-Grammatik Rek. Aufz.
 Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
5. Universelle Maschinen und uniform rekursive Klassen
 5. Universelle Maschinen und uniform rekursive Klassen Die Existenz universeller Maschinen erlaubt effektive Aufzählungen der Klasse der r.a. Mengen, der Klasse der partiell rekursiven Funktionen und der
5. Universelle Maschinen und uniform rekursive Klassen Die Existenz universeller Maschinen erlaubt effektive Aufzählungen der Klasse der r.a. Mengen, der Klasse der partiell rekursiven Funktionen und der
Vorkurs Mathematik-Physik, Teil 5 c 2016 A. Kersch
 Vorkurs Mathematik-Physik, Teil 5 c 206 A. Kersch Vektoren. Vektorrechnung Definition Ein Vektor ist eine gerichtete Größe welche einen Betrag ( Zahl und eine Richtung ( in 2D, 2 in 3D hat. Alternativ
Vorkurs Mathematik-Physik, Teil 5 c 206 A. Kersch Vektoren. Vektorrechnung Definition Ein Vektor ist eine gerichtete Größe welche einen Betrag ( Zahl und eine Richtung ( in 2D, 2 in 3D hat. Alternativ
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
MPCP das modifizierte PCP
 MPCP das modifizierte PCP Das modifizierte PCP (MPCP) ist definiert wie PCP, einzige Ausnahme: Lösungen müssen mit i 1 = 1 beginnen! Lemma: H apple MPCP Zum Beweis muss eine Eingabe w#x in eine Instanz
MPCP das modifizierte PCP Das modifizierte PCP (MPCP) ist definiert wie PCP, einzige Ausnahme: Lösungen müssen mit i 1 = 1 beginnen! Lemma: H apple MPCP Zum Beweis muss eine Eingabe w#x in eine Instanz
Integralrechnung - Einführung Seite 1 von 6. Vergleicht man die Ergebnisse miteinander, so kann man folgende Entdeckung machen:
 Integralrechnung - Einführung Seite von 6 Berechnung von Flächeninhalten zwischen dem Graphen einer Funktion und der x-achse: Beispiel : f(x)= Fläche zwischen Graph und x-achse üer dem Intervall [;]: Bei
Integralrechnung - Einführung Seite von 6 Berechnung von Flächeninhalten zwischen dem Graphen einer Funktion und der x-achse: Beispiel : f(x)= Fläche zwischen Graph und x-achse üer dem Intervall [;]: Bei
Präsenzübung Berechenbarkeit und Komplexität
 Lehrstuhl für Informatik 1 WS 2013/14 Prof. Dr. Berthold Vöcking 28.01.2014 Kamal Al-Bawani Benjamin Ries Präsenzübung Berechenbarkeit und Komplexität Musterlösung Name:...................................
Lehrstuhl für Informatik 1 WS 2013/14 Prof. Dr. Berthold Vöcking 28.01.2014 Kamal Al-Bawani Benjamin Ries Präsenzübung Berechenbarkeit und Komplexität Musterlösung Name:...................................
Organisatorisches... Formale Grundlagen der Informatik 1 Kapitel 1. Endliche Automaten. Organisatorisches. Organisatorisches. Eine typische Woche:
 Organisatorisches... Formale der Informatik 1 Kapitel 1 Frank Heitmann heitmann@informatik.uni-hamurg.de 7. April 215 Eine typische Woche: Mo+Di: Vorlesung Di-Fr: Üungsgruppen Neuer Zettel und Beareiten
Organisatorisches... Formale der Informatik 1 Kapitel 1 Frank Heitmann heitmann@informatik.uni-hamurg.de 7. April 215 Eine typische Woche: Mo+Di: Vorlesung Di-Fr: Üungsgruppen Neuer Zettel und Beareiten
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Turingautomaten Jörg Roth Turingautomaten
 Turingautomaten Jörg Roth 331 5 Turingautomaten Wir führen nochmals ein neues Automatenmodell ein und erweitern die Fähigkeit, Sprachen zu erkennen: Problem vom Kellerautomaten: wir können zwar beliebig
Turingautomaten Jörg Roth 331 5 Turingautomaten Wir führen nochmals ein neues Automatenmodell ein und erweitern die Fähigkeit, Sprachen zu erkennen: Problem vom Kellerautomaten: wir können zwar beliebig
