2 Allgemeine Integrationstheorie
|
|
|
- Benjamin Jaeger
- vor 9 Jahren
- Abrufe
Transkript
1 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns vorgegeben, was das Integral der charakteristischen Funktion einer messbaren Menge sein soll. Davon ausgehend definieren wir das Integral von messbaren Funktionen mit nur endlich vielen Werten (Stufenfunktionen) und dann für nichtnegative messbare Funktionen, die wir von unten durch Stufenfunktionen annähern. Schließlich spalten wir allgemeine messbare Funktionen in ihren Positiv und Negativteil auf, für die wir die Integrale bereits definiert haben. Wir werden sehen, dass das so erklärte Lebesgue Integral wesentlich allgemeiner und flexibler als das Riemann Integral ist. 2.1 Stufenfunktionen ine messbare Funktion s : R heißt Stufenfunktion, wenn s() endlich ist. Jede konstante Funktion ist eine Stufenfunktion. Wie sieht es mit Funktionen aus, die zwei Werte annehmen? Dazu betrachten wir für jede Menge ihre charakteristische Funktion { 1 wenn x χ (x) := 0 wenn x. Diese Funktion ist genau dann messbar (und damit eine Stufenfunktion), wenn S. Insbesondere ist χ Q eine Stufenfunktion für (,S) = (R,B(R)). Lemma 2.1 ine Funktion s : R ist genau dann eine Stufenfunktion, wenn es Zahlen α 1,...,α k R und paarweise disjunkte Mengen A 1,...,A k S so gibt, dass s = k α jχ Aj. Beweis Sind α j R und A j S für j = 1,...,k, so ist k α jχ Aj messbar nach Satz 1.13 und damit Stufenfunktion. Sei umgekehrt s eine Stufenfunktion und s() = {α 1,...,α k } (mit paarweise verschiedenen Zahlen α j ). Dann sind die Mengen A j := s 1 ({α j }) messbar und paarweise disjunkt, und es ist s = k α jχ Aj. Die folgenden Sätze zeigen, dass nichtnegative messbare Funktionen durch Stufenfunktionen approximiert werden können. Satz 2.2 Sei f : [0, ] eine messbare Funktion. Dann gibt es eine monoton wachsende Folge von Stufenfunktionen s n : [0, ) so, dass lim s n(x) = f(x) für alle x und dass die Konvergenz auf jeder Menge {x : f(x) c} mit c [0, ) gleichmäßig ist. 16
2 Beweis Für n 1 sei k [ k falls f(x) s n (x) = 2 n 2, k + 1 ) n 2 n n falls f(x) [n, ]. mit 0 k n 2 n 1, Dann ist (s n ) n 1 eine monoton wachsende Folge von Stufenfunktionen, und ist c [0, ) und n > c, so ist f(x) s n (x) < 1 2 n für alle x mit f(x) c. Hieraus folgt die gleichmäßige Konvergenz auf {x : f(x) c} sowie die punktweise Konvergenz auf {x : f(x) < }. Die punktweise Konvergenz auf {x : f(x) = } ist offensichtlich. Folgerung 2.3 ine Funktion f : R ist genau dann messbar, wenn sie punktweiser Grenzwert einer Folge von Stufenfunktionen ist. Beweis Punktweise Grenzwerte messbarer Funktionen sind messbar (Satz 1.15). Ist umgekehrt f messbar, so sind nach Satz 1.13 f + := max (0,f) und f := max (0, f) messbar und nichtnegativ. Nach Satz 2.2 sind beide Funktionen punktweise Grenzwerte von Stufenfunktionen, und damit auch f = f + f. 2.2 Das Lebesgue Integral Sei (,S,µ) Maßraum, S und f : R messbar. Wir definieren das Integral von f über bzgl. des Maßes µ in mehreren Schritten. Schritt A Sei f = χ A mit A S. Dann setzen wir I (f) := µ(a ). Schritt B Sei f nichtnegative Stufenfunktion. Wir schreiben f als k α jχ Aj mit α j [0, ) und mit paarweise disjunkten Mengen A j S (vgl. Lemma 2.1), und wir definieren I (f) := k α j I (χ Aj ) = k α j µ(a j ). Schritt C Ist f messbar und nicht negativ, so definieren wir fdµ := sup {I (s) : s Stufenfunktion mit 0 s f}. Die Menge auf der rechten Seite ist nach Satz 2.2 nicht leer. Man beachte, dass fdµ den Wert + annehmen kann. Ist f selbst eine nichtnegative Stufenfunktion, so ist fdµ = I (f). Für alle Stufenfunktionen 0 s f ist nämlich 17
3 I (s) I (f). Schritt D Nun sei f : R messbar. Nach Satz 1.13 sind die Funktionen f + := max (0,f) und f := max (0, f) messbar, und die Integrale f + dµ, f dµ (2.1) sind wie in Schritt C erklärt. Definition 2.4 Ist eines der Integrale (2.1) endlich, so definieren wir fdµ := f + dµ f dµ R. (2.2) Sind beide Integrale in (2.1) endlich, so heißt f Lebesgue integrierbar, und wir schreiben f L 1 (µ,) bzw. f L 1 (µ) falls =. Man beachte, dass wir das Integral von f auch dann definiert haben, wenn f nicht Lebesgue integrierbar ist, aber eine der Funktionen f +,f diese igenschaft hat. Das ist in vielen Situationen bequem. Wir sehen uns einige elementare igenschaften des Lebesgue Integrals an. Lemma 2.5 (a) Ist f messbar und beschränkt auf und µ() <, so ist f L 1 (µ,). (b) Sind f,g L 1 (µ,) und ist f g auf, so ist f dµ g dµ. (c) Ist f messbar und a,b R mit a f b auf und µ() <, so ist a µ() f dµ bµ(). (d) Ist f L 1 (µ,) und c R, so ist cf L 1 (µ,) und cfdµ = c fdµ. (e) Ist f messbar und µ() = 0, so ist fdµ = 0. (f) Ist f L 1 (µ,) und A S Teilmenge von, so ist f L 1 (µ,a). A Beweis (a) Sei f M < auf. Dann ist auch f ± M auf, und hieraus folgt sofort f ±dµ Mµ(), denn diese Relation überträgt sich offenbar auf die entsprechenden Stufenfunktionen. (b) Aus f g folgt f + g + und g f auf. Hieraus folgt f + dµ g + dµ und g dµ f dµ 18
4 (jede Stufenfunktion s mit 0 s f + erfüllt ja erst recht 0 s g + ) und daher fdµ = f + dµ f dµ g + dµ g dµ = gdµ. (c) Dies folgt sofort aus (b), wenn wir f mit den Konstanten a,b vergleichen. (d) Für nichtnegative Stufenfunktionen s ist trivialerweise I (cs) = ci (s). Ist nun etwa c > 0 und f 0, so folgt cfdµ = sup {I (s) : 0 s cf} = sup {I (s) : 0 1 } c s f ( 1 ) = sup {ci c s : 0 1 } { } c s f = c sup I (t) : 0 t f = c fdµ. Die übrigen Fälle behandelt man analog. (e) Für alle Stufenfunktionen s ist I (s) = 0. Also ist f ±dµ = 0 und fdµ = 0. (f) Für alle Stufenfunktionen 0 s f + ist I A (s) I (s) und daher f + dµ = sup {I A (s) : 0 s f + } sup {I (s) : 0 s f + } = f + dµ <. A Für f argumentiert man analog. Satz 2.6 (a) Sei f 0 messbar auf. Für A S definieren wir ϕ(a) := fdµ. (2.3) Dann ist ϕ ein Maß auf (,S). (b) Ist f L 1 (µ), so wird durch (2.3) eine σ additive Funktion definiert. Beweis Aussage (b) folgt sofort, wenn wir (a) auf die Funktionen f ± anwenden und f = f + f benutzen. Wir zeigen (a). Da ϕ( ) = 0 nach Lemma 2.5 (e) und ϕ(a) 0 nach Lemma 2.5 (c) ist, müssen wir noch die σ Additivität zeigen. Sei also A = n 1 A n mit paarweise disjunkten messbaren Mengen A n. Wir haben zu zeigen, dass ϕ(a) = n 1 ϕ(a n). Ist f = χ C die charakteristische Funktion einer messbaren Menge C, so ist fdµ = µ(a C), und die Behauptung folgt aus der σ Additivität von µ. A Ist f = k c iχ Ci eine nichtnegative Stufenfunktion mit paarweise disjunkten Mengen C i S, so ist A fdµ = A k c j µ(a C j ), 19
5 und die Behauptung folgt aus der σ Additivität der einzelnen Summanden. Sei nun f 0 messbar. Aus dem bereits Bewiesenen folgt für jede Stufenfunktion s mit 0 s f, dass s dµ = s dµ f dµ = ϕ(a n ). A n 1 A n n 1 A n n 1 Bilden wir links das Supremum über alle Stufenfunktionen s mit 0 s f, so folgt ϕ(a) = fdµ ϕ(a n ). A n 1 Wir haben noch n 1 ϕ(a n) ϕ(a) zu zeigen. Für ϕ(a) = ist dies klar. Sei also ϕ(a) < und damit auch ϕ(a n ) < für alle n. Mit der Definition des Integrals finden wir für jedes ε > 0 eine Stufenfunktion s mit 0 s f und s dµ A 1 f dµ ε sowie A 1 s dµ A 2 f dµ ε. A 2 Folglich ist ϕ(a 1 A 2 ) s dµ = A 1 A 2 s dµ + A 1 s dµ ϕ(a 1 ) + ϕ(a 2 ) 2ε. A 2 Da ε > 0 beliebig war, folgt ϕ(a 1 A 2 ) ϕ(a 1 ) + ϕ(a 2 ). Induktiv erhalten wir ( n ϕ A j ) n ϕ(a j ) für alle n 1, und wegen n A j A führt dies auf ( n ϕ(a) lim ϕ A j ) lim n ϕ(a j ) = ϕ(a j ). Damit ist alles gezeigt. Folgerung 2.7 Sind A B messbare Mengen mit µ(b \ A) = 0 und ist f Lebesgue integrierbar, so ist fdµ = fdµ. A B Beweis Die Funktion ϕ() := f dµ ist additiv nach Satz 2.6. Folglich ist ϕ(b) = ϕ(a) + ϕ(b \ A), und nach Lemma 2.5 (e) ist ϕ(b \ A) = 0. 20
6 Folgerung 2.8 Sei (,S,µ) vollständig, die Funktionen f,g : R seien fast überall gleich, und sei f L 1 (µ,) für S. Dann ist auch g L 1 (µ,) und f dµ = g dµ. Beweis Die Funktion g ist messbar nach Lemma Sei N eine µ Nullmenge so, dass f(x) = g(x) für alle x \ N. Dann ist auch f ± (x) = g ± (x) für alle x \ N, und wir erhalten f ± dµ = f ± dµ nach Folgerung 2.7 \N = g ± dµ nach Voraussetzung \N = g ± dµ + g ± dµ nach Lemma 2.5 (e) \N N = g ± dµ. Hieraus folgt die Behauptung. Satz 2.9 Mit f L 1 (µ,) ist auch f L 1 (µ,), und es gilt fdµ f dµ. Beweis Sei A = {x : f(x) 0} und B = \ A. Nach Satz 2.6 (a) ist f dµ = f dµ + f dµ = f + dµ + f dµ < A B und somit f L 1 (µ,). Wegen f f und f f ist nach Lemma 2.5 (b), (d) fdµ f dµ und fdµ f dµ. Hieraus folgt die Behauptung. Satz 2.10 (a) Ist f messbar, f g und g L 1 (µ,), so ist auch f L 1 (µ,). (b) Ist (,S,µ) vollständig, f messbar, f g fast überall und g L 1 (µ,), so ist f L 1 (µ,). Beweis (a) Dies folgt sofort aus f + g und f g. (b) Sei N eine µ Nullmenge so, dass f(x) g(x) für alle x \ N, und sei { f(x) falls x \ N f(x) = g(x) falls x N. Nach Lemma 1.24 ist f messbar, und es gilt f g. Nach Teil (a) ist f L 1 (µ,), und mit Folgerung 2.8 finden wir f L 1 (µ,). 21 A B
7 2.3 Konvergenzsätze Wir behandeln in diesem Abschnitt die Lebesgue schen Konvergenzsätze. Diese Sätze sind unentbehrliche Werkzeuge der Analysis. Satz 2.11 (Satz über monotone Konvergenz) Sei (,S,µ) vollständig, S, und (f n ) n 1 sei eine Folge messbarer Funktionen mit 0 f 1 (x) f 2 (x)... für fast alle x. (2.4) Dann konvergiert (f n ) fast überall punktweise gegen eine messbare Funktion f, und f ndµ fdµ. Ohne die Voraussetzung der Vollständigkeit gilt die Aussage immer noch, wenn man (2.4) für alle x fordert. Beweis Sei N eine µ Nullmenge so, dass (2.4) für alle x \N erfüllt ist. Für alle x \ N konvergiert dann die Folge (f n (x)) gegen f(x) [0, ], und wir setzen f(x) für x \ N f(x) := für x N. Nach Lemma 1.25 ist f messbar. Sei α n := f ndµ. Nach Lemma 2.5 (b) und Folgerung 2.7 ist die Folge (α n ) monoton wachsend. Sei α := sup {α n : n 1} = lim α n [0, ]. Für jede Stufenfunktion s mit s f n gilt auch s f und somit f ndµ fdµ. Folglich ist α fdµ. Wir zeigen noch die umgekehrte Ungleichung α fdµ. Dazu nehmen wir α < an (sonst ist nichts zu beweisen). Sei s eine Stufenfunktion mit 0 s f, c (0, 1) und n := {x \ N : f n (x) cs(x)} für n 1. Dann ist n n+1 für alle n (Monotonie der Folge (f n ) außerhalb von N) und n 1 n = \ N (wegen f n (x) f(x) und cs(x) < f(x) für alle x \ N mit f(x) > 0). Mit Satz 2.6 (a) und Lemma 2.5 (b) erhalten wir außerdem, dass f n dµ f n dµ c n sdµ. n (2.5) Für n ergibt sich daher wieder mit Satz 2.6 (a), (2.5) und Lemma 1.17 (c) α = lim f n dµ c lim sdµ = c sdµ = c sdµ. n \N 22
8 Da c (0, 1) beliebig war, folgt α sdµ für alle Stufenfunktionen s mit 0 s f. Dann ist aber α fdµ. Der folgende Satz zeigt zusammen mit Lemma 2.5 (d), dass die reellwertigen Funktionen aus L 1 (µ,) einen reellen Vektorraum bilden. Satz 2.12 Ist f 1,f 2 L 1 (µ,) und ist f 1 + f 2 erklärt, so ist auch f 1 + f 2 L 1 (µ,) und es gilt (f 1 + f 2 )dµ = f 1 dµ + f 2 dµ. (2.6) Beweis Zuerst zeigen wir (2.6) für nichtnegative Stufenfunktionen. Ist s = j c jχ j eine nichtnegative Stufenfunktion (mit nicht notwendig paarweise disjunkten Mengen i ), so kann man s schreiben als k d kχ Fk mit paarweise disjunkten Mengen F k und mit d k := j:f k j c j. Damit folgt sdµ = d k µ(f k ) = c j µ(f k ) k k j:f k j = c j µ(f k ) = c j µ( j ) = c j χ j dµ. j k:f k j j j Da man zwei Stufenfunktionen s 1,s 2 immer als s 1 = j c jχ j und s 2 = j d jχ j (mit gleichen Mengen j ) schreiben kann, folgt hieraus (2.6) für nichtnegative Stufenfunktionen. Seien nun f 1,f 2 L 1 (µ,) nichtnegativ. Nach Satz 2.2 gibt es monoton wachsende Folgen (s n ) bzw. (t n ) von Stufenfunktionen, die punktweise gegen f 1 bzw. f 2 konvergieren. Dann ist (s n + t n ) eine monoton wachsende Folge von Stufenfunktionen, die punktweise gegen f 1 + f 2 konvergiert. Der Satz von der monotonen Konvergenz liefert s n dµ f 1 dµ, t n dµ f 2 dµ, (s n + t n )dµ (f 1 + f 2 )dµ. Aus s ndµ + t ndµ = (s n + t n )dµ folgt (2.6) auch in diesem Fall. Im allgemeinen Fall zerlegt man in vier paarweise disjunkte messbare Mengen, auf denen f 1 und f 2 ihr Vorzeichen nicht wechseln, und benutzt (2.6) für nichtnegative Funktionen sowie die Beziehung ( f)dµ = fdµ aus Lemma 2.5 (d). Wir haben hier nur die schwächere Form von Satz 2.11 benutzt. Satz 2.12 gilt also ohne Vollständigkeitsvoraussetzung. Für Reihen liefert Satz 2.11: Folgerung 2.13 Sei (,S,µ) vollständig, f n : [0, ] und f = n=1 f n fast überall. Damit ist f messbar, und für S ist f dµ = f n dµ. n=1 23
9 Beweis Sei g n := n f n. Die Folge (g n ) ist monoton wachsend und konvergiert fast überall gegen f. Nach Lemma 1.25 ist f messbar, und die Sätze 2.11 und 2.12 liefern fdµ 2.11 = lim n 2.12 = lim g n dµ = lim f j dµ = n f j dµ f j dµ. Unser nächstes Ziel ist der Satz von der majorisierten Konvergenz, das vermutlich wichtigste Werkzeug, um die Vertauschbarkeit von Grenzübergang und Integration zu zeigen. Vorbereitend überlegen wir uns ein Lemma. Lemma 2.14 (Fatou) Sind f n : [0, ] messbare Funktionen und ist S, so ist lim inf f ndµ lim inf f n dµ. Beweis Für k 1 sei g k := inf j k f j. Dann ist g k f k und somit g kdµ f kdµ. Weiter ist die Folge (g k ) monoton wachsend, und sie konvergiert punktweise gegen lim inf f n. Der Satz über montone Konvergenz (schwache Fassung) liefert f k dµ g k dµ lim inf f ndµ und damit lim inf k f k dµ lim inf f ndµ. Satz 2.15 (Lebesgues Satz über majorisierte Konvergenz) Sei (,S,µ) ein vollständiger Maßraum, S, und (f n ) sei eine Folge messbarer Funktionen f n : R, die fast überall gegen eine Funktion f konvergieren. Weiter sei g : R eine messbare Funktion mit f n g für alle n fast überall. Ist g L 1 (µ,), so gehören auch f und f n zu L 1 (µ,), und es gilt f n dµ fdµ. Beweis Sei N eine µ Nullmenge so, dass f n (x) f(x) für n und f n (x) g(x) für alle n und alle x \ N. Dann ist f messbar nach Lemma 1.25, und es ist f(x) g(x) für alle x \ N. Nach Satz 2.10 (b) sind f,f n L 1 (µ,). Weiter ist f f n 2g auf \ N. Wir wenden das Fatousche Lemma auf die 24
10 Folge der Funktionen (2g f f n ) \N an und erhalten 2gdµ = 2gdµ = lim inf (2g f n f )dµ \N \N lim inf (2g f n f )dµ \N = 2gdµ + lim inf f n f dµ \N \N = 2gdµ lim sup f n f dµ 2gdµ. Da 2gdµ = 2 gdµ < ist, erhalten wir lim f n f dµ = 0. Dies hat f n dµ fdµ f n f dµ 0 zur Folge (Satz 2.12 und Satz 2.9). Ohne Vollständigkeitsvoraussetzung gilt der Satz 2.15 noch, wenn alle fast in seiner Formulierung gestrichen werden. Beispiel Wir betrachten eine Funktionenfolge, auf die sich der Satz von der majorisierten Konvergenz nicht anwenden lässt ( der gleitende Buckel ). Dazu sei (,S,µ) = (R, B(R),λ) und f n = χ [n,n+1] für n N. Die Funktionen f n konvergieren punktweise gegen f 0, aber 0 = fdλ = lim f ndλ lim f n dλ = 1. R R R 2.4 Lebesgue und Riemann Integral Wir vergleichen in diesem Abschnitt das Riemann Integral über Intervallen in R mit dem Lebesgue Integral. Die Resultate hängen davon ab, ob die Intervalle beschränkt oder unbeschränkt sind. Wir vereinbaren: wenn wir über Lebesgue Integration auf R n sprechen, legen wir stets den vervollständigten Maßraum (R n, B(R n ),λ) zu Grunde, betrachten also messbare Funktionen f : ( R n, B(R ) n ),λ ( ) R, B(R). Satz 2.16 Ist R ein kompaktes Intervall, so ist jede auf Riemann integrierbare Funktion f auch Lebesgue integrierbar, und fdλ = b a f(x)dx. 25
11 Beweis Ist f auf Riemann integrierbar, so gibt es für jedes n 1 Treppenfunktionen ϕ n f ψ n mit b (ψ a n(x) ϕ n (x))dx < 1 (Ana II, Folgerung 8.9). n O..d.A. können wir die Folgen (ϕ n ) bzw. (ψ n ) als monoton wachsend bzw. fallend voraussetzen (andernfalls ersetzen wir ϕ n durch max (ϕ 1,...,ϕ n ) und ψ n durch min (ψ 1,...,ψ n )). Nach den Integraldefinitionen stimmen Riemann und Lebesgue Integral für Treppenfunktionen überein. s ist also auch (ψ n ϕ n )dλ < 1/n. (2.7) Die monotonen Funktionenfolgen (ϕ n ) bzw. (ψ n ) konvergieren punktweise auf gegen messbare Funktionen ϕ bzw ψ mit ϕ f ψ. Aus ϕ 1 ϕ n ψ n ψ 1 und der Lebesgue Integrierbarkeit von ϕ 1 und ψ 1 folgt mit dem Satz über die majorisierte Konvergenz, dass ϕ,ψ L 1 (λ, ) und dass ϕ n dλ ϕdλ sowie ψ n dλ ψdλ. Der gleiche Satz liefert mit (2.7), dass (ψ ϕ)dλ = 0. Aus der Übung wissen wir, dass dann ϕ = ψ fast überall, und wegen ϕ f ψ ist auch ϕ = f fast überall. Folglich ist auch f L 1 (λ, ), und fdλ = b ϕdλ = lim ϕ n dλ = lim ϕ n (x)dx = a b a f(x)dx. In diesem Zusammenhang erinnern wir an das Lebesguesche Integrabilitätskriterium (Ana II, Abschnitt 8.4). Satz 2.17 ine beschränkte Funktion f : R ist genau dann Riemann integrierbar, wenn ihre Unstetigkeitsstellen eine λ Nullmenge bilden. Die Klasse der Lebensgue integrierbaren Funktionen ist aber wesentlich größer als die der Riemann integrierbaren Funktionen. in einfaches Beispiel ist die charakteristische Funktion χ Q der Menge der rationalen Zahlen, die nicht Riemann aber Lebesgue integrierbar ist (beachte: Mengen, die nur aus einem Punkt bestehen, sind Borelmengen vom Maß 0, und Q ist eine abzählbare Vereinigung solcher Mengen). s folgt ein Beispiel einer Lebesgue integrierbaren Funktion, die sich (im Gegensatz zu χ Q ) nicht einmal durch Abändern auf einer Nullmenge zu einer Riemann integrierbaren Funktion machen lässt. Beispiel Sei Q = Q (0, 1). Diese Menge ist abzählbar: Q = {q n : n 1}. Sei ε > 0 und U n (0, 1) ein offenes Intervall einer Länge ε/2 n, das q n enthält. Dann ist Q U := n 1U n (0, 1) und λ(u) 26 λ(u n ) n=1 n=1 ε 2 n = ε.
12 Sei f = χ U und f n := χ U1... U n. Die Funktionen f n sind Riemann integrierbar, [0,1] f n dλ = 1 0 f n (x)dx ε, und die Folge (f n ) ist monoton wachsend und konvergiert punktweise gegen f. Nach dem Satz über monotone Konvergenz ist f Lebesgue integrierbar und fdλ ε. Zeigen Sie als Übung, dass f die behauptete igenschaft hat. [0,1] Bei uneigentlichen Riemann Integralen, die nicht absolut konvergieren, ist die Situation subtiler. Da die Lebesgue Integrabilität die absolute Konvergenz des Integrals voraussetzt, können uneigentliche Riemann Integrale existieren, die man nicht als Lebesgue Integrale interpretieren kann. Bevor wir ein Beispiel geben, fassen wir diesen Zusammenhang präziser. Dazu benötigen wir folgenden Satz. Satz 2.18 (Ausschöpfungssatz) Sei (M n ) eine wachsende Folge messbarer Teilmengen von,m := n 1 M n und f : M R. Dann ist f genau dann in L 1 (µ,m), wenn f L 1 (µ,m n ) für jedes n und wenn die Folge der M n f dµ konvergiert (gegen eine endliche Zahl). Ist dies der Fall, so ist fdµ = lim fdµ. M M n Beweis Aus f L 1 (µ,m) folgt f L 1 (µ,m) (Satz 2.9) und damit f L 1 (µ,m n ), und es gilt M n f dµ M f dµ. Der interessante Teil des Beweises betrifft die Umkehrung dieser Aussage. Zunächst konvergiert die monoton wachsende Folge (χ Mn f ) punktweise gegen χ M f, so dass χ Mn f dµ χ M f dµ bzw. f dµ f dµ M n nach dem Satz über monotone Konvergenz. Nach Voraussetzung ist f dµ also M endlich, d. h. χ M f L 1 (µ,m). Weiter ist χ Mn f χ M f, und die Funktionen χ Mn f konvergieren punktweise wegen χ M f, so dass wir mit dem Satz über majorisierte Konvergenz f L 1 (µ,m) sowie lim f dµ = lim χ Mn fdµ = χ M fdµ = fdµ M n erhalten. M M 27
13 Folgerung 2.19 Seien a,b R und a < b. Ist f : (a,b) R Riemann integrierbar auf jedem kompakten Teilintervall von (a, b), so ist f genau dann Lebesgue integrierbar auf (a,b), wenn das uneigentliche Riemann Integral b f(x) dx konvergiert. a Beweis Wir wählen eine monoton fallende Folge (x n ) mit a < x n < b und x n a und eine monoton wachsende Folge (y n ) mit x n < y n < b und y n b, und wir setzen M n := [x n,y n ]. Dann ist M = n 1 M n = (a,b), und nach dem Ausschöpfungssatz ist f genau dann Lebesgue integrierbar auf M, wenn der Grenzwert endlich ist. lim yn f dλ = lim M n x n f(x) dx Beispiel Auf [1, ) sei f(x) = sin x. Wir wissen aus Ana II, Abschnitt , x dass das uneigentliche Riemann Integral sin x dx konvergiert. Dieses Integral 1 x sin x konvergiert aber nicht absolut, denn für x [kπ, (k +1)π] ist f(x) und (k+1)π folglich (k+1)π kπ = f(x) dx 1 (k + 1)π π 0 1 (k + 1)π sin xdx = kπ+π kπ 2 (k + 1)π. sin x dx Wegen der Divergenz der harmonischen Reihe konvergiert 1 f(x) dx nicht, und nach Folgerung 2.19 ist f nicht Lebesgue integrierbar auf [1, ). rgänzend gehen wir noch kurz auf zwei Resultate ein. Das erste betrifft parameterabhängige Integrale, wo wir nun wesentlich stärkere Aussagen als früher zeigen können. Satz 2.20 Sei (,S,µ) ein Maßraum und U R n offen. Weiter sei f : U R eine Funktion, so dass für jedes u U die Funktion ˆf u : R, x f(x,u) zu L 1 (µ,) gehört, und sei g : U R, u ˆf u dµ = f(x,u)dµ(x). (a) Sind alle Funktionen f x : U R, u f(x,u) stetig in p U und existiert eine Funktion h L 1 (µ,) mit f(x,u) h(x) für alle (x,u) U, so ist g in p stetig. 28
14 (b) Sei 1 j n. Haben alle Funktionen f x eine stetige partielle Ableitung D j f x = fx u j und gibt es eine Funktion h L 1 (µ,) mit D j f x (u) h(x) für alle (x,u) U, so existiert auch D j g, diese Funktion ist stetig, und für alle p U ist (D j g)(p) = D j f(x,p)dµ(x). Beweis Aussage (a) folgt direkt aus dem Satz über majorisierte Konvergenz, da man Stetigkeit durch konvergente Folgen testen kann. Zu (b): Mit dem Mittelwertsatz finden wir für jedes t R mit u + µte j U für alle µ [0, 1] ein θ [0, 1] so, dass 1 t f(x,u + te j) f(x,u) = (D j f)(x,u + θte j ) h(x). Mit dem Satz über majorisierte Konvergenz erhalten wir für jede Folge (t n ) mit t n 0 die Beziehung lim g(p + t n e j ) g(p) f(x,p + t n e j ) f(x,p) = lim dµ t n t n = D j f(x,p)dµ. Die zweite rgänzung betrifft Funktionenräume, die man mit dem Lebensgue Integral sehr bequem definieren kann. Für einen vollständigen Maßraum (, S, µ) und p [1, ) sei L p (µ,) die Menge aller messbaren Funktionen f mit f p L 1 (µ,). Man kann zeigen, dass L p (µ,) ein linearer Raum ist und dass die Abbildung ( ) 1/p L p (µ,) [0, ), f f p := f p dµ alle igenschaften einer Norm mit Ausnahme von f p = 0 f = 0 hat. Um diese igenschaft zu erzwingen, setzt man N p := {f L p (µ,) : f p = 0} und faktorisiert N p weg. Auf den Räumen L p (µ,) := L p (µ,)/n p wird durch p eine Norm induziert, die man wieder mit p bezeichnet. Die dominierende Rolle dieser Räume in der Analysis liegt an folgendem Satz: Satz 2.21 Die Räume (L p (µ,), p ) sind vollständig, also Banachräume. Literatur: Forster, Analysis 3,
2. Integration. {x : f(x) <a+ 1 n }
 9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
9. Übung zur Maß- und Integrationstheorie, Lösungsskizze Aufgaben
 9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
Mathematik III. Vorlesung 71
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 athematik III Vorlesung 71 Ausschöpfungseigenschaften Die folgenden Rechenregeln für Integrale beruhen auf dem Ausschöpfungssatz für aße. an kann den Subgraphen
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 athematik III Vorlesung 71 Ausschöpfungseigenschaften Die folgenden Rechenregeln für Integrale beruhen auf dem Ausschöpfungssatz für aße. an kann den Subgraphen
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Serie 2 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
Analysis 2. Vorlesungsausarbeitung zum SS von Prof. Dr. Klaus Fritzsche. Inhaltsverzeichnis
 Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Lebesgue-Integral und L p -Räume
 Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie
 Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
1 Konvergenz im p ten Mittel
 Konvergenz im p ten Mittel 1 1 Konvergenz im p ten Mittel In diesem Paragraphen werden zunächst in Abschnitt 1.1 die L p Räume eingeführt. Diese erweisen sich als vollständige, lineare Räume über R. In
Konvergenz im p ten Mittel 1 1 Konvergenz im p ten Mittel In diesem Paragraphen werden zunächst in Abschnitt 1.1 die L p Räume eingeführt. Diese erweisen sich als vollständige, lineare Räume über R. In
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
3 Messbare Funktionen
 3. Messbare Funktionen 1 3 Messbare Funktionen Sei (, A, µ) ein beliebiger Maßraum. Definition. ine Funktion f : R = [, + ] heißt messbar (bezüglich A), falls die Menge {f < c} = {x : f(x) < c} = f 1 ([,
3. Messbare Funktionen 1 3 Messbare Funktionen Sei (, A, µ) ein beliebiger Maßraum. Definition. ine Funktion f : R = [, + ] heißt messbar (bezüglich A), falls die Menge {f < c} = {x : f(x) < c} = f 1 ([,
Darstellungssatz von Riesz in vollständig regulären Räumen. Carina Pöll Wintersemester 2012
 Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Höhere Analysis. dω = Reiner Lauterbach. Vorlesung. Universität Hamburg, WS 2015/2016
 Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
Maßtheorie. Skript zur Vorlesung von Prof. Dr. Michael Kohler. Sommersemester 2005 und Wintersemester 2005/2006
 Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
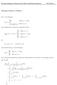 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
L p Räume und der Satz von Riesz-Fischer
 Kolloqium Partielle Differentialgleichungen 8.5.28 Carsten Erdmann L p Räume und der Satz von Riesz-Fischer 1.1. Definition. Sei p R, p >, dann setzen wir p :=, p :=. Sei f : K meßbar, dann ist f M + (,
Kolloqium Partielle Differentialgleichungen 8.5.28 Carsten Erdmann L p Räume und der Satz von Riesz-Fischer 1.1. Definition. Sei p R, p >, dann setzen wir p :=, p :=. Sei f : K meßbar, dann ist f M + (,
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 30.11.2016 5. Teilmengen von R und von R n Der R n ist eine mathematische Verallgemeinerung: R n = {x = (x 1,..., x n ) : x i R} = } R. {{.. R }. n mal Für x R ist x der Abstand zum
Universität Freiburg 30.11.2016 5. Teilmengen von R und von R n Der R n ist eine mathematische Verallgemeinerung: R n = {x = (x 1,..., x n ) : x i R} = } R. {{.. R }. n mal Für x R ist x der Abstand zum
Erwartungswert als Integral
 Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
30 Metriken und Normen
 31 Metriken und Normen 153 30 Metriken und Normen Lernziele: Konzepte: Metriken, Normen, Skalarprodukte, Konvergenz von Folgen Frage: Versuchen Sie, möglichst viele verschiedene Konvergenzbegriffe für
31 Metriken und Normen 153 30 Metriken und Normen Lernziele: Konzepte: Metriken, Normen, Skalarprodukte, Konvergenz von Folgen Frage: Versuchen Sie, möglichst viele verschiedene Konvergenzbegriffe für
Kapitel 19. Das Lebesgue Maß σ Algebren und Maße
 Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Analysis III Wintersemester 2003/2004. W. Ebeling
 Analysis III Wintersemester 2003/2004 W. Ebeling 1 c Wolfgang Ebeling Institut für Algebraische Geometrie Leibniz Universität Hannover Postfach 6009 30060 Hannover E-mail: [email protected]
Analysis III Wintersemester 2003/2004 W. Ebeling 1 c Wolfgang Ebeling Institut für Algebraische Geometrie Leibniz Universität Hannover Postfach 6009 30060 Hannover E-mail: [email protected]
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
2. Stetige lineare Funktionale
 -21-2. Stetige lineare Funktionale Die am Ende von 1 angedeutete Eigenschaft, die ein lineares Funktional T : D(ú) 6 verallgemeinerten Funktion macht, ist die Stetigkeit von T in jedem n 0 0 D(ú). Wenn
-21-2. Stetige lineare Funktionale Die am Ende von 1 angedeutete Eigenschaft, die ein lineares Funktional T : D(ú) 6 verallgemeinerten Funktion macht, ist die Stetigkeit von T in jedem n 0 0 D(ú). Wenn
9 Folgen und Reihen von Funktionen
 9 Folgen und Reihen von Funktionen In diesem Abschnitt betrachten wir verschiedene Arten der Konvergenz einer Funktionenfolge Besonders interessiert uns die Frage, ob sich Eigenschaften der einzelnen Glieder
9 Folgen und Reihen von Funktionen In diesem Abschnitt betrachten wir verschiedene Arten der Konvergenz einer Funktionenfolge Besonders interessiert uns die Frage, ob sich Eigenschaften der einzelnen Glieder
Optimale Steuerung, Prof.Dr. L. Blank 1. II Linear-quadratische elliptische Steuerungsprobleme
 Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN
 8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN (vi) Konvergenz von Folgen ist in topologischen Räumen folgendermaßen definiert: Ist (a n ) M eine Folge, so heißt sie konvergent gegen a M, wenn es
8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN (vi) Konvergenz von Folgen ist in topologischen Räumen folgendermaßen definiert: Ist (a n ) M eine Folge, so heißt sie konvergent gegen a M, wenn es
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version A)
 Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, 10.1.009 (Version A) Kennwort: Übungsgruppe: (Sie können ein beliebiges Kennwort wählen, um Ihre Anonymität zu wahren! Da die Probeklausur
Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, 10.1.009 (Version A) Kennwort: Übungsgruppe: (Sie können ein beliebiges Kennwort wählen, um Ihre Anonymität zu wahren! Da die Probeklausur
Inverse Fourier Transformation
 ETH Zürich HS 27 Departement Mathematik Seminararbeit Inverse Fourier Transformation Patricia Hinder Sandra König Oktober 27 Prof. M. Struwe Im Vortrag der letzten Woche haben wir gesehen, dass die Faltung
ETH Zürich HS 27 Departement Mathematik Seminararbeit Inverse Fourier Transformation Patricia Hinder Sandra König Oktober 27 Prof. M. Struwe Im Vortrag der letzten Woche haben wir gesehen, dass die Faltung
1.3 Zufallsvariablen
 1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
Kapitel 3. Konvergenz von Folgen und Reihen
 Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS-
 ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
Funktionsgrenzwerte, Stetigkeit
 Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Vorlesungen Analysis von B. Bank
 Vorlesungen Analysis von B. Bank vom 23.4.2002 und 26.4.2002 Zunächst noch zur Stetigkeit von Funktionen f : D(f) C, wobei D(f) C. (Der Text schliesst unmittelbar an die Vorlesung vom 19.4.2002 an.) Auf
Vorlesungen Analysis von B. Bank vom 23.4.2002 und 26.4.2002 Zunächst noch zur Stetigkeit von Funktionen f : D(f) C, wobei D(f) C. (Der Text schliesst unmittelbar an die Vorlesung vom 19.4.2002 an.) Auf
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Mathematik III. Vorlesung 74. Folgerungen aus dem Satz von Fubini. (( 1 3 x3 1 2 x2 y +2y 3 x) 1 2)dy. ( y +2y y +4y3 )dy
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Maß und Integral I und II. SS 2004 und WS 2004/05
 Maß und Integral I und II SS 2004 und WS 2004/05 Vorlesung von Priv.-Doz. Dr. J. Dippon unter Verwendung einer Vorlesung von Prof. Dr. H. Walk im SS 2003 Inhaltsverzeichnis Bezeichnungen 3 1 Grundbegriffe
Maß und Integral I und II SS 2004 und WS 2004/05 Vorlesung von Priv.-Doz. Dr. J. Dippon unter Verwendung einer Vorlesung von Prof. Dr. H. Walk im SS 2003 Inhaltsverzeichnis Bezeichnungen 3 1 Grundbegriffe
(b) Man nennt die Menge M beschränkt, wenn sie nach oben und unten beschränkt ist.
 8 Punktmengen Für die Menge M = { 1 n ; n N } ist 1 = max(m), denn 1 M und 1 n 1 für alle n N. Die Menge M besitzt aber kein Minimum, denn zu jeder Zahl x = 1 n M existiert ein y M mit y < x, etwa y =
8 Punktmengen Für die Menge M = { 1 n ; n N } ist 1 = max(m), denn 1 M und 1 n 1 für alle n N. Die Menge M besitzt aber kein Minimum, denn zu jeder Zahl x = 1 n M existiert ein y M mit y < x, etwa y =
Analysis III. Vorlesung 69. Integrierbare Funktionen
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Wichtige Klassen reeller Funktionen
 0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
Schwache Konvergenz. Kapitel 8
 Im Hinblick auf die funktionalen Grenzwertsätze wird in diesem Kapitel die Theorie der schwachen Konvergenz endlicher Maße auf separablen metrischen, vorallem polnischen Räumen entwickelt. In dieser Situation
Im Hinblick auf die funktionalen Grenzwertsätze wird in diesem Kapitel die Theorie der schwachen Konvergenz endlicher Maße auf separablen metrischen, vorallem polnischen Räumen entwickelt. In dieser Situation
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
3 Das n-dimensionale Integral
 3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Maßtheoretische Konzepte der Stochastik
 Maßtheoretische Konzepte der Stochastik Sommersemester 2016 Mathias Trabs Universität Hamburg 17. November 2016 Inhaltsverzeichnis 1 Wozu brauchen wir Maßtheorie? in Beispiel. 2 2 σ-algebren und Maße 4
Maßtheoretische Konzepte der Stochastik Sommersemester 2016 Mathias Trabs Universität Hamburg 17. November 2016 Inhaltsverzeichnis 1 Wozu brauchen wir Maßtheorie? in Beispiel. 2 2 σ-algebren und Maße 4
Analysis I - Stetige Funktionen
 Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kurzskript zur Maßtheorie (Teil der Vorlesung Analysis III, Wintersemester 2010/11, gehalten von D. Grieser)
 Kurzskript zur Maßtheorie (Teil der Vorlesung Analysis III, Wintersemester 2010/11, gehalten von D. Grieser) 13. Januar 2011 Inhaltsverzeichnis Vorwort..................................................
Kurzskript zur Maßtheorie (Teil der Vorlesung Analysis III, Wintersemester 2010/11, gehalten von D. Grieser) 13. Januar 2011 Inhaltsverzeichnis Vorwort..................................................
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
3. Übungsblatt zur Analysis II
 Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno WS 9/ 9..9 3. Übungsblatt zur Analysis II Gruppenübung Majorantenkriterium für uneigentliche Riemann-Integrale: Es seien f : [, ) [, ) und g
Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno WS 9/ 9..9 3. Übungsblatt zur Analysis II Gruppenübung Majorantenkriterium für uneigentliche Riemann-Integrale: Es seien f : [, ) [, ) und g
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Ljapunov Exponenten. Reiner Lauterbach
 Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Maß- und Integrationstheorie
 Maß- und Integrationstheorie Manuskript zur Vorlesung in SS26 Bálint Farkas [email protected] Inhaltsverzeichnis Einführung...................................................................
Maß- und Integrationstheorie Manuskript zur Vorlesung in SS26 Bálint Farkas [email protected] Inhaltsverzeichnis Einführung...................................................................
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
Existenz des Lebesgue-Borel-Maßes
 A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
Skript zur Vorlesung. Mass und Integral. Urs Lang. Sommersemester 2005 ETH Zürich
 Skript zur Vorlesung Mass und Integral Urs Lang Sommersemester 2005 ETH Zürich Version vom 12. September 2006 Literatur [Rudin] W. Rudin, Real and Complex Analysis, Third Edition. McGraw-Hill Book Co.,
Skript zur Vorlesung Mass und Integral Urs Lang Sommersemester 2005 ETH Zürich Version vom 12. September 2006 Literatur [Rudin] W. Rudin, Real and Complex Analysis, Third Edition. McGraw-Hill Book Co.,
Meßbare Funktionen. Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen.
 Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Vollständigkeit. 1 Konstruktion der reellen Zahlen
 Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
Rechenoperationen mit Folgen. Rekursion und Iteration.
 Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
4.1 Grundlegende Konstruktionen Stetigkeit von Funktionen Eigenschaften stetiger Funktionen... 92
 Kapitel 4 Funktionen und Stetigkeit In diesem Kapitel beginnen wir Funktionen f : Ê Ê systematisch zu untersuchen. Dazu bauen wir auf den Begriff des metrischen Raumes auf und erhalten offene und abgeschlossene
Kapitel 4 Funktionen und Stetigkeit In diesem Kapitel beginnen wir Funktionen f : Ê Ê systematisch zu untersuchen. Dazu bauen wir auf den Begriff des metrischen Raumes auf und erhalten offene und abgeschlossene
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
5 Teilmengen von R und von R n
 5 Teilmengen von R und von R n Der R n ist eine mathematische Verallgemeinerung: R n = {x = (x 1,...,x n ) : x i R} = R }... {{ R }. n mal Für x R ist x der Abstand zum Nullpunkt. Die entsprechende Verallgemeinerung
5 Teilmengen von R und von R n Der R n ist eine mathematische Verallgemeinerung: R n = {x = (x 1,...,x n ) : x i R} = R }... {{ R }. n mal Für x R ist x der Abstand zum Nullpunkt. Die entsprechende Verallgemeinerung
DIFFERENTIATION PARAMETERABHÄNGIGER INTEGRALE
 DIFFERENTIATION PARAMETERABHÄNGIGER INTEGRALE Zusammenfassung. Ergänzend zur Übung vom 06.06.203 soll hier die Leibnizregel für die Differentiation parameterabhängiger Integrale formuliert und bewiesen
DIFFERENTIATION PARAMETERABHÄNGIGER INTEGRALE Zusammenfassung. Ergänzend zur Übung vom 06.06.203 soll hier die Leibnizregel für die Differentiation parameterabhängiger Integrale formuliert und bewiesen
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
9 Metrische und normierte Räume
 9 Metrische und normierte Räume Idee: Wir wollen Abstände zwischen Punkten messen. Der Abstand soll eine reelle Zahl 0 sein (ohne Dimensionsangabe wie Meter...). 9.1 Definition Sei X eine Menge. Eine Metrik
9 Metrische und normierte Räume Idee: Wir wollen Abstände zwischen Punkten messen. Der Abstand soll eine reelle Zahl 0 sein (ohne Dimensionsangabe wie Meter...). 9.1 Definition Sei X eine Menge. Eine Metrik
12 Der Gaußsche Integralsatz
 12. Der Gaußsche Integralsatz 1 12 Der Gaußsche Integralsatz Das Ziel dieses Abschnitts ist die folgende zentrale Aussage der mehrdimensionalen Analysis und der Theorie der partiellen Differentialgleichungen:
12. Der Gaußsche Integralsatz 1 12 Der Gaußsche Integralsatz Das Ziel dieses Abschnitts ist die folgende zentrale Aussage der mehrdimensionalen Analysis und der Theorie der partiellen Differentialgleichungen:
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Analysis III. Inhaltsverzeichnis. Martin Brokate. 1 Maße 1. 2 Das Lebesgue-Integral Normierte und metrische Räume 38
 Analysis III Martin Brokate Inhaltsverzeichnis 1 Maße 1 2 Das Lebesgue-Integral 26 3 Normierte und metrische Räume 38 4 Konvergenzsätze und L p -Räume 48 5 Mehrfachintegrale, Satz von Fubini 63 6 Metrische
Analysis III Martin Brokate Inhaltsverzeichnis 1 Maße 1 2 Das Lebesgue-Integral 26 3 Normierte und metrische Räume 38 4 Konvergenzsätze und L p -Räume 48 5 Mehrfachintegrale, Satz von Fubini 63 6 Metrische
13 Auswahlaxiom und Zornsches Lemma
 13 Auswahlaxiom und Zornsches Lemma Handout zur Funktionalanalysis I von H. Glöckner, 25.11.2008 Wichtige Teile der modernen Mathematik beruhen auf dem sogenannten Auswahlaxiom der Mengenlehre. Dieses
13 Auswahlaxiom und Zornsches Lemma Handout zur Funktionalanalysis I von H. Glöckner, 25.11.2008 Wichtige Teile der modernen Mathematik beruhen auf dem sogenannten Auswahlaxiom der Mengenlehre. Dieses
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Erwartungswert und Varianz von Zufallsvariablen
 Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Definition 3.1. Sei A X. Unter einer offenen Überdeckung von A versteht man eine Familie (U i ) i I offener Mengen U i X mit U i
 3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
Übersicht Wahrscheinlichkeitsheorie
 Übersicht Wahrscheinlichkeitsheorie Gunther Leobacher und Friedrich Pillichshammer Universität Linz, Institut für Finanzmathematik, Altenbergerstrasse 69, 4040 Linz, Austria E-mail: [email protected],
Übersicht Wahrscheinlichkeitsheorie Gunther Leobacher und Friedrich Pillichshammer Universität Linz, Institut für Finanzmathematik, Altenbergerstrasse 69, 4040 Linz, Austria E-mail: [email protected],
