Räumliche Darstellung
|
|
|
- Willi Richter
- vor 9 Jahren
- Abrufe
Transkript
1 Räumliche Darstellung
2 Einleitung Stellen wir uns mal vor, jemand möchte einen Rubiks-Cube abzeichnen, dann wird sich diese Person diesen Würfel vor sich auf einen Tisch stellen, wird ein Papier hinlegen und verschiedene Zeichnmaterialien bereitstellen. Das Grundproblem besteht nun darin, dass der Ausgangspunkt (der Würfel) ein dreidimensionales Objekt, die Zeichnung aber nur zweidimensional ist. Im zweidimensionalen Raum (auf dem Zeichenblatt) gibt es nur zwei Raumrichtungen, die horizontale (links - rechts) und die vertikale (oben - unten). Im dreidimensionalen Raum kommt die Richtung in die Tiefe hinzu. Dieses Wegfallen der dritten Dimension hat fatale Folgen, denn man kann nicht das Objekt so übernehmen, wie es in Wirklichkeit ist, sondern kann es nur so wiedergeben, wie es sich genau aus einem Beobachtungspunkt zeigt. Man übersetzt also etwas Räumliches in etwas Flächiges. Text lesen wichtige Stellen markieren Eine räumliche Darstellung ist im Endeffekt also nichts anderes, als etwas Zweidimensionales, das so tut, als ob es dreidimensional wäre. Die Übersetzung von drei Dimensionen in deren zwei kann über zwei verschiedene Methoden geschehen, über die Beobachtung oder die Konstruktion. Die Methode der Beobachtung hat den Vorteil, dass sie eine relativ schnelle Methode ist. Ihr Nachteil liegt in der Ungenauigkeit (symbolhaftes Sehen, optische Täuschungen). Die Methode der Konstruktion hat den Vorteil, dass sie ziemlich genaue Ergebnisse erzielt (mit den oben genannten Einschränkungen). Ihr Nachteil liegt wohl darin, dass sie sehr zeitaufwändig ist. So benötigt man beispielsweise für eine konstruierte Abbildung eines Holzstuhles mit Lehne auch als geübter Zeichner schnell vier bis fünf Stunden. Im eigenen gestaltersischen Schaffen verschmelzen diese beiden Methoden oft. Darüber hinaus können im eigenen Gestalten noch weitere raumgebende Methoden berücksichtigt werden (z. B.: Verdeckung, Modulierung). Diese Werkstatt führt in die Wahrnehmung des Raumes ein. Sie gibt einen Einblick in die beiden Methoden (beobachten und konstruieren), zeigt auf, welche weiteren raumgebenden Methoden angewendet werden können und erweitert das eigene räumliche Denken und Vorstellungsvermögen. Dadurch wird die eigene Wahrnehmung, wie auch das künstlerische / gestalterische Schaffen differenzierter. li: Rubiks-Würfel re: Der Beobachtungspunkt entscheidet über die Erscheinung eines Objektes. Räumliche Darstellung 1
3 Raumgebende Verfahren: Die Perspektiven 1. Geometrische Projektionsverfahren 1A - Parallelprojektion Sehstrahlen verlaufen parallel, raumparallele Kanten werden in der Projektion ebenfalls parallel abgebildet. rechtwinklig (orthogonal): Sehstrahlen treffen rechtwinklig auf die Projektionsfläche. Hauptriss (Dreitafelprojektion) Axonometrie: isometrisch, dimetrisch oder trimetrisch schiefwinklig: Sehstrahlen treffen in einem schrägen Winkel auf die Projektionsfläche. Kavalier-, Kabinett- und Militärperspektive 1B - Zentralprojektion Sehstrahlen gehen von einem Augpunkt aus, raumparallele Kanten fluchten in der Projektion in einem Punkt Zentralperspektive Zentralprojektion, eine Raumfläche liegt parallel zur Bildebene, diese wird bildparallel abgebildet, die andere orthogonal dazu deren Raumflächen fluchten in einem Punkt 2-Punktperspektive (Übereckperspektive) Zentralprojektion, die horizontparallelen Raumkanten sind nicht bildebenenparallel und fluchten in ihrem jeweiligen Fluchtpunkt, die Vertikalen werden bildparallel abgebildet. 3-Punktperspektive Zentralprojektion, die horizontparallelen Raumkanten sind nicht bildebenenparallel und fluchten in ihrem jeweiligen Fluchtpunkt, ebenso die Vertikalen. Froschperspektive Zentralprojektion, es gibt keine bildebenenparallelen Raumkanten, der Augpunkt liegt unter dem abgebildeten Gegenstand Vogelperspektive Zentralprojektion, es gibt keine bildebenenparallelen Raumkanten, der Augpunkt liegt über dem abgebildeten Gegenstand 1C - weitere geometrische Projektionsverfahren Fischaugprojektion Sphärische Projektion. Linien, die nicht durch das Zentrum gehen, werden gekrümmt, Flächen am Rand kleiner abgebildet, als in Bildmitte, der Blickwinkel erreicht 180 Grad und mehr. Panoramabild Beim Panoramabild erfolgt die Abbildung zunächst auf eine zylinderförmige Fläche, die dann in eine Ebene abgerollt werden kann. Es gibt aber auch große Panoramen, die als Zylinder aufgestellt sind. Parallele Linien werden nur im Sonderfall parallel abgebildet. Man erreicht einen Blickwinkel von 180 Grad und mehr (bis 360 Grad). Zylinderperspektive Reliefperspektive Umgekehrte Perspektive 2. Bedeutungsperspektive Begriff in der Malerei. Die Größe der dargestellten Figuren und Gegenstände hängt von deren Bildbedeutung ab, nicht von den räumlich-geometrischen Gegebenheiten. 3. Luft- und Farbperspektive Die Farb- und Helligkeitskontraste nehmen in die Ferne ab Farben erscheinen matter, meistens heller und ins blau verschoben Räumliche Darstellung 2
4 Raumgebende Verfahren: Weitere Methoden Neben den perspektivischen Methoden gibt es auch andere Verfahren, ein Bild räumlich wirken zu lassen. Hier eine Übersicht: Verdeckung In einer räumlichen Situation stehen Gegenstände nicht nur neben-, sondern auch hintereinander. So ist es wahrscheinlich, dass Gegenstände, die sich näher beim Betrachter befinden, andere teilweise verdecken. Veränderung der Grösse Je grösser der Abstand zwischen Betrachter und Gegenstand ist, desto kleiner erscheint dieser. Dies gilt sowohl für die die Gegenstände selber, wie auch für die Zwischenräume. Modellierung Die zu zeichnenden Objekte werden immer auf eine bestimmte Art und Weise beleuchtet. Das Licht wird je nach Einfallswinkel stärker oder schwächer reflektiert, der Gegenstand erscheint heller oder dünkler. Die Lichtsituation bringt auch Schatten hervor, meistens mehrere. Details + Schärfe Abb aus «Perspective Without Pain», 1988, bei North Light/F&W Publications, Ohio Je grösser der Abstand zwischen Betrachter und Gegenstand ist, desto weniger Details sind auf dem Gegenstand zu erkennen. Ebenso kann nur ein Teil des Bildes mit scharfem Umriss gezeichnet werden. Veränderung des Kontrastes Mit zunehmendem Abstand verändert sich das Objekt auch in Bezug auf seinen Kontrast. Je weiter weg ein Objekt ist, desto vergrauter erscheint es. Das hat mit der Luft zu tun, die zwischen Objekt und Betrachter liegt. Luft enthält Wasser und Staub, und je nach dem, wie hoch diese Anteile sind, desto stärker wird der Schleier sichtbar. Ein anderer Grund ist, dass von weiter entfernten Objekten weniger Licht unser Auge erreicht. Räumliche Darstellung 3
5 Die Perspektiven: Geometrische Projektionsverfahren Zwei häufige und wichtige perspektivische Zeichenmethoden sind die Zentral- und Parallel-Projektion. Sie gehören beide zu den geometrischen Verfahren und werden beispielsweise in der Architektur oder in der Produktegestaltung angewendet. Text lesen wichtige Stellen markieren Die Parallelprojektion (1A) Linien, die in der Wirklichkeit parallel verlaufen, werden bei der parallelperspektivischen Abbildung gleichfalls parallel dargestellt. Dadurch wird ein Zusammenlaufen der Linien in Richtung der Fluchtpunkte vermieden, so dass die abgebildeten Flächen gut erkenntlich bleiben. Diese Darstellungsweise findet man oft bei Anleitungen (zum Beispiel Zusammenbaus eines Möbelstückes). In besonderen Formen der Parallel- Projektion sind die Linien längentreu wiedergegeben, dies kann, bei der Anwendung auf einem Plan, äusserst praktisch sein. Die Zentralprojektion (1B) Die Zentralprojektion ist eine Darstellungsmethode, die dem menschlichen Wahrnehmung sehr nahe kommt. Zu ihr gehören die 1-, 2- und 3-Fluchtpunkt-Perspektive. o-li: Isometrische Darstellung o-mi: Schrägprojektion, «Militärperspektive» o-re:schrägprojektion, «Kabinettperspektive» (auch «Kavalierperspektive») li: 2-Fluchtpunkt-Perspektive u-1: 1-Fluchtpunkt-Perspektive u-2: 2-Fluchtpunkt-Perspektive u-3: 3-Fluchtpunkt-Perspektive (Frosch-Persp.) u-4: 3-Fluchtpunkt-Perspektive (Vogel-Persp.) Räumliche Darstellung 4
6 Augenpunkt Die Perspektiven: Geometrische Projektionsverfahren Text lesen wichtige Stellen markieren Die Zentralprojektion (Fortsetzung) Die Bildebene Bei der Zentralprojektion werden die Punkte eines dreidimensionalen Raumes oder Objektes auf einer Ebene abgebildet. Diese Ebene nennt man Bildebene. Augenpunkt Bildebene Bildebene Horizont Hauptsehstrahl Horizont + Sehstrahl Parallelität in Bezug zur Bildfläche In der Zentralprojektion werden die im Raum parallelen Linien nicht parallel gezeichnet mit einer Ausnahme: wenn sich diese genau parallel zur Bildfläche (=zum Betrachter) verhalten. Schliesst man diesen Sonderfall aus, so kann man eine weitere Regel formulieren: Linien, die raumparallel sind (= in Wirklichkeit, am Objekt parallel), schneiden sich auf einem gemeinsamen Punkt. Diesen Punkt nennt man Fluchtpunkt. Sind nun diese Linien im Raum waagrecht, so befindet sich ihr Fluchtpunkt auf dem Horizont. Die Horizontallinie Stellen wir uns vor, wir würden aufrecht an einem Sandstrand stehen und ins Meer hinaussehen. Würde man diese räumliche Konfiguration auf ein Blatt übertragen, müsste man nur den Horizont zeichnen. Doch so einfach, wie das auch tönt, diese nur eine Linie würde dem Betrachter schon mehr verraten, als dass man gemeinhin annimmt. Befindet sich die Horizontale im oberen Bildbereich, wäre man sehr gross, oder befindet sich auf einem Aussichtsturm. Ist die Horizontale am unteren Bildrand, hat der Zeichner im Sand gelegen. Die Horizontallinie befindet sich dort, wo der Sehstrahl die Bildebene in einem rechten Winkel schneidet. Den Schneidepunkt nennt man Augenpunkt. Räumliche Darstellung 5
7 Die Perspektiven: Geometrische Projektionsverfahren Weitere Projektionsverfahren (1C) Fischaugenprojektion Die Fischaugenprojektion ist eine sphärische Projektion. Linien, die nicht durch das Zentrum gehen, werden gekrümmt, Flächen am Rand kleiner abgebildet, als in der Bildmitte. Die Krümmung ist stark tonnenförmig. Dafür bildet dieses Projektionsverfahren Flächenverhältnisse meist getreuer ab. Die Fischaugprojektion bedient sich eines sehr grossen Blickwinkels (bis zu 220 ). Der Name dieses Projektionverfahrens kommt übrigens von der Vorstellung, wie ein Fisch die Welt sieht, wenn er von unten durch die Wasseroberfläche schaut. Die Fischaugprojektion wird heute vorallem in der Fotografie angewendet, da es spezielle Objektive gibt, die diese Projektion quasi automatisch herstellen. Panoramabild Beim Panoramabild erfolgt die Abbildung zunächst auf eine zylinderförmige Fläche, die dann in eine Ebene aufgerollt werden kann. Es gibt aber auch große Panoramen, die als Zylinder aufgestellt sind. Parallele Linien werden nur im Sonderfall parallel abgebildet. Man erreicht einen Blickwinkel von 180 Grad und mehr (bis 360 Grad). Zylindrische Projektion Verschiedene Künstler wie M. C. Escher haben mit der zylindrischen Projektion experimentiert. Mit dieser Perspektive sind Panoramen von mehr als 180 perspektivisch real darstellbar, dabei verzerren sich gerade Linien zu gekrümmten Kurven. Ein Beispiel dafür ist Eschers Lithografie Treppenhaus I., Umgekehrte Perspektive Mit zwei Augen sieht man im Nahbereich näher liegende Gegenstände schmaler als weiter entfernt liegende. Der Effekt entsteht durch das zweiäugige (räumliche) Sehen. Die umgekehrte Perspektive wurde zum Beispiel in der byzantinischen Ikonenmalerei angewandt, zusammen mit der Bedeutungsperspektive. Dabei laufen parallele Linien in Bildteilen auf den Betrachter zu, wie es bei den Fussbänken der Dreifaltigkeitsikone zu sehen ist. Räumliche Darstellung 6
8 Die Perspektiven: Bedeutungsperspektive, Luft- und Farbperspektive Bedeutungsperspektive (2) In der Zeit vor der Wiederentdeckung der geometrischen Perspektive wird in Tafelbildern die sogenannte Bedeutungsperspektive benutzt. Die Größe und Ausrichtung der im Bild dargestellten Personen richtet sich nach deren Bedeutung: wichtige Protagonisten erscheinen groß, weniger wichtige werden kleiner dargestellt, auch wenn diese sich räumlich vor der anderen Person befinden. In dem Bildbeispiel rechts bezieht sich die quasi-isometrische Perspektive der Fußbänke nur auf die jeweilige Figur in grafisch-kompositorischer Hinsicht ermöglicht diese Anordnung die (flächige) Öffnung des Bildraumes zum Hintergrund. Die Bedeutungsperspektive wird bereits in der altägyptischen Kunst angewandt: Während der Pharao nebst Gemahlin in voller Größe dargestellt wird, zeigt man Sklaven und Hofstaat sehr viel kleiner. In der Ikonenmalerei findet sich diese Art der Darstellung ebenso wie in der Malerei der Romanik und Gotik. Die Bedeutungsperspektive ist auch heute noch in der naiven Malerei zu finden Luft- und Farbperspektive (3) Luft- und Farbperspektive müssen unterschieden werden. Bei der Luftperspektive wird ein Tiefeneindruck erzeugt, indem die Kontraste von vorne nach hinten abnehmen und die Helligkeit von vorne nach hinten zunimmt. Unabhängig von der Farbe entsteht gleichzeitig durch die nach hinten undeutlicher werdenden Konturen ein Scharf/Unscharf-Kontrast. Die Farbperspektive sorgt für einen Tiefeneindruck, indem im Vorder-, Mittel- und Hintergrund unterschiedliche Farbtöne dominant eingesetzt werden. Im Vordergrund dominieren warme Farben (gelb, orange, rot, braun), im Mittelgrund und im Hintergrund Grün- und Blautöne. Stattdessen kann auch eine Grün- bzw. Blaustichigkeit vorliegen. Räumliche Darstellung 7
9 Geschichte der perspektivischen Darstellung T1 Text lesen wichtige Stellen markieren Von der Antike... Um räumliche Situationen darzustellen oder abzubilden, waren perspektivische Verfahren bereits den Römern bekannt (siehe auch Skenographie). In Pompeji (dies war eine antike Stadt am Golf von Neapel, 1000 v. Chr. 79 n. Chr.) wurden Wandfresken gefunden, die den Raum in einen gemalten Garten fortsetzen sollten. In den darauf folgenden Jahrhunderten wurde dieses Wissen nicht weiterentwickelt; die frühchristliche und mittelalterliche Malerei bediente sich fast ausschließlich der Bedeutungsperspektive, d. h. die Größe der dargestellten Personen und Gegenstände wurde durch deren Bedeutung im Bild bestimmt, nicht durch ihre räumliche Anordnung. Räumliche Wirkung erzielte man fast ausschließlich durch die Kulissenwirkung, die eine Vordergrundebene vor einem Hintergrund unterschied.... zur Renaissance In der Renaissance wurde die Zentralperspektive (im Zusammenhang mit der Camera Obscura) (wieder-) entdeckt, die in etwa dem Sehen mit einem Auge oder einer verzerrungsfreien fotografischen Abbildung entspricht. Malerarchitekten wie Filippo Brunelleschi (gilt als der Erfinder der Perspektive), Giotto und Leon Battista Alberti schufen Werke, die Motive der christlichen Ikonographie in räumlich korrekt konstruierten Architekturkulissen zeigten. Anfänglich wurde die Zentralperspektive, die unser Auge produziert, in ihren Gesetzmäßigkeiten nicht erkannt, und die Darstellung erfolgte mittels einer Schnur, die, von einem festen Punkt ausgehend, über ein einfaches Raster in Form eines Drahtgitters zu den abzubildenden Objekten gespannt wurde. Der Zeichner saß neben dem Gitter und übertrug die Messungen in das Raster seiner Zeichenfläche («perspektivisches Abschnüren»). In einem Buch aus dem Jahre 1436 erläuterte Leon Battista Alberti die mathematischen Methoden, mit denen auf Gemälden eine perspektivische Wirkung zu erzielen sei. o: In Rom wurde das Prinzip der griechischen Bühnendekoration übernommen, weleches in pompejianischen Villen erhalten ist. Die in Griechenland verfolgte Tendenz einer räumlichen Erfassung von Landschaft wurde jedoch nicht weitergeführt. Beim Übergang spätrömischer Kunst zur frühchristlichen spielten Plastizität der Figuren und Raumillusion nur mehr eine untergeordnete Rolle. u: Abbildung aus Dürers Underweysung, 1525 Albrecht Dürer veröffentlichte 1525 sein Buch «Underweysung der messung mit dem zirckel un richtscheyt» [2], das die erste Zusammenfassung der mathematisch-geometrischen Verfahren der Zentralperspektive darstellte und damit auch die Grundlagen der perspektivischen Konstruktionsverfahren als Teilbereich der Darstellenden Geometrie bildet. Räumliche Darstellung 8
10 Die Erfindung der Linearperspektive Die Erfindung der Linearperspektive A1 Text abschreiben Bilder ausschneiden und aufkleben Das System der Perspektive entstand am Anfang des 15. Jahrhunderts, also in der Kunstepoche, die der Renaissance zugeschreiben wird. Ihre Erfindung bzw. Wiederentdeckung wird zwei Florentinern zugeschrieben - dem Architekten und Schriftsteller Leon Battista Alberti ( ) und dem Bildhauer und Architekten Filippo Brunelleschi ( ). Mit sehr einfach anzuwendenden Methoden konnten Künstler von da an auf einer Fläche dreidimensionale Gegenstände exakt wiedergeben - und veränderten damit die Kunst des Abendlandes entscheidend. Das Wort Perspektive stammt vom lateinischen Wortbegriff «perspicere» und bedeutet soviel wie durchschauen (deutlich sehen, in den Raum hinein sehen). Um die Gesetze der Perspektive zu studieren, hielt Leonardo da Vinci die Ansicht einer Landschaft mit Kriede auf einer Glasplatte fest. Damit klärt sich der Begriff «perspicere» (durchschauen). Statue von Leon Battista Alberti im Hof der Uffizien; Florenz Statue von Filippo Brunelleschi, zur Kuppel des Domes Santa Maria del Fiore hinaufblickend; Florenz Papier Schreibzeug Schere Leim Räumliche Darstellung 9
11 Raumsituation auf Folie A2 Raumsituation auswählen Raumgebende Linien nachzeichnen Folie aufkleben Suche dir eine eindeutige Raumsituation im Schulgang. Lege die Folie, welche du in diesem Mäppchen findest, auf eine Glasplatte und befestige sie mit Klebeband, damit sie nicht mehr verrutscht. Nun zeichne sehr genau auf der Folie mit einem wasserfesten Filzstift alles nacht, was du durch die Glasplatte siehst. Klebe die Folie sauber auf ein Blatt. Folie Glasplatte Klebeband wasserfester Filzstift Leim Papier (120g) «Ein Mann zeichnet eine Amphore» aus Dürers Lehrbuch «Underweisung der Messung». Dieser Netzrahmen wurde zum Studium perspektivischer Verkürzungen am Körper benutzt. Die Bildebene Die Glasplatte bzw. die Folie, auf welcher du deine Zeichnung anfertigst, ist die sogenannte Bildebene. Nur diejenigen Raumlinien, die parallel zur Bildebene verlaufen, verhalten sich auch auf der Bildebene parallel. Dort, wo der Sehstrahl die Bildebene in einem rechten Winkel schneidet, befindet sich der sogenannte Augenpunkt. Durch ihn geht der Horizont. A ugen B il d e b e punk t ne enebedlib Horizont lhartshestpuah Horizont + tkn u e pn gu A Sehstrahl Räumliche Darstellung 10
12 Zentralprojektion: Die 1-Fluchtpunkt-Perspektive A3 Die 1-Fluchtpunkt-Perspektive ist eigentlich ein Spezialfall unter den Linearperspektiven. Sie kommt nur dann zum Einsatz, wenn sich ein Objekt genau parallel zur Bildfläche verhält. Regeln zur 1-Fluchtpunkt-Perspektive Senkrechte Linien bleiben senkrecht. Waagrechte Linien bleiben waagrecht. Senk- und Waagrechte werden mit zunehmender Distanz kürzer. Tiefenlinien, welche raumparallel sind, treffen sich im Fluchtpunkt. Der Augenpunkt ist gleich Fluchtpunkt. Augenhöhe ist gleich Horizontallinie Die Abbildung rechts ist eine spezielle Situation. der Fluchtpunkt ist genau in der Mitte der gegenüberliegenden Wand, so dass die Tiefenlinien eine Diagonale bilden und genau in den Ecken der näheren Wand enden. Man nennt sie deshalb: Zentralperspektive Horizontallinie Fluchtpunkt Sehstrahl Tiefenlinie Augenpunkt Augenhöhe Bildebene Fluchtpunkt = Augenpunkt Horizontallinie = Augenhöhe Räumliche Darstellung 11
13 Zentralprojektion: Die 1-Fluchtpunkt-Perspektive A3 Die 1-Fluchtpunkt-Perspektive ist eigentlich ein Spezialfall unter den Linearperspektiven. Sie kommt nur dann zum Einsatz, wenn sich ein Objekt genau parallel zur Bildfläche verhält. Regeln zur 1-Fluchtpunkt-Perspektive Senkrechte Linien bleiben senkrecht. Waagrechte Linien bleiben waagrecht. Senk- und Waagrechte werden mit zunehmender Distanz kürzer. Tiefenlinien, welche raumparallel sind, treffen sich im Fluchtpunkt. Der Augenpunkt ist gleich Fluchtpunkt. Augenhöhe ist gleich Horizontallinie Die Abbildung rechts ist eine spezielle Situation. der Fluchtpunkt ist genau in der Mitte der gegenüberliegenden Wand, so dass die Tiefenlinien eine Diagonale bilden und genau in den Ecken der näheren Wand enden. Man nennt sie deshalb: Zentralperspektive Horizontallinie Fluchtpunkt Zeichne unten ein: Tiefenlinien Horizontallinie Augenhöhe Fluchtpunkt Augenpunkt Sehstrahl Tiefenlinie Augenpunkt Augenhöhe Bildebene Räumliche Darstellung 12
14 Übung zur 1-Fluchtpunkt-Perspektive Zeichne unten ein: Tiefenlinien Horizontallinie Augenhöhe Fluchtpunkt + Augenpunkt Sammle aus Zeitschriften mindestens zwei typische Bilder mit einem Fluchtpunkt. Klebe sie auf die Rückseite dieses Blattes und zeichne folgendes ein: Tiefenlinien Horizontallinie Augenhöhe Fluchtpunkt + Augenpunkt Räumliche Darstellung 13
15 Lösung zur Übung zur 1-Fluchtpunkt-Perspektive Räumliche Darstellung 14
16 Übung zur 1-Fluchtpunkt-Perspektive A4 4/5 der Höhe der 1/3 der Breite der 1/3 der Höhe der 1/4 der Breite der Räumliche Darstellung 15
17 Lösung zur Übung zur 1-Fluchtpunkt-Perspektive L4 4/5 der Höhe der 1/3 der Breite der 1/3 der Höhe der 1/4 der Breite der Räumliche Darstellung 16
18 Weitere Übungungen zur 1-Fluchtpunkt-Perspektive A5 Räumliche Darstellung 17
19 Zentralprojektion: Die 2-Fluchtpunkt-Perspektive A3 Die 2-Fluchtpunkt-Perspektive kommt der alltäglichen Sicht des Menschen am nächsten (solange er nicht nach oben oder unten schaut). Der Name trügt allerdings ein wenig, denn die Zahl zwei des Namens bezieht sich nicht auf das ganze Bild, sondern auf jedes Objekt. Die 2-Fluchtpunkt-Perspektive kommt dann zum Einsatz, wenn sich das Objekt nicht parallel zur Bildebene verhält. Regeln zur 2-Fluchtpunkt-Perspektive Senkrechte Linien bleiben senkrecht. Senkrechte werden mit zunehmender Distanz kürzer. Raumparallele Tiefenlinien treffen sich im jeweiligen Fluchtpunkt. Sind die Objektkanten parallel zur Grundfläche, liegen die Fluchtpunkte auf der Horizontlinie. Augenhöhe ist gleich Horizontallinie Augenpunkt Augenhöhe Bildebene Räumliche Darstellung 18
20 Übung zur 2-Fluchtpunkt-Perspektive Zeichne unten ein: Tiefenlinien Horizontallinie Augenhöhe Fluchtpunkt + Augenpunkt Sammle aus Zeitschriften mindestens zwei typische Bilder mit zwei Fluchtpunkten. Klebe sie auf die Rückseite dieses Blattes und zeichne folgendes ein: Tiefenlinien Horizontallinie Augenhöhe Fluchtpunkt + Augenpunkt Räumliche Darstellung 19
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Raumdarstellung. Arbeitsheft. Perspektive
 Arbeitsheft Perspektive Wie kann man Tiefe darstellen auf einer Ebene? Trick 1 vorne = im Bild unten sind die Teile größer und auch Abstände größer hinten = im Bild oben werden die Teile kleiner und die
Arbeitsheft Perspektive Wie kann man Tiefe darstellen auf einer Ebene? Trick 1 vorne = im Bild unten sind die Teile größer und auch Abstände größer hinten = im Bild oben werden die Teile kleiner und die
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Die Grundlagen der Gestaltung Die Perspektive
 Gute Bildgestaltung in Theorie und Praxis Die Grundlagen der Gestaltung Die Perspektive Kaum mit einem anderen Wort wird, selbst von namhaften Autoren in der Fotografie, derart Schindluderei getrieben
Gute Bildgestaltung in Theorie und Praxis Die Grundlagen der Gestaltung Die Perspektive Kaum mit einem anderen Wort wird, selbst von namhaften Autoren in der Fotografie, derart Schindluderei getrieben
01 Räumlich zeichnen lernen 03 Räumlich zeichnen lernen info Blicklinien info Blickwinkel und Größe im Bild
 01 Räumlich zeichnen lernen 03 Räumlich zeichnen lernen info Blicklinien info Blickwinkel und Größe im Bild Frage: Was sind Blicklinien? Glasscheibe: Meine Lehrer sind der Architekt Leon Battista Alberti
01 Räumlich zeichnen lernen 03 Räumlich zeichnen lernen info Blicklinien info Blickwinkel und Größe im Bild Frage: Was sind Blicklinien? Glasscheibe: Meine Lehrer sind der Architekt Leon Battista Alberti
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Raum.Stationen.zu.linearen.
 Raum.Stationen.zu.linearen. Perspektiven Bearbeite die Stationen A bis K und mache dir Notizen im Hefter. Für die Übungen benutze bitte Zeichenpapier. Bsp.: (F) kannst du nur besuchen, wenn du (E) erledigt
Raum.Stationen.zu.linearen. Perspektiven Bearbeite die Stationen A bis K und mache dir Notizen im Hefter. Für die Übungen benutze bitte Zeichenpapier. Bsp.: (F) kannst du nur besuchen, wenn du (E) erledigt
Projektionen und Perspektive
 Projektionen und Perspektive 2 Beim räumlichen Zeichnen geht es um das Problem, dreidimensionale Objekte auf einer meist ebenen Zeichenfläche darzustellen. Allgemein wird diese Tätigkeit (bzw. deren Ergebnis)
Projektionen und Perspektive 2 Beim räumlichen Zeichnen geht es um das Problem, dreidimensionale Objekte auf einer meist ebenen Zeichenfläche darzustellen. Allgemein wird diese Tätigkeit (bzw. deren Ergebnis)
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Thomae. Perspektive und Axonometrie
 Thomae. Perspektive und Axonometrie Reiner Thomae Perspektive und Axonometrie 7. Auflage Verlag W Kohlhammer Die Deutsche Bibliothek - CIP-Einheitsaufnahme Thomae, Reiner: Perspektive und Axonometrie/Reiner
Thomae. Perspektive und Axonometrie Reiner Thomae Perspektive und Axonometrie 7. Auflage Verlag W Kohlhammer Die Deutsche Bibliothek - CIP-Einheitsaufnahme Thomae, Reiner: Perspektive und Axonometrie/Reiner
Optische Täuschungen Lehrerinformation
 Lehrerinformation 1/6 Arbeitsauftrag Die SuS betrachten die optischen Täuschungen und lassen diese auf sich wirken. Anschliessend zeichnen sie selber geometrische Figuren. Ziel Die SuS kennen einige optische
Lehrerinformation 1/6 Arbeitsauftrag Die SuS betrachten die optischen Täuschungen und lassen diese auf sich wirken. Anschliessend zeichnen sie selber geometrische Figuren. Ziel Die SuS kennen einige optische
Nach Lage der Winkel im Achsenkreuz wird unterschieden zwischen:
 Darstellung In der Zeichnung gibt es verschiedene Möglichkeiten einen Körper darzustellen. Die echte perspektivische Darstellung ist gekennzeichnet, durch einen Fluchtpunkt in dem alle Linien, die in der
Darstellung In der Zeichnung gibt es verschiedene Möglichkeiten einen Körper darzustellen. Die echte perspektivische Darstellung ist gekennzeichnet, durch einen Fluchtpunkt in dem alle Linien, die in der
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Perspektivische Darstellung in der Renaissance
 Perspektivische Darstellung in der Renaissance Die Perspektive ist ein konstruierendes Darstellungsmittel, das von den Künstlern der Renaissance (1400 - ca. 1620) entwickelt wurde. In dieser Zeit entstand
Perspektivische Darstellung in der Renaissance Die Perspektive ist ein konstruierendes Darstellungsmittel, das von den Künstlern der Renaissance (1400 - ca. 1620) entwickelt wurde. In dieser Zeit entstand
Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. 3-Punkt-Fluchtpunktp.
 Ein Auftrag: Eine Frage der Perspektive... Isometrie Dimetrie Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. Sphärische Perspektive curvilinear perspective Kavalliersperspektive, Kabinettperspektive (Eine
Ein Auftrag: Eine Frage der Perspektive... Isometrie Dimetrie Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. Sphärische Perspektive curvilinear perspective Kavalliersperspektive, Kabinettperspektive (Eine
Zeichnen und Skizzieren von Szenarien
 Zeichnen und Skizzieren von Szenarien 2. Anatomie 3. Komposition 4. Struktur und Kontraste 5. Abstraktion 6. Abgabe Körper im Raum. Perspektivisches Umdenken. Räumlichkeit & Perspektive. Räumlichkeit
Zeichnen und Skizzieren von Szenarien 2. Anatomie 3. Komposition 4. Struktur und Kontraste 5. Abstraktion 6. Abgabe Körper im Raum. Perspektivisches Umdenken. Räumlichkeit & Perspektive. Räumlichkeit
Themenpaket für die 7./8. Jahrgangsstufe
 Themenpaket für die 7./8. Jahrgangsstufe Fritz Overbeck: Im Vorfrühling, 1896 (Öl auf Leinwand) Perspektive Inhalt: Franziska Hell Arbeitsblatt Fritz Overbeck (1869-1909) gehört zu den Gründungsvätern
Themenpaket für die 7./8. Jahrgangsstufe Fritz Overbeck: Im Vorfrühling, 1896 (Öl auf Leinwand) Perspektive Inhalt: Franziska Hell Arbeitsblatt Fritz Overbeck (1869-1909) gehört zu den Gründungsvätern
Zeichnen in der Gartengestaltung
 Daniel Nies Zeichnen in der Gartengestaltung 2., erweiterte Auflage 70 Das zweidimensionale Bild Lageplan-Grafik In diesem Teil befassen wir uns mit der zweidimensiona len Darstellung der Gestaltungsidee.
Daniel Nies Zeichnen in der Gartengestaltung 2., erweiterte Auflage 70 Das zweidimensionale Bild Lageplan-Grafik In diesem Teil befassen wir uns mit der zweidimensiona len Darstellung der Gestaltungsidee.
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
5A. Von der Perspektive zu den projektiven Ebenen.
 5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
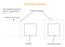 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Thema Geometrie Räumliche Vorstellung
 Seite 1 1. Drei-Tafel-Projektion Eine wunderbar einfache Visualisierungsmöglichkeit der 3-Tafel-Projektion besteht im entsprechenden Falten eines DIN-A 4 Blattes. Hier besteht einerseits die Möglichkeit
Seite 1 1. Drei-Tafel-Projektion Eine wunderbar einfache Visualisierungsmöglichkeit der 3-Tafel-Projektion besteht im entsprechenden Falten eines DIN-A 4 Blattes. Hier besteht einerseits die Möglichkeit
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien. Tutorial 02. Zentralperspektive Rekonstruktion
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial 02 Zentralperspektive Rekonstruktion Um ein perspektives Bild zu rekonstruieren, dh. die realen Abmessungen eines dreidimensionalen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial 02 Zentralperspektive Rekonstruktion Um ein perspektives Bild zu rekonstruieren, dh. die realen Abmessungen eines dreidimensionalen
Bildnerisches Gestalten
 Anzahl der Lektionen Bildungsziel Bildnerische Gestaltung ist Teil der Kultur. Sie visualisiert und verknüpft individuelle und gesellschaftliche Inhalte. Sie ist eine Form der Kommunikation und setzt sich
Anzahl der Lektionen Bildungsziel Bildnerische Gestaltung ist Teil der Kultur. Sie visualisiert und verknüpft individuelle und gesellschaftliche Inhalte. Sie ist eine Form der Kommunikation und setzt sich
Bild 1: Gegeben ist der in der Zentralperspektive zentrale Fluchtpunkt, der Distanzpunkt und der Grundriss des zu zeichnenden Vierecks.
 Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Raum Zeich(n)en. 1. Zeichnen heißt Vereinfachen
 1 1. Zeichnen heißt Vereinfachen Zeichnen heißt Vereinfachen Diese einfache Skizze zeigt, worauf es beim Raumzeichnen ankommt: Hilfslinien (Mittelachsen vertikal und horizontal) erleichtern die Übertragung
1 1. Zeichnen heißt Vereinfachen Zeichnen heißt Vereinfachen Diese einfache Skizze zeigt, worauf es beim Raumzeichnen ankommt: Hilfslinien (Mittelachsen vertikal und horizontal) erleichtern die Übertragung
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Unmögliche Figuren perspektivisches Zeichnen:
 Unmögliche Figuren perspektivisches Zeichnen: Kompetenzen: Die Schüler/innen sollen Ein quaderförmiges Werkstück in der Schrägbildperspektive darstellen und bemaßen können. Ein Werkstück mit veränderter
Unmögliche Figuren perspektivisches Zeichnen: Kompetenzen: Die Schüler/innen sollen Ein quaderförmiges Werkstück in der Schrägbildperspektive darstellen und bemaßen können. Ein Werkstück mit veränderter
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Was sagt der Totenschdel? Das komplette Material finden Sie hier:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Was sagt der Totenschdel? Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT - Malerei interpretieren lernen Seite
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Was sagt der Totenschdel? Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT - Malerei interpretieren lernen Seite
Malen für Anfänger: Erste Grundlagen. Farbe
 Malen für Anfänger: Erste Grundlagen Die unten angeführten ersten Grundlagen sind Ihnen bereits aus Ihrer Schulzeit bekannt. Bitte wiederholen Sie die Informationen. Die Arbeitsaufträge sind auszuführen
Malen für Anfänger: Erste Grundlagen Die unten angeführten ersten Grundlagen sind Ihnen bereits aus Ihrer Schulzeit bekannt. Bitte wiederholen Sie die Informationen. Die Arbeitsaufträge sind auszuführen
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Prüfungsfach: Methoden der Darstellung Termin: 13. September 2013 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.30 Uhr 11.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
Hans Walser. Raumgeometrie. Modul 5 Projektionen
 Hans Walser Raumgeometrie Modul 5 Projektionen Hans Walser: Modul 5, Projektionen ii Inhalt 1 Schatten und Bilder... 1 1.1 Eigenschatten und Schlagschatten... 1 1.2 Eigenschattengrenze?... 2 1.3 Schatten
Hans Walser Raumgeometrie Modul 5 Projektionen Hans Walser: Modul 5, Projektionen ii Inhalt 1 Schatten und Bilder... 1 1.1 Eigenschatten und Schlagschatten... 1 1.2 Eigenschattengrenze?... 2 1.3 Schatten
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
1. Licht, Lichtausbreitung, Schatten, Projektion
 1. Licht, Lichtausbreitung, Schatten, Projektion Was ist Licht? Definition: Die Optik ist das Gebiet der Physik, das sich mit dem Licht befasst. Der Begriff aus dem Griechischen bedeutet Lehre vom Sichtbaren.
1. Licht, Lichtausbreitung, Schatten, Projektion Was ist Licht? Definition: Die Optik ist das Gebiet der Physik, das sich mit dem Licht befasst. Der Begriff aus dem Griechischen bedeutet Lehre vom Sichtbaren.
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 25. August 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 16.00 Uhr 17.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 25. Februar 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 10.00 Uhr 11.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
Dreiecke, Quadrate, Rechtecke, Kreise erkennen und benennen Würfel, Quader, Kugeln erkennen und benennen
 Geometrie Ich kann... Formen und Körper erkennen und beschreiben Dreiecke, Quadrate, Rechtecke, Kreise erkennen und benennen Würfel, Quader, Kugeln erkennen und benennen Symmetrien in Figuren erkennen
Geometrie Ich kann... Formen und Körper erkennen und beschreiben Dreiecke, Quadrate, Rechtecke, Kreise erkennen und benennen Würfel, Quader, Kugeln erkennen und benennen Symmetrien in Figuren erkennen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Grundschraffur Metalle feste Stoffe Gase. Kunststoffe Naturstoffe Flüssigkeiten
 Anleitung für Schraffuren beim Zeichnen Die Bezeichnung Schraffur leitet sich von dem italienischen Verb sgraffiare ab, was übersetzt etwa soviel bedeutet wie kratzen und eine Vielzahl feiner, paralleler
Anleitung für Schraffuren beim Zeichnen Die Bezeichnung Schraffur leitet sich von dem italienischen Verb sgraffiare ab, was übersetzt etwa soviel bedeutet wie kratzen und eine Vielzahl feiner, paralleler
4^ Springer Vieweg. Geometrische Grundlagen der Architekturdarstellung. Cornelie Leopold. 5V überarbeitete und erweiterte Auflage.
 Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
Cornelie Leopold Geometrische Grundlagen der Architekturdarstellung 5V überarbeitete und erweiterte Auflage Unter Mitwirkung von Andreas Matievits 4^ Springer Vieweg Affinität INHALTSVERZEICHNIS Vorwort
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Fotografieren mit der Digitalkamera
 Fotografieren mit der Digitalkamera 1 Zielsetzung Näher ran! Grundsätzlich sollte man sich bei jedem Bild überlegen, wozu man es aufnimmt: Familienfotos für kleine Ausdrucke? Bilder zum Verschicken? Produktfotos
Fotografieren mit der Digitalkamera 1 Zielsetzung Näher ran! Grundsätzlich sollte man sich bei jedem Bild überlegen, wozu man es aufnimmt: Familienfotos für kleine Ausdrucke? Bilder zum Verschicken? Produktfotos
Gebrochener Stab. Martin Lieberherr Mathematisch Naturwissenschaftliches Gymnasium Rämibühl, 8001 Zürich
 Gebrochener Stab Martin Lieberherr Mathematisch Naturwissenschaftliches Gymnasium Rämibühl, 8001 Zürich Einleitung Hält man einen geraden Wanderstab in einen spiegelglatten, klaren Bergsee, so schaut der
Gebrochener Stab Martin Lieberherr Mathematisch Naturwissenschaftliches Gymnasium Rämibühl, 8001 Zürich Einleitung Hält man einen geraden Wanderstab in einen spiegelglatten, klaren Bergsee, so schaut der
Optische Täuschungen Jacqueline Musil , A
 Optische Täuschungen Jacqueline Musil 0401823, A 190 445 299 Optische Täuschungen Wahrnehmungstäuschungen Gestaltpsychologie Optische Täuschungen / Visuelle Illusionen Gestaltpsychologie Die Gestalt (Das
Optische Täuschungen Jacqueline Musil 0401823, A 190 445 299 Optische Täuschungen Wahrnehmungstäuschungen Gestaltpsychologie Optische Täuschungen / Visuelle Illusionen Gestaltpsychologie Die Gestalt (Das
G1.02 In jedes der drei Muster hat sich ein Fehler eingeschlichen. Kennzeichne diesen, indem du den Bereich mit roter Farbe einringelst!
 1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
1 Muster (Teil 1) G1.01 Vervollständige das Muster, sodass der gesamte Raster ausgefüllt ist! Verwende dazu ein Geodreieck und einen gespitzten Bleistift oder einen Druckbleistift mit einer 0,5 mm HB-Mine
2.3 Linienarten und Linienbreiten nach DIN 15 T1
 Angebots- Zeichnung Fundament- Zeichnung Zeichnung zur Erläuterung einer Ausschreibung oder zur Abgabe eines Angebotes Enthält Angaben über die Fertigung des Fundamentes für die Aufstellung der Maschine
Angebots- Zeichnung Fundament- Zeichnung Zeichnung zur Erläuterung einer Ausschreibung oder zur Abgabe eines Angebotes Enthält Angaben über die Fertigung des Fundamentes für die Aufstellung der Maschine
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Projektionen von geometrischen Objekten
 Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Optische Phänomene. Hier täuscht uns die Perspektive und die Gewohnheit. Der kleine Junge ist eigentlich genauso groß wie der ältere Herr.
 Optische Phänomene Der Strahlenförmige Verlauf lässt den linken Würfel kleiner erscheinen als den rechten. Der Effekt wurde von einigen Malern zu Beginn der Renaissance in Italien aufgegriffen um durch
Optische Phänomene Der Strahlenförmige Verlauf lässt den linken Würfel kleiner erscheinen als den rechten. Der Effekt wurde von einigen Malern zu Beginn der Renaissance in Italien aufgegriffen um durch
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Kornflakes und räumliche Darstellung - Technisches Zeichnen - Teil 2
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Kornflakes und räumliche Darstellung - Technisches Zeichnen - Teil 2 Das komplette Material finden Sie hier: School-Scout.de 2.21
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Kornflakes und räumliche Darstellung - Technisches Zeichnen - Teil 2 Das komplette Material finden Sie hier: School-Scout.de 2.21
Stundenbild Unmögliche Figuren
 Stundenbild Unmögliche Figuren Schulform: Gymnasium, 7. Klasse. Pflichtfach Psychologie. Klassengröße: 25 Schüler. Lehrplanbezug: Aspekte der Sinneswahrnehmung, der räumlichen und zeitlichen Wahrnehmung
Stundenbild Unmögliche Figuren Schulform: Gymnasium, 7. Klasse. Pflichtfach Psychologie. Klassengröße: 25 Schüler. Lehrplanbezug: Aspekte der Sinneswahrnehmung, der räumlichen und zeitlichen Wahrnehmung
Körper erkennen und beschreiben
 Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Grundsätzliche Konstruktionshilfen:
 Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Der Satz von Gérard Desargues
 2008 Jens Scherdin Andreas Meyburg Universität Bremen Juni 2008 Der Satz von Gérard Desargues Veranstaltung: Geometrie Seminarleiter: Dr. Reimund Albers Bearbeiter: Andreas Meyburg, Matrikel-Nr.: 2172110
2008 Jens Scherdin Andreas Meyburg Universität Bremen Juni 2008 Der Satz von Gérard Desargues Veranstaltung: Geometrie Seminarleiter: Dr. Reimund Albers Bearbeiter: Andreas Meyburg, Matrikel-Nr.: 2172110
RaumZeich(n)en Zeichnerische Raumerfahrungen
 RaumZeich(n)en Zeichnerische Raumerfahrungen Entwickelt aus einem Unterrichtsprojekt 6 ab, SS 2005 Regina Öschlberger (Architektin), Peter Haas, Wolfgang Richter, Thomas Stadler Privatgymnasium der Herz-Jesu-Missionare,
RaumZeich(n)en Zeichnerische Raumerfahrungen Entwickelt aus einem Unterrichtsprojekt 6 ab, SS 2005 Regina Öschlberger (Architektin), Peter Haas, Wolfgang Richter, Thomas Stadler Privatgymnasium der Herz-Jesu-Missionare,
A K K O M M O D A T I O N
 biologie aktiv 4/Auge/Station 2/Lösung Welche Teile des Auges sind von außen sichtbar? Augenbraue, Augenlid, Wimpern, Pupille, Iris, Lederhaut, Hornhaut (durchsichtiger Bereich der Lederhaut) Leuchte nun
biologie aktiv 4/Auge/Station 2/Lösung Welche Teile des Auges sind von außen sichtbar? Augenbraue, Augenlid, Wimpern, Pupille, Iris, Lederhaut, Hornhaut (durchsichtiger Bereich der Lederhaut) Leuchte nun
Physik-Prüfung. vom 4. Oktober Lichtausbreitung, Schatten
 Physik-Prüfung vom 4. Oktober 2011 Lichtausbreitung, Schatten Hinweise und Modalitäten: - Beginnen Sie erst mit der Prüfung, wenn das Zeichen dafür gegeben wurde. - Erlaubte Hilfsmittel: Papier, Schreibzeug,
Physik-Prüfung vom 4. Oktober 2011 Lichtausbreitung, Schatten Hinweise und Modalitäten: - Beginnen Sie erst mit der Prüfung, wenn das Zeichen dafür gegeben wurde. - Erlaubte Hilfsmittel: Papier, Schreibzeug,
Kartenverwandte Ausdrucksformen
 Kartenverwandte Ausdrucksformen 612 440 VU Karel Kriz Institut für Geographie und Regionalforschung Kartographie und Geoinformation Universität Wien Ebene kartenverwandte Darstellungen Art der Projektion
Kartenverwandte Ausdrucksformen 612 440 VU Karel Kriz Institut für Geographie und Regionalforschung Kartographie und Geoinformation Universität Wien Ebene kartenverwandte Darstellungen Art der Projektion
Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV)
 Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV) 1. Schülerleistungen 2. Darstellenden Geometrie und RVV im MU 3. Fachliche und begriffliche Probleme 4. Ergebnisse
Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV) 1. Schülerleistungen 2. Darstellenden Geometrie und RVV im MU 3. Fachliche und begriffliche Probleme 4. Ergebnisse
5. Optische Täuschungen
 5. Hat der Betrachter den Eindruck, es besteht ein Unterschied zwischen dem was er sieht und dem was er vor sich hat, spricht er von einer optischen Täuschung. So stellen optische Täuschungen die Ansicht
5. Hat der Betrachter den Eindruck, es besteht ein Unterschied zwischen dem was er sieht und dem was er vor sich hat, spricht er von einer optischen Täuschung. So stellen optische Täuschungen die Ansicht
8. Projektionsarten und Perspektive
 8. Projektionsarten un Perspektive Projektionen: transformieren 3D-Objekte in 2D-Biler (mathematisch: lineare Abb., aber nicht bijektiv ugehörige Matri singulär,.h. Determinante ) Projektion ist Grunaufgabe
8. Projektionsarten un Perspektive Projektionen: transformieren 3D-Objekte in 2D-Biler (mathematisch: lineare Abb., aber nicht bijektiv ugehörige Matri singulär,.h. Determinante ) Projektion ist Grunaufgabe
Grundregeln der Perspektive und ihre elementargeometrische Herleitung
 Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Arena Medien. Fotoguide
 Arena Medien Fotoguide 1 Inhaltsverzeichnis 1. Blende und Zeit... Seite 3 2. Format..Seite 5 3. Ausschnitt Seite 6 4. Kameraperspektive..Seite 7 5. Tiefenschärfe...Seite 9 6. Beleuchtung...Seite 11 2 Blende
Arena Medien Fotoguide 1 Inhaltsverzeichnis 1. Blende und Zeit... Seite 3 2. Format..Seite 5 3. Ausschnitt Seite 6 4. Kameraperspektive..Seite 7 5. Tiefenschärfe...Seite 9 6. Beleuchtung...Seite 11 2 Blende
5. Sitzung Propädeutikum - Einführung in die Kunstwissenschaften und ihre Methoden (Propädeutikum)
 Propädeutikum - Einführung in die Kunstwissenschaften und ihre Methoden (Propädeutikum) Oliver Müller, M.A. SEMINAR Montag, 16:15 17:45 Raum 103/104, Villa Neuwerk 7 5. Sitzung 26.11.2018 Eine erste
Propädeutikum - Einführung in die Kunstwissenschaften und ihre Methoden (Propädeutikum) Oliver Müller, M.A. SEMINAR Montag, 16:15 17:45 Raum 103/104, Villa Neuwerk 7 5. Sitzung 26.11.2018 Eine erste
Abstand etwa 7cm. Zwei Waagerechten werden gezeichnet (parallel zum Blattrand). Abstand etwa 7cm. Seite 1
 Um auf einem A4-Blatt einen Raum in der Einpunktperspektive zu zeichnen, werden zuerst die Flächen für den Fußboden, die Wände und die Decke festgelegt. Dazu sind folgende Schritte von Seite 1 bis Seite
Um auf einem A4-Blatt einen Raum in der Einpunktperspektive zu zeichnen, werden zuerst die Flächen für den Fußboden, die Wände und die Decke festgelegt. Dazu sind folgende Schritte von Seite 1 bis Seite
D a r s t e l l u n g s g r u n d l a g e n a m L e h r s t u h l G D A Perspektive konstruieren
 D a r s t e l l u n g s g r u n d l a g e n a m L e h r s t u h l G D A Perspektive konstruieren T u t o r i u m s h e f t N o. I I Technische Universität Dortmund Lehrstuhl Grundlagen der Architektur
D a r s t e l l u n g s g r u n d l a g e n a m L e h r s t u h l G D A Perspektive konstruieren T u t o r i u m s h e f t N o. I I Technische Universität Dortmund Lehrstuhl Grundlagen der Architektur
Darstellende Geometrie Übungen. Tutorial 06. Übungsblatt: Schatten - Perspektive 04. Wohnhaus
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Anamorphosen Jürgen Becker: Anamorphosen 1
 Anamorphosen 2010 Jürgen Becker: Anamorphosen 1 Anamorphosen 2010 Jürgen Becker: Anamorphosen 2 Anamorphosen - Definition Anamorphosen sind Bilder, die auf eine bestimmte Art verzerrt worden sind, so dass
Anamorphosen 2010 Jürgen Becker: Anamorphosen 1 Anamorphosen 2010 Jürgen Becker: Anamorphosen 2 Anamorphosen - Definition Anamorphosen sind Bilder, die auf eine bestimmte Art verzerrt worden sind, so dass
Projektion. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
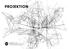 Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Anschauliche Parallelrisse und Hauptrisse
 Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Die Zentral-Perspektive & deren [Innen-]Raumwirkung
![Die Zentral-Perspektive & deren [Innen-]Raumwirkung Die Zentral-Perspektive & deren [Innen-]Raumwirkung](/thumbs/50/27002574.jpg) Arch. Bmstr. DI URSULA ENDER www.atelierender.at Mai 2012 Die Zentral-Perspektive & deren [Innen-]Raumwirkung Perspektive verstehen, anwenden und die Raumwirkung spielerisch manipulieren. 1. Begriffserklärung
Arch. Bmstr. DI URSULA ENDER www.atelierender.at Mai 2012 Die Zentral-Perspektive & deren [Innen-]Raumwirkung Perspektive verstehen, anwenden und die Raumwirkung spielerisch manipulieren. 1. Begriffserklärung
Praktikum Schau Geometrie
 Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Architektur-Fotografie
 Architektur-Fotografie Überblick Günther Keil, 26.2.2007 Grundlagen Architektur-Fotografie Abbildung von Bauwerken Eher in der Totalen als im Detail: 1 Foto statt einer Serie Dokumentarisches Erfassen
Architektur-Fotografie Überblick Günther Keil, 26.2.2007 Grundlagen Architektur-Fotografie Abbildung von Bauwerken Eher in der Totalen als im Detail: 1 Foto statt einer Serie Dokumentarisches Erfassen
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Zentral- und parallelprojektive Darstellungen in Cabri 3D
 Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Schaffenswelten Kunst: Mit Drer durch die Renaissance
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Schaffenswelten Kunst: Mit Drer durch die Renaissance Das komplette Material finden Sie hier: School-Scout.de Thema: Schaffenswelten
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Schaffenswelten Kunst: Mit Drer durch die Renaissance Das komplette Material finden Sie hier: School-Scout.de Thema: Schaffenswelten
Die nachfolgenden Bildbeispiele wurden mit Windows 7 und Photoshop Elements 8 erstellt.
 2 Die nachfolgenden Bildbeispiele wurden mit Windows 7 und Photoshop Elements 8 erstellt. Seite / Thema 3 Ordner und Dateien öffnen 4 Kontrast mindern mit Tiefen/Lichter 5 Kontrast erhöhen mit Tonwertkorrektur
2 Die nachfolgenden Bildbeispiele wurden mit Windows 7 und Photoshop Elements 8 erstellt. Seite / Thema 3 Ordner und Dateien öffnen 4 Kontrast mindern mit Tiefen/Lichter 5 Kontrast erhöhen mit Tonwertkorrektur
Experimente. mit Licht cc Corinna Burtscher. Name: Klasse:
 F ORSCHERTAGEBUCH Experimente mit Licht Name: Klasse: Forscherauftrag Nr. 1 Kann eine gespiegelte Lampe Schatten werfen? 1 Spiegel 1 Kerze 1 beliebiger Gegenstand Spiegel 1. Stelle in einem dunklen Raum
F ORSCHERTAGEBUCH Experimente mit Licht Name: Klasse: Forscherauftrag Nr. 1 Kann eine gespiegelte Lampe Schatten werfen? 1 Spiegel 1 Kerze 1 beliebiger Gegenstand Spiegel 1. Stelle in einem dunklen Raum
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Am einfachsten bekommt man einen Körper durch Aufklappen in eine Ebene.
 Grraphiische Darrsttellllung Netz eines Körpers Wie kommtt ein Körrperr auffs Papierr? Am einfachsten bekommt man einen Körper durch Aufklappen in eine Ebene. Beispiel. Netz eines Würfels Aufgabe. Zu welchem
Grraphiische Darrsttellllung Netz eines Körpers Wie kommtt ein Körrperr auffs Papierr? Am einfachsten bekommt man einen Körper durch Aufklappen in eine Ebene. Beispiel. Netz eines Würfels Aufgabe. Zu welchem
Inhalt. Einleitung Eine kleine Einführung in die Optik Der 30 Grad-Blickwinkel und die Seitenansicht Der Abstandspunkt 15 19
 Inhalt Einleitung 06-07 Eine kleine Einführung in die Optik 08 11 Der 30 Grad-Blickwinkel und die Seitenansicht 12 14 Der Abstandspunkt 15 19 Der Betrachter in der Draufsicht 20 21 Die Konstruktion eines
Inhalt Einleitung 06-07 Eine kleine Einführung in die Optik 08 11 Der 30 Grad-Blickwinkel und die Seitenansicht 12 14 Der Abstandspunkt 15 19 Der Betrachter in der Draufsicht 20 21 Die Konstruktion eines
Einführung in die Grundlagen des Technischen Zeichnens: Thema dieser Präsentation: Die Parallelprojektion
 Einführung in die Grundlagen des Technischen Zeichnens: Thema dieser Präsentation: Die Parallelprojektion 1. Was ist eine Projektion? 2. Alles Ansichtssache!? 3. Isometrische Projektion 4. Kabinett-Projektion
Einführung in die Grundlagen des Technischen Zeichnens: Thema dieser Präsentation: Die Parallelprojektion 1. Was ist eine Projektion? 2. Alles Ansichtssache!? 3. Isometrische Projektion 4. Kabinett-Projektion
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
Farbe. 6. Welche Farben hat es alles auf Deinem Bild? Lege die Karte weg und versuche aus der Erinnerung die Farben aus den
 Farbe 1. Betrachtet den Farbkreis. Nehmt die Kreisel und lasst die Grundfarben kreisen. Was ergibt sich aus rot und blau? Was ergibt sich aus gelb und rot? Was ergibt sich aus blau und gelb? 2. Nehmt eine
Farbe 1. Betrachtet den Farbkreis. Nehmt die Kreisel und lasst die Grundfarben kreisen. Was ergibt sich aus rot und blau? Was ergibt sich aus gelb und rot? Was ergibt sich aus blau und gelb? 2. Nehmt eine
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
18.7 Übungen Übungen 341
 18.7 Übungen 341 18.7 Übungen 18.1 Skizzieren Sie die dargestellten Körper (freihand) in Vorder-, Seiten- und Draufsicht. Wenn Sie Schwierigkeiten mit der räumlichen Vorstellung haben, bauen Sie die Körper
18.7 Übungen 341 18.7 Übungen 18.1 Skizzieren Sie die dargestellten Körper (freihand) in Vorder-, Seiten- und Draufsicht. Wenn Sie Schwierigkeiten mit der räumlichen Vorstellung haben, bauen Sie die Körper
