Aufgabe 2.1. Ergebnis, Ergebnismenge, Ereignis
|
|
|
- Detlef Feld
- vor 8 Jahren
- Abrufe
Transkript
1 Aufgabe 2. Ergebnis, Ergebnismenge, Ereignis
2 Ergebnis und Ergebnismenge Vorgänge mit zufälligem Ergebnis, oft Zufallsexperiment genannt Bei der Beschreibung der Ergebnisse wird stets ein bestimmtes Merkmal des Zufallsexperiments benannt. Zufallsexperiment Merkmal Ergebnisse Hochsprung von Schülern Ziehen von Kugeln aus Urne Werfen einer Münze Werfen eines Würfels Kontrolle einer Bonbontüte Sprunghöhe Lage der Oberseite der Münze Höhen zwischen 0,75m und,70 m gelb, grün, blau 24,25,26,27,28
3 Beispiel: Würfeln mit einem Würfel Mögliche Ergebnismenge, je nach Fragestellung: Ω = {,2,3,4,5,6, Ecke, Kante} Die Ergebnismenge Ω (sprich: Omega ) enthält alle möglichen Ergebnisse eines Zufallsexperiments. Ω 2 = {,2,3,4,5,6} Ω 3 = {6, keine 6} Ω 4 = {gerade, ungerade Augenzahl} Welche Ergebnismenge erscheint am geeignetsten - d. h. nicht zu grob und ohne überflüssige Ergebnisse - für die Frage nach der Wahrscheinlichkeit einer Augenzahl? Begründe.
4 Die Ergebnisse sind also die Elemente der Ergebnismenge. Sie sollen höchstens einmal in Ω vorkommen. Keine Ergebnismenge: Ω = {gerade Zahlen oder Primzahlen kleiner gleich 6} Warum?
5 Nenne einen geeigneten Ergebnisraum für die folgenden Zufallsexperimente:. Würfeln eines Tetraeders mit den Augenzahlen,2,3 und Beim Werfen zweier Tetraederwürfels ( zweistufiges Zufallsexperiment ) bietet jemand folgende Ergebnismengen an: Bemerkung: Das Ergebnis (3 4) bedeutet, dass im ersten Wurf eine 3 und im zweiten Wurf eine 4 gewürfelt wird. Ω = {( );( 2),( 3),( 4), (2 );(2 2),(2 3),(2 4),(3 );(3 2),(3 3),(3 4),(4 );(4 2),(4 3),(4 4)} Ω 2 = {( );( 2),( 3),( 4),(2 2),(2 3),(2 4),(3 3),(3 4),(4 4)} Ω 2 = {Augensumme größer als und kleiner als 9} Welches sind Ergebnismengen des Experiments? 3. In einer Klinik wir eine Statistik über das Geschlecht der Neugeborenen geführt. a) Einzelkinder b) eineiige Zwillinge c) zweieiige Zwillinge
6 Aufgaben. Bei einem Wettrennen starten die vier Personen A,B,C und D. Man geht davon aus, dass alle Läufer zu verschiedenen Zeiten das Ziel passieren. a) Nenne die verschiedenen Einlaufreihenfolgen. Wie viele sind es? b) Gib die Ergebnismenge Ω an, wenn nur der. Sieger interessiert. c) Gib die Ergebnismenge Ω 2 an, wenn nur der. und 2. Sieger festgestellt werden soll. 2. Die drei Triebwerke eines Flugzeugs werden getestet. Gib die Ergebnismenge an, wenn interessiert, a) wie viele b) welche Triebwerke nicht einwandfrei laufen. 3. In einem Land gibt es vier politische Parteien. A, B, C und D. Welche der Mengen sind mögliche Ergebnismengen zu der Umfrage: Welche Partei würden Sie wählen, wenn morgen Wahltag wäre? a) {A;B;C;D; keine} b) {A; B oder C; keine} c) {A;sonstige; keine} d) {A oder B}
7 Aufgaben. Bei einem Wettrennen starten die vier Personen A,B,C und D. Man geht davon aus, dass alle Läufer zu verschiedenen Zeiten das Ziel passieren. a) Nenne die verschiedenen Einlaufreihenfolgen. Wie viele sind es? b) Gib die Ergebnismenge Ω an, wenn nur der. Sieger interessiert. c) Gib die Ergebnismenge Ω 2 an, wenn nur der. und 2. Sieger festgestellt werden soll. 2. Die drei Triebwerke eines Flugzeugs werden getestet. Gib die Ergebnismenge an, wenn interessiert, a) wie viele b) welche Triebwerke nicht einwandfrei laufen. 3. In einem Land gibt es vier politische Parteien. A, B, C und D. Welche der Mengen sind mögliche Ergebnismengen zu der Umfrage: Welche Partei würden Sie wählen, wenn morgen Wahltag wäre? a) {A;B;C;D; keine} b) {A; B oder C; keine} c) {A;sonstige; keine} d) {A oder B}
8 Ereignis Jede Teilmenge von Ω heißt Ereignis. Beispiel: Einmaliges Würfeln mit Ω = {,2,3,4,5,6} E: gerade Augenzahl E = {2;4;6}
9 Besondere Ereignisse Enthält ein Ereignis nur ein Ergebnis, so nennt man es Elementareignis Ω heißt sicheres Ereignis Die leere Menge {} oder heißt das unmögliche Ereignis Beispiel: E ={6} Wähle ich Ω ={,2,3,4,5,6} so betrachte ich es als sicher, dass eine der 6 Zahlen der Menge gewürfelt wird. Ich betrachte es als unmöglich, keine der 6 Zahlen zu würfeln.
10 Aufgaben. Zwei Freunde spielen das Knobelspiel Schere (S), Stein (St), Papier (P) Notiere die Ergebnismenge Ω, das sichere und das unmögliche Ereignis sowie die Ereignisse E und E 2 mit E : Erster Spieler gewinnt, E 2 : Keiner gewinnt. 2. Gib die Mengen an, die folgende Ereignisse beim zweimaligen Würfeln mit dem Tetraeder beschreiben: E : Pasch, E 2 : Augensumme gerade, E 3 : Erste Augenzahl kleiner als zweite
11 Verknüpfung von Ereignissen Ereignisse sind Mengen. Verknüpfungen von Mengen: Schnittmenge von A und B: A B A und B Vereinigungsmenge von A und B: A B A oder B Komplementärmenge von A: A nicht A Stelle für das Würfeln mit einem Würfel die Schnittund Vereinigungsmenge von A: Augenzahl prim und B: Augenzahl höchstens 4 dar. Nenne auch die Komplementärmengen zu A und B.
12 Aufgabe Auf Karins Schulweg gibt es drei Ampeln, die unabhängig voneinander den Verkehr regeln. Katrin muss sie alle drei passieren. a) Nenne die Ergebnismenge Ω für die Möglichkeiten der Ampelschaltungen, falls nur Rot und Grün beachtet werden soll. b) Gib die folgenden Ereignisse an. A: Alle Ampeln zeigen die gleiche Farbe. B: Die erste Ampel zeigt Rot. C: Die zweite Ampel zeigt Rot. D: Höchstens eine Ampel zeigt Rot. c) Notiere die folgenden Ereignisse und beschreibe sie verbal: R = B C, S = B C, T = A C, U = D, V = A C
13 Laplace-Experimente a) Werft in Gruppenarbeit zwei Münzen mit den Prägungen Kopf und Zahl und notiert die relativen Häufigkeiten nach 200-maligem Werfen für die Ereignisse E : beide Kopf, E 2 : beide Zahl und E 3 : unterschiedliche Prägung Ereignisse E E 2 E 3 relative Häufigkeit h 200 (E)
14 Laplace-Experimente b) Einigen Schülern ist es zu langweilig, die Würfe durchzuführen. Sie wollen lieber durch Berechnungen, den Ausfall des Zufallsexperiments vorhersagen. Sie schlagen folgende Modelle zur Beschreibung des Versuchs vor: Ω = {beide Kopf, beide Zahl, unterschiedlich} Ereignisse beide Kopf beide Zahl unterschiedlich Wahrscheinlichkeit P(E) Ereignisse beide Kopf beide Zahl unterschiedlich Ω 2 = Ω Wahrscheinlichkeit P(E) Ω 3 = {(K K),(Z Z),(Z K),(K Z)} Ereignisse (K K) (Z Z) (Z K) (K Z) Wahrscheinlichkeit P(E)
15 Aufgabe (Fortsetzung) Vergleicht mit den relativen Häufigkeiten aus a) und beschreibt, welche Modelle das Zufallsexperiment tatsächlich widerspiegeln. Welche Ergebnismenge ist zur Berechnung der Wahrscheinlichkeiten am geeignetsten? Begründet.
16 Laplace-Experiment Ein Zufallsexperiment, dessen Ergebnisse als gleichwahrscheinlich angenommen werden, heißt Laplace-Experiment.
Übungsaufgaben Wahrscheinlichkeit
 Übungsaufgaben Wahrscheinlichkeit Aufgabe 1 (mdb500405): In einer Urne befinden sich gelbe (g), rote (r), blaue (b) und weiße (w) Kugel (s. Bild). Ohne Hinsehen sollen aus der Urne in einem Zug Kugeln
Übungsaufgaben Wahrscheinlichkeit Aufgabe 1 (mdb500405): In einer Urne befinden sich gelbe (g), rote (r), blaue (b) und weiße (w) Kugel (s. Bild). Ohne Hinsehen sollen aus der Urne in einem Zug Kugeln
15.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit
 5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
y 1 2 3 4 5 6 P (Y = y) 1/6 1/6 1/6 1/6 1/6 1/6
 Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Statistik für Prüfungskandidaten und Prüfungskandidatinnen Unabhängigkeit
Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Statistik für Prüfungskandidaten und Prüfungskandidatinnen Unabhängigkeit
Kugel-Fächer-Modell. 1fach. 3fach. Für die Einzelkugel gibt es 3 Möglichkeiten. 6fach. 3! Möglichkeiten
 Kugel-Fächer-Modell n Kugeln (Rosinen) sollen auf m Fächer (Brötchen) verteilt werden, zunächst 3 Kugeln auf 3 Fächer. 1fach 3fach Für die Einzelkugel gibt es 3 Möglichkeiten } 6fach 3! Möglichkeiten Es
Kugel-Fächer-Modell n Kugeln (Rosinen) sollen auf m Fächer (Brötchen) verteilt werden, zunächst 3 Kugeln auf 3 Fächer. 1fach 3fach Für die Einzelkugel gibt es 3 Möglichkeiten } 6fach 3! Möglichkeiten Es
Bei vielen Zufallsexperimenten interessiert man sich lediglich für das Eintreten bzw. das Nichteintreten eines bestimmten Ereignisses.
 XI. Binomialverteilung ================================================================== 11.1 Definitionen -----------------------------------------------------------------------------------------------------------------
XI. Binomialverteilung ================================================================== 11.1 Definitionen -----------------------------------------------------------------------------------------------------------------
 Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
R. Brinkmann http://brinkmann-du.de Seite 1 30.11.2013 Schriftliche Übung Mathematik Stochastik II (Nachschreiber) Jan. 2007
 R. Brinkmann http://brinkmann-du.de Seite 1 30.11.2013 Schriftliche Übung Mathematik Stochastik II (Nachschreiber) Jan. 2007 SG15/25D NAME: Lösungen 1. In einer Packung sind Glühbirnen, davon sind zwei
R. Brinkmann http://brinkmann-du.de Seite 1 30.11.2013 Schriftliche Übung Mathematik Stochastik II (Nachschreiber) Jan. 2007 SG15/25D NAME: Lösungen 1. In einer Packung sind Glühbirnen, davon sind zwei
Wahrscheinlichkeit Klasse 8 7
 7 Wahrscheinlichkeit Klasse 8 Ereignisse Seite 8 a) Ω {Herz 7; Herz 8; Herz 9; Herz 0; Herz Unter; Herz Ober; Herz König; Herz Ass; Eichel 7; Eichel 8; Eichel 9; Eichel 0; Eichel Unter; Eichel Ober; Eichel
7 Wahrscheinlichkeit Klasse 8 Ereignisse Seite 8 a) Ω {Herz 7; Herz 8; Herz 9; Herz 0; Herz Unter; Herz Ober; Herz König; Herz Ass; Eichel 7; Eichel 8; Eichel 9; Eichel 0; Eichel Unter; Eichel Ober; Eichel
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
6 Mehrstufige zufällige Vorgänge Lösungshinweise
 6 Mehrstufige zufällige Vorgänge Lösungshinweise Aufgabe 6.: Begründen Sie, warum die stochastische Unabhängigkeit zweier Ereignisse bzw. zufälliger Vorgänge nur ein Modell der Realität darstellen kann.
6 Mehrstufige zufällige Vorgänge Lösungshinweise Aufgabe 6.: Begründen Sie, warum die stochastische Unabhängigkeit zweier Ereignisse bzw. zufälliger Vorgänge nur ein Modell der Realität darstellen kann.
P X =3 = 2 36 P X =5 = 4 P X =6 = 5 36 P X =8 = 5 36 P X =9 = 4 P X =10 = 3 36 P X =11 = 2 36 P X =12 = 1
 Übungen zur Stochastik - Lösungen 1. Ein Glücksrad ist in 3 kongruente Segmente aufgeteilt. Jedes Segment wird mit genau einer Zahl beschriftet, zwei Segmente mit der Zahl 0 und ein Segment mit der Zahl
Übungen zur Stochastik - Lösungen 1. Ein Glücksrad ist in 3 kongruente Segmente aufgeteilt. Jedes Segment wird mit genau einer Zahl beschriftet, zwei Segmente mit der Zahl 0 und ein Segment mit der Zahl
Melanie Kaspar, Prof. Dr. B. Grabowski 1
 7. Hypothesentests Ausgangssituation: Man muss sich zwischen 2 Möglichkeiten (=Hypothesen) entscheiden. Diese Entscheidung soll mit Hilfe von Beobachtungen ( Stichprobe ) getroffen werden. Die Hypothesen
7. Hypothesentests Ausgangssituation: Man muss sich zwischen 2 Möglichkeiten (=Hypothesen) entscheiden. Diese Entscheidung soll mit Hilfe von Beobachtungen ( Stichprobe ) getroffen werden. Die Hypothesen
(für Grund- und Leistungskurse Mathematik) 26W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP
 .RPELQDWRULN (für Grund- und Leistungsurse Mathemati) 6W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP Nach dem Studium dieses Sripts sollten folgende Begriffe beannt sein: n-menge, Kreuzprodut, n-tupel Zählprinzip
.RPELQDWRULN (für Grund- und Leistungsurse Mathemati) 6W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP Nach dem Studium dieses Sripts sollten folgende Begriffe beannt sein: n-menge, Kreuzprodut, n-tupel Zählprinzip
Übungen zur Mathematik für Pharmazeuten
 Blatt 1 Aufgabe 1. Wir betrachten den Ereignisraum Ω = {(i,j) 1 i,j 6} zum Zufallsexperiment des zweimaligem Würfelns. Sei A Ω das Ereignis Pasch, und B Ω das Ereignis, daß der erste Wurf eine gerade Augenzahl
Blatt 1 Aufgabe 1. Wir betrachten den Ereignisraum Ω = {(i,j) 1 i,j 6} zum Zufallsexperiment des zweimaligem Würfelns. Sei A Ω das Ereignis Pasch, und B Ω das Ereignis, daß der erste Wurf eine gerade Augenzahl
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Statuten in leichter Sprache
 Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Variationen Permutationen Kombinationen
 Variationen Permutationen Kombinationen Mit diesen Rechenregeln lässt sich die Wahrscheinlichkeit bestimmter Ereigniskombinationen von gleichwahrscheinlichen Elementarereignissen ermitteln, und erleichtert
Variationen Permutationen Kombinationen Mit diesen Rechenregeln lässt sich die Wahrscheinlichkeit bestimmter Ereigniskombinationen von gleichwahrscheinlichen Elementarereignissen ermitteln, und erleichtert
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Maristengymnasium Fürstenzell zuletzt geändert am 10.03.2001 Aufgaben zur Kombinatorik (mit Lösungen)
 Maristengymnasium Fürstenzell zuletzt geändert am 0.0.00 Aufgaben zur Kombinatorik (mit Lösungen) 0.. Wieviele Möglichkeiten gibt es für Kinder, sich auf einen Schlitten zu setzen, wenn ihn nur davon steuern
Maristengymnasium Fürstenzell zuletzt geändert am 0.0.00 Aufgaben zur Kombinatorik (mit Lösungen) 0.. Wieviele Möglichkeiten gibt es für Kinder, sich auf einen Schlitten zu setzen, wenn ihn nur davon steuern
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zufallsgrößen. Vorlesung Statistik für KW 29.04.2008 Helmut Küchenhoff
 Zufallsgrößen 2.5 Zufallsgrößen 2.5.1 Verteilungsfunktion einer Zufallsgröße 2.5.2 Wahrscheinlichkeits- und Dichtefunktion Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße Dichtefunktion einer
Zufallsgrößen 2.5 Zufallsgrößen 2.5.1 Verteilungsfunktion einer Zufallsgröße 2.5.2 Wahrscheinlichkeits- und Dichtefunktion Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße Dichtefunktion einer
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Gibt es einen Geschmacksunterschied zwischen Coca Cola und Cola Zero?
 Gibt es einen Geschmacksunterschied zwischen Coca Cola und Cola Zero? Manche sagen: Ja, manche sagen: Nein Wie soll man das objektiv feststellen? Kann man Geschmack objektiv messen? - Geschmack ist subjektiv
Gibt es einen Geschmacksunterschied zwischen Coca Cola und Cola Zero? Manche sagen: Ja, manche sagen: Nein Wie soll man das objektiv feststellen? Kann man Geschmack objektiv messen? - Geschmack ist subjektiv
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Linienland, Flächenland und der Hyperraum Ein Ausflug durch die Dimensionen
 Linienland, Flächenland und der Hyperraum Ein Ausflug durch die Dimensionen Stephan Rosebrock Pädagogische Hochschule Karlsruhe 23. März 2013 Stephan Rosebrock (Pädagogische Hochschule Linienland, Karlsruhe)
Linienland, Flächenland und der Hyperraum Ein Ausflug durch die Dimensionen Stephan Rosebrock Pädagogische Hochschule Karlsruhe 23. März 2013 Stephan Rosebrock (Pädagogische Hochschule Linienland, Karlsruhe)
Übungsaufgaben - Kombinatorik. Übungsaufgaben - Kombinatorik. Aufgabe 1 Schwierigkeit: X. Aufgabe 3 Schwierigkeit: X
 Aufgabe 1 Schwierigkeit: X Aufgabe 3 Schwierigkeit: X Einer Gruppe von 15 Schülern werden 3 Theaterkarten angeboten. Auf wie viele Arten können die Karten verteilt werden, wenn sich die Karten auf nummerierte
Aufgabe 1 Schwierigkeit: X Aufgabe 3 Schwierigkeit: X Einer Gruppe von 15 Schülern werden 3 Theaterkarten angeboten. Auf wie viele Arten können die Karten verteilt werden, wenn sich die Karten auf nummerierte
MATHEMATIK 3 STUNDEN. DATUM: 8. Juni 2009
 EUROPÄISCHES ABITUR 2009 MATHEMATIK 3 STUNDEN DATUM: 8. Juni 2009 DAUER DES EXAMENS : 3 Stunden (180 Minuten) ZUGELASSENE HILFSMITTEL : Europäische Formelsammlung Nicht graphischer und nicht programmierbarer
EUROPÄISCHES ABITUR 2009 MATHEMATIK 3 STUNDEN DATUM: 8. Juni 2009 DAUER DES EXAMENS : 3 Stunden (180 Minuten) ZUGELASSENE HILFSMITTEL : Europäische Formelsammlung Nicht graphischer und nicht programmierbarer
Mädchen Jungen Smartphone 42 52 Computer 77 87 Fernsehgerät 54 65 feste Spielkonsole 37 62
 Unabhängigkeit ================================================================== 1. Im Rahmen der sogenannten JIM-Studie wurde in Deutschland im Jahr 2012 der Umgang von Jugendlichen im Alter von 12 bis
Unabhängigkeit ================================================================== 1. Im Rahmen der sogenannten JIM-Studie wurde in Deutschland im Jahr 2012 der Umgang von Jugendlichen im Alter von 12 bis
Kapitel 3: Etwas Informationstheorie
 Stefan Lucks 3: Informationstheorie 28 orlesung Kryptographie (SS06) Kapitel 3: Etwas Informationstheorie Komplexitätstheoretische Sicherheit: Der schnellste Algorithmus, K zu knacken erfordert mindestens
Stefan Lucks 3: Informationstheorie 28 orlesung Kryptographie (SS06) Kapitel 3: Etwas Informationstheorie Komplexitätstheoretische Sicherheit: Der schnellste Algorithmus, K zu knacken erfordert mindestens
AUFFRISCHERKURS 2. Kreuze für jede der Zahlen bzw. Rechenausdrücke an, zu welchen der angegebenen Zahlenmengen sie gehören!
 AUFFRISCHERKURS 2 AUFGABE 1 Kreuze für jede der Zahlen bzw. Rechenausdrücke an, zu welchen der angegebenen Zahlenmengen sie gehören! Zahl keine davon ( ) AUFGABE 2 Löse alle vorhandenen Klammern auf und
AUFFRISCHERKURS 2 AUFGABE 1 Kreuze für jede der Zahlen bzw. Rechenausdrücke an, zu welchen der angegebenen Zahlenmengen sie gehören! Zahl keine davon ( ) AUFGABE 2 Löse alle vorhandenen Klammern auf und
Lösung. Prüfungsteil 1: Aufgabe 1
 Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Abitur 2007 Mathematik GK Stochastik Aufgabe C1
 Seite 1 Abiturloesung.de - Abituraufgaben Abitur 2007 Mathematik GK Stochastik Aufgabe C1 Eine Werbeagentur ermittelte durch eine Umfrage im Auftrag eines Kosmetikunternehmens vor Beginn einer Werbekampagne
Seite 1 Abiturloesung.de - Abituraufgaben Abitur 2007 Mathematik GK Stochastik Aufgabe C1 Eine Werbeagentur ermittelte durch eine Umfrage im Auftrag eines Kosmetikunternehmens vor Beginn einer Werbekampagne
Wie löst man Mathematikaufgaben?
 Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Wie löst man Mathematikaufgaben? Manfred Dobrowolski Universität Würzburg Wie löst man Mathematikaufgaben? 1 Das Schubfachprinzip 2 Das Invarianzprinzip 3 Das Extremalprinzip Das Schubfachprinzip Verteilt
Wie Sie beliebig viele PINs, die nur aus Ziffern bestehen dürfen, mit einem beliebigen Kennwort verschlüsseln: Schritt 1
 Wie Sie beliebig viele PINs, die nur aus Ziffern bestehen dürfen, mit einem beliebigen Kennwort verschlüsseln: Schritt 1 Zunächst einmal: Keine Angst, die Beschreibung des Verfahrens sieht komplizierter
Wie Sie beliebig viele PINs, die nur aus Ziffern bestehen dürfen, mit einem beliebigen Kennwort verschlüsseln: Schritt 1 Zunächst einmal: Keine Angst, die Beschreibung des Verfahrens sieht komplizierter
Zufallsgrößen und Wahrscheinlichkeitsverteilungen
 RS 24.2.2005 Zufallsgroessen_i.mcd 1) Zufallsgröße Zufallsgrößen und Wahrscheinlichkeitsverteilungen Zu jedem Zufallsexeriment gehört ein Ergebnisraum Ω. Die einzelnen Ergebnisse ω i können Buchstaben,
RS 24.2.2005 Zufallsgroessen_i.mcd 1) Zufallsgröße Zufallsgrößen und Wahrscheinlichkeitsverteilungen Zu jedem Zufallsexeriment gehört ein Ergebnisraum Ω. Die einzelnen Ergebnisse ω i können Buchstaben,
R ist freie Software und kann von der Website. www.r-project.org
 R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
Einstellungen der Deutschen gegenüber dem Beruf der Putzfrau
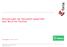 Auftraggeber: Helpling GmbH Frankfurt a.m.: 5. November 05 3367/n5447 Go/Bü Untersuchungsdesign Zielgruppe: Stichprobengröße: Die in Privathaushalten in Deutschland lebenden deutschsprachigen Personen
Auftraggeber: Helpling GmbH Frankfurt a.m.: 5. November 05 3367/n5447 Go/Bü Untersuchungsdesign Zielgruppe: Stichprobengröße: Die in Privathaushalten in Deutschland lebenden deutschsprachigen Personen
Impulse Inklusion 2014 Beteiligungskulturen - Netzwerke - Kooperationen (Leichte Sprache Version)
 Impulse Inklusion 2014 Beteiligungskulturen - Netzwerke - Kooperationen (Leichte Sprache Version) Das heißt: Beteiligungskultur: Wie können Menschen mit Behinderungen überall mitmachen und mitsprechen.
Impulse Inklusion 2014 Beteiligungskulturen - Netzwerke - Kooperationen (Leichte Sprache Version) Das heißt: Beteiligungskultur: Wie können Menschen mit Behinderungen überall mitmachen und mitsprechen.
i x k k=1 i u i x i v i 1 0,2 24 24 0,08 2 0,4 30 54 0,18 3 0,6 54 108 0,36 4 0,8 72 180 0,60 5 1,0 120 300 1,00 2,22 G = 1 + 1 n 2 n i=1
 1. Aufgabe: Der E-Commerce-Umsatz (in Millionen Euro) der fünf größten Online- Shopping-Clubs liegt wie folgt vor: Club Nr. Umsatz 1 120 2 72 3 54 4 30 5 24 a) Bestimmen Sie den Ginikoeffizienten. b) Zeichnen
1. Aufgabe: Der E-Commerce-Umsatz (in Millionen Euro) der fünf größten Online- Shopping-Clubs liegt wie folgt vor: Club Nr. Umsatz 1 120 2 72 3 54 4 30 5 24 a) Bestimmen Sie den Ginikoeffizienten. b) Zeichnen
Kapitel 7 und Kapitel 8: Gleichgewichte in gemischten Strategien. Einleitung. Übersicht Teil 2 2. Übersicht 3
 Übersicht Teil 2 Kaitel 7 und Kaitel 8: Gleichgewichte in gemischten Strategien Übersicht Teil 2 2 Übersicht Einleitung Was ist eine gemischte Strategie? Nutzen aus gemischten Strategien Reaktionsfunktionen
Übersicht Teil 2 Kaitel 7 und Kaitel 8: Gleichgewichte in gemischten Strategien Übersicht Teil 2 2 Übersicht Einleitung Was ist eine gemischte Strategie? Nutzen aus gemischten Strategien Reaktionsfunktionen
Wir machen neue Politik für Baden-Württemberg
 Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Ein Rechenspiel auf der Hunderter-Tafel. Reinhold Wittig
 Ein Rechenspiel auf der Hunderter-Tafel Reinhold Wittig Ein Rechenspiel auf der Hunderter-Tafel für 2 Spieler ab 8 Jahren Autor Reinhold Wittig Inhalt 1 Spielbrett (Hunderter-Tafel) 1 transparente Maske
Ein Rechenspiel auf der Hunderter-Tafel Reinhold Wittig Ein Rechenspiel auf der Hunderter-Tafel für 2 Spieler ab 8 Jahren Autor Reinhold Wittig Inhalt 1 Spielbrett (Hunderter-Tafel) 1 transparente Maske
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
MI - Mission Impossible Sind Sie gut versichert? Ein kurzes Beispiel zur Versicherungsmathematik
 MI - Mission Impossible Sind Sie gut versichert? Ein kurzes Beispiel zur Versicherungsmathematik Seite 1 Vorstellung Organisation: Deutsche Aktuarvereinigung e.v. (DAV) berufsständische Vertretung der
MI - Mission Impossible Sind Sie gut versichert? Ein kurzes Beispiel zur Versicherungsmathematik Seite 1 Vorstellung Organisation: Deutsche Aktuarvereinigung e.v. (DAV) berufsständische Vertretung der
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009)
 Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Alle gehören dazu. Vorwort
 Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
Kreativ visualisieren
 Kreativ visualisieren Haben Sie schon einmal etwas von sogenannten»sich selbst erfüllenden Prophezeiungen«gehört? Damit ist gemeint, dass ein Ereignis mit hoher Wahrscheinlichkeit eintritt, wenn wir uns
Kreativ visualisieren Haben Sie schon einmal etwas von sogenannten»sich selbst erfüllenden Prophezeiungen«gehört? Damit ist gemeint, dass ein Ereignis mit hoher Wahrscheinlichkeit eintritt, wenn wir uns
Regelmäßigkeit (Erkennen von Mustern und Zusammenhängen) versus Zufall
 Wahrscheinlichkeitstheorie Was will die Sozialwissenschaft damit? Regelmäßigkeit (Erkennen von Mustern und Zusammenhängen) versus Zufall Auch im Alltagsleben arbeiten wir mit Wahrscheinlichkeiten, besteigen
Wahrscheinlichkeitstheorie Was will die Sozialwissenschaft damit? Regelmäßigkeit (Erkennen von Mustern und Zusammenhängen) versus Zufall Auch im Alltagsleben arbeiten wir mit Wahrscheinlichkeiten, besteigen
Gründe für fehlende Vorsorgemaßnahmen gegen Krankheit
 Gründe für fehlende Vorsorgemaßnahmen gegen Krankheit politische Lage verlassen sich auf Familie persönliche, finanzielle Lage meinen, sich Vorsorge leisten zu können meinen, sie seien zu alt nicht mit
Gründe für fehlende Vorsorgemaßnahmen gegen Krankheit politische Lage verlassen sich auf Familie persönliche, finanzielle Lage meinen, sich Vorsorge leisten zu können meinen, sie seien zu alt nicht mit
Statistik 1: Einführung
 Seite Stat- Statistik : Einführung Die mathematische Disziplin der Stochastik, die die Teilgebiete Wahrscheinlichkeitstheorie und mathematische Statistik umfaßt, beschäftigt sich mit der Beobachtung, Aufzeichnung
Seite Stat- Statistik : Einführung Die mathematische Disziplin der Stochastik, die die Teilgebiete Wahrscheinlichkeitstheorie und mathematische Statistik umfaßt, beschäftigt sich mit der Beobachtung, Aufzeichnung
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: If-clauses - conditional sentences - Nie mehr Probleme mit Satzbau im Englischen! Das komplette Material finden Sie hier: School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: If-clauses - conditional sentences - Nie mehr Probleme mit Satzbau im Englischen! Das komplette Material finden Sie hier: School-Scout.de
Dr. Guido Schwarz Forschung, Schulung, Beratung; A - 1180 Wien, Edelhofgasse 31/8; Tel: +43-1-478 34 44 Mobil: +43-676 431 91 12 E-mail:
 1 PROTOKOLL 2 Der Startschuss verlief erfolgreich, wenn auch mit Geburtswehen. Bei herrlichem Wetter gab es einen diskussionsreichen Nachmittag mit dem Fazit: Lauter nette Menschen und interessant genug,
1 PROTOKOLL 2 Der Startschuss verlief erfolgreich, wenn auch mit Geburtswehen. Bei herrlichem Wetter gab es einen diskussionsreichen Nachmittag mit dem Fazit: Lauter nette Menschen und interessant genug,
Ideen für die Zukunft haben.
 BREMEN WÄHLT AM 10. MAI 2015 Ideen für die Zukunft haben. Leichte Sprache Kurz und bündig. www.spd-land-bremen.de Bürgermeister, Hanseat, Bremer. Foto: Patrice Kunde Liebe Menschen in Bremen, am 10. Mai
BREMEN WÄHLT AM 10. MAI 2015 Ideen für die Zukunft haben. Leichte Sprache Kurz und bündig. www.spd-land-bremen.de Bürgermeister, Hanseat, Bremer. Foto: Patrice Kunde Liebe Menschen in Bremen, am 10. Mai
Fachwirt. Geprüfter. werden. Intensivtraining für eine erfolgreiche IHK-Prüfung. Teil A wirtschaftsübergreifende Qualifikationen
 Intensivtraining für eine erfolgreiche IHK-Prüfung Geprüfter Fachwirt werden Teil A wirtschaftsübergreifende Qualifikationen Peter Collier, Reinhard Fresow, Klaus Steines Mit Aufgaben- und Lösungssätzen
Intensivtraining für eine erfolgreiche IHK-Prüfung Geprüfter Fachwirt werden Teil A wirtschaftsübergreifende Qualifikationen Peter Collier, Reinhard Fresow, Klaus Steines Mit Aufgaben- und Lösungssätzen
Statistik I für Betriebswirte Vorlesung 5
 Statistik I für Betriebswirte Vorlesung 5 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik 07. Mai 2015 PD Dr. Frank Heyde Statistik I für Betriebswirte Vorlesung 5 1 Klassische Wahrscheinlichkeitsdefinition
Statistik I für Betriebswirte Vorlesung 5 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik 07. Mai 2015 PD Dr. Frank Heyde Statistik I für Betriebswirte Vorlesung 5 1 Klassische Wahrscheinlichkeitsdefinition
Fragebogen zur Erhebung der Zufriedenheit und Kooperation der Ausbildungsbetriebe mit unserer Schule
 Fragebogen zur Erhebung der Zufriedenheit und Kooperation der Ausbildungsbetriebe mit unserer Schule Sehr geehrte Ausbilderinnen und Ausbilder, die bbs1celle betreiben nun bereits seit einigen Jahren ein
Fragebogen zur Erhebung der Zufriedenheit und Kooperation der Ausbildungsbetriebe mit unserer Schule Sehr geehrte Ausbilderinnen und Ausbilder, die bbs1celle betreiben nun bereits seit einigen Jahren ein
Erstellen einer digitalen Signatur für Adobe-Formulare
 Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Eisenbahnspiel. (Dokumentation)
 Eisenbahnspiel (Dokumentation) Abbildung 1: Hier sieht man den Gleisparcour In der Mitte ist das Depot mit den Einnahmetalern und den dunkelfarbigen Kreditsteinen und den Sparsäcken zu sehen. Außerdem
Eisenbahnspiel (Dokumentation) Abbildung 1: Hier sieht man den Gleisparcour In der Mitte ist das Depot mit den Einnahmetalern und den dunkelfarbigen Kreditsteinen und den Sparsäcken zu sehen. Außerdem
Die neue Aufgabe von der Monitoring-Stelle. Das ist die Monitoring-Stelle:
 Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Die neue Aufgabe von der Monitoring-Stelle Das ist die Monitoring-Stelle: Am Deutschen Institut für Menschen-Rechte in Berlin gibt es ein besonderes Büro. Dieses Büro heißt Monitoring-Stelle. Mo-ni-to-ring
Kombinatorik Platzierungsproblem 3 Berechnungsarten
 Kombinatorik Platzierungsproblem 3 Berechnungsarten 10 Weinflaschen, davon Rotweinflaschen, werden rechteckförmig zufällig angeordnet 7 7 Wie groß ist die Wahrscheinlichkeit, dass die Rotweinflaschen die
Kombinatorik Platzierungsproblem 3 Berechnungsarten 10 Weinflaschen, davon Rotweinflaschen, werden rechteckförmig zufällig angeordnet 7 7 Wie groß ist die Wahrscheinlichkeit, dass die Rotweinflaschen die
TIPS-Crash und zwei Hindenburg-Omen
 TIPS-Crash und zwei Hindenburg-Omen In den USA bezeichnet das Kürzel TIPS eine Anleihe, die gegen Kaufkraftverlust schützt. Ein Investment in TIPS ( Treasury Inflation Protected Security, deutsch: Inflationsgeschützte
TIPS-Crash und zwei Hindenburg-Omen In den USA bezeichnet das Kürzel TIPS eine Anleihe, die gegen Kaufkraftverlust schützt. Ein Investment in TIPS ( Treasury Inflation Protected Security, deutsch: Inflationsgeschützte
 194 Beweis eines Satzes von Tschebyschef. Von P. E RDŐS in Budapest. Für den zuerst von T SCHEBYSCHEF bewiesenen Satz, laut dessen es zwischen einer natürlichen Zahl und ihrer zweifachen stets wenigstens
194 Beweis eines Satzes von Tschebyschef. Von P. E RDŐS in Budapest. Für den zuerst von T SCHEBYSCHEF bewiesenen Satz, laut dessen es zwischen einer natürlichen Zahl und ihrer zweifachen stets wenigstens
Wärmebildkamera. Arbeitszeit: 15 Minuten
 Wärmebildkamera Arbeitszeit: 15 Minuten Ob Menschen, Tiere oder Gegenstände: Sie alle senden unsichtbare Wärmestrahlen aus. Mit sogenannten Wärmebildkameras können diese sichtbar gemacht werden. Dadurch
Wärmebildkamera Arbeitszeit: 15 Minuten Ob Menschen, Tiere oder Gegenstände: Sie alle senden unsichtbare Wärmestrahlen aus. Mit sogenannten Wärmebildkameras können diese sichtbar gemacht werden. Dadurch
Tipp III: Leiten Sie eine immer direkt anwendbare Formel her zur Berechnung der sogenannten "bedingten Wahrscheinlichkeit".
 Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
EINMALEINS BEZIEHUNGSREICH
 EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder
EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder
1.5 Folgerungen aus dem Kolmogoroff- Axiomensystem P( ) = 0.
 1.5 Folgerungen aus dem Kolmogoroff- Axiomensystem Folg. 2 Sei (Ω, E, P) W.-raum. Seien A, B,A 1,...,A n Ereignisse. Es gelten die folgenden Aussagen: 1. P(A) = 1 P(A). 2. Für das unmögliche Ereignis gilt:
1.5 Folgerungen aus dem Kolmogoroff- Axiomensystem Folg. 2 Sei (Ω, E, P) W.-raum. Seien A, B,A 1,...,A n Ereignisse. Es gelten die folgenden Aussagen: 1. P(A) = 1 P(A). 2. Für das unmögliche Ereignis gilt:
Beispiel(unten ist der Spielfeldrand):
 Anleitung Side by Side ist ein Puzzle mit einfachen Regeln, das in einem 6x6 (oder größerem) Gitter gespielt wird. Ziel des Spieles ist es, die leeren Kästchen mit den Zahlen 1, 2, 3, 4 oder einem X zu
Anleitung Side by Side ist ein Puzzle mit einfachen Regeln, das in einem 6x6 (oder größerem) Gitter gespielt wird. Ziel des Spieles ist es, die leeren Kästchen mit den Zahlen 1, 2, 3, 4 oder einem X zu
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Die Invaliden-Versicherung ändert sich
 Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Grundlagen der Inferenzstatistik
 Grundlagen der Inferenzstatistik (Induktive Statistik oder schließende Statistik) Dr. Winfried Zinn 1 Deskriptive Statistik versus Inferenzstatistik Die Deskriptive Statistik stellt Kenngrößen zur Verfügung,
Grundlagen der Inferenzstatistik (Induktive Statistik oder schließende Statistik) Dr. Winfried Zinn 1 Deskriptive Statistik versus Inferenzstatistik Die Deskriptive Statistik stellt Kenngrößen zur Verfügung,
Auslotung der Gefühle & Wünsche von Eltern und SchülerInnen zum Schuljahr 2011/2012
 Chart Auslotung der Gefühle & Wünsche von Eltern und SchülerInnen zum Schuljahr 0/0 Projektleiter: Studien-Nr.: Mag. Reinhard Födermayr Z85.08.P.O n=5, Online Interviews mit Eltern von SchülerInnen und
Chart Auslotung der Gefühle & Wünsche von Eltern und SchülerInnen zum Schuljahr 0/0 Projektleiter: Studien-Nr.: Mag. Reinhard Födermayr Z85.08.P.O n=5, Online Interviews mit Eltern von SchülerInnen und
Eine der Aktien hat immer einen höheren Gewinn als die andere Aktie. Ihre Aufgabe ist es diese auszuwählen.
 Instruktionen am Anfang von Experiment 1 (auf Papier ausgeteilt: grünmarkierte Textstellen zeigen den Instruktionstext in der jeweiligen Bedingung an; Kommentare sind gelb markiert.) Stellen Sie sich vor,
Instruktionen am Anfang von Experiment 1 (auf Papier ausgeteilt: grünmarkierte Textstellen zeigen den Instruktionstext in der jeweiligen Bedingung an; Kommentare sind gelb markiert.) Stellen Sie sich vor,
Ein Spiel für 2-3 goldhungrige Spieler ab 8 Jahren.
 Ein Spiel für 2-3 goldhungrige Spieler ab 8 Jahren. Gold! Gold! Nichts als Gold, soweit das Auge reicht. So ein Goldesel ist schon was Praktisches. Doch Vorsicht: Die störrischen Viecher können einem auch
Ein Spiel für 2-3 goldhungrige Spieler ab 8 Jahren. Gold! Gold! Nichts als Gold, soweit das Auge reicht. So ein Goldesel ist schon was Praktisches. Doch Vorsicht: Die störrischen Viecher können einem auch
Geld Verdienen im Internet leicht gemacht
 Geld Verdienen im Internet leicht gemacht Hallo, Sie haben sich dieses E-book wahrscheinlich herunter geladen, weil Sie gerne lernen würden wie sie im Internet Geld verdienen können, oder? Denn genau das
Geld Verdienen im Internet leicht gemacht Hallo, Sie haben sich dieses E-book wahrscheinlich herunter geladen, weil Sie gerne lernen würden wie sie im Internet Geld verdienen können, oder? Denn genau das
Zahlenmauern. Dr. Maria Koth. Ausgehend von dieser einfachen Bauvorschrift ergibt sich eine Vielzahl an möglichen Aufgabenstellungen.
 Zahlenmauern Dr. Maria Koth Zahlenmauern sind nach einer einfachen Regel gebaut: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Ausgehend von dieser einfachen Bauvorschrift ergibt
Zahlenmauern Dr. Maria Koth Zahlenmauern sind nach einer einfachen Regel gebaut: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Ausgehend von dieser einfachen Bauvorschrift ergibt
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
 AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
Ministerium für Bildung und Wissenschaft des Landes Schleswig-Holstein. Zentrale Abschlussarbeit 2013. Realschulabschluss
 Ministerium für Bildung und Wissenschaft des Landes Schleswig-Holstein Zentrale Abschlussarbeit 2013 Realschulabschluss Impressum Herausgeber Ministerium für Bildung und Wissenschaft des Landes Schleswig-Holstein
Ministerium für Bildung und Wissenschaft des Landes Schleswig-Holstein Zentrale Abschlussarbeit 2013 Realschulabschluss Impressum Herausgeber Ministerium für Bildung und Wissenschaft des Landes Schleswig-Holstein
Der Wert von Lebensmitteln Umfragen im Auftrag des BMELV
 Der Wert von Lebensmitteln Umfragen im Auftrag des BMELV Teil 1 Datenbasis: 1.001 Bundesbürger ab 14 Jahre Erhebungszeitraum: 4. bis 7. Januar 2011 statistische Fehlertoleranz: +/- 3 Prozentpunkte Auftraggeber:
Der Wert von Lebensmitteln Umfragen im Auftrag des BMELV Teil 1 Datenbasis: 1.001 Bundesbürger ab 14 Jahre Erhebungszeitraum: 4. bis 7. Januar 2011 statistische Fehlertoleranz: +/- 3 Prozentpunkte Auftraggeber:
Dieses erste Kreisdiagramm, bezieht sich auf das gesamte Testergebnis der kompletten 182 getesteten Personen. Ergebnis
 Datenanalyse Auswertung Der Kern unseres Projektes liegt ganz klar bei der Fragestellung, ob es möglich ist, Biere von und geschmacklich auseinander halten zu können. Anhand der folgenden Grafiken, sollte
Datenanalyse Auswertung Der Kern unseres Projektes liegt ganz klar bei der Fragestellung, ob es möglich ist, Biere von und geschmacklich auseinander halten zu können. Anhand der folgenden Grafiken, sollte
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Zentrale Aufnahmeprüfung 2015 für die Handelsmittelschulen des Kantons Zürich. Vorname:... Aufgaben 1 2 3 4 5 6 7 8 9 Total Note
 Zentrale Aufnahmeprüfung 2015 für die Handelsmittelschulen des Kantons Zürich Mathematik Name:... Vorname:... Prüfungsnummer:... Du hast 90 Minuten Zeit. Du musst alle Aufgaben in dieses Heft lösen. Wenn
Zentrale Aufnahmeprüfung 2015 für die Handelsmittelschulen des Kantons Zürich Mathematik Name:... Vorname:... Prüfungsnummer:... Du hast 90 Minuten Zeit. Du musst alle Aufgaben in dieses Heft lösen. Wenn
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Bürger legen Wert auf selbstbestimmtes Leben
 PRESSEINFORMATION Umfrage Patientenverfügung Bürger legen Wert auf selbstbestimmtes Leben Ergebnisse der forsa-umfrage zur Patientenverfügung im Auftrag von VorsorgeAnwalt e.v. Der Verband VorsorgeAnwalt
PRESSEINFORMATION Umfrage Patientenverfügung Bürger legen Wert auf selbstbestimmtes Leben Ergebnisse der forsa-umfrage zur Patientenverfügung im Auftrag von VorsorgeAnwalt e.v. Der Verband VorsorgeAnwalt
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG
 Frist berechnen BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG Sie erwägen die Kündigung eines Mitarbeiters und Ihr Unternehmen hat einen Betriebsrat? Dann müssen Sie die Kündigung
Frist berechnen BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG Sie erwägen die Kündigung eines Mitarbeiters und Ihr Unternehmen hat einen Betriebsrat? Dann müssen Sie die Kündigung
13 Öffentliche Güter
 1 13ÖffentlicheGüter Deregriffdes"öffentlichenGutes"hateinigespekte,dieÄhnlichkeitenzuderDiskussion vonexterneneffektenaufweisen.einsolchergemeinsamerspektist,daßnichtmehralle EntscheidungsträgerunabhängigvoneinanderüberdasNiveaueinesdesKonsumsoderdes
1 13ÖffentlicheGüter Deregriffdes"öffentlichenGutes"hateinigespekte,dieÄhnlichkeitenzuderDiskussion vonexterneneffektenaufweisen.einsolchergemeinsamerspektist,daßnichtmehralle EntscheidungsträgerunabhängigvoneinanderüberdasNiveaueinesdesKonsumsoderdes
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 3914 jutta.arrenberg@th-koeln.
 Übungen zur Vorlesung Wirtschaftsstatistik Zufallsvariablen Aufgabe 4.1 Ein Unternehmen fertigt einen Teil der Produktion in seinem Werk in München und den anderen Teil in seinem Werk in Köln. Auf Grund
Übungen zur Vorlesung Wirtschaftsstatistik Zufallsvariablen Aufgabe 4.1 Ein Unternehmen fertigt einen Teil der Produktion in seinem Werk in München und den anderen Teil in seinem Werk in Köln. Auf Grund
Informatik für Schüler, Foliensatz 12 Pseudo-Zufallszahlen
 rof. G. Kemnitz Institut für Informatik, Technische Universität Clausthal 14. April 2010 1/14 Informatik für Schüler, Foliensatz 12 Pseudo-Zufallszahlen Prof. G. Kemnitz Institut für Informatik, Technische
rof. G. Kemnitz Institut für Informatik, Technische Universität Clausthal 14. April 2010 1/14 Informatik für Schüler, Foliensatz 12 Pseudo-Zufallszahlen Prof. G. Kemnitz Institut für Informatik, Technische
Ebenenmasken Grundlagen
 Ebenenmasken Grundlagen Was sind Ebenmasken? Was machen sie? Wofür braucht man sie? Wie funktionieren sie? Ebenmasken sind eines der sinnvollsten Tools in anspruchvollen EBV Programmen (EBV = elektronische
Ebenenmasken Grundlagen Was sind Ebenmasken? Was machen sie? Wofür braucht man sie? Wie funktionieren sie? Ebenmasken sind eines der sinnvollsten Tools in anspruchvollen EBV Programmen (EBV = elektronische
1. Weniger Steuern zahlen
 1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
Professionelle Seminare im Bereich MS-Office
 Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
