|
|
|
- Hans Holtzer
- vor 9 Jahren
- Abrufe
Transkript
1 Statik I Ergänzungen zum Vorlesungsskript Dr.-Ing. Stephan Salber Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen
2 Statik I Vorlesungs- und Übungsmaterial Vorlesung Benutzername: Vorlesungsskript Passwort: **koesa** Übungen Benutzername: Uebungsskript Passwort: **koenig** Ergänzungen Benutzername: Zusatzinfos Passwort: **stesa** Tutorübungen Benutzername: Tutoruebungen Passwort: **stesa**
3 Werkstoffmodelle linear-elastisches Werkstoffverhalten Elasto-plastisches Werkstoffverhalten Linear-elastisches Material- dreidimensionaler Fall: Normalspannungen Schubspannungen
4 Vereinfachungen und Beschränkungen Werkstoff Idealisierung: 1.) isotropes Verhalten Werkstoffverhalten in alle Richtungen gleich im Gegensatz dazu orthotrop z.b. bei Faserverbundwerkstoffen E 1 E3 in Statik I sind ausschließlich Spannungen und Dehnungen in Längsrichung (eindimensional) E 2 2.) lineares Werkstoff- Zusammenhang zwischen verhalten bzw. Spannung σ und Materialgesetz Dehnung ε σ= ε E E = const σ Gummi Hooksche Gerade Metalle ε
5 Elementare Theorie der Biegung (ETB) Querschnitte bleiben eben und normal zur verformten Mittellinie Demo Materialgesetz: daraus ergibt sich der Zusammenhang zwischen Verzerrungs- und Kraftgrößen Erläuterung
6 Zusammenhang: Verzerrungs- und Kraftgrößen Biegung: Verzerrung Kraft Materialgesetz Krümmung verallgem. Spannungsgröße Biegesteifigkeit Zug-Druck: verallgem. Verzerrung verallgem. Spannungsgröße (Längskraft) Längssteifigkeit
7 Schnittprinzip Anwendung zur Bestimmung von inneren Kraftgrößen für Rahmentragwerke = Stabwerke aus Biegestäben hier: Abzählkriterium für den Grad der statischen Unbestimmtheit für Rahmentragwerke: 2
8 Schnittprinzip für Fachwerke Abzählkriterium für den Grad der statischen Unbestimmtheit von Fachwerken: = 4 = 2 = 3 im obigen Beispiel: n = (4 + 2) 2 3 = 0 Allgem. Formel für den Grad der statischen Unbestimmtheit:
9 Arbeit Prinzip der Virtuellen Arbeiten GG-Punkt A a u u A i A a äußere Arbeit P Verschiebung A ges gesamte Arbeit Last A a u A a u Verschiebung Spannung s A i innere Arbeit A i e A i A ges A i A a! 0 Dehnung
10 Prinzip der Virtuellen Arbeiten Prinzip der Virtuellen Verrückungen PVV (auch Prinzip der Virtuellen Verschiebungen) äußere Arbeit innere Arbeit Das PVV gilt auch bei geometrischer Nichtlinearität und bei nichtlinearem Materialverhalten
11 P INSTITUT FÜR STATIK UND DYNAMIK DER Prinzip der Virtuellen Arbeiten Prinzip der Virtuellen Kräfte PVK Last P A a komplementäre Arbeit u A a Verschiebung Spannung s A A i i e Dehnung Bei Beschränkung auf lineare Probleme gilt: u äußere Arbeit innere Arbeit
12 Prinzip der Virtuellen Arbeiten PVV: Zur Berechnung von Lasten (z.b. Schnittlasten, Auflagerraktionen) PVK: Bei stat. unbest. Systemen werden die virtuellen Größen auf stat. best. Untersysteme aufgebracht Zur Berechnung von Verformungen (PVK gilt nur bei linearen Problemen)
13 PVV: INSTITUT FÜR STATIK UND DYNAMIK DER Prinzip der Virtuellen Arbeiten Anwendung auf den Zug-Druckstab (Skipt: Seite 60) (heutige Tutorübungen: Aufgabe 4) =? Zug-Druck-Stab PVV: innere Arbeit N verallgemeinerte wahre Spannung (Belastung) verallgemeinerte virtuelle Verzerrung (Dehnung) analog im PVK: innere Arbeit N verallgemeinerte virtuelle Spannung (Belastung) verallgemeinerte wahre Verzerrung (Dehnung) mit N E A
14 INSTITUT FÜR STATIK UND DYNAMIK DER Prinzip der Virtuellen Arbeiten Anwendung auf den Biegestab (Skipt: Seite 61) Zusammenhang von Verzerrungs-und Kraftgrößen: M verallgem. Spannungsgröße verallgem. Verzerrungsgröße (Krümmung) I Trägheitsmoment PVV: innere Arbeit M verallgemeinerte wahre Spannung (Belastung) verallgemeinerte virtuelle Verzerrung (Krümmung) Erläuterung Anwendungsbeispiel analog im PVK: innere Arbeit M verallgemeinerte wahre Verzerrung (Dehnung) verallgemeinerte virtuelle Spannung (Belastung) mit M E I
15 Prinzip der Virtuellen Arbeiten Berechnung statisch unbestimmter Systeme mit dem Kraftgrößenverfahren Idee: Statisch unbestimmte Tragwerke Superposition aus statisch bestimmten Untersystemen Der Berechnung liegt ein statisch bestimmtes Grundsystem 0 zugrunde Bindungen (Lagerungen) müssen gelöst werden, um ein statisch unbestimmtes System bestimmt zu machen (bewusste Verletzung der Kinematik) Gelöste Bindungen werden als äußere Lasten angesetzt Skalierung, bis Kinematik wieder eingehalten wird
16 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren-Reduktionssatz M, M,Q,N=? P P v =? n=1 = P + X 1 Kraftgrößenverfahren dm 1, dq 1, dn 1 1 Ergebnis: tatsächliche M-, Q-, N-Verlauf des stat. unbest. Systems M,Q,N im stat. unbest. System nun bekannt M 0, Q 0, N 0 M, P =? l 1 M, l 1 l1 M M P v dx =1 E I 0 P=1 P im stat. best. Untersystem am Ort der gesuchten Verschiebung aufbringen M, l l 1 M=1 l1 M M M dx =1 E I 0 M im stat. best. Untersystem am Ort der gesuchten Verdrehung aufbringen
17 Prinzip der Virtuellen Arbeiten Berechnung statisch unbestimmter Systeme mit dem Kraftgrößenverfahren Allgemeine Vorgehensweise
18 Prinzip der Virtuellen Arbeiten Berechnung statisch unbestimmter Systeme mit dem Kraftgrößenverfahren Allgemeine Vorgehensweise
19 Kraftgrößenverfahren für mehrfach statisch unbestimmte Systeme
20 Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: 2-fach statisch unbestimmtes System belastet mit der äußeren Punktlast P P Idee hinter dem Kraftkrößenverfahren: Aufteilen in stat. best. Untersysteme und anschließende Superposition! statisch bestîmmtes Untersystem wird durch Schneiden erzeugt Hinweis: Das rechte Lager zwar nur 1 mal weggeschnitten. Dadurch entstehen jedoch 2 Reaktionen
21 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: 2-fach statisch unbestimmtes System stat. unbest. Gesamtsystem P stat. best. Grundsystem 0 -System (nur äußere Lasten) P erstes Einheitslastsystem 1 -System (Schnitt 1 bzw. Richtung 1 ) 1 X 1 zweites Einheitslastsystem 2 -System (Schnitt 2 bzw. Richtung 2 ) X 2 1 = = 10 + X 1 + X 2
22 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: 2-fach statisch unbestimmtes System Wie werden die Verschiebungen ij berechnet? am Beispiel von Einheitslastsystem 1 1 Verschiebung aufgrund von Last 1 in Richtung bzw. an der Stelle 2 11 =? Ausgangssystem 1 Hier ist das Ausgangs- System zugleich mit der Einheitslast beaufschlagt Virtuelles Lastsystem 11 =? P=1 am Ort der gesuchten Verschiebung Einheitslast P=1 aufbringen (Einheitslastgestz) 21 M=M 1 N=N 1 M 1 N 1 11 Verschiebung aufgrund von Last 1 in Richtung bzw. an der Stelle 1 Prinzip der virtuellen Arbeit (hier PVK): Zusammenhang von Verformung 11 und der im Gesamttragwerk gespeicherten Energie. Abhängig von Normalkräften, Momenten (Querkräften)
23 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: 2-fach statisch unbestimmtes System Wie werden die Verschiebungen d ij berechnet? analog für weitere ij =? =0 20 = X 1 + X s. Skipt S Verträglichkeitsbedingung Forderung : =0 X 1, X 2, bestimmen (lin. Gl.-System)
24 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Belastungen des statisch unbestimmten Tragwerks? stat. unbest. Gesamtsystem M Verformung ~ Belastung X 1, X 2, auch auf Belastung anwendbar = - stat. best. Grundsystem 0 -System (nur äußere Lasten) - M 0 P + erstes Einheitslastsystem 1 -System (Schnitt 1 bzw. Richtung 1 ) M 1 + X 1 X 2 + zweites Einheitslastsystem 2 -System (Schnitt 2 bzw. Richtung 2 ) M 2 1 P - 1 N = - N N 1 + X 1 X 2 N 2
25 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant E, I, A F R a + z - 3b = n = 3 Das Gesamtsystem ist 3-fach statisch unbestimmt. F/2 ausnutzen der Symmetrie 1 2 a + z - 3b = n = 2 symmetriesches Halbmodell 3 Das reduzierte System ist 2-fach statisch unbestimmt.
26 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant Zustandslinien ermitteln 0-System 0 F/2 1-System F/2 statisch bestimmtes Grundsystem erzeugen durch Entfernen des 2-wertigen Lagers System R
27 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant Verträglichkeitsbedingung formulieren Verschiebung aufgrund von Last 1 in Richtung bzw. an der Stelle 1 Verschiebung aufgrund von Last 1 in Richtung bzw. an der Stelle 2 Skalierfaktor für Einheits - Lastrichtung 2
28 / INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant Koeffizienten bestimmen / / / =0 / / / / 1cos /
29 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant Koeffizienten bestimmen / / / / / =0 1cos / / / / 1 1 =0 / 1 1
30 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant Skalierfaktoren bestimmen Verträglichkeitsbedingung: = Gleichungssystem nach X 1 und X 2 auflösen
31 INSTITUT FÜR STATIK UND DYNAMIK DER Kraftgrößenverfahren - mehrfach stat. unbest. Systeme Beispiel: Ringspant Endsystem berechnen und darstellen
ERLÄUTERUNGEN ZUM KRAFTGRÖßENVERFAHREN An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.
 FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
Bachelor of Science Luft- und Raumfahrttechnik Modulprüfung Statik Kernmodul
 UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. R. Reichel Bachelor of Science Luft- und Raumfahrttechnik Modulprüfung Statik Kernmodul
UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. R. Reichel Bachelor of Science Luft- und Raumfahrttechnik Modulprüfung Statik Kernmodul
Hauptdiplomprüfung Statik und Dynamik Pflichtfach
 UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. S. Staudacher Hauptdiplomprüfung Statik und Dynamik Pflichtfach Herbst 2011 Aufgabenteil
UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. S. Staudacher Hauptdiplomprüfung Statik und Dynamik Pflichtfach Herbst 2011 Aufgabenteil
Inhaltsverzeichnis. 1 Einführung in die Statik der Tragwerke 1
 1 Einführung in die Statik der Tragwerke 1 1.1 Vorbemerkungen 1 1.1.1 Definition und Aufgabe der Baustatik l 1.1.2 Tragwerksformen irnd deren Idealisierung 2 1.1.2.1 Dreidimensionale Tragelemcnte: Räume
1 Einführung in die Statik der Tragwerke 1 1.1 Vorbemerkungen 1 1.1.1 Definition und Aufgabe der Baustatik l 1.1.2 Tragwerksformen irnd deren Idealisierung 2 1.1.2.1 Dreidimensionale Tragelemcnte: Räume
Baustatik kompakt. Statisch bestimmte und statisch/unbestimmte Systeme
 Prof. Dipl.-Ing. Klaus-Jürgen Schneider Prof. Dipl.-Ing. Erwin Schweda Baustatik kompakt Statisch bestimmte und statisch/unbestimmte Systeme / Neu bearbeitet von: Prof. Dr.-Ing. Christoph Seeßelberg Prof.JDr.-Ing.
Prof. Dipl.-Ing. Klaus-Jürgen Schneider Prof. Dipl.-Ing. Erwin Schweda Baustatik kompakt Statisch bestimmte und statisch/unbestimmte Systeme / Neu bearbeitet von: Prof. Dr.-Ing. Christoph Seeßelberg Prof.JDr.-Ing.
1. EINFLUSSLINIEN FÜR KRAFTGRÖßEN
 Arbeitsblätter 1 Hinweise zur Konstruktion und Berechnung von Einflusslinien Definition: Eine Einflusslinie (EL) liefert den Einfluss einer Wanderlast P = 1 von festgelegter Wirkungsrichtung. längs des
Arbeitsblätter 1 Hinweise zur Konstruktion und Berechnung von Einflusslinien Definition: Eine Einflusslinie (EL) liefert den Einfluss einer Wanderlast P = 1 von festgelegter Wirkungsrichtung. längs des
BAUSTATIK I KOLLOQUIUM 10, Lösung
 BAUSTATIK I KOLLOQUIUM 10, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: Unterspanntes Fachwerk, EA = konstant für alle Stäbe Stabkräfte S i Grad der statischen Unbestimmtheit:
BAUSTATIK I KOLLOQUIUM 10, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: Unterspanntes Fachwerk, EA = konstant für alle Stäbe Stabkräfte S i Grad der statischen Unbestimmtheit:
Hauptdiplomprüfung Statik und Dynamik Pflichtfach
 UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. S. Staudacher Hauptdiplomprüfung Statik und Dynamik Pflichtfach Herbst 2011 Aufgabenteil
UNIVERSITÄT STUTTGART Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Komm. Leiter: Prof. Dr.-Ing. S. Staudacher Hauptdiplomprüfung Statik und Dynamik Pflichtfach Herbst 2011 Aufgabenteil
Baustatik II und III (PO 2013)
 Bachelorprüfung Frühjahr 2016 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 20.02.2016 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
Bachelorprüfung Frühjahr 2016 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 20.02.2016 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
1. Zug und Druck in Stäben
 1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
5.1 Grundlagen zum Prinzip der virtuellen Kräfte
 5 Prinzip der virtuellen Kräfte 5. Grundlagen zum Prinzip der virtuellen Kräfte Das Prinzip der virtuellen Kräfte (PvK) stellt eine nwendung des Prinzips der virtuellen rbeit dar. Es dient zur Bestimmung
5 Prinzip der virtuellen Kräfte 5. Grundlagen zum Prinzip der virtuellen Kräfte Das Prinzip der virtuellen Kräfte (PvK) stellt eine nwendung des Prinzips der virtuellen rbeit dar. Es dient zur Bestimmung
Potentielle Energie, P.d.v.K. und P.d.v.V.
 IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Potentielle Energie, P.d.v.K. und P.d.v.V. Fachgebiet Baustatik 2. Februar 26 Inhaltsverzeichnis 1 Die potentielle Energie 1 1.1
IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Potentielle Energie, P.d.v.K. und P.d.v.V. Fachgebiet Baustatik 2. Februar 26 Inhaltsverzeichnis 1 Die potentielle Energie 1 1.1
3. Kraftgrößenverfahren
 .Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
.Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
1. Formänderungsenergie
 1. Formänderungsenergie 1.1 Grundlagen 1. Grundlastfälle 1.3 Beispiele.1-1 1.1 Grundlagen Zugstab: F L F x E, A F W u u An einem am linken Ende eingespannten linear elastischen Stab greift am rechten Ende
1. Formänderungsenergie 1.1 Grundlagen 1. Grundlastfälle 1.3 Beispiele.1-1 1.1 Grundlagen Zugstab: F L F x E, A F W u u An einem am linken Ende eingespannten linear elastischen Stab greift am rechten Ende
6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK)
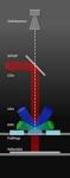 Technische Mechanik 2 (SS 2011) 6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK) Arbeit: 6.1 Grundbegriffe und Arbeitssatz 6.1 Grundbegriffe und Arbeitssatz
Technische Mechanik 2 (SS 2011) 6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK) Arbeit: 6.1 Grundbegriffe und Arbeitssatz 6.1 Grundbegriffe und Arbeitssatz
Eigenspannungszustand: Ermittlung der Schnittgrößen, die durch die Ersatzkräfte hervorgerufen
 www.statik-lernen.de Beispiele (Ein-) Gelenkrahmen Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines 2-fach
www.statik-lernen.de Beispiele (Ein-) Gelenkrahmen Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines 2-fach
Baustatik II. Kapitel IV. Einflusslinien für statisch unbestimmte Systeme. Institute of Structural Engineering Seite 1
 Institute of Structural Engineering Seite Baustatik II Kapitel IV Einflusslinien für statisch unbestimmte Systeme Institute of Structural Engineering Seite 2 Lernziele dieses Kapitels. Sich mit der Form
Institute of Structural Engineering Seite Baustatik II Kapitel IV Einflusslinien für statisch unbestimmte Systeme Institute of Structural Engineering Seite 2 Lernziele dieses Kapitels. Sich mit der Form
11 Balkenbiegung Technische Mechanik Balkenbiegung
 11 Balkenbiegung Balkenbiegung 2 Motivation / Einführung Ziele: Berechnung der Balkendurchbiegung (Deformation) Berechnung der Schnittgrößen für statisch unbestimmte Systeme Balken Definition Stabförmig;
11 Balkenbiegung Balkenbiegung 2 Motivation / Einführung Ziele: Berechnung der Balkendurchbiegung (Deformation) Berechnung der Schnittgrößen für statisch unbestimmte Systeme Balken Definition Stabförmig;
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Frühjahr 2009 Prüfungsfach Statik Klausur am 23.02.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Diplomprüfung Frühjahr 2009 Prüfungsfach Statik Klausur am 23.02.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Berechnung von Tragwerken
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 09.09.2005 (Bearbeitungszeit 90 Minuten)
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 09.09.2005 (Bearbeitungszeit 90 Minuten)
Biegung
 2. Biegung Wie die Normalkraft resultiert auch das Biegemoment aus einer Normalspannung. Das Koordinatensystem des Balkens wird so gewählt, dass die Flächenschwerpunkte der Querschnitte auf der x-achse
2. Biegung Wie die Normalkraft resultiert auch das Biegemoment aus einer Normalspannung. Das Koordinatensystem des Balkens wird so gewählt, dass die Flächenschwerpunkte der Querschnitte auf der x-achse
RUHR-UNIVERSITÄT BOCHUM FAKULTÄT FÜR BAUINGENIEURWESEN STATIK UND DYNAMIK. Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Baustatik & Festigkeitslehre Vorlesung & Übung
 Baustatik & Festigkeitslehre Vorlesung & Übung Vortragender: O.Univ.Prof. DI Dr. Dr. Konrad Bergmeister Kraftgrößenverfahren Wenn statisch unbestimmte Systeme berechnet werden sollen, müssen zusätzliche
Baustatik & Festigkeitslehre Vorlesung & Übung Vortragender: O.Univ.Prof. DI Dr. Dr. Konrad Bergmeister Kraftgrößenverfahren Wenn statisch unbestimmte Systeme berechnet werden sollen, müssen zusätzliche
Leseprobe. Kai-Uwe Bletzinger, Falko Dieringer, Rupert Fisch, Benedikt Philipp. Aufgabensammlung zur Baustatik
 Leseprobe Kai-Uwe Bletzinger, Falko Dieringer, Rupert Fisch, Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke ISBN (Buch): 978-3-446-4478-8 Weitere Informationen
Leseprobe Kai-Uwe Bletzinger, Falko Dieringer, Rupert Fisch, Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke ISBN (Buch): 978-3-446-4478-8 Weitere Informationen
Aufgabensammlung zur Baustatik
 Kai-Uwe Bletzinger Falko Dieringer Rupert Fisch Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke 5 Carl Hanser Verlag München PDF Bletzinger/Dieringer/Fisch/Philipp,
Kai-Uwe Bletzinger Falko Dieringer Rupert Fisch Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke 5 Carl Hanser Verlag München PDF Bletzinger/Dieringer/Fisch/Philipp,
Berechnung von Tragwerken
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Wintersemester 2004/2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 11.03.2005 (Bearbeitungszeit 90
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Wintersemester 2004/2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 11.03.2005 (Bearbeitungszeit 90
1. Aufgabe: (ca. 12 % der Gesamtpunkte)
 . August 07. Aufgabe: (ca. % der Gesamtunkte) a) Skizzieren Sie an den dargestellten Stäben die Knickformen der vier Euler-Knickfälle inklusive Lagerung und geben Sie zum Eulerfall mit der höchsten Knicklast
. August 07. Aufgabe: (ca. % der Gesamtunkte) a) Skizzieren Sie an den dargestellten Stäben die Knickformen der vier Euler-Knickfälle inklusive Lagerung und geben Sie zum Eulerfall mit der höchsten Knicklast
2. Sätze von Castigliano und Menabrea
 2. Sätze von Castigliano und Menabrea us der Gleichheit von äußerer rbeit und Formänderungsenergie kann die Verschiebung am Lastangriffspunkt berechnet werden, wenn an der Struktur nur eine Last angreift.
2. Sätze von Castigliano und Menabrea us der Gleichheit von äußerer rbeit und Formänderungsenergie kann die Verschiebung am Lastangriffspunkt berechnet werden, wenn an der Struktur nur eine Last angreift.
4. Balken. Brücken Tragflügel KFZ-Karosserie: A-Säule, B-Säule Rahmen: Fahrrad, Motorrad. Prof. Dr. Wandinger 2. Festigkeitslehre TM 2.
 4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
Arbeitsunterlagen. Statik 2
 Arbeitsunterlagen Statik 2 WS 2014/15 Stand 07.10.2014 Inhalt 1. Vertiefung KGV 1.1 Eingeprägte Auflagerverformungen 1.2 Vorspannung 1.3 Systeme mit elastischer Lagerung 1.4 Ermittlung von Federsteifigkeiten
Arbeitsunterlagen Statik 2 WS 2014/15 Stand 07.10.2014 Inhalt 1. Vertiefung KGV 1.1 Eingeprägte Auflagerverformungen 1.2 Vorspannung 1.3 Systeme mit elastischer Lagerung 1.4 Ermittlung von Federsteifigkeiten
Modulprüfung Baustatik II am 16. Februar 2012
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik II am. Februar Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik II am. Februar Name:.................................................................
Kleines Einmaleins der
 Wolfram Franke, Thorsten Kunow Kleines Einmaleins der Baustatik Wissenswertes für Neu- und Wiederlerner ULB Darmstadt Illlllllllllllllllllllll 16544701 kassel univershy Grundwissen 1 1.1 Statik sehen 1
Wolfram Franke, Thorsten Kunow Kleines Einmaleins der Baustatik Wissenswertes für Neu- und Wiederlerner ULB Darmstadt Illlllllllllllllllllllll 16544701 kassel univershy Grundwissen 1 1.1 Statik sehen 1
Baustatik I (WS 2017/2018) 1. Einführung. 1.2 Modellbildung LEHRSTUHL FÜR BAUSTATIK UNIVERSITÄT SIEGEN
 Baustatik I (WS 2017/2018) 1. Einführung 1.2 Modellbildung 1 Statische Berechnungen Für die statischen Berechnungen sind geeignete Tragwerksmodelle mit den maßgebenden Einflussgrößen zu wählen, welche
Baustatik I (WS 2017/2018) 1. Einführung 1.2 Modellbildung 1 Statische Berechnungen Für die statischen Berechnungen sind geeignete Tragwerksmodelle mit den maßgebenden Einflussgrößen zu wählen, welche
Statik im Bauwesen. HUSS-MEDIEN GmbH Verlag Bauwesen Berlin. Fritz Bochmann/Werner Kirsch. Band 3: Statisch unbestimmte ebene Systeme
 Fritz Bochmann/Werner Kirsch Statik im Bauwesen Band 3: Statisch unbestimmte ebene Systeme 13. Auflage HUSS-MEDIEN GmbH Verlag Bauwesen 10400 Berlin Inhaltsverzeichnis Einführung 11.1. Allgemeine Grundlagen
Fritz Bochmann/Werner Kirsch Statik im Bauwesen Band 3: Statisch unbestimmte ebene Systeme 13. Auflage HUSS-MEDIEN GmbH Verlag Bauwesen 10400 Berlin Inhaltsverzeichnis Einführung 11.1. Allgemeine Grundlagen
Statik 1 Hausübungen - 3. Semester (Bachelor)
 Statik 1 Hausübungen - 3. Semester (Bachelor) Aufgabenstellung Download als PDF per Internet: Homepage Fachbereich B: www.fbb.h-da.de Studium / Bachelor (B.Eng.) Grundstudium Modul-Übersicht Grundstudium
Statik 1 Hausübungen - 3. Semester (Bachelor) Aufgabenstellung Download als PDF per Internet: Homepage Fachbereich B: www.fbb.h-da.de Studium / Bachelor (B.Eng.) Grundstudium Modul-Übersicht Grundstudium
Grundfachklausur Teil 2 / Statik II
 Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 2 / Statik II im Sommersemester 204, am 08.09.204
Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 2 / Statik II im Sommersemester 204, am 08.09.204
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Herbst 2009 Prüfungsfach Statik Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Diplomprüfung Herbst 2009 Prüfungsfach Statik Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Vorlesung L Leichtbau, HS Fachwerke. Paolo Ermanni 7. Oktober 2015
 Vorlesung 151-3207-00L Leichtbau, HS 2015 Fachwerke Paolo Ermanni 7. Oktober 2015 PAOLO ERMANNI - 151-3207-K3-FACHWERKE 01.10.2015 1 Leitfaden Allgemeines Ebene statisch bestimmte Fachwerke Aufgabe 1 und
Vorlesung 151-3207-00L Leichtbau, HS 2015 Fachwerke Paolo Ermanni 7. Oktober 2015 PAOLO ERMANNI - 151-3207-K3-FACHWERKE 01.10.2015 1 Leitfaden Allgemeines Ebene statisch bestimmte Fachwerke Aufgabe 1 und
Praktikum Nichtlineare FEM
 Praktikum Nichtlineare FEM Einführung FEM II - Einführung 1 [email protected] Ziele des Praktikums Überblick über die Berechnung nichtlinearer Strukturen Umgang mit der kommerziellen FEM-Software
Praktikum Nichtlineare FEM Einführung FEM II - Einführung 1 [email protected] Ziele des Praktikums Überblick über die Berechnung nichtlinearer Strukturen Umgang mit der kommerziellen FEM-Software
Eigenspannungszustand: Ermittlung der Schnittgrößen, die durch die Ersatzkräfte hervorgerufen
 www.statik-lernen.de Beispiele Zweifeldträger Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines -fach statisch
www.statik-lernen.de Beispiele Zweifeldträger Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines -fach statisch
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:...
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 13.7.2004 (Bearbeitungszeit 45 Minuten) max. Punkte
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 13.7.2004 (Bearbeitungszeit 45 Minuten) max. Punkte
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Frühjahr 2006 Prüfungsfach Statik Klausur am 20.02.2006 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 4 6 25 20 30
Diplomprüfung Frühjahr 2006 Prüfungsfach Statik Klausur am 20.02.2006 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 4 6 25 20 30
Technische Mechanik für Wirtschaftsingenieure
 Technische Mechanik für Wirtschaftsingenieure Bearbeitet von Ulrich Gabbert, Ingo Raecke 3., aktualisierte und erweiterte Auflage 2006. Buch. 324 S. Hardcover ISBN 978 3 446 40960 6 Format (B x L): 16,2
Technische Mechanik für Wirtschaftsingenieure Bearbeitet von Ulrich Gabbert, Ingo Raecke 3., aktualisierte und erweiterte Auflage 2006. Buch. 324 S. Hardcover ISBN 978 3 446 40960 6 Format (B x L): 16,2
3. Elastizitätsgesetz
 3. Elastizitätsgesetz 3.1 Grundlagen 3.2 Isotropes Material 3.3 Orthotropes Material 3.4 Temperaturdehnungen 1.3-1 3.1 Grundlagen Elastisches Material: Bei einem elastischen Material besteht ein eindeutig
3. Elastizitätsgesetz 3.1 Grundlagen 3.2 Isotropes Material 3.3 Orthotropes Material 3.4 Temperaturdehnungen 1.3-1 3.1 Grundlagen Elastisches Material: Bei einem elastischen Material besteht ein eindeutig
Inhaltsverzeichnis. Teil I. Lehrbuch
 Teil I. Lehrbuch 1. Spannungen... 3 1.1 Der Spannungsvektor. Normal- und Schubspannungen... 3 1.1.1 Gleichheit zugeordneter Schubspannungen... 5 1.2 Der allgemeine räumliche Spannungszustand... 7 1.2.1
Teil I. Lehrbuch 1. Spannungen... 3 1.1 Der Spannungsvektor. Normal- und Schubspannungen... 3 1.1.1 Gleichheit zugeordneter Schubspannungen... 5 1.2 Der allgemeine räumliche Spannungszustand... 7 1.2.1
MECHANIK & WERKSTOFFE
 MECHANIK & WERKSTOFFE Statik Lagerung von Körpern 1-wertig Pendelstütze Seil (keine Lasten dazwischen) (nur Zug) Loslager Anliegender Stab Kraft in Stabrichtung Kraft in Seilrichtung Kraft in Auflagefläche
MECHANIK & WERKSTOFFE Statik Lagerung von Körpern 1-wertig Pendelstütze Seil (keine Lasten dazwischen) (nur Zug) Loslager Anliegender Stab Kraft in Stabrichtung Kraft in Seilrichtung Kraft in Auflagefläche
Baustatik I und II. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Bachelorprüfung Herbst 2010 Prüfungsfach Baustatik I und II Klausur am 23.08.2010 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche Punkte 30 29
Bachelorprüfung Herbst 2010 Prüfungsfach Baustatik I und II Klausur am 23.08.2010 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche Punkte 30 29
7.1 Grundregeln der Kinematik: Polplan
 7 Einflusslinien 7. Grundregeln der Kinematik: Polplan Trotz der Erfüllung der Bedingungsgleichungen für statisch (un)bestimmte Tragwerke (Abzählkriterien A/B) kann es vorkommen, dass Stabwerksstrukturen
7 Einflusslinien 7. Grundregeln der Kinematik: Polplan Trotz der Erfüllung der Bedingungsgleichungen für statisch (un)bestimmte Tragwerke (Abzählkriterien A/B) kann es vorkommen, dass Stabwerksstrukturen
4. Das Verfahren von Galerkin
 4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
Lehrveranstaltung Stereostatik
 ehrveranstaltung Stereostatik Thema 7: Berechnung ebener Rahmen Bergische Universität Wuppertal Baumechanik und Numerische Methoden Prof. Dr.-Ing. W. Zahlten Mechanik 1 Ebene Rahmen 7.1 Problemstellung
ehrveranstaltung Stereostatik Thema 7: Berechnung ebener Rahmen Bergische Universität Wuppertal Baumechanik und Numerische Methoden Prof. Dr.-Ing. W. Zahlten Mechanik 1 Ebene Rahmen 7.1 Problemstellung
BAUMECHANIK I Prof. Dr.-Ing. Christian Barth
 BAUMECHANIK I Umfang V/Ü/P (ECTS) 2/2/0 (5) 2/2/0 2/2/0 2/2/0-2*/2*/0 - Diplom 5. 6. 7. 8. 9. 10. Definitionen und Klassifizierungen Kräfte und Kraftarten, Vektor, Vektorsysteme Darstellung vektorieller
BAUMECHANIK I Umfang V/Ü/P (ECTS) 2/2/0 (5) 2/2/0 2/2/0 2/2/0-2*/2*/0 - Diplom 5. 6. 7. 8. 9. 10. Definitionen und Klassifizierungen Kräfte und Kraftarten, Vektor, Vektorsysteme Darstellung vektorieller
Universität für Bodenkultur
 Baustatik Übungen Kolloquiumsvorbereitung Universität für Bodenkultur Department für Bautechnik und Naturgefahren Wien, am 15. Oktober 2004 DI Dr. techn. Roman Geier Theoretischer Teil: Ziele / Allgemeine
Baustatik Übungen Kolloquiumsvorbereitung Universität für Bodenkultur Department für Bautechnik und Naturgefahren Wien, am 15. Oktober 2004 DI Dr. techn. Roman Geier Theoretischer Teil: Ziele / Allgemeine
Elastizitätslehre Biegebalken
 3. Semester Seite 1/9 Elastizitätslehre Biegebalken 0. Inhalt 0. Inhalt 1 1. Allgemeines 1 2. Begriffe 2 3. Grundlagen 2 4. Biegebalken 2 4.1 Allgemeines 2 4.2 Werkstoff und Randfaserdehnung 3 4.3 Geometrische
3. Semester Seite 1/9 Elastizitätslehre Biegebalken 0. Inhalt 0. Inhalt 1 1. Allgemeines 1 2. Begriffe 2 3. Grundlagen 2 4. Biegebalken 2 4.1 Allgemeines 2 4.2 Werkstoff und Randfaserdehnung 3 4.3 Geometrische
( ) Winter Montag, 19. Januar 2015, Uhr, HIL E 1. Name, Vorname: Studenten-Nr.:
 Baustatik I+II Sessionsprüfung (101-0113-00) Winter 2015 Montag, 19. Januar 2015, 09.00 12.00 Uhr, HIL E 1 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet
Baustatik I+II Sessionsprüfung (101-0113-00) Winter 2015 Montag, 19. Januar 2015, 09.00 12.00 Uhr, HIL E 1 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet
Technische Mechanik für Wirtschaftsingenieure
 Ulrich Gabbert/Ingo Raecke Technische Mechanik für Wirtschaftsingenieure 5., aktualisierte Auflage Mit 301 Abbildungen, 16 Tabellen, 83 Beispielen sowie einer CD-ROM Wi im Carl Hanser Verlag 1 Statik 11
Ulrich Gabbert/Ingo Raecke Technische Mechanik für Wirtschaftsingenieure 5., aktualisierte Auflage Mit 301 Abbildungen, 16 Tabellen, 83 Beispielen sowie einer CD-ROM Wi im Carl Hanser Verlag 1 Statik 11
Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am (bitte deutlich schreiben!)
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 04.0.00 Name: Vorname: (bitte deutlich schreiben) Matr.-Nr.: (9-stellig) Aufgabe 4 5 6 7 8 9 Summe mögliche Punkte 7 5 4 6 6 4 4 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 04.0.00 Name: Vorname: (bitte deutlich schreiben) Matr.-Nr.: (9-stellig) Aufgabe 4 5 6 7 8 9 Summe mögliche Punkte 7 5 4 6 6 4 4 0 erreichte Punkte
Euler-Bernoulli-Balken
 Euler-Bernoulli-Balken 2 2.1 Einführende Bemerkungen Ein Balken ist als langer prismatischer Körper, der schematisch in Abb. 2.1 dargestellt ist, definiert. Die folgenden Ableitungen unterliegen hierbei
Euler-Bernoulli-Balken 2 2.1 Einführende Bemerkungen Ein Balken ist als langer prismatischer Körper, der schematisch in Abb. 2.1 dargestellt ist, definiert. Die folgenden Ableitungen unterliegen hierbei
2. Statisch bestimmte Systeme
 1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
Einführung in die Plastizitätstheorie
 Einführung in die Plastizitätstheorie Mit technischen Anwendungen von Dr.-lng. habil. Reiner Kreißig Mit 151 Bildern Fachbuchverlag Leipzig-Köln Inhalt sverzeichnls 1. Mechanisches Verhalten metallischer
Einführung in die Plastizitätstheorie Mit technischen Anwendungen von Dr.-lng. habil. Reiner Kreißig Mit 151 Bildern Fachbuchverlag Leipzig-Köln Inhalt sverzeichnls 1. Mechanisches Verhalten metallischer
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Lösung zur Diplomprüfung Frühjahr 2007 Prüfungsfach Statik Klausur am 26.02.2007 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 5 6 7 8 9 Summe mögliche Punkte 20 5
Lösung zur Diplomprüfung Frühjahr 2007 Prüfungsfach Statik Klausur am 26.02.2007 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 5 6 7 8 9 Summe mögliche Punkte 20 5
2. Der ebene Spannungszustand
 2. Der ebene Spannungszustand 2.1 Schubspannung 2.2 Dünnwandiger Kessel 2.3 Ebener Spannungszustand 2.4 Spannungstransformation 2.5 Hauptspannungen 2.6 Dehnungen 2.7 Elastizitätsgesetz Prof. Dr. Wandinger
2. Der ebene Spannungszustand 2.1 Schubspannung 2.2 Dünnwandiger Kessel 2.3 Ebener Spannungszustand 2.4 Spannungstransformation 2.5 Hauptspannungen 2.6 Dehnungen 2.7 Elastizitätsgesetz Prof. Dr. Wandinger
5. Elastizitätsgesetz
 5. Elastizitätsgesetz Das Materialgesetz ist eine Beziehung zwischen den Spannungen, den Verzerrungen und den Temperaturänderungen. Das Materialgesetz für einen elastischen Körper wird als Elastizitätsgesetz
5. Elastizitätsgesetz Das Materialgesetz ist eine Beziehung zwischen den Spannungen, den Verzerrungen und den Temperaturänderungen. Das Materialgesetz für einen elastischen Körper wird als Elastizitätsgesetz
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
Ruhr-Universität Bochum Bau- und Umweltingenieurwissenschaften Statik und Dynamik. Bachelorprüfung Herbst Klausur am
 Bachelorprüfung Herbst 2012 Modul 13 (BI) / Modul IV 3b (UTRM) Baustatik I und II Klausur am 27.08.2012 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 Summe mögliche
Bachelorprüfung Herbst 2012 Modul 13 (BI) / Modul IV 3b (UTRM) Baustatik I und II Klausur am 27.08.2012 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 Summe mögliche
Baustatik Theorie I. und II. Ordnung
 Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 3., völlig neu bearbeitete und erweiterte Auflage 1996 Werner-Verlag Inhaltsverzeichnis 1 Einfuhrung
Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 3., völlig neu bearbeitete und erweiterte Auflage 1996 Werner-Verlag Inhaltsverzeichnis 1 Einfuhrung
Baumechanik - Repetitorium
 Mechanik und Numerische Methoden Thema 1: Fachwerke Aufgabe 1.1 Ein ebenes Fachwerk wird durch eine Reihe von Einzelkräften unterschiedlicher Größe belastet. a) Weisen Sie nach, dass das Fachwerk statisch
Mechanik und Numerische Methoden Thema 1: Fachwerke Aufgabe 1.1 Ein ebenes Fachwerk wird durch eine Reihe von Einzelkräften unterschiedlicher Größe belastet. a) Weisen Sie nach, dass das Fachwerk statisch
Stahlbau 1. Name:... Matr. Nr.:...
 1/12 Name:... Matr. Nr.:... A. Rechnerischer steil 1. Knicknachweis eines zentrisch gedrückten Stabes Zwei zentrisch gedrückte Gelenkstäbe [HEA 220, E= 210000N/mm²] werden in der x-z Ebene durch Seile
1/12 Name:... Matr. Nr.:... A. Rechnerischer steil 1. Knicknachweis eines zentrisch gedrückten Stabes Zwei zentrisch gedrückte Gelenkstäbe [HEA 220, E= 210000N/mm²] werden in der x-z Ebene durch Seile
Herbert Mang Günter Hofstetter. Festigkeitslehre. Mit einem Beitrag von Josef Eberhardsteiner. Dritte, aktualisierte Auflage
 Herbert Mang Günter Hofstetter Festigkeitslehre Mit einem Beitrag von Josef Eberhardsteiner Dritte, aktualisierte Auflage SpringerWienNewYork Inhaltsverzeichnis 1 Einleitung 1 2 Mathematische Grundlagen
Herbert Mang Günter Hofstetter Festigkeitslehre Mit einem Beitrag von Josef Eberhardsteiner Dritte, aktualisierte Auflage SpringerWienNewYork Inhaltsverzeichnis 1 Einleitung 1 2 Mathematische Grundlagen
2.1.8 Praktische Berechnung von statisch unbestimmten, homogenen
 Inhaltsverzeichnis 1 Einleitung... 1 1.1 Aufgaben der Elastostatik.... 1 1.2 Einige Meilensteine in der Geschichte der Elastostatik... 4 1.3 Methodisches Vorgehen zur Erarbeitung der vier Grundlastfälle...
Inhaltsverzeichnis 1 Einleitung... 1 1.1 Aufgaben der Elastostatik.... 1 1.2 Einige Meilensteine in der Geschichte der Elastostatik... 4 1.3 Methodisches Vorgehen zur Erarbeitung der vier Grundlastfälle...
Grundfachklausur Teil 1 / Statik I
 Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 1 / Statik I im Wintersemester 2013/2014, am 21.03.2014
Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 1 / Statik I im Wintersemester 2013/2014, am 21.03.2014
2. Materialgesetze und Festigkeitshypothesen
 Baustatik III SS 2016 2. Materialgesetze und Festigkeitshypothesen 2.3 Festigkeitshypothesen Vergleichsspannung Die Vergleichsspannung ist eine fiktive einachsige Spannung, die dieselbe Materialbeanspruchung
Baustatik III SS 2016 2. Materialgesetze und Festigkeitshypothesen 2.3 Festigkeitshypothesen Vergleichsspannung Die Vergleichsspannung ist eine fiktive einachsige Spannung, die dieselbe Materialbeanspruchung
Institut für Allgemeine Mechanik der RWTH Aachen
 Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
Kleines Einmaleins der Baustatik
 IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Buchvorstellung Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher
IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Buchvorstellung Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher
Technische Mechanik für Wirtschaftsingenieure
 Technische Mechanik für Wirtschaftsingenieure von Ulrich Gabbert, Ingo Raecke 2. Auflage Hanser München 2004 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 22807 8 Zu Leseprobe schnell und portofrei
Technische Mechanik für Wirtschaftsingenieure von Ulrich Gabbert, Ingo Raecke 2. Auflage Hanser München 2004 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 22807 8 Zu Leseprobe schnell und portofrei
Baustatik 2. Semestrale am Aufgabe 2 (3 Punkte) (Biegemoment u. Krümmung infolge T) (Normalkraft u. Dehnung infolge T s ) (Senkfeder)
 Baustatik 2 --- Sommersemester 2001 Semestrale Seite 2 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2001 Matr.---Nr. :... Fachsemester:... Aufgabe 1 (4 Punkte)
Baustatik 2 --- Sommersemester 2001 Semestrale Seite 2 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2001 Matr.---Nr. :... Fachsemester:... Aufgabe 1 (4 Punkte)
Grundkurs Technische Mechanik
 Frank Mestemacher Grundkurs Technische Mechanik Statik der Starrk6rper, Elastostatik, Dynamik Inhaltsverzeichnis Vorwort v I Statik der St.arrkorper 1 1 Mathematische Voriiberlegungen 3 1.1 Skalare.. 3
Frank Mestemacher Grundkurs Technische Mechanik Statik der Starrk6rper, Elastostatik, Dynamik Inhaltsverzeichnis Vorwort v I Statik der St.arrkorper 1 1 Mathematische Voriiberlegungen 3 1.1 Skalare.. 3
Skript zur Vorlesung Baustatik II
 BS III Skript zur Vorlesung Baustatik II an der Hochschule Augsburg Hochschule für angewandte Wissenschaften University of Applied Sciences Prof. Dr.-Ing. Gerhard Zirwas BS III Inhalt I. Wiederholungen
BS III Skript zur Vorlesung Baustatik II an der Hochschule Augsburg Hochschule für angewandte Wissenschaften University of Applied Sciences Prof. Dr.-Ing. Gerhard Zirwas BS III Inhalt I. Wiederholungen
Sommer Baustatik I+II Sessionsprüfung. Bemerkungen. ( und ) Montag, 08. August 2016, Uhr, HIL G 61 / HIL E 9
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2016 Montag, 08. August 2016, 09.00 12.00 Uhr, HIL G 61 / HIL E 9 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2016 Montag, 08. August 2016, 09.00 12.00 Uhr, HIL G 61 / HIL E 9 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
Schnittgrößen und Vorzeichenkonvention
 Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Baustatik Theorie I. und II. Ordnung
 Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 4., neu bearbeitete und erweiterte Auflage 2002 Werner Verlag Inhaltsverzeichnis 1 Einführung 11
Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 4., neu bearbeitete und erweiterte Auflage 2002 Werner Verlag Inhaltsverzeichnis 1 Einführung 11
Technische Mechanik. Fachwerke
 7 Fachwerke Fachwerke Fachwerke Anwendungsbeispiele... Beispiele aus dem Ingenieurwesen (wikipedia.org) Fachwerke 1 Fachwerke Anwendungsbeispiele nanowerk.com (T. Bückmann) wikipedia.org Beispiele aus
7 Fachwerke Fachwerke Fachwerke Anwendungsbeispiele... Beispiele aus dem Ingenieurwesen (wikipedia.org) Fachwerke 1 Fachwerke Anwendungsbeispiele nanowerk.com (T. Bückmann) wikipedia.org Beispiele aus
Modulprüfung Baustatik I am 8. Juli 2015
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 8. Juli 015 Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 8. Juli 015 Name:.................................................................
Übungsaufgaben Systemmodellierung WT 2015
 Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
Inhaltsverzeichnis. I Starrkörperstatik 17. Vorwort 5
 Inhaltsverzeichnis Vorwort 5 1 Allgemeine Einführung 13 1.1 Aufgabe und Einteilung der Mechanik.............. 13 1.2 Vorgehen in der Mechanik..................... 14 1.3 Physikalische Größen und Einheiten................
Inhaltsverzeichnis Vorwort 5 1 Allgemeine Einführung 13 1.1 Aufgabe und Einteilung der Mechanik.............. 13 1.2 Vorgehen in der Mechanik..................... 14 1.3 Physikalische Größen und Einheiten................
a) b) c) d) e) f) g) h) i)
 Ausgabe: 8.1.15 Übung 5: Schub Einleitung und Lernziele strukturen bestehen meist aus dünnwandigen Profilen. Während bei vollen Querschnitten die Schubspannungen oft kaum eine Rolle spielen, ist der Einfluss
Ausgabe: 8.1.15 Übung 5: Schub Einleitung und Lernziele strukturen bestehen meist aus dünnwandigen Profilen. Während bei vollen Querschnitten die Schubspannungen oft kaum eine Rolle spielen, ist der Einfluss
Mechanisches Verhalten und numerische Simulationen von TPE im Vergleich zu Elastomeren
 Mechanisches Verhalten und numerische Simulationen von TPE im Vergleich zu Elastomeren O. Haeusler & H. Baaser Computer Aided Engineering TPE@DKT / Nürnberg, 3. Juli 2012 Agenda Materialverhalten aus Ingenieur-Sicht
Mechanisches Verhalten und numerische Simulationen von TPE im Vergleich zu Elastomeren O. Haeusler & H. Baaser Computer Aided Engineering TPE@DKT / Nürnberg, 3. Juli 2012 Agenda Materialverhalten aus Ingenieur-Sicht
Teil 1 Zehn einfache Prüfbeispiele zur Verifikation von Software-Ergebnissen. Beispiel 1 Einachsige Biegung mit Druck 11
 Inhaltsverzeichnis Vorwort Zum Gebrauch dieses Buches 1 Teil 1 Zehn einfache Prüfbeispiele zur Verifikation von Software-Ergebnissen Beispiel 1 Einachsige Biegung mit Druck 11 Kragstütze mit aufgesetztem
Inhaltsverzeichnis Vorwort Zum Gebrauch dieses Buches 1 Teil 1 Zehn einfache Prüfbeispiele zur Verifikation von Software-Ergebnissen Beispiel 1 Einachsige Biegung mit Druck 11 Kragstütze mit aufgesetztem
Modulprüfung Baustatik I am 3. Februar 2016
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 3. Februar 016 Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 3. Februar 016 Name:.................................................................
1. Einführung Festigkeitslehre
 1. Einführung estigkeitslehre Themen der estigkeitslehre Zugbeanspruchung Hooksches Gesetz lächenmomente. Grades estigkeitslehre Druckbeanspruchung Abscherung lächenpressung www.lernen-interaktiv.ch 1
1. Einführung estigkeitslehre Themen der estigkeitslehre Zugbeanspruchung Hooksches Gesetz lächenmomente. Grades estigkeitslehre Druckbeanspruchung Abscherung lächenpressung www.lernen-interaktiv.ch 1
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Herbst 27 Prüfungsfach Statik Klausur am 27.8.27 ame: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 2 5 5 25 25 25 25 25
Diplomprüfung Herbst 27 Prüfungsfach Statik Klausur am 27.8.27 ame: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 2 5 5 25 25 25 25 25
2. Definieren Sie die 2 Arten von Verzerrungen. Vorzeichenregeln.
 FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
3.7 Sonderprobleme Ausnutzung der Symmetrie und Antimetrie. Größe. Belastung
 VORLESUGSAUSKRIPT BAUSTATIK I II (UVERTIEFT).7 Sonderrobeme.7. Ausnutzung der Symmetrie und Antimetrie Durch die Ausnutzung der Symmetrie und Antimetrie kann der Grad der statischen Unbestimmtheit (u.
VORLESUGSAUSKRIPT BAUSTATIK I II (UVERTIEFT).7 Sonderrobeme.7. Ausnutzung der Symmetrie und Antimetrie Durch die Ausnutzung der Symmetrie und Antimetrie kann der Grad der statischen Unbestimmtheit (u.
Technische Mechanik 2 Festigkeitslehre
 Technische Mechanik 2 Festigkeitslehre Bearbeitet von Russell C. Hibbeler 8., aktualisierte Auflage 2013. Buch. 928 S. Hardcover ISBN 978 3 86894 126 5 Format (B x L): 19,5 x 24,6 cm Gewicht: 1835 g Weitere
Technische Mechanik 2 Festigkeitslehre Bearbeitet von Russell C. Hibbeler 8., aktualisierte Auflage 2013. Buch. 928 S. Hardcover ISBN 978 3 86894 126 5 Format (B x L): 19,5 x 24,6 cm Gewicht: 1835 g Weitere
Baustatik - einfach und anschaulich. Bauwerk. Herausgeber: Dr.-Ing. Eddy Widjaja
 Herausgeber: Dr.-Ing. Eddy Widjaja Autoren: Prof. Dr.-Ing. Klaus Holschemacher Prof. Dipl.-Ing. Klaus-Jürgen Schneider Dr.-Ing. Eddy Widjaja Baustatik - einfach und anschaulich Baustatische Grundlagen
Herausgeber: Dr.-Ing. Eddy Widjaja Autoren: Prof. Dr.-Ing. Klaus Holschemacher Prof. Dipl.-Ing. Klaus-Jürgen Schneider Dr.-Ing. Eddy Widjaja Baustatik - einfach und anschaulich Baustatische Grundlagen
Verzerrungen und Festigkeiten
 Verzerrungen und Festigkeiten Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Verzerrungen
Verzerrungen und Festigkeiten Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Verzerrungen
Klausur Technische Mechanik
 Institut für Mechanik und Fluiddynamik Institut für Mechanik und Fluiddynamik Klausur Technische Mechanik 10/02/10 Aufgabe S1 Gegeben ist ein durch eine Pendelstütze und ein Festlager A abgestütztes Fachwerk.
Institut für Mechanik und Fluiddynamik Institut für Mechanik und Fluiddynamik Klausur Technische Mechanik 10/02/10 Aufgabe S1 Gegeben ist ein durch eine Pendelstütze und ein Festlager A abgestütztes Fachwerk.
Prüfung - Technische Mechanik II
 Prüfung - Technische Mechanik II SoSe 2013 2. August 2013 FB 13, Festkörpermechanik Prof. Dr.-Ing. F. Gruttmann Name: Matr.-Nr.: Studiengang: Platznummer Raumnummer Die Aufgaben sind nicht nach ihrem Schwierigkeitsgrad
Prüfung - Technische Mechanik II SoSe 2013 2. August 2013 FB 13, Festkörpermechanik Prof. Dr.-Ing. F. Gruttmann Name: Matr.-Nr.: Studiengang: Platznummer Raumnummer Die Aufgaben sind nicht nach ihrem Schwierigkeitsgrad
