Hamiltonsche Graphen (2. Teil)
|
|
|
- Leon Hofmann
- vor 9 Jahren
- Abrufe
Transkript
1 Hamiltonsche Graphen (2. Teil)
2 Themen des Vortrages Für Schachspieler Hamiltons Spiel Sitzordnungen Eine billige Rundreise Ein vielleicht unlösbares Problem Bäcker mit Kenntnissen in Graphentheorie Fazit Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 2
3 Für Schachspieler Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 3
4 Für Schachspieler Problematik für die Figur TURM: Turm nur geradeaus und quer, nicht diagonal Frage 1: Kann Turm über alle Felder eines Schachbrettes genau einmal ziehen und am Ausgangspunkt wieder auskommen? Frage 2: Hat das irgendwie was mit Graphen zu tun? Aufgabe: Überlegung für ein 4x4 Schachbrett Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 4
5 Für Schachspieler Lösungsansatz: Definieren Felder als Ecken und Zugmöglichkeiten als Kanten Zusätzliche Restriktion: Turm darf nur 1 Feld ziehen erhalten gleiche Aufgabe wie einen hamiltonschen Kreis zu finden dieser existiert Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 5
6 Für Schachspieler Turm zieht über jedes Feld genau einmal Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 6
7 Für Schachspieler Überlegung für ein 5x5 Schachbrett: jedes Feld 1 mal besuchen und wieder zurück zum Start 25 mal ziehen Aber: je Schritt ein Farbwechsel des Feldes Start auf schwarz, dann jedes ungerade Feld weiß, auch das 25. also unmöglich zu lösen Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 7
8 Für Schachspieler Allgemein: Soll ein Turm auf einem (n x n)-schachbrett über alle Felder genau einmal ziehen und zum Ausgangspunkt zurückkehren, so ist dies nur möglich, falls n gerade ist Sind aber auch größere Schritte erlaubt, so kann ein Turm durchaus auf einem Schachbrett mit ungerader Eckenzahl (nach Def.: Felderzahl) alle Felder besuchen und wieder zum Ausgangspunkt zurückkehren Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 8
9 Für Schachspieler (Bsp. Für Schachbrett mit ungerader Eckenzahl) Hamiltonscher Kreis mit einem großen Schritt Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 9
10 Für Schachspieler Aufgabe: Käse der Form eines Würfels mit Maßen 3x3x3 soll von Maus links unten beginnend aufgefressen werden. Kann sie sich durch alle kleinen Würfel der Maße 1x1x1 mit jeweils Einerschritten hindurch fressen und in der Mitte aufhören? Kann sie es schaffen wenn sie an einer anderen Stelle anfängt zu fressen? Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 10
11 Für Schachspieler Lösung: Nein, es ist unmöglich! 1. Ebene 2. Ebene 3. Ebene Man kann Würfelfelder wie ein dreidimensionales Schachbrett einfärben (siehe oben). Startet Maus egal wo, z.b. auf schwarz (1. Feld) so muss sie um zuletzt in die Mitte zu gelangen weitere 26 Felder durchqueren, wobei jedes ungerade wieder schwarz ist. Das heißt, die Mitte (27. Feld) kann unmöglich weiß sein, was aber nach Schachbrettfärbung sein müsste. Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 11
12 Für Schachspieler Problematik nun für die Figur Pferd: nur Sprünge in L-Form möglich Frage : Kann denn ein Pferd über alle Felder eines Schachbrettes genau einmal ziehen und am Ausgangspunkt wieder auskommen? Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 12
13 Für Schachspieler Lösungsansatz: Auch Pferd wechselt bei jedem Zug die Farbe des Feldes wenn Lösung existiert nur für Schachbretter mit gerader Anzahl von Feldern Aufgabe: Überlegung für ein 4x4 Spielfeld? Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 13
14 Für Schachspieler Lösung: Auf 4x4 Spielfeld trotzdem nicht lösbar Problem sind Ecken: Nur von 2 bestimmten Feldern erreichbar Von denen aus direkt auch zu beiden Ecken, sonst nie wieder Es entsteht Kreis aus 4 Feldern, aus dem nie wieder raus Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 14
15 Für Schachspieler Allgemein: Für 6 x 6 Schachbretter und größer mit gerader Eckenzahl kann das Pferd jedes Feld besuchen und wieder zum Ausgangspunkt zurückkehren. Es ist jedoch sehr aufwändig eine Lösung für größere Schachbretter zu finden Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 15
16 Für Schachspieler Lösung für ein 6 x 6 Schachbrett Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 16
17 Hamiltons Spiel Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 17
18 Hamiltons Spiel Hamilton erfand ein Spiel für 2 Personen: Reise um die Welt Jeder, der 20 Punkte stellt dabei eine Stadt dar Außerdem gibt es 20 durchnummerierte Steine Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 18
19 Hamiltons Spiel Spielablauf: Spieler 1 beginnt Reise und setzt Steine 1 bis 5 nacheinander so, dass zusammenhängende Kette entsteht Spieler 2 setzt Reise fort und muss restliche 15 Steine so legen, dass insgesamt eine Rundreise entsteht Aufgabe: Formuliert Aufgabe nach Kenntnissen über Graphen Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 19
20 Hamiltons Spiel Lösung: Erster Spieler gibt Weg vor, der aus 4 Kanten besteht Der 2. Spieler ergänzt ihn zum hamiltonschen Kreis => Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 20
21 Sitzordnungen Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 21
22 Sitzordnungen Überlegung: Können 6 Personen an einem rundem Tisch so platziert werden, dass jeder zwischen 2 Personen sitzt, die er schon kennt? Personen heißen A, B, C, D, E, F In folgenden Gruppen kennt jeder die jeweils anderen: A, B, D, E B, C, F A, F C, D Aufgabe: 1) Löst Aufgabe mit Hilfe der Graphentheorie 2) Existiert ein hamiltonscher Kreis als Lösung? Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 22
23 Sitzordnungen Lösung: Definiere Personen als Ecken und Kanten wenn sich 2 Personen kennen Wir sehen: Graph ist hamiltonsch Setzt man Leute nun entsprechend einem hamiltonschen Kreis Erhält man erwünschtes Ergebnis Eine mögliche Lösung Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 23
24 Eine billige Rundreise Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 24
25 Eine billige Rundreise Überlegung: Wie im 1. Teil von Karina: Reise durch alle Städte, jede aber nur einmal Nun kein Pauschalpreis, sondern Fahrpreis ist streckenlängenabhängig Planung der Rundreise nun durch knappe Kasse der Reiseteilnehmer erschwert Reise soll so günstig wie möglich werden Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 25
26 Eine billige Rundreise Welche ist die billigste Rundreise 3 versch. Rundfahrtmöglichkeiten (richtungsunabh.) Kürzeste A-B-D-C-A mit Preis 49 GE Städte mit Verbindungen => wieder Graph, neu sind Zahlen an den Kanten Wir erhalten einen Bewerteten Graphen Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 26
27 Ein vielleicht unlösbares Problem Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 27
28 Ein vielleicht unlösbares Problem Geschäftsmann hat Kunden in mehreren Orten zu betreuen und danach in sein Büro zurückkehren Fahrtroute so planen, dass er jeden Ort an fährt und die zurückgelegte Strecke möglichst kurz ist Traveling Salesman Problem Im vorherigen Bsp. Der billigen Rundreise ist das kein Problem, weil nur kleiner Graph Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 28
29 Ein vielleicht unlösbares Problem Wie wir im 1. Teil gesehen haben, ist die Anzahl der hamiltonschen Kreise eines vollständigen n-ecks genau Bei 6 Städten macht das schon 60 Möglichkeiten Bei 20 Städten sind es: n 1! Möglichkeiten Rechner mit 1 Mio. Rechnungen/sec würde 14 Milliarden Jahre an dieser Aufgabe rechnen Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 29
30 Ein vielleicht unlösbares Problem Aufgabe: Ein Radfahrer will Rundfahrt durch alle Orte der Karte machen, wobei dir gesamte Fahrtzeit möglichst kurz sein soll. In der Karte sieht man als Wertung des Graphen die jeweiligen Fahrtzeiten zwischen 2 Orten. Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 30
31 Ein vielleicht unlösbares Problem Lösung: Verwende das Prinzip längste Wege zu vermeiden. Als einzig mögliche Lösung ergibt sich die eingezeichnete Route. Die Fahrt dauert 130 min. Was ist aber mit folgendem Problem? Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 31
32 Ein vielleicht unlösbares Problem Aufgabe: Ein LKW-Fahrer will auf seiner Fahrt den größtmöglichen Gewinn machen. Hier gibt es auch negative Zahlen, die Verlust auf einer Strecke bedeuten, z.b. durch eine Leerfahrt hervorgerufen. Gilt hier nun auch, alle dem Wert nach kleinsten Kanten zu meiden? Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 32
33 Ein vielleicht unlösbares Problem Lösung: Nein! Es existieren 2 beste Routen, wobei, die eine sogar eine Kante besucht, deren Wert kleiner als 0 ist, dies aber mit großen Werten der nächsten Kanten ausgleicht. (s. Bild) Das heißt, nicht immer kann man davon ausgehen, die beste Route zu finden, wenn man die Kanten mit den kleinsten (im anderen Bsp. größten) Werten meidet. Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 33
34 Ein vielleicht unlösbares Problem Erwünscht wäre Algorithmus, der zu jedem beliebigen bewerteten Graphen den hamiltonschen Kreis mit dem niedrigsten Wert findet Zur Zeit gibt es lediglich gute Näherungen, die mehr oder weniger schnell sind und darauf beruhen Kanten mit großen Werten zu meiden (nicht immer optimal, s. Bsp.) Annahme: Hätte man eine Lösung des TSP gefunden, wäre dies gleichzeitig auch die Lösung des Problems der hamiltonschen Graphen Man könnte darauf basierend untersuchen ob Graph hamiltonsch ist oder nicht Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 34
35 Ein vielleicht unlösbares Problem Beweis: Ergänzen den zu untersuchenden Graphen zu einem vollständigen An Kanten des ursprünglichen Graphen schreiben wir eine 0, an neue Kanten eine 1 Ist TSP gelöst erhalten wir hamiltonschen Kreis mit kleinstem Wert z als Summe der Kanten: Ist z = 0: nur Kanten des urspr. Graphen benutzt Ursprünglicher Graph ist hamiltonsch Ist z > 0: auch neue Kanten benutzt Ursprünglicher Graph ist nicht hamiltonsch Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 35
36 Bäcker mit Kenntnissen in Graphentheorie Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 36
37 Bäcker mit Kenntnissen in Graphentheorie Bewertete Graphen in Produktionsprozessen Beispiel: Bäcker backt an einem Tag Mischbrot, Baguettebrot, Zwiebelbrötchen, Rosinenbrötchen und Knusperbrötchen Nach einer Sorte Maschine reinigen und neu einstellen Jede Änderung dauert gewisse Zeit Ziel: Unproduktive Zwischenzeiten möglichst kurz halten Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 37
38 Bäcker mit Kenntnissen in Graphentheorie Umwandlung in Graphenaufgabe: Erhalten wieder bekannte Aufgabe: Ges.: hamiltonscher Kreis mit möglichst geringer Gesamtbewertung 2 verschiedene Lösungen: M-r-k-z-B-M oder M-r-z-k-B-M mit je 70 ZE en Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 38
39 Fazit Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 39
40 Fazit Konnten Graphen finden, die nicht hamiltonsch waren Wurde Ecke entfernt und mit ihr alle dazugehörigen Kanten, war Restgraph nicht zusammenhängend Eckengelöschte Graphen Es war jedoch unmöglich einen Algorithmus zu finden, der uns zeigen konnte, dass ein Graph hamiltonsch ist Nils Gröblinghoff Hamiltonsche Graphen 2.Teil 40
Diskrete Mathematik. Hamiltonsche Graphen Teil I. Karina Arndt
 Diskrete Mathematik Hamiltonsche Graphen Teil I Karina Arndt 21.06.2006 Übersicht Einleitung Hamiltonsch und eulersch Hamiltonsche Kreise Hamiltonsche Graphen neu zeichnen Kreise und Wege Reguläre Graphen
Diskrete Mathematik Hamiltonsche Graphen Teil I Karina Arndt 21.06.2006 Übersicht Einleitung Hamiltonsch und eulersch Hamiltonsche Kreise Hamiltonsche Graphen neu zeichnen Kreise und Wege Reguläre Graphen
Eulerweg, Eulerkreis. Das Königsberger Brückenproblem. Definition 3.1. Ein Weg, der jede Kante von G genau einmal
 3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
Hamiltonsche Graphen
 Hamiltonsche Graphen Definition 3.2. Es sei G = (V, E) ein Graph. Ein Weg, der jeden Knoten von G genau einmal enthält, heißt hamiltonscher Weg. Ein Kreis, der jeden Knoten von G genau einmal enthält,
Hamiltonsche Graphen Definition 3.2. Es sei G = (V, E) ein Graph. Ein Weg, der jeden Knoten von G genau einmal enthält, heißt hamiltonscher Weg. Ein Kreis, der jeden Knoten von G genau einmal enthält,
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein
 Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Graphen für Einsteiger
 Manfred Nitzsche Graphen für Einsteiger Rund um das Haus vom Nikolaus vieweg 1 Erste Graphen 1 Das Haus vom Nikolaus 1 Was ist ein Graph? 2 Auch das ist bei Graphen möglich! 3 Der Grad einer Ecke 4 Verschiedene
Manfred Nitzsche Graphen für Einsteiger Rund um das Haus vom Nikolaus vieweg 1 Erste Graphen 1 Das Haus vom Nikolaus 1 Was ist ein Graph? 2 Auch das ist bei Graphen möglich! 3 Der Grad einer Ecke 4 Verschiedene
9: Gewichtete Graphen
 Chr.Nelius: Graphentheorie (WS 06/7) 9 9: Gewichtete Graphen Beispiel: Eine Straßenkarte mit Entfernungsangaben zwischen den Orten ist ein Beispiel für einen gewichteten Graphen. (9.) DEF: Ein Graph G
Chr.Nelius: Graphentheorie (WS 06/7) 9 9: Gewichtete Graphen Beispiel: Eine Straßenkarte mit Entfernungsangaben zwischen den Orten ist ein Beispiel für einen gewichteten Graphen. (9.) DEF: Ein Graph G
Was ändert sich, wenn zu Beginn eine andere Anzahl n an Streichhölzern auf dem Haufen liegt?
 NIM Auf dem Tisch liegen mehrere Haufen mit Spielsteinen. Zum Beispiel drei Haufen mit 4, 5 und 6 Steinen. Jeder Spiele nimmt abwechselnd von einem Haufen eine beliebige Anzahl an Steinen. Der Spieler,
NIM Auf dem Tisch liegen mehrere Haufen mit Spielsteinen. Zum Beispiel drei Haufen mit 4, 5 und 6 Steinen. Jeder Spiele nimmt abwechselnd von einem Haufen eine beliebige Anzahl an Steinen. Der Spieler,
Graphentheorie: Das Hamiltonische-Kreis-Problem: Definitionen, Resultate und Anwendungen
 Graphentheorie: Das Hamiltonische-Kreis-Problem: Definitionen, Resultate und Anwendungen Dr. Gerold Jäger Habilitationsvorlesung Christian-Albrechts-Universität zu Kiel Institut für Informatik 21. April
Graphentheorie: Das Hamiltonische-Kreis-Problem: Definitionen, Resultate und Anwendungen Dr. Gerold Jäger Habilitationsvorlesung Christian-Albrechts-Universität zu Kiel Institut für Informatik 21. April
Schach Spielanleitung
 Schach Spielanleitung 1. Schachbrett Untenstehend sieht man ein Schachbrett inklusive Figuren in Grundstellung. Hierbei handelt es sich immer um die Ausgangsposition. Zu beachten ist, dass jedes Feld seinen
Schach Spielanleitung 1. Schachbrett Untenstehend sieht man ein Schachbrett inklusive Figuren in Grundstellung. Hierbei handelt es sich immer um die Ausgangsposition. Zu beachten ist, dass jedes Feld seinen
Kapitel 3. Kapitel 3 Graphentheorie
 Graphentheorie Inhalt 3.1 3.1 Grundlagen 3.2 3.2 Das Das Königsberger Brückenproblem 3.3 3.3 Bäume 3.4. 3.4. Planare Graphen 3.5 3.5 Färbungen Seite 2 3.1 Grundlagen Definition. Ein Ein Graph besteht aus
Graphentheorie Inhalt 3.1 3.1 Grundlagen 3.2 3.2 Das Das Königsberger Brückenproblem 3.3 3.3 Bäume 3.4. 3.4. Planare Graphen 3.5 3.5 Färbungen Seite 2 3.1 Grundlagen Definition. Ein Ein Graph besteht aus
Grundlagen der Informatik Kapitel 20. Harald Krottmaier Sven Havemann
 Grundlagen der Informatik Kapitel 20 Harald Krottmaier Sven Havemann Agenda Klassen von Problemen Einige Probleme... Approximationsalgorithmen WS2007 2 Klassen P NP NP-vollständig WS2007 3 Klasse P praktisch
Grundlagen der Informatik Kapitel 20 Harald Krottmaier Sven Havemann Agenda Klassen von Problemen Einige Probleme... Approximationsalgorithmen WS2007 2 Klassen P NP NP-vollständig WS2007 3 Klasse P praktisch
4. Kreis- und Wegeprobleme
 4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung
4. Kreis- und Wegeprobleme Kapitelübersicht 4. Kreis- und Wegeprobleme Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Abstände in Graphen Berechnung
Paper Computer Science Experiment. Computation (NP-Vollständigkeit) Traveling Salesman
 Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Traveling Salesman Unterrichtsform Lernen am Modell Voraussetzung Wahrscheinlich kennen viele Schüler/innen
Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Traveling Salesman Unterrichtsform Lernen am Modell Voraussetzung Wahrscheinlich kennen viele Schüler/innen
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie
 Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
Wiederholung aus Diskreter Mathematik I: I: Graphentheorie Inhalt: W.1 Grundlagen W.2 Das Königsberger Brückenproblem W.3 Bäume W.4 Planare Graphen W.5 Färbungen W.1 Grundlagen Ein Ein Graph besteht aus
Graphentheorie. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
 Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Schach für Anfänger. Hier möchte ich für Anfänger das Schachspiel näher bringen.
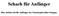 Schach für Anfänger Hier möchte ich für Anfänger das Schachspiel näher bringen. Bild 1 Die Grundstellung Das Schachbrett sollte man immer so legen, daß rechts unten ein weißes Feld ist (Bild1: rotes Feld).
Schach für Anfänger Hier möchte ich für Anfänger das Schachspiel näher bringen. Bild 1 Die Grundstellung Das Schachbrett sollte man immer so legen, daß rechts unten ein weißes Feld ist (Bild1: rotes Feld).
Graphen. Graphen und ihre Darstellungen
 Graphen Graphen und ihre Darstellungen Ein Graph beschreibt Beziehungen zwischen den Elementen einer Menge von Objekten. Die Objekte werden als Knoten des Graphen bezeichnet; besteht zwischen zwei Knoten
Graphen Graphen und ihre Darstellungen Ein Graph beschreibt Beziehungen zwischen den Elementen einer Menge von Objekten. Die Objekte werden als Knoten des Graphen bezeichnet; besteht zwischen zwei Knoten
Formale Grundlagen. bis , Lösungen. 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist.
 Formale Grundlagen 4. Übungsaufgaben bis 2011-06-03, Lösungen 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist. 2. Finden Sie einen Eulerschen Weg im Briefumschlag, d.h. in: { ((1,
Formale Grundlagen 4. Übungsaufgaben bis 2011-06-03, Lösungen 1. Beweisen Sie, daß die Summe aller Grade der Knoten stets gerade ist. 2. Finden Sie einen Eulerschen Weg im Briefumschlag, d.h. in: { ((1,
Hackenbusch und Spieltheorie
 Hackenbusch und Spieltheorie Was sind Spiele? Definition. Ein Spiel besteht für uns aus zwei Spielern, Positionen oder Stellungen, in welchen sich das Spiel befinden kann (insbesondere eine besondere Startposition)
Hackenbusch und Spieltheorie Was sind Spiele? Definition. Ein Spiel besteht für uns aus zwei Spielern, Positionen oder Stellungen, in welchen sich das Spiel befinden kann (insbesondere eine besondere Startposition)
Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten
 Graphentheorie Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten gerichteter Graph (DiGraph (directed graph) E: Teilmenge E
Graphentheorie Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten gerichteter Graph (DiGraph (directed graph) E: Teilmenge E
Algorithmen und Datenstrukturen 2-1. Seminar -
 Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Algorithmen und Datenstrukturen 2-1. Seminar - Dominic Rose Bioinformatics Group, University of Leipzig Sommersemster 2010 Outline 1. Übungsserie: 3 Aufgaben, insgesamt 30 28 Punkte A1 Spannbäume (10 8
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Hausaufgabe 2 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Verflixt, warum geht das nicht? Unmöglichkeitsbeweise in der Mathematik
 Verflixt, warum geht das nicht? Unmöglichkeitsbeweise in der Mathematik Daniel Grieser Institut für Mathematik Universität Oldenburg Tag der Mathematik, 5. November 2008 Der Läufer Ein Läufer im Schach
Verflixt, warum geht das nicht? Unmöglichkeitsbeweise in der Mathematik Daniel Grieser Institut für Mathematik Universität Oldenburg Tag der Mathematik, 5. November 2008 Der Läufer Ein Läufer im Schach
3 Klassifikation wichtiger Optimierungsprobleme
 3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Theoretische Informatik 1
 Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 10.06.2016 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 10.06.2016 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
Mathematik ohne Formeln gibt s denn das?
 Mathematik ohne Formeln gibt s denn das? Ein Stück Mathematik der anderen Art Daniel Grieser Institut für Mathematik Universität Oldenburg Der Läufer Ein Läufer im Schach kann nur schräg ziehen. Kann er......
Mathematik ohne Formeln gibt s denn das? Ein Stück Mathematik der anderen Art Daniel Grieser Institut für Mathematik Universität Oldenburg Der Läufer Ein Läufer im Schach kann nur schräg ziehen. Kann er......
Gruppengröße: 4-5 Teilnehmer bilden eine Gruppe, dabei ist zu. Spielidee: Immer zwei Gruppen spielen gegeneinander Schach. Ein.
 Gruppengröße: 4-5 Teilnehmer bilden eine Gruppe, dabei ist zu beachten, dass in jeder Gruppe mindestens ein Teilnehmer eingeteilt ist, der die Spielregeln von Schach kann. Die Gruppen sollten möglichst
Gruppengröße: 4-5 Teilnehmer bilden eine Gruppe, dabei ist zu beachten, dass in jeder Gruppe mindestens ein Teilnehmer eingeteilt ist, der die Spielregeln von Schach kann. Die Gruppen sollten möglichst
Euler und Hamiltonkreise
 Euler und Hamiltonkreise 1. Königsberger Brücken 2. Eulerwege und Kreise Definition, Algorithmus mit Tiefensuche 3. Hamiltonwege und Kreise Definition 4. Problem des Handlungsreisenden Enumeration und
Euler und Hamiltonkreise 1. Königsberger Brücken 2. Eulerwege und Kreise Definition, Algorithmus mit Tiefensuche 3. Hamiltonwege und Kreise Definition 4. Problem des Handlungsreisenden Enumeration und
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter WS 2013/14 1 Eulersche Graphen Kantenzug Ein Kantenzug in einem Graphen (V, E) ist eine Folge (a 0, a 1,..., a n ) von Knoten
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter WS 2013/14 1 Eulersche Graphen Kantenzug Ein Kantenzug in einem Graphen (V, E) ist eine Folge (a 0, a 1,..., a n ) von Knoten
6in1 Deluxe Spiele-Koffer. Spielanleitung
 6in1 Deluxe Spiele-Koffer Spielanleitung 1 ihr neuer spielekoffer Sehr gehrte Kunden, wir danken Ihnen für den Kauf dieses Spiele- Koffers. Mit diesem eleganten Koffer sind Sie für Spiele-Abende und lange
6in1 Deluxe Spiele-Koffer Spielanleitung 1 ihr neuer spielekoffer Sehr gehrte Kunden, wir danken Ihnen für den Kauf dieses Spiele- Koffers. Mit diesem eleganten Koffer sind Sie für Spiele-Abende und lange
Graphentheorie Graphentheorie. Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke
 Graphen Graphentheorie Graphentheorie Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke 2 Was ist ein Graph? Ein Graph ist in der Graphentheorie eine abstrakte Struktur,
Graphen Graphentheorie Graphentheorie Grundlagen Bäume Eigenschaften von Graphen Graphen-Algorithmen Matchings und Netzwerke 2 Was ist ein Graph? Ein Graph ist in der Graphentheorie eine abstrakte Struktur,
Rechenzeit für A. Sei t B die Rechenzeit eines Algo für B. Seien p,q,r monotone Polynome ( +).
 Rechenzeit für A Sei t B die Rechenzeit eines Algo für B. Seien p,q,r monotone Polynome ( +). Rechenzeit des resultierenden Algo für A: t A (n) p(n) + q(n) t B (r(n)). Ist polynomiell, falls t B Polynom.
Rechenzeit für A Sei t B die Rechenzeit eines Algo für B. Seien p,q,r monotone Polynome ( +). Rechenzeit des resultierenden Algo für A: t A (n) p(n) + q(n) t B (r(n)). Ist polynomiell, falls t B Polynom.
MATHEMATIK. Name: Vorname: maximale Punkte 1 a), b) 4 2 a), b), c) 6 3 a), b) Gesamtpunktzahl 38. Die Experten: 1.
 Berufsmaturität Kanton Glarus Aufnahmeprüfung 2013 Kaufmännische Berufsfachschule Glarus Kaufmännische Richtung MATHEMATIK Name: Vorname: Note Aufgabe Nr. Teilaufgaben erreichte Punkte maximale Punkte
Berufsmaturität Kanton Glarus Aufnahmeprüfung 2013 Kaufmännische Berufsfachschule Glarus Kaufmännische Richtung MATHEMATIK Name: Vorname: Note Aufgabe Nr. Teilaufgaben erreichte Punkte maximale Punkte
Theoretische Informatik 1
 Theoretische Informatik 1 Nichtdeterminismus David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Nichtdeterminismus NTM Nichtdeterministische Turingmaschine Die
Theoretische Informatik 1 Nichtdeterminismus David Kappel Institut für Grundlagen der Informationsverarbeitung TU Graz SS 2012 Übersicht Nichtdeterminismus NTM Nichtdeterministische Turingmaschine Die
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. wer das Problem löste 4
 Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Minimal spannender Baum
 Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Wie findet man den optimalen Weg zum Ziel? Klassische Probleme der Kombinatorischen Optimierung
 Wie findet man den optimalen Weg zum Ziel? Klassische Probleme der Kombinatorischen Optimierung Teilnehmer/innen: Markus Dahinten, Graf Münster Gymnasium Bayreuth Robert Fay, Herder Gymnasium Berlin Falko
Wie findet man den optimalen Weg zum Ziel? Klassische Probleme der Kombinatorischen Optimierung Teilnehmer/innen: Markus Dahinten, Graf Münster Gymnasium Bayreuth Robert Fay, Herder Gymnasium Berlin Falko
Ausarbeitung zum Modulabschluss. Graphentheorie. spannende Bäume, bewertete Graphen, optimale Bäume, Verbindungsprobleme
 Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Das Multi Traveling Salesman Problem
 Das Multi Traveling Salesman Problem Harald Voit Seminar Ganzzahlige Optimierung 19. bis 21. Januar 2007 Wallenfels Das Multi Traveling Salesman Problem p.1/26 Übersicht Vom TSP zum ATSP Das Multi Traveling
Das Multi Traveling Salesman Problem Harald Voit Seminar Ganzzahlige Optimierung 19. bis 21. Januar 2007 Wallenfels Das Multi Traveling Salesman Problem p.1/26 Übersicht Vom TSP zum ATSP Das Multi Traveling
Erste Schritte um Schach zu lernen
 Erste Schritte um Schach zu lernen Erstellt durch wikihow Übersetzungen: Schach ist ein sehr beliebtes Spiel und weithin als eines der ältesten noch gespielten Spiele anerkannt. Obwohl die Regeln von Schach
Erste Schritte um Schach zu lernen Erstellt durch wikihow Übersetzungen: Schach ist ein sehr beliebtes Spiel und weithin als eines der ältesten noch gespielten Spiele anerkannt. Obwohl die Regeln von Schach
Name:... Vorname:...
 Zentrale Aufnahmeprüfung 2012 für die Kurzgymnasien des Kantons Zürich Mathematik 2./3. Sekundarschule Bisheriges Lehrmittel Bitte zuerst auszufüllen: Name:... Vorname:... Prüfungsnummer:... Du hast 90
Zentrale Aufnahmeprüfung 2012 für die Kurzgymnasien des Kantons Zürich Mathematik 2./3. Sekundarschule Bisheriges Lehrmittel Bitte zuerst auszufüllen: Name:... Vorname:... Prüfungsnummer:... Du hast 90
Färbungsbeweise. 1 Aufgaben
 Schweizer Mathematik-Olympiade smo osm Färbungsbeweise Aktualisiert: 1. Dezember 2015 vers. 1.0.0 1 Aufgaben Einstieg 1.1 Kann man überlappungsfrei und ohne Löcher die Figuren auf den Bildern unten mit
Schweizer Mathematik-Olympiade smo osm Färbungsbeweise Aktualisiert: 1. Dezember 2015 vers. 1.0.0 1 Aufgaben Einstieg 1.1 Kann man überlappungsfrei und ohne Löcher die Figuren auf den Bildern unten mit
Zahlenfolgen. Aufgabe 1 (Streichholzfiguren)
 Zahlenfolgen Aufgabe (Streichholzfiguren) a) Wie viele Streichhölzer benötigt man für die 0. Figur? b) Gib für die Streichholzfolge eine rekursive und eine explizite Berechnungsvorschrift an. Aufgabe (Quadratzahlen)
Zahlenfolgen Aufgabe (Streichholzfiguren) a) Wie viele Streichhölzer benötigt man für die 0. Figur? b) Gib für die Streichholzfolge eine rekursive und eine explizite Berechnungsvorschrift an. Aufgabe (Quadratzahlen)
Das Problem des Handlungsreisenden
 Seite 1 Das Problem des Handlungsreisenden Abbildung 1: Alle möglichen Rundreisen für 4 Städte Das TSP-Problem tritt in der Praxis in vielen Anwendungen als Teilproblem auf. Hierzu gehören z.b. Optimierungsprobleme
Seite 1 Das Problem des Handlungsreisenden Abbildung 1: Alle möglichen Rundreisen für 4 Städte Das TSP-Problem tritt in der Praxis in vielen Anwendungen als Teilproblem auf. Hierzu gehören z.b. Optimierungsprobleme
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Algorithmen und Datenstrukturen (für ET/IT)
 Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 05 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute Einführung Grundlagen von Algorithmen Grundlagen
Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 05 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Programm heute Einführung Grundlagen von Algorithmen Grundlagen
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 6: Graphentheorie
 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Spielregeln für Schach
 Gebrauchsartikel mit sozialer Herkunft B-Vertrieb GmbH Anerkannt gemeinnütziges Unternehmen gem. Art. 80 Abs. 1 lit. g und Art. 56 Bst. g DBG Lehnstrasse 90 l CH-9014 St.Gallen Tel. +41 (0)71 280 83 20
Gebrauchsartikel mit sozialer Herkunft B-Vertrieb GmbH Anerkannt gemeinnütziges Unternehmen gem. Art. 80 Abs. 1 lit. g und Art. 56 Bst. g DBG Lehnstrasse 90 l CH-9014 St.Gallen Tel. +41 (0)71 280 83 20
Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert?
 Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? Königsberger Brückenproblem Gibt es in Königsberg einen Spaziergang, bei dem man
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? Königsberger Brückenproblem Gibt es in Königsberg einen Spaziergang, bei dem man
Einführung in das Invarianzprinzip
 15.03.2016 Motivation Betrachtet diesen Kreis, der in sechs Sektoren eingeteilt ist. Wir erlauben, die Zahl in je zwei benachbarten Feldern um jeweils 1 zu erhöhen. In welcher Reihenfolge muss man die
15.03.2016 Motivation Betrachtet diesen Kreis, der in sechs Sektoren eingeteilt ist. Wir erlauben, die Zahl in je zwei benachbarten Feldern um jeweils 1 zu erhöhen. In welcher Reihenfolge muss man die
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
 Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Breitensuche BFS (Breadth First Search)
 Breitensuche BFS (Breadth First Search) Algorithmus BREITENSUCHE EINGABE: G = (V, E) als Adjazenzliste, Startknoten s V 1 Für alle v V 1 If (v = s) then d[v] 0 else d[v] ; 2 pred[v] nil; 2 Q new Queue;
Breitensuche BFS (Breadth First Search) Algorithmus BREITENSUCHE EINGABE: G = (V, E) als Adjazenzliste, Startknoten s V 1 Für alle v V 1 If (v = s) then d[v] 0 else d[v] ; 2 pred[v] nil; 2 Q new Queue;
Übung zur Vorlesung Berechenbarkeit und Komplexität
 RWTH Aachen Lehrgebiet Theoretische Informatik Reidl Ries Rossmanith Sanchez Tönnis WS 2012/13 Übungsblatt 9 10.12.2012 Übung zur Vorlesung Berechenbarkeit und Komplexität Aufgabe T20 Beweisen Sie die
RWTH Aachen Lehrgebiet Theoretische Informatik Reidl Ries Rossmanith Sanchez Tönnis WS 2012/13 Übungsblatt 9 10.12.2012 Übung zur Vorlesung Berechenbarkeit und Komplexität Aufgabe T20 Beweisen Sie die
Bauerndiplom. 2 Der König
 1 Das Schachbrett Bauerndiplom 2 Der König Das Schlagen Diagramm 1 Das Schachbrett besteht aus 8x8 Feldern. In der rechten Ecke, auf beiden Seiten, muss sich ein weißes Feld befinden. Die Felder sind bezeichnet.
1 Das Schachbrett Bauerndiplom 2 Der König Das Schlagen Diagramm 1 Das Schachbrett besteht aus 8x8 Feldern. In der rechten Ecke, auf beiden Seiten, muss sich ein weißes Feld befinden. Die Felder sind bezeichnet.
Aufgaben zur Klausurvorbereitung
 Vorlesung Graphen und Optimierung Sommersemester 2013/14 Prof. S. Lange Aufgaben zur Klausurvorbereitung Hier finden Sie eine Reihe von Übungsaufgaben, die wir an den beiden Vorlesungsterminen am 29.01.2014
Vorlesung Graphen und Optimierung Sommersemester 2013/14 Prof. S. Lange Aufgaben zur Klausurvorbereitung Hier finden Sie eine Reihe von Übungsaufgaben, die wir an den beiden Vorlesungsterminen am 29.01.2014
Graphentheorie. Kürzeste Wege. Kürzeste Wege. Kürzeste Wege. Rainer Schrader. 25. Oktober 2007
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 25. Oktober 2007 1 / 20 2 / 20 Wir werden Optimierungsprobleme vom folgenden Typ betrachten: gegeben eine Menge X und eine Funktion
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 25. Oktober 2007 1 / 20 2 / 20 Wir werden Optimierungsprobleme vom folgenden Typ betrachten: gegeben eine Menge X und eine Funktion
Graphentheorie Mathe-Club Klasse 5/6
 Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
Westfählische Wilhelms-Universität. Eulersche Graphen. Autor: Jan-Hendrik Hoffeld
 Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Musterlösung MafI 1 - Blatt 5
 Musterlösung MafI 1 - Blatt 5 Titus Laska Aufgabe 1 (Relationen). Die drei Relationen R, S, T N N sind jeweils auf Reflexivität, Symmetrie und Antisymmetrie zu untersuchen. Lösung. Erinnerung. Sei R A
Musterlösung MafI 1 - Blatt 5 Titus Laska Aufgabe 1 (Relationen). Die drei Relationen R, S, T N N sind jeweils auf Reflexivität, Symmetrie und Antisymmetrie zu untersuchen. Lösung. Erinnerung. Sei R A
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel1 aus "Abenteuer Informatik" von Jens
Bemerkung: Der vollständige Graph K n hat n(n 1)
 Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Bemerkung: Der vollständige Graph K n hat n(n 1) 2 Kanten. Bew: Abzählen! Definition 111. Graphen mit n paarweise zyklisch verbundenen Kanten heißen Kreise (vom Grad n) und werden mit C n bezeichnet. Beispiel
Schach für Anfänger Hier möchte ich für Anfänger das Schachspiel näher bringen.
 Schach für Anfänger Hier möchte ich für Anfänger das Schachspiel näher bringen. Viele glauben, daß das Schachspiel schwierig zu erlernen ist, da es sechs verschiedene Figuren gibt. Wenn man sich aber die
Schach für Anfänger Hier möchte ich für Anfänger das Schachspiel näher bringen. Viele glauben, daß das Schachspiel schwierig zu erlernen ist, da es sechs verschiedene Figuren gibt. Wenn man sich aber die
Nachbarschaft, Grad, regulär, Inzidenz
 Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Nachbarschaft, Grad, regulär, Inzidenz Definition Eigenschaften von Graphen Sei G = (V, E) ein ungerichteter Graph. 1 Die Nachbarschaftschaft Γ(u) eines Knoten u V ist Γ(u) := {v V {u, v} E}. 2 Der Grad
Graphalgorithmen 2. Dominik Paulus Dominik Paulus Graphalgorithmen / 47
 Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
Graphalgorithmen Dominik Paulus.0.01 Dominik Paulus Graphalgorithmen.0.01 1 / 7 1 Spannbäume Kruskal Prim Edmonds/Chu-Liu Datenstrukturen Fibonacci-Heap Union/Find Kürzeste Pfade Dijkstra Bellman-Ford
INHALT 32 Schmetterlingskarten 8 Aufgabenkarten (4 Form en + 4 Farben) 8 Spielsteine (4 Sch m etterlingsnetze + 4 Spinnweben)
 INHALT 32 Schmetterlingskarten 8 Aufgabenkarten (4 Form en + 4 Farben) 8 Spielsteine (4 Sch m etterlingsnetze + 4 Spinnweben) SPIELZIEL Wer als Erster vier Schmetterlinge seiner Form oder Farbe waagrecht,
INHALT 32 Schmetterlingskarten 8 Aufgabenkarten (4 Form en + 4 Farben) 8 Spielsteine (4 Sch m etterlingsnetze + 4 Spinnweben) SPIELZIEL Wer als Erster vier Schmetterlinge seiner Form oder Farbe waagrecht,
Aufnahmeprüfung 2014 LÖSUNGEN Mathematik Serie 5 (60 Min.)
 Aufnahmeprüfung 014 LÖSUNGEN Mathematik Serie 5 (60 Min.) Hilfsmittel: Taschenrechner Name... Vorname... Adresse...... ACHTUNG: - Resultate ohne Ausrechnungen bzw. Doppellösungen werden nicht berücksichtigt!
Aufnahmeprüfung 014 LÖSUNGEN Mathematik Serie 5 (60 Min.) Hilfsmittel: Taschenrechner Name... Vorname... Adresse...... ACHTUNG: - Resultate ohne Ausrechnungen bzw. Doppellösungen werden nicht berücksichtigt!
12.4 Traveling Salesman Problem
 96 KOMBINATORISCHE SUCHE.4 Traveling Salesman Problem Definition.3(TSP, Problem des Handlungsreisenden): Wir betrachten einen gerichteten, gewichteten Graphen G = (V,E) mit K : V R. K({u,v}) sind die Kosten
96 KOMBINATORISCHE SUCHE.4 Traveling Salesman Problem Definition.3(TSP, Problem des Handlungsreisenden): Wir betrachten einen gerichteten, gewichteten Graphen G = (V,E) mit K : V R. K({u,v}) sind die Kosten
Das ist nicht besonders spannend. Wir ändern daher die Regeln für den Turm leicht ab.
 Hans Walser, [20150101] Schachbrett-Geometrie 1 Worum es geht Auf dem Schachbrett wird eine Metrik definiert, die sich an den Bewegungen von Schachfiguren orientiert. Für eine bestimmte Schachfigur ist
Hans Walser, [20150101] Schachbrett-Geometrie 1 Worum es geht Auf dem Schachbrett wird eine Metrik definiert, die sich an den Bewegungen von Schachfiguren orientiert. Für eine bestimmte Schachfigur ist
11: Die Euler sche Polyederformel für planare Graphen
 Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Traveling Salesman Problem (TSP)
 Traveling Salesman Problem (TSP) Das Traveling Salesman Problem (TSP) ist ein bekanntes Optimierungsproblem. Ein Handlungsreisender soll in einer Rundreise (auch Tour genannt) n vorgegebene Städte besuchen.
Traveling Salesman Problem (TSP) Das Traveling Salesman Problem (TSP) ist ein bekanntes Optimierungsproblem. Ein Handlungsreisender soll in einer Rundreise (auch Tour genannt) n vorgegebene Städte besuchen.
Graphentheorie und Anwendungen. Peter Eichelsbacher, Ruhr-Universität Bochum
 Graphentheorie und Anwendungen Peter Eichelsbacher, Ruhr-Universität Bochum 2005 Inhaltsverzeichnis 1 Motivation, Beispiele 3 2 Grundbegriffe der Graphentheorie 7 3 Hamiltonkreise und Eulertouren 15 4
Graphentheorie und Anwendungen Peter Eichelsbacher, Ruhr-Universität Bochum 2005 Inhaltsverzeichnis 1 Motivation, Beispiele 3 2 Grundbegriffe der Graphentheorie 7 3 Hamiltonkreise und Eulertouren 15 4
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
Der folgende Vortrag basiert auf dem Text A Polynomial Time Algorithm for the N-Queens Problem von Rok Sosic und Jun Gu aus dem Jahre 1990.
 Ein polynomieller Algorithmus für das N-Damen Problem 1 Einführung Der folgende Vortrag basiert auf dem Text A Polynomial Time Algorithm for the N-Queens Problem von Rok Sosic und Jun Gu aus dem Jahre
Ein polynomieller Algorithmus für das N-Damen Problem 1 Einführung Der folgende Vortrag basiert auf dem Text A Polynomial Time Algorithm for the N-Queens Problem von Rok Sosic und Jun Gu aus dem Jahre
Spielmaterial 1 Spielplan 1 Würfelturm 4 Würfel 16 Spielfiguren (4 pro Farbe)
 Spielanleitung Für den kleinen Ärger unterwegs! Spielmaterial 1 Spielplan 1 Würfelturm 4 Würfel 16 Spielfiguren (4 pro Farbe) Spielbeschreibung Die Spieler laufen mit ihren eigenen Spielfiguren so schnell
Spielanleitung Für den kleinen Ärger unterwegs! Spielmaterial 1 Spielplan 1 Würfelturm 4 Würfel 16 Spielfiguren (4 pro Farbe) Spielbeschreibung Die Spieler laufen mit ihren eigenen Spielfiguren so schnell
2. Optimierungsprobleme 6
 6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
Bernd Döring. Wege, Plätten, Färben. Vom Problem zur Theorie der Graphen
 Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen Bernd Döring, 2002-2005 Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg 28 26721 Emden - 2 - Inhaltsverzeichnis 0. Einleitung
Bernd Döring Wege, Plätten, Färben Vom Problem zur Theorie der Graphen Bernd Döring, 2002-2005 Bernd Döring Johannes-Althusius-Gymnasium Früchteburger Weg 28 26721 Emden - 2 - Inhaltsverzeichnis 0. Einleitung
Zahlenluchs. von Anja Strobach. Spielanleitung
 von Anja Strobach Spielanleitung Die Zahlen von 1 bis 25 laden dich zum spannenden Kombinationstraining ein. Noch während du Aufgaben durch ausgeklügelte Rechenkunst löst, jonglieren deine Mitspieler mit
von Anja Strobach Spielanleitung Die Zahlen von 1 bis 25 laden dich zum spannenden Kombinationstraining ein. Noch während du Aufgaben durch ausgeklügelte Rechenkunst löst, jonglieren deine Mitspieler mit
Übungen zu Kombinatorik und Graphentheorie
 Übungen zu Kombinatorik und Graphentheorie Ilse Fischer, SS 07 (1) (a) In einer Schachtel sind 4 rote, 2 blaue, 5 gelbe und 3 grüne Stifte. Wenn man die Stifte mit geschlossenen Augen zieht, wieviele muss
Übungen zu Kombinatorik und Graphentheorie Ilse Fischer, SS 07 (1) (a) In einer Schachtel sind 4 rote, 2 blaue, 5 gelbe und 3 grüne Stifte. Wenn man die Stifte mit geschlossenen Augen zieht, wieviele muss
Heuristische und exakte Lösungsansätze für das Handelsreisendenproblem. Dr. Gerold Jäger
 Heuristische und exakte Lösungsansätze für das Handelsreisendenproblem Dr. Gerold Jäger Arbeitsgruppe Prof. Dr. Paul Molitor Institut für Informatik Martin-Luther-Universität Halle-Wittenberg 30. September
Heuristische und exakte Lösungsansätze für das Handelsreisendenproblem Dr. Gerold Jäger Arbeitsgruppe Prof. Dr. Paul Molitor Institut für Informatik Martin-Luther-Universität Halle-Wittenberg 30. September
Algorithmische Methoden für schwere Optimierungsprobleme
 Algorithmische Methoden für schwere Optimierungsprobleme Prof. Dr. Henning Meyerhenke Institut für Theoretische Informatik 1 KIT Henning Universität desmeyerhenke, Landes Baden-Württemberg Institutund
Algorithmische Methoden für schwere Optimierungsprobleme Prof. Dr. Henning Meyerhenke Institut für Theoretische Informatik 1 KIT Henning Universität desmeyerhenke, Landes Baden-Württemberg Institutund
Toleranzbasierte Algorithmen für das Travelling Salesman Problem. Gerold Jäger
 Toleranzbasierte Algorithmen für das Travelling Salesman Problem Gerold Jäger (Zusammenarbeit mit Jop Sibeyn, Boris Goldengorin) Institut für Informatik Martin-Luther-Universität Halle-Wittenberg [email protected]
Toleranzbasierte Algorithmen für das Travelling Salesman Problem Gerold Jäger (Zusammenarbeit mit Jop Sibeyn, Boris Goldengorin) Institut für Informatik Martin-Luther-Universität Halle-Wittenberg [email protected]
Schnittebenenverfahren für das symmetrische
 Schnittebenenverfahren für das symmetrische TSP Sebastian Peetz Mathematisches Institut Universität Bayreuth 19. Januar 2007 / Blockseminar Ganzzahlige Optimierung, Bayreuth Gliederung 1 Das symmetrische
Schnittebenenverfahren für das symmetrische TSP Sebastian Peetz Mathematisches Institut Universität Bayreuth 19. Januar 2007 / Blockseminar Ganzzahlige Optimierung, Bayreuth Gliederung 1 Das symmetrische
NP-Vollständigkeit. Krautgartner Martin (9920077) Markgraf Waldomir (9921041) Rattensberger Martin (9921846) Rieder Caroline (0020984)
 NP-Vollständigkeit Krautgartner Martin (9920077) Markgraf Waldomir (9921041) Rattensberger Martin (9921846) Rieder Caroline (0020984) 0 Übersicht: Einleitung Einteilung in Klassen Die Klassen P und NP
NP-Vollständigkeit Krautgartner Martin (9920077) Markgraf Waldomir (9921041) Rattensberger Martin (9921846) Rieder Caroline (0020984) 0 Übersicht: Einleitung Einteilung in Klassen Die Klassen P und NP
Algo&Komp. - Wichtige Begriffe Mattia Bergomi Woche 6 7
 1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
1 Kürzeste Pfade Woche 6 7 Hier arbeiten wir mit gewichteten Graphen, d.h. Graphen, deren Kanten mit einer Zahl gewichtet werden. Wir bezeichnen die Gewichtsfunktion mit l : E R. Wir wollen einen kürzesten
Brückenkurs Mathematik. Jörn Steuding (Uni Würzburg), 13. Januar 2018
 Brückenkurs Mathematik Jörn Steuding (Uni Würzburg), 3. Januar 08 unser Programm. November:. Zahlen und einfache Gleichungen Zahlen, Rechengesetze, lineare u. quadratische Gleichungen, Dezimalbrüche, ein
Brückenkurs Mathematik Jörn Steuding (Uni Würzburg), 3. Januar 08 unser Programm. November:. Zahlen und einfache Gleichungen Zahlen, Rechengesetze, lineare u. quadratische Gleichungen, Dezimalbrüche, ein
Der Fünf-Farben-Satz. Lukas Schweighofer. Feb.2014
 Der Fünf-Farben-Satz Lukas Schweighofer Feb.2014 1 Contents 1 Vorwort 3 2 Graphentheoretische Grundlagen 4 3 Satz 2 (Eulerscher Polyedersatz) 8 4 Satz 3 9 5 Der Fnf-Farben-Satz 10 5.1 Beweis 1..............................
Der Fünf-Farben-Satz Lukas Schweighofer Feb.2014 1 Contents 1 Vorwort 3 2 Graphentheoretische Grundlagen 4 3 Satz 2 (Eulerscher Polyedersatz) 8 4 Satz 3 9 5 Der Fnf-Farben-Satz 10 5.1 Beweis 1..............................
Graphentheorie. Kardinalitätsmatchings. Kardinalitätsmatchings. Kardinalitätsmatchings. Rainer Schrader. 11. Dezember 2007
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 11. Dezember 2007 1 / 47 2 / 47 wir wenden uns jetzt einem weiteren Optimierungsproblem zu Gliederung Matchings in bipartiten Graphen
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 11. Dezember 2007 1 / 47 2 / 47 wir wenden uns jetzt einem weiteren Optimierungsproblem zu Gliederung Matchings in bipartiten Graphen
Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen)
 WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 4: Graphentheorie (Grundlagen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Sachrechnen/Größen WS 14/15-
 Kapitel Daten & Wahrscheinlichkeit 3.1 Kombinatorische Grundlagen 3.2 Kombinatorik & Wahrscheinlichkeit in der Grundschule 3.3 Daten Darstellen 3.1 Kombinatorische Grundlagen Verschiedene Bereiche der
Kapitel Daten & Wahrscheinlichkeit 3.1 Kombinatorische Grundlagen 3.2 Kombinatorik & Wahrscheinlichkeit in der Grundschule 3.3 Daten Darstellen 3.1 Kombinatorische Grundlagen Verschiedene Bereiche der
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden [email protected] WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Die Zeilen mit geraden Zahlen beim Halbieren werden gestrichen.
 Napier s Rechenbrett Die Bedeutung des Zweiersystems ist im Computer-Zeitalter kein Geheimnis mehr. Verdoppeln und Halbieren sind Tätigkeiten, welche uralt sind. Sie erfordern weder ein Zählen noch Rechnen,
Napier s Rechenbrett Die Bedeutung des Zweiersystems ist im Computer-Zeitalter kein Geheimnis mehr. Verdoppeln und Halbieren sind Tätigkeiten, welche uralt sind. Sie erfordern weder ein Zählen noch Rechnen,
