Ganzzahlige Optimierung (IP)

Transkript

1 Thema Ganzzahlige Optimierung (IP) Systematik * Problematik * Pragmatik IP und Branch and Bound 1

2 Agenda 1. Relevanz der Ganzzahligkeit? 2. Formulierung ganzzahliger Modelle 3. Zur Lösung ganzzahliger Probleme 4. Entscheidungsbaumverfahren IP und Branch and Bound 2

3 Ein Beispiel Max z mit z = x 1 + 5x 2 u.d.n. x x 2 20 x 1 2 x 1,x 2 0 ganzzahlig Max x 1 x 2 RS Max x 1 x 3 RS Max x 4 x 3 RS z z z x x x x x x IP und Branch and Bound 3

4 Problematik der Ganzzahligkeit x 2 2 OPTganz. OPTkont x 1 IP und Branch and Bound 4

5 Runden ist keine Lösung x 2 3 OPTganz OPTkont x 1 IP und Branch and Bound 5

6 Ganzzahligkeit - sinnlos oder sinnvoll? 1. Direkte Modelle 2. Codierte Modelle 3. Transformierte Modelle IP und Branch and Bound 6

7 2. Codierte Modelle Eine Binärvariable, die nur die beiden Werte 1 (ja) oder 0 (nein) annimmt, dient als Code für die Entscheidung: Kapitalbudgetierung Maschinenbelegung Stundenplanerstellung Knapsackproblem Travelling Salesman P. Lieferplan Standort (Investition x: ja oder nein) (Auftrag x auf Anlage A: ja oder nein) (Lehrer x zur Stunde i in Raum j für Klasse k: ja oder nein) (Gut x in Rucksack: ja oder nein) (Strecke x in Rundreise: ja oder nein) (Lieferung x auf Fahrt i: ja oder nein) (Standort x: ja oder nein) IP und Branch and Bound 7

8 3. Transformierte Modelle Eine Binärvariable wird als sog. Indikatorvariable benutzt, um Konditionalsätze "Wenn dann " zu formulieren: Wenn Produkt A gefertigt wird, dann auch B. Solange Produkt nicht gefertigt wird, entstehen keine Kosten. Erst wenn auch nur eine Einheit von A produziert wird, fallen neben variablen Kosten auch Fixkosten an. Eine von zwei Nebenbedingungen soll erfüllt werden. Eine Variable soll entweder den Wert Null, oder aber einen Wert zwischen 0 < l x u annehmen. IP und Branch and Bound 8

9 Diskretwertprobleme Ist x j die Entscheidungsvariable, die einen der in der Menge W = {w 1, w 2,..., w p } zusammengefaßten Werte annehmen darf, dann leisten folgende Nebenbedingungen die Auswahl: x j (w 1 y 1 + w 2 y w p y p ) = 0 y 1 + y y p = 1 y 1,... y p {0,1} IP und Branch and Bound 9

10 Batchsize-Problem = Losgrößen-Problem Eine Variable x j soll entweder null sein oder - falls sie positiv ist - eine gegebene Untergrenze l j nicht unterschreiten. Zur Formulierung derartiger, einander ausschließender Bedingungen muss für x j eine praktische Obergrenze u j eingeführt werden, das ist ein hinreichend großer Wert, der mit Sicherheit nicht überschritten wird. Dann ergibt sich als Bedingung: x j l j y j 0 (1) x j u j y j 0 (2) y j {0,1} x j 0 IP und Branch and Bound 10

11 Disjunkte Variablen Von p Aktivitäten, beschrieben durch die kontinuierlichen Variablen x 1, x 2,..., x p, soll (i) höchstens eine mit einem Wert größer null in der Lösung enthalten sein bzw. (ii) höchstens k in der Lösung größer null sein oder (iii) mindestens k in der Lösung größer null sein. Mit den Indikatorvariablen y i (i = 1,2,...,p) ergibt sich: x i u i y i 0 für i = 1,2,...,p Fall (i): y i 1 Fall (ii): yi k Fall (iii): y k i i i i y i {0,1} für i = 1,2,...,p IP und Branch and Bound 11

12 Disjunkte Nebenbedingungen Aus einer Menge von Nebenbedingungen sollen nur einzelne erfüllt werden. Es seien etwa f i (x 1,x 2,...,x n ) b i (i = 1,2,...,m) beliebige Restriktionen, von denen (i) genau k erfüllt werden soll bzw. (ii) höchstens k wirksam sein oder (iii) mindestens k gelten sollen. Erneut führt man y i {0,1} und eine große Zahl M ein, die wesentlich größer als jede Rechte Seite b i : ist. f i (x 1,x 2,...,x n ) b i + M y i i i Fall (i) y = m k Fall (ii) yi m k Fall (iii) yi m k i i y i {0,1} für i = 1,2,... m IP und Branch and Bound 12

13 NB mit alternativen Rechten Seiten Über die Indikatorvariable y i {0,1} wird gesteuert, dass nur eine der drei Rechte Seiten wirksam wird. Verallgemeinert gilt eine der Rechten Seiten f(x) = b 1 oder b 2 oder... oder b k, wenn formuliert wird: f ( x) = yk bk k k y y k k = 1 { 01, } IP und Branch and Bound 13

14 Fixed Charge Problem 0 für x j = 0 Die Kostenfunktion k(x j ) laute: k(x j ) = f j + cj xj für xj > 0 Für alle Aktivitäten mit einer derartigen Struktur werden wieder Indikatorvariablen y i eingeführt: Min k mit k = c x + f y j j j j j j u.d.n. aij xj bi für i = 1,2,...,m (1) j x j M y j für j = 1,2,...,n (2) x j 0 y i {0,1} IP und Branch and Bound 14

15 3. Lösung ganzzahliger Modelle 1. Runden ist nur bei natürlicher Ganzzahligkeit und großen Werte der Entscheidungsvariablen eine sinnvolle (jedoch nicht unumstrittene) Strategie. 2. Schnittebenenverfahren sind zunächst faszinierend intelligente Ansätze, die jedoch in der Praxis versagen. 3. Entscheidungsbaumverfahren haben sich in der Praxis bewährt, jedoch ist der Aufwand zur Lösung ganzzahliger Probleme außerordentlich schwer anzuschätzen. IP und Branch and Bound 15

16 3.2 Schnittebenenverfahren x2 o x1 {or3ab401.pre} IP und Branch and Bound 16

17 Problem mit generierten Cuts x2 4 NB1 3 C1 NB2 2 C3 C2 1 Zielfktn. C4 o x1 {or3ab403.pre} IP und Branch and Bound 17

18 3.3 Lösung durch Entscheidungsbaumverfahren Prinzip des Teilens und Besiegens als Lösungsstrategie Ein schwieriges Problem wird in mehrere weniger schwierig zu lösende Probleme geteilt. Ein schwierig zu lösendes Problem wird eingegrenzt. IP und Branch and Bound 18

19 Branching Branching = Verzweigen Eine sinnvolle Verzweigung muss ein im Prinzip in einfacher zu lösende Probleme erfolgen. Beim Verzweigen durch Problemteilung darf keine relevante Lösung verloren gehen. IP und Branch and Bound 19

20 Bounding Bounding = Beschränken Für Max-Probleme sucht man obere Schranken Für Min-Probleme untere Schranken Zu diesem Zweck werden im Problem eine oder mehrere Bedingungen relaxiert, mit der Folge, dass für das Max- Problem eine obere bzw. für das Min-Problem eine untere Schranke berechnet wird. Relaxiert werden grundsätzlich schwierige Bedingungen. IP und Branch and Bound 20

21 Entscheidungsbaum (generelle Vorgehensweise) IP0 LP0: z0 Branching = Verzweigen IP11 IP12 IP13 LP11: z11 Bounding = Beschränken LP12: z12 LP13: z13 Kandidatenliste IP und Branch and Bound 21

22 Abbruchkriterien (1) FC1: L(LP j ) = Ø L(IPj) = Ø FC2: FC3: Lösung des LP j ist schlechter als die beste bisher bekannte Lösung des IP: z j z lfd Falls die Lösung von LP j eine Lösung des IP j ist, wird geprüft, ob sie besser ist als die beste bekannte Lösung: z j > z lfd z lfd *= z j IP und Branch and Bound 22

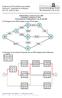
23 Abbruchkriterien (2) IP0 LP0: z0 IP11 IP12 IP12 LP11: z11 LP12: z12 LP13: z13 IP24 LP24: z24 IP25 LP25: z25 IP21 IP22 IP23 LP21: z21 LP22: z22 LP23: z23 FC1: L(LP13) = FC1: L(LP24) = FC2: z25 < zlfd. FC2. FC3: zlfd. = z23 IP31 LP31: z31 IP32 LP32: z32 FC2. FC3: zlfd. = z32 IP und Branch and Bound 23

24 Branch and Bound Beispiel LP0 Max z mit z = 21x + 11x 1 2 u.d.n. 6x + 4x x, x Max x 1 x 2 RS Max x 3 x 2 RS z z x x entweder ist x 2 oder x IP und Branch and Bound 24

25 Graphische Lösung von LP0 x LP0 o x1 Zielfunktion IP und Branch and Bound 25

26 Verzweigen an der Variablen x1 IP: max z A x <= b ganzz. x >= 0 LP0: z0 = 52,5 x1 = 2,5; x2 = 0 x1 <= 2 x1 >= 3 LP11: LP12 IP und Branch and Bound 26

27 B&B Lösung der Probleme LP11 und LP12 Max x 1 x 2 RS Max x 1 ' x 2 RS Max x 1 ' x 3 RS z z z x x x x 1 ' x x Max x 1 x 2 RS Max x 4 x 2 RS z z x x keine zul. Lösung! x x IP und Branch and Bound 27

28 B&B Graphische Lösung LP11 und LP12 x LP12 1 LP11 o x1 Zielfunktion IP und Branch and Bound 28 4

29 Baum nach ersten B&B-Schritt IP: max z A x <= b ganzz. x >= 0 LP0: z0 = 52,5 x1 = 2,5; x2 = 0 x1 <= 2 x1 >= 3 LP11: z11 = 50,25 x1 = 2; x2 = 0,75 LP12 = FC1 IP und Branch and Bound 29

30 B&B Graphische Lösung LP21 und LP22 x LP22 o 1 LP x1 Zielfunktion IP und Branch and Bound 30

31 B&B Baum nach 2 Verzweigungen IP LP0 x1 <= 2 LP11: z11 = 50,25 x1 >= 3 LP12 x1 = 2; x2 = 0,75 x2 = 0 x2 >= 1 FC1 LP21: z21 = 42 x1 = 2; x2 = 0 LP22: z22 = 49,50 x1 = 11/6; x2 = 1 FC3 IP und Branch and Bound 31

32 B&B Graph LP31 und LP 32 x LP31 o x1 4 Zielfunktion IP und Branch and Bound 32

33 B&B Baum nach 3 Verzweigungen IP LP0 x1 <= 2 x1 >= 3 LP11 LP12 x2 = 0 x2 >= 1 LP21 LP22: z22 = 49,50 x1 = 1 5/6; x2 = 1 x1 <= 1 x1 = 2 FC1 LP31: z31 = 43 3/4 LP32: x1 = 1; x2 = 2 1/4 IP und Branch and Bound FC1 33

34 B&B Graph LP41 und LP42 x2 4 3 LP42 2 LP41 1 o x1 4 Zielfunktion IP und Branch and Bound 34

35 B&B Vollständiger Entscheidungsbaum IP LP0 x1 <= 2 x1 >= 3 LP11 LP12 x2 = 0 x2 >= 1 LP21 LP22 FC1 FC3 x1 <= 1 x1 = 2 LP31 LP32 x2 <= 2 x2 >= 3 FC1 LP41 LP42 FC3 FC2 IP und Branch and Bound 35

36 B&B Problemlösung Da alle Knoten abgearbeitet sind, ist die gesuchte Lösung erreicht und es wurde nachgewiesen, dass die Lösung wirklich optimal ist. Branching: Grundsätzlich kann man in beliebig viele Knoten verzweigen. Alle so erzeugten Knoten kommen in die sog. Kandidatenliste. Bounding: An dieser Stelle können alle Hilfsmittel eingesetzt werden, um eine möglichst Schranke zu berechnen. IP und Branch and Bound 36

37 B&B Vor- und Nachteile Anbindung an das LP-Modul Gestaltungsfreiheit des Baumbaus Heuristische Unterstützung Verwendbarkeit der Lösung bei Abbruch Hoher Speicheraufwand Hoher Rechenaufwand Veränderliche Problemgröße IP und Branch and Bound 37