Algorithmische Abstraktion mit Python
|
|
|
- Helene Arnold
- vor 8 Jahren
- Abrufe
Transkript
1 Kapitel 3 Algorithmische Abstraktion mit Python 3.1 Allgemeines zu Python Python ist eine imperative und objekt-orientierte Programmiersprache mit dynamischer Typisierung. Sie ist gut geeignet zum schnellen Ausprobieren von Algorithmen (rapid prototyping) und auch als Script-Sprache. Sie hat als Basiswerte ganze Zahlen, Gleitkommazahlen (Double), und Strings. Sie hat eine umfangreiche Fehlerbehandlung zur Laufzeit (Exception-Handling). Es gibt bereits vordefinierte Datentypen wie Tupel und Listen und auch vordefinierte Listenfunktionen. Auf weitere Möglichkeiten von Python wie eigene Datentypen, Klassen, Methoden, Aus- und Eingabe werden wir hier nicht explizit eingehen. 3.2 Programmierung in Python Wir verwenden den Interpreter in Python zur Auswertung von Definitionen und Ausdrücken. Ziel ist nicht die volle Programmiersprache Python zu lernen, sondern die typischen Programmiermethoden und das Speicher- und Auswertungsmodell einer imperativen Programmiersprache zu verstehen. Zunächst führen wir nur die Programmierung ohne Listen und Listenfunktionen ein Python: Struktur eines imperativen Programms Ein Python-Programm-File besteht, ähnlich wie ein Haskell-Programm, aus Definitionen von Funktionen. Es können Deklarationsteile wie Import- Deklarationen enthalten sein. 1
2 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Die wesentlichen Bausteine einer Funktionsdefinition sind Befehle (Anweisungen, Kommandos), wie Zuweisungen Sprungbefehle, Ein/Ausgabebefehle, usw.. Die meisten Befehle haben das Ziel, irgendeinen Seiteneffekt zu bewirken wie Änderung des Speichers, Ausgabe auf einen Drucker, u.ä. oder den aktuellen Zustand zu ermitteln. Innerhalb der Anweisungen gibt es auch die Möglichkeit Ausdrücke zu schreiben, deren Auswertung ähnlich zu Haskell erfolgt, allerdings ist es immer die strikte Auswertungsreihenfolge. In diesen Ausdrücken ist die Verwendung selbstdefinierter Funktionen möglich, wobei auch die Ergebnisse der Funktionsaufrufe (Returnwert) bei der Berechnung verwendet wird Zuweisung und Kontrollstrukturen in Python Python erlaubt die Eingabe von arithmetischen Ausdrücken. Man kann den Interpreter wie einen Taschenrechner, aber mit änderbarem Speicher, verwenden: >>> a = 3 >>> b = 4 >>> c = a**2 + b**2 >>> c 25 >>> print math.sqrt(c) 5.0 >>> Wir werden die Syntax von wesentlichen Konstrukten in Python nun kurz erklären, für weitere Konstrukte sowie Details zur Syntax von Python sei auf Tutorials und Handbücher verwiesen. Die Syntax der Zuweisung (Assignment) ist: variable = ausdruck Zunächst wird das Ergebnis des Ausdruckes berechnet, wobei die Werte von Variablen im Speicher nachgeschaut werden. Das Resultat ist ein im Speicher liegendes Objekt. Objekte können hierbei einfache Zahlen, Strings aber auch komplexe Datenstrukturen sein. Anschließend weist die Zuweisung der Variablen als Wert das Objekt zu. Alternative Sichtweise ist, dass das Objekt als Name den Namen der Variablen erhält. Ein Objekt kann durchaus mehrere Namen besitzen. Die Deklaration der Variablen(namen) geschieht in Python mit der ersten Zuweisung, Variablen müssen somit nicht explizit vorher deklariert werden. Man kann auch arithmetische Operatoren mit der Zuweisung verknüpfen: ist möglich: x op = Ausdruck
3 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember >>> a= 100 >>> a /= 5 >>> a 20 >>> a *= 5 >>> a 100 Es ist auch eine (scheinbar parallele) Mehrfach-Zuweisung möglich: wobei e i Ausdrücke sind. Die Auswertung des Ausdrucks x 1,... x n = e 1,..., e n x 1,... x n = s 1,..., s n ist folgendermaßen: Der Wert aller Ausdrücke s i wird zuerst ermittelt, und danach werden den Variablennamen x i die Werte (d.h. Objekte ) s i zugewiesen. Das if-then-else-konstrukt hat in Python die Syntax: if Bedingung: Anweisungen wenn Bedingung wahr else: Anweisungen, wenn Bedingung falsch Eine Besonderheit von Python ist, dass es das Schlüsselwort then nicht gibt, dafür Doppelpunkte zur Trennung einzelner Teilkonstrukte verwendet werden. Zusätzlich bestimmt die Einrückung die Blockstruktur, und sorgt dafür, dass man Klammern weglassen kann. Es gibt noch weitere Varianten von if-then-else in Python, ohne else Zweig oder mit zusätzlichen Abfragen (elif-zweigen). Die while-schleife dient zur Iteration, die Syntax ist: while Bedingung: Schleifenkörper Der Anweisungsblock des Schleifenkörpers wird solange ausgeführt bis die Bedingung nicht (mehr) erfüllt ist. Im Schleifenrumpf können die Statements break und continue verwendet werden. Beispiel >>> a=10 >>> while a > 0:... print a... a = a-1...
4 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Funktions- bzw Prozedurdefinitionen, werden mit dem Schlüsselwort def eingeleitet: def Funktioname(parameter1, parameter2,...) : Anweisungen return Wert Der Rückgabewert der Funktion ist der mit dem Schlüsselwort return zurück gereichte Wert. Die return-anweisung darf auch weggelassen werden, dann liefert die Funktion nichts zurück (bzw. None). Prozeduraufrufe finden immer mit voller Argumentanzahl und mit eingeklammerten Argumenten statt: f(a, b, c). Komplexe Zahlen sind verfügbar. Sie werden als Paar von zwei Double- Zahlen repräsentiert, der Real- und der Imaginär-Teil. Will man diese aus der komplexen Zahl z extrahieren, dann benutzt man z.real und z.imag. >>> a= j >>> a.real 1.5 >>> a.imag 0.5 >>> abs(a) >>> a*a (2+1.5j) >>> Neben einfachen Strings kann man Unicode Strings in Python auf folgende Art erzeugen: >>> u Hello World! u Hello World! Es gibt eine Menge von Modulen, die zur Verfügung stehen. Man kann sie im Interpreter verwenden durch entsprechende import-anweisungen und qualifizierte Aufrufe:
5 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember >>> import cmath >>> a= j >>> cmath.sin(a) ( j) >>> Eine genauere Beschreibung folgt noch. 3.3 Beispiele und Besonderheiten in Python Einige einfache Funktionen in Python In Python kann man wie in Haskell Funktionen definieren. Die Syntax ist etwas anders: Z.B. die Wurzelberechnung mittels Iteration kann man so programmieren wenn man sie selbst programmieren will, und nicht math.sqrt verwenden will. def wurzel(x): return wurzeliter(1.0,x) def wurzeliter(schaetzwert,x): if gutgenug(schaetzwert,x): return schaetzwert else: return wurzeliter(verbessern(schaetzwert, x), x) def quadrat(x): return x*x def gutgenug(schaetzwert,x): return (abs ((quadrat(schaetzwert) - x) / x) < ) def verbessern(schaetzwert,x): return mittelwert(schaetzwert, (x / schaetzwert)) def mittelwert(x,y): return (x + y) / 2.0 >>> wurzel(2.0) >>> Verletzung der referentiellen Transparenz Die referentielle Transparenz, die in Haskell galt, wird in Python, wie in allen imperativen Programmiersprachen, verletzt: count = 0 def f(x):
6 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember global count count = count + x return count Der Test f (1) == f (1) ergibt 0, d.h. falsch bei diesem Beispiel, da die globale Variable count durch Seiteneffekte verändert wird Flussdiagramme Der größte gemeinsame Teiler kann durch die Prozedur ggtpy berechnet werden: def ggtpy(x,y): if x <= 0 or y <= 0: print Eingabe in GGT muss positiv sein else: while x!= y: if x > y: x = x - y else: y = y - x return x Die schnellere Version von ggt, hier rekursiv: def ggt(x,y): if y == 0: return x else: return ggt(y, (x % y)) Einige Beispielauswertungen: >>> ggtpy(4,6) 2 >>> ggtpy(100,85) 5 >>> ggtpy(3,3) 3 >>> ggtpy(0,0) Eingabe in GGT muss positiv sein 0 >>> ggtpy(1234,4321) 1 >>> ggtpy(1243,3421) 11 Man kann ein sogenanntes Flussdiagramm verwenden, um die Wirkungsweise dieses Programms zu veranschaulichen (siehe Figur 3.1). Allerdings sind Flussdiagramme als Entwurfsmethode oft von begrenztem Nutzen, da zu große Diagramme entstehen.
7 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember x := a; y := b drucke x Ja x = y nein Stop Ja x > y nein x := x-y y := y-x Abbildung 3.1: Flußdiagramm für ggt Vertauschung ohne Hilfsvariable Mit der Mehrfach-Zuweisung kann man die Vertauschung von Variablenwerten ohne Hilfsvariable durchführen: >>> a = 1 >>> b = 2 >>> a,b = b,a >>> a 2 >>> b 1 >>> In anderen imperativen Programmiersprachen braucht man i.a. die Sequenz:
8 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember c = a a = b b = c ####### Im Python Interpreter: >>> a = 1 >>> b = 2 >>> c = a >>> a = b >>> b = c >>> a 2 >>> b 1 >>> Die Implementierung der Mehrfach-Zuweisung ist doch nicht ganz so parallel wie vermutet >>> a,b,a = 1,2,3 >>> a 3 >>> Berechnung der Fibonacci-Zahlen Die Berechnung der Fibonacci-Zahlen kleiner als n kann man in Python (optimiert) so hinschreiben: def fib(n): a,b = 0,1 while b < n: print b, a,b = b,a+b Die formale Definition ist fib n = fib n 1 + fib n 2 für n > 1 und fib 0 = 0, fib 1 = 1. >>> fib(1000) Implementierung der 3 n + 1-Funktion Der Fairness halber die Python-Implementierung von drein in Python: def drein(x): while x!= 1: print(x) if x % 2 == 0: x = x/2
9 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember else: x = print(1) 3*x Boolesche Funktionen Beispiel Zur Demonstration erläutern wir kurz die Wirkungsweise der Booleschen Funktionen: >>> a = 1 >>> not a False >>> a = 0 >>> b = 1 >>> a or b 1 >>> a and b 0 >>> del b >>> b Traceback (most recent call last): File "<input>", line 1, in? NameError: name b is not defined >>> a 1 >>> a or b 1 D.h. not, or, and wirken (fast) wie die Booleschen Operatoren. Es gibt eine kleine Besonderheit: or und and werten von links nach rechts aus und geben ihr Ergebnis sofort zurück, wenn der Wert aufgrund des ersten Arguments schon bekannt ist, auch wenn das zweite undefiniert ist. Sie wirken wie folgende Funktionen: def or(x,y): if x: return x else: return y def and(x,y): if x: return y else: return x
10 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Iterative Prozesse Funktionen, die iterative Prozesse erzeugen, lassen sich leicht mittels einer while-schleife (oder einer for-schleife) programmieren: Hier die den Haskell- Funktionen entsprechenden Funktionen zur Fakultät in Python. Beachte, dass man die Anweisung zur strikten Auswertung in Python nicht braucht. def fakultaetlin(n): a = faktiter(1,1,n) return a def faktiter(produkt,zaehler,max): if zaehler > max: return produkt else: return faktiter(zaehler * produkt,zaehler + 1,max) def faktwhile(n): produkt = 1 zaehler = 1 max = n while zaehler <= max: produkt = (zaehler * produkt) zaehler = zaehler + 1 return produkt Module in Python Module dienen zur Strukturierung / Hierarchisierung: Einzelne Programmteile können innerhalb verschiedener Module definiert werden; eine (z. B. inhaltliche) Unterteilung des gesamten Programms ist somit möglich. Hierarchisierung ist möglich, indem kleinere Programmteile mittels Modulimport zu größeren Programmen zusammen gesetzt werden. Kapselung: Nur über Schnittstellen kann auf bestimmte Funktionalitäten zugegriffen werden, die Implementierung bleibt verdeckt. Sie kann somit unabhängig von anderen Programmteilen geändert werden, solange die Funktionalität (bzgl. einer vorher festgelegten Spezifikation) erhalten bleibt. Wiederverwendbarkeit: Ein Modul kann für verschiedene Programme benutzt (d.h. importiert) werden. In Python gibt es ebenfalls Module, hierbei gibt es jedoch keinen Modulkopf wie in Haskell, der eine Datei als Modul auszeichnet. Vielmehr ist jede Datei, die Python-Code enthält, ein Modul und kann von anderen Modulen aus importiert werden.
11 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Modulimport mittels import In einfachster Weise kann ein Modul, durch die Anweisung import Modulname importiert werden, wobei der Modulname dem Dateinamen ohne Dateiendung entspricht. Bei erstmaliger Ausführung der import-anweisung werden die auf oberster Ebene des Moduls definierten Befehle (d.h. solche die nicht innerhalb einer Funktionsdefinition stehen) ausgeführt. Bei nochmaligem Ausführen der import-anweisung werden diese Anweisungen nicht erneut ausgeführt. Zur Reinitialisierung eines geladenen Moduls steht jedoch die Funktion reload zur Verfügung, die als Argument das Modulobjekt erwartet, d.h. reload(modulname) kompiliert den Quellcode erneut (in interpretierbaren Byte-Code) und führt anschließend die Anweisungen auf oberster Ebene des importierten Moduls erneut aus. Beispiel Wir betrachten die Datei Fib.py, d.h. das Modul Fib: def fib(n): a,b = 0,1 while b < n: print b, a,b = b,a+b X=10 # Diese Zeilen werden beim Import fib(x) # ausgefuehrt Beim Import des Moduls werden die beiden letzten Befehle (im Namensraum des Modules Fib) ausgeführt: >>> import Fib Auf die Funktionsdefinitionen und globalen Variablen des mittels import eingebundenen Moduls kann nur qualifiziert, d.h. in der Form Modulname.Funktionsname bzw. Modulname.Variablenname, zugegriffen werden. Beispiel Nach Laden des Moduls Fib aus Beispiel ist die (globale) Variable X unbekannt, sie existiert jedoch qualifiziert, gleiches gilt für die Funktion fib: >>> X Traceback (most recent call last): File "<stdin>", line 1, in? NameError: name X is not defined >>> Fib.X 10 >>> Fib.fib(5)
12 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Lokale Aliase für Modulnamen Importierte Module können analog wie in Haskell unter einem Alias-Namen importiert werden, hierfür gibt es in Python das Schlüsselwort as, z.b. kann man das Modul Fib aus Beispiel unter dem Namen Fibonacci importieren: >>> import Fib as Fibonacci >>> Fibonacci.fib(5) Einbinden mittels from Mit der from-anweisung können zum einen die zu importierenden Definitionen selektiert werden, zum anderen sind sie direkt im Namensraum des importierenden Moduls, d.h. unqualifiziert, verfügbar, die Syntax hierbei ist from Modulname import Definitionsliste Z.B. kann man ausschließlich die Funktion fib importieren: >>> from Fib import fib >>> fib(5) Es gibt noch die Variante from Modulname import * die sämtliche Namen eines Moduls in den Namensraum des importierenden Moduls kopiert. Hiervon sei aber abgeraten, da unerwartete Seiteneffekte auftreten können: Beispiel Wir betrachten das Modul Printer: X = 10; def printer(): global X: print X Wird dieses Modul mit der from *-Anweisung importiert und die importierte globale Variable X verändert, so gilt diese Änderung nur im Namensraum des importierenden Moduls, nicht jedoch im Namensraum der Funktion printer: >>> from Printer import * >>> X 10 >>> printer() 10
13 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember >>> X = 20 >>> printer() 10 >>> X 20 Keine Datenkapselung in Python In Python gibt es keine (echte) Möglichkeit bestimmte Funktionsdefinitionen, o.ä. vom Export auszuschließen, d.h. das importierende Modul kann auf sämtliche definierten Namen des importierten Moduls zugreifen. Eine Datenkapselung ist somit in Python nicht möglich. Es gibt lediglich die Konvention, dass man Definitionen deren Namen mit einem Unterstrich _ beginnen, als versteckt ansehen sollte, und im importierenden Modul nicht benutzen soll. Der Interpreter verbietet den Zugriff jedoch nicht. 3.4 Auswertung von Python-Programmen Der von-neumann-rechner ist ein von John von Neumann ( ) vorgeschlagenes Modell eines universellen Rechners, der zum Konzept der imperativen Programmiersprachen passt, genauer: zu einem primitiven Assembler- Programm. Das Konzept des von-neumann Rechners ist hilfreich beim Verständnis der Auswertung von imperativen Programmen. Um die volle Auswirkung der Zuweisung zu verstehen, insbesondere die Gültigkeitsbereiche von Variablen, ist es hilfreich, ein solches Modell des Rechners und Speichers zu betrachten.
14 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Haupt-Speicher Daten Programm Ein/ Ausgabe Rechenwerk Steuerwerk Bus Register Programmzähler Datenzeiger Akkumulator Der Speicher ist in gleichlange Einheiten, die Speicherzellen zu je einem Byte = 8 Bits, eingeteilt, die fortlaufend nummeriert sind und unter dieser Nummer adressierbar sind, und direkt, unter Angabe der Adresse, gelesen und geschrieben werden können. Als weitere größere Einheit hat man manchmal auch (Speicher-)Worte (normalerweise 1 Wort = 4 Byte = 32 Bit). Eine zentrale Idee ist die Speicherung von Daten und Programmen im gleichen Speicher in Binärcode, wobei die Programme in kodierter Form vorliegen. Selbst die von-neumann Maschine in der einfachsten Form benötigt zumindest: ein Adressregister für das Programm (den Programmzähler), ein Register für Datenadressierung, und ein Register zum Rechnen (Akkumulator). Heutzutage sind die Register 32 oder 64 Bit lang. Mit 32 Bit ist der adressierbare Speicher auf 2 32 Bytes beschränkt (ca. 4 Gigabyte). Im Steuerwerk werden die Programmbefehle interpretiert, und im Rechenwerk die arithmetischen Operationen ausgeführt. Ein Programm für eine von-neumann-maschine besteht aus Befehlen, die man sich durchnummeriert vorstellt: 1.,2.,3...., und die hintereinander im Speicher abgelegt sind. Als Befehle sind möglich: arithmetische: Addiere Konstante zum Akkumulator. Auch indirekt adressierte: mulitpliziere Zahl an Adresse xxx mit dem Akkumulator und speichere das Ergebnis im Akkumulator. Auch arithmetische Vergleiche sind möglich.
15 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember bedingte und unbedingte Sprungbefehle. Z.B. springe zu Programmbefehl 108. Oder: Wenn Akkumulator 0, dann springe zu Befehl 101, sonst zu 201. Ein-Ausgabe-Befehle: Drucke den Inhalt des Akkumulators. Oder: Speichere den Inhalt des Akkumulators an der Adresse, die im Datenregister steht. Die zweite zentrale Idee des von-neumann Rechner-Modells ist die Methode der Abarbeitung des Programms: Es gibt einen Befehlszyklus, der in etwa so abläuft. Start des Programms ist mit dem Programmbefehl 1. Der Befehlszyklus: 1. Lade den Programmbefehl mit der Nummer, die im Programmzähler angegeben ist, in das Steuerwerk. Das Steuerwerk steuert dann, abhängig vom Inhalt des Programmbefehle, die weitere Abarbeitung. 2. Wenn es ein Sprungbefehl ist, setze den Programmzähler neu. Ende des Zyklus. Wenn es ein arithmetischer Befehl ist, dann entsprechend abarbeiten. Diese Abarbeitung wird vom Rechenwerk erledigt. Der Programmzähler wird danach um 1 erhöht. Ende des Zyklus. Wenn es ein Ein-Ausgabebefehle ist, dann entsprechend abarbeiten. Der Programmzähler wird danach um 1 erhöht. Ende des Zyklus. 3. Bei dem speziellen Befehl Stop wird das Programm beendet. Natürlich ist ein richtiger Computer (bzw. Prozessor) komplizierter. Zum Beispiel hat die Recheneinheit noch weitere universelle Register, die meist so groß sind, dass eine Adresse gespeichert werden kann Auswertung von Pythonprogrammen In diesem Abschnitt werden wir einen Ausschnitt aus der operationalen Semantik von Python angeben. Das soll das Verständnis der Vorgänge vertiefen. Auch wenn es zunächst wie eine umständliche Erklärung von Zusammenhängen wirkt, die man nach dem Erlernen der Programmiersprache einfach weiß, braucht man eine solche formale Begriffsbildung und Regeln, um die Auswertung von Programmen und Ausdrücken rechnerunabhängig mitteilen und beschreiben zu können. Dieser Formalismus ist es auch notwendig, um zu spezifizieren bzw. zu verstehen, wie man geschachtelte Ausdrücke mit Seiteneffekten und Funktionsaufrufen auswertet. Zudem versteht man danach auch, welche Implementierungen der Modellvorstellung nicht entsprechen.
16 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom 9. Dezember Wir nehmen an, dass nur sehr einfach strukturierte Programme vorliegen. D.h. als Python-Programm betrachten wir eine Menge von Funktionsdefinitionen und Variablendefinitionen, wobei nur Zuweisung, if-then-else, while, arithmetische und logische Operationen benutzt werden. Funktionsaufrufe werden erst mal ausgeschlossen, da sie Seiteneffekte auf globalen Variablen bewirken können und auch etwas komplizierter sind. Diese werden später behandelt. An Basiswerten betrachten wir im Moment nur Zahlen, wobei auch Boolesche Werte als Zahlen gespeichert werden 1 bedeutet wahr und 0 bedeutet falsch Die formale Modellierung Wir betrachten auch die globale Umgebung, damit wir Seiteneffekte auf globale Variablen angeben und modellieren können, da dies in den meisten imperativen Programmiersprachen vorkommt. Insbesondere muss die operationale Semantik dann die Reihenfolge der Operationen beschreiben, denn die Seiteneffekte ändern sich, wenn die Reihenfolge der Auswertungen verändert wird. Unsere Modellierung in diesem Abschnitt ist vereinfacht und ist nicht einfach erweiterbar auf geschachtelte Funktionsdefinitionen, da man dazu weitere Konzepte benötigt. Definition Eine Bindung ist ein Paar (x, v), wobei x ein Variablenname und v ein Basiswert ist oder. Das schreiben wir etwas deutlicher als x v. Ein Umgebungsrahmen (Frame) ist eine endliche Menge von Bindungen. Pro Variablennamen x kann nur eine Bindung x v in einem Umgebungsrahmen enthalten sein. Eine Umgebung (Variablenumgebung) ist ein Paar (R 1, R 2 ) von zwei Umgebungsrahmen, des lokalen Umgebungsrahmens R 1 und des globalen Umgebungsrahmens R 2. Um das Modell zu vereinfachen, nehmen wir an, dass in unserer Modellierung lokale Variablennamen niemals gleich globalen Variablennamen sind. Das kann man erreichen, indem lokale Variablen in Funktionsrümpfen so umbenannt werden, dass diese disjunkt zu allen anderen Variablen sind. Der Wert wert(x, Z) einer Variablen x in einer Umgebung Z = (R 1, R 2 ) ist definiert als der Wert v der Bindung x v in der Umgebung R 1 R 2. Kommt kein solches Paar in R 1 R 2 vor, oder ergibt sich, so ist der Wert undefiniert. Normalerweise wird bei einer solchen Anfrage das Programm abgebrochen. Die Funktion update(x, v, Z) hat als Ergebnis die Umgebung Z neu, die aus Z = (R 1, R 2 ) folgendermaßen entsteht: Wenn x lokale Variable ist, und es eine Bindung x v in R 1 gibt, wird diese durch x v ersetzt. Das ergibt einen veränderten Umgebungsrahmen R 1, so dass Z neu := (R 1, R 2 ). Wenn x lokale Variable ist und wenn es keine Bindung x v in R 1 gibt, dann ergibt sich ein Fehler: Wert wird referenziert ohne dass er angelegt wurde.
17 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Wenn x globale Variable ist, und es eine Bindung x v in R 2 gibt, wird diese durch x v ersetzt. Das ergibt einen veränderten Umgebungsrahmen R 2, so dass Z neu := (R 1, R 2). Wenn x globale Variable ist und wenn es keine Bindung x v in R 2 gibt, dann ergibt sich ein Fehler: Wert wird referenziert ohne dass er angelegt wurde. Beispiel Sei die Umgebung definiert als Z = ({x 1, y 2, z 3}, {gx 2, gu 100}) Dann ist wert(x, Z) = 1, wert(gu, Z) = 100, und update(x, 30, Z) = ({x 30, y 2, z 3}, {gx 2, gu 100}). Definition Der Wert eines Ausdrucks s in der Umgebung Z ist der Wert, der bei Berechnung des Ausdrucks entsteht, wobei der Wert der Variablen in der Umgebung Z ermittelt wurde. Ist eine (für die Berechnung benötigte) Variable x in s undefiniert, dann ist der Wert von s ebenfalls undefiniert. D.h. wir nehmen bei der Auswertung von Ausdrücken in einfachem Python im Moment an, dass keine Seiteneffekte (d.h. keine Zustandsänderungen) durch Auswertungen von Ausdrücken entstehen. Hier einige formale Definitionen für die Auswertung von arithmetischen und Booleschen Ausdrücken, die seiteneffektfrei sind, d.h. ohne weitere Funktionsaufrufe, wobei der Operator rechts in der Tabelle jeweils der arithmetische Operator ist. Funktionsanwendungen und Kombinationen mit arithmetischen Ausdrücken werden wir weiter unten behandeln. wert(s 1 + s 2, Z) := wert(s 1, Z) + wert(s 2, Z) wert(s 1 s 2, Z) := { wert(s 1, Z) wert(s 2, Z) 1 wenn wert(s1, Z) wert(s wert(s 1 s 2, Z) := 2, Z) { 0 sonst 1 wenn wert(s, Z) = 0 wert(not s, Z) := { 0 wenn wert(s, Z) 0 0 wenn wert(s1, Z) = 0 wert(s 1 and s 2, Z) := wert(s 2, Z) wenn wert(s 1, Z) Beispiel Wert eines seiteneffektfreien Ausdrucks in einer Umgebung. Sei Z = ({x 1, y 2, z 3}, {u 100}). Dann ergibt sich mit obiger Definition als Wert von x+(y*z):
18 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom wert(x + (y z), Z) = wert(x, Z) + wert(y z, Z) = 1 + (wert(y, Z) wert(z, Z)) = 1 + (2 3) = 7 Als Wert von x+u ergibt sich, wobei u global definiert ist: Auswertung von Zuweisungen wert(x + u, Z) = wert(x, Z) + wert(u, Z) = = 101 Definition Wir werden im folgenden die Schreibweise der logischen Regeln verwenden: V oraussetzungen Konsequenz Oberhalb des Striches werden evtl. mehrere Voraussetzungen notiert und unterhalb die Konsequenz. Wenn es keine Voraussetzung gibt, wird nur die Konsequenz notiert (ohne Bruchstrich) Effekt der Ausführung eines Python-Befehls Wir schreiben den Effekt einer Befehlsausführung folgendermaßen hin: (Z; B) Z, wenn, nach Ausführung des Befehls (des Programmstücks) B im Zustand Z der Zustand Z danach hinterlassen wird. Zuweisung: (Z; x = s) update(x, wert(s, Z), Z) Auch hier ist zu beachten, dass wir erst mal annehmen, dass s keine Seiteneffekte bewirkt. Mehrfachzuweisung: (Z; x 1,..., x n = s 1,..., s n ) update(x n, wert(s n, Z), update(x n 1, wert(s n 1, Z),... update(x 1, wert(s 1, Z), Z)...))
19 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Man erkennt, dass diese Zuweisung ein Potential zur Parallelisierbarkeit hat, aber nur unter der Annahme, dass die Auswertung der Ausdrücke keine Seiteneffekte bewirkt, und dass die Variablennamen der Zuweisung alle verschieden sind. Beispiel Sei Z = ({x 3, y 4, z 5}, ). Die Auswertung von x,y = y,x im Zustand Z ergibt: Z = update(y, wert(x, Z), update(x, wert(y, Z), Z)) = update(y, wert(x, Z), update(x, 4, Z)) = update(y, wert(x, ({x 3, y 4, z 5}, )), ({x 4, y 4, z 5}, )) = update(y, 3, ({x 4, y 4, z 5}, )) = ({x 4, y 3, z 5}, ) Hier muss man beachten, dass Z in den Berechnungen immer die gleiche Umgebung referenziert. Beispiel Sei Z = ({x 3, y 4, z 5}, ). Die Auswertung von x,x = y,0 im Zustand Z ergibt: Z = update(x, wert(0, Z), update(x, wert(y, Z), Z)) = update(x, 0, update(x, 4, Z)) = update(x, 0, update(x, 4, ({x 3, y 4, z 5}, ))), = update(x, 0, ({x 4, y 4, z 5}, ), = ({x 0, y 4, z 5}, ), Auswertung der Sequenz Dies ist ein Konzept, das in Haskell unnötig ist, aber in imperativen Programmiersprachen wie Python notwendig ist. {c 1 ; c 2 } ist die Hintereinanderausführung der beiden Kommandos c 1, c 2. Die Regel zur operationalen Semantik ist: (Z; c 1 ) Z 1 (Z 1 ; c 2 ) Z 2 (Z; {c 1 ; c 2 }) Z 2 Beispiel Sei Z = ({x 3, y 4, z 5}, ). Die Auswertung von x = y; y = x im Zustand Z ergibt: 1. (Z, x = y) update(x, wert(y, Z), Z) = update(x, 4, Z) = ({x 4, y 4, z 5}, ) =: Z 1 2. (Z 1, y = x) update(y, wert(x, Z 1 ), Z 1 ) = update(y, 4, Z 1 ) = ({x 4, y 4, z 5}, ) = Z 1 Fallunterscheidung Auswertungsregeln:
20 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom wert(b, Z) 0 (Z, c 1 ) Z 1 (Z; if b : c 1 else : c 2 ) Z 1 wert(b, Z) = 0 (Z, c 2 ) Z 2 (Z; if b : c 1 else : c 2 ) Z 2 Die Auswertung einer Fallunterscheidung ohne else-fall oder mit weiteren elseif-fällen ist jetzt eine einfache Verallgemeinerung. Bei der Abarbeitung muss man sich merken, dass zunächst nur die Bedingung ausgewertet wird, und abhängig von ihrem Wert entweder die Befehle des jaoder des nein-falles. While-Schleife Bei der formalen Definition der Auswertung der while-schleife muss man beachten, dass diese evtl. nicht stoppt. Die folgende Regel berücksichtigt das. Ebenso beachte man, dass die Regel rekursiv ist. wert(b, Z) = 0 (Z; while b : c) Z wert(b, Z) 0 (Z, c) Z 1 (Z 1 ; while b : c) Z 2 (Z; while b : c) Z 2 Die erste Regel behandelt den Fall, dass die Bedingung falsch ist, und die while-schleife nicht durchlaufen wird. In dem Fall bleibt die Umgebung erhalten. Die zweite Regel behandelt den Fall, dass Die Bedingung wahr ist, und die Schleife durchlaufen wird. In der Bedingung steht: wenn der Rumpf einmal durchlaufen wird, danach die While-Schleife und sich dann die Umgebung Z 2 ergibt, dann auch nach der While-Abarbeitung alleine. Die for-schleife werden wir noch behandeln. Beispiel Sei die Umgebung vor der Auswertung der while-schleife: Z = ({x 0, n 5}, ). Der Befehl sei while (n > 0): x = x+n; n = n-1 Wir gehen die Auswertung durch, entsprechend den Regeln: 1. wert(n > 0, Z) ergibt Wir wenden die zweite Regel an. Die zweite Voraussetzung ist (Z, c) Z 1. c ist hierbei der Rumpf des while-ausdrucks und Z 1 die Umgebung nach einmaliger Ausführung. Es ergibt sich Z 1 = ({x 5, n 4}, ). Um die dritte Voraussetzung zu erfüllen, muss man jetzt wieder einen while-ausdruck, jetzt im Zustand Z 1 auswerten. D.h. man muss wieder die volle Regel für while verwenden. Das kommt mehrfach vor und ergibt
21 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom eine Folge von Umgebungen: ({x 9, n 3}, ). ({x 12, n 2}, ). ({x 14, n 1}, ). ({x 15, n 0}, ). 3. Danach muss man, um die letzte Voraussetzung zu erfüllen, die erste Regel anwenden, es ergibt sich, dass die Umgebung erhalten bleibt. 4. Jetzt kann man alle Voraussetzungen nach und nach erfüllen, die letzte Umgebung wird jeweils weitergegeben. Es ergibt sich am Ende Z 2 = ({x 15, n 0}, ) Anzahl der Schritte bei Auswertung Die Regeln der operationalen Semantik sind zwar nicht so formuliert, dass sie die Reihenfolge der Operationen genau festlegen, aber man kann an der Weitergabe der Umgebungen die notwendige Reihenfolge der Schritte ablesen. Aufbauend auf der operationalen Semantik können wir jetzt die Anzahl der Auswertungsschritte definieren und auch zählen. Wir vereinbaren: Bei Auswertung eines Ausdrucks werden folgende Auswertungsschritte gezählt: Einzelauswertung einer Operation in einem Ausdruck Auswertung eines Befehls Zuweisung Wertermittlung bei Variablen Nicht gezählt wird die implizite Initialisierung von Variablen. Bei Operationen wir += nehmen wir an, dass diese zunächst in eine normale Zuweisung transformiert wurden. Beispiel Die Auswertung der Sequenz x = y; y = x ergibt: Auswertung von y Zuweisung auf x Auswertung von x Zuweisung auf y Das sind insgesamt 4 Auswertungsschritte. Beispiel Auswertung einer while-schleife, die fib (10) berechnet. Wir zählen die Schritte.
22 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom n = 10; a,b = 0,1; while n > 0: print b; a,b = b,a+b; n = n-1; Die Anzahl der Auswertungsschritte ergibt: 1 Zuweisung zu n 2 Mehrfachzuweisung 1 Aufruf von while 2 Bedingung 2 print 2 Mehrfachzuweisung a = b 4 Mehrfachzuweisung b = a+b; (a;b;+;=) 3 Zuweisung n=n-1 Ergebnis: 3 für Initialisierung 1 für while-aufruf 14 pro while-durchlauf (10 mal) 2 Bedingung zur While-Beendigung In der Summe ergibt das: n Auswertungsschritte, d.h. O(n) Auswertung unter Benutzung von Funktionsaufrufen und Seiteneffekten Hier erweitern wir die Auswertung um die Behandlung von Funktionsaufrufen und auch Seiteneffekten. Die (echten) Seiteneffekte können in unserer Modellierung nur von Funktionsanwendungen herrühren, in denen globale Variablen verändert werden. Bevor wir die Formalisierung durchführen, hier noch zwei Beispiele. Beispiel Ein Beispiel einer Booleschen Funktion mit Seiteneffekt. Die Funktion schonmalda testet, ob der Wert schon einmal eingegeben wurde. schonmaldakenn = False def schonmalda(x): global schonmaldakenn; if (x == 12345): if schonmaldakenn: return True else: schonmaldakenn = True def InitKenn(): global schonmaldakenn; schonmaldakenn = False >>> kap3.schonmalda(3) False
23 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom >>> kap3.schonmalda(12345) False >>> kap3.schonmalda(12345) True >>> kap3.initkenn() >>> kap3.schonmalda(12345) False >>> kap3.schonmalda(12345) True >>> Beispiel Die Funktion addtoakku addiert das Argument jeweils zu einem Akkumulator, der als globale Variable vereinbart ist. Akkumulator = 0 def addtoakku(x): global Akkumulator; Akkumulator = Akkumulator + x return Akkumulator def ShowAkku(): return Akkumulator >>> kap3.addtoakku(2) 2 >>> kap3.showakku() 2 >>> kap3.addtoakku(2) * kap3.addtoakku(2) 24 >>> Die letzte Rechnung kommt von 4 6 = 24, da der Akkumulator jeweils um 2 erhöht wird. Da Python keine explizite Variablendeklaration für lokale Variablen in Funktionen hat, aber doch eine implizite Variablendeklaration macht, müssen wir diese Variablen hier behandeln. Mit LV(f) bezeichnen wir die lokalen Variablen von f: Das sind solche, die nicht als formale Parameter von f vereinbart sind, die aber auf der linken Seite von Zuweisungen innerhalb des Rumpfs vorkommen. Ein Funktionsaufruf in Python ist von der Form f(s 1,..., s n ). Um die Auswertung zu verstehen, muss man sich klarmachen, dass die s i wieder Funktionsaufrufe enthalten können, und dass Argumente von links nach rechts ausgewertet werden. Da als Ergebnis einer Auswertung der Wert eines Funktionsaufrufs und der Zustand benötigt wird, schreiben wir (Z; s) e (Z ; v)
24 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom falls es sich um die Auswertung eines Ausdrucks (expressions) s im Zustand Z handelt, Z der Zustand danach ist und v der return-wert von s. Aufgrund der Regeln wird bei der Auswertung e nur der globale Anteil in Z und Z unterschiedlich sein, im Gegensatz zu Auswertung von Befehlen. Eine (kleine) Schwierigkeit bereitet die spezielle Methode der Rückgabe mittels return, die nicht nur einen Wert zurückgibt, sondern auch die Ausführung der Funktion beendet, und damit einen Rücksprung bewirkt. Das kann in unserer Methode nicht genau modelliert werden, statt eines Rücksprungs sind nach einem return innerhalb der Funktion alle Befehle ohne Wirkung. Wir erweitern deshalb den bisher benutzten Formalismus, indem wir im Umgebungsrahmen zwei spezielle Variablennamen zur Steuerung der Ausführung hinzufügen: rj enthält true bzw. false, wenn ein Rücksprung aktiv ist. rw enthält den Rückgabewert, wenn ein Rücksprung aktiv ist. Wir geben nacheinander die operationale Semantik der Befehle an, wenn Seiteneffekte erlaubt sind. Zunächst die einfachen Auswertungen: (Z, x) e (Z, wert(x, Z)) wenn x Variable ist (Z, v) e (Z, v) wenn v Basiswert ist Wenn ein Rücksprung aktiv ist, sollen Anweisungen c nichts tun: return v 0 (({..., rj v,...}, R), c) ({..., rj v,...}, R) (Z; s) e (Z ; w) (Z, return s) update( rj, 1, update( rw, w, Z )) Die operationale Semantik der Konstrukte muss jetzt so erweitert werden, dass diese nur unter der Bedingung ausgeführt werden, dass rj den Wert 0 hat. Es reicht aus, das jeweils in den Bedingungen aller Regeln mit aufzuführen. Wir lassen diese Vorbedingung bei der Notation unten weg, damit die Notation Regeln nicht zu kompliziert wird. Zuweisung Mehrfachzuweisung: (Z, s) e (Z 1, v) (Z; x = s) update(x, v, Z 1 )
25 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom (Z, s 1 ) e (Z 1, v 1 ), (Z 1, s 2 ) e (Z 2, v 2 ),..., (Z n 1, s n ) e (Z n, v n ) (Z; x 1,..., x n = s 1,..., s n ) update(x n, v n, update(x n 1, v n 1,... update(x 1, v 1, Z n )...)) Man erkennt, dass die Mehrfach-Zuweisung jetzt nicht mehr parallelisierbar ist, da die Umgebungen jeweils übergeben werden müssen. Fallunterscheidung: While-Schleife (Z, b) e (Z 1, v) v 0 (Z 1, c 1 ) Z 2 (Z; if b : c 1 else : c 2 ) Z 2 (Z, b) e (Z 1, v) v = 0 (Z 1, c 2 ) Z 2 (Z; if b : c 1 else : c 2 ) Z 2 (Z, b) e (Z 1, v) v = 0 (Z; while b : c) Z 1 (Z, b) e (Z 1, v) v 0 (Z 1, c) Z 2 (Z 2 ; while b : c) Z 3 (Z; while b : c) Z 3 Auswertung eines Ausdrucks Wir müssen auch den Fall betrachten, dass eine Funktion ohne ein return beendet wird. Dann wird auch kein Wert zurückgegeben. Diesen Nicht-Wert kann man durch einen eigenen Wert beschreiben, in Python ist es None. Er verhält sich ähnlich wie das Objekt () des unit-types in Haskell. Damit kann man die Auswertung eines Ausdrucks beschreiben. Hierbei gehen wir davon aus, dass f den Rumpf rumpf f hat, die formalen Parameter x 1,..., x n und die lokalen Variablen LV (f) = {y 1,..., y m }. (Z, s 1 ) e (Z 1, v 1 ),..., (Z n 1, s n ) e (Z n, v n ), R = {x 1 v 1,..., x n v n, y 1,..., y m, rj 0, rw None} Z n = (R 1, R 2 ) ((R, R 2 ), rumpf f ) ({..., rw w}, R 2) (Z, f(s 1,..., s n )) e ((R 1, R 2 ), w) Das kann man so beschreiben: Zeile 1: Zuerst werden die Argumente von f von links nach rechts ausgewertet. Da man damit rechnen muss, dass die Auswertung Seiteneffekte in der lokalen Umgebung und in der globalen hat, darf man das nur sequentiell machen, und der veränderte Zustand muss jeweils mitübergeben werden. Das kann einen rekursiven Abstieg in die Auswertung von Unterargumenten bedeuten.
26 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Zeile 2: Wenn die Auswertung der Argumente beendet ist, kann man die lokale Umgebung R definieren, die die LV-Variablen initialisiert und den formalen Variablen die entsprechenden Werte zuweist. Zeile 3: aus Z n wird die globale Umgebung extrahiert. Zeile 4: Jetzt kann man den Rumpf der Funktion auswerten. Am Ende des Aufrufs ist der Rückgabe-Wert bekannt, falls alles terminiert. Wenn kein return gemacht wurde, wird als Wert das Objekt None zurückgegeben, das als Initialisierung verwendet wurde. Da in den Argumenten eines Ausdrucks ein return unzulässig ist 1, braucht man nicht damit zu rechnen, dass die Zustände Z i einen Sprung erzwingen. Ergebnis am Ende ist der evtl. veränderte Zustand, und der berechnete Wert. Zu beachten ist, dass die Berechnung wert(s, Z) jetzt nur noch für Variablen s stimmt. Die Berechnung des Wertes für arithmetische (auch Boolesche) Ausdrücke muss angepasst werden und sieht jetzt so aus: (Z, s 1 ) e (Z 1, v 1 ), (Z 1, s 2 ) e (Z 2, v 2 ), v 1 op v 2 = v 3 (Z, s 1 op s 2 ) e (Z 2, v 3 ) wobei op ein arithmetischer (bzw. Boolescher) Operator ist. Beispiel Als Abkürzung verwenden wir in den Beispielen rj statt und rw statt rw rj def fakultaet(x): if x <= 1: return 1 else: return x*fakultaet(x-1) Die jeweiligen lokalen Umgebungen bei Auswertung von fakultaet(3) ohne die globale Umgebung sind in zeitlicher Reihenfolge wie folgt: Aufruf von fakultaet(3) im Zustand Z {x 3, rj 0, rw None} rekursives Auswerten von fakultaet (2) x 2, rj 0, rw None} rekursives Auswerten von fakultaet (1) {x 1, rj 0, rw None} Auswerten von return 1 {x 1, rj 1, rw 1} Auswerten von return 2 {x 2, rj 1, rw 2} Auswerten von return 6 {x 3, rj 1, rw 6} Resultat am Ende ist 6. Beispiel Veränderung einer globalen Variablen durch eine Zuweisung. Hier kann man die dauerhafte Veränderung der Umgebung nachvollziehen. 1 Hier gibt es doch eine Typprüfung in Python
27 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom count = 0 def nreft(x): global count count = count + x return count Die Ausführung von nreft(1) ergibt: Aufruf von nreft(1) ({x 1, rj 0, rw None}, {count 0}) nach count = count + x ({x 1, rj 0, rw None}, {count 1}) nach return count ({x 1, rj 1, rw 1}, {count 1}) Die globale Umgebung nach dem nreft(1)-aufruf ist {count 1} und der Rückgabewert ist = 1. Die Bedingung nreft(1) == nreft(1) kann jetzt nicht zu True auswerten, denn nach Auswertung des linken Ausdrucks hat count den Wert 1, nach Aufruf des zweiten hat count den Wert 2, das sind auch die jeweiligen Rückgabewerte, somit ergibt sich False. Beispiel Wir zeigen die Zustände bei Auswertung von eulerzahl(0.0001) in zeitlicher Reihenfolge. def eulerzahl(x): s = 1 e = 0 n = 1 while x < s: e = e + s s = 1.0 / (fakultaet(n)) n = n+1 return e Abfolge der Zustände, wobei wir die globale Umgebung weglassen.
28 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Aufruf von eulerzahl(0.0001) {x , rj 0, rw None} Aufruf von eulerzahl {s, e, n, x , rj 0, rw None} 3 Zuweisungen {s 1, e 0, n 1, x , rj 0, rw None} 1. Zuweisungen im while {s 1, e 1, n 1, x , rj 0, rw None} fakultaet im while, nur dessen lokale Umgebung {x 1, rj 0, rw None} nach Aufruf fakultaet und Zuweisung: {s 1, e 1, n 1, x , rj 0, rw None)] nach n = n+1 {s 1, e 1, n 2, x , rj 0, rw None)] nach e = e+s {s 1, e 2, n 2, x , rj 0, rw None)]... Bemerkung Man sieht, dass Zuweisungen bzw. allein die Vermutung, dass welche erfolgen könnten, die Parallelisierbarkeit von Programmen verhindert. Die Reihenfolge der Auswertung in Python spielt eine große Rolle und kann nicht verändert werden, ohne die Bedeutung der Programme zu ändern. In Python wird das Ausmaß der Seiteneffekte etwas zurückgedrängt, auch wenn es noch ein normales Mittel der Programmierung ist Anzahl Auswertungsschritte mit Funktionsanwendungen und return Die Anzahl der Auswertungsschritte einer Auswertung kann man auf Programme mit Funktionsanwendung erweitern, wenn man vereinbart, dass return selbst als eine Auswertung zählt, während das Überspringen der nachfolgenden Anweisungen, bis die Funktion verlassen wird, nicht mitzählt. Ebenso zählt die Initialisierung von internen Variablen nicht mit. Beispiel Anzahl der Schritte am Beispiel der rekursiven Fibonacci- Funktion. def fib(n): if n == 0: return 0 elif n == 1: return 1 else: return (fib(n-2) + fib(n-1)) Anzahl Schritte für fib(3):
29 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Anzahl Schritte welche Auswertung 1 fib(3)-aufruf 1 if- Aufruf 2 n == 0 1 if- Aufruf 2 n == 1 1 return- Aufruf 1 +- Aufruf 2 n-2-auswertung 1 fib-aufruf (fib(1)) 1 if- Aufruf (rekursiv in fib(1)) 2 n == 0 1 if- Aufruf 2 n == 1 1 return- Aufruf: fib(1) zu Ende 2 n-2-auswertung 1 fib-aufruf (fib(2)) Argumentieren mittels operationeller Semantik Man kann die Definition der operationellen Semantik verwenden, um Beweise über Python-Programme zu führen. Als Beispiel nehmen wir die Funktion, die die Fibonacci-Zahlen berechnet. def fibw (n): a,b = 0,1 while n > 0: print b, a,b = b,a+b n = n-1 Wir zeigen: fibw(n) druckt F ib n als letzten Wert, unter der Voraussetzung, dass n > 0 und kein Überlauf eintritt. Man braucht noch eine Klarstellung, die nicht ganz offensichtlich ist: Die Operationen, die das Programm ausführt, sind konzeptuell etwas anderes als die mathematischen Operationen. Wir können aber annehmen, dass nach einer Übersetzung der internen Datenstrukturen in mathematische Objekte sich die Python-Operatoren +,,, /, > wie die mathematischen Operationen verhalten, insbesondere da wir angenommen haben, dass kein Überlauf eintritt. Der Nachweis geschieht mit vollständiger Induktion nach Anzahl der Durchläufe des while-rumpfs. Eigentlich muss man zunächst beweisen, dass die Schleife terminiert. Das ist aber einfach, da der Wert n immer kleiner wird. Man braucht eine Idee, was man beweisen will. I.a. braucht man dafür eine sogenannte Schleifeninvariante. Hier kann man diese leicht raten und erhält: wenn man den Zeitpunkt vor Durchlauf der while-schleife nimmt, und mit m
30 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom den Wert der Eingabe bezeichnet: a = F ib m n, b = F ib m n+1 Diese Schleifeninvariante wird jetzt mit vollständiger Induktion nachgewiesen: Die Induktion nach Anzahl der Schleifendurchläufe ergibt jetzt: Basisfall m = n : a = F ib n n = F ib 0 = 0 stimmt. Und b = F ib 1 = 1 stimmt. Induktionsfall: Wenn n > 0: Die Schleife wird durchlaufen. (Wir schreiben a, b, n für die alten Werte.) print b ändert den Zustand nicht. a,b = b,a+b ergibt: a = b, b = a + b n = n-1 ergibt n = n 1. Vor der Schleife galt: a = F ib m n, b = F ib m n+1 Wir berechnen a = b = F ib m n+1 = F ib m n. Das ist der erste Teil der Schleifeninvariante. Die Berechnung für b ergibt: b = a + b = F ib m n + F ib m n+1 Einsetzen des veränderten Index n ergibt: b = F ib m n 1 + F ib m n. Nach der Definition der Fibonacci-Zahlen ist das gerade b = F ib m n 1 + F ib m n = F ib m n+1. Damit ist die Behauptung mit Induktion bewiesen. Wir müssen noch argumentieren, was das letzte gedruckte b ist. Offenbar ist dann n = 1. Es ergibt sich, dass b = F ib m 1+1 = F ib m gedruckt wurde. Beispiel Dieses Beispiel soll zeigen, dass man auch in Python mit einem let doppelte Auswertungen vermeiden kann. Die Funktion f(x, y) := x(1 + xy) 2 + y(1 y) + (1 + xy)(1 y) läßt sich effizienter berechnen, wenn man definiert: a := 1 + xy b := 1 y f(x, y) := xa 2 + yb + ab Die entsprechende Definition sieht so aus: def polyf(x,y): a = 1 + x *y b = 1 - y return (x * a**2 + y* b + a*b) Lokale Funktionen und geschachtelten Gültigkeitsbereiche Python erlaubt in der Version 2.3 geschachtelte Funktionsdefinitionen, d.h. solche, die innerhalb einer Funktionsdefinition gemacht werden und auf die lokalen Variablen der Ober-Funktion zugreifen dürfen. Hier gibt es Beschränkungen bei Zuweisungen: Externe Variablen (außer globale) dürfen nicht verändert werden, aber sie dürfen referenziert werden.
31 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Beispiel def f(x): def g(y): return x+y; return g(11); Der Aufruf f(4)ergibt 15. Hier ist die textuelle Sichtbarkeit (lexikalischer Gültigkeits-Bereich) entscheidend. Der Aufruf f(11) hat als Rückgabewert den Wert von g(11). Im Rumpf von g wird x+y ausgewertet: Da g die Variable x von f sieht, ergibt sich 4+11, d.h. 15. Bei folgender unabhängiger Definition von f und g ergibt sich ein Fehler. def f(x): return g(11); def g(y): return x+y; Der Grund ist, dass g die lokale Variable x von f nicht sieht. Das Prinzip, das dahintersteht ist der lexikalische Gültigkeits-Bereich von Variablen. Die Semantik von Funktionen soll erhalten bleiben, wenn man die formalen und lokalen Parameter einer Funktion nur in dieser Funktion umbenennt. Würde der externe Zugriff auf x oben noch funktionieren, so wäre das nach Umbenennung nicht mehr möglich: def f(z): return g(11); def g(y): return x+y; Die allgemein verwendete Variante der Variablensichtbarkeit ist der lexikalische Gültigkeitsbereich, d.h., man darf nur Variablennamen verwenden, die im Programmtext auf derselben oder einer höheren Stufe verwendet werden. Die andere Methode, die oben im Beispiel nicht funktionierte, und die man in Ausnahmefällen (mit global-definition) verwendet, allerdings so, dass man sie wieder als Variante der lexikalische Sichtbarkeit sehen kann, nennt man dynamischen Gültigkeitsbereich der Variablen (hier x). Die Funktion g sieht x in der Ablaufumgebung und versucht diese zu ändern. In Python wird das Prinzip für globale Variablen verwendet, nachdem sie als solche deklariert wurden. Diese Methode hat ohne extra Deklaration schwerwiegende Nachteile, da sie die theoretische Behandlung der Bedeutung von Programmen sehr schwierig macht und zudem Namensabhängigkeiten einführt. Der Effekt der Auswertung in Python bei geschachtelten Funktionsdefinitionen kann so beschrieben werden: Wird ein undeklarierter Name referenziert, d.h. der Wert abgefragt, dann wird im nächsthöheren Gültigkeitsbereich gesucht.
32 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Wird im innersten Gültigkeitsbereich ein Variablenname definiert, kann man nicht mehr auf den gleichen Variablennamen im höheren Gültigkeitsbereich zugreifen, auch wenn man den ganz unten definierten Variablennamen wieder löscht (mit del) Variablennamen aus höheren Gültigkeitsbereichen können nicht gelöscht werden (mit del) und sie können auch nicht neu gebunden werden. (mit x =...), ein solches Assignment führt dazu, dass eine neue lokale Deklaration angelegt, und gleichzeitig auch dazu, dass sämtliche Anweisungen im selben Gültigkeitsbereich, die x referenzieren, sich nur auf diesen Gültigkeitsbereich beziehen Wir betrachten noch ein Beispiel: Beispiel def fff(): v = 2; def ggg(): v = 3; return hhh (); def hhh(): return v return ggg(); Hier ist die Frage, welchen Wert fff()zurückgibt: 2 oder 3? Analyse ergibt, dass der lexikalische Gültigkeitsbereich der lokalen Variablen v der Rumpf von fff ist außer dem Rumpf von ggg, ebenso der Rumpf von hhh. Damit ergibt sich 2 als Wert. Betrachten wir das Prinzip der Umbenennung und das Python-Prinzip der Lokalisierung aller veränderbaren Variablen, dann ist das v in ggg lokal in ggg, also kann man folgendermaßen umbenennen: def fff(): v = 2; def ggg(): w = 3; return hhh (); def hhh(): return v return ggg(); Dann ergibt fff() immer noch Listenverarbeitung in Python Es gibt Datentypen, die Sequenzen von Objekten implementieren: Tupel, Listen und Strings. Tupel und Listen werden analog zu Haskell dargestellt. Z.B. (1, 2, 3)
33 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom ist das 3-Tupel aus den Zahlen 1,2,3, und [1, 2, 3] die Liste dazu. Tupel sind in der Länge festgelegt, während Listen ihre Länge ändern können. Es gibt in Python die Listenfunktionen map, +, filter, und reduce, die vordefiniert sind. Sie haben analoge Ergebnisse und Funktionalitt wie die Funktionen map, ++, filter, und foldl in Haskell. Beachte: Die Listenfunktionen in Prfixschreibweise verndern die Liste nicht, whrend die Listenfunktionen in Attributschreibweise die Liste verndern knnen. Hier ein Auszug aus einer Dokumentation zu Python. Operationen auf allen Arten von Folgen (Listen, Tupel, Strings) 2 Operation Resultat Bem. x in s True wenn ein Eintrag von s = x, sonst False x not in s False wenn ein Eintrag von s gleich x, sonst True s + t Konkatenation von s und t s n n Kopien von s aneinander gehängt s[i] i-es Element von s, Start mit 0 (1) s[i : j] Teilstück s ab i (incl.) bis j (excl.) (1), (2) len(s) Länge von s min(s) Kleinstes Element von s max(s) Größtes Element von s Bemerkungen (1) Wenn i oder j negativ ist, dann ist der Index relativ zum Ende des String, d.h. len(s)+i oder len(s)+j wird eingesetzt. Beachte, dass -0 = 0. (2) Das Teilstück von s von i bis j wird definiert als die Folge von Elementen mit Index k mit i <= k < j. Wenn i oder j größer als len(s) sind, nehme len(s). Wenn i weggelassen wurde, nehme len(s). Wenn i j, dann ist das Teilstück leer. Operation auf Listen (mutable sequences) 3 Operation Resultat Bemerkungen s[i] = x item i von s ersetzt durch x s[i : j] = t Unterliste s von i bis j ersetzt durch t del s[i : j] dasselbe wie s[i : j] = [] s.append(x) dasselbe wie s[len(s) : len(s)] = [x] s.extend(x) dasselbe wie s[len(s) : len(s)] = x (5) s.count(x) Return: Anzahl der i mit s[i] == x s.index(x) Return: kleinstes i mit s[i] == x (1) s.insert(i, x) dasselbe wie s[i : i] = [x] wenn i >= 0 s.remove(x) dasselbe wie del s[s.index(x)] (1) s.pop([i]) dasselbe wie x = s[i]; del s[i]; return x (4) s.reverse() Umdrehen von s in place (3) s.sort([cmpf ct]) Sortiere s in place (2), (3) 2 Aus Quick-Reference 3 Aus Quick-Reference
34 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Kommentare: (1) Ergibt eine ValueError-Exception, wenn x nicht in s, d.h. wenn der Index außerhalb des gültigen Bereichs ist. (2) Die sort()-methode nimmt ein optionales Argument, das eine Vergleichsfunktion für 2 Argumente ist, die -1, 0, or 1 als Wert ergeben muss, abhängig davon, ob das erste Elemente kleiner als, gleich oder größer als das zweite Argument sein soll. Beachte dass dadurch das Sortieren sehr viel langsamer wird. (3) Die sort() und reverse()-methoden ändern die Liste in-place. Es gibt keinen Rückgabewert zur Warnung vor diesem Seiteneffekt. (4) Die pop()-methode wird nur für Listen unterstützt. Das optionale Argument i wird automatisch als -1 definiert, so dass normalerweise das letzte Element entfernt und zurückgegeben wird. (5) Ergibt eine TypeError-Exception, wenn x kein Listenobjekt ist. Weitere Funktionen, die nicht in Attributschreibweise angewendet werden: Operation Resultat map(f,s) Liste [f s[0], f s[1],... ] filter(p,s) Liste der Elemente mit p(s[i]) = True reduce(op,s) s[0] op s[1] op... reduce(op,s,init) Dasselbe wie init op (reduce(op,s)) zip(s,t) Liste der Paare der Elemente von s,t. Der Rückgabewert (return... ) der Funktionen entspricht im allgemeinen dem der Haskellfunktionen. Bei Seiteneffekten haben die Listen-Funktionen von Python ein ganz anderes Verhalten als in Haskell. Haskell ist referentiell transparent, was bewirkt, dass die Listenargumente nach einer Funktionsanwendung unverändert sind, während eine Funktionsanwendung bzw. Operatoranwendung in Python oft eine Veränderung der Listenstruktur, und damit der Werte von Argumentvariablen nach sich zieht. Einige Funktionen sind nur dazu gemacht, genau dies zu bewirken. Z.B. reverse dreht die Python-Liste um. Wir geben zur Listenverarbeitung in Python einige Beispiele an: >>> range(20) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19] >>> range(5,10) [5, 6, 7, 8, 9] >>> len(range(10)) 10 >>> len(range( )) Traceback (most recent call last): File "<input>", line 1, in? MemoryError
35 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom >>>len(xrange( )) >>> a = [ a, b, c ] >>> a [ a, b, c ] >>> b = [3,4,5] >>> a.extend(b) >>> a [ a, b, c, 3, 4, 5] ## a ist modifiziert >>> b [3, 4, 5] >>> a.append(b) >>> a [ a, b, c, 3, 4, 5, [3, 4, 5]] >>> a.reverse() >>> a [[3, 4, 5], 5, 4, 3, c, b, a ] >>> b [3, 4, 5] ## b bleibt >>> b.reverse() >>> a [[5, 4, 3], 5, 4, 3, c, b, a ] ## a ist modifiziert! Variablen, die in einem Aufruf f(t 1,..., t n ) nicht erwähnt werden, können trotzdem nach der Auswertung dieses Aufrufs andere Werte haben. Das passiert durch sogenanntes aliasing: der gleiche Speicherbereich hat verschiedene Namen. Schleifen in Python Schleifen kann man in Python programmieren mittels while oder for: Hier ein Beispiel für for: >>> for i in range(1,11):... print(i) >>>
36 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Beispiel zu vordefinierten Listenfunktionen Beispiele zu den Listenfunktionen map, +, filter, und reduce, die analog zu map, ++, filter, und foldl in Haskell sind. Folgende Funktion listcopy erzeugt eine Kopie einer Liste: def id(x): return x def listcopy(x): return map(id, x) def geradeq(n): return n%2 == 0 >>> filter(geradeq,range(20)) [0, 2, 4, 6, 8, 10, 12, 14, 16, 18] >>> map(quadrat,range(1,10)) [1, 4, 9, 16, 25, 36, 49, 64, 81] >>>[1,2,3]+[11,12,13] >>>[1,2,3,11,12,13] Die Summe aller Elemente einer Liste kann man ebenfalls analog zu den Haskell-Methoden berechnen: def add(x,y): return x+y >>> reduce(add,range(100)) 4950 def mal(x,y): return x*y def fak(n): return reduce(mal,range(1,n+1)) Alias-Namens-Problematik Alias-Namens-Problematik (Aliasing): Der gleiche Speicherbereich wird von mehreren Variablen (-Namen) referenziert. Effekte: Der Wert (bzw. das Datenobjekt) zu einer Variablen x kann sich im Laufe der Programmbearbeitung verändern, ohne dass diese Variable im Programm in einem Befehl, der den Speicher verändert, vorkommt. Allgemeiner kann auch ein Objekt unter dem Namen A erreichbar sein, und Teile des Objekts unter anderen Namen. Das bedeutet, dass der einfache Schluss: B wurde im Aufruf nicht erwähnt, also ist es nach der Auswertung des Aufrufs nicht verändert! falsch sein kann. Ein weiteres Beispiel für die Effekte der Alias-Namens-Problematik:
37 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom >>> a = [3,2,1] >>> b = a >>> a [3, 2, 1] >>> b [3, 2, 1] >>> a.sort() >>> a [1, 2, 3] >>> b [1, 2, 3] Um sich ein Bild von verketteten Listen zu machen, ist folgendes Darstellungsweise von Listen in einem Diagramm hilfreich, das die Situation nach der Zuweisung a = [1,2,3]; b = a repräsentiert. Pfeile ausgehend von Namen bedeuten Bindungen: a.... Andere Pfeile kann man ebenfalls als Bindung ansehen, nur sind die Namen implizit. Eine Box repräsentiert ein Paar von zwei impliziten Namen. In einer Implementierung wird man das als Adressen (Zeiger) darstellen. Der erste Pfeil von der linken Zelle einer Box ausgehend ist die Bindung des Listenelementes. Der zweite Pfeil ist die Bindung an die Restliste (Liste ohne das erste Element). Die zweite Zelle der letzten Box symbolisiert einen Zeiger auf die leere Liste (Nil). a b Nil Es ist zu beachten, dass bei a.extend(b) eine Kopie der Liste b an a angehängt wird. Bei append wird nur der Verweis genommen: >>> a = [1,2,3] >>> b = [4,5,6] >>> a.append(b) >>> a [1, 2, 3, [4, 5, 6]] >>> b.reverse()
38 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom >>> a [1, 2, 3, [6, 5, 4]] >>> Bild des Speichers nach den obigen Befehlen: a Nil b Nil Python nutzt die Flexibilität der Listendarstellung nicht aus, sondern es wird intern optimiert. D.h. Man hat Listenobjekte, die keine Teillisten haben, so dass man eigentlich ein anderes Diagramm verwenden könnte: >>> a = [1,2,3] a Nil >>> b = [4,5,6] >>> a.append(b) >>> a [1, 2, 3, [4, 5, 6]] >>> b.reverse() >>> a
39 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom [1, 2, 3, [6, 5, 4]] >>> a Nil b Nil Stacks und Queues Ein Stack (bzw. Keller, Stapel) ist eine oft verwendete Datenstruktur. In Python kann man einen Stack leicht implementieren, man kann sogar eine Liste von beiden Seiten als Stack verwenden: push e auf Stack a: a.insert(0,e) Benutzung der Listen von links: a.insert(0,b) a.pop(0) ##push(b) Benutzung der Listen von rechts: a.append(b) a.pop() Es tritt ein Fehler auf, wenn man vom leeren Stapel etwas herunternehmen will. Beispiel Ein Beispiel, das sich eines Stacks bedient, ist die Verwendung eines Umgebungsstacks zur Auswertung von (Python-)Ausdrücken. Das Umdrehen einer Liste wurde schon im Haskell-Kapitel besprochen.
40 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Eine Schlange, Queue ist eine Datenstruktur, die sich wie eine Warteschlange verhält: Vorne wird bedient (abgearbeitet), und hinten stellen sich Leute an (first-in first out, fifo). In Python kann man das effizient implementieren mit einer der folgenden Kombination von Operationen. a.insert(0,b), a.pop() oder a.append(b), a.pop(0) Auswertungsregeln für Listenfunktionen in Python: operationale Semantik Dieser Paragraph soll verdeutlichen, dass man die operationale Semantik der Listenverarbeitung in einer imperativen Programmiersprache wie Python formal darstellen kann, wobei man den Speicher nur als abstrakte Schnittstelle benötigt, Natürlich wird dies dann letztlich doch auf einen adressierbaren Speicher abgebildet, aber man kann danach konzeptuell trennen zwischen den minimalen Erfordernissen der Auswertung und den zufälligen Eigenschaften der Implementierung. Z.B. ist die Größe der Adressen oder die Lokalität eher eine Eigenschaft der Implementierung auf einem Rechner mit linearem Speicher. Der Heap (Halde) dient dazu, Daten mit Struktur, die vom Programm modelliert werden, darzustellen, und deren Veränderung korrekt zu beschreiben. Dazu werden Heap-Variablen verwendet, deren Zweck es ist, Zeiger abstrakt zu modellieren und Objekte bereitzustellen, die vom Programm aus referenziert werden können. 4. Um auch die Problematik der nicht mehr erreichbaren Speicherteile korrekt zu behandeln, führen wir zusätzlich noch den Begriff der Wurzelvariablen ein. Die Wurzelvariablen haben nur den Zweck, den garbagecollector zu unterstützen. Definition Eine Halde (Heap) besteht aus folgenden Komponenten: Einer Menge V H von Heap-Variablen, d.h. einer Menge von Namen. Einer Menge von HH-Bindungen an Heapvariablen, wobei zwei Arten von HH-Bindungen vorkommen: x v: eine HH-Bindung eines Wertes v (Zahl, Character oder Nil) an die Heap-Variable x, oder x, x None. x [x 1 x 2 ]: eine HH-Bindung eines Paares (einer Box) aus zwei Heap-Variablen [x 1 x 2 ] an die Heap-Variable x. Folgende Zusatzbedingungen müssen erfüllt sein: Es darf pro Heap-Variable nur eine HH-Bindung im Heap sein. Jede Heap-Variable, die in einer Box vorkommt, muss auch eine HH-Bindung im Heap haben. Meist werden einige Heapvariablen als Wurzel-Variablen markiert. Die Menge der Wurzelvariablen nennen wir V W ; wobei V W V H gelten muss. 4 Wie bei anderen Namen ist die Implementierung sinnvoll als Zeiger.
41 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Die beiden Formen der HH-Bindung kann man folgendermaßen darstellen: x x v x 1 x 2 Jede Heapvariable repräsentiert ein komplexes Objekt, das man als gerichteten Graphen sehen kann, wobei nur binäre Verzweigungen vorkommen und die Daten an den Blättern sind. Eine Programmvariable z wird dann durch die (PH-) Bindung {z x}, an ein Objekt gebunden, wobei x die Heapvariable ist, die das Objekt repräsentiert. Wir wiederholen die Definition der Bindungen und Umgebung zu Programmen (siehe Def ), wobei statt Zahlen und Zeichen auch Objekte aus einer Halde verwendet werden. Definition Gegeben eine Halde H. Eine (Programmvariablen- bzw. PH- ) Bindung (bzgl. der Halde H) ist ein Paar x y, wobei x eine Programm- Variable und y eine Heap-Variable ist. Ein Umgebungsrahmen (Frame) zu einer Halde H ist eine endliche Menge R von PH-Bindungen zur Halde H. Pro Programm-Variablennamen kann nur eine PH-Bindung in R enthalten sein. Eine Umgebung (Variablenumgebung, Zustand) ist ein Tripel (R 1, R 2, H) von zwei Umgebungsrahmen, des lokalen Umgebungsrahmens R 1 bezüglich der Halde H, und des globalen Umgebungsrahmens R 2 bezüglich der Halde H; und der Halde H. Wir nehmen an, dass die Wurzel-Variablen von H mindestens die Heap- Variablen sind, die in den Variablenumgebungen R 1, R 2 als Ziele vorkommen. Oft ist die Umgebung als Stack organisiert, der die Auswertung von Ausdrücken unterstützt. Unsere Modellierung erlaubt keine Werte direkt auf dem Stack. In realen Implementierung werden zur Optimierung oft Werte direkt auf dem Auswertungsstack abgelegt und verarbeitet, da dies effizienter ist. Beispiel Die Darstellung der Liste [100] nach dem Aufruf z1 = [100] mit Umgebung und Halde ist folgendermaßen: lokaler Umgebungsrahmen {z1 z2} globaler Umgebungsrahmen Halde {z2 [z3 z4] z3 100 z4 Nil}
42 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom z1 z2 z3 z4 100 Nil Beispiel Darstellung einer zyklischen Liste, wobei man diese nur so drucken kann: [[[[[...]]]]]] AA AB Nil Die Halde dazu sieht so aus: {AA [AA AB], AB Nil} Definition Die Erreichbarkeitsrelation H, des Heaps H kann man folgendermaßen definieren: Eine Heap-Variable y ist von der Heap-Variablen x aus erreichbar, Notation x H, y, wenn x = y, oder wenn es eine endliche Folge von Variablen x 1,..., x n gibt, so dass x = x 1 und y = x n und für alle i = 1,... n 1 entweder x i [x i+1 x i+1 ] H oder x i [x i+1 x i+1] H wobei x i+1 irgendwelche Heap-Variablen sein dürfen. Eine Heap-Variable x ist erreichbar (aktiv), wenn es eine Wurzelvariable x 0 H, gibt mit x 0 x, andernfalls heißt sie unerreichbar (redundant). Bemerkung Die Erreichbarkeitsrelation H, des Heaps H kann man auch als die reflexiv-transitive Hülle der folgenden Relation definieren: Wenn x [x 1 x 2 ] H, dann gilt x H, x 1 und x H, x 2. Die Bindungen von unerreichbaren Variablen kann man aus dem Heap entfernen. In einer Implementierung nennt man das garbage collection. Wurzelvariablen sind i.a. die Heap-Variablen, auf die vom Stack aus referenziert wird und die Heap-Variablen, auf die das Programm referenziert.
43 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Jede Variable der Halde repräsentiert einen Basiswert oder eine komplexere Datenstruktur. z.b.: In der Halde H = {x [x 1 x 2 ], x 1 1, x 2 Nil)} repräsentiert die Halden-Variable x die Liste [1] und x 2 die leere Liste. x x 1 x 2 Nil 1 Regeln der (erweiterten) operationalen Semantik Der Aufwand dafür ist etwas höher als bei der ersten Variante der operationalen Semantik von Python, die nur mit Zahlen umgehen konnte, da auch zyklische Strukturen beschreibbar sein sollen. Der Zustand besteht aus Bindungsumgebung und Heap. Die übliche Umgebung wird so verallgemeinert, dass jeder Programmvariablen eine Heapvariable zugeordnet wird, die ihrerseits auf einen (evtl. komplexeren) Wert im Heap verweist. Jetzt können wir die Auswertung von Listenausdrücken und Listenfunktionen in Python mittels dieser Halden-Modellierung beschreiben: Wir verwenden die Klammer [.], um syntaktische Konstrukte einzuklammern, damit diese von den Operationen deutlich getrennt werden, und verwenden die Notation (Z, s) e (Z, x) um eine Auswertung des Ausdrucks s im Zustand Z zu bezeichnen, wobei x die Heapvariable ist, die den zurückgegebenen Wert repräsentiert und Z der neue Zustand ist. Definition Eine Auswertung des Listenausdrucks [a 1,..., a n ] in einer Halde H folgt der Regel (n 1): (Z; [[a 1 ]) e (Z 1 ; x 1 ) (Z 1 ; [[[a 2,..., a n ]]) e (Z 2 ; x 2 ) Z 2 = (R 2,1, R 2,2, H 2 ) (Z; [[[a 1,..., a n ]]) e ( (R2,1, R 2,2, H 2 {x [x 1 x 2 ]}); x ) Am Ende der Listen verwenden wir die spezielle Konstante Nil: ((R 1, R 2, H); [[]]) e ((R 1, R 2, H {x Nil}); x) Die Auswertung des Listenausdrucks [a 1,..., a n ] kann man so umschreiben: Zuerst wird a 1 ausgewertet, danach a 2 usw., bis a n. Der Zustand am Ende ist der letzte Zustand nach dieser Auswertung. In der Halde repräsentiert die Haldenvariable x die ausgewertete Liste.
44 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Die Alias-Namens-Problematik tritt jetzt auch bei Zuweisung von Listenvariablen auf. Sei die Folge der Befehle gegeben: a = [1,2] b = a Dann entsteht folgende Struktur in der Umgebung und in der Halde: Nach a = [1,2]: Bindungen:..., a u 1,... Heap: {u 1 [u 2 u 3 ], u 2 1, u 3 [u 4 u 5 ], u 4 2, u 5 Nil,...} Nach der weiteren Zuweisung b = a entsteht der Zustand Bindungen:..., a u 1,..., b u 1,... Heap: {u 1 [u 2 u 3 ], u 2 1, u 3 [u 4 u 5 ], u 4 2, u 5 Nil,...} Wenn jetzt innerhalb der Liste zu a etwas verändert wird, dann ändert sich automatisch etwas in der Liste, auf die b zeigt. a u 1 b u 2 u 3 u 4 u 5 Nil 1 2 Jetzt können wir auch die Auswertung von Funktionen wie len, append, insert,... angeben. Für die folgende Regel nehmen wir der Einfachheit halber an, dass a, b Programm-Variablen sind. ((R 1, R 2, H); [a.append(b)]) e ((R 1, R 2, H ); None) Wobei H = H 0 {x Nil} der Heap vor der Auswertung ist. x sei letzte Heap-Variable der Liste zu a die auf Nil zeigt, b x 1 ist Bindung in der Umgebung R 1, und H = H 0 {x [x 1 x 2 ], x 2 Nil} mit der neu erzeugten Heap- Variablen x 2. D.h. die x-bindung {x Nil} im Heap wird ersetzt durch {x [x 1 x 2 ]}, wobei x 2 neu eingeführt wird. Die Auswertung von a.append(b) kann man sich so veranschaulichen:
45 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Vorher: a u 1 x Nil b x 1 w Nachher: a u 1 x x 1 x 2 Nil b x 1 w Dadurch wird (die Liste) b als letztes Element an die Liste angehängt. Durch append-anwendungen kann auch eine Liste entstehen, die unendlich tiefe Verschachtelung hat, indem man z.b. a.append(a) ausführt. Die zugehörige Halde für die Liste a = [1, 2] sieht so aus: {u 1 [u 2 u 3 ], u 2 1, u 3 [u 4 u 5 ], u 4 2, u 5 [u 1 u 7 ], u 7 Nil,...} Diese Halde ist ein Graph, der Zyklen hat. Man sieht auch, dass im Diagramm u 1 zweimal vorkommt, aber die zwei Pfeile der gleichen Bindung entsprechen. a u 1 u 2 u 3 u 4 u 5 u 1 u 7 Nil 1 2 Als weiteres Beispiel die operationelle Semantik der Funktion insert. Für diese Regel nehmen wir ebenfalls an, dass a, b Programm-Variablen sind. ((R 1, R 2, H); [a.insert(i, b)]) e ((R 1, R 2, H ); None) wobei x i die Heap-Variable zum i-ten Listen-Tail ist. H = H 0 {x i [e i+1 x i+1 ]}, b y 1 R 1, und H = H 0 {x i [y 1 y 2 ], y 2 [e i+1 x i+1 ]}, wobei y 2 neue Heap-Variable ist.
46 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom vorher: e i x i e i+1 x i+1... nach insert: e i x i e i+1 x i+1... y 1 y 2 Der Fall, dass die Liste zu Ende ist, geht analog: H = H 0 {x i Nil}, b z 1 S, und H = H 0 {x i [z 1 z 2 ], z 2 Nil}. Die operationelle Semantik von map kann damit ebenfalls beschrieben werden, allerdings ist diese Funktion aus kleineren Operationen zusammengesetzt, so dass es einfacher wäre, für die Implementierung der Funktion map die operationale Semantik der kleineren Operationen zu beschreiben. Zum Beispiel, indem man ersatzweise die folgende Funktion betrachtet. def map_demo(f,xs): if len(xs) == 0: return []; else: wert = map_demo(f, xs[1:len(xs)]); wert.insert(0,f(xs[0])); ## Seiteneffekt return wert; Den Inhalt des Elements mit Index i der Liste a kann man mittels a[i] = b verändern. Wir geben hierfür die operationelle Semantik an, wobei wir annehmen, dass b eine Programmvariable ist, und bei der Auswertung von Anweisungen rechts nur den veränderten Zustand angeben. ((R 1, R 2, H); [a[i] = b]) (R 1, R 2, H ) wobei H = H 0 {x i [y 1 y 2 ]}, x i ist die Heap-Variable zum i-ten Listen-Tail, b z R 1, und H = H 0 {x i [z y 2 ]}.
47 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Indirektionen Diese könnte man auch in der Halde erlauben. Es sind Bindungen von der Art x 1 x 2, wobei x 1, x 2 beides Heap-Variablen sind. Deren Bedeutung ist, dass der Wert von x 1 erst über die Referenz x 2 und evtl. weitere Indirektionen gefunden werden kann, wobei die Indirektionen für die Programmiersprache nicht sichtbar sind. Das formale Modell würde dadurch etwas komplizierter, da man den Wert nicht direkt finden kann. Man muss auch Indirektionszyklen beachten, die eine Nichtterminierung des Wertesuchens bewirken könnten. In Implementierungen werden Indirektionen z.t. verwendet, aus verschiedenen Gründen: manche Operationen lassen sich leichter implementieren bzw. formulieren, und manchmal ist es effizienter, Indirektionen zu verwenden Implementierung der Halde in einem Speichermodell Zunächst das Speichermodell in dem die Halde implementiert werden soll. Definition Einen RAM-Speicher S kann man definieren als endliche Folge von Bytes (1 Byte = 8 Bit), (alternativ: von Zahlen zwischen 0 und = 255), nummeriert mit Indices 0,..., L 1. L ist die Größe des Speichers. Der gespeicherte Wert unter der Adresse i ist das Byte S(i), d.h. das i te Element der Folge, wenn die Zählung mit 0 beginnt. Die benötigte Adresslänge in Bits ist log 2 (L). Die Zugriffsfunktion get(s, i, l) hat als Ergebnis die Subfolge von S der Länge l ab i Eine Implementierung von Adressen eines Speichers mit Adresslänge 32 Bit kann man durchführen, indem man eine Binärzahl, die durch eine Folge von 4 Bytes repräsentiert wird, als Adresse im gleichen Speicher interpretiert. Heapvariablen kann man dann implementieren als Folge von 4 Bytes (auch Wort genannt), die im Speicher direkt hintereinanderliegen, d.h. S(i), S(i + 1), S(i + 2), S(i + 3). Diese werden als Adressen interpretiert. Ein Paar [x 1 x 2 ] von zwei Heapvariablen kann man als hintereinanderliegende Folge von 8 Bytes implementieren, d.h. S(i),..., S(i + 7). Eine Zahl kann man implementieren wie eine Adresse, nur wird der Wert als die binäre Zahl selbst interpretiert.
48 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Beispiel Hat man z.b. (mit Programmvariable b, Heapvariable x) eine Bindung b x und x 4, so kann man x als 4-Byte Adresse implementieren. Wenn an der Stelle mit der Adresse x die Adresse i steht, dann ist der Wert der Heapvariablen x ist dann der Wert unter dieser Adresse, d.h. S(i). Hat x die Adresse 100, dann erhält man durch a = get(h, 100, 4) die Adresse i, die zu x assoziiert ist, get(h, i, 1) ergibt dann den Wert, der bei korrekter Implementierung dann 4 ist. 100 b x In dieser Implementierung geht die Information verloren, welcher Typ von Daten gemeint ist. Das sieht man daran, dass man damit Indirektionen, Paare, Nil, und Zahlen nicht unterscheiden kann. Je nach Implementierung benötigt man daher i.a. 5 noch eine Markierung (englisch: Tag), die diese verschiedenen Daten im Speicher voneinander unterscheidet. D.h. man könnte vereinbaren: Adresse: 1 Byte Markierung (z.b. binär 1), und 4 Byte Adresse. Paar: 1 Byte Markierung (z.b. binär 2), und 8 Byte Adressen. Ganze Zahl: 1 Byte Markierung (z.b. binär 3), und 4 Byte Zahl. Nil: 1 Byte Markierung (z.b. binär 4). kein Wert: 1 Byte Markierung (z.b. binär 5). Durch diese Haldenimplementierung haben wir eine abstrakte Schnittstelle angedeutet, die auch anders implementiert sein kann, ohne dass sich die Funktionalität der Halde bzw. der Umgebung ändert. Z.B. braucht folgendes nicht zu gelten: die Adressen eines Adresspaares (einer Box) [x 1 x 2 ] liegen direkt nebeneinander. Adressen sind als aufsteigende Folge von Bytes repräsentiert. Der nächste Eintrag im Array (Feld) hat Adresse des aktuellen Feldes +4. Auch die Länge der Adressen ist nicht festgelegt. soll. 5 Diese Markierung wird nicht benötigt, wenn ein Programm vorher weiß, was dort stehen
49 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Felder, Arrays in Python In Python sind die Listen (und Tupel) gleichzeitig eindimensionale Felder, die auch heterogen (d.h. mit Elementen unterschiedlichen Typs) sein dürfen. Mehrdimensionale Arrays und Matrizen kann man mit einem Array von Arrays, d.h. mit Listen von Listen modellieren. Die interne Implementierung eines Feldes macht es möglich, eine (praktisch) konstante Zugriffszeit zu realisieren, wenn der Index bekannt ist. Allerdings ist die Handhabung eines Feldes im Programm etwas aufwändiger, da man bei Zugriffen stets den Index berechnen muss und da man im allgemeinen ein Feld nicht so ohne weiteres verkleinern oder erweitern kann. Folgend einige Beispiele: Beispiel Transposition einer 2-dimensionalen quadratischen Matrix in Python def transpose(a,n): for i in range(n): for j in range(i+1,n): a[i][j], a[j][i] = a[j][i], a[i][j] return a def testtranspose(n): b = range(n) for i in range(n): b[i] = range(n) for i in range(n): print b[i]; c = transpose(b,n) print " "; print "Nach Transposition:" for i in range(n): print c[i] Beispiel Matrixmultiplikation für quadratische Matrizen und Determinante einer Matrix def matrixmult(a,b): leng = len(a); c = range(leng); for i in range(leng): c[i] = range(leng); for j in range(leng): c[i] [j] = 0; for i in range(leng): for j in range(leng): sum = 0
50 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom for k in range(leng): sum = sum + a[i][k]*b[k][j] c[i][j] = sum return c def testmatmult(leng): a = range(leng); b = range(leng); print a; print b; for i in range(leng): a[i] = range(leng); b[i] = range(leng); for j in range(leng): a[i] [j] = i; b[i] [j] = j; print a; print b; return (matrixmult(a,b)) ###Determinante einer Matrix: rekursiv, exponentiell \begin{verbatim} def determinante(a): n = len(a); if n <= 0: return 1; else: if n == 1: return a[0][0] else: sum = 0; flip = -1; for i in range(n): flip = (-1)*flip; b = matrixcopy(a); for j in range(n): b[j].pop(0); b.pop(i); sum = sum + flip*a[i] [0] * determinante(b); return(sum); Beachte, dass es unter Benutzung der Gauß-Elimination einen ALgorithmus mit Laufzeit O(n 3 ) gibt.
51 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom Operationale Semantik: C C ist eine wichtige und verbreitete Programmiersprache für maschinennahes Programmieren, insbesondere Betriebssysteme. C-Compiler ergeben effizienten Code. Der Abstraktionsgrad von C bzw. der C-Programme ist zwar höher als der von Assembler-Sprachen, aber nicht so hoch wie der von Python oder Haskell. Wir untersuchen die Eigenschaften der operationalen Semantik von C anhand eines Konstruktes. Aus Kernighan/Ritchie: Programmieren in C: Diese Regeln sind außerordentlich kompliziert, denn sie müssen mit einer Mischung von Funktionen alten und neuen Stils fertigwerden. Wenn möglich, sollten Mischungen vermieden werden. Die Reihenfolge, in der Argumente bewertet werden, ist nicht festgelegt; man beachte, dass sich verschiedene Übersetzer hierin unter- scheiden. Die Argumente und Funktionsbezeichner werden jedoch vollständig bewertet [d.h. ausgewertet], mit allen Nebenwirkungen, bevor die Ausführung der Funktion beginnt... Ein anderes Zitat zum Versuch einer Andeutung der (funktionalen) operationellen Semantik von C:... In anderen Worten, wenn das n-te Kode-Fragment durch die Funktion f n repräsentiert wird, und s 0 ist der Anfangszustand, dann ist der Endzustand definiert durch s n = f n (f n 1 (... f 1 (f 0 (s 0 ))...)) Die Ausführung der einzelnen Funktionen erlaubt... Parallelismus. Wir wollen hier mal explizit ein Code-Fragment untersuchen, dass wir im Prinzip ala Python analysieren können. Dazu schnell die Erklärung eines C- Operators: i++ bewirkt, wenn ausgewertet, den Seiteneffekt i := i+1 wobei i Programmvariable sein muss. Die Nebenbedingung ist: Wenn es in einem Ausdruck vorkommt, dann ist der Return-Wert i, und der Wert danach ist i+1. Um die operationale Semantik hinzuschreiben, nehmen wir mal an, dass das auch in Python geht. Die operationale Semantik ist dann: v = wert(i, Z) w = v + 1 Z = update(i, w, Z) (Z; [[i++]) e (Z ; v) Zum Vergleich hier die operationale Semantik des Ausdrucks ++i, der sich von i++ nur dadurch unterscheidet, dass der Returnwert bereits i+1 ist: v = wert(i, Z) w = v + 1 Z = update(i, w, Z) (Z; [[++i]) e (Z ; w) Als Beispiel für i++ betrachte das C-Code-Fragment
52 Praktische Informatik 1, WS 2004/05, Kapitel 3, vom i = 7; j = i++ * i++ Informelle Begründung für den erwarteten Zustand danach: Die Multiplikation wertet i++ zweimal aus: Der Wert des linken Argument ist 7, des rechten Argument 8, da es um 1 erhöht wurde, danach hat i den Wert 9. Der Wert von j ist 7 8 = 56. Zunächst mal eine Überraschung beim Ausprobieren (aus Dissertation Ronald Moore). Der C-Code i = 7; j = i++ * i++; kompiliert in gcc hinterlässt den Zustand j = 49, i = 8 statt j = 56, i = 9! Erklärungsversuch: der Compiler versucht, die Doppelauswertung von i++ zu vermeiden und ändert daher das Programm ab zu: i = 7; j = let x = i++ in x*x; bzw. in let-freier Schreibweise: i = 7; x = i++; j = x*x; Die operationale Semantik ergibt jetzt: Nach Auswertung von x: {x 7, i 8,...}. Danach wertet man x*x aus und erhält 49, wie vom gcc berechnet. Fazit: Die Verwirrung, die beim Programmierer entsteht, wird bewirkt durch eine (optimierende) Programmtransformation, die die operationale Semantik nur erhält, wenn die Unterausdrücke keine Seiteneffekte bewirken; im Fall, dass die Unterausdrücke Seiteneffekte bewirken, wird die operationale Semantik nicht erhalten.
Programmierung in Python
 Programmierung in Python imperativ, objekt-orientiert dynamische Typisierung rapid prototyping Script-Sprache Funktionales und rekursives Programmieren P raktische Informatik 1, W S 2004/05, F olien P
Programmierung in Python imperativ, objekt-orientiert dynamische Typisierung rapid prototyping Script-Sprache Funktionales und rekursives Programmieren P raktische Informatik 1, W S 2004/05, F olien P
Listenverarbeitung in Python
 Listenverarbeitung in Python Datentypen für Sequenzen von Objekten: Tupel, Listen und Strings Tupel und Listen sind analog zu Haskells Tupel und Listen: (1, 2, 3) 3-Tupel aus den Zahlen 1,2,3, [1, 2, 3]
Listenverarbeitung in Python Datentypen für Sequenzen von Objekten: Tupel, Listen und Strings Tupel und Listen sind analog zu Haskells Tupel und Listen: (1, 2, 3) 3-Tupel aus den Zahlen 1,2,3, [1, 2, 3]
JavaScript. Dies ist normales HTML. Hallo Welt! Dies ist JavaScript. Wieder normales HTML.
 JavaScript JavaScript wird direkt in HTML-Dokumente eingebunden. Gib folgende Zeilen mit einem Texteditor (Notepad) ein: (Falls der Editor nicht gefunden wird, öffne im Browser eine Datei mit der Endung
JavaScript JavaScript wird direkt in HTML-Dokumente eingebunden. Gib folgende Zeilen mit einem Texteditor (Notepad) ein: (Falls der Editor nicht gefunden wird, öffne im Browser eine Datei mit der Endung
C.3 Funktionen und Prozeduren
 C3 - Funktionen und Prozeduren Funktionsdeklarationen in Pascal auch in Pascal kann man selbstdefinierte Funktionen einführen: Funktionen und Prozeduren THEN sign:= 0 Funktion zur Bestimmung des Vorzeichens
C3 - Funktionen und Prozeduren Funktionsdeklarationen in Pascal auch in Pascal kann man selbstdefinierte Funktionen einführen: Funktionen und Prozeduren THEN sign:= 0 Funktion zur Bestimmung des Vorzeichens
Java 8. Elmar Fuchs Grundlagen Programmierung. 1. Ausgabe, Oktober 2014 JAV8
 Java 8 Elmar Fuchs Grundlagen Programmierung 1. Ausgabe, Oktober 2014 JAV8 5 Java 8 - Grundlagen Programmierung 5 Kontrollstrukturen In diesem Kapitel erfahren Sie wie Sie die Ausführung von von Bedingungen
Java 8 Elmar Fuchs Grundlagen Programmierung 1. Ausgabe, Oktober 2014 JAV8 5 Java 8 - Grundlagen Programmierung 5 Kontrollstrukturen In diesem Kapitel erfahren Sie wie Sie die Ausführung von von Bedingungen
zu große Programme (Bildschirmseite!) zerlegen in (weitgehend) unabhängige Einheiten: Unterprogramme
 Bisher Datentypen: einfach Zahlen, Wahrheitswerte, Zeichenketten zusammengesetzt Arrays (Felder) zur Verwaltung mehrerer zusammengehörender Daten desselben Datentypes eindimensional, mehrdimensional, Array-Grenzen
Bisher Datentypen: einfach Zahlen, Wahrheitswerte, Zeichenketten zusammengesetzt Arrays (Felder) zur Verwaltung mehrerer zusammengehörender Daten desselben Datentypes eindimensional, mehrdimensional, Array-Grenzen
1 Bedingungen und der Typ bool. Informatik I: Einführung in die Programmierung 5. Bedingungen, bedingte Ausführung und Schleifen. Vergleichsoperatoren
 1 und der Informatik I: Einführung in die Programmierung 5., bedingte Ausführung und Albert-Ludwigs-Universität Freiburg Bernhard Nebel 27. Oktober 2015 27. Oktober 2015 B. Nebel Info I 3 / 21 Der Vergleichsoperatoren
1 und der Informatik I: Einführung in die Programmierung 5., bedingte Ausführung und Albert-Ludwigs-Universität Freiburg Bernhard Nebel 27. Oktober 2015 27. Oktober 2015 B. Nebel Info I 3 / 21 Der Vergleichsoperatoren
Informatik I. 4. Funktionen: Aufrufe und Definitionen. 25. Oktober Albert-Ludwigs-Universität Freiburg. Informatik I.
 4. Funktionen: Aufrufe und en Aufrufe Albert-Ludwigs-Universität Freiburg 25. Oktober 2013 1 / 23 Aufrufe Funktionsaufrufe 2 / 23 Funktionsaufrufe Innerhalb von Programmiersprachen ist eine Funktion ein
4. Funktionen: Aufrufe und en Aufrufe Albert-Ludwigs-Universität Freiburg 25. Oktober 2013 1 / 23 Aufrufe Funktionsaufrufe 2 / 23 Funktionsaufrufe Innerhalb von Programmiersprachen ist eine Funktion ein
zu große Programme (Bildschirmseite!) zerlegen in (weitgehend) unabhängige Einheiten: Unterprogramme
 Bisher Datentypen: einfach Zahlen, Wahrheitswerte, Zeichenketten zusammengesetzt Arrays (Felder) zur Verwaltung mehrerer zusammengehörender Daten desselben Datentypes eindimensional, mehrdimensional, Array-Grenzen
Bisher Datentypen: einfach Zahlen, Wahrheitswerte, Zeichenketten zusammengesetzt Arrays (Felder) zur Verwaltung mehrerer zusammengehörender Daten desselben Datentypes eindimensional, mehrdimensional, Array-Grenzen
S. d. I.: Programieren in C Folie 4-1. im Gegensatz zu Pascal gibt es in C kein Schlüsselwort "then"
 S. d. I.: Programieren in C Folie 4-1 4 Anweisungen 4.1 if-anweisung 1) if (Ausdruck) 2) if (Ausdruck) } else im Gegensatz zu Pascal gibt es in C kein Schlüsselwort "then" es wird nur der numerische Wert
S. d. I.: Programieren in C Folie 4-1 4 Anweisungen 4.1 if-anweisung 1) if (Ausdruck) 2) if (Ausdruck) } else im Gegensatz zu Pascal gibt es in C kein Schlüsselwort "then" es wird nur der numerische Wert
Programmiersprache 1 (C++) Prof. Dr. Stefan Enderle NTA Isny
 Programmiersprache 1 (C++) Prof. Dr. Stefan Enderle NTA Isny 5. Kontrollstrukturen Allgemein Kontrollstrukturen dienen zur Steuerung des Programmablaufs. (Bemerkung: C und C++ besitzen die selben Kontrollstrukturen.)
Programmiersprache 1 (C++) Prof. Dr. Stefan Enderle NTA Isny 5. Kontrollstrukturen Allgemein Kontrollstrukturen dienen zur Steuerung des Programmablaufs. (Bemerkung: C und C++ besitzen die selben Kontrollstrukturen.)
3AA. Prof. Dr. Wolfgang P. Kowalk. Universität Oldenburg WS 2005/2006
 3AA Prof. Dr. Wolfgang P. Kowalk Universität Oldenburg WS 2005/2006 Version vom 24.10.2005 Übersicht Einführung in maschinennahe Programmierung Verständnis für grundlegende Vorgänge im Computer Jedes Programm
3AA Prof. Dr. Wolfgang P. Kowalk Universität Oldenburg WS 2005/2006 Version vom 24.10.2005 Übersicht Einführung in maschinennahe Programmierung Verständnis für grundlegende Vorgänge im Computer Jedes Programm
Funktionale Programmiersprachen
 Funktionale Programmiersprachen An den Beispielen Haskell und Erlang Übersicht Programmiersprachen λ-kalkül Syntax, Definitionen Besonderheiten von funktionalen Programmiersprache, bzw. Haskell Objektorientierte
Funktionale Programmiersprachen An den Beispielen Haskell und Erlang Übersicht Programmiersprachen λ-kalkül Syntax, Definitionen Besonderheiten von funktionalen Programmiersprache, bzw. Haskell Objektorientierte
JAVA-Datentypen und deren Wertebereich
 Folge 8 Variablen & Operatoren JAVA 8.1 Variablen JAVA nutzt zum Ablegen (Zwischenspeichern) von Daten Variablen. (Dies funktioniert wie beim Taschenrechner. Dort können Sie mit der Taste eine Zahl zwischenspeichern).
Folge 8 Variablen & Operatoren JAVA 8.1 Variablen JAVA nutzt zum Ablegen (Zwischenspeichern) von Daten Variablen. (Dies funktioniert wie beim Taschenrechner. Dort können Sie mit der Taste eine Zahl zwischenspeichern).
3. Anweisungen und Kontrollstrukturen
 3. Kontrollstrukturen Anweisungen und Blöcke 3. Anweisungen und Kontrollstrukturen Mit Kontrollstrukturen können wir den Ablauf eines Programmes beeinflussen, z.b. ob oder in welcher Reihenfolge Anweisungen
3. Kontrollstrukturen Anweisungen und Blöcke 3. Anweisungen und Kontrollstrukturen Mit Kontrollstrukturen können wir den Ablauf eines Programmes beeinflussen, z.b. ob oder in welcher Reihenfolge Anweisungen
Modul Entscheidungsunterstützung in der Logistik. Einführung in die Programmierung mit C++ Übung 2
 Fakultät Verkehrswissenschaften Friedrich List, Professur für Verkehrsbetriebslehre und Logistik Modul Entscheidungsunterstützung in der Logistik Einführung in die Programmierung mit C++ Übung 2 SS 2016
Fakultät Verkehrswissenschaften Friedrich List, Professur für Verkehrsbetriebslehre und Logistik Modul Entscheidungsunterstützung in der Logistik Einführung in die Programmierung mit C++ Übung 2 SS 2016
Entwurf von Algorithmen - Kontrollstrukturen
 Entwurf von Algorithmen - Kontrollstrukturen Eine wichtige Phase in der Entwicklung von Computerprogrammen ist der Entwurf von Algorithmen. Dieser Arbeitsschritt vor dem Schreiben des Programmes in einer
Entwurf von Algorithmen - Kontrollstrukturen Eine wichtige Phase in der Entwicklung von Computerprogrammen ist der Entwurf von Algorithmen. Dieser Arbeitsschritt vor dem Schreiben des Programmes in einer
Informatik. Studiengang Chemische Technologie. Michael Roth WS 2012/2013. [email protected]. Hochschule Darmstadt -Fachbereich Informatik-
 Informatik Studiengang Chemische Technologie Michael Roth [email protected] Hochschule Darmstadt -Fachbereich Informatik- WS 2012/2013 Inhalt Teil VII Einstieg in Java I Michael Roth (h_da) Informatik
Informatik Studiengang Chemische Technologie Michael Roth [email protected] Hochschule Darmstadt -Fachbereich Informatik- WS 2012/2013 Inhalt Teil VII Einstieg in Java I Michael Roth (h_da) Informatik
Kapitel 5. Programmierkurs. Kontrollstrukturen. Arten von Kontrollstrukturen. Kontrollstrukturen Die if-anweisung Die switch-anweisung
 Kapitel 5 Programmierkurs Birgit Engels, Anna Schulze ZAIK Universität zu Köln Kontrollstrukturen Die if-anweisung Die switch-anweisung Die for-schleife Die while-schleife Die do-schleife WS 7/8 /55 Kontrollstrukturen
Kapitel 5 Programmierkurs Birgit Engels, Anna Schulze ZAIK Universität zu Köln Kontrollstrukturen Die if-anweisung Die switch-anweisung Die for-schleife Die while-schleife Die do-schleife WS 7/8 /55 Kontrollstrukturen
Präzedenz von Operatoren
 Präzedenz von Operatoren SWE-30 Die Präzedenz von Operatoren bestimmt die Struktur von Ausdrücken. Ein Operator höherer Präzedenz bindet die Operanden stärker als ein Operator geringerer Präzedenz. Mit
Präzedenz von Operatoren SWE-30 Die Präzedenz von Operatoren bestimmt die Struktur von Ausdrücken. Ein Operator höherer Präzedenz bindet die Operanden stärker als ein Operator geringerer Präzedenz. Mit
Übungen zur Vorlesung Wissenschaftliches Rechnen I. Grundelemente von Java. Eine Anweisung. wird mit dem Wertzuweisungsoperator = geschrieben.
 Eine Anweisung wird mit dem Wertzuweisungsoperator = geschrieben. Eine Anweisung wird mit dem Wertzuweisungsoperator = geschrieben. Daher ist y = x + 5.6; keine Gleichung, sondern die Anweisung den Wert
Eine Anweisung wird mit dem Wertzuweisungsoperator = geschrieben. Eine Anweisung wird mit dem Wertzuweisungsoperator = geschrieben. Daher ist y = x + 5.6; keine Gleichung, sondern die Anweisung den Wert
Grundlagen der Programmierung
 Grundlagen der Programmierung 7. Vorlesung 18.05.2016 1 Konstanten Ganzzahlkonstante Dezimal: 42, 23, -2 Oktal (0 vorangestellt): 052 Hexadezimal (0x vorangestellt): 0x2A Gleitkommazahlen: 3.1415, 2.71,
Grundlagen der Programmierung 7. Vorlesung 18.05.2016 1 Konstanten Ganzzahlkonstante Dezimal: 42, 23, -2 Oktal (0 vorangestellt): 052 Hexadezimal (0x vorangestellt): 0x2A Gleitkommazahlen: 3.1415, 2.71,
Theoretische Informatik SS 03 Übung 3
 Theoretische Informatik SS 03 Übung 3 Aufgabe 1 a) Sind die folgenden Funktionen f : partiell oder total: f(x, y) = x + y f(x, y) = x y f(x, y) = x y f(x, y) = x DIV y? Hierbei ist x DIV y = x y der ganzzahlige
Theoretische Informatik SS 03 Übung 3 Aufgabe 1 a) Sind die folgenden Funktionen f : partiell oder total: f(x, y) = x + y f(x, y) = x y f(x, y) = x y f(x, y) = x DIV y? Hierbei ist x DIV y = x y der ganzzahlige
RO-Tutorien 3 / 6 / 12
 RO-Tutorien 3 / 6 / 12 Tutorien zur Vorlesung Rechnerorganisation Christian A. Mandery WOCHE 2 AM 06./07.05.2013 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
RO-Tutorien 3 / 6 / 12 Tutorien zur Vorlesung Rechnerorganisation Christian A. Mandery WOCHE 2 AM 06./07.05.2013 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
4 Kontrollfluss-Diagramme
 4 Kontrollfluss-Diagramme In welcher Weise die Operationen eines Programms nacheinander ausgeführt werden, läßt sich anschaulich mithilfe von Kontrollfluss-Diagrammen darstellen. Ingredienzien: Start Stop
4 Kontrollfluss-Diagramme In welcher Weise die Operationen eines Programms nacheinander ausgeführt werden, läßt sich anschaulich mithilfe von Kontrollfluss-Diagrammen darstellen. Ingredienzien: Start Stop
Einfache Rechenstrukturen und Kontrollfluss II
 Einfache Rechenstrukturen und Kontrollfluss II Martin Wirsing in Zusammenarbeit mit Moritz Hammer und Axel Rauschmayer http://www.pst.informatik.uni-muenchen.de/lehre/ss06/infoii/ SS 06 Ziele Lernen imperative
Einfache Rechenstrukturen und Kontrollfluss II Martin Wirsing in Zusammenarbeit mit Moritz Hammer und Axel Rauschmayer http://www.pst.informatik.uni-muenchen.de/lehre/ss06/infoii/ SS 06 Ziele Lernen imperative
Kapitel 5: Abstrakte Algorithmen und Sprachkonzepte. Elementare Schritte
 Elementare Schritte Ein elementarer Berechnungsschritt eines Algorithmus ändert im Allgemeinen den Wert von Variablen Zuweisungsoperation von fundamentaler Bedeutung Zuweisungsoperator In Pascal := In
Elementare Schritte Ein elementarer Berechnungsschritt eines Algorithmus ändert im Allgemeinen den Wert von Variablen Zuweisungsoperation von fundamentaler Bedeutung Zuweisungsoperator In Pascal := In
Grundlagen der Informatik I (Studiengang Medieninformatik)
 Grundlagen der Informatik I (Studiengang Medieninformatik) Thema: 3. Datentypen, Datenstrukturen und imperative Programme Prof. Dr. S. Kühn Fachbereich Informatik/Mathematik Email: [email protected]
Grundlagen der Informatik I (Studiengang Medieninformatik) Thema: 3. Datentypen, Datenstrukturen und imperative Programme Prof. Dr. S. Kühn Fachbereich Informatik/Mathematik Email: [email protected]
Schleifen in C/C++/Java
 Schleifen in C/C++/Java Alle 3 Sprachen stellen mindestens die folgenden 3 Schleifenkonstruktionen zur Verfügung. In C gibt es auch keine weiteren, C++, Java und C# haben noch weitere nützliche Varianten.
Schleifen in C/C++/Java Alle 3 Sprachen stellen mindestens die folgenden 3 Schleifenkonstruktionen zur Verfügung. In C gibt es auch keine weiteren, C++, Java und C# haben noch weitere nützliche Varianten.
5. Elementare Befehle und Struktogramme
 5. Elementare Befehle und Struktogramme Programmablauf Beschreibung des Programmablaufs mittel grafischer Symbole Beispiel : Flussdiagramme ja nein Besser : Struktogramme Dr. Norbert Spangler / Grundlagen
5. Elementare Befehle und Struktogramme Programmablauf Beschreibung des Programmablaufs mittel grafischer Symbole Beispiel : Flussdiagramme ja nein Besser : Struktogramme Dr. Norbert Spangler / Grundlagen
Einführung Datentypen Verzweigung Schleifen. Java Crashkurs. Kim-Manuel Klein May 4, 2015
 Java Crashkurs Kim-Manuel Klein ([email protected]) May 4, 2015 Quellen und Editoren Internet Tutorial: z.b. http://www.java-tutorial.org Editoren Normaler Texteditor (Gedit, Scite oder ähnliche)
Java Crashkurs Kim-Manuel Klein ([email protected]) May 4, 2015 Quellen und Editoren Internet Tutorial: z.b. http://www.java-tutorial.org Editoren Normaler Texteditor (Gedit, Scite oder ähnliche)
Objektorientierte Programmierung
 Objektorientierte Programmierung Eine Einführung mit anschaulichen Beispielen aus der Java-Welt apl. Prof. Dr. Achim Ebert Inhalt Kapitel 3: Kontrollstrukturen Einfache Anweisungen Anweisungsblöcke Steuerung
Objektorientierte Programmierung Eine Einführung mit anschaulichen Beispielen aus der Java-Welt apl. Prof. Dr. Achim Ebert Inhalt Kapitel 3: Kontrollstrukturen Einfache Anweisungen Anweisungsblöcke Steuerung
VBA-Programmierung: Zusammenfassung
 VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
Die Programmiersprache C
 Die Programmiersprache C höhere Programmiersprache (mit einigen Assembler-ähnlichen Konstrukten) gut verständliche Kommandos muss von Compiler in maschinenlesbaren Code (Binärdatei) übersetzt werden universell,
Die Programmiersprache C höhere Programmiersprache (mit einigen Assembler-ähnlichen Konstrukten) gut verständliche Kommandos muss von Compiler in maschinenlesbaren Code (Binärdatei) übersetzt werden universell,
4.2 Selbstdefinierte Matlab-Funktionen 1. Teil
 4.2 Selbstdefinierte Matlab-Funktionen 1. Teil 37 Ein m-file mit Namen Funktionsname.m und einer ersten Zeile der folgen Form: function Funktionsname(input1,input2,...,inputn) oder function output1=funktionsname(input1,input2,...,inputn)
4.2 Selbstdefinierte Matlab-Funktionen 1. Teil 37 Ein m-file mit Namen Funktionsname.m und einer ersten Zeile der folgen Form: function Funktionsname(input1,input2,...,inputn) oder function output1=funktionsname(input1,input2,...,inputn)
Einführung in die Informatik 1
 Einführung in die Informatik 1 Algorithmen und algorithmische Sprachkonzepte Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 [email protected] Sprechstunde: Freitag,
Einführung in die Informatik 1 Algorithmen und algorithmische Sprachkonzepte Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 [email protected] Sprechstunde: Freitag,
Vorlesung Programmieren
 Vorlesung Programmieren 3. Kontrollstrukturen 04.11.2015 Prof. Dr. Ralf H. Reussner Version 1.1 LEHRSTUHL FÜR SOFTWARE-DESIGN UND QUALITÄT (SDQ) INSTITUT FÜR PROGRAMMSTRUKTUREN UND DATENORGANISATION (IPD),
Vorlesung Programmieren 3. Kontrollstrukturen 04.11.2015 Prof. Dr. Ralf H. Reussner Version 1.1 LEHRSTUHL FÜR SOFTWARE-DESIGN UND QUALITÄT (SDQ) INSTITUT FÜR PROGRAMMSTRUKTUREN UND DATENORGANISATION (IPD),
Deklarationen in C. Prof. Dr. Margarita Esponda
 Deklarationen in C 1 Deklarationen Deklarationen spielen eine zentrale Rolle in der C-Programmiersprache. Deklarationen Variablen Funktionen Die Deklarationen von Variablen und Funktionen haben viele Gemeinsamkeiten.
Deklarationen in C 1 Deklarationen Deklarationen spielen eine zentrale Rolle in der C-Programmiersprache. Deklarationen Variablen Funktionen Die Deklarationen von Variablen und Funktionen haben viele Gemeinsamkeiten.
Imperative vs. Funktionale Programmierung
 Beispiel: Entwerfe eine Funktion, die testet, ob eine Zahl n eine Primzahl ist oder nicht. Beobachtung: (1) Wenn n Primzahl ist, ist die Menge der Teiler von n leer. (2) Die Menge der Teiler von n sind
Beispiel: Entwerfe eine Funktion, die testet, ob eine Zahl n eine Primzahl ist oder nicht. Beobachtung: (1) Wenn n Primzahl ist, ist die Menge der Teiler von n leer. (2) Die Menge der Teiler von n sind
2. Programmierung in C
 2. Programmierung in C Inhalt: Überblick über Programmiersprachen, Allgemeines zur Sprache C C: Basisdatentypen, Variablen, Konstanten Operatoren, Ausdrücke und Anweisungen Kontrollstrukturen (Steuerfluss)
2. Programmierung in C Inhalt: Überblick über Programmiersprachen, Allgemeines zur Sprache C C: Basisdatentypen, Variablen, Konstanten Operatoren, Ausdrücke und Anweisungen Kontrollstrukturen (Steuerfluss)
Einführung in den Einsatz von Objekt-Orientierung mit C++ I
 Einführung in den Einsatz von Objekt-Orientierung mit C++ I ADV-Seminar Leiter: Mag. Michael Hahsler Syntax von C++ Grundlagen Übersetzung Formale Syntaxüberprüfung Ausgabe/Eingabe Funktion main() Variablen
Einführung in den Einsatz von Objekt-Orientierung mit C++ I ADV-Seminar Leiter: Mag. Michael Hahsler Syntax von C++ Grundlagen Übersetzung Formale Syntaxüberprüfung Ausgabe/Eingabe Funktion main() Variablen
Kontrollstrukturen, Pseudocode und Modulo-Rechnung
 Kontrollstrukturen, Pseudocode und Modulo-Rechnung CoMa-Übung III TU Berlin 29.10.2012 CoMa-Übung III (TU Berlin) Kontrollstrukturen, Pseudocode und Modulo-Rechnung 29.10.2012 1 / 1 Themen der Übung 1
Kontrollstrukturen, Pseudocode und Modulo-Rechnung CoMa-Übung III TU Berlin 29.10.2012 CoMa-Übung III (TU Berlin) Kontrollstrukturen, Pseudocode und Modulo-Rechnung 29.10.2012 1 / 1 Themen der Übung 1
Welche Informatik-Kenntnisse bringen Sie mit?
 Welche Informatik-Kenntnisse bringen Sie mit? So gehen Sie vor! Lösen Sie die Aufgaben der Reihe nach von 1 bis 20, ohne das Lösungsblatt zur Hilfe zu nehmen. Der Schwierigkeitsgrad der Aufgaben nimmt
Welche Informatik-Kenntnisse bringen Sie mit? So gehen Sie vor! Lösen Sie die Aufgaben der Reihe nach von 1 bis 20, ohne das Lösungsblatt zur Hilfe zu nehmen. Der Schwierigkeitsgrad der Aufgaben nimmt
Programmierung WS12/13 Lösung - Übung 1 M. Brockschmidt, F. Emmes, C. Otto, T. Ströder
 Prof. aa Dr. J. Giesl Programmierung WS12/13 M. Brockschmidt, F. Emmes, C. Otto, T. Ströder Tutoraufgabe 1 (Syntax und Semantik): 1. Was ist Syntax? Was ist Semantik? Erläutern Sie den Unterschied. 2.
Prof. aa Dr. J. Giesl Programmierung WS12/13 M. Brockschmidt, F. Emmes, C. Otto, T. Ströder Tutoraufgabe 1 (Syntax und Semantik): 1. Was ist Syntax? Was ist Semantik? Erläutern Sie den Unterschied. 2.
Einleitung Entwicklung in C Hello-World! Konstrukte in C Zusammenfassung Literatur. Grundlagen von C. Jonas Gresens
 Grundlagen von C Jonas Gresens Proseminar C Grundlagen und Konzepte Arbeitsbereich Wissenschaftliches Rechnen Fachbereich Informatik Fakultät für Mathematik, Informatik und Naturwissenschaften Universität
Grundlagen von C Jonas Gresens Proseminar C Grundlagen und Konzepte Arbeitsbereich Wissenschaftliches Rechnen Fachbereich Informatik Fakultät für Mathematik, Informatik und Naturwissenschaften Universität
Algorithmen & Programmierung. Ausdrücke & Operatoren (1)
 Algorithmen & Programmierung Ausdrücke & Operatoren (1) Ausdrücke Was ist ein Ausdruck? Literal Variable Funktionsaufruf Ausdruck, der durch Anwendung eines einstelligen (unären) Operators auf einen Ausdruck
Algorithmen & Programmierung Ausdrücke & Operatoren (1) Ausdrücke Was ist ein Ausdruck? Literal Variable Funktionsaufruf Ausdruck, der durch Anwendung eines einstelligen (unären) Operators auf einen Ausdruck
Einführung in die Informatik I (autip)
 Einführung in die Informatik I (autip) Dr. Stefan Lewandowski Fakultät 5: Informatik, Elektrotechnik und Informationstechnik Abteilung Formale Konzepte Universität Stuttgart 24. Oktober 2007 Was Sie bis
Einführung in die Informatik I (autip) Dr. Stefan Lewandowski Fakultät 5: Informatik, Elektrotechnik und Informationstechnik Abteilung Formale Konzepte Universität Stuttgart 24. Oktober 2007 Was Sie bis
= 7 (In Binärdarstellung: = 0111; Unterlauf) = -8 (In Binärdarstellung: = 1000; Überlauf)
 Musterlösung Übung 2 Aufgabe 1: Große Zahlen Das Ergebnis ist nicht immer richtig. Die Maschine erzeugt bei Zahlen, die zu groß sind um sie darstellen zu können einen Über- bzw. einen Unterlauf. Beispiele
Musterlösung Übung 2 Aufgabe 1: Große Zahlen Das Ergebnis ist nicht immer richtig. Die Maschine erzeugt bei Zahlen, die zu groß sind um sie darstellen zu können einen Über- bzw. einen Unterlauf. Beispiele
Kapitel 3: Variablen
 Kapitel 3: Variablen Thema: Programmieren Seite: 1 Kapitel 3: Variablen Im letzten Kapitel haben wir gelernt, bestimmte Ereignisse zu wiederholen solange eine Bedingung erfüllt ist. Nun möchten wir aber
Kapitel 3: Variablen Thema: Programmieren Seite: 1 Kapitel 3: Variablen Im letzten Kapitel haben wir gelernt, bestimmte Ereignisse zu wiederholen solange eine Bedingung erfüllt ist. Nun möchten wir aber
Die Programmiersprache C99: Zusammenfassung
 Die Programmiersprache C99: Zusammenfassung Jörn Loviscach Versionsstand: 7. Dezember 2010, 19:30 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.youtube.com/joernloviscach
Die Programmiersprache C99: Zusammenfassung Jörn Loviscach Versionsstand: 7. Dezember 2010, 19:30 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.youtube.com/joernloviscach
Elementare Datentypen in C++
 Elementare Datentypen in C++ bool signed/unsigned char signed/unsigned short int signed/unsigned int signed/unsigned long int (signed/unsigned long long int) float double long double void enum char Der
Elementare Datentypen in C++ bool signed/unsigned char signed/unsigned short int signed/unsigned int signed/unsigned long int (signed/unsigned long long int) float double long double void enum char Der
Werkzeuge zur Programmentwicklung
 Werkzeuge zur Programmentwicklung B-15 Bibliothek Modulschnittstellen vorübersetzte Module Eingabe Editor Übersetzer (Compiler) Binder (Linker) Rechner mit Systemsoftware Quellmodul (Source) Zielmodul
Werkzeuge zur Programmentwicklung B-15 Bibliothek Modulschnittstellen vorübersetzte Module Eingabe Editor Übersetzer (Compiler) Binder (Linker) Rechner mit Systemsoftware Quellmodul (Source) Zielmodul
C- Kurs 04 Anweisungen
 C- Kurs 04 Anweisungen Dipl.- Inf. Jörn Hoffmann jhoffmann@[email protected] leipzig.de Universität Leipzig Ins@tut für Informa@k Technische Informa@k Ausdrücke Institut für Informatik Anweisungen C-Programm
C- Kurs 04 Anweisungen Dipl.- Inf. Jörn Hoffmann jhoffmann@[email protected] leipzig.de Universität Leipzig Ins@tut für Informa@k Technische Informa@k Ausdrücke Institut für Informatik Anweisungen C-Programm
4. Ablaufsteuerung (Kontrollstrukturen)
 4. Ablaufsteuerung (Kontrollstrukturen) 4.1 Anweisungen 4.2 Selektion (bedingte Anweisung) 4.3 Iteration 4.4 Flussdiagramm (Programmablaufplan) 4. Ablaufsteuerung 4-1 4.1 Anweisungen Ein Programm besteht
4. Ablaufsteuerung (Kontrollstrukturen) 4.1 Anweisungen 4.2 Selektion (bedingte Anweisung) 4.3 Iteration 4.4 Flussdiagramm (Programmablaufplan) 4. Ablaufsteuerung 4-1 4.1 Anweisungen Ein Programm besteht
Algorithmen & Programmierung. Rekursive Funktionen (1)
 Algorithmen & Programmierung Rekursive Funktionen (1) Berechnung der Fakultät Fakultät Die Fakultät N! einer nichtnegativen ganzen Zahl N kann folgendermaßen definiert werden: d.h. zur Berechnung werden
Algorithmen & Programmierung Rekursive Funktionen (1) Berechnung der Fakultät Fakultät Die Fakultät N! einer nichtnegativen ganzen Zahl N kann folgendermaßen definiert werden: d.h. zur Berechnung werden
PHP 5.4 ISBN 978-3-86249-327-2. Stephan Heller, Andreas Dittfurth 1. Ausgabe, September 2012. Grundlagen zur Erstellung dynamischer Webseiten GPHP54
 PHP 5.4 Stephan Heller, Andreas Dittfurth 1. Ausgabe, September 2012 Grundlagen zur Erstellung dynamischer Webseiten ISBN 978-3-86249-327-2 GPHP54 5 PHP 5.4 - Grundlagen zur Erstellung dynamischer Webseiten
PHP 5.4 Stephan Heller, Andreas Dittfurth 1. Ausgabe, September 2012 Grundlagen zur Erstellung dynamischer Webseiten ISBN 978-3-86249-327-2 GPHP54 5 PHP 5.4 - Grundlagen zur Erstellung dynamischer Webseiten
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Registermaschine (random access machine, RAM) 0 I 0 1 I 1 2 I 2 m I m Programm
Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Die Registermaschine (random access machine, RAM) 0 I 0 1 I 1 2 I 2 m I m Programm
2017/01/23 15:50 1/5 Bedienung
 2017/01/23 15:50 1/5 Bedienung Bedienung (J.Müller, Hilfe zu JTCEMU) Das originale 2K-System Das 2 KByte große Betriebssystem bietet die wichtigsten Funktionen zur Eingabe und Verwaltung von BASIC-Programmen.
2017/01/23 15:50 1/5 Bedienung Bedienung (J.Müller, Hilfe zu JTCEMU) Das originale 2K-System Das 2 KByte große Betriebssystem bietet die wichtigsten Funktionen zur Eingabe und Verwaltung von BASIC-Programmen.
Kapitel 9: Klassen und höhere Datentypen. Klassen und höhere. Objekte, Felder, Methoden. Küchlin/Weber: Einführung in die Informatik
 Klassen und höhere Datentypen Objekte, Felder, Methoden Küchlin/Weber: Einführung in die Informatik Klassen Klasse (class) stellt einen (i.a. benutzerdefinierten) Verbund-Datentyp dar Objekte sind Instanzen
Klassen und höhere Datentypen Objekte, Felder, Methoden Küchlin/Weber: Einführung in die Informatik Klassen Klasse (class) stellt einen (i.a. benutzerdefinierten) Verbund-Datentyp dar Objekte sind Instanzen
Flussdiagramm / Programmablaufplan (PAP)
 Flussdiagramm / Programmablaufplan (PAP) Basissysmbole Grenzstelle (Anfang, Zwischenhalt oder Ende des Programms/Algorithmus) Verbindung Zur Verdeutlichung der Ablaufrichtung werden Linien mit einer Pfeilspitze
Flussdiagramm / Programmablaufplan (PAP) Basissysmbole Grenzstelle (Anfang, Zwischenhalt oder Ende des Programms/Algorithmus) Verbindung Zur Verdeutlichung der Ablaufrichtung werden Linien mit einer Pfeilspitze
Operatoren für elementare Datentypen Bedingte Anweisungen Schleifen. Programmieren I. Martin Schultheiß. Hochschule Darmstadt Wintersemester 2010/2011
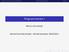 Programmieren I Martin Schultheiß Hochschule Darmstadt Wintersemester 2010/2011 1 Operatoren für elementare Datentypen 2 Bedingte Anweisungen 3 Schleifen Zuweisungsoperator Die Zuweisung von Werten an
Programmieren I Martin Schultheiß Hochschule Darmstadt Wintersemester 2010/2011 1 Operatoren für elementare Datentypen 2 Bedingte Anweisungen 3 Schleifen Zuweisungsoperator Die Zuweisung von Werten an
Webbasierte Programmierung
 Webbasierte Programmierung Eine Einführung mit anschaulichen Beispielen aus der HTML5-Welt apl. Prof. Dr. Achim Ebert Inhalt Kapitel 6: JavaScript Kontrollstrukturen Verzweigungen Einseitig, zweiseitig,
Webbasierte Programmierung Eine Einführung mit anschaulichen Beispielen aus der HTML5-Welt apl. Prof. Dr. Achim Ebert Inhalt Kapitel 6: JavaScript Kontrollstrukturen Verzweigungen Einseitig, zweiseitig,
Inhaltsverzeichnis. Einführende Bemerkungen 11. Das Fach Informatik 11 Zielsetzung der Vorlesung Grundbegriffe
 Inhaltsverzeichnis Einführende Bemerkungen 11 Das Fach Informatik 11 Zielsetzung der Vorlesung 12 1. Grundbegriffe 1 3 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Information und Nachricht 1.1.1 Information 1.1.2 Nachricht
Inhaltsverzeichnis Einführende Bemerkungen 11 Das Fach Informatik 11 Zielsetzung der Vorlesung 12 1. Grundbegriffe 1 3 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Information und Nachricht 1.1.1 Information 1.1.2 Nachricht
4.Grundsätzliche Programmentwicklungsmethoden
 4.Grundsätzliche Programmentwicklungsmethoden 1.1 Grundlage strukturierter und objektorientierter Programmierung Begriff Software Engineering - umfaßt den gezielten Einsatz von Beschreibungsmitteln, Methoden
4.Grundsätzliche Programmentwicklungsmethoden 1.1 Grundlage strukturierter und objektorientierter Programmierung Begriff Software Engineering - umfaßt den gezielten Einsatz von Beschreibungsmitteln, Methoden
Modul Entscheidungsunterstützung in der Logistik. Einführung in die Programmierung mit C++ Übung 4
 Fakultät Verkehrswissenschaften Friedrich List, Professur für Verkehrsbetriebslehre und Logistik Modul Entscheidungsunterstützung in der Logistik Einführung in die Programmierung mit C++ Übung 4 SS 2016
Fakultät Verkehrswissenschaften Friedrich List, Professur für Verkehrsbetriebslehre und Logistik Modul Entscheidungsunterstützung in der Logistik Einführung in die Programmierung mit C++ Übung 4 SS 2016
2. Computer (Hardware) K. Bothe, Institut für Informatik, HU Berlin, GdP, WS 2015/16
 2. Computer (Hardware) K. Bothe, Institut für Informatik, HU Berlin, GdP, WS 2015/16 Version: 14. Okt. 2015 Computeraufbau: nur ein Überblick Genauer: Modul Digitale Systeme (2. Semester) Jetzt: Grundverständnis
2. Computer (Hardware) K. Bothe, Institut für Informatik, HU Berlin, GdP, WS 2015/16 Version: 14. Okt. 2015 Computeraufbau: nur ein Überblick Genauer: Modul Digitale Systeme (2. Semester) Jetzt: Grundverständnis
Korn-Shell: Einführung in Shellscripte 1. Übersicht: Einführung - 2. Die Kornshell im Detail - 3.Grundlagen der Programmierung
 1. Übersicht: Einführung - 2. Die Kornshell im Detail - 3.Grundlagen der Programmierung 1. Übersicht und Einführung 1.1 Die Shell allgemein 1.2 Die korn-shell 1.3 Der Weg zum ersten Skript 1.4 Nutzen und
1. Übersicht: Einführung - 2. Die Kornshell im Detail - 3.Grundlagen der Programmierung 1. Übersicht und Einführung 1.1 Die Shell allgemein 1.2 Die korn-shell 1.3 Der Weg zum ersten Skript 1.4 Nutzen und
II. Grundlagen der Programmierung. 9. Datenstrukturen. Daten zusammenfassen. In Java (Forts.): In Java:
 Technische Informatik für Ingenieure (TIfI) WS 2005/2006, Vorlesung 9 II. Grundlagen der Programmierung Ekkart Kindler Funktionen und Prozeduren Datenstrukturen 9. Datenstrukturen Daten zusammenfassen
Technische Informatik für Ingenieure (TIfI) WS 2005/2006, Vorlesung 9 II. Grundlagen der Programmierung Ekkart Kindler Funktionen und Prozeduren Datenstrukturen 9. Datenstrukturen Daten zusammenfassen
Erwin Grüner 09.02.2006
 FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
Zugriff auf Matrizen. Anhängen von Elementen. Punktweise Operatoren. Vektoren und Matrizen in MATLAB II
 Zugriff auf Matrizen. Anhängen von Elementen. Punktweise Operatoren. Vektoren und Matrizen in MATLAB II Matrixzugriff Wir wollen nun unsere Einführung in die Arbeit mit Vektoren und Matrizen in MATLAB
Zugriff auf Matrizen. Anhängen von Elementen. Punktweise Operatoren. Vektoren und Matrizen in MATLAB II Matrixzugriff Wir wollen nun unsere Einführung in die Arbeit mit Vektoren und Matrizen in MATLAB
Gliederung. Tutorium zur Vorlesung. Gliederung. Gliederung. 1. Gliederung der Informatik. 1. Gliederung der Informatik. 1. Gliederung der Informatik
 Informatik I WS 2012/13 Tutorium zur Vorlesung 1. Alexander Zietlow [email protected] Wilhelm-Schickard-Institut für Informatik Eberhard Karls Universität Tübingen 11.02.2013 1. 2. 1.
Informatik I WS 2012/13 Tutorium zur Vorlesung 1. Alexander Zietlow [email protected] Wilhelm-Schickard-Institut für Informatik Eberhard Karls Universität Tübingen 11.02.2013 1. 2. 1.
Variablen in MATLAB. Unterschiede zur Mathematik: Symbolisches und numerisches Rechnen. Skriptdateien. for-schleifen.
 Variablen in MATLAB. Unterschiede zur Mathematik: Symbolisches und numerisches Rechnen. Skriptdateien. for-schleifen. Wir wollen uns heute dem Thema Variablen widmen und uns damit beschäftigen, wie sich
Variablen in MATLAB. Unterschiede zur Mathematik: Symbolisches und numerisches Rechnen. Skriptdateien. for-schleifen. Wir wollen uns heute dem Thema Variablen widmen und uns damit beschäftigen, wie sich
Programmieren mit Python
 Programmieren mit Python Programmieren heisst: Dem Computer sagen, was er tun soll. Die Befehle muss man übrigens in einer Sprache geben, die der Computer versteht. Darum sind verschiedene Programmiersprachen
Programmieren mit Python Programmieren heisst: Dem Computer sagen, was er tun soll. Die Befehle muss man übrigens in einer Sprache geben, die der Computer versteht. Darum sind verschiedene Programmiersprachen
Komplexität von Algorithmen
 Komplexität von Algorithmen Prof. Dr. Christian Böhm WS 07/08 in Zusammenarbeit mit Gefei Zhang http://www.dbs.informatik.uni-muenchen.de/lehre/nfinfosw Ressourcenbedarf - Größenordnungen Prozesse verbrauchen
Komplexität von Algorithmen Prof. Dr. Christian Böhm WS 07/08 in Zusammenarbeit mit Gefei Zhang http://www.dbs.informatik.uni-muenchen.de/lehre/nfinfosw Ressourcenbedarf - Größenordnungen Prozesse verbrauchen
1.8 Kontrollstrukturen 73. default : ziffer = 0; if (ziffer > 0) { cout << "Ziffer = " << ziffer; else { cout << "keine römische Ziffer!
 1.8 Kontrollstrukturen 73 default : ziffer = 0; if (ziffer > 0) { cout
1.8 Kontrollstrukturen 73 default : ziffer = 0; if (ziffer > 0) { cout
5 DATEN. 5.1. Variablen. Variablen können beliebige Werte zugewiesen und im Gegensatz zu
 Daten Makro + VBA effektiv 5 DATEN 5.1. Variablen Variablen können beliebige Werte zugewiesen und im Gegensatz zu Konstanten jederzeit im Programm verändert werden. Als Variablen können beliebige Zeichenketten
Daten Makro + VBA effektiv 5 DATEN 5.1. Variablen Variablen können beliebige Werte zugewiesen und im Gegensatz zu Konstanten jederzeit im Programm verändert werden. Als Variablen können beliebige Zeichenketten
Interpreter - Gliederung
 Institut für Informatik Ludwig-Maximilian Universität Interpreter - Gliederung Programmiersprache Syntax Konkrete Syntax Abstrakter Syntax Baum (Abstrakte Syntax) Parser Syntaktische Struktur einer Sprache
Institut für Informatik Ludwig-Maximilian Universität Interpreter - Gliederung Programmiersprache Syntax Konkrete Syntax Abstrakter Syntax Baum (Abstrakte Syntax) Parser Syntaktische Struktur einer Sprache
Schleifenanweisungen
 Schleifenanweisungen Bisher: sequentielle Abarbeitung von Befehlen (von oben nach unten) Nun: Befehle mehrfach ausführen (= Programmschleife): for-anweisung - wenn feststeht, wie oft z.b.: eine Berechnung
Schleifenanweisungen Bisher: sequentielle Abarbeitung von Befehlen (von oben nach unten) Nun: Befehle mehrfach ausführen (= Programmschleife): for-anweisung - wenn feststeht, wie oft z.b.: eine Berechnung
Shell-Scripting Linux-Kurs der Unix-AG
 Shell-Scripting Linux-Kurs der Unix-AG Andreas Teuchert 8. Juli 2014 Was ist ein Shell-Script? Aneinanderreihung von Befehlen, die ausgeführt werden Bedingte und wiederholende Ausführung möglich Nützlich
Shell-Scripting Linux-Kurs der Unix-AG Andreas Teuchert 8. Juli 2014 Was ist ein Shell-Script? Aneinanderreihung von Befehlen, die ausgeführt werden Bedingte und wiederholende Ausführung möglich Nützlich
Probeklausur: Programmierung WS04/05
 Probeklausur: Programmierung WS04/05 Name: Hinweise zur Bearbeitung Nimm Dir für diese Klausur ausreichend Zeit, und sorge dafür, dass Du nicht gestört wirst. Die Klausur ist für 90 Minuten angesetzt,
Probeklausur: Programmierung WS04/05 Name: Hinweise zur Bearbeitung Nimm Dir für diese Klausur ausreichend Zeit, und sorge dafür, dass Du nicht gestört wirst. Die Klausur ist für 90 Minuten angesetzt,
1. Grundzüge der Objektorientierung 2. Methoden, Unterprogramme und Parameter 3. Datenabstraktion 4. Konstruktoren 5. Vordefinierte Klassen
 1. Grundzüge der Objektorientierung 2. Methoden, Unterprogramme und Parameter 3. Datenabstraktion 4. Konstruktoren 5. Vordefinierte Klassen II.2.2 Methoden, Unterprogramme und Parameter - 1 - 2. Methoden
1. Grundzüge der Objektorientierung 2. Methoden, Unterprogramme und Parameter 3. Datenabstraktion 4. Konstruktoren 5. Vordefinierte Klassen II.2.2 Methoden, Unterprogramme und Parameter - 1 - 2. Methoden
Java Einführung Methoden. Kapitel 6
 Java Einführung Methoden Kapitel 6 Inhalt Deklaration und Aufruf von Methoden Lokale und globale Namen (Bezeichner) Sichtbarkeit und Lebensdauer von Variablen in Methoden Überladen von Methoden 2 Methoden
Java Einführung Methoden Kapitel 6 Inhalt Deklaration und Aufruf von Methoden Lokale und globale Namen (Bezeichner) Sichtbarkeit und Lebensdauer von Variablen in Methoden Überladen von Methoden 2 Methoden
Syntax von LOOP-Programmen
 LOOP-Berechenbarkeit Syntax von LOOP-Programmen Definition LOOP-Programme bestehen aus: Variablen: x 0, x 1, x 2, x 3,... Konstanten: 0, 1, 2, 3,... Trennsymbolen:; und := Operationen: + und Befehlen:
LOOP-Berechenbarkeit Syntax von LOOP-Programmen Definition LOOP-Programme bestehen aus: Variablen: x 0, x 1, x 2, x 3,... Konstanten: 0, 1, 2, 3,... Trennsymbolen:; und := Operationen: + und Befehlen:
12 == 12 true 12 == 21 false 4 === 7 true 4 === "vier" false 4 === 4.0 false 12!= 13 true 12!== 12 false 12!== 12.0 true. 1 < 3 true 3 < 1 false
 Die if-anweisung if (Bedingung 1) { Code 1 else { Code 2 ; Anm.1: Das ; kann entfallen, da innerhalb { ein sog. Codeblock geschrieben wird. Anm.2: Es gibt noch andere Schreibweisen, aber wir wollen uns
Die if-anweisung if (Bedingung 1) { Code 1 else { Code 2 ; Anm.1: Das ; kann entfallen, da innerhalb { ein sog. Codeblock geschrieben wird. Anm.2: Es gibt noch andere Schreibweisen, aber wir wollen uns
Programmieren in C / C++ Grundlagen C 4
 Programmieren in C / C++ Grundlagen C 4 Hochschule Fulda FB AI Wintersemester 2016/17 http://c.rz.hs-fulda.de Peter Klingebiel, HS Fulda, FB AI Anweisungen Anweisung im allgemeinsten Sinn: Programmieren
Programmieren in C / C++ Grundlagen C 4 Hochschule Fulda FB AI Wintersemester 2016/17 http://c.rz.hs-fulda.de Peter Klingebiel, HS Fulda, FB AI Anweisungen Anweisung im allgemeinsten Sinn: Programmieren
Grundlagen der Programmierung Prof. H. Mössenböck. 6. Methoden
 Grundlagen der Programmierung Prof. H. Mössenböck 6. Methoden Parameterlose Methoden Beispiel: Ausgabe einer Überschrift class Sample { static void printheader() { // Methodenkopf Out.println("Artikelliste");
Grundlagen der Programmierung Prof. H. Mössenböck 6. Methoden Parameterlose Methoden Beispiel: Ausgabe einer Überschrift class Sample { static void printheader() { // Methodenkopf Out.println("Artikelliste");
Java Einführung VARIABLEN und DATENTYPEN Kapitel 2
 Java Einführung VARIABLEN und DATENTYPEN Kapitel 2 Inhalt dieser Einheit Variablen (Sinn und Aufgabe) Bezeichner Datentypen, Deklaration und Operationen Typenumwandlung (implizit/explizit) 2 Variablen
Java Einführung VARIABLEN und DATENTYPEN Kapitel 2 Inhalt dieser Einheit Variablen (Sinn und Aufgabe) Bezeichner Datentypen, Deklaration und Operationen Typenumwandlung (implizit/explizit) 2 Variablen
1. LPC - Lehmanns Programmier Contest - Lehmanns Logo
 Aufgabe ist die Entwicklung einer vereinfachten Variante der beliebten Programmiersprache Logo. Die Aufgabe ist in drei Stufen zu erledigen, von der wir zunächst nur die erste Stufe bekannt geben. Die
Aufgabe ist die Entwicklung einer vereinfachten Variante der beliebten Programmiersprache Logo. Die Aufgabe ist in drei Stufen zu erledigen, von der wir zunächst nur die erste Stufe bekannt geben. Die
Kapitel 8. Programmierkurs. Methoden. 8.1 Methoden
 Kapitel 8 Programmierkurs Birgit Engels Anna Schulze Zentrum für Angewandte Informatik Köln Objektorientierte Programmierung Methoden Überladen von Methoden Der this-zeiger Konstruktoren Vererbung WS 07/08
Kapitel 8 Programmierkurs Birgit Engels Anna Schulze Zentrum für Angewandte Informatik Köln Objektorientierte Programmierung Methoden Überladen von Methoden Der this-zeiger Konstruktoren Vererbung WS 07/08
Programmieren in Haskell Programmiermethodik
 Programmieren in Haskell Programmiermethodik Peter Steffen Universität Bielefeld Technische Fakultät 12.01.2011 1 Programmieren in Haskell Bisherige Themen Was soll wiederholt werden? Bedienung von hugs
Programmieren in Haskell Programmiermethodik Peter Steffen Universität Bielefeld Technische Fakultät 12.01.2011 1 Programmieren in Haskell Bisherige Themen Was soll wiederholt werden? Bedienung von hugs
Einführung in die C-Programmierung
 Einführung in die C-Programmierung Warum C? Sehr stark verbreitet (Praxisnähe) Höhere Programmiersprache Objektorientierte Erweiterung: C++ Aber auch hardwarenahe Programmierung möglich (z.b. Mikrokontroller).
Einführung in die C-Programmierung Warum C? Sehr stark verbreitet (Praxisnähe) Höhere Programmiersprache Objektorientierte Erweiterung: C++ Aber auch hardwarenahe Programmierung möglich (z.b. Mikrokontroller).
Speicher und Adressraum
 Linearer Speicher (Adressraum) Technische Universität München Speicher und Adressraum Freie Speicherhalde (Heap) Freier Speicherstapel (Stack) Globale Variablen Bibliotheksfunktionen Laufzeitsystem Programmcode
Linearer Speicher (Adressraum) Technische Universität München Speicher und Adressraum Freie Speicherhalde (Heap) Freier Speicherstapel (Stack) Globale Variablen Bibliotheksfunktionen Laufzeitsystem Programmcode
Übersicht. Datenstrukturen und Algorithmen Vorlesung 5: Rekursionsgleichungen (K4) Übersicht. Binäre Suche. Joost-Pieter Katoen. 20.
 Übersicht Datenstrukturen und Algorithmen Vorlesung 5: (K4) Joost-Pieter Katoen Lehrstuhl für Informatik 2 Software Modeling and Verification Group http://www-i2.informatik.rwth-aachen.de/i2/dsal12/ 20.
Übersicht Datenstrukturen und Algorithmen Vorlesung 5: (K4) Joost-Pieter Katoen Lehrstuhl für Informatik 2 Software Modeling and Verification Group http://www-i2.informatik.rwth-aachen.de/i2/dsal12/ 20.
Funktionale Programmierung. Funktionale Programmierung: Vorlesungsüberblick. Eigenschaften rein funktionaler Programmierung
 Funktionale Programmierung 1 Funktionale Programmierung: Vorlesungsüberblick 1. Funktionale Programmierung Prinzipien funktionaler Programmierung Funktionale Programmierung in prozeduralen Sprachen Rekursive
Funktionale Programmierung 1 Funktionale Programmierung: Vorlesungsüberblick 1. Funktionale Programmierung Prinzipien funktionaler Programmierung Funktionale Programmierung in prozeduralen Sprachen Rekursive
C/C++ Programmierung
 1 C/C++ Programmierung Grundlagen: Der Präprozessor Sebastian Hack Christoph Mallon (hack mallon)@cs.uni-sb.de Fachbereich Informatik Universität des Saarlandes Wintersemester 2009/2010 2 Der Präprozessor
1 C/C++ Programmierung Grundlagen: Der Präprozessor Sebastian Hack Christoph Mallon (hack mallon)@cs.uni-sb.de Fachbereich Informatik Universität des Saarlandes Wintersemester 2009/2010 2 Der Präprozessor
Informatik I Übung, Woche 40
 Giuseppe Accaputo 2. Oktober, 2014 Plan für heute 1. Fragen & Nachbesprechung Übung 2 2. Zusammenfassung der bisherigen Vorlesungsslides 3. Tipps zur Übung 3 Informatik 1 (D-BAUG) Giuseppe Accaputo 2 Nachbesprechung
Giuseppe Accaputo 2. Oktober, 2014 Plan für heute 1. Fragen & Nachbesprechung Übung 2 2. Zusammenfassung der bisherigen Vorlesungsslides 3. Tipps zur Übung 3 Informatik 1 (D-BAUG) Giuseppe Accaputo 2 Nachbesprechung
Im Original veränderbare Word-Dateien
 Das Von-Neumann-Prinzip Prinzipien der Datenverarbeitung Fast alle modernen Computer funktionieren nach dem Von- Neumann-Prinzip. Der Erfinder dieses Konzeptes John von Neumann (1903-1957) war ein in den
Das Von-Neumann-Prinzip Prinzipien der Datenverarbeitung Fast alle modernen Computer funktionieren nach dem Von- Neumann-Prinzip. Der Erfinder dieses Konzeptes John von Neumann (1903-1957) war ein in den
Einstieg in die Informatik mit Java
 1 / 26 Einstieg in die Informatik mit Java Felder Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 26 1 Was sind Felder? 2 Vereinbarung von Feldern 3 Erzeugen von Feldern
1 / 26 Einstieg in die Informatik mit Java Felder Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 26 1 Was sind Felder? 2 Vereinbarung von Feldern 3 Erzeugen von Feldern
Java 7. Elmar Fuchs Grundlagen Programmierung. 1. Ausgabe, Dezember 2011 JAV7
 Java 7 Elmar Fuchs Grundlagen Programmierung 1. Ausgabe, Dezember 2011 JAV7 5 Java 7 - Grundlagen Programmierung 5 Kontrollstrukturen In diesem Kapitel erfahren Sie wie Sie die Ausführung von von Bedingungen
Java 7 Elmar Fuchs Grundlagen Programmierung 1. Ausgabe, Dezember 2011 JAV7 5 Java 7 - Grundlagen Programmierung 5 Kontrollstrukturen In diesem Kapitel erfahren Sie wie Sie die Ausführung von von Bedingungen
