Empirischer Vergleich ordinaler Regressionsmodelle
|
|
|
- Lioba Weiss
- vor 6 Jahren
- Abrufe
Transkript
1 Ludwig-Maximilians-Universität, München Institut für Statistik Empirischer Vergleich ordinaler Regressionsmodelle Bachelorarbeit Verfasser: Susanne Dandl Betreuer: Prof. Dr. Gerhard Tutz, Institut für Statistik, LMU Moritz Berger, Institut für Statistik, LMU Eingereicht am: 30. Mai 2016
2 Zusammenfassung In vielen Regressionsproblemen mit kategorialem, ordinalem Response ist dem Anwender zwar die Multinomialverteilung der Zielvariable bewusst, jedoch wird die Ordnung der Kategorien häufig in der Wahl der Linkfunktion missachtet. Somit wird nicht der volle Informationsgehalt der Variablen genutzt. Zwei Modelle, welche die Rangordnung einer Variablen beachten, sind das kumulative und Adjacent-Type Logit-Modell. Diese unterscheiden sich in der Art der verwendeten Logits. Während beim Adjacent-Type Modell die Logits benachbarter Kategorien genutzt werden, sind es beim kumulativen Modell kumulierte Logits. Dies führt zu unterschiedlichen Interpretationen. Welches Verfahren nun für die Berechnung von Regressionsmodellen zu bevorzugen ist, wird anhand mehrerer Datenbeispiele erläutert. Dazu werden zunächst, auf Grundlage des multinomialen Modells, die Komponenten des kumulativen Modells und des Adjacent-Type Modells genauer spezifiziert. Für beide Verfahren können sowohl Modelle unter Partial-Proportional-Odds Annahme als auch unter Annahme kategoriespezifischer Koeffizienten modelliert werden. Ein Likelihood-Ratio-Test kann darüber Aufschluss geben, welche Annahme getroffen werden sollte. Das kumulative Modell hat jedoch den Nachteil, dass es bei einer großen Anzahl geordneter Kategorien der Zielvariablen und mehreren kategorialen Einflussgrößen zu keinem Schätzwerten führen kann. Die Konzepte beider Methoden können auch auf die Modellierung longitudinaler Daten übertragen werden, indem zusätzlich ein Random Intercept in den Prädiktor aufgenommen wird. Für die Modellierung der Vertrauensskalen des Allbus-Datensatzes wird das R-Package vgam mit der Funktion vglm() verwendet. Für die Modellierung der Schmerzkategorien des Knee-Datensatzes kann das vcrpart Package mit der Funktion olmm() genutzt werden. Der Vergleich beider Verfahren anhand des Allbus-Datensatzes und Knee-Datensatzes gibt Aufschluss darüber, dass sowohl das kumulative Logit-Modell als auch das Adjacent- Category Logit-Modell in ähnlichen Situationen einen vergleichbaren Fit aufweisen. Dies bestätigen auch die Werte des AICs und der Devianz, welche als Vergleichskriterien für den Modellfit verwendet werden. Allgemein sollte das Verfahren genutzt werden, dessen Art der Logits bzw. dessen Interpretationsform präferiert wird. i
3 Inhaltsverzeichnis 1 Einleitung 1 2 Grundlagen Multinomialverteilung Inferenz Multinomiales Logit-Modell Vorteile ordinaler Methoden Ordinale Modelle Kumulatives Modell Motivation Definition des kumulativen Logit-Modells Kumulatives Logit-Modell für Kontingenztabellen Inferenz Methoden zur Modellüberprüfung Erweiterung des kumulativen Logit-Modells Adjacent-Type Modell Definition des Adjacent-Type Logit-Modells Verbindung zum multinomialen Logit-Modell Adjacent-Type Logit-Modell für Kontingenztabellen Inferenz Vergleich der Methoden VGAM Package Allbus-Datenbeispiel Variablenbeschreibung und Modellspezifikationen Vergleich der Testergebnisse Zielvariable government Vergleich der Testergebnisse Zielvariable fellow Zusammenfassung des Vergleichs Longitudinale Daten Ordinale gemischte Modelle Methodenvergleich anhand des Knee-Datensatzes Fazit 62 ii
4 Literaturverzeichnis 63 A Verfügbare Dateien 68 B R-Code und Ergebnistabellen 71 B.1 Likelihood-Ratio-Test kumulatives Logit-Modell Variable government B.2 Auswertung Zielvariable justice iii
5 1 EINLEITUNG 1 Einleitung Die Theorie der ordinalen, kategorialen Daten und die Unterscheidung ihrer Methoden zu den ungeordneten Skalen erhalten seit 1980 durch Publikationen wie Regression Models for Ordinal Data von McCullagh (siehe Peter McCullagh (1980)) Aufmerksamkeit in der Datenana- lyse. Ordinale Skalen unterscheiden sich von nominalen Skalen darin, dass ihre Ausprägungen geordnet werden können. Zum Beispiel lassen sich Augenfarben in keine hierarchische Anordung bringen. Somit gehören sie zu den nominalen Variablen. Ordinale Kategorien werden besonders häufig im Bereich medizinischer Gesundheitseinschätzungen und Messungen von Einstellungen und Meinungen zu öffentlichen Themen verwendet (vgl. Agresti (2010): S. 1 f.). Beispiele sind die in Kapitel 4 verwendeten Skalen zum Vertrauen in die Regierung und die Mitmenschen sowie die in Kapitel 5 verwendete Skala mit Stufen von 1 bis 5 für die Einschätzung von Knieschmerzen. Es gibt zwei Arten geordneter kategorialer Variablen. Sie können zum einen auf festgesetzten, ordinalen Skalen beruhen. Ein Beispiel sind die Kategorien verschiedener Schulformen, welche anhand ihrer Abschlüsse in Hauptschule, Realschule und Gymnasium gestaffelt werden können. Zum anderen können sie durch das Zusammenfassen stetiger Größen entstehen (vgl. Tutz (2012): S. 241). Diese werden Intervallskalen genannt (vgl. Agresti (2010): S. 2). Ein Beispiel ist die Einteilung des Body Mass Indexes (BMI) in verschiedene Gruppen. Der BMI wird anhand des Gewichts in Kilogramm dividiert durch die quadrierte Größe in Metern berechnet. Wird ein Index von kleiner als 18.5 errechnet, so wird die Person der Gruppe der Untergewichtigen zugeordnet. Bei einem BMI von erfolgt die Zuteilung zu den Normalgewichtigen, bei Werten zwischen 25 und zu den Übergewichtigen und ab 30 zur Personengruppe der Fettleibigen. Diese Gruppengrenzwerte wurden von der World Health Organization (kurz: WHO) festgelegt (vgl. WHO - World Health Organization (2000)). Ein Nachteil dieses Vorgehens ist der Verlust von Information durch die Bildung von Intervallen. Im Gegensatz zu festgesetzten, ordinalen Skalen ist bei den Intervallskalen die Distanz zwischen den Kategorien genau festgelegt. In vielen Regressionsproblemen mit kategorialem, ordinalem Response ist dem Anwender zwar die Multinomialverteilung der Zielvariable bewusst, jedoch wird die Ordnung der Kategorien in der Wahl seiner Methoden häufig nicht genutzt. Somit wird nicht der volle Informationsgehalt der Variablen verwendet (vgl. Agresti (2010): S. 1 ff.). Nach einer Einführung in das Multinomialmodell, seine Inferenz und das multinomiale Logit- Modell, werden am Ende von Kapitel 2 die Vorteile ordinaler Methoden erläutert. In Kapitel 3 wird näher auf das kumulative Modell und das Adjacent-Type Modell eingegangen, welche die 1
6 2 GRUNDLAGEN ordinale Struktur der Daten ausnutzen. Diese beiden Methoden werden in Kapitel 4 anhand des Allbus-Datensatzes verglichen. Anschließend folgt in Kapitel 5 ein kurzer Überblick über die Verwendung gemischter ordinaler Modelle im kumulativen und im Adjacent-Category Modell für Daten mit Messwiederholungen, den sogenannten longitudinalen Daten. Beide Methoden werden dann anhand des Knee-Datensatzes kontrastiert. Zum Abschluss folgt eine Zusammenfassung der Erkenntnisse in einem Fazit. 2 Grundlagen Ist die Zielvariable in einem Regressionsproblem kategorial, so kann angenommen werden, dass diese einer Multinomialverteilung folgt (Fahrmeir et al. (2009): S. 236). Bei der Verteilung wird nicht zwischen ordinalen und nominalen Skalen unterschieden. Die Ordnung fließt in die Wahl der Linkfunktion ein. In diesem Kapitel werden Annahmen, Wahrscheinlichkeitsfunktionen und Inferenz des Multinomialmodells sowie das multinomiale Logit-Modell näher erläutert. 2.1 Multinomialverteilung Die folgenden Spezifikationen der Multinomialverteilung beziehen sich auf Fahrmeir et al. (2009) S. 236 ff. sowie Tutz (2012) S.209. Ausgehend von einer Variable Y mit Kategorien 1, 2,..., k ist die Wahrscheinlichkeit auf Kategorie r 1, 2,..., k als P (Y = r) = π r mit π r [0, 1] und k π r = 1 (1) r=1 definiert. Jede Kategorie hat also eine eigene Wahrscheinlichkeit aufzutreten, sodass Y ein multivariater Response ist mit y T = (y 1, y 2,..., y k ). Wird nur eine Person, eine Befragung oder ein Messpunkt i betrachtet, so kann eine binäre Variable y ir definiert werden mit { 1, Y i = r y ir = mit r 1,..., k 0, sonst Gilt Y i = r, so entspricht y T i = (y i1, y i2,..., y ik ) dem Vektor (0,..., 0, 1, 0,..., 0), wobei die 1 an der r-ten Stelle des Vektors für die Wahl der r-ten Kategorie steht. y i folgt einer Multinomialverteilung und hat mit der Wahrscheinlichkeit π T i = (π i1,..., π ik ) und π ir = P (Y i = r) = 2
7 2.1 Multinomialverteilung 2 GRUNDLAGEN P (y ir = 1) die Wahrscheinlichkeitsfunktion f(y i π i ) = π y i1 i1... πy ik ik Werden nun n Befragungen durchgeführt, so entspricht y r mit r 1,..., k nicht mehr binären Variablen, sondern der Anzahl an Wiederholungen in denen Kategorie r bei den n Befragungen aufgetreten ist. Der Vektor y T = (y 1,..., y k ) ist dann multinomialverteilt mit y M(n, π) und π T = (π 1,..., π k ). Die Wahrscheinlichkeitsfunktion wird folgendermaßen definiert: f(y π) = n! y 1!... y k! πy π y k k Da y k durch y 1,..., y k 1 ausgedrückt werden kann, wie die Umformung von n i=1 y i = n zu k 1 y k = n y i = n y 1... y k 1, i=1 zeigt, kann eine Reduzierung des Vektors y T zu y T = (y 1,..., y q ) mit q = k 1 vorgenommen werden. Zudem kann π k nach Umformung von (1) zu k 1 π k = 1 π r = 1 π 1... π k 1 r=1 durch π 1,..., π q mit q = k 1 berechnet werden. Somit ergibt sich die Wahrscheinlichkeitsfunktion unter Reduzierung der verwendeten Anzahl an Parametern mit π T = (π 1,..., π q ) als: f(y π) = n! y 1!... y q! (n y 1... y q )! πy πq yq (1 π 1... π q ) n y 1... y q Für den Erwartungswert von y gilt E(y) = nπ = nπ 1. nπ q 3
8 2.1 Multinomialverteilung 2 GRUNDLAGEN und für die Kovarianz von y nπ 1 (1 π 1 )... nπ 1 π q Cov(y) =..... nπ q π 1... nπ q (1 π q ) Anstelle der multinomialen Verteilung y M(n, π) kann auch die skalierte Multinomialverteilung verwendet werden, sodass nicht die absolute Anzahl betrachtet wird, sondern die relativen Häufigkeiten der Ausprägungen 1,..., q ȳ = y ( n = y1 n,..., y ) T q = (ȳ1,..., ȳ q ) T n In diesem Fall gilt ȳ M(n, π)/n. Der Erwartungswert ist gegeben als E(ȳ) = π = π 1. π q und die Kovarianz als Cov(ȳ) = 1 π 1 (1 π 1 )... π 1 π q. n.... π q π 1... π q (1 π q ) Inferenz Im vorherigen Kapitel wurde die Wahrscheinlichkeitsfunktion für eine Person i 1,..., n als multinomialverteilt mit f(y i π i ) = π y i1 i1... πy ik ik definiert (vgl. Tutz (2012): S. 218). Alle folgenden Spezifikationen des Abschnitts beziehen sich nun auf Fahrmeir et al. (2009) S. 247 ff.. Werden n Subjekte betrachtet, so folgt unter Annahme der Unabhängigkeit der Beobachtungen die Likelihoodfunktion als: L(β) = n f(y i π i ) = i=1 n i=1 π y i1 i1... πy iq iq (1 π i1... π iq ) (n y i1... y iq ) (2) 4
9 2.1 Multinomialverteilung 2 GRUNDLAGEN Dabei gilt q = k 1. Die Funktion wird verwendet, um die Parameter nach dem Maximum-Likelihood-Prinzip zu schätzen. Zur Vereinfachung wird sie zunächst zur Log-Likelihood-Funktion l(β) = n (y i1 log(π i1 ) y iq log(π iq ) + (n y i1... y iq )log(1 π i1... π iq )) i=1 logarithmiert. Nach Ableitung der Log-Likelihood-Funktion nach β ergibt sich s(β) = l(β) β. Wird diese Score-Funktion nun 0 gesetzt und nach β aufgelöst, so erhält man ˆβ, für das s(ˆβ)! = 0 gilt. Durch die zweite Ableitung wird überprüft, ob es sich um ein Maximum handelt. Im Folgenden wird von p Einflussgrößen und damit von einer Designmatrix der Form x T i = (1, x i1,..., x ip ) ausgegangen. Der Zusammenhang zwischen π i und dem Prädiktor x T i β mit β T = (β 0, β 1,..., β p ) wird über die Responsefunktion h festgelegt. Es gilt: π ir = h(η ir ) = h(x T i β) Die Schätzung von ˆβ erfolgt in iterativer Weise nach dem Fisher-Scoring-Algorithmus, welcher in Kapitel 3.1 zum kumulativen Modell näher erläutert wird. Dazu wird die erwartete Fischerinformationsmatrix benötigt. Diese Matrix F (β) wird als F (β) = E ( ) 2 l(β) β β T definiert. Der ML-Schätzer ˆβ ist dann asymptotisch normalverteilt mit ˆβ N(β, F 1 (ˆβ)) und F 1 (ˆβ) als Inverses der Fisher-Informationsmatrix Multinomiales Logit-Modell Das multinomiale oder mehrkategoriale Logit-Modell ist der natürliche Link der Multinomialverteilung. Sie verbindet eine Responsevariable Y mit geordneten oder ungeordneten Kategorien 1,..., k durch eine Linkfunktion mit dem Designvektor x T = (1, x 1,..., x p ). Die folgenden Definitionen zum Logit-Modell sind in Fahrmeir et al. (2009) S. 239 zu finden. Zur Verein- 5
10 2.1 Multinomialverteilung 2 GRUNDLAGEN fachung wird angenommen, dass für jede Kategorie der Zielvariable der Kovariablenvektor x identisch ist. Für die Auftrittswahrscheinlichkeit π r von Kategorie r gilt: π r = P (Y = r x) = exp(x T β r ) 1 + q mit q = k 1 und r = 1,..., q (3) s=1 exp(xt β s ) Zudem gilt β T r = (β r0, β r1,..., β rp ) mit r = 1,..., q, wenn die Wirkung der Einflussvariablen über die Kategorien variiert. Wird dies nicht angenommen, so entspricht β T r dem Vektor (β r0, β 1,..., β p ). Bei dem mehrkategorialen Logit-Modell wird die (logarithmierte) Chance zwischen der betrachteten Kategorie r und einer Referenzkategorie betrachtet. In Softwareprogrammen wie R wird als Referenzkategorie häufig die letzte Kategorie k verwendet. Die Auftrittswahrscheinlichkeit für Kategorie k ist gegeben durch: π k = 1 π 1... π q = q s=1 exp(xt β s ) Um nun die Chance oder das relative Risiko von Kategorie r zu der letzten Kategorie k zu betrachten, wird die Auftrittswahrscheinlichkeit von Kategorie r mit der von Kategorie k verglichen: P (Y = r x) P (Y = k x) = π r π k = exp(x T β r ) mit r = 1,..., q (4) Nach dem Logarithmieren von (4) wird folgende äquivalente Log-Odds-Darstellung erhalten, wenn kategoriespezifische Koeffizienten angenommen werden: log π r π k = log ( exp(x T β r ) ) = x T β r = β ro + x 1 β r x p β rp (5) Der Koeffizientenvektor β r hängt von der betrachteten Kategorie r und der gewählten Referenzgruppe ab. Zur Interpretation des Einflusses einer Variablen x j mit j 1,..., p auf die Wahl der Kategorie r, wird die Veränderung der Chance zwischen Kategorie r und k bei einer Steigerung von x j um c Einheiten betrachtet: (4) = (5) P (Y = r x mit x j + c)/p (Y = k x mit x j + c)) P (Y = r x)/p (Y = k x) exp(β ro + x 1 β r (x j + c)β rj x p β rp ) exp(β ro + x 1 β r x j β rj x p β rp ) = exp((x j + c)β rj ) exp(x j β rj ) = exp(x jβ rj + cβ rj ) exp(x j β rj ) = exp(cβ rj ) 6
11 2.1 Multinomialverteilung 2 GRUNDLAGEN Je nach Vorzeichen kann die Chance für Kategorie r im Gegensatz zu Kategorie k um den Faktor exp(cβ rj ) steigen (bei einem positiven Vorzeichen) oder sinken (bei einem negativen Vorzeichen), wenn sich x j um c Einheiten verändert und alle anderen Variablen festgehalten werden. Gilt c = 1, so wird die Veränderung der Chance auf Kategorie r zu k um den Faktor exp(β rj ) bei Steigerung der Einflussgröße x j um eine Einheit betrachtet, unter Konstanthalten aller anderen Kovariablen. Zur Interpretation der Veränderung der Chance auf Stufe r zu l 1,..., (k 1), also einer anderen Kategorie als k, wird folgender Bruch betrachtet: P (Y = r x mit x j + c) P (Y = l x mit x j + c) (3) = exp(β ro+...+(x j +c)β rj +...+x pβ rp) 1+ q s=1 exp(βso+...+(x j+c)β sj +...+x pβ sp) exp(β lo +...+(x j +c)β lj +...+x pβ lp ) 1+ q s=1 exp(βso+...+(x j+c)β sj +...+x pβ sp) = exp(β ro (x j + c)β rj x p β rp ) exp(β lo (x j + c)β lj x p β lp ) (6) Für den Vergleich der Chance der Kategorie r zu der Kategorie l folgt: P (Y =r x mit x j +c) P (Y =l x mit x j +c) P (Y =r x) P (Y =l x) 6 = exp(β ro+...+(x j +c)β rj +...+x pβ rp) exp(β lo +...+(x j +c)β lj +...+x pβ lp ) exp(β ro+...+x j β rj +...+x pβ rp) exp(β lo +...+x j β lj +...+x pβ lp ) = exp((x j + c)β rj )exp(x j β lj ) exp((x j + c)β lj )exp(x j β rj ) = exp((x j + c)β rj x j β rj ) exp((x j + c)β lj x j β lj ) = exp(cβ rj) exp(cβ lj ) ) = exp(c(β rj β lj )) Alternativen zum Logit-Modell sind das Probit-Modell und das c-log-log-modell. Beim Probit- Modell wird für die Auftrittswahrscheinlichkeit π r nicht (3) angenommen, sondern die Standardnormalverteilung: π r = φ(x T β r ) Beim c-log-log Modell wird die Auftrittswahrscheinlichkeit π r = 1 exp( exp(x T β r )) verwendet. 7
12 2.2 Vorteile ordinaler Methoden 2 GRUNDLAGEN 2.2 Vorteile ordinaler Methoden Das mehrkategoriale Logit-Modell missachtet bei Anwendung auf geordnete, kategoriale Daten die ordinale Struktur der Variablen und nutzt damit nicht die volle Information aus. Deshalb sind ordinale Methoden für Daten mit geordneten Kategorien zu bevorzugen. Agresti gibt in seinem Buch Analysis of Ordinal Categorical Data (siehe Agresti (2010): S. 3 f.) den Hinweis, dass beim Aufdecken relevanter Trends und alternativer Nachweise bei Tests des Effekts von Kovariablen auf eine ordinale Zielvariable ordinale Methoden eine größere Power aufweisen als nominale Methoden. Die Power ist ein Maß für die Qualität eines statistischen Tests. Sie gibt die Wahrscheinlichkeit an eine Nullhypothese zu verwerfen, wenn die Alternative richtig ist (vgl. Fahrmeir et al. (2011): S ). Zudem kann bei der Analyse ordinaler Daten auf ein größeres Verfahrensspektrum zurückgegriffen werden, da Methoden stetiger Variablen wie Korrelation oder Mittelwerte in ähnlicher Form angewendet werden können (vgl. Agresti (2010): S. 3). Der Grund dafür ist, dass sowohl bei den stetigen als auch ordinalen Skalen eine Ordnung der Daten vorliegt. Außerdem können aus stetigen Variablen durch Intervallbildung ordinale Größen gebildet werden (siehe Einleitung). Das folgende Kapitel, welches das kumulative und das Adjacent- Type Logit-Modell vorstellt, beweist zudem, dass die ordinalen Modelle parametersparsamer als das multinomiale Logit-Modell sind (vgl. Tutz (2012): S. 241). 8
13 3 ORDINALE MODELLE 3 Ordinale Modelle In Kapitel 2 wurde das multinomiale Modell vorgestellt, aus dessen kanonischem Link das multinomiale Logit-Modell resultiert. Es missachtet jedoch bei Anwendung auf Regressionsprobleme mit ordinaler Zielvariable deren zugrundeliegende Ordnung. Deshalb werden in diesem Kapitel zwei Modelle vorgestellt, welche die Ordnung der Kategorien ausnutzen. Zunächst wird das kumulative Modell erläutert. 3.1 Kumulatives Modell Eine Möglichkeit zur Konstruktion von Modellen, welche die Ordnung beachten, ist benachbarte Kategorien in zwei Gruppen zusammenzufassen, sodass eine binäre Variable entsteht (vgl. Agresti (2010): S. 44). Deren kumulierte Wahrscheinlichkeiten werden dann miteinander verglichen Motivation Die folgende Motivation des kumulativen Modells basiert auf Fahrmeir et al. (2009) S Es wird angenommen, dass es hinter der ordinalen, beobachtbaren Responsevariable Y i mit Kategorien r = 1,..., k eine latente (nicht beobachtbare) Variable Yi gibt. Dieses Yi ist definiert als: Y i = x T i β + ɛ i (7) mit x i als Designvektor, β als Parametervektor und ɛ i als Störvariable mit Verteilungsfunktion F. Das sogenannte Schwellenwertkonzept verknüpft die latente Variable und die Beobachtungen durch folgende Annahme: Y i = r θ r 1 < Y i θ r mit r = 1,..., k 1 (8) Für die Schwellenwerte θ 0,..., θ k wird angenommen, dass diese geordnet sind mit = θ 0 < θ 1 <... < θ k =. Liegt also eine latente Variable zwischen den Schwellen θ r 1 und θ r, so liegt eine Beobachtung der Kategorie r vor. Da beim kumulativen Modell durch Zusammenfassung aneinandergrenzender Kategorien eine binäre Zielvariable mit Ausprägungen Y i r und Y i > r entstehen soll, wird folgende Auftrittswahrscheinlichkeit betrachtet: P (Y i r) = P (Y i = 1) P (Y i = r) mit r = 1,..., q (9) 9
14 3.1 Kumulatives Modell 3 ORDINALE MODELLE Diese werden als kumulierte Wahrscheinlichkeiten bezeichnet. Bei Anwendung des Schwellenwertkonzeptes ergibt sich als Zielvariable Y i r, falls Yi θ r und Y i > r, wenn Yi > θ r ist. Abbildung 1 zeigt, wie sich die Chance auf eine Kategorie bei einer Veränderung der Einflussgrößen ändert. Es sind die Dichten der latenten Variable Yi für zwei unterschiedliche Ausprägungen von x i, also x i1 und x i2, dargestellt. Beide Dichten haben die gleiche Form, da jeweils ɛ i F gilt. Auf der x-achse sind die Schwellenwerte markiert. Die Fläche zwischen zwei Schwellenwerten unter der Dichtekurve gibt an mit welcher Wahrscheinlichkeit eine bestimmte Kategorie auftritt. Dadurch, dass die Dichtekurven aufgrund der unterschiedlichen Ausprägungen der Einflussgrößen auf den latenten Kontinuum verschoben sind, verändert sich die Wahrscheinlichkeit für eine bestimmte Responsekategorie bei Änderung von x i1 zu x i2. Zum Beispiel ist die Wahrscheinlichkeit für ein Subjekt mit Ausprägungen x i2 auf Kategorie 2 viel kleiner als die Wahrscheinlichkeit für ein Subjekt mit den Ausprägungen x i1 auf Kategorie 2, wie die grauen Flächen unter den Dichtekurven zwischen θ 1 und θ 2 zeigen. Aus (7) und (8) folgt die Definition des kumulativen Modells: P (Y i r x i ) = F (θ r + x T i β), r = 1,..., k Die Auftrittswahrscheinlichkeit einer Kategorie r wird definiert als: P (Y i = r x i ) = F (θ r + x T i β) F (θ r 1 + x T i β), r = 2,..., k 1 Abbildung 1: Schwellenwerte und Dichten der latenten Variable für die unterschiedlichen Designvektoren x i1 und x i2 (eigene Darstellung nach Fahrmeir et al. (2009): S. 243) 10
15 3.1 Kumulatives Modell 3 ORDINALE MODELLE Für die Verteilungsfunktion F von ɛ i können verschiedene Varianten verwendet werden. Für das kumulative Proportional-Odds Modell, welches im nächsten Abschnitt vorgestellt wird, gilt: P (Y i r x i ) = exp(θ r + x T i β) 1 + exp(θ r + x T i β) Die äquivalente Form dazu ist: log P (Y i r x i ) P (Y i > r x i ) = θ r + x T i β Wird für F jedoch die Minimum-Extremwertverteilung bzw. Gompertzverteilung F (x) = 1 exp( exp(x)) gewählt, so ergibt sich das kumulative Extremwertmodell bzw. Complementary Log-Log-Modell: Dieses ist äquivalent zu P (Y i r x i ) = 1 exp( exp(θ r + x T i β)) log( log(p (Y i > r x i ))) = θ r + x T i β Es wird auch als gruppiertes Cox - bzw. Proportional Hazards -Modell bezeichnet, da es in der Verweildaueranalyse Anwendung findet Definition des kumulativen Logit-Modells unter Proportionalitätsannahme Beim kumulativen Modell werden die Kategorien in zwei Gruppen aufgeteilt. Einmal in die Gruppe Y j und in die Gruppe Y > j. Die folgenden Definitionen basieren auf Agresti (2010) S sowie Agresti (2013) S.275. Die kumulativen Logits werden unter Verwendung der kumulativen Wahrscheinlichkeiten (9) wie folgt definiert: P (Y r) logit(p (Y r)) = log P (Y > r) = log P (Y r) 1 P (Y r) = log π π r π r π k mit r = 1,..., (k 1) = 1,..., q Mit Variation von r über alle möglichen Responsekategorien von Y ergeben sich k 1 verschiedene Logits. Der Vorteil dieser Logits zu den ursprünglichen mehrkategorialen Logits aus Kapitel ist, dass bei der Berechnung alle k Responsekategorien einfließen. Im Folgenden wird das Proportional-Odds Modell vorgestellt, welches alle k 1 kumulativen Logits in einem 11
16 3.1 Kumulatives Modell 3 ORDINALE MODELLE einzigen, sparsamen Modell verwendet und die erklärenden Variablen für die betrachtete Responsevariable mit einbezieht. Das Proportional-Odds Modell ist unter Berücksichtigung des Vektors der Kovariablen x = (x 1,..., x p ) definiert als: logit(p (Y r x)) = log ( ) P (Y r x) = α r + β T x = α r + β 1 x i1 + β 2 x i β p x ip P (Y > r x) mit r = 1,..., (k 1) Dabei hat jeder kumulative Logit einen eigenen Intercept α r, wobei sich P (Y r x) und somit die Intercepts bei steigendem r erhöhen. Zudem gilt α 0 = und α k =. Äquivalent dazu kann die Wahrscheinlichkeit für Y r definiert werden als: Für die Wahrscheinlichkeit von Y = r gilt: P (Y r x) = exp(α r + β T x) 1 + exp(α r + β T x) P (Y = r x) = P (Y r x) P (Y r 1 x) = exp(α r + β T x) 1 + exp(α r + β T x) exp(α r 1 + β T x) 1 + exp(α r 1 + β T x) (10) Beim Proportional-Odds Modell wird angenommen, dass für jeden Logit der Koeffizientenvektor β identisch ist. Dies führt zu einem sparsameren Modell als das mehrkategoriale Logit- Modell in Kapitel 2, welches für jeden Logit einen eigenen separaten Parameter annimmt. Zur Motivation des kumulativen Logit-Modells und zum besseren Verständnis seiner Interpretation wird zunächst angenommen, dass die einzige Einflussgröße eine stetige Variable x ist. Das Proportional-Odds Modell ist dann definiert als: logit(p (Y r x)) = α r + βx Abbildung 2 zeigt für eine ordinale Variable Y mit vier Kategorien die zugehörigen kumulativen Wahrscheinlichkeiten. Diese haben durch die Annahme der Proportionalität einen gleichen Kurvenverlauf, da der Parameter β als identisch angenommen wird. Die Größe von β gibt an wie stark die Kurve steigt bzw. fällt. Bei fixierten x sind die Werte der kumulierten Wahrscheinlichkeiten geordnet, wobei der Wert für P (Y 1) immer am kleinsten und für P (Y k 1) am größten ist. 12
17 3.1 Kumulatives Modell 3 ORDINALE MODELLE Abbildung 2: Darstellung der Wahrscheinlichkeiten des kumulativen Proportional-Odds Logit- Modell bei vier Kategorien der Zielvariablen Y (eigene Darstellung nach (Agresti (2010): S. 47)) Für s > r und s 1,..., k 1 entspricht der Kurvenverlauf von P (Y s) dem von P (Y r), wobei dieser um α s α r /β Einheiten verschoben ist. Je größer die Differenz zwischen α s und α r ist, desto größer ist der horizontale Abstand zwischen den Kurven. Zur Interpretation der Koeffizienten wird die Veränderung der Chance auf Y r zu Y > r bei Änderung des Wertes der einzigen Einflussvariable x von x 1 zu x 2, mit x 1 x 2, betrachtet: logit(p (Y r x 2 )) logit(p (Y r x 1 )) = log P (Y r x 2)/P (Y > r x 2 ) P (Y r x 1 )/P (Y > r x 1 ) = α r + βx 1 α r + βx 2 = β(x 2 x 1 ) (11) Der kumulative Log-Odds-Ratio ist also proportional zu der Distanz zwischen x 2 und x 1. Zur Interpretation wird exp(β(x 2 x 1 ))) betrachtet. Dieses besagt, dass die Chance für die Responsekategorie r oder niedriger im Verhältnis zu höheren Kategorien um den Faktor exp(β(x 2 x 1 )) bei einem positiven Vorzeichen steigt bzw. bei einem negativen Vorzeichen sinkt, wenn sich x 1 zu x 2 ändert. Beträgt die Distanz zwischen x 2 und x 1 gleich 1, so ändert sich die Chance um den Faktor exp(β). Formel (11) zeigt, dass die Odds unabhängig von den betrachteten Kategorien sind. Durch diese Eigenschaft erhält das Modell den Namen Proportional-Odds Modell Kumulatives Logit-Modell für Kontingenztabellen Die folgenden Ausführungen beruhen auf Agresti (2010) S Zur Vereinfachung wird nur eine einzige Einflussgröße betrachtet, welche kategorial ist. Somit wird der Prädiktor als Faktor in das Modell aufgenommen. Dargestellt in einer Kreuztabelle entsprechen die Zeilen den Ausprägungen der erklärenden Variablen X und die Spalten den Kategorien der Responsevariable Y. Im Fall einer nominal skalierten Prädiktorvariable mit Kategorien 1, 2,..., l erhalten die 13
18 3.1 Kumulatives Modell 3 ORDINALE MODELLE Logits die Form logit(p (Y r)) = α r + τ 1 z 1 + τ 2 z τ l 1 z l 1 mit r = 1,..., q und z j = 1, wenn es sich um eine Beobachtung aus Zeile j handelt, wobei gilt j 1,..., l. Ansonsten gilt z j = 0. Für die Identifizierbarkeit des Modells wird zudem τ l = 0 oder l i=1 τ j = 0 angenommen. Dabei entspricht τ j dem Effektparameter für Zeile j. Die Differenz zwischen den Effektparametern von Kategorie a zu b der ordinalen Variable X entsprechen dem kumulativen Log-Odds-Ratio für ordinale erklärende Variablen: logit(p (Y r X = b)) logit(p (Y r X = a)) = τ b τ a Der kumulative Log-Odds-Ratio für die Zeilen a und b ist für alle Kategorien r = 1,..., q identisch. Gilt τ 1 = τ 2 =... = τ l, so sind Y und X unabhängig. Ist die erklärende Variable ordinal, so ist es besser jeder Kategorie bzw. Zeile numerische Scores zuzuordnen, da damit die Ordnung der Kategorien beachtet wird. Diese Scores werden anschließend wie eine quantitative Variable behandelt. Sie werden im Folgenden als u j mit j = 1,..., l bezeichnet und sind geordnet in u 1 u 2... u l. Werden diese in das Logit-Modell aufgenommen, so wird das Modell logit(p (Y r X = u j )) = α r + βu j mit r = 1,..., q und j = 1,..., (l 1) erhalten. Für die Interpretation von β werden zwei Zeilen j und j + 1 mit j = 1,..., l 1 und die Differenz der Log-Odds betrachtet: logit(p (Y r X = u j+1 )) logit(p (Y r X = u j )) = β(u j+1 u j ) (12) Dieser sogenannte kumulative Log-Odds-Ratio ist proportional zur Distanz zwischen den Zeilen und für fixiertes j sind die Werte der Odds-Ratios über alle Kategorien 1,..., q identisch. Beträgt die Distanz zwischen u j und u j + 1 gleich 1, so vereinfacht sich (12) zu: logit(p (Y r X = u j+1 )) logit(p (Y r X = u j )) = β Bei gleicher Distanz zwischen den Zeilenscores wird dieses Modell mit nur einer ordinalen Einflussgröße und Zielgröße auch als kumulatives Logit Uniform Association Modell bezeichnet. 14
19 3.1 Kumulatives Modell 3 ORDINALE MODELLE Inferenz Die Erläuterungen zu der Inferenz über Modellparameter und Wahrscheinlichkeiten in diesem Abschnitt basieren auf Agresti (2010) S Wenn x i der Vektor mehrerer erklärender Variablen für Person i ist, so ist die Wahrscheinlichkeit von Kategorie r bei gegebenen x i gleich π r (x i ) = P (Y i = r X = x i ) = P (Y i r x i ) P (Y i r 1 x i ). Die Likelihood-Funktion des multinomialen Modells (2) erweitert sich dann im Fall einer ordinaler Responsevariable zu: L(β) = (10) = ( n k ) π r (x i ) y ir = i=1 i=1 r=1 r=1 ( n k ) [P (Y i r x i ) P (Y i r 1 x i )] y ir i=1 r=1 ( n k [ exp(αr + β T x i ) 1 + exp(α r + β T x i ) exp(α r 1 + β T ] yir ) x i ) 1 + exp(α r 1 + β T x i ) Zur Berechnung der Log-Likelihood-Funktion wird G(z) = exp(z) 1 + exp(z) g(z) = exp(z) (1 + exp(z)) 2 verwendet, woraus folgt: l(β) = ( n k ) g(α r + β T x i ) g(α r 1 + β T x i ) y ir x ik G(α r + β T x i ) G(α r 1 + β T x i ) i=1 r=1 Zur Lösung von s(β) = l(β)! = 0 wird der Fisher-Scoring-Algorithmus verwendet, ein iteratives Verfahren bei dem in jedem Schritt neu gewichtete kleinste Quadrate verwendet β werden. Bei jeder Iteration wird also die nicht konstante Varianz der Beobachtungen beachtet, indem die Gewichte variieren bis die Schätzung konvergiert. Bereits 1980 hat McCullagh in seinem Artikel Regression Models for Ordinal Data (siehe Peter McCullagh (1980)) gezeigt, dass bei einem suffizient großen Stichprobenumfang n ein einziges Maximum der Likelihood-Funktion erreicht wird. Zu beachten ist, dass für endliches n die Einzigartigkeit der Lösung nicht gewährleistet sein kann oder unendliche Koeffizienten geschätzt werden können. Um zu testen, ob eine Variable x j mit j 1,..., p Einfluss auf die Wahl der Responsekategorie hat, werden Nullhypothesen der Form H 0 : β j = 0 betrachtet. Wird als Testverfahren der Wald-Test verwendet, so wird für seine Testgröße z = ˆβ j /SE der Standardfehler SE benötigt. Zur Schätzung des Standardfehlers wird die Fisher-Informationsmatrix verwendet. Die Informationsmatrix hat zwei mögliche Versionen. Zum einen gibt es die beobachtete Fisher- 15
20 3.1 Kumulatives Modell 3 ORDINALE MODELLE Informationsmatrix (vgl. Fahrmeir et al. (2009) S. 469) F obs (β) = 2 l(β) β β T und zum anderen die erwartete Fisher-Informationsmatrix (vgl. Fahrmeir et al. (2009): S. 470) F (β) = E(F obs (β)) = E ( ) 2 l(β) β β T Das Inverse der erwarteten Informationsmatrix fließt beim Fisher-Scoring-Algorithmus ein. Wird stattdessen die beobachtete Fisher-Informationsmatrix benutzt, so wird der Newton-Raphson-Algorithmus verwendet. Die Standardfehler ergeben sich aus der Wurzel der Diagonalelemente beider Versionen von Informationsmatrizen. Somit kann der Wald-Test zum Testen der Nullhypothese H 0 : β j = 0 angewendet werden. Unter H 0 wird z als approximativ χ 2 (df = 1)- verteilt angenommen. Allerdings weißt Agresti darauf hin, dass bei der Anwendung des Tests die Stichprobengröße nicht zu klein sein und kein großer Anteil der Beobachtungen in die höchste oder niedrigste Kategorie der Responsevariable fallen sollte (siehe Agresti (2010): S. 60). Dann kann die Annahme, dass ( ˆβ j β j )/SE standardnormalverteilt ist, nicht mehr erfüllt sein und es sollte auf einen Likelihood-Ratio-Test zurückgegriffen werden. Er spezifiziert allerdings nicht, ab welcher Anzahl der Beobachtungen und welchem Anteil dies der Fall ist. Für die Teststatistik des Likelihood-Ratio-Tests gilt: LR = 2(L 0 L 1 ) (13) L 0 ist die maximierte Log-Likelihood-Funktion unter Annahme der Nullhypothese und L 1 die maximierte Log-Likelihood-Funktion ohne Einschränkung. Die Teststatistik ist unter Annahme der Nullhypothese wie beim Wald-Test approximativ χ 2 (df = 1) verteilt Methoden zur Modellüberprüfung Liegen die Daten als Kreuztabelle vor, so ist ein Test der Anpassungsgüte durch eine Pearsonoder Likelihood-Ratio-Statistik möglich. Diese testen das vorhandene Modell gegen ein Modell, welches die Daten perfekt fittet. Für die Tests wird die beobachtete Anzahl in einer Zelle der Tabelle mit der erwarteten Anzahl im perfekt gefitteten Modell verglichen. Die folgenden Spezifikationen beruhen auf Agresti (2010) S Wenn n i die Anzahl an Beobachtungen für einen Vektor der Einflussgrößen x i und n ir mit r = 1,..., k die beobachtete Anzahl für die 16
21 3.1 Kumulatives Modell 3 ORDINALE MODELLE r-te Responsekategorie sind, dann wird die erwartete Anzahl folgendermaßen geschätzt: µ ˆ ir = n i ˆP (Y = r xi ) mit r = 1,..., k Die Pearson-Statistik zum Test der Anpassungsgüte unter Verwendung der geschätzten erwarteten Anzahl wird definiert als: χ 2 = n k (n ir µ ˆ ir ) 2 ˆ i=1 r=1 µ ir Daraus folgt die Likelihood-Ratio-Statistik: G 2 = 2 n i=1 k r=1 n ir log n ir ˆ µ ir Unter der Nullhypothese sind sowohl die Pearson-Statistik als auch die Likelihood-Ratio-Statistik χ 2 -verteilt. Die Anzahl der Freiheitsgrade ergibt sich aus der Differenz der Anzahl der modellierten kumulativen Logits zu der Zahl der Modellparameter. Die Anzahl der modellierten kumulativen Logits erhält man aus der Anzahl der multinomialen Parameter im perfekt gefitteten Modell, also (k 1)-mal die Anzahl der Kategorien der erklärenden Variable. In einer (l x k)-kontingenztabelle wären dies also l(k 1) Parameter. Im Fall einer ordinalen Einflussgröße mit dem Logits logit(p (Y r X = j)) = α r + βu j mit r = 1,..., q ist die Anzahl der Modellparameter gleich q + 1 = k. Somit ergeben sich die Freiheitsgrade in diesem Fall als df = l(k 1) k = lk l k. Ist die kategoriale Einflussgröße nicht geordnet, dann werden die Logits logit(p (Y r X = j)) = α r + τ j betrachtet. In diesem Fall sind es (k 1) + (l 1) Modellparameter. Somit werden für die χ 2 -Verteilung df = l(k 1) ((k 1) + (l 1)) = (l 1)(k 2) Freiheitsgrade betrachtet. In Abschnitt wurde bereits erwähnt, dass bei Daten mit wenigen Beobachtungen oder einer Verteilung der Beobachtungen auf wenige Kategorien unendliche Koeffizienten geschätzt werden könnten. In diesem Fall ist die Anwendung eines globalen Goodness of Fit-Tests nicht möglich. Es kann aber auf eine Pearson-Statistik zurückgegriffen werden, welche die ursprünglichen, ungruppierten Daten verwendet. Genauere Informationen dazu befinden sich in Lipsitz et al. (1996). Sind die Einflussgrößen nicht qualitativ, sondern stetig, so kann der oben beschriebenen Goodness of Fit-Test nicht angewendet werden. Um trotzdem zu testen, wie gut das Modell die Daten fittet, kann auf den Vergleich zu alternativen, komplexeren Modellen zurückgegriffen werden. Wird nur eine Einflussgröße betrachtet, so kann dessen Fit zum Beispiel mit einem Modell 17
22 3.1 Kumulatives Modell 3 ORDINALE MODELLE unter zusätzlicher quadratischer Aufnahme der Einflussgröße verglichen werden. Falls mehrere Einflussgrößen in das Modell aufgenommen werden, kann zum Vergleich ein Modell mit zusätzlicher Aufnahme von Interaktionstermen verwendet werden. Ob das größere, komplexere Modell mit zusätzlichen Term(en) einen besseren Fit bewirkt, kann anhand eines Likelihood- Ratio-Tests, wie er bereits in Abschnitt vorgestellt wurde, beurteilt werden. Dessen Teststatistik LR = 2(L 0 L 1 ) ist approximativ χ 2 -verteilt mit der Anzahl an zusätzlichen Parametern des komplexeren Modells als Freiheitsgrade. Ein kleiner p-wert besagt, dass das einfachere Modell verworfen werden sollte. Alternativ kann auch das Akaike Information Criterion, kurz AIC, betrachtet werden (vgl. Agresti (2010): S. 75)). Dieses ist definiert als (vgl. Fahrmeir et al. (2009): S. 206) AIC = 2(l( ˆβ) p) mit p als Anzahl an Parametern im Modell. Der Vorteil des AICs ist, dass die Zahl der Parameter bei der Berechnung einfließt und mit steigender Anzahl ein höheres AIC zur Folge hat. Sparsame Modelle können ebenfalls eine den wahren Werten nahe Schätzung liefern und sind dabei einfacher in ihrer Berechnung. Ist die Anzahl an Parametern identisch, so kann auch die Devianz (vgl. Tutz (2012): S. 67) n D = 2φ (l( ˆβ) l(y)) als Vergleichskriterium verwendet werden, mit φ als zugehöriger Dispersionsparameter. i= Erweiterung des kumulativen Logit-Modells Häufig ist die Annahme der Proportionalität nicht angemessen und statt eines einzigen Parametervektors β für alle Kategorien der Zielgröße, sollte für jede Responsekategorie ein eigenes β r mit r = 1,..., q geschätzt werden. Somit ergibt sich ein komplexeres Logit-Modell nach Agresti (2010) S. 70f.. Dieses wird definiert als: logit(p (Y r)) = α r + β T r x Das um (k 2) Parameter erweiterte Modell hat jedoch das strukturelle Problem, dass es vor allem bei einer großen Anzahl an Prädiktoren nicht verwendet werden kann, da die Maximierung der Likelihood-Funktion und damit die Schätzung der Parameter zu komplex ist. Um zu testen, ob ein Modell ohne Annahme der Proportionalität verwendet werden sollte, kann ein Score- 18
23 3.1 Kumulatives Modell 3 ORDINALE MODELLE Test durchgeführt werden. Dieser liefert asymptotisch ähnliche Ergebnisse wie der Wald- und Likelihood-Ratio-Test. Er hat aber den Vorteil, dass er nur die Log-Likelihood-Funktion unter der Nullhypothese H 0 : β 1 = β 2 =... = β q betrachtet und nicht die Funktion unter der komplexen Alternative. Ist der p-wert größer als 0.05, so kann angenommen werden, dass das komplexere Modell keinen signifikant besseren Fit liefert. Dieser Wert gibt jedoch nur Auskunft über die statistische Signifikanz, reflektiert aber nicht die Praktikabilität. Deshalb wird trotz Tests häufig das einfachere Modell wegen seiner Sparsamkeit bevorzugt. Das Ergebnis des Score-Tests ist zudem fragwürdig bei Daten mit wenigen Gesamtbeobachtungen oder wenn ein großer Teil der Beobachtungen in wenige Responsekategorien fallen. Einen besonderen Fall bildet das kumulative Partial-Proportional-Odds Logit-Modell. Dieses beinhaltet sowohl Einflussgrößen x mit Annahme von Koeffizienten mit Proportional-Odds Struktur als auch Kovariablen mit kategoriespezifischen Koeffizienten. Letztere werden im Folgenden im Vektor u zusammengefasst. Das Modell wird dann nach Agresti (2010) S. 78 als logit(p (Y r)) = α r + β T x + γ T r u (14) mit r = 1,..., q definiert. Zur Identifizierbarkeit wird angenommen, dass γ 1 = 0 gilt, wobei ein anderes γ r auch gewählt werden kann. Bei der Interpretation sollte beachtet werden, dass die Parameter des Vektors β (ohne Proportionalitätsannahme) wie bisher im kumulativen Logit- Modell für jede Kategorie identisch interpretiert werden. Bei Annahme kategoriespezifischer Parameter γ r ergibt sich für jede Kategorie eine eigene Interpretation der Wirkung der betrachteten Einflussgrößen. Gilt γ 2 =... = γ q, so wird das gewöhnliche Proportional-Odds Modell angenommen. 19
24 3.2 Adjacent-Type Modell 3 ORDINALE MODELLE 3.2 Adjacent-Type Modell In Kapitel 3.1. wurde das kumulative Logit-Modell vorgestellt, welches durch Verwendung der kumulierten Wahrscheinlichkeiten die Ordnung der Responsekategorien beachtet. Eine Alternative dazu ist das Adjacent-Category Logit-Modell. Dieses verwendet nicht die kumulierten Logits, sondern paarweise, lokale Logits (vgl. Agresti (2010): S. 96). Im Folgenden wird dieses Modell zunächst mit und ohne Annahme von Proportional-Odds sowie deren Verbindung zum multinomialen Logit-Modell vorgestellt. Danach wird das resultierende Modell für eine kategoriale Einflussgröße und die Inferenz erläutert. Die Definitionen und ihre Ergänzungen dieses Kapitels basieren auf Agresti (2010) S Definition des Adjacent-Type Logit-Modells Sind die multinomialen Wahrscheinlichkeiten π r (x) für die Responsevariable Y mit Kategorien 1,..., k, wie beim kumulativen Modell (10), als π r (x) = P (Y = r x) = exp(α r + β T x) mit r = 1,..., k 1 + exp(α r + β T x) gegeben, dann sind die Adjacent-Category Logits mit Annahme der Proportionalität definiert als: logit(p (Y = r Y = r oder Y = r + 1, x)) = log mit r = 1,..., k 1 ( ) πr+1 (x) = α r + β T x π r (x) In diesem Modell werden also zwei benachbarte Kategorien r und r + 1 beachtet, sodass nicht von einem kumulativen Odds-Ratio, sondern von einem lokalen Odds-Ratio gesprochen wird. β T x gibt die Präferenz für die Kategorie r + 1 im Gegensatz zu der Kategorie r an. Für jeden Logit ergibt sich, unter Annahme, dass die erklärende Variable einen ähnlichen Effekt für jede Responsekategorie hat, ein einziges β, statt k 1 unterschiedlichen Parametervektoren für jede Betrachtung benachbarter Kategorien. Zur Interpretation des Einflusses einer Variable x j mit j = 1,..., p auf die Chance einer Responsekategorie r + 1 zu r, wird exp(β j ) betrachtet. Die Chance auf ein höhere Kategorie r + 1 zu einer niedrigeren Stufe r entspricht dem Faktor exp(β j ), wenn die j-te Einflussvariable um eine Einheit steigt. Dieses Chanceverhältnis bzw. dieser Odds-Ratio ist für alle Paare benachbarter Kategorien von Y identisch, also unabhängig von r, sodass β j = β j1 =... = β jk gilt. Das Vorzeichen von β j gibt an, ob bei steigenden x j niedrigere oder höhere Kategorien getroffen werden. Gilt β j > 0 so fällt Y eher in höhere Kategorien und für β j < 0 eher in niedrigere. 20
25 3.2 Adjacent-Type Modell 3 ORDINALE MODELLE Eine Erweiterung des Modells mit Proportionalitätsannahme ist die Annahme eines eigenen Koeffizientenvektors β r für jede Kategorie r 1,..., k, sodass für das Logit-Modell folgt: log ( ) πr+1 (x) = α r + β T r x mit r = 2,..., k (15) π r (x) Proportional-Odds können aber auch nur für einen Teil der Einflussgrößen, aber nicht bei allen, angenommen werden. Dieses Modell wird als Partial-Proportional-Odds Modell bezeichnet und ist analog zum Partial-Proportional-Odds Modell (14) bei der Verwendung kumulierter Logits. Zum Test der Proportionalitätsannahme können die gleichen Tests wie beim kumulativen Modell verwendet werden Verbindung zum multinomialen Logit-Modell In Kapitel wurde das multinomiale Logit-Modell vorgestellt. Dieses missachtet die Ordnung der Kategorien bei ordinalen Responsevariablen. Zur Definition benötigt es die Wahl einer Referenzkategorie. Wird als Referenz die erste Ausprägung gewählt, so erhält man als Logits log π 2 π 1, log π 3 π 1,..., log π k 1 π 1, log π k π 1 für das multinomiale Logit-Modell. Folgende Umformung zeigt die Verbindung zu den Adjacent-Category Logits (vgl. Agresti (2010): S. 91): log π r π 1 = log π 2 π 1 + log π 3 π log π r π r 1 mit r = 2,..., k Zusammen mit (15) folgt das mehrkategoriale Logit-Modell: log π r(x) π 1 (x) = α 1 + β T 1 x + α 2 + β T 2 x α r 1 + β T r 1x ( r 1 r 1 ) = α s + β T s x = αr + β T r x mit r = 2,..., k s=1 s=1 (16) Unter Proportionalitätsannahme für alle Parameter vereinfacht sich das Modell zu log π r 1 r(x) π 1 (x) = α s + (r 1)β T x = αr + β T z r, r = 2,..., k (17) s=1 mit z r = (r 1)x. Die Logits des mehrkategorialen Logit-Modells können also durch Adjacent- Type Logits ersetzt werden, allerdings wird dann die Designmatrix x durch den Vektor z r ersetzt. 21
26 3.2 Adjacent-Type Modell 3 ORDINALE MODELLE Adjacent-Type Logit-Modell für Kontingenztabellen Wird eine einzige Einflussgröße X mit l Kategorien betrachtet, so ergibt sich eine (l x k)- Kontingenztabelle (vgl. Agresti (2010): S. 90). Die konditionale Wahrscheinlichkeit ist dann gegeben durch π r j = P (Y = r X = j) mit r = 1,..., k 1 und j = 1,..., l 1. Im ersten Fall wird die Einflussgröße X als ordinal angenommen. Die geordneten Reihenscores von X werden im Folgenden als u j mit j = 1,..., l 1 bezeichnet. Um die Ordnung der Reihen nun in der proportionalen Form zu beachten, kann ähnlich wie bei Formel (12) logit(p (Y = r Y = r oder Y = r + 1)) = log π r+1 j π r j = α r + βu j r = 1,..., k 1 verwendet werden. Für die Interpretation von β werden zwei Zeilen j+1 und j und die Differenz ihrer Logits betrachtet: logit(p (Y = r X = j + 1)) logit(p (Y = r X = j)) = β(u j+1 u j ) Ist die Distanz zwischen den Reihenscores identisch, so erfüllt das Modell die Uniform Association für lokale Odds-Ratios. Falls gilt u j+1 u j = 1, so ist der uniforme lokale Odds-Ratio gleich exp(β). Im zweiten Fall wird von einem nominalen X mit ungeordneten Kategorien 1,..., l ausgegangen. Es kann ein generelleres Row Effects Modell definiert werden, bei dem statt den Parametern βu j die ungeordneten Parameter τ j auftreten mit j = 1,..., l: logit(p (Y = r Y = r oder Y = r + 1)) = log π r+1 j π r j = α r + τ j mit r = 2,..., k Für die Interpretation des Einflusses wird wieder die Differenz betrachtet: logit(p (Y = r X = j + 1)) logit(p (Y = r X = j)) = τ j+1 τ j Für zwei Paare von Reihen sind die k 1 Log-Odds-Ratios identisch Inferenz Die Spezifikationen der Inferenz basieren auf Agresti (2010) S. 92 ff.. Für Subjekt i ist y ir der binäre Indikator, ob der Response sich in der Kategorie r befindet und x ij mit j 1,..., p ist der Wert der erklärenden Variable mit x i = (x i1,..., x ip ) T. Mit der Annahme von n unabhängigen 22
27 3.2 Adjacent-Type Modell 3 ORDINALE MODELLE Beobachtungen ist die Log-Likelihood-Funktion über alle n Beobachtungen definiert als: log [ n k ] π r (x i ) y ir = i=1 r=1 = i=1 n i=1 r=2 [ k 1 ( y ir logπ r (x i ) + 1 r=2 ) ] k y ir logπ 1 (x i ) r=2 [ n k ] y ir log π r(x i ) π 1 (x i ) + logπ 1(x i ) Für das Modell unter Annahme der Proportionalität ergibt sich die Log-Likelihood für das Adjacent-Category Modell mit (17) zu: log [ n k ] π r (x i ) y ir = i=1 r=1 [ n k ( y ir (αr + β T z ir ) + log 1 + i=1 r=2 )] k αr + β T z ir r=2 mit z ir = (r 1)x i und mit kategoriespezifischen Parametern (siehe (16)) als: log [ n k ] π r (x i ) y ir = i=1 r=1 [ n k ( y ir (αr + β T r x i ) + log 1 + i=1 r=2 k r=2 α r + β T r x i )] Wie beim kumulativen Modell kann auch hier ein Test auf Anpassungsgüte für Kontingenztabellen durch einen Pearson-Test oder durch einen Likelihood-Ratio-Test erfolgen. Fittet das Modell die Daten schlecht, so können weitere Terme zum Beispiel Interaktionsterme hinzugefügt oder im Fall der Annahme von Proportionalität kategoriespezifische Parameter zugelassen werden. Eine Besonderheit des Adjacent-Category Logit-Modells ist, dass bei ihm im Gegensatz zu dem kumulativen Modell die erwartete Fisher-Matrix für β (bzw. β r ) gleich der beobachteten Fisher-Matrix ist, also F (β) = F obs (β) gilt. Die Fisher-Matrix wird anhand von F (β) = ( 2 l(β))/( β β T ) = E( ( 2 l(β))/( β β T )) erhalten. Zur Schätzung der Parameter wird wie beim kumulativen Modell der Fisher-Scoring-Algorithmus verwendet. Dieser entspricht durch die Äquivalenz der erwarteten und beobachteten Fisher-Information dem Newton-Raphson- Verfahren. Weitere Gemeinsamkeiten und Unterschiede des kumulativen und des Adjacent-Category Logit- Modells werden im nächsten Kapitel anhand des Allbus-Datensatzes veranschaulicht. 23
28 4 VERGLEICH DER METHODEN 4 Vergleich der Methoden Anhand der Definitionen des kumulativen und des Adjacent-Category Modells aus Kapitel 3 zeigen sich einige Parallelen und Unterschiede der beiden Verfahren. Während das kumulative Modell auf kumulierten Logits basiert, werden beim Adjacent-Category Modell die lokalen Logits benachbarter Kategorien betrachtet. Für letzteres Modell gilt, im Gegensatz zum kumulativen Modell, dass die beobachtete Fisher-Informationsmatrix äquivalent zu ihrem Erwartungswert ist. Für beide Modelle können flexible Annahmen über die Proportionalität der Koeffizienten getroffen werden, sodass Partial-Proportional-Odds Modelle gebildet werden können. Für den Test der Proportionalitätsannahme und des Modellfits können die gleichen Teststatistiken und Kennzahlen verwendet werden. Um weitere Unterschiede und Gemeinsamkeiten der beiden Verfahren aufzudecken, wurde das Vertrauen in die Regierung und das Vertrauen in die Mitmenschen des sogenannten Allbus- Datensatzes sowohl durch ein kumulatives als auch durch ein Adjacent-Category Logit-Modell gefittet. Dazu wurde zunächst durch einen Likelihood-Ratio-Test die Proportional-Odds Annahme überprüft. Die Anpassungsgüte wird anhand des AIC Kriteriums und der Devianz verglichen. Zur Berechnung wurde das VGAM Package in R verwendet, welches nun zunächst erläutert wird. Der Allbus-Datensatz und die Ergebnisse der Modellierung der Vertrauensskalen durch beide Verfahren werden in Abschnitt 4.2 vorgestellt. 4.1 VGAM Package Für die Berechnung des Adjacent-Type und des kumulativen Modells wurde die Funktion vglm() verwendet, welche in dem Package VGAM implementiert ist. Die folgenden Erläuterungen basieren auf Yee (2010) S. 1 f. und Yee (2016) S.727 f.. Die Funktion vglm() bietet den Vorteil, dass es durch die flexible Spezifikation des family -Arguments für das Fitten beider Modelle verwendet werden kann. In R sind zwar noch weitere Funktionen zur Modellierung von kategorialen Daten vorhanden, diese sind aber entweder nur für eine Linkfunktion implementiert oder benötigen vorherige Prozesse oder Startwerte zur Berechnung. Beispiele wären die Funktionen polr() aus dem Package MASS, welches nur Proportional-Odds Modelle fittet, und multinom() aus dem Paket nnet für multinomiale Logit-Modelle. Diese sind im Comprehensive R Archive Network (kurz: CRAN) zu finden. Zudem gibt es noch weitere Funktionen von nicht-cran Paketen wie die Funktion nordr() aus dem Package gnlm. Dieses fittet zwar das Proportional-Odds und das Adjacent-Category Modell, zur Anwendung werden aber Startwerte benötigt. Deshalb wird das VGAM Package mit der Funktion vglm() bevorzugt. 24
Kapitel 4: Binäre Regression
 Kapitel 4: Binäre Regression Steffen Unkel (basierend auf Folien von Nora Fenske) Statistik III für Nebenfachstudierende WS 2013/2014 4.1 Motivation Ausgangssituation Gegeben sind Daten (y i, x i1,...,
Kapitel 4: Binäre Regression Steffen Unkel (basierend auf Folien von Nora Fenske) Statistik III für Nebenfachstudierende WS 2013/2014 4.1 Motivation Ausgangssituation Gegeben sind Daten (y i, x i1,...,
2.Tutorium Generalisierte Regression
 2.Tutorium Generalisierte Regression - Binäre Regression - Moritz Berger: 04.11.2013 und 11.11.2013 Shuai Shao: 06.11.2013 und 13.11.2013 Institut für Statistik, LMU München 1 / 16 Gliederung 1 Erweiterte
2.Tutorium Generalisierte Regression - Binäre Regression - Moritz Berger: 04.11.2013 und 11.11.2013 Shuai Shao: 06.11.2013 und 13.11.2013 Institut für Statistik, LMU München 1 / 16 Gliederung 1 Erweiterte
Schätzverfahren ML vs. REML & Modellbeurteilung mittels Devianz, AIC und BIC. Referenten: Linda Gräfe & Konstantin Falk
 Schätzverfahren ML vs. REML & Modellbeurteilung mittels Devianz, AIC und BIC Referenten: Linda Gräfe & Konstantin Falk 1 Agenda Schätzverfahren ML REML Beispiel in SPSS Modellbeurteilung Devianz AIC BIC
Schätzverfahren ML vs. REML & Modellbeurteilung mittels Devianz, AIC und BIC Referenten: Linda Gräfe & Konstantin Falk 1 Agenda Schätzverfahren ML REML Beispiel in SPSS Modellbeurteilung Devianz AIC BIC
Statistische Modellierung Merkblatt
 Inhaltsverzeichnis Statistische Modellierung Merkblatt Welches Modell nimmt man wann?... 1 Logit:... 2 Probit:... 2 Poisson:...2 Loglinear:... 2 multinomiales Logit:... 2 Ordinales Logit (PROC LOGISTIC
Inhaltsverzeichnis Statistische Modellierung Merkblatt Welches Modell nimmt man wann?... 1 Logit:... 2 Probit:... 2 Poisson:...2 Loglinear:... 2 multinomiales Logit:... 2 Ordinales Logit (PROC LOGISTIC
1 Gemischte Lineare Modelle
 1 Gemischte Lineare Modelle Wir betrachten zunächst einige allgemeine Aussagen für Gemischte Lineare Modelle, ohne zu tief in die mathematisch-statistische Theorie vorzustoßen. Danach betrachten wir zunächst
1 Gemischte Lineare Modelle Wir betrachten zunächst einige allgemeine Aussagen für Gemischte Lineare Modelle, ohne zu tief in die mathematisch-statistische Theorie vorzustoßen. Danach betrachten wir zunächst
Übung zur Empirischen Wirtschaftsforschung V. Das Lineare Regressionsmodell
 Universität Ulm 89069 Ulm Germany Dipl.-WiWi Christian Peukert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2010
Universität Ulm 89069 Ulm Germany Dipl.-WiWi Christian Peukert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2010
Bivariate Kreuztabellen
 Bivariate Kreuztabellen Kühnel, Krebs 2001 S. 307-342 Gabriele Doblhammer: Empirische Sozialforschung Teil II, SS 2004 1/33 Häufigkeit in Zelle y 1 x 1 Kreuztabellen Randverteilung x 1... x j... x J Σ
Bivariate Kreuztabellen Kühnel, Krebs 2001 S. 307-342 Gabriele Doblhammer: Empirische Sozialforschung Teil II, SS 2004 1/33 Häufigkeit in Zelle y 1 x 1 Kreuztabellen Randverteilung x 1... x j... x J Σ
Bivariater Zusammenhang in der Mehrfeldertafel PEΣO
 Bivariater Zusammenhang in der Mehrfeldertafel PEΣO 9. November 2001 Bivariate Häufigkeitsverteilungen in Mehrfeldertabellen In der Mehrfeldertabelle werden im Gegensatz zur Vierfeldertabelle keine dichotomen
Bivariater Zusammenhang in der Mehrfeldertafel PEΣO 9. November 2001 Bivariate Häufigkeitsverteilungen in Mehrfeldertabellen In der Mehrfeldertabelle werden im Gegensatz zur Vierfeldertabelle keine dichotomen
Unterlagen zu Fisher s Exact Test, Vergleich von Anteilswerten und logistischer Regression. Robin Ristl. Wintersemester 2012/13
 Unterlagen zu Fisher s Exact Test, Vergleich von Anteilswerten und logistischer Regression Robin Ristl Wintersemester 2012/13 1 Exakter Test nach Fisher Alternative zum Chi-Quadrat Unabhängigkeitstest
Unterlagen zu Fisher s Exact Test, Vergleich von Anteilswerten und logistischer Regression Robin Ristl Wintersemester 2012/13 1 Exakter Test nach Fisher Alternative zum Chi-Quadrat Unabhängigkeitstest
Multinomiale logistische Regression
 Multinomiale logistische Regression Die multinomiale logistische Regression dient zur Schätzung von Gruppenzugehörigkeiten bzw. einer entsprechenden Wahrscheinlichkeit hierfür, wobei als abhänginge Variable
Multinomiale logistische Regression Die multinomiale logistische Regression dient zur Schätzung von Gruppenzugehörigkeiten bzw. einer entsprechenden Wahrscheinlichkeit hierfür, wobei als abhänginge Variable
Zusammenhangsanalyse in Kontingenztabellen
 Zusammenhangsanalyse in Kontingenztabellen Bisher: Tabellarische / graphische Präsentation Jetzt: Maßzahlen für Stärke des Zusammenhangs zwischen X und Y. Chancen und relative Chancen Zunächst 2 2 - Kontingenztafel
Zusammenhangsanalyse in Kontingenztabellen Bisher: Tabellarische / graphische Präsentation Jetzt: Maßzahlen für Stärke des Zusammenhangs zwischen X und Y. Chancen und relative Chancen Zunächst 2 2 - Kontingenztafel
Multivariate Statistik
 Hermann Singer Multivariate Statistik 1 Auflage 15 Oktober 2012 Seite: 12 KAPITEL 1 FALLSTUDIEN Abbildung 12: Logistische Regression: Geschätzte Wahrscheinlichkeit für schlechte und gute Kredite (rot/blau)
Hermann Singer Multivariate Statistik 1 Auflage 15 Oktober 2012 Seite: 12 KAPITEL 1 FALLSTUDIEN Abbildung 12: Logistische Regression: Geschätzte Wahrscheinlichkeit für schlechte und gute Kredite (rot/blau)
Kategorielle Daten. Seminar für Statistik Markus Kalisch
 Kategorielle Daten Markus Kalisch 1 Phase 3 Studie: Wirksamer als Placebo? Medikament Placebo Total Geheilt 15 9 24 Nicht geheilt 10 11 21 Total 25 20 45 Grundfrage: Sind Heilung und Medikamentengabe unabhängig?
Kategorielle Daten Markus Kalisch 1 Phase 3 Studie: Wirksamer als Placebo? Medikament Placebo Total Geheilt 15 9 24 Nicht geheilt 10 11 21 Total 25 20 45 Grundfrage: Sind Heilung und Medikamentengabe unabhängig?
8. Februar 2007. 5. Bei Unterschleif gilt die Klausur als nicht bestanden und es erfolgt eine Meldung an das Prüfungsamt.
 L. Fahrmeir, C. Belitz Department für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit Wahlfach Statistik 8. Februar 2007 Hinweise:
L. Fahrmeir, C. Belitz Department für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit Wahlfach Statistik 8. Februar 2007 Hinweise:
Generalisierte lineare Modelle. Statistik 3 im Nebenfach. Binäre Regressionsmodelle. 4.1 Binäre Regression
 Generalisierte lineare Modelle Statistik 3 im Nebenfach Friedrich Leisch Institut für Statistik Ludwig-Maximilians-Universität München WS 2010/2011 basierend auf Fahrmeir, Kneib & Lang (2007) 4 Generalisierte
Generalisierte lineare Modelle Statistik 3 im Nebenfach Friedrich Leisch Institut für Statistik Ludwig-Maximilians-Universität München WS 2010/2011 basierend auf Fahrmeir, Kneib & Lang (2007) 4 Generalisierte
Klausur zur Vorlesung Statistik III für Studenten mit dem Wahlfach Statistik
 Ludwig Fahrmeir, Nora Fenske Institut für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit dem Wahlfach Statistik 29. März 21 Hinweise:
Ludwig Fahrmeir, Nora Fenske Institut für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit dem Wahlfach Statistik 29. März 21 Hinweise:
Berechnung des LOG-RANK-Tests bei Überlebenskurven
 Statistik 1 Berechnung des LOG-RANK-Tests bei Überlebenskurven Hans-Dieter Spies inventiv Health Germany GmbH Brandenburger Weg 3 60437 Frankfurt hd.spies@t-online.de Zusammenfassung Mit Hilfe von Überlebenskurven
Statistik 1 Berechnung des LOG-RANK-Tests bei Überlebenskurven Hans-Dieter Spies inventiv Health Germany GmbH Brandenburger Weg 3 60437 Frankfurt hd.spies@t-online.de Zusammenfassung Mit Hilfe von Überlebenskurven
Lösungen zu den Übungsaufgaben in Kapitel 10
 Lösungen zu den Übungsaufgaben in Kapitel 10 (1) In einer Stichprobe mit n = 10 Personen werden für X folgende Werte beobachtet: {9; 96; 96; 106; 11; 114; 114; 118; 13; 14}. Sie gehen davon aus, dass Mittelwert
Lösungen zu den Übungsaufgaben in Kapitel 10 (1) In einer Stichprobe mit n = 10 Personen werden für X folgende Werte beobachtet: {9; 96; 96; 106; 11; 114; 114; 118; 13; 14}. Sie gehen davon aus, dass Mittelwert
Tutorial: Vergleich von Anteilen
 Tutorial: Vergleich von Anteilen Die Sicherung des Pensionssystems ist in vielen Ländern ein heikles Thema. Noch stärker als der Streit, wer wann welche Pension beziehen können soll, tobt ein Streit, welche
Tutorial: Vergleich von Anteilen Die Sicherung des Pensionssystems ist in vielen Ländern ein heikles Thema. Noch stärker als der Streit, wer wann welche Pension beziehen können soll, tobt ein Streit, welche
Bivariate Zusammenhänge
 Bivariate Zusammenhänge Tabellenanalyse: Kreuztabellierung und Kontingenzanalyse Philosophische Fakultät Institut für Soziologie Berufsverläufe und Berufserfolg von Hochschulabsolventen Dozent: Mike Kühne
Bivariate Zusammenhänge Tabellenanalyse: Kreuztabellierung und Kontingenzanalyse Philosophische Fakultät Institut für Soziologie Berufsverläufe und Berufserfolg von Hochschulabsolventen Dozent: Mike Kühne
Fortgeschrittene Statistik Logistische Regression
 Fortgeschrittene Statistik Logistische Regression O D D S, O D D S - R A T I O, L O G I T T R A N S F O R M A T I O N, I N T E R P R E T A T I O N V O N K O E F F I Z I E N T E N, L O G I S T I S C H E
Fortgeschrittene Statistik Logistische Regression O D D S, O D D S - R A T I O, L O G I T T R A N S F O R M A T I O N, I N T E R P R E T A T I O N V O N K O E F F I Z I E N T E N, L O G I S T I S C H E
Aufgabenblock 4. Da Körpergröße normalverteilt ist, erhalten wir aus der Tabelle der t-verteilung bei df = 19 und α = 0.05 den Wert t 19,97.
 Aufgabenblock 4 Aufgabe ) Da s = 8. cm nur eine Schätzung für die Streuung der Population ist, müssen wir den geschätzten Standardfehler verwenden. Dieser berechnet sich als n s s 8. ˆ = = =.88. ( n )
Aufgabenblock 4 Aufgabe ) Da s = 8. cm nur eine Schätzung für die Streuung der Population ist, müssen wir den geschätzten Standardfehler verwenden. Dieser berechnet sich als n s s 8. ˆ = = =.88. ( n )
b) Bestimmen Sie die Varianz der beiden Schätzer. c) Ist ein oder sind beide Schätzer konsistent? Begründen Sie!
 Aufgabe 1 (3 + 3 + 2 Punkte) Ein Landwirt möchte das durchschnittliche Gewicht von einjährigen Ferkeln bestimmen lassen. Dies möchte er aus seinem diesjährigen Bestand an n Tieren schätzen. Er kann dies
Aufgabe 1 (3 + 3 + 2 Punkte) Ein Landwirt möchte das durchschnittliche Gewicht von einjährigen Ferkeln bestimmen lassen. Dies möchte er aus seinem diesjährigen Bestand an n Tieren schätzen. Er kann dies
Chi-Quadrat Verfahren
 Chi-Quadrat Verfahren Chi-Quadrat Verfahren werden bei nominalskalierten Daten verwendet. Die einzige Information, die wir bei Nominalskalenniveau zur Verfügung haben, sind Häufigkeiten. Die Quintessenz
Chi-Quadrat Verfahren Chi-Quadrat Verfahren werden bei nominalskalierten Daten verwendet. Die einzige Information, die wir bei Nominalskalenniveau zur Verfügung haben, sind Häufigkeiten. Die Quintessenz
Wiederholung Hypothesentests Zusammenfassung. Hypothesentests. Statistik I. Sommersemester Statistik I Hypothesentests I (1/36)
 Statistik I Sommersemester 2009 Statistik I I (1/36) Wiederholung Grenzwertsatz Konfidenzintervalle Logik des 0.0 0.1 0.2 0.3 0.4 4 2 0 2 4 Statistik I I (2/36) Zum Nachlesen Agresti/Finlay: Kapitel 6+7
Statistik I Sommersemester 2009 Statistik I I (1/36) Wiederholung Grenzwertsatz Konfidenzintervalle Logik des 0.0 0.1 0.2 0.3 0.4 4 2 0 2 4 Statistik I I (2/36) Zum Nachlesen Agresti/Finlay: Kapitel 6+7
Angewandte Statistik 3. Semester
 Angewandte Statistik 3. Semester Übung 5 Grundlagen der Statistik Übersicht Semester 1 Einführung ins SPSS Auswertung im SPSS anhand eines Beispieles Häufigkeitsauswertungen Grafiken Statistische Grundlagen
Angewandte Statistik 3. Semester Übung 5 Grundlagen der Statistik Übersicht Semester 1 Einführung ins SPSS Auswertung im SPSS anhand eines Beispieles Häufigkeitsauswertungen Grafiken Statistische Grundlagen
Grundlegende Eigenschaften von Punktschätzern
 Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Kommentierter SPSS-Ausdruck zur logistischen Regression
 Daten: POK V AG 3 (POKV_AG3_V07.SAV) Kommentierter SPSS-Ausdruck zur logistischen Regression Fragestellung: Welchen Einfluss hat die Fachnähe und das Geschlecht auf die interpersonale Attraktion einer
Daten: POK V AG 3 (POKV_AG3_V07.SAV) Kommentierter SPSS-Ausdruck zur logistischen Regression Fragestellung: Welchen Einfluss hat die Fachnähe und das Geschlecht auf die interpersonale Attraktion einer
Mathematische und statistische Methoden II
 Statistik & Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte
Statistik & Methodenlehre e e Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-206) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden II Dr. Malte
Chi-Quadrat-Verteilung
 Chi-Quadrat-Verteilung Die Verteilung einer Summe X +X +...+X n, wobei X,..., X n unabhängige standardnormalverteilte Zufallsvariablen sind, heißt χ -Verteilung mit n Freiheitsgraden. Eine N(, )-verteilte
Chi-Quadrat-Verteilung Die Verteilung einer Summe X +X +...+X n, wobei X,..., X n unabhängige standardnormalverteilte Zufallsvariablen sind, heißt χ -Verteilung mit n Freiheitsgraden. Eine N(, )-verteilte
Statistik. Jan Müller
 Statistik Jan Müller Skalenniveau Nominalskala: Diese Skala basiert auf einem Satz von qualitativen Attributen. Es existiert kein Kriterium, nach dem die Punkte einer nominal skalierten Variablen anzuordnen
Statistik Jan Müller Skalenniveau Nominalskala: Diese Skala basiert auf einem Satz von qualitativen Attributen. Es existiert kein Kriterium, nach dem die Punkte einer nominal skalierten Variablen anzuordnen
4 Binäre Regressionsmodelle, Folien 2
 4 Binäre Regressionsmodelle, Folien 2 Ludwig Bothmann (basierend auf Unterlagen von Nora Fenske) Statistik III für Nebenfachstudierende WS 2014/2015 4.5 Hypothesentests Lineare Hypothesen Betrachtet werden
4 Binäre Regressionsmodelle, Folien 2 Ludwig Bothmann (basierend auf Unterlagen von Nora Fenske) Statistik III für Nebenfachstudierende WS 2014/2015 4.5 Hypothesentests Lineare Hypothesen Betrachtet werden
ε heteroskedastisch BINARY CHOICE MODELS Beispiele: Wahlentscheidung Kauf langlebiger Konsumgüter Arbeitslosigkeit Schätzung mit OLS?
 BINARY CHOICE MODELS 1 mit Pr( Y = 1) = P Y = 0 mit Pr( Y = 0) = 1 P Beispiele: Wahlentscheidung Kauf langlebiger Konsumgüter Arbeitslosigkeit Schätzung mit OLS? Y i = X i β + ε i Probleme: Nonsense Predictions
BINARY CHOICE MODELS 1 mit Pr( Y = 1) = P Y = 0 mit Pr( Y = 0) = 1 P Beispiele: Wahlentscheidung Kauf langlebiger Konsumgüter Arbeitslosigkeit Schätzung mit OLS? Y i = X i β + ε i Probleme: Nonsense Predictions
Regression ein kleiner Rückblick. Methodenseminar Dozent: Uwe Altmann Alexandra Kuhn, Melanie Spate
 Regression ein kleiner Rückblick Methodenseminar Dozent: Uwe Altmann Alexandra Kuhn, Melanie Spate 05.11.2009 Gliederung 1. Stochastische Abhängigkeit 2. Definition Zufallsvariable 3. Kennwerte 3.1 für
Regression ein kleiner Rückblick Methodenseminar Dozent: Uwe Altmann Alexandra Kuhn, Melanie Spate 05.11.2009 Gliederung 1. Stochastische Abhängigkeit 2. Definition Zufallsvariable 3. Kennwerte 3.1 für
Aufgaben zu Kapitel 9
 Aufgaben zu Kapitel 9 Aufgabe 1 Für diese Aufgabe benötigen Sie den Datensatz Nominaldaten.sav. a) Sie arbeiten für eine Marktforschungsfirma und sollen überprüfen, ob die in diesem Datensatz untersuchte
Aufgaben zu Kapitel 9 Aufgabe 1 Für diese Aufgabe benötigen Sie den Datensatz Nominaldaten.sav. a) Sie arbeiten für eine Marktforschungsfirma und sollen überprüfen, ob die in diesem Datensatz untersuchte
Univariates Datenmaterial
 Univariates Datenmaterial 1.6.1 Deskriptive Statistik Zufallstichprobe: Umfang n, d.h. Stichprobe von n Zufallsvariablen o Merkmal/Zufallsvariablen: Y = {Y 1, Y 2,..., Y n } o Realisationen/Daten: x =
Univariates Datenmaterial 1.6.1 Deskriptive Statistik Zufallstichprobe: Umfang n, d.h. Stichprobe von n Zufallsvariablen o Merkmal/Zufallsvariablen: Y = {Y 1, Y 2,..., Y n } o Realisationen/Daten: x =
Kategoriale abhängige Variablen: Logit- und Probit -Modelle. Statistik II
 Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Wiederholung Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell
Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Wiederholung Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell
Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester Aufgabe 1
 Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester 2013 Aufgabe 1 In einer Urne
Lehrstuhl für Statistik und Ökonometrie der Otto-Friedrich-Universität Bamberg Prof. Dr. Susanne Rässler Klausur zu Methoden der Statistik II (mit Kurzlösung) Sommersemester 2013 Aufgabe 1 In einer Urne
Kategoriale Daten. Johannes Hain. Lehrstuhl für Mathematik VIII Statistik 1/17
 Johannes Hain Lehrstuhl für Mathematik VIII Statistik 1/17 Übersicht Besitzen die Daten, die statistisch ausgewertet werden sollen, kategoriales Skalenniveau, unterscheidet man die folgenden Szenarien:
Johannes Hain Lehrstuhl für Mathematik VIII Statistik 1/17 Übersicht Besitzen die Daten, die statistisch ausgewertet werden sollen, kategoriales Skalenniveau, unterscheidet man die folgenden Szenarien:
Hypothesenprüfung. Darüber hinaus existieren zahlreiche andere Testverfahren, die alle auf der gleichen Logik basieren
 Hypothesenprüfung Teil der Inferenzstatistik Befaßt sich mit der Frage, wie Hypothesen über eine (in der Regel unbekannte) Grundgesamtheit an einer Stichprobe überprüft werden können Behandelt werden drei
Hypothesenprüfung Teil der Inferenzstatistik Befaßt sich mit der Frage, wie Hypothesen über eine (in der Regel unbekannte) Grundgesamtheit an einer Stichprobe überprüft werden können Behandelt werden drei
8. Konfidenzintervalle und Hypothesentests
 8. Konfidenzintervalle und Hypothesentests Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Beispiel. Sie wollen den durchschnittlichen Fruchtsaftgehalt eines bestimmten Orangennektars
8. Konfidenzintervalle und Hypothesentests Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Beispiel. Sie wollen den durchschnittlichen Fruchtsaftgehalt eines bestimmten Orangennektars
die wir als Realisationen von unabhängig und identisch verteilten Zufallsvariablen
 Kapitel 8 Schätzung von Parametern 8.1 Schätzmethoden Gegeben seien Beobachtungen Ü Ü ¾ Ü Ò die wir als Realisationen von unabhängig und identisch verteilten Zufallsvariablen ¾ Ò auffassen. Die Verteilung
Kapitel 8 Schätzung von Parametern 8.1 Schätzmethoden Gegeben seien Beobachtungen Ü Ü ¾ Ü Ò die wir als Realisationen von unabhängig und identisch verteilten Zufallsvariablen ¾ Ò auffassen. Die Verteilung
3 Häufigkeitsverteilungen
 3 Häufigkeitsverteilungen 3.1 Absolute und relative Häufigkeiten 3.2 Klassierung von Daten 3.3 Verteilungsverläufe 3.1 Absolute und relative Häufigkeiten Datenaggregation: Bildung von Häufigkeiten X nominal
3 Häufigkeitsverteilungen 3.1 Absolute und relative Häufigkeiten 3.2 Klassierung von Daten 3.3 Verteilungsverläufe 3.1 Absolute und relative Häufigkeiten Datenaggregation: Bildung von Häufigkeiten X nominal
6.0 Logistische Regression. 6 Logistische Regression. 6.1 Das binäre Modell. 6 Logistische Regression
 6.0 Logistische Regression 6.1 Das binäre Modell 6.1 Das binäre Modell Sei x der Vektor der Einflussgrößen mit einem Eins-Element, um die Regressionskonstante zu modellieren. Angenommen, es gilt das Regressionsmodell:
6.0 Logistische Regression 6.1 Das binäre Modell 6.1 Das binäre Modell Sei x der Vektor der Einflussgrößen mit einem Eins-Element, um die Regressionskonstante zu modellieren. Angenommen, es gilt das Regressionsmodell:
Kategoriale abhängige Variablen:
 Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell Statistik II
Kategoriale abhängige Variablen: Logit- und Probit -Modelle Statistik II Literatur Annahmen und Annahmeverletzungen Funktionen Exponenten, Wurzeln usw. Das Problem Das binäre Logit-Modell Statistik II
VS PLUS
 VS PLUS Zusatzinformationen zu Medien des VS Verlags Statistik II Inferenzstatistik 2010 Übungsaufgaben und Lösungen Inferenzstatistik 2 [Übungsaufgaben und Lösungenn - Inferenzstatistik 2] ÜBUNGSAUFGABEN
VS PLUS Zusatzinformationen zu Medien des VS Verlags Statistik II Inferenzstatistik 2010 Übungsaufgaben und Lösungen Inferenzstatistik 2 [Übungsaufgaben und Lösungenn - Inferenzstatistik 2] ÜBUNGSAUFGABEN
Online-Aufgaben Statistik (BIOL, CHAB) Auswertung und Lösung
 Online-Aufgaben Statistik (BIOL, CHAB) Auswertung und Lösung Abgaben: 92 / 234 Maximal erreichte Punktzahl: 7 Minimal erreichte Punktzahl: 1 Durchschnitt: 4 Frage 1 (Diese Frage haben ca. 0% nicht beantwortet.)
Online-Aufgaben Statistik (BIOL, CHAB) Auswertung und Lösung Abgaben: 92 / 234 Maximal erreichte Punktzahl: 7 Minimal erreichte Punktzahl: 1 Durchschnitt: 4 Frage 1 (Diese Frage haben ca. 0% nicht beantwortet.)
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 19. Januar 2011 1 Nichtparametrische Tests Ordinalskalierte Daten 2 Test für ein Merkmal mit nur zwei Ausprägungen
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 19. Januar 2011 1 Nichtparametrische Tests Ordinalskalierte Daten 2 Test für ein Merkmal mit nur zwei Ausprägungen
Anhang 4. Bias durch Überdiagnose von papillären Mikrokarzinomen
 Anhang 4 Bias durch Überdiagnose von papillären Mikrokarzinomen Bias durch Überdiagnose von papillären Mikrokarzinomen H. Bertelsmann AG Epidemiologie und Medizinische Statistik Universität Bielefeld Dezember
Anhang 4 Bias durch Überdiagnose von papillären Mikrokarzinomen Bias durch Überdiagnose von papillären Mikrokarzinomen H. Bertelsmann AG Epidemiologie und Medizinische Statistik Universität Bielefeld Dezember
Logit Modelle mit ordinaler Response Variable. Diplomarbeit
 Logit Modelle mit ordinaler Response Variable Diplomarbeit zur Erlangung des Grades eines Diplom-Volkswirtes an der Wirtschaftswissenschaftlichen Fakultät der Humboldt-Universität zu Berlin vorgelegt von
Logit Modelle mit ordinaler Response Variable Diplomarbeit zur Erlangung des Grades eines Diplom-Volkswirtes an der Wirtschaftswissenschaftlichen Fakultät der Humboldt-Universität zu Berlin vorgelegt von
SPSS V Gruppenvergleiche ( 2 Gruppen) abhängige (verbundene) Stichproben
 SPSS V Gruppenvergleiche ( 2 Gruppen) abhängige (verbundene) Stichproben ÜBERSICHT: Testverfahren bei abhängigen (verbundenen) Stichproben parametrisch nicht-parametrisch 2 Gruppen t-test bei verbundenen
SPSS V Gruppenvergleiche ( 2 Gruppen) abhängige (verbundene) Stichproben ÜBERSICHT: Testverfahren bei abhängigen (verbundenen) Stichproben parametrisch nicht-parametrisch 2 Gruppen t-test bei verbundenen
Exemplar für Prüfer/innen
 Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2016 Mathematik Kompensationsprüfung 3 Angabe für Prüfer/innen Hinweise zur
Exemplar für Prüfer/innen Kompensationsprüfung zur standardisierten kompetenzorientierten schriftlichen Reifeprüfung AHS Juni 2016 Mathematik Kompensationsprüfung 3 Angabe für Prüfer/innen Hinweise zur
Jost Reinecke. 7. Juni 2005
 Universität Bielefeld 7. Juni 2005 Testtheorie Test für unabhängige Stichproben Test für abhängige Stichproben Testtheorie Die Testtheorie beinhaltet eine Reihe von Testverfahren, die sich mit der Überprüfung
Universität Bielefeld 7. Juni 2005 Testtheorie Test für unabhängige Stichproben Test für abhängige Stichproben Testtheorie Die Testtheorie beinhaltet eine Reihe von Testverfahren, die sich mit der Überprüfung
Kapitel 5: Einfaktorielle Varianzanalyse
 Rasch, Friese, Hofmann & Naumann (006). Quantitative Methoden. Band (. Auflage). Heidelberg: Springer. Kapitel 5: Einfaktorielle Varianzanalyse Berechnen der Teststärke a priori bzw. Stichprobenumfangsplanung
Rasch, Friese, Hofmann & Naumann (006). Quantitative Methoden. Band (. Auflage). Heidelberg: Springer. Kapitel 5: Einfaktorielle Varianzanalyse Berechnen der Teststärke a priori bzw. Stichprobenumfangsplanung
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 9. Dezember 2010 1 Konfidenzintervalle Idee Schätzung eines Konfidenzintervalls mit der 3-sigma-Regel Grundlagen
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 9. Dezember 2010 1 Konfidenzintervalle Idee Schätzung eines Konfidenzintervalls mit der 3-sigma-Regel Grundlagen
Lage- und Streuungsparameter
 Lage- und Streuungsparameter Beziehen sich auf die Verteilung der Ausprägungen von intervall- und ratio-skalierten Variablen Versuchen, diese Verteilung durch Zahlen zu beschreiben, statt sie graphisch
Lage- und Streuungsparameter Beziehen sich auf die Verteilung der Ausprägungen von intervall- und ratio-skalierten Variablen Versuchen, diese Verteilung durch Zahlen zu beschreiben, statt sie graphisch
Zusammenhangsanalyse mit SPSS. Messung der Intensität und/oder der Richtung des Zusammenhangs zwischen 2 oder mehr Variablen
 - nominal, ordinal, metrisch In SPSS: - Einfache -> Mittelwerte vergleichen -> Einfaktorielle - Mehrfaktorielle -> Allgemeines lineares Modell -> Univariat In SPSS: -> Nichtparametrische Tests -> K unabhängige
- nominal, ordinal, metrisch In SPSS: - Einfache -> Mittelwerte vergleichen -> Einfaktorielle - Mehrfaktorielle -> Allgemeines lineares Modell -> Univariat In SPSS: -> Nichtparametrische Tests -> K unabhängige
Datenanalyse mit Excel und Gretl
 Dozent: Christoph Hindermann christoph.hindermann@uni-erfurt.de Datenanalyse mit Excel und Gretl Teil Titel 2: Gretl 1 Teil 2: Gretl Datenanalyse mit Excel und Gretl Teil Titel 2: Gretl 2 Modellannahmen
Dozent: Christoph Hindermann christoph.hindermann@uni-erfurt.de Datenanalyse mit Excel und Gretl Teil Titel 2: Gretl 1 Teil 2: Gretl Datenanalyse mit Excel und Gretl Teil Titel 2: Gretl 2 Modellannahmen
Binäre abhängige Variablen
 Binäre abhängige Variablen Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Einführung Oft wollen wir qualitative Variablen
Binäre abhängige Variablen Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Einführung Oft wollen wir qualitative Variablen
9 Die Normalverteilung
 9 Die Normalverteilung Dichte: f(x) = 1 2πσ e (x µ)2 /2σ 2, µ R,σ > 0 9.1 Standard-Normalverteilung µ = 0, σ 2 = 1 ϕ(x) = 1 2π e x2 /2 Dichte Φ(x) = 1 x 2π e t2 /2 dt Verteilungsfunktion 331 W.Kössler,
9 Die Normalverteilung Dichte: f(x) = 1 2πσ e (x µ)2 /2σ 2, µ R,σ > 0 9.1 Standard-Normalverteilung µ = 0, σ 2 = 1 ϕ(x) = 1 2π e x2 /2 Dichte Φ(x) = 1 x 2π e t2 /2 dt Verteilungsfunktion 331 W.Kössler,
Technische Universität München. Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Modellwahl bei der KFZ Haftpflicht-Versicherung mit Hilfe von GLMs Diplomarbeit von Ivonne Siegelin Themenstellerin: Prof. Dr. C. Czado, Dr. G. Sussmann
Technische Universität München Zentrum Mathematik Modellwahl bei der KFZ Haftpflicht-Versicherung mit Hilfe von GLMs Diplomarbeit von Ivonne Siegelin Themenstellerin: Prof. Dr. C. Czado, Dr. G. Sussmann
1 Statistische Grundlagen
 Konzepte in Empirische Ökonomie 1 (Winter) Hier findest Du ein paar Tipps zu den Konzepten in Empirische 1. Wenn Du aber noch etwas Unterstützung kurz vor der Klausur brauchst, schreib uns eine kurze Email.
Konzepte in Empirische Ökonomie 1 (Winter) Hier findest Du ein paar Tipps zu den Konzepten in Empirische 1. Wenn Du aber noch etwas Unterstützung kurz vor der Klausur brauchst, schreib uns eine kurze Email.
Statistik eindimensionaler Größen
 Statistik eindimensionaler Größen Michael Spielmann Inhaltsverzeichnis 1 Aufgabe der eindimensionalen Statistik 2 2 Grundbegriffe 2 3 Aufbereiten der Stichprobe 3 4 Die Kennzahlen Mittelwert und Streuung,
Statistik eindimensionaler Größen Michael Spielmann Inhaltsverzeichnis 1 Aufgabe der eindimensionalen Statistik 2 2 Grundbegriffe 2 3 Aufbereiten der Stichprobe 3 4 Die Kennzahlen Mittelwert und Streuung,
Kapitel 5: Einfaktorielle Varianzanalyse
 Kapitel 5: Einfaktorielle Varianzanalyse Durchführung einer einfaktoriellen Varianzanalyse ohne Messwiederholung Dieser Abschnitt zeigt die Durchführung der in Kapitel 5 vorgestellten einfaktoriellen Varianzanalyse
Kapitel 5: Einfaktorielle Varianzanalyse Durchführung einer einfaktoriellen Varianzanalyse ohne Messwiederholung Dieser Abschnitt zeigt die Durchführung der in Kapitel 5 vorgestellten einfaktoriellen Varianzanalyse
Lineare Gleichungssysteme (Teschl/Teschl 11.1)
 Lineare Gleichungssysteme (Teschl/Teschl.) Ein Lineares Gleichungssystem (LGS) besteht aus m Gleichungen mit n Unbekannten x,...,x n und hat die Form a x + a 2 x 2 +... + a n x n b a 2 x + a 22 x 2 +...
Lineare Gleichungssysteme (Teschl/Teschl.) Ein Lineares Gleichungssystem (LGS) besteht aus m Gleichungen mit n Unbekannten x,...,x n und hat die Form a x + a 2 x 2 +... + a n x n b a 2 x + a 22 x 2 +...
Kap. 9: Regression mit einer binären abhängigen Variablen
 Kap. 9: Regression mit einer binären abhängigen Variablen Motivation Lineares Wahrscheinlichkeitsmodell Probit- und Logit-Regression Maximum Likelihood Empirisches Beispiel: Analyse der HMDA-Daten Ausblick:
Kap. 9: Regression mit einer binären abhängigen Variablen Motivation Lineares Wahrscheinlichkeitsmodell Probit- und Logit-Regression Maximum Likelihood Empirisches Beispiel: Analyse der HMDA-Daten Ausblick:
Prof. Dr. Christoph Kleinn Institut für Waldinventur und Waldwachstum Arbeitsbereich Waldinventur und Fernerkundung
 Systematische Stichprobe Rel. große Gruppe von Stichprobenverfahren. Allgemeines Merkmal: es existiert ein festes, systematisches Muster bei der Auswahl. Wie passt das zur allgemeinen Forderung nach Randomisierung
Systematische Stichprobe Rel. große Gruppe von Stichprobenverfahren. Allgemeines Merkmal: es existiert ein festes, systematisches Muster bei der Auswahl. Wie passt das zur allgemeinen Forderung nach Randomisierung
K8 Stetige Zufallsvariablen Theorie und Praxis
 K8 Stetige Zufallsvariablen Theorie und Praxis 8.1 Theoretischer Hintergrund Wir haben (nicht abzählbare) Wahrscheinlichkeitsräume Meßbare Funktionen Zufallsvariablen Verteilungsfunktionen Dichten in R
K8 Stetige Zufallsvariablen Theorie und Praxis 8.1 Theoretischer Hintergrund Wir haben (nicht abzählbare) Wahrscheinlichkeitsräume Meßbare Funktionen Zufallsvariablen Verteilungsfunktionen Dichten in R
1.1.1 Ergebnismengen Wahrscheinlichkeiten Formale Definition der Wahrscheinlichkeit Laplace-Experimente...
 Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Zeit zum Kochen [in min] [10, 20[ [20, 30[ [30, 40[ [40, 50[ [50,60[ [60, 100] Hi
![Zeit zum Kochen [in min] [10, 20[ [20, 30[ [30, 40[ [40, 50[ [50,60[ [60, 100] Hi Zeit zum Kochen [in min] [10, 20[ [20, 30[ [30, 40[ [40, 50[ [50,60[ [60, 100] Hi](/thumbs/48/24644287.jpg) 1. Susi und Fritzi bereiten ein Faschingsfest vor, dazu gehört natürlich ein Faschingsmenü. Ideen haben sie genug, aber sie möchten nicht zu viel Zeit fürs Kochen aufwenden. In einer Zeitschrift fanden
1. Susi und Fritzi bereiten ein Faschingsfest vor, dazu gehört natürlich ein Faschingsmenü. Ideen haben sie genug, aber sie möchten nicht zu viel Zeit fürs Kochen aufwenden. In einer Zeitschrift fanden
Armutsquotenberechnung aus gerundeten Einkommensangaben
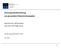 Armutsquotenberechnung aus gerundeten Einkommensangaben Jörg Drechsler, IAB Nürnberg Hans Kiesl, OTH Regensburg Statistik Tage Bamberg Fürth 2016 20.7.2016 S. 1 Panelerhebung PASS (Panel Arbeitsmarkt und
Armutsquotenberechnung aus gerundeten Einkommensangaben Jörg Drechsler, IAB Nürnberg Hans Kiesl, OTH Regensburg Statistik Tage Bamberg Fürth 2016 20.7.2016 S. 1 Panelerhebung PASS (Panel Arbeitsmarkt und
Scheinklausur Stochastik 1 für Studierende des Lehramts und der Diplom-Pädagogik
 Universität Karlsruhe (TH) Institut für Stochastik Dr. Bernhard Klar Dipl.-Math. oec. Volker Baumstark Name Vorname Matr.-Nr.: Scheinklausur Stochastik für Studierende des Lehramts und der Diplom-Pädagogik
Universität Karlsruhe (TH) Institut für Stochastik Dr. Bernhard Klar Dipl.-Math. oec. Volker Baumstark Name Vorname Matr.-Nr.: Scheinklausur Stochastik für Studierende des Lehramts und der Diplom-Pädagogik
Faktorenanalysen höherer Ordnung
 Faktorenanalysen höherer Ordnung 1 Ausgangssituation Übliche Faktorenanalysen (erster Ordnung) gehen von Zusammenhängen zwischen manifesten, beobachteten Variablen aus und führen diese Zusammenhänge auf
Faktorenanalysen höherer Ordnung 1 Ausgangssituation Übliche Faktorenanalysen (erster Ordnung) gehen von Zusammenhängen zwischen manifesten, beobachteten Variablen aus und führen diese Zusammenhänge auf
Vorlesung Wirtschaftsstatistik 2 (FK ) Wiederholungen deskriptive Statistik und Einleitung Normalverteilungsverfahren. Dipl.-Ing.
 Vorlesung Wirtschaftsstatistik 2 (FK 040637) Wiederholungen deskriptive Statistik und Einleitung Normalverteilungsverfahren Dipl.-Ing. Robin Ristl Wintersemester 2012/13 1 Vorlesungsinhalte Wiederholung:
Vorlesung Wirtschaftsstatistik 2 (FK 040637) Wiederholungen deskriptive Statistik und Einleitung Normalverteilungsverfahren Dipl.-Ing. Robin Ristl Wintersemester 2012/13 1 Vorlesungsinhalte Wiederholung:
3.4 Asymptotische Evaluierung von Sch atzer Konsistenz Konsistenz Definition 3.4.1: konsistente Folge von Sch atzer
 3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
Projekt Kaffeemaschine Welche Faktoren beeinflussen das Geschmacksurteil?
 AKULTÄT ANGEWANDTE SOZIALWISSENSCHATEN PRO. DR. SONJA HAUG Projekt Kaffeemaschine Welche aktoren beeinflussen das Geschmacksurteil? Ausgehend von der Verkostung an der Hochschule Regensburg und der dabei
AKULTÄT ANGEWANDTE SOZIALWISSENSCHATEN PRO. DR. SONJA HAUG Projekt Kaffeemaschine Welche aktoren beeinflussen das Geschmacksurteil? Ausgehend von der Verkostung an der Hochschule Regensburg und der dabei
Standardisierte Vorgehensweisen und Regeln zur Gewährleistung von: Eindeutigkeit Schlussfolgerungen aus empirischen Befunden sind nur dann zwingend
 Standardisierte Vorgehensweisen und Regeln zur Gewährleistung von: Eindeutigkeit Schlussfolgerungen aus empirischen Befunden sind nur dann zwingend oder eindeutig, wenn keine alternativen Interpretationsmöglichkeiten
Standardisierte Vorgehensweisen und Regeln zur Gewährleistung von: Eindeutigkeit Schlussfolgerungen aus empirischen Befunden sind nur dann zwingend oder eindeutig, wenn keine alternativen Interpretationsmöglichkeiten
Statistik II für Betriebswirte Vorlesung 3
 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik Statistik II für Betriebswirte Vorlesung 3 5. November 2013 Beispiel: Aktiensplit (Aczel & Sounderpandan, Aufg. 14-28) Ein Börsenanalyst
PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik Statistik II für Betriebswirte Vorlesung 3 5. November 2013 Beispiel: Aktiensplit (Aczel & Sounderpandan, Aufg. 14-28) Ein Börsenanalyst
10. Vorlesung. Grundlagen in Statistik. Seite 291. Martin-Luther-Universität Halle/Wittenberg
 . Vorlesung Grundlagen in Statistik Seite 29 Beispiel Gegeben: Termhäufigkeiten von Dokumenten Problemstellung der Sprachmodellierung Was sagen die Termhäufigkeiten über die Wahrscheinlichkeit eines Dokuments
. Vorlesung Grundlagen in Statistik Seite 29 Beispiel Gegeben: Termhäufigkeiten von Dokumenten Problemstellung der Sprachmodellierung Was sagen die Termhäufigkeiten über die Wahrscheinlichkeit eines Dokuments
Gliederung. Bachelorseminar: Graphiken in R Visualisierung Kategorialer Daten. Einführung. Visualisierung von zweidimensionalen Kontingenztafeln
 Gliederung Bachelorseinar: Graphiken in R Visualisierung Kategorialer Daten Matthias Mitterayer betreut durch Sebastian Kaiser Einführung Institut für Statistik, LMU München 13. Januar 2011 Fazit Visualisierung
Gliederung Bachelorseinar: Graphiken in R Visualisierung Kategorialer Daten Matthias Mitterayer betreut durch Sebastian Kaiser Einführung Institut für Statistik, LMU München 13. Januar 2011 Fazit Visualisierung
Mehr-Ebenen-Analyse I. Regressionsmodelle für Politikwissenschaftler
 Mehr-Ebenen-Analyse I Regressionsmodelle für Politikwissenschaftler Was sind strukturierte Daten? Was ist Struktur? Probleme Bisher sind wir stets von einfachen Zufallsstichproben ausgegangen (Registerstichprobe)
Mehr-Ebenen-Analyse I Regressionsmodelle für Politikwissenschaftler Was sind strukturierte Daten? Was ist Struktur? Probleme Bisher sind wir stets von einfachen Zufallsstichproben ausgegangen (Registerstichprobe)
Statistik II. Statistische Tests. Statistik II
 Statistik II Statistische Tests Statistik II - 12.5.2006 1 Test auf Anteilswert: Binomialtest Sei eine Stichprobe unabhängig, identisch verteilter ZV (i.i.d.). Teile diese Stichprobe in zwei Teilmengen
Statistik II Statistische Tests Statistik II - 12.5.2006 1 Test auf Anteilswert: Binomialtest Sei eine Stichprobe unabhängig, identisch verteilter ZV (i.i.d.). Teile diese Stichprobe in zwei Teilmengen
Zufallsgröße. Würfelwurf mit fairem Würfel. Wahrscheinlichkeitsverteilung einer diskreten
 Zufallsgrößen Ergebnisse von Zufallsexperimenten werden als Zahlen dargestellt 0 Einführung Wahrscheinlichkeitsrechnung 2 Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Hypothesentests
Zufallsgrößen Ergebnisse von Zufallsexperimenten werden als Zahlen dargestellt 0 Einführung Wahrscheinlichkeitsrechnung 2 Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Hypothesentests
Regression I. Statistik I. Sommersemester Lineare Regression Zusammenhang und Modell Ein Beispiel: Armut und Gewaltverbrechen Zusammenfassung
 Sommersemester 2009 Ein Beispiel: Armut und Gewaltverbrechen Rechtswahl 15 10 5 0 5 10 Arbeitslosigkeit Zum Nachlesen Agresti: 9.1-9.4 Gehring/Weins: 8 Schumann: 8.1-8.2 Was ist ein Zusammenhang? Gemeinsame
Sommersemester 2009 Ein Beispiel: Armut und Gewaltverbrechen Rechtswahl 15 10 5 0 5 10 Arbeitslosigkeit Zum Nachlesen Agresti: 9.1-9.4 Gehring/Weins: 8 Schumann: 8.1-8.2 Was ist ein Zusammenhang? Gemeinsame
Hypothesentests mit SPSS. Beispiel für eine einfaktorielle Varianzanalyse Daten: museum_m_v05.sav
 Beispiel für eine einfaktorielle Varianzanalyse Daten: museum_m_v05.sav Hypothese: Die Beschäftigung mit Kunst ist vom Bildungsgrad abhängig. 1. Annahmen Messniveau: Modell: Die Skala zur Erfassung der
Beispiel für eine einfaktorielle Varianzanalyse Daten: museum_m_v05.sav Hypothese: Die Beschäftigung mit Kunst ist vom Bildungsgrad abhängig. 1. Annahmen Messniveau: Modell: Die Skala zur Erfassung der
Kapitel 6 Martingale
 Kapitel 6 Martingale Martingale spielen eine große Rolle in der Finanzmathematik, und sind zudem ein wichtiges Hilfsmittel für die statistische Inferenz stochastischer Prozesse, insbesondere auch für Zählprozesse
Kapitel 6 Martingale Martingale spielen eine große Rolle in der Finanzmathematik, und sind zudem ein wichtiges Hilfsmittel für die statistische Inferenz stochastischer Prozesse, insbesondere auch für Zählprozesse
9. Schätzen und Testen bei unbekannter Varianz
 9. Schätzen und Testen bei unbekannter Varianz Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Schätzen und Testen bei unbekannter Varianz Wenn wir die Standardabweichung σ nicht kennen,
9. Schätzen und Testen bei unbekannter Varianz Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Schätzen und Testen bei unbekannter Varianz Wenn wir die Standardabweichung σ nicht kennen,
Vorlesung Wirtschaftsstatistik 2 (FK 040637) Multiple lineare Regression. Dipl.-Ing. Robin Ristl Wintersemester 2012/13
 Vorlesung Wirtschaftsstatistik 2 (FK 040637) Multiple lineare Regression Dipl.-Ing. Robin Ristl Wintersemester 2012/13 1 Grundidee: Eine abhängige Variable soll als Linearkombination mehrerer unabhängiger
Vorlesung Wirtschaftsstatistik 2 (FK 040637) Multiple lineare Regression Dipl.-Ing. Robin Ristl Wintersemester 2012/13 1 Grundidee: Eine abhängige Variable soll als Linearkombination mehrerer unabhängiger
Kapitel 12 Stetige Zufallsvariablen Dichtefunktion und Verteilungsfunktion. stetig. Verteilungsfunktion
 Kapitel 12 Stetige Zufallsvariablen 12.1. Dichtefunktion und Verteilungsfunktion stetig Verteilungsfunktion Trägermenge T, also die Menge der möglichen Realisationen, ist durch ein Intervall gegeben Häufig
Kapitel 12 Stetige Zufallsvariablen 12.1. Dichtefunktion und Verteilungsfunktion stetig Verteilungsfunktion Trägermenge T, also die Menge der möglichen Realisationen, ist durch ein Intervall gegeben Häufig
Multiplizitätskorrektur bei Variablenselektion
 Multiplizitätskorrektur bei Variablenselektion Seminar: Multiples Testen Dozent: Prof. Dr. T. Dickhaus Referent: Maximilian Mönch - 22.11.2010 - Überblick 1) Einleitung 2) Multiplizitätskorrektur 3) Median
Multiplizitätskorrektur bei Variablenselektion Seminar: Multiples Testen Dozent: Prof. Dr. T. Dickhaus Referent: Maximilian Mönch - 22.11.2010 - Überblick 1) Einleitung 2) Multiplizitätskorrektur 3) Median
Freisetzen und Fixieren von Parametern in Strukturgleichungsmodellen
 Freisetzen und Fixieren von Parametern in Strukturgleichungsmodellen 1 Variablen und Parameter Variablen haben für verschiedene Personen unterschiedliche Werte. Parameter haben für eine gegebene Population
Freisetzen und Fixieren von Parametern in Strukturgleichungsmodellen 1 Variablen und Parameter Variablen haben für verschiedene Personen unterschiedliche Werte. Parameter haben für eine gegebene Population
2. Statistische Methoden in der Diagnostik. Elemente des Studiendesigns
 2. Statistische Methoden in der Diagnostik Elemente des Studiendesigns Diagnosestudien in der Medizin Klassifikation in krank - nicht krank basierend auf diagnostischem Test Beispiel: Diagnose von Brustkrebs
2. Statistische Methoden in der Diagnostik Elemente des Studiendesigns Diagnosestudien in der Medizin Klassifikation in krank - nicht krank basierend auf diagnostischem Test Beispiel: Diagnose von Brustkrebs
STATISTISCHE MUSTERANALYSE - DARSTELLUNGSVORSCHLAG
 STATISTISCHE MUSTERANALYSE - DARSTELLUNGSVORSCHLAG Statistische Methoden In der vorliegenden fiktiven Musterstudie wurden X Patienten mit XY Syndrom (im folgenden: Gruppe XY) mit Y Patienten eines unauffälligem
STATISTISCHE MUSTERANALYSE - DARSTELLUNGSVORSCHLAG Statistische Methoden In der vorliegenden fiktiven Musterstudie wurden X Patienten mit XY Syndrom (im folgenden: Gruppe XY) mit Y Patienten eines unauffälligem
Einfache statistische Auswertungen mit dem Programm SPSS
 Einfache statistische Auswertungen mit dem Programm SPSS Datensatz: fiktive_daten.sav Dipl. Päd. Anne Haßelkus Dr. Dorothea Dette-Hagenmeyer 11/2011 Überblick 1 Deskriptive Statistiken; Mittelwert berechnen...
Einfache statistische Auswertungen mit dem Programm SPSS Datensatz: fiktive_daten.sav Dipl. Päd. Anne Haßelkus Dr. Dorothea Dette-Hagenmeyer 11/2011 Überblick 1 Deskriptive Statistiken; Mittelwert berechnen...
METHODENLEHRE I WS 2013/14 THOMAS SCHÄFER
 METHODENLEHRE I WS 2013/14 THOMAS SCHÄFER DAS THEMA: INFERENZSTATISTIK IV INFERENZSTATISTISCHE AUSSAGEN FÜR ZUSAMMENHÄNGE UND UNTERSCHIEDE Inferenzstatistik für Zusammenhänge Inferenzstatistik für Unterschiede
METHODENLEHRE I WS 2013/14 THOMAS SCHÄFER DAS THEMA: INFERENZSTATISTIK IV INFERENZSTATISTISCHE AUSSAGEN FÜR ZUSAMMENHÄNGE UND UNTERSCHIEDE Inferenzstatistik für Zusammenhänge Inferenzstatistik für Unterschiede
