Der Greedy-Algorithmus und unendliche Matroide
|
|
|
- Laura Lehmann
- vor 7 Jahren
- Abrufe
Transkript
1 FernUniversität in Hagen Fakultät für Mathematik und Informatik Bachelorarbeit Der Greedy-Algorithmus und unendliche Matroide Christoph Horst Paderborn, 25. September 2012 Betreuer: Prof. Dr. Winfried Hochstättler
2 Inhaltsverzeichnis Selbständigkeitserklärung Kurzzusammenfassung ii iii 1 Einleitung Der Greedy-Algorithmus und Matroide Der Algorithmus von Kruskal Greedy-Algorithmen ohne Matroide Zu dieser Arbeit Der Greedy-Algorithmus und unendliche Matroide Problemstellung Struktur der Arbeit Notation Endliche und unendliche Matroide Endliche Matroide Dualität Pre-independence spaces Matroide endlichen Ranges Finitäre Matroide Matroide Beziehungen zwischen den Klassen Matroid-ähnlicher Objekte Der Greedy-Algorithmus Gewichtete Matroide Wohlgeordnete Matroide Die Klee sche Formulierung des Greedy-Algorithmus Äquivalenz der beiden Formen Unendliche Matroide und der Greedy-Algorithmus Der iterative Greedy-Algorithmus Der transfinite Greedy-Algorithmus nach Klee Die Rückrichtung Zusammenfassung und offene Fragen 41 A Hypothetisch: Greedy-Algorithmus impliziert finitäres Matroid? 42 Literaturverzeichnis 44 i
3 Selbständigkeitserklärung Hiermit erkläre ich, dass ich diese Bachelorarbeit selbständig verfasst und keine anderen als die angegebenen Quellen und Hilfsmittel verwendet habe. Die Stellen der Arbeit, die anderen Werken dem Wortlaut oder dem Sinn nach entnommen sind, habe ich unter Angabe der Quellen der Entlehnung kenntlich gemacht. Desweiteren versichere ich, dass diese Arbeit noch keiner anderen Prüfungsbehörde vorgelegt wurde. Paderborn, 25. September 2012 Christoph Horst
4 Kurzzusammenfassung In dieser Bachelorarbeit werden die Zusammenhänge zwischen Matroiden und dem Greedy- Algorithmus auf unendliche Matroide erweitert. Es ist bekannt (Klee, 1971), dass der Greedy- Algorithmus für wohlgeordnete finitäre Matroide stets eine optimale Basis liefert. In dieser Arbeit wird gezeigt, dass die Umkehrung dieser Aussage teilweise gilt: Unabhängigkeitssysteme mit abzählbarer Grundmenge, für die der Greedy-Algorithmus stets eine optimale Basis liefert, sind finitäre Matroide.
5 1 Einleitung 1.1 Der Greedy-Algorithmus und Matroide Bei der Lösung von Problemen der kombinatorischen Optimierung ist im Allgemeinen eine Reihe von Entscheidungen darüber zu treffen, welche Elemente aus einer gewissen Menge auszuwählen sind. Oft gibt es dabei mehrere Wahlmöglichkeiten, von denen sich einige später als falsch herausstellen können. Die Greedy-Strategie 1 besteht darin, sich stets lokal optimal zu verhalten, d. h. sich in jedem Schritt für die gerade am günstigsten erscheinende Wahl zu entscheiden und diese Wahl in späteren Schritten niemals zurückzunehmen. Die Greedy-Strategie garantiert nicht in jedem Fall eine optimale Lösung. Eine Vielzahl von Problemen ist jedoch so gestaltet, dass ein Greedy-Algorithmus stets eine optimale Lösung findet. Ein klassisches Problem der kombinatorischen Optimierung ist das Problem des minimalen aufspannenden Baumes (Minimum spanning tree, MST). Gegeben sei ein zusammenhängender Graph G = (V, E) mit der Knotenmenge V und der Kantenmenge E sowie einer Gewichtsfunktion w : E R, die jeder Kante e ein Gewicht w(e) zuordnet. Gesucht ist ein aufspannender Baum, d. h. ein zusammenhängender und zyklenfreier Teilgraph (V, T ) von G mit derselben Knotenmenge wie G, für den das Gesamtgewicht w(t ) = e T w(e) minimal wird. Das MST-Problem wurde erstmals von Borůvka (1926) 2 algorithmisch gelöst. Es existieren eine Vielzahl weiterer Algorithmen zu seiner Lösung; die bekanntesten die Algorithmen von Kruskal und Prim werden wir im Folgenden besprechen Der Algorithmus von Kruskal Der Algorithmus von Kruskal zur Bestimmung eines minimalen aufspannenden Baumes in einem Graphen G = (V, E) beginnt mit einem Teilgraphen (V, T 0 := ), den man als einen Wald mit V Komponenten auffassen kann. In jedem Schritt wird diesem Teilgraphen eine Kante aus E hinzugefügt, die minimales Gewicht hat und deren Hinzufügen nicht dazu führt, dass ein Zyklus entsteht oder anders gesagt, die zwei bisher getrennte Komponenten des 1 gierig. Das englische greedy ist aber auch in deutschsprachigen Texten ein feststehender Begriff. 2 Zu dem tschechischsprachigen Originalartikel gibt es eine Übersetzung des ursprünglichen Wortlautes sowie eine Übersetzung in moderne mathematische Sprache von Nešetřil et al. (2001). 1
6 1.1. Der Greedy-Algorithmus und Matroide Waldes verbindet. Der Algorithmus terminiert nach V 1 Schritten mit einem minimalen aufspannenden Baum. 3 Algorithmus 1 Algorithmus von Kruskal. 1: T 0 := 2: k := 0 3: while T k ist kein aufspannender Baum do 4: Finde eine Kante e E \T k mit minimalem Gewicht, so dass der Teilgraph (V, T k {e}) zyklenfrei ist 5: T k+1 := T k {e} 6: k := k + 1 7: end while 8: return T k Das Interessante an diesem Algorithmus ist die Struktur des Systems der möglichen Kantenmengen, die während der Laufzeit des Algorithmus gebildet werden. Man überlegt sich leicht, dass bei gegebenem Graphen G durch passende Wahl der Gewichtsfunktion w jeder mögliche Wald mit k Kanten im k-ten Schritt des Algorithmus gebildet werden kann. Für Wälder gilt nun: Jede Teilmenge eines Waldes ist wieder ein Wald. Ein nichtleeres Mengensystem mit dieser Eigenschaft ist ein Unabhängigkeitssystem. Außerdem gilt für zwei Wälder verschiedener Größe, dass es stets eine Kante in dem größeren Wald gibt, um die der kleinere Wald ergänzt werden kann, ohne dass ein Zyklus entsteht und er damit die Wald-Eigenschaft verliert. 4 Ein Unabhängigkeitssystem, das auch diese Ergänzungseigenschaft besitzt, heißt Matroid. Im Vorgriff auf spätere Kapitel soll hier bereits die Definition des Begriffes Matroid über die Unabhängigkeitsaxiome gegeben werden. Definition 1.1 (Matroid). Sei E eine endliche Menge und I P(E) ein System von Teilmengen von E. Dann heißt M = (E, I ) Matroid über der Grundmenge E, falls die folgenden Unabhängigkeitsaxiome erfüllt sind: (I1) I. (I2) Ist I I und I I, so ist auch I I. (I3) Sind I 1, I 2 I mit I 1 < I 2, dann gibt es ein Element e I 2 \I 1, so dass I 1 {e} I. Die Elemente von I heißen in diesem Fall unabhängige Mengen, die Elemente des Komplements P(E) \ I entsprechend abhängige Mengen. Eine Basis ist eine maximale unabhängige Menge. Die Existenz von Basen sowie die Gleichmächtigkeit aller Basen eines gegebenen Matroids sind einfache Folgerungen aus Definition 1.1. Man kann nun mithilfe des Matroidbegriffes einen allgemeinen Greedy-Algorithmus formulieren, der für jedes gewichtete Matroid schrittweise eine Basis mit minimalem Gesamtgewicht aufbaut. 3 vgl. Cormen et al. (2001, Kapitel 23) für eine ausführlichere Darstellung der Algorithmen von Kruskal und Prim, die auch detailliert auf den hier unberücksichtigten Aspekt der benutzten Datenstrukturen, die eine effiziente Implementierung erst möglich machen, eingehen. 4 Beweis siehe Aigner (2006, Abschnitt 7.4). 2
7 1.1. Der Greedy-Algorithmus und Matroide Definition 1.2. Sei M = (E, I ) ein Matroid und w : E R eine Funktion. Dann heißt M gewichtetes Matroid über der Grundmenge E mit der Gewichtsfunktion w. Algorithmus 2 Greedy-Algorithmus für gewichtete Matroide. 1: A 0 := { I (I1)} 2: k := 0 3: while A k ist keine Basis do 4: Finde ein Element e A k mit minimalem Gewicht w(e), so dass A k {e} I {Existiert wegen (I3)} 5: A k+1 := A k {e} 6: k := k + 1 7: end while 8: return A k Falls wir ein Optimierungsproblem mithilfe von Matroiden formulieren können, haben wir damit sofort einen allgemeinen effizienten Lösungsalgorithmus zur Verfügung. Umgekehrt folgt aus dem Funktionieren des Greedy-Algorithmus für ein Unabhängigkeitssystem bereits die Ergänzungseigenschaft (I3), so dass Matroide in gewisser Weise eine natürliche Struktur hinter dem Greedy-Algorithmus darstellen Greedy-Algorithmen ohne Matroide In diesem Abschnitt wollen wir dem Eindruck entgegentreten, dass Matroide hinter jedem Greedy-Algorithmus stecken. Dazu sehen wir uns den Algorithmus von Prim an, der dem Algorithmus von Kruskal oberflächlich ziemlich ähnlich ist. Algorithmus 3 Algorithmus von Prim. 1: T 0 := 2: Lege Startknoten v 0 V beliebig fest 3: S 0 := {v 0 } 4: k := 0 5: while S 0 V do 6: Finde eine Kante e = {u, v} mit minimalem Gewicht und u S k, v V \ S k 7: {Der Teilgraph (S k, T k ) ist zusammenhängend und zyklenfrei} 8: T k+1 := T k {e} 9: S k+1 := S k {v} 10: k := k : end while 12: return T k Beim Algorithmus von Kruskal wird ein anfänglich leerer Wald nach und nach um Kanten zwischen den Komponenten ergänzt, so dass am Ende ein aufspannender Baum entsteht. Beim Algorithmus von Prim wird dagegen von vornherein ein Baum aufgebaut und in jedem Schritt um eine weitere Kante ergänzt, bis am Ende ein aufspannender Baum entsteht. 3
8 1.2. Zu dieser Arbeit Wie der Algorithmus von Kruskal ist auch der Algorithmus von Prim vom Greedy-Typ. Ihm liegt jedoch kein Matroid zugrunde, denn die möglichen Kantenmengen, die während des Ablaufs des Algorithmus gebildet werden, sind Bäume, und im Allgemeinen ist eine Teilmenge eines Baumes nicht wieder ein Baum, so dass Bedingung (I2) verletzt ist. Es liegt damit kein Unabhängigkeitssystem vor: Nur bestimmte Teilmengen von Bäumen sind wieder Bäume. Die hier vorliegende Struktur wird Greedoid genannt. 5 Definition 1.3. Sei E eine Menge und F ein nichtleeres System von Teilmengen von E. Dann heißt G = (E, F ) Greedoid über E, falls folgende Axiome erfüllt sind: (G1) Ist X F nicht leer, so existiert ein x X, so dass X \ {x} F. (G2) Sind X 1, X 2 F mit X 1 < X 2, dann gibt es ein Element x X 2 \ X 1, so dass X 1 {x} F. Die Elemente von F werden erreichbare Mengen genannt. Das Greedoid ist eine Verallgemeinerung des Matroids: Das Axiom (G2) entspricht dem Ergänzungsaxiom (I3), (G1) ist eine Abschwächung der Erblichkeitsbedingung (I2) und da F nicht leer ist, folgt mit (G1) die Erreichbarkeit der leeren Menge, also (I1). Greedoide stellen damit noch mehr als Matroide eine natürliche Struktur für den Greedy-Algorithmus dar. Die Theorie der unendlichen Greedoide ist allerdings noch wesentlich weniger ausgearbeitet als die Theorie der unendlichen Matroide. Wir werden deshalb die Diskussion über Greedoide auf die Erwähnung in diesem Abschnitt beschränken und uns sonst auf Matroide konzentrieren. Der Vollständigkeit halber sei erwähnt, dass es auch Greedy-Algorithmen gibt, denen kein Greedoid zugrunde liegt, beispielsweise der Huffman-Algorithmus zur Erstellung eines optimalen Präfixcodes Zu dieser Arbeit Der Greedy-Algorithmus und unendliche Matroide Problemstellung Für endliche Matroide ist bekannt, dass für sie der Greedy-Algorithmus immer eine optimale Basis liefert. Umgekehrt ist auch bekannt, dass ein endliches Unabhängigkeitssystem, für das der Greedy-Algorithmus funktioniert, ein Matroid sein muss. Wir interessieren uns für die Erweiterung dieser Aussagen auf den Fall unendlicher Matroide. Zunächst ist weder klar, welche Form ein unendlicher Greedy-Algorithmus überhaupt haben sollte, noch nach welchen Kriterien man die produzierte Menge als optimal bezeichnen kann. Wir werden uns in diesen Punkten weitgehend Klee (1971) anschließen, der für finitäre Matroide gezeigt hat, dass der Greedy-Algorithmus stets eine in einem bestimmten Sinne optimale Basis liefert. Die Problemstellung besteht nun darin, zu untersuchen, ob auch die Umkehrung dieses Satzes gilt, d. h. ob man aus dem Funktionieren des Greedy-Algorithmus für ein unendliche Unabhängigkeitssysteme folgern kann, dass dieses ein finitäres Matroid sein muss, oder ob der Greedy-Algorithmus möglicherweise auch für andere Klassen von Matroiden funktioniert. 5 siehe Björner u. Ziegler (1992). 6 siehe Cormen et al. (2001, Abschnitt 16.3). 4
9 1.2. Zu dieser Arbeit Struktur der Arbeit Nach der informalen Einführung werden wir im Kapitel 2 den Begriff des Matroids nochmals rigoros definieren. Wir beginnen mit den endlichen Matroiden, um die Grundbegriffe der Matroidtheorie einzuführen. Wir erweitern den Begriff dann schrittweise auf verschiedene Klassen von unendlichen Matroiden. Bei der Frage, was ein unendliches Matroid ist, stützen wir uns hauptsächlich auf den kürzlich veröffentlichten Artikel von Bruhn et al. (2010), in dem äquivalente Axiomensysteme für unendliche Matroide angegeben werden. Danach werden wir in Kapitel 3 die Theorie des Greedy-Algorithmus für endliche Matroide aufarbeiten. Wir werden sehen, dass die Greedy-Strategie bei gewichteten Matroiden im unendlichen Fall zu gewissen Schwierigkeiten führt, die sich umgehen lassen, indem man statt der Gewichtsfunktion eine Wohlordnung auf den Elementen des Matroids vorgibt. Es wird sich herausstellen, dass die Definition von Klee (1971) auch für endliche Matroide geeignet ist und zu identischen Ergebnissen führt, wodurch eine Rechtfertigung für den unendlichen Fall gegeben ist. In Kapitel 4 werden wir den Greedy-Algorithmus für unendliche Matroide betrachten. Wir werden uns zunächst einen iterativen Greedy-Algorithmus ansehen, der nach und nach immer größere unabhängige Mengen produziert, aber nach endlich vielen Schritten abgebrochen wird. Dass die erzeugten Mengen optimal sind, lässt sich mit der Theorie endlicher Matroide zeigen; wir werden aber auch zeigen, dass dieser Algorithmus selbst für Unabhängigkeitssysteme funktioniert, die keine Matroide sind. Danach geben wir Klees Formulierung des Greedy- Algorithmus sowie seinen Satz, dass der Greedy-Algorithmus für finitäre Matroide stets eine optimale Basis liefert, an. Schließlich gehen wir in Abschnitt 4.3 die Umkehrung des Satzes an Notation Die in dieser Arbeit verwendete Notation wird keine größere Überraschung hervorrufen. In der Regel bezeichnen große Buchstaben wie A Mengen, kalligraphische Großbuchstaben wie A Mengensysteme und kleine Buchstaben wie a Elemente, die nicht selbst Mengen sind. Die Potenzmenge wird mit P(A), die Kardinalität einer Menge mit A, die Mengendifferenz mit A \ B notiert. Falls aus dem Kontext eine Grundmenge U ersichtlich ist, wird für A U das relative Komplement U \ A auch einfach A c geschrieben. Eine in der Matroidtheorie übliche vereinfachte Schreibweise wird benutzt: Falls es nicht zu Missverständnissen kommen kann, fallen die Mengenklammern bisweilen weg. Beispielsweise schreiben wir A x statt A {x} und B \ y statt B \ {y}. Die lineare Hülle einer (Multi-)Menge S von Vektoren schreiben wir S ; falls K ein Körper ist schreiben wir den Vektorraum der n-spaltenvektoren K n. 5
10 2 Endliche und unendliche Matroide Dieses Kapitel soll eine Einführung in den Matroidbegriff sein. Es werden zunächst die endlichen Matroide vorgestellt und grundlegende, damit zusammenhängende Konzepte erarbeitet, die für das Verständnis der weiteren Untersuchungen wesentlich sind. Dann wird die Endlichkeitsbedingung weggelassen, so dass die wesentlich größere Klasse der pre-independence spaces entsteht. Diese wird dann durch geeignete Zusatzbedingungen wieder eingeschränkt, um zu einem handhabbaren unendlichen Matroidbegriff zu kommen, der die wesentlichen Eigenschaften endlicher Matroide auch im Unendlichen zeigt. Wir werden folgende Klassen Matroid-ähnlicher Objekte besprechen: endliche Matroide (siehe Abschnitt 2.1) Matroide endlichen Ranges (siehe Abschnitt 2.4) finitäre Matroide (siehe Abschnitt 2.5) Matroide (siehe Abschnitt 2.6) pre-independence spaces (siehe Abschnitt 2.3) Diese Begriffe sind in eine echte Inklusionshierarchie eingeordnet, siehe Abbildung Endliche Matroide Die Theorie der unendlichen Matroide führt innerhalb der Matroidtheorie vergleichsweise ein Schattendasein. Wenn der Begriff Matroid fällt, ist damit folglich in der Regel ein endliches Matroid gemeint. Wir werden uns in diesem und nur in diesem Abschnitt dieser Sprechweise pre-independence spaces Matroide finitäre Matroide Matroide mit endlichem Rang endliche Matroide Abbildung 2.1: Hierarchie Matroid-ähnlicher Begriffe. Die Teilmengenbeziehung ist jeweils echt. 6
11 2.1. Endliche Matroide weitestgehend anschließen. Im restlichen Teil der Arbeit werden wir dann jedoch explizit von endlichen Matroiden sprechen und mit Matroid eine bestimmte unendliche Verallgemeinerung bezeichnen. Eine interessante Eigenart des Matroidbegriffs ist die Existenz einer Vielzahl äquivalenter Definitionen, sogenannter kryptomorpher Axiomensysteme. Neben der Definition über die Unabhängigkeitsaxiome werden wir endliche Matroide in diesem Abschnitt über die Basis-, Kreis- und Abschlussaxiome charakterisieren. Eine Vielzahl weiterer Definitionen findet sich z. B. bei Nicoletti u. White (1986). Die Definitionen und Sätze in diesem Abschnitt stammen, soweit nicht anders angegeben, von Oxley (1992a). Beginnen wir mit der Definition über die in der Einleitung schon genannten unabhängigen Mengen. Definition 2.1 (Unabhängigkeitsaxiome). Sei E eine endliche Menge, und sei I P(E) ein System von Teilmengen von E. Dann heißt M = (E, I ) (endliches) Matroid über der Grundmenge E, falls die folgenden Unabhängigkeitsaxiome erfüllt sind: (I1) I. (I2) Falls I I und I I, so folgt I I. (Erblichkeitsbedingung) (I3 F ) Falls I 1, I 2 I und I 1 < I 2, so existiert ein x I 2 \I 1, so dass I 1 x I. ((endliche) Ergänzungseigenschaft) Die Elemente von I werden unabhängige Mengen genannt. Die Elemente von P(E) \ I heißen entsprechend abhängige Mengen. Wie üblich gelten zwei Matroide als isomorph, wenn sie durch Umbenennen der Elemente ineinander übergehen, formal: M 1 = (E 1, I 1 ) und M 2 = (E 2, I 2 ) sind isomorph, M 1 = M2, falls eine bijektive Abbildung ψ : E 1 E 2 existiert, so dass ψ(x) I 2 X I 1 für alle X E 1. Beispiel 2.2 (Darstellbare Matroide). Sei K ein Körper und A eine n m-matrix mit Elementen aus K. Wir schreiben A spaltenweise als A = ( a 1 a 2 a n ). Definieren wir nun S = {a 1, a 2,..., a n } (S ist eine Multimenge, d. h. zwei gleiche Spalten mit unterschiedlichem Index sollen beide in S auftauchen) und I = {I S I ist linear unabhängig}, (2.1) so ist (S, I ) ein Matroid, das sogenannte Vektormatroid von A. Ein zu einem Vektormatroid isomorphes Matroid heißt (K-)darstellbar. In der Literatur sind teilweise auch die Begriffe matrisches oder lineares Matroid gebräuchlich. Beweis. Wir überprüfen die Unabhängigkeitsaxiome. (I1) und (I2) gelten offensichtlich. Seien I 1, I 2 mit I 1 < I 2 linear unabhängige Teilmengen von S. Angenommen, (I3 F ) gilt nicht. Dann ist I 1 e für alle e I 2 \ I 1 linear abhängig, d. h. e I 1 für alle e I 2 I 1. Daraus folgt I 1 I 2 = I 1, also I 2 dim I 1 I 2 = dim I 1 = I 1 < I 2, Widerspruch. 7
12 2.1. Endliche Matroide In der linearen Algebra ist eine Basis eine maximale linear unabhängige Menge. Einen entsprechenden Begriff gibt es auch in der Matroidtheorie. Definition 2.3. Sei M = (E, I ) ein Matroid. Eine Basis von M ist eine (bezüglich der Inklusion) maximale unabhängige Menge von M. Die unabhängigen Mengen sind nach oben durch E beschränkt. Da E endlich ist, ist somit jede unabhängige Menge in einer Basis enthalten. Aus (I1) folgt damit, dass es stets Basen gibt. Die Ergänzungseigenschaft (I3 F ) sichert die Gleichmächtigkeit sämtlicher Basen eines Matroids. Satz 2.4. Seien B 1, B 2 Basen eines endlichen Matroids (E, I ). Dann gilt B 1 = B 2. Beweis. Sei o. B. d. A. angenommen, dass B 1 < B 2. Dann gibt es nach (I3 F ) ein e B 2 \B 1, so dass B 1 e I, im Widerspruch zur Maximalität von B 1. Satz 2.5. Sei M = (E, I ) ein endliches Matroid und X eine Teilmenge von E. Dann ist auch M X := (X, I P(X)) (2.2) ein Matroid, die Restriktion von M auf X. Beweis. Einfaches Nachprüfen der Unabhängigkeitsaxiome zeigt die Behauptung. Definition 2.6 (Rang). Sei B eine beliebige Basis des Matroids M = (E, I ). Die nach Satz 2.4 von der konkreten Wahl von B unabhängige Anzahl der Elemente von B heißt Rang von M und wird mit r(m) bezeichnet. Ist X eine Teilmenge von E, so schreiben wir abkürzend auch r(x) für r(m X). Satz 2.7 (Basisaxiome). Die Menge B der Basen eines Matroids M besitzt folgende Eigenschaften: (B1) B. (B2) Falls B 1, B 2 B und x B 1 \B 2, dann gibt es ein y B 2 \B 1, so dass (B 1 \x) y B. (Austauscheigenschaft) Beweis. (B1) folgt aus (I1) und der Endlichkeit von E. Nach (I2) ist B 1 \ x I, und da B 1 \ x < B 2 gibt es nach (I3 F ) ein y B 2 \ (B 1 \ x), so dass (B 1 \ x) y I. Wegen x B 2 ist offenbar y B 2 \ B 1. Es ist noch zu zeigen, dass (B 1 \x) y maximal ist. (B 1 \x) y ist in einer Basis B 1 enthalten. Da wir (B 1 \ x) y = B 1 und wegen Satz 2.4 B 1 = B 1 haben, folgt (B 1 \ x) y = B 1, also ist (B 1 \ x) y eine Basis, womit (B2) gezeigt ist. Matroide lassen sich durch ihre Basenmenge B charakterisieren. Anders gesagt, die Basisaxiome bilden ein kryptomorphes Axiomensystem. 8
13 2.1. Endliche Matroide Satz 2.8 (Charakterisierung von Matroiden durch ihre Basen). Sei E eine endliche Menge und besitze B P(E) die Eigenschaften (B1) und (B2). Setzt man dann ist (E, I ) ein Matroid mit der Basenmenge B. Beweis. Siehe Oxley (1992a, Theorem 1.2.3). I = {I B B B}, (2.3) Definition 2.9. Sei M = (E, I ) ein Matroid. Ein Kreis 1 von M ist eine (bezüglich der Inklusion) minimale abhängige Menge von M. Satz 2.10 (Kreisaxiome). Die Menge C der Kreise eines Matroids M besitzt folgende Eigenschaften: (C1) C. (C2) Falls C 1, C 2 C und C 1 C 2, so folgt C 1 = C 2. (C3) Falls C 1, C 2 voneinander verschiedene Elemente von C sind und e C 1 C 2 ist, dann gibt es ein Element C 3 C, so dass C 3 (C 1 C 2 ) \ e. (Kreiseliminationseigenschaft) Beweis. (C1) folgt direkt aus (I1), (C2) aus der Minimalität von C 1 und C 2. Zum Beweis von (C3) sei angenommen, dass es keinen Kreis in (C 1 C 2 ) \ e gibt. Dann muss (C 1 C 2 ) \ e eine unabhängige Menge sein. Sei f ein beliebiges Element aus der nach (C2) nichtleeren Menge C 2 \ C 1. Da C 2 als Kreis eine minimale abhängige Menge ist, muss C 2 \ f unabhängig sein. Sei nun I I maximal mit C 2 \ f I C 1 C 2 gewählt. Dann ist offenbar f I, da sonst C 2 I wäre, im Widerspruch zur Unabhängigkeit von I. Da C 1 abhängig ist und somit C 1 keine Teilmenge von I ist, gibt es ein g C 1 \ I, das wegen f C 2 \ C 1 von f verschieden sein muss. Es folgt I (C 1 C 2 ) \ {f, g} = C 1 C 2 2 < (C 1 C 2 ) \ e. Wendet man nun (I3 F ) auf I und (C 1 C 2 ) \ e an, erhält man ein x (C 1 C 2 ) \ e, so dass I x I und C 2 \ f I x C 1 C 2, im Widerspruch dazu, dass I bereits maximal gewählt war. Wie durch ihre Basen lassen sich Matroide auch durch ihre Kreise charakterisieren. Die Kreisaxiome bilden damit ein weiteres kryptomorphes Axiomensystem. Satz 2.11 (Charakterisierung von Matroiden durch ihre Kreise). Sei E eine endliche Menge und besitze C P(E) die Eigenschaften (C1), (C2) und (C3). Setzt man so ist (E, I ) ein Matroid, dessen Kreismenge gerade C ist. Beweis. Siehe Oxley (1992a, Theorem 1.1.4). 1 engl. circuit. I = {I E C C : C I}, (2.4) 9
14 2.1. Endliche Matroide w C 3 u C 1 C 2 e v, x Abbildung 2.2: Kreiseliminationsaxiom. In der Vereinigung von C 1 und C 2 ist ein Kreis C 3 enthalten, hier grau hinterlegt, der die gemeinsame Kante e nicht enthält. Die Begriffe Matroid (von Matrix 2 ), unabhängig und Basis sind offensichtlich von der Linearen Algebra inspiriert. Der Begriff des Kreises stammt aus der zweiten großen Inspirationsquelle der Matroidtheorie, der Graphentheorie. Beispiel 2.12 (Graphische Matroide). Sei G = (V, E) ein endlicher Graph mit der Knotenmenge V und der Kantenmenge E ( V 2). Sei C die Menge der Kantenmengen von G, die einen Zyklus bilden, d. h. einen zusammenhängenden Teilgraphen induzieren, in dem jeder Knoten den Grad 2 hat. Dann ist C die Menge der Kreise eines Matroids über E, des sogenannten Zyklen- oder Polygonmatroids von G. Zu Zyklenmatroiden isomorphe Matroide heißen graphisch. Beweis. Die leere Kantenmenge bildet keinen Zyklus, also ist C, so dass (C1) gilt. Es gilt auch (C2), denn ein Zyklus kann keinen anderen Zyklus echt enthalten. Zum Beweis von (C3) seien C 1 und C 2 die Kantenmengen zweier verschiedener Zyklen von G, die eine gemeinsame Kante e = {u, v} besitzen. Wir konstruieren einen Zyklus C 3, dessen Kantenmenge in (C 1 C 2 ) \ e enthalten ist. Für i = 1, 2 sei P i jeweils der Pfad von u nach v mit der Kantenmenge C i \ e. Durchlaufe P 1 von u nach v. Sei w der erste Knoten, dessen folgende Kante in P 1 \ P 2 liegt, und sei x der erste Knoten ungleich w, dessen folgende Kante aus P 1 auch in P 2 liegt. Vereinige nun den P 1 -Abschnitt von w nach x mit dem P 2 -Abschnitt von x nach w. Das Ergebnis ist ein Zyklus mit einer Kantenmenge in (C 1 C 2 ) \ e. Damit gilt auch (C3). Oxley (1992a) führt den Abschlussoperator eines Matroids über die Rangfunktion eines Matroids, r : P(E) N, X r(x), siehe Definition 2.6, ein. Der Abschluss einer Teilmenge X von E ist damit durch definiert. cl(x) := {x E r(x x) = r(x)} Im Hinblick auf unendliche Matroide ist die Rangfunktion in dieser Form allerdings recht unpraktisch 3, weshalb wir uns Bruhn et al. (2010) für die Definition des Abschlusses anschließen wollen. 2 siehe Whitney (1935). 3 Siehe Bruhn et al. (2010). Dort wird für unendliche Matroide statt dieser Rangfunktion eine relative Rangfunktion einführt. 10
15 2.1. Endliche Matroide X cl(x) Abbildung 2.3: Der Abschluss cl(x) der mit dicken Linien markierten Kantenmenge X besteht aus den Kanten aus X sowie den Kanten, die in X einen Zyklus schließen. Definition Sei M = (E, I ) ein Matroid. Die Abbildung cl: P(E) P(E) cl(x) := X {x E I X : I I I x I } für X E heißt Abschlussoperator von M. Die Menge cl(x) heißt Abschluss von X. Vor der Untersuchung der Eigenschaften des Abschlussoperators wollen wir uns noch jeweils ein Beispiel für darstellbare und für graphische Matroide anschauen. Beispiel Sei A eine n m-matrix über einem Körper K mit der Spaltenmenge E und M[A] = (E, I ) das Vektormatroid von A. Ist X eine Teilmenge der Spalten von A, dann ist ein Element e E im Abschluss cl(x) genau dann enthalten, wenn e in der linearen Hülle X enthalten ist, das heißt cl(x) = E X. Beispiel Sei G = (V, E) ein Graph und M(G) = (E, I ) sein Zyklenmatroid. Ist X eine Teilmenge der Kanten von G, dann besteht der Abschluss von X gerade aus den Kanten e, die bereits in X enthalten sind, oder durch deren Hinzufügen zu X ein Zyklus geschlossen wird (siehe Abbildung 2.3.) Satz 2.16 (Abschlussaxiome). Der Abschlussoperator cl eines Matroids M über E besitzt folgende Eigenschaften. (CL1) Für alle X E ist X cl(x). (CL2) Sind X, Y Teilmengen von E mit X Y, so gilt cl(x) cl(y ). (Isotonie) (CL3) Für alle X E gilt cl(cl(x)) = cl(x). (Idempotenz) (CL4) Für alle X E gilt: Ist x E und y cl(x x) \ cl(x), so folgt x cl(x y). (Austauscheigenschaft) Beweis. (CL1) und (CL2) folgen direkt aus der Definition. (CL3) Der Beweis stützt sich auf das folgende Lemma. Lemma Sei X E und B eine Basis von M X, dann gilt cl(b) = cl(x). Beweis. Wir müssen wegen (CL2) nur die Inklusion cl(x) cl(b) zeigen. Für y B ist die Aussage trivial, sei also zunächst y X \ B. Dann ist B I und B y I, also y cl(b). 11
16 2.1. Endliche Matroide Sei nun y cl(x) \ X. Dann gibt es laut Definition eine unabhängige Teilmenge I X mit I y I. Wir erweitern I zu einer Basis B von M (X y). Dann ist offenbar y B, also ist B auch eine Basis von M X. Nach Satz 2.4 gilt B = B, so dass B auch eine Basis von M (X y) sein muss. Dann muss also B y I sein, also y cl(b), und es folgt die behauptete Inklusion. Aus dem Beweis des Lemmas lässt sich auch die folgende Aussage ableiten. Korollar Sei B eine Basis von M X für ein X E. Dann ist B eine Basis von M cl(x). Beweis. Im Beweis des Lemmas ist B y I für alle y cl(x) \ X, also ist B in cl(x) eine maximale unabhängige Menge. Wir fahren mit dem Beweis von (CL3) fort. Sei X E, und sei B eine Basis von M X. Nach dem Korollar ist B auch eine Basis von M cl(x). Mit dem Lemma schließen wir cl(x) = cl(b) = cl(cl(x)). (CL4) In den Fällen x X und x = y ist die Behauptung trivial erfüllt, sei also x E\(X y). Es gibt dann per Definition ein I X x mit I I und I y I mit x I. Wegen y cl(x) ist (I \ x) y I, und mit ((I \ x) y) x = I y I folgt x cl(x y). Die Abschlussaxiome bilden ein weiteres kryptomorphes Axiomensystem für Matroide. Satz Sei E eine endliche Menge und cl : P(E) P(E) eine Abbildung, die die Eigenschaften (CL1) (CL4) erfüllt. Dann ist cl der Abschlussoperator eines Matroids M = (E, I ), und es gilt I = {I E x I : x cl(i \ x)}. (2.5) Beweis. Siehe Oxley (1992a), Theorem inkl. Lemma und Korollar Der Abschlussbegriff bringt eine Reihe von Bezeichnungen für spezielle Teilmengen von E mit sich. X E heißt abgeschlossene Menge oder Fläche, falls X = cl(x). X E heißt aufspannende Menge, falls cl(x) = E. X E heißt Hyperebene, falls X eine maximale nicht-aufspannende Menge ist. Korollar Sei M = (E, I ) ein Matroid. Dann gilt: B E ist eine Basis genau dann, wenn B unabhängig und aufspannend ist. Beweis. B ist Basis B I und B x I für alle x B c B I und B c cl(b) B ist unabhängig und aufspannend. Zusätzlich zu den hier aufgezählten Axiomensystemen lassen sich endliche Matroide auch durch ihre Rangfunktion, ihre abhängigen, aufspannenden oder nicht-aufspannenden Mengen sowie ihre Hyperebenen charakterisieren. Dazu sei auf Nicoletti u. White (1986) verwiesen. 12
17 2.2. Dualität 2.2 Dualität Der Begriff der Dualität zieht sich durch viele Bereiche der Mathematik. In der Matroidtheorie beruht die Dualität von Matroiden über einer endlichen Menge E darauf, die Inklusionsteilordnung auf P(E) umzukehren und dadurch duale Begriffe und Aussagen zu gewinnen. Wir werden diese Herleitung aber nicht von Grund auf durchführen, sondern uns an der existierenden Literatur orientieren, die in der Regel mit der Definition der dualen Basen beginnt. Satz Sei M ein endliches Matroid über E mit der Basenmenge B. Setzt man so ist B die Basenmenge eines endlichen Matroids über E. Beweis. Siehe Oxley (1992a, Theorem 2.1.1). B := {E \ B B B}, (2.6) Das Matroid mit der Basenmenge B wird duales Matroid zu M genannt und mit M bezeichnet. Da die dualen Basen durch Komplementbildung aus den Basen hervorgehen, führt eine erneute Bildung des Duals wieder zum Ausgangspunkt: (M ) = M, d. h. die Dualisierung M M ist eine Involution. Die Basen von M heißen Kobasen von M. Entsprechend heißen beispielsweise die unabhängigen Mengen, Kreise, aufspannenden Mengen von M kounabhängige Mengen, Kokreise, koaufspannende Mengen von M. Dabei gelten folgende Beziehungen: Satz Sei M ein Matroid über E und sei X eine Teilmenge von E. Dann gilt: (i) X ist unabhängig E \ X ist koaufspannend. (ii) X ist aufspannend E \ X ist kounabhängig. (iii) X ist eine Hyperebene E \ X ist ein Kokreis. (iv) X ist ein Kreis E \ X ist eine Kohyperebene. Beweis. Siehe Oxley (1992a, Theorem 2.1.6). Die Bedeutung der Dualität liegt zum großen Teil im Dualitätsprinzip, welches besagt, dass man zu jeder Aussage über Matroide eine äquivalente duale Aussage erhält, indem man alle Begriffe durch ihre Dualen ersetzt. Dualität spielt eine zentrale Rolle in der Matroidtheorie und, wie wir bei der Untersuchung unendlicher Matroide sehen werden, insbesondere bei der Entscheidung, welche Klasse ins Unendliche verallgemeinerter Matroide überhaupt wert ist, weiter betrachtet zu werden. 13
18 2.3. Pre-independence spaces 2.3 Pre-independence spaces Lässt man in der Definition 2.1 die Bedingung weg, dass die Grundmenge E endlich sei, erhält man die Klasse der pre-independence spaces. 4 Diese Definition ist so allgemein, dass sie aus Sicht der Matroidtheorie relativ uninteressant ist. Beispielsweise müssen pre-independence spaces im Allgemeinen nicht einmal Basen oder Kreise besitzen. Beispiel Wir betrachten auf der Grundmenge R die Menge I der abzählbaren Teilmengen von R. Dann sind die Axiome (I1),(I2),(I3 F ) sicher erfüllt, es gibt jedoch weder maximale abzählbare noch minimale überabzählbare Teilmengen und somit keine Basen oder Kreise. 2.4 Matroide endlichen Ranges Die Klasse der Matroide endlichen Ranges erhalten wir aus Definition 2.1, indem wir die Bedingung, dass die Grundmenge E endlich sei, entfernen, und durch die folgende Bedingung ersetzen: (R F ) Es gibt ein n N, so dass I n für alle I I. Matroide endlichen Ranges besitzen Basen und Kreise. Überhaupt ist die Theorie ähnlich der der endlichen Matroide, mit Ausnahme der Dualität: Die Komplemente der Basen sind bei unendlicher Grundmenge unendlich, das Dual ist also kein Matroid endlichen Ranges. Beispiele für Matroide endlichen Ranges sind endlichdimensionale Vektorräume bzw. Teilmengen endlichdimensionaler Vektorräume, wobei wie im Beispiel 2.2 die unabhängigen Mengen durch die linear unabhängigen Mengen gebildet werden. 2.5 Finitäre Matroide Dehnen wir das Beispiel 2.2 der darstellbaren Matroide nicht nur auf unendliche Grundmengen, sondern sogar auf unendliche (Vektorraum-)Basen aus, erhalten wir den Begriff des finitären Matroids. Definition Sei E eine Menge und I P(E) ein System von Teilmengen von E. Dann heißt M = (E, I ) finitäres Matroid, falls zusätzlich zu den in Definition 2.1 aufgeführten Unabhängigkeitsaxiomen (I1), (I2), (I3 F )das folgende Axiom gilt: (I4) Falls für alle endlichen Teilmengen Y von X E gilt, dass Y I, dann folgt X I. (endlicher Charakter) Bemerkung Finitäre Matroide werden in manchen Publikationen, z. B. bei Oxley (1992), auch als independence spaces bezeichnet. 4 siehe Oxley (1992). 14
19 2.5. Finitäre Matroide Beispiel Sei V ein möglicherweise unendlichdimensionaler K-Vektorraum. Bekanntlich 5 heißt eine Teilmenge M V linear unabhängig, falls jede endliche Teilmenge N M linear unabhängig ist. Eine Teilmenge von V zusammen mit den linear unabhängigen Teilmengen von V ist dann ein finitäres Matroid. Eine zu (I4) äquivalente Eigenschaft führt uns direkt zum nächsten Beispiel aus der Graphentheorie. Satz Für einen pre-independence space M = (E, I ) gilt (I4) genau dann, wenn jede abhängige Menge einen endlichen Kreis enthält. Beweis. Die Kontraposition von (I4) lautet: Jede abhängige Menge enthält eine endliche abhängige Menge. Die Äquivalenz zur Existenz eines endlichen Kreises ist dann trivial. Beispiel Wir erweitern Beispiel 2.12, indem wir nun einen unendlichen Graphen G zulassen. Die Menge C bestehe nach wie vor aus den Zyklen von G. Da alle Zyklen aus endlich vielen Kanten bestehen, ist das Zyklenmatroid von G ein finitäres Matroid. Finitäre Matroide besitzen viele der Eigenschaften endlicher Matroide. Die Klasse der finitären Matroide ist jedoch nicht unter Dualität abgeschlossen. Die dualen Matroide zu finitären Matroiden werden kofinitäre Matroide genannt. Die folgenden Aussagen werden wir später benötigen. Satz Finitäre Matroide erfüllen die Kreisaxiome (C1) (C3). Beweis. Man prüft leicht nach, dass im Beweis von Satz 2.10 lediglich die Unabhängigkeitsaxiome, nicht jedoch die Endlichkeit der Grundmenge verwendet wurde. Bemerkung Durch Hinzunahme der Bedingung (C4) Jede abhängige Menge enthält einen endlichen Kreis. erhält man laut Oxley (1992, Theorem 3.1.3) sogar eine Charakterisierung der finitären Matroide durch die Kreisaxiome. Satz Sei M = (E, I ) ein finitäres Matroid und I I. Falls I x I für ein x E gilt, dann gibt es einen eindeutig bestimmten Kreis C von M mit x C I x. (2.7) Beweis. (1) I x ist abhängig und enthält daher nach (I4) mindestens einen Kreis. Jeder dieser Kreise muss x enthalten, denn sonst wäre er auch in I enthalten. (2) Zum Nachweis der Eindeutigkeit sei angenommen, C 1, C 2 wären zwei verschiedene Kreise, die (2.7) erfüllen. Dann existiert mit (C3) ein Kreis C 3 mit C 3 (C 1 C 2 )\x I, Widerspruch. 5 siehe Unger (2003, Definition (b)) 15
20 2.5. Finitäre Matroide Eine Folgerung aus (C3), das starke Kreiseliminationsaxiom 6, werden wir zum Beweis der Abschlusseigenschaften benötigen. Satz Falls C 1, C 2 voneinander verschiedene Kreise sind und e C 1 C 2 ist, dann gibt es für jedes f C 1 \ C 2 einen Kreis C 3 mit f C 3 (C 1 C 2 ) \ e. (2.8) Beweis. 7 Angenommen, die Behauptung ist falsch, und sei durch Kreise C 1, C 2 sowie Elemente e C 1 C 2 und f C 1 \ C 2 ein Gegenbeispiel gegeben, wobei o. B. d. A. C 1 C 2 minimal sei. Nach (C3) existiert ein Kreis C 3 mit C 3 (C 1 C 2 ) \ e, und nach der Annahme ist f C 3. Nun muss es ein g C 3 (C 2 \ C 1 ) geben, denn sonst wäre C 3 eine echte Teilmenge von C 1. Betrachte C 2, C 3. Es ist g C 2 C 3, e C 2 \ C 3, und da f C 2 C 3 ist C 2 C 3 C 1 C 2, also C 2 C 3 < C 1 C 2, d. h. C 2, C 3, g, e ist kein Gegenbeispiel für die Behauptung. Es existiert daher ein Kreis C 4 mit e C 4 (C 2 C 3 ) \ g. Betrachte nun C 1, C 4. Es ist e C 1 C 4 und f C 2 C 3, also f C 1 \C 4. Da C 1 C 4 C 1 C 2 wegen g C 2 \ (C 1 C 4 ) ist, haben wir wieder C 1 C 4 < C 1 C 2, d. h. C 1, C 4, e, f ist kein Gegenbeispiel für die Behauptung. Es existiert daher ein Kreis C 5 mit f C 5 (C 1 C 4 ) \ e, aber wegen C 1 C 4 C 1 C 2 gilt für diesen Kreis auch f C 5 (C 1 C 2 ) \ e, Widerspruch. Der Abschlussoperator ist für finitäre Matroide genauso definiert wie in Definition 2.13 für endliche Matroide, d. h. cl(x) := X {x E I X : I I I x I } für X E. (2.9) Satz Der Abschlussoperator eines finitären Matroids erfüllt die Abschlussaxiome (CL1) (CL4) aus Satz 2.16: (CL1) Für alle X E ist X cl(x). (CL2) Sind X, Y Teilmengen von E mit X Y, so gilt cl(x) cl(y ). (CL3) Für alle X E gilt cl(cl(x)) = cl(x). (CL4) Für alle X E gilt: Ist x E und y cl(x x) \ cl(x), so folgt x cl(x y). Beweis. (CL1) und (CL2) folgen direkt aus der Definition von cl; für (CL4) kann der Beweis des endlichen Falls aus Satz 2.16 übertragen werden. Zu (CL3): Es genügt wegen (CL1), cl(cl(x)) cl(x) für alle X E zu zeigen. 6 Die Bezeichnung als Axiom rührt daher, dass das starke Kreiseliminationsaxiom äquivalent zum (schwachen) Kreiseliminationsaxiom ist und daher dessen Platz innerhalb der Kreisaxiome einnehmen kann. 7 siehe Welsh (1976, Theorem 9.2). 16
21 2.5. Finitäre Matroide Sei das Gegenteil angenommen, dann gibt es y cl(cl(x))\cl(x). Dann existiert ein I cl(x) mit I I und I y I. Nach Satz 2.31 gibt es einen Kreis C y mit Sei o. B. d. A. C y von allen Kreisen mit y C y I y. y C y cl(x) y derjenige, für den C y (cl(x) \ X) = C y \ (X y) (2.10) minimal ist. Falls C y \ (X y) = 0, sind wir fertig, da dann mit I := C y \ y X gilt: I I und I y I, also y cl(x), im Widerspruch zur Annahme. Sei also C y \ (X y) > 0, und sei ein x C y \ (X y) gewählt. Wegen x cl(x) \ X gibt es dann einen Kreis C x mit x C x X x. Wir können nun das starke Kreiseliminationsaxiom, Satz 2.32, auf C y, C x, x C y C x, y C y \ C x anwenden und erhalten einen Kreis C mit y C (C y C x ) \ x. Für diesen gilt: C \ (X y) ((C y C x ) \ x) \ (X y) = (C y C x ) \ (X {x, y}) = C y \ (X {x, y}) da C x X x C y \ (X y) da x C y \ (X y), also ist C \ (X y) C y \ (X y) 1, im Widerspruch dazu, dass C y (2.10) minimiert. Satz Für jeden Kreis C gilt x cl(c \ x) für alle x C. Beweis. Wegen der Minimalität von C gilt C \x I für alle x C, außerdem ist (C \x) x = C I, also x cl(c \ x). 17
22 2.6. Matroide 2.6 Matroide Eigentlich müsste dieser Abschnitt mit B-Matroide überschrieben sein. B-Matroide wurden bereits von Higgs (1969) beschrieben und stellen einen von vielen Versuchen zur Verallgemeinerung des Matroidbegriffs auf unendliche Grundmengen dar. Sie haben gegenüber finitären Matroiden den Vorteil, unter Dualität abgeschlossen zu sein. Später hat Oxley (1978) bewiesen, dass B-Matroide die größte Klasse von pre-independence spaces bilden, die unter einem Begriff von Dualität abgeschlossen ist, der die von endlichen Matroiden bekannten Konstruktionen zulässt. Man kann, wie das Bruhn et al. (2010) getan haben, also mit Fug und Recht allgemein von Matroiden sprechen, wenn man B-Matroide meint. Bruhn et al. (2010) geben für Matroide fünf äquivalente Axiomensysteme an, darunter die im folgenden zitierten Unabhängigkeits- und Abschlussaxiome. Definition 2.35 (Unabhängigkeitsaxiome). Sei E eine Menge und I P(E), so dass die folgenden Unabhängigkeitsaxiome erfüllt sind. (I1) I. (I2) Falls I I und I I, so folgt I I. (I3) Falls I 1, I 2 I, wobei I 2 maximal und I 1 nicht maximal seien, dann existiert ein x I 2 \ I 1, so dass I 1 x I. (Ergänzungseigenschaft) (IM) Falls I X E und I I, dann gibt es in {I I I I X} ein maximales Element. Dann heißt M = (E, I ) Matroid über E. Wie für endliche Matroide heißen die Elemente von I unabhängige Mengen, die Elemente von P(E) \ I heißen abhängige Mengen. Maximale unabhängige Mengen heißen Basen, minimale abhängige Mengen heißen Kreise. Der Abschlussoperator wird genauso wie im endlichen Fall definiert: cl(x) := X {x E I X : I I I x I }. (2.11) Die Abschlussaxiome für Matroide lauten: (CL1) Für alle X E ist X cl(x). (CL2) Sind X, Y Teilmengen von E mit X Y, so gilt cl(x) cl(y ). (CL3) Für alle X E gilt cl(cl(x)) = cl(x). (CL4) Für alle X E gilt: Ist x E und y cl(x x) \ cl(x), so folgt x cl(x y). (CLM) Für die Menge I cl der cl-unabhängigen Mengen, I cl := {I E x I : x cl(i \ x)}, gilt: Falls I X E und I I cl, dann gibt es in {I I cl I I X} ein maximales Element. 18
23 2.7. Beziehungen zwischen den Klassen Matroid-ähnlicher Objekte Die von endlichen oder finitären Matroiden bekannten Eigenschaften sind teilweise für Matroide erstaunlich schwierig zu beweisen. Für die Beweise der folgenden Sätze sei auf Bruhn et al. (2010) verwiesen. Es sei angemerkt, dass beispielsweise für den Beweis, dass die Restriktion M X eines Matroids wieder ein Matroid ist, bereits die Abgeschlossenheit der Matroide unter Dualität sowie eine Reihe sehr technischer Lemmata benötigt wird. Satz 2.36 (Restriktion). Sei M = (E, I ) ein Matroid und X E. Dann ist die Restriktion ein Matroid. M X := (X, I P(X)) Satz 2.37 (Kreise). Sei M = (E, I ) ein Matroid und X E eine abhängige Menge. Dann enthält X eine minimale abhängige Menge C, einen Kreis. 2.7 Beziehungen zwischen den Klassen Matroid-ähnlicher Objekte Wir wollen in diesem Abschnitt zeigen, dass die in Abbildung 2.1 auf Seite 6 dargestellte Inklusionshierarchie gilt. Folgende Beziehungen ergeben sich unmittelbar aus den jeweiligen Definitionen: Satz Jedes endliche Matroid ist ein Matroid mit endlichem Rang. 2. Jedes Matroid mit endlichem Rang, das eine endliche Grundmenge hat, ist ein endliches Matroid. 3. Jedes Matroid mit endlichem Rang ist ein finitäres Matroid. 4. Jedes finitäres Matroid, für dessen System unabhängiger Mengen I gilt, dass I n für alle I I und ein n N, ist ein Matroid mit endlichem Rang. Satz Jedes finitäre Matroid ist ein Matroid. Beweis. Wir müssen die Gültigkeit der Axiome (I3) und (IM) für finitäre Matroide zeigen. Zu (I3): Angenommen, es gibt ein Gegenbeispiel I 1, I 2 I, wobei I 2 maximal und I 1 nichtmaximal sei. Für alle y I 2 \ I 1 gilt dann I 1 y I, d. h. y cl(i 1 ), und damit I 2 cl(i 1 ). Mit (CL2) und (CL3) folgt nun cl(i 2 ) cl(cl(i 1 )) = cl(i 1 ), also, da I 2 eine Basis und damit aufspannend ist, cl(i 1 ) = E. Also muss auch I 1 maximal sein, Widerspruch. Zu (IM): Sei I I und X E, und sei K eine aufsteigende Kette in S := {I I I I X}, und sei I K := K. Für jede endliche Teilmenge F I K gibt es dann ein Kettenglied G K mit F G, es ist also F I. Mit (I4) folgt nun I K I, und da offenbar I K S ist, ist I K eine obere Schranke von S. Nach dem Lemma von Zorn besitzt S dann ein maximales Element. Damit ist (IM) bewiesen. 19
24 2.7. Beziehungen zwischen den Klassen Matroid-ähnlicher Objekte Für den folgenden Satz benötigen wir noch ein Lemma von Bruhn et al. (2010). Lemma Sei M = (E, I ) ein Matroid. Dann gilt (I3 ) Für I 1, I 2 I, wobei I 2 maximal sei, gibt es eine maximale unabhängige Menge B mit I 1 B I 1 I 2. Beweis. Nach (IM) gibt es ein maximales Element B der Menge {I I I 1 I I 1 I 2 }. Angenommen, B ist keine Basis von M. Dann gibt es nach (I3) ein x I 2 \ B mit B x I, aber dann wäre auch I 1 B x I 1 I 2, Widerspruch, denn B ist maximal mit dieser Eigenschaft. Satz Sei M = (E, I ) ein Matroid. Dann gilt für M die endliche Ergänzungseigenschaft (I3 F ). Beweis. Angenommen, I 1, I 2 I mit I 1 < I 2 < bilden ein Gegenbeispiel, d. h. für alle x I 2 \ I 1 ist I 1 x eine abhängige Menge. Den Beweis kann man beispielsweise leicht führen, indem man auf der Restriktion M (I 1 I 2 ), die nach Satz 2.36 ein Matroid ist, das Axiom (I3) anwendet. Hier soll jedoch ein anderer Weg beschritten werden: (1) Ergänze I 1 unter Verwendung von (IM) zu einer Basis B 1. Nach der Annahme gilt dann B 1 I 2 = I 1 I 2. (2.12) (2) Ergänze I 2 unter Verwendung von (I3 ) aus Lemma 2.40 zu einer Basis B 2 mit I 2 B 2 I 2 B 1. (2.13) (3) Ergänze I 1 unter Verwendung von (I3 ) zu einer Basis B 3 mit I 1 B 3 I 1 B 2. (2.14) Nach der Annahme gilt dann B 3 I 2 = I 1 I 2. (2.15) (4) Aus (2.13) und (2.14) folgt B 3 I 1 B 2 I 1 I 2 B 1 = I 2 B 1, also mit (2.15) B 3 \ I 2 B 1 \ I 2 und (2.16) B 3 I 2 = I 1 I 2 = B 1 I 2, (2.17) also B 3 B 1 und daher B 3 = B 1. Aus (2.14) schließt man also I 1 B 1 I 1 B 2. (2.18) 20
25 2.7. Beziehungen zwischen den Klassen Matroid-ähnlicher Objekte (5) Aus (2.13) folgt durch Bilden der Mengendifferenz mit B 1 I 2 \ B 1 B 2 \ B 1 I 2 \ B 1, also (2.19) B 2 \ B 1 = I 2 \ B 1 = I 2 \ I 1, (2.20) wobei die letzte Gleichung aus (2.12) folgt. Aus (2.18) folgt analog I 1 \ B 2 B 1 \ B 2 I 1 \ B 2, also (2.21) B 1 \ B 2 = I 1 \ B 2 I 1 \ I 2 (2.22) Wir haben also B 1 \ B 2 I 1 \ I 2 < I 2 \ I 1 = B 2 \ B 1, (2.23) und damit einen Widerspruch zum folgenden Lemma. Lemma Sind B 1, B 2 Basen mit B 1 \ B 2 <, so folgt B 1 \ B 2 = B 2 \ B 1. Beweis. 8 Angenommen, B 1, B 2 bilden ein Gegenbeispiel, für das o. B. d. A. B 1 \ B 2 minimal ist. Es gilt also B 1 \ B 2 < B 2 \ B 1. Sei x B 2 \ B 1 gewählt. Mit (I3 ) existiert eine Basis B 3 mit B 2 \ x B 3 (B 2 \ x) B 1. Da B 3 keine echte Teilmenge von B 2 sein kann, muss es einen nichtleeren Schnitt B 3 (B 1 \B 2 ) geben. Es folgt B 1 \ B 3 < B 1 \ B 2, laut der Annahme bildet das Paar B 1, B 3 also kein Gegenbeispiel, d. h. es gilt B 1 \ B 3 = B 3 \ B 1, und es folgt B 3 \ B 1 = B 1 \ B 3 < B 1 \ B 2 < B 2 \ B 1, im Widerspruch dazu, dass sich B 3 \ B 1 und B 2 \ B 1 nur um ein Element unterscheiden. Korollar Ein Matroid, das zusätzlich (I4) erfüllt, ist ein finitäres Matroid. Da wir gerade (I3 F ) für Matroide bewiesen haben, folgt: Korollar Matroide sind pre-independence spaces. 8 Bruhn et al. (2010, Lemma 3.7) 21
26 3 Der Greedy-Algorithmus Dieses Kapitel ist zunächst der Darstellung der bekannten Aussagen über den endlichen Greedy-Algorithmus gewidmet. Wir werden zeigen, dass endliche Matroide dadurch charakterisiert sind, dass auf ihnen der (endliche) Greedy-Algorithmus für jede Gewichtsfunktion eine optimale Lösung liefert. Danach werden wir die Anpassung der Definition des Greedy-Algorithmus auf unendliche Unabhängigkeitssysteme vorbereiten, indem wir die Gewichtsfunktion durch eine Wohlordnung auf der Grundmenge ersetzen. 3.1 Gewichtete Matroide Definition 3.1. Ein gewichtetes Matroid ist ein Matroid (E, I ) mit einer Gewichtsfunktion w : E R. Wir betrachten in diesem Abschnitt das folgende Optimierungsproblem: Gesucht ist ein maximales Element A von I mit minimalem Gesamtgewicht w(a) := x A w(x). (3.1) So gestellt handelt es sich um ein Minimierungsproblem. Maximierungsprobleme können durch Negieren der Gewichtsfunktion in Minimierungsprobleme überführt werden und bedürfen daher keiner gesonderten Betrachtung. Algorithmus 4 Greedy-Algorithmus für gewichtete Matroide. 1: A 0 := 2: k := 0 3: while A k ist keine Basis do 4: Wähle x k A k so, dass w(x k ) minimal und A k x k I ist. 5: A k+1 := A k x k 6: k := k + 1 7: end while 8: return A k 22
27 3.1. Gewichtete Matroide Satz 3.2. Sei M = (E, I ) ein endliches Matroid mit einer beliebigen Gewichtsfunktion w : E R. Dann liefert der Greedy-Algorithmus (Algorithmus 4) eine Basis A mit minimalem Gesamtgewicht, d. h. es gilt für jede Basis B von M: w(x). (3.2) x A w(x) x B Der Beweis findet sich bei Oxley (1992a, Abschnitt 1.8). Er ist jedoch so erhellend, dass er hier wiedergegeben werden soll. Beweis. Der Algorithmus terminiert offenbar nach r = r(m) Schritten mit einer Basis A = A r = {x 0, x 1,..., x r 1 }. Sei B = {y 0, y 1,..., y r 1 } eine beliebige Basis von M mit w(y 0 ) w(y 1 ) w(y r 1 ). Die Behauptung folgt nun mit dem folgenden Lemma. Lemma 3.3. Für 0 k < r gilt w(x k ) w(y k ). Beweis. Annahme des Gegenteils. Sei k der kleinste Index mit w(x k ) > w(y k ). Sei I 1 := {x 0, x 1,..., x k 1 } und I 2 := {y 0, y 1,..., y k }. Da I 1 < I 2 gibt es nach (I3) ein y t I 2 \ I 1, so dass I 1 y t I. Da nun aber w(y t ) w(y k ) < w(x k ) laut Annahme ist, hätte der Greedy-Algorithmus y t statt x k wählen müssen, um A k+1 zu bilden, Widerspruch. Die Aussage des Lemmas 3.3 ist wesentlich stärker als von Satz 3.2 benötigt. Nicht nur ist das Gesamtgewicht von A minimal, auch das Gewicht jedes einzelnen Basiselements ist kleiner oder gleich dem des korrespondierenden Elementes einer beliebigen anderen Basis. Wir werden darauf im nächsten Abschnitt zurückkommen. Wie in der Einleitung schon erwähnt, gilt in gewisser Weise sogar die Umkehrung von Satz 3.2. Während es zwar andere Strukturen gibt, auf denen der Greedy-Algorithmus funktioniert, so sind doch die endlichen Matroide genau diejenigen endlichen Unabhängigkeitssysteme, für die das der Fall ist. Definition 3.4. Sei E eine (endliche) Menge und I P(E) ein System von Teilmengen von E. Dann heißt das Paar U = (E, I ) (endliches) Unabhängigkeitssystem, falls die Unabhängigkeitsaxiome (I1) und (I2) erfüllt sind. Soweit anwendbar gilt für Unabhängigkeitssysteme die gleiche Terminologie wie für Matroide. Die Elemente von I heißen unabhängige Mengen, maximale unabhängige Mengen heißen Basen usw. Satz 3.5. Sei U = (E, I ) ein endliches Unabhängigkeitssystem. Für jede Gewichtsfunktion w : E R liefere der Greedy-Algorithmus 4 eine Basis A mit minimalem Gewicht. Dann ist U ein endliches Matroid. Der folgende Beweis nutzt die Formulierung des Optimierungsproblems als Maximierungsproblem. Es sei nochmals darauf hingewiesen, dass Minimierungs- und Maximierungsprobleme äquivalent sind, da sie ineinander überführt werden können. 23
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 6 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 16. Mai 2018 [Letzte Aktualisierung: 18/05/2018,
ADS: Algorithmen und Datenstrukturen 2 Teil 6 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 16. Mai 2018 [Letzte Aktualisierung: 18/05/2018,
3.2 Unabhängigkeitsstrukturen
 80 3.2 Unabhängigkeitsstrukturen Unser Ziel ist der Nachweis, daß in Vektorräumen, also in Moduln über Körpern, Basen existieren und zwei endliche Basen gegebenenfalls von derselben Ordnung sind. (Basen
80 3.2 Unabhängigkeitsstrukturen Unser Ziel ist der Nachweis, daß in Vektorräumen, also in Moduln über Körpern, Basen existieren und zwei endliche Basen gegebenenfalls von derselben Ordnung sind. (Basen
Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl. Beispiele für optimale Greedy-Lösungen
 Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 24. April 2019 [Letzte Aktualisierung: 24/04/2019,
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 24. April 2019 [Letzte Aktualisierung: 24/04/2019,
1 Matroide. 1.1 Definitionen und Beispiele. Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler
 Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler 1 Matroide 1.1 Definitionen und Beispiele 1. Definition (Unabhängigkeitssystem): Ein Mengensystem
Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler 1 Matroide 1.1 Definitionen und Beispiele 1. Definition (Unabhängigkeitssystem): Ein Mengensystem
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph.
 Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Durchschnitt von Matroiden
 Durchschnitt von Matroiden Satz von Edmonds Dany Sattler 18. Januar 2007/ Seminar zur ganzzahligen Optimierung / Wallenfels Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt
Durchschnitt von Matroiden Satz von Edmonds Dany Sattler 18. Januar 2007/ Seminar zur ganzzahligen Optimierung / Wallenfels Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide
 Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
2.3 Basis und Dimension
 Lineare Algebra I WS 205/6 c Rudolf Scharlau 65 2.3 Basis und Dimension In diesem zentralen Abschnitt werden einige für die gesamte Lineare Algebra fundamentale Grundbegriffe eingeführt: Lineare Abhängigkeit
Lineare Algebra I WS 205/6 c Rudolf Scharlau 65 2.3 Basis und Dimension In diesem zentralen Abschnitt werden einige für die gesamte Lineare Algebra fundamentale Grundbegriffe eingeführt: Lineare Abhängigkeit
9 Minimum Spanning Trees
 Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
technische universität dortmund Dortmund, im Dezember 2011 Fakultät für Mathematik Prof. Dr. H. M. Möller
 technische universität dortmund Dortmund, im Dezember 2011 Fakultät für Mathematik Prof. Dr. H. M. Möller Lineare Algebra für Lehramt Gymnasien und Berufskolleg Zusammenfassung der Abschnitte 4.3 und 4.4
technische universität dortmund Dortmund, im Dezember 2011 Fakultät für Mathematik Prof. Dr. H. M. Möller Lineare Algebra für Lehramt Gymnasien und Berufskolleg Zusammenfassung der Abschnitte 4.3 und 4.4
Lineare Algebra und analytische Geometrie I
 Prof Dr H Brenner Osnabrück WS 25/26 Lineare Algebra und analytische Geometrie I Schläft ein Lied in allen Dingen, Die da träumen fort und fort, Und die Welt hebt an zu singen, Triffst du nur das Zauberwort
Prof Dr H Brenner Osnabrück WS 25/26 Lineare Algebra und analytische Geometrie I Schläft ein Lied in allen Dingen, Die da träumen fort und fort, Und die Welt hebt an zu singen, Triffst du nur das Zauberwort
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Mengenlehre und vollständige Induktion
 Fachschaft MathPhys Heidelberg Mengenlehre und vollständige Induktion Vladislav Olkhovskiy Vorkurs 018 Inhaltsverzeichnis 1 Motivation 1 Mengen.1 Grundbegriffe.................................. Kostruktionen
Fachschaft MathPhys Heidelberg Mengenlehre und vollständige Induktion Vladislav Olkhovskiy Vorkurs 018 Inhaltsverzeichnis 1 Motivation 1 Mengen.1 Grundbegriffe.................................. Kostruktionen
Informatik II, SS 2016
 Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Graphentheorie. Zusammenhang. Zusammenhang. Zusammenhang. Rainer Schrader. 13. November 2007
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 13. November 2007 1 / 84 2 / 84 Gliederung stest und Schnittkanten älder und Bäume minimal aufspannende Bäume Der Satz von Menger 2-zusammenhängende
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 13. November 2007 1 / 84 2 / 84 Gliederung stest und Schnittkanten älder und Bäume minimal aufspannende Bäume Der Satz von Menger 2-zusammenhängende
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
 Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Einführung in die mathematische Logik
 Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 5 Das Lemma von Zorn Wir möchten im Folgenden zeigen, dass eine widerpruchsfreie Menge Γ L V von Aussagen nicht nur
Prof. Dr. H. Brenner Osnabrück SS 2014 Einführung in die mathematische Logik Vorlesung 5 Das Lemma von Zorn Wir möchten im Folgenden zeigen, dass eine widerpruchsfreie Menge Γ L V von Aussagen nicht nur
Lösungen zu Kapitel 5
 Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
4.2 Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition 4.2.1
 Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
Kapitel IV Minimale Spannbäume
 Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
Kapitel IV Minimale Spannbäume 1. Grundlagen Ein Graph G = (V, E) besteht aus einer Menge V von Knoten und einer Menge E von Kanten. Wir werden nur endliche Knoten- (und damit auch Kanten-) Mengen betrachten.
3.3 Austauschsatz, Basisergänzungssatz und Dimension
 66 Kapitel III: Vektorräume und Lineare Abbildungen 3.3 Austauschsatz, Basisergänzungssatz und Dimension Montag, 15. Dezember 2003 Es sei V ein Vektorraum. Jedes Teilsystem eines linear unabhängigen Systems
66 Kapitel III: Vektorräume und Lineare Abbildungen 3.3 Austauschsatz, Basisergänzungssatz und Dimension Montag, 15. Dezember 2003 Es sei V ein Vektorraum. Jedes Teilsystem eines linear unabhängigen Systems
Wir betrachten einen einfachen Algorithmus, der den Zusammenhang eines Graphen testen soll.
 Kapitel 2 Zusammenhang 2.1 Zusammenhängende Graphen Wir betrachten einen einfachen Algorithmus, der den Zusammenhang eines Graphen testen soll. (1) Setze E = E, F =. (2) Wähle e E und setze F = F {e},
Kapitel 2 Zusammenhang 2.1 Zusammenhängende Graphen Wir betrachten einen einfachen Algorithmus, der den Zusammenhang eines Graphen testen soll. (1) Setze E = E, F =. (2) Wähle e E und setze F = F {e},
Auswahlaxiom, Zornsches Lemma und Wohlordnungssatz. 14.Oktober 97
 Auswahlaxiom, Zornsches Lemma und Wohlordnungssatz Uwe Liebe Sven Hermann 14.Oktober 97 Inhaltsverzeichnis 1 Einleitung 3 2 Auswahlaxiom 4 3 Ordnung 5 4 Zornsches Lemma 9 5 Wohlordnungssatz 11 6 Zurück
Auswahlaxiom, Zornsches Lemma und Wohlordnungssatz Uwe Liebe Sven Hermann 14.Oktober 97 Inhaltsverzeichnis 1 Einleitung 3 2 Auswahlaxiom 4 3 Ordnung 5 4 Zornsches Lemma 9 5 Wohlordnungssatz 11 6 Zurück
Mathematik I. Vorlesung 11. Lineare Unabhängigkeit
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 11 Lineare Unabhängigkeit Definition 11.1. Es sei K ein Körper und V ein K-Vektorraum. Dann heißt eine Familie von Vektoren v i, i I,
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 11 Lineare Unabhängigkeit Definition 11.1. Es sei K ein Körper und V ein K-Vektorraum. Dann heißt eine Familie von Vektoren v i, i I,
Übung zur Vorlesung Diskrete Strukturen I
 Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Technische Universität München WS 00/0 Institut für Informatik Aufgabenblatt Prof. Dr. J. Csirik. November 00 Brandt & Stein Übung zur Vorlesung Diskrete Strukturen I Abgabetermin: Tutorübungen am. und.
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Konvergenz, Filter und der Satz von Tychonoff
 Abschnitt 4 Konvergenz, Filter und der Satz von Tychonoff In metrischen Räumen kann man topologische Begriffe wie Stetigkeit, Abschluss, Kompaktheit auch mit Hilfe von Konvergenz von Folgen charakterisieren.
Abschnitt 4 Konvergenz, Filter und der Satz von Tychonoff In metrischen Räumen kann man topologische Begriffe wie Stetigkeit, Abschluss, Kompaktheit auch mit Hilfe von Konvergenz von Folgen charakterisieren.
Kapitel 5: Minimale spannende Bäume Gliederung der Vorlesung
 Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
13 Auswahlaxiom und Zornsches Lemma
 13 Auswahlaxiom und Zornsches Lemma Handout zur Funktionalanalysis I von H. Glöckner, 25.11.2008 Wichtige Teile der modernen Mathematik beruhen auf dem sogenannten Auswahlaxiom der Mengenlehre. Dieses
13 Auswahlaxiom und Zornsches Lemma Handout zur Funktionalanalysis I von H. Glöckner, 25.11.2008 Wichtige Teile der modernen Mathematik beruhen auf dem sogenannten Auswahlaxiom der Mengenlehre. Dieses
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 7 und 8: Euler- und Hamilton-Graphen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 17. April 2018 1/96 WIEDERHOLUNG Eulersche
Algorithmische Graphentheorie Vorlesung 7 und 8: Euler- und Hamilton-Graphen Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 17. April 2018 1/96 WIEDERHOLUNG Eulersche
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 16 (2.7.2014) Graphtraversierung II, Minimale Spannbäume I Algorithmen und Komplexität Tiefensuche: Pseusocode DFS Traversal: for all u in
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 16 (2.7.2014) Graphtraversierung II, Minimale Spannbäume I Algorithmen und Komplexität Tiefensuche: Pseusocode DFS Traversal: for all u in
Übungsblatt 5 Lösungsvorschläge
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 5 Lösungsvorschläge Vorlesung Algorithmentechnik im WS 09/10 Problem 1: Lineare Weihnachtsalgebra Kreisbasen [vgl. Kapitel
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 5 Lösungsvorschläge Vorlesung Algorithmentechnik im WS 09/10 Problem 1: Lineare Weihnachtsalgebra Kreisbasen [vgl. Kapitel
Hrushovskis primordiales Amalgam
 Hrushovskis primordiales Amalgam M.Z. 27. September 2009 Zusammenfassung Hrushovskis originale Fusion [1]. Seminarvortrag, Freiburg 4.Mai 2005 We prove that the resulting theory is model-complete (26.11.2005).
Hrushovskis primordiales Amalgam M.Z. 27. September 2009 Zusammenfassung Hrushovskis originale Fusion [1]. Seminarvortrag, Freiburg 4.Mai 2005 We prove that the resulting theory is model-complete (26.11.2005).
Algorithmische Graphentheorie
 Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
7 Polymatroide Submodulare Funktionen Die Sätze von Hall und Rado Die Komplexe Vereinigung von Matroiden...
 Inhaltsverzeichnis 1 Einstimmung 3 1.1 Organisatorisches......................................... 3 1.2 Einführende Beispiele...................................... 4 1.3 Bedeutung der Matroidtheorie..................................
Inhaltsverzeichnis 1 Einstimmung 3 1.1 Organisatorisches......................................... 3 1.2 Einführende Beispiele...................................... 4 1.3 Bedeutung der Matroidtheorie..................................
5 Komplementäre Verbände
 5 Komplementäre Verbände Die Bestimmung von Verbandselementen durch Punkte hat in modularen längenendlichen Verbänden im Falle der Existenz sinnvolle Eigenschaften (vgl. 4.5), die Existenz kann aber mit
5 Komplementäre Verbände Die Bestimmung von Verbandselementen durch Punkte hat in modularen längenendlichen Verbänden im Falle der Existenz sinnvolle Eigenschaften (vgl. 4.5), die Existenz kann aber mit
Freie Bäume und Wälder
 (Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
(Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
ADS: Algorithmen und Datenstrukturen 2
 ADS: Algorithmen und Datenstrukturen 2 Teil XIII Peter F. Stadler & Konstantin Klemm Bioinformatics Group, Dept. of Computer Science & Interdisciplinary Center for Bioinformatics, University of Leipzig
ADS: Algorithmen und Datenstrukturen 2 Teil XIII Peter F. Stadler & Konstantin Klemm Bioinformatics Group, Dept. of Computer Science & Interdisciplinary Center for Bioinformatics, University of Leipzig
3. Minimale Spannbäume. Definition 99 T heißt minimaler Spannbaum (MSB, MST) von G, falls T Spannbaum von G ist und gilt:
 3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
3. Minimale Spannbäume Sei G = (V, E) ein einfacher ungerichteter Graph, der o.b.d.a. zusammenhängend ist. Sei weiter w : E R eine Gewichtsfunktion auf den Kanten von G. Wir setzen E E: w(e ) = e E w(e),
1. Gruppen. 1. Gruppen 7
 1. Gruppen 7 1. Gruppen Wie schon in der Einleitung erläutert wollen wir uns in dieser Vorlesung mit Mengen beschäftigen, auf denen algebraische Verknüpfungen mit gewissen Eigenschaften definiert sind.
1. Gruppen 7 1. Gruppen Wie schon in der Einleitung erläutert wollen wir uns in dieser Vorlesung mit Mengen beschäftigen, auf denen algebraische Verknüpfungen mit gewissen Eigenschaften definiert sind.
Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo?
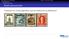 Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
Ausarbeitung zum Modulabschluss. Graphentheorie. spannende Bäume, bewertete Graphen, optimale Bäume, Verbindungsprobleme
 Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion
 Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion Saskia Klaus 07.10.016 1 Motivation In den ersten beiden Vorträgen des Vorkurses haben wir gesehen, wie man aus schon bekannten Wahrheiten
Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion Saskia Klaus 07.10.016 1 Motivation In den ersten beiden Vorträgen des Vorkurses haben wir gesehen, wie man aus schon bekannten Wahrheiten
3. Musterlösung. Problem 1: Boruvka MST
 Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 06/07 ITI Wagner. Musterlösung Problem : Boruvka MST pt (a) Beweis durch Widerspruch. Sei T MST von G, e die lokal minimale Kante eines
Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 06/07 ITI Wagner. Musterlösung Problem : Boruvka MST pt (a) Beweis durch Widerspruch. Sei T MST von G, e die lokal minimale Kante eines
Überabzählbarkeit der reellen Zahlen
 Überabzählbarkeit der reellen Zahlen Mathematik M4 Dozentin: Dr. Regula Krapf Jan Lukas Schallenberg Matr. Nr.: 214202241 November 2017 1 Inhaltsverzeichnis 1 Dedekindsche Schnitte 3 2 Addition und Multiplikation
Überabzählbarkeit der reellen Zahlen Mathematik M4 Dozentin: Dr. Regula Krapf Jan Lukas Schallenberg Matr. Nr.: 214202241 November 2017 1 Inhaltsverzeichnis 1 Dedekindsche Schnitte 3 2 Addition und Multiplikation
\ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E.
 Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
1. Gruppen. 1. Gruppen 7
 1. Gruppen 7 1. Gruppen Wie schon in der Einleitung erläutert wollen wir uns in dieser Vorlesung mit Mengen beschäftigen, auf denen algebraische Verknüpfungen mit gewissen Eigenschaften definiert sind.
1. Gruppen 7 1. Gruppen Wie schon in der Einleitung erläutert wollen wir uns in dieser Vorlesung mit Mengen beschäftigen, auf denen algebraische Verknüpfungen mit gewissen Eigenschaften definiert sind.
Mathematisches Argumentieren und Beweisen Beweisarten Besipiele. Hagen Knaf, WS 2014/15
 Mathematisches Argumentieren und Beweisen Beweisarten Besipiele Hagen Knaf, WS 2014/15 Im Folgenden sind einige der in der Vorlesung besprochenen Beispielbeweise für die verschiedenen Beweisarten aufgeführt
Mathematisches Argumentieren und Beweisen Beweisarten Besipiele Hagen Knaf, WS 2014/15 Im Folgenden sind einige der in der Vorlesung besprochenen Beispielbeweise für die verschiedenen Beweisarten aufgeführt
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Lerneinheit 3: Greedy Algorithmen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2016 10.5.2016 Einleitung Einleitung Diese Lerneinheit
Algorithmen und Datenstrukturen 2 Lerneinheit 3: Greedy Algorithmen Prof. Dr. Christoph Karg Studiengang Informatik Hochschule Aalen Sommersemester 2016 10.5.2016 Einleitung Einleitung Diese Lerneinheit
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Elemente in Φ werden Wurzeln genannt. Bemerkung 3.2. (a) Zu einem Wurzelsystem können wir immer eine Spiegelungsgruppe definieren
 3. Wurzelsysteme Als erstes führen wir den Begriff eines Wurzelsystems ein. Definition 3.1 (Wurzelsystem). Eine endliche Teilmenge Φ V {0} heißt Wurzelsystem falls gilt: (R1) Φ Rα = {±α} für α Φ, (R2)
3. Wurzelsysteme Als erstes führen wir den Begriff eines Wurzelsystems ein. Definition 3.1 (Wurzelsystem). Eine endliche Teilmenge Φ V {0} heißt Wurzelsystem falls gilt: (R1) Φ Rα = {±α} für α Φ, (R2)
Ausgewählte Lösungen zu den Übungsblättern 4-5
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Ausgewählte en zu den Übungsblättern -5 Aufgabe, Lineare Unabhängigkeit
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Ausgewählte en zu den Übungsblättern -5 Aufgabe, Lineare Unabhängigkeit
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen Safe
Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen Safe
Kantengraphen und Planare Graphen. Seminararbeit
 Kantengraphen und Planare Graphen Seminararbeit in Mathematisches Seminar für LAK 621.378 SS 2018 vorgelegt von Anna Maria Gärtner bei: Baur, Karin, Univ.-Prof. Dr.phil. Graz, 2018 Inhaltsverzeichnis 1
Kantengraphen und Planare Graphen Seminararbeit in Mathematisches Seminar für LAK 621.378 SS 2018 vorgelegt von Anna Maria Gärtner bei: Baur, Karin, Univ.-Prof. Dr.phil. Graz, 2018 Inhaltsverzeichnis 1
Kapitel II. Vektorräume
 Inhalt der Vorlesung LAAG I Prof. Dr. Arno Fehm TU Dresden WS2017/18 Kapitel II. Vektorräume In diesem ganzen Kapitel sei K ein Körper. 1 Definition und Beispiele 1.1 Beispiel. Ist K = R, so haben wir
Inhalt der Vorlesung LAAG I Prof. Dr. Arno Fehm TU Dresden WS2017/18 Kapitel II. Vektorräume In diesem ganzen Kapitel sei K ein Körper. 1 Definition und Beispiele 1.1 Beispiel. Ist K = R, so haben wir
5 Der Transzendenzgrad
 $Id: trgrad.tex,v 1.6 2009/05/11 14:48:57 hk Exp $ 5 Der Transzendenzgrad Wir stellen nun einige der Tatsachen über die Mächtigkeit von Mengen zusammen, die Ihnen wahrscheinlich aus den ersten Semester
$Id: trgrad.tex,v 1.6 2009/05/11 14:48:57 hk Exp $ 5 Der Transzendenzgrad Wir stellen nun einige der Tatsachen über die Mächtigkeit von Mengen zusammen, die Ihnen wahrscheinlich aus den ersten Semester
Kapitel 3: Die Sätze von Euler, Fermat und Wilson. 8 Der Satz von Euler
 Kapitel 3: Die Sätze von Euler, Fermat und Wilson In diesem Kapitel wollen wir nun die eulersche -Funktion verwenden, um einen berühmten Satz von Euler zu formulieren, aus dem wir dann mehrere interessante
Kapitel 3: Die Sätze von Euler, Fermat und Wilson In diesem Kapitel wollen wir nun die eulersche -Funktion verwenden, um einen berühmten Satz von Euler zu formulieren, aus dem wir dann mehrere interessante
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/42 Graphische Darstellung von Zusammenhängen schon an vielen Stellen
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/42 Graphische Darstellung von Zusammenhängen schon an vielen Stellen
Übungsblatt 2 - Lösung
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik quasthoff@informatik.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen
Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik quasthoff@informatik.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen
Kapitel 13. Lineare Gleichungssysteme und Basen
 Kapitel 13. Lineare Gleichungssysteme und Basen Matrixform des Rangsatzes Satz. Sei A eine m n-matrix mit den Spalten v 1, v 2,..., v n. A habe den Rang r. Dann ist die Lösungsmenge L := x 1 x 2. x n x
Kapitel 13. Lineare Gleichungssysteme und Basen Matrixform des Rangsatzes Satz. Sei A eine m n-matrix mit den Spalten v 1, v 2,..., v n. A habe den Rang r. Dann ist die Lösungsmenge L := x 1 x 2. x n x
Skriptbausteine zur Vorlesung Maßtheorie
 Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Algorithmik WS 07/ Vorlesung, Andreas Jakoby Universität zu Lübeck. 10 Matching-Probleme
 10 Matching-Probleme 10.1 Definition von Matching-Probleme Definition 21 [2-dimensionales Matching] Sei G = (V, E) ein ungerichteter Graph und E E. E ist ein Matching, wenn für alle Kantenpaare e 1, e
10 Matching-Probleme 10.1 Definition von Matching-Probleme Definition 21 [2-dimensionales Matching] Sei G = (V, E) ein ungerichteter Graph und E E. E ist ein Matching, wenn für alle Kantenpaare e 1, e
Dieser Graph hat 3 Zusammenhangskomponenten
 Vl 2, Informatik B, 19. 04. 02 1.1.3 Definitionen und wichtige Graphen Sei im folgenden G =(V;E) ein schlichter ungerichteter Graph. Definition: Der Grad eines Knoten v in einem ungerichteten Graphen ist
Vl 2, Informatik B, 19. 04. 02 1.1.3 Definitionen und wichtige Graphen Sei im folgenden G =(V;E) ein schlichter ungerichteter Graph. Definition: Der Grad eines Knoten v in einem ungerichteten Graphen ist
Argumentationen zu ermöglichen, verlangen wir, dass diese Eigenschaft auch für induzierte Teilgraphen
 Kapitel 9 Perfekte Graphen 9.1 α- und χ-perfektheit Eine Clique in einem Graphen G ist ein induzierter vollstäniger Teilgraph. Die Cliquenzahl ω(g) ist die Kardinalität einer größten in G enthaltene Clique.
Kapitel 9 Perfekte Graphen 9.1 α- und χ-perfektheit Eine Clique in einem Graphen G ist ein induzierter vollstäniger Teilgraph. Die Cliquenzahl ω(g) ist die Kardinalität einer größten in G enthaltene Clique.
5.7 Lineare Abhängigkeit, Basis und Dimension
 8 Kapitel 5. Lineare Algebra 5.7 Lineare Abhängigkeit, Basis und Dimension Seien v,...,v n Vektoren auseinemvektorraumv über einem KörperK. DieMenge aller Linearkombinationen von v,...,v n, nämlich { n
8 Kapitel 5. Lineare Algebra 5.7 Lineare Abhängigkeit, Basis und Dimension Seien v,...,v n Vektoren auseinemvektorraumv über einem KörperK. DieMenge aller Linearkombinationen von v,...,v n, nämlich { n
1. Topologische Räume
 1. Topologische Räume 5 1. Topologische Räume Wie schon in der Einleitung erwähnt wollen wir uns in dieser Vorlesung mit stetigen Abbildungen beschäftigen. Als Erstes müssen wir uns daher fragen, welche
1. Topologische Räume 5 1. Topologische Räume Wie schon in der Einleitung erwähnt wollen wir uns in dieser Vorlesung mit stetigen Abbildungen beschäftigen. Als Erstes müssen wir uns daher fragen, welche
Folgen. Definition. Sei M eine beliebige Menge. Eine Abbildung a : N M oder a : N 0 M heißt eine Folge.
 Folgen Eine Folge stellt man sich am einfachsten als eine Aneinanderreihung von Zahlen (oder Elementen irgendeiner anderen Menge) vor, die immer weiter geht Etwa,,,,,, oder,,, 8,,,, oder 0,,,,,,,, In vielen
Folgen Eine Folge stellt man sich am einfachsten als eine Aneinanderreihung von Zahlen (oder Elementen irgendeiner anderen Menge) vor, die immer weiter geht Etwa,,,,,, oder,,, 8,,,, oder 0,,,,,,,, In vielen
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
 3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
U = U, v i λ i = o und (z.b.) λ 1 0. i=1 1 = i=2. i=2
 7 Lineare Unabhängigkeit, asis Existenzsatz M Am Ende des vorigen Paragraphen betrachteten wir bei vorgegebener Teilmenge T eines K-Vektorraumes V das Erzeugnis U von T in V. Die ildung des Erzeugnisses
7 Lineare Unabhängigkeit, asis Existenzsatz M Am Ende des vorigen Paragraphen betrachteten wir bei vorgegebener Teilmenge T eines K-Vektorraumes V das Erzeugnis U von T in V. Die ildung des Erzeugnisses
Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume)
 WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Analyis I -Metrische Räume - eine Einführung in die Topologie
 Analyis I -Metrische Räume - eine Einführung in die Topologie E = E isolierter Punkte x 1 x 2 x 3 E ist abgeschlossen U ɛ (x) x innerer Punkt Ω Häufungspunkte Ω Metrik Metrische Räume Definition Sei X
Analyis I -Metrische Räume - eine Einführung in die Topologie E = E isolierter Punkte x 1 x 2 x 3 E ist abgeschlossen U ɛ (x) x innerer Punkt Ω Häufungspunkte Ω Metrik Metrische Räume Definition Sei X
Ordnung ins Chaos bringen
 Ordnung ins Chaos bringen 1 1 Einleitung Ordnung ins Chaos bringen Vor kurzem tauchte in einer Diskussion auf dem Weg von einer Vorlesung zur nächsten innerhalb einer Gruppe von Studenten (größtenteils
Ordnung ins Chaos bringen 1 1 Einleitung Ordnung ins Chaos bringen Vor kurzem tauchte in einer Diskussion auf dem Weg von einer Vorlesung zur nächsten innerhalb einer Gruppe von Studenten (größtenteils
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 15. April 2018 1/46 Die Dimension eines Vektorraums Satz 2.27 (Basisergänzungssatz) Sei V ein Vektorraum über einem Körper K. Weiter seien v 1,...,
(Analysis und lineare Algebra) im Sommersemester 2018 15. April 2018 1/46 Die Dimension eines Vektorraums Satz 2.27 (Basisergänzungssatz) Sei V ein Vektorraum über einem Körper K. Weiter seien v 1,...,
Theoretische Informatik. Exkurs: Komplexität von Optimierungsproblemen. Optimierungsprobleme. Optimierungsprobleme. Exkurs Optimierungsprobleme
 Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
5.1 Affine Räume und affine Abbildungen
 402 LinAlg II Version 1.2 21. Juli 2006 c Rudolf Scharlau 5.1 Affine Räume und affine Abbildungen Ein affiner Raum besteht aus zwei Mengen P und G zusammen mit einer Relation der Inzidenz zwischen ihnen.
402 LinAlg II Version 1.2 21. Juli 2006 c Rudolf Scharlau 5.1 Affine Räume und affine Abbildungen Ein affiner Raum besteht aus zwei Mengen P und G zusammen mit einer Relation der Inzidenz zwischen ihnen.
3 Längenendliche Verbände. Dimension
 3 Längenendliche Verbände. Dimension Unser Ziel ist es, projektive Geometrien endlicher Dimension durch Spezialisierung der betrachteten Verbände zu kennzeichnen. Dazu gehört sicher, dass es endliche viele
3 Längenendliche Verbände. Dimension Unser Ziel ist es, projektive Geometrien endlicher Dimension durch Spezialisierung der betrachteten Verbände zu kennzeichnen. Dazu gehört sicher, dass es endliche viele
Cauchy-Folgen und Kompaktheit. 1 Cauchy-Folgen und Beschränktheit
 Vortrag zum Seminar zur Analysis, 10.05.2010 Michael Engeländer, Jonathan Fell Dieser Vortrag stellt als erstes einige Sätze zu Cauchy-Folgen auf allgemeinen metrischen Räumen vor. Speziell wird auch das
Vortrag zum Seminar zur Analysis, 10.05.2010 Michael Engeländer, Jonathan Fell Dieser Vortrag stellt als erstes einige Sätze zu Cauchy-Folgen auf allgemeinen metrischen Räumen vor. Speziell wird auch das
8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN
 8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN (vi) Konvergenz von Folgen ist in topologischen Räumen folgendermaßen definiert: Ist (a n ) M eine Folge, so heißt sie konvergent gegen a M, wenn es
8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN (vi) Konvergenz von Folgen ist in topologischen Räumen folgendermaßen definiert: Ist (a n ) M eine Folge, so heißt sie konvergent gegen a M, wenn es
1 Axiomatische Charakterisierung der reellen. 3 Die natürlichen, die ganzen und die rationalen. 4 Das Vollständigkeitsaxiom und irrationale
 Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Analysis 1, Woche 2. Reelle Zahlen. 2.1 Anordnung. Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität).
 Analysis 1, Woche 2 Reelle Zahlen 2.1 Anordnung Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität). 2. Für jeden a, b K mit a b und b a gilt a = b (Antisymmetrie).
Analysis 1, Woche 2 Reelle Zahlen 2.1 Anordnung Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität). 2. Für jeden a, b K mit a b und b a gilt a = b (Antisymmetrie).
Distanzprobleme in der Ebene
 Distanzprobleme in der Ebene (Literatur: deberg et al., Kapitel 7,9) Christian Knauer 1 Motivation: Alle nächsten Nachbarn Gegeben: Eine Menge von Punkten P in der Ebene Berechne: Zu jedem Punkt aus P
Distanzprobleme in der Ebene (Literatur: deberg et al., Kapitel 7,9) Christian Knauer 1 Motivation: Alle nächsten Nachbarn Gegeben: Eine Menge von Punkten P in der Ebene Berechne: Zu jedem Punkt aus P
Graphen KAPITEL 3. Dieses Problem wird durch folgenden Graph modelliert:
 KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
Mengen und Relationen
 KAPITEL 1 Mengen und Relationen 1.1. Mengenlehre Georg Cantor (3.3.1845 6.1.1918: Cantor ist der Vater der modernen Mengenlehre, er definierte 1895: DEFINITION 1.1.1. Unter einer Menge verstehen wir jede
KAPITEL 1 Mengen und Relationen 1.1. Mengenlehre Georg Cantor (3.3.1845 6.1.1918: Cantor ist der Vater der modernen Mengenlehre, er definierte 1895: DEFINITION 1.1.1. Unter einer Menge verstehen wir jede
5. Bäume und Minimalgerüste
 5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
Aufbau der Projektiven Geometrie
 Seminararbeit zum Seminar aus Reiner Mathematik Aufbau der Projektiven Geometrie Leonie Knittelfelder Matr. Nr. 1011654 WS 2012/13 Inhaltsverzeichnis 1 Einleitung 3 2 Linearmengen 4 2.1 Satz (1.3.1): Das
Seminararbeit zum Seminar aus Reiner Mathematik Aufbau der Projektiven Geometrie Leonie Knittelfelder Matr. Nr. 1011654 WS 2012/13 Inhaltsverzeichnis 1 Einleitung 3 2 Linearmengen 4 2.1 Satz (1.3.1): Das
8 Der Kompaktheitssatz und der Satz von Löwenheim und Skolem
 8 Der Kompaktheitssatz und der Satz von Löwenheim und Skolem 8.1 Der Kompaktheitssatz Kompaktheitssatz Endlichkeitssatz Der Kompaktheitssatz ist auch unter dem Namen Endlichkeitssatz bekannt. Unter Verwendung
8 Der Kompaktheitssatz und der Satz von Löwenheim und Skolem 8.1 Der Kompaktheitssatz Kompaktheitssatz Endlichkeitssatz Der Kompaktheitssatz ist auch unter dem Namen Endlichkeitssatz bekannt. Unter Verwendung
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
2 Die Dimension eines Vektorraums
 2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Kapitel 1. Mengen und Abbildungen. 1.1 Mengen
 Kapitel 1 Mengen und Abbildungen 1.1 Mengen Die Objekte der modernen Mathematik sind die Mengen. Obwohl die Logik einen axiomatischen Zugang zur Mengenlehre bietet, wollen wir uns in dieser Vorlesung auf
Kapitel 1 Mengen und Abbildungen 1.1 Mengen Die Objekte der modernen Mathematik sind die Mengen. Obwohl die Logik einen axiomatischen Zugang zur Mengenlehre bietet, wollen wir uns in dieser Vorlesung auf
1.9 Beweis durch Kontraposition
 1.9 Beweis durch Kontraposition 1.9 Beweis durch Kontraposition Ein Beweis durch Kontraposition ist ein Spezialfall des indirekten Beweises. Wir betrachten zwei Aussagen A und B und wollen A B zeigen,
1.9 Beweis durch Kontraposition 1.9 Beweis durch Kontraposition Ein Beweis durch Kontraposition ist ein Spezialfall des indirekten Beweises. Wir betrachten zwei Aussagen A und B und wollen A B zeigen,
