Durchschnitt von Matroiden
|
|
|
- Norbert Klein
- vor 7 Jahren
- Abrufe
Transkript
1 Durchschnitt von Matroiden Satz von Edmonds Dany Sattler 18. Januar 2007/ Seminar zur ganzzahligen Optimierung / Wallenfels
2 Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt man Unabhängigkeitssystem, falls folgende Axiome erfüllt sind: (M1) : J (M2) : I 1 I 2, I 2 J I 1 J
3 Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt man Unabhängigkeitssystem, falls folgende Axiome erfüllt sind: (M1) : J (M2) : I 1 I 2, I 2 J I 1 J
4 Definition: Unabhängigkeitssystem Definition: Ein Mengensystem (S, J ) nennt man Unabhängigkeitssystem, falls folgende Axiome erfüllt sind: (M1) : J (M2) : I 1 I 2, I 2 J I 1 J
5 Definition: Unabhängigkeitssystem Die Elemente von J werden unabhängig genannt, die Elemente von 2 S \J abhängig. Minimale abhängige Mengen heißen Kreise, maximale unabhängige Mengen heißen Basen
6 Definition: Unabhängigkeitssystem Die Elemente von J werden unabhängig genannt, die Elemente von 2 S \J abhängig. Minimale abhängige Mengen heißen Kreise, maximale unabhängige Mengen heißen Basen
7 Definition: Matroid Definition: Ein Unabhängigkeitssystem (S, J ) heißt Matroid, falls gilt: (M3) : I 1, I 2 J und I 1 > I 2 dann gibt es ein x I 1 \I 2 mit I 2 {x} J
8 Definition: Matroid Definition: Ein Unabhängigkeitssystem (S, J ) heißt Matroid, falls gilt: (M3) : I 1, I 2 J und I 1 > I 2 dann gibt es ein x I 1 \I 2 mit I 2 {x} J
9 Definition: Rang eines Matroiden Definition: Sei (S, J ) ein Matroid. Dann ist für U S der Rang von U definiert durch: r (U) := max { I : I U, I J }
10 Beispiel: Matrixmatroid Matrixmatroid Sei A eine Matrix mit A = Die Spalten der Matrix A, also {(1)... (7)}, bilden die Menge S. Diejenigen Spalten von A, die zusammen linear unabhängig sind, bilden das System aus Teilmengen J von S.
11 Beispiel: Matrixmatroid Dann enthält J alle diejenigen Teilmengen von S \ {(7}) mit höchstens 3 Elementen, außer: {(1), (2), (4)}, {(2), (3), (5)}, {(2), (3), (6)} und außer allen Teilmengen, die {(5), (6)} gemeinsam enthalten. S stellt somit die Grundmenge des Matroiden dar und J das Unabhängigkeitssystem das Paar (S, J ) ist ein Matroid.
12 Beispiel: Matrixmatroid Dann enthält J alle diejenigen Teilmengen von S \ {(7}) mit höchstens 3 Elementen, außer: {(1), (2), (4)}, {(2), (3), (5)}, {(2), (3), (6)} und außer allen Teilmengen, die {(5), (6)} gemeinsam enthalten. S stellt somit die Grundmenge des Matroiden dar und J das Unabhängigkeitssystem das Paar (S, J ) ist ein Matroid.
13 Beispiel: Matrixmatroid Dann enthält J alle diejenigen Teilmengen von S \ {(7}) mit höchstens 3 Elementen, außer: {(1), (2), (4)}, {(2), (3), (5)}, {(2), (3), (6)} und außer allen Teilmengen, die {(5), (6)} gemeinsam enthalten. S stellt somit die Grundmenge des Matroiden dar und J das Unabhängigkeitssystem das Paar (S, J ) ist ein Matroid.
14 Beispiel: Graphenmatroid Graphenmatroid Wir haben den Graphen G = (V, E) mit 4 Ecken {a, b, c, d} und mit 7 Kanten {1, 2, 3, 4, 5, 6, 7} Sei S die Menge der Kanten, also S = E und J sei das System der Teilmengen von S, die kreisfrei sind. Die Kreise von G haben die Kantenmenge: {(7), (5, 6), (1, 2, 4), (2, 3, 5), (2, 3, 6), (1, 3, 4, 5), (1, 3, 4, 6)} (S, J ) ist somit ein Matroid, genauer ein Graphen-Matroid,der mitm (G) bezeichnet wird.
15 Beispiel: Graphenmatroid Graphenmatroid Wir haben den Graphen G = (V, E) mit 4 Ecken {a, b, c, d} und mit 7 Kanten {1, 2, 3, 4, 5, 6, 7} Sei S die Menge der Kanten, also S = E und J sei das System der Teilmengen von S, die kreisfrei sind. Die Kreise von G haben die Kantenmenge: {(7), (5, 6), (1, 2, 4), (2, 3, 5), (2, 3, 6), (1, 3, 4, 5), (1, 3, 4, 6)} (S, J ) ist somit ein Matroid, genauer ein Graphen-Matroid,der mitm (G) bezeichnet wird.
16 Beispiel: Graphenmatroid Graphenmatroid Wir haben den Graphen G = (V, E) mit 4 Ecken {a, b, c, d} und mit 7 Kanten {1, 2, 3, 4, 5, 6, 7} Sei S die Menge der Kanten, also S = E und J sei das System der Teilmengen von S, die kreisfrei sind. Die Kreise von G haben die Kantenmenge: {(7), (5, 6), (1, 2, 4), (2, 3, 5), (2, 3, 6), (1, 3, 4, 5), (1, 3, 4, 6)} (S, J ) ist somit ein Matroid, genauer ein Graphen-Matroid,der mitm (G) bezeichnet wird.
17 Beispiel: Graphenmatroid Graphenmatroid Wir haben den Graphen G = (V, E) mit 4 Ecken {a, b, c, d} und mit 7 Kanten {1, 2, 3, 4, 5, 6, 7} Sei S die Menge der Kanten, also S = E und J sei das System der Teilmengen von S, die kreisfrei sind. Die Kreise von G haben die Kantenmenge: {(7), (5, 6), (1, 2, 4), (2, 3, 5), (2, 3, 6), (1, 3, 4, 5), (1, 3, 4, 6)} (S, J ) ist somit ein Matroid, genauer ein Graphen-Matroid,der mitm (G) bezeichnet wird.
18 Beispiel: Graphenmatroid Dieser Matroid kann auch in eine Matrix umgeformt werden über Ecken-Kanten-Indizes Dabei: Falls Verbindung besteht: = 1; sonst: = 0; wobei hier gilt: Spalte i = Kante i mit i = 1,...,7 und Zeile j = Ecke j mit j = a,b,c,d
19 Beispiel: Graphenmatroid Dieser Matroid kann auch in eine Matrix umgeformt werden über Ecken-Kanten-Indizes Dabei: Falls Verbindung besteht: = 1; sonst: = 0; wobei hier gilt: Spalte i = Kante i mit i = 1,...,7 und Zeile j = Ecke j mit j = a,b,c,d
20 Wiederholung: Bipartiter Graph und Matching 1 Bipartiter Graph ein Graph G = (V, E) heißt bipartit, falls sich seine Knoten V in zwei disjunkte Teilmengen V 1, V 2 aufteilen lassen, s.d. zwischen den Knoten innerhalb beider Teilmengen keine Kanten verlaufen. 2 Matching Ein Matching ist eine Teilmenge der Kanten eines Graphen G, in der keine zwei Kanten einen gemeinsamen Knoten besitzen.
21 Wiederholung: Bipartiter Graph und Matching 1 Bipartiter Graph ein Graph G = (V, E) heißt bipartit, falls sich seine Knoten V in zwei disjunkte Teilmengen V 1, V 2 aufteilen lassen, s.d. zwischen den Knoten innerhalb beider Teilmengen keine Kanten verlaufen. 2 Matching Ein Matching ist eine Teilmenge der Kanten eines Graphen G, in der keine zwei Kanten einen gemeinsamen Knoten besitzen.
22 Motivation 1 Matching in bipartiten Graphen M stellt die Menge aller Matchings in einem bipartiten Graphen G = {V 1 V 2, E = (V 1 V 2 )} dar. M 2 E, 2 Proposition (E, M) ist kein Matroid.
23 Motivation 1 Matching in bipartiten Graphen M stellt die Menge aller Matchings in einem bipartiten Graphen G = {V 1 V 2, E = (V 1 V 2 )} dar. M 2 E, 2 Proposition (E, M) ist kein Matroid.
24 Motivation Beobachtung Sei (E, M) = (E, J 1 J 2 ) mit (E, J 1 ), (E, J 2 ) Matroide, mit: J 1 := {F E : (v 1, w 1 ) F, (v 2, w 2 ) F v 1 v 2 } J 2 := {F E : (v 1, w 1 ) F, (v 2, w 2 ) F w 1 w 2 } Dann ist J 1 ein Matroid.
25 Charakterisierung anhand von Kreisen (S, J ) ein Matroid und C ein System von Teilmengen. Dann heißt C die Menge der Kreise von (S, J ), wenn gilt: (C1): Die leere Menge liegt nicht in C: / C (C2): Kein Element von C ist eine echte Teilmenge eines weiteren Elements von C (C3): C 1, C 2 sind zwei Elemente von C und e C 1 C 2, dann enthält (C 1 C 2 ) \ {e} ein Element von C. (S, J ) ist ein Matroid, wenn C den Axiomen (C1), (C2), (C3) genügt und J aus denjenigen Teilmengen von S besteht, die kein Element von C enthalten
26 Charakterisierung anhand von Kreisen (S, J ) ein Matroid und C ein System von Teilmengen. Dann heißt C die Menge der Kreise von (S, J ), wenn gilt: (C1): Die leere Menge liegt nicht in C: / C (C2): Kein Element von C ist eine echte Teilmenge eines weiteren Elements von C (C3): C 1, C 2 sind zwei Elemente von C und e C 1 C 2, dann enthält (C 1 C 2 ) \ {e} ein Element von C. (S, J ) ist ein Matroid, wenn C den Axiomen (C1), (C2), (C3) genügt und J aus denjenigen Teilmengen von S besteht, die kein Element von C enthalten
27 Charakterisierung anhand von Kreisen (S, J ) ein Matroid und C ein System von Teilmengen. Dann heißt C die Menge der Kreise von (S, J ), wenn gilt: (C1): Die leere Menge liegt nicht in C: / C (C2): Kein Element von C ist eine echte Teilmenge eines weiteren Elements von C (C3): C 1, C 2 sind zwei Elemente von C und e C 1 C 2, dann enthält (C 1 C 2 ) \ {e} ein Element von C. (S, J ) ist ein Matroid, wenn C den Axiomen (C1), (C2), (C3) genügt und J aus denjenigen Teilmengen von S besteht, die kein Element von C enthalten
28 Charakterisierung anhand von Kreisen (S, J ) ein Matroid und C ein System von Teilmengen. Dann heißt C die Menge der Kreise von (S, J ), wenn gilt: (C1): Die leere Menge liegt nicht in C: / C (C2): Kein Element von C ist eine echte Teilmenge eines weiteren Elements von C (C3): C 1, C 2 sind zwei Elemente von C und e C 1 C 2, dann enthält (C 1 C 2 ) \ {e} ein Element von C. (S, J ) ist ein Matroid, wenn C den Axiomen (C1), (C2), (C3) genügt und J aus denjenigen Teilmengen von S besteht, die kein Element von C enthalten
29 Charakterisierung anhand von Kreisen (S, J ) ein Matroid und C ein System von Teilmengen. Dann heißt C die Menge der Kreise von (S, J ), wenn gilt: (C1): Die leere Menge liegt nicht in C: / C (C2): Kein Element von C ist eine echte Teilmenge eines weiteren Elements von C (C3): C 1, C 2 sind zwei Elemente von C und e C 1 C 2, dann enthält (C 1 C 2 ) \ {e} ein Element von C. (S, J ) ist ein Matroid, wenn C den Axiomen (C1), (C2), (C3) genügt und J aus denjenigen Teilmengen von S besteht, die kein Element von C enthalten
30 Charakterisierung anhand einer Basis Sei B ein System von Teilmengen einer endlichen Menge S. Dann ist B die Menge der Basen des Matroiden (S, J ) B erfüllt folgende Axiome: (B1) : B ist nicht leer (B2) : (B 1, B 2 ) B und x B 1 \B 2, dann y B 1 \B 2 so, dass (B 1 \ {x}) {y} B
31 Charakterisierung anhand einer Basis Sei B ein System von Teilmengen einer endlichen Menge S. Dann ist B die Menge der Basen des Matroiden (S, J ) B erfüllt folgende Axiome: (B1) : B ist nicht leer (B2) : (B 1, B 2 ) B und x B 1 \B 2, dann y B 1 \B 2 so, dass (B 1 \ {x}) {y} B
32 Charakterisierung anhand einer Rangfunktion Sei S eine endliche Menge und r definiert durch r : 2 S Z + Dann sind folgende Aussagen äquivalent: 1 r ist die Rangfunktion des Matroiden (S, J ) und J = {I S : r (I) = I } 2 X, Y S gilt: (R1) : r (X) X (R2) : Falls X Y, gilt r (X) r (Y ) (R3) : r (X Y ) + r (X Y ) r (X) + r (Y )
33 Charakterisierung anhand einer Rangfunktion Sei S eine endliche Menge und r definiert durch r : 2 S Z + Dann sind folgende Aussagen äquivalent: 1 r ist die Rangfunktion des Matroiden (S, J ) und J = {I S : r (I) = I } 2 X, Y S gilt: (R1) : r (X) X (R2) : Falls X Y, gilt r (X) r (Y ) (R3) : r (X Y ) + r (X Y ) r (X) + r (Y )
34 Charakterisierung anhand einer Rangfunktion Sei S eine endliche Menge und r definiert durch r : 2 S Z + Dann sind folgende Aussagen äquivalent: 1 r ist die Rangfunktion des Matroiden (S, J ) und J = {I S : r (I) = I } 2 X, Y S gilt: (R1) : r (X) X (R2) : Falls X Y, gilt r (X) r (Y ) (R3) : r (X Y ) + r (X Y ) r (X) + r (Y )
35 Charakterisierung anhand einer Rangfunktion Sei S eine endliche Menge und r definiert durch r : 2 S Z + Dann sind folgende Aussagen äquivalent: 1 r ist die Rangfunktion des Matroiden (S, J ) und J = {I S : r (I) = I } 2 X, Y S gilt: (R1) : r (X) X (R2) : Falls X Y, gilt r (X) r (Y ) (R3) : r (X Y ) + r (X Y ) r (X) + r (Y )
36 Charakterisierung anhand einer Rangfunktion Sei S eine endliche Menge und r definiert durch r : 2 S Z + Dann sind folgende Aussagen äquivalent: 1 r ist die Rangfunktion des Matroiden (S, J ) und J = {I S : r (I) = I } 2 X, Y S gilt: (R1) : r (X) X (R2) : Falls X Y, gilt r (X) r (Y ) (R3) : r (X Y ) + r (X Y ) r (X) + r (Y )
37 Optimierungsproblem: maximale unabhängige Menge Gegeben:(S, J ) ein Unabhängigkeitssystem und c : S R + eine positive Gewichtsfunktion auf den Elementen von S. Gesucht:ein maximales Element I J, dessen Gesamtgewicht c (I) = s I c (s) maximal ist.
38 Unabhängigkeitsorakel Problem: kompakte Darstellung von J. Ein Orakel allgemein, in diesem Fall ein Unabhängigkeitsorakel, ist ein Algorithmus, der mit dem Input einer Menge J S entscheidet, ob I J unabhängig ist oder nicht. Vorteil: Orakelaufrufe werden in der Komplexitätsanalyse nur einmal gezählt und sie sind polynomial.
39 Unabhängigkeitsorakel Problem: kompakte Darstellung von J. Ein Orakel allgemein, in diesem Fall ein Unabhängigkeitsorakel, ist ein Algorithmus, der mit dem Input einer Menge J S entscheidet, ob I J unabhängig ist oder nicht. Vorteil: Orakelaufrufe werden in der Komplexitätsanalyse nur einmal gezählt und sie sind polynomial.
40 Greedy-Algorithmus MAX-INDEPENDENT-SET Input: Ein Unabhängigkeitssystem (S, J ) gegeben durch ein Unabhängigkeitsorakel und eine Gewichtsfunktion c. Output: Eine Menge I J 1 Ordne die Elemente in S = {s 1,..., s n } absteigend nach ihrem Gewicht, d.h. c (s 1 )... c (s n ) 2 Setze I = 3 Wiederhole für k = 1,..., n: FallsI {s k } J füge {s k } zu I hinzu 4 Gib die Menge I aus.
41 Greedy-Algorithmus MAX-INDEPENDENT-SET Input: Ein Unabhängigkeitssystem (S, J ) gegeben durch ein Unabhängigkeitsorakel und eine Gewichtsfunktion c. Output: Eine Menge I J 1 Ordne die Elemente in S = {s 1,..., s n } absteigend nach ihrem Gewicht, d.h. c (s 1 )... c (s n ) 2 Setze I = 3 Wiederhole für k = 1,..., n: FallsI {s k } J füge {s k } zu I hinzu 4 Gib die Menge I aus.
42 Greedy-Algorithmus MAX-INDEPENDENT-SET Input: Ein Unabhängigkeitssystem (S, J ) gegeben durch ein Unabhängigkeitsorakel und eine Gewichtsfunktion c. Output: Eine Menge I J 1 Ordne die Elemente in S = {s 1,..., s n } absteigend nach ihrem Gewicht, d.h. c (s 1 )... c (s n ) 2 Setze I = 3 Wiederhole für k = 1,..., n: FallsI {s k } J füge {s k } zu I hinzu 4 Gib die Menge I aus.
43 Greedy-Algorithmus MAX-INDEPENDENT-SET Input: Ein Unabhängigkeitssystem (S, J ) gegeben durch ein Unabhängigkeitsorakel und eine Gewichtsfunktion c. Output: Eine Menge I J 1 Ordne die Elemente in S = {s 1,..., s n } absteigend nach ihrem Gewicht, d.h. c (s 1 )... c (s n ) 2 Setze I = 3 Wiederhole für k = 1,..., n: FallsI {s k } J füge {s k } zu I hinzu 4 Gib die Menge I aus.
44 Greedy-Algorithmus: max aufspannender Wald WH: Ein aufspannender Wald in einem Graphen G ist ein Wald der alle Knoten des des Graphen enthält. Wald bedeutet: der Graph enthält keine Kreise. Greedy-Max-Algorithmus: aufspannender Wald Input: Graph G = (V, E) mit Kantengewichten c e Output: Ein Wald W E mit maximalem Gewicht. Schritt 1, 2, 4 sind wie oben. Schritt 3: Für k = 1,..., n führe durch: Falls W {e k } keinen Kreis enthält, setze W := W {e k }
45 Greedy-Algorithmus: max aufspannender Wald WH: Ein aufspannender Wald in einem Graphen G ist ein Wald der alle Knoten des des Graphen enthält. Wald bedeutet: der Graph enthält keine Kreise. Greedy-Max-Algorithmus: aufspannender Wald Input: Graph G = (V, E) mit Kantengewichten c e Output: Ein Wald W E mit maximalem Gewicht. Schritt 1, 2, 4 sind wie oben. Schritt 3: Für k = 1,..., n führe durch: Falls W {e k } keinen Kreis enthält, setze W := W {e k }
46 Anwendung und Probleme 1 Anwendung Vorallem beim Design von Transport-, Kommunikations,- Energie- und Computernetzwerken. 2 Problem Der Greedy-Algorithmus findet optimale Lösungen, wenn er auf Matroiden angewendet wird. Auf Mengensystemen die das Axiom (M3) nicht erfüllen sind die Lösungen nicht optimal. Zum Beispiel bei bipartitem Matching
47 Anwendung und Probleme 1 Anwendung Vorallem beim Design von Transport-, Kommunikations,- Energie- und Computernetzwerken. 2 Problem Der Greedy-Algorithmus findet optimale Lösungen, wenn er auf Matroiden angewendet wird. Auf Mengensystemen die das Axiom (M3) nicht erfüllen sind die Lösungen nicht optimal. Zum Beispiel bei bipartitem Matching
48 Satz von Edmonds 1 Satz Seien (S, J 1 ) und (S, J 2 ) zwei Matroide und r 1, r 2 die zugehörigen Rangfunktionen. Dann gilt: max { I : I J 1 J 2 } = min U S (r 1 (U) + r 2 (S\U)) 2 Anwendung: Matching in bipartiten Graphen Satz von König.
49 Satz von Edmonds 1 Satz Seien (S, J 1 ) und (S, J 2 ) zwei Matroide und r 1, r 2 die zugehörigen Rangfunktionen. Dann gilt: max { I : I J 1 J 2 } = min U S (r 1 (U) + r 2 (S\U)) 2 Anwendung: Matching in bipartiten Graphen Satz von König.
50 Satz von Edmonds Algorithmus von Edmonds Edmonds entwickelte einen Algorithmus für den Schnitt von zwei Matroiden, der die Unabhängigkeitsmengen durch ein Orakel bestimmt und ein Element I J 1 J 2 ausgibt, das von maximaler Mächtigkeit ist. Er arbeitet über kürzeste Wege in bipartiten Hilfsgraphen und kann im Vgl. mit Greedy-Alg. Knoten hinzufügen und entfernen. Er löst das MATROID-INTERSECTION-PROBLEM in polynomialer Zeit.
1 Matroide. 1.1 Definitionen und Beispiele. Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler
Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler 1 Matroide 1.1 Definitionen und Beispiele 1. Definition (Unabhängigkeitssystem): Ein Mengensystem
ADS: Algorithmen und Datenstrukturen 2
ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 3: Minimal aufspannende Bäume und Matroide Dipl-Math. Wolfgang Kinzner 3.4.2012 Kapitel 3: Minimal aufspannende Bäume und Matroide Minimal aufspannende
ADS: Algorithmen und Datenstrukturen 2
ADS: Algorithmen und Datenstrukturen 2 Teil 6 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 16. Mai 2018 [Letzte Aktualisierung: 18/05/2018,
ADS: Algorithmen und Datenstrukturen 2
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 24. April 2019 [Letzte Aktualisierung: 24/04/2019,
Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl. Beispiele für optimale Greedy-Lösungen
Wiederholung Optimale Lösungen mit Greedy-Strategie erfordern Optimalität der Greedy-Wahl unabhängig von Subproblemen Optimalität der Subprobleme Beispiele für optimale Greedy-Lösungen Scheduling Problem
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph.
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Optimierung. Optimierung. Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung Fabian Kuhn
Optimierung Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung 1 Assignment Problem (Zuordnungsproblem) Gewichtetes Perfektes Bipartites Matching agents Costs tasks Weise jedem Agenten genau
Satz 324 Sei M wie oben. Dann gibt es für ein geeignetes k Konstanten c i > 0 und Permutationsmatrizen P i, i = 1,...
Satz 324 Sei M wie oben. Dann gibt es für ein geeignetes k Konstanten c i > 0 und Permutationsmatrizen P i, i = 1,..., k, so dass gilt M = k c i P i i=1 k c i = r. i=1 Diskrete Strukturen 7.1 Matchings
KAPITEL 3 MATCHINGS IN BIPARTITEN GRAPHEN
KAPITEL 3 MATCHINGS IN BIPARTITEN GRAPHEN F. VALLENTIN, A. GUNDERT 1. Definitionen Notation 1.1. Ähnlich wie im vorangegangenen Kapitel zunächst etwas Notation. Wir beschäftigen uns jetzt mit ungerichteten
EDM, Algorithmen und Graphenspeicherung
EDM, Algorithmen und Graphenspeicherung 1 Graphenspeicherung Gespeichert werden soll ein Graph G = (V, E) bzw. Digraph D = (V, A). Man beachte: E ( ) V 2 bzw. E V 2 1.1 Adjazenzmatrix Graph G: A = (a vw
Kapitel 5: Minimale spannende Bäume Gliederung der Vorlesung
Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
6. Übung zur Linearen Optimierung SS08
6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
Übungsblatt 2 - Lösung
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 2 - Lösung Vorlesung Algorithmentechnik im WS 08/09 Ausgabe 04. November 2008 Abgabe 8. November, 5:0 Uhr (im Kasten vor Zimmer
Studientag zur Algorithmischen Mathematik
Studientag zur Algorithmischen Mathematik Minimale aufspannende Bäume und Matchings Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 22. Mai 2011 Outline Minimale aufspannende
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 1: Grundlagen der algorithmischen Graphentheorie Dipl-Math. Wolfgang Kinzner 2.4.2012 Kapitel 1: Grundlagen der algorithmischen Graphgentheorie
ADS: Algorithmen und Datenstrukturen 2
ADS: Algorithmen und Datenstrukturen 2 Teil XIII Peter F. Stadler & Konstantin Klemm Bioinformatics Group, Dept. of Computer Science & Interdisciplinary Center for Bioinformatics, University of Leipzig
Freie Bäume und Wälder
(Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
Name:... Vorname:... Matr.-Nr.:... Studiengang:...
Technische Universität Braunschweig Sommersemester 2013 IBR - Abteilung Algorithmik Prof. Dr. Sándor P. Fekete Dr. Christiane Schmidt Stephan Friedrichs Klausur Netzwerkalgorithmen 16.07.2013 Name:.....................................
Operations Research. Flüsse in Netzwerken. Flüsse in Netzwerken. Unimodularität. Rainer Schrader. 2. Juli Gliederung.
Operations Research Rainer Schrader Flüsse in Netzwerken Zentrum für Angewandte Informatik Köln 2. Juli 2007 1 / 53 2 / 53 Flüsse in Netzwerken Unimodularität Gliederung Netzwerke und Flüsse bipartite
1.Aufgabe: Minimal aufspannender Baum
1.Aufgabe: Minimal aufspannender Baum 11+4+8 Punkte v 1 v 2 1 3 4 9 v 3 v 4 v 5 v 7 7 4 3 5 8 1 4 v 7 v 8 v 9 3 2 7 v 10 Abbildung 1: Der Graph G mit Kantengewichten (a) Bestimme mit Hilfe des Algorithmus
Graphalgorithmen Netzwerkalgorithmen. Laufzeit
Netzwerkalgorithmen Laufzeit (Folie 390, Seite 78 im Skript) Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{
Algorithmik WS 07/ Vorlesung, Andreas Jakoby Universität zu Lübeck. 10 Matching-Probleme
10 Matching-Probleme 10.1 Definition von Matching-Probleme Definition 21 [2-dimensionales Matching] Sei G = (V, E) ein ungerichteter Graph und E E. E ist ein Matching, wenn für alle Kantenpaare e 1, e
Richtig oder falsch? Richtig oder falsch? Richtig oder falsch? Mit dynamischer Programmierung ist das Knapsack- Problem in Polynomialzeit lösbar.
Gegeben sei ein Netzwerk N = (V, A, c, s, t) wie in der Vorlesung. Ein maximaler s-t-fluss kann immer mit Hilfe einer Folge von höchstens A Augmentationsschritten gefunden werden. Wendet man den Dijkstra-Algorithmus
Betriebliche Optimierung
Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 21 1 Approximationsalgorithmen auf
Bäume und Wälder. Definition 1
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Bäume und Wälder. Definition 1
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Diskrete Mathematik Graphentheorie (Übersicht)
Diskrete Mathematik Graphentheorie (Übersicht) Dr. C. Löh 2. Februar 2010 0 Graphentheorie Grundlagen Definition (Graph, gerichteter Graph). Ein Graph ist ein Paar G = (V, E), wobei V eine Menge ist (die
Betriebswirtschaftliche Optimierung
Institut für Statistik und OR Uni Graz 1 Approximationsalgorithmen auf metrischen Instanzen Minimum Spanning Tree Definition (Spannbaum) Ein Spannbaum in einem Graphen G = (V,E) ist ein kreisfreier Teilgraph
Vorlesung Datenstrukturen
Vorlesung Datenstrukturen Minimale Spannbäume Maike Buchin 18.7., 20.7.2017 Einführung Motivation: Verbinde Inseln mit Fähren oder Städte mit Schienen und verbrauche dabei möglichst wenig Länge. Problem:
f h c 7 a 1 b 1 g 2 2 d
) Man bestimme mit Hilfe des Dijkstra-Algorithmus einen kürzesten Weg von a nach h: c 7 a b f 5 h 3 4 5 i e 6 g 2 2 d Beim Dijkstra-Algorithmus wird in jedem Schritt von den noch unmarkierten Knoten jener
Graphentheorie. Kardinalitätsmatchings. Kardinalitätsmatchings. Kardinalitätsmatchings. Rainer Schrader. 11. Dezember 2007
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 11. Dezember 2007 1 / 47 2 / 47 wir wenden uns jetzt einem weiteren Optimierungsproblem zu Gliederung Matchings in bipartiten Graphen
Ganzzahlige lineare Programme
KAPITEL 5 Ganzzahlige lineare Programme Wir betrachten nun Optimierungsprobleme vom Typ (42) min c T x s.d. Ax = b, x 0, x ganzzahlig, wobei die Matrix A R m n und die Vektoren c R n, b R m gegeben seien.
Formale Grundlagen. Graphentheorie 2008W. Vorlesung im 2008S
Minimale Formale Grundlagen Graphentheorie Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt Minimale
Trennender Schnitt. Wie groß kann der Fluss in dem folgenden Flussnetzwerk höchstens sein?
6. Flüsse und Zuordnungen max-flow min-cut Trennender Schnitt Wie groß kann der Fluss in dem folgenden Flussnetzwerk höchstens sein? a e s c d t b f Der Fluss kann nicht größer als die Kapazität der der
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 22.
Note: Name Vorname Matrikelnummer Studiengang Unterschrift der Kandidatin/des Kandidaten Hörsaal Reihe Platz Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS
5 Graphen. Repräsentationen endlicher Graphen. 5.1 Gerichtete Graphen. 5.2 Ungerichtete Graphen. Ordnung von Graphen
Grundlagen der Mathematik für Informatiker 1 Grundlagen der Mathematik für Informatiker 5 Graphen 5.1 Gerichtete Graphen Definition 5.1 (V, E) heißt gerichteter Graph (Digraph), wenn V Menge von Knoten
4.2 Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition 4.2.1
Allgemeines. Minimale Spannbäume: Der Algorithmus von Jarník/Prim Definition.. (a) Ein Graph G =(V, E) heißt kreisfrei, wenn er keinen Kreis besitzt. Beispiel: Ein kreisfreier Graph: FG KTuEA, TU Ilmenau
9 Minimum Spanning Trees
Im Folgenden wollen wir uns genauer mit dem Minimum Spanning Tree -Problem auseinandersetzen. 9.1 MST-Problem Gegeben ein ungerichteter Graph G = (V,E) und eine Gewichtsfunktion w w : E R Man berechne
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
Gliederung der Vorlesung. Fallstudie Bipartite Graphen. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen. Minimal spannende Bäume. Kürzeste Pfade. Traveling Salesman Problem. Flüsse in Netzwerken
Das Matching Polytop
Das Matching Polytop Manuel Schneider Institut für Mathematik, TU Berlin Seminar: Algorithmische Diskrete Mathematik 27. Mai 2008 Überblick 1 Beschreibungen durch Ungleichungen Das Perfekte Matching Polytop
Matching. Organisatorisches. VL-18: Matching. (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger. Tanzabend
Organisatorisches VL-18: Matching (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11:15 12:00 Übungen: Tim Hartmann,
Kapitel 8: Bipartite Graphen Gliederung der Vorlesung
Gliederung der Vorlesung 1. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege 4. Minimale spannende Bäume 5. Färbungen und Cliquen 6. Traveling Salesman Problem 7. Flüsse in Netzwerken
Bipartite Graphen. Beispiele
Bipartite Graphen Ein Graph G = (V, E) heiÿt bipartit (oder paar), wenn die Knotenmenge in zwei disjunkte Teilmengen zerfällt (V = S T mit S T = ), sodass jede Kante einen Knoten aus S mit einem Knoten
Systems of Distinct Representatives
Systems of Distinct Representatives Seminar: Extremal Combinatorics Peter Fritz Lehr- und Forschungsgebiet Theoretische Informatik RWTH Aachen Systems of Distinct Representatives p. 1/41 Gliederung Einführung
Überblick. Kap. 1.4: Minimum Weight Perfect Matching. 1.3 Blüten-Schrumpf Algorithmus für Maximum Matching
Kap. 1.4: Minimum Weight Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 4. VO 6. November 2006 Überblick kurze Wiederholung: 1.2 Blüten-Schrumpf-Algorithmus für Perfektes Matching
Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo?
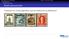Briefmarkensammeln (Folie 413, Seite 80 im Skript) Funktioniert der Greedy-Algorithmus auch für Briefmarken aus Manchukuo? Welche Briefmarken für einen 20 fen Brief? Der Greedy-Algorithmus führt nicht
3. Musterlösung. Problem 1: Heapsort
Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 05/06 ITI Wagner 3. Musterlösung Problem : Heapsort ** 2 3 4 5 Algorithmus : Heapsort (A) Eingabe : Array A der Länge n Ausgabe : Aufsteigend
2. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2008/2009
2. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2008/2009 Lösung! Beachten Sie: Bringen Sie den Aufkleber mit Ihrem Namen und Matrikelnummer auf diesem Deckblatt an und beschriften Sie jedes
5. Bäume und Minimalgerüste
5. Bäume und Minimalgerüste Charakterisierung von Minimalgerüsten 5. Bäume und Minimalgerüste Definition 5.1. Es ein G = (V, E) ein zusammenhängender Graph. H = (V,E ) heißt Gerüst von G gdw. wenn H ein
Ferienkurs Propädeutikum Diskrete Mathematik
Ferienkurs Propädeutikum Diskrete Mathematik Teil 3: Grundlagen Graphentheorie Tina Janne Schmidt Technische Universität München April 2012 Tina Janne Schmidt (TU München) Ferienkurs Propädeutikum Diskrete
Wiederholung zu Flüssen
Universität Konstanz Methoden der Netzwerkanalyse Fachbereich Informatik & Informationswissenschaft SS 2008 Prof. Dr. Ulrik Brandes / Melanie Badent Wiederholung zu Flüssen Wir untersuchen Flüsse in Netzwerken:
Graphen KAPITEL 3. Dieses Problem wird durch folgenden Graph modelliert:
KAPITEL 3 Graphen Man kann als Ursprung der Graphentheorie ein Problem sehen, welches Euler 1736 von Studenten aus Königsberg gestellt bekam. Der Fluss Pregel wird von 7 Brücken überquert, und die Frage
Informatik II, SS 2014
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 16 (2.7.2014) Graphtraversierung II, Minimale Spannbäume I Algorithmen und Komplexität Tiefensuche: Pseusocode DFS Traversal: for all u in
Vorlesung Lineare Optimierung (Sommersemester 2007)
1 Vorlesung Lineare Optimierung (Sommersemester 007) Kapitel 9: Ganzzahlige Polyeder und Kombinatorische Dualität Volker Kaibel Otto-von-Guericke Universität Magdeburg Montag, 9. Juli 007 Gliederung Ganzzahlige
2. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2009/2010
2. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2009/2010 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie den Aufkleber mit
Effiziente Algorithmen I
H 10. Präsenzaufgabenblatt, Wintersemester 2015/16 Übungstunde am 18.01.2015 Aufgabe Q Ein Reiseveranstalter besitzt ein Flugzeug, das maximal p Personen aufnehmen kann. Der Veranstalter bietet einen Flug
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume)
WS 2016/17 Diskrete Strukturen Kapitel 4: Graphentheorie (Bäume) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Fortgeschrittene Netzwerk- und Graph-Algorithmen
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Flüsse, Schnitte, Bipartite Graphen II
Flüsse, Schnitte, Bipartite Graphen II Jonathan Hacker 06.06.2016 Jonathan Hacker Flüsse, Schnitte, Bipartite Graphen II 06.06.2016 1 / 42 Gliederung Einführung Jonathan Hacker Flüsse, Schnitte, Bipartite
3.2 Unabhängigkeitsstrukturen
80 3.2 Unabhängigkeitsstrukturen Unser Ziel ist der Nachweis, daß in Vektorräumen, also in Moduln über Körpern, Basen existieren und zwei endliche Basen gegebenenfalls von derselben Ordnung sind. (Basen
Wie findet man den optimalen Weg zum Ziel? Klassische Probleme der Kombinatorischen Optimierung
Wie findet man den optimalen Weg zum Ziel? Klassische Probleme der Kombinatorischen Optimierung Teilnehmer/innen: Markus Dahinten, Graf Münster Gymnasium Bayreuth Robert Fay, Herder Gymnasium Berlin Falko
Informatik II, SS 2016
Informatik II - SS 208 (Algorithmen & Datenstrukturen) Vorlesung 4 (..208) Graphenalgorithmen III Algorithmen und Komplexität Bäume Gegeben: Zusammenhängender, ungerichteter Graph G = V, E Baum: Zusammenhängender,
Graphentheorie. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
Minimale Graphentheorie Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Minimale Inhalt
Matchings in Graphen. Praktikum Diskrete Optimierung (Teil 5)
Praktikum Diskrete Optimierung (Teil 5) 6.05.009 Matchings in Graphen Es sei ein ungerichteter Graph G = (V, E) gegeben. Ein Matching in G ist eine Teilmenge M E, so dass keine zwei Kanten aus M einen
WS 2013/14. Diskrete Strukturen
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
Einführung in die Mathematik des Operations Research
Universität zu Köln Mathematisches Institut Prof. Dr. F. Vallentin Einführung in die Mathematik des Operations Research Sommersemester 3 en zur Klausur (7. Oktober 3) Aufgabe ( + 3 + 5 = Punkte). Es sei
Univ.-Prof. Dr. Goulnara ARZHANTSEVA
Diskrete Mathematik Univ.-Prof. Dr. Goulnara ARZHANTSEVA SS 2018 c Univ.-Prof. Dr. Goulnara Arzhantseva Kapitel 08: Menger, König und Hall / Planare Graphen 1 / 30 Der Satz von Menger: s t trennende Kantenmenge
Übungsaufgaben Graphentheorie, Wintersemester 2011/12
Übungsaufgaben Graphentheorie, Wintersemester 2011/12 Frank Göring 25. Januar 2012 Zusammenfassung Übungsaufgaben zur Graphentheorievorlesung. 1 Bis 19.10.2011 1. Wir hatten einen Graphen G als zusammenhängend
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od
Algorithmus zur topologischen Nummerierung: while V = 0 do nummeriere eine Quelle mit der nächsten Nummer streiche diese Quelle aus V od Diskrete Strukturen 3.7 dag 473/556 3.8 Zusammenhang Definition
Vorlesung 3: Logik und Mengenlehre
28102013 Erinnerung: Zeilen-Stufen-Form (ZSF) eines LGS 0 0 1 c 1 0 0 0 1 0 0 1 c r 0 0 0 c r+1 0 0 0 0 0 0 0 0 0 c m Erinnerung: Information der Zeilen-Stufen-Form Aus der ZSF liest man ab: Folgerung
Graphentheorie. Zusammenhang. Zusammenhang. Zusammenhang. Rainer Schrader. 13. November 2007
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 13. November 2007 1 / 84 2 / 84 Gliederung stest und Schnittkanten älder und Bäume minimal aufspannende Bäume Der Satz von Menger 2-zusammenhängende
1. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2009/2010
. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2009/200 Lösung! Beachten Sie: Bringen Sie den Aufkleber mit Ihrem Namen und Matrikelnummer auf diesem Deckblatt an und beschriften Sie jedes Aufgabenblatt
Algorithmische Graphentheorie
Algorithmische Graphentheorie Vorlesung 4: Suchstrategien Babeş-Bolyai Universität, Department für Informatik, Cluj-Napoca csacarea@cs.ubbcluj.ro 14. April 2017 HALBORDNUNG TOPOLOGISCHE ORDNUNG TOPOLOGISCHES
Das Multi Traveling Salesman Problem
Das Multi Traveling Salesman Problem Harald Voit Seminar Ganzzahlige Optimierung 19. bis 21. Januar 2007 Wallenfels Das Multi Traveling Salesman Problem p.1/26 Übersicht Vom TSP zum ATSP Das Multi Traveling
Kapitel 4: Minimal spannende Bäume Gliederung der Vorlesung
Kapitel : Minimal spannende Bäume Gliederung der Vorlesung. Fallstudie Bipartite Graphen 2. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen. Minimal spannende Bäume. Kürzeste Wege. Traveling
Formale Grundlagen der Informatik
Formale Grundlagen der Informatik / 2015 1 Die Elemente einer (endlichen) Menge sollen den Elementen einer zweiten, gleichmächtigen Menge zugeordnet werden Problemstellung Bipartite Graphen Zuordnungsprobleme
Flüsse und Zuordnungen. Kapitel 6. Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/ / 296
Kapitel 6 Peter Becker (H-BRS) Graphentheorie Wintersemester 2018/19 227 / 296 Inhalt Inhalt 6 Flussnetzwerke Berechnung maximaler Flüsse Max-Flow-Min-Cut Matchings Peter Becker (H-BRS) Graphentheorie
Effiziente Algorithmen I
9. Präsenzaufgabenblatt, WiSe 2013/14 Übungstunden am 13.01. & 15.01.2014 Aufgabe Q Gegeben sei ein Fluss-Netzwerk mit Digraph D = (V, A), Knotenkapazitäten c(u, v) 0, Quelle s und Senke t. Kann sich der
Ecken des Zuordnungsproblems
Total unimodulare Matrizen Ecken des Zuordnungsproblems Definition.6 Ein Zuordnungsproblem mit den Vorzeichenbedingungen 0 apple x ij apple für i, j =,...,n statt x ij 2{0, } heißt relaxiertes Zuordnungproblem.
Informatik III - WS07/08
Informatik III - WS07/08 Kapitel 4 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 4 : Komplexitätsklassen Informatik III - WS07/08 Kapitel 4 2 Sprachen, Probleme, Zeitkomplexität
Kapitel 4: Minimale spannende Bäume Gliederung der Vorlesung
Kapitel : Minimale spannende Bäume Gliederung der Vorlesung. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman
Grundlagen Theoretischer Informatik 3 SoSe 2012 in Trier. Henning Fernau Universität Trier
Grundlagen Theoretischer Informatik 3 SoSe 2012 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Zum Umgang mit NP-harten Problemen In manchen Anwendungen ist das garantierte Auffinden exakter
1. Klausur zur Vorlesung Algorithmentechnik Wintersemester 2008/2009
. Klausur zur Vorlesung Algorithmentechnik Wintersemester 008/009 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie den Aufkleber mit Ihrem
ADS: Algorithmen und Datenstrukturen 2
ADS: Algorithmen und Datenstrukturen 2 Teil 4 Prof. Dr. Gerhard Heyer Institut für Informatik Abteilung Automatische Sprachverarbeitung Universität Leipzig 02. Mai 2017 [Letzte Aktualisierung: 10/07/2018,
Algorithmische Graphentheorie
1 Algorithmische Graphentheorie Sommersemester 2014 5. Vorlesung Matchings / Paarungen II Kombinatorischer Algorithmus, Anwendung für Handlungsreisende, LP-Runden Dr. Joachim Spoerhase Prof. Dr. Alexander
Auslastungs- und Potenzialspiele
Definition Existenz Konvergenzzeit Matroidspiele Algorithmische Spieltheorie Sommer 2017 Definition Existenz Konvergenzzeit Matroidspiele Auslastungsspiele Existenz eines reinen Nash-Gleichgewichtes Konvergenzzeit
Der Greedy-Algorithmus und unendliche Matroide
FernUniversität in Hagen Fakultät für Mathematik und Informatik Bachelorarbeit Der Greedy-Algorithmus und unendliche Matroide Christoph Horst Paderborn, 25. September 2012 Betreuer: Prof. Dr. Winfried
Flüsse, Schnitte, Bipartite Graphen
Flüsse, Schnitte, Bipartite Graphen Sebastian Hahn 4. Juni 2013 Sebastian Hahn Flüsse, Schnitte, Bipartite Graphen 4. Juni 2013 1 / 48 Überblick Flussnetzwerke Ford-Fulkerson-Methode Edmonds-Karp-Strategie
2. Optimierungsprobleme 6
6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
Algorithmen und Datenstrukturen 2
Algorithmen und Datenstrukturen 2 Sommersemester 2007 11. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen Safe
Algorithmen und Datenstrukturen 2
Algorithmen und Datenstrukturen 2 Sommersemester 2009 11. Vorlesung Uwe Quasthoff Universität Leipzig Institut für Informatik quasthoff@informatik.uni-leipzig.de Das Rucksack-Problem Ein Dieb, der einen
Ausarbeitung über den Satz von Menger und den Satz von König
Ausarbeitung über den Satz von Menger und den Satz von König Myriam Ezzedine, 0326943 Anton Ksernofontov, 0327064 Jürgen Platzer, 0025360 Nataliya Sokolovska, 0326991 1. Beweis des Satzes von Menger Bevor
Berechnung minimaler Spannbäume. Beispiel
Minimale Spannbäume Definition Sei G pv, Eq ein ungerichteter Graph und sei w : E Ñ R eine Funktion, die jeder Kante ein Gewicht zuordnet. Ein Teilgraph T pv 1, E 1 q von G heißt Spannbaum von G genau
Algorithmische Mathematik I
Algorithmische Mathematik I Wintersemester 2011 / 2012 Prof. Dr. Sven Beuchler Peter Zaspel Übungsblatt zur Wiederholung Teil 1. Abgabe am -. Aufgabe 1. a) Was ist eine B-adische Darstellung mit fixer
8. Konvexe Polytope. Tobias Boelter. Mittwoch, 5. März TopMath Frühlingsschule
1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
Zugeordneter bipartiter Graph
Zugeordneter bipartiter Graph Für ein Transportproblem sei A = {A 1,...,A m } die Menge der Fabriken und B = {B 1,...,B n } sei die Menge der Warenhäuser. Wir ordnen nun einem Transportproblem einen bipartiten
KAPITEL 4 FLÜSSE IN NETZWERKEN
KAPITEL 4 FLÜSSE IN NETZWERKEN F. VALLENTIN, A. GUNDERT 1. Das Max-Flow-Min-Cut Theorem Es sei D = (V, A) ein gerichteter Graph, s, t V zwei Knoten. Wir nennen s Quelle und t Senke. Definition 1.1. Eine