Momentanpol
|
|
|
- Reiner Schreiber
- vor 6 Jahren
- Abrufe
Transkript
1 Momentanpol
2 Momentanpol allgemein Der Momentanpol - ist eine geometrische Größe - ist ein Bezugspunkt für den momentanen/augenblicklichen Bewegungszustand eines Körpers / Gegenstands - ist der Drehpunkt für den augenblicklichen Bewegungszustand - verändert ständig seine Lage Befindet sich ein Körper in Bewegung, so genügen 2 Bewegungsrichtungen und eine Geschwindigkeitskomponente, um den Bewegungszustand des Körpers eindeutig zu beschreiben. Mit dem Momentanpol lassen sich dann Geschwindigkeiten anderer Körperteile bestimmen. Wofür braucht man den Momentanpol? Alle Bewegungen, Geschwindigkeiten, Kräfte und Drehmomente, die für einen vorgesehenen Arbeitsgang benötigt werden, beziehen sich auf diesen Punkt.
3 Momentanpol eines bewegten Körpers 2 Bewegungsrichtungen eines Körpers sind bekannt. Geschwindigkeitsrichtung Geschwindigkeitsrichtung
4 Momentanpol eines bewegten Körpers Geschwindigkeitsrichtung Geschwindigkeitsrichtung Momentanpol
5 Momentanpol eines bewegten Körpers Geschwindigkeitsrichtung Geschwindigkeitsrichtung Momentanpol
6 Momentanpol eines bewegten Körpers P2 Bewegungsrichtung ist bekannt Geschwindigkeit ist ein Vektor mit Betrag und Richtung Bewegungsgeschwindigkeit durch Momentanpol und v1 vorgegeben P3 l3 l1 P1 Bewegungsgeschwindigkeit ist bekannt l1 Momentanpol Strahlensatz v 3 l 3 v l 1 1 v 3 l 3 v l 1 1
7 Bestimmung des Momentanpols
8 Momentanpol in Verbindung mit Fahrwerken Bei den mobilen Arbeitsgeräten werden oftmals anspruchsvolle Fahrwerke eingesetzt, um bestimmte Bewegungsabläufe zu realisieren. Im Vordergrund steht in der Regel das Ziel, bodenschonend und verschleißarm zu arbeiten.
9 Geschwindigkeiten an Traktorrädern α a α i Die Räder bewegen sich auf unterschiedlichen Kreisbögen. v a v i Die Geschwindigkeiten aller Räder sind unterschiedlich. Die Einschlagwinkel der Vorderräder sind unterschiedlich. l a l i α a < α i l a v a l i v i Momentanpol
10 Momentanpol bei Geradeausfahrt v M = Momentanpol Bei Geradeausfahrt wandert der Momentanpol ins Unendliche. Alle Räder haben identische Umfangsgeschwindigkeiten. Alle Geschwindigkeiten sind identisch - Betrag und Richtung.
11 Gezogene Pflanzenschutzspritze mit starrer Deichsel Momentanpol
12 Gezogene Pflanzenschutzspritze mit gelenkter Deichsel Momentanpol
13 Gezogene Pflanzenschutzspritze mit gelenkten Rädern Momentanpol
14 Radstellungen bei einem Tandemfahrwerk Momentanpol
15 Momentanpol in Verbindung mit dem Viergelenkgetriebe In der Agrartechnik hat insbesondere das Viergelenkgetriebe eine besondere Bedeutung. Viergelenkgetriebe kommen zur Anwendung bei Heckkraftheber Förderelement Klappmechanismus Schließmechanismus Geräteaufhängung Gestängeaufhängung - Verbindung Schlepper und Gerät - Raffer in Ballenpresse - Rahmen Einzelkornsämaschine - Deckel, Hauben - Säaggregate - Pflanzenschutzspritze
16 Bestimmung des Momentanpols bei Gelenkgetrieben Bei Gelenkgetrieben (Kurbel, usw) ist die Richtung der Schneidlinien für den Momentanpol bereits vorgegeben. Es ist die Verlängerung der Verbindungslinie der Gelenkpunkte, da die Geschwindigkeitsrichtung im rechten Winkel zum Radius des Gelenks/der Kurbel verläuft.
17 Antrieb des Viergelenkgetriebes Koppelkurve C Koppel B A Schwinge Kurbel A0 B0 Gestell
18 Viergelenkgetriebe Die Kurbel wird angetrieben mit n = min = 2 1 s Der Radius der Kurbel beträgt r = 30 cm Die Umfangsgeschwindigkeit errechnet sich zu B v 1 2 n r v1 2 π 2 0,3 m s v1 3,8 m s A A 0 B 0
19 Geschwindigkeiten im Viergelenkgetriebe entsprechend dem Strahlensatz gilt v 2 l 2 Momentanpol l 2 v2 v 1 l 1 v 2 l 2 v 1 l 1 l 1 = 1,3 m l 1 v2 P 2 l 2 = 0,5 m v 2 v 2 0,5 3,8 m 1,3 s 1,5 m s P 1
20 Bestimmen des Momentanpols C B A0 B0 A Momentanpol
21 Bestimmen des Momentanpols C Momentanpol B A0 B0 A
22 Kurbelschwinge für ein Raffergetriebe Schwinge Kurbel Guttransport Förderkanal
23 Raffergetriebe in der Hochdruckpresse
24 Kräfte im Viergelenkgetriebe Die verschiedenen punktuell am Körper (Koppel beim Viergelenkgetriebe) auftretenden Geschwindigkeiten stehen in einem bestimmten Verhältnis zu einander, wie auf der Folie dargestellt. Die Bewegungsgeschwindigkeiten v 1 an der Antriebskurbel wird beispielsweise mit Hilfe der Koppel übersetzt in die Abtriebsgeschwindigkeit v 2 am Koppelendpunkt. Das Verhältnis der Geschwindigkeiten beträgt An dem Koppelendpunkt wirkt die Kraft F 2 in Richtung der Bewegungsgeschwindigkeit - z.b. beim Raffergetriebe während des Transports von Halmgut. Diese Kraft F 2 verursacht an der Kurbel die Kraft F 1. Diese Kräfte stehen im umgekehrten Verhältnis wie die Geschwindigkeiten zu einander. Die Produkte aus Geschwindigkeit und Kräften sind konstant ( Energie-Erhaltungssatz)
25 Kräfte und Geschwindigkeiten im Viergelenkgetriebe l 2 v1 v 2 F2 l 1 F1 v1 v1 F 2 F 1 = v 1 v 2 = l 1 l 2
26 Kräfte im Viergelenkgetriebe Das Geschwindigkeitsverhältnis lässt sich durch das Längenverhältnis ersetzen so dass sich ergibt Daraus lässt sich wiederum das Momentengleichgewicht bilden Die durch einen Körper übertragbaren Kräfte lassen sich somit wie die Geschwindigkeiten bezogen auf den Momentanpol berechnen.
27 Schubkurbelgetriebe ω F1 v 1 v 2 M kleine Geschwindigkeit hohe Kraft F 2 v 1 M v 1 v 1 ω F 1 hohe Geschwindigkeit kleine Kraft F 2 v 2
28 Ballenpresse Schubkurbelgetriebe a
29 Dreipunktkraftheber Oberlenker Hubzylinder Unterlenker
30 Dreipunktkraftheber als Viergelenkgetriebe Hubrahmen Anlenkpunkte am Traktor (Gestell) Oberlenker Rahmen am Gerät für Dreipunktanbau (Koppel) Hub- Zylinder Unterlenker
31 Düngerstreuer in der Dreipunkthydraulik Ventil in Sperrstellung fixe Drehpunkte am Traktor Oberlenker Hubgestell F D virtuelle Krafteinleitung Momentanpol Unterlenker In der gezeichneten Situation der Dreipunkthydraulik ergibt sich der Momentanpol durch die Schnittlinien von Oberlenker und Unterlenker. Entsprechend den Grundlagen der Mechanik ist der Momentanpol der augenblickliche Drehpunkt für das Gelenksystem Dreipunkthydraulik mit angebautem Gerät. Alle Kräfte und Bewegungsgeschwindigkeiten, die in Zusammenwirken mit dem angebauten Gerät stehen, beziehen sich auf diesenpunkt.
32 Berechnen der Radlasten F G F D F V V a f H F H b Zum Berechnen der Radlasten F V und F H sind die Aufstandspunkte V und H die Bezugspunkte für die auftretenden Drehmomente. M H F V a F G f F D b 0 F V a F G f F D b FV 1 F G f FD b F 1 a H a M V F G a f F H a F D a b 0 F H a F G a f F D a b F G a f F D a b
33 Berechnen der Hubkräfte M F H F D e g Zur Berechnung der Kräfte F H im Dreipunktanbau ist der Momentanpol M der Bezugspunkt für die auftretenden Drehmomente. M F D g F H e 0 F H e F D g g F H F D e
34 Berechnen der Hubkräfte F H D F U c d Zur Berechnung der Kräfte F U um den Unterlenker anzuheben, ist das Gelenk D am Traktor der Bezugspunkt für die auftretenden Drehmomente. M D F H d F U c 0 F U c F H d d F U F H c
35 Dreipunktkraftheber Versuch 1
36 1 2 3
37 Kraftverhältnisse bei angebauter Dreipunktmaschine I Beispiel m st kg Masse des Düngerstreuers m D kg Masse des eingefüllten Düngers F g N Gewichtskraft A Zy cm² Kolbenfläche im Hubzylinder a m Abstand Gewichtskraft c, d, f, b m Hebelarme a = 0,50m e = 3,50m b = 0,38m c = 0,60m d = 1,00m f = 0,40m m st = 900 kg m D = 3000 kg A Zy = 50,2 cm² F Zy b f F H > F G F D F H F G Momentanpol c e q = e + a d a
38 Kraftverhältnisse bei angebauter Dreipunktmaschine II F H = F G f F Zy b F H F G Momentanpol F D c e q = e e + + aa d a
39 Kraftverhältnisse bei angebauter Dreipunktmaschine III q = e + a
40 Berechnung der Hubkraft und des Hydraulikdrucks Beispiel
41 Aushubkräfte Gleichung für Drehmomente bezogen auf den Momentanpol F H e = F G q Die Hubkraft ergibt sich somit zu M F H F G e q
42 q FH 1 F 1 G e 1 Während des Aushebens verändern sich die Längenverhältnisse bezogen auf dem Momentanpol q 1 q e 1 e Die Hubkraft vergrößert sich während des Aushebens F H F H 1 Aushubkräfte F H1 F G M e 1 q 1
43 Einstellungen am Pflug Pflüge müssen an der Dreipunkthydraulik so angebaut werden, dass - die Pflugschare sich selbst einziehen, das Stützrad aber nur wenig belastet wird - keine Querkräfte auftreten, die durch Lenkeinschlag ausgeglichen werden müssen. Zwei Momentanpole kommen dabei zur Wirkung. 1. Ideeller Führungspunkt 2. Ideeller Zugpunkt Quelle: Meiners/Bucks/Hegemann/Rempfer Fachkenntnisse Landmaschinen Mechaniker
44 Kräfte am Mähwerk v F v F M M Beim Auftreffen auf ein Hindernis wird das Mähwerk angehoben. Durch die Schubkräfte wird das Mähwerk entlastet. Es entsteht ein unruhiger Lauf. Beim Auftreffen auf ein Hindernis wird das Mähwerk nach unten gedrückt. Durch die Schubkraft wird das Mähwerk auf den Boden gedrückt. Es erhöhen sich die Reibkräfte.
45 M v F Kräfte am Mähwerk M v F Kette v F v F
46 Übertragene Kräfte beim angebauten Scheibengrubber virtuelle Krafteinleitung Momentanpol F 0 F U F 0 F B k F U Bodenkräfte M D = F B x k F U
47 Optimieren der Verdichtungsdrücke durch Verändern des Momentanpols Quelle: Lemken
48 Beispiel Momentanpol
49 Schubkurbelgetriebe Aufgabe Der Pressdruck beträgt in der momentanen Situation p D = 50 kn m² 1. Zeichnen Sie für diesen Zustand den Momentanpol ein. 2. Wie groß ist die auf den Kolben wirkende Presskraft F p? Die Kolbenfläche hat die Maße b = 1,2 m und h = 0,92 m F p = kn
50 Schubkurbelgetriebe Aufgabe 3. Die Kolbengeschwindigkeit in dem dargestellten Zustand beträgt v k = 1,5 m / s. Wie groß ist die Umfangsgeschwindigkeit v n an der Antriebskurbel? v n = m/ s 4. Wie groß ist die augenblickliche Pressleistung P p? P p = kw 5. Wie groß ist die Antriebsleistung an der Antriebskurbel? Der Wirkungsgrad des Gelenkgetriebes beträgt η = 0,8 P A = kw
51 Schubkurbelgetriebe Aufgabe n = 1/ min M A = knm F A = kn F k = kn
1. Grundlagen der ebenen Kinematik
 Lage: Die Lage eines starren Körpers in der Ebene ist durch die Angabe von zwei Punkten A und P eindeutig festgelegt. Die Lage eines beliebigen Punktes P wird durch Polarkoordinaten bezüglich des Bezugspunktes
Lage: Die Lage eines starren Körpers in der Ebene ist durch die Angabe von zwei Punkten A und P eindeutig festgelegt. Die Lage eines beliebigen Punktes P wird durch Polarkoordinaten bezüglich des Bezugspunktes
Drehmoment
 Drehmoment Drehmoment Ein Drehmoment entsteht, wenn eine Kraft in einem Abstand zu einem bestimmten Drehpunkt wirkt. Das Drehmoment ist ein Vektorprodukt. Der Betrag des Drehmoments ist gleich dem Produkt
Drehmoment Drehmoment Ein Drehmoment entsteht, wenn eine Kraft in einem Abstand zu einem bestimmten Drehpunkt wirkt. Das Drehmoment ist ein Vektorprodukt. Der Betrag des Drehmoments ist gleich dem Produkt
Formelsammlung
 Formelsammlung Geradlinige Bewegung Bewegung eines Körpers Geschwindigkeit Weg Zeit - Diagramme Zeit s s ~ t v v = const t a a = 0 t t Bewegung eines Körpers Beschleunigte Bewegung Beschleunigung Geschwindigkeit
Formelsammlung Geradlinige Bewegung Bewegung eines Körpers Geschwindigkeit Weg Zeit - Diagramme Zeit s s ~ t v v = const t a a = 0 t t Bewegung eines Körpers Beschleunigte Bewegung Beschleunigung Geschwindigkeit
2. Momentanpol. Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: y A ), v Py. =v Ay
 ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
Tutorium Physik 2. Rotation
 1 Tutorium Physik 2. Rotation SS 16 2.Semester BSc. Oec. und BSc. CH 2 Themen 7. Fluide 8. Rotation 9. Schwingungen 10. Elektrizität 11. Optik 12. Radioaktivität 3 8. ROTATION 8.1 Rotation: Lösungen a
1 Tutorium Physik 2. Rotation SS 16 2.Semester BSc. Oec. und BSc. CH 2 Themen 7. Fluide 8. Rotation 9. Schwingungen 10. Elektrizität 11. Optik 12. Radioaktivität 3 8. ROTATION 8.1 Rotation: Lösungen a
M1 Maxwellsches Rad. 1. Grundlagen
 M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler"
 Aufgaben 5 Rotations-Mechanik Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler" Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen, dass sich die Wirkung einer Kraft nicht
Aufgaben 5 Rotations-Mechanik Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler" Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen, dass sich die Wirkung einer Kraft nicht
Massenträgheitsmomente homogener Körper
 http://www.youtube.com/watch?v=naocmb7jsxe&feature=playlist&p=d30d6966531d5daf&playnext=1&playnext_from=pl&index=8 Massenträgheitsmomente homogener Körper 1 Ma 1 Lubov Vassilevskaya Drehbewegung um c eine
http://www.youtube.com/watch?v=naocmb7jsxe&feature=playlist&p=d30d6966531d5daf&playnext=1&playnext_from=pl&index=8 Massenträgheitsmomente homogener Körper 1 Ma 1 Lubov Vassilevskaya Drehbewegung um c eine
Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler"
 Aufgaben 5 Rotations-Mechanik Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler" Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen und verstehen, dass sich die Wirkung einer
Aufgaben 5 Rotations-Mechanik Drehimpuls, Drehmoment, Kraft-/Drehmoment-"Wandler" Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen und verstehen, dass sich die Wirkung einer
Klassische Experimentalphysik I (Mechanik) (WS 16/17)
 Klassische Experimentalphysik I (Mechanik) (WS 16/17) http://ekpwww.physik.uni-karlsruhe.de/~rwolf/teaching/ws16-17-mechanik.html Übungsblatt 7 Name des Übungsgruppenleiters und Gruppenbuchstabe: Namen
Klassische Experimentalphysik I (Mechanik) (WS 16/17) http://ekpwww.physik.uni-karlsruhe.de/~rwolf/teaching/ws16-17-mechanik.html Übungsblatt 7 Name des Übungsgruppenleiters und Gruppenbuchstabe: Namen
Ein Fahrzeug ohne eigenen Antrieb startet auf der abgebildeten Bahn von dem Punkt (1) und fährt reibungsfrei über den Punkt (2) zum Punkt (3).
 Achterbahn Ein Fahrzeug ohne eigenen Antrieb startet auf der abgebildeten Bahn von dem Punkt (1) und fährt reibungsfrei über den Punkt (2) zum Punkt (3). a) Warum bewegt sich das Fahrzeug? sidee b) Welche
Achterbahn Ein Fahrzeug ohne eigenen Antrieb startet auf der abgebildeten Bahn von dem Punkt (1) und fährt reibungsfrei über den Punkt (2) zum Punkt (3). a) Warum bewegt sich das Fahrzeug? sidee b) Welche
Parameterdarstellung einer Funktion
 Parameterdarstellung einer Funktion 1-E Eine ebene Kurve Abb. 1-1: Die Kurve C beschreibt die ebene Bewegung eines Teilchens 1-1 Eine ebene Kurve Ein Teilchen bewegt sich in einer Ebene. Eine ebene Kurve
Parameterdarstellung einer Funktion 1-E Eine ebene Kurve Abb. 1-1: Die Kurve C beschreibt die ebene Bewegung eines Teilchens 1-1 Eine ebene Kurve Ein Teilchen bewegt sich in einer Ebene. Eine ebene Kurve
Übung zu Mechanik 1 Seite 65
 Übung zu Mechanik 1 Seite 65 Aufgabe 109 Gegeben ist das skizzierte System. a) Bis zu welcher Größe kann F gesteigert werden, ohne daß Rutschen eintritt? b) Welches Teil rutscht, wenn F darüber hinaus
Übung zu Mechanik 1 Seite 65 Aufgabe 109 Gegeben ist das skizzierte System. a) Bis zu welcher Größe kann F gesteigert werden, ohne daß Rutschen eintritt? b) Welches Teil rutscht, wenn F darüber hinaus
TECHNISCHE MECHANIK III (DYNAMIK)
 Klausur im Fach TECHNISCHE MECHANIK III (DYNAMIK) WS 2014 / 2015 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 Summe Punkte: 15 7 23 15 60 Davon erreicht Bearbeitungszeit: Hilfsmittel:
Klausur im Fach TECHNISCHE MECHANIK III (DYNAMIK) WS 2014 / 2015 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 Summe Punkte: 15 7 23 15 60 Davon erreicht Bearbeitungszeit: Hilfsmittel:
tgt HP 1987/88-1: Drehschwenktisch für Schweißarbeiten
 tgt HP 1987/88-1: Drehschwenktisch für Schweißarbeiten maximales Werkstückgewicht Gewichtskraft des Tischoberteiles Geiwchtskraft des Tischunterteiles F G1 = 18 kn F G = 6 kn F G3 = 8 kn Mit einem Drehschwenktisch
tgt HP 1987/88-1: Drehschwenktisch für Schweißarbeiten maximales Werkstückgewicht Gewichtskraft des Tischoberteiles Geiwchtskraft des Tischunterteiles F G1 = 18 kn F G = 6 kn F G3 = 8 kn Mit einem Drehschwenktisch
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 5: Drehmoment, Gleichgewicht und Rotation Dr. Daniel Bick 16. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 16. November 2016 1 / 39 Impuls
Physik für Biologen und Zahnmediziner Kapitel 5: Drehmoment, Gleichgewicht und Rotation Dr. Daniel Bick 16. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 16. November 2016 1 / 39 Impuls
Übung zu Mechanik 1 Seite 50
 Übung zu Mechanik 1 Seite 50 Aufgabe 83 Eine quadratische Platte mit dem Gewicht G und der Kantenlänge a liegt wie skizziert auf drei Böcken, so daß nur Druckkräfte übertragen werden können. Welches Gewicht
Übung zu Mechanik 1 Seite 50 Aufgabe 83 Eine quadratische Platte mit dem Gewicht G und der Kantenlänge a liegt wie skizziert auf drei Böcken, so daß nur Druckkräfte übertragen werden können. Welches Gewicht
Schwingungen. a. Wie lautet die Gleichung für die Position der Masse als Funktion der Zeit? b. Die höchste Geschwindigkeit des Körpers.
 Schwingungen Aufgabe 1 Sie finden im Labor eine Feder. Wenn Sie ein Gewicht von 100g daran hängen, dehnt die Feder sich um 10cm. Dann ziehen Sie das Gewicht 6cm herunter von seiner Gleichgewichtsposition
Schwingungen Aufgabe 1 Sie finden im Labor eine Feder. Wenn Sie ein Gewicht von 100g daran hängen, dehnt die Feder sich um 10cm. Dann ziehen Sie das Gewicht 6cm herunter von seiner Gleichgewichtsposition
4.9 Der starre Körper
 4.9 Der starre Körper Unter einem starren Körper versteht man ein physikalische Modell von einem Körper der nicht verformbar ist. Es erfolgt eine Idealisierung durch die Annahme, das zwei beliebig Punkte
4.9 Der starre Körper Unter einem starren Körper versteht man ein physikalische Modell von einem Körper der nicht verformbar ist. Es erfolgt eine Idealisierung durch die Annahme, das zwei beliebig Punkte
Experimentalphysik 1
 Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg ([email protected]) Katharina Scheidt ([email protected]) Aufgabe 1: Superposition
Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg ([email protected]) Katharina Scheidt ([email protected]) Aufgabe 1: Superposition
Abschlußprüfung an Fachoberschulen: Physik 1996 Aufgabe III
 Abschlußprüfung an Fachoberschulen: Physik 1996 Aufgabe III 1.0 Die Abhängigkeit des Betrags der Coulombkraft F C von den Punktladungen gen Q 1, Q und ihrem Abstand r im Vakuum wird durch das Coulombgesetz
Abschlußprüfung an Fachoberschulen: Physik 1996 Aufgabe III 1.0 Die Abhängigkeit des Betrags der Coulombkraft F C von den Punktladungen gen Q 1, Q und ihrem Abstand r im Vakuum wird durch das Coulombgesetz
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 4: Arbeit, Energie und Meachnik starrer Körper Dr. Daniel Bick 17. November 2017 Daniel Bick Physik für Biologen und Zahnmediziner 17. November 2017 1 / 39
Physik für Biologen und Zahnmediziner Kapitel 4: Arbeit, Energie und Meachnik starrer Körper Dr. Daniel Bick 17. November 2017 Daniel Bick Physik für Biologen und Zahnmediziner 17. November 2017 1 / 39
tgt HP 2011/12-5: Klappbrücke
 tgt HP 2011/12-5: Klappbrücke Klappbrücken werden an Kanälen eingesetzt um Schiffe mit höheren Aufbauten die Durchfahrt zu ermöglichen. Das Hochklappen des Brückenbodens erfolgt durch eine Zahnstange und
tgt HP 2011/12-5: Klappbrücke Klappbrücken werden an Kanälen eingesetzt um Schiffe mit höheren Aufbauten die Durchfahrt zu ermöglichen. Das Hochklappen des Brückenbodens erfolgt durch eine Zahnstange und
Matr.-Nummer Fachrichtung
 Institut für Technische und Num. Mechanik Technische Mechanik II+III Profs. P. Eberhard, M. Hanss WS 2015/16 P 1 18. Februar 2016 Bachelor-Prüfung in Technischer Mechanik II+III Nachname, Vorname E-Mail-Adresse
Institut für Technische und Num. Mechanik Technische Mechanik II+III Profs. P. Eberhard, M. Hanss WS 2015/16 P 1 18. Februar 2016 Bachelor-Prüfung in Technischer Mechanik II+III Nachname, Vorname E-Mail-Adresse
Mechanik I. Arbeitsblätter. (Lehrerversion) GIDA 2010
 Arbeitsblätter (Lehrerversion) Sek. I Arbeitsblatt 1 Kräfte: Vervollständige den Lückentext! Überall in der Welt begegnen uns Kräfte. Man kann sie nicht direkt sehen, man erkennt sie nur an ihrer Wirkung.
Arbeitsblätter (Lehrerversion) Sek. I Arbeitsblatt 1 Kräfte: Vervollständige den Lückentext! Überall in der Welt begegnen uns Kräfte. Man kann sie nicht direkt sehen, man erkennt sie nur an ihrer Wirkung.
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 5: Drehmoment, Gleichgewicht und Rotation Dr. Daniel Bick 16. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 16. November 2016 1 / 39 Impuls
Physik für Biologen und Zahnmediziner Kapitel 5: Drehmoment, Gleichgewicht und Rotation Dr. Daniel Bick 16. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 16. November 2016 1 / 39 Impuls
3 Kinematik des Körpers
 22 3 Kinematik des Körpers 3. Ebene Bewegung eines starren Körpers Liegen die Bahnkurven aller Punkte eines starren Körpers in parallelen Ebenen, so spricht man von einer ebenen Bewegung. Solche Bewegungen
22 3 Kinematik des Körpers 3. Ebene Bewegung eines starren Körpers Liegen die Bahnkurven aller Punkte eines starren Körpers in parallelen Ebenen, so spricht man von einer ebenen Bewegung. Solche Bewegungen
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
ERGEBNISSE TECHNISCHE MECHANIK III-IV Lehrstuhl für Technische Mechanik, TU Kaiserslautern
 ERGEBNISSE TECHNISCHE MECHANIK III-IV Lehrstuhl für Technische Mechanik, TU Kaiserslautern WS 12/13, 13.02.2013 1. Aufgabe: (TM III) Um vom Boden aufzustehen, rutscht ein Mensch mit konstanter Geschwindigkeitv
ERGEBNISSE TECHNISCHE MECHANIK III-IV Lehrstuhl für Technische Mechanik, TU Kaiserslautern WS 12/13, 13.02.2013 1. Aufgabe: (TM III) Um vom Boden aufzustehen, rutscht ein Mensch mit konstanter Geschwindigkeitv
0,6 m. 0,4m. Gegeben seien die obigen drei auf den Balken wirkenden Kräfte mit:
 Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
5.4. KINETISCHE ENERGIE EINES STARREN KÖRPERS 203. Abbildung 5.12: Koordinaten zur Berechnung der kinetischen Energie (siehe Diskussion im Text)
 5.4. KINETISCHE ENERGIE EINES STARREN KÖRPERS 03 ρ α r α R Abbildung 5.1: Koordinaten zur Berechnung der kinetischen Energie (siehe Diskussion im Text) 5.4 Kinetische Energie eines Starren Körpers In diesem
5.4. KINETISCHE ENERGIE EINES STARREN KÖRPERS 03 ρ α r α R Abbildung 5.1: Koordinaten zur Berechnung der kinetischen Energie (siehe Diskussion im Text) 5.4 Kinetische Energie eines Starren Körpers In diesem
6 Mechanik des Starren Körpers
 6 Mechanik des Starren Körpers Ein Starrer Körper läßt sich als System von N Massenpunkten m (mit = 1,...,N) auffassen, die durch starre, masselose Stangen miteinander verbunden sind. Dabei ist N M :=
6 Mechanik des Starren Körpers Ein Starrer Körper läßt sich als System von N Massenpunkten m (mit = 1,...,N) auffassen, die durch starre, masselose Stangen miteinander verbunden sind. Dabei ist N M :=
Physikalisches Praktikum M 7 Kreisel
 1 Physikalisches Praktikum M 7 Kreisel Versuchsziel Quantitative Untersuchung des Zusammenhangs von Präzessionsfrequenz, Rotationsfrequenz und dem auf die Kreiselachse ausgeübten Kippmoment Literatur /1/
1 Physikalisches Praktikum M 7 Kreisel Versuchsziel Quantitative Untersuchung des Zusammenhangs von Präzessionsfrequenz, Rotationsfrequenz und dem auf die Kreiselachse ausgeübten Kippmoment Literatur /1/
Zykloide als Bewegungsbahn
 Zykloide als Bewegungsbahn Zykloide als Bewegungsbahn Eine Zykloide ist die Kurvenbahn eines Punktes einer Scheibe, die z.b. beim Abrollen der Scheibe auf einer Geraden entsteht. Die Kurvenbahn lässt sich
Zykloide als Bewegungsbahn Zykloide als Bewegungsbahn Eine Zykloide ist die Kurvenbahn eines Punktes einer Scheibe, die z.b. beim Abrollen der Scheibe auf einer Geraden entsteht. Die Kurvenbahn lässt sich
Tutorium Physik 2. Rotation
 1 Tutorium Physik 2. Rotation SS 16 2.Semester BSc. Oec. und BSc. CH 2 Themen 7. Fluide 8. Rotation 9. Schwingungen 10. Elektrizität 11. Optik 12. Radioaktivität 3 8. ROTATION 8.1 Rotation: Aufgabe (*)
1 Tutorium Physik 2. Rotation SS 16 2.Semester BSc. Oec. und BSc. CH 2 Themen 7. Fluide 8. Rotation 9. Schwingungen 10. Elektrizität 11. Optik 12. Radioaktivität 3 8. ROTATION 8.1 Rotation: Aufgabe (*)
FACHHOCHSCHULE HEILBRONN Hochschule für Technik und Wirtschaft Studiengang Mikro- und Feinwerktechnik Prof. Dr.-Ing. Jörg Wild
 FACHHOCHSCHULE HEILBRONN Hochschule für Technik und Wirtschaft Studiengang Mikro- und Feinwerktechnik Prof. Dr.-Ing. Jörg Wild Leistungsnachweis im WS 1996/97 zum Diplomzeugnis Prüfungsfach: 3382 Getriebelehre
FACHHOCHSCHULE HEILBRONN Hochschule für Technik und Wirtschaft Studiengang Mikro- und Feinwerktechnik Prof. Dr.-Ing. Jörg Wild Leistungsnachweis im WS 1996/97 zum Diplomzeugnis Prüfungsfach: 3382 Getriebelehre
Kräftepaar und Drehmoment
 Kräftepaar und Drehmoment Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Kräftepaar
Kräftepaar und Drehmoment Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Kräftepaar
Übung zur Vorlesung Grundlagen der Fahrzeugtechnik I. Übung
 Institut für Fahrzeugsystemtechnik Lehrstuhl für Fahrzeugtechnik Leiter: Prof. Dr. rer. nat. Frank Gauterin Fritz-Erler-Str. 1-3 76133 Karlsruhe Übung zur Vorlesung Grundlagen der Fahrzeugtechnik I 1 Aufgaben
Institut für Fahrzeugsystemtechnik Lehrstuhl für Fahrzeugtechnik Leiter: Prof. Dr. rer. nat. Frank Gauterin Fritz-Erler-Str. 1-3 76133 Karlsruhe Übung zur Vorlesung Grundlagen der Fahrzeugtechnik I 1 Aufgaben
Drehimpuls, Drehmoment, Einfache Maschinen
 Aufgaben 4 Rotations-Mechanik Drehimpuls, Drehmoment, Einfache Maschinen Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen, dass sich die Wirkung einer Kraft nicht ändert,
Aufgaben 4 Rotations-Mechanik Drehimpuls, Drehmoment, Einfache Maschinen Lernziele - das Drehimpulsbilanzgesetz verstehen und anwenden können. - wissen, dass sich die Wirkung einer Kraft nicht ändert,
! den Ausdruck W = F. s schreiben darf?
 Probeklausur 1. ufgabe Ohne die Luftreibung wären Regentropfen sehr gefährlich, sie könnten uns "erschießen". Welchen Betrag in km/h hätte die Geschwindigkeit eines Regentropfens, der frei (ohne Luftreibung)
Probeklausur 1. ufgabe Ohne die Luftreibung wären Regentropfen sehr gefährlich, sie könnten uns "erschießen". Welchen Betrag in km/h hätte die Geschwindigkeit eines Regentropfens, der frei (ohne Luftreibung)
06/02/12. Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise:
 Prof Dr-Ing Ams Klausur Technische Mechanik C 06/0/1 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: - Die Prüfungszeit beträgt zwei Stunden - Erlaubte Hilfsmittel
Prof Dr-Ing Ams Klausur Technische Mechanik C 06/0/1 Matrikelnummer: Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: - Die Prüfungszeit beträgt zwei Stunden - Erlaubte Hilfsmittel
Klausur zur Experimentalphysik I für Geowissenschaftler und Geoökologen (Prof. Philipp Richter)
 Übungsgruppenleiter: Universität Potsdam Institut für Physik und Astronomie 14.02.2012 Klausur zur Experimentalphysik I für Geowissenschaftler und Geoökologen (Prof. Philipp Richter) Gesamtpunktzahl: 52
Übungsgruppenleiter: Universität Potsdam Institut für Physik und Astronomie 14.02.2012 Klausur zur Experimentalphysik I für Geowissenschaftler und Geoökologen (Prof. Philipp Richter) Gesamtpunktzahl: 52
Aufgabe 1: (18 Punkte)
 MODULPRÜFUNG TECHNISCHE MECHANIK IV (PO 2004) VOM 26.07.2011 Seite 1 Aufgabe 1: (18 Punkte) Zwei Massenpunkte m 1 = 5 kg und m 2 = 2 kg sind durch ein dehnstarres und massenloses Seil über eine reibungsfrei
MODULPRÜFUNG TECHNISCHE MECHANIK IV (PO 2004) VOM 26.07.2011 Seite 1 Aufgabe 1: (18 Punkte) Zwei Massenpunkte m 1 = 5 kg und m 2 = 2 kg sind durch ein dehnstarres und massenloses Seil über eine reibungsfrei
Biomechanik. Was ist denn das??? Copyright by Birgit Naberfeld & Sascha Kühnel
 Biomechanik Was ist denn das??? Was ist Biomechanik Seite 2 Was ist Biomechanik? Definitionen: "Die Biomechanik des Sports ist die Wissenschaft von der mechanischen Beschreibung und Erklärung der Erscheinungen
Biomechanik Was ist denn das??? Was ist Biomechanik Seite 2 Was ist Biomechanik? Definitionen: "Die Biomechanik des Sports ist die Wissenschaft von der mechanischen Beschreibung und Erklärung der Erscheinungen
Physik 1. Kinematik, Dynamik.
 Physik Mechanik 3 Physik 1. Kinematik, Dynamik. WS 15/16 1. Sem. B.Sc. Oec. und B.Sc. CH Physik Mechanik 5 Themen Definitionen Kinematik Dynamik Physik Mechanik 6 DEFINITIONEN Physik Mechanik 7 Was ist
Physik Mechanik 3 Physik 1. Kinematik, Dynamik. WS 15/16 1. Sem. B.Sc. Oec. und B.Sc. CH Physik Mechanik 5 Themen Definitionen Kinematik Dynamik Physik Mechanik 6 DEFINITIONEN Physik Mechanik 7 Was ist
Eine Last von 120kg hängt an einer Dreieckskonstruktion. Ermittle die Kräfte im Zug- und im Druckstab graphisch. 1200N
 400 Eine Last von 120kg hängt an einer Dreieckskonstruktion. Ermittle die Kräfte im Zug- und im Druckstab graphisch. Zugstab 1) Zeichen der geometrischen Angaben maßstabsgetreu. Z.B. 1cm = 10cm in Wirklichkeit.
400 Eine Last von 120kg hängt an einer Dreieckskonstruktion. Ermittle die Kräfte im Zug- und im Druckstab graphisch. Zugstab 1) Zeichen der geometrischen Angaben maßstabsgetreu. Z.B. 1cm = 10cm in Wirklichkeit.
Aufgaben zum Skalarprodukt
 Aufgaben zum Skalarprodukt 3 1.0 Gegeben ist der Vektor a= 4. 5 0 0 1.1 Berechnen Sie a und a. 1.2 Berechnen Sie denjenigen Vektor der Länge 5 LE, der dieselbe Orientierung hat wie der Gegenvektor von
Aufgaben zum Skalarprodukt 3 1.0 Gegeben ist der Vektor a= 4. 5 0 0 1.1 Berechnen Sie a und a. 1.2 Berechnen Sie denjenigen Vektor der Länge 5 LE, der dieselbe Orientierung hat wie der Gegenvektor von
Grund- und Angleichungsvorlesung Kinematik, Dynamik.
 2 Grund- und Angleichungsvorlesung Physik. Kinematik, Dynamik. WS 18/19 1. Sem. B.Sc. LM-Wissenschaften Diese Präsentation ist lizenziert unter einer Creative Commons Namensnennung Nichtkommerziell Weitergabe
2 Grund- und Angleichungsvorlesung Physik. Kinematik, Dynamik. WS 18/19 1. Sem. B.Sc. LM-Wissenschaften Diese Präsentation ist lizenziert unter einer Creative Commons Namensnennung Nichtkommerziell Weitergabe
Physik 1 Mechanik Tutorium Gravitation Schweredruck - Wasser. Diesmal 6 Aufgaben, davon 2 sehr leicht zu beantworten.
 Seite1(6) Übung 7 Gravitation Schweredruck - Wasser. Diesmal 6 Aufgaben, davon 2 sehr leicht zu beantworten. Aufgabe 1 ISS (IRS) Die ISS (IRS) hat eine Masse von 455 t und fliegt aktuell in einer mittleren
Seite1(6) Übung 7 Gravitation Schweredruck - Wasser. Diesmal 6 Aufgaben, davon 2 sehr leicht zu beantworten. Aufgabe 1 ISS (IRS) Die ISS (IRS) hat eine Masse von 455 t und fliegt aktuell in einer mittleren
Unregelmäßig geformte Scheibe Best.- Nr. MD02256
 Unregelmäßig geformte Scheibe Best.- Nr. MD02256 Momentenlehre Ziel Die unregelmäßig geformte Scheibe wurde gewählt, um den Statik-Kurs zu vervollständigen und um einige praktische Versuche durchzuführen.
Unregelmäßig geformte Scheibe Best.- Nr. MD02256 Momentenlehre Ziel Die unregelmäßig geformte Scheibe wurde gewählt, um den Statik-Kurs zu vervollständigen und um einige praktische Versuche durchzuführen.
Wirkungslinie einer Kraft, Drehmoment, Einfache Maschinen
 Übung 4 Rotations-Mechanik Wirkungslinie einer Kraft, Drehmoment, Einfache Maschinen Lernziele - wissen, dass sich die Wirkung einer Kraft nicht ändert, wenn man die Kraft auf ihrer Wirkungslinie verschiebt.
Übung 4 Rotations-Mechanik Wirkungslinie einer Kraft, Drehmoment, Einfache Maschinen Lernziele - wissen, dass sich die Wirkung einer Kraft nicht ändert, wenn man die Kraft auf ihrer Wirkungslinie verschiebt.
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 17. März 2012 Die Bearbeitungszeit für alle drei Aufgaben beträgt 90 Minuten.
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
Klassische Experimentalphysik I (Mechanik) (WS 16/17)
 Klassische Experimentalphysik I (Mechanik) (WS 16/17) http://ekpwww.physik.uni-karlsruhe.de/~rwolf/teaching/ws16-17-mechanik.html Übungsblatt 8 Name des Übungsgruppenleiters und Gruppenbuchstabe: Namen
Klassische Experimentalphysik I (Mechanik) (WS 16/17) http://ekpwww.physik.uni-karlsruhe.de/~rwolf/teaching/ws16-17-mechanik.html Übungsblatt 8 Name des Übungsgruppenleiters und Gruppenbuchstabe: Namen
Lehrstuhl für Maschinenelemente TU München Prof. Dr.-Ing. B.-R. Höhn. Prüfung Antriebssystemtechnik für Fahrzeuge SS 2010.
 Lehrstuhl für Maschinenelemente TU München Prof. Dr.-Ing. B.-R. Höhn Prüfung Antriebssystemtechnik für Fahrzeuge SS 2010 - Berechnung - (Bearbeitungszeit: 60 min) Hinweise: Die Angaben werden mit den Arbeitsblättern
Lehrstuhl für Maschinenelemente TU München Prof. Dr.-Ing. B.-R. Höhn Prüfung Antriebssystemtechnik für Fahrzeuge SS 2010 - Berechnung - (Bearbeitungszeit: 60 min) Hinweise: Die Angaben werden mit den Arbeitsblättern
Körperberechnung. Würfel - Einheitswürfel. Pyramide. - Oberfläche - Volumen. - Oberfläche. - Volumen. Kegel. Quader. - Oberfläche - Volumen
 Körperberechnung Würfel - Einheitswürfel - Oberfläche - Volumen Quader - Oberfläche - Volumen - zusammengesetzte Körper Prisma - Oberfläche Zylinder - Oberfläche Pyramide - Oberfläche - Volumen Kegel -
Körperberechnung Würfel - Einheitswürfel - Oberfläche - Volumen Quader - Oberfläche - Volumen - zusammengesetzte Körper Prisma - Oberfläche Zylinder - Oberfläche Pyramide - Oberfläche - Volumen Kegel -
Kinematik des starren Körpers
 Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Probeklausur zur Vorlesung PN I Einführung in die Physik für Chemiker und Biologen Priv. Doz. Dr. P. Gilch
 Name: Martrikelnr.: Semester: Biologie Chemie Probeklausur zur Vorlesung PN I Einführung in die Physik für Chemiker und Biologen Priv. Doz. Dr. P. Gilch 12. 2. 2007 Bitte schreiben Sie Ihren Namen auf
Name: Martrikelnr.: Semester: Biologie Chemie Probeklausur zur Vorlesung PN I Einführung in die Physik für Chemiker und Biologen Priv. Doz. Dr. P. Gilch 12. 2. 2007 Bitte schreiben Sie Ihren Namen auf
Aufgabenübersicht für tägliche Übungen mit zugehörigen Klassenstufen:
 Aufgabenübersicht für tägliche Übungen mit zugehörigen Klassenstufen: Größen mit Formelzeichen, Einheiten und Umrechnungen: Bsp.: 520 mm : 10 = 52 cm Bsp.: 120 h : 24 = 5 d 6 Weg FZ: s Einheiten: mm; cm;
Aufgabenübersicht für tägliche Übungen mit zugehörigen Klassenstufen: Größen mit Formelzeichen, Einheiten und Umrechnungen: Bsp.: 520 mm : 10 = 52 cm Bsp.: 120 h : 24 = 5 d 6 Weg FZ: s Einheiten: mm; cm;
Mechanik I. Arbeitsblätter. (Schülerversion) GIDA 2010
 Arbeitsblätter (Schülerversion) Sek. I Arbeitsblatt 1 Kräfte: Vervollständige den Lückentext! Überall in der Welt begegnen uns. Man kann sie nicht direkt sehen, man erkennt sie nur an ihrer. Kräfte können
Arbeitsblätter (Schülerversion) Sek. I Arbeitsblatt 1 Kräfte: Vervollständige den Lückentext! Überall in der Welt begegnen uns. Man kann sie nicht direkt sehen, man erkennt sie nur an ihrer. Kräfte können
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Illustrierende Aufgaben zum LehrplanPLUS. Realschule, Physik, Jahrgangsstufe 7 (I), 8 (II/III), 10 (I) g-kraft. Stand:
 g-kraft Stand: 03.05.2018 Schulart Jahrgangsstufen Fach Übergreifende Bildungs- und Erziehungsziele Zeitrahmen Realschule 7 (I), 8 (II/III), 10 (I) Physik Medienbildung / Digitale Bildung Teil einer Unterrichtsstunde
g-kraft Stand: 03.05.2018 Schulart Jahrgangsstufen Fach Übergreifende Bildungs- und Erziehungsziele Zeitrahmen Realschule 7 (I), 8 (II/III), 10 (I) Physik Medienbildung / Digitale Bildung Teil einer Unterrichtsstunde
Grundwissen. Physik. Jahrgangsstufe 10
 Grundwissen Physik Jahrgangsstufe 10 1. Impuls Grundwissen Physik Jahrgangsstufe 10 Seite 1 Definition: p=m v [ p]=1 kg m s Impulserhaltungssatz: p vorher = p nachher p= p ' p 1 p = p' 1 p ' m 1 =1kg stößt
Grundwissen Physik Jahrgangsstufe 10 1. Impuls Grundwissen Physik Jahrgangsstufe 10 Seite 1 Definition: p=m v [ p]=1 kg m s Impulserhaltungssatz: p vorher = p nachher p= p ' p 1 p = p' 1 p ' m 1 =1kg stößt
2.5 Ausgleichswellen im Verbrennungsmotor
 90 2 Dynamik der starren Maschine 2.5 Ausgleichswellen im Verbrennungsmotor Die periodische Hubbewegung der Kolben in Verbrennungsmotoren verursacht Massenkräfte in Zylinderachsenrichtung. Die periodischen
90 2 Dynamik der starren Maschine 2.5 Ausgleichswellen im Verbrennungsmotor Die periodische Hubbewegung der Kolben in Verbrennungsmotoren verursacht Massenkräfte in Zylinderachsenrichtung. Die periodischen
2.5 Ausgleichswellen im Verbrennungsmotor
 78 2 Dnamik der starren Maschine 2.5 Ausgleichswellen im Verbrennungsmotor Die periodische Hubbewegung der Kolben in Verbrennungsmotoren verursacht Massenkräfte in Zlinderachsenrichtung. Die periodischen
78 2 Dnamik der starren Maschine 2.5 Ausgleichswellen im Verbrennungsmotor Die periodische Hubbewegung der Kolben in Verbrennungsmotoren verursacht Massenkräfte in Zlinderachsenrichtung. Die periodischen
Kinematik des Viergelenk-Koppelgetriebes
 HTL-LiTec Viergelenk - Koppelgetriebe Seite 1 von 7 Dipl.-Ing. Paul MOHR email: [email protected] Kinematik des Viergelenk-Koppelgetriebes Mathematische / Fachliche Inhalte in Stichworten: Kinematik; Getriebelehre;
HTL-LiTec Viergelenk - Koppelgetriebe Seite 1 von 7 Dipl.-Ing. Paul MOHR email: [email protected] Kinematik des Viergelenk-Koppelgetriebes Mathematische / Fachliche Inhalte in Stichworten: Kinematik; Getriebelehre;
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 19. März AUFGABE 1 (16 Punkte)
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
tgt HP 2005/06-2: Exzenterantrieb
 tgt HP 2005/06-2: Exzenterantrieb Der Exzenter wird über eine Welle, die mit einem Getriebe und Motor verbunden ist, angetrieben. Die Kraft wird über Tellerstößel und Stange übertragen, an deren oberen
tgt HP 2005/06-2: Exzenterantrieb Der Exzenter wird über eine Welle, die mit einem Getriebe und Motor verbunden ist, angetrieben. Die Kraft wird über Tellerstößel und Stange übertragen, an deren oberen
TG TECHNOLOGISCHE GRUNDLAGEN 4 MECHANIK REPETITIONEN 4 DREHMOMENT UND SEILROLLEN 1 DREHMOMENT. 1 Drehbewegung erkennen. 06. Februar
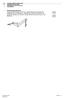 1 Drehbewegung erkennen Dreht sich dieser Körper? Wenn ja, in welche Richtung? Die Länge der Kraftpfeile bzw. der Hebelarme entspricht der Grösse der Kraft bzw. der Länge des Hebelarmes! Zeichnen sie das
1 Drehbewegung erkennen Dreht sich dieser Körper? Wenn ja, in welche Richtung? Die Länge der Kraftpfeile bzw. der Hebelarme entspricht der Grösse der Kraft bzw. der Länge des Hebelarmes! Zeichnen sie das
1. Aufgabenstellung Vorbereitung der Aufgabe Zeichnung in AutoCAD Zeichnung in SAM Lösung der Teilaufgaben...
 Inhaltsverzeichnis 1. Aufgabenstellung... 2 2. Vorbereitung der Aufgabe... 3 2.1 Zeichnung in AutoCAD... 3 2.2 Zeichnung in SAM... 4 3. Lösung der Teilaufgaben... 6 3.1 Geschwindigkeitsverlauf am Schwingenzapfen...
Inhaltsverzeichnis 1. Aufgabenstellung... 2 2. Vorbereitung der Aufgabe... 3 2.1 Zeichnung in AutoCAD... 3 2.2 Zeichnung in SAM... 4 3. Lösung der Teilaufgaben... 6 3.1 Geschwindigkeitsverlauf am Schwingenzapfen...
1. Geradlinige Bewegung
 1. Geradlinige Bewegung 1.1 Kinematik 1.2 Schwerpunktsatz 1.3 Dynamisches Gleichgewicht 1.4 Arbeit und Energie 1.5 Leistung Prof. Dr. Wandinger 3. Kinematik und Kinetik TM 3.1-1 1.1 Kinematik Ort: Bei
1. Geradlinige Bewegung 1.1 Kinematik 1.2 Schwerpunktsatz 1.3 Dynamisches Gleichgewicht 1.4 Arbeit und Energie 1.5 Leistung Prof. Dr. Wandinger 3. Kinematik und Kinetik TM 3.1-1 1.1 Kinematik Ort: Bei
Impuls, Kraft, Impulsbilanz, Grundgesetz der Mechanik
 Aufgaben Translations-Mechanik Impuls, Kraft, Impulsbilanz, Grundgesetz der Mechanik Lernziele - die Eigenschaften des Impulses und den Zusammenhang zwischen Impuls, Masse und Geschwindigkeit eines Körpers
Aufgaben Translations-Mechanik Impuls, Kraft, Impulsbilanz, Grundgesetz der Mechanik Lernziele - die Eigenschaften des Impulses und den Zusammenhang zwischen Impuls, Masse und Geschwindigkeit eines Körpers
Aufgabe 1 Um welche Strecke verlängert sich eine Feder mit D = 50 N/m, wenn eine Masse von 1 kg angehängt wird? Lösung: s = 0.2 m
 13. Statik 13.1. Federgesetz Federgesetz F =D s [ D]= [ F ] [s] = N m Umrechnung 1 N cm =100 N m Um welche Strecke verlängert sich eine Feder mit D = 50 N/m, wenn eine Masse von 1 kg angehängt wird? Lösung:
13. Statik 13.1. Federgesetz Federgesetz F =D s [ D]= [ F ] [s] = N m Umrechnung 1 N cm =100 N m Um welche Strecke verlängert sich eine Feder mit D = 50 N/m, wenn eine Masse von 1 kg angehängt wird? Lösung:
Kraftwinder S = a = a
 Prof. Dr.-ng. Prof. E.h. P. Eberhard A Kraftwinder Der skizzierte Eckpfosten eines Gartenzaunes ist bei A fest im Boden verankert. Er wird in B durch die Kräfte, und belastet. Die Punkte B und C sind durch
Prof. Dr.-ng. Prof. E.h. P. Eberhard A Kraftwinder Der skizzierte Eckpfosten eines Gartenzaunes ist bei A fest im Boden verankert. Er wird in B durch die Kräfte, und belastet. Die Punkte B und C sind durch
3. Systeme von starren Körpern
 Systeme von starren Körpern lassen sich folgendermaßen berechnen: Die einzelnen starren Körper werden freigeschnitten. Für jeden einzelnen Körper werden die Bewegungsgleichungen aufgestellt. Die kinematischen
Systeme von starren Körpern lassen sich folgendermaßen berechnen: Die einzelnen starren Körper werden freigeschnitten. Für jeden einzelnen Körper werden die Bewegungsgleichungen aufgestellt. Die kinematischen
Mehr Zugleistung, größere Arbeitsbreiten- wie bleibt das Pflügen noch optimierbar? Peter Baumgärtner
 Mehr Zugleistung, größere Arbeitsbreiten- wie bleibt das Pflügen noch optimierbar? Peter Baumgärtner Gliederung des Vortrages: Vorstellung der eigenen Person Umsatzverteilung bei LEMKEN Absatzzahlen im
Mehr Zugleistung, größere Arbeitsbreiten- wie bleibt das Pflügen noch optimierbar? Peter Baumgärtner Gliederung des Vortrages: Vorstellung der eigenen Person Umsatzverteilung bei LEMKEN Absatzzahlen im
F r = m v2 r. Bewegt sich der Körper mit der konstanten Winkelgeschwindigkeit ω = 2π, T
 Kreisbewegung ================================================================== Damit sich ein Körper der Masse m auf einer Kreisbahn vom Radius r, dannmuss die Summe aller an diesem Körper angreifenden
Kreisbewegung ================================================================== Damit sich ein Körper der Masse m auf einer Kreisbahn vom Radius r, dannmuss die Summe aller an diesem Körper angreifenden
Übung zu Mechanik 3 Seite 36
 Übung zu Mechanik 3 Seite 36 Aufgabe 61 Ein Faden, an dem eine Masse m C hängt, wird über eine Rolle mit der Masse m B geführt und auf eine Scheibe A (Masse m A, Radius R A ) gewickelt. Diese Scheibe rollt
Übung zu Mechanik 3 Seite 36 Aufgabe 61 Ein Faden, an dem eine Masse m C hängt, wird über eine Rolle mit der Masse m B geführt und auf eine Scheibe A (Masse m A, Radius R A ) gewickelt. Diese Scheibe rollt
KG-Oberkurs 2011 Vorlesungen: Grundlagen der Kinematik und Dynamik
 KG-Oberkurs 011 Vorlesungen: Grundlagen der Kinematik und Dynamik Dr.-Ing. Ulrich Simon 1 Allgemeines Biomechanik Biologie Mechanik Ziel der Vorlesung: Mechanische Grundlagen in anschaulicher Form aufzufrischen.
KG-Oberkurs 011 Vorlesungen: Grundlagen der Kinematik und Dynamik Dr.-Ing. Ulrich Simon 1 Allgemeines Biomechanik Biologie Mechanik Ziel der Vorlesung: Mechanische Grundlagen in anschaulicher Form aufzufrischen.
2.2 Arbeit und Energie. Aufgaben
 2.2 Arbeit und Energie Aufgaben Aufgabe 1: Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt. Für die
2.2 Arbeit und Energie Aufgaben Aufgabe 1: Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt. Für die
Das Hebelgesetz zur Lösung technischer Aufgaben
 Es gibt einseitige Hebel, zweiseitige Hebel und Winkelhebel. Mit allen Hebeln kann man die Größe und Richtung von Kräften ändern. In der Regel verwendet man Hebel zur Vergrößerung von Kräften. Das Hebelgesetz
Es gibt einseitige Hebel, zweiseitige Hebel und Winkelhebel. Mit allen Hebeln kann man die Größe und Richtung von Kräften ändern. In der Regel verwendet man Hebel zur Vergrößerung von Kräften. Das Hebelgesetz
Impuls, Kraft, Impulsbilanz, Grundgesetz der Mechanik
 Aufgaben Translations-Mechanik Impuls, Kraft, Impulsbilanz, Grundgesetz der Mechanik Lernziele - die Eigenschaften des Impulses und den Zusammenhang zwischen Impuls, Masse und Geschwindigkeit eines Körpers
Aufgaben Translations-Mechanik Impuls, Kraft, Impulsbilanz, Grundgesetz der Mechanik Lernziele - die Eigenschaften des Impulses und den Zusammenhang zwischen Impuls, Masse und Geschwindigkeit eines Körpers
Übungen zur Vorlesung Fahrdynamik
 Seite 1 Aufgabe 1 : Der skizzierte Manipulator mit den Hebeln r 1,2 und r 2,3 besitzt zwei Drehgelenke (Drehachsen u 1, u 2 u 1 ). Gegeben seien die Drehwinkel Θ 1 und Θ 2 sowie die Winkelgeschwindigkeiten
Seite 1 Aufgabe 1 : Der skizzierte Manipulator mit den Hebeln r 1,2 und r 2,3 besitzt zwei Drehgelenke (Drehachsen u 1, u 2 u 1 ). Gegeben seien die Drehwinkel Θ 1 und Θ 2 sowie die Winkelgeschwindigkeiten
Im abgebildeten rechtwinkligen Dreieck ( ein Winkel ist 90 groß ) ist β = 40. Wie groß ist Winkel γ?
 LM Gleichungen Seite 30 Übergang Schule - Betrieb Beispiel 1: γ α β Im abgebildeten rechtwinkligen Dreieck ( ein Winkel ist 90 groß ) ist β = 40. Wie groß ist Winkel γ? gegeben: α = 90 β = 40 Winkelsumme
LM Gleichungen Seite 30 Übergang Schule - Betrieb Beispiel 1: γ α β Im abgebildeten rechtwinkligen Dreieck ( ein Winkel ist 90 groß ) ist β = 40. Wie groß ist Winkel γ? gegeben: α = 90 β = 40 Winkelsumme
2.4 Stoßprozesse. entweder nicht interessiert o- der keine Möglichkeit hat, sie zu untersuchen oder zu beeinflussen.
 - 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
- 52-2.4 Stoßprozesse 2.4.1 Definition und Motivation Unter einem Stoß versteht man eine zeitlich begrenzte Wechselwirkung zwischen zwei oder mehr Systemen, wobei man sich für die Einzelheiten der Wechselwirkung
PN1 Einführung in die Physik für Chemiker 1 Prof. J. Lipfert
 PN1 Einführung in die Physik für Chemiker 1 Prof. J. Lipfert WS 015/16 Übungsblatt 6 Übungsblatt 6 Lösung Aufgabe 1 Gravitation. a) Berechnen Sie die Beschleunigung g auf der Sonnenoberfläche. Gegeben
PN1 Einführung in die Physik für Chemiker 1 Prof. J. Lipfert WS 015/16 Übungsblatt 6 Übungsblatt 6 Lösung Aufgabe 1 Gravitation. a) Berechnen Sie die Beschleunigung g auf der Sonnenoberfläche. Gegeben
Aufgabenstellung. Aufgabe 9: Gegeben ist eine Doppelkurbel (siehe folgende Abbildung) mit den Maßen a=30mm, b=70mm, c=60mm, d=80mm. Zu ermitteln sind:
 Aufgabenstellung Die folgende Aufgabenstellung ist entnommen aus Hagedorn, Thonfeld, Rankers: Konstruktive Getriebelehre, 5. Auflage, Springer, Berlin, 996, kurz [Hag96]. (Im Lösungsteil dieses Belegs
Aufgabenstellung Die folgende Aufgabenstellung ist entnommen aus Hagedorn, Thonfeld, Rankers: Konstruktive Getriebelehre, 5. Auflage, Springer, Berlin, 996, kurz [Hag96]. (Im Lösungsteil dieses Belegs
tgtm HP 2017/18-1: Holzrückeschlepper
 Holzrückeschlepper: F G1 40 kn in S1 Abmessungen: l 1 800 mm Holzstämme: F G 70 kn in S l 3800 mm Ladekran: F G3 5 kn in S3 l 3 4500 mm l 4 6000 mm 1 Holzrückeschlepper 1.1 Machen Sie den vollbeladenen
Holzrückeschlepper: F G1 40 kn in S1 Abmessungen: l 1 800 mm Holzstämme: F G 70 kn in S l 3800 mm Ladekran: F G3 5 kn in S3 l 3 4500 mm l 4 6000 mm 1 Holzrückeschlepper 1.1 Machen Sie den vollbeladenen
VHS Floridsdorf elopa Manfred Gurtner Was ist der Differentialquotient in der Physik?
 Was ist der Differentialquotient in der Physik? Ein Auto fährt auf der A1 von Wien nach Salzburg. Wir können diese Fahrt durch eine Funktion Y(T) beschreiben, die zu jedem Zeitpunkt T (Stunden oder Sekunden)
Was ist der Differentialquotient in der Physik? Ein Auto fährt auf der A1 von Wien nach Salzburg. Wir können diese Fahrt durch eine Funktion Y(T) beschreiben, die zu jedem Zeitpunkt T (Stunden oder Sekunden)
tgt HP 1995/96-2: Säulenschwenkkran
 tgt HP 1995/96-2: Säulenschwenkkran Der skizzierte Säulenschwenkkran darf maximal mit der Kraft F L belastet werden. Die Eigengewichtskraft des Schwenkarms mit Hubeinrichtung und Schwenkwerk beträgt F
tgt HP 1995/96-2: Säulenschwenkkran Der skizzierte Säulenschwenkkran darf maximal mit der Kraft F L belastet werden. Die Eigengewichtskraft des Schwenkarms mit Hubeinrichtung und Schwenkwerk beträgt F
2.2 Arbeit und Energie. Aufgaben
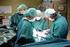 Technische Mechanik 3 2.2-1 Prof. Dr. Wandinger Aufgabe 1 Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt.
Technische Mechanik 3 2.2-1 Prof. Dr. Wandinger Aufgabe 1 Auf eine Katapult befindet sich eine Kugel der Masse, die durch eine Feder beschleunigt wird. Die Feder ist a Anfang u die Strecke s 0 zusaengedrückt.
tgt HP 2007/08-5: Krabbenkutter
 tgt HP 2007/08-5: Krabbenkutter Zum Fang von Krabben werden die Ausleger in die Waagrechte gebracht. Die Fanggeschirre werden zum Meeresboden abgesenkt. Nach Beendigung des Fanges werden die Ausleger in
tgt HP 2007/08-5: Krabbenkutter Zum Fang von Krabben werden die Ausleger in die Waagrechte gebracht. Die Fanggeschirre werden zum Meeresboden abgesenkt. Nach Beendigung des Fanges werden die Ausleger in
Brückenkurs Höhere Mathematik
 Vorkurse der Hochschule Aalen Brückenkurs Höhere Mathematik Aufgabensammlung März 209 Das Grundlagenzentrum (GLZ) wird aus Mitteln des Bundesministeriums für Bildung und Forschung (BMBF) unter dem Förderkennzeichen
Vorkurse der Hochschule Aalen Brückenkurs Höhere Mathematik Aufgabensammlung März 209 Das Grundlagenzentrum (GLZ) wird aus Mitteln des Bundesministeriums für Bildung und Forschung (BMBF) unter dem Förderkennzeichen
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 3: Dynamik und Kräfte Dr. Daniel Bick 09. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 09. November 2016 1 / 25 Übersicht 1 Wiederholung
Physik für Biologen und Zahnmediziner Kapitel 3: Dynamik und Kräfte Dr. Daniel Bick 09. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 09. November 2016 1 / 25 Übersicht 1 Wiederholung
Mathematik verstehen 7 Lösungsblatt Aufgabe 6.67
 Aufgabenstellung: Berechne die Schnittpunkte der e k1 und k mit den Mittelpunkten M1 bzw. M und den Radien r1 bzw. r a. k1: M1 3, 4, P 5, 3 k 1, k geht durch A 0 und B 4 0 r 5 M liegt im 1. Quadranten
Aufgabenstellung: Berechne die Schnittpunkte der e k1 und k mit den Mittelpunkten M1 bzw. M und den Radien r1 bzw. r a. k1: M1 3, 4, P 5, 3 k 1, k geht durch A 0 und B 4 0 r 5 M liegt im 1. Quadranten
TECHNISCHE MECHANIK A (STATIK)
 Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 4 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 31 9 15 10 9 6 80 Davon erreicht Punkte: Gesamtergebnis
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 4 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 31 9 15 10 9 6 80 Davon erreicht Punkte: Gesamtergebnis
