9. Turbulenz in Flüssigkeiten
|
|
|
- Joachim Becker
- vor 9 Jahren
- Abrufe
Transkript
1 9. Turbulenz in Flüssigkeiten Experimentelle Beobachtungen bei strömungen in Rohren (Osborne, Reynolds 1883) Laminare Strömung laminare Strömung bei geringer Strömungsgeschwindigkeit Durchfluss j ist proportional zur Druckdifferenz p Hagen-Poisseuille-Gesetz: j = π r 4 p 8ηl η: Viskosität, l: Rohrlänge, r: Rohrradius turbulente Strömung bei hoher Strömungsgeschwindigkeit Durchfluss j nicht proportional zur Druckdifferenz 1
2 Beispiele turbulenter Strömung In der Natur vorkommende turbulente Strömungen: Wasserströmungen in Flüssen Wasserfall Atmospärische Luftströmungen Ozeanische Wasserströmungen Blutströmungen im Herzen In der Technik auftretende turbulente Strömungen: Strömung von Flüssigkeiten und Gasen in Rohrleitungen Luft-/Wasserströmung um Kraftfahrzeuge/Flugzeuge/Schiffe... Austritt von Flüssigkeiten und Gasen aus Düsen/Rohrenden (Schornsteine, Düsentriebwerke, Raketentriebwerke...) Umrühren von Flüssigkeiten (z. B. Kaffee) Brennkammern Maschinen (z.b. Pumpen, Turbinen, Verbrennungsmotoren) Test eines Feststoffraketen- Motors der Titan IV Rakete 2
3 Das Geschwindigkeitsfeld turbulenter Strömungen Axiale Komponente u l einer turbulenten Strömung auf der Mittelachse als Funktion der Zeit t Normierter Mittelwert der axialen Geschwindigkeit u l einer turbulenten Strömung als Funktion des Normierten radialen Abstands x 2 Ausgeprägte, nicht periodische Fluktuationen der Strömungsgeschwindigkeitskomponente u l (t) um den Mittelwert u l Mittelwerte der Geschwindigkeiten ändern sich kontinuierlich als Funktion des Orts 3
4 Eigenschaften turbulenter Strömung: Der Hauptbewegung sind Querbewegungen überlagert Turbulenz führt zur Durchmischung Wirbelbildung Geschwindigkeitsfeld variiert nicht periodisch in Ort und Zeit selbstähnlich deterministisch chaotisch! Turbulente Strömung eines Wasserstrahls, der in ruhendes Wasser strömt. Turbulente Flüssigkeitsströmung durch ein Rohr. 4
5 Mathematische Beschreibung der Strömung in Fluiden Eulersche Bewegungsgleichung: ρ du dt = ρ u t + u2 2 u rot(u) Kontinuitätsgleichung: ρ t + div( ρ u(x,t) ) = 0 = ρk p u(x,t): Strömungsgeschwindigkeit am Ort x zur Zeit t K = df/dm F: äußere Kraft (z. B. Rührkraft, Schwerkraft, Druckdifferenz) P: isotroper Druck Berücksichtigung von Reibung: Navier-Stokes Gleichung: u t + u2 2 u rot(u) = K 1 4η p + ρ 3ρ div(u) η ρ rot(rot(u)) η: Viskosität ρ: Dichte Navier-Stokes Gleichung besitzt nichtlineare Glieder ==> Instabilität 5
6 Annahme: Inkompressible Fluide Inkompressibilität ==> Dichte: ρ = ρ o = const. Kontinuitätsgleichung: div(u(x,t)) = 0 Navier-Stokes Gleichung: u t u2 = 2 + u rot(u) + K 1 p η rot ( rot(u) ) ρ o ρ o = (u )u u rot(u) + K 1 [ div(u) u] ρ o = (u )u + K 1 ρ o p + η ρ o Δu Randbedingungen bei Strömung durch ein Rohr: Fluid haftet an den Rändern, Rand (V) des Strömungsvolumens: u( x Rand(V ),t ) = u L (x Rand(V ),t) u: konstante Geschwindigkeit am Rand L: typische geometrische Länge des Strömungsvolumens 6
7 Die Reynoldszahl Navier-Stokes Gleichung und Kontinuitätsgleichung beinhalten keine explizite Längen- und Zeitskala (nur Ableitungen der Felder) sowie keine Geschwindigkeitsskala (Galileiinvarianz) Erst die Randbedingungen definieren eine Längen (L) bzw. Geschwindigkeitsskala (u L )! Weitere Skala gegeben durch die Materialeigenschaften des Fluids: η/ρ (Einheit: m 2 /s) Reynoldszahl: Re = Lu Lρ η kleine Reynoldszahlen: lineare (dämpfende) Terme in Navier-Stokes Gleichung dominieren ==> laminare Strömung Typische Reynoldszahlen: Schmieren von Honig auf Brot Re 10-4 Umrühren von Kaffee Re 10 4 Luftströmung um ein Auto bei u = 50 km/h Re Wasserströmung eines Flusses: Re 10 7 Luftströmung um ein Verkehrsflugzeug: Re Gasaustritt aus Feststoffraketenmotor (Titan IV) Re Atmosphärische Strömungen /Zyklon/Antizyklon) Re
8 Windkanäle Unverzichtbares Mittel zum experimentellen Studium und zur Optimierung der aerodynamischen Eigenschaften von Objekten (z. B. Fahrzeugen) Aerodynamische Eigenschaften lassen sich vor dem Bau eines Prototypen an einfachen (preisgünstigen) Modellen testen. Problem bei großen Objekten: Windkanäle, in die große Objekte (z.b. Verkehrsflugzeuge) in Originalgröße hineinpassen, können nicht mit vertretbarem Aufwand gebaut werden! Die Reynoldszahl Re skaliert mit der Größe L des Objektes, während die Schallgeschwindigkeit (Machzahl = 1) größenunabhängig ist! ==> Die aerodynamischen Eigenschaften großer Objektekönnen in konventionellen Windkanälen nicht vollständig an verkleinerten Modellen studiert werden. Re = Lu Lρ η Lösung: Kryogene Windkanäle Mit fallender Temperatur sinken die Viskosität η und die Schallgeschwindigkeit von Luft, während die Dichte ρ ansteigt! ==> Bei niedrigen Temperaturen können in kryogenen Windkanälen an ca. 2m großen Modellen für Verkehrsflugzeuge typische Reynolds- und Machzahlen erreicht werden! 8
9 Der ETW (European Transonic Windtunnel) Der ETW in Köln-Porz Modell eines Airbus A340 im ETW 9
10 Technische Daten des ETW: Machzahlen: ,35 Lufttemperaturen: 110 K K Druck: 1.25 bar bar Typische Modellspannweite: 1.6 m Max. Reynoldszahl: (für Flugzeughälften) 10
11 Energiedissipation Viskosität (Reibung) führt zu Energiedissipation ==> Turbulenz erfordert stete Energiezufuhr zu ihrer Aufrechterhaltung! offenes System Lokal dissipierte Energie (pro Masse und Zeit): ε(x,t) = η ρ u i x j u i x j ; i, j = 1,2, 3 Einheit: [m 2 /s 3 ] Laminare Strömungen weisen kleineres ε als turbulente Strömungen auf! Typische Werte der Energiedissipationsrate: Atmosphärische Strömung: ε = 10-6 m 2 /s 3 Strömung in Grenzschichten: ε = 10-1 m 2 /s 3 Windkanal Stachelschwein in Modane (F): ε = 1.75 m 2 /s 3 11
12 Die Strukturfunktion Strukturfunktion: D(r) = < u(x+r) - u(x) 2 > Beschreibung der Änderung der Geschwindigkeit zwischen zwei Punkten als Funktion des Abstands r Wellenzahlspektrum: 0 E(k)dk = Falls nur ε die Struktur der turbulenten Strömung beeinflusst: u2 2 E(k) ε 2/3 k 5/3 D(r) ε 2/3 r 2/3 Andererseits: Für kleine r muss u(x+r) analytisch sein wegen glättender Wirkung der Viskosität ==> u(x+r) - u(x) ~ r ==> D(r) ~ r 2 Flüssigkeitsströmung durch ein Rohr 12
13 Skizze eines turbulenten Scherfeldes sowie zugehörige Strukturfunktion Zwei Bereiche: 1.) zähigkeitsbeherrschter Bereich (viscous subrange VSR) D(r) = ε ρ η r 2 D hängt explizit von Materialeigenschaften (η/ρ) ab! 2.) nichtlinearer, trägheitsbeherrschter Bereich (inertial subrange ISR) D r 2/3 keine Abhängigkeit von Materialeigenschaften (η/ρ) Wirbelfeld ist statistisch selbstähnlich (Skalierung der Längenskala um λ und Skalierung der Geschwindigkeitsdifferenzen um λ 1/3 ) D( r ) bestimmt durch parameterfreie Meanfeldtheorie 13
14 Selbstähnlichkeit turbulenter Strömungen Strukturfunktion: D(r) = < u(x+r) - u(x) 2 > = <v 2 (r)> Skalenverhalten der Strukturfunktion: D(λr) = λ df D(r) VSR-Bereich: v(r) r ==> d f = 2 ISR-Bereich: v(r) r 1/3 ==> d f = 2/3 Strömungsfelder sind fraktal! ISR Bereich ist begrenzt durch 2 Skalen: Äußere Skala: Abmessung L des Systems Innere Skala: Dämpfung durch Viskosität 1 Re = rν(r)ρ ; ν(r) ε 1/3 r 1/3 η Dissipationslänge: r d := η3 ρ 3 ε 1/4 Übergang von turbulenter (ISR-Bereich) zu laminarer Strömung (VSR-Bereich) bei r 9 r d L r ISR 9 r d VSR 14
15 Einfluss der Viskosität Strömung zweier Fluide unterschiedlicher Viskosität (daher unterschiedlicher Renoldszahlen) unter sonst gleichen Bedingungen in Draufsicht (links unds als Schattenwurf (rechts) Die äußere Form des Strahls ist weitgehend unabhängig von der Viskosität Die minimale Wirbelgröße ist bei dem Fluid mit niedriger Viskosität (große Reynoldszahl) deutlich kleiner als beim höherviskosen Fluid. 15
Dr.-Ing. habil. Jörg Wollnack 18.12.2008 GHY.1. Hydraulische Systeme
 GHY.1 Hydraulische Systeme GHY.2 Hydraulische Motoren GHY.3 p i const, p i Fi i F F 1 2 1 2 F 1 2 F 1 2 Hydraulische Presse I GHY.4 Energieerhaltungssatz S + s S + s 01 1 02 2 S F ds F ds 1 1 2 2 S 01
GHY.1 Hydraulische Systeme GHY.2 Hydraulische Motoren GHY.3 p i const, p i Fi i F F 1 2 1 2 F 1 2 F 1 2 Hydraulische Presse I GHY.4 Energieerhaltungssatz S + s S + s 01 1 02 2 S F ds F ds 1 1 2 2 S 01
Stationäre Rohrströmung ohne Reibung. 2002 Büsching, F.: Hydromechanik 07.1
 Stationäre Rohrströmung ohne Reibung. 00 Büsching, F.: Hydromechanik 07.1 Stationäre Rohrströmung mit Reibung. 00 Büsching, F.: Hydromechanik 07. FLIEßVORGANG REALER FLÜSSIGKEITEN: 1. Laminare und turbulente
Stationäre Rohrströmung ohne Reibung. 00 Büsching, F.: Hydromechanik 07.1 Stationäre Rohrströmung mit Reibung. 00 Büsching, F.: Hydromechanik 07. FLIEßVORGANG REALER FLÜSSIGKEITEN: 1. Laminare und turbulente
Versuch 1. Bestimmung des Umschlagpunktes laminar-turbulent bei einer Rohrströmung (Reynoldsversuch)
 Versuch 1 Bestimmung des Umschlagpunktes laminar-turbulent bei einer Rohrströmung (Reynoldsversuch) Strömungsmechanisches Praktikum des Deutschen Zentrums für Luft- und Raumfahrt Georg-August-Universität
Versuch 1 Bestimmung des Umschlagpunktes laminar-turbulent bei einer Rohrströmung (Reynoldsversuch) Strömungsmechanisches Praktikum des Deutschen Zentrums für Luft- und Raumfahrt Georg-August-Universität
Klausur Strömungsmechanik 1 WS 2009/2010
 Klausur Strömungsmechanik 1 WS 2009/2010 03. März 2010, Beginn 15:00 Uhr Prüfungszeit: 90 Minuten Zugelassene Hilfsmittel sind: Taschenrechner (nicht programmierbar) TFD-Formelsammlung (ohne handschriftliche
Klausur Strömungsmechanik 1 WS 2009/2010 03. März 2010, Beginn 15:00 Uhr Prüfungszeit: 90 Minuten Zugelassene Hilfsmittel sind: Taschenrechner (nicht programmierbar) TFD-Formelsammlung (ohne handschriftliche
Strömung realer inkompressibler Fluide
 4 STRÖMUNG REALER INKOMPRESSIBLER FLUIDE 4.1 EIGENSCHAFTEN REALER FLUIDE 4.1.1 Fluidreibung und Viskosität Wesentlichstes Merkmal realer Fluide ist die Fluidreibung. Sie wurde erstmals von I. Newton (engl.
4 STRÖMUNG REALER INKOMPRESSIBLER FLUIDE 4.1 EIGENSCHAFTEN REALER FLUIDE 4.1.1 Fluidreibung und Viskosität Wesentlichstes Merkmal realer Fluide ist die Fluidreibung. Sie wurde erstmals von I. Newton (engl.
5. Hydro- und Aerodynamik
 Hydro- und Aerodynamik: 5. Hydro- und Aerodynamik (Strömung von Fluiden, also flüssigen und gasförmigen Substanzen) blaue Linien Bahnen von Partikeln der Flüssigkeit Dichte der Linien ist ein Maß für die
Hydro- und Aerodynamik: 5. Hydro- und Aerodynamik (Strömung von Fluiden, also flüssigen und gasförmigen Substanzen) blaue Linien Bahnen von Partikeln der Flüssigkeit Dichte der Linien ist ein Maß für die
Zusammenfassung der hämodynamischen Modellierung Typische medizinische Gegebenheiten und auftretende Probleme bei der Modellierung
 Zusammenfassung der hämodynamischen Modellierung Typische medizinische Gegebenheiten und auftretende Probleme bei der Modellierung 1. Blut (Bettina Wiebe) 2. Gefäße und Kreislaufsystem (Stella Preußler)
Zusammenfassung der hämodynamischen Modellierung Typische medizinische Gegebenheiten und auftretende Probleme bei der Modellierung 1. Blut (Bettina Wiebe) 2. Gefäße und Kreislaufsystem (Stella Preußler)
Aerodynamische Untersuchungen. 1.2 Grundgleichungen von Strömungen idealer, inkompressibler Fluide
 M7 Aerodynamische Untersuchungen Die Abhängigkeiten von Druck und Strömungsgeschwindigkeit in einer Luftströmung sowie die Kraftwirkung auf Körper in dieser Luftströmung sollen veranschaulicht werden..
M7 Aerodynamische Untersuchungen Die Abhängigkeiten von Druck und Strömungsgeschwindigkeit in einer Luftströmung sowie die Kraftwirkung auf Körper in dieser Luftströmung sollen veranschaulicht werden..
Zusammenfassung 23.10.2006, 0. Einführung
 Zusammenfassung 23.10.2006, 0. Einführung - Umrechnung der gebräuchlichen Einheiten - Teilung/Vervielfachung von Einheiten - Kenngrößen des reinen Wassers (z.b. Dichte 1000 kg/m 3 ) Zusammenfassung 30.10.2006,
Zusammenfassung 23.10.2006, 0. Einführung - Umrechnung der gebräuchlichen Einheiten - Teilung/Vervielfachung von Einheiten - Kenngrößen des reinen Wassers (z.b. Dichte 1000 kg/m 3 ) Zusammenfassung 30.10.2006,
I. Mechanik. I.4 Fluid-Dynamik: Strömungen in Flüssigkeiten und Gasen. Physik für Mediziner 1
 I. Mechanik I.4 Fluid-Dynamik: Strömungen in Flüssigkeiten und Gasen Physik für Mediziner Stromdichte Stromstärke = durch einen Querschnitt (senkrecht zur Flussrichtung) fließende Menge pro Zeit ( Menge
I. Mechanik I.4 Fluid-Dynamik: Strömungen in Flüssigkeiten und Gasen Physik für Mediziner Stromdichte Stromstärke = durch einen Querschnitt (senkrecht zur Flussrichtung) fließende Menge pro Zeit ( Menge
Elektrostatik. Freie Ladungen im elektrischen Feld. Was passiert mit einem Elektron in einer Vakuumröhre? Elektron
 Elektrostatik 1. Ladungen Phänomenologie. Eigenschaften von Ladungen 3. Kräfte zwischen Ladungen, quantitativ 4. Elektrisches Feld 5. Der Satz von Gauß 6. Das elektrische Potenzial und Potenzialdifferenz
Elektrostatik 1. Ladungen Phänomenologie. Eigenschaften von Ladungen 3. Kräfte zwischen Ladungen, quantitativ 4. Elektrisches Feld 5. Der Satz von Gauß 6. Das elektrische Potenzial und Potenzialdifferenz
durch Ratengleichungen der Form t t = F 2 N 1 t, N 2 t d N 1 t
 5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
Mathcad Berechnung hydraulischer Verluste fluidführender Systeme
 WARMWASSER ERNEUERBARE ENERGIEN KLIMA RAUMHEIZUNG Mathcad Berechnung hydraulischer Verluste fluidführender Systeme Dipl.-Ing. Carsten Hüge Agenda > Beschreibung der Problemstellung Definition der Druckverluste
WARMWASSER ERNEUERBARE ENERGIEN KLIMA RAUMHEIZUNG Mathcad Berechnung hydraulischer Verluste fluidführender Systeme Dipl.-Ing. Carsten Hüge Agenda > Beschreibung der Problemstellung Definition der Druckverluste
I. Mechanik. 10.Vorlesung EP WS2009/10
 10.Vorlesung EP WS2009/10 I. Mechanik 6. Hydro- und Aerodynamik a) Kontinuitäts- und Bernoulli-Gleichung b) Definition von Viskosität Hagen-Poiseuille - und Stokes - Gesetz 7. Schwingungen Versuche: Druckabfall
10.Vorlesung EP WS2009/10 I. Mechanik 6. Hydro- und Aerodynamik a) Kontinuitäts- und Bernoulli-Gleichung b) Definition von Viskosität Hagen-Poiseuille - und Stokes - Gesetz 7. Schwingungen Versuche: Druckabfall
laminare Grenzschichten Wofür Grenzschichttheorie?
 laminare Grenzschichten Wofür Grenzschichttheorie? mit der Potentialtheorie können nur Druckverteilungen berechnet werden Auftriebskraft Die Widerstandskräfte können nicht berechnet werden. Reibungskräfte
laminare Grenzschichten Wofür Grenzschichttheorie? mit der Potentialtheorie können nur Druckverteilungen berechnet werden Auftriebskraft Die Widerstandskräfte können nicht berechnet werden. Reibungskräfte
Physik I TU Dortmund WS2017/18 Gudrun Hiller Shaukat Khan Kapitel 7
 1 Ergänzungen zur Hydrodynamik Fluide = Flüssigkeiten oder Gase - ideale Fluide - reale Fluide mit "innerer Reibung", ausgedrückt durch die sog. Viskosität Strömungen von Flüssigkeiten, d.h. räumliche
1 Ergänzungen zur Hydrodynamik Fluide = Flüssigkeiten oder Gase - ideale Fluide - reale Fluide mit "innerer Reibung", ausgedrückt durch die sog. Viskosität Strömungen von Flüssigkeiten, d.h. räumliche
10.3.1 Druckverlust in Rohrleitungen bei laminarer Strömung (Re < 2320)
 0.3-0.3 Rohrströmung 0.3. Druckverlust in Rohrleitungen bei laminarer Strömung (Re < 30) Bei laminarer Rohrströmung läßt sich der Reibungsverlust theoretisch berechnen, as bei der turbulenten Strömung
0.3-0.3 Rohrströmung 0.3. Druckverlust in Rohrleitungen bei laminarer Strömung (Re < 30) Bei laminarer Rohrströmung läßt sich der Reibungsverlust theoretisch berechnen, as bei der turbulenten Strömung
Labor Medizinische Gerätetechnologie
 Labor Medizinische Gerätetechnologie Anleitung Flusscharakteristik von Implantaten Versuch 2 1 Vorbereitung Zentralvenöser Katheter Laminare Strömung (Bernoulli, Hagen- Poiseuille) Turbulente Strömung
Labor Medizinische Gerätetechnologie Anleitung Flusscharakteristik von Implantaten Versuch 2 1 Vorbereitung Zentralvenöser Katheter Laminare Strömung (Bernoulli, Hagen- Poiseuille) Turbulente Strömung
lokaler und globaler konvektiver Wärmeübergang (Oberflächentemperatur T s = const.)
 lokaler und globaler konvektiver Wärmeübergang (Oberflächentemperatur T s = const.) Temperaturgrenzschicht Geschwindigkeitsgrenzschicht Vergleich von Geschwindigkeits- und Temperaturgrenzschicht laminare
lokaler und globaler konvektiver Wärmeübergang (Oberflächentemperatur T s = const.) Temperaturgrenzschicht Geschwindigkeitsgrenzschicht Vergleich von Geschwindigkeits- und Temperaturgrenzschicht laminare
14. Strömende Flüssigkeiten und Gase
 14. Strömende Flüssigkeiten und Gase 14.1. orbemerkungen Es gibt viele Analogien zwischen Flüssigkeiten und Gasen (wegen der freien erschiebbarkeit der Teilchen); Hauptunterschied liegt in der Kompressibilität
14. Strömende Flüssigkeiten und Gase 14.1. orbemerkungen Es gibt viele Analogien zwischen Flüssigkeiten und Gasen (wegen der freien erschiebbarkeit der Teilchen); Hauptunterschied liegt in der Kompressibilität
74 Gewöhnliche Differentialgleichungen / Sommersemester 2008
 74 Gewöhnliche Differentialgleichungen / Sommersemester 2008 15 Flüsse Bisher wurde im wesentlichen die Abhängigkeit der Lösungen autonomer Systeme von der Zeit bei festem Anfangswert untersucht. Nun wird
74 Gewöhnliche Differentialgleichungen / Sommersemester 2008 15 Flüsse Bisher wurde im wesentlichen die Abhängigkeit der Lösungen autonomer Systeme von der Zeit bei festem Anfangswert untersucht. Nun wird
Grundpraktikum der Physik. Versuch 05. Viskosität von Flüssigkeiten. Durchführung am 09.11.2007. Gruppe D12 Betreuer: Anne Kröske
 Grundpraktikum der Physik Versuch 05 Viskosität von Flüssigkeiten Durchführung am 09.11.2007 Gruppe D12 Betreuer: Anne Kröske Nadine Kremer [email protected] Rainer Pfeiffer [email protected]
Grundpraktikum der Physik Versuch 05 Viskosität von Flüssigkeiten Durchführung am 09.11.2007 Gruppe D12 Betreuer: Anne Kröske Nadine Kremer [email protected] Rainer Pfeiffer [email protected]
10. Vorlesung EP I. Mechanik 7. Schwingungen (freie, gedämpfte und erzwungene Schwingung, Resonanz, Schwebung)
 10. Vorlesung EP I. Mechanik 7. Schwingungen (freie, gedämpfte und erzwungene Schwingung, Resonanz, Schwebung) Versuche: Pendel mit zwei Längen Sandpendel ohne/mit Dämpfung erzwungene Schwingung mit ω
10. Vorlesung EP I. Mechanik 7. Schwingungen (freie, gedämpfte und erzwungene Schwingung, Resonanz, Schwebung) Versuche: Pendel mit zwei Längen Sandpendel ohne/mit Dämpfung erzwungene Schwingung mit ω
3. Laminar oder turbulent?
 3. Laminar oder turbulent? Die Reynoldszahl Stokes- Gleichung Typisch erreichbare Reynoldszahlen in der Mikrofluik Laminare Strömung Turbulente Strömung 1 Durchmesser L Dichte ρ TrägheitskraG: F ρ ρu 2
3. Laminar oder turbulent? Die Reynoldszahl Stokes- Gleichung Typisch erreichbare Reynoldszahlen in der Mikrofluik Laminare Strömung Turbulente Strömung 1 Durchmesser L Dichte ρ TrägheitskraG: F ρ ρu 2
2.9 Hydrodynamik und Ärodynamik
 - 92-2.9 Hydrodynamik und Ärodynamik In diesem Kapitel werden ebenfalls Fluide diskutiert, wobei wir jetzt bewegte Medien betrachten. Der wichtigste Unterschied zwischen den strömenden Flüssigkeiten und
- 92-2.9 Hydrodynamik und Ärodynamik In diesem Kapitel werden ebenfalls Fluide diskutiert, wobei wir jetzt bewegte Medien betrachten. Der wichtigste Unterschied zwischen den strömenden Flüssigkeiten und
Turbulente Strömung. Benedikt Urbanek. 15. Dezember 2012
 Turbulente Strömung Benedikt Urbanek 15. Dezember 2012 Inhaltsverzeichnis 1 Herleitung der Navier-Stokes-Gleichung 2 1.1 Mathematische Grundlage - Die Substantielle Ableitung.... 2 1.2 Die Kontinuitätsgleichung....................
Turbulente Strömung Benedikt Urbanek 15. Dezember 2012 Inhaltsverzeichnis 1 Herleitung der Navier-Stokes-Gleichung 2 1.1 Mathematische Grundlage - Die Substantielle Ableitung.... 2 1.2 Die Kontinuitätsgleichung....................
Fragen zur Prüfungsvorbereitung Strömungsmechanik II. Stand Sommersemester 2009
 Fragen zur Prüfungsvorbereitung Strömungsmechanik II Stand Sommersemester 2009 Allgemein Sicherer Umgang in der für die im Vorlesungsrahmen benötigte Tensorrechnung. Insbesondere Kenntnis der einzelnen
Fragen zur Prüfungsvorbereitung Strömungsmechanik II Stand Sommersemester 2009 Allgemein Sicherer Umgang in der für die im Vorlesungsrahmen benötigte Tensorrechnung. Insbesondere Kenntnis der einzelnen
Die Burgers Gleichung
 Die Burgers Gleichung Vortrag im Rahmen der Vorlesung Spektralmethoden Elena Frenkel Samuel Voit Balthasar Meyer 29. Mai 2008 1 Einfürung Ein kurzer Überblick Physikalische Motivation 2 Cole-Hopf Transformation
Die Burgers Gleichung Vortrag im Rahmen der Vorlesung Spektralmethoden Elena Frenkel Samuel Voit Balthasar Meyer 29. Mai 2008 1 Einfürung Ein kurzer Überblick Physikalische Motivation 2 Cole-Hopf Transformation
KAPITEL 6. Nichtlineare Ausgleichsrechnung
 KAPITEL 6 Nichtlineare Ausgleichsrechnung Beispiel 61 Gedämpfte Schwingung: u + b m u + D m u = 0, Lösungen haben die Form: u(t) = u 0 e δt sin(ω d t + ϕ 0 ) Modell einer gedämpften Schwingung y(t; x 1,
KAPITEL 6 Nichtlineare Ausgleichsrechnung Beispiel 61 Gedämpfte Schwingung: u + b m u + D m u = 0, Lösungen haben die Form: u(t) = u 0 e δt sin(ω d t + ϕ 0 ) Modell einer gedämpften Schwingung y(t; x 1,
Aufgaben Hydraulik I, 11. Februar 2010, total 150 Pkt.
 Aufgaben Hydraulik I, 11. Februar 2010, total 150 Pkt. Aufgabe 1: Kommunizierende Gefässe (20 Pkt.) Ein System von zwei kommunizierenden Gefässen besteht aus einem oben offenen Behälter A und einem geschlossenen
Aufgaben Hydraulik I, 11. Februar 2010, total 150 Pkt. Aufgabe 1: Kommunizierende Gefässe (20 Pkt.) Ein System von zwei kommunizierenden Gefässen besteht aus einem oben offenen Behälter A und einem geschlossenen
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 10. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung Auswertung Parameter und Kennzahlen
Angewandte Strömungssimulation 10. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung Auswertung Parameter und Kennzahlen
2. Potentialströmungen
 2. Potentialströmungen Bei der Umströmung schlanker Körper ist Reibung oft nur in einer dünnen Schicht um den Körper signifikant groß. Erinnerung: Strömung um ein zweidimensionales Tragflügelprofil: 1
2. Potentialströmungen Bei der Umströmung schlanker Körper ist Reibung oft nur in einer dünnen Schicht um den Körper signifikant groß. Erinnerung: Strömung um ein zweidimensionales Tragflügelprofil: 1
Labor zur Vorlesung Physik
 Labor zur Vorlesung Physik 1 Zur Vorbereitung Die folgenden Begriffe sollten Sie kennen und erklären können: Laminare und turbulente Strömung, Kontinuitätsgleichung, Bernoulli Gleichung, statischer und
Labor zur Vorlesung Physik 1 Zur Vorbereitung Die folgenden Begriffe sollten Sie kennen und erklären können: Laminare und turbulente Strömung, Kontinuitätsgleichung, Bernoulli Gleichung, statischer und
Physik I Mechanik und Thermodynamik
 Physik I Mechanik und Thermodynamik 1 Einführung: 1.1 Was ist Physik? 1.2 Experiment - Modell - Theorie 1.3 Geschichte der Physik 1.4 Physik und andere Wissenschaften 1.5 Maßsysteme 1.6 Messfehler und
Physik I Mechanik und Thermodynamik 1 Einführung: 1.1 Was ist Physik? 1.2 Experiment - Modell - Theorie 1.3 Geschichte der Physik 1.4 Physik und andere Wissenschaften 1.5 Maßsysteme 1.6 Messfehler und
b) Hydrostatik, Aerostatik (Fortsetzung) Schweredruck:
 b) Hydrostatik, Aerostatik (Fortsetzung) Schweredruck: = Druck einer senkrecht über einer Fläche A Stehenden Substanz (auch Flächen innerhalb der Flüssigkeit, nicht nur am Boden) Schweredruck steigt linear
b) Hydrostatik, Aerostatik (Fortsetzung) Schweredruck: = Druck einer senkrecht über einer Fläche A Stehenden Substanz (auch Flächen innerhalb der Flüssigkeit, nicht nur am Boden) Schweredruck steigt linear
... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre ρ L0
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 03. 08. 007 1. Aufgabe (10 Punkte) Ein mit elium gefüllter Ballon (Volumen V 0 für z = 0) steigt in einer Atmosphäre mit der Gaskonstante R
...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 03. 08. 007 1. Aufgabe (10 Punkte) Ein mit elium gefüllter Ballon (Volumen V 0 für z = 0) steigt in einer Atmosphäre mit der Gaskonstante R
1.4 Gradient, Divergenz und Rotation
 .4 Gradient, Divergenz und Rotation 5.4 Gradient, Divergenz und Rotation Die Begriffe Gradient, Divergenz und Rotation erfordern die partiellen Ableitung aus Abschnitt.. sowie das Konzept des Differentialoperators.
.4 Gradient, Divergenz und Rotation 5.4 Gradient, Divergenz und Rotation Die Begriffe Gradient, Divergenz und Rotation erfordern die partiellen Ableitung aus Abschnitt.. sowie das Konzept des Differentialoperators.
Simulations-Untersuchungen des Entleerungsvorgangs eines adiabaten Behälters durch eine angeschlossene Laval-Düse
 TTS-Labor Prof. Dr.-Ing. Victor Gheorghiu Simulations-Untersuchungen es Entleerungsvorgangs eines aiabaten Behälters urch eine angeschlossene Laval-Düse Die Strömung urch ie Laval-Düse von Länge L un minimalem
TTS-Labor Prof. Dr.-Ing. Victor Gheorghiu Simulations-Untersuchungen es Entleerungsvorgangs eines aiabaten Behälters urch eine angeschlossene Laval-Düse Die Strömung urch ie Laval-Düse von Länge L un minimalem
I. Mechanik. 10.Vorlesung EP WS2008/9. 6. Hydro- und Aerodynamik a) Kontinuitäts- und Bernoulli-Gleichung b) Viskosität Fortsetzung: Hagen-Poisenille
 10.Vorlesung EP WS2008/9 I. Mechanik 6. Hydro- und Aerodynamik a) Kontinuitäts- und Bernoulli-Gleichung b) Viskosität Fortsetzung: Hagen-Poisenille 7. Schwingungen Versuche: Pendel mit zwei Längen Sandpendel
10.Vorlesung EP WS2008/9 I. Mechanik 6. Hydro- und Aerodynamik a) Kontinuitäts- und Bernoulli-Gleichung b) Viskosität Fortsetzung: Hagen-Poisenille 7. Schwingungen Versuche: Pendel mit zwei Längen Sandpendel
a.) Wie beeinflussen in einer Verbrennungsreaktion Brennstoffe in fester bzw. flüssiger Phase das chemische Gleichgewicht? Begründung!
 Klausur F2004 (Grundlagen der motorischen Verbrennung) 2 Aufgabe 1.) ( 2 Punkte) Wie beeinflussen in einer Verbrennungsreaktion Brennstoffe in fester bzw. flüssiger Phase das chemische Gleichgewicht? Begründung!
Klausur F2004 (Grundlagen der motorischen Verbrennung) 2 Aufgabe 1.) ( 2 Punkte) Wie beeinflussen in einer Verbrennungsreaktion Brennstoffe in fester bzw. flüssiger Phase das chemische Gleichgewicht? Begründung!
Grundlagen der Strömungsmechanik
 Franz Durst Grundlagen der Strömungsmechanik Eine Einführung in die Theorie der Strömungen von Fluiden Mit 349 Abbildungen, davon 8 farbig QA Springer Inhaltsverzeichnis Bedeutung und Entwicklung der Strömungsmechanik
Franz Durst Grundlagen der Strömungsmechanik Eine Einführung in die Theorie der Strömungen von Fluiden Mit 349 Abbildungen, davon 8 farbig QA Springer Inhaltsverzeichnis Bedeutung und Entwicklung der Strömungsmechanik
7 Turbulenz (7.1) L. L oder ausgerückt durch das Verhältnis (7.2)
 7 Turbulenz In einer laminaren Strömung fliessen die Flüssigkeitselemente in benachbarten Stromlinien aneinander vorbei ohne sich zu mischen. Im Gegensatz dazu hat die turbulente Strömung einen stark unregelmässigen,
7 Turbulenz In einer laminaren Strömung fliessen die Flüssigkeitselemente in benachbarten Stromlinien aneinander vorbei ohne sich zu mischen. Im Gegensatz dazu hat die turbulente Strömung einen stark unregelmässigen,
Berechnungsmethoden der Energie- und Verfahrenstechnik
 Institute of Fluid Dynamics Berechnungsmethoden der Energie- und Verfahrenstechnik Prof. Dr. Leonhard Kleiser c L. Kleiser, ETH Zürich Transition zur Turbulenz in einem drahlbehafteten Freistrahl. S. Müller,
Institute of Fluid Dynamics Berechnungsmethoden der Energie- und Verfahrenstechnik Prof. Dr. Leonhard Kleiser c L. Kleiser, ETH Zürich Transition zur Turbulenz in einem drahlbehafteten Freistrahl. S. Müller,
Prüfungsfragen und Prüfungsaufgaben
 Mathematische Modelle in der Technik WS 3/4 Prüfungsfragen und Prüfungsaufgaben Fragen - 9:. Modellieren Sie ein örtlich eindimensionales, stationäres Wärmeleitproblem (Integralbilanzformulierung, differentielle
Mathematische Modelle in der Technik WS 3/4 Prüfungsfragen und Prüfungsaufgaben Fragen - 9:. Modellieren Sie ein örtlich eindimensionales, stationäres Wärmeleitproblem (Integralbilanzformulierung, differentielle
Übung 4 - SIMPLE-Verfahren
 Übung 4 - SIMPLE-Verfahren Musterlösung C. Baur, M. Schäfer Fachgebiet für Numerische Berechnungsverfahren im Maschinenbau 27.11.2008 TU Darmstadt FNB 27.11.2008 1/26 Aufgabe 1 - Problembeschreibung Geometrie
Übung 4 - SIMPLE-Verfahren Musterlösung C. Baur, M. Schäfer Fachgebiet für Numerische Berechnungsverfahren im Maschinenbau 27.11.2008 TU Darmstadt FNB 27.11.2008 1/26 Aufgabe 1 - Problembeschreibung Geometrie
Grundlage für das Verständnis der Gegebenheiten unter Wasser Erkennen der sich daraus ableitenden Vorgänge in diesem für den Taucher
 Tauchphysik Grundlage für das Verständnis der Gegebenheiten unter Wasser Erkennen der sich daraus ableitenden Vorgänge in diesem für den Taucher lebensfeindlichen Milieu Einhaltung wichtiger Verhaltens-regeln,
Tauchphysik Grundlage für das Verständnis der Gegebenheiten unter Wasser Erkennen der sich daraus ableitenden Vorgänge in diesem für den Taucher lebensfeindlichen Milieu Einhaltung wichtiger Verhaltens-regeln,
Kompressible Gasdynamik
 Hauptseminar Lineare und Nichtlineare Wellenphänomene 14. Januar 2013 Inhaltsverzeichnis 1 Thermodynamische Grundlagen 2 Bewegungsgleichungen 3 Konstruktion der Charakteristiken Allgemeine Konstruktion
Hauptseminar Lineare und Nichtlineare Wellenphänomene 14. Januar 2013 Inhaltsverzeichnis 1 Thermodynamische Grundlagen 2 Bewegungsgleichungen 3 Konstruktion der Charakteristiken Allgemeine Konstruktion
Strömung im Rohr. Versuch: Inhaltsverzeichnis. Fachrichtung Physik. Physikalisches Grundpraktikum. 1 Aufgabenstellung 2
 Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
VON DER GALAXIE ZUR ZELLE
 VON DER GALAXIE ZUR ZELLE Michael Bestehorn Lehrstuhl Theoretische Physik II BTU Cottbus Selbstorganisierte Strukturen Unter bestimmten äußeren Bedingungen entstehen Strukturen (räumliche und zeitliche)
VON DER GALAXIE ZUR ZELLE Michael Bestehorn Lehrstuhl Theoretische Physik II BTU Cottbus Selbstorganisierte Strukturen Unter bestimmten äußeren Bedingungen entstehen Strukturen (räumliche und zeitliche)
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
3. Grenzschichtströmungen Grenzschichtablösung
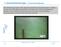 3. Grenzschichtströmungen - 3. Grenzschichtablösung Eine Strömung ist nicht in der Lage sehr schnellen Konturänderungen zu folgen, da dies sehr hohe Beschleunigungen und daher sehr hohe Druckgradienten
3. Grenzschichtströmungen - 3. Grenzschichtablösung Eine Strömung ist nicht in der Lage sehr schnellen Konturänderungen zu folgen, da dies sehr hohe Beschleunigungen und daher sehr hohe Druckgradienten
Strömungsmechanik I - Fluideigenschaften
 Strömungsmechanik I - R. Hinkelmann,, Folie 1 Fachbezeichnungen Strömungsmechanik: sehr allgemein; i.d.r. kompressibel und inkompressibel Strömungsmechanik für Bauingenieure: i.d.r. Fokus auf Wasser und
Strömungsmechanik I - R. Hinkelmann,, Folie 1 Fachbezeichnungen Strömungsmechanik: sehr allgemein; i.d.r. kompressibel und inkompressibel Strömungsmechanik für Bauingenieure: i.d.r. Fokus auf Wasser und
Präzisionsstahlrohre
 Hydraulik Ermeto Original Präzisionsstahlrohre INDUSTRIETECHNIK GMBH. Brunshofstraße 10. D-45470 Mülheim an der Ruhr Tel. (0208) 3783-0. Fax (0208) 3783-158. E-Mail: [email protected]. Internet: Angaben zu EO-Rohren
Hydraulik Ermeto Original Präzisionsstahlrohre INDUSTRIETECHNIK GMBH. Brunshofstraße 10. D-45470 Mülheim an der Ruhr Tel. (0208) 3783-0. Fax (0208) 3783-158. E-Mail: [email protected]. Internet: Angaben zu EO-Rohren
Lineare Antwort, Green-Kubo, Fluktuations-Dissipations Theorem
 Lineare Antwort, Green-Kubo, Fluktuations-Dissipations Theorem Franziska Böhme, Sophie Seidenbecher 05.07.2012 1 Lineare Antwort 2 3 4 Theorie der Linearen Antwort Einführung der Linearen Antworttheorie
Lineare Antwort, Green-Kubo, Fluktuations-Dissipations Theorem Franziska Böhme, Sophie Seidenbecher 05.07.2012 1 Lineare Antwort 2 3 4 Theorie der Linearen Antwort Einführung der Linearen Antworttheorie
Inhaltsverzeichnis. Gerd Junge. Einführung in die Technische Strömungslehre ISBN: Weitere Informationen oder Bestellungen unter
 Inhaltsverzeichnis Gerd Junge Einführung in die Technische Strömungslehre ISBN: 978-3-446-42300-8 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42300-8 sowie im Buchhandel.
Inhaltsverzeichnis Gerd Junge Einführung in die Technische Strömungslehre ISBN: 978-3-446-42300-8 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42300-8 sowie im Buchhandel.
Hydrodynamische Wechselwirkung und Stokes Reibung
 Hydrodynamische Wechselwirkung und Stokes Reibung 9. Februar 2008 Problemstellung Kolloidsuspension aus Teilchen und Lösungsmittel Teilchen bewegen sich aufgrund von externen Kräften Schwerkraft Äußere
Hydrodynamische Wechselwirkung und Stokes Reibung 9. Februar 2008 Problemstellung Kolloidsuspension aus Teilchen und Lösungsmittel Teilchen bewegen sich aufgrund von externen Kräften Schwerkraft Äußere
Allgemein gilt: Die Erdbeschleunigung g kann vereinfachend mit g= 10 m/s² angenommen
 Allgemein gilt: Die Erdbeschleunigung g kann vereinfachend mit g= 10 m/s² angenommen werden. (1) Eigenschaften von Fluiden In Weimar soll ein etwa 25 m hohes Gebäude errichtet werden (siehe Anlage für
Allgemein gilt: Die Erdbeschleunigung g kann vereinfachend mit g= 10 m/s² angenommen werden. (1) Eigenschaften von Fluiden In Weimar soll ein etwa 25 m hohes Gebäude errichtet werden (siehe Anlage für
Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume. Klausur Frühjahr Strömungsmechanik I. Name Vorname Matr.
 Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume Klausur Frühjahr 003 Strömungsmechanik I Bearbeitungsdauer: PO 000 : 90 min zugelassene Hilfsmittel: Taschenrechner Formelsammlung-IfS,
Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume Klausur Frühjahr 003 Strömungsmechanik I Bearbeitungsdauer: PO 000 : 90 min zugelassene Hilfsmittel: Taschenrechner Formelsammlung-IfS,
Vektoren, Tensoren, Operatoren Tensoren Rang 0 Skalar p,ρ,t,... Rang 1 Vektor F, v, I,... Spannungstensor
 Vektoren, Tensoren, Operatoren Tensoren Rang 0 Skalar p,ρ,t,... Rang 1 Vektor F, v, I,... Rang 2 Dyade }{{} σ, τ,... Spannungstensor Differential-Operatoren Nabla- / x Operator / y in kartesischen / Koordinaten
Vektoren, Tensoren, Operatoren Tensoren Rang 0 Skalar p,ρ,t,... Rang 1 Vektor F, v, I,... Rang 2 Dyade }{{} σ, τ,... Spannungstensor Differential-Operatoren Nabla- / x Operator / y in kartesischen / Koordinaten
Strömungen. Kapitel 10
 Kapitel 10 Strömungen In Kapitel 9 behandelten wir die statistische Bewegung einzelner Moleküle in einem Gas, aber noch keine makroskopische Bewegung des Mediums. Der Mittelwert der Impulse aller Teilchen
Kapitel 10 Strömungen In Kapitel 9 behandelten wir die statistische Bewegung einzelner Moleküle in einem Gas, aber noch keine makroskopische Bewegung des Mediums. Der Mittelwert der Impulse aller Teilchen
III. Schwingungen und Wellen
 III. Schwingungen und Wellen III.1 Schwingungen Physik für Mediziner 1 Schwingungen Eine Schwingung ist ein zeitlich periodischer Vorgang Schwingungen finden im allgemeinen um eine stabile Gleichgewichtslage
III. Schwingungen und Wellen III.1 Schwingungen Physik für Mediziner 1 Schwingungen Eine Schwingung ist ein zeitlich periodischer Vorgang Schwingungen finden im allgemeinen um eine stabile Gleichgewichtslage
Mathematik in Strömungen
 Mathematik in Strömungen Ein Rätsel und ein Paradoxon László Székelyhidi Jr. Leonardo da Vinci 1452-1519 Tinte und Sirup Tinte und Sirup Wirbelstürme Tinte und Sirup Wirbelstürme Turbulenzen beim Fliegen
Mathematik in Strömungen Ein Rätsel und ein Paradoxon László Székelyhidi Jr. Leonardo da Vinci 1452-1519 Tinte und Sirup Tinte und Sirup Wirbelstürme Tinte und Sirup Wirbelstürme Turbulenzen beim Fliegen
Die Funktion f sei (zumindest) in einem Intervall I = [a, b] definiert und dort hinreichend oft differenzierbar. f(x 0 ) f(x)
![Die Funktion f sei (zumindest) in einem Intervall I = [a, b] definiert und dort hinreichend oft differenzierbar. f(x 0 ) f(x) Die Funktion f sei (zumindest) in einem Intervall I = [a, b] definiert und dort hinreichend oft differenzierbar. f(x 0 ) f(x)](/thumbs/40/21100650.jpg) 3.2.4. Analyse von Funktionen Die Funktion f sei (zumindest) in einem Intervall I = [a, b] definiert und dort hinreichend oft differenzierbar. Begriffe: Die Funktion f hat in x 0 I eine stationäre Stelle,
3.2.4. Analyse von Funktionen Die Funktion f sei (zumindest) in einem Intervall I = [a, b] definiert und dort hinreichend oft differenzierbar. Begriffe: Die Funktion f hat in x 0 I eine stationäre Stelle,
Klausur Strömungsmechanik I
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungsmechanik I 08. 08. 2014 1. Aufgabe (12 Punkte) Eine Ölbarriere in der Form eines Zylinders mit dem Durchmesser D schwimmt im Meer. Sie taucht in dem
...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungsmechanik I 08. 08. 2014 1. Aufgabe (12 Punkte) Eine Ölbarriere in der Form eines Zylinders mit dem Durchmesser D schwimmt im Meer. Sie taucht in dem
3.2 Streuungsmaße. 3 Lage- und Streuungsmaße 133. mittlere Variabilität. geringe Variabilität. große Variabilität 0.0 0.1 0.2 0.3 0.4 0.
 Eine Verteilung ist durch die Angabe von einem oder mehreren Mittelwerten nur unzureichend beschrieben. Beispiel: Häufigkeitsverteilungen mit gleicher zentraler Tendenz: geringe Variabilität mittlere Variabilität
Eine Verteilung ist durch die Angabe von einem oder mehreren Mittelwerten nur unzureichend beschrieben. Beispiel: Häufigkeitsverteilungen mit gleicher zentraler Tendenz: geringe Variabilität mittlere Variabilität
Pumpenkennlinie. Matthias Prielhofer
 Matthias Prielhfer 1. Zielsetzung Im Rahmen der Übung sllen auf einem dafür eingerichteten Pumpenprüfstand Parameter gemessen werden um eine erstellen zu können. Weiters sll vn einem Stellglied, in diesem
Matthias Prielhfer 1. Zielsetzung Im Rahmen der Übung sllen auf einem dafür eingerichteten Pumpenprüfstand Parameter gemessen werden um eine erstellen zu können. Weiters sll vn einem Stellglied, in diesem
Kapitel 6. Variationsrechnung
 Kapitel 6 Variationsrechnung Die vorangegangenen Kapitel waren der relativistischen Kinematik gewidmet, also der Beschreibung der Bewegung von Teilchen, deren Geschwindigkeit nicht vernachlässigbar klein
Kapitel 6 Variationsrechnung Die vorangegangenen Kapitel waren der relativistischen Kinematik gewidmet, also der Beschreibung der Bewegung von Teilchen, deren Geschwindigkeit nicht vernachlässigbar klein
3. Magnetostatik 3.1. Grundbegriffe
 3. Magnetostatik 3.1. Grundbegriffe In der Natur existieren magnetische Felder. Es gibt allerdings keine Quellen des magnetischen Feldes, d. h. es wurden noch nie magnetischen Ladungen (magnetische Monopole)
3. Magnetostatik 3.1. Grundbegriffe In der Natur existieren magnetische Felder. Es gibt allerdings keine Quellen des magnetischen Feldes, d. h. es wurden noch nie magnetischen Ladungen (magnetische Monopole)
B.3 Lösungsskizzen der Übungsaufgaben zum Kapitel 3
 B sskizzen B.3 sskizzen der Übungsaufgaben zum Kapitel 3 Aufgabe 9 (Stahlseil) An einem Stahlseil (Länge L 0, Querschnittsfläche A, Dichte ρ, Elastizitätsmodul E) hängt ein Körper der Masse m. Um welchen
B sskizzen B.3 sskizzen der Übungsaufgaben zum Kapitel 3 Aufgabe 9 (Stahlseil) An einem Stahlseil (Länge L 0, Querschnittsfläche A, Dichte ρ, Elastizitätsmodul E) hängt ein Körper der Masse m. Um welchen
Hydrodynamik Kontinuitätsgleichung. Massenerhaltung: ρ. Massenfluss. inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms : v
 Hydrodynamik Kontinuitätsgleichung A2, rho2, v2 A1, rho1, v1 Stromröhre Massenerhaltung: ρ } 1 v {{ 1 A } 1 = ρ } 2 v {{ 2 A } 2 m 1 inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms
Hydrodynamik Kontinuitätsgleichung A2, rho2, v2 A1, rho1, v1 Stromröhre Massenerhaltung: ρ } 1 v {{ 1 A } 1 = ρ } 2 v {{ 2 A } 2 m 1 inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms
Prüfungsfrage Strömung der Flüssigkeiten. Fluideigenschaften. Strömungslehre. HYDROSTATIK keine Bewegung
 016.11.18. Prüfungsfrage Strömung der Flüssigkeiten Typen der Flüssigkeitsströmung. Die Reynolds-Zahl. Die Viskosität. Die Gesetzmäßigkeiten der Flüssigkeitsströmung: die Gleichung der Kontinuität, das
016.11.18. Prüfungsfrage Strömung der Flüssigkeiten Typen der Flüssigkeitsströmung. Die Reynolds-Zahl. Die Viskosität. Die Gesetzmäßigkeiten der Flüssigkeitsströmung: die Gleichung der Kontinuität, das
Die Anzahl der Keime in 1 cm 3 Milch wird im zeitlichen Abstand von 1 h bestimmt.
 7. Anwendungen ================================================================== 7.1 Exponentielles Wachstum ------------------------------------------------------------------------------------------------------------------
7. Anwendungen ================================================================== 7.1 Exponentielles Wachstum ------------------------------------------------------------------------------------------------------------------
1. Die Wellengleichung
 1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt
 Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt f 1 : W D, y wobei D mit f() = y die Umkehrfunktion zu f. Der Graph G f 1 = {(y,
Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt f 1 : W D, y wobei D mit f() = y die Umkehrfunktion zu f. Der Graph G f 1 = {(y,
Allgemeine Vorgehensweise
 Allgemeine Vorgehensweise 1. Skizze zeichnen und Systemgrenze ziehen 2. Art des Systems festlegen (offen, geschlossen, abgeschlossen) und Eigenschaften charakterisieren (z.b. adiabat, stationär, ruhend...)
Allgemeine Vorgehensweise 1. Skizze zeichnen und Systemgrenze ziehen 2. Art des Systems festlegen (offen, geschlossen, abgeschlossen) und Eigenschaften charakterisieren (z.b. adiabat, stationär, ruhend...)
Bem. Die mittlere Geschwindigkeit hängt i.a. nicht nur von t, sondern auch von t ab.
 40 8. Anwendungen der Differentialrechnung Beispiele aus der Phsik: Momentangeschwindigkeit Die Bewegung eines Massenpunktes wird mathematisch durch die zugrundeliegende Weg- Zeitfunktion beschrieben,
40 8. Anwendungen der Differentialrechnung Beispiele aus der Phsik: Momentangeschwindigkeit Die Bewegung eines Massenpunktes wird mathematisch durch die zugrundeliegende Weg- Zeitfunktion beschrieben,
Kompetenzcheck. Mathematik (AHS) Oktober 2013. Lösungsheft
 Kompetenzcheck Mathematik (AH) Oktober 2013 Lösungsheft Lösung zu Aufgabe 1 Rationale Zahlen 1 2 3,5 16 Ein Punkt ist nur dann zu geben, wenn alle Kreuze richtig gesetzt sind. 2 Lösung zu Aufgabe 2 Rechenoperationen
Kompetenzcheck Mathematik (AH) Oktober 2013 Lösungsheft Lösung zu Aufgabe 1 Rationale Zahlen 1 2 3,5 16 Ein Punkt ist nur dann zu geben, wenn alle Kreuze richtig gesetzt sind. 2 Lösung zu Aufgabe 2 Rechenoperationen
Materialien WS 2014/15 Dozent: Dr. Andreas Will.
 Master Umweltingenieur, 1. Semester, Modul 42439,, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will [email protected] Reynoldszahl
Master Umweltingenieur, 1. Semester, Modul 42439,, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will [email protected] Reynoldszahl
Klausur Technische Strömungslehre z g
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Technische Strömungslehre 11. 03. 2009 1. Aufgabe (12 Punkte) p a z g Ein Forscher taucht mit einem kleinen U-Boot der Masse m B = 3200kg (Taucher und Boot)
...... (Name, Matr.-Nr, Unterschrift) Klausur Technische Strömungslehre 11. 03. 2009 1. Aufgabe (12 Punkte) p a z g Ein Forscher taucht mit einem kleinen U-Boot der Masse m B = 3200kg (Taucher und Boot)
Differentialrechnung
 Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 205/6 7 Differentialrechnung / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f () f ( 0) 0 heißt
Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 205/6 7 Differentialrechnung / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f () f ( 0) 0 heißt
Übungsblatt 1 (13.05.2011)
 Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 11 Übungsblatt 1 (13.5.11) 1) Wasserstrahl Der aus einem Wasserhahn senkrecht nach unten ausfließende Wasserstrahl verjüngt
Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 11 Übungsblatt 1 (13.5.11) 1) Wasserstrahl Der aus einem Wasserhahn senkrecht nach unten ausfließende Wasserstrahl verjüngt
3. Innere Reibung von Flüssigkeiten
 IR1 3. Innere Reibung von Flüssigkeiten 3.1 Einleitung Zwischen den Molekülen in Flüssigkeiten wirken anziehende Van der Waals Kräfte oder wie im Falle des Wassers Kräfte, die von sogenannten Wasserstoffbrückenbindungen
IR1 3. Innere Reibung von Flüssigkeiten 3.1 Einleitung Zwischen den Molekülen in Flüssigkeiten wirken anziehende Van der Waals Kräfte oder wie im Falle des Wassers Kräfte, die von sogenannten Wasserstoffbrückenbindungen
Versuch Eichung und Linearisierung eines Hitzdrahtes Wirbelbildung am quer angeströmten Kreiszylinder (Kármánsche Wirbelstraße)
 Versuch 7 + 8 Eichung und Linearisierung eines Hitzdrahtes Wirbelbildung am quer angeströmten Kreiszylinder (Kármánsche Wirbelstraße) Strömungsmechanisches Praktikum des Deutschen Zentrums für Luft- und
Versuch 7 + 8 Eichung und Linearisierung eines Hitzdrahtes Wirbelbildung am quer angeströmten Kreiszylinder (Kármánsche Wirbelstraße) Strömungsmechanisches Praktikum des Deutschen Zentrums für Luft- und
Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide
 Daniel Janocha Aus der Reihe: e-fellows.net stipendiaten-wissen e-fellows.net (Hrsg.) Band 1064 Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide Weak solution of the Stokes equations
Daniel Janocha Aus der Reihe: e-fellows.net stipendiaten-wissen e-fellows.net (Hrsg.) Band 1064 Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide Weak solution of the Stokes equations
Physikalisches Grundpraktikum
 Ernst-Moritz-Arndt-Universität Greifswald / Institut für Physik Physikalisches Grundpraktikum Praktikum für Mediziner M1 Viskose Strömung durch Kapillaren Name: Versuchsgruppe: Datum: Mitarbeiter der Versuchsgruppe:
Ernst-Moritz-Arndt-Universität Greifswald / Institut für Physik Physikalisches Grundpraktikum Praktikum für Mediziner M1 Viskose Strömung durch Kapillaren Name: Versuchsgruppe: Datum: Mitarbeiter der Versuchsgruppe:
Aufgabe 1 (LGS mit Parameter): Bestimmen Sie die Lösungsmengen des folgenden LGS in Abhängigkeit vom Parameter :
 Mathematik MB Übungsblatt Termin Lösungen Themen: Grundlagen Vektoren und LGS ( Aufgaben) DHBW STUTTGART WS / Termin SEITE VON Aufgabe (LGS mit Parameter): Bestimmen Sie die Lösungsmengen des folgenden
Mathematik MB Übungsblatt Termin Lösungen Themen: Grundlagen Vektoren und LGS ( Aufgaben) DHBW STUTTGART WS / Termin SEITE VON Aufgabe (LGS mit Parameter): Bestimmen Sie die Lösungsmengen des folgenden
V.2 Ähnlichkeitsgesetz
 V2 Ähnlichkeitsgesetz Die inkompressible Strömung eines Fluids genügt der Kontinuitätsgleichung vt, r = 0 und der Navier Stokes-Gleichung III34 Um den Einfluss der Eigenschaften des Fluids ρ und η bzw
V2 Ähnlichkeitsgesetz Die inkompressible Strömung eines Fluids genügt der Kontinuitätsgleichung vt, r = 0 und der Navier Stokes-Gleichung III34 Um den Einfluss der Eigenschaften des Fluids ρ und η bzw
NTB Druckdatum: SC. typische Zeitkonstante für die Wärmeleitungsgleichung Beispiel
 SCIENTIFIC COMPUTING Die eindimensionale Wärmeleitungsgleichung (WLG) Begriffe Temperatur Spezifische Wärmekapazität Wärmefluss Wärmeleitkoeffizient Fourier'sche Gesetz Spezifische Wärmeleistung Mass für
SCIENTIFIC COMPUTING Die eindimensionale Wärmeleitungsgleichung (WLG) Begriffe Temperatur Spezifische Wärmekapazität Wärmefluss Wärmeleitkoeffizient Fourier'sche Gesetz Spezifische Wärmeleistung Mass für
Differentialgleichungen der Strömungsmechanik
 Differentialgleichungen der Strömungsmechanik Teil 2 Seminarvortrag: Regulär oder Singulär? Mathematische und numerische Rätsel in der Strömungsmechanik Referentin: Irena Vogel Inhalt Grundgleichungen
Differentialgleichungen der Strömungsmechanik Teil 2 Seminarvortrag: Regulär oder Singulär? Mathematische und numerische Rätsel in der Strömungsmechanik Referentin: Irena Vogel Inhalt Grundgleichungen
Fluidmechanik. Thema Erfassung der Druckverluste in verschiedenen Rohrleitungselementen. -Laborübung- 3. Semester. Namen: Datum: Abgabe:
 Strömungsanlage 1 Fachhochschule Trier Studiengang Lebensmitteltechnik Fluidmechanik -Laborübung-. Semester Thema Erfassung der Druckverluste in verschiedenen Rohrleitungselementen Namen: Datum: Abgabe:
Strömungsanlage 1 Fachhochschule Trier Studiengang Lebensmitteltechnik Fluidmechanik -Laborübung-. Semester Thema Erfassung der Druckverluste in verschiedenen Rohrleitungselementen Namen: Datum: Abgabe:
Vergleich von experimentellen Ergebnissen mit realen Konfigurationen
 Ähnlichkeitstheorie Vergleich von experimentellen Ergebnissen mit realen Konfigurationen Verringerung der Anzahl der physikalischen Größen ( Anzahl der Experimente) Experimentelle Ergebnisse sind unabhängig
Ähnlichkeitstheorie Vergleich von experimentellen Ergebnissen mit realen Konfigurationen Verringerung der Anzahl der physikalischen Größen ( Anzahl der Experimente) Experimentelle Ergebnisse sind unabhängig
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
Anwendung der Mikrofonarraymesstechnik in kryogenen und druckbeaufschlagten Windkanälen
 Anwendung der Mikrofonarraymesstechnik in kryogenen und druckbeaufschlagten Windkanälen Thomas Ahlefeldt Deutsches Zentrum für Luft- und Raumfahrt (DLR) Institut für Aerodynamik und Strömungstechnik Abteilung
Anwendung der Mikrofonarraymesstechnik in kryogenen und druckbeaufschlagten Windkanälen Thomas Ahlefeldt Deutsches Zentrum für Luft- und Raumfahrt (DLR) Institut für Aerodynamik und Strömungstechnik Abteilung
1. Angebot und Nachfrage
 1. Angebot und Nachfrage Georg Nöldeke WWZ, Universität Basel Intermediate Microeconomics, HS 11 1. Angebot und Nachfrage 1/40 2 / 40 1.1 Gleichgewicht in Wettbewerbsmärkten Wir betrachten einen Markt
1. Angebot und Nachfrage Georg Nöldeke WWZ, Universität Basel Intermediate Microeconomics, HS 11 1. Angebot und Nachfrage 1/40 2 / 40 1.1 Gleichgewicht in Wettbewerbsmärkten Wir betrachten einen Markt
Hydrodynamik y II - Viskosität
 Physik A VL9 (..0) Hydrodynamik y II - Viskosität Die Viskosität ität Das Gesetz on Hagen-Poiseuille Die Stokes sche Reibung Die Reynolds-Zahl Viskose Fluide Viskosität bisher: Kräfte zwischen dem strömenden
Physik A VL9 (..0) Hydrodynamik y II - Viskosität Die Viskosität ität Das Gesetz on Hagen-Poiseuille Die Stokes sche Reibung Die Reynolds-Zahl Viskose Fluide Viskosität bisher: Kräfte zwischen dem strömenden
