Demo für
|
|
|
- Kurt Lennart Lorentz
- vor 9 Jahren
- Abrufe
Transkript
1 Wahrscheinlichkeitsrechnung Warenprüfungen Themenheft und Trainingsheft Anwendung der Binomialverteilung und der hypergeometrischen Verteilung Datei Nr. 0 Stand. Juni 00 Wird noch fortgesetzt Friedrich W. Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Demo für
2 0 Warenprüfungen Inhalt Warenprüfungsverfahren. Es gibt prinzipiell zwei Verfahren. Das Modul-Prüfverfahren Aufgabensammlung mit Binomialverteilung 0 Lösungen dazu Aufgaben mit hypergeometrische Verteilung mit Lösungen Vorwort Ein beliebtes Thema für umfangreichere Stochastik-Aufgaben ist die Fehlersuche. Da gibt es defekte Geräte aller Art. Durch Tests will man herausfinden, wie hoch deren Anteil ist. Oder wenn sie Fehler aufweisen, dann können diese einzeln oder zusammen in Erscheinung treten. Dieses Aufgabenfeld scheint sich endlos auszudehnen. Wenn man sich dieses Themas genauer annimmt, erkennt man, dass es einige prinzipielle Aufgabenstellungen gibt, die man nicht einfach so nebenbei mitbekommen soll, sondern, die man gezielt gründlich angehen sollte, weil der Lerneffekt und das Aha-Erlebnis groß sein kann. Daher habe ich hier begonnen, eine Sammlung aufzubauen, aus der man auswählen kann, und die (auch Lehrern) zeigt, was es so alles gibt. Dabei bin ich sicher, dass auch ich noch vieles nicht kenne. Demo für
3 0 Warenprüfungen Warenprüfungsverfahren. Zur Überprüfung der Qualität einer Ware gibt es prinzipiell zwei Verfahren: () Man kann die fertig produzierte Ware direkt der Produktion entnehmen. In diesem Falle wird man davon ausgehen, dass die Produktionsanlage mit einigermaßen konstanter Wahrscheinlichkeit immer wieder ein nicht der Norm entsprechendes Gerät produziert. Ich nenne dieses dann der Einheitlichkeit halber defekt. Derjenige, der die Qualitätsprüfung vornimmt, arbeitet dann entweder im Auftrag des Herstellers oder des Verkäufers. Dessen Interesse an guter Qualität beruht natürlich darauf, dass er seine Kunden zufrieden stellen will. () Es gibt aber auch den Abnehmer, der die Ware bestellt hat und nach Empfang erst einmal der Lieferung eine Stichprobe entnimmt, um sie auf Qualität zu prüfen. Wie groß diese Stichprobe sein wird, muss er abwägen. Hier steht Sicherheit gegen Kosten. Es wird zu teuer, jedes Einzelstück zu überprüfen, dann aber hätte der Abnehmer die volle Sicherheit. Daher wird er sich auf eine Stichprobe beschränken und eine gewisse Unsicherheit in Kauf nehmen, um Kosten zu sparen. In diesem Fall ist es dann wichtig zu wissen, mit wie vielen defekten Geräten er rechnen kann, wie sicher das Testergebnis ist (denn es wurde ja nur eine Stichprobe überprüft), und ob er überhaupt den Angaben des Herstellers vertrauen kann. Die Rechenverfahren, die man zu diesen Tests verwendet, richten sich nach der Testmethode. Wir beschränken uns hier auf die beiden Verfahren, die man üblicherweise in der Schule behandelt. () Bei der direkten Herstellungskontrolle nach der Produktion geht man, wie oben schon gesagt wurde, davon aus, dass die Wahrscheinlichkeit, mit der die Fertigungsanlage defekte Geräte produziert, konstant ist. Dann entspricht das Testverfahren dem Urnenmodell Ziehen mit Zurücklegen. Denn nur dabei ist die Wahrscheinlichkeit für das Ziehen einer Kugel der Sorte (= defektes Gerät) konstant. Zur Berechnung von Wahrscheinlichkeiten verwendet man dann die Binomialverteilung. () Bei der Kontrolle einer Lieferung muss man unterscheiden, ob man ahnungslos testet und erst einmal herausfinden muss, wie viele defekte Geräte im Durchschnitt vorkommen. Dann kann man nichts voraussagen und auch wenig planen. Oder ob man eine Information darüber besitzt, mit welchem Prozentsatz defekter Geräte man rechnen muss. Dies kann man dann Demo für durch die Stichprobe überprüfen und dann entscheiden, ob man die Lieferung annimmt oder ablehnt. Kennt man eine zugrunde liegende Fehlerwahrscheinlichkeit, kann man berechnen, dass dann unter 00 Geräten z. B. defekte und 9 brauchbare sein sollten. Dann verwendet man zur Rechnung die hypergeometrische Verteilung.
4 0 Warenprüfungen. Das Modul-Prüfverfahren Um mehrere Elemente einer Schaltung zu testen oder mehrere Blutuntersuchungen vorzunehmen, gibt es eine kostensparende Variante: Das sogenannte Modulverfahren. Beispiel -. Möglichkeit: Durchführung von Einzeltests. In einer Schaltung mit Transistoren ist genau einer defekt. Mit wie vielen Einzeltests und welchen Kosten muss man dann rechnen, wenn Test,0 kostet?.test T wählen.test.test.test.test Erklärung: Ein defekter Transistor ist sicher dabei. Beim. Test findet man ihn mit der Wahrscheinlichkeit und mit der Wahrscheinlichkeit findet man einen guten. Nun sind unter den restlichen Transistoren gute und defekter, den man beim. Test mit der Wahrscheinlichkeit findet, während man mit der Wahrscheinlichkeit einen. guten findet. Dann sind noch gute und defekter vorhanden, so dass man bei. Test mit der Wahrscheinlichkeit den defekten findet oder mit wieder einen guten. In diesem Fall sind noch gute und defekter vorrätig, so dass man mit den defekten findet oder mit einen der restlichen guten. In diesem Fall sind noch vorrätig. Jetzt genügt Test, um daraus den defekten zu entlarven. Dies ergibt nun folgende Tabelle: T i bedeute der i. Transistor. Tabelle zur Berechnung des Erwartungswerts: Z = Anzahl der Tests Ereignis Wahrscheinlichkeit Preis K ( ) T ist defekt T ist defekt T ist defekt T ist defekt T wird getestet. Entweder T oder T ist dann defekt,0 =,00 =,0 =,00 = (Es sind Pfade!) Berechnung des Erwartungswerts für die Anzahl der Tests (aus den Spalten und ): E Z = = = =, ( ) ( ) 0 0 Berechnung des Erwartungswerts für die Kosten der Tests: (aus den Spalten und ): E K =, + +, + + 7,0 =, + +, + + = 0 = ( ) ( ) 7,0 Demo für Ergebnis: Man muss mit durchschnittlich, Tests rechnen und dafür ( ) bezahlen.
5 0 Warenprüfungen. Möglichkeit: Durchführung von Modultests. a) Jetzt fasst man (beispielsweise) Transistoren zu einem Modul zusammen. Ist das erste Modul fehlerhaft, dann muss es einer dieser drei Transistoren sein. Man testet den ersten, ist er gut, dann muss es der. oder. sein. Man hat dann entweder oder Tests durchgeführt. Ist das erste Modul aber gut, dann muss man die Transistoren des. Moduls einzeln testen. Man testet den ersten, ist er gut, dann muss es der. oder. sein. Man hat dann entweder oder Tests durchgeführt. Im Diagramm sieht das so aus:. Test : Modul Preis :,70. Modul defekt. Modul gut =. Moduldefekt. Test : Einzeln Preis :,0. Trans. defekt. Trans. gut dann. oder. Trans. testen. Trans. defekt. Trans. gut dann. oder. Trans. testen Die Pfade und benötigen Tests, die Pfade,, und benötigen Tests. Tabelle zur Berechnung des Erwartungswerts: Info: Ein Modultest kostet,70, ein Einzeltest,0. Weiter auf der Mathe-CD!. Test : Einzeln Preis :,0 Demo für. Trans. defekt. Trans. gut =. Trans.defekt. Trans. defekt. Trans. gut =. Trans.defekt
DEMO für Wahrscheinlichkeitsrechnung Erwartungswert u.a. 1. Erwartungswert INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
 Wahrscheinlichkeitsrechnung Erwartungswert u.a.. Erwartungswert. Varianz und Standardabweichung. Spiele bewerten Datei Nr. Stand. April 0 Friedrich W. Buckel DEMO für INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Wahrscheinlichkeitsrechnung Erwartungswert u.a.. Erwartungswert. Varianz und Standardabweichung. Spiele bewerten Datei Nr. Stand. April 0 Friedrich W. Buckel DEMO für INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
DEMO für STOCHASTIK. Testen von Hypothesen. Datei Nr INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 STOCHASTIK Testen von Hypothesen Teil 1 rundlagen der Signifikanztests Hier: Berechnungen mit Binomialverteilung Datei Nr. 35010 Stand: 9. November 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
STOCHASTIK Testen von Hypothesen Teil 1 rundlagen der Signifikanztests Hier: Berechnungen mit Binomialverteilung Datei Nr. 35010 Stand: 9. November 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Einführung: Kaum Theorie, aber viel Training. Mehr Theorie in Zusätzliche Aufgabensammlung in 34021
 STOCHASTIK Binomialverteilung Einführung: Kaum Theorie, aber viel Training Mehr Theorie in 3402 Zusätzliche Aufgabensammlung in 3402 Ausführliche Erklärung des Einsatzes dreier Rechner: Grafikrechner:
STOCHASTIK Binomialverteilung Einführung: Kaum Theorie, aber viel Training Mehr Theorie in 3402 Zusätzliche Aufgabensammlung in 3402 Ausführliche Erklärung des Einsatzes dreier Rechner: Grafikrechner:
Trainings und Übungstext. für Klasse 5 oder 6. Auch ggt und kgv ohne Primfaktorzerlegung. Datei Nr. 10101. Friedrich W. Buckel. Stand 11.
 Orientierungsstufe 5/6 Teiler und Vielfache Trainings und Übungstext für Klasse 5 oder 6 Auch ggt und kgv ohne Primfaktorzerlegung Datei Nr. 00 Friedrich W. Buckel Stand. Juli 2 DEMO für INTERNETBIBLIOTHEK
Orientierungsstufe 5/6 Teiler und Vielfache Trainings und Übungstext für Klasse 5 oder 6 Auch ggt und kgv ohne Primfaktorzerlegung Datei Nr. 00 Friedrich W. Buckel Stand. Juli 2 DEMO für INTERNETBIBLIOTHEK
Demo-Text für STOCHASTIK. Tschebyscheff-Ungleichung. Einführung mit Anwendungsbeispielen. Datei Nr Friedrich W.
 STOCHASTIK Tschebyscheff-Ungleichung Einführung mit Anwendungsbeispielen Datei Nr. 36111 Friedrich W. Buckel Stand 1. April 010 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mathe-cd.de Inhalt 1 Wiederholung:
STOCHASTIK Tschebyscheff-Ungleichung Einführung mit Anwendungsbeispielen Datei Nr. 36111 Friedrich W. Buckel Stand 1. April 010 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mathe-cd.de Inhalt 1 Wiederholung:
Wahrscheinlichkeitsverteilungen
 Wahrscheinlichkeitsverteilungen 1. Binomialverteilung 1.1 Abzählverfahren 1.2 Urnenmodell Ziehen mit Zurücklegen, Formel von Bernoulli 1.3 Berechnung von Werten 1.4 Erwartungswert und Standardabweichung
Wahrscheinlichkeitsverteilungen 1. Binomialverteilung 1.1 Abzählverfahren 1.2 Urnenmodell Ziehen mit Zurücklegen, Formel von Bernoulli 1.3 Berechnung von Werten 1.4 Erwartungswert und Standardabweichung
Abitur 2013 Mathematik Stochastik III
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2013 Mathematik Stochastik III Folgende Tabelle gibt die Verteilung der Blutgruppen und der Rhesusfaktoren innerhalb der Bevölkerung Deutschlands wieder:
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2013 Mathematik Stochastik III Folgende Tabelle gibt die Verteilung der Blutgruppen und der Rhesusfaktoren innerhalb der Bevölkerung Deutschlands wieder:
Aufgabensammlung mit sehr ausführlichen Lösungen
 Stochastik Binomialverteilung Aufgabensammlung mit sehr ausführlichen Lösungen Berücksichtigung dreier Rechner: Grafikrechner: CASIO fx 9860 CAS-Rechner: CASIO ClassPad 330 Texas Instruments: TI Nspire
Stochastik Binomialverteilung Aufgabensammlung mit sehr ausführlichen Lösungen Berücksichtigung dreier Rechner: Grafikrechner: CASIO fx 9860 CAS-Rechner: CASIO ClassPad 330 Texas Instruments: TI Nspire
Hypergeometrische Verteilung
 Hypergeometrische Verteilung Aufgaben Aufgabe 1 Eine Firma produziert insgesamt 30 elektronische Bauteile des gleichen Typs. Aus langjähriger Erfahrung weiß man das davon jedes 70te defekt ist. Um die
Hypergeometrische Verteilung Aufgaben Aufgabe 1 Eine Firma produziert insgesamt 30 elektronische Bauteile des gleichen Typs. Aus langjähriger Erfahrung weiß man das davon jedes 70te defekt ist. Um die
Abiturprüfung. Mecklenburg-Vorpommern Stochastik. Wahl- und Pflichtaufgaben. Aus den Jahren 2009 bis Datei Nr Stand 5.
 Abiturprüfung Mecklenburg-Vorpommern Stochastik Wahl- und Pflichtaufgaben Aus den Jahren 2009 bis 2016 Datei Nr. 73111 Stand 5. August 2016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 73111
Abiturprüfung Mecklenburg-Vorpommern Stochastik Wahl- und Pflichtaufgaben Aus den Jahren 2009 bis 2016 Datei Nr. 73111 Stand 5. August 2016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 73111
Lineare Gleichungen Lineare Gleichungssysteme. Lineare Algebra 5. Ein Trainingsheft für Schüler
 Lineare Gleichungen Lineare Gleichungssysteme Lineare Algebra Ein Trainingsheft für Schüler Manuelle Lösungen ohne Rechnerhilfen und (hier) ohne Determinanten Datei Nr. 600 Stand 8. September 04 FRIEDRICH
Lineare Gleichungen Lineare Gleichungssysteme Lineare Algebra Ein Trainingsheft für Schüler Manuelle Lösungen ohne Rechnerhilfen und (hier) ohne Determinanten Datei Nr. 600 Stand 8. September 04 FRIEDRICH
Lösungsskizzen zur Präsenzübung 09
 Lösungsskizzen zur Präsenzübung 09 Hilfestellung zur Vorlesung Anwendungen der Mathematik im Wintersemester 2015/2016 Fakultät für Mathematik Universität Bielefeld Veröffentlicht am 07. Februar 2016 von:
Lösungsskizzen zur Präsenzübung 09 Hilfestellung zur Vorlesung Anwendungen der Mathematik im Wintersemester 2015/2016 Fakultät für Mathematik Universität Bielefeld Veröffentlicht am 07. Februar 2016 von:
Demoseiten für www.mathe-cd.de
 ANALYSIS Näherungsweises Lösen von Gleichungen mit speziellen Methoden für CAS-Rechner TI Nspire und CASIO ClassPad Viele Musteraufgaben und Trainingsaufgaben Datei Nr. 41 150 Theorieteil neu geschrieben!
ANALYSIS Näherungsweises Lösen von Gleichungen mit speziellen Methoden für CAS-Rechner TI Nspire und CASIO ClassPad Viele Musteraufgaben und Trainingsaufgaben Datei Nr. 41 150 Theorieteil neu geschrieben!
ALGEBRA Quadratische Gleichungen
 ALGEBRA Quadratische Gleichungen Übungsprogramm Teil 1 Ein Frage-Antwort-Spiel zum intensiven Wiederholen. Zu jeder Aufgabe sofort die Erklärung und die Lösung. Datei Nr. 1 Friedrich W. Buckel Stand: 1.
ALGEBRA Quadratische Gleichungen Übungsprogramm Teil 1 Ein Frage-Antwort-Spiel zum intensiven Wiederholen. Zu jeder Aufgabe sofort die Erklärung und die Lösung. Datei Nr. 1 Friedrich W. Buckel Stand: 1.
Aufgabensammlung. Demo: Mathe-CD. Datei Nr Friedrich W. Buckel. Stand 7. April 2008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Zuorrdnungen Teill Aufgabensammlung Datei Nr. 101 Friedrich W. Buckel Stand 7. April 008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Inhalt 1. Dreisatzaufgaben (1 bis 1) 1 Lösungen dazu 17. Vorbereitungsaufgaben
Zuorrdnungen Teill Aufgabensammlung Datei Nr. 101 Friedrich W. Buckel Stand 7. April 008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK Inhalt 1. Dreisatzaufgaben (1 bis 1) 1 Lösungen dazu 17. Vorbereitungsaufgaben
Abitur 2015 Mathematik Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Urne befinden sich vier rote und sechs blaue Kugeln. Aus dieser wird achtmal eine Kugel zufällig gezogen, die Farbe
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Urne befinden sich vier rote und sechs blaue Kugeln. Aus dieser wird achtmal eine Kugel zufällig gezogen, die Farbe
(1) Werte berechnen und Definitionsbereich finden. (2) Kürzen und Erweitern von Bruchtermen
 () Werte berechnen und Definitionsbereich finden () Kürzen und Erweitern von Bruchtermen Die Aufgaben dieses Tetes findet man auch als reine Aufgabensammlung mit Lösungen im Tet zum Einsatz im Unterricht
() Werte berechnen und Definitionsbereich finden () Kürzen und Erweitern von Bruchtermen Die Aufgaben dieses Tetes findet man auch als reine Aufgabensammlung mit Lösungen im Tet zum Einsatz im Unterricht
SS 2017 Torsten Schreiber
 173 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird die Anordnung von unterschiedlichen Objekten eines Experiments untersucht, so handelt es sich um eine. Möchte man die Anzahl der möglichen
173 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird die Anordnung von unterschiedlichen Objekten eines Experiments untersucht, so handelt es sich um eine. Möchte man die Anzahl der möglichen
Beispielaufgaben Binomialverteilung Lösungen
 L. Schmeink 05a_beispielaufgaben_binomialverteilung_lösungen.doc 1 Beispielaufgaben Binomialverteilung Lösungen Übung 1 Der Würfel mit zwei roten (A) und vier weißen Seitenflächen (B) soll fünfmal geworfen
L. Schmeink 05a_beispielaufgaben_binomialverteilung_lösungen.doc 1 Beispielaufgaben Binomialverteilung Lösungen Übung 1 Der Würfel mit zwei roten (A) und vier weißen Seitenflächen (B) soll fünfmal geworfen
Grundlagen der Wahrscheinlichkeitstheorie und Statistik für Studierende der Informatik
 INSTITUT FÜR STOCHASTIK WS 07/08 UNIVERSITÄT KARLSRUHE Blatt 4 Dr. B. Klar Übungen zur Vorlesung Grundlagen der Wahrscheinlichkeitstheorie und Statistik für Studierende der Informatik Musterlösungen Aufgabe
INSTITUT FÜR STOCHASTIK WS 07/08 UNIVERSITÄT KARLSRUHE Blatt 4 Dr. B. Klar Übungen zur Vorlesung Grundlagen der Wahrscheinlichkeitstheorie und Statistik für Studierende der Informatik Musterlösungen Aufgabe
Dr. Jürgen Senger INDUKTIVE STATISTIK. Wahrscheinlichkeitstheorie, Schätz- und Testverfahren
 Dr. Jürgen Senger INDUKTIVE STATISTIK Wahrscheinlichkeitstheorie, Schätz- und Testverfahren ÜBUNG 7.2 - LÖSUNGEN POISSONVERTEILUNG. Fahrzeuge, die eine Brücke passieren Zufallsexperiment: Zeitpunkt des
Dr. Jürgen Senger INDUKTIVE STATISTIK Wahrscheinlichkeitstheorie, Schätz- und Testverfahren ÜBUNG 7.2 - LÖSUNGEN POISSONVERTEILUNG. Fahrzeuge, die eine Brücke passieren Zufallsexperiment: Zeitpunkt des
Bruchrechnen. 1. Teil. Brüche kennen lernen Erweitern und Kürzen. Schüler-Lese- und Übungstext für Klasse 6
 Bruchrechnen. Teil Brüche kennen lernen Erweitern und Kürzen Schüler-Lese- und Übungstext für Klasse Die Aufgaben dieses Textes findet man auch noch als Sammlung von Aufgabenblättern im Text 020 Datei
Bruchrechnen. Teil Brüche kennen lernen Erweitern und Kürzen Schüler-Lese- und Übungstext für Klasse Die Aufgaben dieses Textes findet man auch noch als Sammlung von Aufgabenblättern im Text 020 Datei
Demoseiten für
 Lineare Ungleichungen mit Variablen Anwendung (Vorübungen für das Thema Lineare Optimierung) Datei Nr. 90 bzw. 500 Stand 0. Dezember 009 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 90 / 500 Lineare Ungleichungen
Lineare Ungleichungen mit Variablen Anwendung (Vorübungen für das Thema Lineare Optimierung) Datei Nr. 90 bzw. 500 Stand 0. Dezember 009 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 90 / 500 Lineare Ungleichungen
DEMO für Übergangsmatrizen. Abiturprüfung. Matrizenrechnung INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Abiturprüfung Matrizenrechnung Aufgaben aus Bremen zum Thema Übergangsmatrizen Datei Nr 750 Stand: 5 März 03 FRIEDRICH W BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 750 Übergangsmatrizen Abituraufgaben
Abiturprüfung Matrizenrechnung Aufgaben aus Bremen zum Thema Übergangsmatrizen Datei Nr 750 Stand: 5 März 03 FRIEDRICH W BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 750 Übergangsmatrizen Abituraufgaben
Abschlussprûfung Berufskolleg. Prüfungsaufgaben aus Baden-Württemberg. Stochastik. Jahrgänge 2002 bis Text Nr Stand 12.
 Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Stochastik Jahrgänge 2002 bis 2016 Text Nr. 74341 Stand 12. Juli 2016 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 74341
Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Stochastik Jahrgänge 2002 bis 2016 Text Nr. 74341 Stand 12. Juli 2016 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 74341
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 17.3.21 Grundlagen zum Hypothesentest Einführung: Wer Entscheidungen zu treffen hat, weiß oft erst im nachhinein ob seine Entscheidung richtig war. Die Unsicherheit
R. Brinkmann http://brinkmann-du.de Seite 1 17.3.21 Grundlagen zum Hypothesentest Einführung: Wer Entscheidungen zu treffen hat, weiß oft erst im nachhinein ob seine Entscheidung richtig war. Die Unsicherheit
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Klett Wahrscheinlichkeitsrechnung im Griff - Mathematik
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Klett Wahrscheinlichkeitsrechnung im Griff - Mathematik 5.-10. Klasse Das komplette Material finden Sie hier: School-Scout.de Wahrscheinlichkeitsrechnung
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Klett Wahrscheinlichkeitsrechnung im Griff - Mathematik 5.-10. Klasse Das komplette Material finden Sie hier: School-Scout.de Wahrscheinlichkeitsrechnung
Es gibt insgesamt 14 Grundkompetenzpunkte: Je einen für jede der 12 Teil-1-Aufgaben und jede der beiden mit A gekennzeichnete Aufgaben aus Teil 2.
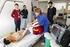 Prototypische Schularbeit 2 Klasse 8 Autor: Mag. Paul Schranz Begleittext Die vorliegende Schularbeit behandelt größtenteils Grundkompetenzen der Inhaltsbereiche Analysis und Wahrscheinlichkeitsrechnung
Prototypische Schularbeit 2 Klasse 8 Autor: Mag. Paul Schranz Begleittext Die vorliegende Schularbeit behandelt größtenteils Grundkompetenzen der Inhaltsbereiche Analysis und Wahrscheinlichkeitsrechnung
Mathematik 12. Jahrgangsstufe - Hausaufgaben
 Mathematik 2. Jahrgangsstufe - Hausaufgaben Inhaltsverzeichnis Wahrscheinlichkeitsrechnung 2. Wahrscheinlichkeitsrechnung.......................... 2.. Binomialkoeffizienten Berechnen....................
Mathematik 2. Jahrgangsstufe - Hausaufgaben Inhaltsverzeichnis Wahrscheinlichkeitsrechnung 2. Wahrscheinlichkeitsrechnung.......................... 2.. Binomialkoeffizienten Berechnen....................
Alternativtest Einführung und Aufgabenbeispiele
 Alternativtest Einführung und Aufgabenbeispiele Ac Einführendes Beispiel: Ein Medikament half bisher 10% aller Patienten. Von einem neuen Medikament behauptet der Hersteller, dass es 20% aller Patienten
Alternativtest Einführung und Aufgabenbeispiele Ac Einführendes Beispiel: Ein Medikament half bisher 10% aller Patienten. Von einem neuen Medikament behauptet der Hersteller, dass es 20% aller Patienten
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 24.2.214 Grundlagen zum Hypothesentest Einführung: Wer Entscheidungen zu treffen hat, weiß oft erst im nachhinein ob seine Entscheidung richtig war. Die Unsicherheit
R. Brinkmann http://brinkmann-du.de Seite 1 24.2.214 Grundlagen zum Hypothesentest Einführung: Wer Entscheidungen zu treffen hat, weiß oft erst im nachhinein ob seine Entscheidung richtig war. Die Unsicherheit
Elemente der Stochastik (SoSe 2016) 9. Übungsblatt
 Dr. M. Weimar 06.06.2016 Elemente der Stochastik (SoSe 2016) 9. Übungsblatt Aufgabe 1 (2+2+2+2+1=9 Punkte) In einer Urne befinden sich sieben Lose, darunter genau ein Gewinnlos. Diese Lose werden nacheinander
Dr. M. Weimar 06.06.2016 Elemente der Stochastik (SoSe 2016) 9. Übungsblatt Aufgabe 1 (2+2+2+2+1=9 Punkte) In einer Urne befinden sich sieben Lose, darunter genau ein Gewinnlos. Diese Lose werden nacheinander
A: Beispiele Beispiel 1: Zwei Zufallsvariablen X und Y besitzen die beiden folgenden Wahrscheinlichkeitsfunktionen:
 5 Diskrete Verteilungen 1 Kapitel 5: Diskrete Verteilungen A: Beispiele Beispiel 1: Zwei Zufallsvariablen X und Y besitzen die beiden folgenden Wahrscheinlichkeitsfunktionen: 5 0.6 x 0.4 5 x (i) P x (x)
5 Diskrete Verteilungen 1 Kapitel 5: Diskrete Verteilungen A: Beispiele Beispiel 1: Zwei Zufallsvariablen X und Y besitzen die beiden folgenden Wahrscheinlichkeitsfunktionen: 5 0.6 x 0.4 5 x (i) P x (x)
Biometrieübung 5 Spezielle Verteilungen. 1. Anzahl von weiblichen Mäusen in Würfen von jeweils 4 Mäusen
 Biometrieübung 5 (Spezielle Verteilungen) - Aufgabe Biometrieübung 5 Spezielle Verteilungen Aufgabe 1. Anzahl von weiblichen Mäusen in Würfen von jeweils 4 Mäusen Anzahl weiblicher Mäuse (k) Anzahl Würfe
Biometrieübung 5 (Spezielle Verteilungen) - Aufgabe Biometrieübung 5 Spezielle Verteilungen Aufgabe 1. Anzahl von weiblichen Mäusen in Würfen von jeweils 4 Mäusen Anzahl weiblicher Mäuse (k) Anzahl Würfe
Bruchrechnen. 3. Teil. Addition und Subtraktion. Schüler-Lese- und Übungstext. Die Aufgaben dieses Textes sind zusätzlich ausgelagert in 10206
 Bruchrechnen 3. Teil Addition und Subtraktion Schüler-Lese- und Übungstext Die Aufgaben dieses Textes sind zusätzlich ausgelagert in 10206 Datei Nr. 1020 Stand 12. April 2012 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK
Bruchrechnen 3. Teil Addition und Subtraktion Schüler-Lese- und Übungstext Die Aufgaben dieses Textes sind zusätzlich ausgelagert in 10206 Datei Nr. 1020 Stand 12. April 2012 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK
Abitur 2009 Mathematik GK Stochastik Aufgabe C1
 Seite 1 Abiturloesung.de - Abituraufgaben Abitur 009 Mathematik GK Stochastik Aufgabe C1 Auf einem Spielbrett rollt eine Kugel vom Start bis in eines der Fächer F 1 bis F 5. An jeder Verzweigung rollt
Seite 1 Abiturloesung.de - Abituraufgaben Abitur 009 Mathematik GK Stochastik Aufgabe C1 Auf einem Spielbrett rollt eine Kugel vom Start bis in eines der Fächer F 1 bis F 5. An jeder Verzweigung rollt
DEMO für www.mathe-cd.de
 (1) Rechnen mit Paaren und Tripeln () Eine Gleichung mit oder 3 Unbekannten (3) Zwei Gleichungen mit 3 Unbekannten Datei Nr. 61 011 Stand 19. Oktober 010 Friedrich W. Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
(1) Rechnen mit Paaren und Tripeln () Eine Gleichung mit oder 3 Unbekannten (3) Zwei Gleichungen mit 3 Unbekannten Datei Nr. 61 011 Stand 19. Oktober 010 Friedrich W. Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Lernblatt: Lagebeziehungen
 Dieser Trainingstext ist ungekürzt. ls Demoversion ist allerdings der usdruck gesperrt. Vektorrechnung Lernblatt: Lagebeziehungen ufgabenversion ohne Lösungen Untersuchung der gegenseitigen Lage von Punkt
Dieser Trainingstext ist ungekürzt. ls Demoversion ist allerdings der usdruck gesperrt. Vektorrechnung Lernblatt: Lagebeziehungen ufgabenversion ohne Lösungen Untersuchung der gegenseitigen Lage von Punkt
Je größer n und je näher p bei 0,5 liegt, desto besser wird i. A. die Näherung. Als Faustregel gilt, dass die Näherung geeignet ist, wenn.
 1. Sigma-Regeln / Sigma-Umgebungen Die Sigma-Regeln geben an: - mit welcher Wahrscheinlichkeit die Werte einer binomialverteilten Zufallsgröße in bestimmten Intervallen um den Erwartungswert liegen. (also
1. Sigma-Regeln / Sigma-Umgebungen Die Sigma-Regeln geben an: - mit welcher Wahrscheinlichkeit die Werte einer binomialverteilten Zufallsgröße in bestimmten Intervallen um den Erwartungswert liegen. (also
4b. Wahrscheinlichkeit und Binomialverteilung
 b. Wahrscheinlichkeit und Binomialverteilung Um was geht es? Häufigkeit in der die Fehlerzahl auftritt 9 6 5 3 2 2 3 5 6 Fehlerzahl in der Stichprobe Wozu dient die Wahrscheinlichkeit? Häfigkeit der Fehlerzahl
b. Wahrscheinlichkeit und Binomialverteilung Um was geht es? Häufigkeit in der die Fehlerzahl auftritt 9 6 5 3 2 2 3 5 6 Fehlerzahl in der Stichprobe Wozu dient die Wahrscheinlichkeit? Häfigkeit der Fehlerzahl
Vorwort Zufallsvariable X, Erwartungswert E(X), Varianz V(X) 1.1 Zufallsvariable oder Zufallsgröße Erwartungswert und Varianz...
 Inhaltsverzeichnis Vorwort... 2 Zum Einstieg... 3 1 Zufallsvariable X, Erwartungswert E(X), Varianz V(X) 1.1 Zufallsvariable oder Zufallsgröße... 5 1.2 Erwartungswert und Varianz... 7 2 Wahrscheinlichkeitsverteilungen
Inhaltsverzeichnis Vorwort... 2 Zum Einstieg... 3 1 Zufallsvariable X, Erwartungswert E(X), Varianz V(X) 1.1 Zufallsvariable oder Zufallsgröße... 5 1.2 Erwartungswert und Varianz... 7 2 Wahrscheinlichkeitsverteilungen
Klausur Nr. 1. Wahrscheinlichkeitsrechnung. Keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt.
 Klausur Nr. 1 2014-02-06 Wahrscheinlichkeitsrechnung Pflichtteil Keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche Darstellung,
Klausur Nr. 1 2014-02-06 Wahrscheinlichkeitsrechnung Pflichtteil Keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche Darstellung,
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Binomialverteilung und Bernoulli- Experiment
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Binomialverteilung und Bernoulli- Experiment Das komplette Material finden Sie hier: Download bei School-Scout.de TOSSNET Der persönliche
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Binomialverteilung und Bernoulli- Experiment Das komplette Material finden Sie hier: Download bei School-Scout.de TOSSNET Der persönliche
Mathematik für Klasse 6 Rechnen mit Dezimalzahlen
 Mathematik für Klasse 6 Rechnen mit Dezimalzahlen 16 Trainingseinheiten zum Unterricht Dazu gehört auch eine Einführung in die Anfänge der Prozentrechnung. Datei Nr. 10310 Friedrich W. Buckel Stand: Stand
Mathematik für Klasse 6 Rechnen mit Dezimalzahlen 16 Trainingseinheiten zum Unterricht Dazu gehört auch eine Einführung in die Anfänge der Prozentrechnung. Datei Nr. 10310 Friedrich W. Buckel Stand: Stand
Aufgabe A1 Ein Glücksrad hat vier Sektoren, wovon die ersten beiden die Winkelgröße 60 haben. Für die Winkelgrößen und des dritten und vierten Sektors
 Level Grundlagen Blatt Dokument mit Aufgaben Aufgabe A Ein Glücksrad hat vier Sektoren, wovon die ersten beiden die Winkelgröße 60 haben. Für die Winkelgrößen und des dritten und vierten Sektors gilt.
Level Grundlagen Blatt Dokument mit Aufgaben Aufgabe A Ein Glücksrad hat vier Sektoren, wovon die ersten beiden die Winkelgröße 60 haben. Für die Winkelgrößen und des dritten und vierten Sektors gilt.
1,00 2,00 3,00 4,00 Bestimme den Gewinnerwartungswert. Entscheide, ob das Spiel fair ist.
 Level Grundlagen Blatt Dokument mit 3 Aufgaben Aufgabe A Ein Glücksrad hat vier Sektoren, wovon die ersten beiden die Winkelgröße 60 haben. Für die Winkelgrößen und des dritten und vierten Sektors gilt.
Level Grundlagen Blatt Dokument mit 3 Aufgaben Aufgabe A Ein Glücksrad hat vier Sektoren, wovon die ersten beiden die Winkelgröße 60 haben. Für die Winkelgrößen und des dritten und vierten Sektors gilt.
Abiturprüfung Mathematik, Leistungskurs
 Seite 1 von 7 Abiturrüfung 215 Mathematik, Leistungskurs Aufgabenstellung: Eine Firma stellt mit zwei verschiedenen Maschinen A und B Bodenfliesen aus Keramik her. Damit eine Fliese als 1. Wahl gilt, muss
Seite 1 von 7 Abiturrüfung 215 Mathematik, Leistungskurs Aufgabenstellung: Eine Firma stellt mit zwei verschiedenen Maschinen A und B Bodenfliesen aus Keramik her. Damit eine Fliese als 1. Wahl gilt, muss
Im nachstehenden Stabdiagramm sind die Wahrscheinlichkeiten dargestellt, beim Kauf einer bestimmten Anzahl von Energydrinks genau x i.
 c) Anlässlich einer Skiweltmeisterschaft erhält man beim Kauf eines bestimmten Energydrinks zusätzlich zu jedem Energydrink ein Sammelbild mit einer Sportlerin. Nach Angaben des Herstellers zeigen 20 %
c) Anlässlich einer Skiweltmeisterschaft erhält man beim Kauf eines bestimmten Energydrinks zusätzlich zu jedem Energydrink ein Sammelbild mit einer Sportlerin. Nach Angaben des Herstellers zeigen 20 %
WHB11 - Mathematik. AFS II: Umgang mit Zufall und Wahrscheinlichkeiten. Thema: Summierte Binomialverteilung
 Binomialverteilung Bisher haben wir berechnet, wie groß die Wahrscheinlichkeit dafür ist, dass bei einer Bernoulli-Kette n der Länge genau k Treffer auftreten. Die Formel dafür war: B (n;p;k) = P (X=k)
Binomialverteilung Bisher haben wir berechnet, wie groß die Wahrscheinlichkeit dafür ist, dass bei einer Bernoulli-Kette n der Länge genau k Treffer auftreten. Die Formel dafür war: B (n;p;k) = P (X=k)
Quadratische Gleichungen. Teil 2
 ALGEBRA Quadratische Gleichungen Teil Wiederholungsaufgaben für Vergessliche Hier ohne quadratische Ergänzung 18 Musterbeispiele 97 Aufgaben 4 Seiten Lösungen Datei 11 Stand 5. Juli 017 Friedrich Buckel
ALGEBRA Quadratische Gleichungen Teil Wiederholungsaufgaben für Vergessliche Hier ohne quadratische Ergänzung 18 Musterbeispiele 97 Aufgaben 4 Seiten Lösungen Datei 11 Stand 5. Juli 017 Friedrich Buckel
Diskrete Wahrscheinlichkeitstheorie - Probeklausur
 Diskrete Wahrscheinlichkeitstheorie - robeklausur Sommersemester 2007 - Lösung Name: Vorname: Matrikelnr.: Studiengang: Hinweise Sie sollten insgesamt Blätter erhalten haben. Tragen Sie bitte Ihre Antworten
Diskrete Wahrscheinlichkeitstheorie - robeklausur Sommersemester 2007 - Lösung Name: Vorname: Matrikelnr.: Studiengang: Hinweise Sie sollten insgesamt Blätter erhalten haben. Tragen Sie bitte Ihre Antworten
Übungen zur Klausur 2 (Wahrscheinlichkeitsrechnung II)
 Übungen zur Klausur 2 (Wahrscheinlichkeitsrechnung II) Aufgabe 1: Für einige Krankheiten, die erst relativ spät zutage treten, gleichwohl aber im Krper vorhanden sind, gibt es Diagnosetests. Wenn diese
Übungen zur Klausur 2 (Wahrscheinlichkeitsrechnung II) Aufgabe 1: Für einige Krankheiten, die erst relativ spät zutage treten, gleichwohl aber im Krper vorhanden sind, gibt es Diagnosetests. Wenn diese
Aufgabe 1. Übung Wahrscheinlichkeitsrechnung Markus Kessler Seite 1 von 8. Die Ereignisse A, B und C erfüllen die Bedingungen
 Ü b u n g 1 Aufgabe 1 Die Ereignisse A, B und C erfüllen die Bedingungen P(A) = 0. 7, P(B) = 0. 6, P(C) = 0. 5 P(A B) = 0. 4, P(A C) = 0. 3, P(B C) = 0. 2, P(A B C) = 0. 1 Bestimmen Sie P(A B), P(A C),
Ü b u n g 1 Aufgabe 1 Die Ereignisse A, B und C erfüllen die Bedingungen P(A) = 0. 7, P(B) = 0. 6, P(C) = 0. 5 P(A B) = 0. 4, P(A C) = 0. 3, P(B C) = 0. 2, P(A B C) = 0. 1 Bestimmen Sie P(A B), P(A C),
Abitur 2012 Mathematik Stochastik III
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2012 Mathematik Stochastik III Für eine Quizshow sucht ein Fernsehsender Abiturientinnen und Abiturienten als Kandidaten. Jeder Bewerber gibt in einem
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2012 Mathematik Stochastik III Für eine Quizshow sucht ein Fernsehsender Abiturientinnen und Abiturienten als Kandidaten. Jeder Bewerber gibt in einem
Handelt es sich bei den folgenden um diskrete oder stetige Zufallsvariablen?
 1. Handelt es sich bei den folgenden um diskrete oder stetige Zufallsvariablen? a.) Anzahl der Kunden, die an der Kasse in der Schlange stehen. b.) Die Menge an Energie, die pro Tag von einem Energieversorgungsunternehmen
1. Handelt es sich bei den folgenden um diskrete oder stetige Zufallsvariablen? a.) Anzahl der Kunden, die an der Kasse in der Schlange stehen. b.) Die Menge an Energie, die pro Tag von einem Energieversorgungsunternehmen
1 Grundlagen der Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsräume. Ein erster mathematischer Blick auf Zufallsexperimente...
 Inhaltsverzeichnis 1 Grundlagen der Wahrscheinlichkeitsrechnung 1 1.1 Wahrscheinlichkeitsräume Ein erster mathematischer Blick auf Zufallsexperimente.......... 1 1.1.1 Wahrscheinlichkeit, Ergebnisraum,
Inhaltsverzeichnis 1 Grundlagen der Wahrscheinlichkeitsrechnung 1 1.1 Wahrscheinlichkeitsräume Ein erster mathematischer Blick auf Zufallsexperimente.......... 1 1.1.1 Wahrscheinlichkeit, Ergebnisraum,
Übungs-Blatt 7 Wahrscheinlichkeitsrechnung
 Übungs-Blatt Wahrscheinlichkeitsrechnung BMT Biostatistik Prof. Dr. B. Grabowski Zu Aufgabe ) Ein bestimmtes Bauteil wird auf seine Zuverlässigkeit untersucht. Die technische Prüfung erfolgt dabei so:
Übungs-Blatt Wahrscheinlichkeitsrechnung BMT Biostatistik Prof. Dr. B. Grabowski Zu Aufgabe ) Ein bestimmtes Bauteil wird auf seine Zuverlässigkeit untersucht. Die technische Prüfung erfolgt dabei so:
Wahrscheinlichkeit3 Binomialverteilung/Bernoulli-Formel
 Wahrscheinlichkeit3 Binomialverteilung/Bernoulli-Formel Aufgaben Lösen Sie A1 und A sowohl mit der Bernoulli-Formel als auch mit dem TR(BV), die anderen Aufgaben lösen sie mit dem TR(BV). A1 Eine Familie
Wahrscheinlichkeit3 Binomialverteilung/Bernoulli-Formel Aufgaben Lösen Sie A1 und A sowohl mit der Bernoulli-Formel als auch mit dem TR(BV), die anderen Aufgaben lösen sie mit dem TR(BV). A1 Eine Familie
Trainingseinheiten. zum Üben und Vertiefen. Teil 1 Grundlagen Teil 2 Anwendungen. Datei Nr. 10551. Friedrich Buckel. Stand 28.
 Demoseiten für Mathematik für Klasse 6/7 Prozentrechnen Trainingseinheiten zum Üben und Vertiefen Teil Grundlagen Teil 2 Anwendungen Datei Nr. 055 Stand 28. März 2008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Demoseiten für Mathematik für Klasse 6/7 Prozentrechnen Trainingseinheiten zum Üben und Vertiefen Teil Grundlagen Teil 2 Anwendungen Datei Nr. 055 Stand 28. März 2008 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
3. Lösungen weitere Übungsaufgaben Statistik für Ingenieure WiSe 16/17
 3. Lösungen weitere Übungsaufgaben Statistik für Ingenieure WiSe 6/7. Aufgabe: 0 Bauteile gleicher Bauart werden vor der Weiterverarbeitung einer Materialprüfung unterzogen. 7 bestanden diese Prüfung,
3. Lösungen weitere Übungsaufgaben Statistik für Ingenieure WiSe 6/7. Aufgabe: 0 Bauteile gleicher Bauart werden vor der Weiterverarbeitung einer Materialprüfung unterzogen. 7 bestanden diese Prüfung,
Übersicht Wahrscheinlichkeitsrechnung EF
 Übersicht Wahrscheinlichkeitsrechnung EF. Grundbegriffe der Wahrscheinlichkeitsrechnung (eite ). Regeln zur Berechnung von Wahrscheinlichkeiten (eite ). Bedingte Wahrscheinlichkeit und Vierfeldertafel
Übersicht Wahrscheinlichkeitsrechnung EF. Grundbegriffe der Wahrscheinlichkeitsrechnung (eite ). Regeln zur Berechnung von Wahrscheinlichkeiten (eite ). Bedingte Wahrscheinlichkeit und Vierfeldertafel
Schleswig-Holstein Kernfach Mathematik
 Aufgabe 5: Stochastik Der Schokoladenhersteller Nikolaus Hase produziert für namhafte Discounter Ostereier. Auf Grund langjähriger Erfahrungen ist davon auszugehen, dass 95 % der Produktion der Norm entsprechen
Aufgabe 5: Stochastik Der Schokoladenhersteller Nikolaus Hase produziert für namhafte Discounter Ostereier. Auf Grund langjähriger Erfahrungen ist davon auszugehen, dass 95 % der Produktion der Norm entsprechen
Aufgabe 8: Stochastik (WTR)
 Abitur Mathematik: Nordrhein-Westfalen 2013 Aufgabe 8 a) (1) WAHRSCHEINLICHKEIT FÜR KEINE ANGABE ERMITTELN Nach der Laplace Formel ist Anzahl der Personen, die keine Angabe machten keine Angabe Gesamtzahl
Abitur Mathematik: Nordrhein-Westfalen 2013 Aufgabe 8 a) (1) WAHRSCHEINLICHKEIT FÜR KEINE ANGABE ERMITTELN Nach der Laplace Formel ist Anzahl der Personen, die keine Angabe machten keine Angabe Gesamtzahl
Biometrische Planung von Versuchsvorhaben
 Biometrische Planung von Versuchsvorhaben Einführung in das Prinzip der Lehrstuhl für Mathematik VIII Statistik http://statistik.mathematik.uni-wuerzburg.de/~hain Ziel des Vortrags Im nachfolgenden Vortrag
Biometrische Planung von Versuchsvorhaben Einführung in das Prinzip der Lehrstuhl für Mathematik VIII Statistik http://statistik.mathematik.uni-wuerzburg.de/~hain Ziel des Vortrags Im nachfolgenden Vortrag
Level 1 Grundlagen Blatt 2
 Level 1 Grundlagen Blatt 2 Dokument mit 1 Aufgaben Aufgabe A9 Ein Glücksrad besteht aus 3 Feldern, die folgendermaßen beschriftet sind: 1.Feld: 2,00 2. Feld: 5,00 3. Feld: 0,00 Das 1. Feld hat einen Mittelpunktswinkel
Level 1 Grundlagen Blatt 2 Dokument mit 1 Aufgaben Aufgabe A9 Ein Glücksrad besteht aus 3 Feldern, die folgendermaßen beschriftet sind: 1.Feld: 2,00 2. Feld: 5,00 3. Feld: 0,00 Das 1. Feld hat einen Mittelpunktswinkel
Trainingsheft Analysis Schaubilder schnell zeichnen
 Trainingsheft Analysis Schaubilder schnell zeichnen Schnelles Zeichnen von Kurven: 6 ausführliche Beispiele! Parabeln, Hyperbeln, Gebrochen rationale Funktionen, Wurzelfunktionen als Parabelbögen oder
Trainingsheft Analysis Schaubilder schnell zeichnen Schnelles Zeichnen von Kurven: 6 ausführliche Beispiele! Parabeln, Hyperbeln, Gebrochen rationale Funktionen, Wurzelfunktionen als Parabelbögen oder
DOWNLOAD. Mein Taschengeld. Mathe-Aufgaben aus dem Alltag. Karin Schwacha. Downloadauszug aus dem Originaltitel:
 DOWNLOAD Karin Schwacha Mein Taschengeld Mathe-Aufgaben aus dem Alltag 7 8 Downloadauszug aus dem Originaltitel: Taschengeld Katrin und Simon sind befreundet und gehen in dieselbe Klasse. Sie verbringen
DOWNLOAD Karin Schwacha Mein Taschengeld Mathe-Aufgaben aus dem Alltag 7 8 Downloadauszug aus dem Originaltitel: Taschengeld Katrin und Simon sind befreundet und gehen in dieselbe Klasse. Sie verbringen
x(n x) cm 2 ) zweier Betonsorten wird überprüft. Dabei ergaben Sorte 1 185 186 184 186 185 187 186 187 185 Sorte 2 183 182 185 182 181 179
 . Aufgabe: Zwei bis drei Millionen deutsche Haushalte sind überschuldet. Einer der Hauptgründe für die Überschuldung privater Haushalte ist eine gescheiterte Selbstständigkeit. In einer Stichprobe von
. Aufgabe: Zwei bis drei Millionen deutsche Haushalte sind überschuldet. Einer der Hauptgründe für die Überschuldung privater Haushalte ist eine gescheiterte Selbstständigkeit. In einer Stichprobe von
Pfadregel. 400 Kugeln durchlaufen die möglichen Pfade. Das Diagramm zeigt das Ergebnis am Ende der Versuchsdurchführung.
 Würfelsimulation 1) Bezeichnen Sie in den Säulendiagrammen (Histogrammen - 2. Graphik) die senkrechten Achsen und vervollständigen Sie im ersten Diagramm die Achseneinteilung. Lesen Sie im Histogramm für
Würfelsimulation 1) Bezeichnen Sie in den Säulendiagrammen (Histogrammen - 2. Graphik) die senkrechten Achsen und vervollständigen Sie im ersten Diagramm die Achseneinteilung. Lesen Sie im Histogramm für
Klausur Mathematik 2, Teil Statistik und Finanzmathematik Lösungen
 Fachhochschule Ravensburg-Weingarten, Fachbereich Elektrotechnik und Informatik Klausur Mathematik 2, Teil Statistik und Finanzmathematik Lösungen Aufgaben (Punkte) 1. Für eine Voraussage der Bürgermeisterwahl
Fachhochschule Ravensburg-Weingarten, Fachbereich Elektrotechnik und Informatik Klausur Mathematik 2, Teil Statistik und Finanzmathematik Lösungen Aufgaben (Punkte) 1. Für eine Voraussage der Bürgermeisterwahl
Θ Mathematik Stochastik
 Θ Mathematik Stochastik Aufgabe 1: Als Spam-Nachricht wird eine unerwünschte E-Mail bezeichnet, die dem Empfänger unverlangt zugestellt wird. a) Statistische Untersuchungen an der Mailbox eines Benutzers
Θ Mathematik Stochastik Aufgabe 1: Als Spam-Nachricht wird eine unerwünschte E-Mail bezeichnet, die dem Empfänger unverlangt zugestellt wird. a) Statistische Untersuchungen an der Mailbox eines Benutzers
Wahrscheinlichkeitsrechnung
 Aufgaben Wahrscheinlichkeitsrechnung 1. Eine Münze wird viermal geworfen. Y sei die Anzahl der Wechsel zwischen 0 und 1 während einer Versuchsfolge, z. B. Y(00) =. Bestimmen Sie die Verteilung von Y, zeichnen
Aufgaben Wahrscheinlichkeitsrechnung 1. Eine Münze wird viermal geworfen. Y sei die Anzahl der Wechsel zwischen 0 und 1 während einer Versuchsfolge, z. B. Y(00) =. Bestimmen Sie die Verteilung von Y, zeichnen
Mathematik: LehrerInnenteam Arbeitsblatt Semester ARBEITSBLATT 12. Erwartungswert, Varianz und Standardabweichung
 Mathematik: LehrerInnenteam Arbeitsblatt 7-7. Semester ARBEITSBLATT Erwartungswert, Varianz und Standardabweichung Die Begriffe Varianz und Standardabweichung sind uns bereits aus der Statistik bekannt
Mathematik: LehrerInnenteam Arbeitsblatt 7-7. Semester ARBEITSBLATT Erwartungswert, Varianz und Standardabweichung Die Begriffe Varianz und Standardabweichung sind uns bereits aus der Statistik bekannt
Rubbeln und gewinnen!
 Abituraufgaben Stochastik BG (Teil 3 mit Hilfsmittel) ab 2017 Aufgabe A1/2017 Beim Strafstoß (Elfmeter) gibt es drei mögliche Ereignisse: (1) Der Schütze erzielt ein Tor. (2) Der Torhüter wehrt den Ball
Abituraufgaben Stochastik BG (Teil 3 mit Hilfsmittel) ab 2017 Aufgabe A1/2017 Beim Strafstoß (Elfmeter) gibt es drei mögliche Ereignisse: (1) Der Schütze erzielt ein Tor. (2) Der Torhüter wehrt den Ball
AUFGABENTYPEN. 2. Bekannt ist die Irrtumswahrscheinlichkeit α ; zu berechnen ist der Annahme- und Ablehnungsbereich, also die Entscheidungsregel.
 AUFGABENTYPEN 1. Bekannt ist die Entscheidungsregel, d.h. K und K ; zu berechnen ist das Risiko 1.Art (bzw. 2. Art). 2. Bekannt ist die Irrtumswahrscheinlichkeit α ; zu berechnen ist der Annahme- und Ablehnungsbereich,
AUFGABENTYPEN 1. Bekannt ist die Entscheidungsregel, d.h. K und K ; zu berechnen ist das Risiko 1.Art (bzw. 2. Art). 2. Bekannt ist die Irrtumswahrscheinlichkeit α ; zu berechnen ist der Annahme- und Ablehnungsbereich,
Proportionale und antiproportionale Zuordnungen
 Proportionale und antiproportionale Zuordnungen Proportionale und antiproportionale Zuordnungen findet man in vielen Bereichen des täglichen Lebens. Zum Beispiel beim Tanken oder beim Einkaufen. Bei proportionalen
Proportionale und antiproportionale Zuordnungen Proportionale und antiproportionale Zuordnungen findet man in vielen Bereichen des täglichen Lebens. Zum Beispiel beim Tanken oder beim Einkaufen. Bei proportionalen
6. Stochastische Modelle II: Stetige Wahrscheinlichkeitsverteilungen, insbesondere Normalverteilungen
 6. Stochastische Modelle II: Stetige Wahrscheinlichkeitsverteilungen, insbesondere Normalverteilungen Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Bisher: Diskrete Zufallsvariablen,
6. Stochastische Modelle II: Stetige Wahrscheinlichkeitsverteilungen, insbesondere Normalverteilungen Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Bisher: Diskrete Zufallsvariablen,
I. Lehrplanauszug. Beispielaufgaben. Grundwissen Mathematik 6. Jahrgangsstufe. In der Jahrgangsstufe 6 erwerben die Schüler folgendes Grundwissen:
 Grundwissen Mathematik 6. Jahrgangsstufe I. Lehrplanauszug In der Jahrgangsstufe 6 erwerben die Schüler folgendes Grundwissen: Sie können rationale Zahlen in verschiedenen Schreibweisen darstellen. Sie
Grundwissen Mathematik 6. Jahrgangsstufe I. Lehrplanauszug In der Jahrgangsstufe 6 erwerben die Schüler folgendes Grundwissen: Sie können rationale Zahlen in verschiedenen Schreibweisen darstellen. Sie
2. Rechnen mit Wahrscheinlichkeiten
 2. Rechnen mit Wahrscheinlichkeiten 2.1 Axiome der Wahrscheinlichkeitsrechnung Die Wahrscheinlichkeitsrechnung ist ein Teilgebiet der Mathematik. Es ist üblich, an den Anfang einer mathematischen Theorie
2. Rechnen mit Wahrscheinlichkeiten 2.1 Axiome der Wahrscheinlichkeitsrechnung Die Wahrscheinlichkeitsrechnung ist ein Teilgebiet der Mathematik. Es ist üblich, an den Anfang einer mathematischen Theorie
Streichholzgeschichten von Dieter Ortner.
 Streichholzgeschichten von Dieter Ortner. 1. Streichholzgeschichte Nr. 1 Aus vier n kann man ein Quadrat bilden. Mit diesem Verfahren sollst du nun selber herausfinden, wie viele es braucht, wenn das grosse
Streichholzgeschichten von Dieter Ortner. 1. Streichholzgeschichte Nr. 1 Aus vier n kann man ein Quadrat bilden. Mit diesem Verfahren sollst du nun selber herausfinden, wie viele es braucht, wenn das grosse
Abitur 2012 Mathematik Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2012 Mathematik Stochastik IV Nachdem die Verfilmung eines bekannten Romans erfolgreich in den Kinos gezeigt wurde, veröffentlicht eine Tageszeitung
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2012 Mathematik Stochastik IV Nachdem die Verfilmung eines bekannten Romans erfolgreich in den Kinos gezeigt wurde, veröffentlicht eine Tageszeitung
Abitur 2011 G8 Musterabitur Mathematik Stochastik III
 Seite 1 http://www.abiturloesung.de/ Seite Abitur 011 G Musterabitur Mathematik Stochastik III Folgendes Diagramm zeigt Daten zum Rauchverhalten in bestimmten Altersgruppen, die das Statistische Bundesamt
Seite 1 http://www.abiturloesung.de/ Seite Abitur 011 G Musterabitur Mathematik Stochastik III Folgendes Diagramm zeigt Daten zum Rauchverhalten in bestimmten Altersgruppen, die das Statistische Bundesamt
1 Dreisatz In diesem Modul werden alle Spielarten des Dreisatzes behandelt
 1 In diesem Modul werden alle Spielarten des es behandelt Inhalt: 1... 1 1.1 Der normale... 2 1.1.1 Erstes direktes Berechnen... 2 1.1.2 Berechnung mittels Schema... 3 1.1.3 Lösen als Tabelle... 4 Seite
1 In diesem Modul werden alle Spielarten des es behandelt Inhalt: 1... 1 1.1 Der normale... 2 1.1.1 Erstes direktes Berechnen... 2 1.1.2 Berechnung mittels Schema... 3 1.1.3 Lösen als Tabelle... 4 Seite
Dieses Quiz soll Ihnen helfen, Kapitel besser zu verstehen.
 Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Mit Dezimalzahlen multiplizieren
 Vertiefen 1 Mit Dezimalzahlen multiplizieren zu Aufgabe 1 Schulbuch, Seite 134 1 Multiplizieren im Bild darstellen Zeichne zur Aufgaben 1,63 2,4 ein Bild und bestimme mit Hilfe des Bildes das Ergebnis
Vertiefen 1 Mit Dezimalzahlen multiplizieren zu Aufgabe 1 Schulbuch, Seite 134 1 Multiplizieren im Bild darstellen Zeichne zur Aufgaben 1,63 2,4 ein Bild und bestimme mit Hilfe des Bildes das Ergebnis
Grundlegende Eigenschaften von Punktschätzern
 Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Demoseiten für
 Matrizenrechnung Anwendungsaufgaben Teil Themenheft Demoseiten für Arbeiten mit Bedarfsmatrizen Herstellung von Zwischen- und Endprodukten aus Rohstoffen Kostenberechnungen Datei 623 Stand: 5. August 2
Matrizenrechnung Anwendungsaufgaben Teil Themenheft Demoseiten für Arbeiten mit Bedarfsmatrizen Herstellung von Zwischen- und Endprodukten aus Rohstoffen Kostenberechnungen Datei 623 Stand: 5. August 2
Statistik im Versicherungs- und Finanzwesen
 Springer Gabler PLUS Zusatzinformationen zu Medien von Springer Gabler Grimmer Statistik im Versicherungs- und Finanzwesen Eine anwendungsorientierte Einführung 2014 1. Auflage Übungsaufgaben zu Kapitel
Springer Gabler PLUS Zusatzinformationen zu Medien von Springer Gabler Grimmer Statistik im Versicherungs- und Finanzwesen Eine anwendungsorientierte Einführung 2014 1. Auflage Übungsaufgaben zu Kapitel
Stochastik. 1 Grundlagen
 1 Grundlagen Stochastik S 1.1 Beim Mensch-ärgere-dich-nicht darf zu Beginn bis zu dreimal gewürfelt werden, um eine Sechs zu bekommen. Mit welcher Wahrscheinlichkeit gelingt dies? S 1.2 Für einen Flug
1 Grundlagen Stochastik S 1.1 Beim Mensch-ärgere-dich-nicht darf zu Beginn bis zu dreimal gewürfelt werden, um eine Sechs zu bekommen. Mit welcher Wahrscheinlichkeit gelingt dies? S 1.2 Für einen Flug
Ringvorlesung Einführung in die Methoden der empirischen Sozialforschung II
 Ringvorlesung Einführung in die Methoden der empirischen Sozialforschung II Auswahlverfahren - Begriffe und theoretische Grundlagen 1 USA 1936: - Wahlstudie mit 10.000.000 Probestimmzetteln - Quelle: Telefonverzeichnis
Ringvorlesung Einführung in die Methoden der empirischen Sozialforschung II Auswahlverfahren - Begriffe und theoretische Grundlagen 1 USA 1936: - Wahlstudie mit 10.000.000 Probestimmzetteln - Quelle: Telefonverzeichnis
Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: k = n (n + 1) 2
 Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k = k=1 n (n + 1). 2 Aufgabe 2. (5 Punkte) Bestimmen Sie das folgende Integral mithilfe partieller
Aufgabe 1. (5 Punkte) Zeigen Sie mittles vollständiger Induktion, dass für jede natürliche Zahl n 1 gilt: n k = k=1 n (n + 1). 2 Aufgabe 2. (5 Punkte) Bestimmen Sie das folgende Integral mithilfe partieller
Abitur 2013 Mathematik Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Großstadt steht die Wahl des Oberbürgermeisters bevor. 12% der Wahlberechtigten sind Jungwähler, d. h. Personen
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Großstadt steht die Wahl des Oberbürgermeisters bevor. 12% der Wahlberechtigten sind Jungwähler, d. h. Personen
