Mathematik und Landkarten
|
|
|
- Kai Hofmann
- vor 9 Jahren
- Abrufe
Transkript
1 Mathematik und Landkarten Hans Havlicek Einleitung Die Kartenentwurfslehre beschäftigt sich mit der Darstellung der (gekrümmten) Erdoberfläche in einer (ebenen) Karte. In diesem Beitrag sollen einige mathematische Grundideen vorgestellt werden. Zu deren präziser Beschreibung werden tiefer liegende Kenntnisse der Differentialgeometrie benötigt, also jenes Teilgebiets der Mathematik, wo Geometrie und Infinitesimalrechnung aufeinander treffen. Die Entwicklung der Infinitesimalrechnung begann erst mit den Untersuchungen von Isaac Newton ( ) und Gottfried Wilhelm Leibniz ( ). Demgegenüber wurde eine Reihe von Kartenentwürfen lange vor dem 17. Jahrhundert gefunden. Jede Darstellung der Erdoberfläche in der Ebene wird als Projektion oder Entwurf bezeichnet. In der geometrischen Literatur dient der Terminus Projektion als Oberbegriff für Parallelund Zentralprojektion. Nur wenige Karten beruhen aber auf einer derartigen Projektion. Daher bevorzugen wir hier die Bezeichnung Kartenentwurf. Geometrie auf der Kugeloberfläche Auf der Kugel können zwei Arten von Kreisen unterschieden werden. Großkreise haben denselben Mittelpunkt und daher auch denselben Radius wie die Kugel. Alle anderen Kreise der Kugel heißen Kleinkreise; ihr Radius ist kleiner als der Kugelradius. Abbildung 1 zeigt die Erdkugel samt Gradnetz. Jene Kreise, die den Nord- mit dem Südpol verbinden, sind Großkreise. Sie werden auch Meridiane genannt. Der Äquator ist ebenfalls ein Großkreis, während die anderen Breitenkreise durchwegs Kleinkreise sind. Die Großkreise spielen auf der Kugel dieselbe Rolle wie die Geraden in der Ebene: Als kürzeste Verbindung zwischen zwei Punkten der Kugel tritt immer ein Stück eines Großkreises auf. Die Länge dieses Bogens ist der sphärische Abstand der beiden Punkte, also der an der Oberfläche gemessene Abstand. Im Gegensatz zur Ebene können zwei Punkte der Kugel nicht beliebig weit entfernt sein: Jeder Punkt der Kugel hat von seinem Abb. 1: Erdkugel Antipoden, also dem auf der Kugel gegenüberliegenden Punkt, den maximalen sphärischen Abstand. Auf der Erdkugel ist der maximale Abstand gleich dem halben Umfang des Äquators (also rund km). Schneiden einander zwei Kurven auf der Kugel in einem Punkt, so wird ihr Winkel als der Winkel der Tangenten im Schnittpunkt erklärt. Damit ist der Winkel krummer Kurven auf den Winkel von Geraden zurückgeführt. Die Berechnung der Oberfläche von Teilen der Kugel lässt sich nicht einfach erklären. Es sollte aber auch ohne theoretischen Hintergrund klar sein, dass es prinzipiell möglich ist, derartige Oberflächen zu berechnen. Problemstellung Die Erde ist näherungsweise eine Kugel mit einem Radius von 6370 km. Um eine bessere anschauliche Vorstellung zu haben, gehen wir von einem Globus, also einem verkleinerten Modell des Erdballs aus. Ein optimaler Kartenentwurf müsste ein (flächenhaftes) Gebiet oder
2 sogar den gesamten Globus isometrisch abbilden. D.h., für je zwei Punkte des Gebiets müsste der sphärische Abstand mit dem Abstand ihrer Bilder in der Karte übereinstimmen. Die Differentialgeometrie lehrt aber, dass es einen isometrischen Entwurf nicht gibt, wie klein auch immer das abzubildende Gebiet gewählt wird. Es lassen sich nur Darstellungen finden, bei denen manche Abstände erhalten bleiben, niemals aber alle Abstände. Jede Darstellung eines Gebiets der Erdkugel ist also hinsichtlich der Abstände an gewissen Stellen verzerrt. Eine andere Forderung ist die Flächentreue. Es muss jeder beliebige Teil eines Gebiets des Globus in der Karte denselben Flächeninhalt besitzen wie im Original. Es zeigt sich, dass diese Forderung relativ einfach zu erfüllen ist. Dementsprechend gibt es eine Fülle von flächentreuen Entwürfen. Flächentreue Karten werden gerne zur Illustration von Wirtschaftsdaten verwendet, da sie jedes Land wenn schon nicht in richtiger Gestalt so dennoch in der richtigen Größe wiedergeben. Weiters seien die winkeltreuen Karten genannt. Hier werden alle Winkel in wahrer Größe dargestellt. Statt winkeltreu wird auch der Begriff konform verwendet. Es gibt zahlreiche Beispiele konformer Karten, ihre mathematische Beschreibung ist aber oft aufwändig. Erwähnt werden muss noch folgendes Ergebnis der Differentialgeometrie: Ein Entwurf kann in einem Gebiet nicht flächentreu und winkeltreu zugleich sein. Ein derartiger Entwurf wäre nämlich isometrisch, was nicht möglich ist. Es kommt aber durchaus vor, dass etwa ein flächentreuer Entwurf in einzelnen Punkten winkeltreu ist. Verzerrung Die in einem Kartenpunkt auftretenden Verzerrungen lassen sich an Hand der nach dem französischen Mathematiker Nicolas Auguste Tissot ( ) benannten Indikatrix illustrieren. Eine präzise Definition kann nur mit Hilfe der Infinitesimalrechnung erfolgen. Wir beschreiben die Indikatrix hier näherungsweise: Um einen Punkt P am Globus wird ein sehr kleiner Kreis gezeichnet, etwa mit einem sphärischen Radius r = 1 mm. Das Kartenbild dieses Kreises weicht dann von einer Ellipse nur ganz wenig ab. Der auftretende Fehler wird hier vernachlässigt. Diese Ellipse in der Karte ist aber meist sehr kein. Daher wird sie in einer fest gewählten Vergrößerung dargestellt. Dies ergibt die Indikatrix im Kartenbild von P. Diese Konstruktion kann für verschiedene Punkte des Globus durchgeführt werden. Um die Indikatrizen vergleichen zu können, muss dabei immer derselbe Kreisradius r und derselbe Vergrößerungsfaktor gewählt werden. In manchen Punkten kann die Indikatrix sogar ein Kreis sein. Dort herrscht in allen Richtungen dieselbe Längenverzerrung und sogar Winkeltreue. Andernfalls bestimmen die große und die kleine Halbachse der Indikatrix die beiden Richtungen mit den extremalen Längenverzerrungen. Bei einem (hypothetischen) isometrischen Entwurf wären alle Indikatrizen Kreise mit demselben Radius. Abbildung 2 zeigt einen abstandstreuen Azimutalentwurf in normaler Lage, d.h., der Nordpol ist in der Bildmitte. Die Abstandstreue bezieht sich Abb. 2: Abstandsteuer Azimutalentwurf mit Tissot-Indikatrizen
3 aber nur auf die Meridiane: Diese werden in richtiger Länge als Stecken dargestellt. Die Indikatrix im Bild des Nordpols ist ein Kreis, alle anderen Indikatrizen sind Ellipsen mit derselben Länge der kleinen Halbachse. Die Breitenkreise erscheinen in der Karte zu lang. Die variable Länge der großen Halbachsen der Indikatrizen zeigt, dass die Breitenkreise verschieden stark verzerrt werden. Nahe am Nordpol ist die Abweichung deutlich geringer als am Äquator. Als weiteres Beispiel betrachten wir in Abbildung 3 den Entwurf von Sanson. Er ist durch zwei Forderungen gekennzeichnet: Erstens wird der Nullmeridian als Strecke in richtiger Länge dargestellt, zweitens sind die Bilder der Breitenkreise dazu rechtwinkelige Strecken, die ebenfalls in richtiger Länge dargestellt werden. Diese Informationen reichen schon aus, um das Bild des Nullmeridians und der Breitenkreise zu zeichnen. Anschließend kann das Bild des gesamten Gradnetzes ergänzt werden. Abb. 3: Entwurf von Sanson mit Tissot-Indikatrizen Was die obige Beschreibung nicht sofort erkennen lässt, ist die Flächentreue des Entwurfs von Sanson. Sie kann daran abgelesen werden, dass alle Indikatrizen denselben Flächeninhalt besitzen. Dennoch treten starke Deformationen auf. Das sehen wir etwa am Bild von Australien. In diesem Bereich weichen die Indikatrizen stark von der Kreisform ab. In den Punkten des Nullmeridians und des Äquators ist die Abbildung isometrisch. Hier sind die Indikatrizen Kreise mit demselben Radius. Dies ist kein Widerspruch zur Nicht-Existenz isometrischer Landkarten. Entlang einzelner Kurven lässt sich Isometrie realisieren, niemals aber in einem (flächenhaften) Gebiet des Globus. Als letztes Beispiel in diesem Abschnitt sei die stereographische Projektion vorgestellt: Jeder Punkt des Globus wird aus dem Südpol auf jene Ebene projiziert, welche den Globus im Nordpol berührt. Das ist eine nette Eigenschaft, die aber beim Betrachten der Karte keine Rolle spielt. Erneut haben wir hier eine Beschreibung, die wesentliche Eigenschaften nicht erkennen lässt: Die stereographische Projektion ist winkeltreu und sogar kreistreu. Letzteres bedeutet: Jeder Kreis am Globus erscheint in der stereographischen Karte wieder als Kreis oder (ausnahmsweise) als Gerade. Alle Tissot-Indikatrizen der stereographischen Projektion sind Kreise. In Abbildung 4 sind keine Indikatrizen eingezeichnet, wir merken aber folgendes an: Der Radius der Indikatrizen in allen Bildpunkten des Äquators ist doppelt so groß wie der Radius der Indikatrix im Bild des Nordpols. Deshalb vermittelt die Karte den völlig falschen Eindruck, Grönland (rund 2,17 Millionen m 2 ) wäre deutlich keiner als die arabische Halbinsel (rund 2,73 Millionen m 2 ). In Abbildung 5 wird ein wesentlich kleinerer Globus vom Nordpol bis hin zum Breitenkreis 80 Süd stereographisch abgebildet. Derartige Darstellungen sind für geographische Karten kaum brauchbar, da der Rand des Bildes rund 131 Mal größer dargestellt wird als die Bildmitte. Hingegen wird die stereographische Projektion gerne für drehbare Sternkarten verwendet.
4 Abb. 4: Stereographische Projektion der Nordhalbkugel Abb. 5: Stereographische Projektion bis 80 Süd Weltkarten Wenn es darum geht, den ganzen Globus darzustellen, spielt neben der im letzten Abschnitt behandelten Verzerrung auch das Gesamtbild des Globus eine wichtige Rolle. Viele vom mathematischen Standpunkt interessante Karten taugen nicht oder nur beschränkt als Weltkarten. Abb. 6: Entwurf von Bonne Abb. 7: Entwurf von Stab-Werner Zum Beispiel stören beim Entwurf von Sanson (Abbildung 3) die beiden Ecken oben und unten. Die kugelförmige Erde hat doch keine Ecken! Ebenso wenig können die beiden Entwürfe in den Abbildungen 6 und 7 überzeugen. Sie sind Varianten des Sanson-Entwurfs. Der Nullmeridian erscheint als Strecke in wahrer Länge, alle Breitenkreise haben konzentrische Kreisbögen als Bilder und erscheinen ebenfalls in richtiger Länge. Der gemeinsame Mittelpunkt der Breitenkreisbilder ist beim Entwurf von Bonne irgendwo oberhalb des Bildes des Nordpols (was einen zusätzlichen Freiheitsgrad ergibt), beim Stab-Werner-Entwurf jedoch im Bild des Nordpols. Beide Entwürfe sind so wie der Entwurf von Sanson flächentreu. Der Preis für die Längentreue entlang der Breitenkreise ist aber hoch: Er bewirkt die Herzform der beiden Entwürfe.
5 Eine einfache und zugleich passable Weltkarte liefert die quadratische Plattkarte in Abbildung 8. Sie hat ihren Namen daher, dass das Bild des Gradnetzes aus Quadraten besteht. Entlang des Äquators ist die Abbildung (so wie der Sanson-Entwurf) isometrisch, alle anderen Breitenkreise erscheinen zu lange. Alle Meridiane haben im Bild die richtige Länge, die Indikatrizen dort sind aber Ellipsen (so wie beim abstandstreuen Azimutalentwurf). Es wird auch vom abstandstreuen Zylinderentwürf gesprochen. Ein Vorteil dieser Karte ist, dass sich aus ihr geographische Längen und Breiten leicht ablesen lassen. Flächentreue ist nicht gegeben. Abb. 8: Quadratische Plattkarte Eine ansprechende Weltkarte liefert der Entwurf von Mollweide in Abbildung 9. Diese Karte hat die bemerkenswerte Eigenschaft, dass die Bilder der Meridiane Ellipsen sind. Als störend kann empfunden werden, dass die Breitenkreise geradlinig erscheinen. Dafür ist der Entwurf aber flächentreu. Abb. 9: Entwurf von Mollweide Es gibt eine Reihe von Darstellungen des ganzen Globus, die als vermittelnde Entwürfe bezeichnet werden. Derartige Entwürfe sind in der Regel bloß nahezu flächentreu und bieten dafür meist bessere Werte bei der Längenverzerrung als eine tatsächlich flächentreue Karte. Kartenausschnitte Landkartenentwürfe lassen sich dadurch verändern, dass der Globus vor der eigentlichen Abbildung verdreht wird. Als Beispiel betrachten wir nochmals den Sanson-Entwurf. In Abbildung 10 liegt der Punkt am Äquator mit der geographischen Länge 30 Ost dort, wo vorher der Nordpol war. Es wird von einer Darstellung in transversaler Lage gesprochen.
6 Abb. 10: Entwurf von Sanson in transversaler Lage Die entstehende Karte folgt nicht der gängigen Konvention, den Nordpol oben darzustellen. Sie ist aber flächentreu, hat dieselben Tissot-Indikatrizen wie Abbildung 3 und liefert in der Bildmitte eine nahezu unverzerrte Darstellung von Südamerika. In einem Atlas könnte daher ein Ausschnitt der Karte aus Abbildung 10 zu finden sein, so wie er in Abbildung 11 (vergrößert und gedreht) wiedergegeben ist. Dass es sich dabei um einen Sanson-Entwurf handelt, ist nun wohl nicht mehr zu erkennen. Denn durch die vorhergehende Drehung des Globus stellen sich die Bilder der Längen- und Breitenkreise als komplizierte Kurven dar. Außerdem geht die charakteristische Gesamtform des Sanson-Entwurfs auf Grund des rechteckigen Bildausschnitts verloren. Dieses Beispiel soll zeigen, dass Kartenentwürfe, die für Weltkarten nur beschränkt geeignet sind, dennoch gute Detailkarten liefern können. Abb. 11: Kartenausschnitt Literaturverzeichnis [1] F. Hohenberg: Konstruktive Geometrie in der Technik, 3. Aufl., Wien New York, Springer, [2] J. Hoschek: Mathematische Grundlagen der Kartographie, 2. Aufl., Mannheim Wien Zürich, BI-Wissenschaftsverlag, [3] E. Müller, E. Kruppa: Lehrbuch der darstellenden Geometrie, 6. Aufl., Springer, Wien, [4] G. Sammet: Der Vermessene Planet, Gruner + Jahr, Hamburg, [5] K. Strubecker, G. Scheffers: Wie findet und zeichnet man Gradnetze von Land- und Sternkarten? 2. Aufl., Stuttgart, Teubner, Die Werke [1] und [3] sind Lehrbücher der Konstruktiven Geometrie, in denen das Thema Landkarten anschaulich behandelt wird. Das Buch [5] kann im Gegensatz zu [2] mit geringen mathematische Kenntnisse gelesen werden. Für historische Anmerkungen und Reproduktionen alter Karten sei auf [4] verwiesen.
Einhundert Projektionsprobleme ein Programm zum Zeichnen von Karten
 Einhundert Projektionsprobleme ein Programm zum Zeichnen von Karten Enter Cartography Universität für Angewandte Kunst Wien, 16. Juni 2011 HANS HAVLICEK FORSCHUNGSGRUPPE DIFFERENTIALGEOMETRIE UND GEOMETRISCHE
Einhundert Projektionsprobleme ein Programm zum Zeichnen von Karten Enter Cartography Universität für Angewandte Kunst Wien, 16. Juni 2011 HANS HAVLICEK FORSCHUNGSGRUPPE DIFFERENTIALGEOMETRIE UND GEOMETRISCHE
Gekrümmte Erdkugel Flache Landkarte Geometrie und Kartenentwürfe
 Gekrümmte Erdkugel Flache Landkarte Geometrie und Kartenentwürfe 29. Fortbildungstagung für Geometrie Bundesinstitut für Erwachsenenbildung, St. Wolfgang, 6. November 2008 HANS HAVLICEK FORSCHUNGSGRUPPE
Gekrümmte Erdkugel Flache Landkarte Geometrie und Kartenentwürfe 29. Fortbildungstagung für Geometrie Bundesinstitut für Erwachsenenbildung, St. Wolfgang, 6. November 2008 HANS HAVLICEK FORSCHUNGSGRUPPE
Kürzester Abstand. Abb.1
 Kürzester Abstand Im Januar 2011 meldete die Lufthansa, dass eines ihrer Flugzeuge des Typs Boeing 747 über Grönland den Flug nach San Francisco wegen Ölverlustes in einem der vier Triebwerke abgebrochen
Kürzester Abstand Im Januar 2011 meldete die Lufthansa, dass eines ihrer Flugzeuge des Typs Boeing 747 über Grönland den Flug nach San Francisco wegen Ölverlustes in einem der vier Triebwerke abgebrochen
Gekrümmte Erdkugel Flache Landkarte Geometrie und Kartenentwürfe
 Gekrümmte Erdkugel Flache Landkarte Geometrie und Kartenentwürfe Arge DG/GZ Wien TU Wien, 5. März 2008 HANS HAVLICEK FORSCHUNGSGRUPPE DIFFERENTIALGEOMETRIE UND GEOMETRISCHE STRUKTUREN INSTITUT FÜR DISKRETE
Gekrümmte Erdkugel Flache Landkarte Geometrie und Kartenentwürfe Arge DG/GZ Wien TU Wien, 5. März 2008 HANS HAVLICEK FORSCHUNGSGRUPPE DIFFERENTIALGEOMETRIE UND GEOMETRISCHE STRUKTUREN INSTITUT FÜR DISKRETE
Ebene Schnitte einer Kugel
 Ebene Schnitte einer Kugel Eine Kugel Φ(M,r) und eine Ebene Σschneiden sich in einem Kreis k(σ, M k, r k ), falls der Abstand d des Kugelmittelpunkts von Σ kleiner r ist. Φ Φ k r=r k d M k r k M=M k k
Ebene Schnitte einer Kugel Eine Kugel Φ(M,r) und eine Ebene Σschneiden sich in einem Kreis k(σ, M k, r k ), falls der Abstand d des Kugelmittelpunkts von Σ kleiner r ist. Φ Φ k r=r k d M k r k M=M k k
Der Entwurf von Winkel oder "Wieviel Geometrie steckt in einer Schulwandkarte?" Von Hans Havlicek, Wien.
 Der Entwurf von Winkel oder "Wieviel Geometrie steckt in einer Schulwandkarte?" Von Hans Havlicek, Wien. In vielen Schulklassen hängen geographische Karten, insbesondere dürfte die in Figur 1 abgebildete
Der Entwurf von Winkel oder "Wieviel Geometrie steckt in einer Schulwandkarte?" Von Hans Havlicek, Wien. In vielen Schulklassen hängen geographische Karten, insbesondere dürfte die in Figur 1 abgebildete
Abb. 1: St. Galler-Brot. 2.1 Formelsammlung In der Formelsammlung finden wir für den Flächeninhalt A einer Kugelzone: A = 2πRh (1)
 Hans Walser, [20180112] Brotkruste Anregungen: Sebastian Baader, Bern, und Anselm Lambert, Saarbrücken 1 Worum geht es? In einigen Gegenden der Schweiz gibt es ein annähernd kugelförmiges Brot, das so
Hans Walser, [20180112] Brotkruste Anregungen: Sebastian Baader, Bern, und Anselm Lambert, Saarbrücken 1 Worum geht es? In einigen Gegenden der Schweiz gibt es ein annähernd kugelförmiges Brot, das so
Formelsammlung zur Vorlesung. Kartenentwürfe. Hans Havlicek
 Formelsammlung zur Vorlesung Kartenentwürfe Hans Havlicek Institut für Diskrete Mathematik und Geometrie der TU Wien Forschungsgruppe Differentialgeometrie und Geometrische Strukturen Internet: www.geometrie.tuwien.ac.at/havlicek/
Formelsammlung zur Vorlesung Kartenentwürfe Hans Havlicek Institut für Diskrete Mathematik und Geometrie der TU Wien Forschungsgruppe Differentialgeometrie und Geometrische Strukturen Internet: www.geometrie.tuwien.ac.at/havlicek/
Abb. 1: Stereografische Projektion
 Hans Walser, [20160808] Stereografische Projektion 1 Ausgangslage Wir projizieren die Erde (Geodaten) vom Nordpol aus auf die Tangentialebene im Südpol. Die Abbildung 1 zeigt die Projektion exemplarisch
Hans Walser, [20160808] Stereografische Projektion 1 Ausgangslage Wir projizieren die Erde (Geodaten) vom Nordpol aus auf die Tangentialebene im Südpol. Die Abbildung 1 zeigt die Projektion exemplarisch
Kartografie I. Hans Walser. Kartenprojektionen Lernumgebung
 Kartografie I Hans Walser Kartenprojektionen Lernumgebung Hans Walser: Kartenprojektionen. Lernumgebung ii Inhalt Parameterdarstellung der Kugel... 2 Geodätische Linien... 3 Kegelprojektion: Variante mit
Kartografie I Hans Walser Kartenprojektionen Lernumgebung Hans Walser: Kartenprojektionen. Lernumgebung ii Inhalt Parameterdarstellung der Kugel... 2 Geodätische Linien... 3 Kegelprojektion: Variante mit
Orthografische Projektion!
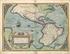 Kartenprojektionen! Orthografische Projektion! Immer der Nase nach! Großkreise statt Geraden! α = 15 Blick von der Seite! Steigungswinkel α { 15, 45, 75 } Was ist denn das?! Verzerrungsellipsen (Indikatrix
Kartenprojektionen! Orthografische Projektion! Immer der Nase nach! Großkreise statt Geraden! α = 15 Blick von der Seite! Steigungswinkel α { 15, 45, 75 } Was ist denn das?! Verzerrungsellipsen (Indikatrix
7 Beziehungen im Raum
 Lange Zeit glaubten die Menschen, die Erde sei eine Scheibe. Heute zeigen dir Bilder aus dem Weltall sehr deutlich, dass die Erde die Gestalt einer Kugel hat. 7 Beziehungen im Raum Gradnetz der Erde Längengrade
Lange Zeit glaubten die Menschen, die Erde sei eine Scheibe. Heute zeigen dir Bilder aus dem Weltall sehr deutlich, dass die Erde die Gestalt einer Kugel hat. 7 Beziehungen im Raum Gradnetz der Erde Längengrade
Nichteuklidische Geometrien und gekrümmte Räume
 Nichteuklidische Geometrien und gekrümmte Räume Es begann mit dem Problem der Landvermessung... Carl Friedrich Gauß (1777-1855): Theorie gekrümmter Flächen Landesvermessung des Königreichs Hannover Entdeckung
Nichteuklidische Geometrien und gekrümmte Räume Es begann mit dem Problem der Landvermessung... Carl Friedrich Gauß (1777-1855): Theorie gekrümmter Flächen Landesvermessung des Königreichs Hannover Entdeckung
Triangulierungen und Kartographie
 Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 30. Oktober 2015 Was
Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 30. Oktober 2015 Was
A. N. Danilewsky 31. Fortsetzung von Kapitel 2
 A. N. Danilewsky 31 Fortsetzung von Kapitel 2 2.3 Darstellung von Körpern... 32 2.3.1 Othogonale Parallelprojektion... 32 2.3.2 Stereographische Projektion... 34 2.3.3 Gnomonische Projektion... 42 32 Kristallographie
A. N. Danilewsky 31 Fortsetzung von Kapitel 2 2.3 Darstellung von Körpern... 32 2.3.1 Othogonale Parallelprojektion... 32 2.3.2 Stereographische Projektion... 34 2.3.3 Gnomonische Projektion... 42 32 Kristallographie
Triangulierungen und Kartographie
 Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 23. Juli 2014 Was verraten
Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 23. Juli 2014 Was verraten
Erfassen der Kugelgestalt der Erde, Abschätzen von Entfernungen und Flächeninhalten
 Semesterarbeit SoSe 2016 UE Digitale Information und Kommunikation Erfassen der Kugelgestalt der Erde, Abschätzen von Entfernungen und Flächeninhalten 1. Klasse AHS (5. Schulstufe) Geographie und Wirtschaftskunde
Semesterarbeit SoSe 2016 UE Digitale Information und Kommunikation Erfassen der Kugelgestalt der Erde, Abschätzen von Entfernungen und Flächeninhalten 1. Klasse AHS (5. Schulstufe) Geographie und Wirtschaftskunde
1. Schreibe die Geografischen Lageangaben in die richtigen Kästchen ein:
 Lösung Das Gradnetz der Erde L1 1. Schreibe die Geografischen Lageangaben in die richtigen Kästchen ein: nördliche Breite / westliche Länge südliche Breite / östliche Länge südliche Breite / westliche
Lösung Das Gradnetz der Erde L1 1. Schreibe die Geografischen Lageangaben in die richtigen Kästchen ein: nördliche Breite / westliche Länge südliche Breite / östliche Länge südliche Breite / westliche
2.1 Steigung 1. Die Geraden mit Steigung ±1 folgen den Diagonalen der Netzquadrate (Abb. 2). Abb. 1: Plattkarte. Abb. 2: Situation auf der Karte
 Hans Walser, [20131216a], [20140308] Sphärische Spiralen 1 Idee Die Idee ist einfach: Wir zeichnen auf einer Weltkarte eine schräg ansteigende Gerade und studieren deren Bild auf der Kugel. Je nach Kartentyp
Hans Walser, [20131216a], [20140308] Sphärische Spiralen 1 Idee Die Idee ist einfach: Wir zeichnen auf einer Weltkarte eine schräg ansteigende Gerade und studieren deren Bild auf der Kugel. Je nach Kartentyp
Klassenarbeit - Die Erde
 Klassenarbeit - Die Erde 5. Klasse / Geografie Erdrotation; Erdbahn; Kontinente; Gradnetz; Karten; Polartag Aufgabe 1 Wie nennt man a) die Drehung der Erde um sich selbst und b) wie ihre Drehung um die
Klassenarbeit - Die Erde 5. Klasse / Geografie Erdrotation; Erdbahn; Kontinente; Gradnetz; Karten; Polartag Aufgabe 1 Wie nennt man a) die Drehung der Erde um sich selbst und b) wie ihre Drehung um die
Koordinatensysteme der Erde
 Koordinatensysteme der Erde Es gibt verschiedene Arten, die Position eines Punktes auf der Oberfläche einer Kugel (manchmal auch Sphäre genannt) darzustellen, jede hat ihre Vor-und Nachteile und ist für
Koordinatensysteme der Erde Es gibt verschiedene Arten, die Position eines Punktes auf der Oberfläche einer Kugel (manchmal auch Sphäre genannt) darzustellen, jede hat ihre Vor-und Nachteile und ist für
Es wird versucht, die geometrischen Grundlagen zur Entscheidung dieser Frage aufzuarbeiten.
 Hans Walser, [20160609] Gestalt der Erde 1 Worum geht es? Im späten 17. Jahrhundert entspann sich ein wissenschaftlicher treit um die Gestalt der Erde (Brotton 2012,. 308): Die Anhänger von Descartes (1596-1650)
Hans Walser, [20160609] Gestalt der Erde 1 Worum geht es? Im späten 17. Jahrhundert entspann sich ein wissenschaftlicher treit um die Gestalt der Erde (Brotton 2012,. 308): Die Anhänger von Descartes (1596-1650)
GPS - Anwendungen. im Zusammenhang mit satellitengestützter Ortung
 im Zusammenhang mit satellitengestützter Ortung Gestalt der Erde und Darstellungsmöglichkeiten auf Karten : Die Erde hat annähernd Kugelform. Durch die Erdrotation entsteht eine Abplattung an den Polen
im Zusammenhang mit satellitengestützter Ortung Gestalt der Erde und Darstellungsmöglichkeiten auf Karten : Die Erde hat annähernd Kugelform. Durch die Erdrotation entsteht eine Abplattung an den Polen
Ptolemäus (2. Jhdt. n. Chr.) gilt als erster Hersteller eines Globus und führt Längen- und Breitengrade zur Positionsangabe ein.
 Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
x 1 x 2 a) Erläutern Sie den prinzipiellen Weg, wie man den Standort der Person aus den gegebenen Daten berechnen kann.
 Lineare Algebra / Analytische Geometrie Leistungskurs Aufgabe 5: GPS Eine Person bestimmt ihre Position auf der Erdoberfläche mit Hilfe eines GPS-Gerätes. Dieser Vorgang soll in dieser Aufgabe prinzipiell
Lineare Algebra / Analytische Geometrie Leistungskurs Aufgabe 5: GPS Eine Person bestimmt ihre Position auf der Erdoberfläche mit Hilfe eines GPS-Gerätes. Dieser Vorgang soll in dieser Aufgabe prinzipiell
r 1 Abb. 1: Schlinge um Kreis im Abstand 1
 Hans Walser, [20130119a] Schlinge um Kreis Anregung: R. S., Z. 1 Die Uralt-Aufgabe Um einen Kreis mit Radius r wird eine Schlinge im Abstand 1 gelegt (Abb. 1). Wie lang ist die Schlinge im Vergleich zum
Hans Walser, [20130119a] Schlinge um Kreis Anregung: R. S., Z. 1 Die Uralt-Aufgabe Um einen Kreis mit Radius r wird eine Schlinge im Abstand 1 gelegt (Abb. 1). Wie lang ist die Schlinge im Vergleich zum
Die Luftfahrtkarte ICAO 1 : ist a) nur winkeltreu b) nur streckentreu c) flächen-, strecken- und winkeltreu d) nur flächentreu
 NAV K1. Welche Aussage ist nicht richtig? a) Die äquatorständige stereographische Projektion findet in der Navigation keine besondere Anwendung b) Die Mercatorkarte dient besonders in niedrigen Breiten
NAV K1. Welche Aussage ist nicht richtig? a) Die äquatorständige stereographische Projektion findet in der Navigation keine besondere Anwendung b) Die Mercatorkarte dient besonders in niedrigen Breiten
Kartenprojektion. gnonomische Projektion. Zylinderentwürfe
 Grundsätze der Kartographie Um die Erdoberfläche für die u. a. navigatorische Nutzung darzustellen, macht es sich erforderlich, mit den Grundlagen der Kartographie vertraut zu sein. Der Globus (lat. Kugel)
Grundsätze der Kartographie Um die Erdoberfläche für die u. a. navigatorische Nutzung darzustellen, macht es sich erforderlich, mit den Grundlagen der Kartographie vertraut zu sein. Der Globus (lat. Kugel)
Ptolemäus (2. Jhdt. n. Chr.) gilt als erster Hersteller eines Globus und führt Längen- und Breitengrade zur Positionsangabe ein.
 Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
Die stereografische Projektion. Hans Walser
 Die stereografische rojektion Hans Walser Die stereografische rojektion ii Inhalt 1 Worum geht es?...1 2 Die stereografische rojektion ist winkeltreu...3 3 Die stereografische rojektion ist kreistreu...5
Die stereografische rojektion Hans Walser Die stereografische rojektion ii Inhalt 1 Worum geht es?...1 2 Die stereografische rojektion ist winkeltreu...3 3 Die stereografische rojektion ist kreistreu...5
100 % Mathematik - Lösungen
 100 % Mathematik: Aus der Geometrie Name: Klasse: Datum: 1 Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm
100 % Mathematik: Aus der Geometrie Name: Klasse: Datum: 1 Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm
Äquatoraufgabe. Der Äquator
 Humboldt Universität zu Berlin Datum: 06.01.09 Institut für Mathematik SE: Ausgewählte Kapitel der Didaktik der Mathematik (Computerunterstützter Mathematikunterricht) Dozent: I. Lehmann Autor: A. Gielsdorf
Humboldt Universität zu Berlin Datum: 06.01.09 Institut für Mathematik SE: Ausgewählte Kapitel der Didaktik der Mathematik (Computerunterstützter Mathematikunterricht) Dozent: I. Lehmann Autor: A. Gielsdorf
Abb. 1: Acht Kartenausschnitte
 Hans Walser, [20161103] Abroll-Globus 1 Worum geht es? Wir bauen einen Papierglobus, der abrollen lässt. 2 Kartengrundlagen Die Abbildung 1 zeigt acht Kartenausschnitte. Jeder Ausschnitt zeigt einen Viertel
Hans Walser, [20161103] Abroll-Globus 1 Worum geht es? Wir bauen einen Papierglobus, der abrollen lässt. 2 Kartengrundlagen Die Abbildung 1 zeigt acht Kartenausschnitte. Jeder Ausschnitt zeigt einen Viertel
Reuleaux-Dreieck, Tetraeder und Seifenblasen Das Reuleaux-Dreieck kann durch geeignete Projektionen aus dem Tetraeder hergeleitet werden.
 Hans Walser, [20120513] Reuleaux-Dreieck, Tetraeder und Seifenblasen Das Reuleaux-Dreieck kann durch geeignete Projektionen aus dem Tetraeder hergeleitet werden. 1 Das Reuleaux-Dreieck Die Abbildung 1
Hans Walser, [20120513] Reuleaux-Dreieck, Tetraeder und Seifenblasen Das Reuleaux-Dreieck kann durch geeignete Projektionen aus dem Tetraeder hergeleitet werden. 1 Das Reuleaux-Dreieck Die Abbildung 1
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
Klassenarbeit - Die Erde
 Klassenarbeit - Die Erde 5. Klasse / Geografie Gradnetz; Kontinente; Weltbilder; Sonnensystem; Ozeane; Karten Aufgabe 1 Ergänze den Text zum Gradnetz der Erde! Damit wir uns auf der Erde orientieren können,
Klassenarbeit - Die Erde 5. Klasse / Geografie Gradnetz; Kontinente; Weltbilder; Sonnensystem; Ozeane; Karten Aufgabe 1 Ergänze den Text zum Gradnetz der Erde! Damit wir uns auf der Erde orientieren können,
DG für Kunstpädagogik
 DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
Die Kugel. Mathematische Betrachtungen von Peter Franzke
 Die Kugel Mathematische Betrachtungen von Die Einheitssphäre S 1. Die Kugel Geometrie: gekrümmte geschlossene Fläche, deren Punkte von einem festen Punkt M (Kugelmittelpunkt) einen festen Abstand r (Kugelradius)
Die Kugel Mathematische Betrachtungen von Die Einheitssphäre S 1. Die Kugel Geometrie: gekrümmte geschlossene Fläche, deren Punkte von einem festen Punkt M (Kugelmittelpunkt) einen festen Abstand r (Kugelradius)
Klassenarbeit - Die Erde
 Klassenarbeit - Die Erde 5. Klasse / Geografie Kontinente; Atlas und Globus; Gestalt; Ozeane; Erdrotation; Gradnetz; Erdbahn; Maßstab Aufgabe 1 Durch welche Erdteile verläuft der Äquator? Aufgabe 2 Nenne
Klassenarbeit - Die Erde 5. Klasse / Geografie Kontinente; Atlas und Globus; Gestalt; Ozeane; Erdrotation; Gradnetz; Erdbahn; Maßstab Aufgabe 1 Durch welche Erdteile verläuft der Äquator? Aufgabe 2 Nenne
Klassenarbeit - Die Erde
 Klassenarbeit - Die Erde Erdrotation; Gradnetz; Erdbahn; Jahreszeiten; Oberflächenformen; Vegetationsgebiete 5. Klasse / Geografie Aufgabe 1 Erläutere die Erdrotation und den damit entstehenden Effekt.
Klassenarbeit - Die Erde Erdrotation; Gradnetz; Erdbahn; Jahreszeiten; Oberflächenformen; Vegetationsgebiete 5. Klasse / Geografie Aufgabe 1 Erläutere die Erdrotation und den damit entstehenden Effekt.
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.17 016/07/1 16:3:40 hk Exp $ 5 Sphärische Trigonometrie 5.5 Geographische Koordinaten Wir beschäftigen uns gerade mit der Berechnung des Weges zwischen zwei in geographischen Koordinaten
$Id: sphaere.tex,v 1.17 016/07/1 16:3:40 hk Exp $ 5 Sphärische Trigonometrie 5.5 Geographische Koordinaten Wir beschäftigen uns gerade mit der Berechnung des Weges zwischen zwei in geographischen Koordinaten
Kreisberechnungen. 2. Kapitel aus meinem Lehrgang Geometrie
 Kreisberechnungen 2. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch e-mail: [email protected] 8. Oktober 08 Überblick über die bisherigen Geometrie
Kreisberechnungen 2. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch e-mail: [email protected] 8. Oktober 08 Überblick über die bisherigen Geometrie
KARTENNETZENTWÜRFE. Grundlagen, Gliederung und Bezeichnung der Netzentwürfe, Literaturverzeichnis. Grundlagen der Kartographie
 HOCHSCHULE FÜR TECHNIK UND WIRTSCHAFT DRESDEN (FH) Fachbereich Vermessungswesen/Kartographie Studiengang Kartographie Prof. Dr.-Ing. Martina Müller KARTENNETZENTWÜRFE Grlagen, Gliederung Bezeichnung der
HOCHSCHULE FÜR TECHNIK UND WIRTSCHAFT DRESDEN (FH) Fachbereich Vermessungswesen/Kartographie Studiengang Kartographie Prof. Dr.-Ing. Martina Müller KARTENNETZENTWÜRFE Grlagen, Gliederung Bezeichnung der
Orthografische Projektion!
 Kartenprojektionen! Orthografische Projektion! Immer der Nase nach! Großkreise statt Geraden! α = 15 Blick von der Seite! Steigungswinkel α { 15, 45, 75 } Was ist denn das?! Verzerrungsellipsen (Indikatrix
Kartenprojektionen! Orthografische Projektion! Immer der Nase nach! Großkreise statt Geraden! α = 15 Blick von der Seite! Steigungswinkel α { 15, 45, 75 } Was ist denn das?! Verzerrungsellipsen (Indikatrix
Magische Kreise 1 Die Probleme 1.1 Drei Kreise Abb. 1: Drei Kreise
 Hans Walser, [20050829a], [20171103] Magische Kreise 1 Die Probleme 1.1 Drei Kreise In die quadratischen Felder sind die Zahlen 1 bis 6 so einzusetzen, dass auf jedem Kreis die Summe gleich ist. Abb. 1:
Hans Walser, [20050829a], [20171103] Magische Kreise 1 Die Probleme 1.1 Drei Kreise In die quadratischen Felder sind die Zahlen 1 bis 6 so einzusetzen, dass auf jedem Kreis die Summe gleich ist. Abb. 1:
Kartografie I. Hans Walser. Koordinatensysteme und Transformationen
 Kartografie I Hans Walser Koordinatenssteme und Transformationen Hans Walser: Koordinatenssteme und Transformationen ii Inhalt Koordinatenssteme.... Kartesische Koordinaten....2 Polarkoordinaten... 2.3
Kartografie I Hans Walser Koordinatenssteme und Transformationen Hans Walser: Koordinatenssteme und Transformationen ii Inhalt Koordinatenssteme.... Kartesische Koordinaten....2 Polarkoordinaten... 2.3
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Hans Walser. Raumgeometrie. Modul 1 Der Würfel Lernumgebung, Teil 1
 Hans Walser Raumgeometrie Modul 1 Der Würfel Lernumgebung, Teil 1 Hans Walser: Modul 1, Der Würfel. Lernumgebung, Teil 1 ii Inhalt 1 Der 12-7-5-Würfel... 1 2 Schnittpunkte am Quader... 2 3 Zwölf oder dreizehn
Hans Walser Raumgeometrie Modul 1 Der Würfel Lernumgebung, Teil 1 Hans Walser: Modul 1, Der Würfel. Lernumgebung, Teil 1 ii Inhalt 1 Der 12-7-5-Würfel... 1 2 Schnittpunkte am Quader... 2 3 Zwölf oder dreizehn
Karten, Projektionen und Referenzsysteme
 Karten, Projektionen und Referenzsysteme Dr. Thomas Schwotzer 23. Oktober 2013 Zusammenfassung In der praktischen Arbeit benötigt man Karten. Die Erde ist aber leider keine Scheibe, sondern (in einer gewissen
Karten, Projektionen und Referenzsysteme Dr. Thomas Schwotzer 23. Oktober 2013 Zusammenfassung In der praktischen Arbeit benötigt man Karten. Die Erde ist aber leider keine Scheibe, sondern (in einer gewissen
Fenchels Theorem. Daniel Weber. Proseminar Kurven. Wintersemester 2012/13. Prof. Dr. Franz Pedit
 Proseminar Kurven Wintersemester 212/13 Prof. Dr. Franz Pedit Inhaltsverzeichnis 1 Einleitung 2 2 Prolog 3 2.1 (Hemi-)Sphären.................................... 3 2.2 Groß- und Kleinkreise................................
Proseminar Kurven Wintersemester 212/13 Prof. Dr. Franz Pedit Inhaltsverzeichnis 1 Einleitung 2 2 Prolog 3 2.1 (Hemi-)Sphären.................................... 3 2.2 Groß- und Kleinkreise................................
Euklid ( v. Chr.) Markus Wurster
 Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Geometrische Grundbegriffe Euklid (365 300 v. Chr.) Punkte und Linien Zwei Linien Markus Wurster Markus Wurster Geometrische Grundbegriffe Winkel Euklid
So viel wie möglich Extremwertaufgaben aus Geometrie
 So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
Zykloide. Lars Ehrenborg. 15. Januar Definition/Erzeugungsweise 2. 2 Herleitung der Parameterdarstellung 2. 4 Fläche eines Zykloidenbogens 4
 Zykloide Lars Ehrenborg 15. Januar 2017 Inhaltsverzeichnis 1 Definition/Erzeugungsweise 2 2 Herleitung der Parameterdarstellung 2 3 hübsche Eigenschaft 3 4 Fläche eines Zykloidenbogens 4 5 Normale und
Zykloide Lars Ehrenborg 15. Januar 2017 Inhaltsverzeichnis 1 Definition/Erzeugungsweise 2 2 Herleitung der Parameterdarstellung 2 3 hübsche Eigenschaft 3 4 Fläche eines Zykloidenbogens 4 5 Normale und
5A. Von der Perspektive zu den projektiven Ebenen.
 5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
1.4. Funktionen, Kurven und Parameterdarstellungen
 .4. Funktionen, Kurven und Parameterdarstellungen Reellwertige Funktionen Eine reelle Relation ist eine beliebige Teilmenge F der Ebene (also eine ebene "Fläche"). Von einer reellen Funktion spricht man,
.4. Funktionen, Kurven und Parameterdarstellungen Reellwertige Funktionen Eine reelle Relation ist eine beliebige Teilmenge F der Ebene (also eine ebene "Fläche"). Von einer reellen Funktion spricht man,
Autodesk CIVIL 3D, MAP 3D 2019 Neuerungen im MAP 2019 Gert Domsch, CAD-Dienstleistung
 Autodesk CIVIL 3D, MAP 3D 2019 Neuerungen im MAP 2019 Gert Domsch, CAD-Dienstleistung 11.07.2018 Inhalt: Vorwort (Grundlage, MAP 3D 2019)...2 Ziel...2 Deutsche Bahn Koordinatensysteme...3 Welche praktische
Autodesk CIVIL 3D, MAP 3D 2019 Neuerungen im MAP 2019 Gert Domsch, CAD-Dienstleistung 11.07.2018 Inhalt: Vorwort (Grundlage, MAP 3D 2019)...2 Ziel...2 Deutsche Bahn Koordinatensysteme...3 Welche praktische
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Mathematik B-Tag Freitag, 20. November, 8:00 15:00 Uhr. Um die Ecke. Mathematik B-Tag Seite 1 von 9 -
 Mathematik B-Tag 2015 Freitag, 20. November, 8:00 15:00 Uhr Um die Ecke Mathematik B-Tag 2015 - Seite 1 von 9 - Erkundung 1 (Klavier) Ein Klavier soll durch einen 1 m breiten Gang um die Ecke (rechter
Mathematik B-Tag 2015 Freitag, 20. November, 8:00 15:00 Uhr Um die Ecke Mathematik B-Tag 2015 - Seite 1 von 9 - Erkundung 1 (Klavier) Ein Klavier soll durch einen 1 m breiten Gang um die Ecke (rechter
Konstruktionen am Dreieck
 Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Aufgaben zur Übung der Anwendung von GeoGebra
 Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Unterrichtsreihe zur Parabel
 Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
2. Die Abbildung der Erdoberfläche
 20 2. Die Abbildung der Erdoberfläche Hieraus ergibt sich mit U= m 360 /Dj ein Kugelumfang von 250000 Stadien. Da der Längeneinheit Stadion je nach Region unterschiedliche Meterangaben entsprachen, ergibt
20 2. Die Abbildung der Erdoberfläche Hieraus ergibt sich mit U= m 360 /Dj ein Kugelumfang von 250000 Stadien. Da der Längeneinheit Stadion je nach Region unterschiedliche Meterangaben entsprachen, ergibt
Weitere geometrische Abbildungen
 Weitere geometrische Abbildungen Anna Wegener, Matthias Wegen, Daniel Kretschmer 15.01.2015 1 / 38 Affinitätsabbildungen - Motivation Kongruenzabbildungen Ähnlichkeitsabbildungen Affinitätsabbildungen
Weitere geometrische Abbildungen Anna Wegener, Matthias Wegen, Daniel Kretschmer 15.01.2015 1 / 38 Affinitätsabbildungen - Motivation Kongruenzabbildungen Ähnlichkeitsabbildungen Affinitätsabbildungen
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Geometrische Grundkonstruktionen
 Geometrische Grundkonstruktionen Strecken...2 Halbierung einer Strecke und Mittelsenkrechte...2 Teilung einer Strecke in eine bestimmte Anzahl gleicher Teile...2 Halbierung eines Winkels...3 Tangente an
Geometrische Grundkonstruktionen Strecken...2 Halbierung einer Strecke und Mittelsenkrechte...2 Teilung einer Strecke in eine bestimmte Anzahl gleicher Teile...2 Halbierung eines Winkels...3 Tangente an
Mathematik III. Vorlesung 76. Das Konzept einer Mannigfaltigkeit
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 76 Das Konzept einer Mannigfaltigkeit In der zweiten Hälfte dieses Kurses werden wir den Begriff der Mannigfaltigkeit entwickeln. Als
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 76 Das Konzept einer Mannigfaltigkeit In der zweiten Hälfte dieses Kurses werden wir den Begriff der Mannigfaltigkeit entwickeln. Als
1.1 Geradenspiegelungen
 1.1 Geradenspiegelungen 1.1.1 Eigenschaften Definition 1.1 Eine Abbildung der Ebene ist eine Vorschrift, die jedem Punkt P der Ebene einen Bildpunkt P zuordnet. Beispiel 1.1 Zentrische Streckung mit Zentrum
1.1 Geradenspiegelungen 1.1.1 Eigenschaften Definition 1.1 Eine Abbildung der Ebene ist eine Vorschrift, die jedem Punkt P der Ebene einen Bildpunkt P zuordnet. Beispiel 1.1 Zentrische Streckung mit Zentrum
I. ZWISCHEN HIMMEL UND ERDE
 I. ZWISCHEN HIMMEL UND ERDE I. 1. Das Sonnensystem Fragen und Aufgaben 1. Welche Planeten befinden sich im Sonnensystem? Ergänze den Wortigel in der Reihenfolge der Planet. Planeten Abb. 1: Planeten 2.
I. ZWISCHEN HIMMEL UND ERDE I. 1. Das Sonnensystem Fragen und Aufgaben 1. Welche Planeten befinden sich im Sonnensystem? Ergänze den Wortigel in der Reihenfolge der Planet. Planeten Abb. 1: Planeten 2.
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.25 2017/07/13 11:11:42 hk Exp $ 5 Sphärische Trigonometrie 5.3 Geographische Koordinaten N N b γ a P α c β P 2 P 1 λ ϕ ϕ2 Längengrad λ und Breitengrad ϕ Abstand auf Großkreis Wir betrachten
$Id: sphaere.tex,v 1.25 2017/07/13 11:11:42 hk Exp $ 5 Sphärische Trigonometrie 5.3 Geographische Koordinaten N N b γ a P α c β P 2 P 1 λ ϕ ϕ2 Längengrad λ und Breitengrad ϕ Abstand auf Großkreis Wir betrachten
Geometrische Aufgaben, die zu DGL mit getrennten Variablen führen
 http://www.outube.com/watch?vm7a cjgldga Geometrische Aufgaben, die zu DGL mit getrennten Variablen führen E Ma Lubov Vassilevskaa Geometrisches Problem von De Beaune Vor etwa 4 Jahrhunderten studierten
http://www.outube.com/watch?vm7a cjgldga Geometrische Aufgaben, die zu DGL mit getrennten Variablen führen E Ma Lubov Vassilevskaa Geometrisches Problem von De Beaune Vor etwa 4 Jahrhunderten studierten
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Aufgabe 5: Analytische Geometrie (WTR)
 Abitur Mathematik: Nordrhein-Westfalen 203 Aufgabe 5 a) () PARALLELOGRAMMEIGENSCHAFTEN NACHWEISEN Zu zeigen ist, dass die gegenüberliegenden Seiten parallel sind, d. h. und. Zunächst ist 0 0 2 0, 3 2 0
Abitur Mathematik: Nordrhein-Westfalen 203 Aufgabe 5 a) () PARALLELOGRAMMEIGENSCHAFTEN NACHWEISEN Zu zeigen ist, dass die gegenüberliegenden Seiten parallel sind, d. h. und. Zunächst ist 0 0 2 0, 3 2 0
Kreisberechnungen. GEOMETRIE Kapitel 1 SprachProfil - Mittelstufe KSOe. Ronald Balestra CH Zürich
 Kreisberechnungen GEOMETRIE Kapitel 1 SprachProfil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 16. November 12 Inhaltsverzeichnis 1 Kreisberechnungen 1 1.1
Kreisberechnungen GEOMETRIE Kapitel 1 SprachProfil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 16. November 12 Inhaltsverzeichnis 1 Kreisberechnungen 1 1.1
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 7 Aufgabe 1. Skizze (mit zusätzlichen Punkten): Die Figur F wird begrenzt durch die Strecken AB und BC und den Kreisbogen CA auf l. Wir werden die Bilder von AB, BC und CA unter der Inversion
Lösungen Übung 7 Aufgabe 1. Skizze (mit zusätzlichen Punkten): Die Figur F wird begrenzt durch die Strecken AB und BC und den Kreisbogen CA auf l. Wir werden die Bilder von AB, BC und CA unter der Inversion
2. UNTERRICHTSTUNDE: DIE LAGE DER VEREINIGTEN STAATEN: EINE LANDKARTE LESEN KÖNNEN
 THEMA: USA 2. UNTERRICHTSTUNDE 34 2. UNTERRICHTSTUNDE: DIE LAGE DER VEREINIGTEN STAATEN: EINE LANDKARTE LESEN KÖNNEN Ziele: die Schüler sollen sich über die Größe der Vereinigten Staaten bewusst werden
THEMA: USA 2. UNTERRICHTSTUNDE 34 2. UNTERRICHTSTUNDE: DIE LAGE DER VEREINIGTEN STAATEN: EINE LANDKARTE LESEN KÖNNEN Ziele: die Schüler sollen sich über die Größe der Vereinigten Staaten bewusst werden
2. Berechnungen mit Pythagoras
 2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
Koordinatensysteme und GPS
 Koordinatensysteme und GPS Koordinatensysteme und GPS Koordinatensysteme: Definition Ein Koordinatensystem ist ein Bezugssystem, mit dem die Positionen von geographischen Features, Bildern und Beobachtungen,
Koordinatensysteme und GPS Koordinatensysteme und GPS Koordinatensysteme: Definition Ein Koordinatensystem ist ein Bezugssystem, mit dem die Positionen von geographischen Features, Bildern und Beobachtungen,
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.4 2013/06/24 23:05:24 hk Exp hk $ 5 Sphärische Trigonometrie 5.2 Sphärische Dreiecksberechnung Wir behandeln gerade die Berechnung sphärischer Dreiecke und haben zu diesem Zweck bereits
$Id: sphaere.tex,v 1.4 2013/06/24 23:05:24 hk Exp hk $ 5 Sphärische Trigonometrie 5.2 Sphärische Dreiecksberechnung Wir behandeln gerade die Berechnung sphärischer Dreiecke und haben zu diesem Zweck bereits
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Kegelschnitte. Evelina Erlacher 13. & 14. M arz 2007
 Workshops zur VO Einfu hrung in das mathematische Arbeiten im SS 2007 Kegelschnitte Evelina Erlacher 13. & 14. M arz 2007 Denken wir uns einen Drehkegel, der nach oben als auch nach unten unbegrenzt ist.
Workshops zur VO Einfu hrung in das mathematische Arbeiten im SS 2007 Kegelschnitte Evelina Erlacher 13. & 14. M arz 2007 Denken wir uns einen Drehkegel, der nach oben als auch nach unten unbegrenzt ist.
Schriftliche Prüfung
 Maximale Punktzahl: 100 Name: Note: Ausgegeben: 26.Mai 2004-13.30 Uhr Abgegeben: 26.Mai 2004 - Uhr Prüfungsfach Aufgabenstellung: Die in den Anlagen 1-13 enthaltenen Aufgaben 1-13 sind zu lösen. Lösungsfrist:
Maximale Punktzahl: 100 Name: Note: Ausgegeben: 26.Mai 2004-13.30 Uhr Abgegeben: 26.Mai 2004 - Uhr Prüfungsfach Aufgabenstellung: Die in den Anlagen 1-13 enthaltenen Aufgaben 1-13 sind zu lösen. Lösungsfrist:
Kartenkunde und GPS Teil 1. Pfadfinder Siedlung Hallimasch
 Kartenkunde und GPS Teil 1 Pfadfinder Siedlung Hallimasch Karte was ist das? Karten sind verkleinerte vereinfachte inhaltlich ergänzte und erläuterte Grundrissbilder der Erdoberfläche oder Teilen davon
Kartenkunde und GPS Teil 1 Pfadfinder Siedlung Hallimasch Karte was ist das? Karten sind verkleinerte vereinfachte inhaltlich ergänzte und erläuterte Grundrissbilder der Erdoberfläche oder Teilen davon
Vorschlag informeller Test zu den Themen Die Grundlagen der Erde sowie Orientierung und Karten
 Vorschlag informeller Test zu den Themen Die Grundlagen der Erde sowie Orientierung und Karten Ziele Erklären können, warum es Tag und Nacht gibt Die Drehbewegungen der Erde erläutern können Über das Gradnetz
Vorschlag informeller Test zu den Themen Die Grundlagen der Erde sowie Orientierung und Karten Ziele Erklären können, warum es Tag und Nacht gibt Die Drehbewegungen der Erde erläutern können Über das Gradnetz
4.15 Buch I der Elemente
 4.15 Buch I der Elemente Das erste Buch der Elemente beginnt mit 23 Definitionen, 5 Postulate und einige Axiomen (von denen man in späteren Ausgaben bis zu 9 findet). Die ersten fünf Definitionen lauten
4.15 Buch I der Elemente Das erste Buch der Elemente beginnt mit 23 Definitionen, 5 Postulate und einige Axiomen (von denen man in späteren Ausgaben bis zu 9 findet). Die ersten fünf Definitionen lauten
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.15 2016/07/08 13:57:53 hk Exp $ 5 Sphärische Trigonometrie 5.3 Kleinkreise als sphärische Kreise In der letzten Sitzung hatten wir eingesehen das die sphärischen Kreise auf einer Sphäre
$Id: sphaere.tex,v 1.15 2016/07/08 13:57:53 hk Exp $ 5 Sphärische Trigonometrie 5.3 Kleinkreise als sphärische Kreise In der letzten Sitzung hatten wir eingesehen das die sphärischen Kreise auf einer Sphäre
Die Quadratur des Kreises
 Die Quadratur des Kreises Häufig hört man Leute sagen, vor allem wenn sie vor großen Schwierigkeiten stehen, so was wie hier wird die Quadratur des Kreises versucht. Was ist mit dieser Redewendung gemeint?
Die Quadratur des Kreises Häufig hört man Leute sagen, vor allem wenn sie vor großen Schwierigkeiten stehen, so was wie hier wird die Quadratur des Kreises versucht. Was ist mit dieser Redewendung gemeint?
Jenseits von Mercator
 Jenseits von Mercator über die Probleme, die Erde in ein Quadrat zu pressen, Salzburg 1 Jenseits von Mercator 2 Jenseits von Mercator 3 Jenseits von Mercator Beispiele von Kartendiensten, die nur Mercator
Jenseits von Mercator über die Probleme, die Erde in ein Quadrat zu pressen, Salzburg 1 Jenseits von Mercator 2 Jenseits von Mercator 3 Jenseits von Mercator Beispiele von Kartendiensten, die nur Mercator
Rotation eines Punktes um eine Achse allgemeiner Lage
 Rotation eines Punktes um eine chse allgemeiner Lage Es gibt eine allgemein, in der arstellenden Geometrie übliche Methode, dieses eispiele zu lösen: 1) chse in Wahrer Größe darstellen - ein weiterer Seitenriss
Rotation eines Punktes um eine chse allgemeiner Lage Es gibt eine allgemein, in der arstellenden Geometrie übliche Methode, dieses eispiele zu lösen: 1) chse in Wahrer Größe darstellen - ein weiterer Seitenriss
x2. Sphärische Trigonometrie Ein sphärisches Dreieck wird durch 3 Grössen bestimmt. Das Ziel der sphärischen Trigonometrie ist es, Beziehungen zwische
 Kapitel II Sphärische Geometrie x1. Sphärische Dreiecke Die 2-dimensionale (Einheit-)Sphäre ist die Fläche S 2 Φ P 2 R 3 jj! OPj 1 Ψ : Zwei Punkte A; B 2 S 2, welche verschieden und nicht antipodal sind,
Kapitel II Sphärische Geometrie x1. Sphärische Dreiecke Die 2-dimensionale (Einheit-)Sphäre ist die Fläche S 2 Φ P 2 R 3 jj! OPj 1 Ψ : Zwei Punkte A; B 2 S 2, welche verschieden und nicht antipodal sind,
kommt zur Kreisinversion eine Spiegelung des Punktes an der reellen Achse dazu. Die folgenden vier Eigenschaften gelten auch für diese Abbildung
 1 3. Die Kreisinversion 3.1. Definition Die Abbildung 1 ordnet der Zahl das folgende Bild zu 1 1 1 1 1 Die Konstruktion des Bildpunkts besteht also aus zwei Schritten: Der Punkt wird in den Bildpunkt abgebildet,
1 3. Die Kreisinversion 3.1. Definition Die Abbildung 1 ordnet der Zahl das folgende Bild zu 1 1 1 1 1 Die Konstruktion des Bildpunkts besteht also aus zwei Schritten: Der Punkt wird in den Bildpunkt abgebildet,
