Symmetrien und Pflasterungen
|
|
|
- Jan Albert
- vor 7 Jahren
- Abrufe
Transkript
1 Symmetrien und Pflasterungen
2 2 Dies ist die ausformulierte Fassung meines Vortrags Symmetrien und Pflasterungen vom 7. Februar 2007 am Tag der offenen Tür an der Universität Mainz.
3 Symmetrien Jeder von Ihnen hat eine intuitive Vorstellung von Symmetrie. In der Natur z.b. haben eine Schneeflocke und auch eine Sonnenblume eine gewisse Symmetrie. Drehen wir die Schneeflocke von einem imaginären Mittelpunkt aus um 60 Grad, dann sieht das Bild genauso wie vorher. Das gleiche gilt für die Sonnenblume. Mathematisch bedeutet das, wir haben eine Transformation angewendet, die das Objekt in sich selbt abgebildet hat. Beispiele von solchen Transformationen sind: Drehungen, Translationen (Verschiebungen) und Spiegelungen. Die Gesamtheit aller Transformationen, die die Schneeflocke (oder die Sonnenblume) auf sich selbst abbilden, heißen Symmetriegruppe der Schneeflocke (bzw. der Sonnenblume). Hier haben wir also zwei mathematische Begriffe: einmal der Begriff der Symmetrie und einmal der Begriff der Gruppe. Diese beiden Begriffe gehen zurück auf die Mathematiker Felix Klein und Èvariste Galois. Felix Klein wurde im 1849 in Düsseldorf geboren und nach seinem Studium der mathematik in Bonn wurde er im Alter von 23 Jahren Professor zuerst in Erlangen und anschließend in Göttingen. In seinem bekannten Erlanger Programm (anlässlich seiner Antrittsvorlesung in Erlangen) vom Jahr 1872 schlägt er eine neue Betrachtung der Geometrie vor, indem er sie als die Gesamtheit der Eigenschaften beschreibt, welche sich bei den Transformationen einer bestimmten Gruppe nicht ändern. Um also Geometrie zu betreiben, braucht man nicht nur Objekte sondern auch Transformationen. Insbesondere in dieser Idee von Klein findet man den Begriff der Symmetrie und der Transformation. Diese beiden Begriffen werden zusammengefasst in dem Begriff der Gruppe. Der Begriff der Gruppe wurde bereits 50 Jahre vor dem Erlanger Programm von dem französischen Mathematiker Èvariste Galois entwickelt, als er die Lösungen von Polynomialgleichungen studierte. Galois lebte in einer unruhigen Zeit und führte ein kurzes, abenteuerliches Leben wurde er bei einem Duell lebensgefährlich verletzt und starb im Alter von 21 Jahren. Seine mathematischen Entdeckungen gerieten für lange Zeit im Vergessenhait und ihre weitreichende Bedeutung wurde erst viel später verstanden. Wir wollen uns nun klar machen, was eine Gruppe ist und insbesondere die Gruppe der Transformationen der Ebene betrachten. Gruppen Betrachten wir einen Kreis K. Die Transformationen, die K invariant lassen, sind 1) Drehungen um einen beliebigen Winkel (K hat Drehsymmetrie). 2) Spiegelungen um einen beliebigen Durchmesser (K hat Spiegelsymmetrie). Dann ist die Symmetriegruppe des Kreises die Gesamtheit aller Transformationen, die man durch Kombinieren von 1) und 2) bekommt. Betrachten wir die Eigenschaften dieser Symmetriegruppe näher (wir werden auch gleich verstehen, warum sie Gruppe heisst): Sei D eine Drehung und S eine Spiegelung des Kreises. Wir schreiben D(P) = Q, als Notation, dass nach der Drehung D der Punkt P nach Q gewandert ist. Für eine Spiegelung schreiben wir S(P) = P. Wenn wir jetzt zuerst D dann S anwenden, bekommen wir eine neue Transformation des Kreises und wir schreiben: (S D)(P) = S(D(P)) = S(Q) = Q 3
4 4 Diese Operation heißt Komposition und hat viele Eigenschaften: 1) Sie ist assoziativ: Sei W eine weitere Transformation, dann (S D) W = S (D W) (d.h es ergibt sich das gleiche Ergebnis, wenn man zuerst W und dann S D ausführt oder zuerst (D W) und dann S). 2) Diese Operation hat ein neutrales Element, d.h. ein Element, das nichts verändert, z. B. die Nulldrehung. Man bezeichnet es mit I, dann gilt für jede Transformation D: D I = I D = D. 3) Jede Transformation hat eine Inverse, wenn man z. B. die Drehung D anwendet, kann man auch dann zurückkommen, wenn man in der anderen Richtung dreht. Diese Transformation heißt D 1 und es gilt offensichtlich: D 1 D = D D 1 = I Diese drei Eigenschaften hat auch (Z, +) aber nicht (Z, ); 1) und 2) gelten noch aber nur 1 und 1 haben eine Inverse bezüglich der Multiplikation, also gilt 3) nicht mehr. Wir können jetzt die genaue Definition von Mengen formulieren, die die Eigenschaften 1), 2) und 3) haben. Eine Gruppe ist eine nicht-leere Menge mit einer Operation, mit den folgenden Eigenschaften: Für x, y, z G gilt (x y) z = x (y z) (Assoziativität). Es gibt ein Element e in G mit e x = x e = x für alle x in G (neutrales Element). Zu jedem Element x aus G gibt es ein Element y mit x y = y x = e (inverses Element zu x). Diese Beschreibung ist sehr wichtig, denn wir können Eigenschaften zeigen, die für alle Gruppen wahr sind, und wir brauchen nicht mehr zu unterscheiden, ob wir an die Symmetriegruppe eines Kreises oder ob wir an (Z, +) denken. Zum Beispiel kann man zeigen, dass das neutrale Element sowie die Inverse eines Elements eindeutig ist. Betrachten wir jetzt die Transformationen der euklidischen Ebenen. Solche Transformationen lassen Abstände, Winkel, Flächen invariant und sind: 1) Translationen, 2) Drehungen, 3) Spiegelungen, 4) Gleitspiegelungen (das ist eine Spiegelung gefolgt von einer Translation in Richtung der Spiegelachse). Diese Transformationen bilden eine Gruppe und sind sehr wichtig, z.b. wenn wir die Symmetriegruppe von Pflasterungen untersuchen.
5 Pflasterungen Jeder von Ihnen kennt Pflasterungen, z.b. Wege im Garten sind gepflastert, Fußboden in Wohnungen (z.b. im Badezimmer), in der Kunst gibt es Pflasterungen (z.b. in dem schönen Bild von dem holländischen Künstler M.C. Escher ( )), usw. 5 Nehmen wir eine einfache Pflasterung, z.b. eine Pflasterung wie man sie oft in Badezimmern oder in Schwimmbäder finden kann, d.h. eine Pflasterung mit regulären Sechsecken, und untersuchen wir ihre Symmetrien, d.h die Transformationen der Ebene, die sie auf sich selbst abbilden. Es gibt Translationen in verschiedene Richtungen, die einen Stein auf einem anderen Stein abbilden, und ihre Komposition ist auch eine Symmetrie der Pflasterung. Nennen wir jetzt die obige Pflasterung τ, dann schreiben wir S(τ) für die Menge aller Symmetrien. Wenn man die Eigenschaften der Komposition studiert, dann entdeckt man, dass S(τ) mit der Komposition eine Gruppe bildet (genauer gesagt ist sie eine Untergruppe der Gruppe der Transformationen der euklidischen Ebene). Wir haben gerade eine Pflasterung mit regulären Sechsecken gesehen. Die Ebene kann man auch mit regulären Dreiecken und Vierecken pflastern (allerdings nicht mit Fünfecken und mit anderen regulären Polygonen). Es gibt einige natürliche Fragen die vorkommen: 1) Wieviele Möglichkeiten gibt es, um eine Ebene zu pflastern? 2) Mit welchen Steinen? 2) Welche sind die Symmetriegruppen, die dabei auftreten können? Die Antwort zu 1) ist natürlich unendlich, aber wir wollen die Frage genauer formulieren. Was wir oft in unserer Umgebung sehen, sind reguläre Pflasterungen wie τ, die Pflasterung mit den Sechsecken. So definieren wir: Eine Pflasterung oder Parkettierung ist eine Überdeckung der euklidischen Ebene mit Parkettsteinen (oder einfach Steine), die sich nicht überlappen (z.b. τ ist eine Pflasterung). Eine Symmetrie der Parkettierung (ich werde ab jetzt beide Wörter benutzen) ist eine Transformation der euklidischen Ebene, die das Parkett auf sich selbst abbildet. Ein Parkett heißt regulär, falls die Steine alle gleich sind, und es für jedes Paar von
6 6 Parkettsteinen eine Transformation gibt, die einen Stein auf den anderen abbildet. Bei einer genauen Untersuchung stellt sich heraus, dass die Symmetriegruppe einer solchen Parkettierung immer Translationen in zwei Richtungen enthält. Wenn man alle solche Gruppen studiert, dann findet man, dass die möglichen Symmetriegruppen nur 17 sind. In diesem Sinn gibt es nur 17 verschiedene mögliche reguläre Parkettierungen der Ebene. Man kann statt Parkettierungen Tapetenmuster betrachten, d.h. wir nehmen ein Muster aus einem Bereich (z.b aus einem Stein einer regulären Parkettierung) und wiederholen das Muster um die ganze Ebene auszufüllen. Die möglichen Symmetriegruppen sind wieder die gleichen 17 wie vorher und zu jeder dieser Gruppe gibt es ein Muster. Man kann 13 von diesen Mustern in der muslimischen Alhambra- Zitadelle (13-14 Jahrhundert) in Granada in Spanien sehen. Da in der muslimischen Kunst keine lebenden Wesen dargestellt werden können, würde die Zitadelle mit sehr komplizierten und schönen Mustern verziert, und man findet darunter die 13 erwähnten Muster. Ähnliche Muster findet man auch in der Kunst z.b. bei dem holländischen Künstler M.C. Escher: wieder gibt es ein Muster, das sich wiederholt. Die Idee hier ist, Steine zu betrachten, die die Ebene regulär parkettieren. Indem man die Form der Steine verändert entstehen diese faszinierenden Bilder. Kehren wir aber zurück zu Parkettierungen. Wir haben Parkettierungen nur mit einem Stein gesehen, aber natürlich kann man Parkettierungen mit mehreren Steine betrachten. Wenn ein bestimmtes Muster sich wiederholt, sprechen wir von periodischen Parkettierungen. In diesem Fall enthält die Symmetriegruppe Translationen in zwei verschiedene Richtungen und die Parkettierung ist translationsinvariant, d.h. es gibt eine Translation, die einen Bereich zu einem anderen Bereich führt. Wieder gibt es nur 17 mögliche Symmetriegruppen (die gleichen wie vorher). Wenn es in der Symmetriegruppe keine Translationen gibt, dann haben wir eine aperiodische Parkettierung.
7 Aperiodische Parkettierungen Das Problem der aperiodischen Parkettierungen ist relativ jung. Die Mathematiker haben für lange Zeit gedacht, dass keine Steine existieren, die die Ebene nur aperiodisch parkettieren können. In den 60-er Jahren stellte sich heraus, dass diese Idee falsch war. Die ersten aperiodischen Parkettierungen enthielten sehr viele Steine (etwa !), dann wurde diese Anzahl reduziert. Im Jahr 1973 fand der englische Mathematiker und Physiker Roger Penrose (er ist bekannt für seine Ergebnisse in der Relativitätstheorie und der Quantummechanik) eine Menge von sechs Steine, die er später zu vier Steinen reduzierte (das Bild auf der Titelseite ist eine Penrose- Pflasterung mit vier Steinen). Später im Jahr 1974 entdeckte er zwei Steine, mit denen man die Ebene aperiodisch parkettieren kann, die sogenannten Kite (=Drache) und Dart (=Pfeil). Man bekommt sie, in dem man die lange Diagonale einer Raute im Verhältnis φ : 1 zerlegt, mit φ = 1+ 5 (der goldene Schnitt). Verbindet 2 man den Punkt, der dadurch entsteht, mit dem stumpfen Winkel der Raute (wie im Bild) so bekommt man die Steine von Penrose: Drache und Pfeil. Um eine aperiodische Pflasterung zu bekommen, darf man Drache und Pfeil nicht so nebeneinander legen, dass sie die Raute wiedergeben (sie pflastert die Ebene natürlich periodisch) aber es gibt andere Regeln. Malt man Kreisbögen von verschiedenen Farben auf dem Drachen und auf dem Pfeil, die die Seiten im Verhältnis φ : 1 zerlegen, (wie im Bild), dann darf man die Steine so nebeneinander legen, dass die Bögen gleicher Farbe fortgesetzt werden, so bekommt man ein Muster von Penrose und hier sehen wir ein Beispiel der Stern-Pflasterung. 7 Die Penrose Pflasterungen sind unendlich viele (unabzählbar viele, also sind sie genauso viele wie die reellen Zahlen) und haben viele interessante und erstaunliche Eigenschaften:
8 8 1) Jeder Bereich einer Pflasterung ist in jeder anderen Pflasterung unendlich viele Male enthalten. 2) Keine besondere Kombination von Steinen erzwingt, dass es sich um eine bestimmte Pflasterung handelt. 3) Einen kreisformigen Bereich vom Durchmesser d kann man spätestens nach einem Abstand 2d wiederfinden. Im Bild können Sie sich von der letzten Eigenschaft überzeugen. Wenn man Penrose-Pflasterungen näher studiert, entdeckt man, wenn man der Regel folgt und man die möglichen Winkeln untersucht, dass es nur sieben Möglichkeiten gibt, um um einer Ecke Drache und Pfeil zu kombinieren. Da die Drachenschwänzen 72 Grad haben und die Pfeilspitzen auch 72 Grad betragen, passen fünf Drachen oder fünf Pfeile um eine Ecke (die Regeln sind auch erfüllt) und so bekommen wir die Sonne (fünf Drachen) und den Stern (fünf Pfeile). Dann gibt es andere mögliche Kombinationen der Winkel (unter der Bedingung, dass die Regeln von Penrose erfüllt werden): man bekommt das Ass (zwei Drachen und ein Pfeil), den Teufel (zwei Pfeile und zwei Drachen), den Bube (drei Drachen und zwei Pfeile), die Königin (vier Drachen und ein Pfeil), den König (zwei Drachen und drei Pfeile). Durch Kombinationen dieser Figuren kann man die Ebene aperiodisch (und nur aperiodisch, wenn man die Regeln folgt) parkettieren. Man hat untersucht, welche Parkettierungen möglich sind, wenn man mit einer diesen Figuren anfängt. Keine von Ihnen erzwingt eine besondere Parkettierung, aber wenn man pentagonale Symmetrie erreichen will (d.h. die Parkettierung ist invariant für Drehungen um 72 Grad) dann gibt es für die Sonne und den Stern jeweils nur eine Möglichkeit, die sogenannten Sonne- und Stern-Pflasterung. Diese zwei Pflasterungen haben eine weitere schöne Eigenschaft: man kann von einer zur anderen durch die Methode der Inflation und Deflation gehen. Diese Methode besteht daraus, aus kleineren Drachen und Pfeilen grössere zu basteln (Inflation) und umgekehrt (Deflation). Im Bild sehen wir es für die Sonne- und Stern-Pflasterung.
9 9 Dieses Verfahren erlaubt auch, aus einer Pflasterung weitere Pflasterungen zu erhalten, und da man es unendlich oft anwenden kann, zeigt sich wieder die Eigenschaft, dass die Penrose Pflasterungen unendlich viele sind und unabzählbar. Eine andere besonders schöne Penrose-Pflasterung ist das Rad: In der Mitte haben wir (rotmarkiert) ein 10-Eck, das eine Figur enthält: die Fledermaus (fünf Drachen und fünf Pfeile). Ausserhalb des roten Bereichs und der Speichen, hat die Pflasterung eine perfekte 10-fache Symmetrie.
10 10 Hoffentlich habe ich Sie überzeugen können, dass die Penrose-Pflasterungen und allgemein aperiodische Pflasterungen ein sehr spannendes Thema der Mathematik sind. Es gibt noch heute viele offene Fragen darüber, z.b.: 1) Kann man nur mit einem Stein die Ebene aperiodisch parkettieren? 2) Gibt es Steine, mit denen man die Ebene parkettieren kann und die mit anderen irrationalen Zahlen zu tun haben? Die erste Frage ist noch ohne Antwort. Bei der zweiten Frage hat der Mathematiker Ammann im Jahr 1977 Pflasterungen mit Steinen gefunden, die mit der Zahl 2 zu tun haben, aber es ist nicht klar, welche anderen irrationalen Zahlen möglich sind. Ich werde hier mit einer lustigen Pflasterung von Penrose schließen. Wir haben schon die schönen Bilder von Escher gesehen, die er durch Deformation von Steinen von periodischen Pflasterungen bekommt. Leider ist Escher im Jahr 1972 gestorben, bevor Penrose seine Steine entdeckte, sonst hätte er bestimmt schöne Bilder mit diesen Steinen produziert. Penrose ist der Idee von Escher gefolgt und durch Deformationen hat er besonders schöne Pflasterungen bekommen z.b. seine aperiodischen Hühner sind deformierte Pfeilen und Drachen! Literatur [BW] H.-G. Bigalke, H. Wippermann, Reguläre Parkettierungen, Wissenschaftsverlag [D] K. Devlin, Muster der Mathematik, Spektrum Akademischer Verlag [G] M. Gardner, Extraordinary nonperiodic tiling that enriches the theory of tiles, Mathematical Games, Scientific American Vol. 236, Januar 1977, pp [GS] B. Grünbaum, G.C. Shephard, Tilings and patterns, W.H. Freemann and Company New York [MSW] D. Mumford, C. Series, D. Wright, Indra s Pearls, the vision of Felix Klein, Cambridge University Press [S] M. Senechal, Quasicrystals and geometry, Cambridge University Press 1995.
Symmetrien und Pflasterungen. Alessandra Sarti Universität Mainz
 Symmetrien und Pflasterungen Alessandra Sarti Universität Mainz Symmetrien Schneeflocken und Sonnenblumen haben viele Symmetrien. Die Gesamtheit aller Transformationen, die eine Schneeflocke (oder eine
Symmetrien und Pflasterungen Alessandra Sarti Universität Mainz Symmetrien Schneeflocken und Sonnenblumen haben viele Symmetrien. Die Gesamtheit aller Transformationen, die eine Schneeflocke (oder eine
Deckabbildungen, Ornamente und Parkettierungen
 27. November 2014 Inhaltsverzeichnis Begrisklärung 1 Begrisklärung 2 3 4 5 6 Deckabbildungen Begrisklärung Deckabbildungen Ornamente Parkettierung Denition Sei h eine Kongruenzabbildung der Ebene E und
27. November 2014 Inhaltsverzeichnis Begrisklärung 1 Begrisklärung 2 3 4 5 6 Deckabbildungen Begrisklärung Deckabbildungen Ornamente Parkettierung Denition Sei h eine Kongruenzabbildung der Ebene E und
Penrose-Parkettierungen
 Penrose-Parkettierungen Daniel Fauser, Clara Löh In diesem Workshop werden wir Penrose-Parkettierungen kennenlernen: Die Penrose-Puzzleteile haben die Eigenheit, dass man mit ihnen die Ebene zwar lückenlos
Penrose-Parkettierungen Daniel Fauser, Clara Löh In diesem Workshop werden wir Penrose-Parkettierungen kennenlernen: Die Penrose-Puzzleteile haben die Eigenheit, dass man mit ihnen die Ebene zwar lückenlos
Escher s Wallpapers. Sophia Lee, Martin Swiontek Brzezinski. 8. April TU Berlin
 Sophia Lee Martin Swiontek Brzezinski TU Berlin 8. April 2014 Übersicht Einführung 1 Einführung 2 3 Kurzbiographie Maurits Cornelis Escher 17.06.1898 in Leeuwarden 1919: 1-wöchiges Architektur-Studium
Sophia Lee Martin Swiontek Brzezinski TU Berlin 8. April 2014 Übersicht Einführung 1 Einführung 2 3 Kurzbiographie Maurits Cornelis Escher 17.06.1898 in Leeuwarden 1919: 1-wöchiges Architektur-Studium
Gegenstände der Geometrie
 Gegenstände der Geometrie Inhalt Quadrat Kreis Würfel Das Das Pentagramm Parkette --- --- Seite 2 1. 1. Das Quadrat Gerade Linien in in der der Natur? Lichtstrahlen, fallende Körper, Wasseroberfläche,
Gegenstände der Geometrie Inhalt Quadrat Kreis Würfel Das Das Pentagramm Parkette --- --- Seite 2 1. 1. Das Quadrat Gerade Linien in in der der Natur? Lichtstrahlen, fallende Körper, Wasseroberfläche,
Friesmuster in der Mathematik
 Friesmuster in der Mathematik Karin Baur Karl-Franzens-Universität Graz 7. Februar 03 Karin Baur (Karl-Franzens-Universität Graz) Friesmuster in der Mathematik 7. Februar 03 / 6 Muster I Muster Friese
Friesmuster in der Mathematik Karin Baur Karl-Franzens-Universität Graz 7. Februar 03 Karin Baur (Karl-Franzens-Universität Graz) Friesmuster in der Mathematik 7. Februar 03 / 6 Muster I Muster Friese
1 Goldener Schnitt. und a = m + M. 1, und wird im Allgemeinen mit τ (griechisch: tau) bezeichnet. Das Verhältnis M m hat den Wert 1+ 5
 1 Goldener Schnitt Definition und Satz 1.1 (Goldener Schnitt) Sei AB die Strecke zwischen den Punkten A und B. Ein Punkt S von AB teilt AB im Goldenen Schnitt, falls sich die größere Teilstrecke M (Major)
1 Goldener Schnitt Definition und Satz 1.1 (Goldener Schnitt) Sei AB die Strecke zwischen den Punkten A und B. Ein Punkt S von AB teilt AB im Goldenen Schnitt, falls sich die größere Teilstrecke M (Major)
Escher-Parkette. oder. Regelmäßige Flächenaufteilungen
 Escher-Parkette oder Regelmäßige Flächenaufteilungen Parkette Parkettstein: zunächst beliebige Teilmenge der Ebene, die sich durch umkehrbare und stetige Deformation aus einer abgeschlossenen Kreisscheibe
Escher-Parkette oder Regelmäßige Flächenaufteilungen Parkette Parkettstein: zunächst beliebige Teilmenge der Ebene, die sich durch umkehrbare und stetige Deformation aus einer abgeschlossenen Kreisscheibe
Angewandte Mathematik am Rechner 2 WINTERSEMESTER 2017/18 *#$?!! Kapitel 5. Symmetrie. Michael Wand Institut für Informatik.
 Michael Wand Institut für Informatik. Angewandte Mathematik am Rechner 2 WINTERSEMESTER 2017/18 *#$?!! Kapitel 5 Symmetrie Symmetrie Geometrische Symmetrie Beispiele Symmetrische geometrische Objekte (2D)
Michael Wand Institut für Informatik. Angewandte Mathematik am Rechner 2 WINTERSEMESTER 2017/18 *#$?!! Kapitel 5 Symmetrie Symmetrie Geometrische Symmetrie Beispiele Symmetrische geometrische Objekte (2D)
3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen
 TEIL II: GRUPPEN In der modernen Algebra versucht man die Zahlen (Z, Q, R, ) durch die Konzentration auf Rechenoperationen (+,,... ), oder allgemeiner auf strukturelle Eigenschaften dieser Operationen,
TEIL II: GRUPPEN In der modernen Algebra versucht man die Zahlen (Z, Q, R, ) durch die Konzentration auf Rechenoperationen (+,,... ), oder allgemeiner auf strukturelle Eigenschaften dieser Operationen,
3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen
 Inhaltsverzeichnis Teil II: Gruppen 2 3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen.................. 2 3.1.1 Gruppen.......................................... 2 3.1.2 Untergruppen.......................................
Inhaltsverzeichnis Teil II: Gruppen 2 3.1 Gruppen, Untergruppen und Gruppen-Homomorphismen.................. 2 3.1.1 Gruppen.......................................... 2 3.1.2 Untergruppen.......................................
D-MATH Tommaso Goldhirsch. Serie 3
 Serie 3 Aufgabe 1 Sei G eine Gruppe und X eine Teilmenge von G. Die von X erzeugte Untergruppe von G ist die kleinste Untergruppe von G die X enthält. (Dass es eindeutig eine "kleinste" gibt wird in der
Serie 3 Aufgabe 1 Sei G eine Gruppe und X eine Teilmenge von G. Die von X erzeugte Untergruppe von G ist die kleinste Untergruppe von G die X enthält. (Dass es eindeutig eine "kleinste" gibt wird in der
Historisches zur Gruppentheorie
 Historisches zur Gruppentheorie Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Gruppen: Abstrakte Definition Eine Gruppe
Historisches zur Gruppentheorie Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Gruppen: Abstrakte Definition Eine Gruppe
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 10.12.2013 Alexander Lytchak 1 / 15 Motivation Für das Verständis affiner Teilräume eines Vektorraums sind Translationen
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 10.12.2013 Alexander Lytchak 1 / 15 Motivation Für das Verständis affiner Teilräume eines Vektorraums sind Translationen
Platonische und archimedische Parkettierungen. Meisterklasse Mathematik Dresden 2016 Olaf Schimmel
 Platonische und archimedische Parkettierungen Meisterklasse Mathematik Dresden 2016 Olaf Schimmel Inhaltsübersicht 1 Was sind Parkettierungen? 2 Warum Winkel wichtig sind 3 Platonische Parkette 4 Archimedische
Platonische und archimedische Parkettierungen Meisterklasse Mathematik Dresden 2016 Olaf Schimmel Inhaltsübersicht 1 Was sind Parkettierungen? 2 Warum Winkel wichtig sind 3 Platonische Parkette 4 Archimedische
Parkettierungen lassen sich auf zweierlei Arten klassifizieren:
 1 Ein bisschen Theorie 1.1 Definition Ein Parkett- oder Pflasterstein ist eine Figur, welche durch eine endlich lange und geschlossene Linie eingeschlossen ist, die sich weder schneidet noch irgendwo zusammenfällt.
1 Ein bisschen Theorie 1.1 Definition Ein Parkett- oder Pflasterstein ist eine Figur, welche durch eine endlich lange und geschlossene Linie eingeschlossen ist, die sich weder schneidet noch irgendwo zusammenfällt.
Symmetrie von Ornamenten
 Symmetrie von Ornamenten Teilnehmer: Theresa Lechner Alexey Loutchko Dennis Menge Simon Reinke Fynn Strohecker Thimo Wellner Gruppenleiter: Jürg Kramer Anna v. Pippich Gymnasium Ernestinum, Coburg Heinrich-Hertz-Oberschule,
Symmetrie von Ornamenten Teilnehmer: Theresa Lechner Alexey Loutchko Dennis Menge Simon Reinke Fynn Strohecker Thimo Wellner Gruppenleiter: Jürg Kramer Anna v. Pippich Gymnasium Ernestinum, Coburg Heinrich-Hertz-Oberschule,
Symmetrien erzeugen Muster und Zerlegungen Stephan Rosebrock
 Symmetrien erzeugen Zerlegungen S. Rosebrock Seite 1 Symmetrien erzeugen Muster und Zerlegungen Stephan Rosebrock Zusätzliches Material zum Artikel in MU Auf dem Foto sieht man zwei im 45 Grad Winkel zueinander
Symmetrien erzeugen Zerlegungen S. Rosebrock Seite 1 Symmetrien erzeugen Muster und Zerlegungen Stephan Rosebrock Zusätzliches Material zum Artikel in MU Auf dem Foto sieht man zwei im 45 Grad Winkel zueinander
Penrose- Parkett Pfeil und Drachen Markus Wurster
 Penrose- Parkett Pfeil und Drachen Markus Wurster Inhalt Penrose-Parkett mit zwei Formen Pfeil und Drachen... 2 Musterbeispiele... 3 Penrose-Parkett... 6 Pfeil und Drachen... 7 Pfeil und Drachen im Zehneck
Penrose- Parkett Pfeil und Drachen Markus Wurster Inhalt Penrose-Parkett mit zwei Formen Pfeil und Drachen... 2 Musterbeispiele... 3 Penrose-Parkett... 6 Pfeil und Drachen... 7 Pfeil und Drachen im Zehneck
Symmetrie. Wiederholung in der Geometrie. Referat am Kolloquium Wiederholung der Schweiz. Ges. für Symbolforschung. Martin Huber
 Symmetrie Wiederholung in der Geometrie Referat am Kolloquium Wiederholung der Schweiz. Ges. für Symbolforschung Martin Huber Symmetrie Wiederholung in der Geometrie Ablauf 1. Wiederholung in der Mathematik
Symmetrie Wiederholung in der Geometrie Referat am Kolloquium Wiederholung der Schweiz. Ges. für Symbolforschung Martin Huber Symmetrie Wiederholung in der Geometrie Ablauf 1. Wiederholung in der Mathematik
2.6. Aufgaben zu Kongruenzabbildungen
 Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
3. Untergruppen. 3. Untergruppen 23
 3. Untergruppen 23 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
3. Untergruppen 23 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
Escher-Parkettierungen
 Escher-Parkettierungen Manfred Dobrowolski Universität Würzburg Escher-Parkettierungen 1 Maurits Cornelis Escher 2 Symmetrien periodischer Parkettierungen 3 Escher-Parkette 4 Analyse einiger bekannter
Escher-Parkettierungen Manfred Dobrowolski Universität Würzburg Escher-Parkettierungen 1 Maurits Cornelis Escher 2 Symmetrien periodischer Parkettierungen 3 Escher-Parkette 4 Analyse einiger bekannter
Meisterklasse Dresden 2014 Olaf Schimmel
 Meisterklasse Dresden 2014 Olaf Schimmel 1 Was sind Parkettierungen? 2 Warum Winkel wichtig sind 3 Platonische Parkette 4 Archimedische Parkette 5 Welche Kombination von Vielecken erfüllen die Winkelbedingung?
Meisterklasse Dresden 2014 Olaf Schimmel 1 Was sind Parkettierungen? 2 Warum Winkel wichtig sind 3 Platonische Parkette 4 Archimedische Parkette 5 Welche Kombination von Vielecken erfüllen die Winkelbedingung?
Symmetrie als fundamentale Idee
 Symmetrie als fundamentale Idee "Ideen, die starke Bezüge zur Wirklichkeit haben, verschiedene Aspekte und Zugänge aufweisen, sich durch hohen inneren Beziehungsreichtum auszeichnen und in den folgenden
Symmetrie als fundamentale Idee "Ideen, die starke Bezüge zur Wirklichkeit haben, verschiedene Aspekte und Zugänge aufweisen, sich durch hohen inneren Beziehungsreichtum auszeichnen und in den folgenden
(Man sagt dafür auch, dass die Teilmenge U bezüglich der Gruppenoperationen abgeschlossen sein muss.)
 3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
Aufgaben zu Symmetrieoperationen
 Aufgaben zu Symmetrieoperationen Bitte bearbeitet die nachfolgenden Aufgaben innerhalb der nächsten Stunde in kleinen Gruppen. Wenn ihr nicht weiterkommt, überspringt die Aufgabe oder fragt nach Hilfe.
Aufgaben zu Symmetrieoperationen Bitte bearbeitet die nachfolgenden Aufgaben innerhalb der nächsten Stunde in kleinen Gruppen. Wenn ihr nicht weiterkommt, überspringt die Aufgabe oder fragt nach Hilfe.
3.1 Die Gruppe (K,o) aller Kongruenzabbildungen einer Ebene
 Kapitel 3: Deckabbildungen von Figuren - Symmetrie 3.1 Die Gruppe (K,o) aller Kongruenzabbildungen einer Ebene K ist die Menge aller Kongruenzabbildungen E E; o ist die Hintereinanderausführung von Abbildungen
Kapitel 3: Deckabbildungen von Figuren - Symmetrie 3.1 Die Gruppe (K,o) aller Kongruenzabbildungen einer Ebene K ist die Menge aller Kongruenzabbildungen E E; o ist die Hintereinanderausführung von Abbildungen
Musterlösung Serie 3. ITET Diskrete Mathematik WS 02/03 R. Suter. d) Für beliebige a, b G gilt
 ITET Diskrete Mathematik WS 2/3 R. Suter. a) r s = r + )s + ). Assoziativität: Ist erfüllt, denn Musterlösung Serie 3 r s) t = r + )s + ) + ) t + ) = r + )s + )t + ) = r + ) s + )t + ) + ) = r s t) Neutrales
ITET Diskrete Mathematik WS 2/3 R. Suter. a) r s = r + )s + ). Assoziativität: Ist erfüllt, denn Musterlösung Serie 3 r s) t = r + )s + ) + ) t + ) = r + )s + )t + ) = r + ) s + )t + ) + ) = r s t) Neutrales
Universität Bielefeld. Elementare Geometrie. Sommersemester Gruppen, Bewegungen. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Gruppen, Bewegungen Stefan Witzel Gruppen Eine Menge G von Bijektionen X X ist eine Gruppe, wenn 1. die Identität id: X X in G liegt, 2. für
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Gruppen, Bewegungen Stefan Witzel Gruppen Eine Menge G von Bijektionen X X ist eine Gruppe, wenn 1. die Identität id: X X in G liegt, 2. für
Einfache Parkettierungen
 Einfache Definitionen: Unter einer Parkettierung (auch Pflasterung oder Parkett genannt) verstehen wir eine überlappungsfreie Überdeckung der Ebene durch Polygone. Ein Polygon (auch Vieleck oder n-eck
Einfache Definitionen: Unter einer Parkettierung (auch Pflasterung oder Parkett genannt) verstehen wir eine überlappungsfreie Überdeckung der Ebene durch Polygone. Ein Polygon (auch Vieleck oder n-eck
eine O fixierende Bewegung.
 1. Bewegungen der hyperbolischen Ebene Sei nun H eine hyperbolische Ebene. Dann erhält man dieselben Klassen von Bewegungen wie im Euklidischen Fall und eine weitere Klasse. Wir haben oben nur ein einziges
1. Bewegungen der hyperbolischen Ebene Sei nun H eine hyperbolische Ebene. Dann erhält man dieselben Klassen von Bewegungen wie im Euklidischen Fall und eine weitere Klasse. Wir haben oben nur ein einziges
Lösungsvorschläge für die Geometrie-Klausur vom 28.7.
 Lösungsvorschläge für die Geometrie-Klausur vom 28.7. Aufgabe 1: (a) Die beiden Punkte liegen offensichtlich auf der hyperbolischen Geraden g = {z H R(z) = 1}. Die beiden idealen Punkte sind a = 1, b =.
Lösungsvorschläge für die Geometrie-Klausur vom 28.7. Aufgabe 1: (a) Die beiden Punkte liegen offensichtlich auf der hyperbolischen Geraden g = {z H R(z) = 1}. Die beiden idealen Punkte sind a = 1, b =.
Geometrie. Homepage zur Veranstaltung: Lehre Geometrie
 Geometrie 4.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 4.2 Inhaltsverzeichnis Geometrie 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen 3 Längen-,
Geometrie 4.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 4.2 Inhaltsverzeichnis Geometrie 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen 3 Längen-,
Tutorium Mathematik I, M Lösungen
 Tutorium Mathematik I, M Lösungen 9. Oktober 202 *Aufgabe. Ein Fischauge ist ein Objektiv in der Photographie, welches einen sehr großen Bildwinkel (gewöhnlich 80 ) abbilden kann. Hierfür muss das Bild
Tutorium Mathematik I, M Lösungen 9. Oktober 202 *Aufgabe. Ein Fischauge ist ein Objektiv in der Photographie, welches einen sehr großen Bildwinkel (gewöhnlich 80 ) abbilden kann. Hierfür muss das Bild
Universität Bielefeld. Elementare Geometrie. Sommersemester Gruppen, Bewegungen. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Gruppen, Bewegungen Stefan Witzel Gruppen Eine Menge G von Bijektionen X X ist eine Gruppe, wenn 1. die Identität id: X X in G liegt, 2. für
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Gruppen, Bewegungen Stefan Witzel Gruppen Eine Menge G von Bijektionen X X ist eine Gruppe, wenn 1. die Identität id: X X in G liegt, 2. für
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
1.1 Geradenspiegelungen
 1.1 Geradenspiegelungen 1.1.1 Eigenschaften Definition 1.1 Eine Abbildung der Ebene ist eine Vorschrift, die jedem Punkt P der Ebene einen Bildpunkt P zuordnet. Beispiel 1.1 Zentrische Streckung mit Zentrum
1.1 Geradenspiegelungen 1.1.1 Eigenschaften Definition 1.1 Eine Abbildung der Ebene ist eine Vorschrift, die jedem Punkt P der Ebene einen Bildpunkt P zuordnet. Beispiel 1.1 Zentrische Streckung mit Zentrum
1.3 Gruppen. Algebra I 9. April 2008 c Rudolf Scharlau,
 Algebra I 9. April 2008 c Rudolf Scharlau, 2002 2008 18 1.3 Gruppen Der Begriff der Gruppe ordnet sich in gewisser Weise dem allgemeineren Konzept der Verknüpfung (auf einer Menge) unter. So ist zum Beispiel
Algebra I 9. April 2008 c Rudolf Scharlau, 2002 2008 18 1.3 Gruppen Der Begriff der Gruppe ordnet sich in gewisser Weise dem allgemeineren Konzept der Verknüpfung (auf einer Menge) unter. So ist zum Beispiel
GRUPPEN UND RUBIK S WÜRFEL
 GRUPPEN UND RUBIK S WÜRFEL HERBERT KOCH 1. Vorlesung: Notation und Gruppen 1.1. Notation. Der Würfel hat sechs Seiten: Front (vorne), back (hinten), left (links), right (rechts), up (oben) und down (unten).
GRUPPEN UND RUBIK S WÜRFEL HERBERT KOCH 1. Vorlesung: Notation und Gruppen 1.1. Notation. Der Würfel hat sechs Seiten: Front (vorne), back (hinten), left (links), right (rechts), up (oben) und down (unten).
Geometrie der Polygone Konstruktionen Markus Wurster 1
 Geometrie der Polygone Teil 6 Klassische Konstruktionen Geometrie der Polygone Konstruktionen Markus Wurster 1 Sechseck Gegeben ist der Umkreis des Sechsecks Zeichne einen Kreis mit dem gewünschten Radius
Geometrie der Polygone Teil 6 Klassische Konstruktionen Geometrie der Polygone Konstruktionen Markus Wurster 1 Sechseck Gegeben ist der Umkreis des Sechsecks Zeichne einen Kreis mit dem gewünschten Radius
Universität Bielefeld. Elementare Geometrie. Sommersemester Rückblick. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Rückblick Stefan Witzel Outline Grundlagen, Axiome Euklid I Bewegungen Verhältnisse, Ähnlichkeiten Kreise Fundamentale Objekte und Eigenschaften
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Rückblick Stefan Witzel Outline Grundlagen, Axiome Euklid I Bewegungen Verhältnisse, Ähnlichkeiten Kreise Fundamentale Objekte und Eigenschaften
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 8
 Dr. Erwin Schörner Klausurenkurs zum Staatseamen (SS 205): Lineare Algebra und analtische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Dr. Erwin Schörner Klausurenkurs zum Staatseamen (SS 205): Lineare Algebra und analtische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum
 Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Elemente der Mathematik - Winter 2016/2017
 4 Elemente der Mathematik - Winter 2016/2017 Prof. Dr. Peter Koepke, Regula Krapf Lösungen Übungsblatt 7 Aufgabe 29 (8 Punkte). Für eine Menge M ist die Potenzmenge von M definiert als P(M) := {X X M},
4 Elemente der Mathematik - Winter 2016/2017 Prof. Dr. Peter Koepke, Regula Krapf Lösungen Übungsblatt 7 Aufgabe 29 (8 Punkte). Für eine Menge M ist die Potenzmenge von M definiert als P(M) := {X X M},
S T E R N E U N D P O L Y G O N E
 Ornament Stern und Polygon (S. 1 von 11) / www.kunstbrowser.de S T E R N E U N D P O L Y G O N E Polygone und Sterne in regelmäßiger Form sind ein wichtiges Grundmotiv in der Ornamentik, da sie v ielf
Ornament Stern und Polygon (S. 1 von 11) / www.kunstbrowser.de S T E R N E U N D P O L Y G O N E Polygone und Sterne in regelmäßiger Form sind ein wichtiges Grundmotiv in der Ornamentik, da sie v ielf
Symmetrien. Transformationen. Affine und euklidische Räume
 Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Plan für Heute/Morgen
 Plan für Heute/Morgen Kongruenzsätze: aus der Schule wissen wir die SSS, SWS, und SSW Kongruenzsätze für Dreiecke: Wir wollen diese Sätze im Rahmen unseres Modells (wenn Punkte die 2 Tupel von reellen
Plan für Heute/Morgen Kongruenzsätze: aus der Schule wissen wir die SSS, SWS, und SSW Kongruenzsätze für Dreiecke: Wir wollen diese Sätze im Rahmen unseres Modells (wenn Punkte die 2 Tupel von reellen
Universität Bielefeld. Elementare Geometrie. Sommersemester Grundlagen. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Wie misst man Symmetrie?
 Wie misst man Symmetrie? Was ist Symmetrie? Beispiele Bewegungen Friesgruppen Verallgemeinerungen Was ist Symmetrie denn eigentlich? Kann man sie überhaupt messen? Symmetrie = Gleichmaß August Ferdinand
Wie misst man Symmetrie? Was ist Symmetrie? Beispiele Bewegungen Friesgruppen Verallgemeinerungen Was ist Symmetrie denn eigentlich? Kann man sie überhaupt messen? Symmetrie = Gleichmaß August Ferdinand
1 Yin Yang Figur Die Abbildung 1 zeigt das Yin Yang, wie es leibt und lebt. Es ist unter Farbwechsel punktsymmetrisch. Weiter hat es keine Symmetrien.
 Hans Walser, [20130505] Yin Yang Eine nostalgische fraktale Erinnerung. Anregung: Strick (2013) 1 Yin Yang Figur Die Abbildung 1 zeigt das Yin Yang, wie es leibt und lebt. Abb. 1: Yin Yang Es ist unter
Hans Walser, [20130505] Yin Yang Eine nostalgische fraktale Erinnerung. Anregung: Strick (2013) 1 Yin Yang Figur Die Abbildung 1 zeigt das Yin Yang, wie es leibt und lebt. Abb. 1: Yin Yang Es ist unter
D-MATH Tommaso Goldhirsch. Serie 2. Man bezeichnet dies als Assoziativität der Verknüpfung von Abbildungen.
 Serie 2 Aufgabe 1 Es seien ψ 1, ψ 2 und ψ Abbildungen von einer Menge E auf sich selbst. Zeigen Sie, dass die Assoziativität gilt: (ψ 1 ψ 2 ) ψ = ψ 1 (ψ 2 ψ ). Wir zeigen, dass die Abbildungen (ψ 1 ψ 2
Serie 2 Aufgabe 1 Es seien ψ 1, ψ 2 und ψ Abbildungen von einer Menge E auf sich selbst. Zeigen Sie, dass die Assoziativität gilt: (ψ 1 ψ 2 ) ψ = ψ 1 (ψ 2 ψ ). Wir zeigen, dass die Abbildungen (ψ 1 ψ 2
Programm des Hauptseminars Symmetrie
 Programm des Hauptseminars Symmetrie Prof. Dr. Irene Bouw Universität Ulm Institut für Reine Mathematik SS 2008 irene.bouw at uni-ulm.de Vortrag 1: Einführung (2 Personen) Dieser Vortrag soll eine Einführung
Programm des Hauptseminars Symmetrie Prof. Dr. Irene Bouw Universität Ulm Institut für Reine Mathematik SS 2008 irene.bouw at uni-ulm.de Vortrag 1: Einführung (2 Personen) Dieser Vortrag soll eine Einführung
Universität Bielefeld. Elementare Geometrie. Sommersemester Grundlagen. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Trigonometrie. In der Abbildung: der Winkel 120 (Gradenmaß) ist 2π = 2π (Bogenmaß).
 Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
2. Platonische Körper
 2 Platonische Körper 27 2. Platonische Körper Dieses Kapitel legt den Schwerpunkt auf die Geometrie. Geometrie in der Grundschule befasst sich mit zwei zentralen Gebieten: Symmetrie und Raumvorstellung.
2 Platonische Körper 27 2. Platonische Körper Dieses Kapitel legt den Schwerpunkt auf die Geometrie. Geometrie in der Grundschule befasst sich mit zwei zentralen Gebieten: Symmetrie und Raumvorstellung.
Waben-Sudoku. Günter Aumann und Klaus Spitzmüller. Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen.
 Waben-Sudoku Günter Aumann und Klaus Spitzmüller Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen. Eine Vorüberlegung Reguläre Vierecke und Sechsecke zeichnen sich vor allen anderen
Waben-Sudoku Günter Aumann und Klaus Spitzmüller Sudoku ist in. Oder ist es schon wieder langweilig? Es gibt Alternativen. Eine Vorüberlegung Reguläre Vierecke und Sechsecke zeichnen sich vor allen anderen
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF DRDR JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker I (Wintersemester 2003/2004) Aufgabenblatt 3 (7
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF DRDR JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker I (Wintersemester 2003/2004) Aufgabenblatt 3 (7
Muster, Bandornamente und Parkette (1)
 Muster, Bandornamente und Parkette (1) In Mustern, Bandornamenten und Parketten (im Folgenden: Figuren) wird ein Grundelement nach einer gewissen Regel mehrfach arrangiert. Die Regelmäßigkeiten lassen
Muster, Bandornamente und Parkette (1) In Mustern, Bandornamenten und Parketten (im Folgenden: Figuren) wird ein Grundelement nach einer gewissen Regel mehrfach arrangiert. Die Regelmäßigkeiten lassen
Was ist ein Quasikristall? Mathematische Aspekte Stabilität von Quasikristallen Verwendungsmöglichkeiten Quellen. Quasikristalle.
 Quasikristalle Kira Riedl 6. Juli 2011 Gliederung 1 Was ist ein Quasikristall? 2 Mathematische Aspekte 3 Stabilität von Quasikristallen 4 Verwendungsmöglichkeiten 5 Quellen Definition eines Kristalls im
Quasikristalle Kira Riedl 6. Juli 2011 Gliederung 1 Was ist ein Quasikristall? 2 Mathematische Aspekte 3 Stabilität von Quasikristallen 4 Verwendungsmöglichkeiten 5 Quellen Definition eines Kristalls im
Einführung in den Symmetriebegriff und gruppentheoretische Grundlagen
 Einführung in den Symmetriebegriff und gruppentheoretische Grundlagen Stephanie Artmeier WS 0/ Inhaltsverzeichnis Einführung... Gruppen.... Beispiel gleichseitiges Dreieck... 3. Darstellung von Gruppen...
Einführung in den Symmetriebegriff und gruppentheoretische Grundlagen Stephanie Artmeier WS 0/ Inhaltsverzeichnis Einführung... Gruppen.... Beispiel gleichseitiges Dreieck... 3. Darstellung von Gruppen...
DEMO für Verkettung von Kongruenzabbildungen INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. FRIEDRICH W. BUCKEL.
 Abbildungen Verkettung von Kongruenzabbildungen Für Interessenten. Datei Nr. 11059 Stand: 3. Oktober 2013 DEMO für FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 11059 Verkettung von Kongruenzabbildungen
Abbildungen Verkettung von Kongruenzabbildungen Für Interessenten. Datei Nr. 11059 Stand: 3. Oktober 2013 DEMO für FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 11059 Verkettung von Kongruenzabbildungen
Halbgruppen, Gruppen, Ringe
 Halbgruppen-1 Elementare Zahlentheorie Einige Bezeichnungen Halbgruppen, Gruppen, Ringe Die Menge N 0 der natürlichen Zahlen 0, 1, 2, Die Menge N = N 1 der von Null verschiedenen natürlichen Zahlen Die
Halbgruppen-1 Elementare Zahlentheorie Einige Bezeichnungen Halbgruppen, Gruppen, Ringe Die Menge N 0 der natürlichen Zahlen 0, 1, 2, Die Menge N = N 1 der von Null verschiedenen natürlichen Zahlen Die
Semesterklausur zur Elementargeometrie (L) von 60 Punkten bestanden Korrektor
 Technische Universität Berlin Wintersemester 03/04 Fakultät II, Institut für Mathematik Prof. Dr. Ulrich Kortenkamp Sekretariat MA6-2 Andreas Fest Semesterklausur zur Elementargeometrie (L) 06.02.2004
Technische Universität Berlin Wintersemester 03/04 Fakultät II, Institut für Mathematik Prof. Dr. Ulrich Kortenkamp Sekretariat MA6-2 Andreas Fest Semesterklausur zur Elementargeometrie (L) 06.02.2004
Hyperbolische Symmetrien
 Hyperbolische Symmetrien Nina Dietsche Robert Papin 01.07.2010 1 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Hyperbolische Symmetrien 2 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Inhaltsverzeichnis
Hyperbolische Symmetrien Nina Dietsche Robert Papin 01.07.2010 1 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Hyperbolische Symmetrien 2 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Inhaltsverzeichnis
Gruppen, Graphen, Symmetrie Was sind negativ gekrümmte Gruppen?
 Gruppen, Graphen, Symmetrie Was sind negativ gekrümmte Gruppen? MNU-Landestagung. 02/2012. Regensburg Clara Löh Fakultät für Mathematik. Universität Regensburg Überblick Zwei Paradigmen der modernen (theoretischen)
Gruppen, Graphen, Symmetrie Was sind negativ gekrümmte Gruppen? MNU-Landestagung. 02/2012. Regensburg Clara Löh Fakultät für Mathematik. Universität Regensburg Überblick Zwei Paradigmen der modernen (theoretischen)
Download. Mathe an Stationen. Mathe an Stationen. Das 4x4-Geobrett in der Sekundarstufe I. Marco Bettner, Erik Dinges
 Download Marco Bettner, Erik Dinges Mathe an Stationen Das 4x4-Geobrett in der Sekundarstufe I Downloadauszug aus dem Originaltitel: Sekundarstufe I Marco Bettner Erik Dinges Mathe an Stationen Umgang
Download Marco Bettner, Erik Dinges Mathe an Stationen Das 4x4-Geobrett in der Sekundarstufe I Downloadauszug aus dem Originaltitel: Sekundarstufe I Marco Bettner Erik Dinges Mathe an Stationen Umgang
Modulprüfung BA 04 Mathematik: Grundlagen der Mathematik C: Geometrie, Elementare Algebra und Zahlentheorie
 FB 3: Mathematik/Naturwissenschaften Prof. Dr. R. Frank/ Dr. D. Habeck Modulprüfung BA 04 Mathematik: Grundlagen der Mathematik C: Geometrie, Elementare Algebra und Zahlentheorie 06.02.2013 Name: Vorname:
FB 3: Mathematik/Naturwissenschaften Prof. Dr. R. Frank/ Dr. D. Habeck Modulprüfung BA 04 Mathematik: Grundlagen der Mathematik C: Geometrie, Elementare Algebra und Zahlentheorie 06.02.2013 Name: Vorname:
1.3. Beträge, Gleichungen und Ungleichungen
 .3. Beträge, Gleichungen und Ungleichungen Das Maimum zweier Zahlen a, b (also die größere von beiden) wird mit ma(a,b) bezeichnet, ihr Minimum (also die kleinere von beiden) mit min(a,b). Der Absolutbetrag
.3. Beträge, Gleichungen und Ungleichungen Das Maimum zweier Zahlen a, b (also die größere von beiden) wird mit ma(a,b) bezeichnet, ihr Minimum (also die kleinere von beiden) mit min(a,b). Der Absolutbetrag
GRUPPENTHEORIE AUFGABEN ZUR PRÜFUNGSVORBEREITUNG II
 Universität Bielefeld WS 2012/13 GRUPPENTHEORIE AUFGABEN ZUR PRÜFUNGSVORBEREITUNG II DR. PHILIPP LAMPE Rat sucht man deshalb, weil man die einzige Lösung kennt, aber nichts davon wissen will. Erica Jong
Universität Bielefeld WS 2012/13 GRUPPENTHEORIE AUFGABEN ZUR PRÜFUNGSVORBEREITUNG II DR. PHILIPP LAMPE Rat sucht man deshalb, weil man die einzige Lösung kennt, aber nichts davon wissen will. Erica Jong
Ornamente zeichnen und hyprbolisieren
 Ornamente zeichnen und hyprbolisieren Martin von Gagern TU München in Zusammenarbeit mit Prof. Jürgen Richter-Gebert www.mathe-vital.de u.a. mit Applet zu Sierpinski-Dreieck per IFS... ist nicht Thema
Ornamente zeichnen und hyprbolisieren Martin von Gagern TU München in Zusammenarbeit mit Prof. Jürgen Richter-Gebert www.mathe-vital.de u.a. mit Applet zu Sierpinski-Dreieck per IFS... ist nicht Thema
Mengenlehre. ALGEBRA Kapitel 1 MNProfil - Mittelstufe KZN. Ronald Balestra CH Zürich Name: Vorname:
 Mengenlehre ALGEBRA Kapitel 1 MNProfil - Mittelstufe KZN Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 21. August 2016 Inhaltsverzeichnis 1 Mengenlehre 1 1.1 Die Menge im mathematischen
Mengenlehre ALGEBRA Kapitel 1 MNProfil - Mittelstufe KZN Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 21. August 2016 Inhaltsverzeichnis 1 Mengenlehre 1 1.1 Die Menge im mathematischen
Symmetrische Figuren von Prof. Dr. Frank
 Symmetrische Figuren von Prof. Dr. Frank Eckhard Großmann November 3, 2009 1 Mathematische Formeln und Darstellungen vorweggegriffen Dieses Kapitel soll nochmal alle notwendigen mathematischen Grundlagen
Symmetrische Figuren von Prof. Dr. Frank Eckhard Großmann November 3, 2009 1 Mathematische Formeln und Darstellungen vorweggegriffen Dieses Kapitel soll nochmal alle notwendigen mathematischen Grundlagen
Selbstverständnis der Mathematik. Selbstverständnis der Mathematik. Selbstverständnis der Mathematik. Selbstverständnis der Mathematik
 i e 0 Komplexe Zahlen i Geometrie e 0 Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 : = Menge der Menschen, die Mathematik studiert haben : = Menge der Männer, die Mathematik studiert haben : =
i e 0 Komplexe Zahlen i Geometrie e 0 Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 : = Menge der Menschen, die Mathematik studiert haben : = Menge der Männer, die Mathematik studiert haben : =
Übungen zu Geometrie (LGy) Universität Regensburg, Sommersemester 2014 Dr. Raphael Zentner, Dr. Olaf Müller
 Übungen zu Geometrie (LGy) Universität Regensburg, Sommersemester 2014 Dr. Raphael Zentner, Dr. Olaf Müller Übungsblatt 13 Dieses Übungsblatt wird nicht mehr zur Abgabe vorgesehen. Es dient der Wiederholung
Übungen zu Geometrie (LGy) Universität Regensburg, Sommersemester 2014 Dr. Raphael Zentner, Dr. Olaf Müller Übungsblatt 13 Dieses Übungsblatt wird nicht mehr zur Abgabe vorgesehen. Es dient der Wiederholung
1.3. Beträge, Gleichungen und Ungleichungen
 1.3. Beträge, Gleichungen und Ungleichungen Das Maximum zweier Zahlen a, b wird mit max(a,b) bezeichnet, ihr Minimum mit min(a,b). Der Absolutbetrag einer reellen Zahl a ist a = max ( a, a ) oder auch
1.3. Beträge, Gleichungen und Ungleichungen Das Maximum zweier Zahlen a, b wird mit max(a,b) bezeichnet, ihr Minimum mit min(a,b). Der Absolutbetrag einer reellen Zahl a ist a = max ( a, a ) oder auch
Kombinatorik und Polynommultiplikation
 Kombinatorik und Polynommultiplikation 3 Vorträge für Schüler SS 2004 W. Plesken RWTH Aachen, Lehrstuhl B für Mathematik 2 Mengen und Abbildungen: Die Sprache der Mathematik Wir haben in der ersten Vorlesung
Kombinatorik und Polynommultiplikation 3 Vorträge für Schüler SS 2004 W. Plesken RWTH Aachen, Lehrstuhl B für Mathematik 2 Mengen und Abbildungen: Die Sprache der Mathematik Wir haben in der ersten Vorlesung
Geometrie (4b) Wintersemester 2015/16. Kapitel 2. Abbildungsgeometrie. Teil 2
 Kapitel 2 Abbildungsgeometrie Teil 2 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Kapitel 2 Abbildungsgeometrie 2.1 2,3,4 Geradenspiegelungen 2.2 Sinn & Orientierung
Kapitel 2 Abbildungsgeometrie Teil 2 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Kapitel 2 Abbildungsgeometrie 2.1 2,3,4 Geradenspiegelungen 2.2 Sinn & Orientierung
Klassenstufen 7, 8. Fachbereich Mathematik Tag der Mathematik 9. November 2013
 Fachbereich Mathematik Tag der Mathematik 9. November 2013 Klassenstufen 7, 8 12 Aufgabe 1 (5+++5+2 Punkte). Meister Hora hat eine kuriose Uhr: Bei dieser springt der Stundenzeiger nicht wie üblich jede
Fachbereich Mathematik Tag der Mathematik 9. November 2013 Klassenstufen 7, 8 12 Aufgabe 1 (5+++5+2 Punkte). Meister Hora hat eine kuriose Uhr: Bei dieser springt der Stundenzeiger nicht wie üblich jede
Lösung 2: Relationen, Abbildungen, Mächtigkeit, Gruppen
 D-MATH Lineare Algebra I HS 2016 Dr. Meike Akveld Lösung 2: Relationen, Abbildungen, Mächtigkeit, Gruppen 1. Gegeben n, m Z schreiben wir m n k Z : n = km Wir sagen m teilt n. Eine Zahl n Z ist gerade,
D-MATH Lineare Algebra I HS 2016 Dr. Meike Akveld Lösung 2: Relationen, Abbildungen, Mächtigkeit, Gruppen 1. Gegeben n, m Z schreiben wir m n k Z : n = km Wir sagen m teilt n. Eine Zahl n Z ist gerade,
Modulprüfung BA 04 Mathematik: Grundlagen der Mathematik C: Geometrie, Elementare Algebra und Zahlentheorie
 FB 3: Mathematik/Naturwissenschaften Prof. Dr. R. Frank/ Dr. D. Habeck Modulprüfung BA 04 Mathematik: Grundlagen der Mathematik C: Geometrie, Elementare Algebra und Zahlentheorie 11.04.2013 LÖSUNG Name:
FB 3: Mathematik/Naturwissenschaften Prof. Dr. R. Frank/ Dr. D. Habeck Modulprüfung BA 04 Mathematik: Grundlagen der Mathematik C: Geometrie, Elementare Algebra und Zahlentheorie 11.04.2013 LÖSUNG Name:
Analysis 1, Woche 2. Reelle Zahlen. 2.1 Anordnung. Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität).
 Analysis 1, Woche 2 Reelle Zahlen 2.1 Anordnung Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität). 2. Für jeden a, b K mit a b und b a gilt a = b (Antisymmetrie).
Analysis 1, Woche 2 Reelle Zahlen 2.1 Anordnung Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität). 2. Für jeden a, b K mit a b und b a gilt a = b (Antisymmetrie).
Wann hat ein gleichschenkliges Dreieck drei gleich große Winkel? Erkläre.
 Aufgabe 1: Es ist ein Schneekristall abgebildet. Kreuze die wahren Aussagen an: Die abgebildete Figur ist achsensymmetrisch. Die abgebildete Figur ist drehsymmetrisch. Die abgebildete Figur ist keines
Aufgabe 1: Es ist ein Schneekristall abgebildet. Kreuze die wahren Aussagen an: Die abgebildete Figur ist achsensymmetrisch. Die abgebildete Figur ist drehsymmetrisch. Die abgebildete Figur ist keines
Gruppentheorie und Symmetrie in der Chemie
 Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 26. April 2002 Mathematische Definition
Gruppentheorie und Symmetrie in der Chemie Martin Schütz Institut für theoretische Chemie, Universität Stuttgart Pfaffenwaldring 55, D-70569 Stuttgart Stuttgart, 26. April 2002 Mathematische Definition
Andi parkettiert T-Shirts
 Andi parkettiert T-Shirts Der letzte große Teil des Kurses Mathe Macht Mode beschäftigte sich damit, ein TShirt zu bedrucken. Als mathematischen Hintergrund wählten wir das Thema Parkettierung. Unser Ziel
Andi parkettiert T-Shirts Der letzte große Teil des Kurses Mathe Macht Mode beschäftigte sich damit, ein TShirt zu bedrucken. Als mathematischen Hintergrund wählten wir das Thema Parkettierung. Unser Ziel
Übungsblatt 1. Gruppenübungen
 Übungsblatt Gruppenübungen Diese Übungen sollen direkt in der Übungsgruppe in der Woche vom 5.0. bis 9.0. bearbeitet und besprochen werden. Bitte bringen Sie dazu Zirkel und Lineal mit. G Die folgende
Übungsblatt Gruppenübungen Diese Übungen sollen direkt in der Übungsgruppe in der Woche vom 5.0. bis 9.0. bearbeitet und besprochen werden. Bitte bringen Sie dazu Zirkel und Lineal mit. G Die folgende
Grundlagen Mathematik 7. Jahrgangsstufe
 ALGEBRA 1. Grundlagen Grundlagen Mathematik 7. Jahrgangsstufe Menge der ganzen Zahlen Z = {..., -3, -2, -1, 0, 1, 2, 3,... } Menge der rationalen Zahlen Q = { z z Z und n N } (Menge aller n positiven und
ALGEBRA 1. Grundlagen Grundlagen Mathematik 7. Jahrgangsstufe Menge der ganzen Zahlen Z = {..., -3, -2, -1, 0, 1, 2, 3,... } Menge der rationalen Zahlen Q = { z z Z und n N } (Menge aller n positiven und
2. Symmetrische Gruppen
 14 Andreas Gathmann 2 Symmetrische Gruppen Im letzten Kapitel haben wir Gruppen eingeführt und ihre elementaren Eigenschaften untersucht Wir wollen nun eine neue wichtige Klasse von Beispielen von Gruppen
14 Andreas Gathmann 2 Symmetrische Gruppen Im letzten Kapitel haben wir Gruppen eingeführt und ihre elementaren Eigenschaften untersucht Wir wollen nun eine neue wichtige Klasse von Beispielen von Gruppen
Mathematisches Kaleidoskop II Materialien Teil 3. Dr. Hermann Dürkop
 Mathematisches Kaleidoskop II Materialien Teil 3 Dr. Hermann Dürkop E-Mail: info@ermanus.de .3.3 Noch zwei Isomorphie-Beispiele Beispiel : Wir betrachten die Symmetrien eines nichtquadratischen Rechtecks.
Mathematisches Kaleidoskop II Materialien Teil 3 Dr. Hermann Dürkop E-Mail: info@ermanus.de .3.3 Noch zwei Isomorphie-Beispiele Beispiel : Wir betrachten die Symmetrien eines nichtquadratischen Rechtecks.
Warum sind Gullydeckel rund und Pflastersteine viereckig?
 Warum sind Gullydeckel rund und Pflastersteine viereckig? Jörn Steuding Heilbronn, 11. März 2015 Rund - Eckig 1. Runde Warum sind Gullydeckel rund? Was wäre wenn...? Wieso braucht man Gullydeckel überhaupt?
Warum sind Gullydeckel rund und Pflastersteine viereckig? Jörn Steuding Heilbronn, 11. März 2015 Rund - Eckig 1. Runde Warum sind Gullydeckel rund? Was wäre wenn...? Wieso braucht man Gullydeckel überhaupt?
Axiomatische Beschreibung der ganzen Zahlen
 Axiomatische Beschreibung der ganzen Zahlen Peter Feigl JKU Linz peter.feigl@students.jku.at 0055282 Claudia Hemmelmeir JKU Linz darja@gmx.at 0355147 Zusammenfassung Wir möchten in diesem Artikel die ganzen
Axiomatische Beschreibung der ganzen Zahlen Peter Feigl JKU Linz peter.feigl@students.jku.at 0055282 Claudia Hemmelmeir JKU Linz darja@gmx.at 0355147 Zusammenfassung Wir möchten in diesem Artikel die ganzen
Universität Bielefeld. Elementare Geometrie. Sommersemester Rückblick. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Rückblick Stefan Witzel Outline Grundlagen, Axiome Euklid I Bewegungen Verhältnisse, Ähnlichkeiten Kreise Fundamentale Objekte und Eigenschaften
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Rückblick Stefan Witzel Outline Grundlagen, Axiome Euklid I Bewegungen Verhältnisse, Ähnlichkeiten Kreise Fundamentale Objekte und Eigenschaften
2.5 Diskrete Bewegungsgruppen I: die Punktgruppe,
 Diskrete Geometrie (Version 3) 20. November 2011 c Rudolf Scharlau 133 2.5 Diskrete Bewegungsgruppen I: die Punktgruppe, Friesgruppen In diesem Abschnitt ist wie bisher ein euklidischer (Vektor-)Raum E
Diskrete Geometrie (Version 3) 20. November 2011 c Rudolf Scharlau 133 2.5 Diskrete Bewegungsgruppen I: die Punktgruppe, Friesgruppen In diesem Abschnitt ist wie bisher ein euklidischer (Vektor-)Raum E
Prof. Dr. Dörte Haftendorn, Leuphana Universität Lüneburg, 2013
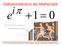 Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
2. Gruppen und Körper
 2. Gruppen und Körper (2.1) Def. Eine Gruppe ist eine Menge, genannt G, und eine Abbildung ( innere Verknüpfung ) von G G nach G, hier bezeichnet als so daß folgende Eigenschaften erfüllt sind: : G G G,
2. Gruppen und Körper (2.1) Def. Eine Gruppe ist eine Menge, genannt G, und eine Abbildung ( innere Verknüpfung ) von G G nach G, hier bezeichnet als so daß folgende Eigenschaften erfüllt sind: : G G G,
1 Angeordnete Körper und Anordnung
 1 ANGEORDNETE KÖRPER UND ANORDNUNG 1 1 Angeordnete Körper und Anordnung Die nächste Idee, die wir interpretieren müssen ist die Anordnung. Man kann zeigen, dass sie nicht über jeden Körper möglich ist.
1 ANGEORDNETE KÖRPER UND ANORDNUNG 1 1 Angeordnete Körper und Anordnung Die nächste Idee, die wir interpretieren müssen ist die Anordnung. Man kann zeigen, dass sie nicht über jeden Körper möglich ist.
2. Isometrien oder Kongruenzabbildungen
 6 2. Isometrien oder Kongruenzabbildungen 2.1 Einführende Überlegungen Kongruente Figuren sind deckungsgleiche Figuren. Eine Figur wird so bewegt, dass sie mit einer anderen Figur zur Deckung gebracht
6 2. Isometrien oder Kongruenzabbildungen 2.1 Einführende Überlegungen Kongruente Figuren sind deckungsgleiche Figuren. Eine Figur wird so bewegt, dass sie mit einer anderen Figur zur Deckung gebracht
