Einführung in die Theoretische Informatik
|
|
|
- Florian Achim Weiß
- vor 6 Jahren
- Abrufe
Transkript
1 Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12
2 Relationalstrukturen Definition Sei A eine nichtleere Menge, R ist eine k-stellige Relation auf A, wenn R A k = A A ist. }{{} k-mal Für i = 1,..., n sei R i eine k i -stellige Relation auf A. Dann heißt (A; R 1,..., R n ) Relationalstruktur. Die Menge A heißt der Individuenbereich, die Trägermenge oder die Grundmenge der Relationalstruktur. Bemerkung Wir werden hier hauptsächlich den Fall n = 1, k 1 = 2, also (A, R) mit R A A betrachten. Man nennt dann R eine (binäre) Relation auf A. Oft wird für (a, b) R auch die Infix-Schreibweise arb benutzt.
3 Relationalstrukturen Beispiel (F, M) mit F = {f f ist Fluss in Europa} und M = {(f, g) F F f mündet in g}, (U, B) mit U = {x x ist Berliner } und B = {(x, y) U U x ist Bruder von y}, (P(M), ), wobei M eine beliebige Menge und die Inklusionsrelation auf den Teilmengen von M ist, (A, Id A ) mit Id A = {(x, x) x A} (die Identität auf A), (R, ), (Z, ), wobei die teilt -Relation bezeichnet.
4 Mengentheoretische Operationen auf Relationen Da Relationen Mengen sind, können wir den Durchschnitt, die Vereinigung, die Differenz und das Komplement von Relationen bilden: R S = {(x, y) A A xry xsy}, R S = {(x, y) A A xry xsy}, R S = {(x, y) A A xry xsy}, R = (A A) R. Sei M P(A A) eine beliebige Menge von Relationen auf A. Dann sind der Schnitt über M und die Vereinigung über M folgende Relationen: M = R M R = {(x, y) R M : xry}, M = R M R = {(x, y) R M : xry}.
5 Weitere Operationen auf Relationen Definition Die transponierte (konverse) Relation zu R ist R T = {(y, x) xry}. R T wird oft auch mit R 1 bezeichnet. Zum Beispiel ist (R, T ) = (R, ). Das Produkt (oder die Komposition) zweier Relationen R und S ist R S = {(x, z) A A y A : xry ysz}. Beispiel Ist B die Relation ist Bruder von, V ist Vater von, M ist Mutter von und E = V M ist Elternteil von, so ist B E die Onkel-Relation.
6 Das Relationenprodukt Notation Für R S wird auch R ;S, R S oder einfach RS geschrieben. Für } R {{ R} schreiben wir auch R n. Dabei ist R 0 = Id. n-mal Vorsicht! Das Relationenprodukt R n sollte nicht mit dem kartesischen Produkt R R }{{} n-mal verwechselt werden. Vereinbarung Wir vereinbaren, dass R n das n-fache Relationenprodukt bezeichnen soll, falls R eine Relation ist.
7 Eigenschaften von Relationen Definition Sei R eine Relation auf A. Dann heißt R reflexiv, falls x A : xrx (also Id A R) irreflexiv, falls x A : xrx (also Id A R) symmetrisch, falls x, y A : xry yrx (also R R T ) asymmetrisch, falls x, y A : xry yrx (also R R T ) antisymmetrisch, falls x, y A : xry yrx x = y (also R R T Id) konnex, falls x, y A : xry yrx (also A A R R T ) semikonnex, falls x, y A : x y xry yrx (also Id R R T ) transitiv, falls x, y, z A : xry yrz xrz (also R 2 R) gilt.
8 Eigenschaften von Relationen Beispiel Die Relation ist Schwester von ist zwar in einer reinen Damengesellschaft symmetrisch, i.a. jedoch weder symmetrisch noch asymmetrisch noch antisymmetrisch. (R, <) ist irreflexiv, asymmetrisch, transitiv und semikonnex. (R, ) und (P(M), ) sind reflexiv, antisymmetrisch und transitiv. (R, ) ist auch konnex. (P(M), ) ist zwar im Fall M 1 konnex, aber im Fall M 2 weder semikonnex noch konnex.
9 Darstellung von endlichen Relationen Graphische Darstellung A = {a, b, c, d} R = {(b, c), (b, d), (c, a), (c, d), (d, d)} a c b d Eine Relation R auf einer (endlichen) Menge A kann durch einen gerichteten Graphen (kurz Digraphen) G = (A, R) mit Knotenmenge A und Kantenmenge R veranschaulicht werden. Hierzu stellen wir jedes Element x A als einen Knoten dar und verbinden jedes Knotenpaar (x, y) R durch eine gerichtete Kante (Pfeil). Zwei durch eine Kante verbundene Knoten heißen adjazent oder benachbart.
10 Darstellung von endlichen Relationen Definition Sei R eine binäre Relation auf A. Die Menge der Nachfolger bzw. Vorgänger von x ist R[x] = {y A xry} bzw. R 1 [x] = {y A yrx}. Der Ausgangsgrad eines Knotens x ist deg + (x) = R[x]. Der Eingangsgrad von x ist deg (x) = R 1 [x]. Ist R symmetrisch, so können wir die Pfeilspitzen auch weglassen. In diesem Fall heißt deg(x) = deg (x) = deg + (x) der Grad von x und R[x] = R 1 [x] die Nachbarschaft von x in G. G ist schleifenfrei, falls R irreflexiv ist. Ist R irreflexiv und symmetrisch, so nennen wir G = (A, R) einen (ungerichteten) Graphen.
11 Darstellung von endlichen Relationen Matrixdarstellung (Adjazenzmatrix) Eine Relation R auf A = {a 1,..., a n } lässt sich auch durch die boolesche (n n)-matrix M R = (m ij ) darstellen mit { 1, ai Ra m ij = j, 0, sonst. Beispiel Die Relation R = {(b, c), (b, d), (c, a), (c, d), (d, d)} auf A = {a, b, c, d} hat beispielsweise die Matrixdarstellung M R =
12 Darstellung von endlichen Relationen Tabellendarstellung (Adjazenzliste) R lässt sich auch durch eine Tabelle darzustellen, die jedem Element x A seine Nachfolger in Form einer Liste zuordnet. Beispiel Die Relation R = {(b, c), (b, d), (c, a), (c, d), (d, d)} auf A = {a, b, c, d} hat beispielsweise die Tabellendarstellung x R[x] a - b c, d c a, d d d
13 Berechnung des Relationenprodukts Berechnung von R S Sind M R = (r ij ) und M S = (s ij ) boolesche n n-matrizen für R und S, so erhalten wir für T = R S die Matrix M T = (t ij ) mit t ij = (r ik s kj ). k=1,...,n Die Nachfolgermenge T [x] von x bzgl. der Relation T = R S berechnet sich zu T [x] = S[y]. y R[x]
14 Das Relationenprodukt Beispiel Betrachte die Relationen R = {(a, a), (a, c), (c, b), (c, d)} und S = {(a, b), (d, a), (d, c)} auf der Menge A = {a, b, c, d}. Relation R S R S S R Digraph Adjazenzmatrix Adjazenzliste a c b d a : a, c b : - c : b, d d : - a c b d a : b b : - c : - d : a, c a c b d a : b b : - c : a, c d : - a c b d a : - b : - c : - d : a, b, c, d
15 Das Relationenprodukt Beobachtung Das Relationenprodukt ist nicht kommutativ, d.h. i.a. gilt nicht R S = S R. Relationenalgebra Als nächstes zeigen wir, dass die Menge R = P(A A) aller binären Relationen auf A mit dem Relationenprodukt als binärer Operation und der Relation Id A als neutralem Element eine Halbgruppe (oder Monoid) bildet. Satz Seien Q, R, S Relationen auf A. Dann gilt 1 (Q R) S = Q (R S), d.h. ist assoziativ, 2 Id R = R Id = R, d.h. Id ist neutrales Element.
16 Relationenalgebra Satz Seien Q, R, S Relationen auf A. Dann gilt 1 (Q R) S = Q (R S), d.h. ist assoziativ, 2 Id R = R Id = R, d.h. Id ist neutrales Element. Beweis. 1 x (Q R) S y u : x (Q R) u u S y u : ( v : x Q v R u) u S y u, v : x Q v R u S y v : x Q v ( u : v R u u S y) v : x Q v (R S) y x Q (R S) y 2 Wegen x Id R y z : x = z z R y x R y folgt Id R = R. Die Gleichheit R Id = R folgt analog.
17 Überblick über Relationalstrukturen Äquivalenz- und Ordnungsrelationen refl. sym. trans. antisym. asym. konnex semikon. Äquivalenzrelation (Halb-)Ordnung Striktordnung lineare Ordnung lin. Striktord. Quasiordnung Bemerkung In der Tabelle sind nur die definierenden Eigenschaften durch ein gekennzeichnet. Das schließt nicht aus, dass noch weitere Eigenschaften vorliegen.
18 Ordnungsrelationen Definition (A, R) heißt Ordnung (auch Halbordnung oder partielle Ordnung), wenn R eine reflexive, antisymmetrische und transitive Relation auf A ist. Beispiel (P(M), ), (Z, ), (R, ), (N, ), sind Ordnungen. (Z, ) ist keine Ordnung. Ist R eine Ordnung auf A und B A, so ist die Einschränkung R B = R (B B) von R auf B eine Ordnung auf B. Beispielsweise ist (N, ) die Einschränkung von (Z, ) auf N.
19 Darstellung einer Ordnung durch ein Hasse-Diagramm Sei eine Ordnung auf A und sei < die Relation \Id A, d.h. x < y x y x y Ein Element x A heißt unterer Nachbar von y (kurz: x y), falls x < y gilt und kein z A existiert mit x < z < y. ist also die Relation < \ < 2. Um die Ordnung (A, ) in einem Hasse-Diagramm darzustellen, wird nur der Digraph der Relation (A, ) gezeichnet. Weiterhin wird im Fall x y der Knoten y oberhalb vom Knoten x gezeichnet, so dass auf die Pfeilspitzen verzichtet werden kann.
20 Das Hasse-Diagramm für (P(M); ) Beispiel Die Inklusion auf P(M) mit M = {a, b, c} lässt sich durch folgendes Hasse-Diagramm darstellen: M {a, b} {a, c} {b, c} {a} {b} {c}
21 Das Hasse-Diagramm der teilt -Relation Beispiel Die Einschränkung der teilt -Relation auf die Menge {1, 2,..., 10} ist durch folgendes Hasse-Diagramm darstellbar:
22 Maximale, minimale, größte und kleinste Elemente Definition Sei eine Ordnung auf A und sei b ein Element in einer Teilmenge B A. b heißt kleinstes Element oder Minimum von B, falls gilt: b B : b b. b heißt größtes Element oder Maximum von B, falls gilt: b B : b b. b heißt minimal in B, falls es in B kein kleineres Element gibt: b B : b b b = b. b heißt maximal in B, falls es in B kein größeres Element gibt: Bemerkung b B : b b b = b. Wegen der Antisymmetrie kann es in B höchstens ein kleinstes und höchstens ein größtes Element geben.
23 Maximale, minimale, größte und kleinste Elemente Beispiel Betrachte folgende Ordnung. a b B minimal in B maximal in B Minimum von B Maximum von B c e d {a, b} a, b a, b - - {c, d} c, d c, d - - {a, b, c} c a, b c - {a, b, c, e} e a, b e - {a, c, d, e} e a e a
24 Obere und untere Schranken Definition Sei eine Ordnung auf A und sei B A. Jedes Element u A mit u b für alle b B heißt untere Schranke von B. Jedes Element o A mit b o für alle b B heißt obere Schranke von B. B heißt nach oben beschränkt, wenn B eine obere Schranke hat. B heißt nach unten beschränkt, wenn B eine untere Schranke hat. B heißt beschränkt, wenn B nach oben und nach unten beschränkt ist.
25 Obere und untere Schranken Beispiel (Fortsetzung) a c e b d B minimal maximal min max untere obere Schranken {a, b} a, b a, b - - c, d, e - {c, d} c, d c, d - - e a, b {a, b, c} c a, b c - c, e - {a, b, c, e} e a, b e - e - {a, c, d, e} e a e a e a
26 Infima und Suprema Definition Sei eine Ordnung auf A und sei B A. Besitzt B eine größte untere Schranke i, d.h. besitzt die Menge U aller unteren Schranken von B ein größtes Element i, so heißt i das Infimum von B (i = inf B): ( b B : b i) [ u A : ( b B : b u) u i]. Besitzt B eine kleinste obere Schranke s, d.h. besitzt die Menge O aller oberen Schranken von B ein kleinstes Element s, so heißt s das Supremum von B (s = sup B): ( b B : b s) [ o A : ( b B : b o) s o] Bemerkung B kann nicht mehr als ein Supremum und ein Infimum haben.
27 Infima und Suprema Beispiel (Schluss) a c e b d B minimal maximal min max untere obere inf sup Schranken {a, b} a, b a, b - - c, d, e {c, d} c, d c, d - - e a, b e - {a, b, c} c a, b c - c, e - c - {a, b, c, e} e a, b e - e - e - {a, c, d, e} e a e a e a e a
28 Infima und Suprema Bemerkung Auch in linearen Ordnungen muss nicht jede beschränkte Teilmenge ein Supremum oder Infimum besitzen. So hat in der linear geordneten Menge (Q, ) die Teilmenge B = {x Q x 2 2} = {x Q x 2 < 2} weder ein Supremum noch ein Infimum. Dagegen hat in einer linearen Ordnung jede endliche Teilmenge ein kleinstes und ein größtes Element und somit erst recht ein Supremum und ein Infimum.
29 Äquivalenzrelationen Definition (A, R) heißt Äquivalenzrelation, wenn R eine reflexive, symmetrische und transitive Relation auf A ist. Beispiel Auf der Menge aller Geraden im R 2 die Parallelität. Auf der Menge aller Menschen im gleichen Jahr geboren wie. Auf Z die Relation gleicher Rest bei Division durch m.
30 Äquivalenzrelationen Ist E eine Äquivalenzrelation, so nennt man die Nachbarschaft E[x] die von x repräsentierte Äquivalenzklasse und bezeichnet sie auch mit [x] E oder einfach mit [x]: [x] E = [x] = {x xex }. Wie wir sehen werden, bilden die Äquivalenzklassen eine Zerlegung (Partition) von A, d.h. je zwei Äquivalenzklassen sind entweder gleich oder disjunkt und ihre Vereinigung ergibt A. Die Zerlegung von A in Äquivalenzklassen wird Quotienten- oder Faktormenge von A bzgl. E genannt und mit A/E bezeichnet: A/E = {[x] E x A}. Die Anzahl A/E der Äquivalenzklassen von E wird auch als der Index von E bezeichnet. Eine Menge S A heißt Repräsentantensystem, falls sie genau ein Element aus jeder Äquivalenzklasse enthält.
31 Äquivalenzrelationen Beispiel Für die weiter oben betrachteten Äquivalenzrelationen erhalten wir folgende Klasseneinteilungen: Für die Parallelität auf der Menge aller Geraden im R 2 : alle Geraden mit derselben Richtung (oder Steigung) bilden jeweils eine Äquivalenzklasse. Ein Repräsentantensystem wird beispielsweise durch die Menge aller Ursprungsgeraden gebildet. Für die Relation im gleichen Jahr geboren wie auf der Menge aller Menschen: jeder Jahrgang bildet eine Äquivalenzklasse. Für die Relation gleicher Rest bei Division durch m auf Z: jede der m Restklassen [0], [1],..., [m 1] mit [r] = {a Z a mod m = r} bildet eine Äquivalenzklasse. Repräsentantensystem: {0, 1,..., m 1}.
32 Verfeinerung und Vergröberung von Äquivalenzrelationen Bemerkungen Die kleinste Äquivalenzrelation auf A ist die Identität Id A, die größte ist die Allrelation A A. Die Äquivalenzklassen der Identität enthalten jeweils nur ein Element, d.h. A/Id A = {{x} x A}. Die Allrelation erzeugt nur eine Äquivalenzklasse, nämlich A, d.h. A/(A A) = {A}. Für zwei Äquivalenzrelationen E E sind auch die Äquivalenzklassen [x] E von E in den Klassen [x] E von E enthalten. Folglich ist jede Äquivalenzklasse von E die Vereinigung von (evtl. mehreren) Äquivalenzklassen von E. Im Fall E E sagt man auch, E bewirkt eine feinere Zerlegung von A als E. Demnach ist die Identität die feinste und die Allrelation die gröbste Äquivalenzrelation.
33 Das Hasse-Diagramm der Feiner-Relation Beispiel Die feiner als Relation auf der Menge aller Partitionen von M = {a, b, c} ist durch folgendes Hasse-Diagramm darstellbar: {M} {{a, b}, {c}} {{a, c}, {b}} {{a}, {b, c}} {{a}, {b}, {c}}
34 Äquivalenzrelationen und Partitionen Satz Sei E eine Relation auf A. Dann sind folgende Aussagen äquivalent: 1 E ist eine Äquivalenzrelation auf A. 2 Für alle x, y A gilt xey E[x] = E[y], 3 E ist reflexiv und {E[x] x A} ist eine Partition von A. Beweis. 1 impliziert 2 : Sei E eine Äquivalenzrelation auf A. Da E transitiv ist, impliziert xey die Inklusion E[y] E[x]: z E[y] yez xez z E[x]. Da E symmetrisch ist, folgt aus xey aber auch E[x] E[y]. Umgekehrt folgt aus E[x] = E[y] wegen der Reflexivität von E, dass y E[y] = E[x] enthalten ist, und somit xey.
35 Äquivalenzrelationen und Partitionen Satz Sei E eine Relation auf A. Dann sind folgende Aussagen äquivalent: 1 E ist eine Äquivalenzrelation auf A. 2 Für alle x, y A gilt xey E[x] = E[y], 3 E ist reflexiv und {E[x] x A} ist eine Partition von A. Beweis. 2 impliziert 3 : Falls E die Bedingung xey E[x] = E[y] erfüllt, so folgt sofort xex (wegen E[x] = E[x]) und folglich überdecken die Mengen E[x] (wegen x E[x]) die Menge A. Ist E[x] E[y] und z ein Element in E[x] E[y], so gilt xez und yez und daher folgt E[x] = E[z] = E[y]. Da also je zwei Mengen E[x] und E[y] entweder gleich oder disjunkt sind, bildet {E[x] x A} sogar eine Partition von A.
36 Äquivalenzrelationen und Partitionen Satz Sei E eine Relation auf A. Dann sind folgende Aussagen äquivalent: 1 E ist eine Äquivalenzrelation auf A. 2 Für alle x, y A gilt xey E[x] = E[y], 3 E ist reflexiv und {E[x] x A} ist eine Partition von A. Beweis. 3 impliziert 1 : Wird schließlich A von den Mengen E[x] partitioniert, wobei x E[x] für alle x A gilt, so folgt xey y E[x] E[y] E[x] = E[y]. Daher übertragen sich die Eigenschaften Reflexivität, Symmetrie und Transitivität unmittelbar von der Gleichheitsrelation auf E.
37 Hüllenoperatoren Bemerkung Es ist leicht zu sehen, dass der Schnitt von transitiven Relationen wieder transitiv ist. Die transitive Hülle von R ist R + = {S A A S ist transitiv und R S}. R + ist also eine transitive Relation, die R enthält. Da R + zudem in jeder Relation mit diesen Eigenschaften enthalten ist, ist R + die kleinste transitive Relation, die R enthält. Da auch die Reflexivität und die Symmetrie bei der Schnittbildung erhalten bleiben, lassen sich nach demselben Muster weitere Hüllenoperatoren definieren.
38 Weitere Hüllenoperatoren Definition Sei R eine Relation auf A. Die reflexive Hülle von R ist h refl (R) = {S A A S ist reflexiv und R S}. Die symmetrische Hülle von R ist h sym (R) = {S A A S ist symmetrisch und R S}. Die reflexiv-transitive Hülle von R ist R = {S A A S ist reflexiv, transitiv und R S}. Die Äquivalenzhülle von R ist h äq (R) = {E A A E ist eine Äquivalenzrelation mit R E}.
39 Transitive und reflexive Hülle Satz h refl (R) = R Id A, h sym (R) = R R T, R + = n 1 Rn, R = n 0 Rn. Beweis Siehe Übungen. Bemerkung Ein Paar (a, b) ist also genau dann in der reflexiv-transitiven Hülle R von R enthalten, wenn es ein n 0 gibt mit ar n b. Dies bedeutet, dass es Elemente x 0,..., x n A gibt mit x 0 = a, x n = b und x 0 Rx 1 Rx 2 x n 1 Rx n. x 0,..., x n heißt Weg der Länge n von a nach b.
40 Abbildungen Definition Sei R eine binäre Relation auf einer Menge M. R heißt rechtseindeutig, falls gilt: x, y, z M : xry xrz y = z. R heißt linkseindeutig, falls gilt: x, y, z M : xrz yrz x = y. Der Nachbereich N(R) und der Vorbereich V (R) von R sind N(R) = R[x] und V (R) = R T [x]. x M x M
41 Abbildungen Abbildungen ordnen jedem Element ihres Definitionsbereichs genau ein Element zu. Definition Eine rechtseindeutige Relation R mit V (R) = A und N(R) B heißt Abbildung oder Funktion von A nach B (kurz R : A B). Bemerkung Wie üblich werden wir Abbildungen meist mit kleinen Buchstaben f, g, h,... bezeichnen und für (x, y) f nicht xfy sondern f (x) = y oder f : x y schreiben. Ist f : A B eine Abbildung, so wird der Vorbereich V (f ) = A der Definitionsbereich und die Menge B der Wertebereich oder Wertevorrat von f genannt. Der Nachbereich N(f ) wird als Bild von f bezeichnet.
42 Abbildungen Definition Sei f : A B eine Abbildung. Im Fall N(f ) = B heißt f surjektiv. Ist f linkseindeutig, so heißt f injektiv. In diesem Fall impliziert f (x) = f (y) die Gleichheit x = y. Eine injektive und surjektive Abbildung heißt bijektiv. Ist f injektiv, so ist auch f 1 eine Abbildung, die als die zu f inverse Abbildung bezeichnet wird. Bemerkung Man beachte, dass der Definitionsbereich V (f 1 ) = N(f ) von f 1 nur dann gleich B ist, wenn f auch surjektiv, also eine Bijektion ist.
43 Homomorphismen Definition Seien (A 1, R 1 ) und (A 2, R 2 ) Relationalstrukturen. Eine Abbildung h : A 1 A 2 heißt Homomorphismus, falls für alle a, b A 1 gilt: ar 1 b h(a)r 2 h(b). Sind (A 1, R 1 ) und (A 2, R 2 ) Ordnungen, so spricht man auch von Ordnungshomomorphismen oder einfach von monotonen Abbildungen. Injektive Ordnungshomomorphismen werden auch streng monotone Abbildungen genannt.
44 Homomorphismen Beispiel b 4 d 3 c 2 a h 1 (A, ) (B, ) Die Abbildung h : A B ist ein bijektiver Ordnungshomomorphismus. Die Umkehrabbildung h 1 ist jedoch kein Homomorphismus, da h 1 nicht monoton ist. Es gilt nämlich 2 3, aber h 1 (2) = b c = h 1 (3).
45 Isomorphismen Definition Seien (A 1, R 1 ) und (A 2, R 2 ) Relationalstrukturen. Ein bijektiver Homomorphismus h : A 1 A 2, bei dem auch h 1 ein Homomorphismus ist, d.h. es gilt a, b A 1 : ar 1 b h(a)r 2 h(b). heißt Isomorphismus. In diesem Fall heißen die Strukturen (A 1, R 1 ) und (A 2, R 2 ) isomorph (kurz: (A 1, R 1 ) = (A 2, R 2 )). Sind (A 1, R 1 ) und (A 2, R 2 ) isomorph, so bedeutet dies, dass sich die eine Struktur aus der anderen durch eine bloße Umbenennung der Elemente gewinnen lässt.
46 Isomorphismen Beispiel Die Bijektion h : x e x ist ein Ordnungsisomorphismus zwischen (R, ) und (R +, ). Für n N sei und T n = {k N k teilt n} P n = {k N k ist Primteiler von n}. Dann ist die Abbildung h : k P k ein Ordnungshomomorphismus von (T n, ) auf (P(P n ), ). h ist sogar ein Isomorphismus, falls n quadratfrei ist (d.h. es gibt kein k 2, so dass k 2 die Zahl n teilt).
47 Isomorphismen Beispiel G = (V, E) v h 1 (v) h 2 (v) G = (V, E ) Die beiden Graphen G und G sind isomorph. Zwei Isomorphismen sind beispielsweise h 1 und h 2.
48 Isomorphismen Beispiel Während auf der Knotenmenge V = {1, 2, 3} insgesamt 2 (3 2) = 2 3 = 8 verschiedene Graphen existieren, gibt es auf dieser Menge nur 4 verschiedene nichtisomorphe Graphen:
49 Isomorphismen Beispiel Es existieren genau 5 nichtisomorphe Ordnungen mit 3 Elementen: Anders ausgedrückt: Die Klasse aller dreielementigen Ordnungen zerfällt unter der Isomorphierelation = in fünf Äquivalenzklassen, die durch obige fünf Hasse-Diagramme repräsentiert werden.
Eine Relation R in einer Menge M ist eine Teilmenge von M x M. Statt (a,b) R schreibt man auch arb.
 4. Relationen 4.1 Grundlegende Definitionen Relation R in einer Menge M: Beziehung zwischen je 2 Elementen von M. Beispiel
4. Relationen 4.1 Grundlegende Definitionen Relation R in einer Menge M: Beziehung zwischen je 2 Elementen von M. Beispiel
(1.18) Def.: Eine Abbildung f : M N heißt
 Zurück zur Mengenlehre: Abbildungen zwischen Mengen (1.17) Def.: Es seien M, N Mengen. Eine Abbildung f : M N von M nach N ist eine Vorschrift, die jedem x M genau ein Element f(x) N zuordnet. a) M = N
Zurück zur Mengenlehre: Abbildungen zwischen Mengen (1.17) Def.: Es seien M, N Mengen. Eine Abbildung f : M N von M nach N ist eine Vorschrift, die jedem x M genau ein Element f(x) N zuordnet. a) M = N
3. Relationen Erläuterungen und Schreibweisen
 3. Relationen Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob
3. Relationen Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob
Diskrete Strukturen Kapitel 2: Grundlagen (Relationen)
 WS 2016/17 Diskrete Strukturen Kapitel 2: Grundlagen (Relationen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 2: Grundlagen (Relationen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Algebra. Eine Menge A heißt abzählbar, wenn A gilt. Insbesondere sind, und abzählbar, und sind nicht abzählbar (überabzählbar).
 Algebra 1 Mengen 1.1 Operationen A Anzahl der Elemente von A (Mächtigkeit, Betrag, Kardinalität) (A) Potenzmenge von X ( (A) = 2 A ) A B wenn jedes Element von A auch Element von B ist. A = B (A B und
Algebra 1 Mengen 1.1 Operationen A Anzahl der Elemente von A (Mächtigkeit, Betrag, Kardinalität) (A) Potenzmenge von X ( (A) = 2 A ) A B wenn jedes Element von A auch Element von B ist. A = B (A B und
Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen
 Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen Dozentin: Wiebke Petersen 4. Foliensatz Wiebke Petersen math. Grundlagen 89 starke / schwache Ordnungen Eine Ordnung R einer Menge A ist
Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen Dozentin: Wiebke Petersen 4. Foliensatz Wiebke Petersen math. Grundlagen 89 starke / schwache Ordnungen Eine Ordnung R einer Menge A ist
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Mengen. (Nicht-) Elemente einer Menge { 3, 4 } { 1, { 2 }, { 3, 4 }, { 5 } } 3 { 1, { 2 }, { 3, 4 }, { 5 } }
 Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1,
Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1,
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Einführung in die Informatik 2
 Einführung in die Informatik 2 Mathematische Grundbegriffe Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr,
Einführung in die Informatik 2 Mathematische Grundbegriffe Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr,
2 Mengen, Relationen, Funktionen
 Grundlagen der Mathematik für Informatiker Grundlagen der Mathematik für Informatiker Mengen, Relationen, Funktionen. Mengen Definition. [Georg Cantor 895] Eine Menge ist eine Zusammenfassung bestimmter,
Grundlagen der Mathematik für Informatiker Grundlagen der Mathematik für Informatiker Mengen, Relationen, Funktionen. Mengen Definition. [Georg Cantor 895] Eine Menge ist eine Zusammenfassung bestimmter,
Mengen. Eigenschaften. Spezielle Mengen (1) Prominente Mengen. ! Mengenzugehörigkeit
 Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen
 Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen Dozentin: Wiebke Petersen 4. Foliensatz Wiebke Petersen math. Grundlagen 86 starke / schwache Ordnungen Eine Ordnung R einer Menge A ist
Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen Dozentin: Wiebke Petersen 4. Foliensatz Wiebke Petersen math. Grundlagen 86 starke / schwache Ordnungen Eine Ordnung R einer Menge A ist
Relationen. Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B.
 Mathematik I für Informatiker Relationen auf einer Menge p. 1 Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B. Ein wichtiger Spezialfall ist der,
Mathematik I für Informatiker Relationen auf einer Menge p. 1 Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von A B. Ein wichtiger Spezialfall ist der,
Grundlagen der linearen Algebra und analytischen Geometrie
 Grundlagen der linearen Algebra und analytischen Geometrie Sascha Trostorff 27. Oktober 2017 Inhaltsverzeichnis I. Einführung in die Mengenlehre 3 1. Grundlagen der Aussagenlogik 4 2. Naive Mengenlehre
Grundlagen der linearen Algebra und analytischen Geometrie Sascha Trostorff 27. Oktober 2017 Inhaltsverzeichnis I. Einführung in die Mengenlehre 3 1. Grundlagen der Aussagenlogik 4 2. Naive Mengenlehre
Einführung in die Theoretische Informatik
 Vorlesungsskript Einführung in die Theoretische Informatik Wintersemester 2011/12 Prof. Dr. Johannes Köbler Humboldt-Universität zu Berlin Lehrstuhl Komplexität und Kryptografie 15. Februar 2012 Inhaltsverzeichnis
Vorlesungsskript Einführung in die Theoretische Informatik Wintersemester 2011/12 Prof. Dr. Johannes Köbler Humboldt-Universität zu Berlin Lehrstuhl Komplexität und Kryptografie 15. Februar 2012 Inhaltsverzeichnis
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018 23. November 2017 1/40 Satz 4.27 (Multinomialsatz) Seien r, n N 0. Dann gilt für
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018 23. November 2017 1/40 Satz 4.27 (Multinomialsatz) Seien r, n N 0. Dann gilt für
Relationen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Relationen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von
Relationen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Relationen Es seien A und B Mengen. Eine (binäre) Relation zwischen A und B ist eine Teilmenge von
Bemerkungen zur Notation
 Bemerkungen zur Notation Wir haben gerade die Symbole für alle und es gibt gebraucht. Dies sind so genannte logische Quantoren, und zwar der All- und der Existenzquantor. Die Formel {a A; ( b B)[(a, b)
Bemerkungen zur Notation Wir haben gerade die Symbole für alle und es gibt gebraucht. Dies sind so genannte logische Quantoren, und zwar der All- und der Existenzquantor. Die Formel {a A; ( b B)[(a, b)
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Theoretische Informatik 2
 Vorlesungsskript Theoretische Informatik 2 Wintersemester 2009/10 Prof. Dr. Johannes Köbler Humboldt-Universität zu Berlin Lehrstuhl Komplexität und Kryptografie 9. Februar 2010 Inhaltsverzeichnis Inhaltsverzeichnis
Vorlesungsskript Theoretische Informatik 2 Wintersemester 2009/10 Prof. Dr. Johannes Köbler Humboldt-Universität zu Berlin Lehrstuhl Komplexität und Kryptografie 9. Februar 2010 Inhaltsverzeichnis Inhaltsverzeichnis
3. Relationen. 3.1 Kartesische Produkte 3.2 Zweistellige Relationen 3.3 Äqivalenzrelationen 3.4 Halbordnungen 3.5 Hüllen. Rolf Linn. 3.
 3. Relationen 3.1 Kartesische Produkte 3.2 Zweistellige Relationen 3.3 Äqivalenzrelationen 3.4 Halbordnungen 3.5 Hüllen 3. Relationen GM 3-1 Wozu Relationen? Mathematik Theoretische Informatik Kryptographie
3. Relationen 3.1 Kartesische Produkte 3.2 Zweistellige Relationen 3.3 Äqivalenzrelationen 3.4 Halbordnungen 3.5 Hüllen 3. Relationen GM 3-1 Wozu Relationen? Mathematik Theoretische Informatik Kryptographie
1.4 Äquivalenzrelationen
 8 1.4 Äquivalenzrelationen achdem nun die axiomatische Grundlage gelegt ist, können wir uns bis zur Einführung der Kategorien das Leben dadurch erleichtern, daß wir bis dorthin, also bis auf weiteres,
8 1.4 Äquivalenzrelationen achdem nun die axiomatische Grundlage gelegt ist, können wir uns bis zur Einführung der Kategorien das Leben dadurch erleichtern, daß wir bis dorthin, also bis auf weiteres,
4. Funktionen und Relationen
 Bestimmung der Umkehrfunktionen c) bei reellen Funktionen geometrisch durch Spiegelung des Funktionsgraphen an der Winkelhalbierenden y = x. y = x 3 y = x y = x y = (x+1)/2 y = x 1/3 y = 2x 1 Seite 27
Bestimmung der Umkehrfunktionen c) bei reellen Funktionen geometrisch durch Spiegelung des Funktionsgraphen an der Winkelhalbierenden y = x. y = x 3 y = x y = x y = (x+1)/2 y = x 1/3 y = 2x 1 Seite 27
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 1-14. Sitzung Dennis Felsing dennis.felsing@student.kit.edu http://www.stud.uni-karlsruhe.de/~ubcqr/2010w/tut gbi/ 2011-02-07 Äquivalenzrelationen 1 Äquivalenzrelationen
Grundbegriffe der Informatik Tutorium 1-14. Sitzung Dennis Felsing dennis.felsing@student.kit.edu http://www.stud.uni-karlsruhe.de/~ubcqr/2010w/tut gbi/ 2011-02-07 Äquivalenzrelationen 1 Äquivalenzrelationen
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Vorbereitung der Bonusklausur am 24.11.2016 (Teil 2) 23. November 2016 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler 23. November 2016
Tutorium: Diskrete Mathematik Vorbereitung der Bonusklausur am 24.11.2016 (Teil 2) 23. November 2016 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler 23. November 2016
Algebraische Strukturen und Verbände
 KAPITEL 4 Algebraische Strukturen und Verbände Definition 4.1. Sei M eine Menge. Eine Abbildung : M M M nennt man eine (zweistellige) Verknüpfung in M. Man schreibt dafür auch a b := (a, b) mit a, b M.
KAPITEL 4 Algebraische Strukturen und Verbände Definition 4.1. Sei M eine Menge. Eine Abbildung : M M M nennt man eine (zweistellige) Verknüpfung in M. Man schreibt dafür auch a b := (a, b) mit a, b M.
mathematische Grundlagen der Modelltheorie: Mengen, Relationen, Funktionen
 Einführung in die Logik - 6 mathematische Grundlagen der Modelltheorie: Mengen, Relationen, Funktionen Modelltheoretische / Denotationelle Semantik der Prdikatenlogik Ein Modell ist ein künstlich geschaffenes
Einführung in die Logik - 6 mathematische Grundlagen der Modelltheorie: Mengen, Relationen, Funktionen Modelltheoretische / Denotationelle Semantik der Prdikatenlogik Ein Modell ist ein künstlich geschaffenes
Mathematische Strukturen
 Mathematische Strukturen Lineare Algebra I Kapitel 3 16. April 2013 Kartesisches Produkt Das kartesische Produkt (benannt nach René Descartes) von n Mengen M 1,..., M n ist M 1 M n := {(x 1,..., x n )
Mathematische Strukturen Lineare Algebra I Kapitel 3 16. April 2013 Kartesisches Produkt Das kartesische Produkt (benannt nach René Descartes) von n Mengen M 1,..., M n ist M 1 M n := {(x 1,..., x n )
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 21: Relationen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 21: Relationen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Kapitel 1. Grundlagen Mengen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Einführung in die Mengenlehre
 Einführung in die Mengenlehre D (Menge von Georg Cantor 845-98) Eine Menge ist eine Zusammenfassung bestimmter wohlunterschiedener Objekte unseres Denkens oder unserer Anschauung zu einem Ganzen wobei
Einführung in die Mengenlehre D (Menge von Georg Cantor 845-98) Eine Menge ist eine Zusammenfassung bestimmter wohlunterschiedener Objekte unseres Denkens oder unserer Anschauung zu einem Ganzen wobei
Beispiele für Relationen
 Text Relationen 2 Beispiele für Relationen eine Person X ist Mutter von einer Person Y eine Person X ist verheiratet mit einer Person Y eine Person X wohnt am gleichen Ort wie eine Person Y eine Person
Text Relationen 2 Beispiele für Relationen eine Person X ist Mutter von einer Person Y eine Person X ist verheiratet mit einer Person Y eine Person X wohnt am gleichen Ort wie eine Person Y eine Person
Kapitel 1. Grundlagen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Vorlesung 4. Tilman Bauer. 13. September 2007
 Vorlesung 4 Universität Münster 13. September 2007 Kartesische Wir befassen uns in dieser Vorlesung noch einmal mit Mengen. Definition Seien M und N zwei Mengen. Dann bezeichnen wir mit M N das (kartesische)
Vorlesung 4 Universität Münster 13. September 2007 Kartesische Wir befassen uns in dieser Vorlesung noch einmal mit Mengen. Definition Seien M und N zwei Mengen. Dann bezeichnen wir mit M N das (kartesische)
Grundlagen der Mathematik
 Grundlagen der Mathematik Übungsaufgaben zu Kapitel 1 Einführung 1.1.1 Für reelle Zahlen a und b gilt (a+b) (a-b) = a 2 -b 2. Was ist die Voraussetzung? Wie lautet die Behauptung? Beweisen Sie die Behauptung.
Grundlagen der Mathematik Übungsaufgaben zu Kapitel 1 Einführung 1.1.1 Für reelle Zahlen a und b gilt (a+b) (a-b) = a 2 -b 2. Was ist die Voraussetzung? Wie lautet die Behauptung? Beweisen Sie die Behauptung.
Mathematik-Vorkurs für Informatiker (Wintersemester 2012/13) Übungsblatt 8 (Relationen und Funktionen)
 DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6. Informatik Universität des Saarlandes Christian Eisentraut, M.Sc. Julia Krämer Mathematik-Vorkurs für Informatiker (Wintersemester 0/3) Übungsblatt 8 (Relationen
DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6. Informatik Universität des Saarlandes Christian Eisentraut, M.Sc. Julia Krämer Mathematik-Vorkurs für Informatiker (Wintersemester 0/3) Übungsblatt 8 (Relationen
Grundbegriffe der Informatik Tutorium 14
 Grundbegriffe der Informatik Tutorium 14 Tutorium Nr. 16 Philipp Oppermann 11. Februar 2015 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Grundbegriffe der Informatik Tutorium 14 Tutorium Nr. 16 Philipp Oppermann 11. Februar 2015 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Vorlesung 4. Tilman Bauer. 13. September Wir befassen uns in dieser Vorlesung noch einmal mit Mengen.
 Vorlesung 4 Universität Münster 13. September 2007 1 Kartesische Wir befassen uns in dieser Vorlesung noch einmal mit Mengen. Seien M und N zwei Mengen. Dann bezeichnen wir mit M N das (kartesische) Produkt
Vorlesung 4 Universität Münster 13. September 2007 1 Kartesische Wir befassen uns in dieser Vorlesung noch einmal mit Mengen. Seien M und N zwei Mengen. Dann bezeichnen wir mit M N das (kartesische) Produkt
Grundlagen. Kapitel Mengen
 Kapitel 1 Grundlagen 1.1 Mengen Grundobjekte mathematischer Theorien sind Mengen. Zwar stellt man sich darunter Gesamtheiten von gewissen Dingen (den Elementen der Menge) vor, doch führt die uneingeschränkte
Kapitel 1 Grundlagen 1.1 Mengen Grundobjekte mathematischer Theorien sind Mengen. Zwar stellt man sich darunter Gesamtheiten von gewissen Dingen (den Elementen der Menge) vor, doch führt die uneingeschränkte
Kapitel 2. Mathematische Grundlagen. Skript zur Vorlesung Einführung in die Programmierung
 LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 2 Mathematische Grundlagen Skript zur Vorlesung Einführung in die Programmierung im Wintersemester 2012/13 Ludwig-Maximilians-Universität
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 2 Mathematische Grundlagen Skript zur Vorlesung Einführung in die Programmierung im Wintersemester 2012/13 Ludwig-Maximilians-Universität
1 Mathematische Grundbegriffe
 1 1 Mathematische Grundbegriffe 1.1 Relationen und Funktionen Seien A 1,..., A n Mengen. Ein n-tupel über A 1,..., A n ist eine Folge (a 1,..., a n ) von Objekten a i A i, für i = 1,..., n. Zwei n-tupel
1 1 Mathematische Grundbegriffe 1.1 Relationen und Funktionen Seien A 1,..., A n Mengen. Ein n-tupel über A 1,..., A n ist eine Folge (a 1,..., a n ) von Objekten a i A i, für i = 1,..., n. Zwei n-tupel
2 Mengen und Abbildungen
 2.1 Mengen Unter einer Menge verstehen wir eine Zusammenfassung von Objekten zu einem Ganzen. Die Objekte heiÿen Elemente. Ist M eine Menge und x ein Element von M so schreiben wir x M. Wir sagen auch:
2.1 Mengen Unter einer Menge verstehen wir eine Zusammenfassung von Objekten zu einem Ganzen. Die Objekte heiÿen Elemente. Ist M eine Menge und x ein Element von M so schreiben wir x M. Wir sagen auch:
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/42 Graphische Darstellung von Zusammenhängen schon an vielen Stellen
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/42 Graphische Darstellung von Zusammenhängen schon an vielen Stellen
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen
 Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 20 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 20 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Grundlagen: 1. Logik. Aussagen und Aussagenformen Wahrheitstabellen; Tautologien und Kontradiktionen Logische Äquivalenz. Prädikate und Quantoren
 Zusammenfassung Grundlagen Logik, Mengen, Relationen, Folgen & Mengenfamilien, Kardinalitäten Techniken Mathematisches Beweisen, Induktion, Kombinatorische Beweise Strukturen Graphen 1 Grundlagen: 1. Logik
Zusammenfassung Grundlagen Logik, Mengen, Relationen, Folgen & Mengenfamilien, Kardinalitäten Techniken Mathematisches Beweisen, Induktion, Kombinatorische Beweise Strukturen Graphen 1 Grundlagen: 1. Logik
Wir starten mit der Entwicklung einer algebraischen Struktur, welche u.a. gut zur Kennzeichnung von Geometrien geeignet ist.
 2 Verbände Wir starten mit der Entwicklung einer algebraischen Struktur, welche u.a. gut zur Kennzeichnung von Geometrien geeignet ist. 2.1 Verbandsdefinition. Beispiele 2.1.1 Definition (Verband): Sei
2 Verbände Wir starten mit der Entwicklung einer algebraischen Struktur, welche u.a. gut zur Kennzeichnung von Geometrien geeignet ist. 2.1 Verbandsdefinition. Beispiele 2.1.1 Definition (Verband): Sei
Konstruktion der reellen Zahlen
 Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Zusammenfassung der letzten LVA. Diskrete Mathematik
 Zusammenfassung Zusammenfassung der letzten LVA Diskrete Mathematik Christina Kohl Georg Moser Oleksandra Panasiuk Christian Sternagel Vincent van Oostrom (Beweisformen) Beweisformen sind etwa (i) deduktive
Zusammenfassung Zusammenfassung der letzten LVA Diskrete Mathematik Christina Kohl Georg Moser Oleksandra Panasiuk Christian Sternagel Vincent van Oostrom (Beweisformen) Beweisformen sind etwa (i) deduktive
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
5.9 Permutationsgruppen. Sei nun π S n. Es existiert folgende naive Darstellung: Kürzer schreibt man auch
 5.9 Permutationsgruppen Definition 103 Eine Permutation ist eine bijektive Abbildung einer endlichen Menge auf sich selbst; o. B. d. A. sei dies die Menge U := {1, 2,..., n}. S n (Symmetrische Gruppe für
5.9 Permutationsgruppen Definition 103 Eine Permutation ist eine bijektive Abbildung einer endlichen Menge auf sich selbst; o. B. d. A. sei dies die Menge U := {1, 2,..., n}. S n (Symmetrische Gruppe für
Anhang B. Relationenalgebraische Definitionen. B.1 Relationen
 Anhang B Relationenalgebraische Definitionen Die relationenalgebraischen Definitionen bilden die Grundlage der formalen Aspekte der Projekte WebReference und InterMediate [Her00]. Sie sind [SS89] entnommen.
Anhang B Relationenalgebraische Definitionen Die relationenalgebraischen Definitionen bilden die Grundlage der formalen Aspekte der Projekte WebReference und InterMediate [Her00]. Sie sind [SS89] entnommen.
Teil 4. Mengen und Relationen
 Teil 4 Mengen und Relationen KAPITEL 10 Äquivalenzrelationen und Faktormengen 1. Äquivalenzrelationen Wir nennen eine Relation von A nach A auch eine Relation auf A. DEFINITION 10.1. SeiΡeine Relation
Teil 4 Mengen und Relationen KAPITEL 10 Äquivalenzrelationen und Faktormengen 1. Äquivalenzrelationen Wir nennen eine Relation von A nach A auch eine Relation auf A. DEFINITION 10.1. SeiΡeine Relation
Logische Grundlagen der Mathematik, WS 2014/15
 Logische Grundlagen der Mathematik, WS 0/ Thomas Timmermann 8. Januar 0 Kardinalzahlen und die Mächtigkeit von Mengen Gleichmächtigkeit von Menge Zur Erinnerung: Wir wollen unendlich große Mengen hinsichtlich
Logische Grundlagen der Mathematik, WS 0/ Thomas Timmermann 8. Januar 0 Kardinalzahlen und die Mächtigkeit von Mengen Gleichmächtigkeit von Menge Zur Erinnerung: Wir wollen unendlich große Mengen hinsichtlich
Kapitel 1. Grundlagen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Diskrete Strukturen 5.9 Permutationsgruppen 168/558 c Ernst W. Mayr
 Bemerkung: Der folgende Abschnitt Boolesche Algebren ist (im WS 2010/11) nicht Teil des Prüfungsstoffs, soweit nicht Teile daraus in der Übung behandelt werden! Diskrete Strukturen 5.9 Permutationsgruppen
Bemerkung: Der folgende Abschnitt Boolesche Algebren ist (im WS 2010/11) nicht Teil des Prüfungsstoffs, soweit nicht Teile daraus in der Übung behandelt werden! Diskrete Strukturen 5.9 Permutationsgruppen
Vorkurs Mathematik für Informatiker
 Vorkurs Mathematik für Informatiker 5. Relationen Thomas Huckle, Kilian Röhner Technische Universität München 9.10.2017 Relationen Mit Relationen können wir Beziehungen zwischen je zwei Dingen ausdrücken.
Vorkurs Mathematik für Informatiker 5. Relationen Thomas Huckle, Kilian Röhner Technische Universität München 9.10.2017 Relationen Mit Relationen können wir Beziehungen zwischen je zwei Dingen ausdrücken.
Zur Zykelschreibweise von Permutationen
 Zur Zykelschreibweise von Permutationen Olivier Sète 16. Juni 2010 1 Grundlagen Definition 1.1. Eine Permutation von {1, 2,..., n} ist eine bijektive Abbildung σ : {1, 2,..., n} {1, 2,..., n}, i σ(i).
Zur Zykelschreibweise von Permutationen Olivier Sète 16. Juni 2010 1 Grundlagen Definition 1.1. Eine Permutation von {1, 2,..., n} ist eine bijektive Abbildung σ : {1, 2,..., n} {1, 2,..., n}, i σ(i).
Relationen (Teschl/Teschl 5.1)
 Relationen (Teschl/Teschl 5.1) Eine (binäre) Relation zwischen den Mengen M und N ist eine Teilmenge R der Produktmenge M N. Beispiele M Menge aller Studierenden, N Menge aller Vorlesungen, R : {(x, y)
Relationen (Teschl/Teschl 5.1) Eine (binäre) Relation zwischen den Mengen M und N ist eine Teilmenge R der Produktmenge M N. Beispiele M Menge aller Studierenden, N Menge aller Vorlesungen, R : {(x, y)
Geordnete Mengen. Eine Relation heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv, transitiv und antisymmetrisch ist.
 Geordnete Mengen Eine Relation heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv, transitiv und antisymmetrisch ist. Ist eine Ordnungsrelation auf eine geordnete Menge., dann nennt man Die Namensgebung
Geordnete Mengen Eine Relation heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv, transitiv und antisymmetrisch ist. Ist eine Ordnungsrelation auf eine geordnete Menge., dann nennt man Die Namensgebung
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
3 Allgemeine Algebren
 Grundlagen der Mathematik für Informatiker 1 3 Allgemeine Algebren Definition 3.1 Für eine Menge A nennen wir eine n-stellige Funktion ω : A n A eine n-äre algebraische Operation. Bemerkung zum Fall n
Grundlagen der Mathematik für Informatiker 1 3 Allgemeine Algebren Definition 3.1 Für eine Menge A nennen wir eine n-stellige Funktion ω : A n A eine n-äre algebraische Operation. Bemerkung zum Fall n
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Boolsche Algebra 3.3 Induktion und Rekursion Peer Kröger (LMU München) Einführung in die Programmierung WS 16/17 46 / 708 Überblick
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Boolsche Algebra 3.3 Induktion und Rekursion Peer Kröger (LMU München) Einführung in die Programmierung WS 16/17 46 / 708 Überblick
Logische Grundlagen der Mathematik, WS 2014/15
 Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 26. November 2014 Was kommt nach den natürlichen Zahlen? Mehr als die natürlichen Zahlen braucht man nicht, um einige der schwierigsten
Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 26. November 2014 Was kommt nach den natürlichen Zahlen? Mehr als die natürlichen Zahlen braucht man nicht, um einige der schwierigsten
5. Äquivalenzrelationen
 5. Äquivalenzrelationen 35 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will, so kann es sinnvoll sein, zunächst kleinere, einfachere Mengen (bzw. Gruppen)
5. Äquivalenzrelationen 35 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will, so kann es sinnvoll sein, zunächst kleinere, einfachere Mengen (bzw. Gruppen)
Diskrete Strukturen und Logik WiSe 2006/07 in Trier. Henning Fernau Universität Trier
 Diskrete Strukturen und Logik WiSe 2006/07 in Trier Henning Fernau Universität Trier fernau@informatik.uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik &
Diskrete Strukturen und Logik WiSe 2006/07 in Trier Henning Fernau Universität Trier fernau@informatik.uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik &
5 Relationen. Formale Grundlagen der Informatik I Herbstsemester 2012. Robert Marti
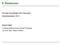 Formale Grundlagen der Informatik I Herbstsemester 2012 Robert Marti Vorlesung teilweise basierend auf Unterlagen von Prof. emer. Helmut Schauer Allgemeine Definition einer Relation Eine n-stellige Relation
Formale Grundlagen der Informatik I Herbstsemester 2012 Robert Marti Vorlesung teilweise basierend auf Unterlagen von Prof. emer. Helmut Schauer Allgemeine Definition einer Relation Eine n-stellige Relation
Ordnungsrelationen auf Mengen. Beispiel einer Ordnungsrelation. Spezielle Elemente von Ordnungen. Spezielle Elemente von Ordnungen
 Ordnungsrelationen auf Mengen! Eine (partielle) Ordnungsrelation oder kurz Ordnung O auf einer Menge M ist eine Relation, die reflexiv, antisymmetrisch und transitiv ist. Beispiel: M = { 1, 2, 3 }, O =
Ordnungsrelationen auf Mengen! Eine (partielle) Ordnungsrelation oder kurz Ordnung O auf einer Menge M ist eine Relation, die reflexiv, antisymmetrisch und transitiv ist. Beispiel: M = { 1, 2, 3 }, O =
(b) Man nennt die Menge M beschränkt, wenn sie nach oben und unten beschränkt ist.
 8 Punktmengen Für die Menge M = { 1 n ; n N } ist 1 = max(m), denn 1 M und 1 n 1 für alle n N. Die Menge M besitzt aber kein Minimum, denn zu jeder Zahl x = 1 n M existiert ein y M mit y < x, etwa y =
8 Punktmengen Für die Menge M = { 1 n ; n N } ist 1 = max(m), denn 1 M und 1 n 1 für alle n N. Die Menge M besitzt aber kein Minimum, denn zu jeder Zahl x = 1 n M existiert ein y M mit y < x, etwa y =
Diskrete Strukturen. Wintersemester 2007/08 Lösungsblatt Januar 2008
 Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 4
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 4
17 Lineare Abbildungen
 Chr.Nelius: Lineare Algebra II (SS2005) 1 17 Lineare Abbildungen Wir beginnen mit der Klärung des Abbildungsbegriffes. (17.1) DEF: M und N seien nichtleere Mengen. Eine Abbildung f von M nach N (in Zeichen:
Chr.Nelius: Lineare Algebra II (SS2005) 1 17 Lineare Abbildungen Wir beginnen mit der Klärung des Abbildungsbegriffes. (17.1) DEF: M und N seien nichtleere Mengen. Eine Abbildung f von M nach N (in Zeichen:
w a is die Anzahl der Vorkommen von a in w Beispiel: abba a = 2
 1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
Mathematische Grundlagen der Computerlinguistik
 Centrum für Informations- und Sprachverarbeitung (CIS) 10. Juni 2014 Table of Contents 1 2 Äquivalenz Der Begriff der Äquivalenz verallgemeinert den Begriff der Gleichheit. Er beinhaltet in einem zu präzisierenden
Centrum für Informations- und Sprachverarbeitung (CIS) 10. Juni 2014 Table of Contents 1 2 Äquivalenz Der Begriff der Äquivalenz verallgemeinert den Begriff der Gleichheit. Er beinhaltet in einem zu präzisierenden
0 Mengen und Abbildungen, Gruppen und Körper
 0 Mengen und Abbildungen, Gruppen und Körper In diesem Paragrafen behandeln wir einige für die Lineare Algebra und für die Analysis wichtige Grundbegriffe. Wir beginnen mit dem Begriff der Menge. Auf Cantor
0 Mengen und Abbildungen, Gruppen und Körper In diesem Paragrafen behandeln wir einige für die Lineare Algebra und für die Analysis wichtige Grundbegriffe. Wir beginnen mit dem Begriff der Menge. Auf Cantor
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen
 Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 25 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 25 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Lineare Algebra 1. Detlev W. Hoffmann. WS 2013/14, TU Dortmund
 Lineare Algebra 1 Detlev W. Hoffmann WS 2013/14, TU Dortmund 1 Mengen und Zahlen 1.1 Mengen und Abbildungen Eine Menge ist eine Zusammenfassung wohlunterscheidbarer Objekte unserer Anschauung/unseres Denkens/unserer
Lineare Algebra 1 Detlev W. Hoffmann WS 2013/14, TU Dortmund 1 Mengen und Zahlen 1.1 Mengen und Abbildungen Eine Menge ist eine Zusammenfassung wohlunterscheidbarer Objekte unserer Anschauung/unseres Denkens/unserer
Formale Methoden 1. Gerhard Jäger 14. November Uni Bielefeld, WS 2007/2008 1/17
 1/17 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 14. November 2007 2/17 Komposition von Relationen und Funktionen seien R A B und S B C Relationen neue
1/17 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 14. November 2007 2/17 Komposition von Relationen und Funktionen seien R A B und S B C Relationen neue
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/18
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/18 9. November 2017 1/34 Beispiel 3.6 Wir können die rationalen Zahlen wie folgt konstruieren:
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/18 9. November 2017 1/34 Beispiel 3.6 Wir können die rationalen Zahlen wie folgt konstruieren:
Serie 2: Relationen, Abbildungen, Mächtigkeit, Gruppen
 D-MATH Lineare Algebra I HS 2016 Dr. Meike Akveld Serie 2: Relationen, Abbildungen, Mächtigkeit, Gruppen 1. Auf Z definieren wir eine Relation durch x, y Z : (x y : x y ist gerade) a) Zeigen Sie, dass
D-MATH Lineare Algebra I HS 2016 Dr. Meike Akveld Serie 2: Relationen, Abbildungen, Mächtigkeit, Gruppen 1. Auf Z definieren wir eine Relation durch x, y Z : (x y : x y ist gerade) a) Zeigen Sie, dass
= n (n 1) 2 dies beruht auf der Auswahl einer zweielementigen Teilmenge aus V = n. Als Folge ergibt sich, dass ein einfacher Graph maximal ( n E = 2
 1 Graphen Definition: Ein Graph G = (V,E) setzt sich aus einer Knotenmenge V und einer (Multi)Menge E V V, die als Kantenmenge bezeichnet wird, zusammen. Falls E symmetrisch ist, d.h.( u,v V)[(u,v) E (v,u)
1 Graphen Definition: Ein Graph G = (V,E) setzt sich aus einer Knotenmenge V und einer (Multi)Menge E V V, die als Kantenmenge bezeichnet wird, zusammen. Falls E symmetrisch ist, d.h.( u,v V)[(u,v) E (v,u)
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/77 Überblick Äquivalenzrelationen Definition Äquivalenzrelationen
Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/77 Überblick Äquivalenzrelationen Definition Äquivalenzrelationen
Grundlagen der Ordnungs- & Verbandstheorie
 Grundlagen der Ordnungs- & Verbandstheorie Francesco Kriegel TU Dresden Fakultät Mathematik Institut Algebra 28. September 2008 Inhaltsverzeichnis Kapitel 1 Grundlagen 1 1.1 Relationen.............................................
Grundlagen der Ordnungs- & Verbandstheorie Francesco Kriegel TU Dresden Fakultät Mathematik Institut Algebra 28. September 2008 Inhaltsverzeichnis Kapitel 1 Grundlagen 1 1.1 Relationen.............................................
Formale Grundlagen 2008W. Vorlesung im 2008S Institut für Algebra Johannes Kepler Universität Linz
 Formale Grundlagen Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Definition Sei A eine Menge und ɛ A A A eine zweistellige
Formale Grundlagen Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Definition Sei A eine Menge und ɛ A A A eine zweistellige
Georg Ferdinand Ludwig Philipp Cantor geb in St. Petersburg, gest in Halle
 Kapitel 1 Mengen, Relationen, Abbildungen 1.1 Mengen Georg Cantor, der Begründer der Mengenlehre, hat 1895 in [1] eine Menge folgendermaßen definiert: Unter einer Menge verstehen wir jede Zusammenfassung
Kapitel 1 Mengen, Relationen, Abbildungen 1.1 Mengen Georg Cantor, der Begründer der Mengenlehre, hat 1895 in [1] eine Menge folgendermaßen definiert: Unter einer Menge verstehen wir jede Zusammenfassung
Theoretische Informatik
 Mathematische Grundlagen Patrick Horster Universität Klagenfurt Informatik Systemsicherheit WS-2007-Anhang-1 Allgemeines In diesem einführenden Kapitel werden zunächst elementare Grundlagen kurz aufgezeigt,
Mathematische Grundlagen Patrick Horster Universität Klagenfurt Informatik Systemsicherheit WS-2007-Anhang-1 Allgemeines In diesem einführenden Kapitel werden zunächst elementare Grundlagen kurz aufgezeigt,
Lineare Algebra und Analytische Geometrie
 Lineare Algebra und Analytische Geometrie Manuel Kauers Institut für Algebra Johannes Kepler Universität Version: 6. Dezember 25 2 Inhalt Teil I Algebraische Strukturen 5 Mengen.......................................
Lineare Algebra und Analytische Geometrie Manuel Kauers Institut für Algebra Johannes Kepler Universität Version: 6. Dezember 25 2 Inhalt Teil I Algebraische Strukturen 5 Mengen.......................................
Einführung in die Semantik, 2./3. Sitzung Mengen / Relatione
 Eigenschaften von Einführung in die Semantik, 2./3. Sitzung Mengen / / Göttingen 2. November 2006 Eigenschaften von Mengenlehre Eigenschaften von Eigenschaften von Das Konzept Menge Eine Menge ist eine
Eigenschaften von Einführung in die Semantik, 2./3. Sitzung Mengen / / Göttingen 2. November 2006 Eigenschaften von Mengenlehre Eigenschaften von Eigenschaften von Das Konzept Menge Eine Menge ist eine
Algorithmen und Datenstrukturen SS09. Foliensatz 16. Michael Brinkmeier. Technische Universität Ilmenau Institut für Theoretische Informatik
 Foliensatz 16 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 2009 TU Ilmenau Seite 1 / 45 Graphen TU Ilmenau Seite 2 / 45 Graphen 1 2 3 4 5 6 7 8
Foliensatz 16 Michael Brinkmeier Technische Universität Ilmenau Institut für Theoretische Informatik Sommersemester 2009 TU Ilmenau Seite 1 / 45 Graphen TU Ilmenau Seite 2 / 45 Graphen 1 2 3 4 5 6 7 8
1.2 Modulare Arithmetik
 Algebra I 8. April 2008 c Rudolf Scharlau, 2002 2008 11 1.2 Modulare Arithmetik Wir erinnern an die Notation für Teilbarkeit: m c für m, c Z heißt, dass ein q Z existiert mit qm = c. Definition 1.2.1 Sei
Algebra I 8. April 2008 c Rudolf Scharlau, 2002 2008 11 1.2 Modulare Arithmetik Wir erinnern an die Notation für Teilbarkeit: m c für m, c Z heißt, dass ein q Z existiert mit qm = c. Definition 1.2.1 Sei
MATHEMATIK FÜR NATURWISSENSCHAFTLER I WINTERSEMESTER 2016/ OKTOBER 2016
 MATHEMATIK FÜR NATURWISSENSCHAFTLER I WINTERSEMESTER 2016/17 MARK HAMILTON LMU MÜNCHEN 1.1. Grundbegriffe zu Mengen. 1. 17. OKTOBER 2016 Definition 1.1 (Mengen und Elemente). Eine Menge ist die Zusammenfassung
MATHEMATIK FÜR NATURWISSENSCHAFTLER I WINTERSEMESTER 2016/17 MARK HAMILTON LMU MÜNCHEN 1.1. Grundbegriffe zu Mengen. 1. 17. OKTOBER 2016 Definition 1.1 (Mengen und Elemente). Eine Menge ist die Zusammenfassung
Kapitel 2 Mathematische Grundlagen
 Kapitel 2 Mathematische Grundlagen Ziel: Einführung/Auffrischung einiger mathematischer Grundlagen 2.1 Mengen, Relationen, Ordnungen Definition: Eine Menge ist eine Zusammenfassung von wohlbestimmten und
Kapitel 2 Mathematische Grundlagen Ziel: Einführung/Auffrischung einiger mathematischer Grundlagen 2.1 Mengen, Relationen, Ordnungen Definition: Eine Menge ist eine Zusammenfassung von wohlbestimmten und
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/76 Überblick Äquivalenzrelationen Definition Äquivalenzrelationen
Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/76 Überblick Äquivalenzrelationen Definition Äquivalenzrelationen
Inhalt der Vorlesung Elemente der Algebra und Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS Grundlegende Definitionen (Wiederholung)
 Inhalt der Vorlesung Elemente der Algebra und Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel I. Gruppen 1 Grundlegende Definitionen (Wiederholung) 1.1 Definition. Eine Gruppe ist ein Paar
Inhalt der Vorlesung Elemente der Algebra und Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel I. Gruppen 1 Grundlegende Definitionen (Wiederholung) 1.1 Definition. Eine Gruppe ist ein Paar
Lineare Algebra I Zusammenfassung
 Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
R = {(1, 1), (2, 2), (3, 3)} K 1 = {1} K 2 = {2} K 3 = {3}
 Äquivalenzrelationen Aufgabe 1. Lesen Sie im Skript nach was eine Äquivalenzrelation und eine Äquivalenzklasse ist. Gegeben ist die Menge A = {1, 2, 3. Finden Sie 3 Äquivalenzrelationen auf A und geben
Äquivalenzrelationen Aufgabe 1. Lesen Sie im Skript nach was eine Äquivalenzrelation und eine Äquivalenzklasse ist. Gegeben ist die Menge A = {1, 2, 3. Finden Sie 3 Äquivalenzrelationen auf A und geben
Ordnungsrelationen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Ordnungsrelationen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Geordnete Mengen Eine Relation R A A heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv,
Ordnungsrelationen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Geordnete Mengen Eine Relation R A A heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv,
7 Äquivalenzrelationen
 71 7 Äquivalenzrelationen 7.1 Äquivalenzrelationen und Klassen Definition Eine Relation R auf einer Menge oder einem allgemeineren Objektbereich heißt eine Äquivalenzrelation, falls sie reflexiv, symmetrisch
71 7 Äquivalenzrelationen 7.1 Äquivalenzrelationen und Klassen Definition Eine Relation R auf einer Menge oder einem allgemeineren Objektbereich heißt eine Äquivalenzrelation, falls sie reflexiv, symmetrisch
Skript und Übungen Teil II
 Vorkurs Mathematik Herbst 2009 M. Carl E. Bönecke Skript und Übungen Teil II Das erste Semester wiederholt die Schulmathematik in einer neuen axiomatischen Sprache; es ähnelt damit dem nachträglichen Erlernen
Vorkurs Mathematik Herbst 2009 M. Carl E. Bönecke Skript und Übungen Teil II Das erste Semester wiederholt die Schulmathematik in einer neuen axiomatischen Sprache; es ähnelt damit dem nachträglichen Erlernen
Lineare Algebra I 5. Tutorium Die Restklassenringe /n
 Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Graphen und Bäume. A.1 Graphen
 Algorithmen und Datenstrukturen 96 A Graphen und Bäume A.1 Graphen Ein gerichteter Graph (auch Digraph) G ist ein Paar (V, E), wobei V eine endliche Menge und E eine Relation auf V ist, d.h. E V V. V heißt
Algorithmen und Datenstrukturen 96 A Graphen und Bäume A.1 Graphen Ein gerichteter Graph (auch Digraph) G ist ein Paar (V, E), wobei V eine endliche Menge und E eine Relation auf V ist, d.h. E V V. V heißt
