Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen
|
|
|
- Hannelore Melsbach
- vor 6 Jahren
- Abrufe
Transkript
1 Mathematische Grundlagen der Computerlinguistik Ordnungsrelationen Dozentin: Wiebke Petersen 4. Foliensatz Wiebke Petersen math. Grundlagen 89
2 starke / schwache Ordnungen Eine Ordnung R einer Menge A ist eine binäre Relation R A A. Man unterscheidet zwischen starken und schwachen Ordnungen: Eine binäre Relation ist eine schwache Ordnung, gdw. sie transitiv, reflexiv und anti-symmetrisch ist. Eine binäre Relation ist eine starke Ordnung, gdw. sie transitiv, irreflexiv und asymmetrisch ist. Starke Ordnungen werden auch strikte Ordnungen genannt. Wiebke Petersen math. Grundlagen 90
3 korrespondierende Ordnungen Eine schwache Ordnung R A A und eine starke Ordnung S korrespondieren zueinander gdw. R = S id A Beispiele: Sei A = {a, b, c, d} R 1 = { a, b, a, c, a, d, b, c, a, a, b, b, c, c, d, d } R 2 = { b, a, c, b, c, a, b, b, a, a, c, c, d, d } R 3 = { d, c, d, b, d, a, c, b, c, a, b, a, a, a, b, b, c, c, d, d } korrespondierende starke Ordnungen: S 1 = { a, b, a, c, a, d, b, c } S 2 = { b, a, c, b, c, a } S 3 = { d, c, d, b, d, a, c, b, c, a, b, a } Wiebke Petersen math. Grundlagen 91
4 geordnete Mengen Eine geordnete Menge ist ein Paar (M, R), bestehend aus einer Menge M und einer Ordnung R von M. Beispiele: (POT (M), ) ist eine schwach geordnete Menge. (POT (M), ) ist die korrespondierende stark geordnete Menge. (N, ) ist eine schwach geordnete Menge. (N, <) ist die korrespondierende stark geordnete Menge. Wiebke Petersen math. Grundlagen 92
5 Terminologie Sei (M, R) eine (stark oder schwach) geordnete Menge. a ist ein Vorgänger von b gdw. R(a, b). a ist ein Nachfolger von b gdw. R(b, a). a ist ein unmittelbarer Vorgänger (oder unterer Nachbar) von b gdw. a b, R(a, b), und es gibt kein c M mit c {a, b} so dass R(a, c) und R(c, b). a ist ein unmittelbarer Nachfolger (oder oberer Nachbar) von b gdw. b ein unmittelbarer Vorgänger von a ist. Wenn a ein unmittelbarer Vorgänger von b ist, dann schreibt man häufig a b. Wiebke Petersen math. Grundlagen 93
6 Hassediagramm Konstruktion Eine endliche geordnete Mengen (M, R) kann durch ein Hassediagramm veranschaulicht werden; dieses erhält man, indem man für jedes Element von M einen Punkt zeichnet und zwar so, daß a unterhalb von b liegt, wenn a b und (a, b) R. Zwei Punkte a und b werden mit einer Linie verbunden, wenn a b. Übung: Zeichnen sie die folgenden Hasse-Diagramme Hasse-Diagramm von ({a, b, c}, R 2) mit R 2 = { b, a, c, b, c, a, b, b, a, a, c, c } Hasse-Diagramm von (POT ({1, 2, 3}), ) Wiebke Petersen math. Grundlagen 94
7 Beispiele Hasse-Diagramm von ({a, b, c}, R 2) mit R 2 = { b, a, c, b, c, a, b, b, a, a, c, c } Hasse-Diagramm von (POT ({1, 2, 3}), ) Wiebke Petersen math. Grundlagen 95
8 Beispiele Hasse-Diagramm von ({a, b, c}, R 2) mit R 2 = { b, a, c, b, c, a, b, b, a, a, c, c } a Hasse-Diagramm von (POT ({1, 2, 3}), ) {1, 2, 3} {1, 2} {1, 3} {2, 3} b {1} {2} {3} c { } Wiebke Petersen math. Grundlagen 95
9 Hasse-Diagramme: Beispiel Teilbarkeit Sei M = {x N 60 ist durch x ohne Rest teilbar}, und R = { x, y M M y ist durch x ohne Rest teilbar}. Hassediagramm der geordneten Menge (M, R): Wiebke Petersen math. Grundlagen 96
10 Hasse-Diagramme: Beispiel Teilbarkeit Sei M = {x N 60 ist durch x ohne Rest teilbar}, und R = { x, y M M y ist durch x ohne Rest teilbar}. Hassediagramm der geordneten Menge (M, R): Wiebke Petersen math. Grundlagen 96
11 Übung Zeichnen sie ein Hasse-Diagramm zur geordneten Menge M = ({{1, 2, 3, 4, 5}, {1, 2, 3, 5}, {1, 3, 4}, {2, 4, 5}, {1, 2, 3}, {1, 3}, {2, 4}, {1, 5}, {1}, {3}, {4}, {5}, {}}, ). Wiebke Petersen math. Grundlagen 97
12 totale/partielle Ordnung Eine binäre Ordnungsrelation ist eine totale Ordnung, gdw. sie konnex ist. Eine binäre Relation R M M ist konnex (bzw. linear) gdw. für alle x, y M mit x y gilt: x, y R oder y, x R (oder beides). Das Hassediagramm einer total geordneten, endlichen Menge bildet eine Linie. Kein Element hat mehr als einen oberen oder unteren Nachbarn. Totale Ordnungen werden auch lineare Ordnungen genannt. In Abgrenzung zu totalen Ordnungen werden allgemeine Ordnungen auch partielle Ordnungen (oder Halbordnungen) genannt. Im Englischen spricht man von poset (partially ordered set). Wiebke Petersen math. Grundlagen 98
13 minimale und maximale Elemente Sei R A A eine Ordnung (stark oder schwach). Hinweise: Ein Element x A ist minimal gdw. es kein y x gibt, das Vorgänger von x ist. Ein Element x A ist maximal gdw. es kein y x gibt, das Nachfolger von x ist. x A ist das Minimum von A, wenn x Vorgänger jedes anderen Elements von A ist (für alle y A mit x y gilt x y). x A ist das Maximum von A, wenn x Nachfolger jedes anderen Elements von A ist (für alle y A mit x y gilt y x). eine total geordnete Menge kann höchstens ein minimales und höchstens ein maximales Element haben. eine partiell geordnete Menge kann beliebig viele minimale und maximale Elemente aber höchstens ein Minimum und höchstens ein Maximum haben. Wiebke Petersen math. Grundlagen 99
14 Beispiel Wiebke Petersen math. Grundlagen 100
15 Beispiel a ist das einzige maximale Element und somit das Maximum der geordneten Menge. d und e sind die minimalen Elemente der geordneten Menge. die geordnete Menge hat kein Minimum, Wiebke Petersen math. Grundlagen 100
16 Vergleichbarkeit / Kette / Antikette Sei (M, R) eine geordnete Menge und seien a und b Elemente von M. a und b heißen vergleichbar, falls arb oder bra; sonst unvergleichbar. Eine Teilmenge K von M heißt Kette, g.d.w. für beliebige a, b K gilt, daß sie vergleichbar sind. Eine Teilmenge A von M heißt Antikette, g.d.w. für beliebige a, b A gilt, daß sie unvergleichbar sind. Wiebke Petersen math. Grundlagen 101
17 Vergleichbarkeit / Kette / Antikette Sei (M, R) eine geordnete Menge und seien a und b Elemente von M. a und b heißen vergleichbar, falls arb oder bra; sonst unvergleichbar. Eine Teilmenge K von M heißt Kette, g.d.w. für beliebige a, b K gilt, daß sie vergleichbar sind. Eine Teilmenge A von M heißt Antikette, g.d.w. für beliebige a, b A gilt, daß sie unvergleichbar sind. Satz von Dilworth Für eine geordnete endliche Menge (M, R) gilt: Die maximale Anzahl von Elementen in einer Antikette von (M, R) ist gleich der kleinsten Anzahl von Ketten von (M, R), die man für eine Partition von M benötigt. Wiebke Petersen math. Grundlagen 101
18 Vergleichbarkeit / Kette / Antikette Sei (M, R) eine geordnete Menge und seien a und b Elemente von M. a und b heißen vergleichbar, falls arb oder bra; sonst unvergleichbar. Eine Teilmenge K von M heißt Kette, g.d.w. für beliebige a, b K gilt, daß sie vergleichbar sind. Eine Teilmenge A von M heißt Antikette, g.d.w. für beliebige a, b A gilt, daß sie unvergleichbar sind. Satz von Dilworth Für eine geordnete endliche Menge (M, R) gilt: Die maximale Anzahl von Elementen in einer Antikette von (M, R) ist gleich der kleinsten Anzahl von Ketten von (M, R), die man für eine Partition von M benötigt. Höhe / Breite Die Höhe einer endlichen geordneten Menge (M, R) ist gleich der maximalen Anzahl von Elementen einer Kette von (M, R). Die Breite einer endlichen geordneten Menge (M, R) ist gleich der maximalen Anzahl von Elementen einer Antikette von (M, R). Wiebke Petersen math. Grundlagen 101
19 Beispiel Wiebke Petersen math. Grundlagen 102
20 Beispiel Die Elemente a und b sind vergleichbar. d und e sind unvergleichbar. {a, b, d} ist eine Kette der geordneten Menge. {b, c} ist Antikette der geordneten Menge. Die geordnete Menge hat die Höhe 3 und die Breite 2. Die Ketten {a, b, d} und {c, e} bilden eine minimale Partition in Ketten der geordneten Menge. Wiebke Petersen math. Grundlagen 102
21 Intervall / Ideal / Filter Sei (M, ) eine geordnete Menge: Intervall: [a, b] := {x M a x b} Hauptideal: (b] := {x M x b} Hauptfilter: [a) := {x M a x} Wiebke Petersen math. Grundlagen 103
22 Beispiel [6, 1] = Wiebke Petersen math. Grundlagen 104
23 Beispiel [6, 1] = {1, 3, 4, 5, 6} (Intervall von 6 bis 1) (4] = Wiebke Petersen math. Grundlagen 104
24 Beispiel [6, 1] = {1, 3, 4, 5, 6} (Intervall von 6 bis 1) (4] = {4, 6, 8} (Hauptideal von 4) [6) = Wiebke Petersen math. Grundlagen 104
25 Beispiel [6, 1] = {1, 3, 4, 5, 6} (Intervall von 6 bis 1) (4] = {4, 6, 8} (Hauptideal von 4) [6) = {1, 2, 3, 4, 5, 6} (Hauptfilter von 6). Wiebke Petersen math. Grundlagen 104
26 Ordnungserhaltende/monotone Abbildungen Definition Seien (M, ) und (M, ) zwei geordnete Mengen. Eine Abbildung (Funktion) f : M M heißt ordnungserhaltend oder monoton, wenn für alle x, y M gilt: Beispiele: wenn x y, dann f (x) f (y) f : N 0 N 0 mit f (x) = 2x ist eine monotone Abbildung von (N 0, ) nach (N 0, ). f : N 0 N 0 mit f (x) = x 2 ist eine monotone Abbildung von (N 0, ) nach (N 0, ). f : Z Z mit f (x) = x 2 ist keine monotone Abbildung von (Z, ) nach (Z, ). Sei M eine endliche Menge. f : POT (M) N 0 mit f (A) = A ist eine ordnungserhaltende Abbildung von (POT (M), ) nach (N 0, ). Wiebke Petersen math. Grundlagen 105
27 Ordnungseinbettung Definition Eine monotone Funktion heißt Ordnungseinbettung, wenn sie injektiv ist, und Ordnungsisomorphismus, wenn sie bijektiv ist. Ein Ordnungsisomorphismus von (M, R) in sich selbst wird auch Ordnungsautomorphismus genannt. Beispiele: f : Z Z mit f (x) = x ist ein Ordnungsisomorphismus von (Z, ) nach (Z, ). f : R R mit f (x) = x ist ein Ordnungsautomorphismus auf (R, ). 2 Wiebke Petersen math. Grundlagen 106
28 Quasiordnung Der Begriff der Quasiordnung ist schwächer als der der Ordnung: Definition Eine binäre Relation R M M ist eine Quasiordnung (oder Präordnung), wenn R Beispiel: reflexiv und transitiv ist. Die Ordnung abs, die die ganzen Zahlen nach ihrem Betrag ordnet ist eine Quasiordnung aber keine Ordnung (beachte, dass 3 abs 3 und 3 abs 3 aber 3 3). Wiebke Petersen math. Grundlagen 107
29 Zusammenfassung: Ordnungen schwache Ordnungen transitiv reflexiv anti- linear/total symmetrisch Quasiordnung partielle Ordnung totale Ordnung Bemerkung: (Schwache) lineare Ordnungsrelationen werden häufig mit, bzw. partielle Ordnungsrelationen mit bezeichnet, auch wenn es sich bei der gegebenen Ordnung weder um eine numerische Größenordnung noch um die Mengeninklusion handelt. Wiebke Petersen math. Grundlagen 108
30 Zusammenfassung: Ordnungen strikte Ordnungen transitiv irreflexiv asymmetrisch linear/total strikte partielle Ordnung strikte totale Ordnung Bemerkung: Strikte Ordnungsrelationen werden häufig mit <, bzw. mit bezeichnet. Man könnte strikte Ordnungen äquivalent auch als transitive, irreflexive und antisymmetrische Relationen definieren, da eine Relation, die irreflexiv und antisymmetrisch ist, immer asymmetrisch ist. Wiebke Petersen math. Grundlagen 109
31 obere / untere Schranke Sei (M, ) eine (partiell) geordnete Menge und K eine Teilmenge von M. Ein Element x von M ist eine obere Schranke von K, g.d.w. für alle y K : y x; eine untere Schranke von K, g.d.w. für alle y K : x y. Die Abbildungen zeigen die Hassediagramme zweier geordneter Mengen. Die rot markierten Elementen haben die blau markierten Elemente als obere und die grün markierten als untere Schranken. Wiebke Petersen math. Grundlagen 110
32 kleinste obere / größte untere Schranke x heißt kleinste obere Schranke oder Supremum von K in M, wenn x eine obere Schranke von K ist und für jede obere Schranke y M von K mit x y die Ungleichung x y gilt. Wir schreiben sup K oder K für das Supremum von K (lese als join ). x heißt größte untere Schranke oder Infimum von K in M, wenn x eine untere Schranke von K ist und für jede untere Schranke y M von K mit x y die Ungleichung y x gilt. Wir schreiben inf K oder K für das Infimum von K (lese als meet ). Wir schreiben x y statt {x, y} und x y statt {x, y}. Die Beispiele der vorangegangenen Folie zeigen, daß es geordnete Mengen M gibt, für die nicht jede Teilmenge K M ein Supremum oder Infimum hat. Wiebke Petersen math. Grundlagen 111
33 kleinste obere / größte untere Schranke x heißt kleinste obere Schranke oder Supremum von K in M, wenn x eine obere Schranke von K ist und für jede obere Schranke y M von K mit x y die Ungleichung x y gilt. Wir schreiben sup K oder K für das Supremum von K (lese als join ). x heißt größte untere Schranke oder Infimum von K in M, wenn x eine untere Schranke von K ist und für jede untere Schranke y M von K mit x y die Ungleichung y x gilt. Wir schreiben inf K oder K für das Infimum von K (lese als meet ). Wir schreiben x y statt {x, y} und x y statt {x, y}. Die Beispiele der vorangegangenen Folie zeigen, daß es geordnete Mengen M gibt, für die nicht jede Teilmenge K M ein Supremum oder Infimum hat. Das Infimum ist also das Maximum aller unteren Schranken und das Supremum ist das Minimum aller oberen Schranken. Wiebke Petersen math. Grundlagen 111
34 Beispiele Für die linear geordnete Menge (R, ) gilt: sup[1, 4] = 4 und inf[1, 4] = 1. Für die partiell geordnete Menge (POT (M), ) mit M = {1, 2, 3, 4} ist das Supremum von K = { {1, 2}, {2, 4}, {1} } die Vereinigung aller Elemente von K, also sup K = {1, 2, 4}. Das Infimum von K ist der Durchschnitt aller Elemente von K, also inf K =. Wiebke Petersen math. Grundlagen 112
35 Verband: ordnungstheoretische Definition Eine geordnete Menge (V, ) ist ein Verband, g.d.w. zu je zwei Elementen x und y aus V auch das Supremum von x und y und das Infimum von x und y Elemente von V sind. vollständiger Verband Ein Verband (V, ) ist ein vollständiger Verband, falls für alle K V gilt, daß sup K V und inf K V. Jeder vollständige Verband hat ein größtes Element sup V, das Einselement (1 V ) genannt, und ein kleinstes Element inf V, das Nullement (0 V ) genannt. Die oberen Nachbarn des Nullelements nennt man die Atome und die unteren Nachbarn des Einselements die Koatome des Verbands. Wiebke Petersen math. Grundlagen 113
36 Bemerkungen Jeder endliche Verband ist vollständig. Da inf = 1 V und sup = 0 V gilt, gibt es keinen vollständigen Verband mit leerer Menge V. Wiebke Petersen math. Grundlagen 114
37 Beispiele (POT (M), ) ist ein vollständiger Verband, entspricht und entspricht. ([2, 5], ) ist ein vollständiger Verband. (R, ) ist ein Verband, aber nicht vollständig. ( {{1, 2}, {2, 4}, {1} }, ) ist kein Verband. Wiebke Petersen math. Grundlagen 115
Diskrete Strukturen Kapitel 2: Grundlagen (Relationen)
 WS 2016/17 Diskrete Strukturen Kapitel 2: Grundlagen (Relationen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
WS 2016/17 Diskrete Strukturen Kapitel 2: Grundlagen (Relationen) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_16
Geordnete Mengen. Eine Relation heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv, transitiv und antisymmetrisch ist.
 Geordnete Mengen Eine Relation heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv, transitiv und antisymmetrisch ist. Ist eine Ordnungsrelation auf eine geordnete Menge., dann nennt man Die Namensgebung
Geordnete Mengen Eine Relation heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv, transitiv und antisymmetrisch ist. Ist eine Ordnungsrelation auf eine geordnete Menge., dann nennt man Die Namensgebung
Ordnungsrelationen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Ordnungsrelationen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Geordnete Mengen Eine Relation R A A heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv,
Ordnungsrelationen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de Geordnete Mengen Eine Relation R A A heißt Ordnung oder Ordnungsrelation, wenn sie reflexiv,
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen
 Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 20 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 20 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
mathematische Grundlagen der Modelltheorie: Mengen, Relationen, Funktionen
 Einführung in die Logik - 6 mathematische Grundlagen der Modelltheorie: Mengen, Relationen, Funktionen Modelltheoretische / Denotationelle Semantik der Prdikatenlogik Ein Modell ist ein künstlich geschaffenes
Einführung in die Logik - 6 mathematische Grundlagen der Modelltheorie: Mengen, Relationen, Funktionen Modelltheoretische / Denotationelle Semantik der Prdikatenlogik Ein Modell ist ein künstlich geschaffenes
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen
 Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 25 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Mathematische Grundlagen der Computerlinguistik Relationen und Funktionen Dozentin: Wiebke Petersen 2. Foliensatz Wiebke Petersen math. Grundlagen 25 n-tupel und Cartesisches Produkt Mengen sind ungeordnet,
Wir starten mit der Entwicklung einer algebraischen Struktur, welche u.a. gut zur Kennzeichnung von Geometrien geeignet ist.
 2 Verbände Wir starten mit der Entwicklung einer algebraischen Struktur, welche u.a. gut zur Kennzeichnung von Geometrien geeignet ist. 2.1 Verbandsdefinition. Beispiele 2.1.1 Definition (Verband): Sei
2 Verbände Wir starten mit der Entwicklung einer algebraischen Struktur, welche u.a. gut zur Kennzeichnung von Geometrien geeignet ist. 2.1 Verbandsdefinition. Beispiele 2.1.1 Definition (Verband): Sei
3. Relationen Erläuterungen und Schreibweisen
 3. Relationen Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob
3. Relationen Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob
Mathematische Grundlagen der Computerlinguistik Bäume
 Mathematische Grundlagen der Computerlinguistik Dozentin: Wiebke Petersen 6. Foliensatz (basierend auf Folien von Gerhard Jäger) Wiebke Petersen math. Grundlagen 1 Baumdiagramme Ein Baumdiagramm eines
Mathematische Grundlagen der Computerlinguistik Dozentin: Wiebke Petersen 6. Foliensatz (basierend auf Folien von Gerhard Jäger) Wiebke Petersen math. Grundlagen 1 Baumdiagramme Ein Baumdiagramm eines
Einführung in die Informatik 2
 Einführung in die Informatik 2 Mathematische Grundbegriffe Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr,
Einführung in die Informatik 2 Mathematische Grundbegriffe Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr,
Anhang B. Relationenalgebraische Definitionen. B.1 Relationen
 Anhang B Relationenalgebraische Definitionen Die relationenalgebraischen Definitionen bilden die Grundlage der formalen Aspekte der Projekte WebReference und InterMediate [Her00]. Sie sind [SS89] entnommen.
Anhang B Relationenalgebraische Definitionen Die relationenalgebraischen Definitionen bilden die Grundlage der formalen Aspekte der Projekte WebReference und InterMediate [Her00]. Sie sind [SS89] entnommen.
Zahlen und metrische Räume
 Zahlen und metrische Räume Natürliche Zahlen : Die natürlichen Zahlen sind die grundlegendste Zahlenmenge, da man diese Menge für das einfache Zählen verwendet. N = {1, 2, 3, 4,...} Ganze Zahlen : Aus
Zahlen und metrische Räume Natürliche Zahlen : Die natürlichen Zahlen sind die grundlegendste Zahlenmenge, da man diese Menge für das einfache Zählen verwendet. N = {1, 2, 3, 4,...} Ganze Zahlen : Aus
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/77 Überblick Äquivalenzrelationen Definition Äquivalenzrelationen
Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/77 Überblick Äquivalenzrelationen Definition Äquivalenzrelationen
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 21: Relationen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 21: Relationen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Vorlesung Diskrete Strukturen Ordnungsrelationen
 Vorlesung Diskrete Strukturen Ordnungsrelationen Bernhard Ganter WS 2009/10 Ein Spiegelei zubereiten... Was muss man tun, wenn man ein Spiegelei brät? HE Herd einschalten PH Pfanne auf den Herd stellen
Vorlesung Diskrete Strukturen Ordnungsrelationen Bernhard Ganter WS 2009/10 Ein Spiegelei zubereiten... Was muss man tun, wenn man ein Spiegelei brät? HE Herd einschalten PH Pfanne auf den Herd stellen
Mengen. Eigenschaften. Spezielle Mengen (1) Prominente Mengen. ! Mengenzugehörigkeit
 Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Zahlen und metrische Räume
 Zahlen und metrische Räume Natürliche Zahlen : Die natürlichen Zahlen sind die grundlegendste Zahlenmenge, da man diese Menge für das einfache Zählen verwendet. N = {1, 2, 3, 4,...} bzw. N 0 = {0, 1, 2,
Zahlen und metrische Räume Natürliche Zahlen : Die natürlichen Zahlen sind die grundlegendste Zahlenmenge, da man diese Menge für das einfache Zählen verwendet. N = {1, 2, 3, 4,...} bzw. N 0 = {0, 1, 2,
Logik für Informatiker. 1. Grundlegende Beweisstrategien. Viorica Sofronie-Stokkermans Universität Koblenz-Landau
 Logik für Informatiker 1. Grundlegende Beweisstrategien Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Mathematisches Beweisen Mathematische ussagen - haben oft
Logik für Informatiker 1. Grundlegende Beweisstrategien Viorica Sofronie-Stokkermans Universität Koblenz-Landau e-mail: sofronie@uni-koblenz.de 1 Mathematisches Beweisen Mathematische ussagen - haben oft
Grundlagen der Mathematik
 Grundlagen der Mathematik Übungsaufgaben zu Kapitel 1 Einführung 1.1.1 Für reelle Zahlen a und b gilt (a+b) (a-b) = a 2 -b 2. Was ist die Voraussetzung? Wie lautet die Behauptung? Beweisen Sie die Behauptung.
Grundlagen der Mathematik Übungsaufgaben zu Kapitel 1 Einführung 1.1.1 Für reelle Zahlen a und b gilt (a+b) (a-b) = a 2 -b 2. Was ist die Voraussetzung? Wie lautet die Behauptung? Beweisen Sie die Behauptung.
6. Induktives Beweisen - Themenübersicht
 6. Induktives Beweisen - Themenübersicht Ordnungsrelationen Partielle Ordnungen Quasiordnungen Totale Ordnungen Striktordnungen Ordnungen und Teilstrukturen Noethersche Induktion Anwendung: Terminierungsbeweise
6. Induktives Beweisen - Themenübersicht Ordnungsrelationen Partielle Ordnungen Quasiordnungen Totale Ordnungen Striktordnungen Ordnungen und Teilstrukturen Noethersche Induktion Anwendung: Terminierungsbeweise
Mathematische Grundlagen der Computerlinguistik
 Centrum für Informations- und Sprachverarbeitung (CIS) 2. Juni 2014 Table of Contents 1 2 Ähnlich wie Funktionen besitzen Relationen charakteristische Eigenschaften. Diese Eigenschaften definieren wie
Centrum für Informations- und Sprachverarbeitung (CIS) 2. Juni 2014 Table of Contents 1 2 Ähnlich wie Funktionen besitzen Relationen charakteristische Eigenschaften. Diese Eigenschaften definieren wie
Mathematik für Informatiker 1 Tutorium
 Mathematik für Informatiker 1 Tutorium Malte Isberner 9.1.2014 M. Isberner MafI1-Tutorium 9.1.2014 1 / 12 Thema heute Thema heute: Verbände M. Isberner MafI1-Tutorium 9.1.2014 2 / 12 Verbände Was ist ein
Mathematik für Informatiker 1 Tutorium Malte Isberner 9.1.2014 M. Isberner MafI1-Tutorium 9.1.2014 1 / 12 Thema heute Thema heute: Verbände M. Isberner MafI1-Tutorium 9.1.2014 2 / 12 Verbände Was ist ein
1 Axiomatische Charakterisierung der reellen. 3 Die natürlichen, die ganzen und die rationalen. 4 Das Vollständigkeitsaxiom und irrationale
 Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Kapitel I Reelle Zahlen 1 Axiomatische Charakterisierung der reellen Zahlen R 2 Angeordnete Körper 3 Die natürlichen, die ganzen und die rationalen Zahlen 4 Das Vollständigkeitsaxiom und irrationale Zahlen
Axiomatik der reellen Zahlen
 Kapitel 13 Axiomatik der reellen Zahlen 13.1 Motivation Analysis beschäftigt sich mit Grenzwerten, Differentiation und Integration. Viele Phänomene in den Natur- und Ingenieurswissenschaften lassen sich
Kapitel 13 Axiomatik der reellen Zahlen 13.1 Motivation Analysis beschäftigt sich mit Grenzwerten, Differentiation und Integration. Viele Phänomene in den Natur- und Ingenieurswissenschaften lassen sich
Kapitel 2 Mathematische Grundlagen
 Kapitel 2 Mathematische Grundlagen Ziel: Einführung/Auffrischung einiger mathematischer Grundlagen 2.1 Mengen, Relationen, Ordnungen Definition: Eine Menge ist eine Zusammenfassung von wohlbestimmten und
Kapitel 2 Mathematische Grundlagen Ziel: Einführung/Auffrischung einiger mathematischer Grundlagen 2.1 Mengen, Relationen, Ordnungen Definition: Eine Menge ist eine Zusammenfassung von wohlbestimmten und
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Formale Methoden 1. Gerhard Jäger 12. Dezember Uni Bielefeld, WS 2007/2008 1/22
 1/22 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 12. Dezember 2007 2/22 Bäume Baumdiagramme Ein Baumdiagramm eines Satzes stellt drei Arten von Information
1/22 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 12. Dezember 2007 2/22 Bäume Baumdiagramme Ein Baumdiagramm eines Satzes stellt drei Arten von Information
Analysis 1, Woche 2. Reelle Zahlen. 2.1 Anordnung. Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität).
 Analysis 1, Woche 2 Reelle Zahlen 2.1 Anordnung Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität). 2. Für jeden a, b K mit a b und b a gilt a = b (Antisymmetrie).
Analysis 1, Woche 2 Reelle Zahlen 2.1 Anordnung Definition 2.1 Man nennt eine Anordnung für K, wenn: 1. Für jeden a K gilt a a (Reflexivität). 2. Für jeden a, b K mit a b und b a gilt a = b (Antisymmetrie).
Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die kontinuierlich ablaufende Zeit.
 Kapitel 4 Reelle Zahlen 4.1 Die reellen Zahlen (Schranken von Mengen; Axiomatik; Anordnung; Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die
Kapitel 4 Reelle Zahlen 4.1 Die reellen Zahlen (Schranken von Mengen; Axiomatik; Anordnung; Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die
2 Modellierung mit Wertebereichen
 2 Modellierung mit Wertebereichen Mod-2.1 In der Modellierung von Systemen, Aufgaben, Lösungen kommen Objekte unterschiedlicher Art und Zusammensetzung vor. Für Teile des Modells wird angegeben, aus welchem
2 Modellierung mit Wertebereichen Mod-2.1 In der Modellierung von Systemen, Aufgaben, Lösungen kommen Objekte unterschiedlicher Art und Zusammensetzung vor. Für Teile des Modells wird angegeben, aus welchem
17 R E L AT I O N E N
 17 R E L AT I O N E N 17.1 äquivalenzrelationen 17.1.1 Definition In Abschnitt 11.2.1 hatten wir schon einmal erwähnt, dass eine Relation R M M auf einer Menge M, die reflexiv, symmetrisch und transitiv
17 R E L AT I O N E N 17.1 äquivalenzrelationen 17.1.1 Definition In Abschnitt 11.2.1 hatten wir schon einmal erwähnt, dass eine Relation R M M auf einer Menge M, die reflexiv, symmetrisch und transitiv
Konstruktion der reellen Zahlen
 Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
(1.18) Def.: Eine Abbildung f : M N heißt
 Zurück zur Mengenlehre: Abbildungen zwischen Mengen (1.17) Def.: Es seien M, N Mengen. Eine Abbildung f : M N von M nach N ist eine Vorschrift, die jedem x M genau ein Element f(x) N zuordnet. a) M = N
Zurück zur Mengenlehre: Abbildungen zwischen Mengen (1.17) Def.: Es seien M, N Mengen. Eine Abbildung f : M N von M nach N ist eine Vorschrift, die jedem x M genau ein Element f(x) N zuordnet. a) M = N
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Boolsche Algebra 3.3 Induktion und Rekursion Peer Kröger (LMU München) Einführung in die Programmierung WS 16/17 46 / 708 Überblick
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Boolsche Algebra 3.3 Induktion und Rekursion Peer Kröger (LMU München) Einführung in die Programmierung WS 16/17 46 / 708 Überblick
3.2 Unabhängigkeitsstrukturen
 80 3.2 Unabhängigkeitsstrukturen Unser Ziel ist der Nachweis, daß in Vektorräumen, also in Moduln über Körpern, Basen existieren und zwei endliche Basen gegebenenfalls von derselben Ordnung sind. (Basen
80 3.2 Unabhängigkeitsstrukturen Unser Ziel ist der Nachweis, daß in Vektorräumen, also in Moduln über Körpern, Basen existieren und zwei endliche Basen gegebenenfalls von derselben Ordnung sind. (Basen
Mathematik-Vorkurs für Informatiker (Wintersemester 2012/13) Übungsblatt 8 (Relationen und Funktionen)
 DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6. Informatik Universität des Saarlandes Christian Eisentraut, M.Sc. Julia Krämer Mathematik-Vorkurs für Informatiker (Wintersemester 0/3) Übungsblatt 8 (Relationen
DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6. Informatik Universität des Saarlandes Christian Eisentraut, M.Sc. Julia Krämer Mathematik-Vorkurs für Informatiker (Wintersemester 0/3) Übungsblatt 8 (Relationen
2. Stetige lineare Funktionale
 -21-2. Stetige lineare Funktionale Die am Ende von 1 angedeutete Eigenschaft, die ein lineares Funktional T : D(ú) 6 verallgemeinerten Funktion macht, ist die Stetigkeit von T in jedem n 0 0 D(ú). Wenn
-21-2. Stetige lineare Funktionale Die am Ende von 1 angedeutete Eigenschaft, die ein lineares Funktional T : D(ú) 6 verallgemeinerten Funktion macht, ist die Stetigkeit von T in jedem n 0 0 D(ú). Wenn
Reelle Zahlen, Gleichungen und Ungleichungen
 9 2. Vorlesung Reelle Zahlen, Gleichungen und Ungleichungen 4 Zahlenmengen und der Körper der reellen Zahlen 4.1 Zahlenmengen * Die Menge der natürlichen Zahlen N = {0,1,2,3,...}. * Die Menge der ganzen
9 2. Vorlesung Reelle Zahlen, Gleichungen und Ungleichungen 4 Zahlenmengen und der Körper der reellen Zahlen 4.1 Zahlenmengen * Die Menge der natürlichen Zahlen N = {0,1,2,3,...}. * Die Menge der ganzen
Kapitel 4 KONSTRUKTION DER REELLEN ZAHLEN
 Kapitel 4 KONSTRUKTION DER REELLEN ZAHLEN Fassung vom 8. Februar 2002 Claude Portenier ANALYSIS 49 4.1 Partitionen 4.1 Partitionen DEFINITION Sei X eine Menge. Eine Familie (X j ) j2j aus nicht-leeren
Kapitel 4 KONSTRUKTION DER REELLEN ZAHLEN Fassung vom 8. Februar 2002 Claude Portenier ANALYSIS 49 4.1 Partitionen 4.1 Partitionen DEFINITION Sei X eine Menge. Eine Familie (X j ) j2j aus nicht-leeren
Formale Sprachen und Automaten
 Mengen Eine Menge ist eine Gruppe von Elementen, die eine Einheit bilden (siehe z.b. Halmos 1976). Formale Sprachen und Automaten Mathematisches Rüstzeug Mengen können verschiedene Typen von Elementen
Mengen Eine Menge ist eine Gruppe von Elementen, die eine Einheit bilden (siehe z.b. Halmos 1976). Formale Sprachen und Automaten Mathematisches Rüstzeug Mengen können verschiedene Typen von Elementen
Mengen und Abbildungen
 1 Mengen und bbildungen sind Hilfsmittel ( Sprache ) zur Formulierung von Sachverhalten; naive Vorstellung gemäß Georg Cantor (1845-1918) (Begründer der Mengenlehre). Definition 1.1 Eine Menge M ist eine
1 Mengen und bbildungen sind Hilfsmittel ( Sprache ) zur Formulierung von Sachverhalten; naive Vorstellung gemäß Georg Cantor (1845-1918) (Begründer der Mengenlehre). Definition 1.1 Eine Menge M ist eine
Mengen, Funktionen und Logik
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Mengen, Funktionen und Logik Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Mengen, Funktionen und Logik Literatur Referenz: Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen,
Mathematik für Ökonomen 1
 Mathematik für Ökonomen 1 Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Herbstemester 2008 Mengen, Funktionen und Logik Inhalt: 1. Mengen 2. Funktionen 3. Logik Teil 1 Mengen
Mathematik für Ökonomen 1 Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Herbstemester 2008 Mengen, Funktionen und Logik Inhalt: 1. Mengen 2. Funktionen 3. Logik Teil 1 Mengen
4 Das Vollständigkeitsaxiom und irrationale Zahlen
 4 Das Vollständigkeitsaxiom und irrationale Zahlen 4.2 R ist archimedisch geordnet 4.5 Q liegt dicht in R 4.7 Existenz von Wurzeln nicht-negativer reeller Zahlen In diesem Paragraphen werden wir zum ersten
4 Das Vollständigkeitsaxiom und irrationale Zahlen 4.2 R ist archimedisch geordnet 4.5 Q liegt dicht in R 4.7 Existenz von Wurzeln nicht-negativer reeller Zahlen In diesem Paragraphen werden wir zum ersten
Technische Universität München
 Stand der Vorlesung Kapitel 2: Auffrischung einiger mathematischer Grundlagen Mengen, Potenzmenge, Kreuzprodukt (Paare, Tripel, n-tupel) Relation: Teilmenge MxN Eigenschaften: reflexiv, symmetrisch, transitiv,
Stand der Vorlesung Kapitel 2: Auffrischung einiger mathematischer Grundlagen Mengen, Potenzmenge, Kreuzprodukt (Paare, Tripel, n-tupel) Relation: Teilmenge MxN Eigenschaften: reflexiv, symmetrisch, transitiv,
Mathematische Grundlagen der Computerlinguistik
 Centrum für Informations- und Sprachverarbeitung (CIS) 10. Juni 2014 Table of Contents 1 2 Äquivalenz Der Begriff der Äquivalenz verallgemeinert den Begriff der Gleichheit. Er beinhaltet in einem zu präzisierenden
Centrum für Informations- und Sprachverarbeitung (CIS) 10. Juni 2014 Table of Contents 1 2 Äquivalenz Der Begriff der Äquivalenz verallgemeinert den Begriff der Gleichheit. Er beinhaltet in einem zu präzisierenden
5. Äquivalenzrelationen
 5. Äquivalenzrelationen 35 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will, so kann es sinnvoll sein, zunächst kleinere, einfachere Mengen (bzw. Gruppen)
5. Äquivalenzrelationen 35 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will, so kann es sinnvoll sein, zunächst kleinere, einfachere Mengen (bzw. Gruppen)
4. Relationen. Beschreibung einer binären Relation
 4. Relationen Relationen spielen bei Datenbanken eine wichtige Rolle. Die meisten Datenbanksysteme sind relational. 4.1 Binäre Relationen Eine binäre Relation (Beziehung) R zwischen zwei Mengen A und B
4. Relationen Relationen spielen bei Datenbanken eine wichtige Rolle. Die meisten Datenbanksysteme sind relational. 4.1 Binäre Relationen Eine binäre Relation (Beziehung) R zwischen zwei Mengen A und B
Spickzettel Mathe C1
 Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
1 Angeordnete Körper. 1.1 Anordnungen und Positivbereiche
 1 1 Angeordnete Körper 1.1 Anordnungen und Positivbereiche Definition 1.1. Eine zweistellige Relation auf einer Menge heißt partielle Ordnung, falls für alle Elemente a, b, c der Menge gilt: (i) a a (ii)
1 1 Angeordnete Körper 1.1 Anordnungen und Positivbereiche Definition 1.1. Eine zweistellige Relation auf einer Menge heißt partielle Ordnung, falls für alle Elemente a, b, c der Menge gilt: (i) a a (ii)
Lineare Algebra I. - 1.Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß. Monday 12 September 16
 Lineare Algebra I - 1.Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß 1. Mengen und Abbildungen: Mengen gehören zu den Grundlegendsten Objekten in der Mathematik Kurze Einführung in die (naive) Mengelehre
Lineare Algebra I - 1.Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß 1. Mengen und Abbildungen: Mengen gehören zu den Grundlegendsten Objekten in der Mathematik Kurze Einführung in die (naive) Mengelehre
Georg Ferdinand Ludwig Philipp Cantor geb in St. Petersburg, gest in Halle
 Kapitel 1 Mengen, Relationen, Abbildungen 1.1 Mengen Georg Cantor, der Begründer der Mengenlehre, hat 1895 in [1] eine Menge folgendermaßen definiert: Unter einer Menge verstehen wir jede Zusammenfassung
Kapitel 1 Mengen, Relationen, Abbildungen 1.1 Mengen Georg Cantor, der Begründer der Mengenlehre, hat 1895 in [1] eine Menge folgendermaßen definiert: Unter einer Menge verstehen wir jede Zusammenfassung
Musterlösung 11.Übung Mathematische Logik
 Lehr- und Forschungsgebiet Mathematische Grundlagen der Informatik RWTH Aachen Prof. Dr. E. Grädel, F. Reinhardt SS 2015 Aufgabe 2 Musterlösung 11.Übung Mathematische Logik Geben Sie für die folgenden
Lehr- und Forschungsgebiet Mathematische Grundlagen der Informatik RWTH Aachen Prof. Dr. E. Grädel, F. Reinhardt SS 2015 Aufgabe 2 Musterlösung 11.Übung Mathematische Logik Geben Sie für die folgenden
Kapitel 1. Grundlagen Mengen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Natürliche Zahlen sind interessant
 Natürliche Zahlen sind interessant N. N. Technische Universität München 16. September 2008 1 Interessante Zahlen Vorbemerkungen Der Zentrale Satz 2 Anwendungen Pädagogik Übersicht 1 Interessante Zahlen
Natürliche Zahlen sind interessant N. N. Technische Universität München 16. September 2008 1 Interessante Zahlen Vorbemerkungen Der Zentrale Satz 2 Anwendungen Pädagogik Übersicht 1 Interessante Zahlen
Kapitel 1. Grundlagen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Einführung in die Mengenlehre
 Einführung in die Mengenlehre D (Menge von Georg Cantor 845-98) Eine Menge ist eine Zusammenfassung bestimmter wohlunterschiedener Objekte unseres Denkens oder unserer Anschauung zu einem Ganzen wobei
Einführung in die Mengenlehre D (Menge von Georg Cantor 845-98) Eine Menge ist eine Zusammenfassung bestimmter wohlunterschiedener Objekte unseres Denkens oder unserer Anschauung zu einem Ganzen wobei
σ-algebren, Definition des Maßraums
 σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
Vorlesung 4. Tilman Bauer. 13. September Wir befassen uns in dieser Vorlesung noch einmal mit Mengen.
 Vorlesung 4 Universität Münster 13. September 2007 1 Kartesische Wir befassen uns in dieser Vorlesung noch einmal mit Mengen. Seien M und N zwei Mengen. Dann bezeichnen wir mit M N das (kartesische) Produkt
Vorlesung 4 Universität Münster 13. September 2007 1 Kartesische Wir befassen uns in dieser Vorlesung noch einmal mit Mengen. Seien M und N zwei Mengen. Dann bezeichnen wir mit M N das (kartesische) Produkt
Vorbereitungskurs Mathematik zum Sommersemester 2015 Mengen und Relationen
 Vorbereitungskurs Mathematik zum Sommersemester 2015 Mengen und Relationen Susanna Pohl Vorkurs Mathematik TU Dortmund 10.03.2015 Mengen und Relationen Mengen Motivation Beschreibung von Mengen Mengenoperationen
Vorbereitungskurs Mathematik zum Sommersemester 2015 Mengen und Relationen Susanna Pohl Vorkurs Mathematik TU Dortmund 10.03.2015 Mengen und Relationen Mengen Motivation Beschreibung von Mengen Mengenoperationen
Mehr über Abbildungen
 Mehr über Abbildungen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de alle Abbildungen Die Menge aller Abbildungen von A nach B wird mit B A bezeichnet. Es
Mehr über Abbildungen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de alle Abbildungen Die Menge aller Abbildungen von A nach B wird mit B A bezeichnet. Es
Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt (Probeklausur) 9
 Prof. Dr. Bernhard Steffen Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt
Prof. Dr. Bernhard Steffen Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt
Über die Existenz von Strong Port Maps zwischen Matroiden. Diplomarbeit von. Alexander Hölzle geboren am 25. Januar 1980 in Kempten (Allgäu)
 FernUniversität in Hagen Fakultät für Mathematik und Informatik Fachbereich Mathematik Über die Existenz von Strong Port Maps zwischen Matroiden Diplomarbeit von Alexander Hölzle geboren am 25. Januar
FernUniversität in Hagen Fakultät für Mathematik und Informatik Fachbereich Mathematik Über die Existenz von Strong Port Maps zwischen Matroiden Diplomarbeit von Alexander Hölzle geboren am 25. Januar
Seminar Kommutative Algebra und Varietäten Vortrag 1: Ideale kommutativer Ringe
 Seminar Kommutative Algebra und Varietäten Vortrag 1: Ideale kommutativer Ringe Sebastian Dobrzynski 17042014 1 Grundsätzliches zu Idealen Vorab legen wir fest: Alle im Vortrag betrachteten Ringe sind
Seminar Kommutative Algebra und Varietäten Vortrag 1: Ideale kommutativer Ringe Sebastian Dobrzynski 17042014 1 Grundsätzliches zu Idealen Vorab legen wir fest: Alle im Vortrag betrachteten Ringe sind
Naive Mengenlehre. ABER: Was ist eine Menge?
 Naive Mengenlehre Im Wörterbuch kann man unter dem Begriff Menge etwa die folgenden Bestimmungen finden : Ansammlung, Konglomerat, Haufen, Klasse, Quantität, Bündel,... usf. Die Mengenlehre ist der (gegenwärtig)
Naive Mengenlehre Im Wörterbuch kann man unter dem Begriff Menge etwa die folgenden Bestimmungen finden : Ansammlung, Konglomerat, Haufen, Klasse, Quantität, Bündel,... usf. Die Mengenlehre ist der (gegenwärtig)
Infimum und Supremum. Definition ) Eine Menge M R heißt nach oben bzw. nach unten beschränkt, falls ein u bzw. o existieren, so dass
 1.5 Teilmengen in R Infimum und Supremum Definition 1.33 1) Eine Menge M R heißt nach oben bzw. nach unten beschränkt, falls ein u bzw. o existieren, so dass u m m M bzw. o m m M. In diesem Fall heiß u
1.5 Teilmengen in R Infimum und Supremum Definition 1.33 1) Eine Menge M R heißt nach oben bzw. nach unten beschränkt, falls ein u bzw. o existieren, so dass u m m M bzw. o m m M. In diesem Fall heiß u
Einführung in die Computerlinguistik deterministische und nichtdeterministische endliche Automaten
 Einführung in die Computerlinguistik deterministische und nichtdeterministische endliche Automaten Dozentin: Wiebke Petersen Foliensatz 4 Wiebke Petersen Einführung CL 1 Äquivalenz von endlichen Automaten
Einführung in die Computerlinguistik deterministische und nichtdeterministische endliche Automaten Dozentin: Wiebke Petersen Foliensatz 4 Wiebke Petersen Einführung CL 1 Äquivalenz von endlichen Automaten
Übungen zu Logik und Künstliche Intelligenz Blatt 8
 Heilbronn, den 14.5.2010 Prof. Dr. V. Stahl WS 10/11 Übungen zu Logik und Künstliche Intelligenz Blatt 8 Aufgabe 1. Überlegen Sie, wie man folgende Relationen R grafisch darstellen könnte und entscheiden
Heilbronn, den 14.5.2010 Prof. Dr. V. Stahl WS 10/11 Übungen zu Logik und Künstliche Intelligenz Blatt 8 Aufgabe 1. Überlegen Sie, wie man folgende Relationen R grafisch darstellen könnte und entscheiden
Lineare Algebra 1. Detlev W. Hoffmann. WS 2013/14, TU Dortmund
 Lineare Algebra 1 Detlev W. Hoffmann WS 2013/14, TU Dortmund 1 Mengen und Zahlen 1.1 Mengen und Abbildungen Eine Menge ist eine Zusammenfassung wohlunterscheidbarer Objekte unserer Anschauung/unseres Denkens/unserer
Lineare Algebra 1 Detlev W. Hoffmann WS 2013/14, TU Dortmund 1 Mengen und Zahlen 1.1 Mengen und Abbildungen Eine Menge ist eine Zusammenfassung wohlunterscheidbarer Objekte unserer Anschauung/unseres Denkens/unserer
Beispiele für Relationen
 Text Relationen 2 Beispiele für Relationen eine Person X ist Mutter von einer Person Y eine Person X ist verheiratet mit einer Person Y eine Person X wohnt am gleichen Ort wie eine Person Y eine Person
Text Relationen 2 Beispiele für Relationen eine Person X ist Mutter von einer Person Y eine Person X ist verheiratet mit einer Person Y eine Person X wohnt am gleichen Ort wie eine Person Y eine Person
In diesem Kapitel wiederholen wir Begriffe und Notationen für grundlegende mathematische
 Kapitel 1 Mathematische Objekte In diesem Kapitel wiederholen wir Begriffe und Notationen für grundlegende mathematische Objekte wie Tupel, Mengen, Relationen und Funktionen. Außerdem erklären wir die
Kapitel 1 Mathematische Objekte In diesem Kapitel wiederholen wir Begriffe und Notationen für grundlegende mathematische Objekte wie Tupel, Mengen, Relationen und Funktionen. Außerdem erklären wir die
Programmieren für Fortgeschrittene
 Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme Wintersemester 2011/12 Programmieren für Fortgeschrittene Rekursive Spezifikationen Die folgende
Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme Wintersemester 2011/12 Programmieren für Fortgeschrittene Rekursive Spezifikationen Die folgende
Mathematik 1 für Informatik Inhalt Grundbegrie
 Mathematik 1 für Informatik Inhalt Grundbegrie Mengen, speziell Zahlenmengen Aussagenlogik, Beweistechniken Funktionen, Relationen Kombinatorik Abzählverfahren Binomialkoezienten Komplexität von Algorithmen
Mathematik 1 für Informatik Inhalt Grundbegrie Mengen, speziell Zahlenmengen Aussagenlogik, Beweistechniken Funktionen, Relationen Kombinatorik Abzählverfahren Binomialkoezienten Komplexität von Algorithmen
2.2 der Größenbegriff
 (mit Äquivalenzrelationen) Maximilian Geier Institut für Mathematik, Landau Universität Koblenz-Landau Zu Größen gelangt man ausgehend von realen Gegenständen durch einen Abstraktionsvorgang. Man geht
(mit Äquivalenzrelationen) Maximilian Geier Institut für Mathematik, Landau Universität Koblenz-Landau Zu Größen gelangt man ausgehend von realen Gegenständen durch einen Abstraktionsvorgang. Man geht
Skript und Übungen Teil II
 Vorkurs Mathematik Herbst 2009 M. Carl E. Bönecke Skript und Übungen Teil II Das erste Semester wiederholt die Schulmathematik in einer neuen axiomatischen Sprache; es ähnelt damit dem nachträglichen Erlernen
Vorkurs Mathematik Herbst 2009 M. Carl E. Bönecke Skript und Übungen Teil II Das erste Semester wiederholt die Schulmathematik in einer neuen axiomatischen Sprache; es ähnelt damit dem nachträglichen Erlernen
Konstruktion reeller Zahlen aus rationalen Zahlen
 Konstruktion reeller Zahlen aus rationalen Zahlen Wir nehmen an, daß der Körper der rationalen Zahlen bekannt ist. Genauer wollen wir annehmen: Gegeben ist eine Menge Q zusammen mit zwei Verknüpfungen
Konstruktion reeller Zahlen aus rationalen Zahlen Wir nehmen an, daß der Körper der rationalen Zahlen bekannt ist. Genauer wollen wir annehmen: Gegeben ist eine Menge Q zusammen mit zwei Verknüpfungen
5 Relationen. Formale Grundlagen der Informatik I Herbstsemester 2012. Robert Marti
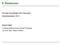 Formale Grundlagen der Informatik I Herbstsemester 2012 Robert Marti Vorlesung teilweise basierend auf Unterlagen von Prof. emer. Helmut Schauer Allgemeine Definition einer Relation Eine n-stellige Relation
Formale Grundlagen der Informatik I Herbstsemester 2012 Robert Marti Vorlesung teilweise basierend auf Unterlagen von Prof. emer. Helmut Schauer Allgemeine Definition einer Relation Eine n-stellige Relation
2. Grundlegende Strukturen 2.1 Wertebereiche beschrieben durch Mengen
 2. Grundlegende Strukturen 2.1 Wertebereiche beschrieben durch Mengen In der Modellierung von Systemen, Aufgaben, Lösungen kommen Objekte unterschiedlicher Art und Zusammensetzung vor. Für Teile des Modells
2. Grundlegende Strukturen 2.1 Wertebereiche beschrieben durch Mengen In der Modellierung von Systemen, Aufgaben, Lösungen kommen Objekte unterschiedlicher Art und Zusammensetzung vor. Für Teile des Modells
Analysis I. Vorlesung 4. Angeordnete Körper
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 4 Angeordnete Körper Zwei reelle Zahlen kann man ihrer Größe nach vergleichen, d.h. die eine ist größer als die andere oder es handelt sich
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 4 Angeordnete Körper Zwei reelle Zahlen kann man ihrer Größe nach vergleichen, d.h. die eine ist größer als die andere oder es handelt sich
FU Berlin: WiSe (Analysis 1 - Lehr.) Übungsaufgaben Zettel 5. Aufgabe 18. Aufgabe 20. (siehe Musterlösung Zettel 4)
 FU Berlin: WiSe 13-14 (Analysis 1 - Lehr.) Übungsaufgaben Zettel 5 Aufgabe 18 (siehe Musterlösung Zettel 4) Aufgabe 20 In der Menge R der reellen Zahlen sei die Relation 2 R 2 definiert durch: x 2 y :
FU Berlin: WiSe 13-14 (Analysis 1 - Lehr.) Übungsaufgaben Zettel 5 Aufgabe 18 (siehe Musterlösung Zettel 4) Aufgabe 20 In der Menge R der reellen Zahlen sei die Relation 2 R 2 definiert durch: x 2 y :
Kapitel 2 MENGENLEHRE
 Kapitel 2 MENGENLEHRE In diesem Kapitel geben wir eine kurze Einführung in die Mengenlehre, mit der man die ganze Mathematik begründen kann. Wir werden sehen, daßjedes mathematische Objekt eine Menge ist.
Kapitel 2 MENGENLEHRE In diesem Kapitel geben wir eine kurze Einführung in die Mengenlehre, mit der man die ganze Mathematik begründen kann. Wir werden sehen, daßjedes mathematische Objekt eine Menge ist.
Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion
 Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion Saskia Klaus 07.10.016 1 Motivation In den ersten beiden Vorträgen des Vorkurses haben wir gesehen, wie man aus schon bekannten Wahrheiten
Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion Saskia Klaus 07.10.016 1 Motivation In den ersten beiden Vorträgen des Vorkurses haben wir gesehen, wie man aus schon bekannten Wahrheiten
eine Folge in R, für die man auch hätte schreiben können, wenn wir alle richtig raten, was auf dem Pünktchen stehen sollte.
 Analysis, Woche 5 Folgen und Konvergenz A 5. Cauchy-Folgen und Konvergenz Eine Folge in R ist eine Abbildung von N nach R und wird meistens dargestellt durch {x n } n=0, {x n} n N oder {x 0, x, x 2,...
Analysis, Woche 5 Folgen und Konvergenz A 5. Cauchy-Folgen und Konvergenz Eine Folge in R ist eine Abbildung von N nach R und wird meistens dargestellt durch {x n } n=0, {x n} n N oder {x 0, x, x 2,...
Musterlösung MafI 1 - Blatt 5
 Musterlösung MafI 1 - Blatt 5 Titus Laska Aufgabe 1 (Relationen). Die drei Relationen R, S, T N N sind jeweils auf Reflexivität, Symmetrie und Antisymmetrie zu untersuchen. Lösung. Erinnerung. Sei R A
Musterlösung MafI 1 - Blatt 5 Titus Laska Aufgabe 1 (Relationen). Die drei Relationen R, S, T N N sind jeweils auf Reflexivität, Symmetrie und Antisymmetrie zu untersuchen. Lösung. Erinnerung. Sei R A
1 Vollständige Induktion
 1 Vollständige Induktion Die vollständige Induktion ist eine machtvolle Methode, um Aussagen zu beweisen, die für alle natürlichen Zahlen gelten sollen. Sei A(n) so eine Aussage, die zu beweisen ist. Bei
1 Vollständige Induktion Die vollständige Induktion ist eine machtvolle Methode, um Aussagen zu beweisen, die für alle natürlichen Zahlen gelten sollen. Sei A(n) so eine Aussage, die zu beweisen ist. Bei
2 Rationale und reelle Zahlen
 2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
2 reelle Es gibt Mathematik mit Grenzwert (Analysis) und Mathematik ohne Grenzwert (z.b Algebra). Grenzwerte existieren sicher nur dann, wenn der Zahlbereich vollständig ist, also keine Lücken aufweist
Mathematische Grundlagen der Computerlinguistik Mengen und Mengenoperationen
 Mathematische Grundlagen der Computerlinguistik Mengen und Mengenoperationen Dozentin: Wiebke Petersen 1. Foliensatz Wiebke Petersen math. Grundlagen 6 Frage Was ist eine Menge? 1 Minute zum Nachdenken
Mathematische Grundlagen der Computerlinguistik Mengen und Mengenoperationen Dozentin: Wiebke Petersen 1. Foliensatz Wiebke Petersen math. Grundlagen 6 Frage Was ist eine Menge? 1 Minute zum Nachdenken
Vollständigkeit der reellen Zahlen
 Vollständigkeit der reellen Zahlen Vorlesung zur Didaktik der Analysis Oliver Passon Vollständigkeit von R 1 take home message I Wollte man mit Zahlen nur rechnen, könnte man mit den rationalen Zahlen
Vollständigkeit der reellen Zahlen Vorlesung zur Didaktik der Analysis Oliver Passon Vollständigkeit von R 1 take home message I Wollte man mit Zahlen nur rechnen, könnte man mit den rationalen Zahlen
Einführung in die Analysis
 Ergänzungen zur Vorlesung Einführung in die Analysis Christian Schmeiser 1 Vorwort In dieser Vorlesung werden Grundbegriffe der Analysis wie Folgen und Reihen, Konvergenz und Vollständigkeit am Beispiel
Ergänzungen zur Vorlesung Einführung in die Analysis Christian Schmeiser 1 Vorwort In dieser Vorlesung werden Grundbegriffe der Analysis wie Folgen und Reihen, Konvergenz und Vollständigkeit am Beispiel
Analysis I - Stetige Funktionen
 Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Mengenlehre. Jörg Witte
 Mengenlehre Jörg Witte 25.10.2007 1 Grbegriffe Die Menegenlehre ist heute für die Mathematik grlegend. Sie spielt aber auch in der Informatik eine entscheidende Rolle. Insbesondere fußt die Theorie der
Mengenlehre Jörg Witte 25.10.2007 1 Grbegriffe Die Menegenlehre ist heute für die Mathematik grlegend. Sie spielt aber auch in der Informatik eine entscheidende Rolle. Insbesondere fußt die Theorie der
Lösungen zum Aufgabenblatt Nr. 1: Konstruktion der reellen Zahlen
 Lösungen zum Aufgabenblatt Nr. 1: Konstruktion der reellen Zahlen Aufgabe 1: Es sei D die Menge aller rationalen Dedekind-Mengen, also D := { M 2 Q M is Dedekind-Menge }. Auf der Menge D definieren wir
Lösungen zum Aufgabenblatt Nr. 1: Konstruktion der reellen Zahlen Aufgabe 1: Es sei D die Menge aller rationalen Dedekind-Mengen, also D := { M 2 Q M is Dedekind-Menge }. Auf der Menge D definieren wir
Warum Mathe? IG/StV-Mathematik der KFU-Graz. 1 Mengen Mengenoperationen Rechenregeln Mengen 4. Funktionen 7
 Warum Mathe? IG/StV-Mathematik der KFU-Graz März 2011 Inhalt 1 Mengen 1 1.1 Mengenoperationen.............................. 2 1.2 Rechenregeln.................................. 3 2 Übungsbeispiele zum
Warum Mathe? IG/StV-Mathematik der KFU-Graz März 2011 Inhalt 1 Mengen 1 1.1 Mengenoperationen.............................. 2 1.2 Rechenregeln.................................. 3 2 Übungsbeispiele zum
3 ist eine Primzahl zugeordnet, während der Zahl 4 die Eigenschaft
 Kapitel 7 Relationen Ω bezeichne die Menge aller Aussagen. 7.1 Grundbegriffe 7.1.1 Definition. Sei n: N, und X 1,...,X n Datentypen. Dann heißt jede Konstruktion P vom Typ ein n-stelliges Prädikat. P :
Kapitel 7 Relationen Ω bezeichne die Menge aller Aussagen. 7.1 Grundbegriffe 7.1.1 Definition. Sei n: N, und X 1,...,X n Datentypen. Dann heißt jede Konstruktion P vom Typ ein n-stelliges Prädikat. P :
Definition 3.1. Sei A X. Unter einer offenen Überdeckung von A versteht man eine Familie (U i ) i I offener Mengen U i X mit U i
 3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
2 Mengen und Abbildungen
 2.1 Mengen Unter einer Menge verstehen wir eine Zusammenfassung von Objekten zu einem Ganzen. Die Objekte heiÿen Elemente. Ist M eine Menge und x ein Element von M so schreiben wir x M. Wir sagen auch:
2.1 Mengen Unter einer Menge verstehen wir eine Zusammenfassung von Objekten zu einem Ganzen. Die Objekte heiÿen Elemente. Ist M eine Menge und x ein Element von M so schreiben wir x M. Wir sagen auch:
Theoretische Informatik
 Mathematische Grundlagen Patrick Horster Universität Klagenfurt Informatik Systemsicherheit WS-2007-Anhang-1 Allgemeines In diesem einführenden Kapitel werden zunächst elementare Grundlagen kurz aufgezeigt,
Mathematische Grundlagen Patrick Horster Universität Klagenfurt Informatik Systemsicherheit WS-2007-Anhang-1 Allgemeines In diesem einführenden Kapitel werden zunächst elementare Grundlagen kurz aufgezeigt,
Verbandstheorie. Udo Hebisch SS 2016
 Verbandstheorie Udo Hebisch SS 2016 Dieses Skript enthält nur den roten Faden einer einführenden Vorlesung über Verbandstheorie. Zur selben Vorlesung gehört noch ein Teil zur Universellen Algebra. Wesentliche
Verbandstheorie Udo Hebisch SS 2016 Dieses Skript enthält nur den roten Faden einer einführenden Vorlesung über Verbandstheorie. Zur selben Vorlesung gehört noch ein Teil zur Universellen Algebra. Wesentliche
Analysis I. Alexander Grigorian Universität Bielefeld
 Analysis I Alexander Grigorian Universität Bielefeld SS 2014 ii Contents 1 Mengen und Zahlen 1 1.1 Grundbegri e der Mengenlehre........................ 1 1.1.1 Mengen und Operationen auf den Mengen..............
Analysis I Alexander Grigorian Universität Bielefeld SS 2014 ii Contents 1 Mengen und Zahlen 1 1.1 Grundbegri e der Mengenlehre........................ 1 1.1.1 Mengen und Operationen auf den Mengen..............
