Dynamische Mengen. Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem & Das Suchproblem.
|
|
|
- Adam Brinkerhoff
- vor 5 Jahren
- Abrufe
Transkript
1 lgorithmen und atenstrukturen Kapitel 7 namische Mengen, das Suchproblem & namische Mengen rundlegende lgorithmen efinition isher hatten wir oft statische Mengen, bei denen sich die nahl der Elemente nicht ändert (.. beim Sortieren). Oft soll eine Menge aber eitabhängig wachsen und schrumpfen können. Man spricht dann von dnamischen Mengen. Kennengelernt haben wir bereits den Stack, die Queue und die verkettete Liste. rank Heitmann heitmann@informatik.uni-hamburg.de 25. November 20 rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 nmerkung Wir beschränken uns oft auf die arstellung der für unsere wichtigen aten. Meist enthalten die Objekte aber usätliche Satellitendaten.. einen Wächter am Ende einer verketteten Liste. rank Heitmann heitmann@informatik.uni-hamburg.de 2/2 rundlegende lgorithmen rundlegende lgorithmen namische Mengen as Suchproblem Wichtige (dnamischer Mengen): Search(S, k). ibt es einen Zeiger x auf ein Element in S mit schlüssel[x] = k? nsert(s, x). elete(s, x). Minimum(S), Maximum(S), Successor(S, x), Predecessor(S, x). Viele hiervon haben wir schon bei.. der verketteten Liste gesehen, aber wie schnell waren die? efinition (as Suchproblem) Eingabe: Eine Sequen < a 1, a 2,..., a n > von n Zahlen und ein Wert k. esucht: Ein ndex i mit k = [i], falls k in vorkommt oder der Wert nil. efinition (as Suchproblem (allgemein)) Eingabe: Eine Menge M und ein Wert k. esucht: Ein Zeiger x auf ein Element in M mit schlüssel[x] = k oder nil, falls kein solches Element existiert. rank Heitmann heitmann@informatik.uni-hamburg.de /2 rank Heitmann heitmann@informatik.uni-hamburg.de 4/2
2 rundlegende lgorithmen rundlegende lgorithmen rute-orce-suche (rra) rute-orce-suche (Liste) lgorithmus 1 Search([1..n], k) 1: for i = 1 to n do 2: if a[i] == k then : return i 4: end if 5: end for 6: return nil lgorithmus 2 Search(L, k) 1: x = kopf[l] 2: while x nil && schlüssel[x] k do : x = nachfolger[x] 4: end while 5: return x nalse Laufeit ist in Θ(n). Korrektheit folgt mit Schleifeninvariante (oder hier auch direkt). nalse Laufeit ist wieder in Θ(n). Korrektheit eigt man wie oben. rank Heitmann heitmann@informatik.uni-hamburg.de 5/2 rank Heitmann heitmann@informatik.uni-hamburg.de 6/2 rundlegende lgorithmen rundlegende lgorithmen inäre Suche rundlegende lgorithmen - Zusammenfassung lgorithmus inäre Suche (rra) 1: while first last idx < 0 do 2: m = first + ((last first)/2) : if a[m] < p then 4: first = m + 1 5: else if a[m] > p then 6: last = m 1 7: else : idx = m 9: end if : end while 11: return idx nalse Laufeit ist in Θ(log n) (T (n) = T (n/2) + c). rank Heitmann heitmann@informatik.uni-hamburg.de 7/2 Zusammenfassung ie Laufeit der rute-orce-suchalgorithmen war in Θ(n), insb. da jedes Element betrachtet werden musste. ie binäre Suche erlaubt eine Laufeit in Θ(log n), ist aber nicht bei jeder atenstruktur anwendbar! Wir suchen nun atenstrukturen, die die Suche und auch die anderen für dnamische Mengen in wenig Zeit (.. in O(log n)) erlauben. Pause to Ponder Unsere bisherigen atenstrukturen erlauben dies nicht. Man überlege sich dies an rra, Stack, Queue, Liste und Heap... rank Heitmann heitmann@informatik.uni-hamburg.de /2
3 - ie dee - ie dee Ein binärer Suchbaum ist eine atenstruktur, die viele auf dnamischen Mengen ermöglicht, insb. die Search, Minimum, Maximum, Predecessor, Successor, nsert und elete. Ein binärer Suchbaum ist ein binärer aum (jeder Knoten hat bis u wei Kindern), wobei der aum noch die speielle Suchbaum-Eigenschaft erfüllt. er aum wird (anders als der Heap!) meist durch eine verkettete atenstruktur (ähnlich der doppelt-verketteten Liste) repräsentiert. Jeder Knoten ist ein Objekt mit den ttributen schlüssel (und den Satellitendaten), links, rechts, p, die auf den jeweiligen linken bw. rechten Nachfolger, bw. den Vaterknoten eigen (fehlen diese, sind die entsprechenden ttribute auf nil gesett). rank Heitmann heitmann@informatik.uni-hamburg.de 9/2 inäre Suchbaum-Eigenschaft: Sei p ein Knoten im binären Suchbaum. Sei l ein Knoten im linken Teilbaum von n, r im rechten, dann gilt stets: schlüssel[l] schlüssel[p] und schlüssel[p] schlüssel[r]. nil nil (m ild sind nicht alle nil-knoten eingeeichnet, nachfolgend verichten wir meist gan auf sie.) rank Heitmann heitmann@informatik.uni-hamburg.de /2 nil nil nil nil - eispiel (gut) - eispiel (schlecht) rank Heitmann heitmann@informatik.uni-hamburg.de 11/2 rank Heitmann heitmann@informatik.uni-hamburg.de /2
4 ie nordertreewalk - ie dee Wir werden nachfolgenden folgende betrachten: nordertreewalk(x). TreeSearch(x, k), terativetreesearch(x, k). TreeMinimum(x), TreeMaximum(x). TreeSuccessor(x), TreePredecessor(x). Treensert(T, x), Treeelete(T, ). ibt die Schlüssel aus, wobei uerst die Schlüssel des linken, dann der Schlüssel der Wurel und dann die Schlüssel des rechten Teilbaumes ausgegeben werden. rank Heitmann heitmann@informatik.uni-hamburg.de /2 rank Heitmann heitmann@informatik.uni-hamburg.de 14/2 nordertreewalk nordertreewalk - eispiel lgorithmus 4 nordertreewalk(x) 1: if x nil then 2: nordertreewalk(links[x]) : print schlüssel[x] 4: nordertreewalk(rechts[x]) 5: end if nmerkung Ähnlich kann man auch PreorderTreeWalk (Wurel uerst) und PostorderTreeWalk (Wurel ulett) schreiben. rank Heitmann heitmann@informatik.uni-hamburg.de /2 rank Heitmann heitmann@informatik.uni-hamburg.de /2
5 nordertreewalk - eispiel nordertreewalk - eispiel 2 2 rank Heitmann heitmann@informatik.uni-hamburg.de 17/2 rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 nordertreewalk - eispiel nordertreewalk - eispiel rank Heitmann heitmann@informatik.uni-hamburg.de 19/2 rank Heitmann heitmann@informatik.uni-hamburg.de 20/2
6 nordertreewalk - eispiel nordertreewalk - eispiel rank Heitmann heitmann@informatik.uni-hamburg.de 21/2 rank Heitmann heitmann@informatik.uni-hamburg.de 22/2 nordertreewalk - eispiel nordertreewalk - eispiel rank Heitmann heitmann@informatik.uni-hamburg.de 2/2 rank Heitmann heitmann@informatik.uni-hamburg.de 24/2
7 nordertreewalk nordertreewalk nmerkung ei einem binären Suchbaum werden die Schlüssel bei nordertreewalk in sortierter Reihenfolge ausgegeben! (er Sat, dass dies korrekt ist, folgt gleich. er eweis mündlich.) lgorithmus 5 nordertreewalk(x) 1: if x nil then 2: nordertreewalk(links[x]) : print schlüssel[x] 4: nordertreewalk(rechts[x]) 5: end if Pause to Ponder Laufeit? Sat Wenn x die Wurel eines Teilbaums mit n Knoten ist, dann ist nordertreewalk(x) korrekt (folgt per nduktion aus den Eigenschaften binärer Suchbäume). rank Heitmann heitmann@informatik.uni-hamburg.de 25/2 rank Heitmann heitmann@informatik.uni-hamburg.de 26/2 nordertreewalk - Laufeitanalse (1/4) nordertreewalk - Laufeitanalse (2/4) Sat Wenn x die Wurel eines Teilbaums mit n Knoten ist, dann ist nordertreewalk(x) in Zeit Θ(n). eweis. ufstellen der Rekurrengleichung: eim einem leeren (Teil-)aum gilt T (0) = c. erner gilt bei ufruf auf einen Knoten dessen linker Teilbaum k und dessen rechter Teilbaum n k 1 Knoten hat T (n) = T (k) + T (n k 1) + d. Wir vermuten nun T (n) Θ(n), d.h. wir vermuten T (n) = e n für eine Konstante e. eweis. ehauptung: T (n) = e n. Wollen wir dies mit nduktion beweisen, so merken wir gleich beim nduktionsanfang T (0) = e 0 = 0 c. Wir müssen unsere Vermutung also verbessern! Neue Vermutung: T (n) = e n + c. amit ist immer noch T (n) Θ(n), aber der nduktionsanfang klappt jett! rank Heitmann heitmann@informatik.uni-hamburg.de 27/2 rank Heitmann heitmann@informatik.uni-hamburg.de 2/2
8 nordertreewalk - Laufeitanalse (/4) nordertreewalk - Laufeitanalse eweis. ehauptung: T (n) = e n + c. nduktionsschritt (n 1 n): T (n) = T (k) + T (n k 1) + d = (e k + c) + (e (n k 1) + c) + d = e n e + 2c + d Seten wir e = c + d (denn wir wollen ja T (n) = e n + c erreichen (nicht T (n + 1) =..., da wir den nduktionsschritt ja auf n machen)) und verfeinern auf diese Weise also unsere ehauptung erneut (!), so wird gleich alles klappen! nmerkung Nimmt man als ehauptung gleich T (n) = (c+d)n+c, so klappt alles sofort, aber die leichung fällt dann vom Himmel. Oben kommt man auf e = c + d, weil man ja möchte, dass sich T (n) = e n + c ergibt. rank Heitmann heitmann@informatik.uni-hamburg.de 29/2 rank Heitmann heitmann@informatik.uni-hamburg.de 0/2 nordertreewalk - Laufeitanalse (4/4) TreeSearch - ie dee am eispiel eweis. egeben (aus dem ode): T (n) mit T (0) = c und T (n) = T (k) + T (n k 1) + d. ehauptung: T (n) = (c + d) n + c. nduktionsanfang: T (0) = c. nduktionsannahme: ehauptung gelte schon für Werte kleiner n. nduktionsschritt (n 1 n): T (n) = T (k) + T (n k 1) + d = ((c + d) k + c) + ((c + d) (n k 1) + c) + d = (c + d) n (c + d) + 2c + d = (c + d) n + c lso gilt T (n) Θ(n). TreeSearch 7?? 11? rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 rank Heitmann heitmann@informatik.uni-hamburg.de 2/2
9 TreeSearch - ie dee TreeSearch - Pseudocode eginne mit der Wurel. st diese kleiner als der Schlüssel, so suche im rechten Teilbaum, ist sie grösser, suche im linken. ahre wie oben mit der Wurel diese Teilbaumes fort. reche ab, wenn Schlüssel gefunden oder, wenn nil- Knoten erreicht wird. lgorithmus 6 TreeSearch(x, k) 1: if x == nil or k == schlüssel[x] then 2: return x : else if k < schlüssel[x] then 4: return TreeSearch(links[x], k) 5: else 6: return TreeSearch(rechts[x], k) 7: end if nalse ie Knoten, die während der Rekursion besucht werden, bilden einen Pfad von der Wurel bis maximal u einem latt. ie Korrektheit folgt aus den Eigenschaften binärer Suchbäume. ie Laufeit ist in O(h), wobei h die Höhe des aumes ist. rank Heitmann heitmann@informatik.uni-hamburg.de /2 rank Heitmann heitmann@informatik.uni-hamburg.de 4/2 TreeSearch - Pseudocode (iterativ) TreeSearch, Minimum und Maximum am eispiel lgorithmus 7 terativetreesearch(x, k) 1: while x nil and k schlüssel[x] do 2: if k < schlüssel[x] then : x = links[x] 4: else 5: x = rechts[x] 6: end if 7: end while : return x TreeSearch 5? Minimum? Maximum? rank Heitmann heitmann@informatik.uni-hamburg.de 5/2 rank Heitmann heitmann@informatik.uni-hamburg.de 6/2
10 Minimum und Maximum Vorgänger und Nachfolger lgorithmus TreeMinimum(x) 1: while links[x] nil do 2: x = links[x] : end while 4: return x Wir wollen den Nachfolger eines Knotens in der sortierten Reihenfolge ausgeben. (en Vorgänger ermittelt man analog.) lgorithmus 9 TreeMaximum(x) 1: while rechts[x] nil do 2: x = rechts[x] : end while 4: return x nalse (Korrektheit und Laufeit) wie bei TreeSearch. rank Heitmann heitmann@informatik.uni-hamburg.de 7/2 Wir können dies machen ohne jemals Schlüssel u vergleichen! rank Heitmann heitmann@informatik.uni-hamburg.de /2 Nachfolger - eispiel Nachfolger - eispiel rank Heitmann heitmann@informatik.uni-hamburg.de 9/2 rank Heitmann heitmann@informatik.uni-hamburg.de 40/2
11 Nachfolger - eispiel Nachfolger - eispiel rank Heitmann heitmann@informatik.uni-hamburg.de 41/2 rank Heitmann heitmann@informatik.uni-hamburg.de 42/2 Nachfolger - ie dee Nachfolger - ie dee er Nachfolger eines Knotens x ist der Knoten mit dem kleinsten Schlüssel, der größer ist als schlüssel[x]. rößer als schlüssel[x] heisst im rechten Teilbaum von x und dort am kleinsten heisst das Minimum ( gan links ). Problem: x muss gar keinen rechten Teilbaum haben! ann ist der Nachfolger der jüngste Vorfahre von x, dessen linkes Kind ebenfalls ein Vorfahre von x ist. (eht das auch nicht, dann ist x das größte Element und hat keinen Nachfolger.) ann ist der Nachfolger der jüngste Vorfahre von x, dessen linkes Kind ebenfalls ein Vorfahre von x ist. as heißt wir gehen von x aus nach oben und der erste Knoten auf den wir treffen von dem aus gesehen x in seinem linken Teilbaum ist, ist der gesuchte. ann gilt nämlich gerade schlüssel[x] < schlüssel[] (wegen linken oben) und es gibt auch keinen Schlüssel dawischen (wegen erste oben). (Obiges kann in einen eweis um-/ausformuliert werden.) emerkung Umgangssprachlich: Wir gehen im aum immer weiter nach oben, wenn wir das erste Mal nach rechts gehen, haben wir den gesuchten Knoten. rank Heitmann heitmann@informatik.uni-hamburg.de 4/2 rank Heitmann heitmann@informatik.uni-hamburg.de 44/2
12 Nachfolger - ie dee Nachfolger - ie dee ann ist der Nachfolger der jüngste Vorfahre von x, dessen linkes Kind ebenfalls ein Vorfahre von x ist. ann ist der Nachfolger der jüngste Vorfahre von x, dessen linkes Kind ebenfalls ein Vorfahre von x ist. rank Heitmann heitmann@informatik.uni-hamburg.de 45/2 rank Heitmann heitmann@informatik.uni-hamburg.de 46/2 Nachfolger - Pseudocode Einfügen - ie dee lgorithmus TreeSucessor(x) 1: if rechts[x] nil then 2: return TreeMinimum(rechts[x]) : end if 4: = p[x] 5: while nil and x == rechts[] do 6: x = 7: = p[] : end while 9: return Wir manipulieren nun die (dnamische!) atenstruktur, indem wir ein Element hinufügen. abei soll die Suchbaum-Eigenschaft erhalten bleiben. m Prinip suchen wir (ähnlich der Suche) den richtigen Plat und fügen das neue Element einfach als latt an... nalse Korrektheit folgt aus obigen Überlegungen. Laufeit ist wieder in O(h). ie Routine TreePredecessor implementiert man analog. rank Heitmann heitmann@informatik.uni-hamburg.de 47/2 rank Heitmann heitmann@informatik.uni-hamburg.de 4/2
13 Einfügen - eispiel Einfügen - eispiel 11 nsert 11? nsert 4? rank Heitmann heitmann@informatik.uni-hamburg.de 49/2 rank Heitmann heitmann@informatik.uni-hamburg.de 50/2 Einfügen - eispiel Einfügen - ie dee m ode halten wir nun einen Zeiger auf x (hier soll das neue Element hin) und einen Zeiger auf p[x]. n wird dann das neue Element angehängt rank Heitmann heitmann@informatik.uni-hamburg.de 51/2 rank Heitmann heitmann@informatik.uni-hamburg.de 52/2
14 Einfügen - Pseudocode Teil 1 Einfügen - Pseudocode Teil 2 lgorithmus 11 Treensert(T, ) - Teil 1 1: = nil 2: x = wurel[t ] : while x nil do 4: = x 5: if schlüssel[] < schlüssel[x] then 6: x = links[x] 7: else : x = rechts[x] 9: end if : end while Erklärung x eigt jett auf nil. auf den ulett besuchten Knoten an den jett der neue Knoten angefügt werden soll. Oft ist ein latt. rank Heitmann heitmann@informatik.uni-hamburg.de 5/2 lgorithmus Treensert(T, ) - Teil 2 1: p[] = 2: if == nil then : wurel[t ] = 4: else 5: if schlüssel[] < schlüssel[] then 6: links[] = 7: else : rechts[] = 9: end if : end if Erklärung er Vater von ist und ist linkes oder rechtes Kind von (je nach Schlüssel). links[] und rechts[] sind ferner nil. rank Heitmann heitmann@informatik.uni-hamburg.de 54/2 Löschen - ie dee Löschen - eispiel as Löschen eines Knotens ist kompliierter. Es gibt drei älle: 1 hat keine Kinder. ann kann er einfach gelöscht werden. (p[] eigt auf nil statt auf ). 2 hat genau ein Kind. ann werden p[] und left[] bw. right[] verbunden und damit ausgeschnitten. (Man vergleiche dies mit der Lösch-Operation bei verketteten Listen!) hat wei Kinder. ann wird s Nachfolger genommen (hat kein linkes Kind!), ausgeschnitten (siehe 2. oben) und mit seinen aten die aten von ersett. rank Heitmann heitmann@informatik.uni-hamburg.de 55/2 rank Heitmann heitmann@informatik.uni-hamburg.de 56/2
15 Löschen - eispiel Löschen - eispiel 5 rank Heitmann heitmann@informatik.uni-hamburg.de 57/2 rank Heitmann heitmann@informatik.uni-hamburg.de 5/2 Löschen - eispiel Löschen - eispiel 5 5 rank Heitmann heitmann@informatik.uni-hamburg.de 59/2 rank Heitmann heitmann@informatik.uni-hamburg.de 60/2
16 Löschen - eispiel Löschen - eispiel 5 5 rank Heitmann heitmann@informatik.uni-hamburg.de 61/2 rank Heitmann heitmann@informatik.uni-hamburg.de 62/2 Löschen - eispiel Löschen - eispiel 5 5 rank Heitmann heitmann@informatik.uni-hamburg.de 6/2 rank Heitmann heitmann@informatik.uni-hamburg.de 64/2
17 Löschen - eispiel Löschen - eispiel 5 5 rank Heitmann heitmann@informatik.uni-hamburg.de 65/2 rank Heitmann heitmann@informatik.uni-hamburg.de 66/2 Löschen - eispiel Löschen - eispiel 5 5 rank Heitmann heitmann@informatik.uni-hamburg.de 67/2 rank Heitmann heitmann@informatik.uni-hamburg.de 6/2
18 Löschen - eispiel Löschen - eispiel 5 5 rank Heitmann heitmann@informatik.uni-hamburg.de 69/2 rank Heitmann heitmann@informatik.uni-hamburg.de 70/2 Löschen - Pseudocode - Zusammenfassung (1/4) uf den Sourcecode verichten wir hier. Ähnlich wie beim Einfügen müssen die Zeigern umgebogen werden. Weitere etails findet man im [ormen] in Kapitel.. Zusammenfassung der nordertreewalk Rekursiv erst die Elemente des linken Teilbaumes ausgeben, dann das Element selbst, dann die Elemente des rechten Teilbaumes. ibt bei einem binären Suchbaum die Elemente in sortierter Reihenfolge aus. TreeSearch Suche im linken Teilbaum weiter, wenn u suchendes Element kleiner ist als das Wurelelement, sonst im rechten Teilbaum. rank Heitmann heitmann@informatik.uni-hamburg.de 71/2 rank Heitmann heitmann@informatik.uni-hamburg.de 72/2
19 - Zusammenfassung (2/4) - Zusammenfassung (/4) Zusammenfassung der Minimum Element gan links. Maximum Element gan rechts. Nachfolger (von x) der Knoten mit dem kleinsten Schlüssel, der größer ist als schlüssel[x]. Minimum im rechten Teilbaum oder der jüngste Vorfahre von x, dessen linkes Kind ebenfalls ein Vorfahre von x ist. Vorgänger (von x) analog... Zusammenfassung der Einfügen Ähnnlich wie beim Suchen die geeignete Position suchen und das neue Element als neues latt anfügen. Löschen rei älle: 1 hat keine Kinder. ann kann er einfach gelöscht werden. (p[] eigt auf nil statt auf ). 2 hat genau ein Kind. ann werden p[] und left[] bw. right[] verbunden und damit ausgeschnitten. hat wei Kinder. ann wird s Nachfolger genommen (hat kein linkes Kind!), ausgeschnitten (siehe 2. oben) und mit seinen aten die aten von ersett. rank Heitmann heitmann@informatik.uni-hamburg.de 7/2 rank Heitmann heitmann@informatik.uni-hamburg.de 74/2 - Zusammenfassung (4/4) Zusammenfassung der ie nordertreewalk, TreeSearch, Minimum, Maximum, Successor, nsert und elete sind alle korrekt, was man stets recht einfach über die Eigenschaften binärer Suchbäume eigen kann (ggf. mit nduktion über die nahl der Knoten oder die Tiefe des aumes). ei einem binären Suchbaum mit n Knoten der Höhe h, ist die Laufeit von nordertreewalk in O(n), die aller anderen in O(h). nmerkung iese Laufeiten sind war gut, da bei einem (ungefähr) ausgeglichenen aum h log n ist. as Problem ist aber, dass binäre Suchbäume nicht ausgeglichen sein müssen! m worst-case sind obige alle in Θ(n)! rank Heitmann heitmann@informatik.uni-hamburg.de 75/2 - ie dee sind binäre Suchbäume, bei denen jeder Knoten eine arbe hat (rot oder schwar). urch Einschränkungen (Rot-Schwar-Eigenschaften) wird sichergestellt, dass der aum annähernd balanciert ist, so dass die dann auch im worst-case in O(log n) laufen. as Problem ist es dann die wie insb. Einfügen und Löschen so u implementieren, dass die Rot-Schwar-Eigenschaften erhalten bleiben (und sie dann trotdem in O(log n) sind)! rank Heitmann heitmann@informatik.uni-hamburg.de 76/2
20 Rot-Schwar-Eigenschaften VL-äume - ie dee 1 Jeder Knoten ist entweder rot oder schwar. 2 ie Wurel ist schwar. Jedes latt ist schwar. 4 Wenn ein Knoten rot ist, dann sind seine beiden Kinder schwar. 5 ür jeden Knoten enthalten alle Pfade, die an diesem Knoten starten und in einem latt des Teilbaumes dieses Knotens enden, die gleiche nahl schwarer Knoten Sat Ein Rot-Schwar-aum mit n inneren Knoten hat höchstens die Höhe 2 log(n + 1). Ein VL-aum ist ein binärer Suchbaum, der höhenbalanciert ist, d.h. für jeden Knoten x unterscheiden sich die Höhen des linken und rechten Teilbaumes maximal um 1. st also h[links[x]] die Höhe des linken und h[rechts[x]] die Höhe des rechten Teilbaumes, dann gilt bei einem VL-aum für jeden Knoten x h[links[x]] h[rechts[x]] { 1, 0, 1} ei VL-äumen spielt wie auch bei n die Rotation eine wichtige Rolle. Mit ihr wird der aum nach einer Einfügeoperation stets wieder ausbalanciert. rank Heitmann heitmann@informatik.uni-hamburg.de 77/2 rank Heitmann heitmann@informatik.uni-hamburg.de 7/2 Zusammenfassung des Suchens: rute-orce-lgorithmus inäres Suchen (rra muss sortiert sein!) Suchbäume efinition TreeWalk, Suchen, Minimum, Maximum Vorgänger, Nachfolger Einfügen, Entfernen VL-äume rank Heitmann heitmann@informatik.uni-hamburg.de 79/2 rank Heitmann heitmann@informatik.uni-hamburg.de 0/2
21 Rot-Schwar-Eigenschaften Ein Rot-Schwar-aum (noch ohne ärbung) 1 Jeder Knoten ist entweder rot oder schwar. 2 ie Wurel ist schwar. Jedes latt ist schwar. 4 Wenn ein Knoten rot ist, dann sind seine beiden Kinder schwar. 5 ür jeden Knoten enthalten alle Pfade, die an diesem Knoten starten und in einem latt des Teilbaumes dieses Knotens enden, die gleiche nahl schwarer Knoten nil nil nil nil nil nil rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 rank Heitmann heitmann@informatik.uni-hamburg.de 2/2 Ein Rot-Schwar-aum (noch ohne ärbung) Ein Rot-Schwar-aum (Wurel und lätter gefärbt) nil [T] nil [T] rank Heitmann heitmann@informatik.uni-hamburg.de /2 rank Heitmann heitmann@informatik.uni-hamburg.de 4/2
22 Ein Rot-Schwar-aum (gefärbt) Ein Rot-Schwar-aum (in schön) nil [T] rank Heitmann 5/2 rank Heitmann 6/2 Rot-Schwar-Eigenschaften (Wiederholung) alanciertheit 1 Jeder Knoten ist entweder rot oder schwar. 2 ie Wurel ist schwar. Jedes latt ist schwar. 4 Wenn ein Knoten rot ist, dann sind seine beiden Kinder schwar. 5 ür jeden Knoten enthalten alle Pfade, die an diesem Knoten starten und in einem latt des Teilbaumes dieses Knotens enden, die gleiche nahl schwarer Knoten nmerkung ie lätter sind alle nil-knoten (der Wächter nil[t ]) und schwar. ie Wurel hat als Vorgänger auch nil[t ] (Siehe die beiden vorherigen ilder.) Sat Ein Rot-Schwar-aum mit n inneren Knoten hat höchstens die Höhe 2 log(n + 1). Sat ie Search, Minimum, Maximum, Successor, Predecessor für dnamische Mengen lassen sich auf n in Zeit O(log n) implementieren, wobei n die nahl der Knoten ist. rank Heitmann heitmann@informatik.uni-hamburg.de 7/2 rank Heitmann heitmann@informatik.uni-hamburg.de /2
23 Rotationen Rotation - ildlich uch die Treensert und Treeelete sind in Zeit O(log n), aber da sie den aum modifiieren, kann es passieren, dass die Rot-Schwar-Eigenschaften danach nicht mehr erfüllt sind. Um die Eigenschaften wiederherustellen, müssen ggf. arben und die Zeigerstruktur geändert werden. Ein wichtiges Hilfsmittel hierbei (ur Änderung der Zeigerstruktur) ist die Rotation... x LeftRotate(x) RightRotate(x) x rank Heitmann heitmann@informatik.uni-hamburg.de 9/2 rank Heitmann heitmann@informatik.uni-hamburg.de 90/2 Linksrotation Linksrotation - um Merken x LeftRotate(x) x LeftRotate(x) x x as rechte Kind () von x ist nicht nil. wird neue Wurel des Teilbaumes. x wird das linke Kind von. as linke Kind von wird rechtes Kinds von x. rank Heitmann heitmann@informatik.uni-hamburg.de 91/2 Ziehe an -x-- wie an einer Schnur. und x rutschen nach unten, und nach oben bleibt übrig. Einiger sinnvoller Plat: rechts von x. Erhälte die binäre Suchbaum-Eigenschaft! rank Heitmann heitmann@informatik.uni-hamburg.de 92/2
24 Rechtsrotation Rechtsrotation - um Merken x x RightRotate(x) x RightRotate(x) x as linke Kind (x) von ist nicht nil. x wird neue Wurel des Teilbaumes. wird das rechte Kind von. as rechte Kind von x wird linkes Kinds von. rank Heitmann heitmann@informatik.uni-hamburg.de 9/2 Ziehe an -x-- wie an einer Schnur. und rutschen nach unten, x und nach oben bleibt übrig. Einiger sinnvoller Plat: links von. Erhälte die binäre Suchbaum-Eigenschaft! rank Heitmann heitmann@informatik.uni-hamburg.de 94/2 Rotation - ildlich Rotation - eispiel x LeftRotate(x) RightRotate(x) x ie Rotation erhält die binäre Suchbaum-Eigenschaft! rank Heitmann heitmann@informatik.uni-hamburg.de 95/2 rank Heitmann heitmann@informatik.uni-hamburg.de 96/2
25 Rotation - eispiel Rotation - eispiel ??? 7? rank Heitmann heitmann@informatik.uni-hamburg.de 97/2 rank Heitmann heitmann@informatik.uni-hamburg.de 9/2 Rotation - eispiel Rotation - mplementation ie mplementierung ist wieder Zeigerspielerei. (Ähnlich des usschneidens in verketteten Listen.) etails sind im [ormen] u finden. Laufeit ist in O(1), da nur (eine konstante nahl von) Zeiger verändert werden. 7 rank Heitmann heitmann@informatik.uni-hamburg.de 99/2 rank Heitmann heitmann@informatik.uni-hamburg.de 0/2
26 Einfügen Einfügen - rossvater, Onkel und Vater... eim Einfügen passiert nun unächst das gleiche wie bei normalen binären Suchbäumen. ie arbe des neu eingefügten Knotens wird auf rot gesett. ann wird eine Routine aufgerufen, die die Rot-Schwar-Eigenschaften wiederherstellt... ist der neu eingefügte, rote Knoten. n einer while-schleife, in der immer geprüft wird, ob der Vater von rot ist (nur dann muss man fortfahren), werden nun drei älle unterschieden. ie drei älle treten spiegelverkehrt auf, je nachdem ob im linken Teilbaum seines rossvaters ist, oder im rechten. Wir behandeln nachfolgend die erste Variante ( ist im linken Teilbaum seines rossvaters). Eine wichtige Rolle spielt der Onkel (= rechts[p[p[]]]) von und insb. dessen arbe sowie, ob ein linkes oder rechtes Kind ist. ( hat nachfolgend Kinder, weil in der Routine der Zeiger nach oben wandern kann.) rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 rank Heitmann heitmann@informatik.uni-hamburg.de 2/2 Einfügen - all 1 Einfügen - all 1 all 1: s Onkel ist rot. Umfärben und neu (!) seten. all 1: s Onkel ist rot. Umfärben und neu (!) seten. neu neu H H H H E E E E rank Heitmann heitmann@informatik.uni-hamburg.de /2 rank Heitmann heitmann@informatik.uni-hamburg.de 4/2
27 Einfügen - all 1b Einfügen - all 1b all 1b: s Onkel ist rot. Umfärben und neu (!) seten. all 1b: s Onkel ist rot. Umfärben und neu (!) seten. neu neu H H H H E E E E rank Heitmann heitmann@informatik.uni-hamburg.de 5/2 rank Heitmann heitmann@informatik.uni-hamburg.de 6/2 Einfügen - all 2 Einfügen - all 2 all 2: s Onkel ist schwar und ist rechtes Kind seines Vaters. wird auf p[] gesett und eine Linksrotation wird um (das neue) gemacht. ann weiter mit all. (er gilt jett!) all 2: s Onkel ist schwar und ist rechtes Kind seines Vaters. wird auf p[] gesett und eine Linksrotation wird um (das neue) gemacht. ann weiter mit all. (er gilt jett!) neu H E rank Heitmann heitmann@informatik.uni-hamburg.de 7/2 rank Heitmann heitmann@informatik.uni-hamburg.de /2
28 Einfügen - all Einfügen - all all : s Onkel ist schwar und ist linkes Kind seines Vaters. arbe von p[] auf schwar (bisher rot), von p[p[]] auf rot (bisher schwar) und Rechtsrotation um p[p[]]. ( nicht neu seten!) all : s Onkel ist schwar und ist linkes Kind seines Vaters. arbe von p[] auf schwar (bisher rot), von p[p[]] auf rot (bisher schwar) und Rechtsrotation um p[p[]]. ( nicht neu seten!) rank Heitmann heitmann@informatik.uni-hamburg.de 9/2 rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 Einfügen - all 2 & in olge Einfügen - eispiel Nun einmal am eispiel. er Knoten 4 wird hier neu eingefügt... rank Heitmann heitmann@informatik.uni-hamburg.de 111/2 rank Heitmann heitmann@informatik.uni-hamburg.de 1/2
29 Einfügen - eispiel Einfügen - eispiel all 1: s Onkel ist rot. Umfärben und auf p[p[]] neu seten. all 1: s Onkel ist rot. Umfärben und auf p[p[]] neu seten. rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 rank Heitmann heitmann@informatik.uni-hamburg.de 114/2 Einfügen - eispiel Einfügen - eispiel all 2: s Onkel ist schwar und ist rechtes Kind seines Vaters. wird auf p[] gesett und eine Linksrotation wird um (das neue) gemacht. ann weiter mit all. (er gilt jett!) rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 all 2: s Onkel ist schwar und ist rechtes Kind seines Vaters. wird auf p[] gesett und eine Linksrotation wird um (das neue) gemacht. ann weiter mit all. (er gilt jett!) rank Heitmann heitmann@informatik.uni-hamburg.de 1/2
30 Einfügen - eispiel Einfügen - eispiel all : s Onkel ist schwar und ist linkes Kind seines Vaters. arbe von p[] auf schwar (bisher rot), von p[p[]] auf rot (bisher schwar) und Rechtsrotation um p[p[]]. rank Heitmann heitmann@informatik.uni-hamburg.de 117/2 all : s Onkel ist schwar und ist linkes Kind seines Vaters. arbe von p[] auf schwar (bisher rot), von p[p[]] auf rot (bisher schwar) und Rechtsrotation um p[p[]]. rank Heitmann heitmann@informatik.uni-hamburg.de 11/2 Einfügen - Zusammenfassung Einfügen - ie Schleifeninvariante er neu eingefüge Knoten ist im linken Teilbaum seines rossvaters. und sein Vater sind rot. all 1: s Onkel ist rot. Umfärben und auf p[p[]] neu seten. (Es gibt hier wei älle, die gleich behandelt werden.) all 2: s Onkel ist schwar und ist rechtes Kind seines Vaters. wird auf p[] gesett und eine Linksrotation wird um (das neue) gemacht. ann weiter mit all. (er gilt jett!) all : s Onkel ist schwar und ist linkes Kind seines Vaters. arbe von p[] auf schwar (bisher rot), von p[p[]] auf rot (bisher schwar) und Rechtsrotation um p[p[]]. ( nicht neu seten, die Routine terminiert hier.) st im rechten Teilbaum seines rossvaters treten obige älle spiegelverkehrt auf. Überall muss dann links und rechts vertauscht werden. rank Heitmann heitmann@informatik.uni-hamburg.de 119/2 ie Schleifeninvariante: a) er Knoten ist rot. b) alls p[] die Wurel ist, ist p[] schwar. c) alls es eine Verletung der Rot-Schwar-Eigenschaften gibt, gibt es höchstens eine und diese verlett Eigenschaft 2 oder 4. st es 2, so ist die Wurel und rot, ist es 4, so sind und p[] beide rot. rank Heitmann heitmann@informatik.uni-hamburg.de 0/2
31 Einfügen - Jett u tun... Zusammenfassung Wir müssten jett - wir könnten jett... 1 en Pseudocode ausführlicher schreiben. abei insb. auf Randfälle achten (leerer aum, hat keinen Onkel,...) 2 ie Schleifeninvariante bei nitialisierung eigen. ortsetung eigen, wobei hier primär geeigt werden muss, dass die drei obigen älle die nvariante u eginn der nächsten teration erhalten. 4 Terminierung eigen und (unter Nutung der Schleifeninvarianten) dann die Korrektheit des lgorithmus eigen, d.h. dass wieder ein Rot-Schwar-aum vorliegt. en genauen eweis der Schleifeninvarianten und den Pseudocode der Einfügeoperation (sowie der Rotation) findet man im [ormen]. ort ist auch eine ehandlung der Löschoperation u finden. rank Heitmann heitmann@informatik.uni-hamburg.de 1/2 Zusammenfassung sind binäre Suchbäume, die die usätlichen Rot-Schwar-Eigenschaften erfüllen. Ein aum der die Rot-Schwar-Eigenschaften erfüllt ist in etwa ausgeglichen (h 2 log(n + 1)). er Erhalt der Rot-Schwar-Eigenschaften ist insb. bei der Einfüge- und der Löschoperation u beachten. Sie können in O(log n) implementiert werden. amit erlauben die wichtigen für dnamische Mengen alle in O(log n) Zeit! (llerdings sind sie dafür aufwändiger als normale binäre Suchbäume.) rank Heitmann heitmann@informatik.uni-hamburg.de 2/2
Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem &
 Grundlagen Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem & Frank Heitmann heitmann@informatik.uni-hamburg.de 25. November 2015 Frank Heitmann heitmann@informatik.uni-hamburg.de
Grundlagen Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem & Frank Heitmann heitmann@informatik.uni-hamburg.de 25. November 2015 Frank Heitmann heitmann@informatik.uni-hamburg.de
Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem &
 Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem & Frank Heitmann heitmann@informatik.uni-hamburg.de 25. November 2015 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/122
Algorithmen und Datenstrukturen Kapitel 7 Dynamische Mengen, das Suchproblem & Frank Heitmann heitmann@informatik.uni-hamburg.de 25. November 2015 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/122
Typische Struktur eines Baumknotens ( Class TreeNode ):
 inäre Suchbäume 1 Suchbäume unterstüten alle unten angegebenen Operationen für dynamische Mengen K effiient: Search(K,k) ---- Suche ein Element x von K mit Schlüssel k. Insert(K,x) ---- Füge das Element
inäre Suchbäume 1 Suchbäume unterstüten alle unten angegebenen Operationen für dynamische Mengen K effiient: Search(K,k) ---- Suche ein Element x von K mit Schlüssel k. Insert(K,x) ---- Füge das Element
Datenstruktur, die viele Operationen dynamischer Mengen unterstützt
 Algorithmen und Datenstrukturen 265 10 Binäre Suchbäume Suchbäume Datenstruktur, die viele Operationen dynamischer Mengen unterstützt Kann als Wörterbuch, aber auch zu mehr eingesetzt werden (Prioritätsschlange)
Algorithmen und Datenstrukturen 265 10 Binäre Suchbäume Suchbäume Datenstruktur, die viele Operationen dynamischer Mengen unterstützt Kann als Wörterbuch, aber auch zu mehr eingesetzt werden (Prioritätsschlange)
13. Binäre Suchbäume
 1. Binäre Suchbäume Binäre Suchbäume realiesieren Wörterbücher. Sie unterstützen die Operationen 1. Einfügen (Insert) 2. Entfernen (Delete). Suchen (Search) 4. Maximum/Minimum-Suche 5. Vorgänger (Predecessor),
1. Binäre Suchbäume Binäre Suchbäume realiesieren Wörterbücher. Sie unterstützen die Operationen 1. Einfügen (Insert) 2. Entfernen (Delete). Suchen (Search) 4. Maximum/Minimum-Suche 5. Vorgänger (Predecessor),
Binäre Suchbäume. Organisatorisches. VL-10: Binäre Suchbäume. (Datenstrukturen und Algorithmen, SS 2017) Gerhard Woeginger.
 Organisatorisches VL-10: inäre Suchbäume (Datenstrukturen und lgorithmen, SS 17) Gerhard Woeginger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11: 12:00 Übungen: Tim Hartmann,
Organisatorisches VL-10: inäre Suchbäume (Datenstrukturen und lgorithmen, SS 17) Gerhard Woeginger Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Sprechstunde: Mittwoch 11: 12:00 Übungen: Tim Hartmann,
Übersicht. Rot-schwarz Bäume. Rot-schwarz Bäume. Beispiel. Eigenschaften. Datenstrukturen & Algorithmen. Rot-schwarz Bäume Eigenschaften Einfügen
 Datenstrukturen & Algorithmen Übersicht Rot-schwarz Bäume Eigenschaften Einfügen Matthias Zwicker Universität Bern Frühling 2009 2 Rot-schwarz Bäume Binäre Suchbäume sind nur effizient wenn Höhe des Baumes
Datenstrukturen & Algorithmen Übersicht Rot-schwarz Bäume Eigenschaften Einfügen Matthias Zwicker Universität Bern Frühling 2009 2 Rot-schwarz Bäume Binäre Suchbäume sind nur effizient wenn Höhe des Baumes
Algorithmen und Datenstrukturen
 1 Algorithmen und Datenstrukturen Wintersemester 2016/17 13. Vorlesung Binäre Suchbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Dynamische Menge verwaltet Elemente einer sich ändernden Menge
1 Algorithmen und Datenstrukturen Wintersemester 2016/17 13. Vorlesung Binäre Suchbäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I 2 Dynamische Menge verwaltet Elemente einer sich ändernden Menge
Übersicht. Datenstrukturen und Algorithmen. Übersicht. Motivation. Vorlesung 10: Binäre Suchbäume
 Übersicht Datenstrukturen und lgorithmen Vorlesung : Joost-Pieter Katoen Lehrstuhl für Informatik 2 Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-/dsal/ 1 Suche Einfügen
Übersicht Datenstrukturen und lgorithmen Vorlesung : Joost-Pieter Katoen Lehrstuhl für Informatik 2 Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-/dsal/ 1 Suche Einfügen
Kapitel 9 Suchalgorithmen
 Kapitel 9 Suchalgorithmen Suchverfahren: Verfahren, das in einem Suchraum nach Mustern oder Objekten mit bestimmten Eigenschaften sucht. Vielfältige Anwendungsbereiche für Suchverfahren: u.a. Suchen in
Kapitel 9 Suchalgorithmen Suchverfahren: Verfahren, das in einem Suchraum nach Mustern oder Objekten mit bestimmten Eigenschaften sucht. Vielfältige Anwendungsbereiche für Suchverfahren: u.a. Suchen in
Wörterbücher ihre Implementierung mit AVL Bäumen
 Wörterbücher ihre Implementierung mit AVL Bäumen Wörterbücher - der Dictionar AD Auch in diesem Vorlesungsthema geht es um die Verwaltung von Objekten mit einem Schlüssel. Wir nennen die aus einem Schüssel
Wörterbücher ihre Implementierung mit AVL Bäumen Wörterbücher - der Dictionar AD Auch in diesem Vorlesungsthema geht es um die Verwaltung von Objekten mit einem Schlüssel. Wir nennen die aus einem Schüssel
Dynamische Mengen. Realisierungen durch Bäume
 Dynamische Mengen Eine dynamische Menge ist eine Datenstruktur, die eine Menge von Objekten verwaltet. Jedes Objekt x trägt einen eindeutigen Schlüssel key[x]. Die Datenstruktur soll mindestens die folgenden
Dynamische Mengen Eine dynamische Menge ist eine Datenstruktur, die eine Menge von Objekten verwaltet. Jedes Objekt x trägt einen eindeutigen Schlüssel key[x]. Die Datenstruktur soll mindestens die folgenden
14. Rot-Schwarz-Bäume
 Bislang: Wörterbuchoperationen bei binären Suchbäume effizient durchführbar, falls Höhe des Baums klein. Rot-Schwarz-Bäume spezielle Suchbäume. Rot-Schwarz-Baum mit n Knoten hat Höhe höchstens 2 log(n+1).
Bislang: Wörterbuchoperationen bei binären Suchbäume effizient durchführbar, falls Höhe des Baums klein. Rot-Schwarz-Bäume spezielle Suchbäume. Rot-Schwarz-Baum mit n Knoten hat Höhe höchstens 2 log(n+1).
Informatik II, SS 2016
 Informatik II - SS 2016 (Algorithmen & Datenstrukturen) Vorlesung 11 (1.6.2016) Binäre Suchbäume III Algorithmen und Komplexität Tiefe eines binären Suchbaums Worst-Case Laufzeit der Operationen in binären
Informatik II - SS 2016 (Algorithmen & Datenstrukturen) Vorlesung 11 (1.6.2016) Binäre Suchbäume III Algorithmen und Komplexität Tiefe eines binären Suchbaums Worst-Case Laufzeit der Operationen in binären
Beispiellösung zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 5
 Robert Elsässer Paderborn, den 15. Mai 2008 u.v.a. Beispiellösung zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 5 AUFGABE 1 (6 Punkte): Nehmen wir an, Anfang bezeichne in einer normalen
Robert Elsässer Paderborn, den 15. Mai 2008 u.v.a. Beispiellösung zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 5 AUFGABE 1 (6 Punkte): Nehmen wir an, Anfang bezeichne in einer normalen
1 AVL-Bäume. 1.1 Aufgabentyp. 1.2 Überblick. 1.3 Grundidee
 AVL-Bäume. Aufgabentyp Fügen Sie in einen anfangs leeren AVL Baum die folgenden Schlüssel ein:... Wenden Sie hierbei konsequent den Einfüge /Balancierungsalgorithmus an und dokumentieren Sie die ausgeführten
AVL-Bäume. Aufgabentyp Fügen Sie in einen anfangs leeren AVL Baum die folgenden Schlüssel ein:... Wenden Sie hierbei konsequent den Einfüge /Balancierungsalgorithmus an und dokumentieren Sie die ausgeführten
ContainerDatenstrukturen. Große Übung 4
 ContainerDatenstrukturen Große Übung 4 Aufgabenstellung Verwalte Kollektion S von n Objekten Grundaufgaben: Iterieren/Auflistung Suche nach Objekt x mit Wert/Schlüssel k Füge ein Objekt x hinzu Entferne
ContainerDatenstrukturen Große Übung 4 Aufgabenstellung Verwalte Kollektion S von n Objekten Grundaufgaben: Iterieren/Auflistung Suche nach Objekt x mit Wert/Schlüssel k Füge ein Objekt x hinzu Entferne
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Einfache binäre Suchbäume können entarten, so dass sich die Tiefen ihrer Blattknoten stark unterscheiden
 5.6.2 AVL-Bäume Einfache binäre Suchbäume können entarten, so dass sich die Tiefen ihrer Blattknoten stark unterscheiden AVL-Bäume, benannt nach ihren Erfindern G. M. Adelson- Velskii und E. M. Landis,
5.6.2 AVL-Bäume Einfache binäre Suchbäume können entarten, so dass sich die Tiefen ihrer Blattknoten stark unterscheiden AVL-Bäume, benannt nach ihren Erfindern G. M. Adelson- Velskii und E. M. Landis,
VL-11: Rot-Schwarz Bäume. (Datenstrukturen und Algorithmen, SS 2017) Janosch Fuchs
 VL-11: Rot-Schwarz Bäume (Datenstrukturen und Algorithmen, SS 2017) Janosch Fuchs SS 2017, RWTH DSAL/SS 2017 VL-11: Rot-Schwarz Bäume 1/41 Organisatorisches Vorlesung: Gerhard Woeginger (Zimmer 4024 im
VL-11: Rot-Schwarz Bäume (Datenstrukturen und Algorithmen, SS 2017) Janosch Fuchs SS 2017, RWTH DSAL/SS 2017 VL-11: Rot-Schwarz Bäume 1/41 Organisatorisches Vorlesung: Gerhard Woeginger (Zimmer 4024 im
Kapitel 4: Dynamische Datenstrukturen. Algorithmen und Datenstrukturen WS 2012/13. Prof. Dr. Sándor Fekete
 Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 4.4 Binäre Suche Aufgabenstellung: Rate eine Zahl zwischen 100 und 114! Algorithmus 4.1 INPUT: OUTPUT:
Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2012/13 Prof. Dr. Sándor Fekete 4.4 Binäre Suche Aufgabenstellung: Rate eine Zahl zwischen 100 und 114! Algorithmus 4.1 INPUT: OUTPUT:
9. Natürliche Suchbäume
 Bäume Bäume sind. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Verallgemeinerte Listen: Knoten können mehrere Nachfolger haben Spezielle Graphen: Graphen bestehen aus Knoten
Bäume Bäume sind. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Verallgemeinerte Listen: Knoten können mehrere Nachfolger haben Spezielle Graphen: Graphen bestehen aus Knoten
Informatik II, SS 2016
 Informatik II - SS 2016 (Algorithmen & Datenstrukturen) Vorlesung 10 (27.5.2016) Binäre Suchbäume II Algorithmen und Komplexität Zusätzliche Dictionary Operationen Dictionary: Zusätzliche mögliche Operationen:
Informatik II - SS 2016 (Algorithmen & Datenstrukturen) Vorlesung 10 (27.5.2016) Binäre Suchbäume II Algorithmen und Komplexität Zusätzliche Dictionary Operationen Dictionary: Zusätzliche mögliche Operationen:
Vorlesung Informatik 2 Algorithmen und Datenstrukturen
 Vorlesung Informatik 2 Algorithmen und Datenstrukturen (21 - Balancierte Bäume, AVL-Bäume) Prof. Dr. Susanne Albers Balancierte Bäume Eine Klasse von binären Suchbäumen ist balanciert, wenn jede der drei
Vorlesung Informatik 2 Algorithmen und Datenstrukturen (21 - Balancierte Bäume, AVL-Bäume) Prof. Dr. Susanne Albers Balancierte Bäume Eine Klasse von binären Suchbäumen ist balanciert, wenn jede der drei
Kapitel 4: Dynamische Datenstrukturen. Algorithmen und Datenstrukturen WS 2017/18. Pro f. Dr. Sán do r Fe k e te
 Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 4.1 Grundoperationen Aufgabenstellung: 3 4.1 Grundoperationen Aufgabenstellung: Verwalten
Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 4.1 Grundoperationen Aufgabenstellung: 3 4.1 Grundoperationen Aufgabenstellung: Verwalten
Anwendungsbeispiel MinHeap
 Anwendungsbeispiel MinHeap Uns seien n ganze Zahlen gegeben und wir möchten darin die k größten Zahlen bestimmen; zudem gelten, dass n deutlich größer als k ist Wir können das Problem mit Laufzeit in O(n
Anwendungsbeispiel MinHeap Uns seien n ganze Zahlen gegeben und wir möchten darin die k größten Zahlen bestimmen; zudem gelten, dass n deutlich größer als k ist Wir können das Problem mit Laufzeit in O(n
Sortieren II / HeapSort Heaps
 Organisatorisches VL-07: Sortieren II: HeapSort (Datenstrukturen und Algorithmen, SS 2017) Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Email: dsal-i1@algo.rwth-aachen.de Webseite: http://algo.rwth-aachen.de/lehre/ss17/dsa.php
Organisatorisches VL-07: Sortieren II: HeapSort (Datenstrukturen und Algorithmen, SS 2017) Vorlesung: Gerhard Woeginger (Zimmer 4024 im E1) Email: dsal-i1@algo.rwth-aachen.de Webseite: http://algo.rwth-aachen.de/lehre/ss17/dsa.php
Suchbäume. Suchbäume. Einfügen in Binären Suchbäumen. Suchen in Binären Suchbäumen. Prinzip Suchbaum. Algorithmen und Datenstrukturen
 Suchbäume Suchbäume Prinzip Suchbaum Der Wert eines Knotens wird als Schlüssel verstanden Knoten kann auch weitere Daten enthalten, die aber hier nicht weiter betrachtet werden Werte der Schlüssel müssen
Suchbäume Suchbäume Prinzip Suchbaum Der Wert eines Knotens wird als Schlüssel verstanden Knoten kann auch weitere Daten enthalten, die aber hier nicht weiter betrachtet werden Werte der Schlüssel müssen
Informatik II, SS 2018
 Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 10 (28.5.2018) Binäre Suchbäume II Algorithmen und Komplexität Binäre Suchbäume Binäre Suchbäume müssen nicht immer so schön symmetrisch
Informatik II - SS 2018 (Algorithmen & Datenstrukturen) Vorlesung 10 (28.5.2018) Binäre Suchbäume II Algorithmen und Komplexität Binäre Suchbäume Binäre Suchbäume müssen nicht immer so schön symmetrisch
Kapitel 9 Suchalgorithmen
 Kapitel 9 Suchalgorithmen Technische Universität München Suchverfahren: Verfahren, das in einem Suchraum nach Mustern oder Objekten mit bestimmten Eigenschaften sucht. Vielfältige Anwendungsbereiche für
Kapitel 9 Suchalgorithmen Technische Universität München Suchverfahren: Verfahren, das in einem Suchraum nach Mustern oder Objekten mit bestimmten Eigenschaften sucht. Vielfältige Anwendungsbereiche für
Kap. 4.2 Binäre Suchbäume ff Kap. 4.3: AVL-Bäume
 Kap. 4.2 Binäre Suchbäume ff Kap. 4.3: AVL-Bäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 12./13. VO DAP2 SS 2009 28.5./2.6.2009 1 Motivation Warum soll
Kap. 4.2 Binäre Suchbäume ff Kap. 4.3: AVL-Bäume Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 12./13. VO DAP2 SS 2009 28.5./2.6.2009 1 Motivation Warum soll
Datenstrukturen und Algorithmen SS17 Lösung - Übung 5
 Prof. aa Dr. Ir. G. Woeginger T. Hartmann, D. Korzeniewski, B. Tauer Hausaufgabe (Inorder-Traversierung binärer Suchbäume): (3 + 3 Punkte) Es soll bewiesen werden, dass die Inorder-Traversierung alle Schlüssel
Prof. aa Dr. Ir. G. Woeginger T. Hartmann, D. Korzeniewski, B. Tauer Hausaufgabe (Inorder-Traversierung binärer Suchbäume): (3 + 3 Punkte) Es soll bewiesen werden, dass die Inorder-Traversierung alle Schlüssel
Definition 14 Rot-Schwarz-Bäume sind externe Binärbäume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt:
 2.1.2 Rot-Schwarz-Bäume Definition 14 Rot-Schwarz-Bäume sind externe Binärbäume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt: 1 alle Blätter hängen an schwarzen Kanten
2.1.2 Rot-Schwarz-Bäume Definition 14 Rot-Schwarz-Bäume sind externe Binärbäume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt: 1 alle Blätter hängen an schwarzen Kanten
1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie
 Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/3, Folie 1 2010 Prof. Steffen Lange - HDa/FbI
Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/3, Folie 1 2010 Prof. Steffen Lange - HDa/FbI
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Rot-schwarz Bäume Eigenschaften Rotationen Einfügen (Löschen) 2 Einführung Binäre Suchbäume Höhe h O(h) für Operationen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Rot-schwarz Bäume Eigenschaften Rotationen Einfügen (Löschen) 2 Einführung Binäre Suchbäume Höhe h O(h) für Operationen
Datenstrukturen Teil 2. Bäume. Definition. Definition. Definition. Bäume sind verallgemeinerte Listen. Sie sind weiter spezielle Graphen
 Bäume sind verallgemeinerte Listen Datenstrukturen Teil 2 Bäume Jeder Knoten kann mehrere Nachfolger haben Sie sind weiter spezielle Graphen Graphen bestehen aus Knoten und Kanten Kanten können gerichtet
Bäume sind verallgemeinerte Listen Datenstrukturen Teil 2 Bäume Jeder Knoten kann mehrere Nachfolger haben Sie sind weiter spezielle Graphen Graphen bestehen aus Knoten und Kanten Kanten können gerichtet
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 11 (4.6.2014) Binäre Suchbäume II Algorithmen und Komplexität Binäre Suchbäume Binäre Suchbäume müssen nicht immer so schön symmetrisch sein
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 11 (4.6.2014) Binäre Suchbäume II Algorithmen und Komplexität Binäre Suchbäume Binäre Suchbäume müssen nicht immer so schön symmetrisch sein
2 i. i=0. und beweisen Sie mittels eines geeigneten Verfahrens die Korrektheit der geschlossenen Form.
 für Informatik Prof. aa Dr. Ir. Joost-Pieter Katoen Christian Dehnert, Friedrich Gretz, Benjamin Kaminski, Thomas Ströder Tutoraufgabe (Vollständige Induktion): Finden Sie eine geschlossene Form für die
für Informatik Prof. aa Dr. Ir. Joost-Pieter Katoen Christian Dehnert, Friedrich Gretz, Benjamin Kaminski, Thomas Ströder Tutoraufgabe (Vollständige Induktion): Finden Sie eine geschlossene Form für die
Mengen. Binäre Suchbäume. Mengen: Anwendungen (II) Mengen: Lösung mit Listen 12/3/12. Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps
 // Mengen Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps n Ziel: ufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: n eines Elements n eines Elements
// Mengen Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps n Ziel: ufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: n eines Elements n eines Elements
3. Binäre Suchbäume. 3.1 Natürliche binäre Suchbäume. EADS 3.1 Natürliche binäre Suchbäume 78/598 ľernst W. Mayr
 3. Binäre Suchbäume 3.1 Natürliche binäre Suchbäume Definition 18 Ein natürlicher binärer Suchbaum über einem durch total geordneten Universum U ist ein als interner Suchbaum organisierter Binärbaum (also:
3. Binäre Suchbäume 3.1 Natürliche binäre Suchbäume Definition 18 Ein natürlicher binärer Suchbaum über einem durch total geordneten Universum U ist ein als interner Suchbaum organisierter Binärbaum (also:
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 13 (18.6.2014) Binäre Suchbäume IV (Rot Schwarz Bäume) Algorithmen und Komplexität Rot Schwarz Bäume Ziel: Binäre Suchbäume, welche immer
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 13 (18.6.2014) Binäre Suchbäume IV (Rot Schwarz Bäume) Algorithmen und Komplexität Rot Schwarz Bäume Ziel: Binäre Suchbäume, welche immer
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Sortierte Folgen Maike Buchin 30.5., 1.6., 13.6.2017 Sortierte Folgen Häufiges Szenario: in einer Menge von Objekten mit Schlüsseln (aus geordnetem Universum) sollen Elemente
Vorlesung Datenstrukturen Sortierte Folgen Maike Buchin 30.5., 1.6., 13.6.2017 Sortierte Folgen Häufiges Szenario: in einer Menge von Objekten mit Schlüsseln (aus geordnetem Universum) sollen Elemente
Christian Rieck, Arne Schmidt
 Institute of Operating Systems and Computer Networks Algorithms Group Algorithmen und Datenstrukturen Wintersemester 207/208 Übung#5, 2.2.207 Christian Rieck, Arne Schmidt Bäume Satz Jeder gerichtete Baum
Institute of Operating Systems and Computer Networks Algorithms Group Algorithmen und Datenstrukturen Wintersemester 207/208 Übung#5, 2.2.207 Christian Rieck, Arne Schmidt Bäume Satz Jeder gerichtete Baum
Algorithmen und Datenstrukturen 2. Dynamische Datenstrukturen
 Algorithmen und Datenstrukturen 2 Dynamische Datenstrukturen Algorithmen für dynamische Datenstrukturen Zugriff auf Variable und Felder durch einen Ausdruck: Namen durch feste Adressen referenziert Anzahl
Algorithmen und Datenstrukturen 2 Dynamische Datenstrukturen Algorithmen für dynamische Datenstrukturen Zugriff auf Variable und Felder durch einen Ausdruck: Namen durch feste Adressen referenziert Anzahl
Übersicht. Datenstrukturen und Algorithmen. Übersicht. Heaps. Vorlesung 8: Heapsort (K6) Joost-Pieter Katoen. 7. Mai 2015
 Datenstrukturen und Algorithmen Vorlesung 8: (K6) 1 Joost-Pieter Katoen Lehrstuhl für Informatik Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-15/dsal/ 7. Mai 015 3 Joost-Pieter
Datenstrukturen und Algorithmen Vorlesung 8: (K6) 1 Joost-Pieter Katoen Lehrstuhl für Informatik Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-15/dsal/ 7. Mai 015 3 Joost-Pieter
Binäre Suchbäume. Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps
 Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps Mengen n Ziel: Aufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: Mengen n Ziel: Aufrechterhalten einer
Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps Mengen n Ziel: Aufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: Mengen n Ziel: Aufrechterhalten einer
Programm heute. Algorithmen und Datenstrukturen (für ET/IT) Suchen. Lineare Suche. Such-Algorithmen. Sommersemester Dr.
 Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 0 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Fortgeschrittene Datenstrukturen Such-Algorithmen
Programm heute Algorithmen und Datenstrukturen (für ET/IT) Sommersemester 0 Dr. Tobias Lasser Computer Aided Medical Procedures Technische Universität München Fortgeschrittene Datenstrukturen Such-Algorithmen
11. Elementare Datenstrukturen
 11. Elementare Datenstrukturen Definition 11.1: Eine dynamische Menge ist gegeben durch eine oder mehrer Mengen von Objekten sowie Operationen auf diesen Mengen und den Objekten der Mengen. Dynamische
11. Elementare Datenstrukturen Definition 11.1: Eine dynamische Menge ist gegeben durch eine oder mehrer Mengen von Objekten sowie Operationen auf diesen Mengen und den Objekten der Mengen. Dynamische
Informatik II, SS 2014
 Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 10 (3.6.2014) Binäre Suchbäume I Algorithmen und Komplexität Zusätzliche Dictionary Operationen Dictionary: Zusätzliche mögliche Operationen:
Informatik II SS 2014 (Algorithmen & Datenstrukturen) Vorlesung 10 (3.6.2014) Binäre Suchbäume I Algorithmen und Komplexität Zusätzliche Dictionary Operationen Dictionary: Zusätzliche mögliche Operationen:
1 Raumwechsel: Gr. 15 (Do 10-12, F-235) ab sofort in G Studie zum Arbeitsverhalten von Studierenden unter Leitung
 Organisatorisches Algorithmen und Datenstrukturen Kapitel 3: Divide & Conquer Frank Heitmann heitmann@informatik.uni-hamburg.de 1 Raumwechsel: Gr. 15 (Do 10-12, F-235) ab sofort in G-021. 2 Studie zum
Organisatorisches Algorithmen und Datenstrukturen Kapitel 3: Divide & Conquer Frank Heitmann heitmann@informatik.uni-hamburg.de 1 Raumwechsel: Gr. 15 (Do 10-12, F-235) ab sofort in G-021. 2 Studie zum
Algorithmen I. Tutorium 1-6. Sitzung. Dennis Felsing
 Algorithmen I Tutorium 1-6. Sitzung Dennis Felsing dennis.felsing@student.kit.edu www.stud.uni-karlsruhe.de/~ubcqr/algo 2011-05-23 Überblick 1 Binäre Suchbäume 2 Dennis Felsing Algorithmen I 2/20 Binäre
Algorithmen I Tutorium 1-6. Sitzung Dennis Felsing dennis.felsing@student.kit.edu www.stud.uni-karlsruhe.de/~ubcqr/algo 2011-05-23 Überblick 1 Binäre Suchbäume 2 Dennis Felsing Algorithmen I 2/20 Binäre
18. Natürliche Suchbäume
 Wörterbuchimplementationen 1. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Hashing: Implementierung von Wörterbüchern mit erwartet sehr schnellen Zugriffszeiten. Nachteile
Wörterbuchimplementationen 1. Natürliche Suchbäume [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Hashing: Implementierung von Wörterbüchern mit erwartet sehr schnellen Zugriffszeiten. Nachteile
Literatur: Kapitel 2.1 des Skripts Rot-Schwarz-Bäume Kapitel 2.2 des Skripts Treaps Cormen. Kapitel 13, Red-Black-Trees
 Algorithmische Anwendungen WS 2006/2007 Praktikum 3: Aufgabe 1: Einfügen eines Knotens ist einen Rot-Schwarz-Baum Aufgabe 2: Erklärungen für die Beobachtungen auf Folie 2.1/67 Aufgabe 3: Zeige wie RB-DELETE-FIXUP
Algorithmische Anwendungen WS 2006/2007 Praktikum 3: Aufgabe 1: Einfügen eines Knotens ist einen Rot-Schwarz-Baum Aufgabe 2: Erklärungen für die Beobachtungen auf Folie 2.1/67 Aufgabe 3: Zeige wie RB-DELETE-FIXUP
Algorithmen und Datenstrukturen Heapsort
 Algorithmen und Datenstrukturen 2 5 Heapsort In diesem Kapitel wird Heapsort, ein weiterer Sortieralgorithmus, vorgestellt. Dieser besitzt wie MERGE-SORT eine Laufzeit von O(n log n), sortiert jedoch das
Algorithmen und Datenstrukturen 2 5 Heapsort In diesem Kapitel wird Heapsort, ein weiterer Sortieralgorithmus, vorgestellt. Dieser besitzt wie MERGE-SORT eine Laufzeit von O(n log n), sortiert jedoch das
Algorithmen und Datenstrukturen Suchbaum
 Algorithmen und Datenstrukturen Suchbaum Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Motivation Datenstruktur zur Repräsentation dynamischer Mengen
Algorithmen und Datenstrukturen Suchbaum Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Motivation Datenstruktur zur Repräsentation dynamischer Mengen
Binäre Suchbäume. Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps
 Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps Mengen n Ziel: Aufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: Mengen n Ziel: Aufrechterhalten einer
Binäre Suchbäume Mengen, Funktionalität, Binäre Suchbäume, Heaps, Treaps Mengen n Ziel: Aufrechterhalten einer Menge (hier: ganzer Zahlen) unter folgenden Operationen: Mengen n Ziel: Aufrechterhalten einer
3.6 AVL-Bäume. (AVL = Adel son-velskii und Landis (1962)) . Seite 326/726
 3.6 VL-Bäume (VL = del son-velskii und Landis (1962)) 2-3-Bäume... sind Basis der B-Bäume, sind gut auf eitere Operationen ereiterbar (SPLIT, CONCTENTE), haben Worstcase-Zeiten on O(log n), aber sie nuten
3.6 VL-Bäume (VL = del son-velskii und Landis (1962)) 2-3-Bäume... sind Basis der B-Bäume, sind gut auf eitere Operationen ereiterbar (SPLIT, CONCTENTE), haben Worstcase-Zeiten on O(log n), aber sie nuten
9. Rekursion. 1 falls n 1 n (n 1)!, andernfalls. Experiment: Die Türme von Hanoi. Links Mitte Rechts. Mathematische Rekursion
 Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
14. Sortieren II Heapsort. Heapsort. [Max-]Heap 7. Heapsort, Quicksort, Mergesort. Binärer Baum mit folgenden Eigenschaften
![14. Sortieren II Heapsort. Heapsort. [Max-]Heap 7. Heapsort, Quicksort, Mergesort. Binärer Baum mit folgenden Eigenschaften 14. Sortieren II Heapsort. Heapsort. [Max-]Heap 7. Heapsort, Quicksort, Mergesort. Binärer Baum mit folgenden Eigenschaften](/thumbs/86/93979187.jpg) Heapsort, Quicksort, Mergesort 14. Sortieren II 14.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] 397 398 Heapsort [Max-]Heap 7 Inspiration von Selectsort: Schnelles Einfügen Binärer Baum
Heapsort, Quicksort, Mergesort 14. Sortieren II 14.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] 397 398 Heapsort [Max-]Heap 7 Inspiration von Selectsort: Schnelles Einfügen Binärer Baum
Das Suchproblem 4. Suchen Das Auswahlproblem Suche in Array
 Das Suchproblem Gegeben. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.-3,2.2-3,2.3-] Menge von Datensätzen. Beispiele
Das Suchproblem Gegeben. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.-3,2.2-3,2.3-] Menge von Datensätzen. Beispiele
Das Suchproblem. Gegeben Menge von Datensätzen. Beispiele Telefonverzeichnis, Wörterbuch, Symboltabelle
 119 4. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Exponentielle Suche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.1-3,2.2-3,2.3-5] 120 Das Suchproblem Gegeben
119 4. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Exponentielle Suche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.1-3,2.2-3,2.3-5] 120 Das Suchproblem Gegeben
Das Suchproblem 4. Suchen Das Auswahlproblem Suche in Array
 Das Suchproblem Gegeben. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Exponentielle Suche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.-3,2.2-3,2.3-] Menge
Das Suchproblem Gegeben. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Exponentielle Suche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.-3,2.2-3,2.3-] Menge
Kapitel 4: Dynamische Datenstrukturen. Algorithmen und Datenstrukturen WS 2017/18. Pro f. Dr. Sán do r Fe k e te
 Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 Binärer Suchbaum Außerdem wichtig: Struktur der Schlüsselwerte! 2 Ordnungsstruktur Linker
Kapitel 4: Dynamische Datenstrukturen Algorithmen und Datenstrukturen WS 2017/18 Pro f. Dr. Sán do r Fe k e te 1 Binärer Suchbaum Außerdem wichtig: Struktur der Schlüsselwerte! 2 Ordnungsstruktur Linker
Das Suchproblem. Gegeben Menge von Datensätzen. Beispiele Telefonverzeichnis, Wörterbuch, Symboltabelle
 122 4. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.1-3,2.2-3,2.3-5] 123 Das Suchproblem Gegeben Menge von Datensätzen.
122 4. Suchen Lineare Suche, Binäre Suche, Interpolationssuche, Untere Schranken [Ottman/Widmayer, Kap. 3.2, Cormen et al, Kap. 2: Problems 2.1-3,2.2-3,2.3-5] 123 Das Suchproblem Gegeben Menge von Datensätzen.
Übung zur Vorlesung Algorithmische Geometrie
 Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Technische Universität München. Vorlesungsgrobstruktur: wo stehen wir, wie geht s weiter
 Vorlesungsgrobstruktur: wo stehen wir, wie geht s weiter Kapitel 7 Fortgeschrittene Datenstrukturen Motivation: Lineare Liste: Suchen eines Elements ist schnell O(log n) Einfügen eines Elements ist langsam
Vorlesungsgrobstruktur: wo stehen wir, wie geht s weiter Kapitel 7 Fortgeschrittene Datenstrukturen Motivation: Lineare Liste: Suchen eines Elements ist schnell O(log n) Einfügen eines Elements ist langsam
Algorithmen 1 Tutorium
 Algorithmen 1 Tutorium Tutorium 13 Misch Sadler 18. Juli 2011 INHALT: VIELES Übersicht 1 Dynamische Programmierung 2 Wiederholung 3 Klausuraufgaben 4 Ende Misch Sadler Algo 1 Tut 18. Juli 2011 2/21 Übersicht
Algorithmen 1 Tutorium Tutorium 13 Misch Sadler 18. Juli 2011 INHALT: VIELES Übersicht 1 Dynamische Programmierung 2 Wiederholung 3 Klausuraufgaben 4 Ende Misch Sadler Algo 1 Tut 18. Juli 2011 2/21 Übersicht
Wiederholung. Datenstrukturen und. Bäume. Wiederholung. Suchen in linearen Feldern VO
 Wiederholung Datenstrukturen und Algorithmen VO 708.031 Suchen in linearen Feldern Ohne Vorsortierung: Sequentielle Suche Speicherung nach Zugriffswahrscheinlichkeit Selbstanordnende Felder Mit Vorsortierung:
Wiederholung Datenstrukturen und Algorithmen VO 708.031 Suchen in linearen Feldern Ohne Vorsortierung: Sequentielle Suche Speicherung nach Zugriffswahrscheinlichkeit Selbstanordnende Felder Mit Vorsortierung:
11.1 Grundlagen - Denitionen
 11 Binärbäume 11.1 Grundlagen - Denitionen Denition: Ein Baum ist eine Menge, die durch eine sog. Nachfolgerrelation strukturiert ist. In einem Baum gilt: (I) (II) 1 Knoten w ohne VATER(w), das ist die
11 Binärbäume 11.1 Grundlagen - Denitionen Denition: Ein Baum ist eine Menge, die durch eine sog. Nachfolgerrelation strukturiert ist. In einem Baum gilt: (I) (II) 1 Knoten w ohne VATER(w), das ist die
Suchen und Sortieren Binäre Suchbäume
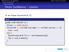 Löschen (Folie 63, Seite 34 im Skript) In der Klasse Searchtree K, : Java public void delete(k k) { if(root == null) return; if(root.left == null && root.right == null && root.key == k) root = null; else
Löschen (Folie 63, Seite 34 im Skript) In der Klasse Searchtree K, : Java public void delete(k k) { if(root == null) return; if(root.left == null && root.right == null && root.key == k) root = null; else
Voronoi-Diagramme. Dr. Martin Nöllenburg Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK
 Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 29.05.2011 Das Postamt-Problem b(p, q) = {x R 2 : xp = xq } p q h(p, q) h(q, p) = {x :
Vorlesung Algorithmische Geometrie INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 29.05.2011 Das Postamt-Problem b(p, q) = {x R 2 : xp = xq } p q h(p, q) h(q, p) = {x :
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Breitensuche, Tiefensuche Wir besprechen nun zwei grundlegende Verfahren, alle Knoten eines Graphen zu
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Breitensuche, Tiefensuche Wir besprechen nun zwei grundlegende Verfahren, alle Knoten eines Graphen zu
1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie
 Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/2, Folie 1 2014 Prof. Steffen Lange - HDa/FbI
Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/2, Folie 1 2014 Prof. Steffen Lange - HDa/FbI
Algorithmen und Datenstrukturen
 Universität Innsbruck Institut für Informatik Zweite Prüfung 16. Oktober 2008 Algorithmen und Datenstrukturen Name: Matrikelnr: Die Prüfung besteht aus 8 Aufgaben. Die verfügbaren Punkte für jede Aufgabe
Universität Innsbruck Institut für Informatik Zweite Prüfung 16. Oktober 2008 Algorithmen und Datenstrukturen Name: Matrikelnr: Die Prüfung besteht aus 8 Aufgaben. Die verfügbaren Punkte für jede Aufgabe
Umstrukturierung durch Rotationen
 Umstrukturierung durch Rotationen (Folie 109, Seite 52 im Skript) P P T A A D B T B C C D Eine Rechtsrotation um T. Die Suchbaumeigenschaft bleibt erhalten. B, C, D können nur aus externen Knoten bestehen.
Umstrukturierung durch Rotationen (Folie 109, Seite 52 im Skript) P P T A A D B T B C C D Eine Rechtsrotation um T. Die Suchbaumeigenschaft bleibt erhalten. B, C, D können nur aus externen Knoten bestehen.
3. Übungsblatt zu Algorithmen I im SoSe 2017
 Karlsruher Institut für Technologie Prof. Dr. Jörn Müller-Quade Institut für Theoretische Informatik Björn Kaidel, Sebastian Schlag, Sascha Witt 3. Übungsblatt zu Algorithmen I im SoSe 2017 http://crypto.iti.kit.edu/index.php?id=799
Karlsruher Institut für Technologie Prof. Dr. Jörn Müller-Quade Institut für Theoretische Informatik Björn Kaidel, Sebastian Schlag, Sascha Witt 3. Übungsblatt zu Algorithmen I im SoSe 2017 http://crypto.iti.kit.edu/index.php?id=799
2.7 Bucket-Sort Bucket-Sort ist ein nicht-vergleichsbasiertes Sortierverfahren. Hier können z.b. n Schlüssel aus
 2.7 Bucket-Sort Bucket-Sort ist ein nicht-vergleichsbasiertes Sortierverfahren. Hier können z.b. n Schlüssel aus {0, 1,..., B 1} d in Zeit O(d(n + B)) sortiert werden, indem sie zuerst gemäß dem letzten
2.7 Bucket-Sort Bucket-Sort ist ein nicht-vergleichsbasiertes Sortierverfahren. Hier können z.b. n Schlüssel aus {0, 1,..., B 1} d in Zeit O(d(n + B)) sortiert werden, indem sie zuerst gemäß dem letzten
Vorlesung Informatik 2 Algorithmen und Datenstrukturen
 Vorlesung Informatik 2 Algorithmen und Datenstrukturen (18 Bäume: Grundlagen und natürliche Suchbäume) Prof. Dr. Susanne Albers Bäume (1) Bäume sind verallgemeinerte Listen (jedes Knoten-Element kann mehr
Vorlesung Informatik 2 Algorithmen und Datenstrukturen (18 Bäume: Grundlagen und natürliche Suchbäume) Prof. Dr. Susanne Albers Bäume (1) Bäume sind verallgemeinerte Listen (jedes Knoten-Element kann mehr
Datenstrukturen & Algorithmen Lösungen zu Blatt 6 FS 14
 Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 2. April
Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 2. April
Mergeable Heaps. C. Komusiewicz 7.1 Fibonacci-Heaps: Überblick 117
 C. Komusiewicz 7.1 Fibonacci-Heaps: Überblick 117 Mergeable Heaps Erweiterung von Standardheaps, die die folgenden fünf Operationen unterstützen. Make-Heappq liefert neuen, leeren Heap. InsertpH, xq fügt
C. Komusiewicz 7.1 Fibonacci-Heaps: Überblick 117 Mergeable Heaps Erweiterung von Standardheaps, die die folgenden fünf Operationen unterstützen. Make-Heappq liefert neuen, leeren Heap. InsertpH, xq fügt
10. Übungsblatt zu Algorithmen I im SoSe 2016
 Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. r. ennis ofheinz Lukas arth, Lisa Kohl 0. Übungsblatt zu lgorithmen I im SoSe 0 https://crypto.iti.kit.edu/index.php?id=algo-sose
Karlsruher Institut für Technologie Institut für Theoretische Informatik Prof. r. ennis ofheinz Lukas arth, Lisa Kohl 0. Übungsblatt zu lgorithmen I im SoSe 0 https://crypto.iti.kit.edu/index.php?id=algo-sose
Definition 15 Rot-Schwarz-Bäume sind externe Binärbäume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt:
 2.2 Rot-Schwarz-Bäume Definition 15 Rot-Schwarz-Bäume sind externe Binäräume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt: 1 alle Blätter hängen an schwarzen Kanten (durchgezogene
2.2 Rot-Schwarz-Bäume Definition 15 Rot-Schwarz-Bäume sind externe Binäräume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt: 1 alle Blätter hängen an schwarzen Kanten (durchgezogene
Algorithmen und Datenstrukturen II
 Algorithmen und Datenstrukturen II und Red-Black-Trees Dr. Georg Sauthoff 1 AG Praktische Informatik July 1, SoSe 2011 1 gsauthof@techfak.uni-bielefeld.de Suchbäume (Indexdatenstrukturen) Zugriff in O(logn)
Algorithmen und Datenstrukturen II und Red-Black-Trees Dr. Georg Sauthoff 1 AG Praktische Informatik July 1, SoSe 2011 1 gsauthof@techfak.uni-bielefeld.de Suchbäume (Indexdatenstrukturen) Zugriff in O(logn)
8. A & D - Heapsort. Werden sehen, wie wir durch geschicktes Organsieren von Daten effiziente Algorithmen entwerfen können.
 8. A & D - Heapsort Werden sehen, wie wir durch geschicktes Organsieren von Daten effiziente Algorithmen entwerfen können. Genauer werden wir immer wieder benötigte Operationen durch Datenstrukturen unterstützen.
8. A & D - Heapsort Werden sehen, wie wir durch geschicktes Organsieren von Daten effiziente Algorithmen entwerfen können. Genauer werden wir immer wieder benötigte Operationen durch Datenstrukturen unterstützen.
Vorlesung Datenstrukturen
 Vorlesung Datenstrukturen Balancieren eines Suchbaums Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 396 Baumgestalt vs. Zeitkomplexität Vorteile eines ausgeglichenen binären Suchbaums
Vorlesung Datenstrukturen Balancieren eines Suchbaums Dr. Frank Seifert Vorlesung Datenstrukturen - Sommersemester 2016 Folie 396 Baumgestalt vs. Zeitkomplexität Vorteile eines ausgeglichenen binären Suchbaums
Heapsort, Quicksort, Mergesort. 8. Sortieren II
 209 Heapsort, Quicksort, Mergesort 8. Sortieren II 210 8.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] Heapsort 211 Inspiration von Selectsort: Schnelles Einfügen Inspiration von Insertionsort:
209 Heapsort, Quicksort, Mergesort 8. Sortieren II 210 8.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] Heapsort 211 Inspiration von Selectsort: Schnelles Einfügen Inspiration von Insertionsort:
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 217 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda: Graphen, Suchbäume, AVL Bäume Heute: Graphen und Bäume Binäre Suchbäume AVL-Bäume Nächste
Übung Algorithmen und Datenstrukturen Sommersemester 217 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda: Graphen, Suchbäume, AVL Bäume Heute: Graphen und Bäume Binäre Suchbäume AVL-Bäume Nächste
Algorithmen und Datenstrukturen Balancierte Suchbäume
 Algorithmen und Datenstrukturen Balancierte Suchbäume Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Überblick Einführung Einfügen und Löschen Einfügen
Algorithmen und Datenstrukturen Balancierte Suchbäume Matthias Teschner Graphische Datenverarbeitung Institut für Informatik Universität Freiburg SS 12 Überblick Einführung Einfügen und Löschen Einfügen
Datenstrukturen & Algorithmen Lösungen zu Blatt 4 FS 15
 Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 18. März
Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 18. März
Algorithmen und Datenstrukturen. Bäume. M. Herpers, Y. Jung, P. Klingebiel
 Algorithmen und Datenstrukturen Bäume M. Herpers, Y. Jung, P. Klingebiel 1 Lernziele Baumstrukturen und Ihre Verwendung kennen Grundbegriffe zu Bäumen anwenden können Baumstruktur in C anlegen können Suchbäume
Algorithmen und Datenstrukturen Bäume M. Herpers, Y. Jung, P. Klingebiel 1 Lernziele Baumstrukturen und Ihre Verwendung kennen Grundbegriffe zu Bäumen anwenden können Baumstruktur in C anlegen können Suchbäume
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Wintersemester 2012/13 16. Vorlesung Rot-Schwarz-Bäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Dynamische Menge verwaltet Elemente einer sich ändernden Menge
Algorithmen und Datenstrukturen Wintersemester 2012/13 16. Vorlesung Rot-Schwarz-Bäume Prof. Dr. Alexander Wolff Lehrstuhl für Informatik I Dynamische Menge verwaltet Elemente einer sich ändernden Menge
B6.1 Introduction. Algorithmen und Datenstrukturen. Algorithmen und Datenstrukturen. B6.1 Introduction. B6.3 Analyse. B6.4 Ordnungsbasierte Methoden
 Algorithmen und Datenstrukturen 11. April 2018 B6. Binäre Suchbäume a Algorithmen und Datenstrukturen B6. Binäre Suchbäume 1 Marcel Lüthi and Gabriele Röger Universität Basel 11. April 2018 a Folien basieren
Algorithmen und Datenstrukturen 11. April 2018 B6. Binäre Suchbäume a Algorithmen und Datenstrukturen B6. Binäre Suchbäume 1 Marcel Lüthi and Gabriele Röger Universität Basel 11. April 2018 a Folien basieren
8. Sortieren II. 8.1 Heapsort. Heapsort. [Max-]Heap 6. Heapsort, Quicksort, Mergesort. Binärer Baum mit folgenden Eigenschaften
![8. Sortieren II. 8.1 Heapsort. Heapsort. [Max-]Heap 6. Heapsort, Quicksort, Mergesort. Binärer Baum mit folgenden Eigenschaften 8. Sortieren II. 8.1 Heapsort. Heapsort. [Max-]Heap 6. Heapsort, Quicksort, Mergesort. Binärer Baum mit folgenden Eigenschaften](/thumbs/72/66389118.jpg) Heapsort, Quicksort, Mergesort 8. Sortieren II 8.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] 9 210 Heapsort [Max-]Heap 6 Inspiration von Selectsort: Schnelles Einfügen Binärer Baum mit
Heapsort, Quicksort, Mergesort 8. Sortieren II 8.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] 9 210 Heapsort [Max-]Heap 6 Inspiration von Selectsort: Schnelles Einfügen Binärer Baum mit
Heapsort, Quicksort, Mergesort. 8. Sortieren II
 209 Heapsort, Quicksort, Mergesort 8. Sortieren II 210 8.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] 211 Heapsort Inspiration von Selectsort: Schnelles Einfügen Inspiration von Insertionsort:
209 Heapsort, Quicksort, Mergesort 8. Sortieren II 210 8.1 Heapsort [Ottman/Widmayer, Kap. 2.3, Cormen et al, Kap. 6] 211 Heapsort Inspiration von Selectsort: Schnelles Einfügen Inspiration von Insertionsort:
Beispiellösungen zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 6
 Robert Elsässer u.v.a. Paderborn, 29. Mai 2008 Beispiellösungen zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 6 Aufgabe 1 (6 Punkte): Zunächst sollte klar sein, daß ein vollständiger Binärer
Robert Elsässer u.v.a. Paderborn, 29. Mai 2008 Beispiellösungen zu den Übungen Datenstrukturen und Algorithmen SS 2008 Blatt 6 Aufgabe 1 (6 Punkte): Zunächst sollte klar sein, daß ein vollständiger Binärer
Wiederholung ADT Menge Ziel: Verwaltung (Finden, Einfügen, Entfernen) einer Menge von Elementen
 Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Was bisher geschah abstrakter Datentyp : Signatur Σ und Axiome Φ z.b. ADT Menge zur Verwaltung (Finden, Einfügen, Entfernen) mehrerer Elemente desselben Typs Spezifikation einer Schnittstelle Konkreter
Satz 172 Jedes vergleichsbasierte Sortierverfahren benötigt im worst-case mindestens n ld n + O(n) Vergleiche und hat damit Laufzeit Ω(n log n).
 2.6 Vergleichsbasierte Sortierverfahren Alle bisher betrachteten Sortierverfahren sind vergleichsbasiert, d.h. sie greifen auf Schlüssel k, k (außer in Zuweisungen) nur in Vergleichsoperationen der Form
2.6 Vergleichsbasierte Sortierverfahren Alle bisher betrachteten Sortierverfahren sind vergleichsbasiert, d.h. sie greifen auf Schlüssel k, k (außer in Zuweisungen) nur in Vergleichsoperationen der Form
Übung Algorithmen und Datenstrukturen
 Übung Algorithmen und Datenstrukturen Sommersemester 216 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda Vorstellung des 6. Übungsblatts. Hashing Binäre Suchbäume AVL-Bäume 2 Aufgabe: Hashing mit
Übung Algorithmen und Datenstrukturen Sommersemester 216 Patrick Schäfer, Humboldt-Universität zu Berlin Agenda Vorstellung des 6. Übungsblatts. Hashing Binäre Suchbäume AVL-Bäume 2 Aufgabe: Hashing mit
