Kapitel 3. Kontextfreie Sprachen. Induktive Charakterisierung der Sprache L der korrekten Klammerausdrücke: (w) L, falls w L vw L, falls v, w L
|
|
|
- Ursula Goldschmidt
- vor 5 Jahren
- Abrufe
Transkript
1 Kapitel 3 Kontextfreie Sprachen Induktive Charakterisierung der Sprache L der korrekten Klammerausdrücke: s. Übung ε L (w) L, falls w L vw L, falls v, w L (R0) (R1) (R2) Für beliebige w {(, )} kann w L nachgewiesen werden durch ngabe der Regeln, nach denen w aufgebaut ist. 3.1 Beispiel w = (()())() 30
2 Theoretische Informatik (SS 2004) 31 Liest man diesen Nachweis umgekehrt, so wird ein noch unbekanntes Wort an der Wurzel entsprechend (R2) durch zwei unbekannte Wörter ersetzt, die dann wiederum durch andere Wörter ersetzt werden, bis an den Blättern ε oder Symbole des lphabets die Ersetzung abschließen. 3.1 Kontextfreie rammatiken 3.2 Def inition Eine kontextfreie rammatik = (V, Σ, P, S) besteht aus einer endlichen Menge von Variablen (Nichtterminalsymbolen) V einem lphabet (Terminalsymbolen) Σ bleitungsregeln (Produktionen) P V (V Σ) einem Startsymbol S V. Jedes α (V Σ) heißt Satzform. Für Produktionen (, α) P schreiben wir α, und für alternative Produktionen α, β auch kurz α β. 3.3 Bemerkung nwenden einer bleitungsregel α bedeutet, in einer Satzform ein Vorkommen von durch α zu ersetzen: β 1 β 2 β 1 αβ 2 (bzw. β 1 β 2 β 1 αβ 2 ). Dies geschieht ohne Berücksichtigung des Kontextes β 1, β 2 von. eht eine Satzform β aus einer Satzform α durch nwenden einer endlichen nzahl von bleitungsregeln hervor, schreiben wir α β (bzw. α β). 3.4 Def inition Eine kontextfreie rammatik = (V, Σ, P, S) erzeugt ein Wort w Σ (w kann in abgeleitet werden), { falls S } w. Die Menge L() := w Σ : S w ist die von erzeugte Sprache. Eine Sprache heißt kontextfrei, wenn sie von einer kontextfreien rammatik erzeugt wird.
3 Theoretische Informatik (SS 2004) Beispiele 1. Die Sprache der korrekten Klammerausdrücke wird von der rammatik = ({S}, {(, )}, P, S) mit P : S ε (R0) S SS S (S) (R1) (R2) erzeugt. Z.B. ist (()())() L(), da S SS (S)S (SS)S ((S)S)S (()S)S (()(S))S (()())S (()())(S) (()())(). 2. Für w = a 1 a n sei w R := a n a n 1 a 1. Die Sprache L = { w Σ : w = w R} der Palindrome über einem beliebigen lphabet Σ ist nicht regulär. Es s. Übung ist aber L = L() für = ({S}, Σ, P, S) mit P : S ε S a S asa für alle a Σ für alle a Σ 3. Sei L = {w {0, 1} : w 0 = w 1 > 0} die Sprache der nichtleeren Binärwörter mit gleich vielen 0 en und 1 en. Eine rammatik, die L erzeugt, muss sich in jeder während einer bleitung auftretenden Satzform merken, wieviele 0 en oder 1 en zusätzlich benötigt werden, um das Verhältnis später wieder auszugleichen: = (V, Σ, P, S) mit V = {, B, S} und P : S 0B 1 0 0S 1 B 1 1S 0BB Reihenfolge der bleitungsschritte egal
4 Theoretische Informatik (SS 2004) 33 Ein Syntaxbaum ist die graphische Darstellung der bleitung eines Wortes, z.b. für und die rammatik aus Beispiel 3.5(??.): 3.6 Bemerkung In Syntaxbäumen ist die Wurzel mit dem Startsymbol markiert ist jeder innere Knoten ein Nichtterminalsymbol und jedes Blatt ein Terminalsymbol bilden die Kinder eines Nichtterminalsymbols die Satzform einer passenden rechten Regelseite Zu jeder bleitung gehört genau ein Syntaxbaum, aber zu einem Syntaxbaum gehören mehrere bleitungen, insbesondere eine Linksableitung (bei der jeweils das linkeste Nichtterminalsymbol als nächstes ersetzt wird) und eine Rechtsableitung (entsprechend). Zu einem von einer kontextfreien rammatik erzeugten Wort kann es verschiedene bleitungen mit verschiedenen Syntaxbäumen geben. 3.7 Def inition Eine kontextfreie rammatik heißt eindeutig, falls es für jedes Wort w L() genau einen Syntaxbaum gibt; andernfalls heißt mehrdeutig. Eine kontextfreie Sprache L heißt eindeutig, falls es eine eindeutige kontextfreie rammatik gibt, die L erzeugt; andernfalls heißt L inhärent mehrdeutig.
5 Theoretische Informatik (SS 2004) 34 Wir werden auf diese Begriffe zurückkommen, wollen jedoch zunächst das Wortproblem für kontextfreie Sprachen angehen. 3.8 Def inition Eine kontextfreie rammatik = (V, Σ, P, S) ist in Chomsky-Normalform, wenn alle Produktionen von der Form mit, B, C V und a Σ sind. BC oder a 3.9 Bemerkung Für Sprachen L, die das leere Wort enthalten, erhalten rammatiken in Chomsky-Normalform, die L \ {ε} erzeugen, ein neues Startsymbol S und neue Produktionen S ε S Satz Jede kontextfreie rammatik kann in eine kontextfreie rammatik in Chomsky-Normalform mit L( ) = L() \ {ε} transformiert werden. Beweis: wird in 4 Schritten in transformiert: 1. Schritt: (Terminale treten nur allein auf der rechten Seite auf) Führe neue Nichtterminale S a für alle a Σ ein. Danach ersetze alle Vorkommen von a Σ auf der rechten Regelseite durch S a und führe neue Produktionen S a a ein. 2. Schritt: (alle rechten Regelseiten haben höchstens zwei Symbole) Für jede Produktion P i : B 1... B m mit m > 2 führe neue Nichtterminale C i j, j = 1,..., m 2, ein und ersetze P i durch B 1 C i 1 C i j B j+1 C i j+1, j = 1,..., m 3 C i m 2 B m 1 B m. 3. Schritt: (ε-elimination) Berechne zunächst die Menge V der Nichtterminale, aus denen das
6 Theoretische Informatik (SS 2004) 35 leere Wort abgeleitet werden kann, d.h. V ε. Dazu seien V 0 = V 1 = { V : ε in P } V i+1 = V i { V : B oder BC mit B, C V i } für alle i 1. Für das kleinste i 0 mit V i+1 = V i gilt schon V i = V. Füge nun für alle Regeln BC mit B V (bzw. C V ) Regeln C (bzw. B) hinzu und streiche alle Regeln der Form ε. 4. Schritt: (Elimination von Kettenregeln B) usgehend von rechten Regelseiten der Form a Σ und BC mit B, C V berechne rückwärts alle bleitungen der Form k a BC ohne Wiederholungen. Füge für jede der obigen bleitungen a bzw. BC ein und streiche alle Produktionen der Form B. Bis auf den Schritt 3 wird die erzeugte Sprache nicht verändert. Im 3. Schritt geht höchstens ε verloren Satz (Cocke, Younger, Kasami) Für eine kontextfreie rammatik = (V, Σ, P, S) in Chomsky-Normalform kann das Wortproblem w L() für w Σ in Zeit O ( P w 3 ) gelöst werden. } Beweis: Seien w = a 1... a n, a i, w i,j = a i... a j und V i,j = { V : w i,j. Dann ist w L() S V 1,n. Wir konstruieren die V i,j nach wachsender Differenz der nfangs- und Endposition k = j i des abgeleiteten Teilwortes w i,j. k = 0: } V i,i = { V : w ii = { V : a i in P }, da in Chomsky- NF. Die V i,i können daher in der Zeit O( P + w ) durch Prüfen aller Regeln bestimmt werden.
7 Theoretische Informatik (SS 2004) 36 k > 0: Wir suchen alle mit w i,j. Da k = j i > 0 und in Chomsky- NF, muss ein erster bleitungsschritt von der Form BC sein. Wegen der ε-freiheit von gilt w i,j daher genau dann, wenn B w i,l und C w l+1,j, d.h. B V i,l, C V l+1,j, für ein l {i,..., j 1}. Werden alle V i,j als rrays der Länge V gespeichert (sodass V i,j in konstanter Zeit überprüft werden kann), so ist der ufwand in O( P w 3 ), da ( ) w 2 viele Mengen in jeweils O( P w ) konstruiert werden. us dem Beweis erhalten wir den folgenden lgorithmus zur Lösung des Wortproblems für kontextfreie Sprachen. lgorithmus 2: CYK-lgorithmus Eingabe : kontextfreie rammatik in Chomsky-Normalform Wort w = a 1 a n for i = 1,..., n do V i,i { V : a i in P } for k = 1,..., n 1 do for i = 1,..., n k + 1 do j i + k V i,j for l = i,..., j 1 do foreach BC in P do if B V i,l und C V l+1,j then V i,j V i,j {} if S V 1,n then gib aus: w L() else gib aus: w L() 3.12 Beispiel : S S a BS B BB BS b c in Chomsky- Normalform
8 Theoretische Informatik (SS 2004) 37 Frage: abacba L()? i j V i,j S S S 2 B, B B B, B 3 S S 4 B B, B 5 B, B 6 S Von der Diagonalen her konstruieren s V 1,n = w L(). 3.2 Kellerautomaten Für praktische Zwecke ist der CYK-lgorithmus zu aufwändig. Wir betrachten daher auch für kontextfreie Sprachen ein passendes Maschinenmodell Def inition Ein Kellerautomat (K) = (Q, Σ, Γ, δ, s, S, F ) besteht aus einer endlichen Zustandsmenge Q einem (Eingabe-)lphabet Σ einem (Keller-)lphabet Γ einer Übergangsrelation δ ( Q (Σ {ε}) Γ ) (Γ Q) einem Startzustand s Q einem Kellerstartsymbol S Γ einer Endzustandsmenge F Q Wie endliche utomaten liest ein Kellerautomat ein Eingabewort zeichenweise und geht dabei von einem Zustand in einen anderen über. Der zusätzliche Keller erlaubt die blage von Zwischeninformationen:
9 Theoretische Informatik (SS 2004) 38 Die Schreibweise (q, a, Z, γ, q ) δ besagt, dass im Zustand q mit nächstem Eingabesymbol a ε und oberstem Kellersymbol Z der utomat in den Zustand q übergehen darf und dabei das Z durch γ ersetzt. nalog geschieht dies für a = ε, wobei dann kein Zeichen der Eingabe verbraucht wird. Für γ > 1 spricht man von einem push-schritt, für γ = ε von einem pop- Schritt. Übergänge beschreiben wir durch Konfigurationen (q, w, γ) Q Σ Γ mit (q, av, Zγ) (q, v, γ γ) falls (q, a, Z, γ, q ) δ und verwenden wieder für eine Folge von beliebig vielen Übergängen (entsprechend auch, ) Def inition Ein Kellerautomat = (Q, Σ, Γ, δ, s, S, F ) akzeptiert ein Wort w Σ, falls (s, w, S) (q, ε, γ) mit q F, γ Γ. Die Menge } L() := {w Σ : (s, w, S) (q, ε, γ), q F, γ Γ heißt die von akzeptierte Sprache Beispiel Wir konstruieren einen Kellerautomaten, der die Sprache L = { w Σ : w = vv R, v Σ } der Palindrome gerade Länge über dem lphabet Σ = {a, b} akzeptiert. Dazu legen wir auf dem Keller die erste Worthälfte ab und bauen ihn beim Lesen der zweiten Worthälfte wieder ab. Der Kellerautomat besteht aus Q = {s, q 1, q 2, q f }, Σ = {a, b}, Γ = Σ {S},
10 Theoretische Informatik (SS 2004) 39 F = {q f } und δ : s a S as q 1 s b S bs q 1 s ε S S q f q 1 a b ab q 1 q 1 b a ba q 1 q 1 a a aa q 1! q 1 a a ε q 2 q 1 b b bb q 1! q 1 b b ε q 2 q 2 a a ε q 2 q 2 b b ε q 2 q 2 ε S ε q f Beachte, dass der Übergang vom uf- zum bbau des Kellers nichtdeterministisch erfolgt. Ein Kellerautomat kommt auch ohne Endzustände aus: Def inition Sei = (Q, Σ, Γ, δ, s, S, ) ein Kellerautomat ohne ausgezeichnete Endzustände. Ein Wort w Σ wird von mit leerem Keller akzeptiert, falls (s, w, S) (q, ε, ε) für irgendein q Q. Die Menge N() := { } w Σ : (s, w, S) (q, ε, ε) heißt die von mit leerem Keller akzeptierte Sprache.
11 Theoretische Informatik (SS 2004) Satz (Äquivalenz der kzeptanzarten) a) Zu jedem K existiert ein K B mit L() = N(B). b) Zu jedem K existiert ein K B mit N() = L(B). Beweis: a) Zu = (Q, Σ, Γ, δ, s, S, F ) konstruiere K B, der wie arbeitet und von den Endzuständen aus den Keller leert (falls das Wort nicht akzeptiert, darf der Keller nicht leer werden). Ergänze daher um einen neuen nfangszustand s einen Zustand ˆq zum Leeren des Kellers ein neues Kellerstartsymbol S sowie Transitionen s ε S SS s q ε Z ε ˆq für alle q F, Z Γ {S } ˆq ε Z ε ˆq für alle Z Γ {S }. b) Zu = (Q, Σ, Γ, δ, s, S, ) konstruiere K B, der wie arbeitet und genau bei geleertem Keller in einen Endzustand wechselt. Ergänze daher um einen neuen nfangszustand s einen neuen und dann einzigen Endzustand q f ein neues Kellerstartsymbol S sowie Transitionen s ε S SS s q ε S ε q f für alle q Q.
12 Theoretische Informatik (SS 2004) Satz Eine Sprache ist kontextfrei genau dann, wenn sie von einem Kellerautomaten akzeptiert wird. Beweis: = : Sei = (V, Σ, P, S) eine kontextfreie rammatik. Wir zeigen, dass es einen Kellerautomaten mit N() = L() gibt, d.h. akzeptiert ein Wort mit leerem Keller genau dann, wenn es in ableitbar ist. Der utomat simuliert im Keller eine Linksableitung, indem Nichtterminalsymbole an der Kellerspitze durch die Satzform einer rechten Regelseite ersetzt und Terminalsymbole mit der Eingabe abgeglichen werden. Sei daher = ({s}, Σ, Γ, δ, s, S, ) mit Γ = Σ V und δ : s ε γ s für alle γ in P s a a ε s für alle a Σ. Wir zeigen, dass für alle u Σ Terminal beginnen, gilt und α Γ, die nicht mit einem S uα mit Linksableitungen (s, u, S) (s, ε, α). Daraus folgt dann für α = ε genau die von der rammatik erzeugte Sprache erkennt. = : Induktion über die Länge k der Berechnung in. k = 0: Dann sind u = ε, α = S und S S mit Linksableitungen. k > 0: Es gelte (s, u, S) k (s, ε, α) und wir betrachten den letzten Berechnungsschritt: 1. Fall: (Transition der Form (s, ε,, γ, s) δ) Dann gilt (s, u, S) k 1 (s, ε, α ) (s, ε, γα ) mit α = γα, und aus der Induktionsvoraussetzung folgt S uα uγα = uα mit Linksableitungen. 2. Fall: (Transition der Form (s, a, a, ε, s) δ) Dann gilt (s, u a, S) k 1 (s, a, aα) (s, ε, α) mit u = u a,
13 Theoretische Informatik (SS 2004) 42 und aus der Induktionsvoraussetzung folgt S u aα = uα mit Linksableitungen. = : Induktion über die nzahl k der Linksableitungen in. k = 0: Dann sind u = ε, α = S. k > 0: Es gelte S k uα mit Linksableitungen und deren letzte sei γ. Dann gilt S k 1 β 1 β 2 β 1 γβ 2 = uα mit β 1 Σ, da Linksableitungen vorausgesetzt wurden. Mit der Induktionsvoraussetzung gilt also (s, β 1, S) (s, ε, β 2 ) (s, ε, γβ 2 ). ( ) Weil α nicht mit einem Terminal beginnt und das linkeste Nichtterminal in β 1 β 2 ist, gilt β 1 u. Es muss daher ein v Σ mit β 1 v = u und vα = γβ 2 geben. u α β 1 γβ 2 }{{} v Durch nwendung von Transitionen (s, a, a, ε, s) δ, a Σ, erhalten wir (s, u, S) = (s, β 1 v, S) }{{} ( ) (s, v, γβ 2 ) (s, ε, α). = : Zu einem Kellerautomaten = (Q, Σ, Γ, δ, s, S, ) konstruieren wir eine kontextfreie rammatik = (V, Σ, P, S ) mit L() = N(). Die Variablen V = S {[pzq] : p, q Q, Z Γ} der rammatik stehen für mögliche Folgen von Berechnungsschritten des utomaten. Die Idee dahinter ist, dass [pzq] u genau dann gelten soll, wenn beim Übergang von p nach q die Eingabe u verbraucht 4.6.
14 Theoretische Informatik (SS 2004) 43 und das Symbol Z von der Kellerspitze entfernt (ohne die Zeichen darunter anzufassen). Wir nehmen daher folgende Produktionen auf: P : S [ssq] für alle q Q Beachte, dass a Σ {ε}. [pzq] a für alle (p, a, Z, ε, q) δ [pzq] a[p 0 Z 1 p 1 ][p 1 Z 2 p 2 ] [p n 1 Z n q] für alle (p, a, Z, Z 1 Z n, p 0 ) δ mit n > 0 und p 1,..., p n 1 Q Wir zeigen, dass für alle p, q Q, u Σ und Z Γ gilt (p, u, Z) (q, ε, ε) [pzq] u woraus für p = s, Z = S und u = w die Behauptung folgt, weil dann (s, w, S) (q, ε, ε) S [ssq] w. = : Induktion über die Länge k 1 der Berechnung in. k = 1: Dann ist u = a Σ {ε} und der Berechnungsschritt war von der Form (p, a, Z, ε, q) δ. Nach Konstruktion ist [pzq] a in P. k > 1: Sei u = au mit a Σ {ε} und der erste Berechnungsschritt sei (p, a, Z, Z 1 Z n, p 0 ) δ, dann gilt (p, au, Z) (p 0, u, Z 1 Z n ) k 1 (q, ε, ε). Wähle nun u 1,..., u n Σ mit u = u 1 u n gemäß dem bbau der Z 1,..., Z n im Keller, d.h. u 1 u i führt über vom Zustand p 0 mit Kellerspitze Z 1 Z n zum Zustand p i mit Kellerspitze Z i+1 Z n. Die Zahl der für die Übergänge (p i 1, u i, Z i ) (p i, ε, ε) für i = 1,..., n und p n = q benötigten Berechnungsschritte ist jeweils kleiner als k, sodass sich mit der Induktionsvoraussetzung [p i 1 Z i p i ] u i
15 Theoretische Informatik (SS 2004) 44 ergibt. Nach Konstruktion gibt es zum ersten bleitungsschritt die Produktion [pzq] a[p 0 Z 1 p 1 ]... [p n 1 Z n q], sodass wir insgesamt [pzq] a[p 0 Z 1 p 1 ] [p n 1 Z n q] au 1 u n = au = u erhalten. = : Induktion über die nzahl k 1 der bleitungen in. k = 1: Die bleitung muss von der Form [pzq] a sein. Es existiert daher eine Transition (p, a, Z, ε, q) δ und somit (p, a, Z) (q, ε, ε). k > 1: Betrachte die bleitung [pzq] a[p 0 Z 1 p 1 ]... [p n 1 Z n p n ] k 1 au 1 u n. Nach Konstruktion muss (p, a, Z, Z 1... Z n, p 0 ) δ sein und aus der Induktionsvoraussetzung folgt (p i 1, u i, Z i ) (p i, ε, ε), sodass insgesamt (p, u, Z) = (p, au 1... u n, Z) (p n, ε, ε) = (q, ε, ε) Beispiel Wir nutzen die Konstruktion aus der Hinrichtung des obigen Beweises, um einen Kellerautomaten zu konstruieren, der die Sprache der Palindrome gerader Länge mit leerem Keller akzeptiert. : S ε S asa für alle a Σ führt auf : s ε S ε s s ε S asa s für alle a Σ s a a ε s für alle a Σ.
16 Theoretische Informatik (SS 2004) Satz (Pumping-Lemma für kontextfreie Sprachen) Sei L eine kontextfreie Sprache. Dann existiert eine Zahl n jedes Wort w L mit w n darstellen läßt als so, dass sich w = tuvxz mit ux 1, uvx n und tu i vx i z L für alle i 0. Wir beweisen nur die verschärfte Form Satz (Ogdens Lemma: verschärftes PL für kfs) Sei L eine kontextfreie Sprache. Dann existiert eine Zahl n so, dass für jedes Wort w L mit w n gilt: Werden in w mindestens n Buchstaben markiert, dann läßt sich w darstellen als w = tuvxz mit mindestens einer Markierung in ux und höchstens n Markierung in uvx und tu i vx i z L für alle i 0. Beweis: Zu L gibt es eine kontextfreie rammatik = (V, Σ, P, S) in Chomsky-Normalform mit L() = L \ {ε}. Wir setzen n := 2 V +1 und betrachten ein w L mit w > n und mindestens n markierten Buchstaben, sowie einen zugehörigen Syntaxbaum. Der Syntaxbaum hat w Blätter, alle inneren Knoten haben höchstens zwei Kinder und die inneren Knoten mit nur einem Kind sind genau die Eltern der Blätter (da in Chomsky-NF ist). Wir wählen im Baum einen Weg von der Wurzel zu einem Blatt, der immer in Richtung der größeren nzahl der n markierten Blätter weiterläuft (bei leichheit beliebig). Knoten mit markierten Blättern im linken und im rechten Teilbaum heißen Verzweigunsknoten. Wegen n > 2 V liegen mindestens V + 1 Verzweigungsknoten auf dem gewählten Weg. Betrachte die letzten V + 1 davon und beachte, dass mindestens zwei mit der gleichen Variable markiert sein müssen.
17 Theoretische Informatik (SS 2004) 46 Wir erhalten die folgende Darstellung von w: Da die mit beschrifteten Knoten Verzweigunsknoten sind, enthält ux mindestens einen markierten Buchstaben, und da der gewählte Weg ab dem oberen -Knoten nur noch höchstens V + 1 Verzweigunsknoten enthält, folgt aus der uswahlregel für den jeweils nächsten Knoten, dass uvx höchstens 2 V +1 = n markierte Buchstaben enthält. In der rammatik sind offensichtlich folgende bleitungen möglich: S tz (1) ux (2) v (3) Daraus erhalten wir für jedes i 0 eine bleitung S (1) tz tuxz... tu i x i z (2) (2) (2) }{{} i-mal (3) tu i vx i z sodass tu i vx i z L() L für alle i 0.
18 Theoretische Informatik (SS 2004) Beispiel Wie beim Pumping-Lemma für reguläre Sprachen lassen sich diese beiden 8.6. Sätze zum Nachweis der Nicht-Kontextfreiheit einer Sprache einsetzen: Sei L = {a i b j a j b i : i > j > 0} und zum n aus dem Pumping-Lemma betrachte w = a n+1 b n a n b n+1. Sei ferner w = tuvxz eine zugehörige Darstellung aus dem Pumping-Lemma mit ux ε und uvx n. 1. Fall: (uvx ist im Mittelteil b n a n enthalten) Dann kann durch ufpumpen die Bedingung i > j verletzt werden. 2. Fall: (uvx ist in a n+1 b n oder in a n b n+1 enthalten) Dann kann durch ufpumpen die Bedingung der gleichen nzahlen verletzt werden Def inition Ein Kellerautomat = (Q, Σ, Γ, δ, s, S, F ) heißt deterministisch (DK), falls i) Für alle q Q, a Σ {ε}, Z Γ existiert höchstens ein Übergang der Form (q, a, Z,, ) δ. ii) Für alle q Q, Z Γ gilt: Ist ein Übergang der Form (q, ε, Z,, ) δ, dann gibt es keinen Übergang der Form (q, a, Z,, ) mit a Σ. Wir werden zeigen, dass deterministische Kellerautomaten nicht alle kontextfreien Sprachen erkennen Lemma ibt es zu einer Sprache L Σ einen deterministischen Kellerautomaten mit L() = L, so gibt es zu MIN(L) := {w L : es gibt kein echtes Präfix von w in L} einen deterministischen Kellerautomaten B mit L(B) = MIN(L). Beweis: Der DK = (Q, Σ, Γ, δ, s, S, F ) erkenne L. Konstruiere den utomaten B durch Hinzufügen eines neuen Zustands q und der Übergänge q a Z Z q für alle a Σ, Z Γ sowie Umwandeln aller Transition mit q F, a Σ, Z Γ in q a Z Z q. Einmal in F, nie wieder in F
19 Theoretische Informatik (SS 2004) Lemma Sei L = L() Σ für einen (deterministischen) Kellerautomaten und R Σ regulär. Dann ist L R = L() für einen (deterministischen) Kellerautomaten B. Beweis: Sei L = L() für den (D)K = (Q, Σ, Γ, δ, s, S, F ) und R = L( ) für den DE = (Q, Σ, δ, s, F ). Wir schalten und wie folgt zu einem (D)K B = (Q Q, Σ, Γ, ˆδ, (s, s ), S, F F ) zusammen: ( (p, p ), a, Z, γ, (q, q ) ) ˆδ : (p, a, Z, γ, q) δ und δ (p, a) = q für a Σ bzw. a = ε und p = q. Mit Induktion über die Länge k der Berechnung folgt ((s, s ), w, S) k B ((q, q ), ε, γ) (s, w, S) k (q, ε, γ) und δ (s, w) = q, und damit L(B) = L() L( ) = L R Satz Es gibt keinen deterministischen Kellerautomaten, der die kontextfreie Sprache L = { w {a, b} : w = vv R, v {a, b} } der Palindrome gerader Länge über {a, b} akzeptiert. Beweis: ngenommen, es existiert ein DK mit L() = L. Nach Lemma 3.24 und Lemma 3.25 existiert dann zu L := MIN(L) (ab) + (ba) + (ab) + (ba) + ein DK mit L( ) = L. Da alle Wörter in L Palindrome gerader Länge ohne echtes Präfix dieser rt sind, gilt: L = { (ab) i (ba) j (ab) j (ba) i : i > j > 0 } Mit dem Pumping-Lemma lässt sich dann aber wie in Beispiel 3.22 zeigen, dass L nicht kontextfrei ist. Dies ist ein Widerspruch!
10 Kellerautomaten. Kellerautomaten
 10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
10 Kellerautomaten Bisher hatten wir kontextfreie Sprachen nur mit Hilfe von Grammatiken charakterisiert. Wir haben gesehen, dass endliche Automaten nicht in der Lage sind, alle kontextfreien Sprachen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 15.01.2015 INSTITUT FÜR THEORETISCHE 0 KIT 15.01.2015 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 15.01.2015 INSTITUT FÜR THEORETISCHE 0 KIT 15.01.2015 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik. Vorlesung am 8. Januar INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 08.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Letzte Vorlesung Eine
Theoretische Grundlagen der Informatik 0 08.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Letzte Vorlesung Eine
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012
 utomaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink utomaten und Formale Sprachen 1 Der CYK-lgorithmus Beispiel
utomaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink utomaten und Formale Sprachen 1 Der CYK-lgorithmus Beispiel
Kontextfreie Sprachen. Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kontextfreie Sprachen
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 13.01.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 13.01.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Rekursiv aufzählbare Sprachen
 Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Theoretische Grundlagen der Informatik. Vorlesung am 17. Januar INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik 0 17.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Evaluation Ergebnisse
Theoretische Grundlagen der Informatik 0 17.01.2019 Torsten Ueckerdt - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Evaluation Ergebnisse
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Informatik III - WS07/08
 Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Informatik III - WS07/08 Kapitel 5 1 Informatik III - WS07/08 Prof. Dr. Dorothea Wagner dwagner@ira.uka.de Kapitel 5 : Grammatiken und die Chomsky-Hierarchie Informatik III - WS07/08 Kapitel 5 2 Definition
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Kontextfreie Sprachen und Pushdown-Automaten Dozentin: Wiebke Petersen WS 2004/2005 Wiebke Petersen Formale Komplexität natürlicher Sprachen WS 03/04 Wiederholung c
Einführung in die Computerlinguistik Kontextfreie Sprachen und Pushdown-Automaten Dozentin: Wiebke Petersen WS 2004/2005 Wiebke Petersen Formale Komplexität natürlicher Sprachen WS 03/04 Wiederholung c
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Informatik III. Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Informatik III Christian Schindelhauer Wintersemester 2006/07 8. Vorlesung 17.11.2006 schindel@informatik.uni-freiburg.de 1 Prinzip des Kellerautomats Push-Down-Automaton (PDA) Ein Kellerautomat vereinigt
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 18/19
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 18/19 Ausgabe 8. Januar 2019 Abgabe 22. Januar 2019, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 18/19 Ausgabe 8. Januar 2019 Abgabe 22. Januar 2019, 11:00 Uhr (im
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Ogden s Lemma: Der Beweis (1/5)
 Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Ogden s Lemma: Der Beweis (1/5) Wir betrachten zuerst die Rahmenbedingungen : Laut dem auf der vorhergehenden Folie zitierten Satz gibt es zur kontextfreien Sprache L eine Grammatik G = (Σ, V, S, P) in
Klammersprache Definiere
 Klammersprache w=w 1...w n {(,)}* heißt korrekt geklammert, falls die Anzahl ( ist gleich der Anzahl ). in jedem Anfangsstück w 1,...,w i (i n) ist die Anzahl ( nicht kleiner als die Anzahl ). Definiere
Klammersprache w=w 1...w n {(,)}* heißt korrekt geklammert, falls die Anzahl ( ist gleich der Anzahl ). in jedem Anfangsstück w 1,...,w i (i n) ist die Anzahl ( nicht kleiner als die Anzahl ). Definiere
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 4.2.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Übung am 4.2.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Kontextfreie Sprachen werden von PDAs akzeptiert
 Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Kontextfreie Sprachen werden von PDAs akzeptiert Sei G = (Σ, V, S, P) eine kontextfreie Grammatik. Dann gibt es einen PDA A mit L(A) = L(G). Der PDA A arbeitet mit nur einem Zustand q 0, besitzt das Kelleralphabet
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Dank. 1 Ableitungsbäume. 2 Umformung von Grammatiken. 3 Normalformen. 4 Pumping-Lemma für kontextfreie Sprachen. 5 Pushdown-Automaten (PDAs)
 ank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert iese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
ank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert iese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive
 Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Definition 78 Ein NPDA = PDA (= Nichtdeterministischer Pushdown-Automat) besteht aus:
 4.7 Kellerautomaten In der Literatur findet man häufig auch die Bezeichnungen Stack-Automat oder Pushdown-Automat. Kellerautomaten sind, wenn nichts anderes gesagt wird, nichtdeterministisch. Definition
4.7 Kellerautomaten In der Literatur findet man häufig auch die Bezeichnungen Stack-Automat oder Pushdown-Automat. Kellerautomaten sind, wenn nichts anderes gesagt wird, nichtdeterministisch. Definition
Umformung NTM DTM. Charakterisierung rek. aufz. Spr. Chomsky-3-Grammatiken (T5.3) Chomsky-0-Grammatik Rek. Aufz.
 Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Skript zur Vorlesung Ulrik Brandes Sommersemester 2004 (Version vom 13. Juli 2004) Prolog Die theoretischen Grundlagen der Informatik gelten gemeinhin als hartes
Theoretische Grundlagen der Informatik Skript zur Vorlesung Ulrik Brandes Sommersemester 2004 (Version vom 13. Juli 2004) Prolog Die theoretischen Grundlagen der Informatik gelten gemeinhin als hartes
Musterlösung Informatik-III-Nachklausur
 Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Musterlösung Informatik-III-Nachklausur Aufgabe 1 (2+2+4+4 Punkte) (a) L = (0 1) 0(0 1) 11(0 1) 0(0 1) (b) Der Automat ist durch folgendes Übergangsdiagramm gegeben: 0, 1 0, 1 0, 1 0, 1 0 s q 1 1 0 0 q
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Kontextfreie (Typ-2) Sprachen
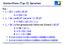 Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Automaten und formale Sprachen Klausurvorbereitung
 Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Beweisidee: 1 Verwende den Keller zur Simulation der Grammatik. Leite ein Wort. 2 Problem: der Keller darf nicht beliebig verwendet werden, man kann
 Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Automaten und Formale prachen alias Theoretische Informatik ommersemester 2011 Dr. ander Bruggink Übungsleitung: Jan tückrath Wir beschäftigen uns ab jetzt einige Wochen mit kontextfreien prachen: Kontextfreie
Ein Fragment von Pascal
 Ein Fragment von Pascal Wir beschreiben einen (allerdings sehr kleinen) Ausschnitt von Pascal durch eine kontextfreie Grammatik. Wir benutzen das Alphabet Σ = {a,..., z, ;, :=, begin, end, while, do} und
Ein Fragment von Pascal Wir beschreiben einen (allerdings sehr kleinen) Ausschnitt von Pascal durch eine kontextfreie Grammatik. Wir benutzen das Alphabet Σ = {a,..., z, ;, :=, begin, end, while, do} und
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Ogden s Lemma (T6.4.2)
 Weiteres Beispiel L={a r b s c t d u r=0 s=t=u} Nahe liegende Vermutung: L nicht kontextfrei. Kann man mit dem Pumping-Lemma nicht zeigen. r=0: Pumpen erzeugt Wort aus L. r>0: Pumpen der a s erzeugt Wort
Weiteres Beispiel L={a r b s c t d u r=0 s=t=u} Nahe liegende Vermutung: L nicht kontextfrei. Kann man mit dem Pumping-Lemma nicht zeigen. r=0: Pumpen erzeugt Wort aus L. r>0: Pumpen der a s erzeugt Wort
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18.01.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 18.01.2011 INSTITUT FÜR THEORETISCHE INFORMATIK 0 KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Übung zur Vorlesung Grundlagen der theoretischen Informatik. Aufgabenblatt 7 Lösungen. Wiederholung: Pumping-Lemma für kontextfreie Sprachen
 Prof. Dr. Viorica Sofronie-Stokkermans Universität Koblenz-Landau Fachbereich 4: Informatik Dennis Peuter 01. Juni 2017 Übung zur Vorlesung Grundlagen der theoretischen Informatik Aufgabenblatt 7 Lösungen
Prof. Dr. Viorica Sofronie-Stokkermans Universität Koblenz-Landau Fachbereich 4: Informatik Dennis Peuter 01. Juni 2017 Übung zur Vorlesung Grundlagen der theoretischen Informatik Aufgabenblatt 7 Lösungen
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Kapitel: Die Chomsky Hierarchie. Die Chomsky Hierarchie 1 / 14
 Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Automaten und formale Sprachen Notizen zu den Folien
 13 Kellerautomaten Automaten und formale Sprachen Notizen zu den Folien Warum ein Automatenmodell für kontextfreien Sprachen (zu Folie 233) Manche Konstruktionen und Verfahren lassen sich besser mit Hilfe
13 Kellerautomaten Automaten und formale Sprachen Notizen zu den Folien Warum ein Automatenmodell für kontextfreien Sprachen (zu Folie 233) Manche Konstruktionen und Verfahren lassen sich besser mit Hilfe
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (IV) 15.06.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (IV) 15.06.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Spracherkennung (Syntaxanalyse)
 Kellerautomaten Kellerautomaten 8 Spracherkennung (Syntaxanalyse) Algorithmus gesucht, der für L T (möglichst schnell) entscheidet, ob w L (Lösung des Wortproblems) Grammatik Automat Aufwand rechtslinear
Kellerautomaten Kellerautomaten 8 Spracherkennung (Syntaxanalyse) Algorithmus gesucht, der für L T (möglichst schnell) entscheidet, ob w L (Lösung des Wortproblems) Grammatik Automat Aufwand rechtslinear
Lösungen zu Übungsblatt 6
 Lösungen zu Übungsblatt 6 Aufgabe 1 Um nachzuweisen, dass eine Sprache L nicht kontextfrei ist, genügt es nach dem (starken) Pumping Lemma für kontextfreie Sprachen zu zeigen: Für jedes n 0 existiert ein
Lösungen zu Übungsblatt 6 Aufgabe 1 Um nachzuweisen, dass eine Sprache L nicht kontextfrei ist, genügt es nach dem (starken) Pumping Lemma für kontextfreie Sprachen zu zeigen: Für jedes n 0 existiert ein
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
4.2 Die Chomsky Normalform
 4.2 Die Chomsky Normalform Für algorithmische Problemstellungen (z.b. das Wortproblem) aber auch für den Nachweis von Eigenschaften kontextfreier Sprachen ist es angenehm, von CFG in Normalformen auszugehen.
4.2 Die Chomsky Normalform Für algorithmische Problemstellungen (z.b. das Wortproblem) aber auch für den Nachweis von Eigenschaften kontextfreier Sprachen ist es angenehm, von CFG in Normalformen auszugehen.
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Ein Satz der deutschen Sprache besitzt ein Subjekt, ein Prädikat und ein Objekt (SPO).
 1 Grammatiken Autor: Tilman Blumenbach Letzte Änderung: 28. Juni 2012 18:15 Ziel von Grammatiken Wollen die Struktur von Sprachen modellieren und charakterisieren. Beispiel Ein Satz der deutschen Sprache
1 Grammatiken Autor: Tilman Blumenbach Letzte Änderung: 28. Juni 2012 18:15 Ziel von Grammatiken Wollen die Struktur von Sprachen modellieren und charakterisieren. Beispiel Ein Satz der deutschen Sprache
Die mathematische Seite
 Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 18/19
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im WS 18/19 Ausgabe 22. Januar 2019 Abgabe 5. Februar 2019, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im WS 18/19 Ausgabe 22. Januar 2019 Abgabe 5. Februar 2019, 11:00 Uhr (im
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Proseminar TI: Kellerautomaten. 1 Motivation. 2 Einführung. Vortrag: Von Sebastian Oltmanns und Dorian Wachsmann. Dozent: Wolfgang Mulzer.
 Proseminar TI: Kellerautomaten Vortrag: 10.11.2015 Von Sebastian Oltmanns und Dorian Wachsmann. Dozent: Wolfgang Mulzer. 1 Motivation Wir kennen bereits die Chomsky-Hierarchie. Sie klassiziert formale
Proseminar TI: Kellerautomaten Vortrag: 10.11.2015 Von Sebastian Oltmanns und Dorian Wachsmann. Dozent: Wolfgang Mulzer. 1 Motivation Wir kennen bereits die Chomsky-Hierarchie. Sie klassiziert formale
11.1 Kontextsensitive und allgemeine Grammatiken
 Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theorie der Informatik 7. April 2014 11. Kontextsensitive und Typ-0-Sprachen Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen 11.1 Kontextsensitive und allgemeine Grammatiken Malte Helmert
Theoretische Informatik I
 (702765) Skript zur Vorlesung am 30.6.2000 Aus der vorherigen Vorlesung: Theoretische Informatik I Satz W: Sei X ein Alphabet. Zu jeder regulären Sprache R X * gibt es ein n N, so daß für alle Wörter z
(702765) Skript zur Vorlesung am 30.6.2000 Aus der vorherigen Vorlesung: Theoretische Informatik I Satz W: Sei X ein Alphabet. Zu jeder regulären Sprache R X * gibt es ein n N, so daß für alle Wörter z
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie prachen (VI) 25.06.2015 Viorica ofronie-tokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
5. Die syntaktische Analyse
 mittels sog. Parser Input: Folge von Token (Symbolen), geliefert vom Scanner/Sieber Aufgabe: Teilfolgen zusammenfassen zu größeren syntaktischen Einheiten Ausdrücke, Anweisungen(-folgen), Deklarationen,
mittels sog. Parser Input: Folge von Token (Symbolen), geliefert vom Scanner/Sieber Aufgabe: Teilfolgen zusammenfassen zu größeren syntaktischen Einheiten Ausdrücke, Anweisungen(-folgen), Deklarationen,
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen
 Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Nichtdeterministischer Kellerautomat
 1 Nichtdeterministischer Kellerautomat endlicher Automat mit Zusatzspeicher in Form eines Kellers (Stapel, Stack) mit Speicheroperationen pro Übergang Keller über X: w X mit den Operationen push, head,
1 Nichtdeterministischer Kellerautomat endlicher Automat mit Zusatzspeicher in Form eines Kellers (Stapel, Stack) mit Speicheroperationen pro Übergang Keller über X: w X mit den Operationen push, head,
Übersicht. 3 3 Kontextfreie Sprachen
 Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Formale Systeme, Automaten, Prozesse Übersicht 3 3.1 Kontextfreie Sprachen und Grammatiken 3.2 Ableitungsbäume 3.3 Die pre -Operation 3.4 Entscheidungsprobleme für CFGs 3.5 Normalformen für CFGs 3.6 Chomsky-Normalform
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch,
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch,
DisMod-Repetitorium Tag 4
 DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
DisMod-Repetitorium Tag 4 Endliche Automaten, Reguläre Sprachen und Kontextfreie Grammatiken 22. März 2018 1 Endliche Automaten Definition DFA Auswertungen Äquivalenzrelationen Verschmelzungsrelation und
Chomsky-Grammatiken 16. Chomsky-Grammatiken
 Chomsky-Grammatiken 16 Chomsky-Grammatiken Ursprünglich von Chomsky in den 1950er Jahren eingeführt zur Beschreibung natürlicher Sprachen. Enge Verwandschaft zu Automaten Grundlage wichtiger Softwarekomponenten
Chomsky-Grammatiken 16 Chomsky-Grammatiken Ursprünglich von Chomsky in den 1950er Jahren eingeführt zur Beschreibung natürlicher Sprachen. Enge Verwandschaft zu Automaten Grundlage wichtiger Softwarekomponenten
Deterministischer Kellerautomat (DPDA)
 Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
ADS-EI 5.2 Struktur einer Turing-Maschine 120/451 ľernst W. Mayr
 Bemerkung: Jede NDTM N (die die Sprache L(N) akzeptiert) kann in eine deterministische Turing-Maschine M konvertiert werden, die ebenfalls genau die Sprache L(N) akzeptiert. Beweisidee: Die Berechnungspfade
Bemerkung: Jede NDTM N (die die Sprache L(N) akzeptiert) kann in eine deterministische Turing-Maschine M konvertiert werden, die ebenfalls genau die Sprache L(N) akzeptiert. Beweisidee: Die Berechnungspfade
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie
 Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.02.2006 28. und letzte Vorlesung 1 Die Chomsky-Klassifizierung Chomsky-Hierachien 3: Reguläre Grammatiken
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.02.2006 28. und letzte Vorlesung 1 Die Chomsky-Klassifizierung Chomsky-Hierachien 3: Reguläre Grammatiken
Das Halteproblem für Turingmaschinen
 Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Das Halteproblem für Turingmaschinen Das Halteproblem für Turingmaschinen ist definiert als die Sprache H := { T w : T ist eine TM, die bei Eingabe w {0, 1} hält }. Behauptung: H {0, 1} ist nicht entscheidbar.
Beschreibungskomplexität von Grammatiken Definitionen
 Beschreibungskomplexität von Grammatiken Definitionen Für eine Grammatik G = (N, T, P, S) führen wir die folgenden drei Komplexitätsmaße ein: Var(G) = #(N), Prod(G) = #(P ), Symb(G) = ( α + β + 1). α β
Beschreibungskomplexität von Grammatiken Definitionen Für eine Grammatik G = (N, T, P, S) führen wir die folgenden drei Komplexitätsmaße ein: Var(G) = #(N), Prod(G) = #(P ), Symb(G) = ( α + β + 1). α β
Informatik III. Christian Schindelhauer Wintersemester 2006/07 7. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 7. Vorlesung 16.11.2006 schindel@informatik.uni-freiburg.de 1 Informatik III 7. Vorlesung - 2 Informatik III 7. Vorlesung - 3 Informatik III
Informatik III Christian Schindelhauer Wintersemester 2006/07 7. Vorlesung 16.11.2006 schindel@informatik.uni-freiburg.de 1 Informatik III 7. Vorlesung - 2 Informatik III 7. Vorlesung - 3 Informatik III
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Grammatiken. Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen
 Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
1. Übungsblatt 6.0 VU Theoretische Informatik und Logik
 . Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
. Übungsblatt 6. VU Theoretische Informatik und Logik 25. September 23 Aufgabe Sind folgende Aussagen korrekt? Begründen Sie jeweils Ihre Antwort. a) Für jede Sprache L gilt: L < L (wobei A die Anzahl
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 24. Januar 2018 Abgabe 6. Februar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 24. Januar 2018 Abgabe 6. Februar 2018, 11:00 Uhr (im
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen Theoretischer Informatik 2 WiSe 2011/12 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik 2 Gesamtübersicht Organisatorisches; Einführung Ersetzungsverfahren:
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Formale Sprachen und Automaten
 Formale Sprachen und Automaten Kapitel 4: Typ 2 kontextfreie Sprachen Vorlesung an der DHBW Karlsruhe Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2012 Kapitel
Formale Sprachen und Automaten Kapitel 4: Typ 2 kontextfreie Sprachen Vorlesung an der DHBW Karlsruhe Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2012 Kapitel
A : z z A : z z : ( z, x, z ) δ
 Informatik IV, SoS2003 1 Definition 1.1 Ein Quintupel A =(X,Z,z 0,δ,Z f )heißt nichtdeterministischer endlicher Automat (NEA): 1. X, Z sind endliche nichtleere Mengen. 2. z 0 Z 4. δ Z X Z Informatik IV,
Informatik IV, SoS2003 1 Definition 1.1 Ein Quintupel A =(X,Z,z 0,δ,Z f )heißt nichtdeterministischer endlicher Automat (NEA): 1. X, Z sind endliche nichtleere Mengen. 2. z 0 Z 4. δ Z X Z Informatik IV,
Grundlagen der Theoretischen Informatik Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
2. Gegeben sei folgender nichtdeterministischer endlicher Automat mit ɛ-übergängen:
 Probeklausur Automatentheorie & Formale Sprachen WiSe 2012/13, Wiebke Petersen Name: Matrikelnummer: Aufgabe A: Typ3-Sprachen 1. Konstruieren Sie einen endlichen Automaten, der die Sprache aller Wörter
Probeklausur Automatentheorie & Formale Sprachen WiSe 2012/13, Wiebke Petersen Name: Matrikelnummer: Aufgabe A: Typ3-Sprachen 1. Konstruieren Sie einen endlichen Automaten, der die Sprache aller Wörter
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 02.02.2012 INSTITUT FÜR THEORETISCHE 0 KIT 06.02.2012 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Übung am 02.02.2012 INSTITUT FÜR THEORETISCHE 0 KIT 06.02.2012 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 7 15. Juni 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 7 15. Juni 2010 Einführung in die Theoretische
a b b a a b b a Dank Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Chart-Parsing Chart-Parsing Vorlesung
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
2.1 Allgemeines. Was ist eine Sprache? Beispiele:
 Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Kapitel 2: Formale Sprachen Gliederung
 Gliederung 0. Motivation und Einordnung 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. 2/5, Folie 1 2017 Prof.
Gliederung 0. Motivation und Einordnung 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. 2/5, Folie 1 2017 Prof.
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik ommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik ommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
1. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004. Mit Lösung!
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 23/4 ILKD Prof. Dr. D. Wagner 2. Februar 24. Klausur zur Vorlesung Informatik III Wintersemester 23/24 Mit Lösung! Beachten Sie:
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 23/4 ILKD Prof. Dr. D. Wagner 2. Februar 24. Klausur zur Vorlesung Informatik III Wintersemester 23/24 Mit Lösung! Beachten Sie:
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik ommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik ommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Theoretische Informatik
 Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 7 Besprechung in KW 48 / Abgabe in KW 49 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
Theoretische Informatik Prof. Meer, Dr. Gengler Aufgabenblatt 7 Besprechung in KW 48 / Abgabe in KW 49 Heften Sie unbedingt alle Blätter Ihrer Lösung zusammen und geben Sie oben auf dem ersten Blatt Ihren
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Vorlesung Theoretische Informatik (Info III)
 1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 22. Januar 2008 Einleitung Motivation 2 Thema heute Kontextfreie Grammatiken: Lemma von Ogden Eigenschaften
1 Vorlesung Theoretische Informatik (Info III) Prof. Dr. Dorothea Wagner Dipl.-Math. Martin Holzer 22. Januar 2008 Einleitung Motivation 2 Thema heute Kontextfreie Grammatiken: Lemma von Ogden Eigenschaften
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
 Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Klausur zur Vorlesung Formale Sprachen und Automaten TIT03G2 mit Lösungsvorschlägen
 Klausur zur Vorlesung Formale Sprachen und Automaten TIT03G2 mit Lösungsvorschlägen Name: Matr.-Nr.: Vorname: Aufgabe 1 2 3 4 5 6 7 max. Punkte 6 7 10 6 8 7 9 err. Punkte Gesamtpunktzahl: Note: Aufgabe
Klausur zur Vorlesung Formale Sprachen und Automaten TIT03G2 mit Lösungsvorschlägen Name: Matr.-Nr.: Vorname: Aufgabe 1 2 3 4 5 6 7 max. Punkte 6 7 10 6 8 7 9 err. Punkte Gesamtpunktzahl: Note: Aufgabe
