146 Sonnenuhren
|
|
|
- Helene Walter
- vor 5 Jahren
- Abrufe
Transkript
1 ' 146 Sonnenuhren Dass das Gnomon hier eine um 48 kleinere Correction hat, als bei der oben S. 142 mitgetheilten Vergleichung, hat in einer veränderten Benützung der Schattenfigur seinen Grund. Die Vergleichung der gegenseitigen Vorzüge und Nachtheile des Gnomons und des Dipleidoskops fällt nach unserer Ansicht zu Gunsten des Gnomons aus. Die Herstellung einer Einrichtung wie die oben bei Fig. 1. S. 141 beschriebene, kostet so viel wie Nichts, das Dipleidoskop kostet 42 Mark. Die Genauigkeit der Beobachtung ist nahezu die gleiche; die Unveränderlichkeit der Vorrichtung selbst und ihrer Correctionselemente spricht zu Gunsten des Gnomons. Ausser für den ersten astronomischen Unterricht und für den Liebhaber der Astronomie sind solche Hülfsmittel, die man auch noch in anderer Form herstellen kann (von denen aber eine Meridianlinie auf dem Boden mit einer Schattenmarke das einfachste ist), auch praktisch in mancher Beziehung bequem, z. B. zeigt unser beim Passage-Instrument angebrachtes Fussboden-Schattenbild immer auf einen Blick, wann es Zeit ist, zu' einer genauen Sonnenbeobachtung an das Passage-Instrument zu treten Sonnenuhren. Die Construction der meisten Sonnenuhren beruht auf der Befestigung einer schattenwerfenden Geraden (Stab oder Kante) parallel der Erdachse, so dass für denselben Stundenwinkel der Schatten dieser Geraden immer in ein und dieselbe Ebene fällt, unabhängig von der Declination der Sonne, d. h. von der Jahreszeit. Die schattenauffangende Fläche kann dann beliebig gelegen und gestaltet sein, sie braucht nicht unbedingt eine Ebene zu sein. Hat man den schattenwerfenden Stab richtig nach der Erd- oder Himmelsachse orientirt, so kann man die Theilung des Ziflerblattes rein empirisch machen, indem man nach anderweitiger Zeitbestimmung eine Uhr auf wahre Ortszeit stellt, und mit dieser Uhr in der Hand den Schatten verfolgend, etwa von 5 zu 5 Minuten einen Strich macht. Die Aufstellung des Schattenstabs in der Meridianebene, und unter der Neigung q) gegen die Horizontalebene, ist eine Aufgabe, welche, etwa nach einer Magnetnadel bei bekannter magnetischer Declination und nach der aus einer Karte entnommenen geographischen wohl unmittelbar mechanisch ausgeführt werden kann; und in diesem Falle wird auch die erwähnte empirische Herstellung des Zifferblattes zu empfehlen sein. Wenn aber die Sonnenuhr möglichst genau werden soll, so ist eine mehr mathematisch-astronomische Behandlung am Platze. Betrachten wir zuerst die theoretisch einfachsten Lagen der schatten auffangenden Ebene, so ist als erste zu nennen die Ebene rechtwinklig zur Erdachse, oder parallel zur Aequatorebene..*
2 5 27. Sonnenuhren Die Schattenstrahlen werden hier für gleiche Zeiten gleiche Winkel bilden, man hat also lediglich den Umfang eines von der Mitte aus gezogenen Kreises in 24 gleiche Theile nebst passenden Unterabtheilungen zu theilen, um ein theoretisch richtiges Zifferblatt zu erhalten. Ist die Zifferblattebene materiell hergestellt (Blech, Kartenpapier etc.) und nicht durchsichtig, so muss sie oben und unten eine Theilung haben. Die obere Theilung wird im Sommerhalbjahr, die untere im Winterhalbjahr gebraucht. Beim Uebergang, zur Zeit der Aequinoctien, wird die Uhr undeutlicbe An gaben machen. Fig. 1. Aequatorialßonuenuhr. (Durchmesser 20 cm.) Eine andere Ausführung desselben Princips zeigt Fig. 1., welche nach einem älteren fein gearbeiteten Instrument unserer hannover schen Sammlung hergestellt ist. (Inschrift: Edm. Culpeper Londini). SN ist parallel der Himmelsachse, MM ' stellt den Meridian und AA den Aequator vor. Auf SN befindet sich, nach der Jahreszeit verstellbar, und um die Achse SN drehbar, ein Sonnenloch B, von welchem ein kleines Sonnenbildchen auf die Innenfiäche des Aequatorringes AA geworfen wird. Diese Innenfläche trägt die gleichförmige Stundentheilung, auf welcher die Tageszeit von 4 zu 4 Minuten an dem Sonnenbild-Kreischen abgelesen wird. Nach diesem ersten und theoretisch einfachsten Princip betrachten wir eine horizontale und eine verticale von West nach Ost gerichtete Bildebene. In Fig. 2. sind diese beiden Ebenen vereinigt. ABC ist die horizontale Bildebene und A B C die verticale Bildebene. AA' ist der 10*
3 148 Sonnenuhren schattenwerfende Stab, dessen Verticalebene ABA rechtwinklig zur Ebene A BC ist. Zur Berechnung der Winkel ac und 31, welche die Schattenlinien AC 'und A C mit dem Meridian Fig. 2. Sonnenubr mit Horizontalebene und mit Verticalebene im ersten Vertical. ABA' bilden, hat man in A ein rechtwinkliges Dreikant, dessen horizontale Kathete = an, dessen verticale Kathete = q) und dessen an letzterer Kathete anliegender Winkel = t (Stundenwinkel) ist. Aus diesem Dreikant, (oder dem zur Veranschaulichung gezeichneten entsprechenden sphärischen Dreieck) findet man: tcmg x = tung t sin q) (1) an der verticalen Bildebene hat man entsprechend tung 31 taugt : m, tung y = taugt cos (p (2) = 50 sind hiernach folgende Hauptwerthe berechnet: t aa temg a; y tung y 011 = , ,000 1 = , ,172 2 = , ,371 3 = , ,643 4 = , ,113 5 = , ,399 6 = oo 90 0 co 7 = , ,399 8 = , ,113 Ein System der horizontalen Schattenstrahlen von Fig. 2. für die Breite q) = von Stuttgart, findet man auf dem Astronomischen Netz zur Bestimmung der Zeit etc. von Professor Riess in Stuttgart. Es ist dieses ein Brettchen von 23 cm X 21 cm, welches ausser den Schattenstrahlen noch die (um A Fig. 2. gezogenen) Kreise für constante Höhenwinkel und die Hyperbeln für constante Sonnendeclinationen enthält. Obgleich eine solche Zeichnung zunächst nur fiir eine gewisse" Breite (po gilt, kann man dieselbe Sonnenubr doch auch für verschiedene Breiten (p brauchen, indem man die Bildebene dann nicht horizontal stellt,
4 g 27. Sonnenuhren. 149 sondern ihr eine Neigung gegen den Horizont: (p - % in der Richtung AB Fig. 2. gibt. Eine andere Ausführung des Princips der Horizontalebene von Fig. 2. _ zeigt Fig. 3.. welche wir aus der Zeitschrift für Instrumentenkunde 1881 S. 165 als Abbildung des Skiostats von August entlehnen. (Verfertiger Ferdinand Ernecke in Berlin.) Die schattenauffangende Ebene KL wird für eine Normalbreite (po, welche bei E eingestellt wird, Fig.3. Horizontal-Sonnenuhr. horizontal gemacht (Dosenlibelle bei B) und der schattenwerfende Faden KM wird parallel der Himmelsachse gestellt. Dann haben wir die Verhältnisse wie in Fig. 2. Für andere Breiten kann man die Einstellung bei E ändern, und KL ist dann nicht mehr horizontal, wohl aber KM noch parallel der Himmelsachse (wie bei dem Legebrett von Riess). Als Beigabe dient der Tageszeiger H J. Da die Scheibe HJ dem Himmels äquator parallel ist, verschiebt sich ihr Schatten auf der Theilung FG entsprechend der Sonnendeclination, und man kann auf FG eine Monatsund Tagesscala anbringen, die indessen an den Enden bei F und G sehr'eng und undeutlich wird. Am 20. März und 23. September wirft die Scheibe JH keinen Schatten, d. h. die Theilung FG wird inh getroffen. Zwar theoretisch weniger einfach, aber für die praktische Ausführung im Grossen viel mehr geeignet, ist die Aufzeichnung einer Schattenbild- Tafel auf einer verticalen Wand, welche nicht genau, aber ungefähr die Richtung West-Ost hat. Es ist dieses die bekannte Figur mit Schatten'stab parallel der Himmelsachse, welche man allenthalben an Kirchenmaueru Rathhäusern u. s. w. angebracht sieht. Die Theorie gibt Fig. 4. in welcher ausser der verticalen Wandebene, auf welcher der Schatten entstehen soll, auch eine horizontale Ebene ABC angenommen ist, in welcher das Azimut a der Wand zur Anschauung kommt. ' Es sei nämlich DB in der Horizontalebene die Normale zur Wand
5 150 Sonnenuhren. % 27. C'A' C, in welcher C' C eine Horizontale ist. AA ist der Schattenstab und AB, BA' sind die Spuren der Meridianebene auf der Horizontal- und Verticalebene. Der Winkel DBA = a ist also die Abweichung der Wan dnormalen BD vom Meridian, d. h. das Azimut der Wand selbst, bezogen auf die West-Ost Richtung. Man wird immer eine Wand aussuchen, bei welcher a möglichst klein ist. Fig. 4. Sonnenuhr auf verticaler Wand mit dem Azimut a. Die Richtung g eines Nachmittagsschattens A'C gegen die Verticale A B erhält man aus einem Dreikant, dessen Spitze in A und dessen drei Strahlen A' B, A C' und A A sind. Das entsprechende sphärische Dreieck ist in Fig. 4. rechts besonders gezeichnet und gibt durch Anwendung der Formel (8) 5 1. S. 2: cotga sin 1) = cos b cos 7 + sin 7 cotg a sin (90 - (p) : cos (90 (p) cos (90 a) + sin (90 a) cotgt (3) cotg 3; cos q) : sin q) sin a + cos a cotgt 608 a cotgy#+sina tung q>+ c cotg t (Nachmittag) (4) OS Diese Gleichung gilt für den Nachmittag, wobei der Stundenwinkel t vom Mittag gegen Abend gezählt ist. Für den Vormittag gilt eine ähnliche Gleichung, wenn der Stundenwinkel vom Mittag an rückwärts gezählt wird; an Stelle von 90 - a tritt dann in dem sphärischen Dreieck 90 + a auf, was in (3) berücksichtigt, statt (4) nun gibt: cotg y = sixn a t(_mg q) + $$$; cotgt (Vormittag) (5) Wenn das Wandazimut a sein Zeichen ändert, d. h. wenn die Wand nach der anderen Seite, als in Fig. 4. angenommen ist, von der West
6 5 27. Sonnenuhren Ost-Richtung abweicht, so bleiben die Formeln (4) und (5) an sich bestehen, gelten dann aber für verwechselten Vormittag und Nachmittag. Man kann auch statt (4) und (5) eine gemeinsame Formel schreiben: 0os a cos cp cotg y = sin a tan!) (P + cotg t (6) wo t Nachmittags positiv, Vormittags negativ und mit entsprechenden Vorzeichen auch 3; gezählt wird. Zur weiteren Veranschaulichung aller bei der Ausführung einer solchen Anlage vorkommenden Einzelheiten nehmen wir das Beispiel einer im Jahr 1871 in Baden-Baden an der v. Plessen schen Villa und einer ähnlichen im Jahr 1877 ebenfalls in Baden-Baden vom Verfasser eingerichteten Sonnenuhr. Von den beiden astronomischen Elementen, Breite (p und Azimut a der Wand wird man die Breite für den vorliegenden Zweck immer hin reichend genau aus einer topographischen oder auch nur aus einer geo graphischen Karte ab stechen. Fiir Baden- Fig. 5. Trigonometrische Orientirung der Wand W. Baden ergab sich so cp : '. Für die Bestimmung des Azimuts a der Wand hat man zwei Mittel: entweder trigonometrische Orientirung nach der Landesvermessung oder unmittelbare astronomische Messung. In dem Falle unserer ersten Badener Sonnenuhr gab sich die trigonometrisché Orientirung nach Fig. 5, sehr ein- +X fach. In die Verlänge & ""'Üerlcur rung der Wandebene WA' wurde ein Theodolit J gestellt, und mit demselben der Brechungswinkel {? zwischen der Wandvisur J W und der Visur JM nach dem trigonometrisch gegebenen 3 Kilometer entfernten Merkur- Thurm gemessen. Die Coordinaten des Standpunktes J wurden aus dem Kataster-Uebersichtsplan in 1 : für den vorliegenden Zweck hinreichend genau abgestochen. Wir haben hiernach in dem badischen System, mit dem Ursprung Mannheim, + a; nach Süden, + y nach Westen: Merkur y = m :c = m PunktJ y= w= Differenzen y y= 2955m x at= 859m
7 152 Sonnenuhren Man berechnet daraus: [ tung (JM) = z, : 3, (JM) = von Süd über West. Gemessen ist der Brechungsminkel ß : , also ist (JW)= (JM) - ß_ = '= a Das ist der Richtungswinkel der Wand, bezogen auf die X-Achse des Landesvermessungs Systems; zur Reduction auf das astronomische Azimut braucht man die Meridianconvergenz, welche nach Jordan, Handb. d. Verm. II S. 283 ist: a a= %gtangcp,odera a =_+% gtang<p= wo R der Querkriimmungshalbmesser ist; für 9) = ist 109 R = , mit dem obigen y = gibt dieses C = + 10, es ist also jetzt a = ' = im Sinne von Fig. 5., und das Wand-Azimut a im Sinne von Fig. 4. S. 150 ist: = (7) Zur Controlle wurde noch eine zweite Visur auf den Kirchthurm von Baden-Baden genommen, welche genügende Uebereinstimmnng gab. Im Falle unserer zweiten Badener Sonnenuhr hätte die trigonometrische Orientirung weit hergeholt werden müssen, weshalb eine unmittelbare astronomische Azimutmessung vorgezogen wurde. Es wurde zu diesem Zweck ein astronomischer Theodolit wieder in die Verlängerung der Wand gestellt, dann abwechselnd Sonnenhöhen und Azimutalwinkel auf die Sonne und auf die Wand gemessen; Die Sonnenhöhen geben nach % 13. die Uhrcorrection, worauf das Sonnenazimut sich für jeden Beobachtungsmoment t nach der Gleichung (2) S. 11 berechnet. Für den vorliegenden Zweck, wo es auf Fehler von 1-2' nicht ankommt, ist das eine leichte Messung und Berechnung. Betrachten wir also die Breite q) und das Wandazimut a als gegeben, und. zwar für unser erstes Beispiel, welchem die Figur 4. S. 150 entspricht, 119 = 48 46' a = ' (8) so hat man die Richtungswinkel y der Schattenstrahlen mit der Verticalen nach den Formeln (4) (5) oder (6) zu berechnen, (1. h. man hat mit Einsetzung von (8) in (4) und (5) Vormittags cotg y = 0, ,4488 cotgt Nachmittags cotg y = + 0, ,4488 cotgt
8 5 27. Sonnenuhren Die Strahlen wurden in ein Rechteck von 1m horizontaler Breite und. 0,7m Höhe, als in einen festen Coordinaten-Rahmen, eingetragen und daher nach Fig. 6. (s. unten) die Functionen X ='0 7In tung y Y = 0,5m cotg 3; soweit sie zum Auftragen brauchbar sind, berechnet, und zwar von 5 zu 5 Zeitminuten. Die Hauptwerthe dieser Berechnungfvon Stunde zu Stunde, sind: Vormittag Nachmittag Zeit X Y - Zeit X Y VII t= 7 = ,025 m VIt=6 l=90.. VIt=6 = ,169 VIIt=5 =75 0,025m Vt=5 = ,363 VIII t = 4- = ,249 IV t=4 = 60 0,596 in 0,588 IX t = 3 = 45 0,631 m 0,555 III t=3 = 45 0,392 0,894 X t = 2 = 30 0,323 1,085 II t=2 = 30 0,246.. Xlt=l =15 0,138.. It=1 = 15 0,122 XIIt=O = 0 0,000.. Xllt=0 = 0 0,000 Nun. fehlen nur noch die Bestimmungsmaasse für den Schattenstab. Hiezu diente das Dreikant AA BB von Fig. 4. Es ist A B = 0,800m bis zum unteren Rand angenommen, dann wird BA =0,800 cotg cp = 0,7012 m, AA = 0,800 cases (p = 1, AB =AB cos a = 0,6696 m BR = AB sin a = 0,2082 m. Zur Controlle noch A B als Hypotenuse = 0, Damit hat der Mechaniker genügende Maasse um dem Stab die richtige Stellung zu geben. Die mechanische Ausführung geschah auf einer Blechtafel, welche nachher an die Wand angeschraubt wurde. Fig. 6. Coordinatennetz zu Fig./ 7 Diese Ausführung ist kostspieliger als 441,5» L> die Frescomalung auf die Wand selbst, hat *,, aber den Vortheil, dass alle Constructionen l,. y Y bequemer und damit auch genauer werden. 5 _i_ Fig. 7. zeigt die fertige Sonnenuhr * \ nach einer Photographie. Das Intervall für -X*"> 5 Minuten ist an der engsten Stelle etwa 1 cm breit, und lässt, trotz der Unsicherheit des Halbschattens, noch Schätzung von 1 2 Minuten zu. Spätere
9 154 Der Spiegelsextant Vergleichungen haben ergeben, dass die Sonnenuhr allerdings innerhalb dieser Genauigkeit richtig geht. Fig. 7. Sonnenuhr an einer verticalen Wand von W.N.W. nach v 1v x ZEIT-UNTEBSCHIEDE WHAM.SRIIHE o'42 umm ammzo'sz V cßeenwicn-baden 32'"57' b ums mm zs'as ZEIT-CI. IJAN + 4 " ISJAN +10 wenn +14 ISFE_BR ISMARZ ISAPRIL MA 3 15mm 4 um 2 ISJUNI +0 X XI ) ///ilii//l [ o 28. Der Spiegelscxtant. Geschichtliche's. Bohnenberger berichtet in seiner Anleitung zur geographischen Ortsbestimmung, Göttingen 1795, auf S Folgendes: Da zur See feste Aufstellung von Instrumenten nicht angeht so sind zur Anstellung astronomischer Beobachtungen auf der See verschiedene Werkzeuge ausgedacht worden. Unter diesen zeichnet sich vorzüglich der nach seinem Erfinder, J oh annhadley, sogenannte Hadley sche Spiegeloctant oder Spiegelsextant aus. Er bekommt den ersten Namen, wenn er ein Kreisausschnitt von 45, den zweiten, wenn er ein solcher von 60 (oder auch etwas mehr, meist 70 ) ist. Hadley legte die erste Be schreibung von seinem Octanten im Mai 1731 der königlichen Societät in London vor (Philos. Trans. Nr. 420), deren Vicepräsident e1 war, und erklärte die Grundsätze, auf welche er gebaut ist. Sein erster Octant war von Holz, er liess nachher einen zweiten von Messing machen (Philos. Trans. Nr. 425), mit welchem Versuche zur See angestellt wurden, welche die Brauchbarkeit dieses Instrumentes an den Tag legten. Demungeachtet verflossen wenigstens zwanzig Jahre bis dieses vortreffliche Werkzeug in Gebrauch kam. Einige Jahre nachher, nämlich im Jahre 1742, wurde unter den hinterlassenen Papieren Hadley s eine Handschrift Newton s gefw1den, welche eine Zeichnung und
154 Der Spiegelsextant Fig. 7. Sonnenuhr an einer verticalen Wand von W.N.W. nach v 1v x
 154 Der Spiegelsextant. 5 28. Vergleichungen haben ergeben, dass die Sonnenuhr allerdings innerhalb dieser Genauigkeit richtig geht. Fig. 7. Sonnenuhr an einer verticalen Wand von W.N.W. nach 0.3.0. v
154 Der Spiegelsextant. 5 28. Vergleichungen haben ergeben, dass die Sonnenuhr allerdings innerhalb dieser Genauigkeit richtig geht. Fig. 7. Sonnenuhr an einer verticalen Wand von W.N.W. nach 0.3.0. v
Stundenwinkel t. 5h 30m 58S m 39S in Bogen S.[3] t= = 4709 (s. o. (15)) gibt log ( 1») )
![Stundenwinkel t. 5h 30m 58S m 39S in Bogen S.[3] t= = 4709 (s. o. (15)) gibt log ( 1») ) Stundenwinkel t. 5h 30m 58S m 39S in Bogen S.[3] t= = 4709 (s. o. (15)) gibt log ( 1») )](/thumbs/75/71600273.jpg) 126 Azimutbestimmung durch den Polarstern. 5 33. Damit erhält man folgende Berechnung: Lage I Lage II Beobachtete Uhrzeit.. 611 OW 26,7S 6h 10m 5,75 Reduction auf mittlere Ortszeit. + 0 30,0 + 0 30,0 Mittlere
126 Azimutbestimmung durch den Polarstern. 5 33. Damit erhält man folgende Berechnung: Lage I Lage II Beobachtete Uhrzeit.. 611 OW 26,7S 6h 10m 5,75 Reduction auf mittlere Ortszeit. + 0 30,0 + 0 30,0 Mittlere
Die Regiomontanus-Sonnenuhr
 Die Regiomontanus-Sonnenuhr Von Günther Zivny Die Regiomontanus-Sonnenuhr gehört zur Gruppe der Höhensonnenuhren. Die Sonnenhöhe, also der Winkel zwischen Horizont und Sonne, ändert sich im aufe des Tages.
Die Regiomontanus-Sonnenuhr Von Günther Zivny Die Regiomontanus-Sonnenuhr gehört zur Gruppe der Höhensonnenuhren. Die Sonnenhöhe, also der Winkel zwischen Horizont und Sonne, ändert sich im aufe des Tages.
= 50 i 15 dt =+ 0,348 10,58 Afp= " (15)
 116 Der Polarstern. % 22. Die Auflösung gibt: = 50 i 15 dt =+ 0,348 10,58 Afp= 65 117" (15) die einzelnen v nach (11) mit (v v') : 344 und mittlerem Gewichtseinheitsfehler : i 7 _ Die Vergleichung der
116 Der Polarstern. % 22. Die Auflösung gibt: = 50 i 15 dt =+ 0,348 10,58 Afp= 65 117" (15) die einzelnen v nach (11) mit (v v') : 344 und mittlerem Gewichtseinheitsfehler : i 7 _ Die Vergleichung der
sin äh = V " 2 " 2 (9)
 5 58. Azimutbestimmung mit dem Sextanten. 283 woraus man findet :.D+(H H ).D (H H ) sin äh = V " 2 " 2 (9). cochosh Um zu sehen, ob diese stengere Rechnung ein merklich anderes Resultat gibt als das frühere
5 58. Azimutbestimmung mit dem Sextanten. 283 woraus man findet :.D+(H H ).D (H H ) sin äh = V " 2 " 2 (9). cochosh Um zu sehen, ob diese stengere Rechnung ein merklich anderes Resultat gibt als das frühere
1.4 Trigonometrie. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 3
 1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
.g 11. ' Fehlertheorie des astronomischen Theodolits. 45. % 11. Fehlertheorie des astronomischen Theodolits.
 .g 11. ' Fehlertheorie des astronomischen Theodolits. 45 % 11. Fehlertheorie des astronomischen Theodolits. Die Achsenfehler des Theodolits haben in der Astronomie wegen der steileren Visuren eine wesentlich
.g 11. ' Fehlertheorie des astronomischen Theodolits. 45 % 11. Fehlertheorie des astronomischen Theodolits. Die Achsenfehler des Theodolits haben in der Astronomie wegen der steileren Visuren eine wesentlich
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras
 Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Schwierigkeitsgrad Projekt 2 Der wahre Mittag Mittelstufe
 Schwierigkeitsgrad Projekt 2 Der wahre Mittag Mittelstufe - GERÄTE ein Solarscope ein Lot eine Uhr mit Sekundenanzeige ein Messschirm. Dieses Experiment kann in einem nach Süden gerichteten Raum oder an
Schwierigkeitsgrad Projekt 2 Der wahre Mittag Mittelstufe - GERÄTE ein Solarscope ein Lot eine Uhr mit Sekundenanzeige ein Messschirm. Dieses Experiment kann in einem nach Süden gerichteten Raum oder an
Eintheilung und Drehung des Himmels.
 6 Eintheilung und Drehung des Himmels. 5 3. @ 3. Eintheilung und Drehung des Himmels. Indem wir nun den Beobachtungspunkt E sammt-seinem Horizont von der Erdoberfläche in den Erdmittelpunkt verschoben
6 Eintheilung und Drehung des Himmels. 5 3. @ 3. Eintheilung und Drehung des Himmels. Indem wir nun den Beobachtungspunkt E sammt-seinem Horizont von der Erdoberfläche in den Erdmittelpunkt verschoben
Über Sonnenuhren. Von
 Über Sonnenuhren. Von HEINZ SCHILT. (Mit 5 Abbildungen im Text.) (Als Manuskript eingegangen am 26. ApriI 1936.) Dieser Aufsatz möchte an die mathematischen und astronomischen Grundlagen der Sonnenuhren
Über Sonnenuhren. Von HEINZ SCHILT. (Mit 5 Abbildungen im Text.) (Als Manuskript eingegangen am 26. ApriI 1936.) Dieser Aufsatz möchte an die mathematischen und astronomischen Grundlagen der Sonnenuhren
g 38.1 Prismatischer Fehler des grossen Spiegels des Sextanten.
 5 88. Prismatischer Fehler des grossen Spiegels des Sextanten. 195 die Fehlergleichungen (9) (und (10) einzusetzen, und man findet dabei das in der Tabelle (14) mit v, v; bezeichnete Fehlersystem, welches
5 88. Prismatischer Fehler des grossen Spiegels des Sextanten. 195 die Fehlergleichungen (9) (und (10) einzusetzen, und man findet dabei das in der Tabelle (14) mit v, v; bezeichnete Fehlersystem, welches
Trigonometrische Berechnungen
 Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Foster-Lambert-Sonnenuhr und analemmatische Sonnenuhr
 Foster-Lambert-Sonnenuhr und analemmatische Sonnenuhr Im Februar 20 wurde in diesem Blog die Bastelanleitung für eine polare Foster-Lambert- Sonnenuhr (auch rektilineare Sonnenuhr genannt) veröffentlicht,
Foster-Lambert-Sonnenuhr und analemmatische Sonnenuhr Im Februar 20 wurde in diesem Blog die Bastelanleitung für eine polare Foster-Lambert- Sonnenuhr (auch rektilineare Sonnenuhr genannt) veröffentlicht,
Astronomie mit einer Sonnenuhr
 Astronomie mit einer Sonnenuhr Udo Backhaus, H Joachim Schlichting, Universität Osnabrück (aus: W Kuhn (Hrsg): Vorträge der Tagung der DPG 987 in Berlin, S 99) Einleitung Im Anschluss an den vorhergehenden
Astronomie mit einer Sonnenuhr Udo Backhaus, H Joachim Schlichting, Universität Osnabrück (aus: W Kuhn (Hrsg): Vorträge der Tagung der DPG 987 in Berlin, S 99) Einleitung Im Anschluss an den vorhergehenden
Astronomische Ortsbestimmung mit dem Sextanten
 Astronomische Ortsbestimmung mit dem Sextanten Der Sextant Die einfachste Art seine Position zu bestimmen ist die Mittagsmethode. Dabei wird die Sonnenhöhe zur Mittagszeit gemessen. Sie hat den Vorteil,
Astronomische Ortsbestimmung mit dem Sextanten Der Sextant Die einfachste Art seine Position zu bestimmen ist die Mittagsmethode. Dabei wird die Sonnenhöhe zur Mittagszeit gemessen. Sie hat den Vorteil,
Wie lang ist Sylt? oder
 Wie lang ist Sylt? oder Wie bestimmt man auf Sylt den Erdradius? Dieter Vornholz, Olbers-Planetarium Bremen Udo Backhaus, Universität Osnabrück, Fachbereich Physik 29. August 2005 Ist Sylt lang genug,
Wie lang ist Sylt? oder Wie bestimmt man auf Sylt den Erdradius? Dieter Vornholz, Olbers-Planetarium Bremen Udo Backhaus, Universität Osnabrück, Fachbereich Physik 29. August 2005 Ist Sylt lang genug,
% 5. Sonnenzeit, Zeitgleichung.
 14 Sonnenzeit, Zeitgleichung. 5 5. Die Auswahl, ob Erg. log sin oder cos zu nehmen ist, dann die Entscheidung über den Quadranten nach Maassgabe der Vorzeichen von Zähler und Nenner, wird genau ebenso
14 Sonnenzeit, Zeitgleichung. 5 5. Die Auswahl, ob Erg. log sin oder cos zu nehmen ist, dann die Entscheidung über den Quadranten nach Maassgabe der Vorzeichen von Zähler und Nenner, wird genau ebenso
1.4 Trigonometrie I. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 4
 1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
2. Strahlensätze Die Strahlensatzfiguren
 2. Strahlensätze 2.1. Die Strahlensatzfiguren 1) Beispiel Die nebenstehende Figur zeigt eine zentrische Streckung mit Zentrum Z. Man kennt einige Streckenlängen. a) Wie gross ist der Streckungsfaktor k?
2. Strahlensätze 2.1. Die Strahlensatzfiguren 1) Beispiel Die nebenstehende Figur zeigt eine zentrische Streckung mit Zentrum Z. Man kennt einige Streckenlängen. a) Wie gross ist der Streckungsfaktor k?
Strahlensätze: Aufgaben
 Strahlensätze: Aufgaben 1. Zwei parallele Geraden schneiden zwei Strahlen mit gemeinsamen Anfangspunkt S. Berechne die in der Tabelle fehlenden Streckenlängen. a b c d (a) 5 cm 4cm 6cm (b) 3.6cm 9.2cm
Strahlensätze: Aufgaben 1. Zwei parallele Geraden schneiden zwei Strahlen mit gemeinsamen Anfangspunkt S. Berechne die in der Tabelle fehlenden Streckenlängen. a b c d (a) 5 cm 4cm 6cm (b) 3.6cm 9.2cm
Berechnung und Messung der Sonnenscheindauer. auf einer Dachschrägen
 Didaktik der Physik Frühjahrstagung Wuppertal 2015 Berechnung und Messung der Sonnenscheindauer auf beliebigen Dachschrägen Tran Ngoc Chat*, Adrian Weber* *Universität Siegen, Didaktik der Physik, Adolf-Reichwein-Straße
Didaktik der Physik Frühjahrstagung Wuppertal 2015 Berechnung und Messung der Sonnenscheindauer auf beliebigen Dachschrägen Tran Ngoc Chat*, Adrian Weber* *Universität Siegen, Didaktik der Physik, Adolf-Reichwein-Straße
Zwei Sonnenuhren aus dem Baumarkt
 Zwei Sonnenuhren aus dem Baumarkt 1 Bauteile 1Holzbrett (15 cm x 20 cm) 1 Einschlagmutter (M5) 1 Gewindestange (M5, l = 25 cm) 2 Schrauben (M5, l = 25 mm) 2 Muttern (M5) 2 Ringe aus Abflussrohr (d = 1
Zwei Sonnenuhren aus dem Baumarkt 1 Bauteile 1Holzbrett (15 cm x 20 cm) 1 Einschlagmutter (M5) 1 Gewindestange (M5, l = 25 cm) 2 Schrauben (M5, l = 25 mm) 2 Muttern (M5) 2 Ringe aus Abflussrohr (d = 1
Eine Viel-Nodus-Sonnenuhr
 Eine Viel-Nodus-Sonnenuhr Inhalt 1. Herleitung der Viel-Nodus- aus der Ein-Nodus-Sonnenuhr 2. Viele fixe Nodi oder nur ein verstellbarer Nodus? 3. Eine auf zwei Arten verwendbare Sonnenuhr 1. Herleitung
Eine Viel-Nodus-Sonnenuhr Inhalt 1. Herleitung der Viel-Nodus- aus der Ein-Nodus-Sonnenuhr 2. Viele fixe Nodi oder nur ein verstellbarer Nodus? 3. Eine auf zwei Arten verwendbare Sonnenuhr 1. Herleitung
DOWNLOAD. Vertretungsstunden Mathematik Klasse: Satzgruppe des Pythagoras. Vertretungsstunden Mathematik 9./10. Klasse
 DOWNLOAD Marco Bettner/Erik Dinges Vertretungsstunden Mathematik 22 9. Klasse: Marco Bettner/Erik Dinges Bergedorfer Unterrichtsideen Downloadauszug aus dem Originaltitel: Vertretungsstunden Mathematik
DOWNLOAD Marco Bettner/Erik Dinges Vertretungsstunden Mathematik 22 9. Klasse: Marco Bettner/Erik Dinges Bergedorfer Unterrichtsideen Downloadauszug aus dem Originaltitel: Vertretungsstunden Mathematik
Erläuterungen zur Funktionsweise der Sonnenuhr
 Erläuterungen zur Funktionsweise der Sonnenuhr Hans Huber 28. November 2016 Lieber Besucher, nehmen Sie sich bitte fünf Minuten Zeit. Vielleicht verändert dies Ihre Sicht auf die Zeit und unser damit verbundenes
Erläuterungen zur Funktionsweise der Sonnenuhr Hans Huber 28. November 2016 Lieber Besucher, nehmen Sie sich bitte fünf Minuten Zeit. Vielleicht verändert dies Ihre Sicht auf die Zeit und unser damit verbundenes
Ellipsoidnormale, Schwerevektor, Normalschwerevektor und Schwerestörungsvektor
 1 von 6 12.02.2006 10:12 Ellipsoidnormale, 1. Ellipsoidnormale Bei der Festlegung der Position eines Punktes bezieht man sich auf ein Referenzellipsoid, welches sich möglichst gut der Erdoberfläche anpaßt.
1 von 6 12.02.2006 10:12 Ellipsoidnormale, 1. Ellipsoidnormale Bei der Festlegung der Position eines Punktes bezieht man sich auf ein Referenzellipsoid, welches sich möglichst gut der Erdoberfläche anpaßt.
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
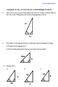 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
2. Berechnungen mit Pythagoras
 2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
1. Aufgabe: Grundwissen
 NAME: Mathematik 3. Klassenarbeit Klasse 10e- Gr. A 06. Feb. 2007 Trigonometrie für Winkel bis 90 Grad - ups - Teil A: Arbeitsblatt ohne Nutzung von Tafelwerk, Formelsammlung und Taschenrechner 1. Aufgabe:
NAME: Mathematik 3. Klassenarbeit Klasse 10e- Gr. A 06. Feb. 2007 Trigonometrie für Winkel bis 90 Grad - ups - Teil A: Arbeitsblatt ohne Nutzung von Tafelwerk, Formelsammlung und Taschenrechner 1. Aufgabe:
Beispiellösungen zu Blatt 96
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 96 Gegeben sei ein Oktaeder. Auf dessen Kanten suchen wir Wege von einer
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 96 Gegeben sei ein Oktaeder. Auf dessen Kanten suchen wir Wege von einer
Aufgabe 1: Anordnung ohne Wiederholung; jedes Element darf nur einmal verwendet werden. Gegeben: 5 Buchstaben: A, b, C, d, E
 Übungen Klasse 9 Aufgabe 1: Anordnung ohne Wiederholung; jedes Element darf nur einmal verwendet werden. Gegeben: 5 Buchstaben: A, b, C, d, E Gesucht: a) Wörter aus 3 Buchstaben b) Wörter aus 5 Buchstaben
Übungen Klasse 9 Aufgabe 1: Anordnung ohne Wiederholung; jedes Element darf nur einmal verwendet werden. Gegeben: 5 Buchstaben: A, b, C, d, E Gesucht: a) Wörter aus 3 Buchstaben b) Wörter aus 5 Buchstaben
Berechnungen am Dreieck
 1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
BMT Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien. Name: Note: Klasse: Punkte: / 21
 BMT8 2012 A Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien Name: Note: Klasse: Punkte: 1 Aufgabe 1 Gegeben ist der Term 3,5kg : 100 g. a) Berechne den Wert des Terms. 3,5kg : 100 g
BMT8 2012 A Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien Name: Note: Klasse: Punkte: 1 Aufgabe 1 Gegeben ist der Term 3,5kg : 100 g. a) Berechne den Wert des Terms. 3,5kg : 100 g
Mathematische Probleme, SS 2018 Dienstag $Id: dreieck.tex,v /06/12 14:54:26 hk Exp $
 $Id: dreieck.tex,v 1.47 018/06/1 14:54:6 hk Exp $ Dreiecke.3 Einige spezielle Punkte im Dreieck Am Ende der letzten Sitzung hatten wir eingesehen, dass sich die drei Winkelhalbierenden eines Dreiecks in
$Id: dreieck.tex,v 1.47 018/06/1 14:54:6 hk Exp $ Dreiecke.3 Einige spezielle Punkte im Dreieck Am Ende der letzten Sitzung hatten wir eingesehen, dass sich die drei Winkelhalbierenden eines Dreiecks in
Klaus Maldener Februar Konstruktionsverfahren zur Herstellung eines Zifferblatts für eine Horizontaluhr
 Klaus Maldener Februar 2013 Konstruktionsverfahren zur Herstellung eines Zifferblatts für eine Horizontaluhr mit einer POLARIS als Konstruktionshilfe und für eine POLARIS als Horizontaluhr Wenn man die
Klaus Maldener Februar 2013 Konstruktionsverfahren zur Herstellung eines Zifferblatts für eine Horizontaluhr mit einer POLARIS als Konstruktionshilfe und für eine POLARIS als Horizontaluhr Wenn man die
Die Strahlensätze machen eine Aussage über Streckenverhältnisse, nämlich:
 Elementargeometrie Der. Strahlensatz Geschichte: In den Elementen des Euklid wird im 5.Buch die Proportionenlehre behandelt, d.h. die geometrische Theorie aller algebraischen Umformungen der Proportion.
Elementargeometrie Der. Strahlensatz Geschichte: In den Elementen des Euklid wird im 5.Buch die Proportionenlehre behandelt, d.h. die geometrische Theorie aller algebraischen Umformungen der Proportion.
7 Beziehungen im Raum
 Lange Zeit glaubten die Menschen, die Erde sei eine Scheibe. Heute zeigen dir Bilder aus dem Weltall sehr deutlich, dass die Erde die Gestalt einer Kugel hat. 7 Beziehungen im Raum Gradnetz der Erde Längengrade
Lange Zeit glaubten die Menschen, die Erde sei eine Scheibe. Heute zeigen dir Bilder aus dem Weltall sehr deutlich, dass die Erde die Gestalt einer Kugel hat. 7 Beziehungen im Raum Gradnetz der Erde Längengrade
Die Oberfläche der Verpackung besteht aus sechs Teilen: 2 Trapeze (vorne und hinten), und 4 Rechtecke.
 Aufgabe 1a) Schritt 1: Oberflächenformel aufstellen Gesucht ist die Oberfläche des Prismas. Das heißt, 2, mit G als Grundfläche und M als Mantel. Die Oberfläche der Verpackung besteht aus sechs Teilen:
Aufgabe 1a) Schritt 1: Oberflächenformel aufstellen Gesucht ist die Oberfläche des Prismas. Das heißt, 2, mit G als Grundfläche und M als Mantel. Die Oberfläche der Verpackung besteht aus sechs Teilen:
Basis Dreieck 2. x = = y. 14 = y. x = = y. x = x = 28. x = 45. x = x = = 2.1+x y = 2.
 3.6 m 1.69 m 6 m 1.69 m Seiten 9 / 10 / 11 1 Vorbemerkung: Alle abgebildeten Dreiecke sind ähnlich (weil sie lauter gleiche Winkel haben). Also gilt jeweils: 2 kurze Seite Dreieck 1 kurze Seite Dreieck
3.6 m 1.69 m 6 m 1.69 m Seiten 9 / 10 / 11 1 Vorbemerkung: Alle abgebildeten Dreiecke sind ähnlich (weil sie lauter gleiche Winkel haben). Also gilt jeweils: 2 kurze Seite Dreieck 1 kurze Seite Dreieck
Eine Sonnenuhr für den Hausgebrauch
 Eine Sonnenuhr für den Hausgebrauch von F.Ostermann, Liebigstraße 13, 50859 Köln, e-mail: Ostermann-fritz@t-online.de Im Sommer 2007 sah ich auf dem Sonnenuhrenweg in Röttingen eine Polaruhr (Abb.1). Abb.1
Eine Sonnenuhr für den Hausgebrauch von F.Ostermann, Liebigstraße 13, 50859 Köln, e-mail: Ostermann-fritz@t-online.de Im Sommer 2007 sah ich auf dem Sonnenuhrenweg in Röttingen eine Polaruhr (Abb.1). Abb.1
Meteoroid von Tscheljabinsk: Bahnberechnung im Unterricht
 Meteoroid von Tscheljabinsk: Bahnberechnung im Unterricht In Bezug auf Aktuelles am Himmel: Das Sonnensystem / Meteore: Mai-Aquariden in der Zeitschrift»Sterne und Weltraum«5/2015. (Die Mai-Aquariden (19.
Meteoroid von Tscheljabinsk: Bahnberechnung im Unterricht In Bezug auf Aktuelles am Himmel: Das Sonnensystem / Meteore: Mai-Aquariden in der Zeitschrift»Sterne und Weltraum«5/2015. (Die Mai-Aquariden (19.
Ähnlichkeit, Strahlensatz
 Ähnlichkeit, Strahlensatz Aufgabe 1 Berechne die Strecken x und y. a) links b) rechts Aufgabe 2 Einem Dreieck wurde die Spitze abgeschnitten. Das Reststück in Form eines Trapezes hat Parallelen von 15
Ähnlichkeit, Strahlensatz Aufgabe 1 Berechne die Strecken x und y. a) links b) rechts Aufgabe 2 Einem Dreieck wurde die Spitze abgeschnitten. Das Reststück in Form eines Trapezes hat Parallelen von 15
Von Sehnen und Sehnenlängen Konstruktion (mit Zirkel und Lineal) und Rechnung
 Die regelmäßige 5-Ecks - Konstruktion des Klaudios Ptolemaios (gelebt ca. 100 bis ca. 160 n. Chr. in Alexandria) 1 : Gegeben ein Kreis mit Durchmesser AB. D ist der Mittelpunkt der trecke MB. C ist Kreispunkt
Die regelmäßige 5-Ecks - Konstruktion des Klaudios Ptolemaios (gelebt ca. 100 bis ca. 160 n. Chr. in Alexandria) 1 : Gegeben ein Kreis mit Durchmesser AB. D ist der Mittelpunkt der trecke MB. C ist Kreispunkt
Inhaltsverzeichnis. 1 Flächen 2. 2 Klammern auflösen 4. 3 Prozentrechnung 6. 4 Zinsrechnung 7. 5 Funktionen 8
 Inhaltsverzeichnis 1 Flächen Klammern auflösen 4 3 Prozentrechnung 6 4 Zinsrechnung 7 5 Funktionen 8 1 Flächen Quadrat Alle Seiten sind gleich lang und alle Winkel sind rechte Winkel. - 4 Symmentriachsen
Inhaltsverzeichnis 1 Flächen Klammern auflösen 4 3 Prozentrechnung 6 4 Zinsrechnung 7 5 Funktionen 8 1 Flächen Quadrat Alle Seiten sind gleich lang und alle Winkel sind rechte Winkel. - 4 Symmentriachsen
5 6. Die Angaben des astronomischen Jahrbuchs. Zeitverwandlung.
 ]8 Die Angaben des astronomischen Jahrbuchs. Zeitwrwandlung. @ 6. Sonnenaufgang : 7h 4' Vormittags Wahre Zeit, Mittag : 12h 0 Wahre Zeit, Sonnenuntergang : 4" 56' Nachmittags Wahre Zeit. Dagegen in mittlerer
]8 Die Angaben des astronomischen Jahrbuchs. Zeitwrwandlung. @ 6. Sonnenaufgang : 7h 4' Vormittags Wahre Zeit, Mittag : 12h 0 Wahre Zeit, Sonnenuntergang : 4" 56' Nachmittags Wahre Zeit. Dagegen in mittlerer
Trigonometrie. Geometrie - Kapitel 3 Sprachprofil - Mittelstufe KSOe. Ronald Balestra CH Zürich
 Trigonometrie Geometrie - Kapitel 3 Sprachprofil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 31. Januar 2013 Überblick über die bisherigen ALGEBRA - Themen:
Trigonometrie Geometrie - Kapitel 3 Sprachprofil - Mittelstufe KSOe Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch Name: Vorname: 31. Januar 2013 Überblick über die bisherigen ALGEBRA - Themen:
Serie 1 Klasse Vereinfache. a) 2(4a 5b) b) 3. Rechne um. a) 456 m =... km b) 7,24 t =... kg
 Serie 1 Klasse 10 1. Berechne. 1 a) 4 3 b) 0,64 : 8 c) 4 6 d) ³. Vereinfache. 1x²y a) (4a 5b) b) 4xy 3. Rechne um. a) 456 m =... km b) 7,4 t =... kg 4. Ermittle. a) 50 % von 30 sind... b) 4 kg von 480
Serie 1 Klasse 10 1. Berechne. 1 a) 4 3 b) 0,64 : 8 c) 4 6 d) ³. Vereinfache. 1x²y a) (4a 5b) b) 4xy 3. Rechne um. a) 456 m =... km b) 7,4 t =... kg 4. Ermittle. a) 50 % von 30 sind... b) 4 kg von 480
a) Wie hoch ist die Leiter? b) Wie weit stehen die beiden Fußpunkte auseinander? Abbildung 1: Eine Stehleiter
 1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
Realschule Abschlussprüfung
 Realschule Abschlussprüfung Annegret Sonntag 4. Januar 2010 Inhaltsverzeichnis 1 Strategie zur Berechnung von ebenen Figuren (Trigonometrie) 3 1.1 Skizze.................................................
Realschule Abschlussprüfung Annegret Sonntag 4. Januar 2010 Inhaltsverzeichnis 1 Strategie zur Berechnung von ebenen Figuren (Trigonometrie) 3 1.1 Skizze.................................................
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis
 Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
Sonnenuhren 1. von Dieter Ortner. Zwei Typen von Sonnenuhren. Die Zeitgleichung. Ortszeit und Mitteleuropäische Zeit
 Sonnenuhren 1 Einige Überlegungen, ein wenig Geometrie, etwas handwerkliches Geschick, damit kann man schon eine Sonnenuhr basteln. In zwei Abschnitten sollen Anleitungen gegeben werden, wie man mit Schülerinnen
Sonnenuhren 1 Einige Überlegungen, ein wenig Geometrie, etwas handwerkliches Geschick, damit kann man schon eine Sonnenuhr basteln. In zwei Abschnitten sollen Anleitungen gegeben werden, wie man mit Schülerinnen
ÜBUNGSBLATT 3 LÖSUNGEN MAT121/MAT131 ANALYSIS I HERBSTSEMESTER 2010 PROF. DR. CAMILLO DE LELLIS
 ÜBUNGSBLATT 3 LÖSUNGEN MAT121/MAT131 ANALYSIS I HERBSTSEMESTER 2010 PROF. DR. CAMILLO DE LELLIS Aufgabe 1. a) Beweisen Sie aus den Axiomen für komplexe Zahlen, dass für alle z, w C gilt: zw = z w; b) Schreiben
ÜBUNGSBLATT 3 LÖSUNGEN MAT121/MAT131 ANALYSIS I HERBSTSEMESTER 2010 PROF. DR. CAMILLO DE LELLIS Aufgabe 1. a) Beweisen Sie aus den Axiomen für komplexe Zahlen, dass für alle z, w C gilt: zw = z w; b) Schreiben
Vektorgeometrie. Schattenspiele. Anwendungen. Friedrich Buckel. Datei Nr INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK. Stand 24.
 Vektorgeometrie Anwendungen Schattenspiele Datei Nr. 6340 Stand 4. September 0 Friedrich Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mathe-cd.de Vorwort Es gibt eine Reihe von Aufgaben, die einen
Vektorgeometrie Anwendungen Schattenspiele Datei Nr. 6340 Stand 4. September 0 Friedrich Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mathe-cd.de Vorwort Es gibt eine Reihe von Aufgaben, die einen
MSA Probearbeit. 2. Berechnen Sie: Ein Viertel des Doppelten der Summe aus 4 und 8.
 MSA Probearbeit www.mathementor.de Stand 22.5.09 1. Fassen Sie die Terme zusammen soweit es geht: x + 10 (4 2x) = (3x + 4)² (x² + 2x + 15) = 4a²b³ : 2a³bz = 5bz 25z² 2. Berechnen Sie: Ein Viertel des Doppelten
MSA Probearbeit www.mathementor.de Stand 22.5.09 1. Fassen Sie die Terme zusammen soweit es geht: x + 10 (4 2x) = (3x + 4)² (x² + 2x + 15) = 4a²b³ : 2a³bz = 5bz 25z² 2. Berechnen Sie: Ein Viertel des Doppelten
Seite 10 Aufgaben Zentrische Streckung 1 a) Konstruktionsbericht (Vorschlag):
 Seite 10 1 a) Konstruktionsbericht (Vorschlag): 1. Alle Eckpunkte mit Z verbinden 2. Die Strecke ZC halbieren (das entspricht der Streckung mit k 0.5) C 3. Parallelverschieben CB // durch C B 4. AB //
Seite 10 1 a) Konstruktionsbericht (Vorschlag): 1. Alle Eckpunkte mit Z verbinden 2. Die Strecke ZC halbieren (das entspricht der Streckung mit k 0.5) C 3. Parallelverschieben CB // durch C B 4. AB //
Übungsaufgaben Repetitionen
 TG TECHNOLOGISCHE GRUNDLAGEN LÖSUNGSSATZ Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Übungsaufgaben Repetitionen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut
TG TECHNOLOGISCHE GRUNDLAGEN LÖSUNGSSATZ Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Übungsaufgaben Repetitionen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut
9.5 Graphen der trigonometrischen Funktionen
 9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
Abschlussprüfung 2011 an den Realschulen in Bayern
 Prüfungsdauer: 150 Minuten Abschlussprüfung 2011 an den Realschulen in Bayern Mathematik I Name: Vorname: Klasse: Platzziffer: Punkte: Aufgabe A 1 Nachtermin A 1.0 Lebensmittelchemiker untersuchten das
Prüfungsdauer: 150 Minuten Abschlussprüfung 2011 an den Realschulen in Bayern Mathematik I Name: Vorname: Klasse: Platzziffer: Punkte: Aufgabe A 1 Nachtermin A 1.0 Lebensmittelchemiker untersuchten das
Drei Flugzeuge unterwegs
 Anwendungsaufgaben: R. 3. 1 Drei Flugzeuge unterwegs Um die Bewegungen dreier Flugzeuge zu analysieren, wird ein räumliches kartesisches Koordinatensystem gewählt, das an die Navigation auf bzw. über der
Anwendungsaufgaben: R. 3. 1 Drei Flugzeuge unterwegs Um die Bewegungen dreier Flugzeuge zu analysieren, wird ein räumliches kartesisches Koordinatensystem gewählt, das an die Navigation auf bzw. über der
8. Helio-Chronometer. Sonnenuhr mit Nonius und Achterschleife zur Kompensation der Zeitgleichung. Bronze, 19. Jahrhundert. Cousins
 8. Helio-Chronometer Diese Äquatorialuhr wird zur Anzeige der Zonenzeit auf die geographische Länge des Standorts eingestellt. Falls nötig, ist auch das Ablesen der Sommerzeit möglich. Zur Anpassung an
8. Helio-Chronometer Diese Äquatorialuhr wird zur Anzeige der Zonenzeit auf die geographische Länge des Standorts eingestellt. Falls nötig, ist auch das Ablesen der Sommerzeit möglich. Zur Anpassung an
Großer Wagen. zum Sternbild. Großer Bär
 B1 Sterne / Sternbilder Termin:....................... 1. Suchen Sie auf einer Sternkarte die Sternbilder Großer Bär, Kleiner Bär und Kassiopeia. 2. Bereiten Sie eine Skizze vor, die den Horizont zeigt
B1 Sterne / Sternbilder Termin:....................... 1. Suchen Sie auf einer Sternkarte die Sternbilder Großer Bär, Kleiner Bär und Kassiopeia. 2. Bereiten Sie eine Skizze vor, die den Horizont zeigt
Mathematisches zur Sonnenreflexionsuhr
 Mathematisches zur Sonnenreflexionsuhr Hellmuth Stachel stachel@dmg.tuwien.ac.at http://www.geometrie.tuwien.ac.at/stachel Zur Präsentation des Buches F. Mayrhofer, G. Liechtenstein (Hrsg.): Die Sonnenreflexionsuhr
Mathematisches zur Sonnenreflexionsuhr Hellmuth Stachel stachel@dmg.tuwien.ac.at http://www.geometrie.tuwien.ac.at/stachel Zur Präsentation des Buches F. Mayrhofer, G. Liechtenstein (Hrsg.): Die Sonnenreflexionsuhr
Beobachtungen am Himmel. Manuel Erdin Gymnasium Liestal, 2010
 Beobachtungen am Himmel Manuel Erdin Gymnasium Liestal, 2010 Grundsätze Alle am Himmel beobachtbaren Objekte befinden sich auf der Innenseite einer Kugel. Wir als Beobachter sind in Ruhe. Die Himmelskugel
Beobachtungen am Himmel Manuel Erdin Gymnasium Liestal, 2010 Grundsätze Alle am Himmel beobachtbaren Objekte befinden sich auf der Innenseite einer Kugel. Wir als Beobachter sind in Ruhe. Die Himmelskugel
ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese Aufgabenblätter
 Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 007 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 007 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Aufgaben für die Klassenstufen 11/12
 Aufgaben für die Klassenstufen 11/12 mit Lösungen Einzelwettbewerb Gruppenwettbewerb Speedwettbewerb Aufgaben OE1, OE2, OE3 Aufgaben OG1, OG2, OG3, OG4 Aufgaben OS1, OS2, OS3, OS4, OS5, OS6, OS7, OS8 Aufgabe
Aufgaben für die Klassenstufen 11/12 mit Lösungen Einzelwettbewerb Gruppenwettbewerb Speedwettbewerb Aufgaben OE1, OE2, OE3 Aufgaben OG1, OG2, OG3, OG4 Aufgaben OS1, OS2, OS3, OS4, OS5, OS6, OS7, OS8 Aufgabe
Einfu hrung in die Geometrie
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul Einfu hrung in die Geometrie Abbildung 0: Winkelkreuz Abbildung 0: Spannen von gleichschenkligen Trapezen auf dem Winkelkreuz
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Teilpru fung, Modul Einfu hrung in die Geometrie Abbildung 0: Winkelkreuz Abbildung 0: Spannen von gleichschenkligen Trapezen auf dem Winkelkreuz
Mathematische Grundlagen II: Einführung in die Geometrie Sekundarstufe
 PH Heidelberg, Fach Mathematik Klausur zur Akademischen Vorprüfung Mathematische Grundlagen II: Einführung in die Geometrie Sekundarstufe Wintersemester 12/13 12. Februar 2013 Aufgabe 8: Definieren Nr.
PH Heidelberg, Fach Mathematik Klausur zur Akademischen Vorprüfung Mathematische Grundlagen II: Einführung in die Geometrie Sekundarstufe Wintersemester 12/13 12. Februar 2013 Aufgabe 8: Definieren Nr.
Abb.1 Kegelschnitte [2]
![Abb.1 Kegelschnitte [2] Abb.1 Kegelschnitte [2]](/thumbs/91/106636815.jpg) und Kegelschnitte DGC-Mitteilungen Nr.106, 2006: "Jede Deklinationslinie der ist ein Stück eines echten Kegelschnittes" Bemerkung von heute, 2008 Im ursprünglichen Aufsatz machte ich auf Fehler in einer
und Kegelschnitte DGC-Mitteilungen Nr.106, 2006: "Jede Deklinationslinie der ist ein Stück eines echten Kegelschnittes" Bemerkung von heute, 2008 Im ursprünglichen Aufsatz machte ich auf Fehler in einer
Analytische Geometrie Seite 1 von 6. Die Addition von Vektoren kann veranschaulicht werden durch das Aneinanderhängen von Pfeilen.
 Analytische Geometrie Seite 1 von 6 1. Wichtige Formeln AB bezeichnet den Vektor, der die Verschiebung beschreibt, durch die der Punkt A auf den Punkt B verschoben wird. Der Vektor, durch den die Verschiebung
Analytische Geometrie Seite 1 von 6 1. Wichtige Formeln AB bezeichnet den Vektor, der die Verschiebung beschreibt, durch die der Punkt A auf den Punkt B verschoben wird. Der Vektor, durch den die Verschiebung
Eingangstest Mathematik
 Eingangstest Mathematik DHBW Mannheim Fachbereich Technik e-mail: Adresse: Gesamtzeit: 20 Minuten Gesamtpunktzahl: 20 Beachten Sie bitte folgende Punkte:. Der folgende Test umfasst neun Aufgabenblöcke.
Eingangstest Mathematik DHBW Mannheim Fachbereich Technik e-mail: Adresse: Gesamtzeit: 20 Minuten Gesamtpunktzahl: 20 Beachten Sie bitte folgende Punkte:. Der folgende Test umfasst neun Aufgabenblöcke.
3. Mathematik Olympiade 1. Stufe (Schulolympiade) Klasse 12 Saison 1963/1964 Aufgaben und Lösungen
 3. Mathematik Olympiade 1. Stufe (Schulolympiade) Klasse 12 Saison 1963/1964 Aufgaben und Lösungen 1 OJM 3. Mathematik-Olympiade 1. Stufe (Schulolympiade) Klasse 12 Aufgaben Hinweis: Der Lösungsweg mit
3. Mathematik Olympiade 1. Stufe (Schulolympiade) Klasse 12 Saison 1963/1964 Aufgaben und Lösungen 1 OJM 3. Mathematik-Olympiade 1. Stufe (Schulolympiade) Klasse 12 Aufgaben Hinweis: Der Lösungsweg mit
Übungsaufgaben Repetitionen
 TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Übungsaufgaben Repetitionen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn
TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Übungsaufgaben Repetitionen Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 877 Nidfurn
Übungsbeispiele- Mathematik 2. Schularbeit, am
 011 Übungsbeispiele- Mathematik. Schularbeit, am 7.1.011 M 3b/I. KL, KV 1.11.011 . Schularbeit: MTHEMTIK KL.: M3b/I. - S. 1) Ergänze die Tabelle! a 1 3 4 5 6 7 8 9 10 a ) Fasse zusammen und schreibe als
011 Übungsbeispiele- Mathematik. Schularbeit, am 7.1.011 M 3b/I. KL, KV 1.11.011 . Schularbeit: MTHEMTIK KL.: M3b/I. - S. 1) Ergänze die Tabelle! a 1 3 4 5 6 7 8 9 10 a ) Fasse zusammen und schreibe als
3.6 Einführung in die Vektorrechnung
 3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
#NN DieAnfangsgründe der Theodoli und der ebenen Polygonometrie.
 ##8,GEODEZIJA,J:NJ A-?2J Die #NN DieAnfangsgründe der Theodoli und der ebenen Polygonometrie. Mit einem Anhange: Von den Fehlern der Messungen. Von #AAGustav Königlichem Oberforstmeister a. D. Dritte Auflage,
##8,GEODEZIJA,J:NJ A-?2J Die #NN DieAnfangsgründe der Theodoli und der ebenen Polygonometrie. Mit einem Anhange: Von den Fehlern der Messungen. Von #AAGustav Königlichem Oberforstmeister a. D. Dritte Auflage,
\ Wir bestimmen zuerst die Projelctionen a, br 0 der Axen. ziehen wir Ofll parallel O'c, SO ist aufl
 Die schiefe axonometrische Projektion. von ~[ermann Linlrolin. Bei axonometrischen Projektionen wird ein System von drei gleich langen von einem Punlrt (Scheitel) ausgehenden auf einander rechtwialrlig
Die schiefe axonometrische Projektion. von ~[ermann Linlrolin. Bei axonometrischen Projektionen wird ein System von drei gleich langen von einem Punlrt (Scheitel) ausgehenden auf einander rechtwialrlig
Dreiecke (in der Ebene)
 Dreiecke (in der Ebene) 1) EinfÄhrung Trigonometrie bedeutet: die Lehre von den Dreiecken. Ein Dreieck entsteht aus drei geraden, nicht parallelen Seiten, die sich jeweils unter einem Winkel treffen. Dies
Dreiecke (in der Ebene) 1) EinfÄhrung Trigonometrie bedeutet: die Lehre von den Dreiecken. Ein Dreieck entsteht aus drei geraden, nicht parallelen Seiten, die sich jeweils unter einem Winkel treffen. Dies
Demo-Text für STOCHASTIK. Tschebyscheff-Ungleichung. Einführung mit Anwendungsbeispielen. Datei Nr Friedrich W.
 STOCHASTIK Tschebyscheff-Ungleichung Einführung mit Anwendungsbeispielen Datei Nr. 36111 Friedrich W. Buckel Stand 1. April 010 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mathe-cd.de Inhalt 1 Wiederholung:
STOCHASTIK Tschebyscheff-Ungleichung Einführung mit Anwendungsbeispielen Datei Nr. 36111 Friedrich W. Buckel Stand 1. April 010 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mathe-cd.de Inhalt 1 Wiederholung:
Projekt. Sonnenuhr. R.Schorpp. Version
 Projekt Sonnenuhr Version 1. - 1-12.1.9 1 INHALTVERZEICHNIS 1 Inhaltverzeichnis...2 1.1 Versionsverwaltung...2 2 Thema...3 2.1 Pflichtenheft...3 3 Astronomische Hintergründe...4 3.1 Nummer des Tages im
Projekt Sonnenuhr Version 1. - 1-12.1.9 1 INHALTVERZEICHNIS 1 Inhaltverzeichnis...2 1.1 Versionsverwaltung...2 2 Thema...3 2.1 Pflichtenheft...3 3 Astronomische Hintergründe...4 3.1 Nummer des Tages im
Themenbereich: Besondere Dreiecke Seite 1 von 6
 Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Die Kanten der Grundfläche mit je 7 cm sind die Katheten a und b des rechtwinkligen Dreiecks, die Hypotenuse c ist die gesuchte Bodendiagonale c.
 Aufgabe 1 Schritt 1: Ansatz und Skizze Bei einem Würfel, bei dem ja alle Kantenlängen gleich sind, kannst du mit einer Raumdiagonale, einer senkrechten Kante und einer Decken oder Bodendiagonalen ein rechtwinkliges
Aufgabe 1 Schritt 1: Ansatz und Skizze Bei einem Würfel, bei dem ja alle Kantenlängen gleich sind, kannst du mit einer Raumdiagonale, einer senkrechten Kante und einer Decken oder Bodendiagonalen ein rechtwinkliges
ASV Astroseminar 2003
 Astronavigation nicht für Prüfungen (C-Schein, SHS) sondern zum Vergnügen. Nichts auswendig lernen, sondern Hintergründe verstehen Nur Verfahren, die auf Sportbooten anwendbar sind Keine HO-Tafeln heutzutage
Astronavigation nicht für Prüfungen (C-Schein, SHS) sondern zum Vergnügen. Nichts auswendig lernen, sondern Hintergründe verstehen Nur Verfahren, die auf Sportbooten anwendbar sind Keine HO-Tafeln heutzutage
Name & Klasse: Naturwissenschaft und Technik Datum: Trigonometrie. Trigonometrie. Wir interessieren uns hier lediglich für rechtwinklige Dreiecke.
 Trigonometrie Trigonometrie Wir interessieren uns hier lediglich für rechtwinklige Dreiecke. Satz des Pythagoras Mit dem Satz des Pythagoras ist es möglich in einem rechtwinkligen Dreieck aus zwei bekannten
Trigonometrie Trigonometrie Wir interessieren uns hier lediglich für rechtwinklige Dreiecke. Satz des Pythagoras Mit dem Satz des Pythagoras ist es möglich in einem rechtwinkligen Dreieck aus zwei bekannten
Funktionen (trigonometrisch)
 Funktionen (trigonometrisch) 1. Einfache trigonometrische Beziehungen (a) Ein rechtwinkliges Dreieck ABC hat die Katheten a = 12 und b = 5. Welche exakten Werte haben sin α, cos α, tan α, sin β, cos β,
Funktionen (trigonometrisch) 1. Einfache trigonometrische Beziehungen (a) Ein rechtwinkliges Dreieck ABC hat die Katheten a = 12 und b = 5. Welche exakten Werte haben sin α, cos α, tan α, sin β, cos β,
Trigonometrische Kurven / Funktionen
 Trigonometrische Kurven / Funktionen Teil Eigenschaften der Funktionen sin, cos und tan Verschiebung und Streckung von Sinuskurven Kurvendiskussion ohne Verwendung der Differenzialrechnung Geeignet ab
Trigonometrische Kurven / Funktionen Teil Eigenschaften der Funktionen sin, cos und tan Verschiebung und Streckung von Sinuskurven Kurvendiskussion ohne Verwendung der Differenzialrechnung Geeignet ab
Name, Klasse, Jahr Schwierigkeit Mathematisches Thema Amelie martin, 9 x trigonometrie. 900m
 Amelie martin, 9 x trigonometrie 600m 900m Welche Länge hat die Hypotenuse dieses Dreiecks und welchen Winkel (α) und welche Steigung haben wir gegeben? Ausrechnung Winkel und Steigung: Steigung: tan(α)
Amelie martin, 9 x trigonometrie 600m 900m Welche Länge hat die Hypotenuse dieses Dreiecks und welchen Winkel (α) und welche Steigung haben wir gegeben? Ausrechnung Winkel und Steigung: Steigung: tan(α)
Geometrie-Aufgaben: Ähnlichkeit & Strahlensätze Berechne die fehlenden Strecken: (Skizzen sind nicht masssabgsgetreu)
 Geometrie-Aufgaben: Ähnlichkeit & Strahlensätze 4 1. Berechne die fehlenden Strecken: (Skizzen sind nicht masssabgsgetreu) 1 2 2. Ein Baum und sein Schatten An einem Baum und an seinem Schatten sind die
Geometrie-Aufgaben: Ähnlichkeit & Strahlensätze 4 1. Berechne die fehlenden Strecken: (Skizzen sind nicht masssabgsgetreu) 1 2 2. Ein Baum und sein Schatten An einem Baum und an seinem Schatten sind die
1 Einleitung. 2 Sinus. Trigonometrie
 1 Einleitung Die Trigonometrie (trigonon - griechisch für Dreieck) und die trigonometrischen Funktionen sind wichtige mathematische Werkzeuge zur Beschreibung der Natur. In der Physik werden trigonometrische
1 Einleitung Die Trigonometrie (trigonon - griechisch für Dreieck) und die trigonometrischen Funktionen sind wichtige mathematische Werkzeuge zur Beschreibung der Natur. In der Physik werden trigonometrische
Ähnlichkeit: 1.1 Welche der Figuren sind ähnlich zueinander? Kreuze an! Miss benötigte Winkel und Längen in der Zeichnung ab!
 Ähnlichkeit: Ähnliche Figuren: https://www.youtube.com/watch?v=xvpd9cep7qu 1.1 Welche der Figuren sind ähnlich zueinander? Kreuze an! Miss benötigte Winkel und Längen in der Zeichnung ab! 1.2 Welche Vierecke
Ähnlichkeit: Ähnliche Figuren: https://www.youtube.com/watch?v=xvpd9cep7qu 1.1 Welche der Figuren sind ähnlich zueinander? Kreuze an! Miss benötigte Winkel und Längen in der Zeichnung ab! 1.2 Welche Vierecke
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
TYPUS MAR. Blutgruppe AB negativ B positiv A positiv Anteil 1
 KANTONSSCHULE KREUZLINGEN MATURITÄTSPRÜFUNGEN 2004 TYPUS MAR MATHEMATIK / 3 Std. Klasse 4 MC / ho Zeit: Hilfsmittel: Beachten Sie: 180 Minuten Taschenrechner, Formelsammlung DMK Jede Aufgabe ist auf ein
KANTONSSCHULE KREUZLINGEN MATURITÄTSPRÜFUNGEN 2004 TYPUS MAR MATHEMATIK / 3 Std. Klasse 4 MC / ho Zeit: Hilfsmittel: Beachten Sie: 180 Minuten Taschenrechner, Formelsammlung DMK Jede Aufgabe ist auf ein
(von Punkt A nach Punkt B) gemessen und auch die entsprechenden Zenitwinkel z B
 Aufgabe a.1 Verwendet dieses elementare geometrische Verhältnis der Strecken, um die Höhe eines Turmes oder eines sonstigen hohen Gebäudes in eurer Nähe zu bestimmen. Dokumentiert euer Experiment. Wiederholt
Aufgabe a.1 Verwendet dieses elementare geometrische Verhältnis der Strecken, um die Höhe eines Turmes oder eines sonstigen hohen Gebäudes in eurer Nähe zu bestimmen. Dokumentiert euer Experiment. Wiederholt
Bin ich in Mathe fit für die Oberstufe? Lösungen der Checkliste der Kompetenzen der Sekundarstufe I
 Gymnasium St. Wolfhelm Bin ich in Mathe fit für die Oberstufe? Lösungen der Checkliste der Kompetenzen der Sekundarstufe I Mit ihrer Hilfe kannst du selbstständig kontrollieren, ob du die abgefragten Kompetenzen
Gymnasium St. Wolfhelm Bin ich in Mathe fit für die Oberstufe? Lösungen der Checkliste der Kompetenzen der Sekundarstufe I Mit ihrer Hilfe kannst du selbstständig kontrollieren, ob du die abgefragten Kompetenzen
Bestimmung der Capaeität mit der Wage
 290 Akademie d. Wissenschaften Wien; download unter www.biologiezentrum.at Bestimmung der Capaeität mit der Wage V. v. Lang, w.m.k.akad. 1. Die im Nachfolgenden gegebene Methode ist wohl nur zur Bestimmung
290 Akademie d. Wissenschaften Wien; download unter www.biologiezentrum.at Bestimmung der Capaeität mit der Wage V. v. Lang, w.m.k.akad. 1. Die im Nachfolgenden gegebene Methode ist wohl nur zur Bestimmung
2.2. Skalarprodukt. Geschwindigkeitsvektoren ergeben sich bei allen Bewegungen. Sie zeigen jeweils in Richtung der Bahnkurve.
 .. Skalarprodukt Kraftvektoren treten bei vielen physikalisch-technischen Problemen auf; sie greifen an einem Punkt in verschiedenen Richtungen an. Die bekannte Formel Arbeit = Kraft mal Weg muß man dann
.. Skalarprodukt Kraftvektoren treten bei vielen physikalisch-technischen Problemen auf; sie greifen an einem Punkt in verschiedenen Richtungen an. Die bekannte Formel Arbeit = Kraft mal Weg muß man dann
Geometrische Optik. Praktikumsversuch am Gruppe: 3. Thomas Himmelbauer Daniel Weiss
 Geometrische Optik Praktikumsversuch am 17.11.2010 Gruppe: 3 Thomas Himmelbauer Daniel Weiss Abgegeben am: 24.11.2010 Inhaltsverzeichnis 1 Einleitung 2 2 Bestimmung der Brennweite einer Linse 2 3 Mikroskop
Geometrische Optik Praktikumsversuch am 17.11.2010 Gruppe: 3 Thomas Himmelbauer Daniel Weiss Abgegeben am: 24.11.2010 Inhaltsverzeichnis 1 Einleitung 2 2 Bestimmung der Brennweite einer Linse 2 3 Mikroskop
Kreisberechnungen. 2. Kapitel aus meinem Lehrgang Geometrie
 Kreisberechnungen 2. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch e-mail: theorie@ronaldbalestra.ch 8. Oktober 08 Überblick über die bisherigen Geometrie
Kreisberechnungen 2. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch e-mail: theorie@ronaldbalestra.ch 8. Oktober 08 Überblick über die bisherigen Geometrie
Wiederholung: Differential- und Integralrechnung1
 Wiederholung: Differential- und Integralrechnung. Richtig, der Differenzenquotient ist die Steigung der Sekante. Durch den Grenzübergang erhält man die Steigung der Tangente (= Differentialquotient. Falsch,
Wiederholung: Differential- und Integralrechnung. Richtig, der Differenzenquotient ist die Steigung der Sekante. Durch den Grenzübergang erhält man die Steigung der Tangente (= Differentialquotient. Falsch,

 _._ -...,.. 5 26. Gnomon und Dipleidoskop. 141 a = 3600 a 2 acas
_._ -...,.. 5 26. Gnomon und Dipleidoskop. 141 a = 3600 a 2 acas