Kapitel I. Maßtheorie
|
|
|
- Damian Beck
- vor 5 Jahren
- Abrufe
Transkript
1 Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine σ-algebra auf Ω, dann gilt σ(a) =A. (b) Ist A Ω und G = A}, dann gilt σ(g) =, A, A c, Ω}. 2 Sei Ω eine Menge und A die σ-algebra aller Teilmengen A Ω, für welche A oder A c (höchstens) abzählbar ist (vgl. VO Beisp.1.3(2)). Zeige, dass das System E aller endlichen Teilmengen von Ω ein Erzeuger für A ist, d.h. dass σ(e) =A gilt. 3 [Zählmaß, vgl. VO Beisp.1.8(2)] Sei Ω eine Menge und definiere ζ : P(Ω) [0, ] durch A nicht endlich, ζ(a) = (A Ω). card(a) A endlich, Zeige, dass ζ ein Maß auf P(Ω) ist. 4 Sei Ω eine überabzählbare Menge und A die σ-algebra aller Teilmengen A Ω, für welche A oder A c (höchstens) abzählbar ist. Definiere µ: A [0, ] durch 0 A abzählbar, µ(a) = (A A). 1 A c abzählbar, Zeige, dass µ ein Maß auf A ist. zu 2. Äußere Maße 5 [Äußeres Lebesgue-Maß auf R n, vgl. VO Bem.2.3] Für (achsenparallele) Quader im R n von der Form Q =[a 1,b 1 ] [a n,b n ] (mit a j b j, j =1,..., n) setzen wir wie üblich Vol(Q) := (b 1 a 1 ) (b n a n ). 1
2 Weiters definieren wir die Abbildung λ : P(R n ) [0, ] durch λ (A) := inf Q UVol(Q) U ist endliche oder abzählbare Überdeckung von A durch Quader}. Zeige, dass λ ein äußeres Maß ist. (Anleitung für den Beweis der σ-subadditivität von λ : Sei A = n=1 A n; falls für ein n N schon λ (A n )= gilt, ist nichts mehr zu zeigen; sei also λ (A n ) < n N und ε> 0 beliebig; dann exisitiert zu jedem n eine Überdeckung (Q n l ) l N von A n durch Quader mit l=1 Vol(Qn l ) < λ (A n )+ε/2 n+1.) 6 Es sei λ wie in der vorigen Aufgabe. Für jede beschränkte Teilmenge A R n definieren wir ein sogenanntes inneres Maß durch λ (A) := Vol(Q) λ (Q \ A), wobei Q ein beliebiger Quader mit Q A ist. Zeige: (a) Der Wert λ (A) ist unabhängig von der Wahl von Q. (b) Die λ -Messbarkeit einer beschränkten Menge A R n ist äquivalent zur Bedingung λ (A) =λ (A). 7 Sei Ω = 1, 2, 3} und µ : P(Ω) [0, ] gegeben durch µ ( ) := 0, µ (Ω) := 2 und µ (B) := 1 für B Ω mit 0 < card(b) < 3. Zeige, dass µ ein äußeres Maß ist, sodass für jede Teilmenge A Ω die Gleichung µ (Ω) = µ (A)+µ (A c ) gilt und dennoch die trivialen Teilmengen und Ω die einzigen µ -messbaren Mengen sind. zu 3. Inhalte und Ringe 8 Sei Ω eine Menge. Wir statten P(Ω) mit der symmetrischen Mengendifferenz als Addition und dem Mengendurchschnitt als Multiplikation aus. Zeige: (a) (P(Ω),, ) ist ein kommutativer Ring mit Nullelement und Einselement Ω. (b) R P(Ω) ist genau dann ein Ring im Sinne der Definition 3.1 aus der VO, wenn R ein Unterring des Ringes (P(Ω),, ) gemäß (a) ist. 2
3 9 Sei Ω eine abzählbar-unendliche Menge und R P(Ω) bestehe aus jenen Teilmengen A Ω, für welche A oder A c endlich ist. (a) Zeige: R ist ein Ring, aber keine σ-algebra. (b) Definiere µ: R [0, ] durch 0 A endlich, µ(a) = 1 A c endlich, (A R). Zeige: µ ist ein Inhalt auf R, aber kein Prämaß. zu 4. Wann ist ein Inhalt ein Maß? 10 Sei Ω eine abzählbar-unendliche Menge und der Ring R P(Ω) bestehe (wie in Aufgabe 9 ) aus jenen Teilmengen A Ω, für welche A oder A c endlich ist. 0 A endlich, Definiere ν : R [0, ] durch ν(a) = (A R). A c endlich, (a) Zeige, dass ν ein Inhalt auf R ist, der die folgende Bedingung aus Proposition 4.1 der VO erfüllt: für jede Folge (A n ) n N in R mit A n gilt lim n ν(a n ) = 0. (b) Zeige, dass ν kein Prämaß ist. Widerspricht das dem oben genannten Satz aus der VO? zu 5, 6 und 7. Maße auf R, Maße auf R n und Borel-σ-Algebren 11 Sei F : R R eine monoton wachsende Funktion. Zeige (evtl. unter Zuhilfenahme eines Lehrbuches der Analysis): (a) F besitzt in jedem Punkt x R einen linksseitigen und rechtsseitigen Grenzwert. (b) Die Menge der Unstetigkeitsstellen von F ist (höchstens) abzählbar und besteht gänzlich aus Sprungstellen. 12 Sei R der von den halboffenen Intervallen der Form ]a, b] (a, b R, a<b) erzeugte Ring (vgl. VO 3.3(3) und Anfang von 5). Weiters sei ein Inhalt µ auf R gegeben. Definiere die Funktion F : R R durch µ(]0,x]) x 0, F (x) := µ(]x, 0]) x<0. und zeige folgende Aussagen: 3
4 (a) F ist monoton wachsend. (b) Ist µ sogar ein Prämaß, so ist F auch rechtsseitig stetig und daher eine Verteilungsfunktion auf R. (c) Sei nun µ ein Maß auf der Borel-σ-Algebra B R und die Funktion F : R R wie oben definiert. Zeige: für jedes x R ist x} B und weiters F ist stetig in x µ(x}) = Sei λ das 1 Lebesgue-(Borel-)Maß auf R n. Zeige: (a) Für beliebige a l <b l (l =1,..., n) sind n ]a l,b l [, l=1 n [a l,b l ] Borelmengen und es gilt l=1 n n n λ( ]a l,b l [) = λ( ]a l,b l ]) = λ( [a l,b l ]). l=1 l=1 l=1 (b) Die affine Hyperebene der Form H = (x 1,..., x n ) R n x i = α}, wobei i 1,..., n} und α R beliebig und fest sind, ist eine Borelmenge und es gilt λ(h) = Seien f und g Verteilungsfunktionen auf R. (a) Zeige, dass (x, y) f(x) g(y) eine Verteilungsfunktion F auf R 2 definiert. (b) Bezeichne µ f bzw. µ g das aus f bzw. g konstruierte Maß auf R und µ F das zu F gehörige Maß auf R 2 (wiederum die Eindeutigkeit gemäß 8 schon vorwegnehmend), dann gilt µ F (]a, b] ]c, d]) = µ f (]a, b]) µ g (]c, d]). zu 8. Eindeutigkeit von Maßen gibt es keine Vorschläge für Aufgaben... 1 Wir nehmen mit dieser Sprechweise schon die in 8 zu beweisende Eindeutigkeit vorweg. 4
5 Kapitel II. Integrationstheorie zu 9. Messbare Funktionen 15 (Rechnen mit Indikatorfunktionen) Seien Ω und I Mengen und A, B Ω sowie A i Ω für i I. Zeige folgende Eigenschaften der entsprechenden charakteristischen Funktionen: (a) A B 1 A 1 B (b) A B = 1 A B = 1 A + 1 B (insbesondere gilt 1 A c =1 1 A ) (c) 1 A B = 1 A 1 B (d) Für A = i I A i ist 1 A = sup i I 1 Ai (punktweise Gleichheit) (Bem.: analog ist 1 T i I A i = inf i I 1 Ai ) 16 Sei (Ω, A) ein messbarer Raum und für n N sei f n :Ω R eine messbare Funktion. Zeige, dass die Menge ω Ω (F n (ω)) n N konvergiert} zu A gehört. 17 Sei (Ω, A) ein messbarer Raum und f :Ω R eine Funktion. Zeige: (a) f ist messbar f + und f sind messbar (b) f ist messbar = f ist messbar, ABER die Umkehrung gilt im Allgemeinen nicht! zu 10. Integral im Stile von Lebesgue 18 Betrachte den Borel-Lebesgue-Maßraum (R, B, λ), wobei B die Borel-σ-Algebra und λ das Lebesgue-Maß bezeichnet. Ist die Dirichletfunktion u = 1 Q eine Elementarfunktion? Falls ja, was ist dann der Wert des Integrals u dλ? 19 Sei (Ω, A) ein messbarer Raum und M + die Menge der nichtnegativen messbaren numerischen Funktionen darauf. Zeige, dass jede beschränkte Funktion aus M + sogar gleichmäßiger Limes einer monoton wachsenden Folge von Elementarfunktionen ist. 20 Sei (Ω, A,µ) ein Maßraum und A A. Ist die charakteristische Funktion 1 A in jedem Fall integrierbar? 21 Sei (Ω, A,µ) ein Maßraum mit endlichem Maß, d.h. µ(ω) <. Zeige, dass dann jede konstante reellwertige Funktion µ-integrierbar ist. Desweiteren ist in diesem Fall auch jede beschränkte, messbare, reellwertige Funktion integrierbar. 22 Sei (Ω, A) ein messbarer Raum und µ und ν zwei Maße auf A. Zeige: 5
6 (a) µ + ν definiert ein Maß auf A (b) L(µ + ν) =L(µ) L(ν) (c) für f L(µ + ν) gilt fd(µ + ν) = f dµ + f dν. zu 11. Bildmaße 23 Wir betrachten wieder den Borel-Lebesgue-Maßraum (R, B, λ). (a) Sei a R und T : R R die Translation T a (x) := x + a. Zeige, dass T a messbar ist und für das Bildmaß von λ unter T a gilt λ Ta = λ, d.h. λ ist translationsinvariant. (b) Sei t R und t>0. Berechne das Bildmaß von λ unter der Dehnung/Streckung D t : R R, x tx. zu 12. Nullmengen 24 Sei (Ω, A,µ) ein Maßraum. Für eine Funktion f in M + oder L und A A setzen wir f dµ := 1 A f dµ. A Zeige, dass für eine Nullmenge N A stets N f dµ = 0 gilt. 25 Beweise oder widerlege folgende Aussagen bzgl. des Lebesgue-Maßes auf R: (a) Für a < b ist 1 [a, b] Q = 1 ]a, b[ fast überall. (b) Jede monotone Funktion R R ist fast überall stetig. (c) Die Dirichletfunktion 1 Q ist fast überall stetig. (d) Die Funktion f : R R, gegeben durch ist fast überall stetig. f(x) = 1 q x = p,p Z,q N,p und q teilerfremd, q 0 x = 0 oder x/ Q, 6
7 zu 13. Konvergenzsätze 26 Wir betrachten wieder den Borel-Lebesgue-Maßraum (R, B, λ). Finde Beispiele für drei Folgen (f n ), (g n ) und (h n ) integrierbarer Funktionen, die allesamt fast überall gegen 0 konvergieren, aber (a) lim n (c) lim inf n f n dλ =+, (b) lim n h n dλ = 1 und lim sup n g n dλ = 1, h n dλ = 1 erfüllen. 27 Seien (R, B,λ) der Borel-Lebesgue-Maßraum, h n (x) := n sin(cos(x)/n) (für x R und n N) und f eine integrierbare Funktion. Existiert lim n hn f dλ? Wenn ja, was ist der Grenzwert? (Hinweis: sin(y) y und lim y 0 sin(y) y =...?) zu 14. Das Riemann-Integral in der Lebesgue-Theorie 28 Welche der Funktionen aus Aufgabe 25 sind auf dem Intervall [0, 1] R-integrierbar? 29 Sei f : [1, [ R gegeben durch f(x) := sin(x) x. Zeige: (a) f ist uneigentlich R-integrierbar (Hinweis: Cauchy-Kriterium und partielle Integration) (b) Die Funktion g : R R, g(x) := 0 (x <1) und g(x) := f(x) (x 1), ist nicht Lebesgue-integrierbar. zu 15. Vervollständigung eines Maßraumes 30 Der Maßraum (Ω, A, µ) sei vollständig, d.h. jede Teilmenge einer Nullmenge gehört ebenfalls zu A. Zeige: Sind f und g numerische Funktionen Ω R mit f = g fast überall, dann impliziert die Messbarkeit von f auch jene von g. zu 16. Die Banachräume L p (µ) 31 Sei (Ω, A,µ) ein Maßraum und sei weiters 1 p, f L p und g :Ω R messbar und fast überall beschränkt. Zeige, dass dann auch g f zu L p gehört. 32 Sei (Ω, A,µ) ein Maßraum mit endlichem Maß (d.h. µ(ω) < ) und 1 p q. Zeige: L q L p. Insbesondere gilt also L q L 1 für jedes p 1. 7
8 33 Sei (R, B,λ) der Borel-Lebesgue-Maßraum. Gilt dann eine der Inklusionen L 1 (λ) L 2 (λ) oder L 2 (λ) L 1 (λ)? (Beweis oder Gegenbeispiel!) 34 Finde ein Beispiel für einen Maßraum (Ω, A,µ) und eine Cauchyfolge (f n ) n N in L 1 (µ), die aber nicht fast überall punktweise konvergent ist. Wie veträgt sich das mit Theorem 16.9 der VO? zu 17. Regularität von Borel-Maßen auf metrischen Räumen gibt es keine Vorschläge für Aufgaben. 8
9 Kapitel III. Grundkonstruktionen mit Maßen zu 18. Signierte Maße und Hahn-Zerlegung 35 Zeige: Jedes signierte Maß ist beschränkt und nimmt ein Maximum und ein Minimum an. (Hinweis: Beweis von Kor.18.6 der VO und Hahn-Zerlegung.) 36 Seien Ω = Ω + Ω sowie Ω = Ω + Ω zwei Hahn-Zerlegungen für das signierte Maß ρ auf der σ-algebra A. (Soll heißen: beide Zerlegungen erfüllen (a) und (b) aus 18.5 der VO.) Zeige, dass Ω + \ Ω + und Ω \ Ω jeweils ρ-nullmengen sind. zu 19. Maße mit Dichten 37 Zeige, dass das Dirac-Maß δ 0 auf R keine Dichte bezüglich des (Borel-)Lebesgue- Maßes λ besitzen kann, d.h. es gibt keine Borel-messbare Funktion f : R [0, [ mit der Eigenschaft δ 0 (A) = f 1 A dλ (A B). 38 Sei F eine stetig differenzierbare Verteilungsfunktion auf R und µ das zugehörige Maß auf der Borel-σ-Algebra B. Zeige, dass µ die Dichte F bezüglich λ (Lebesgue-Maß) besitzt. zu 20 und 21. Produktmaße, mehrfache Integrale 39 Sei a<b.für eine Funktion f :[a, b] [0, [ bezeichne G(f) := (x, y) a x b, y = f(x)} den Graphen und O(f) := (x, y) a x b, 0 y f(x)} die Ordinatenmenge von f, aufgefasst jeweils als Teilmengen von R 2. Es bezeichne B d die Borel-σ-Algebra auf R d und λ d das Borel-Lebesgue-Maß (gegebenenfalls eingeschränkt auf entsprechende Intervalle bzw. Quader). Zeige: (a) f ist Borel-messbar O(f) B 2 (Hinweis: für betrachte g(x, y) := f(x) y, g :[a, b] R R; für denke an Schnitte.) (b) Ist f Borel-messbar, dann gilt die aus der Schule bekannte Formel λ 2 (O(f)) = f dλ 1. 9
10 (c) Ist f Borel-messbar, dann folgt 2 G(f) B 2 und λ 2 (G(f)) = 0. 2 Die Umkehrung davon gilt auch, d.h. G(f) B 2 impliziert, dass f Borel-messbar ist. Eine Referenz dazu ist J. J. Buckley, The American Mathematical Monthly, Vol. 81, No. 10 (Dec., 1974), pp
11 Literatur [Els05] Jürgen Elstrodt. Maß- und Integrationstheorie. Springer-Lehrbuch. [Springer Textbook]. Springer-Verlag, Berlin, fourth edition, Grundwissen Mathematik. [Basic Knowledge in Mathematics]. 11
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit
 2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
KONSTRUKTION VON MASSEN
 KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Der Satz von Lusin. Markus Schuster Juni 2012 Universita t Ulm
 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Universita t Ulm Maßtheorie Seminar 2012 Seite 2 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Inhaltsverzeichnis Motivation Definitionen Der Satz
Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Universita t Ulm Maßtheorie Seminar 2012 Seite 2 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Inhaltsverzeichnis Motivation Definitionen Der Satz
Lemma (Eigenschaften elementarer Mengen) 1. Jede elementare Menge lässt sich als disjunkte Vereinigung halboffener Intervalle schreiben.
 12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
Musterlösung Analysis 3 - Maßtherorie
 Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Skript zur Vorlesung Analysis 3
 Skript zur Vorlesung Analysis 3 Wintersemester 2013/2014 Prof. Dr. Benjamin Schlein Inhaltsverzeichnis 1 Masstheorie 2 1.1 σ-algebren.................................. 6 1.2 Masse.....................................
Skript zur Vorlesung Analysis 3 Wintersemester 2013/2014 Prof. Dr. Benjamin Schlein Inhaltsverzeichnis 1 Masstheorie 2 1.1 σ-algebren.................................. 6 1.2 Masse.....................................
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
σ-algebren, Definition des Maßraums
 σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
2. Integration. {x : f(x) <a+ 1 n }
 9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
Analysis 3. Weihnachtsblatt Prof. Dr. H. Koch Dr. F. Gmeineder Besprechung: TBC, Januar Aufgabe 1: (Besonders prüfungsrelevant)
 Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
Multiplikationsoperatoren
 Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Analysis 2. Vorlesungsausarbeitung zum SS von Prof. Dr. Klaus Fritzsche. Inhaltsverzeichnis
 Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Maßtheorie. Skript zur Vorlesung von Prof. Dr. Michael Kohler. Sommersemester 2005 und Wintersemester 2005/2006
 Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS-
 ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
Maße und Integrale. begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller. Berlin, den 26.
 Maße und Integrale begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller Berlin, den 26. April 2008 Inhaltsverzeichnis 1 Konstruktion von Maßen 3 2 Konstruktion von Integralen
Maße und Integrale begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller Berlin, den 26. April 2008 Inhaltsverzeichnis 1 Konstruktion von Maßen 3 2 Konstruktion von Integralen
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Grundlagen Mengenlehre, Maßtheorie
 Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
2 Allgemeine Integrationstheorie
 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
1 Das Lebesgue-Maß. 1.1 Etwas Maßtheorie. Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}.
 1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
22 KAPITEL 1. GRUNDLAGEN. Um zu zeigen, dass diese Folge nicht konvergent ist, betrachten wir den punktweisen Limes und erhalten die Funktion
 KAPITEL 1. GRUNDLAGEN Um zu zeigen, dass diese Folge nicht konvergent ist, betrachten wir den punktweisen Limes und erhalten die Funktion 1 für 0 x < 1 g 0 (x) = 1 1 für < x 1. Natürlich gibt dies von
KAPITEL 1. GRUNDLAGEN Um zu zeigen, dass diese Folge nicht konvergent ist, betrachten wir den punktweisen Limes und erhalten die Funktion 1 für 0 x < 1 g 0 (x) = 1 1 für < x 1. Natürlich gibt dies von
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Funktionalanalysis und Integrationstheorie
 Funktionalanalysis und Integrationstheorie Vorlesungsnotizen Johannes Kepler Universität Linz Technisch-Naturwissenschaftliche Fakultät Institut für Analysis Prof. Dr. Aicke Hinrichs Wintersemester 2015/16
Funktionalanalysis und Integrationstheorie Vorlesungsnotizen Johannes Kepler Universität Linz Technisch-Naturwissenschaftliche Fakultät Institut für Analysis Prof. Dr. Aicke Hinrichs Wintersemester 2015/16
(alternierendes Vorzeichen) a n := ( 1)n n + 1 a n := 3n 2 7n a n := n(n 1)(n 2), n 3
 ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 43 2. Folgen und Reihen Folgen und Reihen werden in jedem Analysislehrbuch besprochen, siehe etwa [H, Kapitel III], [K, Kapitel 5], [J2, Kapitel 23] oder [M,
ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 43 2. Folgen und Reihen Folgen und Reihen werden in jedem Analysislehrbuch besprochen, siehe etwa [H, Kapitel III], [K, Kapitel 5], [J2, Kapitel 23] oder [M,
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
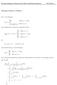 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Liste wichtiger Stammfunktionen
 Liste wichtiger Stammfunktionen Funktion Stammfunktion x n, x ln(x) n R \ { } n + xn+ ln( x ) x ln(x) x a x, a > sin(x) cos(x) sin 2 (x) cos 2 (x) x 2 x 2 a x ln(a) cos(x) sin(x) (x sin(x) cos(x)) 2 (x
Liste wichtiger Stammfunktionen Funktion Stammfunktion x n, x ln(x) n R \ { } n + xn+ ln( x ) x ln(x) x a x, a > sin(x) cos(x) sin 2 (x) cos 2 (x) x 2 x 2 a x ln(a) cos(x) sin(x) (x sin(x) cos(x)) 2 (x
Symmetrische Ableitungen von Massen
 Symmetrische Ableitungen von Massen Hyuksung Kwon 5. Juni 203 Inhaltsverzeichnis Einführung 2 Hardy-Littlewood Maximaloperator 2 3 Symmetrische Ableitung vom positiven Maß 7 Einführung Definition. (Borelmaß
Symmetrische Ableitungen von Massen Hyuksung Kwon 5. Juni 203 Inhaltsverzeichnis Einführung 2 Hardy-Littlewood Maximaloperator 2 3 Symmetrische Ableitung vom positiven Maß 7 Einführung Definition. (Borelmaß
Serie 2 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
Erwartungswert als Integral
 Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Höhere Analysis. dω = Reiner Lauterbach. Vorlesung. Universität Hamburg, WS 2015/2016
 Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
10 Der Satz von Radon-Nikodym
 uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
Analysis III. Vorlesung 69. Integrierbare Funktionen
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
Vollständigkeit. 1 Konstruktion der reellen Zahlen
 Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Maß- und Integrationstheorie
 Maß- und Integrationstheorie Klaus Ritter Kaiserslautern, SS 2014 Literatur Insbesondere J. Elstrodt, Maß- und Integrationstheorie, Springer, Berlin, 1. Auflage 1996, 7. Auflage 2011. Vorkenntnisse Grundlagen
Maß- und Integrationstheorie Klaus Ritter Kaiserslautern, SS 2014 Literatur Insbesondere J. Elstrodt, Maß- und Integrationstheorie, Springer, Berlin, 1. Auflage 1996, 7. Auflage 2011. Vorkenntnisse Grundlagen
Bálint Farkas. Analysis 3. Skript zur Vorlesung in WS2014/ Mai c by B. Farkas. compiled: 21-May-2015/11:13
 Bálint Farkas Analysis 3 Skript zur Vorlesung in WS2014/2015 21. Mai 2015 c by B. Farkas V O R B E M E R K U N G E N Dieses Skript beinhaltet das Material der Vorlesung Analysis 3 gehalten an der Bergischen
Bálint Farkas Analysis 3 Skript zur Vorlesung in WS2014/2015 21. Mai 2015 c by B. Farkas V O R B E M E R K U N G E N Dieses Skript beinhaltet das Material der Vorlesung Analysis 3 gehalten an der Bergischen
Kapitel 19. Das Lebesgue Maß σ Algebren und Maße
 Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
3 Bedingte Erwartungswerte
 3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
Serie 5 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 5 Lösungsvorschläge 1. Finden Sie eine stetige Funktion f : [, ) R, so dass f nicht Lebesgue-integrierbar T ist, jedoch der Grenzwert lim f(t)
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Vorlesung Der Satz von Fubini. 6.2 Der Satz von Beppo Levi 6.1. DER SATZ VON FUBINI 33
 6.1. DER SATZ VON FUBINI 33 Vorlesung 6 6.1 Der Satz von Fubini Das Lebesgue-Integralkann natürlichauchüber mehrdimensionale Gebiete definiert werden. Wir haben uns hier auf den eindimenionalen Fallbeschränkt.
6.1. DER SATZ VON FUBINI 33 Vorlesung 6 6.1 Der Satz von Fubini Das Lebesgue-Integralkann natürlichauchüber mehrdimensionale Gebiete definiert werden. Wir haben uns hier auf den eindimenionalen Fallbeschränkt.
3. Übungsblatt - Lösungsskizzen. so, dass f tatsächlich eine Wahrscheinlichkeitsdichte
 Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Studienbegleitende Prüfung Stochastik 2
 Universität Karlsruhe (TH) Institut für Stochastik Prof. Dr. N. Bäuerle Name: Vorname: Matr.-Nr.: Studienbegleitende Prüfung Stochastik 2 27. März 2007 Diese Klausur hat bestanden, wer mindestens 20 Punkte
Universität Karlsruhe (TH) Institut für Stochastik Prof. Dr. N. Bäuerle Name: Vorname: Matr.-Nr.: Studienbegleitende Prüfung Stochastik 2 27. März 2007 Diese Klausur hat bestanden, wer mindestens 20 Punkte
ANALYSIS 1 Kapitel 6: Stetige Funktionen
 ANALYSIS 1 Kapitel 6: Stetige Funktionen MAB.01012UB MAT.101UB Vorlesung im WS 2017/18 Günter LETTL Institut für Mathematik und wissenschaftliches Rechnen Karl-Franzens-Universität Graz 6.1 Grundbegrie
ANALYSIS 1 Kapitel 6: Stetige Funktionen MAB.01012UB MAT.101UB Vorlesung im WS 2017/18 Günter LETTL Institut für Mathematik und wissenschaftliches Rechnen Karl-Franzens-Universität Graz 6.1 Grundbegrie
Definitionen und Aussagen zur Maßtheorie
 Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Definitionen und Aussagen zur Maßtheorie Man möchte den Teilmengen eines Raumes ein Gewicht zuordnen. Wir werden sehen, daß dies in sinnvoller Weise häufig nicht für alle Teilmengen möglich ist, sondern
Hausdorff-Maß und Hausdorff-Dimension. Jens Krüger
 Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Lösungsvorschlag zu den Hausaufgaben der 3. Übung
 FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume
 Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Existenz des Lebesgue-Borel-Maßes
 A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
3 Konstruktion von Maßräumen
 $Id: caratheodory.tex,v 1.10 2011/11/17 11:43:55 hk Exp hk $ 3 Konstruktion von Maßräumen 3.4 Der Fortsetzungssatz von Caratheodory Wir hatten in der letzten Sitzung mit dem Beweis des Satzes von Caratheodory
$Id: caratheodory.tex,v 1.10 2011/11/17 11:43:55 hk Exp hk $ 3 Konstruktion von Maßräumen 3.4 Der Fortsetzungssatz von Caratheodory Wir hatten in der letzten Sitzung mit dem Beweis des Satzes von Caratheodory
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
1 Grundlagen der Maßtheorie
 1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
Aktuelle Themen aus der Stochastik Wintersemester 2017/2018 Abschnitt 5: Endliche Maße und schwache Konvergenz von Maßen in metrischen Räumen
 Aktuelle Themen aus der Stochastik Wintersemester 2017/2018 Abschnitt 5: Endliche Maße und schwache Konvergenz von Maßen in metrischen Räumen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut
Aktuelle Themen aus der Stochastik Wintersemester 2017/2018 Abschnitt 5: Endliche Maße und schwache Konvergenz von Maßen in metrischen Räumen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut
Kapitel 3. Konvergenz von Folgen und Reihen
 Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Analysis III - Bachelorversion
 Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
1.3 Zufallsvariablen
 1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
Kapitel 1. Übung 1. Bestimmen Sie die Mengen: [ n 0, 1 ) [0,r)
 Kapitel 1 Übungen Übung 1. Bestimmen Sie die Mengen: [ 1.,1 1 ] n 2. 3. 4. 5. n N n N [, 1 n r Q (,1 n N n N [,r [ 1 n+1, 1 n [ 1 n,1+ 1 n Übung 2. Sei X eine Menge und (A i i I eine abzählbare Partition
Kapitel 1 Übungen Übung 1. Bestimmen Sie die Mengen: [ 1.,1 1 ] n 2. 3. 4. 5. n N n N [, 1 n r Q (,1 n N n N [,r [ 1 n+1, 1 n [ 1 n,1+ 1 n Übung 2. Sei X eine Menge und (A i i I eine abzählbare Partition
Maßtheorie und Integralrechnung mehrerer Variablen
 Maßtheorie und Integralrechnung mehrerer Variablen Jan Swoboda 29. März 2014 Inhaltsverzeichnis Einleitung 1 1 Maßtheorie 3 1.1 Messbare Räume und messbare Abbildungen.................. 3 1.2 Maße und
Maßtheorie und Integralrechnung mehrerer Variablen Jan Swoboda 29. März 2014 Inhaltsverzeichnis Einleitung 1 1 Maßtheorie 3 1.1 Messbare Räume und messbare Abbildungen.................. 3 1.2 Maße und
( ) ( ) < b k, 1 k n} (2) < x k
 Technische Universität Dortmund Fakultät für Mathematik Proseminar Analysis Prof. Dr. Röger Benjamin Czyszczon Satz von Heine Borel Gliederung 1. Zellen und offene Überdeckungen 2. Satz von Heine Borel
Technische Universität Dortmund Fakultät für Mathematik Proseminar Analysis Prof. Dr. Röger Benjamin Czyszczon Satz von Heine Borel Gliederung 1. Zellen und offene Überdeckungen 2. Satz von Heine Borel
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis III, WS 2011/2012 Montag $Id: masse.tex,v /10/31 15:48:07 hk Exp $
 $Id: masse.tex,v 1.8 2011/10/31 15:48:07 hk Exp $ 2 Maßräume 2.2 Meßbare Abbildungen Der nächste Grundbegriff sind die meßbaren Abbildungen. Erinnern Sie sich daran das wir eigentlich einen Integralbegriff
$Id: masse.tex,v 1.8 2011/10/31 15:48:07 hk Exp $ 2 Maßräume 2.2 Meßbare Abbildungen Der nächste Grundbegriff sind die meßbaren Abbildungen. Erinnern Sie sich daran das wir eigentlich einen Integralbegriff
3 Produktmaße und Unabhängigkeit
 3 Produktmaße und Unabhängigkeit 3.1 Der allgemeine Fall Im Folgenden sei I eine beliebige Indexmenge. i I sei (Ω i, A i ein messbarer Raum. Weiter sei Ω : i I Ω i ein neuer Ergebnisraum. Wir definieren
3 Produktmaße und Unabhängigkeit 3.1 Der allgemeine Fall Im Folgenden sei I eine beliebige Indexmenge. i I sei (Ω i, A i ein messbarer Raum. Weiter sei Ω : i I Ω i ein neuer Ergebnisraum. Wir definieren
Meßbare Funktionen. Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen.
 Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
3 Das n-dimensionale Integral
 3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
1 Konvergenz im p ten Mittel
 Konvergenz im p ten Mittel 1 1 Konvergenz im p ten Mittel In diesem Paragraphen werden zunächst in Abschnitt 1.1 die L p Räume eingeführt. Diese erweisen sich als vollständige, lineare Räume über R. In
Konvergenz im p ten Mittel 1 1 Konvergenz im p ten Mittel In diesem Paragraphen werden zunächst in Abschnitt 1.1 die L p Räume eingeführt. Diese erweisen sich als vollständige, lineare Räume über R. In
Das Lebesgue-Integral
 Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Teil I: Maß- und Integrationstheorie
 Skript zur Vorlesung Maß- und Wahrscheinlichkeitstheorie Teil I: Maß- und Integrationstheorie Robert Hable Wintersemester 2009/2010 Institut für Statistik LMU München Korrigierte und erweiterte Fassung
Skript zur Vorlesung Maß- und Wahrscheinlichkeitstheorie Teil I: Maß- und Integrationstheorie Robert Hable Wintersemester 2009/2010 Institut für Statistik LMU München Korrigierte und erweiterte Fassung
Universität Leipzig, SoSo 2013
 Vorlesung Wahrscheinlichkeitstheorie I Universität Leipzig, SoSo 2013 Prof. Dr. Max v. Renesse renesse@uni-leipzig.de Sprechstunde: Di 13.15-14.45, A 337 Übungen: Mo 11.15 -- 12.45 A 314 K. Zimmermann
Vorlesung Wahrscheinlichkeitstheorie I Universität Leipzig, SoSo 2013 Prof. Dr. Max v. Renesse renesse@uni-leipzig.de Sprechstunde: Di 13.15-14.45, A 337 Übungen: Mo 11.15 -- 12.45 A 314 K. Zimmermann
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Wahrscheinlichkeitstheorie und Maßtheorie
 KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Maß und Integral I und II. SS 2004 und WS 2004/05
 Maß und Integral I und II SS 2004 und WS 2004/05 Vorlesung von Priv.-Doz. Dr. J. Dippon unter Verwendung einer Vorlesung von Prof. Dr. H. Walk im SS 2003 Inhaltsverzeichnis Bezeichnungen 3 1 Grundbegriffe
Maß und Integral I und II SS 2004 und WS 2004/05 Vorlesung von Priv.-Doz. Dr. J. Dippon unter Verwendung einer Vorlesung von Prof. Dr. H. Walk im SS 2003 Inhaltsverzeichnis Bezeichnungen 3 1 Grundbegriffe
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Analysis I für Studierende der Ingenieurwissenschaften
 Analysis I für Studierende der Ingenieurwissenschaften Ingenuin Gasser Department Mathematik Universität Hamburg Technische Universität Hamburg Harburg Wintersemester 2008/2009 1 Definition: Sei M R, alsom
Analysis I für Studierende der Ingenieurwissenschaften Ingenuin Gasser Department Mathematik Universität Hamburg Technische Universität Hamburg Harburg Wintersemester 2008/2009 1 Definition: Sei M R, alsom
Stetige Funktionen. Definition. Seien (X, d) und (Y, D) metrische Räume und f : X Y eine Abbildung. i) f heißt stetig in x 0 (x 0 D(f)), wenn
 Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Stetige Funktionen Eine zentrale Rolle in der Analysis spielen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume). Dabei sind i.a. nicht beliebige
Maß- und IntegraÖSR? theorie
 Jürgen Elstrodt Maß- und IntegraÖSR? theorie J il Springer Inhaltsverzeichnis Kapitel I. a-algebren und Boreische Mengen 1. Das Inhaltsproblem und das Maßproblem 2. Bezeichnungen und mengentheoretische
Jürgen Elstrodt Maß- und IntegraÖSR? theorie J il Springer Inhaltsverzeichnis Kapitel I. a-algebren und Boreische Mengen 1. Das Inhaltsproblem und das Maßproblem 2. Bezeichnungen und mengentheoretische
Ljapunov Exponenten. Reiner Lauterbach
 Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Übungen zur Analysis 3
 Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Wintersemester 013/01 Blatt 17.10.013 Übungen zur Analysis 3.1ε σ-subadditivität. a Es sei µ ein Inhalt auf einer Mengenalgebra A.
Mathematisches Institut der Universität München Prof. Dr. Franz Merkl Wintersemester 013/01 Blatt 17.10.013 Übungen zur Analysis 3.1ε σ-subadditivität. a Es sei µ ein Inhalt auf einer Mengenalgebra A.
7 Poisson-Punktprozesse
 Poisson-Punktprozesse sind natürliche Modelle für zufällige Konfigurationen von Punkten im Raum Wie der Name sagt, spielt die Poisson-Verteilung eine entscheidende Rolle Wir werden also mit der Definition
Poisson-Punktprozesse sind natürliche Modelle für zufällige Konfigurationen von Punkten im Raum Wie der Name sagt, spielt die Poisson-Verteilung eine entscheidende Rolle Wir werden also mit der Definition
Skript zur Vorlesung. Maßtheorie WS 2017/2018. Peter Junghanns
 Skript zur Vorlesung Maßtheorie WS 2017/2018 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Gerüst zu den Inhalten der Vorlesung dar. Die Vorlesung selbst bietet weiterführende rläuterungen,
Skript zur Vorlesung Maßtheorie WS 2017/2018 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Gerüst zu den Inhalten der Vorlesung dar. Die Vorlesung selbst bietet weiterführende rläuterungen,
