Übungen zur Vorlesung Analysis III Wintersemester 2011/2012. Musterlösung zum Klausurvorbereitungsblatt
|
|
|
- Michaela Geisler
- vor 5 Jahren
- Abrufe
Transkript
1 UNIVESITÄT DES SAALANDES FACHICHTUNG 6. MATHEMATIK Prof. Dr. oland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Analysis III Wintersemester 2/22 Musterlösung zum Klausurvorbereitungsblatt (3) Geben Sie ein Beispiel einer Algebra über einer Menge X, die keine σ-algebra ist. Lösung. Sei zunächst X eine beliebige Menge. In Aufgabe 3 von Blatt haben wir gesehen, dass A : {A X A endlich oder X\A endlich} eine Algebra auf X darstellt, die genau dann auch eine σ-algebra ist, wenn die Grmenge X endlich ist. Wählen wir also speziell X N, so liefert A das geforderte Beispiel. (4) Sei A eine σ-algebra über einer Menge X. Zeigen Sie, dass lim sup A n : {x X x A n für unendlich viele n N} A für jede Folge (A n ) n N von Mengen aus A gilt. Lösung. Wir setzen H : lim sup A n {x X x A n für unendlich viele n N} Wir stellen fest: H 2 : {x X N N n N : x A n } H 3 : A n. N N n N Es gilt H H 2 : Ist x H gegeben, so muss auch x H 2 gelten, da andernfalls (im Widerspruch zur Definition von H ) ein N N existieren würde, so dass x höchstens in den Mengen A,..., A N liegen kann. Ist x H 2 gegeben, so konstruiert man sich mit der definierenden Eigenschaft von H 2 rekursiv eine streng monoton wachsende Folge (n k ) k N aus N mit x A nk, was x H zeigt. Es gilt H 2 H 3, wovon man sich leicht durch Übersetzen der Mengen- in die Quantorenschreibweise überzeugt. Es gilt H 3 A, denn für alle N N gehört B N : n N A n zu A, weshalb auch H 3 N N B N A erfüllt sein muss.
2 Zusammenfassend folgt also lim sup A n H H 2 H 3 A damit die Behauptung. (5) Welche der folgenden Mengen sind λ 2 -Nullmengen in 2? Q, {(x, y) x y Q}, {(x, y) y 2 < x < }. Lösung. Die beiden Mengen Q q Q{q} {(x, y) x y Q} q Q{(x, x q) x } sind als abzählbare (!) Vereinigungen von λ 2 -Nullmengen (vgl. Aufgabe 2 von Blatt ) selbst λ 2 -Nullmengen. Im Gegensatz dazu ist P : {(x, y) y 2 < x < } keine λ 2 -Nullmenge, da das echteck Q : (, ) (, ) in P enthalten ist 4 2 damit (aufgr der Monotonie des Maßes λ 2, vgl. Aufgabe (b) von Blatt 2) gilt. λ 2 (P ) λ 2 (Q) 3 8 > (6) Für r > setzen wir : {x n x r}. Sei f : n C eine messbare Funktion, für die f Kr L (, λ n ) für alle r > gilt. Zeigen Sie die folgende Aussage: f L ( n, λ n ) sup r> f(x) dλ n (x) < Zeigen Sie weiter, dass in diesem Fall gilt: f(x)dλ n (x) lim f(x)dλ n (x). n r Lösung. : Wir nehmen f L ( n, λ n ) an. Dann gilt für jedes r > f(x) dλ n (x) f(x) χ Kr (x)dλ n (x) n f(x) dλ n (x) < n damit : Wir nehmen nun an, dass sup r> f(x) dλ n (x) f(x) dλ n (x) <. n M : sup r> f(x) dλ n (x) <
3 erfüllt ist. Dann wählen wir eine streng monoton wachsende Folge (r k ) k N aus (, ) mit r k für k betrachten die durch g k : n [, ), x f(x) χ Krk (x) definierte Folge (g k ) k N von nichtnegativen (da f L (, λ n ) für alle r > vorausgesetzt ist) auf n bezüglich λ 2 integrierbaren Funktionen, die ferner g (x) g 2 (x) g k (x) g k+ (x) < lim g k(x) f(x) k für alle x n erfüllen. Nach dem Satz von der monotonen Konvergenz können wir also folgern, dass auch f damit f zu L ( n, λ n ) gehört. Zusatz: Sind die äquivalenten Bedingungen erfüllt, so betrachten wir wieder eine Folge (r k ) k N wie oben definieren durch h k : n C, x f(x)χ Krk (x) eine Folge (h k ) k N von integrierbaren Funktionen mit h k f, die auf n punktweise gegen f konvergiert. Der Satz von der majorisierten Konvergenz liefert damit f(x)dλ n (x) lim h k (x)dλ n (x) lim f(x)dλ n (x). n k n k k Weil wir uns (r k ) k N beliebig vorgegeben hatten, folgt nun f(x)dλ n (x) lim f(x)dλ n (x). n r (7) Berechnen Sie das Integral M x yzdλ 3 (x, y, z), wobei M : {(x, y, z) 3 x, y, 2 (x2 + y 2 ) z x 2 + y 2 }. Lösung. Wir betrachten die aus Aufgabe von Blatt bekannte Zylinderkoordinatenabbildung Φ : (, ) (, 2π) 3, (r, ϕ, z) (r cos(ϕ), r sin(ϕ), z), welche die Jacobi-Determinante ( Φ ) det (r, ϕ, z) (r, ϕ, z) r besitzt. Wir setzen nun { I : (r, ϕ, z) < r <, < ϕ < π 2, } 2 r2 z r 2
4 stellen fest, dass Φ(I) eine Teilmenge von M liefert, deren Komplement M\Φ(I) eine λ 3 -Nullmenge ist. Darüber hinaus definieren wir ( I : (, ), π ) (, ), 2 wobei klarerweise I I erfüllt ist. Da die Funktion f(x, y, z) : x yz auf der kompakten Menge M stetig damit insbesondere λ 3 -integrierbar ist, erhalten wir aus dem Transformationssatz x yzdλ 3 (x, y, z) f(x, y, z)dλ 3 (x, y, z) f(φ(r, ϕ, z))rdλ 3 (r, ϕ, z). M Φ(I) Weiter können wir, da die messbare Funktion (r, ϕ, z) (f Φ)(r, ϕ, z)χ I (r, ϕ, z)r auf der beschränkten Menge I Lebesgue-integrierbar ist, unter Verwendung von χ I (r, ϕ, z) χ ( 2 r2,r 2 ) (z) des Satzes von Fubini berechnen: f(φ(r, ϕ, z))rdλ 3 (r, ϕ, z) I (f Φ)(r, ϕ, z)χ I (r, ϕ, z)rdλ 3 (r, ϕ, z) I ( ( ) ) (f Φ)(r, ϕ, z)χ I (r, ϕ, z)rdλ (z) dλ (ϕ) dλ (r) (,) (,) (,) ( ( (, π 2 ) (, π 2 ) (, π 2 ) ( ( (,) (,) ( 2 r2,r 2 ) ) ) (f Φ)(r, ϕ, z)χ ( 2 r2,r 2 ) (z)rdλ (z) dλ (ϕ) dλ (r) ) ) 5 sin(ϕ) cos(ϕ)r 2 zdλ (z) dλ (ϕ) dλ (r) ( ( r 5 2 sin(ϕ) cos(ϕ) (,) (, π 2 ) ( 2 r2,r 2 ) 3 ( ) r 3 2 sin(ϕ) cos(ϕ)dλ (ϕ) dλ (r) 8 (,) (, π 2 ) 3 ( )( sin(ϕ) cos(ϕ)dλ (ϕ) 8 (, π 2 ) (,) 3 zdz 2 r2 I ) ) zdλ (z) dλ (ϕ) dλ (r) ) r 3 2 dλ (r) Hierbei haben wir verwendet, dass wir die folgenden Lebesgue-Integrale nach Aufgabe 2 von Blatt 4 als iemann-integrale berechnen können, nachdem wir jeweils den Integrationsbereich durch Hinzufügen einer λ -Nullmenge abgeschlossen haben: r 2 [ ] r 2 (i) zdλ (z) ( 2 r2,r 2 ) 2 z2 3 8 r4 2 r2 (ii) (, π 2 ) sin(ϕ) cos(ϕ)dλ (ϕ) π 2 sin(ϕ) cos(ϕ)dϕ [ 2 3 sin(ϕ) 3 2 ] π 2 2 3
5 (iii) (,) r 3 2 dλ (r) r 3 2 dr [ 2 5 r 5 2 ] 2 5 (8) Beweisen Sie, dass ( x 2 ) lim cos e x dx n existiert bestimmen Sie den Grenzwert. Lösung. Wir definieren durch ( x 2 ) f n : [, ), x cos e x n eine Folge (f n ) n N von stetigen ( damit messbaren) Funktionen, die mit der Funktion f n (x) e x g(x) für alle x [, ) () g : [, ) [, ), x e x erfüllt. Zudem stellen wir fest, dass die Folge (f n ) n N punktweise auf [, ) gegen g konvergiert. Bei der Lösung zu Aufgabe 4 von Blatt 6 haben wir gesehen, dass eine Borelmessbare uneigentlich iemann-integrierbare Funktion f : [, ) genau dann Lebesgue-integrierbar ist, wenn auch f uneigentlich iemann-integrierbar ist dass in diesem Fall die beiden Integrale übereinstimmen. Wir halten fest: Da g g uneigentlich iemann-integrierbar ist, ist g somit auch Lebesgueintegrierbar es gilt g(x)dλ (x) g(x)dx. [, ) Wegen () sind mit g auch die Funktionen f n uneigentlich iemann-integrierbar gemäß obiger Bemerkung auch Lebesgue-integrierbar mit f n (x)dλ (x) f n (x)dx. [, ) Aus dem Satz von der majorisierten Konvergenz (Satz.32 im Skript zur Vorlesung) erhalten wir nun ( x 2 ) lim cos e x dx lim f n (x)dx n lim [, ) [, ). f n (x)dλ (x) g(x)dλ (x) g(x)dx e x dx
6 (9) Sei n 2 seien E,..., E n Borelmengen in mit E i [, ] für i,..., n λ (E ) + λ (E 2 ) + + λ (E n ) > n. Zeigen Sie, dass es mindestens einen Punkt x [, ] gibt, so dass x E i für alle i,..., n. Lösung. Wir betrachten die Borelmenge E : n i E i [, ] rechnen nach, dass ( n ) λ ([, ]\E) λ ([, ]\E i ) i n λ ([, ]\E i ) i n ( λ ([, ]) λ (E i ) ) i n n λ (E i ) i < n (n ) damit λ (E) λ ([, ]\E) > gelten muss. Insbesondere sehen wir E, was die Behauptung zeigt. () Zeigen Sie, dass es ein eindeutig bestimmtes Maß µ auf gibt, so dass f(x)dµ(x) n f(n) 2 n für alle stetigen Funktionen f : mit kompaktem Träger gilt. Berechnen Sie speziell µ(). Lösung. Existenz: Wir definieren auf dem Vektorraum C c () aller stetigen (komplexwertigen) Funktionen mit kompaktem Träger die Abbildung Λ : C c () C, f n f(n) 2 n. Diese ist wohldefiniert, da für f C c () die eihe f(n) n wegen 2 n n f(n) 2 n f n 2 n f absolut konvergiert. Darüber hinaus ist Λ positiv, denn für f gilt klarerweise Λ(f). Nach dem ieszschen Darstellungssatz (Satz 4.6 im Skript zur Vorlesung) gibt es ein eindeutig bestimmtes Borel-Maß µ auf, so dass Λ(f) f(x)dµ(x) für alle f C c ()
7 damit auch die in der Aufgabenstellung geforderte (schwächere!) Bedingung erfüllt ist. Eindeutigkeit: Sei nun ein weiteres Borel-Maß ν auf gegeben, welches der in der Aufgabenstellung geforderten Bedingung Λ(g) g(x)dν(x) für alle reellwertigen g C c () genügt. Zu jedem f C c () finden wir eine Darstellung f g + ig 2 mit reellwertigen Funktionen g, g 2 C c () können nachrechnen, dass f(x)dν(x) g (x)dν(x) + i g 2 (x)dν(x) Λ(g ) + iλ(g 2 ) g (x)dµ(x) + i f(x)dµ(x) Λ(f) g 2 (x)dµ(x) gilt. Die Eindeutigkeitsaussage des ieszschen Darstellungssatzes impliziert nun µ ν. Zusatz: Definieren wir für n N die Funktion, x (, (n + )] (n + ) + x, x ( (n + ), n) f n :, x, x [ n, n], so gilt f n C c () f n (x)dµ(x) Λ(f n ) (n + ) x, x (n, n + ), x [n +, ) m f n (m) n 2 m 2 m 2. n Da f n punktweise monoton wachsend gegen die Funktion f konvergiert, ergibt sich nach dem Satz von der monotonen Konvergenz m µ() lim f n (x)dµ(x) lim 2 n () Sei T : H H ein kompakter Operator auf einem Hilbertraum (H,, ). Zeigen Sie, dass S : T T kompakt selbstadjungiert ist dass Sx, x für alle x H gilt. Zeigen Sie weiter S T 2.
8 Lösung. Da die Menge K(H) aller kompakten Operatoren auf H nach Satz.2. (3) der Vorlesung ein zweiseitiges Ideal in B(H) darstellt der zu T adjungierte Operator T nach Satz 9.6 der Vorlesung stetig ist, folgt S T T K(H). Weiter erhalten wir mit Satz 9.8 der Vorlesung S (T T ) T T T T S, d.h. S ist selbstadjungiert. Die definierende Eigenschaft von T liefert zudem Sx, x T T x, x T x, T x T x 2 für alle x H. Schließlich ergibt die C -Identität (6) in Satz 9.8 S T T T 2. (2) Sei (H,, ) ein komplexer Hilbertraum seien P Q orthogonale Projektionen auf H. Zeigen Sie die Äquivalenz der folgenden Aussagen: (i) P Q ist eine orthogonale Projektion. (ii) ran(q) ran(p ). (iii) P Q Q. (iv) QP Q. Lösung. (i) (ii) : Nehmen wir an, dass P Q eine Orthogonalprojektion ist, so können wir nachrechnen, dass P Q (P Q) 2 P 2 P Q QP + Q 2 P (P Q + QP ) + Q daher P Q+QP 2Q erfüllt ist. Sei nun x ker(p ) beliebig vorgegeben. Dann erhalten wir 2Qx (P Q + QP )x P (Qx) damit 2 Qx P (Qx) Qx, was aber offensichtlich nur für Qx erfüllt sein kann. Es gilt also Qx damit x ker(q). Die damit bewiesene Inklusion ker(p ) ker(q) führt wegen ker(p ) ran(p ) bzw. ker(q) ran(q) zu ran(p ) ran(q) schließlich zu ran(q) ran(p ). (ii) (iii) : Gilt ran(q) ran(p ), so folgt wegen ran(p ) ker( P ), dass ( P )Q somit P Q Q gelten muss. (iii) (iv) : Aus P Q Q folgt unmittelbar Q Q (P Q) Q P QP. Umgekehrt folgt aus QP Q analog Q Q (QP ) P Q P Q.
9 (iii),(iv) (i) : Es gelte P Q Q QP Q. Wir erhalten dann (P Q) 2 P 2 P Q QP + Q 2 P (P Q + QP ) + Q P Q (P Q) P Q P Q, d.h. P Q ist eine Orthogonalprojektion. (3) Welche der folgenden -Formen auf U : {(x, y) 2 x 2 + y 2 < } sind exakt? dx + 2dy, ydx xdy, ydx + xdy, ye xy dx + xe xy dy Lösung. Da U (etwa bezüglich (, )) sternförmig ist, ist eine -Form auf U nach dem Lemma von Poincaré genau dann exakt, wenn sie geschlossen ist. Wir rechnen also einfach nach: (i) dx + 2dy ist exakt, da d ( dx + 2dy ). (ii) ydx xdy ist nicht exakt, da d ( ydx xdy ) dy dx dx dy 2 dx dy. (iii) ydx + xdy ist exakt, da d ( ydx + xdy ) dy dx + dx dy. (iv) ye xy dx + xe xy dy ist exakt, da d ( ye xy dx + xe xy dy ) ( + xy)e xy dy dx + ( + xy)e xy dx dy. (4) Für welche der folgenden Differentialformen ω auf 4 gilt ω ω? x dx + x 2 dx 3 + dx 4, dx dx 2 + dx 3 dx 4, e x 2 dx dx 4, 2 dx dx 3 dx 2 dx 4. Lösung. Wir berechnen für ω x dx + x 2 dx 3 + dx 4 (ω ω)(x) x x 2 dx dx 3 + x dx dx 4 +x x 2 dx 3 dx + x 2 dx 3 dx 4 +x dx 4 dx + x 2 dx 4 dx 3. für ω dx dx 2 + dx 3 dx 4 (ω ω)(x) dx dx 2 dx 3 dx 4 + dx 3 dx 4 dx dx 2 2dx dx 2 dx 3 dx 4. für ω e x 2 dx dx 4 (ω ω)(x). für ω 2 dx dx 3 dx 2 dx 4 (ω ω)(x) 2 dx dx 3 dx 2 dx 4 2 dx 2 dx 4 dx dx 3 4 dx dx 2 dx 3 dx 4. (5) Sei ω die durch ω(x, y) : y dx dy definierte 2-Form auf 2 sei ϕ : 2 2 definiert durch ϕ(x, y) : (y, e x ). Bestimmen Sie ϕ ω.
10 Lösung. Wir betimmen zunächst dϕ (x, y) ϕ x (x, y) dx + ϕ (x, y) dy dy y damit dϕ 2 (x, y) ϕ 2 x (x, y) dx + ϕ 2 y (x, y) dy ex dx (ϕ ω)(x, y) ϕ 2 (x, y)(dϕ dϕ 2 )(x, y) e 2x dx dy. (6) Sei γ : [, ] 2 der Weg, der den and des von den Punkten (, ), (, ), (, ) (, ) gebildeten Quadrats Q im positiven Sinn durchläuft. Weiter sei ω die durch ω(x, y) : y dx x dy definierte -Form auf 2. Berechnen Sie γ ω. Lösung. Seien a, b 2 gegeben sei γ : γ [a,b] : [, ] 2 die durch γ [a,b] (t) : ( t)a + tb für t [, ] definierte Kurve. Wir rechnen nach, dass (γ ω)(t) ω(γ(t)), γ (t) dt Wir erhalten also (γ 2 (t)γ (t) γ (t)γ 2(t)) dt ( ( t)a 2 + tb 2 )(b a ) (( t)a + tb )(b 2 a 2 ) ) dt ( a 2 (b a ) a (b 2 a 2 ) ) dt ( a 2 b a b 2 ) dt. γ [a,b] ω (γ ω)(t)dt a 2 b a b 2 Für die Teilkurven γ : γ [(, ),(, )], γ 2 : γ [(, ),(,)], γ 3 : γ [(,),(,)] γ 4 : γ [(,),(, )], aus denen sich die Kurve γ zusammensetzt, ergibt sich damit γ j ω 2 für j, 2, 3, 4. Weil ω unter Parametertransformationen der Kurve γ invariant ist, ergibt sich γ schließlich 4 ω ω 8. γ γ j j
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Liste wichtiger Stammfunktionen
 Liste wichtiger Stammfunktionen Funktion Stammfunktion x n, x ln(x) n R \ { } n + xn+ ln( x ) x ln(x) x a x, a > sin(x) cos(x) sin 2 (x) cos 2 (x) x 2 x 2 a x ln(a) cos(x) sin(x) (x sin(x) cos(x)) 2 (x
Liste wichtiger Stammfunktionen Funktion Stammfunktion x n, x ln(x) n R \ { } n + xn+ ln( x ) x ln(x) x a x, a > sin(x) cos(x) sin 2 (x) cos 2 (x) x 2 x 2 a x ln(a) cos(x) sin(x) (x sin(x) cos(x)) 2 (x
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
9. Übung zur Maß- und Integrationstheorie, Lösungsskizze Aufgaben
 9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Übungen zur Vorlesung Funktionentheorie Sommersemester Lösungshinweise zum Klausurvorbereitungsblatt. (z) i f. 2xe (x2 +y 2) i2ye (x2 +y 2 ) 2
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Lösungshinweise zum Klausurvorbereitungsblatt (3
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Lösungshinweise zum Klausurvorbereitungsblatt (3
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Lebesgue-Integral und L p -Räume
 Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Vorlesung Der Satz von Fubini. 6.2 Der Satz von Beppo Levi 6.1. DER SATZ VON FUBINI 33
 6.1. DER SATZ VON FUBINI 33 Vorlesung 6 6.1 Der Satz von Fubini Das Lebesgue-Integralkann natürlichauchüber mehrdimensionale Gebiete definiert werden. Wir haben uns hier auf den eindimenionalen Fallbeschränkt.
6.1. DER SATZ VON FUBINI 33 Vorlesung 6 6.1 Der Satz von Fubini Das Lebesgue-Integralkann natürlichauchüber mehrdimensionale Gebiete definiert werden. Wir haben uns hier auf den eindimenionalen Fallbeschränkt.
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
1 Verbandstheorie. Aufgabensammlung. Höhere Mathematik für Physiker III Wintersemester 2014
 Aufgabensammlung Höhere Mathematik für Physiker III Wintersemester 2014 1 Verbandstheorie 1. Aufgabe: (a) Sei f C(R) eine stetige Funktion. Wenn Rf(x)φ(x)dx = 0 für alle Testfunktionen φ Cc (R) gilt, dann
Aufgabensammlung Höhere Mathematik für Physiker III Wintersemester 2014 1 Verbandstheorie 1. Aufgabe: (a) Sei f C(R) eine stetige Funktion. Wenn Rf(x)φ(x)dx = 0 für alle Testfunktionen φ Cc (R) gilt, dann
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Höhere Funktionalanalysis WS2016/17 Übungsblatt
 Höhere Funktionalanalysis WS2016/17 Übungsblatt 1 11.10.2016 Aufgabe 1. Berechne die Normen der Operatoren (a) f L [0, 1], M f : L 2 [0, 1] L 2 [0, 1], (M f g)(x) = f(x)g(x). (b) g C[0, 1], T g : C[0,
Höhere Funktionalanalysis WS2016/17 Übungsblatt 1 11.10.2016 Aufgabe 1. Berechne die Normen der Operatoren (a) f L [0, 1], M f : L 2 [0, 1] L 2 [0, 1], (M f g)(x) = f(x)g(x). (b) g C[0, 1], T g : C[0,
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
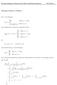 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Musterlösung Analysis 3 - Maßtherorie
 Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1)
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
2. Integration. {x : f(x) <a+ 1 n }
 9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
8 Beispiele von Koordinatentransformationen
 8 Beispiele von Koordinatentransformationen Wir diskutieren nun diejenigen Koordinatentransformationen, die in der Praxis wirklich gebraucht werden (ebene und räumliche Polarkoordinaten sowie Zylinderkoordinaten).
8 Beispiele von Koordinatentransformationen Wir diskutieren nun diejenigen Koordinatentransformationen, die in der Praxis wirklich gebraucht werden (ebene und räumliche Polarkoordinaten sowie Zylinderkoordinaten).
12. Übungsblatt zur Analysis II
 Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno Benno van den Berg WS 9/1 1.1.1 1. Übungsblatt zur Analysis II Gruppenübung Aufgabe G1 Kreuzen Sie die richtigen Aussagen an. Sei V C 1 (R n,
Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno Benno van den Berg WS 9/1 1.1.1 1. Übungsblatt zur Analysis II Gruppenübung Aufgabe G1 Kreuzen Sie die richtigen Aussagen an. Sei V C 1 (R n,
Analysis 3. Weihnachtsblatt Prof. Dr. H. Koch Dr. F. Gmeineder Besprechung: TBC, Januar Aufgabe 1: (Besonders prüfungsrelevant)
 Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
2 Allgemeine Integrationstheorie
 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
Klausur Analysis II
 WS 28/9 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis II 6.2.28 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
WS 28/9 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis II 6.2.28 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
Klausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Karlsruher Institut für Technologie (KIT Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 4.3.3 Klausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((4+3+3 Punkte a Welche
Übungen zur Vorlesung Funktionentheorie Sommersemester Musterlösung zu Blatt 10. f(z) f(z) dz
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
Erwartungswert und Varianz von Zufallsvariablen
 Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Kapitel 7 Erwartungswert und Varianz von Zufallsvariablen Im Folgenden sei (Ω, A, P ) ein Wahrscheinlichkeitsraum. Der Erwartungswert von X ist ein Lebesgue-Integral (allerdings allgemeiner als in Analysis
Das Lebesgue-Integral
 Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Das Lebesgue-Integral Bei der Einführung des Integralbegriffs gehen wir schrittweise vor. Zunächst erklären wir das Integral von charakteristischen Funktionen, danach von positiven einfachen Funktionen
Kommutativität. De Morgansche Regeln
 1. Formale Logik Proposition 1.1. Die logischen Elementarverknüpfungen gehorchen folgenden Äquivalenzen: (1.1) (1.2) p p p p p p Idempotenz (1.3) (1.4) p q q p p q q p Kommutativität (1.5) (1.6) (p q)
1. Formale Logik Proposition 1.1. Die logischen Elementarverknüpfungen gehorchen folgenden Äquivalenzen: (1.1) (1.2) p p p p p p Idempotenz (1.3) (1.4) p q q p p q q p Kommutativität (1.5) (1.6) (p q)
3 Produktmaße und Unabhängigkeit
 3 Produktmaße und Unabhängigkeit 3.1 Der allgemeine Fall Im Folgenden sei I eine beliebige Indexmenge. i I sei (Ω i, A i ein messbarer Raum. Weiter sei Ω : i I Ω i ein neuer Ergebnisraum. Wir definieren
3 Produktmaße und Unabhängigkeit 3.1 Der allgemeine Fall Im Folgenden sei I eine beliebige Indexmenge. i I sei (Ω i, A i ein messbarer Raum. Weiter sei Ω : i I Ω i ein neuer Ergebnisraum. Wir definieren
Grundlagen der Mathematik 2 Nachklausur
 Andreas Gathmann und Yue Ren Sommersemester 6 Grundlagen der Mathematik Nachklausur Bearbeitungszeit: 8 Minuten Aufgabe (6 Punkte): Es sei f : R R, (x,y) xye (x+y). (a) Bestimme alle lokalen Maxima und
Andreas Gathmann und Yue Ren Sommersemester 6 Grundlagen der Mathematik Nachklausur Bearbeitungszeit: 8 Minuten Aufgabe (6 Punkte): Es sei f : R R, (x,y) xye (x+y). (a) Bestimme alle lokalen Maxima und
10 Der Satz von Fubini
 er Satz von Fubini ie Bezeichnungen seien wie in den Paragraphen 8 und 9. Satz. (Satz von Tonelli Es sei f : d [, + ] messbar. (Aus 8 folgt dann, dass f, f y messbar sind, wobei klar ist, dass f, f y sind.
er Satz von Fubini ie Bezeichnungen seien wie in den Paragraphen 8 und 9. Satz. (Satz von Tonelli Es sei f : d [, + ] messbar. (Aus 8 folgt dann, dass f, f y messbar sind, wobei klar ist, dass f, f y sind.
Lösungsvorschlag Klausur MA9802
 Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Multiplikationsoperatoren
 Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Kapitel C. Integrale und Grenzwerte
 Kapitel C Integrale und Grenzwerte Inhalt dieses Kapitels C000 1 Der Satz von Fubini 2 Der Transformationssatz 1 Vertauschen von Integral und eihe 2 Vertauschen von Integral und Limes 3 Vertauschen von
Kapitel C Integrale und Grenzwerte Inhalt dieses Kapitels C000 1 Der Satz von Fubini 2 Der Transformationssatz 1 Vertauschen von Integral und eihe 2 Vertauschen von Integral und Limes 3 Vertauschen von
(y ) 2 0 bis t, so erhalten wir 1 y (t) (t t 0). L sen wir diese Ungleichung nun nach y (t) auf, so folgt
 0.. Lösung der Aufgabe. Wir nehmen an, es existiere eine nicht-triviale globale L sung y. Dann lesen wir direkt von der Gleichung ab, dass y 0 gilt auf ganz R, das heisst, die Funktion ist konvex. Da wir
0.. Lösung der Aufgabe. Wir nehmen an, es existiere eine nicht-triviale globale L sung y. Dann lesen wir direkt von der Gleichung ab, dass y 0 gilt auf ganz R, das heisst, die Funktion ist konvex. Da wir
12 Aufgaben zu linearen Funktionalen
 266 12. Aufgaben zu linearen Funktionalen A B C 12 Aufgaben zu linearen Funktionalen 12.1 Stetige Funktionale (siehe auch 11.6.E, 12.2, 13.4.A) Sei E ein topologischer Vektorraum und ϕ: E K (ϕ ) linear.
266 12. Aufgaben zu linearen Funktionalen A B C 12 Aufgaben zu linearen Funktionalen 12.1 Stetige Funktionale (siehe auch 11.6.E, 12.2, 13.4.A) Sei E ein topologischer Vektorraum und ϕ: E K (ϕ ) linear.
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Mathematik III. Vorlesung 74. Folgerungen aus dem Satz von Fubini. (( 1 3 x3 1 2 x2 y +2y 3 x) 1 2)dy. ( y +2y y +4y3 )dy
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit
 2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
2 Fortsetzung von Prämaßen zu Maßen, Eindeutigkeit a) Fortsetzungssatz, Eindeutigkeit Es wird gezeigt, dass jedes Prämaß µ auf einem Ring R zu einem Maß µ auf A(R) fortgesetzt werden kann, d.h. µ kann
(b) Man nennt die Menge M beschränkt, wenn sie nach oben und unten beschränkt ist.
 8 Punktmengen Für die Menge M = { 1 n ; n N } ist 1 = max(m), denn 1 M und 1 n 1 für alle n N. Die Menge M besitzt aber kein Minimum, denn zu jeder Zahl x = 1 n M existiert ein y M mit y < x, etwa y =
8 Punktmengen Für die Menge M = { 1 n ; n N } ist 1 = max(m), denn 1 M und 1 n 1 für alle n N. Die Menge M besitzt aber kein Minimum, denn zu jeder Zahl x = 1 n M existiert ein y M mit y < x, etwa y =
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
5 Zufallsvariablen, Grundbegriffe
 II. Zufallsvariablen 5 Zufallsvariablen, Grundbegriffe Def. 12 Es seien (Ω 1, E 1,P 1 ) und (Ω 2, E 2,P 2 ) Wahrscheinlichkeitsräume. Eine Abbildung X : Ω 1 Ω 2 heißt E 1 E 2 meßbar, falls für alle Ereignisse
II. Zufallsvariablen 5 Zufallsvariablen, Grundbegriffe Def. 12 Es seien (Ω 1, E 1,P 1 ) und (Ω 2, E 2,P 2 ) Wahrscheinlichkeitsräume. Eine Abbildung X : Ω 1 Ω 2 heißt E 1 E 2 meßbar, falls für alle Ereignisse
Lemma (Eigenschaften elementarer Mengen) 1. Jede elementare Menge lässt sich als disjunkte Vereinigung halboffener Intervalle schreiben.
 12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
12.3. DIE LEBESGUE ALGEBRA 19 Bemerkung 12.3.2 (Bezeichnungen) Im Buch von Bauer [2] werden elementare Mengen als Figuren bezeichnet. Wir folgen mit unserer Nomenklatur Rudin [15]. Natürlich kann man auf
L 2 -Theorie und Plancherel-Theorem
 L -Theorie und Plancherel-Theorem Seminar Grundideen der Harmonischen Analysis bei Porf Dr Michael Struwe HS 007 Vortrag von Manuela Dübendorfer 1 Wiederholung aus der L 1 -Theorie Um die Fourier-Transformation
L -Theorie und Plancherel-Theorem Seminar Grundideen der Harmonischen Analysis bei Porf Dr Michael Struwe HS 007 Vortrag von Manuela Dübendorfer 1 Wiederholung aus der L 1 -Theorie Um die Fourier-Transformation
Nachklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
4 Absolutstetige Verteilungen und Zufallsvariablen 215/1
 4 Absolutstetige Verteilungen und Zufallsvariablen 215/1 23. Bemerkung Integralbegriffe für Funktionen f : R d R (i) Lebesgue-Integral (Vorlesung Analysis IV). Spezialfall: (ii) Uneigentliches Riemann-Integral
4 Absolutstetige Verteilungen und Zufallsvariablen 215/1 23. Bemerkung Integralbegriffe für Funktionen f : R d R (i) Lebesgue-Integral (Vorlesung Analysis IV). Spezialfall: (ii) Uneigentliches Riemann-Integral
D-ITET Analysis II FS 13 Prof. Horst Knörrer. Musterlösung 1. 3xy 2 = 2 x 2. y y. 3 y y. 3 x v x + v = 2 3 v v.
 D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. SS 6 9.4.6 Höhere Mathematik II für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. SS 6 9.4.6 Höhere Mathematik II für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe
Kompakte Operatoren in Hilberträumen
 Kompakte Operatoren in Hilberträumen 1 Vorbemerkungen Im Folgenden bezeichne H immer einen seperablen Hilbertraum über C Mit B(H 1, H 2 ) bezeichnen wir die Menge aller beschränkten linearen Operatoren
Kompakte Operatoren in Hilberträumen 1 Vorbemerkungen Im Folgenden bezeichne H immer einen seperablen Hilbertraum über C Mit B(H 1, H 2 ) bezeichnen wir die Menge aller beschränkten linearen Operatoren
Analysis III. Vorlesungsskriptum WS 2006/07. Fakultät für Mathematik, Ruhr-Universität Bochum
 Analysis III Vorlesungsskriptum WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel IX. Integralrechnung mehrerer Veränderlicher 5 IX.1. Nullmengen 5 IX.2.
Analysis III Vorlesungsskriptum WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel IX. Integralrechnung mehrerer Veränderlicher 5 IX.1. Nullmengen 5 IX.2.
Übungen zu Analysis, SS 2015
 Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
Studienbegleitende Prüfung Stochastik 2
 Universität Karlsruhe (TH) Institut für Stochastik Prof. Dr. N. Bäuerle Name: Vorname: Matr.-Nr.: Studienbegleitende Prüfung Stochastik 2 27. März 2007 Diese Klausur hat bestanden, wer mindestens 20 Punkte
Universität Karlsruhe (TH) Institut für Stochastik Prof. Dr. N. Bäuerle Name: Vorname: Matr.-Nr.: Studienbegleitende Prüfung Stochastik 2 27. März 2007 Diese Klausur hat bestanden, wer mindestens 20 Punkte
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. Michael Wolf Daniel Stilck rança Stefan Huber Zentralübung TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physiker (Analysis 3) MA924 Z3.. Polardarstellung quadratischer Matrizen
Prof. Dr. Michael Wolf Daniel Stilck rança Stefan Huber Zentralübung TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physiker (Analysis 3) MA924 Z3.. Polardarstellung quadratischer Matrizen
3. Übungsblatt - Lösungsskizzen. so, dass f tatsächlich eine Wahrscheinlichkeitsdichte
 Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
1 Die direkte Methode der Variationsrechnung
 Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Wichtige Klassen reeller Funktionen
 0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
0 Wichtige Klassen reeller Funktionen Monotone Funktionen sind i.a. unstetig, aber man kann etwas über das Grenzwertverhalten aussagen, wenn man nur einseitige Grenzwerte betrachtet. Definition 0. : Sei
Analysis 3 - Klausur - Lösung
 Wintersemester 23/24, Universität Bonn Analysis 3 - Klausur - Lösung Aufgabe : Sigma-Algebren (4+6 Punkte) a) Sei X eine Menge. Sei F = {{} : X}. Bestimmen Sie σ(f). b) Sei X eine Menge, Sei S P(X). Zeigen
Wintersemester 23/24, Universität Bonn Analysis 3 - Klausur - Lösung Aufgabe : Sigma-Algebren (4+6 Punkte) a) Sei X eine Menge. Sei F = {{} : X}. Bestimmen Sie σ(f). b) Sei X eine Menge, Sei S P(X). Zeigen
Nachklausur Analysis 2
 Nachklausur Analysis 2. a) Wie ist der Grenzwert einer Folge in einem metrischen Raum definiert? Antwort: Se (a n ) n N eine Folge in dem metrischen Raum (M, d). Diese Folge besitzt den Grenzwert g M,
Nachklausur Analysis 2. a) Wie ist der Grenzwert einer Folge in einem metrischen Raum definiert? Antwort: Se (a n ) n N eine Folge in dem metrischen Raum (M, d). Diese Folge besitzt den Grenzwert g M,
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
KLAUSUR. Analysis (E-Technik/Mechatronik/W-Ing) Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf
 KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
Differentialgleichungen und Hilberträume Sommersemester 2014 Übungsblatt 11
 Institut für Analysis Prof. Dr. Wolfgang Reichel Dipl.-Math. Anton Verbitsky Aufgabe 1 Differentialgleichungen und Hilberträume Sommersemester 14 Übungsblatt 11 5 Punkte In dieser Aufgabe geht es um die
Institut für Analysis Prof. Dr. Wolfgang Reichel Dipl.-Math. Anton Verbitsky Aufgabe 1 Differentialgleichungen und Hilberträume Sommersemester 14 Übungsblatt 11 5 Punkte In dieser Aufgabe geht es um die
Stoppzeiten und Charakteristische Funktionen. Tutorium Stochastische Prozesse 15. November 2016
 Stoppzeiten und Charakteristische Funktionen Tutorium Stochastische Prozesse 15. November 2016 Inhalte des heutigen Tutoriums Im heutigen Tutorium besprechen wir: (1) Eindeutigkeit von Maßen ohne schnittstabilen
Stoppzeiten und Charakteristische Funktionen Tutorium Stochastische Prozesse 15. November 2016 Inhalte des heutigen Tutoriums Im heutigen Tutorium besprechen wir: (1) Eindeutigkeit von Maßen ohne schnittstabilen
Beispiele. Grundlagen. Kompakte Operatoren. Regularisierungsoperatoren
 Beispiele Grundlagen Kompakte Operatoren Regularisierungsoperatoren Transportgleichung Dierenzieren ( nx ) (f δ n ) (x) = f (x) + n cos, x [0, 1], δ Regularisierung!! Inverse Wärmeleitung Durc f (f δ n
Beispiele Grundlagen Kompakte Operatoren Regularisierungsoperatoren Transportgleichung Dierenzieren ( nx ) (f δ n ) (x) = f (x) + n cos, x [0, 1], δ Regularisierung!! Inverse Wärmeleitung Durc f (f δ n
Lösungsvorschlag zur Klausur
 FAKULTÄT FÜ MATHEMATIK Prof. Dr. Patrizio Neff Frank Osterbrink Johannes Lankeit 27.7.23 Lösungsvorschlag zur Klausur Hinweise zur Bearbeitung: - Die Bearbeitungszeit für die Klausur beträgt 8 Minuten.
FAKULTÄT FÜ MATHEMATIK Prof. Dr. Patrizio Neff Frank Osterbrink Johannes Lankeit 27.7.23 Lösungsvorschlag zur Klausur Hinweise zur Bearbeitung: - Die Bearbeitungszeit für die Klausur beträgt 8 Minuten.
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH, D-PHYS, D-CHAB Analysis II FS 2018 Prof. Manfred Einsiedler. Lösung 11
 D-MATH, D-PHYS, D-CHAB Analysis II FS 218 Prof. Manfred Einsiedler Lösung 11 Hinweise 1. Kehren Sie die Integrationsreihenfolge um. Um dabei die korrekten Grenzen zu finden, skizzieren Sie den Integrationsbereich.
D-MATH, D-PHYS, D-CHAB Analysis II FS 218 Prof. Manfred Einsiedler Lösung 11 Hinweise 1. Kehren Sie die Integrationsreihenfolge um. Um dabei die korrekten Grenzen zu finden, skizzieren Sie den Integrationsbereich.
D-MATH Funktionalanalysis II FS 2014 Prof. M. Struwe. Lösung 2
 D-MATH Funktionalanalysis FS 214 Prof. M. Struwe Lösung 2 1. a) Wir unterscheiden zwei Fälle. Fall 1: 1 < p < : Seien u L p () und (u k ) W 1,p () eine beschränkte Folge, so dass u k u in L p () für k.
D-MATH Funktionalanalysis FS 214 Prof. M. Struwe Lösung 2 1. a) Wir unterscheiden zwei Fälle. Fall 1: 1 < p < : Seien u L p () und (u k ) W 1,p () eine beschränkte Folge, so dass u k u in L p () für k.
Erwartungswert als Integral
 Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Spektraltheorie. 9. Übungsblatt - Lösungsvorschläge. (Einiges zum stetigen Funktionalkalkül) PD Dr. Peer Kunstmann M.Sc.
 8.06.208 PD Dr. Peer Kunstmann M.Sc. Michael Ullmann Spektraltheorie 9. Übungsblatt - Lösungsvorschläge Aufgabe (Einiges zum stetigen Funktionalkalkül) Seien (H,, H ) ein Hilbertraum und T selbst-adjungiert.
8.06.208 PD Dr. Peer Kunstmann M.Sc. Michael Ullmann Spektraltheorie 9. Übungsblatt - Lösungsvorschläge Aufgabe (Einiges zum stetigen Funktionalkalkül) Seien (H,, H ) ein Hilbertraum und T selbst-adjungiert.
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
Darstellungssatz von Riesz in vollständig regulären Räumen. Carina Pöll Wintersemester 2012
 Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Spektraltheorie. 8. Übungsblatt - Lösungsvorschläge
 0606208 PD Dr Peer Kunstmann MSc Michael Ullmann Sektraltheorie 8 Übungsblatt - Lösungsvorschläge Aufgabe Nachtrag zur letzten Übung) In dieser Aufgabe wollen wir die Otimalität der Hölder-Ungleichung
0606208 PD Dr Peer Kunstmann MSc Michael Ullmann Sektraltheorie 8 Übungsblatt - Lösungsvorschläge Aufgabe Nachtrag zur letzten Übung) In dieser Aufgabe wollen wir die Otimalität der Hölder-Ungleichung
53 Die Parsevalsche Gleichung
 53 Die Parsevalsche Gleichung 53 Die Parsevalsche Gleichung 5 53. Skalarprodukte auf Räumen quadratintegrierbarer Funktionen. a) Die Orthogonalitätsrelationen (5.5) legen die Interpretation des Ausdrucks
53 Die Parsevalsche Gleichung 53 Die Parsevalsche Gleichung 5 53. Skalarprodukte auf Räumen quadratintegrierbarer Funktionen. a) Die Orthogonalitätsrelationen (5.5) legen die Interpretation des Ausdrucks
ANALYSIS 3. Carsten Schütt WS 2008/9
 1. Es sei f : R 3 R 3 durch f 1 (r, φ 1,φ 2 ) = r cos φ 1 f 2 (r, φ 1,φ 2 ) = r sin φ 1 cos φ 2 f 3 (r, φ 1,φ 2 ) = r sin φ 1 sin φ 2 gegeben. Für welche (r, φ 1,φ 2 ) ist f lokal invertierbar? Ist f global
1. Es sei f : R 3 R 3 durch f 1 (r, φ 1,φ 2 ) = r cos φ 1 f 2 (r, φ 1,φ 2 ) = r sin φ 1 cos φ 2 f 3 (r, φ 1,φ 2 ) = r sin φ 1 sin φ 2 gegeben. Für welche (r, φ 1,φ 2 ) ist f lokal invertierbar? Ist f global
Topologie und Differentialrechnung mehrerer Veränderlicher, SS 2009 Modulprüfung/Abschlussklausur. Aufgabe Punkte
 Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Stetigkeit, Konvergenz, Topologie
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Stetigkeit, Konvergenz, Topologie 21.03.2012 Inhaltsverzeichnis 1 Stetigkeit und Konvergenz
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Stetigkeit, Konvergenz, Topologie 21.03.2012 Inhaltsverzeichnis 1 Stetigkeit und Konvergenz
Kapitel I. Maßtheorie
 Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
Aufgabenvorschläge für das Proseminar zur Maß- und Integrationstheorie (WS 10/11) Shantanu Dave & Günther Hörmann Kapitel I. Maßtheorie zu 1. Maße und σ-algebren 1 Sei Ω eine Menge. Zeige: (a) Ist A eine
6.1 Zerlegungen Ober- und Unterintegrale Existenz des Integrals
 Kapitel 6 Das Riemann-Integral In diesem Abschnitt wollen wir einen Integralbegriff einführen. Dieser Integralbegriff geht auf Riemann 1 zurück und beruht auf einer naheliegenden Anschauung. Es wird sich
Kapitel 6 Das Riemann-Integral In diesem Abschnitt wollen wir einen Integralbegriff einführen. Dieser Integralbegriff geht auf Riemann 1 zurück und beruht auf einer naheliegenden Anschauung. Es wird sich
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Übungen zur Vorlesung: Mehrdimensionale Integralrechnung, Vektoranalysis und Differentialgleichungen B.Sc. Matthias Schulte
 SoSe 17 Blatt 1 07. April 2017 Abgabe: Freitag, 14.04.2017 bis 14:00 Uhr. Persönlich oder per Mail. Aufgabe 1. [4+2 = 6 Punkte] a) Berechnen Sie folgende Integrale! 4 i) 3 7x 2 +6x 4 x 3 3x 2 dx 1 ii)
SoSe 17 Blatt 1 07. April 2017 Abgabe: Freitag, 14.04.2017 bis 14:00 Uhr. Persönlich oder per Mail. Aufgabe 1. [4+2 = 6 Punkte] a) Berechnen Sie folgende Integrale! 4 i) 3 7x 2 +6x 4 x 3 3x 2 dx 1 ii)
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Vorlesung Lineare Funktionale LINEARE FUNKTIONALE 69
 13.1. LINEARE FUNKTIONALE 69 Vorlesung 13 13.1 Lineare Funktionale Der Begriff der schwachen Konvergenz wird klarer, wenn man lineare Funktionale betrachtet. Das Skalarprodukt f, g in Hilberträumenkann
13.1. LINEARE FUNKTIONALE 69 Vorlesung 13 13.1 Lineare Funktionale Der Begriff der schwachen Konvergenz wird klarer, wenn man lineare Funktionale betrachtet. Das Skalarprodukt f, g in Hilberträumenkann
Maß- und Integrationstheorie
 Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn
Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn
