|
|
|
- Sabine Holzmann
- vor 7 Jahren
- Abrufe
Transkript
1 Statitik für Kommunikationienchaftler Winteremeter 010/011 Vorleung Prof. Dr. Nicole Krämer Übung Nicole Krämer, Cornelia Oberhauer, Monia Mahling Löung Thema 5 Homepage zur Verantaltung: Löung Aufgabe 1 (Würfelurf) Ein Würfel ird einmal georfen. E gibt ech mögliche Ergebnie, 1,, 3, 4, 5, 6, je nachdem elche Zahl auf der Obereite ercheint. Dementprechend it Ω {1,, 3, 4, 5, 6}. Wir ind an den Wahrcheinlichkeiten für die folgenden Ereignie intereiert, enn man davon augehen kann, da der Würfel einandfrei it und jede Seite mit der gleichen Wahrcheinlichkeit fällt: a) Der Würfel zeigt die Zahl 1. P ({1}) 1 6 b) Die Anzahl der Augen it nicht gerade. P ({1, 3, 5}) c) Die Augenzahl it gerade, aber nicht größer al 3. P ({, 4, 6} {1,, 3}) P ({}) 1 6 Der Würfel ei nun manipuliert orden, o da die Augenzahlen 1,, 3 nun jeeil mit Wahrcheinlichkeit 1/1 auftreten und die übrigen Augenzahlen eine Eintrittahrcheinlichkeit von 3/1 beitzen. d) Berechnen Sie erneut die Wahrcheinlichkeit für die Ereignie a)-c). a ) Der Würfel zeigt die Zahl 1. P ({1}) 1 1 b ) Die Anzahl der Augen it nicht gerade. P ({1, 3, 5}) P ({1}) + P ({3}) + P ({5}) c ) Die Augenzahl it gerade, aber nicht größer al 3. P ({, 4, 6} {1,, 3}) P ({}) 1 1 Löung Aufgabe (Ergebniraum, Ergebni, Ereigni: Werfen von Würfel und Münze) Ein Experiment betehe au dem gleichzeitigen Werfen eine fairen Würfel und einer fairen Münze. a) Geben Sie den Ergebniraum Ω an. Wieviele Elemente beitzt dieer Ω {(1, K), (, K), (3, K), (4, K), (5, K), (6, K), (1, Z), (, Z), (3, Z), (4, Z), (5, Z), (6, Z)} 1 Elemente b) Geben Sie drei beliebige Ergebnie an. A (3, K), B (, Z), C (5, Z) c) Geben Sie ein unmögliche Ereigni an. D (7, K) d) Wie groß it die Wahrcheinlichkeit de Ereignie der Würfel zeigt 5 und die Münze Kopf Anzahl güntiger Ereignie P ({(5, K)}) Anzahl möglicher Ereignie 1 1 oder über Unabhängigkeit: P (A B) P (A) P (B) P ( Würfel 5 ) 1 6 P ( Münze K ) 1 P ({ Würfel 5 } { Münze K })
2 Löung Aufgabe 3 (Ereignioperationen, Venn-Diagramm) Um ich ein Bild vom Verletzungriiko der ienchaftlichen Mitarbeiter am medizinichen Intitut zu machen, erden alle Mitarbeiter de Intitut befragt. Die 80 Peronen erden danach befragt, ob ie ich bei ihrer Arbeit chon mal verletzt haben (V : chon mal verletzt, V C : noch nie verletzt), und ob ie ihre Schutzkleidung immer getragen haben (S: Schutzkleidung immer getragen, S C : Schutzkleidung nicht immer getragen). Die Ergebnie der Befragung ind in dem folgenden Venn-Diagramm dargetellt: V S Ω 0) Ereignie definieren: V : chon mal verletzt S: Schutzkleidung immer getragen Gegenereignie: V C : noch nie verletzt S C : Schutzkleidung nicht immer getragen a) Bechreiben Sie die folgenden Ereignie verbal und ermitteln Sie die zugehörigen Anzahlen: (V S) C : noch nie verletzt und Schutzkleidung nicht immer getragen (n 35) (V S): chon mal verletzt und / aber Schutzkleidung immer getragen (n 0) S C : Schutzkleidung nicht immer getragen (n45) (V C S): noch nie verletzt und Schutzkleidung immer getragen (n 15) (V S C ): chon mal verletzt und Schutzkleidung nicht immer getragen (n 10) b) Wie groß it die Wahrcheinlichkeit, da eine zufällig gezogene Peron ihre Schutzkleidung immer getragen hat und ich chon mal bei ihrer Arbeit verletzt hat P (V S)
3 Löung Aufgabe 4 (Ergebniraum, Ereigni, Unabhängigkeit) Jemand irft eine faire Münze dreimal hintereinander. a) Geben Sie einen geeigneten Ergebniraum Ω an. Wieviele Elemente hat dieer Ω {(K; K; K), (K; K; Z), (K; Z; K), (K; Z; Z), (Z; Z; Z), (Z; Z; K), (Z; K; Z), (Z; K; K)} 3 8 mögliche Ergebnie [alle gleich ahrcheinlich Laplace-Wahrcheinlichkeitdefinition zur Berechnung der Wahrcheinlichkeiten] b) Geben Sie die zu dem Ereigni E fällt genau zeimal Kopf gehörige Teilmenge A an und berechnen Sie P (A). A: E fällt genau zeimal Kopf. A {(K; K; Z), (K; Z; K), (Z; K; K)} Ω [A it eine Teilmenge der Ergebniraume A it ein Ereigni] P (A) Zahl der güntigen Fälle Zahl aller (gleich) möglichen Fälle 3 8 Betrachten Sie nun zuätzlich da Ereigni B: E fällt genau zeimal Zahl. c) Sind die beiden Ereignie A und B dijunkt B: E fällt genau zeimal Zahl. B {(Z; Z; K), (Z; K; Z), (K; Z; Z)} Zei Ereignie A und B ind dijunkt, enn A B, d.h. enn die Schnittmenge leer it (bz. enn ie keine gemeinamen Elemente aufeien). Hier: A B A und B ind dijunkt d) Geben Sie die Ereignie (A B) und (A B) in Worten ieder und berechnen Sie die zugehörigen Wahrcheinlichkeiten. A B: zeimal Kopf und zeimal Zahl P (A B) P ( ) 1 P (Ω) 0 unmögliche Ereigni A B: zeimal Kopf oder zeimal Zahl P (A B) P (A) + P (B) (Übergang zum Gegenereigni) (A und B dijunkt Axiom der Additivität) 3
4 Betrachten Sie nun noch da Ereigni C: E fällt mindeten einmal Zahl. e) Sind die beiden Ereignie A und C dijunkt C: E fällt mindeten einmal Zahl. C {(K; K; Z), (K; Z; K), (K; Z; Z), (Z; Z; Z), (Z; Z; K), (Z; K; Z), (Z; K; K)} [Zei Ereignie A und B ind dijunkt, enn A B, d.h. enn die Schnittmenge leer it.] Gibt e gemeiname Ergebnie Hier: A C {(K; K; Z), (K; Z; K), (Z; K; K)} e gibt gemeiname Ergebnie A und C ind nicht dijunkt f) Geben Sie die Ereignie (A C) und (A C) in Worten ieder und berechnen Sie die zugehörigen Wahrcheinlichkeiten. A C: zeimal Kopf und mindeten einmal Zahl P (A C) 3 8 [ P (A)] A C: zeimal Kopf oder mindeten einmal Zahl P (A C) P (A) + P (C) P (A C) (Additionatz) g) Sind A und C unabhängig Definition: A und C ind unabhängig, enn P (A C) P (A) und P (C A) P (C) oder P (A C) P (A) P (C) P (A C) 3 8 P (A) P (C) A und C ind nicht unabhängig 4
5 Löung Aufgabe 5 (Bedingte Wahrcheinlichkeit und Unabhängigkeit) Ein fairer Würfel erde einmal georfen. Betrachten Sie dazu folgende Ereignie: A: E ird die Zahl 1 geürfelt. B: E ird die Zahl oder 3 geürfelt. C: E ird eine Zahl größer al 3 geürfelt. Der Würfel ird o georfen, da Sie da Ergebni nicht ehen können. Eine andere Peron konnte da Ergebni jedoch ehen und verrät Ihnen, da eine gerade Zahl geürfelt urde (Ereigni D). 0) Ereignie definieren A{1} B{, 3} C{4, 5, 6} D{, 4, 6} a) Zeichnen Sie alle vier Ereignie in ein Venn-Diagramm ein. b) Berechnen Sie die bedingten Wahrcheinlichkeiten der Ereignie A, B und C, jeeil bedingt auf D. Wa fällt Ihnen auf P (A D) P (A D) P (D) 0 3/6 0 P (B D) P (B D) P (D) 1/6 3/6 1/3 P (C D) P (C D) P (D) /6 3/6 /3 Die Summe der bedingten Wahrcheinlichkeiten it 1. c) Sind die Ereignie A, B und C jeeil von D tochatich unabhängig P (A D) 0 P (A) P (D) P (A D) P (A) P (D) A und D ind tochatich abhängig P (B D) 1 6 P (B) P (D) P (B D) P (B) P (D) B und D ind tochatich unabhängig P (C D) P (C) P (D) P (C D) P (C) P (D) C und D ind tochatich abhängig 5
6 Löung Aufgabe 6 (Unabhängigkeit) Unter einer Gruppe von 60 feiernden Studenten ind 15 Fußballfan. Die Hälfte aller Aneenden ind Germanitik-Studenten mit einem Hang zur Poeie. Beide Eigenchaften eien unabhängig voneinander. Wir betrachten alo hier die beiden Ereignie: F: Die Peron it Fußballfan. P: Die Peron it ein Poet. Ich uche mir an dieem Abend genau eine(n) GeprächpartnerIn zufällig au: 0) Wahrcheinlichkeiten au der Angabe P (F ) P (F C ) 1 P (F ) P (P ) P (P C ) 1 P (P ) a) Mit elcher Wahrcheinlichkeit mu ich mir die chönten Momente der vergangenen Fußball- Saion in Reimform anhören (P (F P )) P (F P ) P (F ) P (P ) (Unabhängigkeit) , 15 8 b) Mit elcher Wahrcheinlichkeit mu ich mich den ganzen Abend über Fußball unterhalten, dafür aber unter keiner poetichen Darbietung leiden (P (F P C )) P (F P C ) P (F ) P (P C ) (Unabhängigkeit) , 15 8 [Wenn F und P unabhängig ind, dann ind auch alle Kombinationen von F, F C mit P, P C unabhängig.] c) Mit elcher Wahrcheinlichkeit kann ich mich gut amüieren (P (F C P C )) P (F C P C ) P (F C ) P (P C ) (Unabhängigkeit) , [Wenn F und P unabhängig ind, dann ind auch alle Kombinationen von F, F C mit P, P C unabhängig.] 6
7 Löung Aufgabe 7 (Wahrcheinlichkeitbaum, bedingte Wahrcheinlichkeiten) Wir betrachten folgende Experiment: Au einer Urne mit drei eißen und drei charzen Kugeln ird dreimal gezogen. Jede Kugel, die gezogen ird, oll nicht mehr in die Urne zurückgelegt erden ( Ziehen ohne Zurücklegen ), o da nach dreimaligem Ziehen nur noch 3 Kugeln in der Urne verbleiben. Der Wahrcheinlichkeitbaum in Abbildung 1 gibt an, ie ich die Auahlahrcheinlichkeit für eine betimmte Farbe im Laufe der dreimaligen Ziehung verändert. 1. Ziehung. Ziehung 3. Ziehung Abbildung 1: Wahrcheinlichkeitbaum zu Aufgabe 7 0) [Wahrcheinlichkeiten ändern ich von Ziehung zu Ziehung, da ohne Zurücklegen gezogen ird.] [Bedingte Wahrcheinlichkeit: Wahrcheinlichkeit für eine betimmte Farbe hängt (ab dem. Zug) von der / den voraugegangenen Ziehungen ab] a) Bechreiben Sie einen beliebigen Pfad (von ganz link nach ganz recht) mit Ihren eigenen Worten. Beipiel: 1. Ziehung: au Urne mit 3 und 3. Ziehung: au Urne mit und 3 3. Ziehung: au Urne mit und 7
8 b) Bechreiben Sie da Ereigni, zu dem die umrandete Wahrcheinlichkeit gehört, mit eigenen Worten. Bei der. Ziehung ird eine eiße Kugel au einer Urne mit 3 und Kugeln gezogen. Im voraugegangenen Zug urde bereit eine charze Kugel gezogen. c) An elchen Stellen müen ich Wahrcheinlichkeiten jeeil immer zu 1 aufummieren Wahrcheinlichkeiten für Kanten (hier Verbindunglinien), die einen gemeinamen Knoten (hier dargetellt durch eine Kugel) haben, ummieren ich zu 1. d) Setzen Sie die richtigen Wahrcheinlichkeiten ein, o jetzt noch Fragezeichen tehen. Alle folgt au c) bi auf: P (3. Ziehung 1. Ziehung und. Ziehung ) P (Ziehe au Urne mit 1 und 3 ) 1 4 e) Berechnen Sie die Wahrcheinlichkeit beim erten Ziehen eine charze und beim zeiten und dritten Mal jeeil eine eiße Kugel zu erhalten. P ({(; ; )}) P (1. Ziehung ) P (. Ziehung 1. Ziehung ) alo einfach am Pfad entlang multiplizieren P (3. Ziehung. Ziehung und 1. Ziehung ) , 15 0 f) Berechnen Sie die Wahrcheinlichkeit eine charze und zei eiße Kugeln zu ziehen. Wieo untercheidet ich Ihr Ergebni von dem in Teilaufgabe e) F : 1 und Kugeln ziehen F {(; ; ), (; ; ), (; ; )} P (F ) P ({(; ; )} {(; ; )} {(; ; )}) P ({(; ; )}) + P ({(; ; )}) + P ({(; ; )}) (Ereignie dijunkt) , 45 Da Ergebni untercheidet ich von dem in e), da hier die Reihenfolge der gezogenen Kugeln egal it. Hier 3 Möglichkeiten gegenüber von einer Möglichkeit in e) Wahrcheinlichkeit größer 8
9 Löung Aufgabe 8 (Wahrcheinlichkeitbaum, Satz von der totalen Wahrcheinlichkeit, Satz von Baye) Gegeben ei eine Urne mit einer charzen und zei roten Kugeln. Wir betrachten die Ereignie R: e ird eine rote Kugel gezogen und S: e ird eine charze Kugel gezogen. E erde nun dreimal au dieer Urne ohne Zurücklegen gezogen - die Urne it alo nach dem letzten Zug leer. 0) Ereignie definieren: R: e ird eine rote Kugel gezogen S: e ird eine charze Kugel gezogen a) Zeichnen Sie hierzu den zugehörigen Wahrcheinlichkeitbaum. b) Wie groß it die Wahrcheinlichkeit im zeiten Zug eine rote Kugel zu ziehen Die Wahrcheinlichkeiten kann man im linken und rechten At ableen, dort teht im. Zug jeeil ein R. P (. Zug R ) P ({(S, R)}) + P ({(R, R)}) P ( 1. Zug S ) P (. Zug R 1. Zug S ) + (Satz von der +P ( 1. Zug R ) P (. Zug R 1. Zug R ) totalen Wahrcheinlichkeit) c) Angenommen e urde im zeiten Zug eine rote Kugel gezogen. Mit elcher Wahrcheinlichkeit urde im erten Zug ebenfall eine rote Kugel gezogen Die Wahrcheinlichkeit lät ich über den Satz von Baye berechnen. Dabei findet da Ergebni der Aufgabe b) (P (. Zug R ) 3 ) Verendung: P ( 1. Zug R. Zug R ) P ( 1. Zug R. Zug R ) (Satz von Baye) P (. Zug R ) P ( 1. Zug R ) P (. Zug R 1. Zug R ) P (. Zug R )
10 Löung Aufgabe 9 (Wahrcheinlichkeitbaum, Satz von der totalen Wahrcheinlichkeit, Satz von Baye) Ein Taxifahrer hat Fahrerflucht begangen. Ein Zeuge hat den Wagen al blau identifiziert. In der Stadt arbeiten nur zei Taxifirmen, die Grünen und die Blauen : 85 Prozent der Taxi ind grün, 15 Prozent blau. Ein Tet ergibt, da der Zeuge die Taxifarbe in 80 Prozent aller Fälle richtig identifiziert. 0) Ereignie definieren: - G: grüne Taxi - B: blaue Taxi - ZG: Zeuge agt, er habe ein grüne Taxi geehen - ZB: Zeuge agt, er habe ein blaue Taxi geehen a) Zeichnen Sie den zugehörigen Wahrcheinlichkeitbaum. Tipp: Gehen Sie dabei von einer Population von 100 Taxi au und berechnen Sie zunächt die zugehörigen (aboluten) Anzahlen von blauen Taxi, die korrekt al blau identifiziert urden bz. fälchlichereie al grün, und dann die Anzahlen der grünen Taxi, die korrekt al grün bz. fälchlichereie al blau identifiziert urden. Tragen Sie dann antelle der Wahrcheinlichkeiten die aboluten Häufigkeiten der Ereignie tatächliche Autofarbe (blau, grün) und vom Zeugen identifizierte Farbe (blau, grün) in den Baum ein. Wahrcheinlichkeitbaum: b) Wie hoch it die Wahrcheinlichkeit, da da Taxi, mit dem die Fahrerflucht begangen urde, blau ar, enn berückichtigt ird, da der Zeuge den Wagen al blau identifiziert hat P (B ZB) P (B ZB) P (ZB) (Satz von Baye) P (ZB B) P (B) P (ZB B) P (B) + P (ZB G) P (G) (Satz von der totalen Wahrcheinlichkeit) 0, 8 0, 15 0, 8 0, , 0, 85 0, 1 0, 1 0, , 4% 0, 1 + 0, 17 0, , 4% 9 (alternativ: Werte direkt au Baum ableen) c) Wie erklären Sie ich da Ergebni Der Zeuge hat doch mit 80-prozentiger Wahrcheinlichkeit ein blaue Taxi identifiziert. Bei der bedingten Wahrcheinlichkeit geht mit ein, da e nur eine Minderheit an blauen Taxi in der Stadt gibt, nämlich nur 15%. Hätte man hier keine Zeugenauage gehabt, ürde man ogar nur mit 15%iger Wahrcheinlichkeit ein blaue Taxi verdächtigen. (Beipiel enttammt: Focu Nr. 17, , S. 114 und urde von Nobelpreiträger Daniel Kahneman erdacht.) 10
11 Löung Aufgabe 10 (Bedingte Wahrcheinlichkeiten, Satz von Baye) Ein Laboratorium hat einen Alkohol-Tet entorfen. Au den biherigen Erfahrungen eiß man, da 60% der von der Polizei kontrollierten Peronen tatächlich betrunken ind. Bezüglich der Funktioneie de Tet urde ermittelt, da - in 95% der Fälle der Tet poitiv reagiert, enn die Peron tatächlich betrunken it, - in 97% der Fälle der Tet negativ reagiert, enn die Peron nicht betrunken it. Ereignie definieren: - B+: Peron it betrunken - T +: Tet it poitiv - B : Peron it nicht betrunken - T : Tet it negativ Wahrcheinlichkeiten au der Angabe: - P (B+) 0, 6 P (B ) 1 P (B+) 1 0, 6 0, 4 - P (T + B+) 0, 95 P (T B+) 1 P (T + B+) 1 0, 95 0, 05 - P (T B ) 0, 97 P (T + B ) 1 P (T B ) 1 0, 97 0, 03 a) Wie groß it die Wahrcheinlichkeit, da eine Peron betrunken it, enn der Tet poitiv reagiert Satz von Baye P (B + T +) P (B + T +) P (T +) P (T + B+) P (B+) P (T + B+) P (B+) + P (T + B ) P (B ) 0, 95 0, 6 0, 95 0, 6 + 0, 03 0, 4 0, 57 0, 979 0, 58 Da heißt, man kann bei einem poitiven Tetergebni mit einer Wahrcheinlichkeit von 97, 9% davon augehen, da die Peron tatächlich betrunken it. b) Angenommen, nur 10% (tatt 60%) der von der Polizei kontrollierten Peronen ind tatächlich betrunken. Wie groß it dann die Wahrcheinlichkeit, da eine Peron betrunken it, enn der Tet poitiv reagiert Veränderte Angabe: P (B+) 0, 1 P (B ) 0, 9 Satz von Baye P (B + T +) P (B + T +) P (T +) P (T + B+) P (B+) P (T + B+) P (B+) + P (T + B ) P (B ) 0, 95 0, 1 0, 95 0, 1 + 0, 03 0, 9 0, 095 0, 779 0, 1 Da heißt, man kann bei einem poitiven Tetergebni jetzt nur noch mit einer Wahrcheinlichkeit von 77, 9% davon augehen, da die Peron tatächlich betrunken it. 11
a) Geben Sie einen geeigneten Ergebnisraum Ω an. Wieviele Elemente hat dieser?
 Statitik für Kommunikationienchaftler Sommeremeter 008 Vorleung Prof. Dr. Helmut Küchenhoff Übung Cornelia Oberhauer, Manuel Wieenfarth, Monia Mahling Löung Thema 3 Homepage zur Verantaltung: http://.tatitik.lmu.de/~helmut/k08.html
Statitik für Kommunikationienchaftler Sommeremeter 008 Vorleung Prof. Dr. Helmut Küchenhoff Übung Cornelia Oberhauer, Manuel Wieenfarth, Monia Mahling Löung Thema 3 Homepage zur Verantaltung: http://.tatitik.lmu.de/~helmut/k08.html
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 1 - Lösungen
 1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
Vier-Felder-Tafel. Medizinische Tests sind grundsätzlich mit zwei Fehlern behaftet: 1. Erkrankte werden als gesund, 2. Gesunde als krank eingestuft.
 Vier-Felder-Tafel Mediziniche Tet ind grundätzlich mit zwei Fehlern behaftet:. Erkrankte werden al geund, 2. Geunde al krank eingetuft. Der. Fehler wird üblicherweie (nicht nur von Tet-Entwicklern) in
Vier-Felder-Tafel Mediziniche Tet ind grundätzlich mit zwei Fehlern behaftet:. Erkrankte werden al geund, 2. Geunde al krank eingetuft. Der. Fehler wird üblicherweie (nicht nur von Tet-Entwicklern) in
Figurierte Zahlen, Urnen und Kugelfarben
 Figurierte Zahlen, Urnen und Kugelfarben KLAUS-ULRICH UDER, Lüneburg HANS HUMENBERER und BERTHOLD SCHUPPAR, Dortmund Zuammenfaung: Bei einem elementaren tochatichen Problem (Ziehung von zei Kugeln au einer
Figurierte Zahlen, Urnen und Kugelfarben KLAUS-ULRICH UDER, Lüneburg HANS HUMENBERER und BERTHOLD SCHUPPAR, Dortmund Zuammenfaung: Bei einem elementaren tochatichen Problem (Ziehung von zei Kugeln au einer
Lösungen I.1. 21/3 = {AA, ABA, ABB, BB, BAB, BAA} (A bzw. B steht für Person A bzw. Person B hat Satz gewonnen )
 Löungen I.1 a) Gundbegiffe 161/1a = {0; 1;...; 9} latt/1 jede mögliche ugang eine Zufallexpeiment daf im Egebniaum nu einmal vokommen (eindeutige Zuodnung); hie gehöt abe z.. de ugang 2 geüfelt oohl zu
Löungen I.1 a) Gundbegiffe 161/1a = {0; 1;...; 9} latt/1 jede mögliche ugang eine Zufallexpeiment daf im Egebniaum nu einmal vokommen (eindeutige Zuodnung); hie gehöt abe z.. de ugang 2 geüfelt oohl zu
Stochastik (Laplace-Formel)
 Stochastik (Laplace-Formel) Übungen Spielwürfel oder Münzen werden ideal (oder fair) genannt, wenn jedes Einzelereignis mit gleicher Wahrscheinlichkeit erwartet werden kann. 1. Ein idealer Spielwürfel
Stochastik (Laplace-Formel) Übungen Spielwürfel oder Münzen werden ideal (oder fair) genannt, wenn jedes Einzelereignis mit gleicher Wahrscheinlichkeit erwartet werden kann. 1. Ein idealer Spielwürfel
Wahrscheinlichkeitsrechnung
 Wahrscheinlichkeitsrechnung Grundbegriffe: Experiment: ein Vorgang, den man unter gleichen Voraussatzungen beliebig oft wiederholen kann. Ergebnis ω : Ausgang eines Experiments Ergebnismenge Ω : Menge
Wahrscheinlichkeitsrechnung Grundbegriffe: Experiment: ein Vorgang, den man unter gleichen Voraussatzungen beliebig oft wiederholen kann. Ergebnis ω : Ausgang eines Experiments Ergebnismenge Ω : Menge
Benutzerhinweise für den PU Bayes-Korrektor V1.0
 PU Dipl.-Kfm. Jörg Petermann Unternehmenberatung Benutzerhinweie für den PU Bae-Korrektor V1.0 Trier, 20. Juli 2007 1 Bae' Theorem Die Wahrcheinlichkeitrechnung hält immer wieder Überrachungen bereit.
PU Dipl.-Kfm. Jörg Petermann Unternehmenberatung Benutzerhinweie für den PU Bae-Korrektor V1.0 Trier, 20. Juli 2007 1 Bae' Theorem Die Wahrcheinlichkeitrechnung hält immer wieder Überrachungen bereit.
UE Statistik 1, SS 2015, letztes Update am 5. März Übungsbeispiele
 UE Statistik, SS 05, letztes Update am 5. März 05 Übungsbeispiele Beispiele mit Musterlösungen finden Sie auch in dem Buch Brannath, W., Futschik, A., Krall, C., (00) Statistik im Studium der Wirtschaftswissenschaften..
UE Statistik, SS 05, letztes Update am 5. März 05 Übungsbeispiele Beispiele mit Musterlösungen finden Sie auch in dem Buch Brannath, W., Futschik, A., Krall, C., (00) Statistik im Studium der Wirtschaftswissenschaften..
2.2 Ereignisse und deren Wahrscheinlichkeit
 2.2 Ereignisse und deren Wahrscheinlichkeit Literatur: [Papula Bd., Kap. II.2 und II.], [Benning, Kap. ], [Bronstein et al., Kap. 1.2.1] Def 1 [Benning] Ein Zufallsexperiment ist ein beliebig oft wiederholbarer,
2.2 Ereignisse und deren Wahrscheinlichkeit Literatur: [Papula Bd., Kap. II.2 und II.], [Benning, Kap. ], [Bronstein et al., Kap. 1.2.1] Def 1 [Benning] Ein Zufallsexperiment ist ein beliebig oft wiederholbarer,
Unabhängigkeit KAPITEL 4
 KAPITEL 4 Unabhängigkeit 4.1. Unabhängigkeit von Ereignissen Wir stellen uns vor, dass zwei Personen jeweils eine Münze werfen. In vielen Fällen kann man annehmen, dass die eine Münze die andere nicht
KAPITEL 4 Unabhängigkeit 4.1. Unabhängigkeit von Ereignissen Wir stellen uns vor, dass zwei Personen jeweils eine Münze werfen. In vielen Fällen kann man annehmen, dass die eine Münze die andere nicht
ÜBUNG: ZUFALLSEREIGNISSE, BAUMDARSTELLUNGEN
 ÜBUNG: ZUFALLSEREIGNISSE, BAUMDARSTELLUNGEN Resultate auf zwei Stellen nach dem Komma runden. 1. Auf einer Speisekarte gibt es 3 Vorspeisen, 5 Hauptspeisen und 2 verschiedene Desserts. Wie viele verschiedene
ÜBUNG: ZUFALLSEREIGNISSE, BAUMDARSTELLUNGEN Resultate auf zwei Stellen nach dem Komma runden. 1. Auf einer Speisekarte gibt es 3 Vorspeisen, 5 Hauptspeisen und 2 verschiedene Desserts. Wie viele verschiedene
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
 Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Korrekturanweisungen für die Mathematikaufgaben 2009
 Korrekturaneiungen für die Mathematikaufgaben 2009 Erläuterungen zu den Korrekturaneiungen Die Korrekturaneiungen ermöglichen eine eindeutige Klaifikation der Schülerantorten in richtig und und damit eine
Korrekturaneiungen für die Mathematikaufgaben 2009 Erläuterungen zu den Korrekturaneiungen Die Korrekturaneiungen ermöglichen eine eindeutige Klaifikation der Schülerantorten in richtig und und damit eine
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datentrukturen Prof. Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Sommeremeter H. Täubig
Grundlagen: Algorithmen und Datentrukturen Prof. Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Sommeremeter H. Täubig
Stochastik - Kapitel 2
 " k " h(a) n = bezeichnet man als die relative Häufigkeit des Ereignisses A bei n Versuchen. n (Anmerkung: für das kleine h wird in der Literatur häufig auch ein r verwendet) k nennt man die absolute Häufigkeit
" k " h(a) n = bezeichnet man als die relative Häufigkeit des Ereignisses A bei n Versuchen. n (Anmerkung: für das kleine h wird in der Literatur häufig auch ein r verwendet) k nennt man die absolute Häufigkeit
5 Die Poisson-Approximation
 5 Die Poion-Approximation Im vierten Kapitel hatten wir mit der Normalverteilung die icherlich wichtigte und meittudierte Verteilung der W.-Theorie kennengelernt und geehen, daß man diee al Lime eine geeignet
5 Die Poion-Approximation Im vierten Kapitel hatten wir mit der Normalverteilung die icherlich wichtigte und meittudierte Verteilung der W.-Theorie kennengelernt und geehen, daß man diee al Lime eine geeignet
Aufgabe 1. Übung Wahrscheinlichkeitsrechnung Markus Kessler Seite 1 von 8. Die Ereignisse A, B und C erfüllen die Bedingungen
 Ü b u n g 1 Aufgabe 1 Die Ereignisse A, B und C erfüllen die Bedingungen P(A) = 0. 7, P(B) = 0. 6, P(C) = 0. 5 P(A B) = 0. 4, P(A C) = 0. 3, P(B C) = 0. 2, P(A B C) = 0. 1 Bestimmen Sie P(A B), P(A C),
Ü b u n g 1 Aufgabe 1 Die Ereignisse A, B und C erfüllen die Bedingungen P(A) = 0. 7, P(B) = 0. 6, P(C) = 0. 5 P(A B) = 0. 4, P(A C) = 0. 3, P(B C) = 0. 2, P(A B C) = 0. 1 Bestimmen Sie P(A B), P(A C),
Lösungsvorschlag. Qq r 2 F C = 1
 Löungvorchlag 1. Zunächt zwei Skizzen zur Verdeutlichung der Situation: Link it da Kügelchen mit der Ladung q zu ehen. Recht it die Kugel mit der Ladung Q 1 µc an die Stelle de Kügelchen gebracht worden.
Löungvorchlag 1. Zunächt zwei Skizzen zur Verdeutlichung der Situation: Link it da Kügelchen mit der Ladung q zu ehen. Recht it die Kugel mit der Ladung Q 1 µc an die Stelle de Kügelchen gebracht worden.
1 Grundlagen Wahrscheinlichkeitsrechung
 1 Grundlagen Wahrscheinlichkeitsrechung 1.1 Grundbegriffe Alle möglichen Ereignisse eines Zufallsexperiments fassen wir in einer Ereignismenge Ω zusammen. Ereignisse sind Teilmengen von Ω. Umfasst das
1 Grundlagen Wahrscheinlichkeitsrechung 1.1 Grundbegriffe Alle möglichen Ereignisse eines Zufallsexperiments fassen wir in einer Ereignismenge Ω zusammen. Ereignisse sind Teilmengen von Ω. Umfasst das
Zusammenfassung Stochastik
 Zusammenfassung Stochastik Die relative Häufigkeit Ein Experiment, dessen Ausgang nicht vorhersagbar ist, heißt Zufallsexperiment (ZE). Ein Würfel wird 40-mal geworfen, mit folgendem Ergebnis Augenzahl
Zusammenfassung Stochastik Die relative Häufigkeit Ein Experiment, dessen Ausgang nicht vorhersagbar ist, heißt Zufallsexperiment (ZE). Ein Würfel wird 40-mal geworfen, mit folgendem Ergebnis Augenzahl
Grundwissen 9. Jahrgangsstufe Mathematik. Wissen / Können Beispiele. 1. Reelle Zahlen, Wurzeln und Potenzen
 Grundwien 9. Jahrgangtufe Mathematik Wien / Können Beiiele. Reelle Zahlen, Wureln und Potenen Die Menge der reellen Zahlen beteht au der Menge der rationalen Zahlen und der Menge der irrationalen Zahlen.
Grundwien 9. Jahrgangtufe Mathematik Wien / Können Beiiele. Reelle Zahlen, Wureln und Potenen Die Menge der reellen Zahlen beteht au der Menge der rationalen Zahlen und der Menge der irrationalen Zahlen.
Übungen zur Vorlesung PN1 Lösung Übungsblatt 12 Besprechung am
 Übungen zur Vorleung PN1 Löung Übungblatt 12 Beprechung am 22.1.2013 Aufgabe 1: Gedämpfte Schwingung An einer Feder mit der Federhärte 20 N/m hängt eine Kugel der Mae 100g. Die Kugel wird um 10 cm nach
Übungen zur Vorleung PN1 Löung Übungblatt 12 Beprechung am 22.1.2013 Aufgabe 1: Gedämpfte Schwingung An einer Feder mit der Federhärte 20 N/m hängt eine Kugel der Mae 100g. Die Kugel wird um 10 cm nach
Dr. Jürgen Senger INDUKTIVE STATISTIK. Wahrscheinlichkeitstheorie, Schätz- und Testverfahren. 1. Zweimaliges Ziehen aus einer Urne (ohne Zurücklegen)
 Dr. Jürgen Senger INDUKTIVE STATISTIK Wahrscheinlichkeitstheorie, Schätz- und Testverfahren ÜUNG. - LÖSUNGEN. Zweimaliges Ziehen aus einer Urne (ohne Zurücklegen Die Urne enthält 4 weiße und 8 rote Kugeln.
Dr. Jürgen Senger INDUKTIVE STATISTIK Wahrscheinlichkeitstheorie, Schätz- und Testverfahren ÜUNG. - LÖSUNGEN. Zweimaliges Ziehen aus einer Urne (ohne Zurücklegen Die Urne enthält 4 weiße und 8 rote Kugeln.
Tag der Mathematik 2016
 Tag der Mathematik 016 Mathematischer Wettbeerb, Klassenstufe 11 1/13 30. April 016, 9.00 1.00 Uhr Aufgabe 1 Zeigt: Die Funktion f : R R, f(x) x, kann nicht als Summe von zei periodischen Funktionen geschrieben
Tag der Mathematik 016 Mathematischer Wettbeerb, Klassenstufe 11 1/13 30. April 016, 9.00 1.00 Uhr Aufgabe 1 Zeigt: Die Funktion f : R R, f(x) x, kann nicht als Summe von zei periodischen Funktionen geschrieben
Prof. Liedl Lösung Blatt 8. Übungen zur Vorlesung PN1. Lösung zum Übungsblatt 8. Besprochen am
 11.12.212 Löung Blatt 8 Übungen zur Vorleung PN1 Löung zum Übungblatt 8 Beprochen am 11.12.212 Aufgabe 1: Moleküle al tarre rotierende Körper Durch Mikrowellen laen ich Rotationen von Molekülen mit einem
11.12.212 Löung Blatt 8 Übungen zur Vorleung PN1 Löung zum Übungblatt 8 Beprochen am 11.12.212 Aufgabe 1: Moleküle al tarre rotierende Körper Durch Mikrowellen laen ich Rotationen von Molekülen mit einem
P A P( A B) Definition Wahrscheinlichkeit
 Unabhaengige Ereignisse edingte Wahrscheinlichkeit Definition Wahrscheinlichkeit Die Wahrscheinlichkeit eines Ereignisses ist das Verhältnis der günstigen Ergebnisse zur Gesamtmenge der Ergebnisse nzahl
Unabhaengige Ereignisse edingte Wahrscheinlichkeit Definition Wahrscheinlichkeit Die Wahrscheinlichkeit eines Ereignisses ist das Verhältnis der günstigen Ergebnisse zur Gesamtmenge der Ergebnisse nzahl
für eine rote Kugel denn von auf den 100% (da rot, rot rot, blau blau, rot blau, blau
 Berechnung von Wahrscheinlichkeiten beim Ziehen mit und ohne Zurücklegenn Ziehen mit Zurücklegenn Wir betrachten folgendes Beispiel: In einer Urne sind 2 rote und 3 blaue Kugeln.. Wenn man hier eine Kugel
Berechnung von Wahrscheinlichkeiten beim Ziehen mit und ohne Zurücklegenn Ziehen mit Zurücklegenn Wir betrachten folgendes Beispiel: In einer Urne sind 2 rote und 3 blaue Kugeln.. Wenn man hier eine Kugel
Prof. Dr. Holger Dette Musterlösung Statistik I Sommersemester 2009 Dr. Melanie Birke Blatt 9
 Prof r Holger ette Muterlöung Statitik I Sommeremeter 009 r Melanie Birke Blatt 9 Aufgabe : 4 Punkte E eien X,, X n unabhängig identich N µ, -verteilt a Man berechne die Fiher-Information I µ für µ b E
Prof r Holger ette Muterlöung Statitik I Sommeremeter 009 r Melanie Birke Blatt 9 Aufgabe : 4 Punkte E eien X,, X n unabhängig identich N µ, -verteilt a Man berechne die Fiher-Information I µ für µ b E
Technische Universität München SS 2006 Zentrum Mathematik Blatt 7 Prof. Dr. J. Hartl Dr. Hannes Petermeier Dr. Cornelia Eder Dipl.-Ing.
 Technische Universität München SS 2006 Zentrum Mathematik Blatt 7 Prof. Dr. J. Hartl Dr. Hannes Petermeier Dr. Cornelia Eder Dipl.-Ing. Martin Nagel Höhere Mathematik 2 (Weihenstephan) 1. In einer Urne
Technische Universität München SS 2006 Zentrum Mathematik Blatt 7 Prof. Dr. J. Hartl Dr. Hannes Petermeier Dr. Cornelia Eder Dipl.-Ing. Martin Nagel Höhere Mathematik 2 (Weihenstephan) 1. In einer Urne
Vorkurs Mathematik. Christoph Hindermann. Wahrscheinlichkeitstheorie
 Kapitel 4 Christoph Hindermann Vorkurs Mathematik 1 4.0 Motivation Wenn 100 Münzen geworfen werden, wie ist dann die Wahrscheinlichkeit, dass genau 50 davon Kopf zeigen? Angenommen, es befinden sich 300
Kapitel 4 Christoph Hindermann Vorkurs Mathematik 1 4.0 Motivation Wenn 100 Münzen geworfen werden, wie ist dann die Wahrscheinlichkeit, dass genau 50 davon Kopf zeigen? Angenommen, es befinden sich 300
Übersicht Wahrscheinlichkeitsrechnung EF
 Übersicht Wahrscheinlichkeitsrechnung EF. Grundbegriffe der Wahrscheinlichkeitsrechnung (eite ). Regeln zur Berechnung von Wahrscheinlichkeiten (eite ). Bedingte Wahrscheinlichkeit und Vierfeldertafel
Übersicht Wahrscheinlichkeitsrechnung EF. Grundbegriffe der Wahrscheinlichkeitsrechnung (eite ). Regeln zur Berechnung von Wahrscheinlichkeiten (eite ). Bedingte Wahrscheinlichkeit und Vierfeldertafel
Wahrscheinlichkeitsrechnung
 Abiturvorbereitung Wahrscheinlichkeitsrechnung S. 1 von 9 Wahrscheinlichkeitsrechnung Kombinatorik Formeln für Wahrscheinlichkeiten Bedingte Wahrscheinlichkeiten Zusammenfassung wichtiger Begriffe Übungsaufgaben
Abiturvorbereitung Wahrscheinlichkeitsrechnung S. 1 von 9 Wahrscheinlichkeitsrechnung Kombinatorik Formeln für Wahrscheinlichkeiten Bedingte Wahrscheinlichkeiten Zusammenfassung wichtiger Begriffe Übungsaufgaben
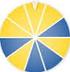
Erwartungswert. c Roolfs
 Erwartungswert 2e b a 4e Der Sektor a des Glücksrads bringt einen Gewinn von 2e, der Sektor b das Doppelte. Um den fairen Einsatz zu ermitteln, ist der durchschnittlich zu erwartende Gewinn pro Spiel zu
Erwartungswert 2e b a 4e Der Sektor a des Glücksrads bringt einen Gewinn von 2e, der Sektor b das Doppelte. Um den fairen Einsatz zu ermitteln, ist der durchschnittlich zu erwartende Gewinn pro Spiel zu
3 Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsversuchen
 Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsversuchen Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsversuchen.1 Pfadregeln.1.1 Pfadmultiplikationsregel Eine faire Münze und
Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsversuchen Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsversuchen.1 Pfadregeln.1.1 Pfadmultiplikationsregel Eine faire Münze und
Wahrscheinlichkeit und Zufall
 Wahrscheinlichkeit und Zufall Rechnen mit Wahrscheinlichkeiten 16. Juni 2009 Dr. Katja Krüger Universität Paderborn 1 Inhalt Ereignisse i und deren Wahrscheinlichkeit h hk i Laplace-Regel Baumdiagramm
Wahrscheinlichkeit und Zufall Rechnen mit Wahrscheinlichkeiten 16. Juni 2009 Dr. Katja Krüger Universität Paderborn 1 Inhalt Ereignisse i und deren Wahrscheinlichkeit h hk i Laplace-Regel Baumdiagramm
Wahrscheinlichkeitsrechnung und Statistik
 3. Vorlesung - 21.10.2016 Bedingte Wahrscheinlichkeit In einer Urne sind 2 grüne und 3 blaue Kugeln. 2 Kugeln werden ohne Zürücklegen gezogen. Welches ist die Wahrscheinlichkeit, dass : a) man eine grüne
3. Vorlesung - 21.10.2016 Bedingte Wahrscheinlichkeit In einer Urne sind 2 grüne und 3 blaue Kugeln. 2 Kugeln werden ohne Zürücklegen gezogen. Welches ist die Wahrscheinlichkeit, dass : a) man eine grüne
2 STOCHASTISCHE GRUNDBEGRIFFE
 2 STOCHASTISCHE GRUNDBEGRIFFE 2.4 Wahrscheinlichkeitsräume 1. Man vereinfache soweit wie möglich (AB A B): (a) (A B)(A B c ) (b) (A B)(B C) (c) (A B)(A c B)(A B c ) (d) (AB) (AB c ) (e) (A B)(A c B)(A
2 STOCHASTISCHE GRUNDBEGRIFFE 2.4 Wahrscheinlichkeitsräume 1. Man vereinfache soweit wie möglich (AB A B): (a) (A B)(A B c ) (b) (A B)(B C) (c) (A B)(A c B)(A B c ) (d) (AB) (AB c ) (e) (A B)(A c B)(A
Beispiel 37. Wir werfen eine Münze so lange, bis zum ersten Mal
 Beispiel 37 Wir werfen eine Münze so lange, bis zum ersten Mal Kopf erscheint. Dies geschehe in jedem Wurf unabhängig mit Wahrscheinlichkeit p. Wir definieren dazu die Zufallsvariable X := Anzahl der Würfe.
Beispiel 37 Wir werfen eine Münze so lange, bis zum ersten Mal Kopf erscheint. Dies geschehe in jedem Wurf unabhängig mit Wahrscheinlichkeit p. Wir definieren dazu die Zufallsvariable X := Anzahl der Würfe.
Zusammengesetzte Zufallsexperimente - Baumdiagramme und Pfadregeln ==================================================================
 Zusammengesetzte Zufallsexperimente - Baumdiagramme und Pfadregeln ================================================================== Ein Zufallsexperiment heißt zusammegesetzt, wenn es es die Kombination
Zusammengesetzte Zufallsexperimente - Baumdiagramme und Pfadregeln ================================================================== Ein Zufallsexperiment heißt zusammegesetzt, wenn es es die Kombination
1.1 Ergebnisräume einfacher Zufallsexperimente. 2) Es gibt mindestens zwei mögliche Ausgänge des Experiments.
 Übungsmaterial 1 1 Zufallsexperimente 1.1 Ergebnisräume einfacher Zufallsexperimente Damit ein Experiment ein Zufallsexperiment ist, müssen folgende Eigenschaften erfüllt sein: 1) Das Experiment lässt
Übungsmaterial 1 1 Zufallsexperimente 1.1 Ergebnisräume einfacher Zufallsexperimente Damit ein Experiment ein Zufallsexperiment ist, müssen folgende Eigenschaften erfüllt sein: 1) Das Experiment lässt
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2014/2015 Prof. Dr. Peter Gritzmann 07.
 Note: Name Vorname Matrikelnummer Studiengang Unterchrift der Kandidatin/de Kandidaten Höraal Reihe Platz Techniche Univerität München Fakultät für Mathematik Algorithmiche Dikrete Mathematik WS 1/1 Prof.
Note: Name Vorname Matrikelnummer Studiengang Unterchrift der Kandidatin/de Kandidaten Höraal Reihe Platz Techniche Univerität München Fakultät für Mathematik Algorithmiche Dikrete Mathematik WS 1/1 Prof.
alte Maturaufgaben zu Stochastik
 Stochastik 01.02.13 alte Maturaufgaben 1 alte Maturaufgaben zu Stochastik 1 07/08 1. (8 P.) In einer Urne liegen 5 rote, 8 gelbe und 7 blaue Kugeln. Es werden nacheinander drei Kugeln gezogen, wobei die
Stochastik 01.02.13 alte Maturaufgaben 1 alte Maturaufgaben zu Stochastik 1 07/08 1. (8 P.) In einer Urne liegen 5 rote, 8 gelbe und 7 blaue Kugeln. Es werden nacheinander drei Kugeln gezogen, wobei die
Grundkurs Codierung Lösungsvorschläge zu den Fragen in den Unterkapiteln Was blieb? Stand Unterkapitel 4.4 Seite 261
 Grundkur Codierung Löungvorchläge zu den Fragen in den Unterkapiteln Wa blieb? Stand 22.04.2007 Unterkapitel 4.4 Seite 261 Zu Frage 1: Nein, damit bleibt da one time pad-verfahren nicht perfekt. Man kann
Grundkur Codierung Löungvorchläge zu den Fragen in den Unterkapiteln Wa blieb? Stand 22.04.2007 Unterkapitel 4.4 Seite 261 Zu Frage 1: Nein, damit bleibt da one time pad-verfahren nicht perfekt. Man kann
C : Genau ein Wurf ergibt Augenzahl D:.Wenigstens ein Wurf ergibt Augenzahl 2
 Lapace-Experimente ================================================================== 1. a) Wie groß ist die W'keit, beim Werfen eines Laplace-Würfels eine Sechs zu erhalten? b) Wie groß ist die W'keit,
Lapace-Experimente ================================================================== 1. a) Wie groß ist die W'keit, beim Werfen eines Laplace-Würfels eine Sechs zu erhalten? b) Wie groß ist die W'keit,
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
KAPITEL 5. Erwartungswert
 KAPITEL 5 Erwartungswert Wir betrachten einen diskreten Wahrscheinlichkeitsraum (Ω, P) und eine Zufallsvariable X : Ω R auf diesem Wahrscheinlichkeitsraum. Die Grundmenge Ω hat also nur endlich oder abzählbar
KAPITEL 5 Erwartungswert Wir betrachten einen diskreten Wahrscheinlichkeitsraum (Ω, P) und eine Zufallsvariable X : Ω R auf diesem Wahrscheinlichkeitsraum. Die Grundmenge Ω hat also nur endlich oder abzählbar
Dieses Quiz soll Ihnen helfen, Kapitel besser zu verstehen.
 Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Dieses Quiz soll Ihnen helfen, Kapitel 2.5-2. besser zu verstehen. Frage Wir betrachten ein Würfelspiel. Man wirft einen fairen, sechsseitigen Würfel. Wenn eine oder eine 2 oben liegt, muss man 2 SFr zahlen.
Wie hoch ist das Risiko, dass ein System, das aus mehreren Komponenten besteht, ausfällt?
 In diesem Kapitel werden wir den egriff Wahrscheinlichkeit und die Grundlagen der Wahrscheinlichkeitsrechnung kennenlernen, um z.. folgende Fragestellungen zu beantworten. Wie hoch ist das Risiko, dass
In diesem Kapitel werden wir den egriff Wahrscheinlichkeit und die Grundlagen der Wahrscheinlichkeitsrechnung kennenlernen, um z.. folgende Fragestellungen zu beantworten. Wie hoch ist das Risiko, dass
Einführung in die Wahrscheinlichkeitsrechnung
 Einführung in die Wahrscheinlichkeitsrechnung. In einer Urne befinden sich 3 schwarze und weiße Kugel. Wir entnehmen der Urne eine Kugel, notieren die Farbe und legen die Kugel in die Urne zurück. Dieses
Einführung in die Wahrscheinlichkeitsrechnung. In einer Urne befinden sich 3 schwarze und weiße Kugel. Wir entnehmen der Urne eine Kugel, notieren die Farbe und legen die Kugel in die Urne zurück. Dieses
7 Unabhängigkeit von Ereignissen; bedingte Wahrscheinlichkeit
 Übungsmaterial 7 Unabhängigkeit von reignissen; bedingte Wahrscheinlichkeit 7. Unabhängigkeit von reignissen Wir betrachten folgendes Beispiel: Zwei unterscheidbare Münzen werden geworfen. Man betrachtet
Übungsmaterial 7 Unabhängigkeit von reignissen; bedingte Wahrscheinlichkeit 7. Unabhängigkeit von reignissen Wir betrachten folgendes Beispiel: Zwei unterscheidbare Münzen werden geworfen. Man betrachtet
Aufgabe 2.4: Temposünder?
 Idee, Aufgabenentwurf und Foto: Barbara Mathea, Ferdinand Weber Weil da Radargerät defekt war, filmte die Polizei in einer 30-km-Zone alle vorbeifahrenden Auto. Von 4 Auto ind je 5 aufeinander folgende
Idee, Aufgabenentwurf und Foto: Barbara Mathea, Ferdinand Weber Weil da Radargerät defekt war, filmte die Polizei in einer 30-km-Zone alle vorbeifahrenden Auto. Von 4 Auto ind je 5 aufeinander folgende
Kapitel N. Wahrscheinlichkeitsrechnung
 Kapitel N Wahrscheinlichkeitsrechnung Inhalt dieses Kapitels N000 1 Diskrete Wahrscheinlichkeitsräume 2 Bedingte Wahrscheinlichkeit und Unabhängigkeit 1 Produktexperimente 2 Kombinatorik und Urnenmodelle
Kapitel N Wahrscheinlichkeitsrechnung Inhalt dieses Kapitels N000 1 Diskrete Wahrscheinlichkeitsräume 2 Bedingte Wahrscheinlichkeit und Unabhängigkeit 1 Produktexperimente 2 Kombinatorik und Urnenmodelle
Wählt man aus n Mengen mit z 1 bzw. z 2,..., bzw. z n Elementen nacheinander aus jeder Menge jeweils ein Element aus,
 V. Stochastik ================================================================== 5.1 Zählprinzip Wählt man aus n Mengen mit z 1 bzw. z 2,..., bzw. z n Elementen nacheinander aus jeder Menge jeweils ein
V. Stochastik ================================================================== 5.1 Zählprinzip Wählt man aus n Mengen mit z 1 bzw. z 2,..., bzw. z n Elementen nacheinander aus jeder Menge jeweils ein
Es werden 120 Schüler befragt, ob sie ein Handy besitzen. Das Ergebnis der Umfrage lautet: Von 120 Schülern besitzen 99 ein Handy.
 R. Brinkmann http://brinkmann-du.de Seite 08..2009 Von der relativen Häufigkeit zur Wahrscheinlichkeit Es werden 20 Schüler befragt, ob sie ein Handy besitzen. Das Ergebnis der Umfrage lautet: Von 20 Schülern
R. Brinkmann http://brinkmann-du.de Seite 08..2009 Von der relativen Häufigkeit zur Wahrscheinlichkeit Es werden 20 Schüler befragt, ob sie ein Handy besitzen. Das Ergebnis der Umfrage lautet: Von 20 Schülern
htw saar 1 KAPITEL 4 BEDINGTE WAHRSCHEINLICHKEIT UND STOCHASTISCHE UNABHÄNGIGKEIT Hans-Peter Hafner WS 2016/2017
 htw saar 1 KAPITEL 4 BEDINGTE WAHRSCHEINLICHKEIT UND STOCHASTISCHE UNABHÄNGIGKEIT htw saar 2 Gliederung 25.01. Bedingte Wahrscheinlichkeit: Motivation und Definition Multiplikationssatz Stochastische Unabhängigkeit:
htw saar 1 KAPITEL 4 BEDINGTE WAHRSCHEINLICHKEIT UND STOCHASTISCHE UNABHÄNGIGKEIT htw saar 2 Gliederung 25.01. Bedingte Wahrscheinlichkeit: Motivation und Definition Multiplikationssatz Stochastische Unabhängigkeit:
Landeswettbewerb Mathematik Baden-Württemberg. Runde 2
 1994 Runde ufgabe 1 Zeige, da 1!! 3!... 1995! mindeten 1 Teiler hat. Hinwei: Unter n! verteht man da Produkt der erten n natürlichen Zahlen. eipiel: 5! = 1 3 4 5 = 10 Löung Die Summe S = 1!! 3!... 1995!
1994 Runde ufgabe 1 Zeige, da 1!! 3!... 1995! mindeten 1 Teiler hat. Hinwei: Unter n! verteht man da Produkt der erten n natürlichen Zahlen. eipiel: 5! = 1 3 4 5 = 10 Löung Die Summe S = 1!! 3!... 1995!
Stochastische Überraschungen beim Spiel BINGO
 Stochatiche Überrachungen beim Spiel BINGO NORBERT HENZE, KARLSRUHE, UND HANS HUMENBERGER, WIEN Zuammenfaung: In dieem Beitrag wird da bekannte Spiel BINGO erläutert und näher analyiert. Augehend vom konkreten
Stochatiche Überrachungen beim Spiel BINGO NORBERT HENZE, KARLSRUHE, UND HANS HUMENBERGER, WIEN Zuammenfaung: In dieem Beitrag wird da bekannte Spiel BINGO erläutert und näher analyiert. Augehend vom konkreten
4. Schularbeit/7C/2-stündig Schularbeit. 7C am
 4. Schularbeit 7C am 24.5.2017 Name: Note: Beispiel-Nr. 1 2 3 4 5 6 7 8 9 10 11 12 AP Teil 1: Teil 2: Punkte Teil 1 (inkl. AP) Punkte Teil 2 Gesamtpunkte Notenschlüssel: 0 7 P von Teil 1 (inkl. Anrechnungspunkte
4. Schularbeit 7C am 24.5.2017 Name: Note: Beispiel-Nr. 1 2 3 4 5 6 7 8 9 10 11 12 AP Teil 1: Teil 2: Punkte Teil 1 (inkl. AP) Punkte Teil 2 Gesamtpunkte Notenschlüssel: 0 7 P von Teil 1 (inkl. Anrechnungspunkte
Kapitel 6. Kapitel 6 Mehrstufige Zufallsexperimente
 Mehrstufige Zufallsexperimente Inhalt 6.1 6.1 Mehrstufige Experimente 6.2 6.2 Bedingte Wahrscheinlichkeiten Seite 2 6.1 Mehrstufige Experimente Grundvorstellung: Viele Viele Experimente werden der der
Mehrstufige Zufallsexperimente Inhalt 6.1 6.1 Mehrstufige Experimente 6.2 6.2 Bedingte Wahrscheinlichkeiten Seite 2 6.1 Mehrstufige Experimente Grundvorstellung: Viele Viele Experimente werden der der
Zufallsprozesse, Ereignisse und Wahrscheinlichkeiten die Grundlagen
 Zufallsprozesse, Ereignisse und Wahrscheinlichkeiten die Grundlagen Wichtige Tatsachen und Formeln zur Vorlesung Mathematische Grundlagen für das Physikstudium 3 Franz Embacher http://homepage.univie.ac.at/franz.embacher/
Zufallsprozesse, Ereignisse und Wahrscheinlichkeiten die Grundlagen Wichtige Tatsachen und Formeln zur Vorlesung Mathematische Grundlagen für das Physikstudium 3 Franz Embacher http://homepage.univie.ac.at/franz.embacher/
Vorlesung Statistik, H&A Mathe, Master M
 Beispiel: Die Wahrscheinlichkeit dafür, dass ein Bewerber von Firma A angenommen wird ist P(A) = 0,2. Die Wahrscheinlichkeit von Firma B angenommen zu werden beträgt P(B) = 0,3. Von mindestens einer der
Beispiel: Die Wahrscheinlichkeit dafür, dass ein Bewerber von Firma A angenommen wird ist P(A) = 0,2. Die Wahrscheinlichkeit von Firma B angenommen zu werden beträgt P(B) = 0,3. Von mindestens einer der
Beispiel-Schulaufgabe 2
 Anregungen zur Ertellung von Aufgaben Aufgaben für Leitungnachweie Die zeichnet ich durch eine augewogene Berückichtigung der allgemeinen mathematichen Kompetenzen au. Aufgaben, deren Bearbeitung in auffallendem
Anregungen zur Ertellung von Aufgaben Aufgaben für Leitungnachweie Die zeichnet ich durch eine augewogene Berückichtigung der allgemeinen mathematichen Kompetenzen au. Aufgaben, deren Bearbeitung in auffallendem
Kurs 2 Stochastik EBBR Vollzeit (1 von 2)
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 281 Bremen Kurs 2 Stochastik EBBR Vollzeit (1 von 2) Name: Ich 1. 2. 3. 4.. 6. 7. So schätze ich meinen Lernzuwachs ein.
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 281 Bremen Kurs 2 Stochastik EBBR Vollzeit (1 von 2) Name: Ich 1. 2. 3. 4.. 6. 7. So schätze ich meinen Lernzuwachs ein.
Einführung. Wahrscheinlichkeit. 1 Wahrscheinlichkeit: Definition und Interpretation. 2 Elementare Wahrscheinlichkeitsrechnung, bedingte
 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2 Elementare Wahrscheinlichkeitsrechnung, bedingte Wahrscheinlichkeit Axiome nach Kolmogorov Gegeben sei ein Zufallsexperiment mit Ergebnisraum
Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2 Elementare Wahrscheinlichkeitsrechnung, bedingte Wahrscheinlichkeit Axiome nach Kolmogorov Gegeben sei ein Zufallsexperiment mit Ergebnisraum
Es wird aus einer Urne mit N Kugeln gezogen, die mit den Zahlen 1,..., N durchnummiert sind. (N n)! n! = N! (N n)!n! =
 Übungsblatt Höhere Mathematik - Weihenstephan SoSe 00 Michael Höhle, Hannes Petermeier, Cornelia Eder Übung: 5.6.00 Die Aufgaben -3 werden in der Übung am Donnerstag (5.6. besprochen. Die Aufgaben -6 sollen
Übungsblatt Höhere Mathematik - Weihenstephan SoSe 00 Michael Höhle, Hannes Petermeier, Cornelia Eder Übung: 5.6.00 Die Aufgaben -3 werden in der Übung am Donnerstag (5.6. besprochen. Die Aufgaben -6 sollen
Ergebnis Ergebnisraum Ω. Ereignis. Elementarereignis
 Stochastik Die Stochastik besteht aus zwei Teilgebieten, der Statistik und der Wahrscheinlichkeitsrechnung. Die Statistik beschreibt die Vergangenheit und verwendet Informationen, die (in realen Versuchen)
Stochastik Die Stochastik besteht aus zwei Teilgebieten, der Statistik und der Wahrscheinlichkeitsrechnung. Die Statistik beschreibt die Vergangenheit und verwendet Informationen, die (in realen Versuchen)
1 Bestimme mit Hilfe eines Baumdiagramms die Wahrscheinlichkeit, beim dreimaligen Werfen einer Münze a) zweimal Kopf und einmal Zahl zu erhalten.
 1 Bestimme mit Hilfe eines Baumdiagramms die Wahrscheinlichkeit, beim dreimaligen Werfen einer Münze a) zweimal Kopf und einmal Zahl zu erhalten. b) erst Zahl, dann zweimal Kopf zu erhalten. c**) mindestens
1 Bestimme mit Hilfe eines Baumdiagramms die Wahrscheinlichkeit, beim dreimaligen Werfen einer Münze a) zweimal Kopf und einmal Zahl zu erhalten. b) erst Zahl, dann zweimal Kopf zu erhalten. c**) mindestens
Universität Basel Wirtschaftswissenschaftliches Zentrum. Kombinatorik. Dr. Thomas Zehrt. Inhalt: 1. Endliche Mengen 2. Einfache Urnenexperimente
 Universität Basel Wirtschaftswissenschaftliches Zentrum Kombinatorik Dr. Thomas Zehrt Inhalt: 1. Endliche Mengen 2. Einfache Urnenexperimente 2 Teil 1 Endliche Mengen Eine endliche Menge M ist eine Menge,
Universität Basel Wirtschaftswissenschaftliches Zentrum Kombinatorik Dr. Thomas Zehrt Inhalt: 1. Endliche Mengen 2. Einfache Urnenexperimente 2 Teil 1 Endliche Mengen Eine endliche Menge M ist eine Menge,
Energiefreisetzung In der Sonne, wie in allen anderen Sternen auch, wird die Energie durch Kernfusion freigesetzt. Wasserstoffkerne(Protonen) können
 Energiefreietzung In der Sonne, wie in allen anderen Sternen auch, wird die Energie durch Kernfuion freigeetzt. Waertoffkerne(Protonen) können bei güntigen Bedingungen zu Heliumkernen verchmelzen, dabei
Energiefreietzung In der Sonne, wie in allen anderen Sternen auch, wird die Energie durch Kernfuion freigeetzt. Waertoffkerne(Protonen) können bei güntigen Bedingungen zu Heliumkernen verchmelzen, dabei
Welche Axiome sind Grundlage der axiomatischen Wahrscheinlichkeitsdefinition von Kolmogoroff?
 2. Übung: Wahrscheinlichkeitsrechnung Aufgabe 1 Welche Axiome sind Grundlage der axiomatischen Wahrscheinlichkeitsdefinition von Kolmogoroff? a) P ist nichtnegativ. b) P ist additiv. c) P ist multiplikativ.
2. Übung: Wahrscheinlichkeitsrechnung Aufgabe 1 Welche Axiome sind Grundlage der axiomatischen Wahrscheinlichkeitsdefinition von Kolmogoroff? a) P ist nichtnegativ. b) P ist additiv. c) P ist multiplikativ.
1. Grundlagen der Wahrscheinlichkeitsrechnung
 1. Grundlagen der Wahrscheinlichkeitsrechnung Ereignisse und Wahrscheinlichkeiten Zufälliger Versuch: Vorgang, der (zumindest gedanklich) beliebig oft wiederholbar ist und dessen Ausgang innerhalb einer
1. Grundlagen der Wahrscheinlichkeitsrechnung Ereignisse und Wahrscheinlichkeiten Zufälliger Versuch: Vorgang, der (zumindest gedanklich) beliebig oft wiederholbar ist und dessen Ausgang innerhalb einer
Greensche Funktion. Frank Essenberger FU Berlin. 30.September Nomenklatur 1. 2 Greensche Theoreme 1. 3 Anwendung in der Elektrostatik 2
 Greenche Funktion Frank Eenberger FU Berlin 30.September 2006 Inhalterzeichni Nomenklatur 2 Greenche Theoreme 3 Anwendung in der Elektrotatik 2 4 Anpaung an Randbedingungen 3 5 Eindeutigkeit der Löung
Greenche Funktion Frank Eenberger FU Berlin 30.September 2006 Inhalterzeichni Nomenklatur 2 Greenche Theoreme 3 Anwendung in der Elektrotatik 2 4 Anpaung an Randbedingungen 3 5 Eindeutigkeit der Löung
Klausur zur Wahrscheinlichkeitstheorie für Lehramtsstudierende
 Universität Duisburg-Essen Essen, den 12.02.2010 Fakultät für Mathematik Prof. Dr. M. Winkler C. Stinner Klausur zur Wahrscheinlichkeitstheorie für Lehramtsstudierende Lösung Die Klausur gilt als bestanden,
Universität Duisburg-Essen Essen, den 12.02.2010 Fakultät für Mathematik Prof. Dr. M. Winkler C. Stinner Klausur zur Wahrscheinlichkeitstheorie für Lehramtsstudierende Lösung Die Klausur gilt als bestanden,
Übungsaufgaben zur Vorlesung. Lineare Algebra II. Komplex VI: Vektoren, Vektorräume und Lineare Unabhängigkeit
 Übungaufgaben zur Vorleung Lineare Algebra II Komplex VI: Vektoren, Vektorräume und Lineare Unabhängigkeit. Seien p = (, k) und q = (, ). Man betimme k o, daß p und q (a) parallel ind. (b) orthogonal ind.
Übungaufgaben zur Vorleung Lineare Algebra II Komplex VI: Vektoren, Vektorräume und Lineare Unabhängigkeit. Seien p = (, k) und q = (, ). Man betimme k o, daß p und q (a) parallel ind. (b) orthogonal ind.
STOCHASTISCHE UNABHÄNGIGKEIT. Annika Pohlmann Philipp Oel Wilhelm Dück
 STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
Verschiebungssatz: Ist F (s) die Laplace-Transformierte von f (t), dann gilt für t 0 > 0
 3.6 Tranformationätze 853 3.6 Tranformationätze In dieem Abchnitt werden weitere Eigenchaften der Laplace-Tranformation vorgetellt, die in vielen technichen Bechreibungen ihre Anwendung finden. Oftmal
3.6 Tranformationätze 853 3.6 Tranformationätze In dieem Abchnitt werden weitere Eigenchaften der Laplace-Tranformation vorgetellt, die in vielen technichen Bechreibungen ihre Anwendung finden. Oftmal
Ableitungsberechnung mit der Grenzwertmethode. Besonders wichtig ist der Zentraltext über Ableitungen Datei Stand 30.
 Analyi Ableitungfunktionen Ableitungberechnung mit der Grenzwertmethode Beonder wichtig it der Zentraltet über Ableitungen 400 Datei 40 Stand 0. Dezember 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 40 Ableitungfunktionen
Analyi Ableitungfunktionen Ableitungberechnung mit der Grenzwertmethode Beonder wichtig it der Zentraltet über Ableitungen 400 Datei 40 Stand 0. Dezember 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 40 Ableitungfunktionen
Diskrete Strukturen. Sebastian Thomas RWTH Aachen https://www2.math.rwth-aachen.de/ds16/ 1. Februar 2017 Vorlesung 21
 Diskrete Strukturen Sebastian Thomas RWTH Aachen https://www2.math.rwth-aachen.de/ds16/ 1. Februar 2017 Vorlesung 21 Quasiendliche Wahrscheinlichkeitsräume Definition quasiendlicher Wahrscheinlichkeitsraum
Diskrete Strukturen Sebastian Thomas RWTH Aachen https://www2.math.rwth-aachen.de/ds16/ 1. Februar 2017 Vorlesung 21 Quasiendliche Wahrscheinlichkeitsräume Definition quasiendlicher Wahrscheinlichkeitsraum
KAPITEL 2. Kombinatorik
 KAPITEL 2 Kombinatori In der Kombinatori geht es um das Abzählen von Kombinationen 21 Geburtstagsproblem Beispiel 211 (Geburtstagsproblem In einem Raum befinden sich 200 Studenten Wie groß ist die Wahrscheinlicheit,
KAPITEL 2 Kombinatori In der Kombinatori geht es um das Abzählen von Kombinationen 21 Geburtstagsproblem Beispiel 211 (Geburtstagsproblem In einem Raum befinden sich 200 Studenten Wie groß ist die Wahrscheinlicheit,
Wahrscheinlichkeitsrechnung für die Mittelstufe
 Wahrscheinlichkeitsrechnung für die Mittelstufe Wir beginnen mit einem Beispiel, dem Münzwurf. Es wird eine faire Münze geworfen mit den Seiten K (für Kopf) und Z (für Zahl). Fair heißt, dass jede Seite
Wahrscheinlichkeitsrechnung für die Mittelstufe Wir beginnen mit einem Beispiel, dem Münzwurf. Es wird eine faire Münze geworfen mit den Seiten K (für Kopf) und Z (für Zahl). Fair heißt, dass jede Seite
Wahrscheinlichkeitstheorie für Informatikstudien Übungsblatt 1
 http://www.stat.tugraz.at/courses/exam/hw_108.pdf 1 Wahrscheinlichkeitstheorie für Informatikstudien 506.000 Übungsblatt 1 04. Nov. 2008 1. [A 2.1] TelematikstudentInnen im 3. Semester werden befragt,
http://www.stat.tugraz.at/courses/exam/hw_108.pdf 1 Wahrscheinlichkeitstheorie für Informatikstudien 506.000 Übungsblatt 1 04. Nov. 2008 1. [A 2.1] TelematikstudentInnen im 3. Semester werden befragt,
Fachhochschule Wedel. Seminararbeit. Flussprobleme in Graphen und ihre Anwendung auf 0/1-Netzwerken
 Fachhochchule Wedel Seminararbeit Thema: Fluprobleme in Graphen und ihre Anwendung auf 0/-Netzwerken Eingereicht von: Erarbeitet im: Claudia Padberg (wi09) An der Windmühle 880 Wedel Tel. (00) 98897 E-Mail:
Fachhochchule Wedel Seminararbeit Thema: Fluprobleme in Graphen und ihre Anwendung auf 0/-Netzwerken Eingereicht von: Erarbeitet im: Claudia Padberg (wi09) An der Windmühle 880 Wedel Tel. (00) 98897 E-Mail:
Zur Bestimmung der ungünstigsten Toleranz zusammengesetzter Systeme können die Einzeltoleranzen entsprechend ihres Zusammenwirkens addiert werden.
 Vorauetzung und verwandte Themen Für diee Bechreibungen ind Vorkenntnie der Statitik und der Verteilungen erforderlich. Weiterführende Thema it: www.veruchmethoden.de/prozedaten_toleranzimulation.pdf Einführung
Vorauetzung und verwandte Themen Für diee Bechreibungen ind Vorkenntnie der Statitik und der Verteilungen erforderlich. Weiterführende Thema it: www.veruchmethoden.de/prozedaten_toleranzimulation.pdf Einführung
Wahrscheinlichkeitstheorie
 Kapitel 2 Wahrscheinlichkeitstheorie Josef Leydold c 2006 Mathematische Methoden II Wahrscheinlichkeitstheorie 1 / 24 Lernziele Experimente, Ereignisse und Ereignisraum Wahrscheinlichkeit Rechnen mit Wahrscheinlichkeiten
Kapitel 2 Wahrscheinlichkeitstheorie Josef Leydold c 2006 Mathematische Methoden II Wahrscheinlichkeitstheorie 1 / 24 Lernziele Experimente, Ereignisse und Ereignisraum Wahrscheinlichkeit Rechnen mit Wahrscheinlichkeiten
Übungsmaterial. Lösen von Anfangswertproblemen mit Laplacetransformation
 Prof. Dr. W. Roenheinrich 30.06.2009 Fachbereich Grundlagenwienchaften Fachhochchule Jena Übungmaterial Löen von Anfangwertproblemen mit Laplacetranformation Nachtehend ind einige Anfangwertprobleme zu
Prof. Dr. W. Roenheinrich 30.06.2009 Fachbereich Grundlagenwienchaften Fachhochchule Jena Übungmaterial Löen von Anfangwertproblemen mit Laplacetranformation Nachtehend ind einige Anfangwertprobleme zu
Übungen zur Kombinatorik
 1. Das Paradoxon des Chevalier de Méré: De Méré fand es paradox, dass beim Würfeln mit drei Würfeln die Augenzahlsumme 11 häufiger zustande kam als die Augenzahlsumme 12. Wie lauten die tatsächlichen Wahrscheinlichkeiten
1. Das Paradoxon des Chevalier de Méré: De Méré fand es paradox, dass beim Würfeln mit drei Würfeln die Augenzahlsumme 11 häufiger zustande kam als die Augenzahlsumme 12. Wie lauten die tatsächlichen Wahrscheinlichkeiten
Vorlesung 3a. Der Erwartungswert. von diskreten reellwertigen Zufallsvariablen
 Vorlesung 3a Der Erwartungswert von diskreten reellwertigen Zufallsvariablen X sei eine diskrete reellwertige Zufallsvariable, d.h. eine ZV e mit Wertebereich R (oder einer Teilmenge davon), sodass eine
Vorlesung 3a Der Erwartungswert von diskreten reellwertigen Zufallsvariablen X sei eine diskrete reellwertige Zufallsvariable, d.h. eine ZV e mit Wertebereich R (oder einer Teilmenge davon), sodass eine
Einführung in die Wahrscheinlichkeitsrechnung
 Einführung in die Wahrscheinlichkeitsrechnung Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) Wahrscheinlichkeitsrechnung
Einführung in die Wahrscheinlichkeitsrechnung Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) Wahrscheinlichkeitsrechnung
TU DORTMUND Sommersemester 2018
 Fakultät Statistik. April 08 Blatt Aufgabe.: Wir betrachten das Zufallsexperiment gleichzeitiges Werfen zweier nicht unterscheidbarer Würfel. Sei A das Ereignis, dass die Augensumme beider Würfel ungerade
Fakultät Statistik. April 08 Blatt Aufgabe.: Wir betrachten das Zufallsexperiment gleichzeitiges Werfen zweier nicht unterscheidbarer Würfel. Sei A das Ereignis, dass die Augensumme beider Würfel ungerade
Wahrscheinlichkeitsrechnung
 Wahrscheinlichkeitsrechnung Was du wissen musst: Die Begriffe Zufallsexperiment, Ereignisse, Gegenereignis, Zufallsvariable und Wahrscheinlichkeit sind dir geläufig. Du kannst mehrstufige Zufallsversuche
Wahrscheinlichkeitsrechnung Was du wissen musst: Die Begriffe Zufallsexperiment, Ereignisse, Gegenereignis, Zufallsvariable und Wahrscheinlichkeit sind dir geläufig. Du kannst mehrstufige Zufallsversuche
Abitur 2015 Mathematik Stochastik IV
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Urne befinden sich vier rote und sechs blaue Kugeln. Aus dieser wird achtmal eine Kugel zufällig gezogen, die Farbe
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 201 Mathematik Stochastik IV In einer Urne befinden sich vier rote und sechs blaue Kugeln. Aus dieser wird achtmal eine Kugel zufällig gezogen, die Farbe
3 Bedingte Wahrscheinlichkeit, Unabhängigkeit von Ereignissen. Bsp (3-maliges Werfen einer Münze) Menge der Elementarereignisse:
 3 Bedingte Wahrscheinlichkeit, Unabhängigkeit von Ereignissen Bsp. 1.19 (3-maliges Werfen einer Münze) Menge der Elementarereignisse: Ω {zzz, zzw,zwz,wzz,zww,wzw,wwz,www}. Dabei gilt: Ω 2 3 8 N. Wir definieren
3 Bedingte Wahrscheinlichkeit, Unabhängigkeit von Ereignissen Bsp. 1.19 (3-maliges Werfen einer Münze) Menge der Elementarereignisse: Ω {zzz, zzw,zwz,wzz,zww,wzw,wwz,www}. Dabei gilt: Ω 2 3 8 N. Wir definieren
Übungsblatt 7 Besprechung am /
 PN - Phyik für Chemiker und Biologen Prof. J. Lipfert WS 07/8 Übungblatt 7 Übungblatt 7 Beprechung am..07/4..07 Aufgabe Raketentechnik: Raketenantriebe funktionieren nach dem Rücktoßprinzip: Der Treibtoff
PN - Phyik für Chemiker und Biologen Prof. J. Lipfert WS 07/8 Übungblatt 7 Übungblatt 7 Beprechung am..07/4..07 Aufgabe Raketentechnik: Raketenantriebe funktionieren nach dem Rücktoßprinzip: Der Treibtoff
1 Elementare Wahrscheinlichkeitstheorie
 1 Elementare Wahrscheinlichkeitstheorie 1.1 Zufallsexperiment Definition 1.1. Ein Zufallsexperiment ist ein Vorgang, der im Prinzip beliebig oft unter identischen Randbedingungen wiederholt werden kann.
1 Elementare Wahrscheinlichkeitstheorie 1.1 Zufallsexperiment Definition 1.1. Ein Zufallsexperiment ist ein Vorgang, der im Prinzip beliebig oft unter identischen Randbedingungen wiederholt werden kann.
,,Schäferhunde sind gefährlich! Denn,,Jeder dritte Biss geht auf das Konto dieser Rasse.
 Wirtschaftswissenschaftliches Zentrum 7 Universität Basel Statistik Dr. Thomas Zehrt Bedingte Wahrscheinlichkeit Motivation Die bedingte Wahrscheinlichkeit eines Ereignisses A bei einem gegebenen Ereignis
Wirtschaftswissenschaftliches Zentrum 7 Universität Basel Statistik Dr. Thomas Zehrt Bedingte Wahrscheinlichkeit Motivation Die bedingte Wahrscheinlichkeit eines Ereignisses A bei einem gegebenen Ereignis
An welchen Wirkungen können wir Kräfte erkennen? Ergebnis Verformung, Beschleunigung, abbremsen, Bewegungsrichtung ändern.
 R. Brinkann http://brinkann-du.de Seite 1 5.11.013 Obertufe: e und auführliche Löungen zur Klaenarbeit zur Mechanik II (Variante A) e: E1 E E3 E4 E5 E6 E7 An welchen Wirkungen können wir Kräfte erkennen?
R. Brinkann http://brinkann-du.de Seite 1 5.11.013 Obertufe: e und auführliche Löungen zur Klaenarbeit zur Mechanik II (Variante A) e: E1 E E3 E4 E5 E6 E7 An welchen Wirkungen können wir Kräfte erkennen?
Allgemeine diskrete Wahrscheinlichkeitsräume II. Beispiel II. Beispiel I. Definition 6.3 (Diskreter Wahrscheinlichkeitsraum)
 Allgemeine diskrete Wahrscheinlichkeitsräume I Allgemeine diskrete Wahrscheinlichkeitsräume II Verallgemeinerung von Laplaceschen Wahrscheinlichkeitsräumen: Diskrete Wahrscheinlichkeitsräume Ω endlich
Allgemeine diskrete Wahrscheinlichkeitsräume I Allgemeine diskrete Wahrscheinlichkeitsräume II Verallgemeinerung von Laplaceschen Wahrscheinlichkeitsräumen: Diskrete Wahrscheinlichkeitsräume Ω endlich
