(Water)Tight-Cocone A.
|
|
|
- Franka Heinrich
- vor 7 Jahren
- Abrufe
Transkript
1 1
2 Wasserdichte Oberfläche Input: Cocone mit Löchern und Artefakten 2
3 Wasserdichte Oberfläche Input: Cocone mit Löchern und Artefakten Bedingung: Prinzip der Lokalität: schlechte Abtastung nur lokal vorhanden 3
4 Wasserdichte Oberfläche Input: Cocone mit Löchern und Artefakten Bedingung: Prinzip der Lokalität: schlechte Abtastung nur lokal vorhanden 2 Arbeitsphasen: Markieren, Schälen Markierung von Dreiecken als in oder out Löschen bzw. schälen aller out-dreiecke 4
5 Topologische Disk: ein Menge homöomorph zur Einheits-Disk einer Ebene Punkte, dessen einfallende Oberflächendreiecke eine topologische Disk bilden sind gut, alle andere Punkte sind arm Schirm(Umbrella): U(p) die Vereinigung von Oberflächendreiecken, die einfallend zu einem guten Punkt p sind 5
6 Markieren: Stack von Paaren (p,t), p ist ein guter Punkt, t ist ein zu p einfallendes out-tetraeder 6
7 Markieren: Stack von Paaren (p,t), p ist ein guter Punkt, t ist ein zu p einfallendes out-tetraeder U(p) = pqr, prs, pqs für ein (p,t): U(p) teilt die in einfallenden Tetraeder in 2 Cluster {absp; asqp; abpq; bqrp; brsp} {cqrp; csrp; cqs} 7
8 Markieren: Cluster mit t wird als out markiert, das andere Cluster als in lokale Schleife über Tetraeder mit U(p) als Grenze (p,bprs) als Initialpaar {absp; asqp; abpq; bqrp; brsp} {cqrp; csrp; cqs} in out 8
9 Markieren: Cluster mit t wird als out markiert, das andere Cluster als in lokale Schleife über Tetraeder mit U(p) als Grenze (p,bprs) als Initialpaar {absp; asqp; abpq; bqrp; brsp} {cqrp; csrp; cqs} in out 9
10 Markieren: wenn die Schleife beim durchgehen eines out-tetraeder t' einen Punkt erreicht, der gut und nicht erforscht ist, wird das paar (q,t') in den Stack aufgenommen 10
11 Markieren: Annahmen: D(P) ist von unendlichen Tetraedern umgeben Initialisierung: ein guter Punkt p und ein unendlicher Tetraeder ut einfallen in p Stack = {(p,ut)} 11
12 Markieren: arme Tetraeder die nur arme Vertices haben wurden bisher ausgelassen einige davon müssen auch markiert werden Reparatur der Löcher und Artefakte 12
13 Markieren: 2 Typen von armen Tetraedern Typ 1: 1 liegen in einzelnen schlecht-abgetasteten Regionen, sind nach dem Prinzip der Lokalität eher klein Typ 2: haben Punkte, die in verschiedenen schlecht abgetasteten Regionen liegen sind oft riesig 13
14 Markieren: Typ 1 Tetraeder werden alle als in markiert, sodass der Schälen-Schritt sie nicht entfernen kann 14
15 Markieren: Typ 1 Tetraeder werden alle als in markiert, sodass der Schälen-Schritt sie nicht entfernen kann Ausserhalb der Oberfläche liegende Typ 2 Tetraeder werden als out markiert auf der Oberfläche liegende Typ 2 Tetraeder werden als in markiert (wie?) 15
16 Markieren: Kleines Dreieck: kleinster Umkreis-Radius von allen Dreiecken im Tetraeder 16
17 Markieren: Kleines Dreieck: kleinster Umkreis-Radius von allen Dreiecken im Tetraeder Beobachtung: wenn Vertices von einem Dreieck des armen Tetraeder in der selben schlecht abgetasteten Region liegen ist er meist klein Typ 2 arme Tetraeder werden beim Schälen-Schritt immer nur über das kleine Dreieck erreicht 17
18 18
19 Schälen: Entfernen aller out-dreiecke und weiterer überflüssiger Dreiecke 19
20 Schälen: Entfernen aller out-dreiecke und weiterer überflüssiger Dreiecke Initialisierung: Stack mit allen Dreiecken der konvexen Hülle 20
21 Schälen: Entfernen aller out-dreiecke und weiterer überflüssiger Dreiecke Initialisierung: Stack mit allen Dreiecken der konvexen Hülle Unendliche Tetraeder sofort als geschält markiert 21
22 Schälen: Dreieck t vom Stack genommen: 1 anliegender Tetraeder tu ist schon geschält, das unendliche für den anderen Tetraeder te bleiben 3 Möglichkeiten: 22
23 Schälen: Dreieck t vom Stack genommen: 1 anliegender Tetraeder tu ist schon geschält, das unendliche für den anderen Tetraeder te bleiben 3 Möglichkeiten: Bereits geschält t löschen Nicht arm und als in markiert t im Output Arm oder als out markiert, oder beides ersetzen von t durch die anderen 3 Dreiecke von te 23
24 Schälen: Dreieck t vom Stack genommen: 1 anliegender Tetraeder tu ist schon geschält, das unendliche für den anderen Tetraeder te bleiben 3 Möglichkeiten: Bereits geschält t löschen Nicht arm und als in markiert t im Output Arm oder als out markiert, oder beides ersetzen von t durch die anderen 3 Dreiecke von te Ausnahme: te ist arm und t ist nicht klein t löschen 24
25 Schälen: Terminierung: Stack leer, Output voll 25
26 26
27 27
28 Quellen N. Amenta, S. Choi, T. K. Dey and N. Leekha. A simple algorithm for homeomorphic surface reconstruction. Proc. 16th. ACM Sympos. Comput. Geom., (2000), 213_222. Also Intl. J. Comput. Geom. Appl., to appear. T. K. Dey and J. Giesen. Detecting undersampling in surface reconstruction. Proc. 17 th Annu. Sympos. Comput. Geom. (2001), Tamal K. Dey, Samrat Goswami, Tight cocone: a water-tight surface reconstructor, Proceedings of the eighth ACM symposium on Solid modeling and applications, June 16-20, 2003, Seattle, Washington, USA Efficient Computation of A Simplified Medial Axis, M.Foskey M.C.Lin D.Manocha Wikipedia Und vieles vieles mehr 28
29 END 29
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am 31.01.2013 Algorithmen für externen Speicher INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 31.01.2013 Algorithmen für externen Speicher INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Pfadgenerierung/Polygone/Polygonoffsetting
 Pfadgenerierung/Polygone/Polygonoffsetting Jan Stenzel 17. Juni 2015 Proseminar: 3D-Druck-Verfahren 1 / 42 Gliederung I 1 Polygone Definition konkav, konvex und überschlagen 2 Clipping Was kann passieren?
Pfadgenerierung/Polygone/Polygonoffsetting Jan Stenzel 17. Juni 2015 Proseminar: 3D-Druck-Verfahren 1 / 42 Gliederung I 1 Polygone Definition konkav, konvex und überschlagen 2 Clipping Was kann passieren?
8. Modelle für feste Körper
 8. Modelle für feste Körper Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
8. Modelle für feste Körper Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
Geometrische Algorithmen
 Geometrische Algorithmen Thomas Röfer Motivation Scan-line-Prinzip Konvexe Hülle Distanzprobleme Voronoi-Diagramm Rückblick Manipulation von Mengen Vorrangwarteschlange Heap HeapSort swap(a, 0, 4) 1 5
Geometrische Algorithmen Thomas Röfer Motivation Scan-line-Prinzip Konvexe Hülle Distanzprobleme Voronoi-Diagramm Rückblick Manipulation von Mengen Vorrangwarteschlange Heap HeapSort swap(a, 0, 4) 1 5
Programmierkurs Python II
 Programmierkurs Python II Stefan Thater & Michaela Regneri Universität des Saarlandes FR 4.7 Allgemeine Linguistik (Computerlinguistik) Übersicht Topologische Sortierung (einfach) Kürzeste Wege finden
Programmierkurs Python II Stefan Thater & Michaela Regneri Universität des Saarlandes FR 4.7 Allgemeine Linguistik (Computerlinguistik) Übersicht Topologische Sortierung (einfach) Kürzeste Wege finden
Approximationsalgorithmen. Durchmesser-, Breite-, kleinster Zylinderund. dünnster Kreisring- Probleme
 Approximationsalgorithmen für Durchmesser-, Breite-, kleinster Zylinderund dünnster Kreisring- Probleme Georgy Sklyarenko Vortrag im Seminar über Algorithmen am 2. December 2005 Kapitel 1. Einführung 1.1.
Approximationsalgorithmen für Durchmesser-, Breite-, kleinster Zylinderund dünnster Kreisring- Probleme Georgy Sklyarenko Vortrag im Seminar über Algorithmen am 2. December 2005 Kapitel 1. Einführung 1.1.
für n-elementige Punktmenge jedenfalls Ω(n log n), da mit VD die konvexe Hülle in linearer Zeit bestimmbar.
 Konstruktion des Voronoi-Diagramms Untere Schranke für den Zeitaufwand: für n-elementige Punktmenge jedenfalls Ω(n log n), da mit VD die konvexe Hülle in linearer Zeit bestimmbar. Wenn man die n Punkte
Konstruktion des Voronoi-Diagramms Untere Schranke für den Zeitaufwand: für n-elementige Punktmenge jedenfalls Ω(n log n), da mit VD die konvexe Hülle in linearer Zeit bestimmbar. Wenn man die n Punkte
Blindennavigation. als Anwendung für Location-based Services. Andreas Hub
 Blindennavigation als Anwendung für Location-based Services Andreas Hub Motivation? Wo bin ich? Was ist vor mir? Wo ist die Tür? Wo ist der Eingang? Kommen Gefahren? Was ist im Weg? Probleme Orientierung
Blindennavigation als Anwendung für Location-based Services Andreas Hub Motivation? Wo bin ich? Was ist vor mir? Wo ist die Tür? Wo ist der Eingang? Kommen Gefahren? Was ist im Weg? Probleme Orientierung
M. Pester 29. Ein konvexes d-polytop ist eine begrenzte d-dimensionale polyedrale Menge. (d = 3 Polyeder, d = 2 Polygon)
 M. Pester 29 6 Konvexe Hülle 6.1 Begriffe Per Definition ist die konvexe Hülle für eine Menge S von lich vielen Punkten die kleinste konvexe Menge, die S enthölt (z.b. in der Ebene durch ein umspannes
M. Pester 29 6 Konvexe Hülle 6.1 Begriffe Per Definition ist die konvexe Hülle für eine Menge S von lich vielen Punkten die kleinste konvexe Menge, die S enthölt (z.b. in der Ebene durch ein umspannes
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung am 24.01.2013 Online Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Algorithmen II Vorlesung am 24.01.2013 Online Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales Forschungszentrum
Mathematische Probleme, SS 2013 Montag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
$Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
Algorithmen zur Berechnung der Transitiven Hülle einer Datenbankrelation
 Algorithmen zur Berechnung der Transitiven Hülle einer Datenbankrelation Daniel Reinhold Shenja Leiser 6. Februar 2006 2/28 Gliederung Einführung Transitive Hülle Definition Iterative Algorithmen 1. Naive
Algorithmen zur Berechnung der Transitiven Hülle einer Datenbankrelation Daniel Reinhold Shenja Leiser 6. Februar 2006 2/28 Gliederung Einführung Transitive Hülle Definition Iterative Algorithmen 1. Naive
Distanzprobleme in der Ebene
 Distanzprobleme in der Ebene (Literatur: deberg et al., Kapitel 7,9) Christian Knauer 1 Motivation: Alle nächsten Nachbarn Gegeben: Eine Menge von Punkten P in der Ebene Berechne: Zu jedem Punkt aus P
Distanzprobleme in der Ebene (Literatur: deberg et al., Kapitel 7,9) Christian Knauer 1 Motivation: Alle nächsten Nachbarn Gegeben: Eine Menge von Punkten P in der Ebene Berechne: Zu jedem Punkt aus P
Triangulierung von einfachen Polygonen
 Triangulierung von einfachen Polygonen - Seminarvortrag von Tobias Kyrion - Inhalt: 1.1 Die Problemstellung Quellenangabe 1.1 Die Problemstellung Definition Polygon: endlich viele paarweise verschiedene
Triangulierung von einfachen Polygonen - Seminarvortrag von Tobias Kyrion - Inhalt: 1.1 Die Problemstellung Quellenangabe 1.1 Die Problemstellung Definition Polygon: endlich viele paarweise verschiedene
Algorithmische Geometrie 4. Schnitte planarer Unterteilungen
 Algorithmische Geometrie 4. Schnitte planarer Unterteilungen JProf. Dr. Heike Leitte Computergraphik und Visualisierung Inhaltsverzeichnis 1. Einführung 2. Konvexe Hülle 3. Schnitte von Liniensegmenten
Algorithmische Geometrie 4. Schnitte planarer Unterteilungen JProf. Dr. Heike Leitte Computergraphik und Visualisierung Inhaltsverzeichnis 1. Einführung 2. Konvexe Hülle 3. Schnitte von Liniensegmenten
Übung zur Vorlesung Algorithmische Geometrie
 Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Übersicht. Datenstrukturen und Algorithmen. Übersicht. Heaps. Vorlesung 8: Heapsort (K6) Joost-Pieter Katoen. 7. Mai 2015
 Datenstrukturen und Algorithmen Vorlesung 8: (K6) 1 Joost-Pieter Katoen Lehrstuhl für Informatik Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-15/dsal/ 7. Mai 015 3 Joost-Pieter
Datenstrukturen und Algorithmen Vorlesung 8: (K6) 1 Joost-Pieter Katoen Lehrstuhl für Informatik Software Modeling and Verification Group http://moves.rwth-aachen.de/teaching/ss-15/dsal/ 7. Mai 015 3 Joost-Pieter
Was bisher geschah. 1. Zerlegung in monotone Polygone 2. Triangulierung der monotonen Teilpolygone
 Was bisher geschah Motivation, Beispiele geometrische Objekte im R 2 : Punkt, Gerade, Halbebene, Strecke, Polygon, ebene Zerlegung in Regionen (planare Graphen) maschinelle Repräsentation geometrischer
Was bisher geschah Motivation, Beispiele geometrische Objekte im R 2 : Punkt, Gerade, Halbebene, Strecke, Polygon, ebene Zerlegung in Regionen (planare Graphen) maschinelle Repräsentation geometrischer
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
8. Konvexe Polytope. Tobias Boelter. Mittwoch, 5. März TopMath Frühlingsschule
 1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
Exploration und Klassifikation von BigData
 Exploration und Klassifikation von BigData Inhalt Einführung Daten Data Mining: Vorbereitungen Clustering Konvexe Hülle Fragen Google: Riesige Datenmengen (2009: Prozessieren von 24 Petabytes pro Tag)
Exploration und Klassifikation von BigData Inhalt Einführung Daten Data Mining: Vorbereitungen Clustering Konvexe Hülle Fragen Google: Riesige Datenmengen (2009: Prozessieren von 24 Petabytes pro Tag)
12. Flächenrekonstruktion aus 3D-Punktwolken und generalisierte Voronoi-Diagramme
 12. Flächenrekonstruktion aus 3D-Punktwolken und generalisierte Voronoi-Diagramme (Einfache) Voronoi-Diagramme: Motivation: gegeben: Raum R, darin Menge S von Objekten Frage nach Zerlegung von R in "Einflusszonen"
12. Flächenrekonstruktion aus 3D-Punktwolken und generalisierte Voronoi-Diagramme (Einfache) Voronoi-Diagramme: Motivation: gegeben: Raum R, darin Menge S von Objekten Frage nach Zerlegung von R in "Einflusszonen"
Lokalisierung von inneren und äußeren Grenzen in Sensornetzwerken
 Lokalisierung von inneren und äußeren Grenzen in Sensornetzwerken Seminararbeit: Algorithmen für Sensornetzwerke Thomas Gramer 1 Thomas Gramer: KIT Universität des Landes Baden-Württemberg und nationales
Lokalisierung von inneren und äußeren Grenzen in Sensornetzwerken Seminararbeit: Algorithmen für Sensornetzwerke Thomas Gramer 1 Thomas Gramer: KIT Universität des Landes Baden-Württemberg und nationales
Programmieren mit dem TI-92
 Sieglinde Fürst Programmieren mit dem TI-92 Programmieren Formeln für Flächeninhalte Inhalte Programm zur Addition zweier Zahlen Programm zur Flächenberechnung eines Dreiecks, Parallelogramms, Trapezes
Sieglinde Fürst Programmieren mit dem TI-92 Programmieren Formeln für Flächeninhalte Inhalte Programm zur Addition zweier Zahlen Programm zur Flächenberechnung eines Dreiecks, Parallelogramms, Trapezes
Binary Space Partitioning Trees: Konzepte und Anwendungen
 Binary Space Partitioning Trees: Konzepte und Anwendungen Bastian Rieck Gliederung 1 Motivation 2 BSP Trees: Der klassische Ansatz Grundlagen Maleralgorithmus Probleme und Erweiterungen 3 BSP Trees: Anwendungen
Binary Space Partitioning Trees: Konzepte und Anwendungen Bastian Rieck Gliederung 1 Motivation 2 BSP Trees: Der klassische Ansatz Grundlagen Maleralgorithmus Probleme und Erweiterungen 3 BSP Trees: Anwendungen
Begriffsklärung: Dominanz
 Einführung Begriffsklärung: Dominanz Gegeben: d-dimensionaler Raum, jeder Punkt p im Raum hat d Attribute: (p 1,,p d ) Definition Dominanz: 1 i d : p i p i und 1 i d : p i < p i Begriffsklärung: Dominanz
Einführung Begriffsklärung: Dominanz Gegeben: d-dimensionaler Raum, jeder Punkt p im Raum hat d Attribute: (p 1,,p d ) Definition Dominanz: 1 i d : p i p i und 1 i d : p i < p i Begriffsklärung: Dominanz
Konvexe Hülle. Konvexe Hülle. Mathematik. Konvexe Hülle: Definition. Mathematik. Konvexe Hülle: Eigenschaften. AK der Algorithmik 5, SS 2005 Hu Bin
 Konvexe Hülle Konvexe Hülle AK der Algorithmik 5, SS 2005 Hu Bin Anwendung: Computergraphik Boundary Kalkulationen Geometrische Optimierungsaufgaben Konvexe Hülle: Definition Mathematik Konvex: Linie zwischen
Konvexe Hülle Konvexe Hülle AK der Algorithmik 5, SS 2005 Hu Bin Anwendung: Computergraphik Boundary Kalkulationen Geometrische Optimierungsaufgaben Konvexe Hülle: Definition Mathematik Konvex: Linie zwischen
Stefan Schmid TU Berlin & T-Labs, Berlin, Germany. Reduktionen in der Berechenbarkeitstheorie
 Stefan Schmid TU Berlin & T-Labs, Berlin, Germany Reduktionen in der Berechenbarkeitstheorie Problem: Wie komme ich von hier zum Hamburger Hbf? 2 Beispiel P1 Wie komme ich von hier zum Hamburger Hbf? kann
Stefan Schmid TU Berlin & T-Labs, Berlin, Germany Reduktionen in der Berechenbarkeitstheorie Problem: Wie komme ich von hier zum Hamburger Hbf? 2 Beispiel P1 Wie komme ich von hier zum Hamburger Hbf? kann
Definition 15 Rot-Schwarz-Bäume sind externe Binärbäume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt:
 2.2 Rot-Schwarz-Bäume Definition 15 Rot-Schwarz-Bäume sind externe Binäräume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt: 1 alle Blätter hängen an schwarzen Kanten (durchgezogene
2.2 Rot-Schwarz-Bäume Definition 15 Rot-Schwarz-Bäume sind externe Binäräume (jeder Knoten hat 0 oder 2 Kinder) mit roten und schwarzen Kanten, so dass gilt: 1 alle Blätter hängen an schwarzen Kanten (durchgezogene
Zum Einstieg. Mittelsenkrechte
 Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Geometrische Algorithmen Voronoi-Diagramme. Lernmodul 7: Geo-Algorithmen und -Datenstrukturen - Voronoi-Diagramme
 Folie 1 von 32 Geometrische Algorithmen Voronoi-Diagramme Folie 2 von 32 Voronoi-Diagramme Übersicht Problemstellung Animation zur Konstruktion eines Voronoi-Diagramms Definition, Eigenschaften eines Voronoi-Diagramms
Folie 1 von 32 Geometrische Algorithmen Voronoi-Diagramme Folie 2 von 32 Voronoi-Diagramme Übersicht Problemstellung Animation zur Konstruktion eines Voronoi-Diagramms Definition, Eigenschaften eines Voronoi-Diagramms
Distributed Algorithms. Image and Video Processing
 Chapter 6 Optical Character Recognition Distributed Algorithms for Übersicht Motivation Texterkennung in Bildern und Videos 1. Erkennung von Textregionen/Textzeilen 2. Segmentierung einzelner Buchstaben
Chapter 6 Optical Character Recognition Distributed Algorithms for Übersicht Motivation Texterkennung in Bildern und Videos 1. Erkennung von Textregionen/Textzeilen 2. Segmentierung einzelner Buchstaben
Wintersemester 2007/2008 Helmut Seidl Institut für Informatik TU München
 Informatik 1 Wintersemester 2007/2008 Helmut Seidl Institut für Informatik TU München 1 Anwendung: Schreibtisch Operation: insert(task) 2 Anwendung: Schreibtisch An uns wird Arbeit delegiert... Operation:
Informatik 1 Wintersemester 2007/2008 Helmut Seidl Institut für Informatik TU München 1 Anwendung: Schreibtisch Operation: insert(task) 2 Anwendung: Schreibtisch An uns wird Arbeit delegiert... Operation:
Algorithmische Geometrie
 Lehrstuhl fu r Informatik I Algorithmische Geometrie Wintersemester 2013/14 Vorlesung: U bung: Alexander Wolff (E29) Philipp Kindermann (E12) Konvexe Hu lle oder Mischungsverha ltnisse 1. Vorlesung Prof.
Lehrstuhl fu r Informatik I Algorithmische Geometrie Wintersemester 2013/14 Vorlesung: U bung: Alexander Wolff (E29) Philipp Kindermann (E12) Konvexe Hu lle oder Mischungsverha ltnisse 1. Vorlesung Prof.
Das Innere eines Oktaeders. Michael Hofer, Workshop: Origami im Geometrieunterricht
 Das Innere eines Oktaeders Michael Hofer, Workshop: Origami im Geometrieunterricht Schritt 1 Halbiere das Quadrat über die Seiten (2x) und öffne die Faltungen wieder. Schritt 2 Drehe das Blatt um und halbiere
Das Innere eines Oktaeders Michael Hofer, Workshop: Origami im Geometrieunterricht Schritt 1 Halbiere das Quadrat über die Seiten (2x) und öffne die Faltungen wieder. Schritt 2 Drehe das Blatt um und halbiere
Mathematische Rekursion
 Rekursion Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die Funktion erscheint in ihrer eigenen Definition. Mathematische Rekursion o Viele mathematische
Rekursion Mathematische Rekursion o Viele mathematische Funktionen sind sehr natürlich rekursiv definierbar, d.h. o die Funktion erscheint in ihrer eigenen Definition. Mathematische Rekursion o Viele mathematische
Dies ist gerade der konstruktive Schritt beim Aufbau von Binomialbäumen.
 Linken von Bäumen: Zwei Bäume desselben Wurzel-Rangs werden unter Einhaltung der Heap-Bedingung verbunden. Sind k 1 und k 2 die Wurzeln der zwei zu linkenden Bäume, so wird ein neuer Baum aufgebaut, dessen
Linken von Bäumen: Zwei Bäume desselben Wurzel-Rangs werden unter Einhaltung der Heap-Bedingung verbunden. Sind k 1 und k 2 die Wurzeln der zwei zu linkenden Bäume, so wird ein neuer Baum aufgebaut, dessen
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Testing for and fixing common security issues
 Testing for and fixing common security issues Fatih Kilic, Thomas Kittel [kilic kittel]@sec.in.tum.de Lehrstuhl für Sicherheit in der Informatik / I20 Prof. Dr. Claudia Eckert Technische Universtität München
Testing for and fixing common security issues Fatih Kilic, Thomas Kittel [kilic kittel]@sec.in.tum.de Lehrstuhl für Sicherheit in der Informatik / I20 Prof. Dr. Claudia Eckert Technische Universtität München
Kapitel 1 Einleitung. Definition: Algorithmus nach M. Broy: aus: Informatik: Eine grundlegende Einführung, Band 1, Springer-Verlag, Berlin
 Kapitel 1 Einleitung 1.1. Begriff des Algorithmus Eine der ältesten Beschreibungstechniken für Abläufe: Benannt nach dem Mathematiker Al-Khwarizmi (ca. 780...840), der am Hof der Kalifen von Bagdad wirkte.
Kapitel 1 Einleitung 1.1. Begriff des Algorithmus Eine der ältesten Beschreibungstechniken für Abläufe: Benannt nach dem Mathematiker Al-Khwarizmi (ca. 780...840), der am Hof der Kalifen von Bagdad wirkte.
Partikelsysteme. Lehrstuhl Computergrafik und Visualisierung Fakultät Informatik TU Dresden. Proseminar Computergrafik.
 58 Partikelsysteme Lehrstuhl Computergrafik und Visualisierung Fakultät Informatik TU Dresden Proseminar Computergrafik Robert Stelzmann Gliederung 1. Einleitung und Motivation 2. Begriffsklärung 3. Einfache
58 Partikelsysteme Lehrstuhl Computergrafik und Visualisierung Fakultät Informatik TU Dresden Proseminar Computergrafik Robert Stelzmann Gliederung 1. Einleitung und Motivation 2. Begriffsklärung 3. Einfache
Die Topologie von R, C und R n
 Die Topologie von R, C und R n Für R haben wir bereits eine Reihe von Strukturen kennengelernt: eine algebraische Struktur (Körper), eine Ordnungsstruktur und eine metrische Struktur (Absolutbetrag, Abstand).
Die Topologie von R, C und R n Für R haben wir bereits eine Reihe von Strukturen kennengelernt: eine algebraische Struktur (Körper), eine Ordnungsstruktur und eine metrische Struktur (Absolutbetrag, Abstand).
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
Detecting Near Duplicates for Web Crawling
 Detecting Near Duplicates for Web Crawling Gurmeet Singh Manku et al., WWW 2007* * 16th international conference on World Wide Web Detecting Near Duplicates for Web Crawling Finde near duplicates in großen
Detecting Near Duplicates for Web Crawling Gurmeet Singh Manku et al., WWW 2007* * 16th international conference on World Wide Web Detecting Near Duplicates for Web Crawling Finde near duplicates in großen
Algorithmen und Datenstrukturen I Bruder-Bäume
 Algorithmen und Datenstrukturen I Bruder-Bäume Prof. Dr. Oliver Braun Letzte Änderung: 11.12.2017 10:50 Algorithmen und Datenstrukturen I, Bruder-Bäume 1/24 Definition ein binärer Baum heißt ein Bruder-Baum,
Algorithmen und Datenstrukturen I Bruder-Bäume Prof. Dr. Oliver Braun Letzte Änderung: 11.12.2017 10:50 Algorithmen und Datenstrukturen I, Bruder-Bäume 1/24 Definition ein binärer Baum heißt ein Bruder-Baum,
Parallele Algorithmen in der Bildverarbeitung
 Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Algorithmen für OBDD s. 1. Reduziere 2. Boole sche Operationen
 Algorithmen für OBDD s 1. Reduziere 2. Boole sche Operationen 1 1. Reduziere siehe auch M.Huth und M.Ryan: Logic in Computer Science - Modelling and Reasoning about Systems, Cambridge Univ.Press, 2000
Algorithmen für OBDD s 1. Reduziere 2. Boole sche Operationen 1 1. Reduziere siehe auch M.Huth und M.Ryan: Logic in Computer Science - Modelling and Reasoning about Systems, Cambridge Univ.Press, 2000
Geradenarrangements und Dualität von Punkten und Geraden
 Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Sudoku ist NP-vollständig
 Sudoku ist NP-vollständig Seminar über Algorithmen und Komplexität Freie Universität Berlin Institut für Informatik SS 007 Sarah Will 8.07.007 Einführung Sudoku ist ein japanisches Logikrätsel und hat
Sudoku ist NP-vollständig Seminar über Algorithmen und Komplexität Freie Universität Berlin Institut für Informatik SS 007 Sarah Will 8.07.007 Einführung Sudoku ist ein japanisches Logikrätsel und hat
A system to integrate the usage of heterogenous input and output devices by the use of a generic interface
 LFE Medieninformatik Ben Blaha Abschlussvortrag Projektarbeit: VISOR Versatile Input Steady Output Remote Control A system to integrate the usage of heterogenous input and output devices by the use of
LFE Medieninformatik Ben Blaha Abschlussvortrag Projektarbeit: VISOR Versatile Input Steady Output Remote Control A system to integrate the usage of heterogenous input and output devices by the use of
Geradenarrangements und Dualität von Punkten und Geraden
 Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Vorlesung Algorithmische Geometrie von Punkten und Geraden INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 12.06.2012 Dualitätsabbildung Bisher haben wir Dualität für planare
Algorithmische Geometrie 8. Voronoidiagramme und Delaunaytriangulierung
 Algorithmische Geometrie 8. Voronoidiagramme und Delaunaytriangulierung JProf. Dr. Heike Leitte Computergraphik und Visualisierung Inhaltsverzeichnis 1. Einführung 2. Konvexe Hülle 3. Schnitte von Liniensegmenten
Algorithmische Geometrie 8. Voronoidiagramme und Delaunaytriangulierung JProf. Dr. Heike Leitte Computergraphik und Visualisierung Inhaltsverzeichnis 1. Einführung 2. Konvexe Hülle 3. Schnitte von Liniensegmenten
Mitschriebe Literatur Taschenrechner
 Name, Vorname... Matrikelnummer... Rechnername... Grundlagen der Darstellung II (Einführung in CAD), Prüfung SS 2014 Allgemeines Ort: Seminarraum 3149 Datum: 17.7.2014 Beginn der Prüfung: Ende der Prüfung:
Name, Vorname... Matrikelnummer... Rechnername... Grundlagen der Darstellung II (Einführung in CAD), Prüfung SS 2014 Allgemeines Ort: Seminarraum 3149 Datum: 17.7.2014 Beginn der Prüfung: Ende der Prüfung:
Vorkurs Informatik WiSe 17/18
 Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Nicole Naczk, 10.10.2017 Technische Universität Braunschweig, IPS Überblick Einleitung Türme von Hanoi Rekursion Beispiele 10.10.2017 Dr. Werner Struckmann
Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Nicole Naczk, 10.10.2017 Technische Universität Braunschweig, IPS Überblick Einleitung Türme von Hanoi Rekursion Beispiele 10.10.2017 Dr. Werner Struckmann
Spline-artige Kurven auf Subdivision Surfaces. Jörn Loviscach Hochschule Bremen, Germany
 Spline-artige Kurven auf Subdivision Surfaces Jörn Loviscach Hochschule Bremen, Germany Überblick Spline-artige Kurven auf Spline-Flächen Kurven auf SDS: Problem, Anwendung Verwandte Arbeiten Spline-artige
Spline-artige Kurven auf Subdivision Surfaces Jörn Loviscach Hochschule Bremen, Germany Überblick Spline-artige Kurven auf Spline-Flächen Kurven auf SDS: Problem, Anwendung Verwandte Arbeiten Spline-artige
Algorithm Engineering. Amortisierung. Stefan Edelkamp
 Algorithm Engineering Amortisierung Stefan Edelkamp Analyse von Algorithmen Best Case Worst Case Average Case Amortisierte Worst Case Was sind die durchschnittlichen Kosten einer schlechtest möglichen
Algorithm Engineering Amortisierung Stefan Edelkamp Analyse von Algorithmen Best Case Worst Case Average Case Amortisierte Worst Case Was sind die durchschnittlichen Kosten einer schlechtest möglichen
Konvexe Hülle. Abbildung: [Wikipedia]: Nicht-konvexe Menge (links), konvexe Menge (rechts) KIT Institut für Theoretische Informatik 510
![Konvexe Hülle. Abbildung: [Wikipedia]: Nicht-konvexe Menge (links), konvexe Menge (rechts) KIT Institut für Theoretische Informatik 510 Konvexe Hülle. Abbildung: [Wikipedia]: Nicht-konvexe Menge (links), konvexe Menge (rechts) KIT Institut für Theoretische Informatik 510](/thumbs/72/66802198.jpg) Konvexe Hülle Definition konvexe Menge: Für je zwei beliebige Punkte, die zur Menge gehören, liegt auch stets deren Verbindungsstrecke ganz in der Menge. Abbildung: [Wikipedia]: Nicht-konvexe Menge (links),
Konvexe Hülle Definition konvexe Menge: Für je zwei beliebige Punkte, die zur Menge gehören, liegt auch stets deren Verbindungsstrecke ganz in der Menge. Abbildung: [Wikipedia]: Nicht-konvexe Menge (links),
Redundanz und Replikation
 Redundanz und Replikation Fehlertoleranz auf Systemebene Kurt Kanzenbach Friedrich Alexander Universität Erlangen-Nürnberg 25. November 2014 1 / 29 Redundanz und Replikation Replikation Replikation: Koordinierter
Redundanz und Replikation Fehlertoleranz auf Systemebene Kurt Kanzenbach Friedrich Alexander Universität Erlangen-Nürnberg 25. November 2014 1 / 29 Redundanz und Replikation Replikation Replikation: Koordinierter
Wie druckt man eine Mannigfaltigkeit? Über die Topologie des 3D-Drucks
 Wie druckt man eine Mannigfaltigkeit? Über die Topologie des 3D-Drucks MNU-Landestagung. 02/2016. Regensburg Clara Löh Fakultät für Mathematik. Universität Regensburg Überblick Ziele Verständnis des Grundprinzip
Wie druckt man eine Mannigfaltigkeit? Über die Topologie des 3D-Drucks MNU-Landestagung. 02/2016. Regensburg Clara Löh Fakultät für Mathematik. Universität Regensburg Überblick Ziele Verständnis des Grundprinzip
Seminararbeit: K-Opt und die Lin-Kernighan-Heuristik für das allgemeine TSP
 Seminararbeit: K-Opt und die Lin-Kernighan-Heuristik für das allgemeine TSP Tobias Boelter 28. Mai 2013 bei Prof. Dr. Rainer Schrader, Universität zu Köln Inhaltsverzeichnis 1 Einleitung 2 2 Lokale Suche
Seminararbeit: K-Opt und die Lin-Kernighan-Heuristik für das allgemeine TSP Tobias Boelter 28. Mai 2013 bei Prof. Dr. Rainer Schrader, Universität zu Köln Inhaltsverzeichnis 1 Einleitung 2 2 Lokale Suche
Anne Groß GI Fachgruppentreffen RE, 24./25.11.2011, Hamburg
 Anforderungen an die Anforderungsspezifikation aus Sicht von Architekten und Usability Experten Anne Groß GI Fachgruppentreffen RE, 24./25.11.2011, Hamburg --- Motivation --- 2 Motivation Informationsquelle
Anforderungen an die Anforderungsspezifikation aus Sicht von Architekten und Usability Experten Anne Groß GI Fachgruppentreffen RE, 24./25.11.2011, Hamburg --- Motivation --- 2 Motivation Informationsquelle
Übung Computergrafik 3
 Übung Computergrafik 3 1.Übungsblatt: Geometrie Stephan Groß (Dank an Irini Schmidt und Jakob Bärz) Institut für Computervisualistik Universität Koblenz-Landau 6. Juli 2011 Aufgabe 1: Fragezeichen Gegeben:
Übung Computergrafik 3 1.Übungsblatt: Geometrie Stephan Groß (Dank an Irini Schmidt und Jakob Bärz) Institut für Computervisualistik Universität Koblenz-Landau 6. Juli 2011 Aufgabe 1: Fragezeichen Gegeben:
Vorkurs Informatik WiSe 16/17
 Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 11.10.2016 Technische Universität Braunschweig, IPS Überblick Einleitung Beispiele 11.10.2016 Dr. Werner Struckmann / Stephan Mielke,
Java Rekursion Dr. Werner Struckmann / Stephan Mielke, Jakob Garbe, 11.10.2016 Technische Universität Braunschweig, IPS Überblick Einleitung Beispiele 11.10.2016 Dr. Werner Struckmann / Stephan Mielke,
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen 13. Übung minimale Spannbäume, topologische Sortierung, AVL-Bäume Clemens Lang Übungen zu AuD 4. Februar 2010 Clemens Lang (Übungen zu AuD) Algorithmen und Datenstrukturen
Algorithmen und Datenstrukturen 13. Übung minimale Spannbäume, topologische Sortierung, AVL-Bäume Clemens Lang Übungen zu AuD 4. Februar 2010 Clemens Lang (Übungen zu AuD) Algorithmen und Datenstrukturen
Algorithmische Geometrie
 Algorithmische Geometrie Martin Peternell TU Wien 31. Fortbildungstagung für Geometrie 2010, Strobl 1 Themen der Algorithmische Geometrie Entwurf von Algorithmen für geometrische Fragestellungen betreffend
Algorithmische Geometrie Martin Peternell TU Wien 31. Fortbildungstagung für Geometrie 2010, Strobl 1 Themen der Algorithmische Geometrie Entwurf von Algorithmen für geometrische Fragestellungen betreffend
1 Rotating Calipers. 2 Antipodal und Copodal. 3 Distanzen Rechtecke Eigenschaften
 1 Rotating Calipers 2 3 Rotating Calipers - Algorithmus Konvexes Polygon mit parallelen Stützgeraden Rotating Calipers - Finder Shamos lässt 1978 zwei Stützgeraden um ein Polygon rotieren Zwei Stützgeraden
1 Rotating Calipers 2 3 Rotating Calipers - Algorithmus Konvexes Polygon mit parallelen Stützgeraden Rotating Calipers - Finder Shamos lässt 1978 zwei Stützgeraden um ein Polygon rotieren Zwei Stützgeraden
Beschleunigung von Bild-Segmentierungs- Algorithmen mit FPGAs
 Fakultät Informatik, Institut für Technische Informatik, Professur für VLSI-Entwurfssysteme, Diagnostik und Architektur Algorithmen mit FPGAs Vortrag von Jan Frenzel Dresden, Gliederung Was ist Bildsegmentierung?
Fakultät Informatik, Institut für Technische Informatik, Professur für VLSI-Entwurfssysteme, Diagnostik und Architektur Algorithmen mit FPGAs Vortrag von Jan Frenzel Dresden, Gliederung Was ist Bildsegmentierung?
Polygontriangulierung
 Vorlesung Algorithmische Geometrie Polygone triangulieren LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 26.04.2011 Das Kunstgalerie-Problem
Vorlesung Algorithmische Geometrie Polygone triangulieren LEHRSTUHL FÜR ALGORITHMIK I INSTITUT FÜR THEORETISCHE INFORMATIK FAKULTÄT FÜR INFORMATIK Martin Nöllenburg 26.04.2011 Das Kunstgalerie-Problem
PROJEKT / SEMINAR DIGITALE FABRIKATION DI
 CONTOURLINES Applikation zur digitalen Fabrikation von Höhenschicht-Modellen PROJEKT / SEMINAR DIGITALE FABRIKATION DI Martin Emmerer Matr.Nr.95 30 952 1 Zielsetzung Höhenlinien, auch Isohypsen, Niveaulinien
CONTOURLINES Applikation zur digitalen Fabrikation von Höhenschicht-Modellen PROJEKT / SEMINAR DIGITALE FABRIKATION DI Martin Emmerer Matr.Nr.95 30 952 1 Zielsetzung Höhenlinien, auch Isohypsen, Niveaulinien
Ultrametrik. Christian Semrau Metrische Räume
 Ultrametrik Christian Semrau 05.11.2002 Inhaltsverzeichnis 1 Metrische Räume 1 1.1 Definition der Metrik.................................. 1 1.2 Offene und abgeschlossene Mengen..........................
Ultrametrik Christian Semrau 05.11.2002 Inhaltsverzeichnis 1 Metrische Räume 1 1.1 Definition der Metrik.................................. 1 1.2 Offene und abgeschlossene Mengen..........................
Textverarbeitung mit Word
 Der Tabelleneditor unterscheidet sich vom Tabulator dadurch, dass die Tabelle in oder mit einem Gitternetz gestaltet wird. Die Elemente der Tabelle, Zeile, Spalte, Zelle oder Feld, bleiben erhalten. Doch
Der Tabelleneditor unterscheidet sich vom Tabulator dadurch, dass die Tabelle in oder mit einem Gitternetz gestaltet wird. Die Elemente der Tabelle, Zeile, Spalte, Zelle oder Feld, bleiben erhalten. Doch
Polygon Triangulation. robot.scr. "Art Gallery Problem" Sichtbarkeitspolygon. Algorithmische Geometrie - SS 99 - Th. Ottmann
 Polygon Triangulation "Art Gallery Problem" Sichtbarkeitspolygon robot.scr Triangulation simpler Polygone P w v u Satz: Triangulation existiert und besitzt n-2 Dreiecke Bew.: Induktion über n> 3. Suche
Polygon Triangulation "Art Gallery Problem" Sichtbarkeitspolygon robot.scr Triangulation simpler Polygone P w v u Satz: Triangulation existiert und besitzt n-2 Dreiecke Bew.: Induktion über n> 3. Suche
Vorbereitung der Bauteil-Abgabe mit netfabb Studio Basic
 TUTORIAL BAUTEIL REPARATUR Vorbereitung der Bauteil-Abgabe mit netfabb Studio Basic Stand 10/2010 netfabb Studio Basic Version 4.6.0 Vorwort Die STL-Schnittstelle (Standard Triangulation Language) oder
TUTORIAL BAUTEIL REPARATUR Vorbereitung der Bauteil-Abgabe mit netfabb Studio Basic Stand 10/2010 netfabb Studio Basic Version 4.6.0 Vorwort Die STL-Schnittstelle (Standard Triangulation Language) oder
Praxiswerkstatt Algorithmen der Signalcodierung
 Praxiswerkstatt Algorithmen der Signalcodierung 2. Termin Themen heute: Abtastung Lineare Zeitinvariante Systeme Seite 1 Abtastung letztes Mal haben wir gesehen: 3,9 khz kaum noch hörbar bei 8 khz Abtastrate.
Praxiswerkstatt Algorithmen der Signalcodierung 2. Termin Themen heute: Abtastung Lineare Zeitinvariante Systeme Seite 1 Abtastung letztes Mal haben wir gesehen: 3,9 khz kaum noch hörbar bei 8 khz Abtastrate.
Informatik B von Adrian Neumann
 Musterlösung zum 7. Aufgabenblatt vom Montag, den 25. Mai 2009 zur Vorlesung Informatik B von Adrian Neumann 1. Java I Schreiben Sie ein Java Programm, das alle positiven ganzen Zahlen 0 < a < b < 1000
Musterlösung zum 7. Aufgabenblatt vom Montag, den 25. Mai 2009 zur Vorlesung Informatik B von Adrian Neumann 1. Java I Schreiben Sie ein Java Programm, das alle positiven ganzen Zahlen 0 < a < b < 1000
Geometrie I. Laura Lawniczak Hallo Welt -Seminar - LS 2
 Geometrie I Laura Lawniczak 12.07.2017 Hallo Welt -Seminar - LS 2 Inhalt Grundlagen Abstandsberechnung Punkt-Gerade Punkt-Segment CCW Polygone Punkt in Polygon Pick s Theorem Konvexe Hülle 12.07.2017 Laura
Geometrie I Laura Lawniczak 12.07.2017 Hallo Welt -Seminar - LS 2 Inhalt Grundlagen Abstandsberechnung Punkt-Gerade Punkt-Segment CCW Polygone Punkt in Polygon Pick s Theorem Konvexe Hülle 12.07.2017 Laura
1. Flash-Anleitung für die SD-Karte
 SD card Flashing Guide Open 1. Flash-Anleitung für die SD-Karte 1)Schritt 1: Erstellen Sie ein Backup Ihrer Daten Erstellen Sie vor dem Upgrade bitte ein Backup Ihrer persönlichen Daten mit dem Google-Service
SD card Flashing Guide Open 1. Flash-Anleitung für die SD-Karte 1)Schritt 1: Erstellen Sie ein Backup Ihrer Daten Erstellen Sie vor dem Upgrade bitte ein Backup Ihrer persönlichen Daten mit dem Google-Service
Algorithm Engineering. Alexander Kröller, Abteilung Algorithmik, IBR
 #7 Terminchaos Nächste Vorlesungen: 27. 5. Vertretung durch Prof. Fekete 3. 6. Exkursionswoche 10. 6. Vertretung durch N.N. 17. 6. back to normal... Experiment Durchlaufe zwei gleichgrosse Arrays: Sortierte
#7 Terminchaos Nächste Vorlesungen: 27. 5. Vertretung durch Prof. Fekete 3. 6. Exkursionswoche 10. 6. Vertretung durch N.N. 17. 6. back to normal... Experiment Durchlaufe zwei gleichgrosse Arrays: Sortierte
KARL-FRANZENS-UNIVERSITÄT GRAZ. Seminar aus Reiner Mathematik. Die Museumswächter. Krupic Mustafa Wintersemester 2013/14
 KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
KARL-FRANZENS-UNIVERSITÄT GRAZ Seminar aus Reiner Mathematik Die Museumswächter Krupic Mustafa Wintersemester 2013/14 Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Museumswächter-Satz 6 2.1
Seminarvortrag über die Euler-Charakteristik einer Fläche
 Dies ist eine Ausarbeitung für einen Seminarvortrag, den ich im Sommersemester 2013/14 an der Humboldt-Universität im Proseminar Differentialgeometrie von Kurven und Flächen bei Christoph Stadtmüller gehalten
Dies ist eine Ausarbeitung für einen Seminarvortrag, den ich im Sommersemester 2013/14 an der Humboldt-Universität im Proseminar Differentialgeometrie von Kurven und Flächen bei Christoph Stadtmüller gehalten
Einheit 11 - Graphen
 Einheit - Graphen Bevor wir in medias res (eigentlich heißt es medias in res) gehen, eine Zusammenfassung der wichtigsten Definitionen und Notationen für Graphen. Graphen bestehen aus Knoten (vertex, vertices)
Einheit - Graphen Bevor wir in medias res (eigentlich heißt es medias in res) gehen, eine Zusammenfassung der wichtigsten Definitionen und Notationen für Graphen. Graphen bestehen aus Knoten (vertex, vertices)
Unendliche Graphen. Daniel Perz 24. Dezember Definition 1. Ein Graph G heißt lokal endlich, wenn alle Knotengrade endlich sind.
 Unendliche Graphen Daniel Perz 24. Dezember 2011 1 Definition Definition 1. Ein Graph G heißt lokal endlich, wenn alle Knotengrade endlich sind. Definition 2. Ein Graph G=(V,E) heißt Strahl, wenn gilt
Unendliche Graphen Daniel Perz 24. Dezember 2011 1 Definition Definition 1. Ein Graph G heißt lokal endlich, wenn alle Knotengrade endlich sind. Definition 2. Ein Graph G=(V,E) heißt Strahl, wenn gilt
Algorithmen und Datenstrukturen 1
 Algorithmen und Datenstrukturen 1 8. Vorlesung Martin Middendorf und Peter F. Stadler Universität Leipzig Institut für Informatik middendorf@informatik.uni-leipzig.de studla@bioinf.uni-leipzig.de Gefädelte
Algorithmen und Datenstrukturen 1 8. Vorlesung Martin Middendorf und Peter F. Stadler Universität Leipzig Institut für Informatik middendorf@informatik.uni-leipzig.de studla@bioinf.uni-leipzig.de Gefädelte
2. Optimierungsprobleme 6
 6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
ShopBot, ein Software-Agent für das Internet
 Software-Agenten p.1/20 ShopBot, ein Software-Agent für das Internet Eine Einführung in (Software-)Agenten Madeleine Theile Software-Agenten p.2/20 Aufbau des Vortrags grundlegende Theorie Definition Autonomy,
Software-Agenten p.1/20 ShopBot, ein Software-Agent für das Internet Eine Einführung in (Software-)Agenten Madeleine Theile Software-Agenten p.2/20 Aufbau des Vortrags grundlegende Theorie Definition Autonomy,
Zahlenschleifen. Schülerzirkel Mathematik. 1 Die Regeln von Slitherlink. Das Slitherlink-Puzzle von nikoli
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg 0 0 Zahlenschleifen Das Slitherlink-Puzzle von nikoli Die Regeln von Slitherlink Slitherlink ist eines von vielen Puzzles, die von
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg 0 0 Zahlenschleifen Das Slitherlink-Puzzle von nikoli Die Regeln von Slitherlink Slitherlink ist eines von vielen Puzzles, die von
Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit
![Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit Counting - Sort [ [ ] [ [ ] 1. SS 2008 Datenstrukturen und Algorithmen Sortieren in linearer Zeit](/thumbs/60/44575606.jpg) Counting-Sort Counting - Sort ( A,B,k ). for i to k. do C[ i]. for j to length[ A]. do C[ A[ j ] C[ A[ j ] +. > C[ i] enthält Anzahl der Elemente in 6. for i to k. do C[ i] C[ i] + C[ i ]. > C[ i] enthält
Counting-Sort Counting - Sort ( A,B,k ). for i to k. do C[ i]. for j to length[ A]. do C[ A[ j ] C[ A[ j ] +. > C[ i] enthält Anzahl der Elemente in 6. for i to k. do C[ i] C[ i] + C[ i ]. > C[ i] enthält
Übersicht. Rot-schwarz Bäume. Rot-schwarz Bäume. Beispiel. Eigenschaften. Datenstrukturen & Algorithmen. Rot-schwarz Bäume Eigenschaften Einfügen
 Datenstrukturen & Algorithmen Übersicht Rot-schwarz Bäume Eigenschaften Einfügen Matthias Zwicker Universität Bern Frühling 2009 2 Rot-schwarz Bäume Binäre Suchbäume sind nur effizient wenn Höhe des Baumes
Datenstrukturen & Algorithmen Übersicht Rot-schwarz Bäume Eigenschaften Einfügen Matthias Zwicker Universität Bern Frühling 2009 2 Rot-schwarz Bäume Binäre Suchbäume sind nur effizient wenn Höhe des Baumes
Topologieseminar. Faserbündel. Michael Espendiller. 16. Oktober 2010 Universität Münster - 3 Faserbündel oder lokal triviale Bündel 4
 Wintersemester 2010/2011 Topologieseminar Faserbündel Michael Espendiller 16. Oktober 2010 Universität Münster - Inhaltsverzeichnis 1 Allgemeine Bündel 1 2 Morphismen und Schnitte 2 3 Faserbündel oder
Wintersemester 2010/2011 Topologieseminar Faserbündel Michael Espendiller 16. Oktober 2010 Universität Münster - Inhaltsverzeichnis 1 Allgemeine Bündel 1 2 Morphismen und Schnitte 2 3 Faserbündel oder
Modelle der Parallelverarbeitung 7. Baumförmige Zellularautomaten
 Modelle der Parallelverarbeitung Modelle der Parallelverarbeitung 7. Baumförmige Zellularautomaten Thomas Worsch Fakultät für Informatik Karlsruher Institut für Technologie Sommersemester 2016 1 / 29 Überblick
Modelle der Parallelverarbeitung Modelle der Parallelverarbeitung 7. Baumförmige Zellularautomaten Thomas Worsch Fakultät für Informatik Karlsruher Institut für Technologie Sommersemester 2016 1 / 29 Überblick
1 Einführung: Algorithmen. Algorithmen und Datenstrukturen WS 2012/13. Pro f. Dr. Sán do r Fe k e te
 1 Einführung: Algorithmen Algorithmen und Datenstrukturen WS 2012/13 Pro f. Dr. Sán do r Fe k e te Literatur 1.1 Was ist ein Algorithmus? Ein Algorithmus ist eine aus endlich vielen Schritten bestehende
1 Einführung: Algorithmen Algorithmen und Datenstrukturen WS 2012/13 Pro f. Dr. Sán do r Fe k e te Literatur 1.1 Was ist ein Algorithmus? Ein Algorithmus ist eine aus endlich vielen Schritten bestehende
Amortisierte Analyse
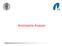 Amortisierte Analyse Amortisierung Betrachte eine Folge a 1, a 2,..., a n von n Operation auf Datenstruktur D T i = Ausführungszeit von a i T = T 1 + T 2 +... + T n, Gesamtlaufzeit Oft kann die Laufzeit
Amortisierte Analyse Amortisierung Betrachte eine Folge a 1, a 2,..., a n von n Operation auf Datenstruktur D T i = Ausführungszeit von a i T = T 1 + T 2 +... + T n, Gesamtlaufzeit Oft kann die Laufzeit
Topologische Isolatoren
 Topologische Isolatoren Ein Überblick Joscha Reichert 6. Juli 2011 1 / 14 Allgemeines Der Topologische Isolator Topologie - Ein Teilbereich der Mathematik 2 / 14 Allgemeines Der Topologische Isolator Topologie
Topologische Isolatoren Ein Überblick Joscha Reichert 6. Juli 2011 1 / 14 Allgemeines Der Topologische Isolator Topologie - Ein Teilbereich der Mathematik 2 / 14 Allgemeines Der Topologische Isolator Topologie
Hidden Markov Model ein Beispiel
 Hidden Markov Model ein Beispiel Gegeben: Folge von Beobachtungen O = o 1,..., o n = nass, nass, trocken, nass, trocken Menge möglicher Systemzustände: Z = {Sonne, Regen} Beobachtungswahrscheinlichkeiten:
Hidden Markov Model ein Beispiel Gegeben: Folge von Beobachtungen O = o 1,..., o n = nass, nass, trocken, nass, trocken Menge möglicher Systemzustände: Z = {Sonne, Regen} Beobachtungswahrscheinlichkeiten:
Algorithmische Geometrie 1. Einführung
 Algorithmische Geometrie 1. Einführung JProf. Dr. Heike Leitte Computergraphik und Visualisierung Algorithmische Geometrie Veranstaltung: 2 SWS Vorlesung: Mi, 9:15 10:45 1 SWS Übung: Do 14:00 16:00 Übungen:
Algorithmische Geometrie 1. Einführung JProf. Dr. Heike Leitte Computergraphik und Visualisierung Algorithmische Geometrie Veranstaltung: 2 SWS Vorlesung: Mi, 9:15 10:45 1 SWS Übung: Do 14:00 16:00 Übungen:
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle. zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"):
 Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
Grundlagen zur Delaunay-Triangulierung und zur konvexen Hülle zum Begriff des Voronoi-Diagramms (vgl. auch Vorlesung "Algorithmische Geometrie"): 1 Erzeugung des Voronoi-Diagramms (siehe Vorlesung "Algorithmische
WINDOWS 10. 1 Der schnelle Einstieg in Windows 10. Apps, Ordner und Dateien suchen und anzeigen
 1 Der schnelle Einstieg in Windows 10 A WINDOWS 10 Apps, Ordner und Dateien suchen und anzeigen Level Zeit ca. 5 min Übungsdatei Elemente suchen Pflanze_1, Pflanze_2, Pflanze_3, Pflanze_4 1. Suchen Sie
1 Der schnelle Einstieg in Windows 10 A WINDOWS 10 Apps, Ordner und Dateien suchen und anzeigen Level Zeit ca. 5 min Übungsdatei Elemente suchen Pflanze_1, Pflanze_2, Pflanze_3, Pflanze_4 1. Suchen Sie
SONNENUHR UND KOMPASS - SET Winkler - Nr
 SONNENUHR UND KOMPSS - SET Winkler - Nr. 102099 Einführung: Die Sonne macht von jedem Ort auf der Erde aus gesehen eine tägliche Wanderung von Ost (Sonnenaufgang) nach West (Sonnenuntergang). Eigentlich
SONNENUHR UND KOMPSS - SET Winkler - Nr. 102099 Einführung: Die Sonne macht von jedem Ort auf der Erde aus gesehen eine tägliche Wanderung von Ost (Sonnenaufgang) nach West (Sonnenuntergang). Eigentlich
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls
 4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
4.9 Deterministische Kellerautomaten Wir haben bereits definiert: Ein PDA heißt deterministisch (DPDA), falls δ(q, a, Z) + δ(q, ɛ, Z) 1 (q, a, Z) Q Σ. Die von einem DPDA, der mit leerem Keller akzeptiert,
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen
 Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
