Perpetuum mobile. Perpetuum mobile erster Art:
|
|
|
- Lothar Adenauer
- vor 9 Jahren
- Abrufe
Transkript
1 Perpetuum mobile Perpetuum mobile erster Art: Maschine, die ständig Arbeit leistet, ohne ihre Umgebung energetisch zu verändern (die also Arbeit leistet, ohne ein Energiereservoir zu benutzen). Verletzt Energieerhaltungssatz (I. HS) Perpetuum mobile zweiter Art: Maschine, die in einem periodische Prozess Wärme vollständig in Arbeit umwandeln kann. Verletzt (II. HS)
2 Plancksche Version des II. HS Es ist unmöglich, eine periodisch arbeitende Wärmekraftmaschine zu bauen, die nur mit einem Wärmereservoir Wärme austauscht. Wäre Perpetuum mobile zweiter Art. Es wäre eine Maschine, die die Wärme, die sie aus dem Reservoir bezieht, zu hundert Prozent in Arbeit umwandelt (wäre die Konversion nicht 100 %, so würde sich die Maschine ständig erhitzen und schließlich selbst zerstören). Problem ist, dass die Maschine die bei der Rückkehr zum Ausgangspunkt anfallende Abwärme Q t nicht los wird. Die höchstmögliche Effizienz η, die eine Wärmekraftmaschine erreichen kann, hat der Carnotprozess: T h -T η = t T h T W Q t S 1 S 2 η = 1 kann nur erreicht werden, wenn T t = 0 K wäre. Selbst dies ist nicht aufrechtzuerhalten, weil die Maschine das untere Reservoir aufheizt. S
3 Stirling-Prozess: p-v- und T-S-Diagramm Stirling-Prozess im p-v-diagramm (idealisiert) Tatsächlicher Verlauf Experiment und nächste Seite p isochor isotherm isochor isotherm V Stirling-Prozess im T-S-Diagramm Isochore Schritte: T = T i e S C V C V : Wärmekapazität C V = ½ f N k B S = (3/2) N k B ln(t/ti) T T h T t isochor W= Q isotherm S 1 S 2 isotherm isochor S 4 S 3 S
4 Stirling-Prozess Heißluftmotor als Beispiel eines praktisch realisierbaren Kreisprozesses nach Robert Stirling (Geistlicher), 1816 Eine Bauform der Maschine Realer Zyklus im p-v-diagramm (gasdurchlässig) Abbildung aus H. J. Leisi, Klassische Physik 2, S. 419, Birkhäuser Verlag Abbildung aus W. Martienssen, Einführung in die Physik III, S. 356, Verlag Harri Deutsch Die im idealisierten Prozess als isochor angenommenen Teilschritte sind in Wahrheit stark verrundet, weil das Zylindervolumen sich zu schnell ändert.
5 A.) Isotherme Expansion: Heißes Gas übt hohen Druck auf den Arbeitskolben aus und drückt ihn nach oben. Der Verdrängerkolben, der sich bei seinem oberen Totpunkt befindet, hält das Gas im heißen Bereich Temperatur bleibt hoch. Schritte beim Stirling-Prozess B.) Isochore Abkühlung: Der Verdrängerkolben drückt nach unten und verdrängt das Gas in den kalten Bereich. Der Arbeitskolben ist beim oberen Totpunkt, das Gasvolumen ist maximal und ändert sich nur langsam. D.) Isochore Erwärmung: Der Arbeitskolben erreicht seinen unteren Totpunkt, das Gasvolumen ändert sich kaum. Der Verdrängerkolben wandert nach oben und drückt das komprimierte Gas in den heißen Bereich, wo es sich im Kontakt mit der Wand erwärmt. p D C A B V C.) Isotherme Kompression: Der Arbeitskolben drückt nach unten und komprimiert das kalte Gas. Der Verdrängerkolben ist im Bereich seines unteren Totpunktes und reduziert den Kontakt des Gases mit der heißen Wand. Abbildungen aus H. J. Leisi, Klassische Physik 2, Birkhäuser Verlag
6 Kühlschrank Schema des Energieflusses Q h Heißes Kühlmedium Q W Kaltes Kühlmedium Innenraum des Kühlschranks Q t Abbildung aus D. C. Giancoli, Physics for Scientists and Engineers, Prentice Hall Kühlschrank als Beispiel einer Kältemaschine Würde zwar auch mit einem idealen Gas funktionieren, aber in der Praxis nutzt man den Phasenübergang eines realen Gases aus, um höhere Kälteleistung zu erzielen.
7 Zahlenbeispiel: Effizienz einer Wärmepumpe Leistungszahl der Wärmepumpe: ε P = Q h W Th T T Eine typische Wärmepumpe hat eine Leistungszahl von 3.0 bei einer mechanischen Leistung von 1500 W. Wieviel Wärmeleistung gibt die Wärmepumpe ab? Pro Sekunde abgegebene Wärme Q h = ε P W = Ws = 4500 Ws. Wärmeleistung: 4500 W. Im Sommer kann man die Wärmepumpe als Klimaanlage (Kältemaschine) verwenden. Wieviel Wärmeleistung kann sie dem Haus entziehen? Wegen der Energieerhaltung Q t = Q h - W ist die dem Haus entzogene Wärmeleistung 4500 W 1500 W = 3000 W. Die Effizienz ist ε Q t W 3000 W 1500 W K = = = 2 h t
8 Reale Gase und Phasenübergang p-v-diagramm von H 2 O kritischer Punkt: Punkt: C, bar, bar, V krit = krit l/mol l/mol reines reines Gas Gas reine reine Flüssigkeit Koexistenzgebiet Gas-Flüssigkeit Abbildung aus W. Martienssen, Einführung in die Physik III, S. 361, Verlag Harri Deutsch
9 p-v-t-diagramm realer Gase Isothermen Tripelpunkt: Koexistenz von von fester, fester, flüssiger und und gasförmiger Phase Phase Abbildungen aus H. J. Leisi, Klassische Physik 2, S. 382, Birkhäuser Verlag
10 Anomalie des Wassers Während sich die meisten Stoffe beim Erstarren etwas zusammenziehen, dehnt sich das Wasser bei der Eisbildung aus. Dichte des Eises ist niedriger, Eis schwimmt auf dem Wasser Eis lässt sich unter Druck schmelzen. Volumenzunahmebeim Schmelzen nahme Volumenabnahmebeim Schmelzen nahme Abbildungen aus Gerthsen Physik, Springer Verlag
11 Komplexes Phasendiagramm von Wasser Abbildung aus Gerthsen Physik, Springer Verlag
12 p-v-diagramm für CO 2 Kritischer Punkt: Punkt: 31 C, 31 C, bar, bar, V krit = krit l/mol l/mol Tripelpunkt: Koexistenz von von fester, fester, flüssiger und und gasförmiger Phase Phase Abbildung aus W. Martienssen, Einführung in die Physik III, S. 300, Verlag Harri Deutsch
13 Unterscheidung flüssig - gasförmig Umlauf um den kritischen Punkt: Rückkehr nach nach A: A: Es Es müsste müsste reines reines Gas Gas vorliegen! Der Der weitere Weg Weg von von B über über C und und D nach nach A führt führt nur nur durch durch das das Gebiet Gebiet der der gasförmigen Phase. Phase. (Scheinbarer) Widerspruch Startpunkt A: A: reine reine Flüssigkeit Nach Nach Durchlaufen des des Koexistenzgebietes liegt liegt bei bei B reines reines Gas Gas vor vor Abbildung aus Martienssen, Einführung in die Physik III, S. 300, Verlag Harri Deutsch Die flüssige und die gasförmige Phase lassen sich nur voneinander unterscheiden, wenn beide gemeinsam vorliegen. Beide Phasen gehen am kritischen Punkt stetig ineinander über und haben dort exakt die gleiche Dichte.
14 Kritische Opaleszenz Bei Temperaturen oberhalb des kritischen Punktes ist die Unterscheidung von flüssiger und gasförmiger Phase nicht mehr sinnvoll. Am kritischen Punkt treten starke Dichteschwankungen auf, die sich in starker Lichtstreuung (opaleszierende Farbwirkung) oder plötzlicher Lichtundurchlässigkeit bei vorheriger Lichtdurchlässigkeit äußern Exp.: mit Freon (C 2 ClF 5 ): T krit = 80ºC, p krit = 30.8 bar (Wegen dem niedrigeren kritischen Druck ist das Experiment noch nicht gefährlich, bei CO 2 wäre das mit p krit = 74 bar schon anders.) Abbildung aus W. Martienssen, Einführung in die Physik III, S. 300, Verlag Harri Deutsch Beobachtung: Bei isochorer Erwärmung einer Küvette mit Freon verschwindet die Phasengrenze flüssig-gasförmig bei Erreichen der kritischen Linie. Dort wird Licht, das man durch die Küvette strahlt, so stark gestreut, dass die Küvette undurchsichtig wird. Bei höheren Temperaturen wird sie wieder durchsichtig.
15 Reale Gase Bisher Wechselwirkung und Ausdehnung der Gasteilchen vernachlässigt. Ihre Berücksichtigung modifiziert die Zustandsgleichung des Gases. Eine der verwendeten Näherungsbeschreibungen für reale Gase: van-der-waals-gleichung realer Gase p + a 2 µ V Binnendruck ( V b µ ) = µ R T Kovolumen µ: Molarität R: Gaskonstante Binnendruck (Kohäsionsdruck): Durch die anziehenden Kräfte zwischen den Atomen/Mole-külen hervorgerufener zusätzlicher Druck auf die Teilchen im Innern des Gases Kovolumen: Ist das von den Teilchen selbst eingenommene Volumen; es reduziert den für die freie Bewegung zur Verfügung stehenden Raum.
16 Kovolumen realer Gase Das Kovolumen gibt unmittelbar an, welches Volumen die Atome/Moleküle in einem Mol eines Gases einnehmen. Kovolumen Gefäßvolumen Das Volumen der Moleküle eines Mols N 2 beträgt l. Der Wert ist mit dem Molvolumen von 22.4 l des Gases bei Normalbedingungen (0 C, bar) zu vergleichen. Bei erhöhtem Druck ist das Kovolumen nicht mehr vernachlässigbar. H 2 H 2 O O 2 N 2 CO 2 b Liter mol
17 Binnendruck realer Gase Wechselwirkung der Teilchen untereinander wirkt sich vor allem an der Oberfläche aus: Rand Gas Auf Teilchen am Rand wirkt eine Nettokraft nach innen (zu Binnendruck ~ (µ/v) 2 siehe H. J. Leisi) Ein Teilchen im Innern des Gases erfährt von allen Seiten Anziehungskräfte, die sich im Zeitmittel aufheben. Die resultierende Kraft bewirkt, dass die Teilchen am Rand weniger Kraft und damit weniger Druck auf die Wand ausüben. H 2 H 2 O O 2 N 2 CO 2 a Liter 2 mol
18 Berechnete van-der- Waals-Isotherme für H 2 O Hohe Temperatur: Verhalten annähernd wie bei idealem Gas Kritische Temperatur: Horizontaler Verlauf am Tripelpunkt Tiefe Temperatur: Verhalten wird instabil. Für einen gegebenen Druck gibt es mehrere mögliche Zustände. Von großem Volumen aus kommend kann das Gas kollabieren. Tatsächliche Gleichgewichtsisotherme ist horizontale Zweiphasenlinie (z.b. Linie AB) Maxwell-Konstruktion Abbildung aus W. Martienssen, Einführung in die Physik III, S. 298, Verlag Harri Deutsch µ R T p = V b µ µ a V Instabilität des des Gasvolumens, es es existieren mehrere erlaubte Volumina Ursache: Binnendruck µ R T µ p = a V b µ V 2 V b µ: b µ: Gasvolumen kann kann nicht nicht unter unter das das Kovolumen absinken; der der Druck Druck steigt steigt bei bei Annäherung V b µ b µ gegen gegen Unendlich 2
19 Übersättigter Dampf, Siedeverzug Dass die van-der-waals-gleichung die tatsächlichen Verhältnisse recht gut wiedergibt, sieht man an der Existenz von Siedeverzug und Dampfübersättigung Übersättigter Dampf tritt bei vorsichtigem Abkühlen (ohne Kondensationskeime) eines Gases auf. Flüssigkeitsbildung ist verzögert. Siedeverzug bei vorsichtigem (siedekeimfreiem Erwärmen) einer Flüssigkeit. Dampfbildung ist verzögert.
20 Sättigungsdampfdruck p Sättigungsdampfdruck: Dampfdruck über Flüssigkeit/Festkörper im Gleichgewicht, gemessen bei geschlossenem Gefäß Dampf Sättigungsdampfdruck von Wasser: Flüssigkeit T [ C] p [mbar]
21 Sättigungsdampfdruck Dampfdruck über Flüssigkeit/Festkörper im Gleichgewicht Sättigungsdampfdruck: pd = const e V kbt E V : V : Verdampfungsenergie pro pro Molekül E
22 Sieden Sieden tritt ein, wenn der Dampfdruck den äußeren Druck erreicht. Sieden von Wasser im Kochtopf tritt ein, wenn der Dampfdruck dem äußeren Luftdruck entspricht Niedrigerer Luftdruck, niedrigerer Siedepunkt (zwar siedet das Wasser schneller, aber Essen wird nicht schneller gar) Mehrkomponentiges System. Es stellen sich Partialdrücke ein: Im Im Reagenzglas herrscht der der Luftdruck plus plus der der Sättigungsdampfdruck von von Äther Äther Abbildung aus W. Martienssen, Einführung in die Physik III, S. 363, Verlag Harri Deutsch
23 Sieden Abbildung aus W. Martienssen, Einführung in die Physik III, S. 372, Verlag Harri Deutsch
Carnotscher Kreisprozess
 Carnotscher Kreisprozess (idealisierter Kreisprozess) 2 p 1, V 1, T 1 p(v) dv > 0 p 2, V 2, T 1 Expansionsarbeit wird geleistet dq fließt aus Wärmebad zu dq > 0 p 2, V 2, T 1 p(v) dv > 0 p 3, V 3, T 2
Carnotscher Kreisprozess (idealisierter Kreisprozess) 2 p 1, V 1, T 1 p(v) dv > 0 p 2, V 2, T 1 Expansionsarbeit wird geleistet dq fließt aus Wärmebad zu dq > 0 p 2, V 2, T 1 p(v) dv > 0 p 3, V 3, T 2
Physik I Mechanik der Kontinua und Wärmelehre Thomas Schörner-Sadenius
 Physik I Mechanik der Kontinua und Wärmelehre Thomas Universität Hamburg Wintersemester 2014/15 ORGANISATORISCHES Thomas : Wissenschaftler (Teilchenphysik) am Deutschen Elektronen-Synchrotron (DESY) Kontakt:
Physik I Mechanik der Kontinua und Wärmelehre Thomas Universität Hamburg Wintersemester 2014/15 ORGANISATORISCHES Thomas : Wissenschaftler (Teilchenphysik) am Deutschen Elektronen-Synchrotron (DESY) Kontakt:
E2: Wärmelehre und Elektromagnetismus 6. Vorlesung
 E2: Wärmelehre und Elektromagnetismus 6. Vorlesung 26.04.2018 Heute: - Kondensationskerne - Van der Waals-Gas - 2. Hauptsatz https://xkcd.com/1166/ Prof. Dr. Jan Lipfert [email protected] 26.04.2018 Prof.
E2: Wärmelehre und Elektromagnetismus 6. Vorlesung 26.04.2018 Heute: - Kondensationskerne - Van der Waals-Gas - 2. Hauptsatz https://xkcd.com/1166/ Prof. Dr. Jan Lipfert [email protected] 26.04.2018 Prof.
Versuch: Sieden durch Abkühlen
 ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
d) Das ideale Gas makroskopisch
 d) Das ideale Gas makroskopisch Beschreibung mit Zustandsgrößen p, V, T Brauchen trotzdem n, R dazu Immer auch Mikroskopische Argumente dazunehmen Annahmen aus mikroskopischer Betrachtung: Moleküle sind
d) Das ideale Gas makroskopisch Beschreibung mit Zustandsgrößen p, V, T Brauchen trotzdem n, R dazu Immer auch Mikroskopische Argumente dazunehmen Annahmen aus mikroskopischer Betrachtung: Moleküle sind
Wärmelehre Zustandsänderungen ideales Gases
 Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Die 4 Phasen des Carnot-Prozesses
 Die 4 Phasen des Carnot-Prozesses isotherme Expansion: A B V V T k N Q ln 1 1 isotherme Kompression: adiabatische Kompression: adiabatische Expansion: 0 Q Q 0 C D V V T k N Q ln 2 2 S Q 1 1 /T1 T 1 T 2
Die 4 Phasen des Carnot-Prozesses isotherme Expansion: A B V V T k N Q ln 1 1 isotherme Kompression: adiabatische Kompression: adiabatische Expansion: 0 Q Q 0 C D V V T k N Q ln 2 2 S Q 1 1 /T1 T 1 T 2
Reale Gase. Versuch: RG. Inhaltsverzeichnis. Fachrichtung Physik. Erstellt: E. Beyer Aktualisiert: am Physikalisches Grundpraktikum
 Versuch: RG Fachrichtung Physik Physikalisches Grundpraktikum Erstellt: E. Beyer Aktualisiert: am 01. 10. 2010 Bearbeitet: J. Kelling F. Lemke S. Majewsky M. Justus Reale Gase Inhaltsverzeichnis 1 Aufgabenstellung
Versuch: RG Fachrichtung Physik Physikalisches Grundpraktikum Erstellt: E. Beyer Aktualisiert: am 01. 10. 2010 Bearbeitet: J. Kelling F. Lemke S. Majewsky M. Justus Reale Gase Inhaltsverzeichnis 1 Aufgabenstellung
Physik III im Studiengang Elektrotechnik
 hysik III im Studiengang Elektrotechnik - reale Gase, hasenübergänge - rof. Dr. Ulrich Hahn WS 2008/09 reale Gase kleine Temperaturen, hohe Drücke: Moleküle weisen Eigenvolumen auf Moleküle ziehen sich
hysik III im Studiengang Elektrotechnik - reale Gase, hasenübergänge - rof. Dr. Ulrich Hahn WS 2008/09 reale Gase kleine Temperaturen, hohe Drücke: Moleküle weisen Eigenvolumen auf Moleküle ziehen sich
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
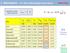 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
II. Wärmelehre. II.2. Die Hauptsätze der Wärmelehre. Physik für Mediziner 1
 II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
Heissluftmotor ******
 luftmotor 8.3.302 luftmotor ****** 1 Motivation Ein luft- bzw. Stirlingmotor erzeugt mechanische Arbeit. Dies funktioniert sowohl mit einer Beheizung als auch mit einem Kältebad. Durch Umkehrung der Laufrichtung
luftmotor 8.3.302 luftmotor ****** 1 Motivation Ein luft- bzw. Stirlingmotor erzeugt mechanische Arbeit. Dies funktioniert sowohl mit einer Beheizung als auch mit einem Kältebad. Durch Umkehrung der Laufrichtung
PC-Übung Nr.3 vom
 PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Isotherme 3. 4 Adiabate 2 T 1. Adiabate Isotherme T 2. Arbeit nach außen = eingeschlossene Kurve
 Carnotscher Kreisprozess Carnot Maschine = idealisierte Maschine, experimentell nicht gut zu realisieren. Einfacher Kreisprozess aus zwei isothermen und zwei adiabatischen Zustandsänderungen. Arbeit nach
Carnotscher Kreisprozess Carnot Maschine = idealisierte Maschine, experimentell nicht gut zu realisieren. Einfacher Kreisprozess aus zwei isothermen und zwei adiabatischen Zustandsänderungen. Arbeit nach
8.4.5 Wasser sieden bei Zimmertemperatur ******
 8.4.5 ****** 1 Motivation Durch Verminderung des Luftdrucks siedet Wasser bei Zimmertemperatur. 2 Experiment Abbildung 1: Ein druckfester Glaskolben ist zur Hälfte mit Wasser gefüllt, so dass die Flüsigkeit
8.4.5 ****** 1 Motivation Durch Verminderung des Luftdrucks siedet Wasser bei Zimmertemperatur. 2 Experiment Abbildung 1: Ein druckfester Glaskolben ist zur Hälfte mit Wasser gefüllt, so dass die Flüsigkeit
FAQ Entropie. S = k B ln W. 1.) Ist die Entropie für einen Zustand eindeutig definiert?
 FAQ Entroie S = k B ln W 1.) Ist die Entroie für einen Zustand eindeutig definiert? Antwort: Nein, zumindest nicht in der klassischen Physik. Es sei an die Betrachtung der Ortsraum-Entroie des idealen
FAQ Entroie S = k B ln W 1.) Ist die Entroie für einen Zustand eindeutig definiert? Antwort: Nein, zumindest nicht in der klassischen Physik. Es sei an die Betrachtung der Ortsraum-Entroie des idealen
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
(VIII) Wärmlehre. Wärmelehre Karim Kouz WS 2014/ Semester Biophysik
 Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Quelle: http://www.pro-physik.de/details/news/1666619/neues_bauprinzip_fuer_ultrapraezise_nuklearuhr.html (VIII) Wärmlehre Karim Kouz WS 2014/2015 1. Semester Biophysik Wärmelehre Ein zentraler Begriff
Stirling-Maschine (STI)
 TUM Anfängerpraktikum für Physiker II Wintersemester 26/27 Stirling-Maschine (STI) Inhaltsverzeichnis 5. Dezember 26 1. Einleitung...2 2. Thermodynamische Kreisprozesse...2 3. Versuchsdurchführung...3
TUM Anfängerpraktikum für Physiker II Wintersemester 26/27 Stirling-Maschine (STI) Inhaltsverzeichnis 5. Dezember 26 1. Einleitung...2 2. Thermodynamische Kreisprozesse...2 3. Versuchsdurchführung...3
Physikalisches Anfaengerpraktikum. Zustandsgleichung idealer Gase und kritischer Punkt
 Physikalisches Anfaengerpraktikum Zustandsgleichung idealer Gase und kritischer Punkt Ausarbeitung von Marcel Engelhardt & David Weisgerber (Gruppe 37) Freitag, 18. März 005 email: [email protected]
Physikalisches Anfaengerpraktikum Zustandsgleichung idealer Gase und kritischer Punkt Ausarbeitung von Marcel Engelhardt & David Weisgerber (Gruppe 37) Freitag, 18. März 005 email: [email protected]
A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C?
 A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C? (-> Tabelle p) A 1.1 b Wie groß ist der Auftrieb eines Helium (Wasserstoff) gefüllten
A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C? (-> Tabelle p) A 1.1 b Wie groß ist der Auftrieb eines Helium (Wasserstoff) gefüllten
Van der Waals-Theorie und Zustandsgleichung
 Van der Waals-Theorie und Zustandsgleichung Eine verbesserte Zustandsgleichung für klassische Gase bei höheren Dichten liefert die Van der Waals-Gleichung. Diese Gleichung beschreibt auch den Phasenübergang
Van der Waals-Theorie und Zustandsgleichung Eine verbesserte Zustandsgleichung für klassische Gase bei höheren Dichten liefert die Van der Waals-Gleichung. Diese Gleichung beschreibt auch den Phasenübergang
Kapitel 10 - Gase. Kapitel 10 - Gase. Gase bestehen aus räumlich weit voneinander getrennten Atome/Moleküle in schneller Bewegung
 Kapitel 0 - Gase Gase bestehen aus räumlich weit voneinander getrennten Atome/Moleküle in schneller ewegung Druck Kraft pro Fläche in Pa(scal) oder bar Normdruck = 760mm = 0,35 KPa =,035 bar = atm Messung
Kapitel 0 - Gase Gase bestehen aus räumlich weit voneinander getrennten Atome/Moleküle in schneller ewegung Druck Kraft pro Fläche in Pa(scal) oder bar Normdruck = 760mm = 0,35 KPa =,035 bar = atm Messung
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 Vladimir Dyakonov #12 am 26.01.2007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 Vladimir Dyakonov #12 am 26.01.2007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Physik 4 Praktikum Auswertung Zustandsdiagramm Ethan
 Physik 4 Praktikum Auswertung Zustandsdiagramm Ethan Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Zustandsgleichung....... 2 2.2. Koexistenzgebiet........ 3 2.3. Kritischer
Physik 4 Praktikum Auswertung Zustandsdiagramm Ethan Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Zustandsgleichung....... 2 2.2. Koexistenzgebiet........ 3 2.3. Kritischer
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
ST Der Stirling-Motor als Wärmekraftmaschine
 ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
Perpetuum Mobile I. Ein Perpetuum mobile erster Art wird durch den ersten Hauptsatz der Thermodynamik ausgeschlossen.
 Perpetuum Mobile I Perpetuum mobile erster Art: Unter einem perpetuum mobile erster Art versteht man eine Vorrichtung, deren Teile, einmal angeregt, nicht nur dauernd in Bewegung bleiben, sondern dabei
Perpetuum Mobile I Perpetuum mobile erster Art: Unter einem perpetuum mobile erster Art versteht man eine Vorrichtung, deren Teile, einmal angeregt, nicht nur dauernd in Bewegung bleiben, sondern dabei
Im Mittel ist die Teilchenenergie im Dampf um die Verdampfungsenergie E V höher als in der Flüssigkeit. Auch hier gilt das BOLTZMANN-Theorem:!
 3. Aggregatzustände 3.1. Flüssigkeit und Dampf Wir betrachten Flüssigkeit + angrenzendes Volumen : Die Flüssigkeitsteilchen besitzen eine gewisse Verteilung der kinetischen Energie Es kommt vor, dass ein
3. Aggregatzustände 3.1. Flüssigkeit und Dampf Wir betrachten Flüssigkeit + angrenzendes Volumen : Die Flüssigkeitsteilchen besitzen eine gewisse Verteilung der kinetischen Energie Es kommt vor, dass ein
O. Sternal, V. Hankele. 5. Thermodynamik
 5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung.
 Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
Thermodynamik 1. Typen der thermodynamischen Systeme. Intensive und extensive Zustandsgröße. Phasenübergänge. Ausdehnung bei Erwärmung. Nullter und Erster Hauptsatz der Thermodynamik. Thermodynamische
Prof. Dr. Peter Vogl, Thomas Eissfeller, Peter Greck. Übung in Thermodynamik und Statistik 4B Blatt 8 (Abgabe Di 3. Juli 2012)
 U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter Vogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 8 Abgabe Di 3. Juli 202). Extremalprinzip
U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter Vogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 8 Abgabe Di 3. Juli 202). Extremalprinzip
Physik 2 Hydrologen et al., SoSe 2013 Lösungen 3. Übung (KW 19/20) Carnot-Wärmekraftmaschine )
 3. Übung KW 19/20) Aufgabe 1 T 4.5 Carnot-Wärmekraftmaschine ) Eine Carnot-Wärmekraftmaschine arbeitet zwischen den Temperaturen und. Während der isothermen Expansion vergrößert sich das Volumen von auf
3. Übung KW 19/20) Aufgabe 1 T 4.5 Carnot-Wärmekraftmaschine ) Eine Carnot-Wärmekraftmaschine arbeitet zwischen den Temperaturen und. Während der isothermen Expansion vergrößert sich das Volumen von auf
Temperatur. Temperaturmessung. Grundgleichung der Kalorik. 2 ² 3 2 T - absolute Temperatur / ºC T / K
 Temperatur Temperatur ist ein Maß für die mittlere kinetische Energie der Teilchen 2 ² 3 2 T - absolute Temperatur [ T ] = 1 K = 1 Kelvin k- Boltzmann-Konst. k = 1,38 10-23 J/K Kelvin- und Celsiusskala
Temperatur Temperatur ist ein Maß für die mittlere kinetische Energie der Teilchen 2 ² 3 2 T - absolute Temperatur [ T ] = 1 K = 1 Kelvin k- Boltzmann-Konst. k = 1,38 10-23 J/K Kelvin- und Celsiusskala
Grundlagen der statistischen Physik und Thermodynamik
 Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
Thermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden.
 Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
4.6.5 Dritter Hauptsatz der Thermodynamik
 4.6 Hauptsätze der Thermodynamik Entropie S: ds = dq rev T (4.97) Zustandsgröße, die den Grad der Irreversibilität eines Vorgangs angibt. Sie ist ein Maß für die Unordnung eines Systems. Vorgänge finden
4.6 Hauptsätze der Thermodynamik Entropie S: ds = dq rev T (4.97) Zustandsgröße, die den Grad der Irreversibilität eines Vorgangs angibt. Sie ist ein Maß für die Unordnung eines Systems. Vorgänge finden
Thermodynamik I. Sommersemester 2012 Kapitel 2, Teil 2. Prof. Dr. Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 2, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 2, Teil 2: Übersicht 2 Zustandsgrößen 2.3 Bestimmung von Zustandsgrößen 2.3.1 Bestimmung der Phase 2.3.2 Der Sättigungszustand
Thermodynamik I Sommersemester 2012 Kapitel 2, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 2, Teil 2: Übersicht 2 Zustandsgrößen 2.3 Bestimmung von Zustandsgrößen 2.3.1 Bestimmung der Phase 2.3.2 Der Sättigungszustand
Versuch Beschreiben Sie die Vorgänge, die in der Nähe des kritischen Punktes zu beobachten sind.
 1 Versuch 220 Reale Gase 1. Aufgaben 1.1 Nehmen Sie ein Isothermennetz für Schwefelhexafluorid (SF 6 ) auf. Bestimmen Sie daraus die kritischen Daten, und berechnen Sie die Konstanten der Van-der-Waals-Gleichung.
1 Versuch 220 Reale Gase 1. Aufgaben 1.1 Nehmen Sie ein Isothermennetz für Schwefelhexafluorid (SF 6 ) auf. Bestimmen Sie daraus die kritischen Daten, und berechnen Sie die Konstanten der Van-der-Waals-Gleichung.
Kapitel IV Wärmelehre und Thermodynamik
 Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Physikalisches Praktikum I
 Fachbereich Physik Physikalisches Praktikum I W21 Name: Verdampfungswärme von Wasser Matrikelnummer: Fachrichtung: Mitarbeiter/in: Assistent/in: Versuchsdatum: Gruppennummer: Endtestat: Folgende Fragen
Fachbereich Physik Physikalisches Praktikum I W21 Name: Verdampfungswärme von Wasser Matrikelnummer: Fachrichtung: Mitarbeiter/in: Assistent/in: Versuchsdatum: Gruppennummer: Endtestat: Folgende Fragen
3.4 Änderung des Aggregatzustandes
 34 Änderung des Aggregatzustandes Man unterscheidet 3 Aggregatzustände: Fest Flüssig Gasförmig Temperatur: niedrig mittel hoch Molekülbindung: Gitter lose Bindung keine Bindung schmelzen sieden erstarren
34 Änderung des Aggregatzustandes Man unterscheidet 3 Aggregatzustände: Fest Flüssig Gasförmig Temperatur: niedrig mittel hoch Molekülbindung: Gitter lose Bindung keine Bindung schmelzen sieden erstarren
Vorlesung 15 II Wärmelehre 15. Wärmetransport und Stoffmischung
 Vorlesung 15 II Wärmelehre 15. Wärmetransport und Stoffmischung a) Wärmestrahlung b) Wärmeleitung c) Wärmeströmung d) Diffusion 16. Phasenübergänge (Verdampfen, Schmelzen, Sublimieren) Versuche: Wärmeleitung
Vorlesung 15 II Wärmelehre 15. Wärmetransport und Stoffmischung a) Wärmestrahlung b) Wärmeleitung c) Wärmeströmung d) Diffusion 16. Phasenübergänge (Verdampfen, Schmelzen, Sublimieren) Versuche: Wärmeleitung
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 U München Reinhard Scholz Physik Department, 33 homas Eissfeller, Peter Greck, illmann Kubis, Christoph Schindler http://www.wsi.tum.de/33/eaching/teaching.htm Übung in heoretischer Physik 5B (hermodynamik)
U München Reinhard Scholz Physik Department, 33 homas Eissfeller, Peter Greck, illmann Kubis, Christoph Schindler http://www.wsi.tum.de/33/eaching/teaching.htm Übung in heoretischer Physik 5B (hermodynamik)
Thermodynamik Thermodynamische Systeme
 Thermodynamik Thermodynamische Systeme p... Druck V... Volumen T... Temperatur (in Kelvin) U... innere Energie Q... Wärme W... Arbeit Idealisierung; für die Betrachtung spielt die Temperatur eine entscheidende
Thermodynamik Thermodynamische Systeme p... Druck V... Volumen T... Temperatur (in Kelvin) U... innere Energie Q... Wärme W... Arbeit Idealisierung; für die Betrachtung spielt die Temperatur eine entscheidende
Physikalisches Praktikum
 Physikalisches Praktikum Versuch 26: Stirling-Motor UNIVERSITÄT DER BUNDESWEHR MÜNCHEN Fakultät für Elektrotechnik und Informationstechnik Institut für Physik Oktober 2015 2 Versuch 26 Stirling-Motor Der
Physikalisches Praktikum Versuch 26: Stirling-Motor UNIVERSITÄT DER BUNDESWEHR MÜNCHEN Fakultät für Elektrotechnik und Informationstechnik Institut für Physik Oktober 2015 2 Versuch 26 Stirling-Motor Der
Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt
 1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 ladimir Dyakonov #0 am 4.0.007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 007 ladimir Dyakonov #0 am 4.0.007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
1 Thermodynamik allgemein
 Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Vorlesung #7. M.Büscher, Physik für Mediziner
 Vorlesung #7 Zustandsänderungen Ideale Gase Luftfeuchtigkeit Reale Gase Phasenumwandlungen Schmelzwärme Verdampfungswärme Dampfdruck van-der-waals Gleichung Zustandsdiagramme realer Gase Allgem. Gasgleichung
Vorlesung #7 Zustandsänderungen Ideale Gase Luftfeuchtigkeit Reale Gase Phasenumwandlungen Schmelzwärme Verdampfungswärme Dampfdruck van-der-waals Gleichung Zustandsdiagramme realer Gase Allgem. Gasgleichung
Dampftafel Für den Homogenen Zustand. HEAT Haus-, Energie- und Anlagentechnik. Vorlesung Thermodynamik
 Dampftafel 1 Zur Berechnung thermodynamischer Prozesse (Kraftwerk, Wärmepumpe, etc.) reicht das ideale Gasgesetz nicht mehr aus Stoffdaten der realen Fluide werden benötigt Für die Bestimmung der Stoffdaten
Dampftafel 1 Zur Berechnung thermodynamischer Prozesse (Kraftwerk, Wärmepumpe, etc.) reicht das ideale Gasgesetz nicht mehr aus Stoffdaten der realen Fluide werden benötigt Für die Bestimmung der Stoffdaten
LMPG1 ÜB1 Phasendiagramme & Dampfdruck Lösungen Seite 1 von 6
 LMPG1 ÜB1 Phasendiagramme & Dampfdruck Lösungen Seite 1 von 6 Aufgabe 1: Phasendiagramm reiner Stoffe. Die Abbildung zeigt das allgemeingültige Phasendiagramm reiner Stoffe. a) Beschriften Sie das Diagramm
LMPG1 ÜB1 Phasendiagramme & Dampfdruck Lösungen Seite 1 von 6 Aufgabe 1: Phasendiagramm reiner Stoffe. Die Abbildung zeigt das allgemeingültige Phasendiagramm reiner Stoffe. a) Beschriften Sie das Diagramm
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 ladimir Dyakonov #13 am 30.01.2007 Folien im PDF Format unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 ladimir Dyakonov #13 am 30.01.2007 Folien im PDF Format unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Physik für Bauingenieure
 Fachbereich Physik Prof. Dr. Rudolf Feile Dipl. Phys. Markus Domschke Sommersemster 2010 17. 21. Mai 2010 Physik für Bauingenieure Übungsblatt 5 Gruppenübungen 1. Wärmepumpe Eine Wärmepumpe hat eine Leistungszahl
Fachbereich Physik Prof. Dr. Rudolf Feile Dipl. Phys. Markus Domschke Sommersemster 2010 17. 21. Mai 2010 Physik für Bauingenieure Übungsblatt 5 Gruppenübungen 1. Wärmepumpe Eine Wärmepumpe hat eine Leistungszahl
-aus theoretischen Ansätzen - Approximationen
 2.3 Bestimmung von Zustandsgrößen Zustand wird bestimmt durch zwei unabhängige, intensive Zustandsgrößen Bestimmung anderer Zustandsgrößen aus Stoffmodellen Zustandsgleichungen Stoffmodelle aus - Experimenten
2.3 Bestimmung von Zustandsgrößen Zustand wird bestimmt durch zwei unabhängige, intensive Zustandsgrößen Bestimmung anderer Zustandsgrößen aus Stoffmodellen Zustandsgleichungen Stoffmodelle aus - Experimenten
1. Klausur zur Vorlesung Physikalische Chemie I
 1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
Übungsblatt 2 ( )
 Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung
Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung
11. Wärmetransport. und Stoffmischung. Q t. b) Wärmeleitung (ohne Materietransport)
 11. Wärmetransport und Stoffmischung b) Wärmeleitung (ohne Materietransport) Wärme(energie) Q wird durch einen Wärmeleiter (Metall) der Querschnittsfläche A vom wärmeren zum kälteren transportiert, also
11. Wärmetransport und Stoffmischung b) Wärmeleitung (ohne Materietransport) Wärme(energie) Q wird durch einen Wärmeleiter (Metall) der Querschnittsfläche A vom wärmeren zum kälteren transportiert, also
1. Klausur ist am 5.12.! (für Vets sowie Bonuspunkte für Zahni-Praktikum) Jetzt lernen!
 1. Klausur ist am 5.12.! (für Vets sowie Bonuspunkte für Zahni-Praktikum) Jetzt lernen! http://www.physik.uni-giessen.de/dueren/ User: duerenvorlesung Password: ****** Druck und Volumen Gesetz von Boyle-Mariotte:
1. Klausur ist am 5.12.! (für Vets sowie Bonuspunkte für Zahni-Praktikum) Jetzt lernen! http://www.physik.uni-giessen.de/dueren/ User: duerenvorlesung Password: ****** Druck und Volumen Gesetz von Boyle-Mariotte:
Versuch 2. Physik für (Zahn-)Mediziner. c Claus Pegel 13. November 2007
 Versuch 2 Physik für (Zahn-)Mediziner c Claus Pegel 13. November 2007 1 Wärmemenge 1 Wärme oder Wärmemenge ist eine makroskopische Größe zur Beschreibung der ungeordneten Bewegung von Molekülen ( Schwingungen,
Versuch 2 Physik für (Zahn-)Mediziner c Claus Pegel 13. November 2007 1 Wärmemenge 1 Wärme oder Wärmemenge ist eine makroskopische Größe zur Beschreibung der ungeordneten Bewegung von Molekülen ( Schwingungen,
T 300K,p 1,00 10 Pa, V 0, m,t 1200K, Kontrolle Physik Leistungskurs Klasse Hauptsatz, Kreisprozesse
 Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Kontrolle Physik Leistungskurs Klasse 2 7.3.207. Hauptsatz, Kreisprozesse. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür offen gelassen. Man merkt es erst, als man
Die Zustandsgleichung realer Gase
 Die Zustandsgleichung realer Gase Grolik Benno, Kopp Joachim 2. Januar 2003 1 Grundlagen des Versuchs Der Zustand eines idealen Gases wird durch die drei elementaren Zustandsgrößen Druck p, Temperatur
Die Zustandsgleichung realer Gase Grolik Benno, Kopp Joachim 2. Januar 2003 1 Grundlagen des Versuchs Der Zustand eines idealen Gases wird durch die drei elementaren Zustandsgrößen Druck p, Temperatur
Grundlagen der Allgemeinen und Anorganischen Chemie. Atome
 Grundlagen der Allgemeinen und Anorganischen Chemie Atome Elemente Chemische Reaktionen Energie Verbindungen 361 4. Chemische Reaktionen 4.1. Allgemeine Grundlagen (Wiederholung) 4.2. Energieumsätze chemischer
Grundlagen der Allgemeinen und Anorganischen Chemie Atome Elemente Chemische Reaktionen Energie Verbindungen 361 4. Chemische Reaktionen 4.1. Allgemeine Grundlagen (Wiederholung) 4.2. Energieumsätze chemischer
1. Klausur ist am 5.12.! Jetzt lernen! Klausuranmeldung: Bitte heute in Listen eintragen!
 1. Klausur ist am 5.12.! Jetzt lernen! Klausuranmeldung: Bitte heute in Listen eintragen! Aggregatzustände Fest, flüssig, gasförmig Schmelz -wärme Kondensations -wärme Die Umwandlung von Aggregatzuständen
1. Klausur ist am 5.12.! Jetzt lernen! Klausuranmeldung: Bitte heute in Listen eintragen! Aggregatzustände Fest, flüssig, gasförmig Schmelz -wärme Kondensations -wärme Die Umwandlung von Aggregatzuständen
Grundlagen der Physik II
 Grundlagen der Physik II Othmar Marti 12. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 12. 07. 2007 Klausur Die Klausur
Grundlagen der Physik II Othmar Marti 12. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 12. 07. 2007 Klausur Die Klausur
Probeklausur STATISTISCHE PHYSIK PLUS
 DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
Mathematisch-Naturwissenschaftliche Grundlegung WS 2014/15 Chemie I Dr. Helge Klemmer
 Mathematisch-Naturwissenschaftliche Grundlegung WS 2014/15 Chemie I 12.12.2014 Gase Flüssigkeiten Feststoffe Wiederholung Teil 2 (05.12.2014) Ideales Gasgesetz: pv Reale Gase: Zwischenmolekularen Wechselwirkungen
Mathematisch-Naturwissenschaftliche Grundlegung WS 2014/15 Chemie I 12.12.2014 Gase Flüssigkeiten Feststoffe Wiederholung Teil 2 (05.12.2014) Ideales Gasgesetz: pv Reale Gase: Zwischenmolekularen Wechselwirkungen
p = Druck R* = universale Gaskonstante n = Stoffmenge V = Volumen R = R*/M spez. Gaskontante T = absolute Temperatur M = molare Masse m = Masse
 1. Wie ist die ideale Gasgleichung definiert? Unter welchen Voraussetzungen ist sie gültig? Unter welchen Bedingungen ist ein Gas "ideal"? pv=nr*t pv = mrt pv = mr*/m T p = Druck R* = universale Gaskonstante
1. Wie ist die ideale Gasgleichung definiert? Unter welchen Voraussetzungen ist sie gültig? Unter welchen Bedingungen ist ein Gas "ideal"? pv=nr*t pv = mrt pv = mr*/m T p = Druck R* = universale Gaskonstante
Thermodynamik I. Sommersemester 2012 Kapitel 4, Teil 1. Prof. Dr.-Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 4, Teil 1 Prof. Dr.-Ing. Heinz Pitsch Kapitel 4, Teil 1: Übersicht 4 Zweiter Hauptsatz der Thermodynamik 4.1Klassische Formulierungen 4.1.1Kelvin-Planck-Formulierung
Thermodynamik I Sommersemester 2012 Kapitel 4, Teil 1 Prof. Dr.-Ing. Heinz Pitsch Kapitel 4, Teil 1: Übersicht 4 Zweiter Hauptsatz der Thermodynamik 4.1Klassische Formulierungen 4.1.1Kelvin-Planck-Formulierung
Beispiel für ein thermodynamisches System: ideales Gas (Edelgas)
 10. Hauptsätze tze der Wärmelehre Thermodynamik: zunächst: Klassische Mechanik punktförmiger Teilchen, starrer und deformierbarer Körper aber: Bewegungsgleichungen für N=10 23 Teilchen mit 6N ariablen
10. Hauptsätze tze der Wärmelehre Thermodynamik: zunächst: Klassische Mechanik punktförmiger Teilchen, starrer und deformierbarer Körper aber: Bewegungsgleichungen für N=10 23 Teilchen mit 6N ariablen
E2: Wärmelehre und Elektromagnetismus 5. Vorlesung
 E2: Wärmelehre und Elektromagnetismus 5. Vorlesung 23.04.2018 Heute: - Phasenübergänge - van der Waals-Gas https://xkcd.com/1561/ Prof. Dr. Jan Lipfert [email protected] 23.04.2018 Prof. Dr. Jan Lipfert
E2: Wärmelehre und Elektromagnetismus 5. Vorlesung 23.04.2018 Heute: - Phasenübergänge - van der Waals-Gas https://xkcd.com/1561/ Prof. Dr. Jan Lipfert [email protected] 23.04.2018 Prof. Dr. Jan Lipfert
A 2.6 Wie ist die Zusammensetzung der Flüssigkeit und des Dampfes eines Stickstoff-Sauerstoff-Gemischs
 A 2.1 Bei - 10 o C beträgt der Dampfdruck des Kohlendioxids 26,47 bar, die Dichte der Flüssigkeit 980,8 kg/m 3 und die Dichte des Dampfes 70,5 kg/m 3. Bei - 7,5 o C beträgt der Dampfdruck 28,44 bar. Man
A 2.1 Bei - 10 o C beträgt der Dampfdruck des Kohlendioxids 26,47 bar, die Dichte der Flüssigkeit 980,8 kg/m 3 und die Dichte des Dampfes 70,5 kg/m 3. Bei - 7,5 o C beträgt der Dampfdruck 28,44 bar. Man
Gesetz von Boyle. Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V.
 Gesetz von Boyle Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V Isothermen Gesetz von Gay-Lussac Jacques Charles und Joseph-Louis Gay-Lussac fanden
Gesetz von Boyle Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V Isothermen Gesetz von Gay-Lussac Jacques Charles und Joseph-Louis Gay-Lussac fanden
Berechnen Sie die Wärmemenge in kj, die erforderlich ist, um 750g H 2 O von
 Aufgabe 1: Berechnen Sie die Wärmemenge in kj, die erforderlich ist, um 750g H O von 0 C bis zum Siedepunkt (100 C) zu erwärmen. Die spezifische Wärmekapazität von Wasser c = 4.18 J K - 1 g -1. Lösung
Aufgabe 1: Berechnen Sie die Wärmemenge in kj, die erforderlich ist, um 750g H O von 0 C bis zum Siedepunkt (100 C) zu erwärmen. Die spezifische Wärmekapazität von Wasser c = 4.18 J K - 1 g -1. Lösung
Hauptsatz der Thermodynamik
 0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14,
 ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14, 12.02.2016 Aufgabe 1 Kreisprozesse Mit einem Mol eines idealen, monoatomaren Gases (cv = 3/2 R) wird, ausgehend
ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14, 12.02.2016 Aufgabe 1 Kreisprozesse Mit einem Mol eines idealen, monoatomaren Gases (cv = 3/2 R) wird, ausgehend
Die kinetische Gastheorie beruht auf den folgenden drei Annahmen:
 Physikalische Chemie Modul II Versuch: Reales Gas 20. Juli 2010 1 Einleitung Die kinetische Gastheorie beruht auf den folgenden drei Annahmen: 1. Das Gas besteht aus Molekülen der Masse m und dem Durchmesser
Physikalische Chemie Modul II Versuch: Reales Gas 20. Juli 2010 1 Einleitung Die kinetische Gastheorie beruht auf den folgenden drei Annahmen: 1. Das Gas besteht aus Molekülen der Masse m und dem Durchmesser
13.Wärmekapazität. EP Vorlesung 14. II) Wärmelehre
 13.Wärmekapazität EP Vorlesung 14 II) Wärmelehre 10. Temperatur und Stoffmenge 11. Ideale Gasgleichung 12. Gaskinetik 13. Wärmekapazität 14. Hauptsätze der Wärmelehre Versuche: Mechanisches Wärmeäquivalent
13.Wärmekapazität EP Vorlesung 14 II) Wärmelehre 10. Temperatur und Stoffmenge 11. Ideale Gasgleichung 12. Gaskinetik 13. Wärmekapazität 14. Hauptsätze der Wärmelehre Versuche: Mechanisches Wärmeäquivalent
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Einführung in die Wärmelehre - Prof. Dr. Ulrich Hahn WS 2008/09 Entwicklung der Wärmelehre Sinnesempfindung: Objekte warm kalt Beschreibung der thermische Eigenschaften
Physik III im Studiengang Elektrotechnik - Einführung in die Wärmelehre - Prof. Dr. Ulrich Hahn WS 2008/09 Entwicklung der Wärmelehre Sinnesempfindung: Objekte warm kalt Beschreibung der thermische Eigenschaften
2.3 Stoffmodelle für Reinstoffe Die Dampftabelle ... MPa C m 3 /kg m 3 /kg ... 0, ,23 0, ,
 2.3 Stoffmodelle für Reinstoffe 2. 3. 1 Die Dampftabelle Beispiel Wasser: 60 kg Nassdampf bei p = 2 bar = 0,2 MPa und V= 3 m 3, v = 0,05 m 3 /kg Drucktafel (Tab. A1.2)... MPa C m 3 /kg m 3 /kg...............
2.3 Stoffmodelle für Reinstoffe 2. 3. 1 Die Dampftabelle Beispiel Wasser: 60 kg Nassdampf bei p = 2 bar = 0,2 MPa und V= 3 m 3, v = 0,05 m 3 /kg Drucktafel (Tab. A1.2)... MPa C m 3 /kg m 3 /kg...............
Skript zur Vorlesung
 Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
4 Hauptsätze der Thermodynamik
 I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
I Wärmelehre -21-4 Hauptsätze der hermodynamik 4.1 Energieformen und Energieumwandlung Innere Energie U Die innere Energie U eines Körpers oder eines Systems ist die gesamte Energie die darin steckt. Es
Musterlösung zur Abschlussklausur PC I Übungen (27. Juni 2018)
 1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
Physikalische Chemie 1 (Thermodyn. u. Elektrochemie) SS09 - Blatt 1 von 13. Klausur PC 1. Sommersemester :15 bis 11:45.
 Physikalische Chemie 1 (Thermodyn. u. Elektrochemie) SS09 - Blatt 1 von 13 Klausur PC 1 Sommersemester 2009 03.08.2007 10:15 bis 11:45 Name: Vorname: geb. am: in: Matrikelnummer: Unterschrift: Für die
Physikalische Chemie 1 (Thermodyn. u. Elektrochemie) SS09 - Blatt 1 von 13 Klausur PC 1 Sommersemester 2009 03.08.2007 10:15 bis 11:45 Name: Vorname: geb. am: in: Matrikelnummer: Unterschrift: Für die
