Höhere Experimentalphysik 1
|
|
|
- Krista Engel
- vor 8 Jahren
- Abrufe
Transkript
1 Höhere Experimentalphysik 1 Institut für Angewandte Physik GoetheUniversität Frankfurt am Main 1. Vorlesung
2 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Ankündigung Übung Die erste Übung findet am von 13h bis 14h im Raum statt.
3 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Inhaltsverzeichnis 1. Elektrodynamik i. Elektrische Ladung ii. MaxwellGleichung iii. Elektrische und magnetische Felder stationär zeitabhängig iv. Elektromagnetische Wellen v. Wellenleiter vi. Hohlraumresonatoren
4 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main 1. Elektrodynamik In der Mechanik gibt es vier Grundkräfte: Starke Elektromagnetische Schwache Gravitative Fast alle diese Kräfte sind elektromagnetischer Natur, aber nur die elektromagnetische Kraft ist bis heute vollständig verstanden. Im Vergleich zur Gravitation ist die elektrische Kraft etwa mal größer.
5 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Messung der Kräfte Cavendish Drehwaage Coulombsche HEMS Darmstadt
6 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Vergleich gravitative und elektromagentische Kraft Gravitation Kraft entlang Verbindungslinie 1/r 2 Abhängigkeit Masse als Quelle anziehend Kraftgesetz Elektromagnetische Kraft Kraft entlang Verbindungslinie 1/r 2 Abhängigkeit Ladung als Quelle anziehend und abstoßend Kraftgesetz Proportionalitätskonstante g= Nm 2 /kg 2 Proportionalitätskonstante k= Nm 2 /C 2 Vergleich:
7 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Alle Erscheinungen, die im Rahmen der Elektrodynamik besprochen werden, beruhen darauf, dass die Materie vorwiegend aus geladenen Teilchen (z.b. Elektronen und Protonen) aufgebaut ist. Eine Ladung ist notwendig, um ein elektromagnetisches Feld zu erzeugen und nachzuweisen. Aber was ist eigentlich die elektrische Ladung?
8 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Positive und negative Ladung Gleichnamige Ladungen stoßen sich ab Ladungserhaltung: Die Summe der positiven und negativen Ladungen in einem abgeschlossenen System ändert sich nie. Ladungsinvarianz: Die Ladung von Elementarteilchen ist relativistisch invariant und ändert sich also nicht mit der Geschwindigkeit des Teilchens. Ladung ist gequantelt Die Kraft zwischen zwei Ladungen ist proportional zu r 2
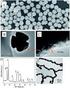
9 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Messung der Elementarladung MilikanVersuch Im Jahre 1910 machte Milikan die wichtige Entdeckung, dass die Ladung nur stückweise vorkommt, d.h. sie ist quantisiert. Zum Nachweis des Elementarquantums benutzte Milikan folgende Versuchsanordnung NobelPreis, 1923 a)
10 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Messung der Elementarladung MilikanVersuch In einen Plattenkondensator werden kleine Öltröpfchen gesprüht, die in der Luft unter dem Einfluss der Gravitationskraft und der Stokesschen Reibungskraft mit konstanter Geschwindigkeit v fallen und zwar desto schneller je größer sie sind: Aus der gemessenen Fallgeschwindigkeit lassen sich der Radius und damit auch die Masse des Öltröpfchens bestimmen, da die Viskosität der Luft und die Öldichte bekannt sind.
11 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Messung der Elementarladung MilikanVersuch Durch Bestrahlung des Tröpfchens mit Röntgenstrahlung kann nun die Ladung q des Tröpfchens verändert werden. Dies wird deutlich sichtbar, sobald am Kondensator ein elektrisches Feld angelegt wird, welches eine zusätzliche Kraft qe ausübt. Die Größe der elektrischen Kraft kann nun durch Variation von E so gewählt werden, dass die elektrische Kraft die Gravitationsanziehung gerade kompensiert, so dass das Tröpfchen schwebt. Somit folgt aus qe=mg: wobei n=1,2,3,
12 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Messung der Elementarladung QuantenHallEffekt Nobelpreis K. von Klitzig D Elektronengas (MOSFET) Bei hohen magnetischen Feldern und tiefe Temperaturen ist der HallWiderstand: R H wobei n=1,2, Die Existenz der Stufen im QuantenHallEffekt und vor allem ihre hohe Reproduzierbarkeit ist bis heute nicht vollständig verstanden,..., Welt der Physik, 2011 Mögliche Erklärung: Quantenphasenübergang
13 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Messung der Elementarladung Wert Standardunsicherheit x C x C Relative Standardunsicherheit 2.2 x , CODATA, recommended values
14 Für eine Punktladung ist die untere Integrationsgrenze r=0 und dies ergibt ein unendliches Integral. Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Energie des Feldes einer Punktladung Das elektrische Feld einer Punktladung ist gegeben durch: Die Energiedichte im Abstand r von der Ladung ist dann: Innerhalb einer Kugelschale mit der Dicke dr und der Fläche A=4pr 2 ist die Gesamtenergie: (1)
15 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main i. Elektrische Ladung Energie des Feldes einer Punktladung Laut Gleichung (1) enthält das Feld einer Punktladung eine unendliche Menge an Energie, obwohl es eigentlich nur Energie zwischen Punktladungen gibt. Ein Ausweg aus dieser Situation würde darin bestehen, die Elementarladung nicht als Punkt sondern in Wirklichkeit als kleine Ladungsverteilung aufzufassen. Die Frage, ob die Energie im Feld lokalisiert ist, bleibt in der Elektrostatik dennoch unbeantwortet.
16 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main ii. Die Maxwellgleichungen Faraday und Maxwell fanden heraus, dass ein zeitlich veränderliches Magnetfeld automatisch in der Umgebung auch ein elektrisches Feld und in analoger Weise führt ein zeitlich veränderliches elektrisches Feld auch zu einem Magnetfeld. Diese symmetrische Kopplung zwischen zeitlich veränderlichen elektrischen und magnetischen Feldern fand ihren mathematischen Ausdruck in den Maxwellgleichungen. Gaußsches Gesetz Gaußsches Gesetz für Magnetfelder Faradaysches Induktionsgesetz Amperesches Gesetz
17 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main ii. Die Maxwellgleichungen Die wichtigste Konsequenz der Maxwellgleichungen liegt in dem erstmaligen Verständnis der Ausbreitung von elektromagnetischen Wellen, deren Erzeugung und Nachweis erstmals Heinrich Hertz gelang. Nach der Maxwellschen Theorie sollten sich elektromagnetische Wellen mit der charakteristischen Geschwindigkeit fortpflanzen, in perfekter Übereinstimmung mit der gemessenen Lichtgeschwindigkeit.
18 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main ii. Die Maxwellgleichungen Gaußsches Gesetz Integralform Das Gaußsche Gesetz stellt die Beziehung zwischen räumlichen Verhalten des elektrischen Feldes und der Ladungsdichteverteilung her, die es hervorruft. Anzahl der Feldlinien durch eine geschlossene Fläche Anzahl der Ladungen, die in der Fläche enthalten sind dividiert durch die Permittivität Elektrische Ladungen produzieren ein elektrisches Feld und der Fluss dieses Feldes durch eine geschlossenen Oberfläche ist proportional zur Gesamtladung innerhalb der Oberfläche.
19 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main ii. Die Maxwellgleichungen Gaußsches Gesetz differentielle Form Die differentielle Form Tendenz des Feldes von einem Punkt wegzufließen. Ladungsdichte dividiert durch die Permittivität wird bei der Lösung von Problemen genutzt, in denen die räumliche Änderung des elektrischen Feldes an bestimmten Stellen bekannt ist, um die Volumenladungsdichte an diesen Positionen zu bestimmen. Das elektrische Feld, das durch elektrische Ladungen produziert wird, divergiert von positiven Ladungen und konvergiert zu negativen Ladungen.
20 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main ii. Die Maxwellgleichungen Gaußsches Gesetz Integralform vs. differentielle Form Es gibt einen fundamentalen Unterschied zwischen differentieller und integraler Form des Gaußschen Gesetzes: Die differentielle Form behandelt die Divergenz des elektrischen Feldes und die Ladungsdichte an individuellen Punkten im Raum, während die integrale Form das Integral der Normalkomponente des elektrischen Felder über einen Oberfläche beinhalt.
21 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Das CoulombGesetz Die elektrostatischen Kräfte sind Zentralkräfte Es gilt das Superpositionsprinzip: Die elektrostatischen Kräfte, die auf eine Probeladung q von mehreren anderen Ladungen q 1, q 2,. ausgeübt werden, überlagern sich ungestört C. De Coulomb, 1785 Kraftwirkung vieler Ladungen auf ein Teilchen am Punkt 1.
22 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Das stationäre elektrische Feld Das elektrische Feld ist eine vektorielle Größe, die direkt proportional zu einer Kraft ist, die auf eine positive Testladung gerichtet ist. field of force Das elektrische Feld kann unabhängig vom magnetischen Feld betrachtet werden d.h. Elektrizität und Magnetismus sind zunächst getrennte Phänomene!
23 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Das stationäre elektrische Feld Im statischen Fall bleiben alle Ladungen fest an einem Punkt im Raum oder wenn sie sich bewegen, dann nur als stationärer Strom. 1. Die Ladungen sind die Quelle des elektrischen Feldes. 2. Das Linienintegral des elektrostatischen Feldes über eine geschlossene Kurve ist null (oder auch das elektrische Feld ist wirbelfrei).
24 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Das stationäre elektrische Feld Der Gaußsche Satz ist eine dem Coulombgesetz äquivalente Darstellung der Elektrostatik. Er gilt nicht nur für die elektrischen Felder ruhender Ladungen, sondern auch für bewegte Ladungen. Während man mit dem Coulombgesetz das elektrische Feld einer Ladung bestimmen kann, erlaubt uns der Gaußsche Satz, aus der Feldverteilung Auskunft über die Ladungsverteilung zu erhalten.
25 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Das elektrische Potential Als elektrostatisches Potential j(r 0 ) am Ort r 0 wird der negative Wert der Arbeit bezeichnet, um eine positive Einheitsladung in einem elektrischen Feld vom Unendlichen bis nach r 0 heranzuführen Potentielle Energie einer Ladung: Potential einer Punktladung:
26 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Influenz (elektrostatische Induktion) Wird ein beliebiges Stück Metall in das elektrische Feld eines Plattenkondensators gebracht, so werden unter dem Einfluss des Feldes Influenzladungen erzeugt. Sie liefern im Inneren des Metalls ein Feld, das dem ursprünglichen Feld entgegengerichtet und dieses im Inneren des Leiters genau zu null kompensiert.
27 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main iii. Elektrostatik Faraday scher Käfig Die freien Ladungen in einem Leiter bewegen sich immer so, das sie das ursprünglich Feld kompensieren und das Feld im Inneren des Leiters gerade null ist. Daher verschwindet auch der Fluss des Feldes durch eine Fläche, die den Hohlraum umschließt. E=0 Nach gilt Feldfreiheit im Hohlraum des Leiters. So erreicht man im Faradayschen Käfig eine vollständige Abschirmung gegen elektrische Felder.
28 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiel: VandeGraaffGenerator Die Feldfreiheit metallischer Hohlräume kann zur Erzeugung hoher Spannungen benutzt werden. Bringt man Ladungen in das Innere einer Hohlkugel, so wandert die Ladung sofort nach außen und der innere Hohlraum bleibt feldfrei, unabhängig wie viel Ladungen die Hohlkugel schon trägt. Dies wird beim VandeGraaffGenerator durch ein rotierendes isolierendes Band bewerkstelligt bis die Kugel ein höheres Potential als die Ladungsquelle hat.
29 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Plattenkondensator: Das elektrische Feld kommt durch Superposition der elektrischen Felder zweier entgegengesetzt geladener Platten gleicher Ladungsdichte. Die Felder im Außenraum kompensieren sich vollständig Das elektrische Feld des Plattenkondensators ist also unabhängig vom Plattenabstand d.
30 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Plattenkondensator: Da die Platten entgegengesetzt geladen sind ziehen sie sich mit einer Kraft F an. E d d F Um die Platten ein Stück auseinanderzubewegen muss von außen Arbeit geleistet werden Da das elektrische Feld unabhängig von d ist, muss sich die Energiedichte entsprechend des Volumens ändern. Mit folgt für die Kraft zwischen den Platten
31 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Plattenkondensator: Das mittlere Feld ist, welches an den Ladungen der Platte angreift ist nur halb so groß wie das Feld zwischen den Platten E d E E/2 Da die Ladungsschicht auf beiden Platten eine endliche Dicke hat, fällt die Feldstärke nach dem Gaußschen Satz innerhalb dieser Schicht d auf null, so dass auf die Ladungen im Mittel nur E/2 wirkt
32 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Kugel E=0 Flammensonde
33 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Kugel im leitenden Medium: Es bildet sich eine Ladungswolke aus, die das Feld der Kugel abschirmt. Die Verteilung der Elektronen im Außenraum ist gegeben durch E=0 Für hohe Temperatur lässt sich die Exponentialfunktion entwickeln zu und man erhält somit die Ladungsdichte
34 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Kugel im leitenden Medium: Mithilfe der eindimensionalen Poissongleichung E=0 erhält man folgende Bestimmungsgleichung für j(x): Diese Gleichung wird gelöst durch wenn für D gilt: DebyeLänge
35 Höhere Experimentalphysik 1 IAP GoetheUniversität Frankfurt am Main Beispiele für elektrische Felder und Potentiale Homogener Teilchenstrahl (siehe Übung 1): & &
Elektrizität und Magnetismus - Einführung
 Elektrizität und Magnetismus - Einführung Elektrostatik - elektrische Ladung - Coulomb Kraft - elektrisches Feld - elektrostatisches Potential - Bewegte Ladung -Strom - Magnetismus - Magnetfelder - Induktionsgesetz
Elektrizität und Magnetismus - Einführung Elektrostatik - elektrische Ladung - Coulomb Kraft - elektrisches Feld - elektrostatisches Potential - Bewegte Ladung -Strom - Magnetismus - Magnetfelder - Induktionsgesetz
Vorlesung 2: Elektrostatik II
 Einheit der elektrischen Ladung: Das Millikan-Experiment (1910, Nobelpreis 1923) Vorlesung 2: Elektrostatik II Sehr feine Öltröpfchen (
Einheit der elektrischen Ladung: Das Millikan-Experiment (1910, Nobelpreis 1923) Vorlesung 2: Elektrostatik II Sehr feine Öltröpfchen (
Wiederholung: Elektrisches Feld und Feldlinien I Feld zwischen zwei Punktladungen (pos. und neg.)
 Wiederholung: Elektrisches Feld und Feldlinien I Feld zwischen zwei Punktladungen (pos. und neg.) 1 Grieskörner schwimmen in Rhizinusöl. Weil sie kleine Dipole werden, richten sie sich entlang der Feldlinien
Wiederholung: Elektrisches Feld und Feldlinien I Feld zwischen zwei Punktladungen (pos. und neg.) 1 Grieskörner schwimmen in Rhizinusöl. Weil sie kleine Dipole werden, richten sie sich entlang der Feldlinien
Elektrizität. Eledrisch is pradisch: wann'st 'as oreibst brennt's!
 Elektrizität Eledrisch is pradisch: wann'st 'as oreibst brennt's! Reibungselektrizität schon vor mehr als 2000 Jahren bei den Griechen bekannt: Reibt man Bernstein mit einem Tuch, zieht er danach Federn
Elektrizität Eledrisch is pradisch: wann'st 'as oreibst brennt's! Reibungselektrizität schon vor mehr als 2000 Jahren bei den Griechen bekannt: Reibt man Bernstein mit einem Tuch, zieht er danach Federn
6.4.8 Induktion von Helmholtzspulen ******
 V648 6.4.8 ****** Motivation Das Induktionsgesetz von Faraday wird mit einer ruhenden Leiterschleife im zeitabhängigen B-Feld und mit einer bewegten Leiterschleife im stationären B-Feld untersucht. 2 Experiment
V648 6.4.8 ****** Motivation Das Induktionsgesetz von Faraday wird mit einer ruhenden Leiterschleife im zeitabhängigen B-Feld und mit einer bewegten Leiterschleife im stationären B-Feld untersucht. 2 Experiment
Experimentalphysik 2
 Ferienkurs Experimentalphysik 2 Sommer 2014 Vorlesung 1 Thema: Elektrostatik Technische Universität München 1 Fakultät für Physik Inhaltsverzeichnis 1 Elektrostatik 3 1.1 Elektrische Ladungen und Coulomb-Gesetz...................
Ferienkurs Experimentalphysik 2 Sommer 2014 Vorlesung 1 Thema: Elektrostatik Technische Universität München 1 Fakultät für Physik Inhaltsverzeichnis 1 Elektrostatik 3 1.1 Elektrische Ladungen und Coulomb-Gesetz...................
Elektromagnetismus und Optik
 Elektromagnetismus und Optik Bilder, Diagramme und Tabellen zur Vorlesung PHYSIK-II -Elektromagnetismus und Optik- SS 2004, Universität Freiburg Prof. Dr. K. Jakobs Physikalisches Institut Universität
Elektromagnetismus und Optik Bilder, Diagramme und Tabellen zur Vorlesung PHYSIK-II -Elektromagnetismus und Optik- SS 2004, Universität Freiburg Prof. Dr. K. Jakobs Physikalisches Institut Universität
ELEKTRIZITÄT & MAGNETISMUS
 ELEKTRIZITÄT & MAGNETISMUS Elektrische Ladung / Coulombkraft / Elektrisches Feld Gravitationsgesetz ( = Gewichtskraft) ist die Ursache von Gravitationskonstante Coulombgesetz ( = Coulombkraft) Elementarladung
ELEKTRIZITÄT & MAGNETISMUS Elektrische Ladung / Coulombkraft / Elektrisches Feld Gravitationsgesetz ( = Gewichtskraft) ist die Ursache von Gravitationskonstante Coulombgesetz ( = Coulombkraft) Elementarladung
12. Elektrodynamik. 12. Elektrodynamik
 12. Elektrodynamik 12.1 Quellen von Magnetfeldern 12.2 Das Ampere sche Gesetz 12.3 Maxwell sche Verschiebungsstrom 12.4 Magnetische Induktion 12.5 Lenz sche Regel 12.6 Magnetische Kraft 12. Elektrodynamik
12. Elektrodynamik 12.1 Quellen von Magnetfeldern 12.2 Das Ampere sche Gesetz 12.3 Maxwell sche Verschiebungsstrom 12.4 Magnetische Induktion 12.5 Lenz sche Regel 12.6 Magnetische Kraft 12. Elektrodynamik
Das Amperesche Gesetz Der Maxwellsche Verschiebungsstrom Magnetische Induktion Lenzsche Regel
 11. Elektrodynamik 11.5.4 Das Amperesche Gesetz 11.5.5 Der Maxwellsche Verschiebungsstrom 11.5.6 Magnetische Induktion 11.5.7 Lenzsche Regel 11.6 Maxwellsche Gleichungen 11.7 Elektromagnetische Wellen
11. Elektrodynamik 11.5.4 Das Amperesche Gesetz 11.5.5 Der Maxwellsche Verschiebungsstrom 11.5.6 Magnetische Induktion 11.5.7 Lenzsche Regel 11.6 Maxwellsche Gleichungen 11.7 Elektromagnetische Wellen
Übungsstunde 2 Montag, 28. September :05
 Übungsstunde 2 Montag, 28. September 2015 19:05 Lernziele: Elektrostatik in Materie Grundgrößen der Elektrostatik: Elektrisches Potential Spannung Elektrostatische Energie Leiter & Nichtleiter Elektrostatik
Übungsstunde 2 Montag, 28. September 2015 19:05 Lernziele: Elektrostatik in Materie Grundgrößen der Elektrostatik: Elektrisches Potential Spannung Elektrostatische Energie Leiter & Nichtleiter Elektrostatik
PhysikI und II fürstudentender Zahnmedizinund Biologie-2. Teil Universität Hamburg Wintersemester 2016/17
 PhysikI und II fürstudentender Zahnmedizinund Biologie-2. Teil Universität Hamburg Wintersemester 2016/17, Folien/Material zur Vorlesung auf: www.desy.de/~steinbru/physikzahnmed Mein Arbeitsgebiet: ExperimentelleElementarteilchenphysikan
PhysikI und II fürstudentender Zahnmedizinund Biologie-2. Teil Universität Hamburg Wintersemester 2016/17, Folien/Material zur Vorlesung auf: www.desy.de/~steinbru/physikzahnmed Mein Arbeitsgebiet: ExperimentelleElementarteilchenphysikan
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde. Sommersemester 2007
 Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #5 am 27.04.2007 Vladimir Dyakonov Frage des Tages Kupfermünze hat die Masse 0.003 kg Atomzahl
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #5 am 27.04.2007 Vladimir Dyakonov Frage des Tages Kupfermünze hat die Masse 0.003 kg Atomzahl
Elektrische und magnetische Felder
 Marlene Marinescu Elektrische und magnetische Felder Eine praxisorientierte Einführung Mit 260 Abbildungen @Nj) Springer Inhaltsverzeichnis I Elektrostatische Felder 1 Wesen des elektrostatischen Feldes
Marlene Marinescu Elektrische und magnetische Felder Eine praxisorientierte Einführung Mit 260 Abbildungen @Nj) Springer Inhaltsverzeichnis I Elektrostatische Felder 1 Wesen des elektrostatischen Feldes
15.Magnetostatik, 16. Induktionsgesetz
 Ablenkung von Teilchenstrahlen im Magnetfeld (Zyklotron u.a.): -> im Magnetfeld B werden geladene Teilchen auf einer Kreisbahn abgelenkt, wenn B senkrecht zu Geschwindigkeit v Kräftegleichgewicht: 2 v
Ablenkung von Teilchenstrahlen im Magnetfeld (Zyklotron u.a.): -> im Magnetfeld B werden geladene Teilchen auf einer Kreisbahn abgelenkt, wenn B senkrecht zu Geschwindigkeit v Kräftegleichgewicht: 2 v
5.5 Elektrisches Zentralfeld, Coulombsches Gesetz
 5 Elektrizität und Magnetismus 5.5 Elektrisches Zentralfeld, Coulombsches Gesetz Elektrisches Zentralfeld Kugel mit Radius r um eine Punktladung = ǫ 0 Ed A = ǫ 0 E E d A Kugel da = ǫ 0 E(4πr 2 ) (5.26)
5 Elektrizität und Magnetismus 5.5 Elektrisches Zentralfeld, Coulombsches Gesetz Elektrisches Zentralfeld Kugel mit Radius r um eine Punktladung = ǫ 0 Ed A = ǫ 0 E E d A Kugel da = ǫ 0 E(4πr 2 ) (5.26)
Das elektrische Feld
 I Das elektrische Feld 0 Wiederholung: Elektrostatik (ruhende Ladungen) Elektrische Ladung ist ebenso wie Masse eine fundamentale Eigenschaft der Materie. Niemand weiß, was Ladung oder Masse letztendlich
I Das elektrische Feld 0 Wiederholung: Elektrostatik (ruhende Ladungen) Elektrische Ladung ist ebenso wie Masse eine fundamentale Eigenschaft der Materie. Niemand weiß, was Ladung oder Masse letztendlich
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 28. 05. 2009 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Elektrizitätslehre und Magnetismus 28. 05. 2009
Elektrizitätslehre und Magnetismus Othmar Marti 28. 05. 2009 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Elektrizitätslehre und Magnetismus 28. 05. 2009
2 Grundgrößen und -gesetze der Elektrodynamik
 Grundgrößen und -gesetze der Elektrodynamik. Grundgrößen der Elektrodynamik.. Ladung und die dreidimensionale δ-distribution Ladung Q, q Ladungen treten in zwei Variationen auf: positiv und negativ Einheit:
Grundgrößen und -gesetze der Elektrodynamik. Grundgrößen der Elektrodynamik.. Ladung und die dreidimensionale δ-distribution Ladung Q, q Ladungen treten in zwei Variationen auf: positiv und negativ Einheit:
Physik. Abiturwiederholung. Das Elektrische Feld
 Das Elektrische Feld Strom Strom ist bewegte Ladung, die Stromstärke ergibt sich also als Veränderung der Ladung nach der Zeit, also durch die Ableitung. Somit kann man die Ladung als Fläche betrachten,
Das Elektrische Feld Strom Strom ist bewegte Ladung, die Stromstärke ergibt sich also als Veränderung der Ladung nach der Zeit, also durch die Ableitung. Somit kann man die Ladung als Fläche betrachten,
Physik 2 Elektrodynamik und Optik
 Physik 2 Elektrodynamik und Optik Notizen zur Vorlesung im Sommersemester 2013 Peter Schleper 6. Juni 2013 Institut für Experimentalphysik, Universität Hamburg [email protected] http://www.desy.de/~schleper/lehre/physik2/ss_2013
Physik 2 Elektrodynamik und Optik Notizen zur Vorlesung im Sommersemester 2013 Peter Schleper 6. Juni 2013 Institut für Experimentalphysik, Universität Hamburg [email protected] http://www.desy.de/~schleper/lehre/physik2/ss_2013
Klassische Elektrodynamik
 Theoretische Physik Band 3 Walter Greiner Klassische Elektrodynamik Institut für Festkörperphysik Fachgebiet Theoretische Physik Technische Hochschule Darmstadt Hochschulstr. 6 1P iu Verlag Harri Deutsch
Theoretische Physik Band 3 Walter Greiner Klassische Elektrodynamik Institut für Festkörperphysik Fachgebiet Theoretische Physik Technische Hochschule Darmstadt Hochschulstr. 6 1P iu Verlag Harri Deutsch
5 Elektrizität und Magnetismus
 5.1 Elektrische Ladung q Ursprung: Existenz von subatomaren Teilchen Proton: positive Ladung Elektron: negative Ladung besitzen jeweils eine Elementarladung e = 1.602 10 19 C (Coulomb) Ladung ist gequantelt
5.1 Elektrische Ladung q Ursprung: Existenz von subatomaren Teilchen Proton: positive Ladung Elektron: negative Ladung besitzen jeweils eine Elementarladung e = 1.602 10 19 C (Coulomb) Ladung ist gequantelt
Kräfte zwischen Ladungen: quantitative Bestimmung
 Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #3 am 25.04.2007 Vladimir Dyakonov Kräfte zwischen Ladungen: quantitative Bestimmung Messmethode:
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #3 am 25.04.2007 Vladimir Dyakonov Kräfte zwischen Ladungen: quantitative Bestimmung Messmethode:
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 27. 04. 2009 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Elektrizitätslehre und Magnetismus 27. 04. 2009
Elektrizitätslehre und Magnetismus Othmar Marti 27. 04. 2009 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Elektrizitätslehre und Magnetismus 27. 04. 2009
Induktion, Polarisierung und Magnetisierung
 Übung 2 Abgabe: 11.03. bzw. 15.03.2016 Elektromagnetische Felder & Wellen Frühjahrssemester 2016 Photonics Laboratory, ETH Zürich www.photonics.ethz.ch Induktion, Polarisierung und Magnetisierung In dieser
Übung 2 Abgabe: 11.03. bzw. 15.03.2016 Elektromagnetische Felder & Wellen Frühjahrssemester 2016 Photonics Laboratory, ETH Zürich www.photonics.ethz.ch Induktion, Polarisierung und Magnetisierung In dieser
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 09. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 09. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 09. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 09. 06.
Physik II. SS 2006 Vorlesung Karsten Danzmann
 Physik II SS 2006 Vorlesung 1 13.4.2006 Karsten Danzmann Max-Planck-Institut für Gravitationsphysik (Albert Einstein Institut) und Universität Hannover Physik bis zum Vordiplom Physik I RdP I Mechanik,
Physik II SS 2006 Vorlesung 1 13.4.2006 Karsten Danzmann Max-Planck-Institut für Gravitationsphysik (Albert Einstein Institut) und Universität Hannover Physik bis zum Vordiplom Physik I RdP I Mechanik,
Zusammenfassung EPII. Elektromagnetismus
 Zusammenfassung EPII Elektromagnetismus Elektrodynamik: Überblick Dynamik (Newton): Elektromagnetische Kräfte zw. Ladungen: Definition EFeld: Kraft auf ruhende Testladung Q: BFeld: Kraft auf bewegte Testladung:
Zusammenfassung EPII Elektromagnetismus Elektrodynamik: Überblick Dynamik (Newton): Elektromagnetische Kräfte zw. Ladungen: Definition EFeld: Kraft auf ruhende Testladung Q: BFeld: Kraft auf bewegte Testladung:
Unter Kapazität versteht man die Eigenschaft von Kondensatoren, Ladung oder elektrische Energie zu speichern.
 16. Kapazität Unter Kapazität versteht man die Eigenschaft von Kondensatoren, Ladung oder elektrische Energie zu speichern. 16.1 Plattenkondensator Das einfachste Beispiel für einen Kondensator ist der
16. Kapazität Unter Kapazität versteht man die Eigenschaft von Kondensatoren, Ladung oder elektrische Energie zu speichern. 16.1 Plattenkondensator Das einfachste Beispiel für einen Kondensator ist der
IIE1. Modul Elektrizitätslehre II. Cavendish-Experiment
 IIE1 Modul Elektrizitätslehre II Cavendish-Experiment Ziel dieses Experiments ist es, dich mit dem Phänomen der elektrischen Influenz vertraut zu machen. Des weiteren sollen Eigenschaften wie Flächenladungsdichte,
IIE1 Modul Elektrizitätslehre II Cavendish-Experiment Ziel dieses Experiments ist es, dich mit dem Phänomen der elektrischen Influenz vertraut zu machen. Des weiteren sollen Eigenschaften wie Flächenladungsdichte,
1 Felder bewegter Ladungen
 Universität Leipzig, Fakultät für Physik und Geowissenschaften Vorlesung zur Experimentalphysik III Wintersemester 2008/2009 Prof. Dr. Josef A. Käs Vorlesungsmitschrift zur Vorlesung vom 16.10.2008 1 Felder
Universität Leipzig, Fakultät für Physik und Geowissenschaften Vorlesung zur Experimentalphysik III Wintersemester 2008/2009 Prof. Dr. Josef A. Käs Vorlesungsmitschrift zur Vorlesung vom 16.10.2008 1 Felder
Ferienkurs - Experimentalphysik 2 - Übungsblatt - Lösungen
 Technische Universität München Department of Physics Ferienkurs - Experimentalphysik 2 - Übungsblatt - Lösungen Montag Daniel Jost Datum 2/8/212 Aufgabe 1: (a) Betrachten Sie eine Ladung, die im Ursprung
Technische Universität München Department of Physics Ferienkurs - Experimentalphysik 2 - Übungsblatt - Lösungen Montag Daniel Jost Datum 2/8/212 Aufgabe 1: (a) Betrachten Sie eine Ladung, die im Ursprung
Ferienkurs Elektrodynamik - Drehmomente, Maxwellgleichungen, Stetigkeiten, Ohm, Induktion, Lenz
 Ferienkurs Elektrodynamik - Drehmomente, Maxwellgleichungen, Stetigkeiten, Ohm, Induktion, Lenz Stephan Huber 19. August 2009 1 Nachtrag zum Drehmoment 1.1 Magnetischer Dipol Ein magnetischer Dipol erfährt
Ferienkurs Elektrodynamik - Drehmomente, Maxwellgleichungen, Stetigkeiten, Ohm, Induktion, Lenz Stephan Huber 19. August 2009 1 Nachtrag zum Drehmoment 1.1 Magnetischer Dipol Ein magnetischer Dipol erfährt
2. Klausur in K1 am
 Name: Punkte: Note: Ø: Physik Kursstufe Abzüge für Darstellung: Rundung:. Klausur in K am 7.. 00 Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: e =,60
Name: Punkte: Note: Ø: Physik Kursstufe Abzüge für Darstellung: Rundung:. Klausur in K am 7.. 00 Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: e =,60
Inhaltsverzeichnis Elektrostatik
 Inhaltsverzeichnis 1 Elektrostatik 1 1.1 Grundbegriffe...................................... 1 1.1.1 Elektrische Ladung, Coulomb-Gesetz..................... 1 1.1.2 Das elektrische Feld..............................
Inhaltsverzeichnis 1 Elektrostatik 1 1.1 Grundbegriffe...................................... 1 1.1.1 Elektrische Ladung, Coulomb-Gesetz..................... 1 1.1.2 Das elektrische Feld..............................
Elektrische und ^magnetische Felder
 Marlene Marinescu Elektrische und ^magnetische Felder Eine praxisorientierte Einführung Zweite, vollständig neu bearbeitete Auflage * j Springer I nhaltsverzeichnis 1 Elektrostatische Felder 1 1.1 Wesen
Marlene Marinescu Elektrische und ^magnetische Felder Eine praxisorientierte Einführung Zweite, vollständig neu bearbeitete Auflage * j Springer I nhaltsverzeichnis 1 Elektrostatische Felder 1 1.1 Wesen
PN 2 Einführung in die Experimentalphysik für Chemiker
 PN 2 Einführung in die Experimentalphysik für Chemiker 2. Vorlesung 25.4.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
PN 2 Einführung in die Experimentalphysik für Chemiker 2. Vorlesung 25.4.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
Einführung Einleitung Grundlagen Bewegung und Energie. 1.1 Grundbegriffe... 16
 3 Inhaltsverzeichnis Einführung..................................................... 12 Einleitung..................................................... 12 Grundlagen.....................................................
3 Inhaltsverzeichnis Einführung..................................................... 12 Einleitung..................................................... 12 Grundlagen.....................................................
Elektrizität und Magnetismus
 Grundlagen- und Orientierungsprüfung Elektrotechnik und Informationstechnik Termin Sommersemester 2010 Elektrizität und Magnetismus Donnerstag, 05. 08. 2010, 8:30 10:30 Uhr Zur Beachtung: Zugelassene Hilfsmittel:
Grundlagen- und Orientierungsprüfung Elektrotechnik und Informationstechnik Termin Sommersemester 2010 Elektrizität und Magnetismus Donnerstag, 05. 08. 2010, 8:30 10:30 Uhr Zur Beachtung: Zugelassene Hilfsmittel:
Skalarfelder. 1-1 Ma 2 Lubov Vassilevskaya
 Skalarfelder 1-1 Ma 2 Lubov Vassilevskaya Einführendes Beispiel r P + q F (P) + Q Abb. 1-1: Kraftwirkung auf eine positive Ladung Wir betrachten das elektrische Feld in der Umgebung einer positiven Punktladung
Skalarfelder 1-1 Ma 2 Lubov Vassilevskaya Einführendes Beispiel r P + q F (P) + Q Abb. 1-1: Kraftwirkung auf eine positive Ladung Wir betrachten das elektrische Feld in der Umgebung einer positiven Punktladung
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 17. 04. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 17. 04.
Elektrizitätslehre und Magnetismus Othmar Marti 17. 04. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 17. 04.
Ferienkurs Experimentalphysik II Elektrodynamik. Magnetostatik. 12. September 2011 Michael Mittermair
 Ferienkurs Experimentalphysik II Elektrodynamik Magnetostatik 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Permanentmagnete und Polstärke 2 2 Magnetfelder stationärer Ströme 3 2.1 Magnetfeldstärke
Ferienkurs Experimentalphysik II Elektrodynamik Magnetostatik 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Permanentmagnete und Polstärke 2 2 Magnetfelder stationärer Ströme 3 2.1 Magnetfeldstärke
PHYSIK. 2. Klausur - Lösung
 EI PH3 2010-11 PHYSIK 2. Klausur - Lösung 1. Aufgabe (2 Punkte) Unten befindet sich ein Proton im elektrischen Feld zwischen einer ortsfesten positiven sowie einer ortsfesten negativen Ladung. a) Beschreibe,
EI PH3 2010-11 PHYSIK 2. Klausur - Lösung 1. Aufgabe (2 Punkte) Unten befindet sich ein Proton im elektrischen Feld zwischen einer ortsfesten positiven sowie einer ortsfesten negativen Ladung. a) Beschreibe,
5.1 Statische und zeitlich veränderliche
 5.1 Statische und zeitlich veränderliche Felder 5 Induktion 5.1 Statische und zeitlich veränderliche Felder Bisher haben wir elektrische und magnetische Felder betrachtet, die durch zeitlich konstante
5.1 Statische und zeitlich veränderliche Felder 5 Induktion 5.1 Statische und zeitlich veränderliche Felder Bisher haben wir elektrische und magnetische Felder betrachtet, die durch zeitlich konstante
Aufbau von Atomen Anzahl der Protonen = Anzahl der Elektronen
 Aufbau von Atomen Ein Atom besteht aus einem positiv geladenen Atomkern und einer negativ geladenen Atomhülle. Träger der positiven Ladung sind Protonen, Träger der negativen Ladung sind Elektronen. Atomhülle
Aufbau von Atomen Ein Atom besteht aus einem positiv geladenen Atomkern und einer negativ geladenen Atomhülle. Träger der positiven Ladung sind Protonen, Träger der negativen Ladung sind Elektronen. Atomhülle
12. Elektrodynamik Quellen von Magnetfeldern 12.2 Das Ampere sche Gesetz 12.3 Magnetische Induktion 12.4 Lenz sche Regel 12.5 Magnetische Kraft
 12. Elektrodynamik 12.1 Quellen von Magnetfeldern 12.2 Das Ampere sche Gesetz 12.3 Magnetische Induktion 12.4 Lenz sche Regel 12.5 Magnetische Kraft 12. Elektrodynamik Beobachtungen zeigen: - Kommt ein
12. Elektrodynamik 12.1 Quellen von Magnetfeldern 12.2 Das Ampere sche Gesetz 12.3 Magnetische Induktion 12.4 Lenz sche Regel 12.5 Magnetische Kraft 12. Elektrodynamik Beobachtungen zeigen: - Kommt ein
1.1.2 Aufladen und Entladen eines Kondensators; elektrische Ladung; Definition der Kapazität
 1.1.2 Aufladen und Entladen eines Kondensators; elektrische Ladung; Definition der Kapazität Ladung und Stromstärke Die Einheit der Stromstärke wurde früher durch einen chemischen Prozess definiert; heute
1.1.2 Aufladen und Entladen eines Kondensators; elektrische Ladung; Definition der Kapazität Ladung und Stromstärke Die Einheit der Stromstärke wurde früher durch einen chemischen Prozess definiert; heute
2 Das elektrostatische Feld
 Das elektrostatische Feld Das elektrostatische Feld wird durch ruhende elektrische Ladungen verursacht, d.h. es fließt kein Strom. Auf die ruhenden Ladungen wirken Coulomb-Kräfte, die über das Coulombsche
Das elektrostatische Feld Das elektrostatische Feld wird durch ruhende elektrische Ladungen verursacht, d.h. es fließt kein Strom. Auf die ruhenden Ladungen wirken Coulomb-Kräfte, die über das Coulombsche
4. Beispiele für Kräfte
 4. Beispiele für Kräfte 4.1 Federkraft 4.2 Gravitation 4.3 Elektrische Kraft 4.4 Reibungskraft 4. Beispiele für Kräfte Man kennt: Federkraft, Reibungskraft, Trägheitskraft, Dipolkraft, Schubskraft, Coulombkraft,
4. Beispiele für Kräfte 4.1 Federkraft 4.2 Gravitation 4.3 Elektrische Kraft 4.4 Reibungskraft 4. Beispiele für Kräfte Man kennt: Federkraft, Reibungskraft, Trägheitskraft, Dipolkraft, Schubskraft, Coulombkraft,
Physik-Skript. Teil II. Melanchthon-Gymnasium Nürnberg
 Physik-Skript Teil II Melanchthon-Gymnasium Nürnberg Volker Dickel 3. überarbeitete Auflage, 2014 2. überarbeitete Auflage, 2012 1. Auflage 2009 Inhaltsverzeichnis EINLEITUNG: ELEMENTARTEILCHEN UND WECHSELWIRKUNGEN...
Physik-Skript Teil II Melanchthon-Gymnasium Nürnberg Volker Dickel 3. überarbeitete Auflage, 2014 2. überarbeitete Auflage, 2012 1. Auflage 2009 Inhaltsverzeichnis EINLEITUNG: ELEMENTARTEILCHEN UND WECHSELWIRKUNGEN...
was besagt das Induktionsgesetz? was besagt die Lenzsche Regel?
 Induktion Einleitung Thema: Induktion Fragen: was ist Induktion? was besagt das Induktionsgesetz? was besagt die Lenzsche Regel? Frage: was, wenn sich zeitlich ändernde E- und -Felder sich gegenseitig
Induktion Einleitung Thema: Induktion Fragen: was ist Induktion? was besagt das Induktionsgesetz? was besagt die Lenzsche Regel? Frage: was, wenn sich zeitlich ändernde E- und -Felder sich gegenseitig
Elektromagnetische Felder und Wellen. Klausur Herbst Aufgabe 1 (5 Punkte) Aufgabe 2 (3 Punkte) Aufgabe 3 (5 Punkte) Aufgabe 4 (12 Punkte) Kern
 Elektromagnetische Felder und Wellen Klausur Herbst 2000 Aufgabe 1 (5 Punkte) Ein magnetischer Dipol hat das Moment m = m e z. Wie groß ist Feld B auf der z- Achse bei z = a, wenn sich der Dipol auf der
Elektromagnetische Felder und Wellen Klausur Herbst 2000 Aufgabe 1 (5 Punkte) Ein magnetischer Dipol hat das Moment m = m e z. Wie groß ist Feld B auf der z- Achse bei z = a, wenn sich der Dipol auf der
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 12. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 12. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 12. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 12. 06.
= Dimension: = (Farad)
 Kapazität / Kondensator Ein Kondensator dient zur Speicherung elektrischer Ladung Die Speicherkapazität eines Kondensators wird mit der Größe 'Kapazität' bezeichnet Die Kapazität C ist definiert als: Dimension:
Kapazität / Kondensator Ein Kondensator dient zur Speicherung elektrischer Ladung Die Speicherkapazität eines Kondensators wird mit der Größe 'Kapazität' bezeichnet Die Kapazität C ist definiert als: Dimension:
10.1 Ampère sches Gesetz und einfache Stromverteilungen
 1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
1. Elektrizität & Magnetismus
 1. Elektrizität & Magnetismus 1.1 Einleitung Elektrische und magnetische Phänomene in der Natur Die vier (bekannten) Wechselwirkungen Elektrometer in der Vorlesung Selbstgebautes Elektrometer -dasideale
1. Elektrizität & Magnetismus 1.1 Einleitung Elektrische und magnetische Phänomene in der Natur Die vier (bekannten) Wechselwirkungen Elektrometer in der Vorlesung Selbstgebautes Elektrometer -dasideale
Inhalt. 10. Elektrostatik. 10. Elektrostatik
 Inhalt 10. Elektrostatik 10.1 Elektrische Ladung 10.2 Coulombsches Gesetz 10.3 Elektrisches Feld 10.4 Kraft auf Ladungen 10.5 Elektrisches Potential 10.6 Elektrische Kapazität 1.1 Der Raum 10.1 Elektrische
Inhalt 10. Elektrostatik 10.1 Elektrische Ladung 10.2 Coulombsches Gesetz 10.3 Elektrisches Feld 10.4 Kraft auf Ladungen 10.5 Elektrisches Potential 10.6 Elektrische Kapazität 1.1 Der Raum 10.1 Elektrische
Der Ladungsbetrag Q, den jede Kondensatorplatten aufnimmt, ist dabei proportional zur angelegten. Q U = konst.
 I. Elektrostatik ==================================================================. Das elektrische Feld eines Plattenkondensators Ein Plattenkondensator besteht aus zwei sich parallel gegenüberliegenden
I. Elektrostatik ==================================================================. Das elektrische Feld eines Plattenkondensators Ein Plattenkondensator besteht aus zwei sich parallel gegenüberliegenden
Übungsblatt 3 - Lösungen
 Übungsblatt 3 - Lösungen zur Vorlesung EP2 (Prof. Grüner) im 2010 3. Juni 2011 Aufgabe 1: Plattenkondensator Ein Kondensator besteht aus parallelen Platten mit einer quadratischen Grundäche von 20cm Kantenlänge.
Übungsblatt 3 - Lösungen zur Vorlesung EP2 (Prof. Grüner) im 2010 3. Juni 2011 Aufgabe 1: Plattenkondensator Ein Kondensator besteht aus parallelen Platten mit einer quadratischen Grundäche von 20cm Kantenlänge.
Felder und Wellen WS 2016/2017
 Felder und Wellen WS 216/217 Musterlösung zum 2. Tutorium 1. Aufgabe (**) Berechnen Sie das el. Feld einer in z-richtung unendlich lang ausgedehnten unendlich dünnen Linienladung der Ladungsdichte η pro
Felder und Wellen WS 216/217 Musterlösung zum 2. Tutorium 1. Aufgabe (**) Berechnen Sie das el. Feld einer in z-richtung unendlich lang ausgedehnten unendlich dünnen Linienladung der Ladungsdichte η pro
Aufgabe 1 ( 3 Punkte)
 Elektromagnetische Felder und Wellen: Klausur 2016-2 1 Aufgabe 1 ( 3 Punkte) Welche elektrische Feldstärke benötigt man, um ein Elektron (Masse m e, Ladung q = e) im Schwerefeld der Erde schweben zu lassen?
Elektromagnetische Felder und Wellen: Klausur 2016-2 1 Aufgabe 1 ( 3 Punkte) Welche elektrische Feldstärke benötigt man, um ein Elektron (Masse m e, Ladung q = e) im Schwerefeld der Erde schweben zu lassen?
Klassische Experimentalphysik II
 Klassische Experimentalphysik II SS 2014 Dozent: Prof. Übungsleitung: Dr. Martin Weides Modul 5520 Beschreibung Lernziele: Verständnis der experimentellen Grundlagen und deren mathematischer Beschreibung
Klassische Experimentalphysik II SS 2014 Dozent: Prof. Übungsleitung: Dr. Martin Weides Modul 5520 Beschreibung Lernziele: Verständnis der experimentellen Grundlagen und deren mathematischer Beschreibung
Physik G8-Abitur 2011 Aufgabenteil Ph 11 LÖSUNG
 3 G8_Physik_2011_Ph11_Loe Seite 1 von 7 Ph 11-1 Physik G8-Abitur 2011 Aufgabenteil Ph 11 LÖSUNG 1) a) b) - - + + + c) In einem Homogenen elektrischen Feld nimmt das Potential in etwa linear. D.h. Es sinkt
3 G8_Physik_2011_Ph11_Loe Seite 1 von 7 Ph 11-1 Physik G8-Abitur 2011 Aufgabenteil Ph 11 LÖSUNG 1) a) b) - - + + + c) In einem Homogenen elektrischen Feld nimmt das Potential in etwa linear. D.h. Es sinkt
Übungen zu Wellen und Elektrodynamik für Chemie- und Bioingenieure und Verfahrenstechniker WS 11/12
 Institut für Experimentelle Kernphysik Übungen zu Wellen und Elektrodynamik für Chemie- und Bioingenieure und Verfahrenstechniker WS 11/12 Prof. Dr. T. Müller Dr. F. Hartmann Blatt 3 Bearbeitung: 25.11.2011
Institut für Experimentelle Kernphysik Übungen zu Wellen und Elektrodynamik für Chemie- und Bioingenieure und Verfahrenstechniker WS 11/12 Prof. Dr. T. Müller Dr. F. Hartmann Blatt 3 Bearbeitung: 25.11.2011
Systematisierung Felder und Bewegung von Ladungsträgern in Feldern
 Systematisierung Felder und Bewegung von Ladungsträgern in Feldern Systematisierung Feld Unterschiede: Beschreibung Ursache Kräfte auf elektrisches Feld Das elektrische Feld ist der besondere Zustand des
Systematisierung Felder und Bewegung von Ladungsträgern in Feldern Systematisierung Feld Unterschiede: Beschreibung Ursache Kräfte auf elektrisches Feld Das elektrische Feld ist der besondere Zustand des
df B = d Φ(F), F = C. (7.1)
 Kapitel 7 Maxwell-Gleichungen 7.1 Induktionsgesetz araday beobachtete 1831, dass in einer Leiterschleife C ein elektrischer Strom entsteht, wenn ein in der Nähe befindlicher Magnet bewegt oder die Leiterschleife
Kapitel 7 Maxwell-Gleichungen 7.1 Induktionsgesetz araday beobachtete 1831, dass in einer Leiterschleife C ein elektrischer Strom entsteht, wenn ein in der Nähe befindlicher Magnet bewegt oder die Leiterschleife
PS III - Rechentest
 Grundlagen der Elektrotechnik PS III - Rechentest 01.03.2011 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 Summe Punkte 3 15 10 12 11 9 60 erreicht Hinweise: Schreiben Sie auf das Deckblatt Ihren Namen und
Grundlagen der Elektrotechnik PS III - Rechentest 01.03.2011 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 Summe Punkte 3 15 10 12 11 9 60 erreicht Hinweise: Schreiben Sie auf das Deckblatt Ihren Namen und
Elektrische und magnetische Felder
 Elektrische und magnetische Felder Eine praxisorientierte Einführung Bearbeitet von Marlene Marinescu 1. Auflage 2012. Buch. xiv, 343 S. Hardcover ISBN 978 3 642 24219 9 Format (B x L): 15,5 x 23,5 cm
Elektrische und magnetische Felder Eine praxisorientierte Einführung Bearbeitet von Marlene Marinescu 1. Auflage 2012. Buch. xiv, 343 S. Hardcover ISBN 978 3 642 24219 9 Format (B x L): 15,5 x 23,5 cm
Klausur 12/1 Physik LK Elsenbruch Di (4h) Thema: elektrische und magnetische Felder Hilfsmittel: Taschenrechner, Formelsammlung
 Klausur 12/1 Physik LK Elsenbruch Di 18.01.05 (4h) Thema: elektrische und magnetische Felder Hilfsmittel: Taschenrechner, Formelsammlung 1) Ein Kondensator besteht aus zwei horizontal angeordneten, quadratischen
Klausur 12/1 Physik LK Elsenbruch Di 18.01.05 (4h) Thema: elektrische und magnetische Felder Hilfsmittel: Taschenrechner, Formelsammlung 1) Ein Kondensator besteht aus zwei horizontal angeordneten, quadratischen
Elektrostatik. 4 Demonstrationsexperimente verwendete Materialien: Polyestertuch, Kunststoffstäbe (einer frei drehbar gelagert), Glasstab
 Elektrostatik 4 Demonstrationsexperimente verwendete Materialien: Polyestertuch, Kunststoffstäbe (einer frei drehbar gelagert), Glasstab Beschreibe und erkläre die Exp. stichpunkartig. Ergebnis: - Es gibt
Elektrostatik 4 Demonstrationsexperimente verwendete Materialien: Polyestertuch, Kunststoffstäbe (einer frei drehbar gelagert), Glasstab Beschreibe und erkläre die Exp. stichpunkartig. Ergebnis: - Es gibt
11. Elektrodynamik Magnetische Kraft auf Stromleiter Quellen von Magnetfeldern. 11. Elektrodynamik. Physik für E-Techniker
 11. Elektrodynamik 11.5.2 Magnetische Kraft auf Stromleiter 11.5.3 Quellen von Magnetfeldern 11.5.2 Magnetische Kraft auf Stromleiter Wir hatten: Frage: Kraft auf einzelne Punktladung Kraft auf Stromleiter
11. Elektrodynamik 11.5.2 Magnetische Kraft auf Stromleiter 11.5.3 Quellen von Magnetfeldern 11.5.2 Magnetische Kraft auf Stromleiter Wir hatten: Frage: Kraft auf einzelne Punktladung Kraft auf Stromleiter
2 Elektromagnetische Wellen
 2 Elektromagnetische Wellen 21 2 Elektromagnetische Wellen In diesem Kapitel tauchen wir erstmals tiefer ein in die Wellennatur des Lichts. Wir werden sehen, dass elektrische Felder sowohl von elektrischen
2 Elektromagnetische Wellen 21 2 Elektromagnetische Wellen In diesem Kapitel tauchen wir erstmals tiefer ein in die Wellennatur des Lichts. Wir werden sehen, dass elektrische Felder sowohl von elektrischen
PN 2 Einführung in die Experimentalphysik für Chemiker
 PN 2 Einführung in die Experimentalphysik für Chemiker 4. Vorlesung 9.5.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
PN 2 Einführung in die Experimentalphysik für Chemiker 4. Vorlesung 9.5.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
7 Maxwell - Gleichungen
 7.1 Der Verschiebungsstrom 7 Maxwell - Gleichungen 7.1 Der Verschiebungsstrom Das Faraday sche Gesetz Eds= t Bd A beschreibt, dass die zeitliche Veränderung des magnetischen Flusses durch eine Fläche wirbelförmige
7.1 Der Verschiebungsstrom 7 Maxwell - Gleichungen 7.1 Der Verschiebungsstrom Das Faraday sche Gesetz Eds= t Bd A beschreibt, dass die zeitliche Veränderung des magnetischen Flusses durch eine Fläche wirbelförmige
9. Elektrostatik Physik für Informatiker. 9. Elektrostatik
 9. Elektrostatik 9.1 Elektrische Ladung 9.2 Coulombsches Gesetz 9.3 Elektrisches Feld 9.4 Kraft auf Ladungen 9.5 Elektrisches Potential 9.6 Elektrische Kapazität 9.1 Elektrische Ladung Es gibt (genau)
9. Elektrostatik 9.1 Elektrische Ladung 9.2 Coulombsches Gesetz 9.3 Elektrisches Feld 9.4 Kraft auf Ladungen 9.5 Elektrisches Potential 9.6 Elektrische Kapazität 9.1 Elektrische Ladung Es gibt (genau)
Klausur 12/1 Physik LK Elsenbruch Di (4h) Thema: elektrische und magnetische Felder Hilfsmittel: Taschenrechner, Formelsammlung
 Klausur 12/1 Physik LK Elsenbruch Di 18.01.05 (4h) Thema: elektrische und magnetische Felder Hilfsmittel: Taschenrechner, Formelsammlung 1) Elektronen im elektrischen Querfeld. Die nebenstehende Skizze
Klausur 12/1 Physik LK Elsenbruch Di 18.01.05 (4h) Thema: elektrische und magnetische Felder Hilfsmittel: Taschenrechner, Formelsammlung 1) Elektronen im elektrischen Querfeld. Die nebenstehende Skizze
Inhaltsverzeichnis. Kurz, G�nther Strà mungslehre, Optik, Elektrizit�tslehre, Magnetismus digitalisiert durch: IDS Basel Bern
 Inhaltsverzeichnis I Strömungslehre 11 1 Ruhende Flüssigkeiten (und Gase) - Hydrostatik 11 1.1 Charakterisierung von Flüssigkeiten 11 1.2 Druck - Definition und abgeleitete 11 1.3 Druckänderungen in ruhenden
Inhaltsverzeichnis I Strömungslehre 11 1 Ruhende Flüssigkeiten (und Gase) - Hydrostatik 11 1.1 Charakterisierung von Flüssigkeiten 11 1.2 Druck - Definition und abgeleitete 11 1.3 Druckänderungen in ruhenden
3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P]
![3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] 3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P]](/thumbs/56/38171884.jpg) 3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] B = µ 0 I 4 π ds (r r ) r r 3 a) Beschreiben Sie die im Gesetz von Biot-Savart vorkommenden Größen (rechts vom Integral). b) Zeigen Sie, dass das Biot-Savartsche
3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] B = µ 0 I 4 π ds (r r ) r r 3 a) Beschreiben Sie die im Gesetz von Biot-Savart vorkommenden Größen (rechts vom Integral). b) Zeigen Sie, dass das Biot-Savartsche
Kraft zwischen zwei Ladungen Q 1 und Q 2 / Coulomb'sches Gesetz
 KRG NW, Physik Klasse 10, Kräfte auf Ladungen, Kondensator, Fachlehrer Stahl Seite 1 Kraft zwischen zwei Ladungen Q 1 und Q 2 / Coulomb'sches Gesetz Kraft auf eine Probeladung q im elektrischen Feld (homogen,
KRG NW, Physik Klasse 10, Kräfte auf Ladungen, Kondensator, Fachlehrer Stahl Seite 1 Kraft zwischen zwei Ladungen Q 1 und Q 2 / Coulomb'sches Gesetz Kraft auf eine Probeladung q im elektrischen Feld (homogen,
v q,m Aufgabensammlung Experimentalphysik für ET
 Experimentalphysik für ET Aufgabensammlung 1. E-Felder Auf einen Plattenkondensator mit quadratischen Platten der Kantenlänge a und dem Plattenabstand d werde die Ladung Q aufgebracht, bevor er vom Netz
Experimentalphysik für ET Aufgabensammlung 1. E-Felder Auf einen Plattenkondensator mit quadratischen Platten der Kantenlänge a und dem Plattenabstand d werde die Ladung Q aufgebracht, bevor er vom Netz
Magnetische Monopole
 Magnetische Monopole Einführung: Aber in der Schule haben wir doch gelernt... Dirac s Idee symmetrischer Maxwell-Gleichungen Konsequenzen aus der Existenz magnetischer Monopole Quantisierung der elektrischen
Magnetische Monopole Einführung: Aber in der Schule haben wir doch gelernt... Dirac s Idee symmetrischer Maxwell-Gleichungen Konsequenzen aus der Existenz magnetischer Monopole Quantisierung der elektrischen
Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t.
![Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t. Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t.](/thumbs/48/24282507.jpg) Formelsammlung Physik Mechanik. Kinematik und Kräfte Kinematik Erstes Newtonsches Axiom (Axio/Reaxio) F axio = F reaxio Zweites Newtonsches Axiom Translationsbewegungen Konstante Beschleunigung F = m a
Formelsammlung Physik Mechanik. Kinematik und Kräfte Kinematik Erstes Newtonsches Axiom (Axio/Reaxio) F axio = F reaxio Zweites Newtonsches Axiom Translationsbewegungen Konstante Beschleunigung F = m a
Grundwissen. Physik. Jahrgangsstufe 7
 Grundwissen Physik Jahrgangsstufe 7 Grundwissen Physik Jahrgangsstufe 7 Seite 1 1. Aufbau der Materie 1.1 Atome Ein Atom besteht aus dem positiv geladenen Atomkern und der negativ geladenen Atomhülle aus
Grundwissen Physik Jahrgangsstufe 7 Grundwissen Physik Jahrgangsstufe 7 Seite 1 1. Aufbau der Materie 1.1 Atome Ein Atom besteht aus dem positiv geladenen Atomkern und der negativ geladenen Atomhülle aus
Experimentalphysik II: Elektrostatik I
 Experimentalphysik II: Elektrostatik I Zweitversuch-Ferienkurs Sommersemester 09 William Hefter 07/09/09 Inhaltsverzeichnis Elektrische Ladung, Coulomb-Kraft 2 2 Das elektrische Feld 2 3 Der Satz von Gauß
Experimentalphysik II: Elektrostatik I Zweitversuch-Ferienkurs Sommersemester 09 William Hefter 07/09/09 Inhaltsverzeichnis Elektrische Ladung, Coulomb-Kraft 2 2 Das elektrische Feld 2 3 Der Satz von Gauß
Energie und Energieerhaltung
 Arbeit und Energie Energie und Energieerhaltung Es gibt keine Evidenz irgendwelcher Art dafür, dass Energieerhaltung in irgendeinem System nicht erfüllt ist. Energie im Austausch In mechanischen und biologischen
Arbeit und Energie Energie und Energieerhaltung Es gibt keine Evidenz irgendwelcher Art dafür, dass Energieerhaltung in irgendeinem System nicht erfüllt ist. Energie im Austausch In mechanischen und biologischen
Übungen: Kraftwirkung in magnetischen Feldern
 Übungen: Kraftwirkung in magnetischen Feldern Aufgabe 1: Zwei metallische Leiter werden durch einen runden, beweglichen Kohlestift verbunden. Welche Beobachtung macht ein(e) Schüler(in), wenn der Stromkreis
Übungen: Kraftwirkung in magnetischen Feldern Aufgabe 1: Zwei metallische Leiter werden durch einen runden, beweglichen Kohlestift verbunden. Welche Beobachtung macht ein(e) Schüler(in), wenn der Stromkreis
Grundgebiete der Elektrotechnik 1 Elektrische Netze bei Gleichstrom, elektrische und magnetische Felder
 Grundgebiete der Elektrotechnik 1 Elektrische Netze bei Gleichstrom, elektrische und magnetische Felder von Prof. Dr.-Ing. Horst Clausert, TH Darmstadt Prof. Dr.-Ing. Günther Wiesemann, FH Braunschweig/Wolfenbüttel
Grundgebiete der Elektrotechnik 1 Elektrische Netze bei Gleichstrom, elektrische und magnetische Felder von Prof. Dr.-Ing. Horst Clausert, TH Darmstadt Prof. Dr.-Ing. Günther Wiesemann, FH Braunschweig/Wolfenbüttel
4 Grenzflächen, Leiter und das elektrostatische Randwertproblem
 4 Grenzflächen, Leiter und das elektrostatische Randwertproblem Bei der Berechnung elektrostatischer Felder und Potentiale mussten wir bisher voraussetzen, dass wir die Ladungsverteilungen im gesamten
4 Grenzflächen, Leiter und das elektrostatische Randwertproblem Bei der Berechnung elektrostatischer Felder und Potentiale mussten wir bisher voraussetzen, dass wir die Ladungsverteilungen im gesamten
1. Statisches elektrisches Feld
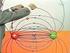 . Statisches elektrisches Feld. Grundlagen der Elektrizitätslehre.. Elektrizität in Natur, Technik und Alltag Altertum: Bernstein reiben Staubteilchen und Wollfasern werden angezogen 794 Coulomb: Gesetz
. Statisches elektrisches Feld. Grundlagen der Elektrizitätslehre.. Elektrizität in Natur, Technik und Alltag Altertum: Bernstein reiben Staubteilchen und Wollfasern werden angezogen 794 Coulomb: Gesetz
Im folgenden Schaltkreis beobachtet man eigenartige Phänomene: = > Beim Einschalten leuchtet die Glühbirne für
 + Kapitel 4 KAPAZITÄT und ENERGIE 4. Kondensator Ein Kondensator besteht typischerweise aus zwei Leiterplatten, die sich in einem kleinen Abstand voneinander befinden. Meist liegt zwischen den Elektroden
+ Kapitel 4 KAPAZITÄT und ENERGIE 4. Kondensator Ein Kondensator besteht typischerweise aus zwei Leiterplatten, die sich in einem kleinen Abstand voneinander befinden. Meist liegt zwischen den Elektroden
Physik für Ingenieure
 Physik für Ingenieure von Prof. Dr. Ulrich Hahn OldenbourgVerlag München Wien 1 Einführung 1 1.1 Wie wird das Wissen gewonnen? 2 1.1.1 Gültigkeitsbereiche physikalischer Gesetze 4 1.1.2 Prinzipien der
Physik für Ingenieure von Prof. Dr. Ulrich Hahn OldenbourgVerlag München Wien 1 Einführung 1 1.1 Wie wird das Wissen gewonnen? 2 1.1.1 Gültigkeitsbereiche physikalischer Gesetze 4 1.1.2 Prinzipien der
Elektrische und magnetische Felder
 Elektrische und magnetische Felder Von Dr.-Ing. Heinrich Frohne Professor an der Universität Hannover Mit 247 Bildern, 5 Tafeln und 140 Beispielen B.G. Teubner Stuttgart 1994 Inhalt s Verzeichnis 1 Wesen
Elektrische und magnetische Felder Von Dr.-Ing. Heinrich Frohne Professor an der Universität Hannover Mit 247 Bildern, 5 Tafeln und 140 Beispielen B.G. Teubner Stuttgart 1994 Inhalt s Verzeichnis 1 Wesen
Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 02/2002 Laborunterlagen
 Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 0/00 7 Magnetismus 7. Grundlagen magnetischer Kreise Im folgenden wird die Vorgehensweise bei der Untersuchung eines magnetischen Kreises
Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 0/00 7 Magnetismus 7. Grundlagen magnetischer Kreise Im folgenden wird die Vorgehensweise bei der Untersuchung eines magnetischen Kreises
Physik LK 12, Klausur 02 Elektrisches Feld und Kondensator Lösung
 Konstanten: Elementarladung e=,602 0 9 2 As 2 C. Elektrische Feldkonstante: 8,8542 0 N m 2 Dielektrizitätszahl: r Luft = Aufgabe : Eine studentische Hilfskraft wurde eingestellt, um acht Stunden lang Ladungen
Konstanten: Elementarladung e=,602 0 9 2 As 2 C. Elektrische Feldkonstante: 8,8542 0 N m 2 Dielektrizitätszahl: r Luft = Aufgabe : Eine studentische Hilfskraft wurde eingestellt, um acht Stunden lang Ladungen
PN 2 Einführung in die Experimentalphysik für Chemiker und Biologen
 PN 2 Einführung in die Experimentalphysik für Chemiker und Biologen 1. Vorlesung 20.4.07 Nadja Regner, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik
PN 2 Einführung in die Experimentalphysik für Chemiker und Biologen 1. Vorlesung 20.4.07 Nadja Regner, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik
Der Millikan-Versuch. Einstiegsfragen. Theorie. betreffenden Feldstärken?
 Der Millikan-Versuch Einstiegsfragen 1. Welche Körper untersuchte Millikan in seinem Versuch? 2. Welche Felder ließ er darauf wirken? Wie "erzeugte" er sie? Welche Richtungen hatten die betreffenden Feldstärken?
Der Millikan-Versuch Einstiegsfragen 1. Welche Körper untersuchte Millikan in seinem Versuch? 2. Welche Felder ließ er darauf wirken? Wie "erzeugte" er sie? Welche Richtungen hatten die betreffenden Feldstärken?
Zusammenfassung. Maxwellgleichungen und elektromagnetische Wellen
 Zusammenfassung Maxwellgleichungen und elektromagnetische Wellen nach dem uch Physik von Paul A. Tipler pektrum Akademischer Verlag Datum:.. von Michael Wack ) http://www.skriptweb.de Hinweise z.. auf
Zusammenfassung Maxwellgleichungen und elektromagnetische Wellen nach dem uch Physik von Paul A. Tipler pektrum Akademischer Verlag Datum:.. von Michael Wack ) http://www.skriptweb.de Hinweise z.. auf
Einführung in die Physik
 Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Klausur: Montag, 11.02. 2008 um 13 16 Uhr (90 min) Willstätter-HS Buchner-HS Nachklausur: Freitag, 18.04.
Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Klausur: Montag, 11.02. 2008 um 13 16 Uhr (90 min) Willstätter-HS Buchner-HS Nachklausur: Freitag, 18.04.
