Neyman-Pearson. - Schulen statistischer Inferenz - Christian Schnell. betreut von Dr. Marco Cattaneo
|
|
|
- Klemens Fuhrmann
- vor 6 Jahren
- Abrufe
Transkript
1 Neyman-Pearson - Schulen statistischer Inferenz - Christian Schnell betreut von Dr. Marco Cattaneo Seminar für methodologische und historische Grundlagen des Wahrscheinlichkeitsbegriffs und der statistischen Inferenz Institut für Statistik Ludwig-Maximilians-Universität München 11. März 2013 Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
2 Gliederung 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss 3.1 Kritik an der klassischen Testtheorie in der Praxis 3.2 Zusammenfassung Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
3 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests 2 Neyman-Pearson Schule 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
4 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests Abbildung: Schotte John Arbuthnot ( d1735) und ein Ausschnitt der 82 Jahre der Londoner Geburtenstatistik Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
5 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests Arbuthnot in der Geschichte des Wahrscheinlichkeitsbegriffs Huygens ( d1695): Zusammenfassung seiner Erkenntnisse über Wahrscheinlichkeitsrechnung Van Rekeningh in Spelen van Geluck (1657) Arbuthnot ( d1735) : Übersetzung auf Englisch mit eigenen Anmerkungen anonym unter dem Titel Of the Laws of Chance (1692) Veröffentlichung seiner Arbeit An argument for Divine Providence (1710) Verwendung des Begriffs Value of Expectation (nach Huygens) Bernoulli ( d1705) : Danach Veröffentlichung von Ars Conjectandi (1713) Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
6 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests Arbuthnots Herangehensweise Ansatz: Überwiegen in einem Jahr Jungen- oder Mädchengeburten? Beweisführung: Annahme: zunächst Gleichverteilung der Geschlechter bei der Geburt Berechnung wie bei einem Münzwurf ( zweiseitiger Würfel ) Erwartungswert : in einem Jahr werden mehr Jungen geboren ˆ= 1 2 Wiederhole 82 mal: in jedem Jahr werden mehr Jungen geboren ˆ= ( 1 2 )82 Schlussfolgerung: Annahme einer Gleichverteilung ist nicht gerechtfertigt! Arbuthnot: göttliche Fügung ist bewiesen. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
7 1 Einleitung John Arbuthnot als Vorreiter des statistischen Tests Aus der heutigen Sichtweise Bemerkenswert: Erweiterung einer logischen Schlussweise zu einer statistischen Schlussweise Gegenteil dessen, was nachgewiesen werden soll als Nullhypothese: Die Wahrscheinlichkeit, dass ein neugeborenes Kind ein Junge bzw. ein Mädchen ist liegt jeweils bei 50%. Durch mathematische Überlegungen folgt der Schluss: Die Wahrscheinlichkeit, dass ein neugeborenes Kind ein Junge ist liegt bei über 50% und ist somit größer als die Wahrscheinlichkeit, dass ein neugeborenes Kind ein Mädchen ist. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
8 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 1 Einleitung 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
9 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern Karl Pearson ( d1936) und d in England Ronald Aylmer Fisher ( d1962) in England d in Australien Jerzy Neyman ( d1981) in Moldawien d in USA/Kalifornien Egon Sharpe Pearson ( d1980) und d in England Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
10 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern Anfänge des Konflikts Karl Pearson: Fisher: Mitbegründer und Lektor des Magazins Biometrika (ab 1901) Professur für Eugenik am University College in London (ab 1913) Gründung: Department of Applied Statistics Statistische Errungenschaften: Korrelations-/Kontingenzkoeffizient, χ 2 -Test Stellenangebot am Institut von Pearson (1919) Forschungsarbeiten: Maximum-Likelihood, t-test, Fisher-Test, Suffizienz, Varianzanalyse und Versuchsplanung Karl Pearson blockierte Veröffentlichungen von Fisher in der Biometrika aufgrund von inhaltlichen Uneinigkeiten bei der Auswertung von Stichproben Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
11 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern Verschärfung des Konflikts Egon Sharpe Pearson: Ab 1924 am Institut und ab 1933 Institutsleitung gemeinsam mit Fisher Weiterhin Blockierung von Fisher in der Biometrika als Lektor Intensive Zusammenarbeit mit Neyman von 1928 bis Anstellung von Neyman am Institut von 1934 bis In dieser Zeit Veröffentlichung von solch grundlegenden Papers wie z.b.: On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference (1928) On the Problem of the Most Efficient Tests of Statistical Hypotheses (1933) Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
12 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern Höhepunkt des Konflikts (zwischen Neyman und Fisher) Vorwurf an Fisher: Unsaubere Beweisführung und umständliche Formulierungen Neyman über Fishers Nullhypothesentest: im mathematischen Sinne schlechter als nutzlos Vorwurf an Neyman: Beschränkt sich auf mathematische Denkweise Fisher über Neyman: Neyman verstehe nichts von Statistik und hat keinen Bezug zu Naturwissenschaften Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
13 2.2 Hypothesentest (mit Alternative) 1 Einleitung 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
14 2.2 Hypothesentest (mit Alternative) Nullhypothese in Fishers Signifikanztest Aufwendige Berechnung der Verteilungstabellen beim t-test (1908) Festlegung des Signifikanzniveaus auf 1% und 5% durch Fisher (1925) anwenderfreundliche Verwendung des Signifikanztests von Fisher Benennung einer Nullhypothese: Unterscheidet sich die tatsächliche Verteilung einer Stichprobe von einer hypothetischen Verteilung? Allgemeine Vorgehensweise: Nullhypothese ohne bedeutenden Effekt Ziel ist die Verwerfung der Nullhypothese Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
15 2.2 Hypothesentest (mit Alternative) Alternativhypothese durch Neyman-Pearson Weiterentwicklung der Ideen von Fisher (Ende 1920er) Betrachtung von Hypothesenpaaren (mit konkreter Alternativhypothese): H 0 : θ Θ 0 gegen H 1 : θ Θ 1 Disjunkte Parameterräume Θ 0 und Θ 1 können sich zu Θ ergänzen Einfachstes Szenario: H 0 und H 1 durch einzelne Parameterwerte repräsentiert einfache Hypothesen vs. zusammengesetzte Hypothesen Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
16 2.2 Hypothesentest (mit Alternative) Mögliche Testentscheidungen H 0 beibehalten H 0 verwerfen richtige Schlussfolgerung falsche Schlussfolgerung H 0 trifft zu Spezifität Fehler 1. Art (Wahrscheinlichkeit 1 α) (auch α-fehler) falsche Schlussfolgerung richtige Schlussfolgerung H 1 trifft zu Fehler 2. Art Power (auch β-fehler) (Wahrscheinlichkeit 1 β) P(Fehler 1. Art) = P(H 0 verwerfen H 0 trifft zu) = α P(Fehler 2. Art) = P(H 0 beibehalten H 1 trifft zu) = 1 P(H 0 verwerfen H 1 trifft zu) = β Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
17 2.3 P-Wert kontra festes α-niveau 1 Einleitung 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
18 2.3 P-Wert kontra festes α-niveau Fishers p-wert Mögliche Annahme: kleine Werte sprechen gegen Nullhypothese p-wert als Maß der Evidenz gegen Nullhypothese: p = F (x) = P(X x) Kumulierung der Wahrscheinlichkeit aller möglichen Beobachtungen kleiner oder gleich der eigentlichen Beobachtung x Je kleiner der p-wert, desto weniger plausibel ist es, dass die beobachteten Werte für die Nullhypothese sprechen. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
19 2.3 P-Wert kontra festes α-niveau Beispiel: Geschlechterverhältnis bei der Geburt Gleichverteilungsannahme unter H 0 : Erwarte bei 1000 Geburten ein Verhältnis von 500 Jungen zu 500 Mädchen Beobachtung: Verhältnis 950 zu 50 (Jungen (J) zu Mädchen (M)) p-wert unter H 0 : p = P(M = 0) + P(M = 1) P(M = m) mit der tatsächlichen Beobachtung m = 50 Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
20 2.3 P-Wert kontra festes α-niveau α-niveau nach Neyman-Pearson Annahme: kleine Werte sprechen gegen Nullhypothese Zusätzlich: Standardnormalverteilte Prüfgröße Z mit α-quantil z α Ablehnbereich der Nullhypothese: P H0 (Z z α ) = α z α entspricht dem kritischen Wert und wird durch α bestimmt Kontrolle des Ablehnbereichs durch α Umso größer α gewählt wird, desto weniger wahrscheinlich spricht eine beobachtete Prüfgröße für die Nullhypothese. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
21 2.3 P-Wert kontra festes α-niveau Vergleich von p-wert und α-niveau Fisher: H 0 wird abgelehnt, falls p-wert kleiner als α-niveau (z.b. 5%) Neyman-Pearson: H 0 wird abgelehnt, falls der Prüfgrößenwert in den kritischen Bereich C fällt Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
22 2.3 P-Wert kontra festes α-niveau Bestimmung des Signifikanzniveaus 1 Fisher (1935): Lege Signifikanzniveau im Sinne einer Konvention fest vor der Durchführung des Tests 2 Fisher (1956): Berechne exaktes Signifikanzniveau aus den Daten (p-wert) nach der Durchführung des Tests 3 Neyman-Pearson: Lege α und β fest nach Kosten-Nutzen Analyse eines möglichen Fehlers 1. oder 2. Art vor der Durchführung des Tests Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
23 2.3 P-Wert kontra festes α-niveau Motivation für Kosten-Nutzen Analyse Beispiel: H 0 : Angeklagter ist schuldig vs. H 1 : Angeklagter ist unschuldig Fehler 1. Art (α): Angeklagte wird freigesprochen, obwohl er schuldig ist. Fehler 2. Art (β): Angeklagte wird verurteilt, obwohl er unschuldig ist. Wichtig: Konsequenzen einer Fehleinschätzung 1 Fehler 1. Art: Gefahr für die Gesellschaft durch Beschuldigten 2 Fehler 2. Art: Art der Bestrafung (z.b. Todesstrafe oder Gefängnisstrafe) Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
24 2.3 P-Wert kontra festes α-niveau Interpretation von Signifikanz Aussage bezieht sich auf Szenario, in dem die Nullhypothese Gültigkeit hat Wahrscheinlichkeit der Beobachtungen unter der Annahme: H 0 trifft zu Die beobachteten Werte sind so klein/groß, dass es (extrem) unwahrscheinlich ist (z.b. 5%), dass sie noch unter H 0 vorkommen. Keine Aussage über die Wahrscheinlichkeit von Hypothesen möglich Nur im Rahmen der Bayes-Inferenz Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
25 2.4 Gütefunktion und Power eines Tests 1 Einleitung 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
26 2.4 Gütefunktion und Power eines Tests Zusammensetzung einer Gütefunktion g φ (θ) = P(H 0 verwerfen θ) α, falls θ Θ 0 1 g φ (θ) = 1 P(H 0 verwerfen θ) = β, falls θ Θ 1 Testproblem einseitiger Gaußtest: H 0 : µ µ 0 gegen H 1 : µ > µ 0 Gütefunktion g φ (µ) = 1 Φ(z 1 α µ µ 0 σ n) eines einseitigen Gaußtests Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
27 2.4 Gütefunktion und Power eines Tests Eigenschaften einer Gütefunktion Beachte: Ein Test ist besser als ein anderer Test, wenn er im Bereich der Alternative eine größere Power besitzt tatsächlich existierende Effekte werden öfter entdeckt 1 Für Werte aus H 1 heißt die Gütefunktion Power eines Tests. 2 Für Werte aus H 0 ist die Gütefunktion kleiner gleich α. 3 Für wachsendes Stichprobenumfang n wird die Power eines Tests größer, d.h. die Gütefunktion wird steiler.. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
28 2.4 Gütefunktion und Power eines Tests Gütefunktion bei verschiedenen Stichprobenumfängen Abbildung: Gütefunktion g φ (µ) = 1 Φ(z 1 α µ µ 0 σ n) für verschiedene Stichprobenumfänge n = 10 ( ), n = 20 (- - -) und n = 50 ( ) und konstantem σ Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
29 2.4 Gütefunktion und Power eines Tests Eigenschaften einer Gütefunktion 1 Für Werte aus H 1 heißt die Gütefunktion Power eines Tests. 2 Für Werte aus H 0 ist die Gütefunktion kleiner gleich α. 3 Für wachsenden Stichprobenumfang n wird die Power eines Tests größer, d.h. die Gütefunktion wird steiler. 4 Für wachsendes α wird die Power eines Tests größer.. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
30 2.4 Gütefunktion und Power eines Tests Gütefunktion bei verschiedenen Signifikanzniveaus Abbildung: Gütefunktion g φ (µ) = 1 Φ(z 1 α µ µ 0 σ n) für verschiedene Signifikanzniveaus α = 0, 01 ( ), α = 0, 05 (- - -) und α = 0, 1 ( ) und konstantem σ Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
31 2.4 Gütefunktion und Power eines Tests Eigenschaften einer Gütefunktion 1 Für Werte aus H 1 heißt die Gütefunktion Power eines Tests. 2 Für Werte aus H 0 ist die Gütefunktion kleiner gleich α. 3 Für wachsenden Stichprobenumfang n wird die Power eines Tests größer, d.h. die Gütefunktion wird steiler. 4 Für wachsendes α wird die Power eines Tests größer. 5 Für eine wachsende Abweichung zwischen Werten aus H 1 und H 0 wird die Power eines Tests größer. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
32 2.4 Gütefunktion und Power eines Tests Power bei wachsender Abweichung zwischen Werten aus H 1 und H 0 Abbildung: Vergleich α- und β-fehler Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
33 2.5 Neyman-Pearson Lemma 1 Einleitung 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
34 2.5 Neyman-Pearson Lemma Wann ist ein Test optimal? 1 Vergleichbarkeit nur für ein bestimmtes Testproblem 2 Zusätzlich gleiches und festes α-niveau fest vorgegeben Wahrscheinlichkeit des Fehlers 1. Art: d.h. für θ Θ 0 ist P(H 0 verwerfen θ) = α fest 3 Test besitzt gleichzeitig minimalst mögliches β Minimierung des Fehlers 2. Art: d.h. für θ Θ 1 wird 1 P(H 0 verwerfen θ) = β minimiert Test hat größtmögliche Power (1 β) und ist somit optimal im Vergleich zu allen anderen Tests unter den beschriebenen Voraussetzungen. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
35 2.5 Neyman-Pearson Lemma Der Likelihood-Quotienten-Test (1/2) Betrachtung eines einfachen Testproblems (θ 0 θ 1 ): H 0 : θ = θ 0 gegen H 1 : θ = θ 1 Likelihood-Quotient: Dichte ist für H 0 gleich f 0 (x) und für H 1 gleich f 1 (x) Λ(x) = f 1(x) f 0 (x) Relatives Maß für bzw. gegen die Nullhypothese Für besten Test wähle kritischen Wert k α für Einhaltung des α-niveaus: H 0 ablehnen Λ(x) > k α Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
36 2.5 Neyman-Pearson Lemma Der Likelihood-Quotienten-Test (2/2) Theoretisches Problem: α-niveau wird bei diskreter Wahrscheinlichkeitsverteilung nicht immer ausgeschöpft Notwendigkeit einer Randomisierung Testfunktion im diskreten Fall: 1, falls f 1 (x) > k α f 0 (x) Λ(x) > k α φ (x) = γ α, falls f 1 (x) = k α f 0 (x) Λ(x) = k α 0, falls f 1 (x) < k α f 0 (x) Λ(x) < k α Testfunktion im stetigen Fall: { φ 1, falls f1 (x) > k (x) = α f 0 (x) Λ(x) > k α 0, sonst. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
37 2.5 Neyman-Pearson Lemma Das Lemma 1 Optimalität: Für jedes k α und γ α hat der Test φ maximale Power unter allen Tests, deren Niveau höchstens gleich dem α-niveau von φ ist. 2 Existenz: Zu vorgegebenem α [0, 1] existieren Konstanten k α und γ α, so dass der LQ-Test φ mit diesem k α und γ α = γ α für alle x exakt das Niveau α besitzt. Es existieren k α und γ α, so dass α-niveau für φ voll ausgeschöpft wird 3 Eindeutigkeit: Falls ein Test φ mit Niveau α maximale Power (= kleinsten Fehler 2. Art) unter allen anderen Tests mit Niveau α besitzt, dann ist φ ein LQ-Test. Optimaler Test ist Likelihood-Quotienten-Test Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
38 2.6 Induktives Verhalten versus induktives Schließen 1 Einleitung 2 Neyman-Pearson Schule 2.1 Konstellation zwischen den wichtigsten Wissenschaftlern 2.2 Hypothesentest (mit Alternative) 2.3 P-Wert kontra festes α-niveau 2.4 Gütefunktion und Power eines Tests 2.5 Neyman-Pearson Lemma 2.6 Induktives Verhalten versus induktives Schließen 3 Schluss Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
39 2.6 Induktives Verhalten versus induktives Schließen Allgemeine Interpretation eines Tests Zentraler Streitpunkt: Unterscheidung zwischen induktivem Verhalten (Neyman-Pearson) und induktivem Schließen (Fisher) Fisher: Erlangen konkreter Erkenntnisse durch signifikante Ergebnisse konkrete Aussagen, wie Alle Schwäne sind weiß! kognitivistische Herangehensweise Neyman-Pearson: Verhaltensempfehlung durch signifikante Ergebnisse Verhalten besteht darin Nullhypothese zu verwerfen oder nicht dezisionistische Herangehensweise Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
40 3 Schluss 3.1 Kritik an der klassischen Testtheorie in der Praxis 1 Einleitung 2 Neyman-Pearson Schule 3 Schluss 3.1 Kritik an der klassischen Testtheorie in der Praxis 3.2 Zusammenfassung Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
41 3 Schluss 3.1 Kritik an der klassischen Testtheorie in der Praxis Häufige Vorgehensweise in der Praxis 1 Benennung einer Null- und einer Alternativhypothese (nach Neyman-Pearson) 2 Berechnung eines exakten p-wertes (nach Fisher); meist automatisiert durch Programme 3 Nachträgliche Kennzeichnung des p-wertes mit Sternen z.b. * bei p < 0, 05, ** bei p < 0, 01 und *** bei p < 0, 001 Problematik: keine Kontrolle des Fehlers 1. Art über α Gefahr: Anpassung des α-niveaus nach der Berechnung des p-werts Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
42 3 Schluss 3.1 Kritik an der klassischen Testtheorie in der Praxis Allgemeine Kritik Verwendung der Nullhypothese als Strohmann Ritualisierte Anwendung von Signifikanztests signifikante Ergebnisse sind notwendig, um beachtet zu werden Stupide Verwendung von Signifikanztests auf Kosten von geeigneteren Methoden 2 2 Siehe hierfür z.b.: Loftus, G. R. (1993). A picture is worth a thousand p values: On the irrelevance of hypothesis testing in the microcomputer age, Behavior Research Methods 25(2): Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
43 3 Schluss 3.2 Zusammenfassung 1 Einleitung 2 Neyman-Pearson Schule 3 Schluss 3.1 Kritik an der klassischen Testtheorie in der Praxis 3.2 Zusammenfassung Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
44 3 Schluss 3.2 Zusammenfassung Die wichtigsten Aspekte im Überblick (1/2) Konflikt zwischen Neyman-Pearson und Fisher hat das heutige Verständnis der Statistik maßgeblich beeinflusst Unterscheidung zwischen Signifikanztest nach Fisher und Hypothesentest nach Neyman-Pearson Benennung einer konkreten Alternativhypothese durch Neyman-Pearson ermöglicht: 1 Bestimmung des β-fehlers 2 Betrachtung einer Gütefunktion 3 Vergleich von Tests über die Power (1 β) 4 Konstruktion eines optimalen Tests über das Neyman-Pearson Lemma Fisher lehnt Benennung einer konkreten Alternativhypothese ab Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
45 3 Schluss 3.2 Zusammenfassung Die wichtigsten Aspekte im Überblick (2/2) Ein optimaler Test hat bei gleichem Testproblem maximale Power im Vergleich zu jedem anderen α-niveau Test Induktives Verhalten (Neyman-Pearson) versus induktives Schließen (Fisher) Fisher: Erlangen konkreter Erkenntnisse durch signifikante Ergebnisse Neyman-Pearson: Verhaltensempfehlung durch signifikante Ergebnisse Heutzutage: inkonsistente Vermischung der Ideen von Fisher und Neyman-Pearson bei der Verwendung von Signifikanztests Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
46 Anhang Empfohlene Literatur und Einstiegsfrage Abschlussdiskussion Empfohlene Literatur Zusätzlich zu den zitierten und genannten Veröffentlichung von Neyman und E. S. Pearson im Vorbereitungsmaterial: 1 Lehmann, E. (1993). The Fisher, Neyman-Pearson theories of testing hypotheses: One theory or two?, Journal of the American Statistical Association 88(424): Saint-Mont, U. (2011). Statistik im Forschungsprozess: Eine Philosophie der Statistik als Baustein einer integrativen Wissenschaftstheorie, Physica-Verlag HD. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
47 Anhang Einstiegsfrage Abschlussdiskussion Abschlussdiskussion Wie ist eure Vorgehensweise bei der Durchführung eines Signifikanztests? Achtet ihr auf eine Kosten-Nutzen Abwägung nach Neyman-Pearson oder ist für euch grundsätzlich der p-wert von Bedeutung? Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
48 Anhang Neyman-Pearson Lemma Beweis der Optimalität (1/2) Sei φ bester Test und φ beliebiger anderer Test mit gleichem α-niveau. E θ0 [φ (X )] = α ˆ= Wahrscheinlichkeit H 0 zu verwerfen, falls θ Θ 0 E θ1 [φ (X )] = 1 β ˆ= Wahrscheinlichkeit H 0 zu verwerfen, falls θ Θ 1 Für Optimalität von φ gilt es zu zeigen: E θ1 [φ(x )] E θ1 [φ (X )] Betrachte hierfür Hilfsfunktion U(x): U(x) = [φ (x)f 1 (x) φ (x)k α f 0 (x)] [φ(x)f 1 (x) φ(x)k α f 0 (x)] = (φ (x) φ(x))(f 1 (x) k α f 0 (x)) Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
49 Anhang Neyman-Pearson Lemma Beweis der Optimalität (2/2) Da U(x) 0 für alle x, gilt somit: 0 = = U(x) dx (φ (x) φ(x))(f 1(x) k αf 0(x)) dx ( φ (x)f 1(x) dx φ(x)f 1(x) dx + k α φ(x)f 0(x) dx ) φ (x)f 0(x) dx = E θ1 [φ (X )] E θ1 [φ(x )] + k α(e θ0 [φ(x )] E θ0 [φ (X )]) }{{} 0, da E θ0 [φ(x )] E θ0 [φ (X )] E θ1 [φ (X )] E θ1 [φ(x )], d.h. die Power von φ ist größer oder zumindest genauso groß wie die Power von φ. Hinweis: E θ0 [φ (X )] = + φ (x)f 0(x) dx Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
50 Anhang Zentrale Eigenschaften eines Inferenzkonzepts frequentistisch vs. nicht-frequentistisch 1 frequentistisch: Güte einer Schlussfolgerung basiert darauf, wie häufig diese im Durchschnitt zu einer wahren Aussage führt (bei Anwendung auf viele verschiedene Beobachtungen). klassische Inferenz 2 nicht-frequentistisch: Güte einer Schlussfolgerung basiert darauf, wie plausibel diese ist (in Hinblick auf die vorliegende Beobachtung). Bayes-Inferenz Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
51 Anhang Zentrale Eigenschaften eines Inferenzkonzepts kognitivistisch vs. dezisionistisch 1 kognitivistisch: Schlussfolgerung als konkrete Erkenntnis klassische Inferenz und Bayes-Inferenz 2 dezisionistisch: Schlussfolgerung dient dem Treffen von Entscheidungen entscheidungstheoretische Inferenz Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
52 Anhang Zentrale Eigenschaften eines Inferenzkonzepts objektivistisch vs. subjektivistisch 1 objektivistisch: Nur Verwendung von objektiven Informationen aus den Beobachtungen klassische Inferenz 2 subjektivistisch: Zusätzlich subjektive Annahmen wie z.b. das a priori Wissen Bayes-Inferenz Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
53 Anhang Herleitung Konfidenzintervall zweiseitiger Gauß-Test Seien X 1,..., X n ZV mit X i N(µ, σ 2 ) bei E(X i ) = µ, V(X i ) = σ 2 und n 30, wobei σ 2 bekannt ist. Für µ = µ 0 ist: X σ N(µ 0, n ) Z = X µ 0 σ n N(0, 1) Betrachte: H 0 : µ = µ 0 gegen H 1 : µ µ 0 Die Nullhypothese H 0 ist beizubehalten falls: z = x µ 0 z 1 α/2 µ 0 x + z 1 α/2 x µ0 n z 1 α/2 x µ 0 z 1 α/2 σ σ n σ n und x µ 0 z 1 α/2 σ n σ n und µ 0 x z 1 α/2 Daraus lässt sich folgendes (1 α)-konfidenzintervall für µ bestimmen: [ ] σ σ x z 1 α/2, x + z 1 α/2 n n σ n Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
54 Anhang Herleitung Gütefunktion einseitiger Gaußtest Seien X 1,..., X n ZV mit X i N(µ, σ 2 ) bei E(X i ) = µ, V(X i ) = σ 2 und n 30, wobei σ 2 bekannt ist. Für µ = µ 0 ist: X σ N(µ 0, n ) Z = X µ 0 σ n N(0, 1) Betrachte: H 0 : µ µ 0 gegen H 1 : µ > µ 0 ( ) X µ0 g φ (µ) = P(H 0 verwerfen µ) = P n > z1 α µ σ ( ) X µ0 + µ µ = P n > z1 α µ σ ( ) X µ µ µ 0 = P n + n > z1 α µ σ σ ( X µ = P n > z1 α µ ) µ0 n µ = 1 Φ(z 1 α µ µ0 n) σ σ σ Da mit µ als wahren Parameter X µ σ n N(0, 1) gilt. Graphische Darstellung der Gütefunktion ist nur in Abhängigkeit von α und n und als Funktion von µ möglich. Neyman-Pearson Schule Institut für Statistik, LMU München 11. März / 54
Deduktive und induktive Aspekte statistischer Methoden
 Deduktive und induktive Aspekte statistischer Methoden Wissenschaftshistorische und -philosophische Grundlagen Felix Günther Institut für Statistik Ludwig-Maximilians-Universität München Prof. Seising
Deduktive und induktive Aspekte statistischer Methoden Wissenschaftshistorische und -philosophische Grundlagen Felix Günther Institut für Statistik Ludwig-Maximilians-Universität München Prof. Seising
Ein möglicher Unterrichtsgang
 Ein möglicher Unterrichtsgang. Wiederholung: Bernoulli Experiment und Binomialverteilung Da der sichere Umgang mit der Binomialverteilung, auch der Umgang mit dem GTR und den Diagrammen, eine notwendige
Ein möglicher Unterrichtsgang. Wiederholung: Bernoulli Experiment und Binomialverteilung Da der sichere Umgang mit der Binomialverteilung, auch der Umgang mit dem GTR und den Diagrammen, eine notwendige
Grundprinzipien der Bayes-Statistik
 Grundprinzipien der Bayes-Statistik Karl-Rudolf Koch Zusammenfassung: In drei wesentlichen Punkten unterscheidet sich die Bayes-Statistik von der traditionellen Statistik. Zunächst beruht die Bayes-Statistik
Grundprinzipien der Bayes-Statistik Karl-Rudolf Koch Zusammenfassung: In drei wesentlichen Punkten unterscheidet sich die Bayes-Statistik von der traditionellen Statistik. Zunächst beruht die Bayes-Statistik
9. StatistischeTests. 9.1 Konzeption
 9. StatistischeTests 9.1 Konzeption Statistische Tests dienen zur Überprüfung von Hypothesen über einen Parameter der Grundgesamtheit (bei einem Ein-Stichproben-Test) oder über die Verteilung einer Zufallsvariablen
9. StatistischeTests 9.1 Konzeption Statistische Tests dienen zur Überprüfung von Hypothesen über einen Parameter der Grundgesamtheit (bei einem Ein-Stichproben-Test) oder über die Verteilung einer Zufallsvariablen
Bachelorabschlussseminar Dipl.-Kfm. Daniel Cracau
 1 Einführung in die statistische Datenanalyse Bachelorabschlussseminar Dipl.-Kfm. Daniel Cracau 2 Gliederung 1.Grundlagen 2.Nicht-parametrische Tests a. Mann-Whitney-Wilcoxon-U Test b. Wilcoxon-Signed-Rank
1 Einführung in die statistische Datenanalyse Bachelorabschlussseminar Dipl.-Kfm. Daniel Cracau 2 Gliederung 1.Grundlagen 2.Nicht-parametrische Tests a. Mann-Whitney-Wilcoxon-U Test b. Wilcoxon-Signed-Rank
9. Schätzen und Testen bei unbekannter Varianz
 9. Schätzen und Testen bei unbekannter Varianz Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Schätzen und Testen bei unbekannter Varianz Wenn wir die Standardabweichung σ nicht kennen,
9. Schätzen und Testen bei unbekannter Varianz Dr. Antje Kiesel Institut für Angewandte Mathematik WS 2011/2012 Schätzen und Testen bei unbekannter Varianz Wenn wir die Standardabweichung σ nicht kennen,
12.1 Wie funktioniert ein Signifikanztest?
 Sedlmeier & Renkewitz Kapitel 12 Signifikanztests 12.1 Wie funktioniert ein Signifikanztest? Zentrales Ergebnis eine Signifikanztests: Wie wahrscheinlich war es unter der Bedingung dass H0 gilt, diesen
Sedlmeier & Renkewitz Kapitel 12 Signifikanztests 12.1 Wie funktioniert ein Signifikanztest? Zentrales Ergebnis eine Signifikanztests: Wie wahrscheinlich war es unter der Bedingung dass H0 gilt, diesen
27. Statistische Tests für Parameter. Was ist ein statistischer Test?
 27. Statistische Tests für Parameter Wenn du eine weise Antwort verlangst, musst du vernünftig fragen Was ist ein statistischer Test? Ein statistischen Test ist ein Verfahren, welches ausgehend von Stichproben
27. Statistische Tests für Parameter Wenn du eine weise Antwort verlangst, musst du vernünftig fragen Was ist ein statistischer Test? Ein statistischen Test ist ein Verfahren, welches ausgehend von Stichproben
14.01.14 DAS THEMA: INFERENZSTATISTIK II. Standardfehler Konfidenzintervalle Signifikanztests. Standardfehler
 DAS THEMA: INFERENZSTATISTIK II INFERENZSTATISTISCHE AUSSAGEN Standardfehler Konfidenzintervalle Signifikanztests Standardfehler der Standardfehler Interpretation Verwendung 1 ZUR WIEDERHOLUNG... Ausgangspunkt:
DAS THEMA: INFERENZSTATISTIK II INFERENZSTATISTISCHE AUSSAGEN Standardfehler Konfidenzintervalle Signifikanztests Standardfehler der Standardfehler Interpretation Verwendung 1 ZUR WIEDERHOLUNG... Ausgangspunkt:
Statistik II für Betriebswirte Vorlesung 3
 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik Statistik II für Betriebswirte Vorlesung 3 5. November 2013 Beispiel: Aktiensplit (Aczel & Sounderpandan, Aufg. 14-28) Ein Börsenanalyst
PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik Statistik II für Betriebswirte Vorlesung 3 5. November 2013 Beispiel: Aktiensplit (Aczel & Sounderpandan, Aufg. 14-28) Ein Börsenanalyst
Fragestellungen der Schließenden Statistik
 Fragestellungen der Schließenden Statistik Bisher: Teil I: Beschreibende Statistik Zusammenfassung von an GesamtheitM N {e,,e N } erhobenem Datensatz x,,x N durch Häufigkeitsverteilung und Kennzahlen für
Fragestellungen der Schließenden Statistik Bisher: Teil I: Beschreibende Statistik Zusammenfassung von an GesamtheitM N {e,,e N } erhobenem Datensatz x,,x N durch Häufigkeitsverteilung und Kennzahlen für
Gibt es einen Geschmacksunterschied zwischen Coca Cola und Cola Zero?
 Gibt es einen Geschmacksunterschied zwischen Coca Cola und Cola Zero? Manche sagen: Ja, manche sagen: Nein Wie soll man das objektiv feststellen? Kann man Geschmack objektiv messen? - Geschmack ist subjektiv
Gibt es einen Geschmacksunterschied zwischen Coca Cola und Cola Zero? Manche sagen: Ja, manche sagen: Nein Wie soll man das objektiv feststellen? Kann man Geschmack objektiv messen? - Geschmack ist subjektiv
5 Statistische Testverfahren
 70 5 Statistische Testverfahren 5.1 Grundlegende Definitionen und Binomialtest Beispiel 5.1.1: (Fortsetzung von Beispiel 4.2.15) Wir nehmen an, dass das Medikament als wenig bedenklich eingestuft werden
70 5 Statistische Testverfahren 5.1 Grundlegende Definitionen und Binomialtest Beispiel 5.1.1: (Fortsetzung von Beispiel 4.2.15) Wir nehmen an, dass das Medikament als wenig bedenklich eingestuft werden
Füllmenge. Füllmenge. Füllmenge. Füllmenge. Mean = 500,0029 Std. Dev. = 3,96016 N = 10.000. 485,00 490,00 495,00 500,00 505,00 510,00 515,00 Füllmenge
 2.4 Stetige Zufallsvariable Beispiel. Abfüllung von 500 Gramm Packungen einer bestimmten Ware auf einer automatischen Abfüllanlage. Die Zufallsvariable X beschreibe die Füllmenge einer zufällig ausgewählten
2.4 Stetige Zufallsvariable Beispiel. Abfüllung von 500 Gramm Packungen einer bestimmten Ware auf einer automatischen Abfüllanlage. Die Zufallsvariable X beschreibe die Füllmenge einer zufällig ausgewählten
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management
 Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg : Gliederung 1 Einführung 2 Deskriptive Statistik
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg : Gliederung 1 Einführung 2 Deskriptive Statistik
werden können. Wenn der Benutzer zudem eine konkrete Differenz mit praktischen Konsequenzen angibt, berechnet der Assistent den Stichprobenumfang,
 Dieses White Paper ist Teil einer Reihe von Veröffentlichungen, welche die Forschungsarbeiten der Minitab-Statistiker erläutern, in deren Rahmen die im Assistenten der Minitab 17 Statistical Software verwendeten
Dieses White Paper ist Teil einer Reihe von Veröffentlichungen, welche die Forschungsarbeiten der Minitab-Statistiker erläutern, in deren Rahmen die im Assistenten der Minitab 17 Statistical Software verwendeten
Statistik im Bachelor-Studium der BWL und VWL
 Max C. Wewel Statistik im Bachelor-Studium der BWL und VWL Methoden, Anwendung, Interpretation Mit herausnehmbarer Formelsammlung ein Imprint von Pearson Education München Boston San Francisco Harlow,
Max C. Wewel Statistik im Bachelor-Studium der BWL und VWL Methoden, Anwendung, Interpretation Mit herausnehmbarer Formelsammlung ein Imprint von Pearson Education München Boston San Francisco Harlow,
METHODENLEHRE I WS 2013/14 THOMAS SCHÄFER
 METHODENLEHRE I WS 2013/14 THOMAS SCHÄFER DAS THEMA: INFERENZSTATISTIK IV INFERENZSTATISTISCHE AUSSAGEN FÜR ZUSAMMENHÄNGE UND UNTERSCHIEDE Inferenzstatistik für Zusammenhänge Inferenzstatistik für Unterschiede
METHODENLEHRE I WS 2013/14 THOMAS SCHÄFER DAS THEMA: INFERENZSTATISTIK IV INFERENZSTATISTISCHE AUSSAGEN FÜR ZUSAMMENHÄNGE UND UNTERSCHIEDE Inferenzstatistik für Zusammenhänge Inferenzstatistik für Unterschiede
Von der Untersuchungsfrage zu statistischen Hypothesen, und wie war das nochmal mit dem α- und
 Von der Untersuchungsfrage zu statistischen Hypothesen, und wie war das nochmal mit dem α- und β-fehler? Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de
Von der Untersuchungsfrage zu statistischen Hypothesen, und wie war das nochmal mit dem α- und β-fehler? Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de
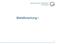
q = 1 p = 0.8 0.2 k 0.8 10 k k = 0, 1,..., 10 1 1 0.8 2 + 10 0.2 0.8 + 10 9 1 2 0.22 1 = 0.8 8 [0.64 + 1.6 + 1.8] = 0.678
![q = 1 p = 0.8 0.2 k 0.8 10 k k = 0, 1,..., 10 1 1 0.8 2 + 10 0.2 0.8 + 10 9 1 2 0.22 1 = 0.8 8 [0.64 + 1.6 + 1.8] = 0.678 q = 1 p = 0.8 0.2 k 0.8 10 k k = 0, 1,..., 10 1 1 0.8 2 + 10 0.2 0.8 + 10 9 1 2 0.22 1 = 0.8 8 [0.64 + 1.6 + 1.8] = 0.678](/thumbs/26/7581163.jpg) Lösungsvorschläge zu Blatt 8 X binomialverteilt mit p = 0. und n = 10: a PX = = 10 q = 1 p = 0.8 0. 0.8 10 = 0, 1,..., 10 PX = PX = 0 + PX = 1 + PX = 10 10 = 0. 0 0.8 10 + 0. 1 0.8 9 + 0 1 10 = 0.8 8 [
Lösungsvorschläge zu Blatt 8 X binomialverteilt mit p = 0. und n = 10: a PX = = 10 q = 1 p = 0.8 0. 0.8 10 = 0, 1,..., 10 PX = PX = 0 + PX = 1 + PX = 10 10 = 0. 0 0.8 10 + 0. 1 0.8 9 + 0 1 10 = 0.8 8 [
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Teil I Beschreibende Statistik 29
 Vorwort zur 2. Auflage 15 Vorwort 15 Kapitel 0 Einführung 19 0.1 Methoden und Aufgaben der Statistik............................. 20 0.2 Ablauf statistischer Untersuchungen..............................
Vorwort zur 2. Auflage 15 Vorwort 15 Kapitel 0 Einführung 19 0.1 Methoden und Aufgaben der Statistik............................. 20 0.2 Ablauf statistischer Untersuchungen..............................
Versuchsplanung. Teil 1 Einführung und Grundlagen. Dr. Tobias Kiesling <kiesling@stat.uni-muenchen.de> Einführung in die Versuchsplanung
 Versuchsplanung Teil 1 Einführung und Grundlagen Dr. Tobias Kiesling Inhalt Einführung in die Versuchsplanung Hintergründe Grundlegende Prinzipien und Begriffe Vorgehensweise
Versuchsplanung Teil 1 Einführung und Grundlagen Dr. Tobias Kiesling Inhalt Einführung in die Versuchsplanung Hintergründe Grundlegende Prinzipien und Begriffe Vorgehensweise
Statistische Auswertung der Daten von Blatt 13
 Statistische Auswertung der Daten von Blatt 13 Problemstellung 1 Graphische Darstellung der Daten 1 Diskussion der Normalverteilung 3 Mittelwerte und deren Konfidenzbereiche 3 Signifikanz der Behandlung
Statistische Auswertung der Daten von Blatt 13 Problemstellung 1 Graphische Darstellung der Daten 1 Diskussion der Normalverteilung 3 Mittelwerte und deren Konfidenzbereiche 3 Signifikanz der Behandlung
Medizinische Statistik Epidemiologie und χ 2 Vierfeldertest
 Universität Wien Institut für Mathematik Wintersemester 2009/2010 Medizinische Statistik Epidemiologie und χ 2 Vierfeldertest Seminar Angewandte Mathematik Ao. Univ. Prof. Dr. Peter Schmitt von Nadja Reiterer
Universität Wien Institut für Mathematik Wintersemester 2009/2010 Medizinische Statistik Epidemiologie und χ 2 Vierfeldertest Seminar Angewandte Mathematik Ao. Univ. Prof. Dr. Peter Schmitt von Nadja Reiterer
Grundlagen der Inferenzstatistik
 Grundlagen der Inferenzstatistik (Induktive Statistik oder schließende Statistik) Dr. Winfried Zinn 1 Deskriptive Statistik versus Inferenzstatistik Die Deskriptive Statistik stellt Kenngrößen zur Verfügung,
Grundlagen der Inferenzstatistik (Induktive Statistik oder schließende Statistik) Dr. Winfried Zinn 1 Deskriptive Statistik versus Inferenzstatistik Die Deskriptive Statistik stellt Kenngrößen zur Verfügung,
Beispiel: Sonntagsfrage. Einführung in die induktive Statistik. Statistische Tests. Statistische Tests
 Beispiel: Sonntagsfrage Vier Wochen vor der österreichischen Nationalratswahl 1999 wurde 499 Haushalten die Sonntagsfrage gestellt: Falls nächsten Sonntag Wahlen wären, welche Partei würden Sie wählen?
Beispiel: Sonntagsfrage Vier Wochen vor der österreichischen Nationalratswahl 1999 wurde 499 Haushalten die Sonntagsfrage gestellt: Falls nächsten Sonntag Wahlen wären, welche Partei würden Sie wählen?
Statistik II für Betriebswirte Vorlesung 2
 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik Statistik II für Betriebswirte Vorlesung 2 21. Oktober 2014 Verbundene Stichproben Liegen zwei Stichproben vor, deren Werte einander
PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik Statistik II für Betriebswirte Vorlesung 2 21. Oktober 2014 Verbundene Stichproben Liegen zwei Stichproben vor, deren Werte einander
5. Schließende Statistik. 5.1. Einführung
 5. Schließende Statistik 5.1. Einführung Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
5. Schließende Statistik 5.1. Einführung Sollen auf der Basis von empirischen Untersuchungen (Daten) Erkenntnisse gewonnen und Entscheidungen gefällt werden, sind die Methoden der Statistik einzusetzen.
Beurteilung der biometrischen Verhältnisse in einem Bestand. Dr. Richard Herrmann, Köln
 Beurteilung der biometrischen Verhältnisse in einem Bestand Dr. Richard Herrmann, Köln Beurteilung der biometrischen Verhältnisse in einem Bestand 1 Fragestellung Methoden.1 Vergleich der Anzahlen. Vergleich
Beurteilung der biometrischen Verhältnisse in einem Bestand Dr. Richard Herrmann, Köln Beurteilung der biometrischen Verhältnisse in einem Bestand 1 Fragestellung Methoden.1 Vergleich der Anzahlen. Vergleich
Die Optimalität von Randomisationstests
 Die Optimalität von Randomisationstests Diplomarbeit Elena Regourd Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Düsseldorf im Dezember 2001 Betreuung: Prof. Dr. A. Janssen Inhaltsverzeichnis
Die Optimalität von Randomisationstests Diplomarbeit Elena Regourd Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Düsseldorf im Dezember 2001 Betreuung: Prof. Dr. A. Janssen Inhaltsverzeichnis
Biostatistik, WS 2015/2016 Der zwei-stichproben-t-test
 1/29 Biostatistik, WS 2015/2016 Der zwei-stichproben-t-test (t-test für ungepaarte Stichproben) Matthias Birkner http://www.staff.uni-mainz.de/birkner/biostatistik1516/ 11.12.2015 2/29 Inhalt 1 t-test
1/29 Biostatistik, WS 2015/2016 Der zwei-stichproben-t-test (t-test für ungepaarte Stichproben) Matthias Birkner http://www.staff.uni-mainz.de/birkner/biostatistik1516/ 11.12.2015 2/29 Inhalt 1 t-test
Wilcoxon-Rangsummen-Test
 Wilcoxon-Rangsummen-Test Theorie: Wilcoxon-Rangsummen-Test Der Wilcoxon-Rangsummen-Test prüft, ob sich die Verteilungen der Grundgesamtheiten zweier Stichproben bezüglich ihrer Lage unterscheiden. Ein
Wilcoxon-Rangsummen-Test Theorie: Wilcoxon-Rangsummen-Test Der Wilcoxon-Rangsummen-Test prüft, ob sich die Verteilungen der Grundgesamtheiten zweier Stichproben bezüglich ihrer Lage unterscheiden. Ein
Studiendesign/ Evaluierungsdesign
 Jennifer Ziegert Studiendesign/ Evaluierungsdesign Praxisprojekt: Nutzerorientierte Evaluierung von Visualisierungen in Daffodil mittels Eyetracker Warum Studien /Evaluierungsdesign Das Design einer Untersuchung
Jennifer Ziegert Studiendesign/ Evaluierungsdesign Praxisprojekt: Nutzerorientierte Evaluierung von Visualisierungen in Daffodil mittels Eyetracker Warum Studien /Evaluierungsdesign Das Design einer Untersuchung
FAKTORIELLE VERSUCHSPLÄNE. Andreas Handl
 FAKTORIELLE VERSUCHSPLÄNE Andreas Handl 1 Inhaltsverzeichnis 1 Versuchsplanung 4 2 Einfaktorielle Varianzanalyse 6 2.1 DieAnnahmen... 6 2.2 Die ANOVA-Tabelle und der F -Test... 6 2.3 Versuche mit zwei
FAKTORIELLE VERSUCHSPLÄNE Andreas Handl 1 Inhaltsverzeichnis 1 Versuchsplanung 4 2 Einfaktorielle Varianzanalyse 6 2.1 DieAnnahmen... 6 2.2 Die ANOVA-Tabelle und der F -Test... 6 2.3 Versuche mit zwei
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Letzte Worte zur Inferenzstatistik, v. a. zu Signifikanztests Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Letzte Worte zur Inferenzstatistik, v. a. zu Signifikanztests Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische
Studiendesign und Statistik: Interpretation publizierter klinischer Daten
 Studiendesign und Statistik: Interpretation publizierter klinischer Daten Dr. Antje Jahn Institut für Medizinische Biometrie, Epidemiologie und Informatik Universitätsmedizin Mainz Hämatologie im Wandel,
Studiendesign und Statistik: Interpretation publizierter klinischer Daten Dr. Antje Jahn Institut für Medizinische Biometrie, Epidemiologie und Informatik Universitätsmedizin Mainz Hämatologie im Wandel,
Einfache statistische Auswertungen mit dem Programm SPSS
 Einfache statistische Auswertungen mit dem Programm SPSS Datensatz: fiktive_daten.sav Dipl. Päd. Anne Haßelkus Dr. Dorothea Dette-Hagenmeyer 11/2011 Überblick 1 Deskriptive Statistiken; Mittelwert berechnen...
Einfache statistische Auswertungen mit dem Programm SPSS Datensatz: fiktive_daten.sav Dipl. Päd. Anne Haßelkus Dr. Dorothea Dette-Hagenmeyer 11/2011 Überblick 1 Deskriptive Statistiken; Mittelwert berechnen...
Klausur zur Vorlesung Statistik III für Studenten mit dem Wahlfach Statistik
 Ludwig Fahrmeir, Nora Fenske Institut für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit dem Wahlfach Statistik 29. März 21 Hinweise:
Ludwig Fahrmeir, Nora Fenske Institut für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit dem Wahlfach Statistik 29. März 21 Hinweise:
Statistische Datenauswertung. Andreas Stoll Kantonsschule Olten
 Statistische Datenauswertung Andreas Stoll Beschreibende vs. schliessende Statistik Wir unterscheiden grundsätzlich zwischen beschreibender (deskriptiver) und schliessender (induktiver) Statistik. Bei
Statistische Datenauswertung Andreas Stoll Beschreibende vs. schliessende Statistik Wir unterscheiden grundsätzlich zwischen beschreibender (deskriptiver) und schliessender (induktiver) Statistik. Bei
Phrasensammlung für wissenschaftliches Arbeiten
 Phrasensammlung für wissenschaftliches Arbeiten Einleitung In diesem Aufsatz/dieser Abhandlung/dieser Arbeit werde ich... untersuchen/ermitteln/bewerten/analysieren... Um diese Frage zu beantworten, beginnen
Phrasensammlung für wissenschaftliches Arbeiten Einleitung In diesem Aufsatz/dieser Abhandlung/dieser Arbeit werde ich... untersuchen/ermitteln/bewerten/analysieren... Um diese Frage zu beantworten, beginnen
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilungsfreie Verfahren Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilungsfreie Verfahren Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Multivariate Statistik
 Hermann Singer Multivariate Statistik 1 Auflage 15 Oktober 2012 Seite: 12 KAPITEL 1 FALLSTUDIEN Abbildung 12: Logistische Regression: Geschätzte Wahrscheinlichkeit für schlechte und gute Kredite (rot/blau)
Hermann Singer Multivariate Statistik 1 Auflage 15 Oktober 2012 Seite: 12 KAPITEL 1 FALLSTUDIEN Abbildung 12: Logistische Regression: Geschätzte Wahrscheinlichkeit für schlechte und gute Kredite (rot/blau)
Klausur: Einführung in die Statistik
 1 Lösungen immer unter die jeweiligen Aufgaben schreiben. Bei Platzmangel auf die Rückseite schreiben (dann Nummer der bearbeiteten Aufgabe mit anmerken!!!). Lösungen, die nicht auf den Aufgabenblättern
1 Lösungen immer unter die jeweiligen Aufgaben schreiben. Bei Platzmangel auf die Rückseite schreiben (dann Nummer der bearbeiteten Aufgabe mit anmerken!!!). Lösungen, die nicht auf den Aufgabenblättern
Gestaltungsempfehlungen
 Professur E-Learning und Neue Medien Institut für Medienforschung Philosophische Fakultät Lehren und Lernen mit Medien I Gestaltungsempfehlungen Überblick Auswahl der Empfehlungen Gestaltungseffekte Empirische
Professur E-Learning und Neue Medien Institut für Medienforschung Philosophische Fakultät Lehren und Lernen mit Medien I Gestaltungsempfehlungen Überblick Auswahl der Empfehlungen Gestaltungseffekte Empirische
8. Methoden der klassischen multivariaten Statistik
 8. Methoden der klassischen multivariaten Statistik 8.1. Darstellung von Daten Voraussetzungen auch in diesem Kapitel: Grundgesamtheit (Datenraum) Ω von Objekten (Fällen, Instanzen), denen J-Tupel von
8. Methoden der klassischen multivariaten Statistik 8.1. Darstellung von Daten Voraussetzungen auch in diesem Kapitel: Grundgesamtheit (Datenraum) Ω von Objekten (Fällen, Instanzen), denen J-Tupel von
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Klausur Nr. 1. Wahrscheinlichkeitsrechnung. Keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt.
 Klausur Nr. 1 2014-02-06 Wahrscheinlichkeitsrechnung Pflichtteil Keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche Darstellung,
Klausur Nr. 1 2014-02-06 Wahrscheinlichkeitsrechnung Pflichtteil Keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche Darstellung,
Eine Einführung in R: Statistische Tests
 Eine Einführung in R: Statistische Tests Bernd Klaus, Verena Zuber Institut für Medizinische Informatik, Statistik und Epidemiologie (IMISE), Universität Leipzig http://www.uni-leipzig.de/ zuber/teaching/ws12/r-kurs/
Eine Einführung in R: Statistische Tests Bernd Klaus, Verena Zuber Institut für Medizinische Informatik, Statistik und Epidemiologie (IMISE), Universität Leipzig http://www.uni-leipzig.de/ zuber/teaching/ws12/r-kurs/
Probeklausur Zeitreihenökonometrie (Sommersemester 2014) 1
 Probeklausur Zeitreihenökonometrie (Sommersemester 2014) 1 Aufgabe 1: Betrachtet wird folgendes Modell zur Erklärung des Managergehalts salary durch den Umsatz sales, die Eigenkapitalrendite roe und die
Probeklausur Zeitreihenökonometrie (Sommersemester 2014) 1 Aufgabe 1: Betrachtet wird folgendes Modell zur Erklärung des Managergehalts salary durch den Umsatz sales, die Eigenkapitalrendite roe und die
Die Pareto Verteilung wird benutzt, um Einkommensverteilungen zu modellieren. Die Verteilungsfunktion ist
 Frage Die Pareto Verteilung wird benutzt, um Einkommensverteilungen zu modellieren. Die Verteilungsfunktion ist k a F (x) =1 k>0,x k x Finden Sie den Erwartungswert und den Median der Dichte für a>1. (Bei
Frage Die Pareto Verteilung wird benutzt, um Einkommensverteilungen zu modellieren. Die Verteilungsfunktion ist k a F (x) =1 k>0,x k x Finden Sie den Erwartungswert und den Median der Dichte für a>1. (Bei
Übungsrunde 7, Gruppe 2 LVA 107.369, Übungsrunde 7, Gruppe 2, 28.11. Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 11/2006
 1 3.34 1.1 Angabe Übungsrunde 7, Gruppe 2 LVA 107.369, Übungsrunde 7, Gruppe 2, 28.11. Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 11/2006 U sei auf dem Intervall (0, 1) uniform verteilt. Zeigen
1 3.34 1.1 Angabe Übungsrunde 7, Gruppe 2 LVA 107.369, Übungsrunde 7, Gruppe 2, 28.11. Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 11/2006 U sei auf dem Intervall (0, 1) uniform verteilt. Zeigen
6. Bayes-Klassifikation. (Schukat-Talamazzini 2002)
 6. Bayes-Klassifikation (Schukat-Talamazzini 2002) (Böhm 2003) (Klawonn 2004) Der Satz von Bayes: Beweis: Klassifikation mittels des Satzes von Bayes (Klawonn 2004) Allgemeine Definition: Davon zu unterscheiden
6. Bayes-Klassifikation (Schukat-Talamazzini 2002) (Böhm 2003) (Klawonn 2004) Der Satz von Bayes: Beweis: Klassifikation mittels des Satzes von Bayes (Klawonn 2004) Allgemeine Definition: Davon zu unterscheiden
Box-and-Whisker Plot -0,2 0,8 1,8 2,8 3,8 4,8
 . Aufgabe: Für zwei verschiedene Aktien wurde der relative Kurszuwachs (in % beobachtet. Aus den jeweils 20 Quartaldaten ergaben sich die folgenden Box-Plots. Box-and-Whisker Plot Aktie Aktie 2-0,2 0,8,8
. Aufgabe: Für zwei verschiedene Aktien wurde der relative Kurszuwachs (in % beobachtet. Aus den jeweils 20 Quartaldaten ergaben sich die folgenden Box-Plots. Box-and-Whisker Plot Aktie Aktie 2-0,2 0,8,8
13.5 Der zentrale Grenzwertsatz
 13.5 Der zentrale Grenzwertsatz Satz 56 (Der Zentrale Grenzwertsatz Es seien X 1,...,X n (n N unabhängige, identisch verteilte zufällige Variablen mit µ := EX i ; σ 2 := VarX i. Wir definieren für alle
13.5 Der zentrale Grenzwertsatz Satz 56 (Der Zentrale Grenzwertsatz Es seien X 1,...,X n (n N unabhängige, identisch verteilte zufällige Variablen mit µ := EX i ; σ 2 := VarX i. Wir definieren für alle
Stochastische Eingangsprüfung, 17.05.2008
 Stochastische Eingangsprüfung, 17.5.8 Wir gehen stets von einem Wahrscheinlichkeitsraum (Ω, A, P) aus. Aufgabe 1 ( Punkte) Sei X : Ω [, ) eine integrierbare Zufallsvariable mit XdP = 1. Sei Q : A R, Q(A)
Stochastische Eingangsprüfung, 17.5.8 Wir gehen stets von einem Wahrscheinlichkeitsraum (Ω, A, P) aus. Aufgabe 1 ( Punkte) Sei X : Ω [, ) eine integrierbare Zufallsvariable mit XdP = 1. Sei Q : A R, Q(A)
Marktforschung I. Marktforschung I 2
 Marktforschung I Marktforschung I Einführung in die Testtheorie (Toporowski) Mathematische Grundlagen (Toporowski) Varianzanalyse (Toporowski) Regressionsanalyse (Boztuğ) Diskriminanzanalyse (Hammerschmidt)
Marktforschung I Marktforschung I Einführung in die Testtheorie (Toporowski) Mathematische Grundlagen (Toporowski) Varianzanalyse (Toporowski) Regressionsanalyse (Boztuğ) Diskriminanzanalyse (Hammerschmidt)
Statistik Musterlösungen
 Statistik Musterlösungen Regina Tüchler & Achim Zeileis Institut für Statistik & Mathematik Wirtschaftsuniversität Wien 1 Grundbegriffe (1.23) Skript Reaktionen auf Videofilm. Aussagen M, E, P, S h(m)
Statistik Musterlösungen Regina Tüchler & Achim Zeileis Institut für Statistik & Mathematik Wirtschaftsuniversität Wien 1 Grundbegriffe (1.23) Skript Reaktionen auf Videofilm. Aussagen M, E, P, S h(m)
7. Das Spannungsfeld von Wissenschaft und Praxis
 Einführung in das Studium der Management- und Wirtschaftswissenschaften WS 2013/14 7. Das Spannungsfeld von Wissenschaft und Praxis Internationales Institut für Management und ökonomische Bildung Professur
Einführung in das Studium der Management- und Wirtschaftswissenschaften WS 2013/14 7. Das Spannungsfeld von Wissenschaft und Praxis Internationales Institut für Management und ökonomische Bildung Professur
Welch-Test. Welch-Test
 Welch-Test Welch-Test Test auf Lageunterschied zweier normalverteilter Grundgesamtheiten mit unbekannten Varianzen durch Vergleich der Mittelwerte zweier unabhängiger Zufallsstichproben. Beispiel Im Labor
Welch-Test Welch-Test Test auf Lageunterschied zweier normalverteilter Grundgesamtheiten mit unbekannten Varianzen durch Vergleich der Mittelwerte zweier unabhängiger Zufallsstichproben. Beispiel Im Labor
2. Korrelation, lineare Regression und multiple Regression
 multiple 2.2 Lineare 2.2 Lineare 1 / 130 2.2 Lineare 2 / 130 2.1 Beispiel: Arbeitsmotivation Untersuchung zur Motivation am Arbeitsplatz in einem Chemie-Konzern 25 Personen werden durch Arbeitsplatz zufällig
multiple 2.2 Lineare 2.2 Lineare 1 / 130 2.2 Lineare 2 / 130 2.1 Beispiel: Arbeitsmotivation Untersuchung zur Motivation am Arbeitsplatz in einem Chemie-Konzern 25 Personen werden durch Arbeitsplatz zufällig
4 Greedy-Algorithmen (gierige Algorithmen)
 Greedy-Algorithmen (gierige Algorithmen) Greedy-Algorithmen werden oft für die exakte oder approximative Lösung von Optimierungsproblemen verwendet. Typischerweise konstruiert ein Greedy-Algorithmus eine
Greedy-Algorithmen (gierige Algorithmen) Greedy-Algorithmen werden oft für die exakte oder approximative Lösung von Optimierungsproblemen verwendet. Typischerweise konstruiert ein Greedy-Algorithmus eine
Business Value Launch 2006
 Quantitative Methoden Inferenzstatistik alea iacta est 11.04.2008 Prof. Dr. Walter Hussy und David Tobinski UDE.EDUcation College im Rahmen des dokforums Universität Duisburg-Essen Inferenzstatistik Erläuterung
Quantitative Methoden Inferenzstatistik alea iacta est 11.04.2008 Prof. Dr. Walter Hussy und David Tobinski UDE.EDUcation College im Rahmen des dokforums Universität Duisburg-Essen Inferenzstatistik Erläuterung
Ausarbeitung des Seminarvortrags zum Thema
 Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Grundlagen der Inferenzstatistik: Was Ihnen nicht erspart bleibt!
 Grundlagen der Inferenzstatistik: Was Ihnen nicht erspart bleibt! 1 Einführung 2 Wahrscheinlichkeiten kurz gefasst 3 Zufallsvariablen und Verteilungen 4 Theoretische Verteilungen (Wahrscheinlichkeitsfunktion)
Grundlagen der Inferenzstatistik: Was Ihnen nicht erspart bleibt! 1 Einführung 2 Wahrscheinlichkeiten kurz gefasst 3 Zufallsvariablen und Verteilungen 4 Theoretische Verteilungen (Wahrscheinlichkeitsfunktion)
Academic Skills - Befragung und Auswertung
 Otto-von-Guericke University Magdeburg Allgemein Befragung Eine Befragung ist eine wissenschaftliche Maßnahme zur Erforschung von Verhalten, Einstellung oder Wissen Des Weiteren können auch demographische
Otto-von-Guericke University Magdeburg Allgemein Befragung Eine Befragung ist eine wissenschaftliche Maßnahme zur Erforschung von Verhalten, Einstellung oder Wissen Des Weiteren können auch demographische
Modul G.1 WS 07/08: Statistik 17.01.2008 1. Die Korrelation ist ein standardisiertes Maß für den linearen Zusammenhangzwischen zwei Variablen.
 Modul G.1 WS 07/08: Statistik 17.01.2008 1 Wiederholung Kovarianz und Korrelation Kovarianz = Maß für den linearen Zusammenhang zwischen zwei Variablen x und y Korrelation Die Korrelation ist ein standardisiertes
Modul G.1 WS 07/08: Statistik 17.01.2008 1 Wiederholung Kovarianz und Korrelation Kovarianz = Maß für den linearen Zusammenhang zwischen zwei Variablen x und y Korrelation Die Korrelation ist ein standardisiertes
Verteilungsanalyse. Johannes Hain. Lehrstuhl für Mathematik VIII Statistik 1/31
 Verteilungsanalyse Johannes Hain Lehrstuhl für Mathematik VIII Statistik 1/31 Datentypen Als Sammeln von Daten bezeichnet man in der Statistik das Aufzeichnen von Fakten. Erhobene Daten klassifziert man
Verteilungsanalyse Johannes Hain Lehrstuhl für Mathematik VIII Statistik 1/31 Datentypen Als Sammeln von Daten bezeichnet man in der Statistik das Aufzeichnen von Fakten. Erhobene Daten klassifziert man
DIPLOMVORPRÜFUNG GRUNDZÜGE DER STATISTIK, TEIL B WINTERSEMESTER 2006/07 28.02.2007
 Wirtschaftswissenschaftliches Prüfungsamt DIPLOMVORPRÜFUNG GRUNDZÜGE DER STATISTIK, TEIL B WINTERSEMESTER 006/07 8.0.007 Lösung Prof. Dr. R Friedmann / Dr. R. Hauser Hinweise für die Klausurteilnehmer
Wirtschaftswissenschaftliches Prüfungsamt DIPLOMVORPRÜFUNG GRUNDZÜGE DER STATISTIK, TEIL B WINTERSEMESTER 006/07 8.0.007 Lösung Prof. Dr. R Friedmann / Dr. R. Hauser Hinweise für die Klausurteilnehmer
Anhang A: Fragebögen und sonstige Unterlagen
 Anhang Anhang A: Fragebögen und sonstige Unterlagen A.: Flyer zur Probandenrekrutierung 46 A.: Fragebogen zur Meditationserfahrung 47 48 A.3: Fragebogen Angaben zur Person 49 5 5 A.4: Termin- und Einladungsschreiben
Anhang Anhang A: Fragebögen und sonstige Unterlagen A.: Flyer zur Probandenrekrutierung 46 A.: Fragebogen zur Meditationserfahrung 47 48 A.3: Fragebogen Angaben zur Person 49 5 5 A.4: Termin- und Einladungsschreiben
Tutorial: Homogenitätstest
 Tutorial: Homogenitätstest Eine Bank möchte die Kreditwürdigkeit potenzieller Kreditnehmer abschätzen. Einerseits lebt die Bank ja von der Vergabe von Krediten, andererseits verursachen Problemkredite
Tutorial: Homogenitätstest Eine Bank möchte die Kreditwürdigkeit potenzieller Kreditnehmer abschätzen. Einerseits lebt die Bank ja von der Vergabe von Krediten, andererseits verursachen Problemkredite
Gestaltungsempfehlungen
 Gestaltungsempfehlungen Prof. Dr. Günter Daniel Rey 1 Überblick Auswahl der Empfehlungen Gestaltungseffekte Empirische Überprüfung Variablenarten Versuchspläne Beispiel eines Experimentes Statistische
Gestaltungsempfehlungen Prof. Dr. Günter Daniel Rey 1 Überblick Auswahl der Empfehlungen Gestaltungseffekte Empirische Überprüfung Variablenarten Versuchspläne Beispiel eines Experimentes Statistische
Einige Statistische Tests für den Ein- Zwei- und k-stichprobenfall (Nach Sachs, Stat. Meth.)
 ue biostatistik: nichtparametrische testverfahren / ergänzung 1/6 h. Lettner / physik Statistische Testverfahren Einige Statistische Tests für den Ein- Zwei- und k-stichprobenfall (Nach Sachs, Stat. Meth.)
ue biostatistik: nichtparametrische testverfahren / ergänzung 1/6 h. Lettner / physik Statistische Testverfahren Einige Statistische Tests für den Ein- Zwei- und k-stichprobenfall (Nach Sachs, Stat. Meth.)
Inhaltsverzeichnis. Vorwort 1. Kapitel 1 Einführung 3. Kapitel 2 Messtheorie und deskriptive Statistik 13
 Inhaltsverzeichnis Vorwort 1 Kapitel 1 Einführung 3 1.1 Ziele... 4 1.2 Messtheorie und deskriptive Statistik... 8 1.3 Grundlagen der Wahrscheinlichkeitsrechnung... 9 1.4 Inferenzstatistik... 9 1.5 Parametrische
Inhaltsverzeichnis Vorwort 1 Kapitel 1 Einführung 3 1.1 Ziele... 4 1.2 Messtheorie und deskriptive Statistik... 8 1.3 Grundlagen der Wahrscheinlichkeitsrechnung... 9 1.4 Inferenzstatistik... 9 1.5 Parametrische
STATISTIK 1 - BEGLEITVERANSTALTUNG
 STATISTIK 1 - BEGLEITVERANSTALTUNG VORLESUNG 4 ALPHA / BETA-FEHLER 12.12.2014 1 12.12.2014 1 Mona Ulrich, Psychologie (M.Sc.) AGENDA 01 STATISTISCHE HYPOTHESEN 02 POPULATION / STICHPROBE 03 ALPHA/ BETA-FEHLER
STATISTIK 1 - BEGLEITVERANSTALTUNG VORLESUNG 4 ALPHA / BETA-FEHLER 12.12.2014 1 12.12.2014 1 Mona Ulrich, Psychologie (M.Sc.) AGENDA 01 STATISTISCHE HYPOTHESEN 02 POPULATION / STICHPROBE 03 ALPHA/ BETA-FEHLER
8. Februar 2007. 5. Bei Unterschleif gilt die Klausur als nicht bestanden und es erfolgt eine Meldung an das Prüfungsamt.
 L. Fahrmeir, C. Belitz Department für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit Wahlfach Statistik 8. Februar 2007 Hinweise:
L. Fahrmeir, C. Belitz Department für Statistik Bitte für die Korrektur freilassen! Aufgabe 1 2 3 4 Punkte Klausur zur Vorlesung Statistik III für Studenten mit Wahlfach Statistik 8. Februar 2007 Hinweise:
Extremwertverteilungen
 Seminar Statistik Institut für Stochastik 12. Februar 2009 Gliederung 1 Grenzwertwahrscheinlichkeiten 2 3 MDA Fréchet MDA Weibull MDA Gumbel 4 5 6 Darstellung von multivariaten, max-stabilen Verteilungsfunktionen
Seminar Statistik Institut für Stochastik 12. Februar 2009 Gliederung 1 Grenzwertwahrscheinlichkeiten 2 3 MDA Fréchet MDA Weibull MDA Gumbel 4 5 6 Darstellung von multivariaten, max-stabilen Verteilungsfunktionen
Varianzanalyse ANOVA
 Varianzanalyse ANOVA Johannes Hain Lehrstuhl für Mathematik VIII Statistik 1/23 Einfaktorielle Varianzanalyse (ANOVA) Bisher war man lediglich in der Lage, mit dem t-test einen Mittelwertsvergleich für
Varianzanalyse ANOVA Johannes Hain Lehrstuhl für Mathematik VIII Statistik 1/23 Einfaktorielle Varianzanalyse (ANOVA) Bisher war man lediglich in der Lage, mit dem t-test einen Mittelwertsvergleich für
Varianzanalyse * (1) Varianzanalyse (2)
 Varianzanalyse * (1) Einfaktorielle Varianzanalyse (I) Die Varianzanalyse (ANOVA = ANalysis Of VAriance) wird benutzt, um Unterschiede zwischen Mittelwerten von drei oder mehr Stichproben auf Signifikanz
Varianzanalyse * (1) Einfaktorielle Varianzanalyse (I) Die Varianzanalyse (ANOVA = ANalysis Of VAriance) wird benutzt, um Unterschiede zwischen Mittelwerten von drei oder mehr Stichproben auf Signifikanz
Varianzanalyse (ANOVA: analysis of variance)
 Varianzanalyse (AOVA: analysis of variance) Einfaktorielle VA Auf der Basis von zwei Stichproben wird bezüglich der Gleichheit der Mittelwerte getestet. Variablen müssen Variablen nur nominalskaliert sein.
Varianzanalyse (AOVA: analysis of variance) Einfaktorielle VA Auf der Basis von zwei Stichproben wird bezüglich der Gleichheit der Mittelwerte getestet. Variablen müssen Variablen nur nominalskaliert sein.
Analog zu Aufgabe 16.1 werden die Daten durch folgenden Befehl eingelesen: > kredit<-read.table("c:\\compaufg\\kredit.
 Lösung 16.3 Analog zu Aufgabe 16.1 werden die Daten durch folgenden Befehl eingelesen: > kredit
Lösung 16.3 Analog zu Aufgabe 16.1 werden die Daten durch folgenden Befehl eingelesen: > kredit
Präsenzübungsaufgaben zur Vorlesung Elementare Sachversicherungsmathematik
 Präsenzübungsaufgaben zur Vorlesung Elementare Sachversicherungsmathematik Dozent: Volker Krätschmer Fakultät für Mathematik, Universität Duisburg-Essen, WS 2012/13 1. Präsenzübung Aufgabe T 1 Sei (Z 1,...,
Präsenzübungsaufgaben zur Vorlesung Elementare Sachversicherungsmathematik Dozent: Volker Krätschmer Fakultät für Mathematik, Universität Duisburg-Essen, WS 2012/13 1. Präsenzübung Aufgabe T 1 Sei (Z 1,...,
 Fixpunktsemantik logischer Programme Pascal Hitzler Juli 1997 Kurzuberblick im Rahmen der Vorlesung Einfuhrung in Prolog von T. Cornell im Sommersemester 1997 an der Universitat Tubingen. Beweise sind
Fixpunktsemantik logischer Programme Pascal Hitzler Juli 1997 Kurzuberblick im Rahmen der Vorlesung Einfuhrung in Prolog von T. Cornell im Sommersemester 1997 an der Universitat Tubingen. Beweise sind
Empathie und prosoziales Verhalten
 Empathie und prosoziales Verhalten 1. Entwicklungskonzept der Empathie 2. Geschlechterspezifische Unterschiede der Empathie 3. Entwicklungsabhängige Veränderung im prosozialen Verhalten 4. Individuelle
Empathie und prosoziales Verhalten 1. Entwicklungskonzept der Empathie 2. Geschlechterspezifische Unterschiede der Empathie 3. Entwicklungsabhängige Veränderung im prosozialen Verhalten 4. Individuelle
Auswertung mit dem Statistikprogramm SPSS: 30.11.05
 Auswertung mit dem Statistikprogramm SPSS: 30.11.05 Seite 1 Einführung SPSS Was ist eine Fragestellung? Beispiel Welche statistische Prozedur gehört zu welcher Hypothese? Statistische Berechnungen mit
Auswertung mit dem Statistikprogramm SPSS: 30.11.05 Seite 1 Einführung SPSS Was ist eine Fragestellung? Beispiel Welche statistische Prozedur gehört zu welcher Hypothese? Statistische Berechnungen mit
Prüfen von Mittelwertsunterschieden: t-test
 Prüfen von Mittelwertsunterschieden: t-test Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) t-test
Prüfen von Mittelwertsunterschieden: t-test Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) t-test
Einführung in statistische Testmethoden
 Einführung in statistische Testmethoden und die Bearbeitung von Messdaten mit Excel 1. Beispielhafte Einführung in den Gebrauch von Testmethoden 2. Typen von Messwerten, Verteilungen 3. Mittelwert, Varianz,
Einführung in statistische Testmethoden und die Bearbeitung von Messdaten mit Excel 1. Beispielhafte Einführung in den Gebrauch von Testmethoden 2. Typen von Messwerten, Verteilungen 3. Mittelwert, Varianz,
90-minütige Klausur Statistik für Studierende der Kommunikationswissenschaft
 Prof. Dr. Helmut Küchenhoff SS08 90-minütige Klausur Statistik für Studierende der Kommunikationswissenschaft am 22.7.2008 Anmerkungen Überprüfen Sie bitte sofort, ob Ihre Angabe vollständig ist. Sie sollte
Prof. Dr. Helmut Küchenhoff SS08 90-minütige Klausur Statistik für Studierende der Kommunikationswissenschaft am 22.7.2008 Anmerkungen Überprüfen Sie bitte sofort, ob Ihre Angabe vollständig ist. Sie sollte
Einfache statistische Testverfahren
 Einfache statistische Testverfahren Johannes Hain Lehrstuhl für Mathematik VIII (Statistik) 1/29 Hypothesentesten: Allgemeine Situation Im Folgenden wird die statistische Vorgehensweise zur Durchführung
Einfache statistische Testverfahren Johannes Hain Lehrstuhl für Mathematik VIII (Statistik) 1/29 Hypothesentesten: Allgemeine Situation Im Folgenden wird die statistische Vorgehensweise zur Durchführung
Parametrische Statistik
 Statistik und ihre Anwendungen Parametrische Statistik Verteilungen, maximum likelihood und GLM in R Bearbeitet von Carsten F. Dormann 1. Auflage 2013. Taschenbuch. xxii, 350 S. Paperback ISBN 978 3 642
Statistik und ihre Anwendungen Parametrische Statistik Verteilungen, maximum likelihood und GLM in R Bearbeitet von Carsten F. Dormann 1. Auflage 2013. Taschenbuch. xxii, 350 S. Paperback ISBN 978 3 642
Stichprobenauslegung. für stetige und binäre Datentypen
 Stichprobenauslegung für stetige und binäre Datentypen Roadmap zu Stichproben Hypothese über das interessierende Merkmal aufstellen Stichprobe entnehmen Beobachtete Messwerte abbilden Schluss von der Beobachtung
Stichprobenauslegung für stetige und binäre Datentypen Roadmap zu Stichproben Hypothese über das interessierende Merkmal aufstellen Stichprobe entnehmen Beobachtete Messwerte abbilden Schluss von der Beobachtung
Konfidenzintervall oder p-wert? Teil 4 der Serie zur Bewertung wissenschaftlicher Publikationen
 ÜBERSICHTSARBEIT Konfidenzintervall oder p-wert? Teil 4 der Serie zur Bewertung wissenschaftlicher Publikationen Jean-Baptist du Prel, Gerhard Hommel, Bernd Röhrig, Maria Blettner ZUSAMMENFASSUNG Einleitung:
ÜBERSICHTSARBEIT Konfidenzintervall oder p-wert? Teil 4 der Serie zur Bewertung wissenschaftlicher Publikationen Jean-Baptist du Prel, Gerhard Hommel, Bernd Röhrig, Maria Blettner ZUSAMMENFASSUNG Einleitung:
Motivation. Wilcoxon-Rangsummentest oder Mann-Whitney U-Test. Wilcoxon Rangsummen-Test Voraussetzungen. Bemerkungen
 Universität Karlsruhe (TH) Forschungsuniversität gegründet 825 Wilcoxon-Rangsummentest oder Mann-Whitney U-Test Motivation In Experimenten ist die Datenmenge oft klein Daten sind nicht normalverteilt Dann
Universität Karlsruhe (TH) Forschungsuniversität gegründet 825 Wilcoxon-Rangsummentest oder Mann-Whitney U-Test Motivation In Experimenten ist die Datenmenge oft klein Daten sind nicht normalverteilt Dann
Nichtparametrische Analyse longitudinaler Daten in faktoriellen Experimenten. Frank Konietschke
 Nichtparametrische Analyse longitudinaler Daten in faktoriellen Experimenten Frank Konietschke Abteilung für Medizinische Statistik Universität Göttingen 1 Übersicht Beispiele CGI (repeated measures) γ-gt
Nichtparametrische Analyse longitudinaler Daten in faktoriellen Experimenten Frank Konietschke Abteilung für Medizinische Statistik Universität Göttingen 1 Übersicht Beispiele CGI (repeated measures) γ-gt
Benchmark-Experimente
 Benchmark-Experimente Viktoria Sander Seminar: Modellwahlkriterien (WS 2009/2010) 04.12.2009 Viktoria Sander (WS 2009/2010) Benchmark-Experimente 04.12.2009 1 / 50 1 Einleitung 2 Ausgangssituation Annahmen
Benchmark-Experimente Viktoria Sander Seminar: Modellwahlkriterien (WS 2009/2010) 04.12.2009 Viktoria Sander (WS 2009/2010) Benchmark-Experimente 04.12.2009 1 / 50 1 Einleitung 2 Ausgangssituation Annahmen
Methoden der empirischen Sozialforschung [Grundkurs]
![Methoden der empirischen Sozialforschung [Grundkurs] Methoden der empirischen Sozialforschung [Grundkurs]](/thumbs/30/14592343.jpg) Methoden der empirischen Sozialforschung [Grundkurs] Mag. Dr. Elfriede Penz MAS Institut für Internationales Marketing und Management Sprechstunde: Mittwoch 16:00-17:00 Uhr UZA1, 3. Stock, Kern B Überblick
Methoden der empirischen Sozialforschung [Grundkurs] Mag. Dr. Elfriede Penz MAS Institut für Internationales Marketing und Management Sprechstunde: Mittwoch 16:00-17:00 Uhr UZA1, 3. Stock, Kern B Überblick
RUPRECHTS-KARLS-UNIVERSITÄT HEIDELBERG
 Die Poisson-Verteilung Jianmin Lu RUPRECHTS-KARLS-UNIVERSITÄT HEIDELBERG Ausarbeitung zum Vortrag im Seminar Stochastik (Wintersemester 2008/09, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: In der Wahrscheinlichkeitstheorie
Die Poisson-Verteilung Jianmin Lu RUPRECHTS-KARLS-UNIVERSITÄT HEIDELBERG Ausarbeitung zum Vortrag im Seminar Stochastik (Wintersemester 2008/09, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: In der Wahrscheinlichkeitstheorie
