3 Bilinearform, Basen und Matrizen
|
|
|
- Leopold Kalb
- vor 5 Jahren
- Abrufe
Transkript
1 Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht unter (CC BY-NC-SA 3.0 DE) Teil I Vorbemerkungen Teil II Bilinearformen 1 Direkte Summen Der Vektorraum U V bzw. U V wird die direkte Summe von U und V genannt Seien U, V W Unterräume. Man sagt W ist die direkte Summe von U, V, falls die kanonische Abbildung U V W, (u, v) u + v ein Isomorphismus ist. Lemma Seien U, V W Unterräume, dann gilt W = U V ( U, V K = W ) (U V = 0). 2 Biliniearform Sei V ein Vektorraum über K. Eine Bilinearform ist eine Abbildung, : V V K, (v, v ) v, v mit der Eigenschaft, dass, biliniear ist, d.h. λ K und alle v, v 1, v 2, v, v 1, v 2 V gilt: v 1 + v 2, v = v 1 v + v 2 v v 1, v 1 + v 2 = v, v 1 + v, v 2 λv, v = v, λv = λ v, v Man nennt die Bilinearform 1
2 symmetrisch, falls v, v V : v, v = v, v schiefsymmetrisch, falls v V : v, v = 0. Ist, schiefsymmetrisch, so gilt wegen der Bilinearität v, v V : v, v = v, v. 3 Bilinearform, Basen und Matrizen Sei V ein n-dimensionaler Vektorraum über K versehen mit einer Bilinearform, : V V K. Ist B = {b 1,..., b n } eine Basis von V, dann kann man der Bilinearform eine quadratische Matrix zuordnen: A, = (a i,j ) mit a i,j = b i, b j genannt die Matrix der Bilinearform bezüglich der Basis B. Sei v = n i=1 x ib i und w = n i=1 y ib i, dann gilt: n n n v, w = x i b i, y i b i = x i y i b i, b j = Lemma i=1 i=1 i,j=1 v, w = v t B A, w B. Die Zuordnung, A, ist bijektiv. n x i y i a i,j = vba t, w B i,j=1 Satz Sei, eine Bilinearform, sei C, A die Matrix von, bezüglich A, CB, die Matrix bezüglich B. Dann gilt ( ) T B t A C A, TA B = C, B 4 Symmetrische Bilinearformen Im Folgenden sei K ein Körper der Charakteristik 0, z.b. C, R oder Q, und V ein n-dimensionaler K-Vektorraum und sei, eine symmetrische Bilinearform auf V V. Das Radikal von, ist deniert als V = {v V v, V = 0} = {v V v, w = 0 w V } Man nennt, nicht ausgeartet, falls V = 0. Satz Sei B = {b 1,..., b n } eine Basis von V und A die zugehörige Matrix von,. Dann gilt: V ist der Unterraum der Lösungen des homogenen linearen Gleichungssystems Ax = 0, ist nicht ausgeartet det A 0 v V heiÿt isotrop bzgl.,, falls v, v = 0 und anisotrop bzgl.,, falls v, v 0. Sei W V ein Unterraum. Dann heiÿt das orthogonale Komplement von W bzgl.,. W = {v V v, w = 0 w W } 2
3 Satz Für jede direkte Summenzerlegung V = V U ist die Einschränkung von, auf U nicht ausgeartet. Satz 2.4.3, nicht ausgeartet ein anisotroper Vektor Sei w V anisotrop, W = K w. Dann ist V = W W und wenn, nicht ausgeartet auf V, W =, W nicht ausgeartet. Satz Sei V ein n-dimensionaler K-Vektorraum und, eine symmetrische Bilinearform auf V. Dann besitzt V eine Basis B, sodass die Matrix A von, bzgl. B folgende Gestalt hat: λ 1... A = λ r, mit n r = dim V. 0 B heiÿt dann Orthogonalbasis von,. Korollar Sei A eine symmetrische Matrix, dann g GL n, sodass t gag in Diagonalgestalt ist. Bemerkung Eine Basis von V mit i j : b i, b j = 0 nennt man Orthogonalbasis. Theorem (Trägheitssatz von Sylvester) Sei V ein reeller Vektorraum mit dim V = n und, eine symmetrische Bilinearform. Dann eine Basis B von V mit der Eigenschaft 1 C, B = 1, (p 1, q 1, s 0) 0 wobei die Zahlen p, q, s unabhängig von der Wahl von B sind Ein Skalarprodukt auf einem reellen Vektorraum V ist eine symmetrische, positiv denite Bilinearform. Satz Die folgenden Aussagen sind äquivalent: A ist eine symmetrische, positiv denite Matrix A repräsentiert das Standardskalarprodukt bzgl. einer geeigneten Basis, d.h. g GL n (R) mit t gag = I Die Signatur der symmetrischen Matrix A ist (n, 0) g GL n (R) mit A = t gg 3
4 Sei, eine symmetrische Biliniearform auf einem reellen, endlich dimensionalen Vektorraum. Eine Orthonormalbasis zu, ist eine Basis B = {b 1,..., b n }, sodass gilt Sei A eine symmetrische, reelle Matrix. b i, b j = 0 i j b i, b i = 1 i = 1,..., n Eine Orthonormalbasis zu A ist eine Basis B = {b 1,..., b n }, sodass gilt t b i Ab j = b i, b j = 0 t b i Ab i = b i, b i = 1 i j i = 1,..., n Korollar 2.6.1, hat eine Orthonormalbasis, positiv denit A hat eine Orthonormalbasis A positiv denit Theorem Sei ( A eine ) symmetrische Matrix. Dann gilt: A ist positiv denit det A i > 0 i = 1,..., n, wobei Ai, d.h. alle Hauptminoren sind positiv Eine hemitesche Form auf V ist eine Funktion, : V V C mit den Eigenschaften: v, w + w = v, w + v, w und v, λw = λ v, w (linear im 2. Argument) v + v, w = v, w + v, w und λv, w = λ v, w (sesquilinear im 1. Argument) v, w V : v, w = w, v Man nennt eine komplexe Matrix A M n,n (C) hermitesch, falls t A = A. Lemma V komplexer Vektorraum, dim V = n, B = {b 1,..., b n } fest gewählte Basis. Dann ist die Abbildung bijektiv. (hermitesche Formen auf V ) (hermitesche n n Matrizen),, H B, Lemma Ist A eine zweite Basis von V, dann gilt H A, = t T A B HB, T A B v V heiÿt isotrop, falls v, v = 0, sonst heiÿt v anisotrop. 4
5 Lemma V komplexer Vektorraum, dim V = n,, hermitesche Form. Dann gibt es eine Orthogonalbasis B, sodass 1 H, B = 1, (p 1, q 1, s 0) 0 wobei die Zahlen p, q, s unabhängig von der Wahl von B sind. Theorem Sei V ein komplexer Vektorraum, dim V = n und, eine hermitesche Form. Sei B eine Basis von V und sei A die zugehörige Basismatrix. Dann sind äquivalent: A (bzw., ) ist positiv denit A repräsentiert die standard hermitesche Form auf dem C n bzgl. einer geeigneten Basis g GL n (C) : A = t gg Alle Hauptminoren sind positiv A hat eine Orthonormalbasis 5
6 Teil III Die orthogonale und die unitäre Gruppe Orthogonale und unitäre Endomorphismen Lemma g M n (C) ist unitär v, w C n : v, w = gv, gw Lemma g M n (C) ist unitär Spalten von g bilden eine Orthonormalbasis zur standard hermiteschen Form. Lemma g M n (R). Dann gilt: g orthogonal gv, gw = v, w g M n (R) ist orthogonal Spalten von g bilden eine Orthonormalbasis Sei V ein endlichdimensional Vektorraum. g End (V ) heiÿt unitär, falls v, w V : φ (v), φ (w) = v, w. Lemma komplexer Fall: V endlichdimensionaler Vektorraum über C,, positiv denite Form, B = {v 1,..., v n } Orthonormalbasis. Sei φ End (V ). Dann gilt φ unitär M B (φ) unitär reeller Fall: V endlichdimensionaler Vektorraum über R,, Skalarprodukt, B = {v 1,..., v n } Orthonormalbasis. Sei φ End (V ). Dann gilt φ unitär M B (φ) orthogonal Die Gruppen O n (R) und U n (C) O n (R) = { g GL n (R) t gg = I } heiÿt die orthogonale Gruppe. U n (R) = { g GL n (C) t gg = I } heiÿt die unitäre Gruppe. Lemma O n ist eine Untergruppe der GL n (R) U n ist eine Untergruppe der GL n (C) 6
7 Orthogonales Komplement und direkte Summen Lemma Sei U = {v V U, v = 0}, dann gilt V = U U Sei φ O (V ) eine orthogonale lineare Abbildung bzgl., : φ (U) = U φ ( U ) = U Sei φ O (V ) mit φ (U) = U. B 1 Orthonormalbasis von U, B 2 Orthonormalbasis von U, B := B 1 B 2. Dann ist ( ) MB1 (φ M B (φ) = U ) 0 0 M B2 (φ U ) Lemma W = {v V W, v = 0} ist ein Untervektorraum von V = W W φ unitär: φ (W ) = W φ ( W ) = W B 1 Orthonormalbasis von W, B 2 Orthonormalbasis von W, B := B 1 B 2. Dann ist ( ) MB1 (φ) 0 M B (φ) = 0 M B2 (φ) Determinante, Eigenwerte und Eigenvektoren Lemma g O n oder g U n det g = SO n = {g O n det g = 1}, SU n = {g U n det g = 1} Sei V ein reeller Vektorraum, dim V = n und, das Standardskalarprodukt. SO (V ) := {φ O (V ) det φ = 1} Sei V ein komplexer Vektorraum, dim V = n und, eine postiv denite hermitesche Form. SU (V ) := {φ U (V ) det φ = 1} Lemma Sei g U n oder g O n, sei λ ein Eigenwert von g. Dann gilt λ = 1. Lemma Seien λ 1 λ 2 Eigenwerte von g O n bzw. g U n und v 1, v 2 die Eigenvektoren von g zu λ 1, λ 2. Dann gilt v 1, v 2 = 0. Satz Jede unitäre Matrix ist diagonalisierbar. (g U n h U n mit h 1 gh = t hgh in Diagonalgestalt) Sei φ U (V ), dann Orthonormalbasis B mit M B (φ) in Diagonalgestalt 7
8 Drehungen & Spiegelungen Satz Zu jeder orthogonalen Abbildung φ O (V ) gibt es eine Orthonormalbasis B mit 1 ( ) M B (φ) = 1 cos α sin α, wobei X := sin α cos α X g O n h O n mit h 1 gh ist von der obigen Form Korollar Jede orthogonale Abbildung ist ein Produkt von Drehungen und Spiegelungen. Euklidische und unitäre Vektorräume Ein reeller Vektorraum V mit dim V = n und einem Skalarprodukt wird ein euklidischer Vektorraum genannt. Ein komplexer Vektorraum V mit dim V = n und einer positiv deniten Form wird ein unitärer Vektorraum genannt. Lemma Sei V ein euklidischer oder unitärer Vektorraum mit dim V ( x, x = x, y = y, y ) x = y = n. Seien x, y V. Dann gilt Satz Seien V, W euklidische oder unitäre Vektorräume mit dim V = n und dim W = m und sei φ : V W eine Abbildung mit der Eigenschaft, dass φ die Formen respektiert: v, v V : v, v V = φ (v), φ (v ) W. Dann ist φ linear und wenn V = W, dann gilt φ O (V ) bzw. φ U (V ). Orthonormalbasen Deniere v := v, v als die Länge von v. Lemma (Schmidtsches Orthonormalisierungsverfahren) Sei A = {v 1,..., v n } eine Basis von einem euklidischen oder unitären Vektorraum V. Dann istb = {b 1,..., b n } mit v b 1 = 1 eine Orthonormalbasis von V. b 2 = b n = v 1 v 2 b 1,v 2 b 1 v 2 b 1,v 2 b 1 v n 1 n j=1 bj,vn bj v n 1 n bj,vn bj j=1 Korollar (Basisergänzungssatz für Orthonormalbasen) Sei B 1 = {v 1,..., v r } eine linear unabhängige Teilmenge eines euklidischen oder unitären Vektorraums V mit dim V = n. Dann gibt es eine Orthonormalbasis B mit B = {v 1,..., v r, v r+1,...v n }. 8
9 Lemma Sei V ein euklidischer oder unitärer Vektorraum mit dim V = n, sei B = {b 1,..., b n } Orthonormalbasis von V und sei v V. Dann gilt: n v = b 1, v b i Lemma Sei B eine Orthonormalbasis. Dann respektiert die Formen, d.h. i=1 p B : V C n, v = Lemma (Basiswechselmatrix) n a i v i i=1 a 1. a n v, v V : v, v V = p B (v), p B (v ) Sei V ein euklidischer oder unitärer Vektorraum, B = {v 1,..., v n } eine Orthonormalbasis von V und sei A = {w 1,..., w n } eine weitere Basis. Sei TB A die Basiswechselmatrix. Dann gilt: A ist Orthonormalbasis T A B Dualraum und Bilinearformen V ist der duale Vektorraum Hom (V, K). ist orthogonal bzw. unitär Sei B = {b 1,.., b n } Basis von V. Die Menge B = {b 1,..., b n} mit { b i : V K, b 1 für i = j i (b j ) = 0 für i j nennt man die duale Basis von V zu B. Lemma B ist eine Basis von V. Lemma Seien V, W Vektorräume mit dim V = n und dim W = m, sei B = {v 1,.., v n } eine Basis von V, B = {w 1,..., w m } eine Basis von W und seien B und B die dualen Basen. Sei φ Hom (V, K). Dann gilt t MB B B (φ) = MB (φ) Lemma Die Abbildungen und sind bijektiv und invers zueinander. Hom (V, V ) Bilinearformen auf V φ, φ Bilinearformen auf V Hom (V, V ), φ, 9
10 Lemma Sei, eine Bilinearform auf V und B eine Basis von V. Dann gilt M B B ( φ, ) = MB (, φ ) Korollar Sei, eine symmetrische Bilinearform. Dann gilt:, nicht ausgeartet φ, Isomorphismus Korollar Sei V ein euklidischer Vektorraum und, ein Skalarprodukt. Dann deniert einen Isomorphismus. : V V v v : V R v v, v Satz Sei V ein unitärer Vektorraum und, eine positiv denite hermitesche Form. Dann deniert : V V v v : V C v v, v einen semilinearen Isomorphismus, d.h. v 1 + v 2 = v 1 + v 2 und λv = λ v. Adjungierter Endomorphismus Sei φ End (V ) und V ein euklidischer oder unitärer Vektorraum. Wir denieren als den adjungierten Endomorphismus von φ. φ a : V V φ V 1 V Satz φ a ist die eindeutig bestimme lineare Abbildung mit φ (v), v = v, φ a (v ) Satz Sei V ein euklidischer oder unitärer Vektorraum,, eine Form, B eine Orthonormalbasis von V und φ End (V ). Dann gilt: M B (φ) T = M B (φ a ) Selbstadjungierte und normale Endomorphismen φ End (V ) heiÿt selbstadjungiert, falls φ a = φ. 10
11 φ End (V ) heiÿt normal, falls φ φ a = φ a φ. Korollar φ selbstadjungiert φ normal. Lemma φ End (V ) normal v V : φ (v), φ (v ) = φ a (v), φ a (v ). Satz Sei φ End (V ) und A = M B (φ). Dann gilt: A a = A selbstadjungiert A hermitesch bzw. symmetrisch φ normal A T A = AA T Man nennt A M n (R oder C) normal, falls A T A = AA T. Bemerkung A hermitesch/symmetrisch A normal. Hermitesche und normale Matrizen Satz Sei V ein unitärer Vektorraum. Dann gilt: φ selbstadjungiert Orthonormalbasis B mit M B (φ) ist Diagonalmatrix φ normal Orthonormalbasis B mit M B (φ) ist Diagonalmatrix Korollar Sei A M n (C). Dann gilt: A normal g U n (C) mit gag 1 ist Diagonalmatrix Korollar Sei A eine hermitesche Matrix mit Signatur (p, q). Dann ist A diagonalisierbar mit einer unitären Matrix, alle Eigenwerte sind reell und die Matrix hat p positive und q negative Eigenwerte. Lemma Sei φ normal und sei V λ φ = {v V φ (v) = λv} für λ C. Dann gilt: V λ φ = V λ φ a V λ φ V µ φ, λ µ 11
12 Lemma V = Vφ λ. λ C Satz φ symmetrisch Orthonormalbasis B mit M B (φ) ist Diagonalmatrix A symmetrische Matrix, (p, q) = Signatur von A. Dann g O n (R) mit gag 1 ist Diagonalmatrix und die Matrix hat p positive und q negative Eigenwerte Satz φ End (V ) ist normal Orthonormalbasis B von V mit M B (φ) ist in verallgemeinerter Diagonalform. Korollar A M n (R): A ist normal g O n mit g 1 Ag ist in verallgemeinerter Diagonalform. Lemma Sei V ein euklidischer Vektorraum und, ein Skalarprodukt. Dann gibt es eine eindeutig bestimmte positiv denite hermitesche Form, C auf V C mit v, w V : v, w C = v, w. 12
13 Teil IV Moduln & Euklidische Ringe Ringe & Moduln Sei R ein kommutativer Ring mit 1 0. Ein Modul M ist eine abelsche Gruppe (M, +), sodass n, m M und r, s R zusammen mit einer Abbildung R M M, (r, m) r m gilt: 1. 1 m = m 2. (r s) m = r (s m) 3. (r + s) m = rm + sm 4. r (m + n) = rm + rn Sei M ein R-Modul. Eine Teilmenge {m j } j J M heiÿt Erzeugendensystem, falls sich jedes Element in M als eine Linearkombination über R mit Elementen aus {m j } j J schreiben lässt. M heiÿt endlich erzeugt, falls es ein endliches Erzeugendensystem gibt. Eine Teilmenge {m j } j J heiÿt linear unabhängig, falls r i1 m i r it m it r i1 =... = r it = 0. Eine Basis ist ein linear unabhängiges Erzeugendensystem. Ein Modul heiÿt frei, falls er eine Basis besitzt. Satz Seien M.M R-Moduln und sei φ : M M eine lineare Abbildung. Dann gibt es eine eindeutige lineare Abbildung φ : M /Kerφ Imφ bestimmt durch die Eigenschaft φ (m) = φ (m) mit φ Isomorphismus Ein R-Modul heiÿt zyklisch, falls m M : {rm r R} = M. Lemma Jeder zyklischer R-Modul ist isomorph zu R /I für ein Ideal I R. Lemma Die Abbildung ist ein Isomorphismus von R-Moduln. Satz φ : M R p m = r 1 m r p m p Sei M ein endlich erzeugter, freier Modul. Dann hat jede Basis die gleiche Anzahl von Elementen, genannt der Rang von M. r 1. r p 13
14 Direkte Summen von Moduln Seien M 1,..., M t R-Moduln. Unter der direkten Summe M 1... M t versteht man die Menge aller Tupel {(m 1,..., m t ) m 1 M 1,..., m t M t } mit der Addition (m 1,..., m t ) + (n 1,..., n t ) = (m 1 + n 1,..., m t + n t ) und der Abbildung R (M 1... M t ) M 1... M t (r, (m 1,..., m t )) (r m 1,..., r m t ) Seien M 1,..., M t M Untermoduln. Man sagt M ist die direkte Summe der M i und schreibt M = M 1... M t, falls M 1... M t M (m 1,..., m t ) m m t ein Isomorphismus ist R heiÿt Integritätsbereich, falls R keine Nullteiler hat, d.h. r 1 r 2 = 0 r 1 = 0 r 2 = 0. Lemma Sei R Integritätsbereich, betrachte R als Modul über sich selbst. Dann ist R unzerlegbar Sei R Integritätsbereich. Eine Gröÿenfunktion oder Betragsfunktion auf R \ {0} ist eine Abbildung S : R \ {0} N Ein Integritätsbereich mit Gröÿenfunktion heiÿt euklidischer Ring, falls es einen Divisionsalgorithmus gibt mit a, b R, a 0 : q, r R mit a = qb + r wobei entweder r = 0 oder r 0 mit S (r) < S (b). Satz Ein euklidischer Ring ist ein Hauptidealring, d.h. I Ideal in R gibt es ein f I mit I = {rf r R}. 14
Klausur zur Vorlesung Lineare Algebra II
 Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
T := {σ S 4 σ 3 = Id}. a) Es seien V ein Vektorraum und Φ ein Endomorphismus von V, sodass
 I. a) Es sei (G, ) eine abelsche Gruppe mit neutralem Element e G. Zeigen Sie, dass U := {g G g 3 = e G } eine Untergruppe von G ist. b) In der symmetrischen Gruppe S 4 definieren wir analog zu a) die
I. a) Es sei (G, ) eine abelsche Gruppe mit neutralem Element e G. Zeigen Sie, dass U := {g G g 3 = e G } eine Untergruppe von G ist. b) In der symmetrischen Gruppe S 4 definieren wir analog zu a) die
Lineare Algebra II (SS 13)
 Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
Lineare Algebra II (SS 13) Bernhard Hanke Universität Augsburg 03.07.2013 Bernhard Hanke 1 / 16 Selbstadjungierte Endomorphismen und der Spektralsatz Definition Es sei (V,, ) ein euklidischer oder unitärer
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.3 Unitäre Operatoren
 Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Wiederholungsserie II
 Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
 Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Universität Bielefeld Sommersemester Lineare Algebra 2 Übungsblatt 1
 Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
Musterlösungen zur Linearen Algebra II Hauptklausur
 Musterlösungen zur Linearen Algebra II Hauptklausur Aufgabe. Q ist unitär genau dann, wenn gilt Q Q = I n. Daraus folgt, dass a) und c) richtig sind. Die -Matrix A := (i) zeigt, dass i.a. A A t, d.h. b)
Musterlösungen zur Linearen Algebra II Hauptklausur Aufgabe. Q ist unitär genau dann, wenn gilt Q Q = I n. Daraus folgt, dass a) und c) richtig sind. Die -Matrix A := (i) zeigt, dass i.a. A A t, d.h. b)
6 Hauptachsentransformation
 6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
1. Übungsblatt: Lineare Algebra II Abgabe: 24./ in den Übungsgruppen
 Hannover, den 0. April 2006. Übungsblatt: Lineare Algebra II Abgabe: 24./25.4.2006 in den Übungsgruppen ( ) 2 5 a) Zeigen Sie, dass A = und B = 2 ( 7 6 invertierbare Matrix T an mit T AT = B. b) Zeigen
Hannover, den 0. April 2006. Übungsblatt: Lineare Algebra II Abgabe: 24./25.4.2006 in den Übungsgruppen ( ) 2 5 a) Zeigen Sie, dass A = und B = 2 ( 7 6 invertierbare Matrix T an mit T AT = B. b) Zeigen
Lineare Algebra I Ferienblatt
 Wintersemester 09/0 Prof. Dr. Frank-Olaf Schreyer Dr. Janko Boehm Lineare Algebra I Ferienblatt. Sei, das Euklidische Skalarprodukt auf R. Das Kreuzprodukt a b von Vektoren a, b R ist durch die Formel
Wintersemester 09/0 Prof. Dr. Frank-Olaf Schreyer Dr. Janko Boehm Lineare Algebra I Ferienblatt. Sei, das Euklidische Skalarprodukt auf R. Das Kreuzprodukt a b von Vektoren a, b R ist durch die Formel
9 Vektorräume mit Skalarprodukt
 9 Skalarprodukt Pink: Lineare Algebra 2014/15 Seite 79 9 Vektorräume mit Skalarprodukt 9.1 Normierte Körper Sei K ein Körper. Definition: Eine Norm auf K ist eine Abbildung : K R 0, x x mit den folgenden
9 Skalarprodukt Pink: Lineare Algebra 2014/15 Seite 79 9 Vektorräume mit Skalarprodukt 9.1 Normierte Körper Sei K ein Körper. Definition: Eine Norm auf K ist eine Abbildung : K R 0, x x mit den folgenden
1. Übungsblatt: Lineare Algebra II Abgabe: 8./ in den Übungsgruppen
 Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
4.3 Bilinearformen. 312 LinAlg II Version Juni 2006 c Rudolf Scharlau
 312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II
 Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II Matrizen, lineare Gleichungssysteme Wie kommt man von einem linearen Gleichungssystem zu einer Matrix? Was ist die Zeilenstufenform?
Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II Matrizen, lineare Gleichungssysteme Wie kommt man von einem linearen Gleichungssystem zu einer Matrix? Was ist die Zeilenstufenform?
Kapitel 11. Bilinearformen über beliebigen Bilinearformen
 Kapitel 11 Bilinearformen über beliebigen Körpern Wir können in diesem Kapitel rasch vorgehen, weil die meisten Konzepte im Zusammenhang mit Sesquilinearformen bereits eingeführt wurden. In diesem Abschnitt
Kapitel 11 Bilinearformen über beliebigen Körpern Wir können in diesem Kapitel rasch vorgehen, weil die meisten Konzepte im Zusammenhang mit Sesquilinearformen bereits eingeführt wurden. In diesem Abschnitt
4 Bilinearformen und Skalarprodukte
 4 Bilinearformen und Skalarprodukte 4 Grundlagen über Bilinearformen Definition 4 Sei V ein K-Vektorraum Eine Bilinearform b auf V ist eine Abbildung b : V V K mit folgenden Eigenschaften: (B) x, y, z
4 Bilinearformen und Skalarprodukte 4 Grundlagen über Bilinearformen Definition 4 Sei V ein K-Vektorraum Eine Bilinearform b auf V ist eine Abbildung b : V V K mit folgenden Eigenschaften: (B) x, y, z
Lineare Algebra II. Inhalt und Begriffe. Lineare Algebra II p. 1
 Lineare Algebra II Inhalt und Begriffe Lineare Algebra II p. 1 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen Algebra... Lineare Algebra II p. 2 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen
Lineare Algebra II Inhalt und Begriffe Lineare Algebra II p. 1 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen Algebra... Lineare Algebra II p. 2 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen
Klausurenkurs zum Staatsexamen (SS 2016): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
Lineare Algebra I für Mathematiker Lösungen
 Lineare Algebra I für Mathematiker Lösungen Anonymous 24. April 2016 Aufgabe 1 Beantworten Sie bitte die folgenden Fragen. Jeder Vektorraum hat mindestens ein Element. Q ist ein R-Vektorraum (mit der Multiplikation
Lineare Algebra I für Mathematiker Lösungen Anonymous 24. April 2016 Aufgabe 1 Beantworten Sie bitte die folgenden Fragen. Jeder Vektorraum hat mindestens ein Element. Q ist ein R-Vektorraum (mit der Multiplikation
Skalarprodukte. Kapitel Bilinearformen
 Kapitel 11 Skalarprodukte Das bekannte Skalarprodukt auf dem n dimensionalen Euklidischen Raum R n ist ein Spezialfall einer für viele Bereiche der linearen Algebra und der Funktionalanalysis außerordentlich
Kapitel 11 Skalarprodukte Das bekannte Skalarprodukt auf dem n dimensionalen Euklidischen Raum R n ist ein Spezialfall einer für viele Bereiche der linearen Algebra und der Funktionalanalysis außerordentlich
Prüfung Lineare Algebra 2
 1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
Sommer 2017 Musterlösung
 Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
Klausurenkurs zum Staatsexamen (SS 2016): Lineare Algebra und analytische Geometrie 6
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Übungen zur Vorlesung Lineare Algebra
 Übungen zur Vorlesung Lineare Algebra Institut für Reine Mathematik WS 2009/10 & SS 2010 Kapitel 1. Vektorräume Was ist ein Vektorraum? Sei X und K ein Körper. Wie macht man Abb (X, K) zu einem K -Vektorraum?
Übungen zur Vorlesung Lineare Algebra Institut für Reine Mathematik WS 2009/10 & SS 2010 Kapitel 1. Vektorräume Was ist ein Vektorraum? Sei X und K ein Körper. Wie macht man Abb (X, K) zu einem K -Vektorraum?
Lösungsskizzen zur Klausur zur Linearen Algebra II. Definitionen
 Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 34 Die Diagonalisierbarkeit von Isometrien im Komplexen Satz 34.1. Es sei V ein endlichdimensionaler C-Vektorraum
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 34 Die Diagonalisierbarkeit von Isometrien im Komplexen Satz 34.1. Es sei V ein endlichdimensionaler C-Vektorraum
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Probeklausur zur Linearen Algebra II
 Probeklausur zur Linearen Algebra II Prof. Dr. C. Löh/D. Fauser/J. Witzig 24. Juli 207 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle
Probeklausur zur Linearen Algebra II Prof. Dr. C. Löh/D. Fauser/J. Witzig 24. Juli 207 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle
Lineare Algebra und analytische Geometrie II
 Prof Dr H Brenner Osnabrück SS 26 Lineare Algebra und analytische Geometrie II Vorlesung 2 Orthogonalität Mit dem Skalarprodukt kann man die Eigenschaft zweier Vektoren, aufeinander senkrecht zu stehen,
Prof Dr H Brenner Osnabrück SS 26 Lineare Algebra und analytische Geometrie II Vorlesung 2 Orthogonalität Mit dem Skalarprodukt kann man die Eigenschaft zweier Vektoren, aufeinander senkrecht zu stehen,
Steilkurs Lineare Algebra 1 einige wichtige Stationen
 Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
8 Eigenwerttheorie I 8. EIGENWERTTHEORIE I 139. Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet:
 8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
8. EIGENWERTTHEORIE I 139 8 Eigenwerttheorie I Wir hatten bereits früher den Polynomring in einer Variablen über einem Körper K betrachtet: K[x] = Abb[N, K] = {P ; P = a n x n + a n 1 x n 1 + + a 0 ; a
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld. Clicker Fragen
 D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 6
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 6 6. (Herbst, Thema, Aufgabe 4) Der Vektorraum R 4 sei mit dem Standard Skalarprodukt versehen. Der Unterraum
Basisprüfung. 18. August 2015
 Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall
 44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
Lineare Algebra für PhysikerInnen
 Universität Wien, SS 2015 Lineare Algebra für PhysikerInnen Beispiele für Multiple-Choice-Fragen Punkteschlüssel: [Typ 1 aus 4] und [Typ 3 aus 4]... 0.8 Punkte [Typ 2 aus 4]... 1 Punkt Bei der schriftlichen
Universität Wien, SS 2015 Lineare Algebra für PhysikerInnen Beispiele für Multiple-Choice-Fragen Punkteschlüssel: [Typ 1 aus 4] und [Typ 3 aus 4]... 0.8 Punkte [Typ 2 aus 4]... 1 Punkt Bei der schriftlichen
a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
 Aufgabe (8 Punkte) Es sei (G, ) eine Gruppe und ϕ: G G die Abbildung, die für jedes g G durch ϕ(g) = g g =: g gegeben ist. a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
Aufgabe (8 Punkte) Es sei (G, ) eine Gruppe und ϕ: G G die Abbildung, die für jedes g G durch ϕ(g) = g g =: g gegeben ist. a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
Mathematik II. Vorlesung 46. Der Gradient
 Prof. Dr. H. Brenner Osnabrück SS 2010 Mathematik II Vorlesung 46 Der Gradient Lemma 46.1. Es sei K ein Körper und V ein K-Vektorraum, der mit einer Bilinearform, versehen sei. Dann gelten folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2010 Mathematik II Vorlesung 46 Der Gradient Lemma 46.1. Es sei K ein Körper und V ein K-Vektorraum, der mit einer Bilinearform, versehen sei. Dann gelten folgende Aussagen
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
17. Orthogonalsysteme
 17. Orthogonalsysteme 17.1. Winkel und Orthogonalität Vorbemerkung: Sei V ein Vektorraum mit Skalaprodukt, und zugehöriger Norm, dann gilt nach Cauchy-Schwarz: x, y V \ {0} : x, y x y 1 Definition: (a)
17. Orthogonalsysteme 17.1. Winkel und Orthogonalität Vorbemerkung: Sei V ein Vektorraum mit Skalaprodukt, und zugehöriger Norm, dann gilt nach Cauchy-Schwarz: x, y V \ {0} : x, y x y 1 Definition: (a)
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 39 Definitheit von Bilinearformen Wir möchten die symmetrischen Bilinearformen über den reellen Zahlen klassifizieren.
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 39 Definitheit von Bilinearformen Wir möchten die symmetrischen Bilinearformen über den reellen Zahlen klassifizieren.
Lineare Algebra 2 (SS 13) Blatt 13: Musterlösung
 Prof. Dr. B. Hanke Dr. J. Bowden Lineare Algebra 2 (SS ) Blatt : Musterlösung Aufgabe. Es sei C (R) der R-Vektorraum der unendlich oft differenzierbaren Funktionen auf R und : C (R) C (R), f f die Abbildung,
Prof. Dr. B. Hanke Dr. J. Bowden Lineare Algebra 2 (SS ) Blatt : Musterlösung Aufgabe. Es sei C (R) der R-Vektorraum der unendlich oft differenzierbaren Funktionen auf R und : C (R) C (R), f f die Abbildung,
4.2 Die adjungierte Abbildung
 4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
Inhalt der Vorlesung Algebraische Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017
 Inhalt der Vorlesung Algebraische Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel II. Moduln 1 Moduln Sei R ein Ring (stets kommutativ und mit 1). 1.1 Definition. 1. Ein R-(links-)Modul ist
Inhalt der Vorlesung Algebraische Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel II. Moduln 1 Moduln Sei R ein Ring (stets kommutativ und mit 1). 1.1 Definition. 1. Ein R-(links-)Modul ist
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra I Zusammenfassung
 Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prüfung Lineare Algebra Sei V ein n-dimensionaler euklidischer Raum. Welche der folgenden Aussagen ist wahr?
 1. Sei V ein n-dimensionaler euklidischer Raum. Welche der folgenden Aussagen ist wahr? A. Wenn n = 3 ist, sind mindestens zwei der drei Euler-Winkel einer Drehung kleiner oder gleich π. B. Wenn n = 2
1. Sei V ein n-dimensionaler euklidischer Raum. Welche der folgenden Aussagen ist wahr? A. Wenn n = 3 ist, sind mindestens zwei der drei Euler-Winkel einer Drehung kleiner oder gleich π. B. Wenn n = 2
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Mathematik I. Vorlesung 18. Vielfachheiten und diagonalisierbare Abbildungen. µ λ = dim(eig λ (ϕ))
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 18 Vielfachheiten und diagonalisierbare Abbildungen Satz 18.1. Es sei K ein Körper und es sei V ein endlichdimensionaler K- Vektorraum.
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 18 Vielfachheiten und diagonalisierbare Abbildungen Satz 18.1. Es sei K ein Körper und es sei V ein endlichdimensionaler K- Vektorraum.
Analysis II. Vorlesung 48. Die Hesse-Form
 Prof. Dr. H. Brenner Osnabrück SS 2015 Analysis II Vorlesung 48 Die Hesse-Form Wir sind natürlich auch an hinreichenden Kriterien für das Vorliegen von lokalen Extrema interessiert. Wie schon im eindimensionalen
Prof. Dr. H. Brenner Osnabrück SS 2015 Analysis II Vorlesung 48 Die Hesse-Form Wir sind natürlich auch an hinreichenden Kriterien für das Vorliegen von lokalen Extrema interessiert. Wie schon im eindimensionalen
1 Euklidische und unitäre Vektorräume
 1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008
 KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
4 Orthogonale Endormorphismen
 4 Orthogonale Endormorphismen Frage: Bei welchen Abbildungen R R bzw. R 3 R 3 bleibt der Abstand zwischen zwei Punkten erhalten? Für α R setzen wir cosα sin α D(α) = und S(α) := sin α cosα ( cos α sin
4 Orthogonale Endormorphismen Frage: Bei welchen Abbildungen R R bzw. R 3 R 3 bleibt der Abstand zwischen zwei Punkten erhalten? Für α R setzen wir cosα sin α D(α) = und S(α) := sin α cosα ( cos α sin
Euklidische und unitäre Vektorräume
 Euklidische und unitäre Vektorräume In allgemeinen Vektorräumen gibt es keine Möglichkeit der Längenmessung von Vektoren und der Winkelmessung zwischen zwei Vektoren. Dafür ist eine zusätzliche Struktur
Euklidische und unitäre Vektorräume In allgemeinen Vektorräumen gibt es keine Möglichkeit der Längenmessung von Vektoren und der Winkelmessung zwischen zwei Vektoren. Dafür ist eine zusätzliche Struktur
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Linear- und Bilinearformen
 Linear- und Bilinearformen Robert Wisbauer 3. Februar 2006 Inhaltsverzeichnis 1 Linearformen 2 2 Bilinearformen 6 3 Orthogonalität 12 4 Vektorräume mit Skalarprodukt 15 5 Isometrien 23 1 1. Linearformen
Linear- und Bilinearformen Robert Wisbauer 3. Februar 2006 Inhaltsverzeichnis 1 Linearformen 2 2 Bilinearformen 6 3 Orthogonalität 12 4 Vektorräume mit Skalarprodukt 15 5 Isometrien 23 1 1. Linearformen
Tagesablauf. Allgemeine Organisation. Programm des Kompaktseminars
 Kompaktseminar Werbellinsee Sept. 2008 1 Tagesablauf 9:00 Frühstück 9:30-13:00 Erste Sitzung (mit Pausen nach Bedarf) 13:00 Mittagessen 14:30-19:00 Zweite Sitzung (mit Pausen nach Bedarf) 19:00 Abendessen
Kompaktseminar Werbellinsee Sept. 2008 1 Tagesablauf 9:00 Frühstück 9:30-13:00 Erste Sitzung (mit Pausen nach Bedarf) 13:00 Mittagessen 14:30-19:00 Zweite Sitzung (mit Pausen nach Bedarf) 19:00 Abendessen
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10)
 Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen
 Technische Universität München Department of Physics Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen Freitag, 16.03.2012 Sascha Frölich Ferienkurs Lin. Alg. -
Technische Universität München Department of Physics Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen Freitag, 16.03.2012 Sascha Frölich Ferienkurs Lin. Alg. -
Lineare Algebra, Analytische Geometrie II
 Skript Lineare Algebra, Analytische Geometrie II gehört bei Prof. Dr. Annette Huber-Klawitter Universität Leipzig Stand: 27. November 26 Zusammengestellt von Marcel Dennhardt Dieses Skript fasst die Mitschriften
Skript Lineare Algebra, Analytische Geometrie II gehört bei Prof. Dr. Annette Huber-Klawitter Universität Leipzig Stand: 27. November 26 Zusammengestellt von Marcel Dennhardt Dieses Skript fasst die Mitschriften
2 Euklidische Vektorräume
 Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Kontrollfragen und Aufgaben zur 3. Konsultation
 1 Technische Universität Ilmenau Fakultät für Mathematik und Naturwissenschaften Institut für Mathematik Prof. Dr. Michael Stiebitz Kontrollfragen und Aufgaben zur 3. Konsultation Termin: Ort: Determinante
1 Technische Universität Ilmenau Fakultät für Mathematik und Naturwissenschaften Institut für Mathematik Prof. Dr. Michael Stiebitz Kontrollfragen und Aufgaben zur 3. Konsultation Termin: Ort: Determinante
Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum
 Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Analytische Geometrie
 21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
Leitfaden 34. , dies ist eine reelle symmetrische Matrix, also diagonalisierbar.
 Leitfaden 34 5. Euklidsche und unitäre Räume (und selbstadjungierte, orthogonale, unitäre, normale Endomorphismen). 5.1. Reelle symmetrische Matrizen sind diagonalisierbar. Satz: Reelle symmetrische Matrizen
Leitfaden 34 5. Euklidsche und unitäre Räume (und selbstadjungierte, orthogonale, unitäre, normale Endomorphismen). 5.1. Reelle symmetrische Matrizen sind diagonalisierbar. Satz: Reelle symmetrische Matrizen
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 11. Übung: Woche vom
 Übungsaufgaben 11. Übung: Woche vom 9. 1.-13. 1. 2017 (Numerik): Heft Ü 1: 12.28.a,b; 12.29.b,c (jeweils mit Fehlerabschätzung); 6.26; 6.27.a (auch mit Lagrange-Interpolationspolynom); 6.25; 6.28 (auch
Übungsaufgaben 11. Übung: Woche vom 9. 1.-13. 1. 2017 (Numerik): Heft Ü 1: 12.28.a,b; 12.29.b,c (jeweils mit Fehlerabschätzung); 6.26; 6.27.a (auch mit Lagrange-Interpolationspolynom); 6.25; 6.28 (auch
Eigenwerte und Diagonalisierung
 Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 0/06 Lineare Algebra und analytische Geometrie I Vorlesung... und ein guter Lehrer kann auch einem schlechten Schüler was beibringen Beziehung zwischen Eigenräumen Wir
Prof. Dr. H. Brenner Osnabrück WS 0/06 Lineare Algebra und analytische Geometrie I Vorlesung... und ein guter Lehrer kann auch einem schlechten Schüler was beibringen Beziehung zwischen Eigenräumen Wir
Richie Gottschalk Lineare Algebra I Seite 1. a) Welche der folgenden Ringe sind kommutativ? Es gibt genau einen Unterraum W von V mit dim(w ) = n.
 Richie Gottschalk Lineare Algebra I Seite Aufgabe Im Folgenden sind K immer ein Körper und V ein K-Vektorraum. a) Welche der folgenden Ringe sind kommutativ? K[x] K[x] ist per se ein kommutativer Polynomring.
Richie Gottschalk Lineare Algebra I Seite Aufgabe Im Folgenden sind K immer ein Körper und V ein K-Vektorraum. a) Welche der folgenden Ringe sind kommutativ? K[x] K[x] ist per se ein kommutativer Polynomring.
Euklidische und unitäre Vektorräume
 Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Lineare Algebra II Zwischentest
 Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
Lineare Algebra II Lösungen zu ausgewählten Aufgaben
 Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Lineare Algebra Weihnachtszettel
 Lineare Algebra Weihnachtszettel 0..08 Die Aufgaben auf diesem Zettel sind zum Üben während der Weihnachtspause gedacht, sie dienen der freiwilligen Selbstkontrolle. Die Aufgaben müssen nicht bearbeitet
Lineare Algebra Weihnachtszettel 0..08 Die Aufgaben auf diesem Zettel sind zum Üben während der Weihnachtspause gedacht, sie dienen der freiwilligen Selbstkontrolle. Die Aufgaben müssen nicht bearbeitet
Klausur zur Vorlesung Lineare Algebra B im SS 2002 an der Universität Hannover
 Dozent: Prof. Dr. Wolfgang Ebeling Übungsleiter: Dr. Detlef Wille Klausur zur Vorlesung Lineare Algebra B im SS an der Universität Hannover Joachim Selke 9. Februar Lineare Algebra B SS Klausur zur Vorlesung
Dozent: Prof. Dr. Wolfgang Ebeling Übungsleiter: Dr. Detlef Wille Klausur zur Vorlesung Lineare Algebra B im SS an der Universität Hannover Joachim Selke 9. Februar Lineare Algebra B SS Klausur zur Vorlesung
Sesqui- und Bilinearformen
 Kapitel 8 Sesqui- und Bilinearformen 8.1 Sesquilinearformen Definition 8.1.1 Sei V ein reeller oder komplexer K-Vektorraum (also K = R oder C). Eine Abbildung f : V V K heißt eine Sesquilinearform wenn
Kapitel 8 Sesqui- und Bilinearformen 8.1 Sesquilinearformen Definition 8.1.1 Sei V ein reeller oder komplexer K-Vektorraum (also K = R oder C). Eine Abbildung f : V V K heißt eine Sesquilinearform wenn
2. Isotropie. Beweis: (i) (ii): β U ist nicht ausgeartet. U U = {0} (ii) (iii): β U ist nicht ausgeartet. Da β nicht ausgeartet ist, gilt U = U:
 2. Isotropie Im folgenden sei V ein K-Vektorraum der Dimension n. Es sei q eine quadratische Form darüber und β die zugehörige symmetrische Bilinearform. Zudem gelte in K: 1 + 1 0. Notation 2.0: Wir nennen
2. Isotropie Im folgenden sei V ein K-Vektorraum der Dimension n. Es sei q eine quadratische Form darüber und β die zugehörige symmetrische Bilinearform. Zudem gelte in K: 1 + 1 0. Notation 2.0: Wir nennen
VII.2. INNERE PRODUKTE 227
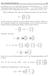 VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
Proseminar Lineare Algebra II, SS 11. Blatt
 Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Lineare Algebra II Zwischentest
 Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG
 KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lineare Algebra Klausur 2
 Lineare Algebra Klausur 2 (24.9.2015 Dozent: Ingo Runkel) Name Vorname Matrikelnr. Anweisungen: Hilfsmittel: Für die Bearbeitung sind nur Stift und Papier erlaubt. Benutzen Sie einen permanenten Stift
Lineare Algebra Klausur 2 (24.9.2015 Dozent: Ingo Runkel) Name Vorname Matrikelnr. Anweisungen: Hilfsmittel: Für die Bearbeitung sind nur Stift und Papier erlaubt. Benutzen Sie einen permanenten Stift
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 33 Das Kreuzprodukt Eine Besonderheit im R 3 ist das sogenannte Kreuzprodukt, das zu zwei gegebenen Vektoren
Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 33 Das Kreuzprodukt Eine Besonderheit im R 3 ist das sogenannte Kreuzprodukt, das zu zwei gegebenen Vektoren
5 Lineare Abbildungen
 5 Lineare Abbildungen Pink: Lineare Algebra 2014/15 Seite 59 5 Lineare Abbildungen 5.1 Definition Gegeben seien Vektorräume U, V, W über einem Körper K. Definition: Eine Abbildung f : V W heisst K-linear,
5 Lineare Abbildungen Pink: Lineare Algebra 2014/15 Seite 59 5 Lineare Abbildungen 5.1 Definition Gegeben seien Vektorräume U, V, W über einem Körper K. Definition: Eine Abbildung f : V W heisst K-linear,
Lineare Algebra I/II LVA ,
 Lineare Algebra I/II LVA 401-1151-00,401-1152-00 Prof. G. Wüstholz, C. Fuchs Lösungen zur Basisprüfung, HS08/FS09 09.02.2010 1. a) (1 Punkt) Wir beginnen mit dem charakteristischen Polynom der Matrix A:
Lineare Algebra I/II LVA 401-1151-00,401-1152-00 Prof. G. Wüstholz, C. Fuchs Lösungen zur Basisprüfung, HS08/FS09 09.02.2010 1. a) (1 Punkt) Wir beginnen mit dem charakteristischen Polynom der Matrix A:
Wiederholungsklausur zur Linearen Algebra II
 Wiederholungsklausur zur Linearen Algebra II Prof. Dr. C. Löh/D. Fauser/J. Witzig 5. Oktober 2017 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie,
Wiederholungsklausur zur Linearen Algebra II Prof. Dr. C. Löh/D. Fauser/J. Witzig 5. Oktober 2017 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie,
7 Lineare Abbildungen und Skalarprodukt
 Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
