a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung
|
|
|
- Carl Müller
- vor 5 Jahren
- Abrufe
Transkript
1 Aufgabe (8 Punkte) Es sei (G, ) eine Gruppe und ϕ: G G die Abbildung, die für jedes g G durch ϕ(g) = g g =: g gegeben ist. a) Zeigen Sie, dass ϕ genau dann ein Gruppenhomomorphismus ist, wenn die Verknüpfung in G kommutativ ist. b) Begründen Sie, weshalb im Fall G = {x R x > } (mit der Multiplikation als Verknüpfung) die Abbildung ϕ injektiv und surjektiv ist. c) Geben Sie ein Beispiel für eine kommutative Gruppe G an, für die ϕ injektiv, aber nicht surjektiv ist. d) Geben Sie ein Beispiel für eine kommutative Gruppe G an, für die ϕ nicht injektiv, aber surjektiv ist. Lösung: a) Laut Definition ist ϕ genau dann ein Homomorphismus, wenn für alle g,h G die Gleichung ϕ(g h) = ϕ(g) ϕ(h) gilt. Linker Hand steht (g h) = g h g h, rechter Hand steht g h. Es ist also ϕ genau dann ein Homomorphismus, wenn für alle g,h G die Gleichung g h g h = g h gilt. Dies ist gleichbedeutend zu (und jetzt lassen wir die Verknüpfungssymbole der Lesbarkeit wegen weg): hg = g (ghgh)h = g ( g h ) h = gh. Also ist ϕ genau dann ein Homomorphismus, wenn G kommutativ ist. b) Im gegebenen Fall ist die Abbildung injektiv, da Kern(ϕ) = {x R x >,x = } = {} nur das neutrale Element enthält. Surjektiv ist ϕ, da sich aus jeder positiven reellen Zahl eine positive Quadratwurzel ziehen lässt. c) Für die Gruppe G = {x Q x > } mit der üblichen Multiplikation ist ϕ mit dem Argument aus b) wieder injektiv. Es ist aber nicht surjektiv, da zum Beispiel die Quadratwurzel aus nicht rational ist. d) Für G = {x C x } mit der üblichen Multiplikation ist ϕ() = ϕ( ), also ϕ nicht injektiv. Es lässt sich aber aus jeder komplexen Zahl eine Quadratwurzel ziehen, denn für x = r(cosα+isinα),r >, α R, ist Daher ist ϕ surjektiv. x = ϕ ( r (cos(α/)+isin(α/)) ).
2 Aufgabe (8 Punkte) In Abhängigkeit von a R seien in R 4 die Vektoren a x := a,x := a gegeben.,x 3 := a a) Für welche Werte von a sind x,x,x 3 linear unabhängig? b) Für welche Werte von a gibt es einen Endomorphismus Φ: R 4 R 4 mit Φ(x ) = x, Φ(x ) = x, Φ(x 3 ) = x 3? Lösung: a) Die drei Vektoren sind genau dann linear unabhängig, wenn die Matrix a a a a Rang 3 hat. Wir führen das Gauß-Verfahren durch: a a a + a a + a a a + a a a + a a und sehen, dass x,x und x 3 genau dann linear unabhängig sind, wenn a gilt, also genau für a R\{, }. b) Wenn x,x,x 3 linear unabhängig sind, lassen sie sich zu einer Basis {x,x,x 3,x 4 } von R 4 ergänzen, und nach dem Satz von der Linearen Fortsetzung gibt es einen Endomorphismus von R 4, der die gewünschten Eigenschaften hat. In den anderen beiden Fällen a = ± sind x und x stets linear unabhängig, es gibt also mit dem eben durchgeführten Argument sicher einen Endomorphismus Φ mit Φ(x ) = x, Φ(x ) = x. Im Fall a = gilt x 3 = x +x, und es folgt Φ(x 3 ) = Φ( x +x ) = x +x = x 3 x 3. Im Fall a = gilt x 3 = x +x, und wir erhalten Φ(x 3 ) = Φ(x +x ) = x +x = x 3. Einen Endomorphismus mit den gewünschten Bildern gibt es also immer dann, wenn a, für a = hingegen nicht.
3 Aufgabe 3 (8 Punkte) Sei 3 A = R Bestimmen Sie a) eine Matrix C GL 3 (R), sodass T := C A Treppenform hat. b) die Menge L T aller Matrizen M R 3 3 mit M T =. c) die Menge L A aller Matrizen N R 3 3 mit N A =. d) die Menge L A,T aller Matrizen D R 3 3 mit D A = T. Lösung: a) Wir hängen rechts an A die Einheitsmatrix an und führen für diese neue Matrix das Gauß-Verfahren durch. Die rechten drei Spalten zeigen jeweils an, mit welcher Matrix A dabei mutlipliziert wurde. ( ) ( ) Die Matrix, die aus den ersten drei Spalten besteht, liegt nunmehr in Treppenform vor, wir erhalten T =, C = b) Wegen a b c a b b a d e f T = d e e d g h i f g g f ergibt sich sofort c L T = { f c,f,i R}. i c) Wegen NA = NC T ist c c c L A = {MC M L T } = { f f f c,f,i R}. i i i d) Wegen DA = T = CA (D C)A = gilt L A,T = {C +N N L A }.
4 Aufgabe 4 (8 Punkte) Seien K ein Körper, V ein endlichdimensionaler Vektorraum über K, V := Hom(V,K) sein Dualraum, B = {b,...,b n } eine Basis von V sowie B := {b,...,b n} die dazu duale Basis von V. Für v V sei Ψ(v): V K die Linearform auf V, die durch gegeben ist. a) Zeigen Sie: Die Abbildung ist linear und bijektiv. b) Zeigen Sie: l V : Ψ(v)(l) := l(v) Ψ: V V := Hom(V,K),v Ψ(v), {Ψ(b ),...,Ψ(b n )} ist die zu B duale Basis B von V. c) Bestimmen Sie die Darstellungsmatrix D B,B(Ψ). Lösung: a) Zu zeigen sind die Identitäten Ψ(v + v ) = Ψ(v ) + Ψ(v ) für beliebige Vektoren v,v V und Ψ(av) = aψ(v) für a K,v V. Das bedeutet, dass für beliebige Linearformen l V und v,v,v,a wie zuvor die Gleichungen gelten müssen. Ψ(v +v )(l) = (Ψ(v )+Ψ(v ))(l), sowie Ψ(av)(l) = a(ψ(v)(l)) Die erste bedeutet l(v +v ) = l(v )+l(v ), die zweite l(av) = a l(v). Beide gelten aufgrund der Vektorraumstruktur von V als Untervektorraum von Abb(V,K). Es ist Kern(Ψ) = {v V l V : l(v) = } = {}, denn für jedes v = n i= a ib i ist mindestens ein a i ungleich und damit Ψ(v)(b i). Da dim(v) = dim(v ) = dim(v ) gilt, folgt wegen der Dimensionsformel aus der Injektivität von Ψ auch die Surjektivität und damit die Bijektivität. b) Für i,j {,...,n} gilt Ψ(b i )(b j) = b j(b i ) = {, falls i = j,, sonst. Damit erfüllen die Linearformen Ψ(b ),...,Ψ(b n ) bezüglich der Basis B genau die definierenden Bedingungen der Dualbasis, also ist b i = Ψ(b i ). c) Da b i auf den i-ten Vektor der Basis B = {Ψ(b ),...,Ψ(b n )} abgebildet wird, ist D B,B(Ψ) die Einheitsmatrix.
5 Aufgabe 5 (8 Punkte) In Abhängigkeit von a R sei A R 4 4 die Matrix 3 4 A = a a 3a 4a+ Weiter sei Φ = Φ A : R 4 R 4 der Endomorphismus von R 4, der durch v Φ(v) := A v gegeben ist. a) Weisen Sie nach, dass ein Eigenwert von Φ ist, und bestimmen Sie die Dimension des zugehörigen Eigenraumes Eig(Φ, ). b) Wählen Sie eine Basis des Eigenraumes Eig(Φ, ) und ergänzen Sie diese zu einer Basis B von R 4. Bestimmen Sie dann die Abbildungsmatrix D B,B (Φ). c) Entscheiden Sie, für welche Werte von a der Endomorphismus Φ diagonalisierbar ist. Lösung: a) Die Matrix 3 4 A I 4 = a a 3a 4a hat Rang, da alle Zeilen Vielfache der ersten sind. Wegen der Dimensionsformel für Endomorphismen ist daher Eig(Φ,) = Kern(A I 4 ) dreidimensional, und damit ist ein Eigenwert, da der Eigenraum nicht der Nullraum ist. b) Es ist b :=, b := 3, b 3 := 4 eine Basis des Eigenraums, da die drei Vektoren im Eigenraum liegen und linear unabhängig sind. Diese wird zum Beispiel von b 4 := zu einer Basis B von R 4 ergänzt, denn b 4 liegt nicht im Eigenraum. Es gilt
6 Φ(b ) = b, Φ(b ) = b, Φ(b 3 ) = b 3, Φ(b 4 ) = A b 4 = = b +b +ab 3 +(7+4a)b 4 a und damit ist D B,B (Φ) = a. 7+4a c) Die Eigenwerte von Φ sind die Eigenwerte der Dreiecksmatrix D BB (Φ), also und 7+4a. Wenn 7 + 4a gilt, also falls a 3, dann gibt es neben dem Eigenwert mit einem dreidimensionalen Eigenraum noch einen weiteren Eigenwert, dessen Eigenraum dann eindimensional ist, Somit ist Φ in diesem Fall diagonalisierbar. Im Fall a = 3 ist der einzige Eigenwert von Φ, aber sein Eigenraum ist nicht alles. Also ist Φ in diesem Fall nicht diagonalisierbar.
7 Aufgabe 6 (8 Punkte) Für einen Körper K und < n N sei A K (n ) n eine Matrix von Rang n. Für einen Zeilenvektor z K n bezeichne ( A z) K n n die Matrix, die durch Anhängen von z als n-te Zeile an A entsteht. Zeigen Sie: a) Es gibt einen Spaltenvektor s = (s,...,s n ), sodass für jeden Zeilenvektor z = (z,...,z n ) gilt: ( ) A n det( ) = z i s i = z s. z b) Der Vektor s aus Teil a) ist durch die genannte Bedingung eindeutig bestimmt. c) Wenn z eine Zeile von A ist, dann erfüllt das s aus Teil a) die Gleichung z s =. d) Der Vektor s aus Teil a) erzeugt den Lösungsraum L(A, ) des linearen Gleichungssystems A x = als K-Vektorraum. i= Lösung: a) Dies folgt aus der Formel für die Laplace-Entwicklung nach der letzten Zeile. Für i {...,n} sei A i diematrix,dieaus A durchstreichender i-tenspalteentsteht, und s i := ( ) i+n deta i. Dann ist ( ) A n det( ) = z i s i, z i= was die Existenz des gesuchten Spaltenvektors zeigt. b) Die Eindeutigkeit von s folgt daraus, dass für i n die Gleichung ( ) A s i = e i s = det( ) gelten muss, wobei e i der i-te Standardbasisvektor ist. c) Für jede Zeile z von A hat ( A z) Rang < n, also gilt ( ) A z s = det( ) =. z d) Da A Rang n hat, ist L(A,) eindimensional. Der Vektor s liegt darin. Da sich die Zeilen von A durch eine geeignete Zeile z zu einer Basis von K n ergänzen lassen, gilt für dieses z ( ) A z s = det( ). z Daher ist s nicht der Nullvektor, und somit eine Basis des ihn enthaltenden eindimensionalen Vektorraums L(A, ). e i
8 Aufgabe II. Für einen reellen Parameter t R sei die Matrix 4 A t = t+4 R4 4 t gegeben. (a) Bestimmen Sie alle t R, für die A t ähnlich ist zur Matrix 3 B = 3 3 R4 4. (b) Berechnen Sie für t = 3 eine Matrix S R 4 4 mit der Eigenschaft B = S A 3 S. Lösungsvorschlag II. (a) Wir bestimmen zunächst die Eigenwerte von A t und berechnen dazu das charakteristische Polynom: 4 X p At = det(a t X E 4 ) = X t+4 X t X 4 X = (t X) X t+4 X = (t X)(t+4 X) 4 X X ( ) = (t X)(t+4 X) 8+6X+X + = (t X)(t+4 X)(3+ X). A t besitzt also die Eigenwerte t, t+4 und 3. Da B den Eigenwert 3 dreifach und den Eigenwert einfach besitzt, muss notwendigerweise {t, t + 4} = {, 3} gelten. Dies trifft genau für t = 3 zu. Die Jordansche Normalform von A 3 besitzt dann einen (3 3)-Jordanblock zum Eigenwert 3 und einen ( )-Jordanblock zum Eigenwert. Die Anzahl der Jordankästchen von A 3 zum Eigenwert 3 ist gleich der Dimension des Eigenraums zu 3. Diese wollen wir nun berechnen: dim ( ker(a 3 ( 3) E 4 ) ) ) ( = dim ker = dim ( ker 4 ) =.
9 Der Jordanblock zum Eigenwert 3 besteht also aus Jordankästchen; als (3 3)-Block kann es sich dabei nur um ein -er Kästchen und ein -er Kästchen handeln. Die Jordansche Normalform von A 3 ist damit gleich der Matrix B. Es folgt, dass A t genau für t = 3 ähnlich zur Matrix B ist. (b) Wir benötigen nun noch eine Jordanbasis. Für den Eigenraum zum Eigenwert 3 gilt nach (a) ker(a 3 ( 3) E 4 ) = ker [ =, ] Für den zweiten Kern erhalten wir ker(a 3 ( 3) E 4 ) = ker [ 4 =,, ] Offensichtlich liegt nicht im Eigenraum zum Eigenwert 3 und es gilt Somit ist (A 3 ( 3) E 4 ) =. {,, } die Teilbasis zum Jordanblock des Eigenwertes 3. Der Eigenraum zum Eigenwert berechnet sich zu 5 ker(a 3 E 4 ) = ker 3 [ = 4 Die gesuchte Matrix S ist daher gegeben durch S =. ].
10 Aufgabe II. Es seien (V,, ) ein endlich dimensionaler Vektorraum mit Skalarprodukt und {b, b,..., b n } eine Orthonormalbasis von V. Zeigen Sie: (a) Für alle x, y V gilt x, y = n i= x, b i b i, y. (b) Für n beliebige Vektoren c, c,..., c n V gilt c, b... c, b n det..... c, c... c, c n = det c n, b... c n, b n c n, c... c n, c n Lösungsvorschlag II. (a) Seien x, y V beliebig. Da {b, b,..., b n } eine Orthonormalbasis ist gilt nach der Fourierformel x = n i= x, b i b i, also dank der Eigenschaften des Skalarproduktes x, y = n i= (b) Für eine quadratische Matrix A gilt x, b i b i, y = n i= x, b i b i, y. det(a) = det(a) det(a) = det(a) det(a) = det(a) det(a ) = det(a A ). Mit c, b... c, b n A =..... c n, b... c n, b n berechnen wir c, b... c, b n c, b... c n, b A A = c n, b... c n, b n c, b n... c n, b n Seien nun i, j {,,..., n}. Für den Eintrag d ij der i-ten Zeile und j-ten Spalte der Matrix A A gilt dann d ij = n k= c i, b k c j, b k = n k= c i, b k b k, c j,
11 da das Skalarprodukt hermitesch ist. Nach Teil (a) folgt d ij = c i, c j und daher c, c... c, c n det(a) = det(a A ) = det....., c n, c... c n, c n was zu zeigen war.
12 Aufgabe II.3 Es sei (V,, ) ein endlich dimensionaler euklidischer Vektorraum. Weiter seien Φ, Ψ End(V) selbstadjungierte Endomorphismen von V. (a) Geben Sie die Definition für selbstadjungiert an. (b) Zeigen Sie, dass sowohl Φ+Ψ als auch Φ Ψ selbstadjungiert sind. (c) Zeigen Sie, dass die Bedingung bereits Φ = Ψ impliziert. Φ(v), v = Ψ(v), v für alle v V Lösungsvorschlag II.3 (a) Ein Endomorphismus Φ eines endlich dimensionalen euklidischen Vektorraums (V,, ) heißt selbstadjungiert, falls für alle v, w V die Bedingung erfüllt ist. Φ(v), w = v, Φ(w) (b) Wir zeigen allgemeiner, dass Φ + αψ für beliebiges α R selbstadjungiert ist, was mit α = und α = die gesuchte Aussage als Spezialfall impliziert. Zu zeigen ist für alle v, w V (Φ+αΨ)(v), w = v,(φ+αψ)(w). Es seien nun v, w V beliebig. Dann gilt (Φ+αΨ)(v), w = ( Φ(v)+αΨ(v) ), w = Φ(v), w +α Ψ(v), w = v, Φ(w) +α v, Ψ(w), da sowohl Φ als auch Ψ selbstadjungiert ist. Weiter folgt (Φ+αΨ)(v), w = v, ( Φ(w)+αΨ(w) ) = v,(φ+αψ)(w). (c) Wir wollen zeigen, dass unter der gegebenen Bedingung Φ = Ψ folgt, das heißt Φ(v) = Ψ(v) für alle v V. Dies ist äquivalent zu Φ(v), w = Ψ(v), w für alle v, w V, da der Nullvektor der einzige Vektor ist, der zu allen Vektoren in V orthogonal ist. Seien also v, w V beliebig. Aus der gegebenen Bedingung folgt = (Φ Ψ)(v+w), v+w = (Φ Ψ)(v), v + (Φ Ψ)(v), w + (Φ Ψ)(w), v + (Φ Ψ)(w), w }{{}}{{} = = = (Φ Ψ)(v), w + w,(φ Ψ)(v) = (Φ Ψ)(v), w, da Φ Ψ selbstadjungiert ist und wegen der Symmetrie des Skalarproduktes. Es folgt direkt die Behauptung.
13 Aufgabe II.4 Gegeben sei die Matrix 3 3 A = R (a) Zeigen Sie, dass die Abbildung Φ : R 3 R 3, x Ax euklidischen Standardraums (R 3,, ) ist. eine Isometrie des (b) Bestimmen Sie die euklidische Normalform à von A. (c) Geben Sie eine orthogonale Matrix S R 3 3 an, sodass S A S = Ã. Lösungsvorschlag II.4 (a) Φ ist genau dann eine Isometrie, wenn die Matrix A orthogonal ist, das heißt wenn A A = I 4 gilt. Dies prüft man durch Rechnung nach. (b) Zur Bestimmung der euklidischen Normalform berechnen wir zunächst das charakteristische Polynom von A: p A = det(a XI 3 ) = det ( 3 4X 3 3 4X 4 3 ) 3 4X 3 4X 3 = ( ) 3 det 3 4X X X 3 = ( ) 3 det 3 4X 4 4 4X 4 4X + = ( 3 4X 3 ) 3 det 3 4X 4 4 4X = ( ( ) ) 3( 4 4X) 3 4X det 4 3 4X = ( ) (X+ ) ( ( 3 4X) + 4 ) 4 = 6 (X+ ) (6X 6 3X+ 6) = (X+ )(X 3X+ ). A hat also den Eigenwert und, aufgefasst als unitäre Matrix in C 3 3, ein Paar 3 konjugiert komplexer Eigenwerte λ, λ C mit λ = + i = cos ω+ i sin ω.
14 Die euklidische Normalform à von A ist damit gegeben durch à = 3. 3 (c) Zur Bestimmung der orthogonalen Matrix S benötigen wir zunächst einen normierten Eigenvektor b zum Eigenwert. Dieser berechnet sich mit Hilfe des homogenen linearen Gleichungssystems (A+ I 3 ) ( 3+) + 3 zu ( 3+) 4 ( 3+) b =. Zur Berechnung der fehlenden beiden Vektoren b, b 3 in der gesuchten Orthonormalbasis können wir b als beliebigen Einheitsvektor im orthogonalen Komplement [b ] von [b ] wählen. Da dieses orthogonale Komplement Φ-invariant ist, gilt auch Ab [b ]. Da in [b ] keine Eigenvektoren von Φ liegen, sind b und Ab linear unabhängig. Konkret wähle man zum Beispiel b = ; dann folgt Ab = 3 4. Wir berechnen mit dem Gram-Schmidt-Verfahren nun eine Orthonormalbasis von [b ] = [{b, Ab }]. Der Vektor b3 = Ab Ab, b b = ist orthogonal zu b ; Normieren liefert b 3 =.
15 Um zu sehen, ob wir gegebenenfalls die Reihenfolge der Basisvektoren (b, b 3 ) von [b ] vertauschen müssen, überprüfen wir ob 3 Ab = b + b 3 gilt. Dies ist tatsächlich der Fall. Somit gilt für die orthogonale Matrix S = mit b, b, b 3 als Spaltenvektoren die Gleichung S A S = Ã.
16 Aufgabe II.5 Es seien V ein endlich dimensionaler unitärer Vektorraum und Φ End(V) ein Endomorphismus von V, sodass für die zu Φ adjungierte Abbildung Φ gilt: Φ = Φ. Zeigen Sie: (a) Es gilt Φ Φ = Φ Φ. (b) Für alle Eigenwerte λ von Φ gilt Re(λ) =. (c) Φ id V ist ein Isomorphismus. (d) (Φ id V ) (Φ+id V ) ist eine Isometrie. Hinweis zu (d): Sie dürfen ohne Beweis verwenden, dass V eine Orthonormalbasis aus Eigenvektoren von Φ besitzt. Lösungsvorschlag II.5 (a) Aufgrund der Voraussetzung ist Φ = Φ und daher Φ Φ = Φ ( Φ) = Φ Φ = ( Φ) Φ = Φ Φ. (b) Für beliebiges v V und λ C gilt Φ(v) λv, Φ(v) λv = Φ(v), Φ(v) λ v, Φ(v) λ Φ(v), v +λ λ v, v = Φ (v), Φ (v) λ Φ (v), v λ v, Φ (v) +λ λ v, v = Φ (v) λv, Φ (v) λv. Hierbei wurde die (vermutlich aus der Vorlesung bekannte) Gleichung Φ (v), Φ (v) = Φ(v), Φ(v) verwendet, die man direkt aus den Definitionen erhält: Φ (v), Φ (v) = v, Φ Φ (v) = v, Φ Φ(v) = Φ(v), Φ(v). Daher ist λ genau dann Eigenwert von Φ zum Eigenvektor v =, wenn λ Eigenwert von Φ zum Eigenvektor v = ist. Ist also λ Eigenwert von Φ zum Eigenvektor v =, so folgt (λ+ λ)v = Φ(v)+Φ (v) = Φ(v) Φ(v) =. Wegen v = erhält man λ+ λ =. Daher ist Re(λ) =. (c) Aus Teil (b) folgt, dass ± kein Eigenwert von Φ ist, also Kern(Φ±id V ) = {} gilt. Somit ist Φ±id V injektiv; da V endlich-dimensional ist, ist Φ±id V sogar bijektiv.
17 (d) Sei nun v ein Eigenvektor von Φ zum Eigenwert λ. Es folgt (Φ+id V )(v) = (λ+)v und (Φ id V )(v) = (λ )v. Die zweite Gleichung ergibt wegen λ = auch (Φ id V ) (v) = (Φ id V ) ( (λ ) (λ )v ) = (λ ) (Φ id V ) ( ) (λ )v = (λ ) v. }{{} =(Φ id V )(v) Zusammen erhält man für den Isomorphismus Ψ := (Φ id V ) (Φ+id V ) Ψ(v) = (Φ id V ) ((λ+)v) = (λ+)(φ id V ) (v) = λ+ λ v. Aus Teil (b) folgt λ = α i für ein α R, und daher ist λ+ λ = α i+ α i = α + α + =. Sei nun v,..., v n eine Orthonormalbasis von V aus Eigenvektoren von Φ mit zugehörigen Eigenwerten λ,..., λ n. Dann hat aber, wie eben gezeigt wurde, Ψ dieselben Eigenvektoren, und die zugehörigen Eigenwerte haben alle Betrag. Dies zeigt, dass Ψ eine lineare Isometrie ist.
18 Aufgabe II.6 Für a R 3 sei die Affinität φ a : R 3 R 3 gegeben durch φ a (x) = 5 4 x+a Ein Element x R 3 heißt Fixpunkt von φ a, falls φ a (x) = x gilt. (a) Geben Sie alle a R 3 an, so dass φ a mindestens einen Fixpunkt hat. Zeigen Sie, dass in diesen Fällen die Menge aller Fixpunkte eine Ebene E a ist. (b) Sei nun a =. Zeigen Sie: Sind P, Q R 3 keine Fixpunkte von φ a, so ist die Gerade durch P und φ a (P) parallel zu der Geraden durch Q und φ a (Q). Lösungsvorschlag II.6 (a) φ a hat einen Fixpunkt genau dann, wenn es ein x R 3 gibt mit φ a (x) = x, das heißt wenn das inhomogene LGS 4 4 a 4 4 x = a = a a 3 eine Lösung besitzt. Wegen 4 4 a a / 4 4 a a + a a 3 a 3 a hat dieses LGS nur dann eine Lösung, wenn a = a und a 3 = a gilt. x Sei nun X = x R 3 ein Fixpunkt von φ a für a = λ mit λ R. x 3 Dann dürfen x = s R und x 3 = t R beliebig gewählt werden, und es muss gelten x = λ x x 3 = λ s t. Die Fixpunktmenge ist also gegeben durch λ/ E a = {X = +s +t s, t R}. Dies ist offensichtlich eine Ebene in A 3 (R).
19 (b) Sei P = p p p 3 ein Punkt außerhalb der Fixpunktmenge von φ a. Die Gerade durch P und φ a (P) hat die Richtung 4 4 p φ a (P) P = 4 4 p p 3 = (p + 4p + 4p 3 ) + = (p + 4p + 4p 3 ),. Dabei gilt p + 4p + 4p 3 =, da P kein Fixpunkt ist. Jede solche Gerade ist also parallel zum Vektor. Die behauptete Aussage folgt nun, da P ein beliebiger Punkt war, der nicht von φ a fixiert wird.
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
a) Die Abbildung µ h ist injektiv, da für alle g 1, g 2 G gilt: Daher ist µ h bijektiv. Zudem folgt aus µ h (g) = g auch
 Aufgabe. (8 Punkte) Es sei (G, ) eine Gruppe und e G ihr neutrales Element. Für h G sei µ h : G G die Abbildung, die durch g G : µ h (g) := h g gegeben ist. a) Zeigen Sie, dass für jedes h G die Abbildung
Aufgabe. (8 Punkte) Es sei (G, ) eine Gruppe und e G ihr neutrales Element. Für h G sei µ h : G G die Abbildung, die durch g G : µ h (g) := h g gegeben ist. a) Zeigen Sie, dass für jedes h G die Abbildung
a) Ein Gruppenhomomorphismus von G nach H ist eine Abbildung Φ : G H, sodass für alle g 1, g 2 G die Gleichung Φ(g 1 g 2 ) = Φ(g 1 ) Φ(g 2 )
 I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
Lineare Algebra und Analytische Geometrie I für die Fachrichtung Informatik
 Universität Karlsruhe (TH) Institut für Algebra und Geometrie Dr. Klaus Spitzmüller Dipl.-Inform. Wolfgang Globke Lineare Algebra und Analytische Geometrie I für die Fachrichtung Informatik Lösungen zum
Universität Karlsruhe (TH) Institut für Algebra und Geometrie Dr. Klaus Spitzmüller Dipl.-Inform. Wolfgang Globke Lineare Algebra und Analytische Geometrie I für die Fachrichtung Informatik Lösungen zum
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
Lösungsvorschlag zur LA-Klausur vom
 I. (4 Punkte) Lösungsvorschlag zur LA-Klausur vom 7.03.008 Es sei M eine Menge mit zwei Verknüpfungen und. Weiter gebe es ein Element e M, das sowohl für als auch für neutrales Element ist. Schließlich
I. (4 Punkte) Lösungsvorschlag zur LA-Klausur vom 7.03.008 Es sei M eine Menge mit zwei Verknüpfungen und. Weiter gebe es ein Element e M, das sowohl für als auch für neutrales Element ist. Schließlich
Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 2015
 sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
Aufgabe I.1 (4 Punkte) Gegeben seien die Matrix H := und die Menge L := {A R 4 4 A HA = H} Zeigen Sie:
 Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
T := {σ S 4 σ 3 = Id}. a) Es seien V ein Vektorraum und Φ ein Endomorphismus von V, sodass
 I. a) Es sei (G, ) eine abelsche Gruppe mit neutralem Element e G. Zeigen Sie, dass U := {g G g 3 = e G } eine Untergruppe von G ist. b) In der symmetrischen Gruppe S 4 definieren wir analog zu a) die
I. a) Es sei (G, ) eine abelsche Gruppe mit neutralem Element e G. Zeigen Sie, dass U := {g G g 3 = e G } eine Untergruppe von G ist. b) In der symmetrischen Gruppe S 4 definieren wir analog zu a) die
Lösungsskizzen zur Klausur zur Linearen Algebra II. Definitionen
 Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
Technische Universität Berlin Sommersemester 2008 Institut für Mathematik 18 Juli 2008 Prof Dr Stefan Felsner Andrea Hoffkamp Lösungsskizzen zur Klausur zur Linearen Algebra II Aufgabe 1 (1+1+1 Punkte)
Zeigen Sie, dass der einzige Gruppenhomomorphismus von (G, ) nach (Z 5, +) die Abbildung Φ : G Z 5
 Aufgabe I (4 Punkte) Es sei G : {e, g, g, g } eine 4-elementige Gruppe mit neutralem Element e Die Verknüpfung auf G werde mit bezeichnet Außerdem seien in G folgende Gleichungen erfüllt: g g g und g g
Aufgabe I (4 Punkte) Es sei G : {e, g, g, g } eine 4-elementige Gruppe mit neutralem Element e Die Verknüpfung auf G werde mit bezeichnet Außerdem seien in G folgende Gleichungen erfüllt: g g g und g g
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Hinweis: Die Klausur Lineare Algebra 2 für die Fachrichtung Informatik besteht aus den Aufgaben 2.1 bis 2.4.
 Hinweis: Die Klausur Lineare Algebra 2 für die Fachrichtung Informatik besteht aus den Aufgaben 2.1 bis 2.4. Aufgabe 2.1 (8 Punkte) Es sei K ein Körper, n N, V ein 2n-dimensionaler K -Vektorraum und U
Hinweis: Die Klausur Lineare Algebra 2 für die Fachrichtung Informatik besteht aus den Aufgaben 2.1 bis 2.4. Aufgabe 2.1 (8 Punkte) Es sei K ein Körper, n N, V ein 2n-dimensionaler K -Vektorraum und U
Basisprüfung. 18. August 2015
 Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Lineare Algebra I/II D-MATH, HS 4/FS 5 Prof Richard Pink Basisprüfung 8 August 25 [6 Punkte] Betrachte den reellen Vektorraum R 3 zusammen mit dem Standardskalarprodukt, und die Vektoren 9 3 v := 6, v
Lösungsvorschläge zur Klausur. Lineare Algebra, Herbst 2010
 Lösungsvorschläge zur Klausur Lineare Algebra, Herbst 200 I. Es seien n eine natürliche Zahl, M = {,..., n} N und S n die Gruppe der Permutationen der Menge M. Zeigen Sie: a) Für jedes a M ist H a := {σ
Lösungsvorschläge zur Klausur Lineare Algebra, Herbst 200 I. Es seien n eine natürliche Zahl, M = {,..., n} N und S n die Gruppe der Permutationen der Menge M. Zeigen Sie: a) Für jedes a M ist H a := {σ
Steilkurs Lineare Algebra 1 einige wichtige Stationen
 Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Wiederholungsserie II
 Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
Lineare Algebra II D-MATH, FS 205 Prof. Richard Pink Wiederholungsserie II. Zeige durch Kopfrechnen, dass die folgende reelle Matrix invertierbar ist: 205 2344 234 990 A := 224 423 990 3026 230 204 9095
{ id, falls sgn(σ) = 1, τ, falls sgn(σ) = 1,
 Aufgabe I1 (4 Punkte) Es seien (G, ) und (H, ) Gruppen a) Wann heißt eine Abbildung Φ : G H ein Gruppenhomomorphismus? b) Es seien Φ, Ψ : G H zwei Gruppenhomomorphismen Zeigen Sie, dass eine Untergruppe
Aufgabe I1 (4 Punkte) Es seien (G, ) und (H, ) Gruppen a) Wann heißt eine Abbildung Φ : G H ein Gruppenhomomorphismus? b) Es seien Φ, Ψ : G H zwei Gruppenhomomorphismen Zeigen Sie, dass eine Untergruppe
Lineare Algebra I für Mathematiker Lösungen
 Lineare Algebra I für Mathematiker Lösungen Anonymous 24. April 2016 Aufgabe 1 Beantworten Sie bitte die folgenden Fragen. Jeder Vektorraum hat mindestens ein Element. Q ist ein R-Vektorraum (mit der Multiplikation
Lineare Algebra I für Mathematiker Lösungen Anonymous 24. April 2016 Aufgabe 1 Beantworten Sie bitte die folgenden Fragen. Jeder Vektorraum hat mindestens ein Element. Q ist ein R-Vektorraum (mit der Multiplikation
Klausurenkurs zum Staatsexamen (SS 2016): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
 Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
1 Die Jordansche Normalform
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
R 3 und U := [e 2, e 3 ] der von e 2, e 3 erzeugte
![R 3 und U := [e 2, e 3 ] der von e 2, e 3 erzeugte R 3 und U := [e 2, e 3 ] der von e 2, e 3 erzeugte](/thumbs/74/70162485.jpg) Aufgabe ( Es seien e =, e = Untervektorraum (, e = ( R und U := [e, e ] der von e, e erzeugte Weiter sei G := {A GL(, R A e = e und A U U} (a Zeigen Sie, dass G eine Untergruppe von GL(, R ist (b Geben
Aufgabe ( Es seien e =, e = Untervektorraum (, e = ( R und U := [e, e ] der von e, e erzeugte Weiter sei G := {A GL(, R A e = e und A U U} (a Zeigen Sie, dass G eine Untergruppe von GL(, R ist (b Geben
Lineare Algebra II Lösungen der Klausur
 Prof Dr K Doerk 673 Jens Mandavid Christian Sevenheck Lineare Algebra II Lösungen der Klausur (a Diese Aussage ist richtig, sie stimmt nämlich für k = Sei nämlich n N beliebig und bezeichne N die Menge
Prof Dr K Doerk 673 Jens Mandavid Christian Sevenheck Lineare Algebra II Lösungen der Klausur (a Diese Aussage ist richtig, sie stimmt nämlich für k = Sei nämlich n N beliebig und bezeichne N die Menge
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 42 Normale Endomorphismen Nach Satz 34.1 besitzt eine Isometrie über C eine Orthonormalbasis aus Eigenvektoren
3 Bilinearform, Basen und Matrizen
 Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht
Lineare Algebra II 2. Oktober 2013 Mitschrift der Vorlesung Lineare Algebra II im SS 2013 bei Prof. Peter Littelmann von Dario Antweiler an der Universität zu Köln. Kann Fehler enthalten. Veröentlicht
Musterlösungen zur Linearen Algebra II Weihnachtszettel
 Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Prüfung Lineare Algebra , B := ( ), C := 1 1 0
 1. Es seien 1 0 2 0 0 1 3 0 A :=, B := ( 1 2 3 4 ), C := 1 1 0 0 1 0. 0 0 0 1 0 0 1 0 0 0 0 Welche der folgenden Aussagen ist richtig? A. A und C haben Stufenform, B nicht. B. A und B haben Stufenform,
1. Es seien 1 0 2 0 0 1 3 0 A :=, B := ( 1 2 3 4 ), C := 1 1 0 0 1 0. 0 0 0 1 0 0 1 0 0 0 0 Welche der folgenden Aussagen ist richtig? A. A und C haben Stufenform, B nicht. B. A und B haben Stufenform,
Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen
 Technische Universität München Department of Physics Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen Freitag, 16.03.2012 Sascha Frölich Ferienkurs Lin. Alg. -
Technische Universität München Department of Physics Ferienkurs zur Linearen Algebra Bilinearformen, Euklidische Vektorräume und Endomorphismen Freitag, 16.03.2012 Sascha Frölich Ferienkurs Lin. Alg. -
Diagonalisierbarkeit symmetrischer Matrizen
 ¾ Diagonalisierbarkeit symmetrischer Matrizen a) Eigenwerte und Eigenvektoren Die Matrix einer linearen Abbildung ³: Î Î bezüglich einer Basis ( Ò ) ist genau dann eine Diagonalmatrix wenn jeder der Basisvektoren
¾ Diagonalisierbarkeit symmetrischer Matrizen a) Eigenwerte und Eigenvektoren Die Matrix einer linearen Abbildung ³: Î Î bezüglich einer Basis ( Ò ) ist genau dann eine Diagonalmatrix wenn jeder der Basisvektoren
Tutorium 3. 1 Nilpotente Endomorphismen. Definition. Sei Φ End(V ). Φ heißt nilpotent: n N : Φ n = 0
 Tutorium 3 1 Nilpotente Endomorphismen Definition. Sei Φ End(V ). Φ heißt nilpotent: n N : Φ n = Bemerkung. Sei V {}. Dann ist λ = einziger EW. Und wegen H(Φ, ) = Kern((Φ id) k ) Kern(Φ n ) = Kern() =
Tutorium 3 1 Nilpotente Endomorphismen Definition. Sei Φ End(V ). Φ heißt nilpotent: n N : Φ n = Bemerkung. Sei V {}. Dann ist λ = einziger EW. Und wegen H(Φ, ) = Kern((Φ id) k ) Kern(Φ n ) = Kern() =
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
Lineare Algebra II Zwischentest
 Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
Lineare Algebra II Zwischentest Dr. Stephan Ehlen, Dr. Chris Jennings-Shaffer, Jonathan Schürr 14.06.18 Dieser Zwischentest besteht aus 7 Aufgaben und enthält insgesamt 12 Seiten. Sie haben für die Bearbeitung
1. Übungsblatt: Lineare Algebra II Abgabe: 24./ in den Übungsgruppen
 Hannover, den 0. April 2006. Übungsblatt: Lineare Algebra II Abgabe: 24./25.4.2006 in den Übungsgruppen ( ) 2 5 a) Zeigen Sie, dass A = und B = 2 ( 7 6 invertierbare Matrix T an mit T AT = B. b) Zeigen
Hannover, den 0. April 2006. Übungsblatt: Lineare Algebra II Abgabe: 24./25.4.2006 in den Übungsgruppen ( ) 2 5 a) Zeigen Sie, dass A = und B = 2 ( 7 6 invertierbare Matrix T an mit T AT = B. b) Zeigen
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
Definitionen. Merkblatt lineare Algebra. affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht
 Seite 1 Definitionen affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht ähnliche Matrizen Matrizen, die das gleiche charakteristische Polynom haben
Seite 1 Definitionen affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht ähnliche Matrizen Matrizen, die das gleiche charakteristische Polynom haben
Lineare Algebra 2 (SS 13) Blatt 13: Musterlösung
 Prof. Dr. B. Hanke Dr. J. Bowden Lineare Algebra 2 (SS ) Blatt : Musterlösung Aufgabe. Es sei C (R) der R-Vektorraum der unendlich oft differenzierbaren Funktionen auf R und : C (R) C (R), f f die Abbildung,
Prof. Dr. B. Hanke Dr. J. Bowden Lineare Algebra 2 (SS ) Blatt : Musterlösung Aufgabe. Es sei C (R) der R-Vektorraum der unendlich oft differenzierbaren Funktionen auf R und : C (R) C (R), f f die Abbildung,
Übungen zur Linearen Algebra 1
 Übungen zur Linearen Algebra 1 Wintersemester 2014/2015 Universität Heidelberg - IWR Prof. Dr. Guido Kanschat Dr. Dörte Beigel Philipp Siehr Blatt 10 Abgabetermin: Freitag, 16.01.2015, 11 Uhr Auf diesem
Übungen zur Linearen Algebra 1 Wintersemester 2014/2015 Universität Heidelberg - IWR Prof. Dr. Guido Kanschat Dr. Dörte Beigel Philipp Siehr Blatt 10 Abgabetermin: Freitag, 16.01.2015, 11 Uhr Auf diesem
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Vorlesung 15 Unterräume und Dualraum Untervektorräume eines K-Vektorraumes stehen in direkter Beziehung zu Untervektorräumen
Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Vorlesung 15 Unterräume und Dualraum Untervektorräume eines K-Vektorraumes stehen in direkter Beziehung zu Untervektorräumen
Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Lineare Algebra I Lösungsvorschlag
 Aufgabe Lineare Algebra I Lösungsvorschlag Wir bezeichnen mit a, a 2, a 3 Q 4 die Spalten der Matrix A. Es ist 7 a + 2a 2 = 7 4 = 7a 3, und wir sehen im l A = a, a 2, a 3 = a, a 2. Da die Vektoren a und
Aufgabe Lineare Algebra I Lösungsvorschlag Wir bezeichnen mit a, a 2, a 3 Q 4 die Spalten der Matrix A. Es ist 7 a + 2a 2 = 7 4 = 7a 3, und wir sehen im l A = a, a 2, a 3 = a, a 2. Da die Vektoren a und
1. Übungsblatt: Lineare Algebra II Abgabe: 8./ in den Übungsgruppen
 Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Hannover, den 7. Februar 2002 Aufgabe. Übungsblatt: Lineare Algebra II Abgabe: 8./9.4.2002 in den Übungsgruppen (2, 2, 3 Punkte) Der Vektorraum V = C[, ] sei mit dem üblichen Skalarprodukt f, g = f(t)g(t)
Lineare Algebra 2. Lösung zu Aufgabe 7.2:
 Technische Universität Dortmund Sommersemester 2017 Fakultät für Mathematik Übungsblatt 7 Prof. Dr. Detlev Hoffmann 15. Juni 2017 Marco Sobiech/ Nico Lorenz Lineare Algebra 2 Lösung zu Aufgabe 7.1: (a)
Technische Universität Dortmund Sommersemester 2017 Fakultät für Mathematik Übungsblatt 7 Prof. Dr. Detlev Hoffmann 15. Juni 2017 Marco Sobiech/ Nico Lorenz Lineare Algebra 2 Lösung zu Aufgabe 7.1: (a)
18 λ 18 + λ 0 A 18I 3 = / Z 2 Z 2 Z Z Z 1
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
Vordiplomsklausur zur Linearen Algebra I
 25.3.2002 Vordiplomsklausur zur Linearen Algebra I Prof. Dr. G. Hiß Tragen Sie bitte auf diesem Deckblatt leserlich und in Blockbuchstaben Ihren Namen und Ihre Matrikelnummer ein und unterschreiben Sie.
25.3.2002 Vordiplomsklausur zur Linearen Algebra I Prof. Dr. G. Hiß Tragen Sie bitte auf diesem Deckblatt leserlich und in Blockbuchstaben Ihren Namen und Ihre Matrikelnummer ein und unterschreiben Sie.
4.2 Die adjungierte Abbildung
 4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
Lineare Algebra I Ferienblatt
 Wintersemester 09/0 Prof. Dr. Frank-Olaf Schreyer Dr. Janko Boehm Lineare Algebra I Ferienblatt. Sei, das Euklidische Skalarprodukt auf R. Das Kreuzprodukt a b von Vektoren a, b R ist durch die Formel
Wintersemester 09/0 Prof. Dr. Frank-Olaf Schreyer Dr. Janko Boehm Lineare Algebra I Ferienblatt. Sei, das Euklidische Skalarprodukt auf R. Das Kreuzprodukt a b von Vektoren a, b R ist durch die Formel
4.3 Bilinearformen. 312 LinAlg II Version Juni 2006 c Rudolf Scharlau
 312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
Lösung zu Serie 18. Lineare Algebra D-MATH, HS Prof. Richard Pink
 Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
Lerndingsbums für LA
 Lerndingsbums für LA Geheim 23. Juli 2010 1. Es seien A, B und C beliebige Mengen. Kreuzen Sie jeweils Ja an, wenn die Aussage stimmt oder Nein, wenn sie nicht stimmt! Hier ist M \ N die Differenzmenge
Lerndingsbums für LA Geheim 23. Juli 2010 1. Es seien A, B und C beliebige Mengen. Kreuzen Sie jeweils Ja an, wenn die Aussage stimmt oder Nein, wenn sie nicht stimmt! Hier ist M \ N die Differenzmenge
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10)
 1 Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 14: Vektorräume und lineare Abbildungen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 6. Oktober 2009) Vektorräume
1 Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 14: Vektorräume und lineare Abbildungen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 6. Oktober 2009) Vektorräume
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Scheinklausur, 2. Teil, Lineare Algebra I, WS 2001, Prof. Dr. G. Hiß. Ja oder
 Gruppe A Scheinklausur 2. Teil 15.2.2002 Lineare Algebra I WS 2001 Prof. Dr. G. Hiß Name: Matrikelnummer: Kreuzen Sie bei jeder Frage entweder Ja oder Nein oder nichts an. Auswertung der Multiple-Choice-Aufgaben:
Gruppe A Scheinklausur 2. Teil 15.2.2002 Lineare Algebra I WS 2001 Prof. Dr. G. Hiß Name: Matrikelnummer: Kreuzen Sie bei jeder Frage entweder Ja oder Nein oder nichts an. Auswertung der Multiple-Choice-Aufgaben:
3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform
 LinAlg II Version 1 29. Mai 2006 c Rudolf Scharlau 219 3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform Das Problem der Normalformen für Endomorphismen handelt kurz gesprochen
LinAlg II Version 1 29. Mai 2006 c Rudolf Scharlau 219 3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform Das Problem der Normalformen für Endomorphismen handelt kurz gesprochen
Klausur Lineare Algebra I am Es sind insgesamt 60 Punkte bei der Klausur zu erreichen.
 Klausur Lineare Algebra I am 03.02.10 Es sind insgesamt 60 Punkte bei der Klausur zu erreichen. Aufgabe 1. (6 Punkte insgesamt) a.) (3P) Definieren Sie, was eine abelsche Gruppe ist. b.) (3P) Definieren
Klausur Lineare Algebra I am 03.02.10 Es sind insgesamt 60 Punkte bei der Klausur zu erreichen. Aufgabe 1. (6 Punkte insgesamt) a.) (3P) Definieren Sie, was eine abelsche Gruppe ist. b.) (3P) Definieren
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
VII.2. INNERE PRODUKTE 227
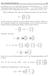 VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
Lineare Abbildungen und Darstellungsmatrizen
 KAPITEL 4 Lineare Abbildungen und Darstellungsmatrizen 1. Lineare Abbildungen Definition 4.1 (Lineare Abbildungen). Seien V und W zwei Vektorräume über den selben Körper K. Eine Abbildung f : V W heißt
KAPITEL 4 Lineare Abbildungen und Darstellungsmatrizen 1. Lineare Abbildungen Definition 4.1 (Lineare Abbildungen). Seien V und W zwei Vektorräume über den selben Körper K. Eine Abbildung f : V W heißt
Lineare Algebra Weihnachtszettel
 Lineare Algebra Weihnachtszettel 0..08 Die Aufgaben auf diesem Zettel sind zum Üben während der Weihnachtspause gedacht, sie dienen der freiwilligen Selbstkontrolle. Die Aufgaben müssen nicht bearbeitet
Lineare Algebra Weihnachtszettel 0..08 Die Aufgaben auf diesem Zettel sind zum Üben während der Weihnachtspause gedacht, sie dienen der freiwilligen Selbstkontrolle. Die Aufgaben müssen nicht bearbeitet
7.3 Unitäre Operatoren
 Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
Wir können jeden Operator T wie folgt schreiben: Dabei gilt T = 1 2 (T + T ) + i( 1 2 i (T T )) (T + T ) = T + T sowie ( 1 2 i (T T )) = 1 2 i (T T) = 1 2 i (T T ). Wir können T also in zwei lineare Operatoren
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG
 KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
Musterlösungen zur Linearen Algebra II Übungsklausur
 Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Lineare Algebra für PhysikerInnen
 Universität Wien, SS 2015 Lineare Algebra für PhysikerInnen Beispiele für Multiple-Choice-Fragen Punkteschlüssel: [Typ 1 aus 4] und [Typ 3 aus 4]... 0.8 Punkte [Typ 2 aus 4]... 1 Punkt Bei der schriftlichen
Universität Wien, SS 2015 Lineare Algebra für PhysikerInnen Beispiele für Multiple-Choice-Fragen Punkteschlüssel: [Typ 1 aus 4] und [Typ 3 aus 4]... 0.8 Punkte [Typ 2 aus 4]... 1 Punkt Bei der schriftlichen
3.5 Duale Vektorräume und Abbildungen
 3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 215/216 Lineare Algebra und analytische Geometrie I Vorlesung 27 In der letzten Vorlesung haben wir die Haupträume zu einem Eigenwert λ zu einem Endomorphismus ϕ als Kern
Prof. Dr. H. Brenner Osnabrück WS 215/216 Lineare Algebra und analytische Geometrie I Vorlesung 27 In der letzten Vorlesung haben wir die Haupträume zu einem Eigenwert λ zu einem Endomorphismus ϕ als Kern
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2015/2016
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS. Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF
 TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07032016-11032016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Lineare Abbildungen 2 11 Homomorphismus 2 12 Kern
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07032016-11032016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Lineare Abbildungen 2 11 Homomorphismus 2 12 Kern
Lineare Algebra II Lösungen zu ausgewählten Aufgaben
 Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
7 Lineare Abbildungen und Skalarprodukt
 Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Übungsblatt
 Prof Dr Fabien Morel Lineare Algebra II Dr Anand Sawant Sommersemester 2018 Übungsblatt 11 20062018 Aufgabe 1 (2 Punkte) Berechnen Sie eine Jordan-Basis für die Matrix 3 1 1 M = 2 2 0 M 3 (R) 1 1 3 Wir
Prof Dr Fabien Morel Lineare Algebra II Dr Anand Sawant Sommersemester 2018 Übungsblatt 11 20062018 Aufgabe 1 (2 Punkte) Berechnen Sie eine Jordan-Basis für die Matrix 3 1 1 M = 2 2 0 M 3 (R) 1 1 3 Wir
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2012/2013
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Prüfung Lineare Algebra 2
 1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
10. Übung zur Linearen Algebra II -
 0. Übung zur Linearen Algebra II - Lösungen Kommentare an Hannes.Klarner@Fu-Berlin.de FU Berlin. SS 00. Aufgabe 7 Der ( linearen ) Abbildung ϕ : R R sei bzgl. der kanonischen Basis die Matrix zugeordnet.
0. Übung zur Linearen Algebra II - Lösungen Kommentare an Hannes.Klarner@Fu-Berlin.de FU Berlin. SS 00. Aufgabe 7 Der ( linearen ) Abbildung ϕ : R R sei bzgl. der kanonischen Basis die Matrix zugeordnet.
Aussagenlogik. 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl. C: 2 ist eine Primzahl D: 7 7. F: 3 ist Teiler von 9
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2018/2019
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Klausur zur Vorlesung Lineare Algebra II
 Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
Mat(2 2, R) Wir bestimmen das charakterische Polynom 1 f A (t) = t 2 t 2 = (t 2)(t + ( 1). ) 2 2. Eigenvektor zu EW 2 ist v 2 = 1 1
 Aufgabe. Bestimmen Sie das Exponential expa) der Matrix ) 5 6 A = Mat, R). 4. Wir bestimmen das charakterische Polynom f A t) = t t = t )t + ). ). Eigenvektor zu EW ist v = ). Eigenvektor zu EW ist v =
Aufgabe. Bestimmen Sie das Exponential expa) der Matrix ) 5 6 A = Mat, R). 4. Wir bestimmen das charakterische Polynom f A t) = t t = t )t + ). ). Eigenvektor zu EW ist v = ). Eigenvektor zu EW ist v =
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 205): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 205): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2 2
Lösungen zu Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Sommer 4 Lösungen zu Prüfung Lineare Algebra I/II für D-MAVT. [ Punkte] Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in
Prof. N. Hungerbühler ETH Zürich, Sommer 4 Lösungen zu Prüfung Lineare Algebra I/II für D-MAVT. [ Punkte] Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in
Beispiellösungen zur Klausur Lineare Algebra bei Prof. Habegger
 Beispiellösungen zur Klausur Lineare Algebra bei Prof. Habegger Stefan Lell 2. Juli 2 Aufgabe. Sei t Q und A t = t 4t + 2 2t + 2 t t 2t 2t Mat 3Q a Bestimmen Sie die Eigenwerte von A t in Abhängigkeit
Beispiellösungen zur Klausur Lineare Algebra bei Prof. Habegger Stefan Lell 2. Juli 2 Aufgabe. Sei t Q und A t = t 4t + 2 2t + 2 t t 2t 2t Mat 3Q a Bestimmen Sie die Eigenwerte von A t in Abhängigkeit
3 Lineare Algebra Vektorräume
 3 Lineare Algebra Vektorräume (31) Sei K ein Körper Eine kommutative Gruppe V bzgl der Operation + ist ein Vektorraum über K, wenn eine Operation : K V V (λ, v) λv existiert mit i) v,w V λ,µ K: λ (v +
3 Lineare Algebra Vektorräume (31) Sei K ein Körper Eine kommutative Gruppe V bzgl der Operation + ist ein Vektorraum über K, wenn eine Operation : K V V (λ, v) λv existiert mit i) v,w V λ,µ K: λ (v +
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Lineare Algebra: Determinanten und Eigenwerte
 : und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
Sommer 2017 Musterlösung
 Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
Sommer 7 Musterlösung. (5 Punkte) a) Sei V ein Vektorraum über K und sei T End(V ). Geben Sie die Definition eines Eigenwertes von T und zeigen Sie für endlichdimensionales V, dass λ K genau dann ein Eigenwert
Lösung 5: Gram-Schmidt Orthogonalisierung, adjungierte Abbildungen
 D-MATH Lineare Algebra II FS 7 Dr. Meike Akveld Lösung 5: Gram-Schmidt Orthogonalisierung, adjungierte Abbildungen. a) Wegen der Linearität im ersten Argument gilt sicherlich w S :, w =. Somit ist S und
D-MATH Lineare Algebra II FS 7 Dr. Meike Akveld Lösung 5: Gram-Schmidt Orthogonalisierung, adjungierte Abbildungen. a) Wegen der Linearität im ersten Argument gilt sicherlich w S :, w =. Somit ist S und
Lösungshinweise zur Klausur. Mathematik für Informatiker III. (Dr. Frank Hoffmann) 18. Februar 2008
 Lösungshinweise zur Klausur Mathematik für Informatiker III (Dr. Frank Hoffmann) 8. Februar 8 Aufgabe Algebraisches I /6++ (a) Rechnen Sie zunächst nach, dass die Menge B = {,, von Vektoren eine Basis
Lösungshinweise zur Klausur Mathematik für Informatiker III (Dr. Frank Hoffmann) 8. Februar 8 Aufgabe Algebraisches I /6++ (a) Rechnen Sie zunächst nach, dass die Menge B = {,, von Vektoren eine Basis
Universität Bielefeld Sommersemester Lineare Algebra 2 Übungsblatt 1
 Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 11. Übung: Woche vom
 Übungsaufgaben 11. Übung: Woche vom 9. 1.-13. 1. 2017 (Numerik): Heft Ü 1: 12.28.a,b; 12.29.b,c (jeweils mit Fehlerabschätzung); 6.26; 6.27.a (auch mit Lagrange-Interpolationspolynom); 6.25; 6.28 (auch
Übungsaufgaben 11. Übung: Woche vom 9. 1.-13. 1. 2017 (Numerik): Heft Ü 1: 12.28.a,b; 12.29.b,c (jeweils mit Fehlerabschätzung); 6.26; 6.27.a (auch mit Lagrange-Interpolationspolynom); 6.25; 6.28 (auch
Mathematik für Informatiker 1 Wintersemester 2013/14 Heimarbeitsblatt 14
 Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker Wintersemester 3/4 Heimarbeitsblatt 4 Die Lösungshinweise dienen
Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker Wintersemester 3/4 Heimarbeitsblatt 4 Die Lösungshinweise dienen
Lineare Algebra für Ingenieure
 TECHNISCHE UNIVERSITÄT BERLIN SS 4 Fakultät II - Mathematik J Liesen/F Lutz/R Seiler Lineare Algebra für Ingenieure Lösungen zur Juli-Klausur Stand: 4 September 4 Rechenteil Aufgabe (8 Punkte Berechnen
TECHNISCHE UNIVERSITÄT BERLIN SS 4 Fakultät II - Mathematik J Liesen/F Lutz/R Seiler Lineare Algebra für Ingenieure Lösungen zur Juli-Klausur Stand: 4 September 4 Rechenteil Aufgabe (8 Punkte Berechnen
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 14.5.218 (Teil 2) 9. Mai 218 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 218 Steven Köhler 9. Mai 218 3 c 218
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 14.5.218 (Teil 2) 9. Mai 218 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 218 Steven Köhler 9. Mai 218 3 c 218
