NUMERIK DER DIFFERENTIALGLEICHUNGEN. Inhaltsverzeichnis
|
|
|
- Joachim Fürst
- vor 5 Jahren
- Abrufe
Transkript
1 NUMERIK DER DIFFERENTIALGLEICHUNGEN FABIAN LUKAS MÜLLER Inhaltsverzeichnis Einschrittverfahren für Anfangsprobleme Beispiele und Problemstellung 2 Ein Existenz- und Eindeutigkeitssatz 2 3 Einschrittverfahren 2 4 Explizite Runge-Kutta Verfahren 3 5 Runge-Kutta-Verfahren höherer Ordnung 4 6 Adaptive Steuerung von Einschrittverfahren 5 2 Mehrschrittverfahren für Anfangswertprobleme 7 2 Explizite Adams-Verfahren 7 22 Implizite Adams-Verfahren 8 23 Die Prädiktor-Korrektor-Verfahren 8 24 Die BDF-Verfahren Backwards-Differentiation-Formulas 9 25 Ordnung eines Mehrschrittverfahrens 9 26 Null-Stabilität 27 Konvergenz der Mehrschrittverfahren 3 3 Steife Differentialgleichungen 5 3 Definition und Motivation 5 32 Stabilität gewöhnlicher Differentialgleichungen 5 33 Stabilitätsgebiete für explizite Runge-Kutta-Verfahren 6 34 Stabilitätsgebiet für lineare Mehrschrittverfahren 7 35 Stabilitätsgebiet für implizite Runge-Kutta-Verfahren 9 4 Geometrische numerische Integration: Eine Einführung 2 4 Erste Beispiele 2 42 Symplektische Abbildungen 2 43 Symplektische Integratoren 22 Anhang A Liste wichtiger Verfahren 23 Einschrittverfahren für Anfangsprobleme Beispiele und Problemstellung Mathematisches Pendel ϑt sei der Auslenkungswinkel, die Länge, die Masse und die Gravitation seien Newton sagt: Masse Beschleunigung = Kraft oder ϑ = sinϑ Setze: y := ϑt und y 2 := ϑt Dann gilt: y = y 2 y 2 siny Allgemeine Problemstellung Wir betrachten ein Anfangswertproblem AWP ẏt = ft,yt yt = y mit f : U R n ; U R R n offen; y R n und t R gegeben gesucht: y : [t,t end ] R n so, dass AWP erfüllt ist Andere Notation: y x = fx,yx yx = y
2 2 FABIAN LUKAS MÜLLER 2 Ein Existenz- und Eindeutigkeitssatz Satz Peano 89 Sei D := {x,y x x a, y y b}, f D stetig, M := max D f und α := min { a, b M } Dann existiert mindestens eine Lösung y des Anfangswertproblems AWP, die erfüllt: y C x α,x + α mit yx = y Satz Cauchy, 824 Seien D,M,L wie oben Sei weiter f D stetig und lipschitzstetig in yt Dann existiert eine eindeutige Lösung y C x α,x + α mit yx = y Bemerkungen Die Beweise der Sätze sind gängigen Lehrbüchern zu entnehmen Auch wenn f nicht lipschitz ist, kann die Lösung existieren Falls f D C, dann ist f D lipschitz Falls f D C k, dann ist y D C k+ 3 Einschrittverfahren Vorgehensweise Sei N N Wir setzen h := x End x N, also ist x k := x + kh, k =,,,N Wir suchen nun eine Approximation der Lösung von AWP an den Punkten x k N k= Allgemeines explizites Einschrittverfahren Wir verwenden für die Approximation eine Iteration der Form ESV y k+ = y k + hφx k,y k,h k =,,,N Der lokalle Fehler des Verfahrens ESV ist definiert als yx + h y Bsp Explizites Eulerverfahren Beim expliziten Eulerverfahren gilt Φx k,y k,h = fx k,y k Def Konsistenz, Fehlerordnung Das Verfahren ESV heisst konsistent, falls yx + h y lim = Anfangswertaufgaben AWP h h Das Verfahren hat Ordnung p N, falls yx + h y = Oh p+ für h und alle Anfangswertaufgaben AWP Satz Konvergenz Sei yx die Lösung des AWP auf [x,x n ] Falls Der lokale Fehler erfüllt x [x,x n ] und h h max yx + h yx hφx,y,h Ch p+ Φ ist Lipschitzstetig bezüglich y für alle x,y,x,z in einer Umgebung der exakten Lösung y und für eine Lipschitzkonstante Λ > Dann erfüllt der globale Fehler für alle h h max : yx n y n Ch peλxn x Λ Beweisskizze Zeige dass für zwei Approximationen gilt y n z n e n ihλ y i z i 2 Schätze die Fehler y n z n Ch p+ e xn xiλ n 3 yx n x n Ch p+ und die Klammer approximiert ein Integral, das man i= exakt rechnen kann, also: Chp Λ exn xλ 4 Pass auf, dass beim Verwenden der Lipschitzstetigkeit alle Approximationen in der Umgebung liegen Nehme also ein h h max he xn x iλ
3 4 Explizite Runge-Kutta Verfahren NUMERIK DER DIFFERENTIALGLEICHUNGEN 3 Verfahren von Runge/Mittelpunktregel Euler benutzt eine Approximation eines Integrals mit f f Besser die Mittelpunktregel: f f 2 Um nun yx + 5h zu approximieren, benutzen wir Euler Wir erhalten: k := fx n,y n k 2 := f x n + h 2,y n + h 2 k das Rungeverfahren mit Ordnung 2 Verfahren von Heun y n+ = y n + hk 2 k = fx n,y k 2 = f x n + h,y n + hk y n+ = y n + h 2 k + k 2 Hat nach Serie 2 die Ordnung 2 Für AWP entspricht Heun der Trapezregel Runge-Kutta-Verfahren Seien: s N, b i s i=, a ij i=,,s; j=,,i i c :=, c i = a ij für i = 2,,s j= k := fx,y k 2 := f x + c 2 h,y + ha 2 k i k i := f x + c i h,y + h a ij k j j= s k s := f x + c s h,y + h a sj k j j= y k+ = y k + h ist ein s-stufiges explizites Runge-Kutta-Verfahren s Es ist ein Einschrittverfahren mit Φx,y,h = b i k i i= s b i k i Man kann ein Runge-Kutta-Verfahren als Tableau schreiben, wobei man die a ij in c i gegen die b i aufträgt: c a b Lemma Wir betrachten ein s-stufiges Runge-Kutta-Verfahren c i,a ij,b i Falls fx,y lipschitzstetig ist in y mit Konstante L, dann ist auch das oben definierte s Φx,y,h := b i k i x,y,h auch lipschitzstetig mit Konstante i= s Λ := L b i + hl i= i= s i b i a ij + Oh 2 i= j=
4 4 FABIAN LUKAS MÜLLER Konvergenz der Runge-Kutta-Verfahren Sei yx die Lösung von AWP mit f : U R, f C p U, R und so, dass {x,y x x x end } U Dann erfüllt ein s-stufiges explizites Runge-Kutta-Verfahren mit lokalen Ordnung p: Beweis mit obigem Lemma yx n y n Ch p x x x end 5 Runge-Kutta-Verfahren höherer Ordnung Problem Um lokale Fehlerordnung p zu zeigen, muss man Taylorentwickeln, was mühsam wird für s 4 Weil es dann sowieso schon mühsam ist, machen wir noch etwas viel Mühsameres Idee von Butcher 963, Hairer 972 und Wanner 973 Definition: Bäume Die Menge der Bäume T ist definiert durch zwei Eigenschaften Die Wurzel T 2 t,,t 2 T [t,t 2,t n ] T, das ist der Baum, an dem t bis t n an einer Wurzel hängt Definition: Elementares Differential Für t T definieren wir das elementare Differential Fty durch F y := fy F[t,,t n ]y := f n y n k= Ft ky Definition: Ordnung eines Baumes Die Ordnung eines Baumes t T ist die Anzahl von Knoten: [ ] =, etc Definition: Koeffizienten von Bäumen Wir definieren die Koeffizienten αt für t T durch: α = αt = t t, t 2,, t n αt αt n für t = [t, t n ] T und wobei gleicher Bäume t i in t = [t,,t n ] µ!µ 2! µ n! t t, t 2,, t n Definition: B-Reihe Sei a : T { } R Eine B-Reihe ist eine formelle Reihe Ba,y := a y + t T := t! t! t n! und µ i ist die Anzahl h t t! atαtfty Gestalt der B-Reihe für die exakte Lösung Die exakte Lösung von AWP hat die B-Reihe Be,y mit Koeffizienten e =, et = t T Gestalt der B-Reihe für ein Runge-Kutta-Verfahren Die numerische Lösung y gegeben durch ein Runge-Kutta-Verfahren ist eine B-Reihe y = Ba,y mit Koeffizienten a =, at = γt s i= b iφ i t, wobei: γ =, γt = t n k= γt k Φ i =, Φ i t = j,,j n a ij a ijn Φ j t Φ jn t Kriterium für Ordnung Ein Runge-Kutta Verfahren hat Ordnung p s γt = b i Φ i t Bäume t, t p Beweis Ordnung p : yx + h y = Oh p+ Vergleich mit B-Reihe: γt b i Φt = folgt i= t mit t p, woraus die Behauptung
5 NUMERIK DER DIFFERENTIALGLEICHUNGEN 5 Regeln für die Baumeigenschaften Regel für γ: Zähle n Knoten ab Wurzel Gehe eine Stufe nach oben und zähle n 2, weiter nach oben bis n t Dann gilt: γt = t k= n k Regel für b i Φ i : Im Ausdruck für Φ i steht jeweils a ij, wenn die Verbindung der Punkte i und j nicht ein Ende des Baumes sind Wenn vom Punkt Nummer i l Äste anfangen, die Ende des Baumes sind, steht im Ausdruck c l i Satz Sei ein s-stufiges Runge-Kutta-Verfahren mit Ordnung p gegeben Dann gilt: s i= b i c q i = q für q =,2,,p Beweis Betrachte fx,y = x q, y = mit exakter Lösung yx = xq q Runge-Kutta: y = h b i c i h q und es gilt y yx = Oh p+ hq q hq b i c q i = Oh p+ = h q q s i= b ic q i = Oh p+ Es folgt: q b i c q i = q =,,p 6 Adaptive Steuerung von Einschrittverfahren Ziel: h an die Abbildung anzupassen, um optimale Fehlerkontrolle zu kriegen Alles in kurz Gegeben: Toleranz Tol, um den lokalen Fehler abzuschätzen 2 Man betrachtet eine numerische Approximation y 3 Falls der Fehler kleiner als Tol: OK Sonst: integriere weiter Satz: Richardson-Extrapolation Um den lokalen Fehler abzuschätzen, benutzt man: eine numerische Lösung mit Schrittweite 2h: y 2 = y + hφx,y,h = y + hφx,y,h + Φx,y + hφx,y,h,h eine numerische Lösung mit zwei Schritten der Schrittweite h: ŷ = y + 2hΦx,y,2h Seien yx die C 2 -Lösung von AWP und y = y +hφx,y,h ein Einschrittvefahren der Ordnung p Für y 2 = y + hφx,y,h und ŷ gilt: yx + 2h y 2 = y 2 ŷ 2 p + Ohp+2 Zusätzlich ist ŷ 2 := y 2 + y 2 ŷ 2 p eine Approximation von yx + 2h der Ordnung p + Beweis Sei zx die exakte Lösung durch x,y Es gilt weiter: yx + h y = Cx,y h p+ + Oh p+2 zx + 2h y 2 = Cx,y h p+ + Oh p+2 Taylor: Cx,y h p+ = Cx,y h p+ + Oh p+2 Das heisst: zx + 2h y 2 = Cx,y h p+ + Oh p+2 zz: := yx + 2h zx + 2h = Cx,y h p+ + Oh p+2 = yx zx + hfx + h,yx + h fx,zx + h2 2 yx + 2h zx + 2h = yx y + hfx,yx fx,y + h2 2 = Cx,y h p+ + Oh p+2 + hfx,yx fx,y + h2 2 fx,yx fx,y yx + yx = f y x,yx y yx + Oh p+ lokalen Fehler einsetzen: = f y x,yx Cx,y h p+ + Oh p+ das zz folgt direkt Nun: yx + 2h y 2 = yx + 2h zx + 2h + zx + 2h y 2 = 2 Cx,y h p+ + Oh p+2 folgt mit den obigen beiden Also: yx + 2h ŷ = Cx,y 2h p+ + Oh p+2 und yx + 2h y 2 = 2Ch p+ + Oh p+2 Wir nehmen die Differenz: y 2 ŷ = 2Ch p+ 2 p + Oh p+2
6 6 FABIAN LUKAS MÜLLER oder 2Ch p+ y 2 ŷ 2 p Das heisst: yx + 2h y 2 = y 2 ŷ 2 p + Ohp+2 oder yx + 2h = y 2 + y 2 ŷ 2 p + Ohp+2 und yx + 2h =: ŷ 2 + Oh p+2 Richardson-Extrapolation: Algorithmus Gegeben seien η min,η max,tol,x,y,h Berechne y 2,ŷ,err = y 2 ŷ 2 p,h opt siehe unten 2 Falls: err < Tol: x = x + h y = ŷ 2 h = h opt 3 Falls: err Tol: h := h opt und gehe damit zu Punkt Richardson-Extrapolation: Wahl von h opt Wir verlangen, dass errh opt = Tol Bekannt ist: Ch p+ = err Ch p+ opt = Tol h p+ opt = Tol h p+ err Tol Daraus folgt: h opt := h p+ err ist die optimale Schrittweite Für die Steuerung in einem bestimmten Intervall h opt [η min,η max ] definiere mit vorgegebenem Sicherheitsfaktor : In den Übungen: = 9, η max = 5, η min = 2
7 NUMERIK DER DIFFERENTIALGLEICHUNGEN 7 2 Mehrschrittverfahren für Anfangswertprobleme Motivation Ein Runge-Kutta-Verfahren braucht viele Auswertungen von f Wir wollen Verfahren mit höherer Ordnung bei wenigsten Auswertungen von f Idee Adams 855 Verwende die Information von früheren Zeitschritten Definition: lineares k - stufiges Mehrschrittverfahren Ein lineares k-stufiges Mehrschrittverfahren ist gegeben durch die Formel LMV α i y n+i = h β i f n+i mit h = x end x N und x j N j= = x + jh N j=, f n+i = fx n+i,y n+i und α i,β i R Koeffizienten mit α k und α + β > Bemerkungen linear : linear in f nicht wie Runge-Kutta β k = : Verfahren ist explizit β k : Verfahren ist implizit: y n+k = η n+k + h β k α k f n+k ist durch eine Fixpunktiteration zu lösen α k : Um y n+k zu berechnen nehme y n+k = α k α + β > : sonst ist α k = β k = und ein k-schrittverfahren kann ein Einschrittverfahren sein Definition: Rückwärtsdifferenzen Die Rückwärtsdifferenzen m f n sind definiert als { f n = f n m f n := m f n m f n Es ist leicht zu zeigen, dass δ j f[x n,x n,,x n j ] = j f n j!h j 2 Explizite Adams-Verfahren Herleitung des expliziten Adams-Verfahren Sei x < x < < x l < x l+ < eine Zerlegung des Intervalls [x,x end ] mit x j = x + jh Nehme an, dass wir k konsekutive Approximationen kennen: y n,y n,,y n k+ mit y j yx j Wir integrieren das Anfangswertproblem: yx n+ = yx n + x n+ x n ft,ytdt Ersetze ft,yt im Integranden durch das Interpolationspolynom p durch die Punkte f n k+,,f n vom Grad k und integriere es exakt Wende dazu die Newtonformel an: pt = k j j= t x n i δ j f[x n,x n,,x n j ] Definiere γ j := j j! s + ids = s+j j ds Übungen Unser Verfahren lautet nun mit t = x n + sh: y n+ = y n + h Zusammenfassend erhalten wir: Das explizite Verfahren von Adams-Bashforth: k px n + shds = y n + h γ j h j j f n h j k y n+ = y n + h γ j j f n γ j = j= s + j j ds j=
8 8 FABIAN LUKAS MÜLLER 22 Implizite Adams-Verfahren Herleitung des impliziten Adams-Verfahren Wir betrachten das Polynom p vom Grad k so, dass p x j = f j für j = n +,n,,n k +, aber f n+ ist unbekannt Das Verfahren lautet y n+ = y n + h x n+ x n p tdt xn+ Newton sagt: y n+ = y n + h k Es gilt: γ j := j= x n j i + sds = t x n+ kdt δ j f[x n+,,x n+ j ] ds j s+j 2 j Zusammenfassend erhalten wir: Das implizite Verfahren von Adams-Moulton: y n+ = y n + h γj j f n+ s + j 2 γj = ds j Bemerkungen zu den Adams-Verfahren Um das Adams-Bashforth-Verfahren zu benutzen brauchen wir die k Werte y n k+,,y n, welche man mit einem Einschrittverfahren berechnet Für die Adams-Bashforth-Verfahren, benutzt man das Interpolationspolynom auch ausserhalb des Intervalls [x n k+,x n ] Nicht gut! Das Adams-Moulton-Verfahren ist implizit, also löse eine nichtlineare Gleichung des Typs y n+ = η n + hβf n+ 23 Die Prädiktor-Korrektor-Verfahren Problem Um ein Adams-Moulton-Verfahren zu benutzen, muss man eine nichtlineare Gleichung lösen: j= FPI y n+ = η n + hβf n+ Beispiel k=2 y n+ = y n + h 2 5f n+ + 8f n f n, also gilt hier: η n = y n + h 2 8f n f n Alles Bekannte β := 5 2 Koeffizient vor dem Unbekannten Idee Man berechnet eine erste Approximation mit einem expliziten Verfahren und man korrigiert diese Werte mithilfe von FPI Hierbei muss man FPI nicht optimal lösen, da y n+ schon eine Approximation ist für yx n+ Algorithmus P: Prädiktor: ŷ n+ := y n + h k j= γ j j f n Adams-Bashforth E: Evaluation: ˆfn+ := fx n+,ŷ n+ C: Corrector: y n+ = η n + hβ ˆf n+ E: Evaluation: f n+ = fx n+,y n+ C: Corrector: y n+ = η n + hβ ˆf n+ Man bekommt die so genannten PEC-Verfahren, falls wir mit ˆf n+ stoppen oder die PEC m -Verfahren in der Praxis m = oder m = 2, falls man m-mal korrigiert
9 NUMERIK DER DIFFERENTIALGLEICHUNGEN 9 24 Die BDF-Verfahren Backwards-Differentiation-Formulas Konstruktion Statt die f j zu interpolieren, benützen wir die Werte y j Man sucht qt ein Polynom vom Grad k so, dass qx j = y j, j = n +,,n + k Da y n+ noch nicht bekannt, verlange, dass q x n+ = fx n+,qx n+, dh dass qt die DGL löst an der Stelle t = x n+ Wie für Moulton, Newton liefert: j qt = t x n+ j δ j y[x n+,x n,,x n+ j ] Beispiele j= Jeder Term in der Summe enthält den Faktor t x n+ so, dass man die Ableitung von q an der Stelle x n+ berechnen kann: q x n+ = j x n+ x n+ i δ j y[x n+,,x n+ j ] =!f n+ j= i= Das ist mit obiger Formel für die dividierten Differenzen das Selbe wie: j= j j y n+ = hf n+ k=: y n+ y n = hf n+ implizites Eulerverfahren k=2: 2 3 y n+ 2y n 2 y n = hf n+ k=3: 6 y n+ 3y n y n 3 y n 2 = hf n+ Bemerkungen Wie man sieht, sind diese Verfahren implizit Diese Verfahren werden oft für steife Differentialgleichungen benutzt 25 Ordnung eines Mehrschrittverfahrens Definition Lokaler Fehler: Sei yx die exakte Lösung von AWP Wir setzen: y i := yx i für i = n,n+,,n + k und definieren den lokalen Fehler als yx n+k y n+k Ordnung: Ein Mehrschrittverfahren LMV hat Ordnung p, falls yx n+k y n+k = Oh p+ Lemma Sei I die N N-Identitätsmatrix Sei y = fx, y mit f stetig differenzierbar mit invertierbarer Jacobimatrix f y x,y Der lokale Fehler erfüllt: f yx n+k y n+k = α k I hβ k y x n+k,η Lyx,x n,h Mit Ly,x,h := α i yx + ih h β i y x + ih
10 FABIAN LUKAS MÜLLER Beweis Mit k exakten Startwerten lautet das Verfahren LMV: k k α i yx n+i + α k y n+k = h β i fx n+i,yx n+i + hβ k f n+k Es folgt: Lyx,x n,h = α k yx n+k y n+k hβ k y x n+k f n+k Mit dem Mittelwertsatz DR folgt: Lyx,x n,h = α k yx n+k y n+k hβ f k y x n+k,η yx n+k y n+k f Schliesslich folgt: Lyx,x n,h = α k I hβ k y x n+k,η yx n+k y n+k, woraus die Behauptung folgt Bemerkungen Im Wesentlichen entspricht α k Lyx,x k,h dem lokalen Fehler Ordnung p α k Lyx,x n,h = Oh p+ Definition: Erzeugende Polynome Für das Verfahren LMV definieren wir zwei Polynome, die erzeugenden Polynome: ζ := α i ζ i, Satz Folgende Bedingungen sind äquivalent: σζ := β i ζ i Das lineare Mehrschrittverfahren LMV hat Ordnung p 2 α i = und α i i q = q β i i q q =,p 3 e h hσe h = Oh p+ für h ζ 4 logζ σζ = Oζ p für ζ Beweis 2 Serie 6, Aufgabe 2 3 Einerseits, per Definitionem von L hat man: Le x,,h = α i e ih h i= β i e ih = e h hσe h Andererseits kriegt man durch Taylorentwicklung von yx + ih = yx + ihy x + : Lyx,x,h = α i yx + h q q! yq x α i i q q β i i q q woraus folgt: Le x,,h = α i + q h q α i i q q q! β i i q 3 2: e h hσe h = Oh p+ Mit : Le x,,y = Oh p+ und mit 2: α i = und α i i q = q β i i q, woraus 2 folgt 2 3: Mit 2: Le x,,h = Oh p+ e h hσe h = Oh p+ 2
11 NUMERIK DER DIFFERENTIALGLEICHUNGEN 3 4: Setze ζ := e h oder logζ = h Approximativ: logt t, wenn t klein 3 ζ logζσζ = Ologζ p+ ζ logζ σζ = Ologζp+ ζ logζ σζ = O p für ζ Definition: Konsistenz eines Verfahrens LMV hat Ordnung p = k α i = und k α i i = k β i = und = σ 26 Null-Stabilität Motivation Dahlquist 956 Man sucht ein k-schrittverfahren mit maximaler Ordnung Sind diese Methoden brauchbar? Beispiel k = 2 Wir suchen ein explizites Verfahren LMV mit α 2 := normiert mit maximaler Ordnung: y n+2 + α y n+ + α y n = hβ f n + hβ f n+ Nach dem obigen Satz hat man Ordnung p wenn p + Gleichungen zutreffen Da wir 4 Parameter haben ist p 3 Übungen: Das Verfahren mit Ordnung p = 3 lautet y n+2 + 4y n+ 5y n = h4f n+ + 2f n Man wendet es auf das Problem y = y, y = an und bekommt: y n hy n hy n =, was man eine Differenzengleichung nennt Man möchte jetzt y : n N y n finden, das sie erfüllt ist für alle n Ansatz: y n = ζ n für ein ζ R Man setzt den Ansatz oben ein und bekommt: ζ hζ 5 + 2hζ n =, also ζ = oder ζ hζ 5 + 2h = Die Wurzeln dieses anderen Polynoms sind ζ = + h + Oh 2 und ζ 2 = 5 + Oh, ie ζ n und ζn 2 lösen für alle erlaubten n die Differenzengleichung Die allgemeine Lösung ist dann y n = c ζ n + c 2ζ2 n für durch Anfangswerte y = exp,y = exph bestimmte Konstanten c,c 2 Für grosse n ist c 2 5 n dominant und die Lösung explodiert Allgemeiner Wir haben Interesse am Verhalten der numerischen Approximation der exakten Lösung für n, h für ein konstantes hn DG Aus LMV bekommen wir für h die Differenzengleichung: α i y n+i = Um diese Gleichung zu lösen, mache Ansatz y n = ζ n für ein ζ R und wir bekommen: Bemerkungen ζ n α i ζ i = Also suchen wir die Wurzeln des erzeugenden Polynoms ζ i= Der Lösungsraum ist linear, ie falls η,η 2 Wurzeln von sind, dann ist y n = c η + c 2 η 2 eine Lösung von DG für alle c,c 2 R Falls die Wurzel η doppelt ist, dann sind η n und nη n zwei linear unabhängige Lösungen von DG
12 2 FABIAN LUKAS MÜLLER Satz Seien η i m i= Wurzeln aus mit Multiplizitäten l i Dann ist die allgemeine Lösung von DG m y n := p j nηj n j= wobei p i ein Polynom vom Grad l i Beweis normiere das Verfahren auf α k = Zuerst: k = Dann ist DG y n+ + α y n = Wir suchen die allgemeine Lösung: y n+ = α y n y n = α n y Untersuche ζ = ζ + α =! ζ = α ist Nullstelle y n = y α n = pnζ n mit pn = y Polynom vom Grad Nun: k = 2 y n+2 + α y n+ + α y n = Allg Lösung: setze z n+ = [y n+2 y n+ ] T und wir haben α α z n+ = =: Az n Wir iterieren: z n = A n z Berechne die Jordanzerlegung von A = V JV Damit folgt: z n = V J n V Falls A zwei Eigenwerte: J ist diagonal und z n = [c λ n +c 2λ n 2 D λ n +D 2λ n 2 ] und es folgt: y n = D λ n + D 2λ n 2 λ Falls λ EW von A mit Vielfachheit 2 ist, dann ist J = und λ λ n nλ z n = V n λ n V z = [c λ n + c 2 nλ n D λ n + D 2 nλ n ] man erhält dann mit D 2 := λ D 2 : y n = D + D 2 nλ n Man zeigt jetzt, dass die Wurzeln von die EW von A sind: = detλi A = deta λi = λ 2 + α λ + α = λ Schlussendlich: y n = p nη n + p 2nη2 n oder y n = pnη n k 3: Übungen Definition: Stabilität Das lineare Mehrschrittverfahren LMV heisst stabil, falls die Wurzeln von folgende Bedingungen erfüllen: Falls ˆζ = hat man ˆζ Falls in diesem Falle ˆζ =, so ist ζ ˆζ, also ist die Wurzel einfach Bemerkungen Wenn LMV stabil ist, bleibt die Approximation der Lösung beschränkt für h Man sagt auch Null-stabil oder D-stabil D wie Dahlquist Erfüllt ein Verfahren diese Bedingungen nicht, dann ist es instabil Beispiel Für ein Adams-Verfahren haben wir ζ = ζ k ζ, also sind die Wurzeln und und ist einfache Wurzel Satz Das k-schritt-bdf-verfahren ist stabil für k =,,, 6 aber instabil für k > 6 Beweis Ansatzweise in den Übungen Satz: Erste Dahlquist-Schranke, 956 Die Ordnung p eines stabilen k-schrittverfahrens LMV erfüllt: p k + 2 k gerade p k + k ungerade ohne Beweis p k falls β k α k
13 NUMERIK DER DIFFERENTIALGLEICHUNGEN 3 27 Konvergenz der Mehrschrittverfahren Annahme für das Kapitel: Das Problem AWP hat eine eindeutige Lösung auf einem Intervall [x,x N ], ie f ist stetig auf D := {x,y x [x,x N ], y yx b} für ein b R und f ist lipschitzstetig: fx,y fx,z L y z für alle x,y D und mit L R > Wir betrachten ein LMV k α iy n+i = h k β if n+i Für x n = x + n h notieren wir y h x n := y n Definition: Konvergenz Das LMV konvergiert, falls für alle AWP mit unserer Annahme gilt yx y h x für h und für alle x [x,x N ] wenn die Startwerte erfüllen yx + ih y h x + ih für i =, k 2 Das LMV konvergiert mit Ordnung p N, falls für alle Anfangswertprobleme AWP ein C R > und ein h R > existiert mit: yx y h x C h p h h x [x,x N ] wenn die Startwerte erfüllen yx + ih y h x + ih Ch p für h klein genug und i =,,k Satz: konvergent ist stabil und konsistent Wenn ein lineares Mehrschrittverfahren konvergiert, dann gilt: Das LMV ist -stabil 2 Das LMV ist konsistent Beweis Betrachte y =,y =, exakte Lösung ist -Abbildung Durch Kontraposition: Nehme an, dass unser Verfahren instabil ist, ie das Polynom ζ hat eine Nullstelle ζ mit ζ > oder ζ 2 = mit Vielfachheit von ζ 2 > Man weiss, dass y j = hζ j und y j = hjζ j 2 die Differenzengleichung k α iy n+i = lösen für j =,, Die Startwerte konvergieren gegen die exakte Lösung, also: lim hζ j = j =,,,k h lim hjζ j 2 = j =,,,k h Aber die numerische Approximationen yh x = hζ x h und yh 2 = x h ζ x h 2 divergieren für fixes x R: lim h y h x =, da ζ > lim h y2 h x =, da ζ 2 = Instabile Verfahren sind nicht konvergent, also sind konvergente Verfahren stabil 2 Betrachte y =, y =, exakte Lösung y Nehme an, unser Verfahren sei konvergent Die Differenzengleichung lautet dann: α k y h x + kh + α k y h x + k h + + α y h x = Nehme in dieser Gleichung h und erhalte wegen Konvergenz a k + α k + + α = =, also ist die erste Vss für Konsistenz erfüllt Betrachte y =,y =,exakte Lösung yx = x und wende unser Verfahren darauf an k α iy n+i = h k β if n+i = h β i = hσ Behauptung: y j = jh κ oder y h = x κ erfüllt obige Gleichung κ = σ Beweis: i α in + ih κ = hσ n κ α i + κ α i i i = σ n κ + κ = σ κ = σ
14 4 FABIAN LUKAS MÜLLER Und mit Konvergenz folgt: x = yx = lim h y h x = x κ κ = σ = Formulierung eines LMV als Einschrittverfahren obda: y R,f : R 2 R,α k = Normierung Idee: Wir definieren implizit ein Vektorfeld durch ψ : R k R k x n,y n,y n+,,y n+k ψx n,y n,,y n+k k k ψ := β i fx n+i,y n+i + β k f x n+k,h ψ α i y n+i Nun lautet unser LMV y n+k = k α iy n+i + hψ Definiere noch den Vektor Y n := y n+k y n+ y n T, womit folgt: Y n+ = y n+k y n+2 y n+ T = α k α k 2 α =: AY n + hφx n,y n,h und dies ist fast ein Einschrittverfahren y n+k y n + h ψx n,y n Lemma Sei yx die exakte Lösung unseres Problems AWP Definiere den Vektor Ŷn als Ŷ n := AY x n + hφx n,y n,h mit Y x n := yx n+k yx n T auf der exakten Lösung Wenn das LMV Ordnung p hat, dann folgt: Y x n+ Ŷn+ Ch p+ oder: das Einschrittverfahren hat Ordnung p Beweis Y x n+ Ŷn+ = y x n+k + α k y x n+k + + α y x n hψ x n,y x n,h T k = α kyx n+k h T k β ifx n+i,yx n+i = Lxn,Y x n,h T = Oh p+ T, da das LMV Ordnung p hat Lemma 2 Wenn das LMV konvergiert so gibt es eine Norm so dass A Beweis Ü Theorem Das LMV ist stabil und konsistent Das LMV konvergiert Beweis siehe obiger Satz Adaption des Konvergenzbeweises von Kapitel Korollar Falls das LMV Ordnung p hat und falls die Startwerte gegen die exakte Lösung konvergieren mit Oh q, dann hat man: Beweis Ü yx n y n C h minp,q h h,x n [x,x N ]
15 3 Definition und Motivation NUMERIK DER DIFFERENTIALGLEICHUNGEN 5 3 Steife Differentialgleichungen Beispiel Das AWP ẏ = λy + λe t,y = y besitzt die Lösung yt = e t + y e λt Für λ << ist yt e t Für λ =,y = wenden wir explizites und implizites Euler mit Schrittweite h = 2 k,k = 2j,j = 2,3,4,5,6 Das explizite Eulerverfahren oszilliert stark und ist nicht brauchbar Im Gegenteil, funktioniert das implizite Eulerverfahren sehr gut! Definitionen: Steife Differentialgleichung nach Curtis/Hirschfelder 952 Eine steife Differentialgleichung ist eine Gleichung, wo bestimmte implizite Verfahren viel besser funktionieren als explizite Verfahren 32 Stabilität gewöhnlicher Differentialgleichungen Definition: Lyapunov-Stabil Die Lösung yt,t,y der Gleichung AWP ist Lyapunov-stabil : Die Lösung existiert für alle t t ε > δ > so, dass man y mit y < δ hat t t : yt,t,y + y yt,t,y < ε Definition: Asymptotisch stabil Die Lösung von AWP heisst asymptotisch stabil : Die Lösung ist Lyapunov-stabil Es existiert ein δ > so, dass für alle y < δ gilt: Beispiel ẏ = λy Für λ < ist y asymptotisch stabil Für λ = ist y stabil Für λ > ist y instabil lim yt,t,y + y yt,t,y = t Lemma Eine Lösung yt von ẏ = Ay + g ist stabil die Lösung z von ż = Az ist stabil Beweis Setze zt := yt,t,y + y yt,t,y zt erfüllt ż = Az: żt = Ayt,t,y + y + gt Ayt,t,y gt = Ayt,t,y + y yt,t,y = Azt Jetzt: yt,t,y ist stabil : ε > δ > mit: y mit y < δ gilt: yt,t,y + y yt,t,y < ε ε so, dass zt < ε : Die Lösung z ist stabil Bemerkungen Dasselbe für asymptotisch stabil und instabil Man redet, da es nur auf die Stabilität der -Abbildung ankommt, von Stabilität einer Gleichung Theorem Wir betrachten ẏ = Ay mit A R n n mit Eigenwerten λ i n i= ẏt = Ayt ist stabil Rλ i i =, n Rλ i < i {, n} mit dimjordanblock zu λ i > 2 ẏ = Ay asymptotisch stabil Rλ i < i {,,n} Beweis Serie 9 Definition: Kritischer Punkt Betrachte ẏt = ft,yt Man nennt y ŷ einen Gleichgewichtszustand oder kritischen Punkt von f, wenn ft,ŷ = t [ˆt,T]
16 6 FABIAN LUKAS MÜLLER Theorem Seien f C und ŷ Gleichgewichtszustand von f Falls die Eigenwerte λ von Dfŷ die Bedingung Rλ < erfüllen, dann ist y ŷ asymptotisch stabil Falls die Eigenwerte λ von Dfŷ die Bedingung Rλ > erfüllt, dann ist y ŷ instabil ohne Beweis Bemerkung Achtung: Man kann nichts aussagen, falls Rλ = Beispiel: ẏ = y 2 hat kritischen Punkt aber y ist instabil ẏ = y 3 hat kritischen Punkt aber y ist asymptotisch stabil 33 Stabilitätsgebiete für explizite Runge-Kutta-Verfahren Motivation Sei ψx eine glatte Lösung von AWP Wir linearisieren f durch Taylor: y = fx,y ψ + ψ = fx,ψx + f y x,ψxy ψx + Wir setzen ỹx := yx ψx Dann: ỹ x = fx,ψx + f y x,ψx ỹx + fx,ψx x,ψx ỹx + = f y Betrachte das approximierte Problem ỹ = f y x,ψxỹx mit f y x,ψ =: Jx die Jacobimatrix von D yf x,ψx Wir setzen Jx auf eine Konstante J und nehmen an, dass J diagonalisierbar ist, also: ẏt = J yt Mit y := Tz bekommen wir: z = T y = T Jy = T JTz oder besser So kommen wir auf żt = Λzt mit Λ = T JT Diagonalform von J Definition: Dahlquist-Testgleichung Die Dahlquist-Testgleichung ist das Anfangswertproblem y = λy, y = und λ C Beispiel: Expl Euler Was geschieht mit dem expliziten Eulerverfahren? y n+ = y n + hλy n = + hλy n = = + hλ n y =: Rhλ n y Setze z := hλ und bekomme: y n = Rz n y mit Rz = + z Die numerische Lösung explodiert nicht Rz Lemma: Stabilitätsfunktion von expliziten RK-Verfahren Für ein explizites RK-Verfahren b,a,c ist die Stabilitätsfunktion Rz gegeben durch das Polynom Rz = + zb T I za wobei b := b,b 2,,b s T A := a ij i,j=,,s :=,, T Beweis RK-Verfahren: Y i := y + h s j= a ijfy j und y = y + h s i= b ify i Wir setzen Y := Y Y s T und z := hλ Erhalte Y = y + zay und y = y + zb T Y Aus der ersten Gleichung: I zay = y und dann y = y + zb T I za y = + zb T I za y = Rzy
17 NUMERIK DER DIFFERENTIALGLEICHUNGEN 7 Bemerkung Die numerische Approximation eines expliziten Runge-Kutta-Verfahrens bleibt beschränkt, falls Rz Definition: Stabilitätsgebiet S := {z C Rz } heisst Stabilitätsgebiet eines Runge-Kutta- Verfahrens Definition: A-Stabilität Wir sagen, dass ein Verfahren A-stabil ist, falls das heisst, dass Rz für z mit Rz {z C Rz } =: C S Bemerkungen Die exakte Lösung von y = λy, y = ist yt = expλt Sie ist beschränkt für λ C mit Rλ Man will nun eben auch, dass die num Approximation diese Eigenschaft hat Beispiel Euler: Rz = +z und S := {z C +z } ist ein Kreis um mit Radius Ein explizites Runge-Kutta-Verfahren kann nicht A-stabil sein, weil S beschränkt ist Das heisst man muss aufpassen, dass die Schrittweite h so gewählt ist, dass hλ = z S und für solche Werte ist die Approximation beschränkt 34 Stabilitätsgebiet für lineare Mehrschrittverfahren Motivation: ϑ-methode Die ϑ-methode lautet für ϑ [,] y n+ = y n + h ϑfy n + ϑfy n+ zum Beispiel: ϑ = : expl Euler ϑ = : implizites Euler = AM = BDF ϑ = 2 : Trapezregel=AM Die Stabilitätsfunktion ist gegeben durch Rz = ϑz ϑz Um S zu zeichnen, betrachten wir S: Rz = + ϑz = ± ϑz, also z = oder z = 2 Wir sehen, dass für ϑ < 2 ein kleines Stabilitätsgebiet resultiert, für ϑ = 2 ist S = C also A-stabil für ϑ > 2 ist C \ S ein Kreisgebilde in C+, also A-stabil 2ϑ Definition: Stabilitätsgebiet Wir definieren für ein LMV das Stabilitätsgebiet als S := {µ C ζ µσζ = ζ für Multiplζ =, ζ < sonst} Bemerkungen Für µ = : Nullstellen von ζ =, also ist Stabilität im Sinne von Kapitel 2 äquivalent zur Bedingung S Deshalb heisst diese Art von Stabilität auch -Stabilität Falls µ = hλ S, dann ist {y n } N n= beschränkt Theorem Falls das LMV explizit ist, dann ist S beschränkt und das Verfahren kann nicht A-stabil sein Beweis Seien ζ µ,,ζ k µ die Nullstellen von ζ µσζ Wir haben α k µβ k ζ ζ µ ζ ζ k µ = ζ µσζ oder ζ ζ µ ζ ζ k µ = ζ µσζ α k Wir nehmen ξ C fest mit σξ Falls ζ j µ für j =,,k, dann hat man ξ ζ µ ξ ζ k µ c für ein von µ unabhängiges c R Aber > c für µ gross genug, also S ist beschränkt ζ µσξ α k Bemerkungen Die Adams-Bashforth-Verfahren sind nicht A-stabil
18 8 FABIAN LUKAS MÜLLER Lemma: Rand von S S erfüllt S Γ mit Γ : [,2π] C ϑ eiϑ eine geschlossene Kurve in σe iϑ C Beweis Betrachte S Falls µ S ζ C, ζ = so, dass ζ µσζ = Also: ϑ [,2π mit expiϑ = ζ und e iϑ µσe iϑ = Es folgt: { } S µ C µ = eiϑ σe iϑ Überprüfe noch, ob innen oder aussen Bemerkungen Γ nennt man root locus curve Die Nullstellen hängen stetig von µ ab Was geschieht mit den Adams-Moulton-Verfahren? y n+ y n = h k j= γ j j f n+i x = x 2 x und σx = k j= γ j xk j x j k = : Implizites Euler, A-stabil k = : Trapezregel, A-stabil k 2? Lemma: Stabilität Adams-Moulton-Verfahren Für k 2 hat das Polynom σx eine Nullstelle x mit Betrag x > S ist dann beschränkt und die AM-Verfahren sind nicht mehr A-stabil Für den Beweis nützliche Tatsachen γ j < für j 2 k j= γ j > für k 2 3 k γ j 2j < für k 2 Beweis Wir zeigen zuerst, dass ζ Nullstelle von σ existiert für AM-Verfahren mit ζ >, dann dass ein solches Verfahren nicht A-stabil sein kann Man hat k σ > und wir haben k σ = k k j= γ j k j 2 j = k j= γ j 2j < nach Es folgt: ζ, mit k σζ = Also ist ζ Nullstelle von σ mit σ > Für µ gross genug sind die Nullstellen von µ σ ungefähr gleich der Nullstellen von σ Aus obiger Überlegung hat man eine Nullstelle x mit x > gefunden und das Verfahren kann nicht A-stabil sein, weil S beschränkt Stabilität der BDF-Verfahren Das BDF-Verfahren der Stufe k ist k j= j j y k+ = hf k+ k = : Implizites Euler, A-stabil k = 2: Auch A-stabil: 3 2 y n 2y n + 2 = hf n Wir haben x = 3 2 x2 2x + 2 und σx = x2 Also: Γϑ = 3 2 2e iϑ + 2 e 2iϑ Wir zeigen jetzt, dass RΓϑ ϑ [, 2π]: RΓϑ = 3 2 2cosϑ + 2 cos2ϑ = 3 2 2cosϑ + cos2 ϑ 2 = cosϑ 2 ϑ [,2π] Also: C S und S unbeschränkt also A-stabil
19 NUMERIK DER DIFFERENTIALGLEICHUNGEN 9 Theorem: Zweite Dahlquist-Schranke 963 Für ein konvergentes LMV gilt: A-stabil Ordnung p 2 2 Falls A-stabil und Ordnung 2: Fehlerkonstante c 2 3 Das einzige A-stabile lineare Mehrschrittverfahren mit p = 2 und c = 2 Definition: Aα-Stabilität Ein LMV heisst Aα-stabil für < α < π 2, falls S α := {µ C arg µ α} S Beispiel: Aα-Stabilität der BDF-Verfahren k α π π Bemerkung Für ẏ = λy mit λ R ist BDF A-stabil 35 Stabilitätsgebiet für implizite Runge-Kutta-Verfahren Ziel: Suche A-stabile Verfahren mit Ordnung p 3 Definition Für s, a ij,c j,b j R ist k i := f x + c i h,y + h s j= a ijk j, i =,,s y := y + h s j= b jk j ein s-stufiges Runge-Kutta Verfahren ist die Trapezregel Bemerkungen Falls a ij = j i: explizit Falls a ij für ein j i: implizites Verfahren und in jedem Schritt muss man eine nichtlineare Gleichung lösen Teuer! Beispiel: s = 2 Das Verfahren sei gegeben durch das Tableau k = fx,y und k 2 = f x + h,y + 2 k + k 2 = fx,y Also: y = y + h 2 k + k 2 und wir erhalten die Trapezregel A-stabil Nun konstruieren wir Verfahren höherer Ordnung Definition: Kollokationspolynom Das Kollokationspolynom ux vom Grad s zu den Stützstellen c c 2 c s ist gegeben durch die Bedingungen { ux = y u x + c i h = f x + c i h,ux + c i h für i =,,s Dh u löst die Gleichung y = fx,y exakt an den Punkten x + c i h,,s Definition: Kollokationsverfahren Sei u das Kollokationspolynom zu Stützstellen c i s i= Das Kollokationsverfahren zur Lösung eines Anfangswertproblems AWP ist gegeben durch die Vorschrift y = ux + h Satz Ein Kollokationsverfahren mit Stützstellen c i s i= ist ein s-stufiges Runge-Kutta-Verfahren mit: a ij = ci l j τdτ und b i = l i τdτ für i,j =, s und mit l j τ := i j τ c i c j c i j-tes Lagrangepolynom Beweis Übungen Satz Falls eine Quadraturformel b i,c i mit b i = l iτdτ für i =, s Ordnung s + m hat, dann hat unser Kollokationsverfahren Ordnung p = s + m ohne Beweis
20 2 FABIAN LUKAS MÜLLER Gaussquadratur Die Gauss-Quadratur ist gegeben durch die Bedingungen: c i sind Nullstellen des Legendre-Polynoms P s 2x und sie hat die Ordnung 2s Es folgt, dass unser RK-Verfahren maximale Ordnung p = 2s hat Beispiel s = : Mittelpunktregel Radau-Verfahren Wir nehmen die Radau-Quadratur, dh c i sind die Nullstellen des Polynoms P s 2x + ap s 2x und a ist so, dass entweder c = oder c s = Diese Quadraturen haben Ordnung 2s, also hat unser Verfahren auch Ordnung p = 2s Beispiel s = : Implizites Euler Lobatto-Verfahren Wir nehmen die Knoten c i als Nullstellen von P s 2x P s 2 2x, also ist c = und c s = Ordnung ist 2s 2 Beispiel s = 2: Trapezregel Nun wollen wir die Stabilitätsgebiete der Kollokationsverfahren untersuchen Lemma: Stabilitätsfunktion der RK-Verfahren Die Stabilitätsfunktion Rz eines s-stufigen RK-Verfahrens c,a,b ist gegeben durch Rz = + zb T I za 2 Rz = deti za+zbt deti za = Pz Qz mit Polynomen P, Q wobei z = hλ, b = b,,b s T, A = a ij, =,,, T Beweis Gleicher Beweis wie für explizite 2 Wir wenden unser RK auf ẏ = λy, y = an und suchen Rz mit y = Rzy = Rz Wir bekommen g i = y + h s j= a ijfg j für i =, s und y = y + h s j= b jfg j Setze g := g g s T und z := hλ g = y + zag und y = y + zb T g I za g zb T = y y = 3 Cramer: Rz = y = det det, mit Zeile := Zeile Zeile 2 Beispiele Beispiel : Gauss mit s = c = 2 = a, b = Pz = deti za + zb T = z 2 + z = + z 2 Qz = deti za = z 2 Mit Lemma: Rz = 2+z 2 z Beispiel 2: Trapezregel s = 2 Hier kommt das selbe raus wie bei Gauss s = Theorem Die Verfahren von Gauss, Radau oder Lobatto sind A-stabil ohne Beweis Konsequenz In der Praxis: Implizites Euler oder Radau IIa: Das Beste zur Zeit ist Radau 5 s =
21 4 Erste Beispiele NUMERIK DER DIFFERENTIALGLEICHUNGEN 2 4 Geometrische numerische Integration: Eine Einführung Problem für das ganze Kapitel D R n offenes Gebiet, f : D R n Betrachte das AWP y = fy, yt = y Definition: Fluss Der Fluss ϕ t y = yt = yt,t,y ist der Wert der Lösungskurve an der Stelle t für jene Lösung y mit yt = y Ziel: Der Fluss ϕ t hat geometrische Eigenschaften Suche also numerische Verfahren mit denselben Eigenschaften Beispiele Falls die Lösung periodisch, symmetrisch, oder falls es eine Invariante gibt Pendel: Sei q der Ausschlagwinkel Die Hamiltonfunktion {ṗ ist Hp,q = p2 2 cosq = H q = sinq Die Bewegungsgleichung lautet dann q = H p = p Es folgt also: q = sinq siehe auch Kapitel Man hat Hpt,qt = Hp,q t > t : d H dthpt,qt = p ṗ + H H q q = p H q Es folgt: Hpt,qt ist konstant + H q H p = Weiter gilt: detϕ tp,q = detϕ p,q wobei ϕ tp,q := ϕt p,q p,q Physikalisch heisst das, dass die Fläche erhalten bleibt Numerische Approximation: Wir wenden das explizite und das symplektische Eulerverfahren auf obiges Problem an, sowie die Mittelpunktregel Man sieht, dass nur für letztere der beiden Verfahren die Fläche auch erhalten bleibt 42 Symplektische Abbildungen Hamilton sche Differentialgleichung Für d N und H : R 2d R betrachten wir die Hamilton sche Differentialgleichung H {ṗk = H q k p,q q k = H p k p,q k =,,d Definition: Symplektisch Sei V ein endlich dimensionaler Vektorraum Wir definieren eine Bilinearform ω auf V durch ω : V 2 V v,w v T Idd Jw wobei J := Id d Eine differenzierbare Abbildung f : V V heisst symplektisch, falls ωdf p v,df p w = ωv,w p V bzw falls Df T p JDf p = J p V Eine lineare Abbildung A : V V heisst symplektisch, falls ωav,aw = ωv,w folgt, da für ein lineares g gilt Dg g
22 22 FABIAN LUKAS MÜLLER Bemerkungen Betrachte R 2d mit Koordinaten p,q R d Seien η = η p,η q,ζ = ζ p,ζ q R 2d linear unabhängig Eindimensionaler Fall: Sei d = Betrachte das Parallelogramm P R 2 aufgespannt von ζ und η Die orientierte Fläche des Parallelogramms ist ωζ,η = detζ,η = ζ p η q ζ q η p Mehrdimensionaler Fall: Wir betrachten die Summe der orientierten Flächen der Projektionen von P auf Koordinatenebenen: d d ωζ,η = detζ i,η i = ζ p i ηq i ζq i ηp i = d Id ζt Jη wobei J := d Id d d i= i= Im Fall dimv = gilt für eine lineare Abb A: A symplektisch Fläche des Parallelogrammsv,w = Fläche des ParallelogrammsAv,Aw, also haben wir hier Flächenerhaltung Satz von Poincaré Sei U R 2d offen, H : U R zweimal stetig differenzierbar Dann gilt: Für alle t R ist der Fluss ϕ t y der Hamilton schen Differentialgleichung ẏ = J Hy eine symplektische Abbildung Beweis Um die Behauptung zu zeigen, beweisen wir zuerst, dass ϕ ty T Jϕ ty konstant ist, dann, dass es J ist Notation: ϕ ty := Dϕ t y =: ϕt y y d dt ϕ ty = d dt y ϕ t y = y d dt ϕ ty = y J Hϕ t y = J 2 Hϕ t y y ϕ t y, wobei 2 die Hessematrix ist d Es folgt: dt ϕ t y = J 2 Hϕ t y ϕ t y und damit d dt ϕ t y T Jϕ t y = d dt ϕ t y T Jϕ t y + ϕ t y T J d dt ϕ t y = ϕ ty T 2 Hϕ t y T J T Jϕ ty + ϕ ty T JJ 2 H ϕ ty = ϕ ty T { 2 H J T J + JJ 2 H } ϕ ty = Bemerkung: J T J = Id Endlich ϕ y T Jϕ y = Id T JId = J, da ϕ y = y 43 Symplektische Integratoren Definition: Symplektischer Integrator Ein numerisches Verfahren y = Φ h y heisst symplektisch, falls DΦ h T y JDΦ h y = J Beispiele Symplektisches Eulerverfahren Mittelpunktregel Störmer-Verlet Die Gauss-Runge-Kutta-Verfahren Satz Falls man ein symplektisches Verfahren auf eine Hamilton-Gleichung anwendet, dann bleibt die Approximation der Gesamtenergie Hp,q für sehr sehr lange Zeiten fast erhalten: mit p die Ordnung des Verfahrens ohne Beweis Hp n,q n = Hp,q + Oh p,
23 NUMERIK DER DIFFERENTIALGLEICHUNGEN 23 Anhang A Liste wichtiger Verfahren Explizites und implizites Eulerverfahren: explizit: y n+ = y n + hfx n,y n implizit: y n+ = y n + hfx n+,y n+ Symplektisches Eulerverfahren: Für ein System u n+ = u n + hf u n,v n+ v n+ = v n + hf 2 u n,v n+ Störmer-Verlet: Für ein System { u = fv v = u { u = f u,v v = f 2 u,v rechnen wir: û = u n + h 2 fv n v n+ = v n + hû u n+ = û + h 2 fv n+ Verfahren von Heun: k = fx n,y n, k 2 = f x n + h,y n + hk und y n+ = y n + h 2 k + k 2 rechnen wir: oder 2 2 Verfahren von Runge/Mittelpunktregel: k := fx n,y n, k 2 := f x n + h 2,y n + h 2 k und oder 2 2 Klassisches Runge-Kutta 4: y n+ = y n + hk Adams-Bashforth LMV: y n+ = y n + h k j= γ j j f n, wobei γ j = Adams-Moulton LMV: y n+ = y n + h k j= γ j j f n+, wobei γ j = BDF LMV: k j= j j y n+ = hf n+ Trapezregel LMV, k = 2: y n+ = y n + h 2 f n+ + f n Milne/Simpson LMV, k = 3: y n+ = y n + h 3 f n+ + 4f n + f n s+j j s+j 2 j ds ds
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
3. Lineare Mehrschrittverfahren 3.1 Begriffe
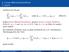 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
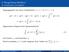 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Lösungsvorschlag zur Nachklausur zur Analysis
 Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
Prof Dr H Garcke, D Depner SS 09 NWF I - Mathematik 080009 Universität Regensburg Lösungsvorschlag zur Nachklausur zur Analysis Aufgabe Untersuchen Sie folgende Reihen auf Konvergenz und berechnen Sie
PVK Numerische Methoden Tag 1
 PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
PVK Numerische Methoden Tag 1 Lucas Böttcher ETH Zürich Institut für Baustoffe Wolfgang-Pauli-Str. 27 HIT G 23.8 8093 Zürich lucasb@ethz.ch June 19, 2017 Lucas Böttcher (ETH Zürich) PVK Numerik June 19,
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Klausur Numerische Mathematik (für Elektrotechniker), 24. Februar 2016
 Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Verständnisfragen-Teil ( Punkte) Jeder der Verständnisfragenblöcke besteht aus Verständnisfragen. Werden alle Fragen in einem Verständnisfragenblock richtig beantwortet, so gibt es für diesen Block Punkte.
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Lösung - Schnellübung 13
 D-MAVT/D-MATL Analysis II FS 7 Dr. Andreas Steiger Lösung - Schnellübung 3. Gegeben sei die Differentialgleichung y + λ 4 y + λ y = 0. Für welche Werte des reellen Parameters λ gibt es eine von Null verschiedene
D-MAVT/D-MATL Analysis II FS 7 Dr. Andreas Steiger Lösung - Schnellübung 3. Gegeben sei die Differentialgleichung y + λ 4 y + λ y = 0. Für welche Werte des reellen Parameters λ gibt es eine von Null verschiedene
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Nichtlineare Gleichungssysteme
 Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Nichtlineare Gleichungssysteme Jetzt: Numerische Behandlung nichtlinearer GS f 1 (x 1,..., x n ) =0. f n (x 1,..., x n ) =0 oder kurz f(x) = 0 mit f : R n R n Bemerkung: Neben dem direkten Entstehen bei
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger. Lösung - Serie 26. ẋ 1 = x 1 + 2x ẋ 2 = 2x 1 + x 2
 D-MAVT/D-MATL Analysis II FS 07 Dr. Andreas Steiger Lösung - Serie 6. Es ist das folgende autonome System ẋ = x + x + 3 ẋ = x + x von linearen Differenzialgleichungen. Ordung gegeben. Welche der folgenden
D-MAVT/D-MATL Analysis II FS 07 Dr. Andreas Steiger Lösung - Serie 6. Es ist das folgende autonome System ẋ = x + x + 3 ẋ = x + x von linearen Differenzialgleichungen. Ordung gegeben. Welche der folgenden
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Seminar Strukturerhaltende Zeitintegratoren für Anfangswertprobleme Hamilton Systeme. Andreas Sturm
 Seminar Strukturerhaltende Zeitintegratoren für Anfangswertprobleme Hamilton Systeme Andreas Sturm 25. November 2010 Inhaltsverzeichnis 1 Einleitung 2 2 Hamilton Systeme 3 2.1 Definition...............................
Seminar Strukturerhaltende Zeitintegratoren für Anfangswertprobleme Hamilton Systeme Andreas Sturm 25. November 2010 Inhaltsverzeichnis 1 Einleitung 2 2 Hamilton Systeme 3 2.1 Definition...............................
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
f f(x ɛξ) f(x) 0, d.h. f (x)ξ = 0 für alle ξ B 1 (0). Also f (x) = 0. In Koordinaten bedeutet dies gerade, dass in Extremstellen gilt: f(x) = 0.
 Mehrdimensionale Dierenzialrechnung 9 Optimierung 9 Optimierung Definition Seien U R n oen, f : U R, x U x heiÿt lokales Maximum, falls eine Umgebung V U von x existiert mit y V : fx fy x heiÿt lokales
Mehrdimensionale Dierenzialrechnung 9 Optimierung 9 Optimierung Definition Seien U R n oen, f : U R, x U x heiÿt lokales Maximum, falls eine Umgebung V U von x existiert mit y V : fx fy x heiÿt lokales
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 12.1 Der Satz von Picard-Lindelöf 12.1.1 Definition (Explizite Differentialgleichung erster Ordnung) Ω 1 R, Ω 2 R n seien offen und f : Ω 1 Ω 2 R n, (x,y) f (x,y)
12 Gewöhnliche Differentialgleichungen 12.1 Der Satz von Picard-Lindelöf 12.1.1 Definition (Explizite Differentialgleichung erster Ordnung) Ω 1 R, Ω 2 R n seien offen und f : Ω 1 Ω 2 R n, (x,y) f (x,y)
Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt
 Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt 9 19.12.2012 Aufgabe 35: Thema: Differenzierbarkeit a) Was bedeutet für eine Funktion f : R n R, dass f an der Stelle x 0 R n differenzierbar ist?
Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt 9 19.12.2012 Aufgabe 35: Thema: Differenzierbarkeit a) Was bedeutet für eine Funktion f : R n R, dass f an der Stelle x 0 R n differenzierbar ist?
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
A 1 A 2 A 3 A 4 A 5 A 6 A 7
 Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
Institut für Geometrie und Praktische Mathematik Numerisches Rechnen für Informatiker WS 7/8 Prof. Dr. H. Esser J. Grande, Dr. M. Larin Klausur Numerisches Rechnen für Informatiker Hilfsmittel: keine (außer
ZWEITE KLAUSUR zur Numerik I mit Lösungen. Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
 MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE FELIX LIEDER DR. GEORG JANSING.9.7 ZWEITE KLAUSUR zur Numerik I mit Lösungen Bitte folgende Angaben ergänzen und DEUTLICH LESBAR in Druckbuchstaben schreiben:
Kapitel 11 Gewöhnliche Differentialgleichungen
 Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Kapitel 11 Gewöhnliche Differentialgleichungen 11.1 Einführung Gesucht wird eine Funktion y = y(t) einer (Zeit-)Variablen t, die der Gleichung und der Anfangsbedingung genügen soll. y (t) = f(t, y(t)),
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Numerische Mathematik Vorlesungs-Script
 Numerische Mathematik Vorlesungs-Script Prof. Martin Gutknecht 19. Oktober 2008 Teil I. Numerische Methoden für Anfangswertprobleme von gewöhnlichen Differentialgleichungen Rohfassung: Bearbeitung: Korrekturen:
Numerische Mathematik Vorlesungs-Script Prof. Martin Gutknecht 19. Oktober 2008 Teil I. Numerische Methoden für Anfangswertprobleme von gewöhnlichen Differentialgleichungen Rohfassung: Bearbeitung: Korrekturen:
KAPITEL 10. Numerische Integration
 KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
KAPITEL 10. Numerische Integration 10.1 Einleitung Sei Es gilt I Ĩ = b I = b a a f(x) f(x) dx f(x) dx, Ĩ = b b a f(x) dx. a f(x) f(x) dx (b a) f f. I Ĩ I (b a) f f b a f(x) dx = ba f dx b a f(x) dx f f
5 Steife Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
Numerik gewöhnlicher Differentialgleichungen 79 5 Steife Differentialgleichungen 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif,
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Topologie und Differentialrechnung mehrerer Veränderlicher, SS 2009 Modulprüfung/Abschlussklausur. Aufgabe Punkte
 Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
5. Steife Differentialgleichungen 5.1 Was sind steife Differentialgleichungen?
 5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
5. Was sind steife Differentialgleichungen? Es gibt keine zufriedenstellende Definition der Bauart eine DG heißt steif, wenn... Wir beschreiben nun verschiedene Aspekte des Phänomens Steifheit einer DG
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Steife Probleme. Motivation
 Steife Probleme Motivation Es gibt Differentialgleichungen mit Lösungen, zu deren Approximation bei Anwendung expliziter Verfahren viel kleinere Schrittweiten benötigt werden, als man erwartet. Diese Probleme
Steife Probleme Motivation Es gibt Differentialgleichungen mit Lösungen, zu deren Approximation bei Anwendung expliziter Verfahren viel kleinere Schrittweiten benötigt werden, als man erwartet. Diese Probleme
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Gewöhnliche Differentialgleichungen Woche 7. Globale Existenz einer Lösung
 Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
Gewöhnliche Differentialgleichungen Woche 7 Globale Existenz einer Lösung 7.1 Von lokal zu global Wir betrachten wiederum das Anfangswertproblem { y (x = f (x, y(x, y( = y 0. (7.1 Eine erste Erweiterung
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi
![Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi](/thumbs/92/110521610.jpg) Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
8 Gewöhnliche Differentialgleichungen
 8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Stabilitätsfragen bei autonomen Systemen
 1 Stabilitätsfragen bei autonomen Systemen M. Schuster 09.08.2006 Inhaltsverzeichnis 1 Allgemeines über autonome Systeme 1 1.1 Oft übliche Bezeichnungen mit Übersetzung.......................... 1 2 Stabilität
1 Stabilitätsfragen bei autonomen Systemen M. Schuster 09.08.2006 Inhaltsverzeichnis 1 Allgemeines über autonome Systeme 1 1.1 Oft übliche Bezeichnungen mit Übersetzung.......................... 1 2 Stabilität
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
A1: Diplomvorprüfung HM II/III WS 2007/
 A: Diplomvorprüfung HM II/III WS 7/8 6..8 Aufgabe. (+68 Punkte) a) Ist die Reihe k+ k k 5k konvergent oder divergent? Begründen Sie ihre Aussage! b) Führen Sie eine Partialbruchzerlegung für n+ durch und
A: Diplomvorprüfung HM II/III WS 7/8 6..8 Aufgabe. (+68 Punkte) a) Ist die Reihe k+ k k 5k konvergent oder divergent? Begründen Sie ihre Aussage! b) Führen Sie eine Partialbruchzerlegung für n+ durch und
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Formelsammlung Analysis I & II
 Formelsammlung Analysis I & II Wichtige eindimensionale Integrale: { x s dx = s+ xs+ + C falls s log x + C falls s = exp(x dx = exp(x + C cos(x dx = sin(x + C sin(x dx = cos(x + C sinh(x dx = cosh(x +
Formelsammlung Analysis I & II Wichtige eindimensionale Integrale: { x s dx = s+ xs+ + C falls s log x + C falls s = exp(x dx = exp(x + C cos(x dx = sin(x + C sin(x dx = cos(x + C sinh(x dx = cosh(x +
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Analysis 2, Woche 9. Mehrdimensionale Differentialrechnung I. 9.1 Differenzierbarkeit
 A Analysis, Woche 9 Mehrdimensionale Differentialrechnung I A 9. Differenzierbarkeit A3 =. (9.) Definition 9. Sei U R m offen, f : U R n eine Funktion und a R m. Die Funktion f heißt differenzierbar in
A Analysis, Woche 9 Mehrdimensionale Differentialrechnung I A 9. Differenzierbarkeit A3 =. (9.) Definition 9. Sei U R m offen, f : U R n eine Funktion und a R m. Die Funktion f heißt differenzierbar in
Numerische Verfahren für gewöhnliche Differentialgleichungen. Literaturliste. P.Deuflhard, F.Bornemann: Numerische Mathematik II, De Gruyter, 1994.
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren
 Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Klausur HM II/III F 2003 HM II/III : 1
 Klausur HM II/III F 3 HM II/III : Aufgabe : (7 Punkte) Untersuchen Sie die Funktion f : R R gegeben durch x 3 y 3 f(x, y) x + y sin, (x, y) (, ) x + y, (x, y) (, ) auf Stetigkeit und Differenzierbarkeit.
Klausur HM II/III F 3 HM II/III : Aufgabe : (7 Punkte) Untersuchen Sie die Funktion f : R R gegeben durch x 3 y 3 f(x, y) x + y sin, (x, y) (, ) x + y, (x, y) (, ) auf Stetigkeit und Differenzierbarkeit.
KARLSRUHER INSTITUT FÜR TECHNOLOGIE Institut für Analysis
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE Institut für Analysis Höhere Mathematik III für die Fachrichtung Elektro- und Informationstechnik D. A MR Frühjahr 2014 T R, M.S. 06.03.2014 Bachelor-Modulprüfung Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE Institut für Analysis Höhere Mathematik III für die Fachrichtung Elektro- und Informationstechnik D. A MR Frühjahr 2014 T R, M.S. 06.03.2014 Bachelor-Modulprüfung Aufgabe
PVK Probeprüfung FS 2017
 PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
Analysis II. Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag
 Prof Dr H Garcke, D Depner SS 9 NWF I - Mathematik 1979 Universität Regensburg Aufgabe 1 Analysis II Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag i Erinnern Sie sich an die Konvergenzkriterien
Prof Dr H Garcke, D Depner SS 9 NWF I - Mathematik 1979 Universität Regensburg Aufgabe 1 Analysis II Aufgaben zum Stoff der Analysis I und II Lösungsvorschlag i Erinnern Sie sich an die Konvergenzkriterien
Orthogonalpolynome Einführung, Eigenschaften und Anwendungen
 Anna Weller Orthogonalpolynome Einführung, Eigenschaften und Anwendungen 1 Orthogonalpolynome Einführung, Eigenschaften und Anwendungen Anna Weller Seminar zur Numerik im SS 2018, Universität zu Köln 10.
Anna Weller Orthogonalpolynome Einführung, Eigenschaften und Anwendungen 1 Orthogonalpolynome Einführung, Eigenschaften und Anwendungen Anna Weller Seminar zur Numerik im SS 2018, Universität zu Köln 10.
Aufgaben GDGL SS 1998
 Aufgaben GDGL SS 1998 Frank Wübbeling 17. September 1998 Aufgabe 1: (4 Punkte) Stellen Sie eine Differentialgleichung 1. Ordnung auf für die Schar der Parabeln mit der x-achse als Achse und dem Ursprung
Aufgaben GDGL SS 1998 Frank Wübbeling 17. September 1998 Aufgabe 1: (4 Punkte) Stellen Sie eine Differentialgleichung 1. Ordnung auf für die Schar der Parabeln mit der x-achse als Achse und dem Ursprung
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 7. Juni 03 Vorbemerkungen Bei diesen Blattern handelt es sich zur Zeit nur um eine begleitende Erganzung des Vorlesungsskriptes von
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 7. Juni 03 Vorbemerkungen Bei diesen Blattern handelt es sich zur Zeit nur um eine begleitende Erganzung des Vorlesungsskriptes von
14 Ljapunov-Funktionen
 14 Ljapunov-Funktionen 67 14 Ljapunov-Funktionen 14.1 Gradientenfelder. a Ein Vektorfeld v C 1 D, R n besitze ein Potential U C 2 D, R, d.h. es sei v = gradu. Dann ist Dvx = HUx symmetrisch, und man hat
14 Ljapunov-Funktionen 67 14 Ljapunov-Funktionen 14.1 Gradientenfelder. a Ein Vektorfeld v C 1 D, R n besitze ein Potential U C 2 D, R, d.h. es sei v = gradu. Dann ist Dvx = HUx symmetrisch, und man hat
Probeklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 21717 Fakultät 4 - Mathematik und Naturwissenschaften Prof N V Shcherbina Dr T P Pawlaschyk wwwkanauni-wuppertalde Probeklausur zur Analysis 2, SoSe 217 Hinweis Die Lösungen
BERGISCHE UNIVERSITÄT WUPPERTAL 21717 Fakultät 4 - Mathematik und Naturwissenschaften Prof N V Shcherbina Dr T P Pawlaschyk wwwkanauni-wuppertalde Probeklausur zur Analysis 2, SoSe 217 Hinweis Die Lösungen
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 2
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Höhere Mathematik III für die Fachrichtung Physik Wintersemester 2016/17. Lösungsvorschlag zu Übungsblatt 5
 Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
Institut für Analysis Dr. Christoph Schmoeger M.Sc. Jonathan Wunderlich Höhere Mathematik III für die Fachrichtung Physik Wintersemester 6/7..7 Lösungsvorschlag zu Übungsblatt 5 Aufgabe 6: Zeigen Sie mit
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
x= f(x) p= U (x). (b) Zeigen Sie, dass auf jeder auf einem Intervall existierenden Lösung t x(t) die Energie E(t) := 1 2 p(t)2 + U(x(t)) x 1
 Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Mehrschrittverfahren und Strukturerhaltung. Valentin Göbel 03. Februar 2011
 Mehrschrittverfahren und Strukturerhaltung Valentin Göbel 03. Februar 2011 1 Inhaltsverzeichnis 1 Einleitung 3 2 Arten von Mehrschrittverfahren 4 2.1 Wiederholung: Lineare Mehrschrittverfahren............
Mehrschrittverfahren und Strukturerhaltung Valentin Göbel 03. Februar 2011 1 Inhaltsverzeichnis 1 Einleitung 3 2 Arten von Mehrschrittverfahren 4 2.1 Wiederholung: Lineare Mehrschrittverfahren............
x 2 y + xp(x)y + q(x)y = 0, (1) wobei p(x) = Satz: Falls ρ 1, ρ 2 R, mit ρ 1 ρ 2 so gibt es für 0 < x < R ein Fundamentalsystem von (1) der Gestalt
 Kurze Zusammenfassung der Vorlesung 6 Am Anfang werden wir einbisschen mehr den Potenzreihenansatz besprechen. Abgewandelter Potenzreihenansatz In Verallgemeinerung der Eulerschen Differentialgleichung
Kurze Zusammenfassung der Vorlesung 6 Am Anfang werden wir einbisschen mehr den Potenzreihenansatz besprechen. Abgewandelter Potenzreihenansatz In Verallgemeinerung der Eulerschen Differentialgleichung
Kapitel 1. Holomorphe Funktionen
 Kapitel 1 Holomorphe Funktionen Zur Erinnerung: I IR sei ein offenes Intervall, und sei z 0 I. Eine Funktion f : I IR heißt differenzierbar in z 0, falls der Limes fz fz 0 lim =: f z 0 z z 0 z z 0 existiert.
Kapitel 1 Holomorphe Funktionen Zur Erinnerung: I IR sei ein offenes Intervall, und sei z 0 I. Eine Funktion f : I IR heißt differenzierbar in z 0, falls der Limes fz fz 0 lim =: f z 0 z z 0 z z 0 existiert.
Klausur,,Algorithmische Mathematik II
 Institut für angewandte Mathematik Sommersemester 017 Andreas Eberle, Matthias Erbar / Behrend Heeren Klausur,,Algorithmische Mathematik II Musterlösung 1 (Unabhängige Zufallsvariablen) a) Wir bezeichnen
Institut für angewandte Mathematik Sommersemester 017 Andreas Eberle, Matthias Erbar / Behrend Heeren Klausur,,Algorithmische Mathematik II Musterlösung 1 (Unabhängige Zufallsvariablen) a) Wir bezeichnen
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Abbildung 5.1: stabile und instabile Ruhelagen
 Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
