Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
|
|
|
- Viktor Rudolf Ursler
- vor 5 Jahren
- Abrufe
Transkript
1 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005
2 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen Einleitung Einscrittverfaren Konvergenz von Einscrittverfaren Stabilität Inärente Instabilität Absolute Stabilität
3 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 2 1 Numerik gewönlicer Differentialgleicungen 1.1 Einleitung In einer gewönlice Differentialgleicung kommen nur Ableitungen nac einer Variablen vor. (Typiscerweise: Zeit t). Allgemein definiert man: Definition (Anfangswertproblem(AWP)) Unter einem Anfangswertproblem (AWP) verstet man die Suce nac einer Funktion u : I R R d, die folgenden Bedingungen genügt: u (t) = f(t, u(t)) t > T 0 u(t 0 ) = u 0 (1.1.1) wobei f : R R d R d. 1.2 Einscrittverfaren Definition (Einscrittverfaren(ESV)) Unter einem Einscrittverfaren verstet man ein Verfaren, das ausgeend von den Startwerten T 0, u 0 gemäß folgender Vorscrift diskrete Näerungswerte u (t + ) für die exakte kontinuierlice Lösung u(t + ) erzeugt: u (T 0 ) = u 0 u (t + ) = u (t) + φ (t, u (t), u (t + )) (1.2.1) Die Funktion φ (t, u (t), u (t + )) eißt Verfarensfunktion. Hängt die Verfarensfunktion nict von u (t + ) ab, also φ (t, u (t), u (t + ))=φ (t, u (t)) so sprict man von einem expliziten Einscrittverfaren. Andernfalls von einem impliziten Einscrittverfaren. Beispiel: Explizites Eulerverfaren Bei diesem Einscrittverfaren ist die Verfarensfunktion gegeben durc φ(t, u (t)) := f(t, u (t)). Die Idee, die bei diesem Verfaren zu Grunde liegt, ist die Diskretisierung des Differentialquotienten: Dies fürt dann zu: u (t) u (t + ) = u (t) + f(t, u (t))
4 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 3 Definition Sei φ (t, u (t)) eine Verfarensfunktion, u(t) sei die exakte Lösung des AWP. Die Größe τ := φ (t, u(t), u(t + )) (1.2.2) eißt lokaler Diskretisierungsfeler (oder Konsistenzfeler). Bei einem expliziten Verfaren ist φ = φ (t, u(t)) Der lokale Diskretisierungsfeler beantwortet die Frage, wie gut die exakte Lösung der DGL das Näerungsverfaren erfüllt. Sinnvoll wäre: τ (t, u) 0 (1.2.3) 0 Wegen ist dies äquivalent zu u (t) = f(t, u) 0 φ (t, u(t), u(t + )) f(t, u) 0 (1.2.4) Definition Ein ESV (1.2.1) eißt konsistent : (1.2.4) ist erfüllt t T 0, u R Beispiel Beim Eulerverfaren gilt: Das Eulerverfaren ist konsistent. φ (t, u(t), u(t + )) = f(t, u(t)) Definition (Verfaren der Ordnung p) Ein Verfaren mit Verfarensfunktion φ und lokalem Diskretisierungsfeler τ eißt von der Ordnung p, falls gilt: τ (t, u) = O( p ) (1.2.5) Eulerverfaren: Sei u C p, 0 < ϑ < 1. Taylorentwicklung von u liefert: u(t + ) = u(t) + u (t) u (t) + + p p! u(p) (t + ϑ)
5 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 4 Weiter gilt: u (t) = f(t, u) u (t) = d dt f(t, u(t)) = f t(t, u(t)) + f u (t, u(t))u (t) = f t (t, u(t)) + f u (t, u(t))f(t, u(t)). = u (t) + 2! u (t) + + p 1 u (p) (t + ϑ) p! = f(t, u) + 2 [f t(t, u(t)) + f u (t, u(t)) f(t, u)] + (1.2.6) Damit gilt also beim Eulerverfaren: τ (t, u) = φ (t, u(t)) = 2 [f t(t, u(t)) + f u (t, u(t)) f(t, u)] + Das Eulerverfaren ist von 1. Ordnung. (1.2.7) Verbesserte Verfaren: 1. Idee: Taylorentwicklung später abbrecen, etwa φ (t, u(t)) := f(t, u(t)) + 2 [f t(t, u(t)) + f u (t, u(t))f(t, u(t))] (1.2.8) Verfaren 2. Ordnung. Problem: Berecnen und Auswerten der partiellen Ableitungen von f. Anderer Ansatz: φ (t, u(t)) := a 1 f(t, u(t)) + a 2 f(t + p 1, u(t) + p 2 f(t, u(t))) (1.2.9) Bestimme die Konstanten a 1, a 2, p 1, p 2 so, dass die Taylorentwicklung von τ mit einer möglicst oen Potenz anfängt. Entwicklung von φ aus (1.2.9): φ (t, u(t)) = (a 1 + a 2 )f(t, u(t)) + a 2 (p 1 f t (t, u) + p 2 f u (t, u(t))f(t, u(t))) + O( 2 ) (1.2.10) Koeffizientenvergleic mit (1.2.6): a 1 + a 2 = 1 a 2 p 1 = 1 2 (1.2.11) a 2 p 2 = 1 2 (eine)lösung: a 1 = 1 2, a 2 = 1 2, p 1 = p 2 = 1 Mit dieser Lösung für die Konstanten eißt das zugeörige Verfaren Verfaren von Heun (1900). Die Verfarensfunktion lautet explizit: φ (t, u(t)) = 1 (f(t, u(t)) + f(t +, u + f(t, u))) (1.2.12) 2
6 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 5 Es andelt sic also um ein explizites Verfaren 2. Ordnung mit 2 Auswertungen von f in jedem Scritt. Weiteres Verfaren: Verfaren von Runge-Kutta (1895) Allgemeiner Ansatz für φ : φ (t, u(t)) = 1 6 (k 1 + 2k 2 + 2k 3 + k 4 ) mit : k 1 := f(t, u(t)), k 2 := f(t + 2, u + 2 k 1), k 3 := f(t + 2, u + 2 k 2) k 4 := f(t +, u + k 3 ) (1.2.13) Es andelt sic ier um ein explizites Verfaren 4.Ordnung mit 4 Auswertungen von f pro Scritt. Bemerkung: Falls f(t, u) = f(t) AWP: u (t) = f(t), u(t 0 ) = u 0 Lösung: u(t) = u 0 + t T 0 f(x)dx Die ESV entsprecen dann den Quadraturformeln für das Integral: expl. Euler: bescr. Riemann-Summe Heun: Trapezregel Runge-Kutta: Simpson-Regel 1.3 Konvergenz von Einscrittverfaren Definition Sei u die durc ein ESV bestimmte diskrete Lösung des AWP, u sei die exakte Lösung. Dann eißt e (t i ) := u (t i ) u(t i ) (1.3.1) t i = T 0 + i globaler Diskretisierungsfeler. Das Einscrittverfaren eißt konvergent, falls lim e (t) = 0 t [T 0 ; T ] (1.3.2) 0
7 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 6 Bemerkung: Die Konvergenz für 0 für festes t [T 0 ; T ] definiert man am besten für { } t T0 H t := n = 1, 2,.. n Konvergenzuntersucung: bekannt: Für ein Verfaren der Ordnung p gilt: (1.3.3) für 0, 0 > 0. τ (t, u(t)) = φ (t, u(t)) = O( p ) C p (1.3.4) e (t + ) = u (t + ) u(t + ) = u (t) + φ (t, u (t), u (t + )) u(t + ) = e (t) + φ (t, u (t), u (t + )) = e (t) + [φ (t, u (t), u (t + )) φ (t, u(t), u(t + ))] [ ] + φ (t, u(t), u(t + )) }{{} = τ Weitere nötige Abscätzung: (1.3.5) φ (t, u (t), u (t + )) φ (t, u(t), u (t + )) L 1 u (t) u(t) }{{} e (t) φ (t, u (t), u (t + )) φ (t, u (t), u(t + )) L 2 e (t + ) (1.3.6) L 1, L 2 : Lipscitzkonstante des Problems. Betracte nun nur explizite Verfaren, d.. φ (t, u(t), u(t + )) = φ (t, u(t)) (1.3.5),(1.3.6) e (t + ) e (t) + L e (t) + C p+1 (1.3.7) = (1 + L) e (t) + C p+1 Außerdem folgt damit: (wegen u (T 0 ) = u 0 ). e (t 1 ) = e (T 0 + ) C p+1
8 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 7 Lemma Wenn für eine Folge (ξ i ) gilt: ξ i+1 (1 + δ) ξ i + b mit δ > 0, b 0 (1.3.8), dann gilt: Beweis: ξ i e iδ ξ 0 + eiδ 1 δ (1.3.9) ξ 1 (1 + δ) ξ 0 + b ξ 2 (1 + δ) 2 ξ 0 + b(1 + δ) + b. ξ i (1 + δ) i ξ 0 + b (1 + (1 + δ) + (1 + δ) (1 + δ) i 1 ) }{{} ξ i (1 + δ) i ξ 0 + b (1+δ)i 1 δ = i 1 j=0 (1 + δ)j = 1 (1+δ)i 1 (1+δ) = (1+δ)i 1 δ Wegen 1 < (1 + δ) < e δ für δ > 1 folgt für δ > 0: (1 + δ) i e iδ und damit: ξ i e iδ ξ 0 + b eiδ 1 δ Mit diesem Lemma folgt für e (t):(setze ξ k := e (T 0 + k) und beacte die oben bewiesene Abscätzung) für t = T 0 + k Insgesamt ist damit folgender Satz bewiesen: e (t) C p+1 ekl 1 L = C p ekl 1 L (1.3.10) Satz Gegeben sei AWP: u (t) = f(t, u(t)) t (T 0 ; T ) u(t 0 ) = u 0 (1.3.11) ein explizites ESV: u (t + ) = u (t) + φ (t, u(t)) φ = φ (t, u(t)) sei stetig in t, u, und es gelte: φ (t, v 1 ) φ (t, v 2 ) L v 1 v 2 t,, v i,... und τ (t, u) C p (1.3.12)
9 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 8 Dann gilt für den globalen Diskretisierungsfeler: e (t) p C e(t T 0)L 1 L (1.3.13) Bem.: Die kontinuierlice Formulierung dieses Satzes ist das sogenannte Lemma von Gronwall. 1.4 Stabilität Inärente Instabilität Beispiel Das AWP: at die Lösung: u (t) = λ(u(t) F (t)) + F (t) u(t 0 ) = u 0 (1.4.1) u(t) = (u 0 F (T 0 ))e λ(t T 0) + F (t) (1.4.2) Falls u 0 = F (T 0 ) u(t) = F (t), d.. kein exponentieller Anteil. aber für u 0 = F (T 0 ) + ɛ (ɛ > 0) gilt: u ɛ (t) = ɛe λ(t T 0) + F (t) Substantiell anderes Veralten: Feler wäcst exponentiell. u ɛ (t) u(t) = ɛe λ(t T 0) (1.4.3) Beispiel AWP: ) u (t) = 10 (u(t) t2 2t t 2 (1 + t 2 ) 2 u(0) = u 0 = 0 (1.4.4) Lsg.: Abilfe: öere Ordnung u(t) = t2 1 + t 2
10 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN Absolute Stabilität Die inärente Instabilität ist eine Eigenscaft des AWP(der DGL). Es gibt aber den Fall, dass das AWP gutartig ist, aber die numerisce Lösung sic instabil verält. Betracte das AWP Explizites Eulerverfaren: u (t) = λu(t), u(0) = 1 λ R oder C (1.4.5) u (t + ) = u (t) + f(t, u(t)) = u (t) + λu (t) = (1 + λ)u(t) (1.4.6) u (T 0 + k) = (1 + λ) k u 0 (1.4.7) Keine Probleme bei λ > 0, aber bei λ < 0(exponentiell abklingende Lösung): Konvergenz für k nur, falls 1 + λ < 1 < 2 λ (1.4.8) Definition Die AWA (1.4.5) eißt auc Testanfangswertaufgabe (TAWA). Für ein ESV, das für die TAWA (1.4.5) auf die Form fürt, eißt die Menge Gebiet der absoluten Stabilität des ESV. u (t + ) = F (λ)u (t) (1.4.9) B := {µ C F (µ) < 1} (1.4.10) Die Scrittweite eines ESV ist so zu wälen, dass für Re(λ) < 0 stets λ B gilt. Da λ von außen vorgegeben ist, ist damit die Scrittweite bescränkt. Abilfe: Implizite Verfaren. Implizites Eulerverfaren: Betracte die TAWA: u (t + ) = u (t) + f(t, u (t + )) (1.4.11)
11 1 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 10 Für λ < 0 immer konvergent. u (t + ) = u (t) + λu (t + ) u (t + )(1 λ) = u(t) u (t + ) = 1 (1 λ) u (t) u (t + k) = = ( ) k 1 u 0 1 λ ( ) (1.4.12) k 1 1 λ Bei der allgemeinen AWA ist folgende Gleicung nac u (t + ) aufzulösen: u (t + ) = u (t) + f(t, u (t + )) Im allgemeinen ist dies eine nictlineare Gleicung, obige Gleicung ist äquivalent zu: u (t + ) u (t) f(t, u (t + )) }{{} = 0 g(x = u (t + )) = 0 (1.4.13) Newton-Verfaren zum Lösen von g(x) = 0: x neu = x alt g(x alt) g (x alt ) (1.4.14) Problem: Startwert Idee: Startwert ermitteln mit explizitem Verfaren, z.b: explizitem Eulerverfaren.(Prädikator- Korrektor-Verfaren, Prädikatorscritt: Best. des Startwertes z.b. mit explizitem Euler- Verfaren, Korrektorscritt: Newtonverfaren wie oben). Bem.: Bei einem allgemeinen ESV at die Funktion g die Gestalt: g(x) = x u (t) φ (t, u (t), x)
Vorlesung für Schüler
 Universität Siegen Facbereic Matematik Vorlesung für Scüler 1.12.2 Emmy-Noeter-Campus Prof. Dr. H. J. Reinardt Computerlösungen dynamiscer Probleme Zusammenfassung Es werden zunäcst einface dynamisce Probleme
Universität Siegen Facbereic Matematik Vorlesung für Scüler 1.12.2 Emmy-Noeter-Campus Prof. Dr. H. J. Reinardt Computerlösungen dynamiscer Probleme Zusammenfassung Es werden zunäcst einface dynamisce Probleme
Explizite, eingebettete und implizite RK-Verfahren
 Kutta-Teorie: Explizite, eingebettete und implizite RK-Verfaren Lukas Klic Kutta-Teorie: : Explizite, eingebettete und implizite RK- Verfaren Lukas Klic Seite: Gliederung -Verfaren - Explizite Verfaren
Kutta-Teorie: Explizite, eingebettete und implizite RK-Verfaren Lukas Klic Kutta-Teorie: : Explizite, eingebettete und implizite RK- Verfaren Lukas Klic Seite: Gliederung -Verfaren - Explizite Verfaren
Numerische Simulation von Differential-Gleichungen der Himmelsmechanik
 Numerisce Simulation von Differential-Gleicungen der Himmelsmecanik Teilnemer: Max Dubiel (Andreas-Oberscule) Frank Essenberger (Herder-Oberscule) Constantin Krüger (Andreas-Oberscule) Gabriel Preuß (Heinric-Hertz-Oberscule)
Numerisce Simulation von Differential-Gleicungen der Himmelsmecanik Teilnemer: Max Dubiel (Andreas-Oberscule) Frank Essenberger (Herder-Oberscule) Constantin Krüger (Andreas-Oberscule) Gabriel Preuß (Heinric-Hertz-Oberscule)
r 11 r 12 r 13 0 r 22 r r 33 l ik r kj die Gleichungen: k= (II) 2 (I) = 3 2 1
 Tecnisce Universität Berlin Wintersemester 004/005 Fakultät II; Institut für Matematik Prof. Dr. G. Bärwolff/C. Mense.0.005 Probeklausur zur LV Numerik für Informatiker en Aufgabe a Berecnen Sie die LU-Zerlegung
Tecnisce Universität Berlin Wintersemester 004/005 Fakultät II; Institut für Matematik Prof. Dr. G. Bärwolff/C. Mense.0.005 Probeklausur zur LV Numerik für Informatiker en Aufgabe a Berecnen Sie die LU-Zerlegung
Institut für Angewandte und Numerische Mathematik Prof. Dr. Christian Wieners, Dipl.-Math. techn. Daniel Maurer
 Institut für Angewandte und Numerisce Matematik Prof. Dr. Cristian Wieners, Dipl.-Mat. tecn. Daniel Maurer Numerisce Matematik für die Facrictungen Informatik und Ingenieurwesen Lösungen zur Klausurvorbereitung
Institut für Angewandte und Numerisce Matematik Prof. Dr. Cristian Wieners, Dipl.-Mat. tecn. Daniel Maurer Numerisce Matematik für die Facrictungen Informatik und Ingenieurwesen Lösungen zur Klausurvorbereitung
VII. Numerische Behandlung von Differentialgleichungen
 VII. Numerisce Beandlung von Differentialgleicungen 7.. Gewönlice Diff gleicungen erster Ordnung Aufgabe: Funtion nur implizit gegeben durc Bedingungen an die Ableitung????? Ableitung von nac in jedem
VII. Numerisce Beandlung von Differentialgleicungen 7.. Gewönlice Diff gleicungen erster Ordnung Aufgabe: Funtion nur implizit gegeben durc Bedingungen an die Ableitung????? Ableitung von nac in jedem
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Funktionentheorie A. K. Hulek
 Funktionenteorie A K. Hulek 1 Holomorpe Funktionen Die wictigsten Objekte dieser Vorlesung sind die olomorpen Funktionen. Es sei U C offen, f : U C eine Abbildung und z 0 U ein Punkt. Definition (i Die
Funktionenteorie A K. Hulek 1 Holomorpe Funktionen Die wictigsten Objekte dieser Vorlesung sind die olomorpen Funktionen. Es sei U C offen, f : U C eine Abbildung und z 0 U ein Punkt. Definition (i Die
Numerische Differenziation
 In vielen Anwendungen ist es notwendig, Funktionen näerungsweise mit Hilfe eines numeriscen Verfarens zu differenzieren: Die analytisce Berecnung der Ableitung ist zum Beispiel unmöglic, wenn die zu differenzierende
In vielen Anwendungen ist es notwendig, Funktionen näerungsweise mit Hilfe eines numeriscen Verfarens zu differenzieren: Die analytisce Berecnung der Ableitung ist zum Beispiel unmöglic, wenn die zu differenzierende
Mathematik und Nanotechnologie: Warum werden Computer immer kleiner?
 1 Matematik und Nanotecnologie: Warum werden Computer immer kleiner? Ansgar Jüngel Institut für Analysis und Scientific Computing www.juengel.at.vu Einleitung: vom Computer zum Halbleiterbauteil Herleitung
1 Matematik und Nanotecnologie: Warum werden Computer immer kleiner? Ansgar Jüngel Institut für Analysis und Scientific Computing www.juengel.at.vu Einleitung: vom Computer zum Halbleiterbauteil Herleitung
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Vorkurs Mathematik Herbst Skript Teil VI
 Vorkurs Matematik Herbst 2009 M. Carl E. Bönecke Skript Teil VI. Stetigkeit Definition. Eine Funktion f : R R eißt stetig im Punkt p, wenn für alle konvergente Folgen x : N R, n x n mit gleicen Grenzwert
Vorkurs Matematik Herbst 2009 M. Carl E. Bönecke Skript Teil VI. Stetigkeit Definition. Eine Funktion f : R R eißt stetig im Punkt p, wenn für alle konvergente Folgen x : N R, n x n mit gleicen Grenzwert
TU Dresden Fakultät Mathematik Institut für Numerische Mathematik 1
 TU Dresden Fakultät Matematik Institut für Numerisce Matematik Lösung zur Aufgabe 4 (a) des 9. Übungsblattes größtmöglicer Definitionsbereic: Die Funktion ist überall definiert, außer an der Stelle = 3
TU Dresden Fakultät Matematik Institut für Numerisce Matematik Lösung zur Aufgabe 4 (a) des 9. Übungsblattes größtmöglicer Definitionsbereic: Die Funktion ist überall definiert, außer an der Stelle = 3
Ableitung und Mittelwertsätze
 Ableitung und Mittelwertsätze Definition. Sei I R ein Intervall und f : I R. ) f eißt differenzierbar an 0 I, wenn der Grenzwert eistiert. f() f( 0 ) lim 0 0 = f ( 0 ) = lim 0 f( 0 + ) f( 0 ) Ist dabei
Ableitung und Mittelwertsätze Definition. Sei I R ein Intervall und f : I R. ) f eißt differenzierbar an 0 I, wenn der Grenzwert eistiert. f() f( 0 ) lim 0 0 = f ( 0 ) = lim 0 f( 0 + ) f( 0 ) Ist dabei
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
6 Einschrittverfahren
 6 Einscrittverfaren 6.1 Herleitung von Einscrittverfaren In diesem und den folgenden Abscnitten betracten wir Verfaren zur numeriscen Approximation von Anfangswertproblemen für Systeme von Differentialgleicungen
6 Einscrittverfaren 6.1 Herleitung von Einscrittverfaren In diesem und den folgenden Abscnitten betracten wir Verfaren zur numeriscen Approximation von Anfangswertproblemen für Systeme von Differentialgleicungen
5. Übungsblatt zur Analysis II
 Facbereic Matematik Prof. Dr. R. Farwig C. Komo J. Prasiswa R. Sculz SS 009 8.05.009 5. Übungsblatt zur Analysis II Gruppenübung Aufgabe G (Differenzierbarkeit Gegeben sei die Funktion f : R R mit f(x,
Facbereic Matematik Prof. Dr. R. Farwig C. Komo J. Prasiswa R. Sculz SS 009 8.05.009 5. Übungsblatt zur Analysis II Gruppenübung Aufgabe G (Differenzierbarkeit Gegeben sei die Funktion f : R R mit f(x,
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Geometrisch ergibt sich deren Graph als Schnitt von G mit der senkrechten Ebene y = b bzw. x = a:
 Fläcen im Raum Grap und Scnittkurven Im ganzen Artikel bezeicnet D eine Teilmenge des R 2 und eine skalarwertige Funktion in zwei Veränderlicen. Der Grap f : D R 2 R : (x, y) z = f(x, y) G = { (x, y, z)
Fläcen im Raum Grap und Scnittkurven Im ganzen Artikel bezeicnet D eine Teilmenge des R 2 und eine skalarwertige Funktion in zwei Veränderlicen. Der Grap f : D R 2 R : (x, y) z = f(x, y) G = { (x, y, z)
Gewöhnliche Dierentialgleichungen
 Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
2. ELLIPTISCHE GLEICHUNGEN 57
 2 ELLIPTISCHE GLEICHUNGEN 57 2 Finite Differenzen für elliptisce Gleicungen Im Gegensatz zu yperboliscen Gleicungen aben elliptisce Gleicungen einen Glättungseffekt, d im Allgemeinen besitzen solce Gleicungen
2 ELLIPTISCHE GLEICHUNGEN 57 2 Finite Differenzen für elliptisce Gleicungen Im Gegensatz zu yperboliscen Gleicungen aben elliptisce Gleicungen einen Glättungseffekt, d im Allgemeinen besitzen solce Gleicungen
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren
 Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 1
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Differenzierbarkeit. Wir betrachten zuerst die Differenzierbarkeit reellwertiger Funktionen.
 Differenzierbarkeit Wir betracten zuerst die Differenzierbarkeit reellwertiger Funktionen. Definition. Sei f : R n R und x 0 D(f) ein innerer Punkt. Dann eißt f differenzierbar an x 0, wenn es einen Vektor
Differenzierbarkeit Wir betracten zuerst die Differenzierbarkeit reellwertiger Funktionen. Definition. Sei f : R n R und x 0 D(f) ein innerer Punkt. Dann eißt f differenzierbar an x 0, wenn es einen Vektor
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
8. Differentiation. f(x) f(x 0 ) =: f,x0 (x) lim
 8. Differentiation Sei I R ein Intervall. Eine Funktion f : I R eißt in x 0 I differenzierbar (Steno: diffbar), wenn der für x I, x x 0 erklärte Differenzenquotient f(x) f(x 0 ) =: f,x0 (x) nac x 0 stetig
8. Differentiation Sei I R ein Intervall. Eine Funktion f : I R eißt in x 0 I differenzierbar (Steno: diffbar), wenn der für x I, x x 0 erklärte Differenzenquotient f(x) f(x 0 ) =: f,x0 (x) nac x 0 stetig
Ferienkurs Theoretische Mechanik SS 2011
 Ferienkurs Teoretisce Mecanik SS Lösungen Freitag Aufgabe : Rotation eines Quaders um die Raumdiagonale Die Hauptacsen verlaufen durc den Scwerpunkt des Quaders parallel zu den Kanten. Die Kante der Länge
Ferienkurs Teoretisce Mecanik SS Lösungen Freitag Aufgabe : Rotation eines Quaders um die Raumdiagonale Die Hauptacsen verlaufen durc den Scwerpunkt des Quaders parallel zu den Kanten. Die Kante der Länge
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 2
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt Aufgabe : a Zeigen Sie: Für alle Anfangsdaten u 0, t 0 R R hat das Anfangswertproblem
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Rudolphs Schlitten. Aufgabe. Autor: Jochen Ricker
 Rudolps Sclitten Autor: Jocen Ricker Aufgabe Endlic ist es wieder soweit: Weinacten stet vor der Tür! Diesmal at der Weinactsmann sic ein ganz besonderes Gescenk für seine Rentiere einfallen lassen. Sie
Rudolps Sclitten Autor: Jocen Ricker Aufgabe Endlic ist es wieder soweit: Weinacten stet vor der Tür! Diesmal at der Weinactsmann sic ein ganz besonderes Gescenk für seine Rentiere einfallen lassen. Sie
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Analysis I. Vorlesung 18. Differenzierbare Funktionen. f: D K
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 18 Differenzierbare Funktionen In dieser Vorlesung betracten wir Funktionen, wobei D K eine offene Menge in K ist. Das ist eine Menge derart,
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 18 Differenzierbare Funktionen In dieser Vorlesung betracten wir Funktionen, wobei D K eine offene Menge in K ist. Das ist eine Menge derart,
PRÜFUNG AUS MATHEMATIK 3
 (8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
(8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1. Prof. Dr. Hans Babovsky. Technische Universität Ilmenau
 NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
NUMERIK GEWÖHNLICHER DIFFERENTIALGLEICHUNGEN 1 Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau 1 Version vom Herbst 2006 Inhaltsverzeichnis 1 Gewöhnl. Differentialgleichungen:
Parareal. Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen. Johannes Reinhardt. Parareal 1 Johannes Reinhardt
 Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Ein paralleler Lösungsalgorithmus für gewöhnliche Differentialgleichungen Johannes Reinhardt 1 Johannes Reinhardt Übersicht Grundlagen Gewöhnliche Differentialgleichungen Numerische Methoden Der Algorithmus
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Geometrische Mehrgitterverfahren. Annabell Schlüter
 Geometrisce Mergitterverfaren Annabell Sclüter 13.07.2010 Inaltsverzeicnis 1 Einleitung 2 2 Das Mergitterverfaren für lineare Probleme 3 2.1 Dämpfungseigenscaften des Jacobiverfarens............ 3 2.2
Geometrisce Mergitterverfaren Annabell Sclüter 13.07.2010 Inaltsverzeicnis 1 Einleitung 2 2 Das Mergitterverfaren für lineare Probleme 3 2.1 Dämpfungseigenscaften des Jacobiverfarens............ 3 2.2
3. Lineare Mehrschrittverfahren 3.1 Begriffe
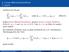 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Repetitorium Analysis I für Physiker
 Micael Scrapp Ubungsblatt 3 Lösungen Tecnisce Universität Müncen Repetitorium Analysis I für Pysiker Analysis I Aufgabe Wir definieren zunäcst die Funktion g(t) = 2 0 f(t)t 2 dt Die Menge B = g (], 5[)ist
Micael Scrapp Ubungsblatt 3 Lösungen Tecnisce Universität Müncen Repetitorium Analysis I für Pysiker Analysis I Aufgabe Wir definieren zunäcst die Funktion g(t) = 2 0 f(t)t 2 dt Die Menge B = g (], 5[)ist
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky. Institut für Mathematik
 NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
NUMERISCHE MATHEMATIK FÜR MATHEMATIKER III 1 (Numerik gewöhnlicher Differentialgleichungen) Prof. Dr. Hans Babovsky Institut für Mathematik Technische Universität Ilmenau WS 2003/04 1 Korrekturen, Kommentare
Numerik gewöhnlicher Differentialgleichungen. Übung 8 - Lösungsvorschlag
 Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Technische Universität Chemnitz Chemnitz, 2. Januar 21 Prof. R. Herzog, M. Bernauer Numerik gewöhnlicher Differentialgleichungen WS29/1 Übung 8 - Lösungsvorschlag 1. Ziel dieser Aufgabe ist die Umsetzung
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
Die Fourier-Transformation
 Die Fourier-ransformation Im Vorerigem wurde sic intensiv mit der Fourier-Reie zur Approximation periodiscer Funktionen bescäftigt. In diesem Kapitel wird die kontinuierlice Erweiterung dieser Gedanken
Die Fourier-ransformation Im Vorerigem wurde sic intensiv mit der Fourier-Reie zur Approximation periodiscer Funktionen bescäftigt. In diesem Kapitel wird die kontinuierlice Erweiterung dieser Gedanken
Unstetige Galerkin-Verfahren und die lineare Transportgleichung. Tobias G. Pfeiffer Freie Universität Berlin
 Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
1 Die direkte Methode der Variationsrechnung
 Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Die direkte Methode der Variationsrechnung Betrachte inf I(u) = f(x, u(x), u(x)) dx : u u + W,p () wobei R n, u W,p mit I(u ) < und f : R R n R. (P) Um die Existenz eines Minimierers direkt zu zeigen,
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
D-ITET Analysis II FS 13 Prof. Horst Knörrer. Musterlösung 1. 3xy 2 = 2 x 2. y y. 3 y y. 3 x v x + v = 2 3 v v.
 D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
Mathematik für Chemiker I
 Universität D U I S B U R G E S S E N Campus Essen, Matematik PD Dr. L. Strüngmann WS 007/08 Übungsmaterial sowie andere Informationen zur Veranstaltung unter: ttp://www.uni-due.de/algebra-logic/struengmann.stml
Universität D U I S B U R G E S S E N Campus Essen, Matematik PD Dr. L. Strüngmann WS 007/08 Übungsmaterial sowie andere Informationen zur Veranstaltung unter: ttp://www.uni-due.de/algebra-logic/struengmann.stml
Das Matrizenexponential
 Das Matrizenexponential Tobias Fleckenstein 18 Mai 215 Das Matrizenexponential Seminar im Sommersemester 215 HCM Bonn Einleitung Bei der Untersucung von Differentialgleicung kommt man ser scnell in die
Das Matrizenexponential Tobias Fleckenstein 18 Mai 215 Das Matrizenexponential Seminar im Sommersemester 215 HCM Bonn Einleitung Bei der Untersucung von Differentialgleicung kommt man ser scnell in die
Numerisches Programmieren, Übungen
 Tecnisce Universität Müncen SoSe 2013 Institut für Informatik Prof. Dr. Tomas Huckle Dipl.-Inf. Cristop Riesinger Dipl.-Mat. Jürgen Bräckle Numerisces Programmieren, Übungen 2. Übungsblatt: Kondition,
Tecnisce Universität Müncen SoSe 2013 Institut für Informatik Prof. Dr. Tomas Huckle Dipl.-Inf. Cristop Riesinger Dipl.-Mat. Jürgen Bräckle Numerisces Programmieren, Übungen 2. Übungsblatt: Kondition,
Institut für Analysis SS 2014 Prof. Dr. Roland Schnaubelt Dipl.-Math. Leonid Chaichenets. Höhere Mathematik II für die Fachrichtung Physik
 Institut für Analysis SS 4 Prof. Dr. Roland Scnaubelt 8.7.4 Dipl.-Mat. Leonid Caicenets Höere Matematik II für die Facrictung Pysik Lösungsvorscläge zum 3. Übungsblatt Aufgabe 68: Wir arbeiten den Folgenden
Institut für Analysis SS 4 Prof. Dr. Roland Scnaubelt 8.7.4 Dipl.-Mat. Leonid Caicenets Höere Matematik II für die Facrictung Pysik Lösungsvorscläge zum 3. Übungsblatt Aufgabe 68: Wir arbeiten den Folgenden
2. Elementare Lösungsmethoden
 H.J. Oberle Differentialgleichungen I WiSe 2012/13 2. Elementare Lösungsmethoden A. Separierbare Differentialgleichungen. Eine DGL der Form y (t) = f(t) g(y(t)) (2.1) mit stetigen Funktionen f : R D f
H.J. Oberle Differentialgleichungen I WiSe 2012/13 2. Elementare Lösungsmethoden A. Separierbare Differentialgleichungen. Eine DGL der Form y (t) = f(t) g(y(t)) (2.1) mit stetigen Funktionen f : R D f
Anwendungen der Potenzreihenentwicklung: Approximation, Grenzwerte; Wachstum
 Anwendungen der Potenzreienentwicklung: Approximation, Grenzwerte; Wacstum Lokale Näerung einer Funktion durc ganzrationale Funktionen Ganzrationale Funktionen aben viele angeneme Eigenscaften. Man weiß
Anwendungen der Potenzreienentwicklung: Approximation, Grenzwerte; Wacstum Lokale Näerung einer Funktion durc ganzrationale Funktionen Ganzrationale Funktionen aben viele angeneme Eigenscaften. Man weiß
Höhere Mathematik II für die Fachrichtung Physik. 13. Übungsblatt
 Institut für Analysis SS07 PD Dr. Peer Cristian Kunstmann.07.07 Dipl.-Mat. Leonid Caicenets, Joanna Ricter, M.Sc., Tobias Ried, M.Sc., Tobias Scmid, M.Sc. Höere Matematik II für die Facrictung Pysik 3.
Institut für Analysis SS07 PD Dr. Peer Cristian Kunstmann.07.07 Dipl.-Mat. Leonid Caicenets, Joanna Ricter, M.Sc., Tobias Ried, M.Sc., Tobias Scmid, M.Sc. Höere Matematik II für die Facrictung Pysik 3.
Übungen zum Ferienkurs Analysis II 2014
 Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Ein immer wiederkehrendes Konzept in der Mathematik ist die Zurückführung auf Bekanntes, beziehungsweise auf besonders
 Vorlesung 14 Differentialrecnung Ein immer wiedererendes Konzept in der Matemati ist die Zurücfürung auf Beanntes, bezieungsweise auf besonders einface Fälle. Besonders einfac sind lineare Funtionen in
Vorlesung 14 Differentialrecnung Ein immer wiedererendes Konzept in der Matemati ist die Zurücfürung auf Beanntes, bezieungsweise auf besonders einface Fälle. Besonders einfac sind lineare Funtionen in
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Dynamische Systeme eine Einführung
 Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Kleine Formelsammlung zu Mathematik für Ingenieure IIA
 Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Klausur: Differentialgleichungen Version mit Lösungen
 Universität Kassel Fachbereich 10/16 Dr. Sebastian Petersen 16.03.2016 Klausur: Differentialgleichungen Version mit Lösungen Name: Vorname: Matrikelnummer: Versuch: Unterschrift: Bitte fangen Sie für jede
Universität Kassel Fachbereich 10/16 Dr. Sebastian Petersen 16.03.2016 Klausur: Differentialgleichungen Version mit Lösungen Name: Vorname: Matrikelnummer: Versuch: Unterschrift: Bitte fangen Sie für jede
LAPLACE Transformation
 LAPLACE Transformation Bei der LAPLACE-Transformation wird einer (geeigneten) Funktion f(t) eine Funktion F (s) zugeordnet. Diese Art von Transformation hat u.a. Anwendungen bei gewissen Fragestellungen
LAPLACE Transformation Bei der LAPLACE-Transformation wird einer (geeigneten) Funktion f(t) eine Funktion F (s) zugeordnet. Diese Art von Transformation hat u.a. Anwendungen bei gewissen Fragestellungen
Numerik III trifft inverse Probleme
 Numerik III trifft inverse Probleme Michael Hönig Heinrich-Heine-Universität Düsseldorf Bad Neuenahr-Ahrweiler, Juli 2009 Inverse Probleme Schließen von einer beobachteten Wirkung auf deren Ursache Beispiel:
Numerik III trifft inverse Probleme Michael Hönig Heinrich-Heine-Universität Düsseldorf Bad Neuenahr-Ahrweiler, Juli 2009 Inverse Probleme Schließen von einer beobachteten Wirkung auf deren Ursache Beispiel:
Musterlösung. TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik. Wiederholungsklausur Mathematik für Physiker 3 (Analysis 2) I... II...
 ................ Note I II Name Vorname Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
................ Note I II Name Vorname Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
Musterlösung. TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik. Klausur Mathematik für Physiker 3 (Analysis 2) I... II...
 ................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Wiederholung von Linearer Algebra und Differentialrechnung im R n
 Wiederholung von Linearer Algebra und Differentialrechnung im R n 1 Lineare Algebra 11 Matrizen Notation: Vektor x R n : x = x 1 x n = (x i ) n i=1, mit den Komponenten x i, i {1,, n} zugehörige Indexmenge:
Wiederholung von Linearer Algebra und Differentialrechnung im R n 1 Lineare Algebra 11 Matrizen Notation: Vektor x R n : x = x 1 x n = (x i ) n i=1, mit den Komponenten x i, i {1,, n} zugehörige Indexmenge:
MATHEMATISCHE METHODEN DER PHYSIK 1
 MATHEMATISCHE METHODEN DER PHYSIK 1 Helmuth Hüffel Fakultät für Physik der Universität Wien Vorlesungsskriptum Sommersemester 2012 Version vom 08-03-2012 Inhaltsverzeichnis 1 Lineare gewöhnliche Differentialgleichungen
MATHEMATISCHE METHODEN DER PHYSIK 1 Helmuth Hüffel Fakultät für Physik der Universität Wien Vorlesungsskriptum Sommersemester 2012 Version vom 08-03-2012 Inhaltsverzeichnis 1 Lineare gewöhnliche Differentialgleichungen
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Differenzialgleichungen erster Ordnung
 Differenzialgleichungen erster Ordnung Fakultät Grundlagen Mai 2011 Fakultät Grundlagen Differenzialgleichungen erster Ordnung Übersicht Grundsätzliches 1 Grundsätzliches Geometrische Deutung Numerik 2
Differenzialgleichungen erster Ordnung Fakultät Grundlagen Mai 2011 Fakultät Grundlagen Differenzialgleichungen erster Ordnung Übersicht Grundsätzliches 1 Grundsätzliches Geometrische Deutung Numerik 2
7. Die eindimensionale Wärmeleitungsgleichung
 H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Hörsaalübung 6 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 28/29 Dr. Hanna Peywand Kiani Hörsaalübung 6 Differentialgleichungen I für Studierende der Ingenieurwissenschaften Autonome Systeme, Stabilität Die ins
Fachbereich Mathematik der Universität Hamburg WiSe 28/29 Dr. Hanna Peywand Kiani Hörsaalübung 6 Differentialgleichungen I für Studierende der Ingenieurwissenschaften Autonome Systeme, Stabilität Die ins
Numerik und Simulation in der Geoökologie
 1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
Analysis 1. Torsten Wedhorn. f(x) f( x) x x. (2) Die Funktion f heißt auf D differenzierbar, falls f in jedem Punkt x D differenzierbar ist.
 Analysis Torsten Wedorn 8 Differentiation (A) Differenzierbare Funktionen (B) Recenregeln für die Ableitung (C) Lokale Extrema und Mittelwertsatz (D) Ableitung und Monotonie (E) Der Satz von l Hospital
Analysis Torsten Wedorn 8 Differentiation (A) Differenzierbare Funktionen (B) Recenregeln für die Ableitung (C) Lokale Extrema und Mittelwertsatz (D) Ableitung und Monotonie (E) Der Satz von l Hospital
Exakte Differenzialgleichungen
 Exakte Differenzialleicunen In der nacfolenden Diskussion benötien wir die so. symmetrisce Darstellun einer Dl 1. Ordnun. Diese lautet (x, y) + (x, y)dy = 0. Dies entsprict im Falle (x, y) 0 der Dl y (x)
Exakte Differenzialleicunen In der nacfolenden Diskussion benötien wir die so. symmetrisce Darstellun einer Dl 1. Ordnun. Diese lautet (x, y) + (x, y)dy = 0. Dies entsprict im Falle (x, y) 0 der Dl y (x)
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Definition A-stabil. Wir betrachen das Modellproblem: y (t) = λy(t) y(0) = 1. für λ C, mit Re(λ) < 0
 Wir betrachen das Modellproblem: { (t) = λ(t) () = Definition A-stabil für λ C, mit Re(λ) < Ein Verfahren heißt absolut stabil, falls lim i i =. Sei i+ = R(z) i, z = hλ, dann die R(z) heißt Stabilitätsfunktion.
Wir betrachen das Modellproblem: { (t) = λ(t) () = Definition A-stabil für λ C, mit Re(λ) < Ein Verfahren heißt absolut stabil, falls lim i i =. Sei i+ = R(z) i, z = hλ, dann die R(z) heißt Stabilitätsfunktion.
PVK Probeprüfung FS 2017
 PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
