Übungen zur Vorlesung Funktionale Programmierung. Wintersemester 2012/2013 Übungsblatt 1
|
|
|
- Manfred Maurer
- vor 8 Jahren
- Abrufe
Transkript
1 Übungsblatt 1 Installieren Sie die Haskell-Platform ( auf ihrem Rechner. Stellen Sie zudem sicher, dass ghci zu ihrer Pfadvariablen hinzugefügt wird. Unter Windows nden Sie im Startmenü nach der Installation unter Programme -> Haskell Platform versionsnummer den Eintrag WinGHCi, der eine grasche Oberäche für den Haskell Interpreter GHCi bereitstellt. Aufgabe 1.1 GHCi-Einführung (a) Önen Sie den Texteditor Ihrer Wahl und tippen Sie folgendes Programm ab: add : : Int > Int > Int add x y = x + y Die Funktion add addiert zwei ganze Zahlen. (b) Speichern Sie das Programm in einer Datei mit der Endung.hs. Den Pfad zu der Datei nennen wir im Folgenden file. (c) Önen Sie die Kommandozeile und laden Sie die Datei mit dem interaktiven Modus des GHC (GHCi genannt), wie folgt: ghci file Sie sollten nun die folgende Ausgabe erhalten: [ 1 o f 1 ] Compiling Main ( f i l e, i n t e r p r e t e d ) Ok, modules loaded : Main. Main> (d) Rufen Sie nun die Funktion add auf, indem Sie add 1 2 eingeben und mit ENTER bestätigen. Das Ergebnis wird ausgegeben und Sie können weitere Funktionsaufrufe auswerten lassen. Um die Funktion add mehrfach zu nutzen, müssen die Parameter geklammert werden, z.b: add 3 (add 5 7). Folgende Kommandos des GHCi haben sich als nützlich erwiesen: :load file (kurz :l) läd die Datei file in den GHCi. :reload (kurz :r) läd die aktuelle Datei neu ein. Nachdem Änderungen an dem Quelltext vorgenommen wurden, kann die aktuelle Datei mit :r leicht neu geladen werden. :type ausdruck (kurz :t) :t add 1 2. zeigt den Typ des Ausdruckes ausdruck an, z.b. :t add oder :help (kurz :h) :quit (kurz :q) önet die Hilfe mit weiteren nützlichen Befehlen. beendet den GHCi.
2 Aufgabe 1.2 Fehlermeldungen des GHCi Die folgende Aufgabe enthält eine Reihe von fehlerhaften Haskell-Ausdrücken. Ziel dieser Aufgabe ist, dass Sie sich mit den Fehlermeldungen des GHCi vertraut machen. Laden Sie dazu die Datei aus Aufgabe 1 und interpretieren Sie die folgenden Ausdrücke mit dem GHCi. Versuchen Sie die Fehlermeldungen nachzuvollziehen. (a) add 3 '2' (b) add (c) Add 3 2 (d) ad 3 2
3 Übungsblatt 2 Aufgabe 2.1 Konstanten Gegeben sei die Funktion add2 von den Folien (dort r genannt) und die konstante Funktion one. add2 :: Int -> Int add2 = (+) 2 one :: Int one = 1 (a) Denieren Sie eine Konstante k :: Int, deren Auswertung die Zahl 11 liefert. Nutzen Sie dabei ausschlieÿlich die Funktionen add2 und one. (b) Denieren Sie eine Funktion add6 :: Int -> Int, die eine ganze Zahl als Parameter erhält und die Summe aus 6 und der Zahl berechnet. Nutzen Sie dafür ausschlieÿlich die Funktion add2. Aufgabe 2.2 ($)-Operator Machen Sie sich mit dem sogenannten Dollar-Operator ($) :: (a -> b) -> a -> b vertraut. (a) Denieren Sie die Konstante k aus Aufgabe 1.a) mit Hilfe des Dollar-Operators. (b) Denieren Sie die Funktion add6 aus Aufgabe 1.b) mit Hilfe des Dollar-Operators. Aufgabe 2.3 Partielle Funktionsanwendung Gegeben sei die folgende Funktion add4ints: add4ints :: Int -> Int -> Int -> Int -> Int add4ints v w x y = v + w + x + y (a) Die Funktionsanwendung in Haskell ist per Denition bekanntermaÿen linksassoziativ. Erweitern Sie dem Ausdruck add4ints um die implizit vorhandenen Klammern. (b) Linksassoziativität der Funktionsanwendung hat direkt Folgen für den Typ von Funktionen mit mehreren Argumenten. Wie sieht die explizite Klammerung für den Typ der Funktion add4ints (also Int -> Int -> Int -> Int -> Int) aus? Hinweis: Die Explikation der Klammerung erhält natürlich die Semantik des Ausdrucks.
4 Musterlösung 2 module Loesung02 where add2 :: Int -> Int add2 = (+) 2 one :: Int one = a k :: Int k = add2 ( add2 ( add2 (add2 (add2 one)))) b add6 :: Int -> Int add6 x = add2 (add2 (add2 x)) a k_dollar :: Int k_dollar = add2 $ add2 $ add2 $ add2 $ add2 one b add6_dollar :: Int -> Int add6_dollar x = add2 $ add2 $ add2 x a --((((add4ints 1) 2) 3) 4) b -- Int -> (Int -> (Int -> (Int -> Int)))
5 Übungsblatt 3 Aufgabe 3.1 Vorfahrtsregeln Gegeben sei eine Funktion add3 die folgendermaÿen deniert ist: add3 x = (+) 3 x (a) Die Ableitung des Funktionstyps sollte keine Schwierigkeiten bereiten. Die Funktion wird in folgendem Kontext aufgerufen: add3 3 * 4 Was ist das Ergebnis dieses Aufrufs - und warum? (b) Nun wird die Funktion leicht verändert aufgerufen und zwar: add3 $ 3 * 4 Wo ist der Unterschied zum vorherigen Aufruf? Welches Ergebnis liefert dieser Aufruf zurück und warum? Aufgabe 3.2 Auswertung anonymer Funktionen Reduzieren Sie die folgendenden Ausdrücke. Geben Sie dabei auch die Zwischenergebnisse an. (a) (\x -> 4 * x) $ (\y -> 3 + y) 1 (b) (\x -> 4 + x + (\x -> 3 + x) 3) 1 (c) (\f -> f (f 2)) (*3) (d) (\x f -> x + f x ) 5 (*3)
6 Aufgabe 3.3 Klassische Logik mit anonymen Funktionen Im folgenden soll gezeigt werden, dass mit anonymen Funktionen klassische Logik (1. Ordnung) realisiert werden kann. Hierzu werden zunächst die beiden Ausdrücke true = (\ x y -> x) false = (\ x y -> y) deniert. (a) Bestimmen sie die Typen der Ausdrücke true und false. Es wird nun der Implikationsoperator als logische Verknüpfung deniert: (==>) = (\ x y -> x y true) (b) Bestimmen sie den Typ von (==>). (c) Wenden sie (==>) auf alle Kombinationen von true und false an, und erstellen sie eine Wertetabelle, um zu verizieren, dass es sich wirklich um die Implikation handelt. (d) Zeigen sie, dass mit λ-ausdrücken alle klassichen logischen Verknüpfungen denierbar sind (Hinweis: Informieren sie sich darüber, welche Funktionen man hierfür mindestens denieren muss).
7 Musterlösung 3 Aufgabe 3.1 Vorfahrtsregeln (a) Addition und Multiplikation add3 :: (Num a) => a -> a add3 x = (+) 3 x add3 3 * 4 = ((+) 3 3) * 4 = 6 * 4 = 24 (b) Addition mit Dollar add3 $ 3 * 4 = add3 $ 12 = 15
8 Aufgabe 3.2 Auswertung anonymer Funktionen (a) Mit Dollar (\ x -> 4 * x) $ (\ y -> 3 + y) 1 = (\ x -> 4 * x) $ = (\ x -> 4 * x) 4 = 4 * 4 = 16 (b) Verschachtelt (\ x -> 4 + x + (\ x -> 3 + x) 3) 1 = (\ x -> 3 + x) 3 = 5 + (3 + 3) = = 11 (c) Mit Funktionsargument (\ f -> f (f 2)) (*3) = (*3) ((*3) 2) = (*3) (6) = 6 * 3 = 18 (d) Mit mehreren Argumenten (\ x f -> x + f x) 5 (*3) = (\ f -> 5 + f 5) (*3) = 5 + (*3) 5 = = 20
9 Aufgabe 3.3 Klassische Logik mit anonymen Funktionen (a) Typen von Wahrheitswerten true :: t -> f -> t true = (\ x y -> x) false :: t -> f -> f false = (\ x y -> y) (b) Implikationstyp (==>) :: (a -> (t -> f -> t) -> r) -> a -> r (==>) = (\ x y -> x y true) (c) Wertetabelle false ==> false = (\ x y -> x y true) false false = false false true = (\ x y -> y) false true = (\ y -> y) true = true false ==> true = (\ x y -> x y true) false true = false true true = (\ x y -> y) true true = (\ y -> y) true = true true ==> false = (\ x y -> x y true) true false = true false true = (\ x y -> x) false true = (\ y -> false) true = false true ==> true = (\ x y -> x y true) true true = true true true = (\ x y -> x) true true = (\ y -> true) true = true (d) NAND-Vollständigkeit OBDD: x true false y true false true false true Teilbäume links und rechts in x und y einsetzen ergibt:
10 nand :: (r -> (t -> f -> t) -> r) -> ((t -> f -> f) -> (t -> f -> t) -> r ) -> r nand = (\ x y -> x (y false true) true) Ausfürhlich: nand false = (\ x y -> x (y false true) true) false = (\ y -> false (y false true) true) = (\ y -> true) nand true false = (\ x y -> x (y false true) true) true false = (\ y -> true (y false true) true) false = (\ y -> y false true) false = false false true = true nand true true = (\ x y -> x (y false true) true) true true = (\ y -> true (y false true) true) true = (\ y -> y false true) true = true false true = false
11 Übungsblatt 4 Aufgabe 4.1 Listen (a) Denieren Sie eine Haskell-Funktion removeoddvalues :: [Int] -> [Int], die alle ungeraden Listenelemente entfernt. (b) Denieren Sie eine Funktion collapse :: (a -> a -> a) -> a -> [a] -> a, die einen kommutativen Operator op :: a -> a -> a, einen Startwert vom Typ e :: a und eine Eingabeliste vom Typ xs :: [a] erhält. Für die leere Liste soll der Startwert e zurückgegeben werden, während bei einer nichtleeren Liste der Operator auf das erste Listenelement und den Wert von collapse für die Restliste angewandt wird. Beispielsweise sollte der Ausdruck collapse (+) 0 [1,2,3,4] zu dem Wert 10 reduzieren. Aufgabe 4.2 Unendliche Listen (a) Denieren Sie eine unendliche Liste squares :: [Integer], die alle Quadratzahlen enthält. Hinweis: mit der Funktion take :: Int -> [a] -> [a] können Sie auf die ersten Listenelemente von Listen zugreifen dies gilt auch für unendliche Listen. (b) Denieren Sie eine unendliche Liste triangle :: [[Int]], die sich zu einer Liste von Listen von der folgenden Form reduziert: []:[1]:[1,2]:[1,2,3]:[1,2,3,4]... Hinweis: bei dieser Aufgabe könnte die Funktion map :: (a -> b) -> [a] -> [b] hilfreich sein. Quizfragen: Beantworten Sie die folgenden Fragen ohne Compiler-Unterstützung. Beachten Sie, dass die leere Liste [] vom Typ [a] und der sogenannte Cons-Operator (:) vom Typ a -> [a] -> [a] ist. (a) Von welchem Typ ist der Ausdruck []:[[]]:[[[]]]? Was ändert sich, wenn wir die Konstruktion unendlich oft fortführen? (b) Was passiert, wenn die inneren Listen mit Werten gefüllt werden, also zum Beispiel der folgende Fall eintritt: ['a']:[['a']]:[[['a']]]?
12 Musterlösung 4 Aufgabe 4.1 Listen (a) removeoddvalues :: [Int] -> [Int] removeoddvalues [] = [] removeoddvalues (x:xs) odd x = removeoddvalues xs otherwise = x : removeoddvalues xs (b) Es existieren zwei mögliche Denitionen für collapse, die sich in der Anwendungsreihenfolge des Operators unterscheiden: -- Operator linksassoziativ anwenden collapsel :: (a -> a -> a) -> a -> [a] -> a collapsel _ e [] = e collapsel op e (x:xs) = collapsel op (op e x) xs -- Operator rechtsassoziativ anwenden collapser :: (a -> a -> a) -> a -> [a] -> a collapser _ e [] = e collapser op e (x:xs) = op x $ collapser op e xs
13 Aufgabe 4.2 Unendliche Listen (a) Quadratzahlen squares :: [Int] squares = map (\x -> x*x) [1,2..] -- list comprehension squarescompr :: [Int] squarescompr = [ x*x x <- [1,2..]] -- Rekursion squaresrec :: [Int] squaresrec = squaresrec' 1 where squaresrec' :: Int -> [Int] squaresrec' n = (n * n) : squaresrec' (n+1) (b) triangle triangle :: [[Int]] triangle = map (\x -> [1..x]) [0,1..] trianglecompr :: [[Int]] trianglecompr = [ [1..x] x <- [0,1..]] trianglerec :: [[Int]] trianglerec = trianglerec' 0 where trianglerec' :: Int -> [[Int]] trianglerec' 0 = []: trianglerec' 1 trianglerec' n = [1..n]: trianglerec' (n+1) Quizfragen: (a) Der Typ von []:[[]]:[[[]]] ist [[[a]]]. Der folgende Haskell-Ausdruck deniert die unendliche Fortsetzung dieser Konstruktion: iterate (\x -> [x]) [] (b) Wir erhalten einen Typfehler, weil kein gröÿtes Element existiert, das die maximale Verschachtelungstiefe beschränkt. Der Trick, dass das erste Element [] genau die leere Liste vom Typ [[a]] ist, funktioniert nur wenn endlich viele Listen verschachtelt werden.
14 Übungsblatt 5 Aufgabe 5.1 Listen (a) Denieren Sie eine Funktion deletechar :: Char -> String -> String, die eine neue Liste erzeugt, die keine Vorkommen des übergebenen Zeichens enthält. (b) Welche Gemeinsamkeiten haben die Funktionen removeoddvalues von Blatt 4 und die Funktion deletechar? Lässt sich von einer gemeinsamen Struktur abstrahieren? Aufgabe 5.2 Komposition (a) Informieren Sie sich über die Funktionskomposition in Haskell. Wie ist der Typ der Funktionskomposition und worin bestehen Unterschiede zum Dollar-Operator? Formulieren Sie dazu die folgende Lösung von Aufgabe 2.2.b) (Blatt 2) unter Verwendung der Komposition neu: add2 :: Int -> Int add2 = (+2) add6 :: Int -> Int add6 x = add2 $ add2 $ add2 x (b) Reduzieren Sie den folgenden Haskell-Ausdruck: ((\x -> 4 * x). (\y -> 3 + y)) 1
15 Aufgabe 5.3 Listen (a) Schreiben Sie eine Haskell-Funktion asciiquersumme :: String -> Int, die zuerst jedes Zeichen in seinen ASCII-Code überführt. Im Anschluss daran soll die Summe von allen ASCII- Codes berechnet werden. Nutzen Sie zur Umformung eines Zeichens in seinen ASCII-Code die Funktion ord :: Char -> Int, die von dem Modul Data.Char angeboten wird. Sie binden das Modul mit dem Befehl import Data.Char am Anfang ihrer Quellcodedatei ein. Zur Berechnung der Summe eignet sich die Funktion collapse von Blatt 4. (b) Schreiben Sie eine Funktion, die eine Liste von als String abgespeicherten Studiengängen und eine Liste von als Int abgespeicherten Matrikelnummern erhält. Die Funktion soll zunächst die beiden Listen mit zip zusammenfügen, um die Zuordnung von Matrikelnummern zu Studiengängen zu erzeugen. Anschlieÿend soll sie eine Liste zurückgeben, die alle Matrikelnummern enthält, denen der Studiengang Diplom zugeordnet wurde. Beispiel: studiengaenge :: [String] studiengaenge = ["Bachelor","Diplom","Bachelor","Diplom","Diplom"] matrikelnr :: [Int] matrikelnr = [31,42,312,89,55,62] Die Funktion soll beispielsweise für die Argumente studiengaenge und matrikelnr zu der Liste [42,89,55] reduzieren.
16 Musterlösung 5 Aufgabe 5.1 (a) deletechar :: Char -> String -> String deletechar _ [] = [] deletechar c (x:xs) c==x = deletechar c xs otherwise = x : deletechar c xs (b) removeoddvalues :: [Int] -> [Int] removeoddvalues [] = [] removeoddvalues (x:xs) odd x = removeoddvalues xs otherwise = x : removeoddvalues xs filt :: (a -> Bool) -> [a] -> [a] filt _ [] = [] filt p (x:xs) p x = filt p xs otherwise = x : filt p xs deletecharf :: Char -> String -> String deletecharf char = filt (\x -> x==char) removeoddvaluesf :: [Int] -> [Int] removeoddvaluesf = filt odd Funktion filter :: (a -> Bool) -> [a] -> [a] existiert bereits - jedoch mit umgekehrter Semantik, so dass sich die Lösungen mit filter wie folgt ergeben: deletecharfilter :: Char -> String -> String deletecharfilter char = filter (\x -> x/=char) removeoddvaluesfilter :: [Int] -> [Int] removeoddvaluesfilter = filter even
17 Aufgabe 5.2 Komposition -- Definition der Komposition: (.) :: (b -> c) -> (a -> b) -> (a -> c) f. g = \ x -> f (g x) (a) add2 :: Int -> Int add2 = (+2) add6 :: Int -> Int add6 = add2. add2. add2 (b) ((\x -> 4 * x). (\y -> 3 + y)) 1 ==> (\x -> 4 * x) ( (\y -> 3 + y) 1) ==> 4 * ( (\y -> 3 + y) 1) ==> 4 * (3+1) ==> 16 Aufgabe 5.3 Listen (a) -- Funktion collapse ist von Blatt 4 bekannt collapse :: (a -> a -> a) -> a -> [a] -> a collapse _ e [] = e collapse op e (x:xs) = op x $ collapse op e xs asciiquersumme :: String -> Int asciiquersumme xs = summe $ map ord xs summe :: [Int] -> Int summe xs = collapse (+) 0 xs -- kürzere Variante mit Benutzung von Funktion sum -- aus der Standardbibliothek ascii :: String -> Int ascii = sum. map ord (b) studiengaenge :: [String] studiengaenge = ["Bachelor","Diplom","Bachelor","Diplom","Diplom"] matrikelnr :: [Int] matrikelnr = [31,42,312,89,55,62] getdiplomer :: [String] -> [Int] -> [Int] getdiplomer ss ms = map snd $ filter (\(s,_) ->s=="diplom") $ zip ss ms
18 Übungsblatt 6 Aufgabe 6.1 Reduktion f x y z = (take x. map (\a -> (a,y a)). filter even) z (a) Bestimmen Sie den Typ der Funktion f. (b) Verdeutlichen Sie sich das Verhalten bei der Reduktion dieser Funktion, indem Sie sich beispielhaft Werte für die Argumente überlegen. Aufgabe 6.2 Punktfreie Notation Betrachten sie den λ-ausdruck (\ x -> f x) 3. Die bekannten Reduktionsregeln ergeben oensichtlich, dass der Ausdruck reduziert identisch ist zu f 3. Die benannte (gebundene) Variable x war also nicht zwingend erforderlich. Wir wissen bereits, dass Funktionen in klassischer Notation oder in λ-notation deniert werden können. Dementsprechend kann man die obige Beobachtung analog für benannte Funktionen machen: f :: a -> b f x =... g :: a -> b g x = f x (g x) 3 = g 3 = f 3 Lassen wir die gebundene Variable x weg, so erhalten wir g :: a -> b g = f Diese Notation wird in der Literatur als /Pointfree/-Notation bezeichnet. (a) Formen Sie die folgenden Ausdrücke in Pointfree-Notation um: manyodd :: [Int] -> [Bool] manyodd xs = map (\ x -> odd x) xs plusdrei :: [Int] -> [Int] plusdrei xs = map (\ x -> add 3 x) xs (b) Implementieren sie eine Funktion sum :: [Int] -> Int unter verwendung der Funktion collapse von Übungsblatt 4, die eine Liste aufsummiert. Verwenden sie bei ihrer Implementierung die Pointfree-Notation.
19 Aufgabe 6.3 Binärkodierung (a) Schreiben Sie eine Haskell-Funktion stringtobinary :: String -> [Int], die eine Zeichenkette in ihre Binärkodierung basierend auf dem ASCII-Wert der Zeichen umformt. Die Binärkodierung wird als Int-Liste mit 0 und 1 als Werten repräsentiert. Gehen Sie davon aus, dass die Funktion ord :: Char -> Int nur Werte zwischen 0 und 127 liefert. Um die Funktion stringtobinary später umkehren zu können, muss sichergestellt werden, dass jede Kodierung eines Zeichens mit führenden Nullen aufgefüllt wird, sofern die Kodierung eine kürzere Länge als 7 (2 7 = 128) hat. Die Länge der durch die Funktion stringtobinary erzeugten Listen ist somit immer durch 7 teilbar. Beispiel: stringtobinary "a b" ==> [1,1,0,0,0,0,1,0,1,0,0,0,0,0,1,1,0,0,0,1,0] (b) Schreiben Sie eine Funktion binarytostring :: [Int] -> String, die genau die Umkehrfunktion zu stringtobinary darstellt. Folgende Bedingung muss also gelten: binarytostring. stringtobinary = id Die Bedingung stringtobinary. binarytostring = id gilt nicht nur für Listen, deren Länge ein Vielfaches von 7 ist. Folgende Funktionen könnten sich bei dieser Aufgabe als hilfreich herausstellen: mod :: Int -> Int -> Int -- Modulo-Operation div :: Int -> Int -> Int -- ganzzahlige Division ord :: Char -> Int chr :: Int -> Char -- ASCII-Repräsentation eines Zeichens -- Umkehrfunktion zu ord Die letzten beiden Funktionen nden Sie im Modul Data.Char, das Sie mit import Data.Char zu Beginn der Haskell-Datei importieren.
20 Musterlösung 6 Aufgabe 6.1 Typisierung und Reduktion (a) f x y z = (take x. map (\a -> (a,y a)). filter even) z -- Annahme: even :: Int -> Bool f :: Int -> (Int -> a) -> [Int] -> [(Int, a)] -- Annahme: even :: Integral a => a -> Bool f :: Integral t1 => Int -> (t1 -> t2) -> [t1] -> [(t1, t2)] (b) f 0 id [0..] ==> (take 0. map (\a -> (a,id a)). filter even) [0..] ==> take 0 (map (\a -> (a,id a)) (filter even [0..]) ) -- Definition der Komposition ==> [] -- Definition von take f 2 (+7) [1,2,3,4] ==> (take 2. map (\a -> (a,(+7) a)). filter even) [0,1,2,3,4] ==> take 2 (map (\a -> (a,(+7) a)) (filter even [0,1,2,3,4])) ==> (0,(+7) 0) : take 1 (map (\a -> (a,(+7) a)) (filter even [1,2,3,4])) ==> (0,(+7) 0) : (2,(+7) 2) : take 0 (map (\a -> (a,(+7) a)) (filter even [3,4])) ==> (0,(+7) 0) : (2,(+7) 2) : [] ==> [(0,7),(2,9)] -- Angenommen wir entfernen den Teil mit filter aus der Definition: f 2 (+7) [1,2,3,4] ==> (take 2. map (\a -> (a,(+7) a))) [0,1,2,3,4] ==> take 2 (map (\a -> (a,(+7) a)) [0,1,2,3,4]) ==> (0,(+7) 0) : take 1 (map (\a -> (a,(+7) a)) [1,2,3,4]) ==> (0,(+7) 0) : (1,(+7) 1) : take 0 (map (\a -> (a,(+7) a)) [2,3,4]) ==> (0,(+7) 0) : (1,(+7) 1) : [] ==> [(0,7),(1,8)] Aufgabe 6.2 Punktfreie Notation (a) manyodd :: [Int] -> [Bool] manyodd = map odd plusdrei :: [Int] -> [Int] plusdrei = map (+3) (b) sum in punktfreier Notation: sum :: [Int] -> Int sum = collapse (+) 0
21 Aufgabe 6.3 Binärcodierung (a) Umformung einer Zeichenkette in ihre Binärkodierung, wobei jedes Zeichen mit einem Bitstring der Länge 7 repräsentiert wird. -- überführt Zahl in Dezimalsystem in Bitstring tobinary :: Int -> [Int] tobinary i i > 1 = tobinary (div i 2) ++ [i `mod` 2] otherwise = [i `mod` 2] -- füllt die Eingabeliste mit führenden Nullen auf, falls Länge kleiner als n fill :: Int -> [Int] -> [Int] fill n xs length xs < n = take (n-length xs) [0,0..] ++ xs otherwise = xs stringtobinary :: String -> [Int] stringtobinary = concatmap (fill 7. tobinary. ord) -- Alternative: erzeugt Repräsentation der gegebenen Länge (kein fill mehr nötig) tobinary2 :: Int -> Int -> [Int] tobinary2 stellen x = map (\ i -> (x `div` 2^i) `mod` 2) [stellen-1, stellen-2.. 0] -- mit alternativer tobinary Implementierung: stringtobinary :: String -> [Int] stringtobinary = concatmap (tobinary2 7. ord) (b) Umkehrfunktion zu stringtobinary. binarytostring :: [Int] -> String binarytostring = map (chr. frombinary). splitbuckets 7 -- zerlegt die Eingabeliste in Listen von Listen der Länge n splitbuckets :: Int -> [Int] -> [[Int]] splitbuckets _ [] = [] splitbuckets n xs = take n xs : splitbuckets n (drop n xs) -- überführt Bitstring in Dezimalsystem frombinary :: [Int] -> Int frombinary is = sum $ zipwith (\p i -> i * 2^p) [0,1..] (reverse is)
22 Übungsblatt 7 Aufgabe 7.1 Die Funktion flip (a) Welchen Typ hat die Funktion flip? (b) Was ist der Typ von flip take? (c) Wozu könnte die Funktion flip hilfreich sein? Aufgabe 7.2 Umkehren von Listen als Faltung In dieser Aufgabe soll eine Funktion zur Umkehrung einer Liste (Typ: [a] -> [a]) auf zwei verschiedene Arten deniert werden. (a) Denieren Sie eine Funktion revl :: [a] -> [a], indem Sie foldl nutzen. (b) Denieren Sie eine Funktion revr :: [a] -> [a], indem Sie foldr nutzen. (c) Vergleichen Sie beide Implementierungen welche würden Sie bevorzugen und warum? Aufgabe 7.3 Faltungen von Funktionslisten (a) Denieren Sie eine Konstante fs :: [Int -> Int] mit der folgenden Struktur: Abwechselnd wird die Summe und das Produkt gebildet. Diese Funktionen werden partiell auf die entsprechenden Elemente der Liste [1,2..] angewandt, so dass die ungeraden Elemente summiert und die gerade Elemente multipliziert. Die ersten Listenelemente sollen sich wie folgt ergeben: [(+1),(*2),(+3),(*4),(+5),(*6),..] Diese Liste kann als Beispieleingabe für die folgenden beiden Aufgabenteile benutzt werden. (b) Schreiben Sie eine Funktion foldlfunc :: [a -> a] -> a -> a, die eine Liste von Funktionen von links auf einen Startwert anwendet. Nutzen Sie foldl für Ihre Implementierung. Beispiel: foldlfunc [f,g,h] x ==> (h (g (f x))) (c) Schreiben Sie eine Funktion foldrfunc :: [a -> a] -> a -> a, die eine Liste von Funktionen von rechts auf einen Startwert anwendet. Nutzen Sie foldr für Ihre Implementierung. Beispiel: foldrfunc [f,g,h] x ==> (f (g (h x)))
23 Musterlösung 7 Aufgabe 7.1 Die Funktion flip flip :: (a -> b -> c) -> b -> a -> c take :: Int -> [a] -> [a] flip take :: [a] -> Int -> [a] Die Funktion flip wird häug genutzt, um Funktionen in punktfreier Notation zu denieren. Vergleiche dazu die folgenden beiden (semantisch äquivalenten) Funktionen f und g: f :: Int -> [Int] f x = take x [1,2..] g :: Int -> [Int] g = flip take [1,2..] Aufgabe 7.2 Listen umkehren mit Faltungen (a) revfoldl :: [a] -> [a] revfoldl = foldl (\xs x -> x : xs) [] -- alternativ mit flip revfoldl = foldl (flip (:)) [] (b) revfoldr :: [a] -> [a] revfoldr = foldr (\x xs -> xs++[x]) [] (c) Die Funktion revfoldl ist ezienter, weil die Operation (:) konstante Zeit benötigt, während xs++[x] die komplette Liste xs durchlaufen muss.
24 Aufgabe 7.3 Faltungen von Funktionsanwendungen (a) -- [(+1),(*2),(+3),(*4),(+5),(*6),..] fs :: [Int -> Int] fs = zipwith (\op x -> op x) ops [1,2..] -- kurz: fs = zipwith ($) ops [1,2..] ops :: [Int -> Int -> Int] ops = [(+),(*)]++ops -- alternative ops = cycle [(+),(*)] -- cycle ist eine Funktion aus der Haskell-Prelude cycle :: [a] -> [a] cycle [] = [] cycle xs@(_:_) = xs ++ cycle xs (b) -- Gewünschtes Verhalten: foldlfunc [f,g,h] x ==> (h (g (f x))) foldlfunc :: [a -> a] -> a -> a foldlfunc fs x = foldl (\x f -> f x) x fs -- alternativ: foldlfunc fs x = foldl (flip ($)) x fs (c) -- Gewünschtes Verhalten: foldrfunc [f,g,h] x ==> (f (g (h x))) foldrfunc :: [a -> a] -> a -> a foldrfunc fs x = foldr (\f x -> f x) x fs --alternativ: foldrfunc fs x = foldr ($) x fs
25 Übungsblatt 8 Aufgabe 8.1 Modellierung (a) Modellieren Sie einen Datentyp mit den folgenden Eigenschaften. Denieren Sie geschickt eigene Typen, um die Modellierung besser zu strukturieren. Eine Firma hat mehrere Abteilungen. Jede Abteilung hat einen Manager und mehrere Mitarbeiter. Manager und Mitarbeiter haben einen Namen und ein Wert für das monatliche Gehalt. (b) Geben Sie eine nichttriviale Beispielinstanz des Datentyps an. (c) Schreiben Sie eine Funktion, die einen Wert des Typs Firma erhält und das Gehalt der Mitarbeiter verdoppelt. Aufgabe 8.2 Binärbäume (a) Denieren Sie einen rekursiven Datentypen BinTree für Binärbäume nach den folgenden Regeln: Ein Binärbaum ist entweder leer oder ein Knoten mit einem Int-Wert und zwei Binärbäumen als Nachfolger. (b) Schreiben Sie eine Haskell-Funktion sumall :: BinTree -> Int, die die Summe aller Werte in dem Baum berechnet. (c) Schreiben Sie eine Haskell-Funktion preorder :: BinTree -> [Int], die den Baum in Preorder- Reihenfolge durchläuft und die Werte der Knoten in dieser Reihenfolge zurückgibt. (d) Schreiben Sie eine Haskell-Funktion mapbintree :: (Int -> Int) -> BinTree -> BinTree, die die übergebene Funktion an jedem Knoten anwendet. (e) Schreiben Sie eine Haskell-Funktion holdseverywhere :: (Int -> Bool) -> BinTree -> Bool, die überprüft, ob das Prädikat an jedem Knoten gilt. (f) Schreiben Sie eine Faltungsfunktion foldbintree :: (Int -> a -> a -> a) -> a -> BinTree -> a so dass der erste Parameter das Verhalten für innere Knoten festlegt, während der zweite Parameter angibt was mit einem leeren Baum passiert. Überlegen Sie sich, wie foldbintree zur Lösung der vorherigen Teilaufgaben genutzt werden kann.
26 Musterlösung 8 Aufgabe 8.1 Modellierung data Firma = Firma { abteilungen :: [Abteilung] } deriving Show data Abteilung = Abteilung { manager :: Manager, mitarbeiter :: [Mitarbeiter] } deriving Show data Manager = Manager { managername :: String, managergehalt :: Float } deriving Show data Mitarbeiter = Mitarbeiter { mitarbeitername :: String, mitarbeitergehalt :: Float} deriving Show meinefirma :: Firma meinefirma = Firma [Abteilung (Manager "Manager" 1000) [Mitarbeiter "Mitarbeiter" 800] ] incsalary :: Firma -> Firma incsalary (Firma as) = Firma $ map incsalaryabt as incsalaryabt :: Abteilung -> Abteilung incsalaryabt (Abteilung manager ms) = Abteilung manager $ map incsalarymit ms incsalarymit :: Mitarbeiter -> Mitarbeiter incsalarymit (Mitarbeiter n s) = Mitarbeiter n (s*2)
27 Aufgabe 8.2 Binärbäume data BinTree = Empty Branch Int BinTree BinTree deriving Show -- rekursive Lösungen sumall :: BinTree -> Int sumall Empty = 0 sumall (Branch i t1 t2) = i + sumall t1 + sumall t2 preorder :: BinTree -> [Int] preorder Empty = [] preorder (Branch i t1 t2) = i : preorder t1 ++ preorder t2 mapbintree :: (Int -> Int) -> BinTree -> BinTree mapbintree _ Empty = Empty mapbintree f (Branch i t1 t2) = Branch (f i) (mapbintree f t1) (mapbintree f t2) holdseverywhere :: (Int -> Bool) -> BinTree -> Bool holdseverywhere _ Empty = True holdseverywhere p (Branch i t1 t2) = p i && holdseverywhere p t1 && holdseverywhere p t2 -- Definition von fold fold :: (Int -> a -> a -> a) -> a -> BinTree -> a fold _ e Empty = e fold f e (Branch i t1 t2) = f i (fold f e t1) (fold f e t2) -- fold-basierte Lösung sumfold :: BinTree -> Int sumfold = fold (\i x1 x2 -> i+x1+x2) 0 preorderfold :: BinTree -> [Int] preorderfold = fold (\i x1 x2 -> i : x1 ++ x2) [] mapfold :: (Int -> Int) -> BinTree -> BinTree mapfold f = fold (\i x1 x2 -> Branch (f i) x1 x2) Empty holdseverywherefold :: (Int -> Bool) -> BinTree -> Bool holdseverywherefold p = fold (\i x1 x2 -> (p i) && x1 && x2) True
28 Übungsblatt 9 Aufgabe 9.1 Intervalle (a) Denieren Sie einen Datentyp Interval für Intervalle [x, y), wobei die Intervallgrenzen vom Typ Float sein sollen. Geben Sie eine Instanz für die Typklasse Show an, um Intervalle anzeigen zu können. (b) Denieren Sie eine Funktion compatible :: Interval -> Interval -> Bool. Zwei Intervalle sind kompatibel, wenn sie sich nicht überlappen. (c) Denieren Sie eine Funktion split :: Interval -> (Interval,Interval), die ein Interval in zwei gleich groÿe Intervalle aufteilt. Beispiel: split (Interval 0 1.0) ==> (Interval 0 0.5, Interval 0.5 1) Aufgabe 9.2 unendliche Datentypen (a) Denieren Sie einen Datentyp BinTreeInf a für unendliche Bäume, die Elemente vom Typ a enthalten. (b) Gegeben sei der Typ für endliche Binärbäume BinTree a: data BinTree a = Empty BinTree a (BinTree a) (BinTree a) Denieren Sie eine Funktion takeinf :: Int -> BinTreeInf a -> Bintree a, die die ersten n Ebenen eines unendlichen Baumes zurückgibt. (c) Denieren Sie eine Funktion buildtree :: (a -> (a,a)) -> a -> BinTreeInf a, die einen unendlichen Baum erzeugt, wobei die übergebene Funktion aus einem Wert die Werte für den linken bzw. rechten Nachfolger bestimmt. Beispielsweise soll die Funktion buildtree split (Interval 0 1.0) zu einem unendlichen Baum reduzieren, bei dem an jedem inneren Knoten die Intervalle geteilt werden. (d) Denieren Sie Instanzen der Typklasse Functor für BinTree und BinTreeInf
29 Aufgabe 9.3 Collections (a) Denieren Sie einen Datentyp Collection a, der als Attribute eine Liste [a] und ein Prädikat a -> [a] -> Bool hat. Die Semantik der Collections ist, dass Werte x nur dann in die Liste xs aufgenommen werden, wenn das Prädikat p für x und xs als Argumente True liefert. Das Prädikat gibt also an, ob ein Wert einen Informationsgewinn liefert. Geben Sie eine Instanz der Typklasse Show für den Typ Collection an. (b) Denieren Sie eine Funktion empty :: (a -> [a] -> Bool) -> Collection a, die eine leere Collection mit einem gegebenen Prädikat erzeugt. (c) Denieren Sie eine Funktion ins :: a -> Collection a -> Collection a, die einen Wert in die Collection aufnimmt, wenn das Prädikat für die aktuelle Liste und den einzufügenden Wert True liefert. (d) Denieren Sie ein Modul Collection, das den Typ Collection und die beiden Funktionen empty und insert exportiert. Der Konstruktor für den Typ Collection wird nicht exportiert, da neue Collections durch die Funktionen empty und ins deniert werden sollen. (e) Denieren Sie ein neues Modul, das das Modul Collection importiert. Denieren Sie in diesem Modul eine leere Collection Int, die einen Wert nur dann aufnimmt, wenn dieser noch nicht enthalten ist. Denieren Sie in diesem Modul eine leere Collection Int, die solange neue Werte aufnimmt wie die Summe der Werte in der Liste kleiner als 50 ist. Denieren Sie zudem eine leere Collection Interval, die ein Intervall nur dann aufnimmt, wenn es kompatibel zu allen Intervallen in der ursprünglichen Collection ist. Überprüfen Sie das Verhalten der Collections, indem Sie beispielhaft Werte einfügen.
30 Musterlösung 9 Aufgabe 9.1 Intervalle data Interval = Interval { lower:: Float, upper :: Float } interval :: Float -> Float -> Interval interval a b a < b = Interval a b a > b = Interval b a instance Show Interval where show (Interval l u) = "["++show l++","++show u++")" overlaps :: Interval -> Interval -> Bool overlaps (Interval a b) (Interval x y) = x < b && a < y compatible :: Interval -> Interval -> Bool compatible i j = not (overlaps i j) split :: Interval -> (Interval, Interval) split (Interval a b) = let m = (a + b) / 2 in (Interval a m, Interval m b) Aufgabe 9.2 unendliche Binärbäume data BinTreeInf a = InfBranch a (BinTreeInf a) (BinTreeInf a) data BinTree a = Empty Branch a (BinTree a) (BinTree a) deriving Show takeinf :: Int -> BinTreeInf a -> BinTree a takeinf 0 _ = Empty takeinf n (InfBranch v t1 t2) = Branch v (takeinf (n-1) t1) (takeinf (n-1) t2) buildtree :: (a -> (a,a)) -> a -> BinTreeInf a buildtree f x = InfBranch x (buildtree f (fst $ f x)) (buildtree f (snd $ f x)) instance Functor BinTreeInf where fmap f (InfBranch x t1 t2) = InfBranch (f x) (fmap f t1) (fmap f t2) instance Functor BinTree where fmap _ Empty = Empty fmap f (Branch x t1 t2) = Branch (f x) (fmap f t1) (fmap f t2)
31 Aufgabe 9.3 Der Datentyp Collection data Collection a = Collection [a] (a -> [a] -> Bool) instance Show a => Show (Collection a) where show (Collection xs _) = show xs ins :: a -> Collection a -> Collection a ins x (Collection xs new) new x xs = Collection (x:xs) new otherwise = Collection xs new empty :: (a -> [a] -> Bool) -> Collection a empty p = Collection [] p intervalcompatibleset :: Collection Interval intervalcompatibleset = ins (Interval ) $ ins (Interval ) $ ins (Interval ) $ empty (\x xs -> all (compatible x) xs) eqbasedset :: Collection Int eqbasedset = ins 4 $ ins 4 $ ins 1 $ empty notelem sumlessthan :: Collection Int sumlessthan = ins 10 $ ins 20 $ ins 5 $ ins 30 $ empty (\x xs -> 50 > sum (x:xs)) list :: Collection Int list = ins 4 $ ins 4 $ ins 1 $ empty (\ -> True)
32 Übungsblatt 10 Aufgabe 10.1 λ-kalkül In dieser Aufgabe sollen einzelne Funktionalitäten des λ-kalküls implementiert werden. Gegeben sei dazu folgender Datentyp für Termvariablen: data Var = Var { var :: String } (a) Denieren Sie einen Datentyp Lambda für λ-terme nach folgenden Vorgaben: jede Termvariable ist ein λ Term. für zwei λ-terme P und Q ist (P Q) ein λ-term (Applikation). für eine Termvariable x und einen λ Term P ist (λx.p ) ein λ-term (λ Abstraktion). Implementieren Sie zudem eine Instanz der Typklasse Show für den Typ Lambda. (b) Repräsentieren Sie die Funktionen true, false und die Implikation von Übungsaufgabe 3.3 als Werte des Typs Lambda. (c) Implementieren Sie eine Funktion freshtermvar :: Lambda -> Var, die für einen gegebenen λ-ausdruck eine Variable zurückgibt, die nicht in dem λ-term vorkommt. (d) Die freien Variablen F V (P ) eines λ-terms P sind die Termvariablen in P, die nicht durch eine λ-abstraktion gebunden sind. Implementieren Sie eine Haskell-Funktion freevars :: Lambda -> [Var], die die freien Variablen eines λ-terms bestimmt. (e) Die Substitution [P/x]Q ersetzt P für jedes freie Vorkommen der Variable x in Q. [P/x]x = N (1) [P/x]y = y, mit x y (2) [P/x](M N) = (([P/x]M) ([P/x]N)) (3) [P/x](λx.N) = λx.n (4) [P/x](λy.N) = λy.n, falls x y und x / F V (N) (5) [P/x](λy.N) = λy.[p/x]n, falls x F V (N) und y / F V (P ) (6) [P/x](λy.N) = λz.[p/x][z/y]n, falls x F V (N) und y F V (P ) (7) In Fall (7) ist z eine frische Termvariable, die nicht in (P N) vorkommt (vgl. Aufgabenteil 10.1.c). Hinweis: der Fall (7) fängt die Situation ab, dass eine ehemals freie Variable durch die Substitution gebunden wird: durch [y/x]λy.x darf nicht die Identitätsfunktion λy.y entstehen, sondern wir ersetzen vor der eigentlichen Substitution alle Vorkommen von y durch eine frische Variable z: Anwendung der Substitution [y/x][z/y]λy.x liefert [y/x]λz.x. Weitere Anwendung der Denition führt zu λz.y.
33 (f) Ein β-redex ist ein Teilterm eines λ-terms der Form (λx.p )Q. Ein λ-term kann durchaus mehrere β-redexe enthalten. Die Ersetzung eines β-redexes (λx.p )Q durch [Q/x]P nennen wir β-reduktion. Es hat sich als sinnvoll erwiesen, dass immer der äuÿerste, linke β-redex reduziert wird. Denieren Sie eine Haskell-Funktion betareduction :: Lambda -> Lambda, die in einem λ- Term den äuÿersten, linken β-redex wie oben gezeigt ersetzt. Achten Sie bei der Applikation (siehe. Teil (a)) darauf, dass betareduction nur maximal einen β-redex substituiert. (g) Ein λ-term ist in β-normalform, wenn er keine β-redexe enthält. Schreiben Sie eine Haskell- Funktion betanormalform :: Lambda -> Lambda, die die β-normalform eines λ-terms berechnet. (h) Lassen Sie von der Funktion betanormalform die β-normalform der Anwendungen der Implikation auf die vier Kombinationen der Wahrheitswerte berechnen, zum Beispiel betanormalform (impl `App` true `App` false), wobei impl, true, false :: Lambda aus Aufgabe 10.1.b und App :: Lambda -> Lambda -> Lambda der Konstruktor für die Applikation sei.
34 Musterlösung 10
35 Aufgabe 10.1 Lambda-Kalkül module Lambda where import Data.List data Var = Var { var :: String } deriving Eq instance Show Var where show (Var v) = v -- a) datentyp für lambda-formeln data Lambda = Lambda Var Lambda App Lambda Lambda LVar Var deriving Eq instance Show Lambda where show (LVar v) = show v show (App (LVar v1) (LVar v2)) = show v1 ++" "++ show v2 show (App e1 e2) = "("++show e1++") ("++show e2++")" show t@(lambda ) = let (vs,p) = multipleabstractions t in" \\"++(concatmap (\v -> show v ++" ") vs) ++ ". ("++show p++")" -- hilfsfunktion, um \x \y.... als \x y. darzustellen multipleabstractions :: Lambda -> ([Var],Lambda) multipleabstractions = helper [] where helper :: [Var] -> Lambda -> ([Var],Lambda) helper vs (Lambda v e) = helper (vs++[v]) e helper vs e = (vs,e) -- b) repräsentation von boolescher algebra x,v,z :: Var x = Var "x" z = Var "z" v = Var "v" true :: Lambda true = Lambda x (Lambda v (LVar x)) false :: Lambda false = Lambda x (Lambda v (LVar v)) implication :: Lambda implication = Lambda x $ Lambda z $ (LVar x) `App` (LVar z) `App` true -- c) liefert eine variable zurück, die nicht im lambda-term vorkommt freshtermvar :: Lambda -> Var freshtermvar = Var. (++"'"). maximumby len. map var. vars where len :: [a] -> [a] -> Ordering len x y = compare (length x) (length y) vars :: Lambda -> [Var] vars (LVar v) = [v] vars (App p q) = union (vars p) (vars q) vars (Lambda v e) = union [v] (vars e)
36 -- d) freie variablen eines lambda-terms freevars :: Lambda -> [Var] freevars (LVar v) = [v] freevars (App p q) = union (freevars p) (freevars q) freevars (Lambda v e) = delete v $ freevars e -- e) substitution sub :: Var -> Lambda -> Lambda -> Lambda sub x n (LVar y) x == y = n x /= y = LVar y sub x n (App p q) = App (sub x n p) (sub x n q) sub x n (Lambda y p) x == y = Lambda x p not $ elem x (freevars p) = Lambda y p elem x (freevars p) && notelem y (freevars n) = Lambda y (sub x n p) elem x (freevars p) && elem y (freevars n) = let z = freshtermvar $ App n p in Lambda z $ sub x n $ sub y (LVar z) p -- f) beta-reduktion betareduction :: Lambda -> Lambda betareduction (App (Lambda v e) a) = sub v a e betareduction (App e1 e2) = if e1 == (betareduction e1) then App e1 (betareduction e2) else App (betareduction e1) e2 betareduction (Lambda v e) = Lambda v $ betareduction e betareduction (LVar v) = LVar v -- g) beta-normalform betanf :: Lambda -> Lambda betanf t t /= (betareduction t) = betanf $ betareduction t otherwise = t -- h) applytoimpl :: Lambda -> Lambda -> Lambda applytoimpl x y = betanf $ implication `App` x `App` y ff = applytoimpl false false ft = applytoimpl false true tf = applytoimpl true false tt = applytoimpl true true -- alternative: applytoimpl auf alle kombinationen von true und false anwenden applyall :: [Lambda] applyall = let args = [false,true] in [applytoimpl x y x <- args, y <- args]
37 Übungsblatt 11 Aufgabe 11.1 Visualisierung der β-reduktion (a) Denieren Sie eine Funktion betanfsteps :: Lambda -> [Lambda], die alle Zwischenergebnisse bei der β-reduktion zur Bestimmung der Normalform (Übungsblatt 10) zurückgibt. (b) Implementieren Sie eine Funktion visualizebetareduction :: Lambda -> IO (), die den λ-ausdruck mit der Funktion aus Aufgabenteil (a) in die β-normalform überführt und die Zwischenergebnisse in der folgenden Form ausgibt: (\x. (\x. x) x) y ==> (\x. x) y ==> y Aufgabe 11.2 Hangman Implementieren Sie das Spiel Hangman. Eine Beschreibung des Spiels nden Sie auf folgender Webseite: Das Spiel soll interaktiv in der Konsole spielbar sein und selbstständig auf Tastatureingaben vom Benutzer reagieren. Beim Programmstart soll eine Datei mit den möglichen Wörtern eingelesen werden. Nutzen Sie die Funktion randomio :: IO a aus dem Modul System.Random, um eine Zufallszahl zu erhalten, mit der Sie zufällig ein Wort aus der Datei auswählen.
38 Musterlösung 11 Aufgabe 11.1 Lambda-Kalkül betanfsteps :: Lambda -> [Lambda] betanfsteps t t /= (betareduction t) = t : (betanfsteps $ betareduction t) t == (betareduction t) = [t] visualize :: [Lambda] -> IO () visualize [] = return () visualize (x:xs) = do putstrln $ "==>" ++ show x visualize xs visualizebeta :: Lambda -> IO () visualizebeta = visualize. betanfsteps
39 Aufgabe 11.2 Hangman module Hangman where import System.Random (randomio) import Data.Char (toupper) data Character = Hidden Char Visible Char instance Show Character where show (Hidden _) = "_ " show (Visible c) = show c ++ " " data Word = Word [Character] fromstring :: String -> Word fromstring = Word. map (Hidden. toupper) instance Show Word where show (Word cs) = foldr (\c acc -> show c ++ " " ++ acc) "" cs unshadowchar :: Char -> Word -> Word unshadowchar c (Word cs) = Word $ map f cs where f :: Character -> Character f (Visible x) = Visible x f (Hidden x) x == c = Visible x x /= c = Hidden x successfulguess :: Char -> Word -> Bool successfulguess c (Word cs) = any p cs where p :: Character -> Bool p (Visible x) x == c = True x /= c = False p (Hidden x) x == c = True x /= c = False iswordsolved:: Word -> Bool iswordsolved (Word cs) = all p cs where p :: Character -> Bool p (Visible _) = True p (Hidden _) = False unshadowall :: Word -> Word unshadowall (Word cs) = Word $ map f cs where f :: Character -> Character f (Visible x) = Visible x f (Hidden x) = Visible x -- * IO-basierte funktionen randomword :: IO Word randomword = do contents <- readfile "dictionary" let words = lines contents randomint <- randomio :: IO Int let index = randomint `mod` length words return $ fromstring $ words!! index
40 allowednumberofmistakes :: IO Int allowednumberofmistakes = do putstrln "How many mistakes should be allowed?" strmistakes <- getline return $ (read strmistakes :: Int) main :: IO () main = do n <- allowednumberofmistakes word <- randomword print word play n word play :: Int -> Word -> IO () play 0 word iswordsolved word = congrats otherwise = loss $ unshadowall word play n word = do putstrln $ "Guess a character: [" ++ show n ++ " mistakes allowed]" c' <- getchar putstrln "" let c = toupper c' newword = unshadowchar c word n' successfulguess c word = n otherwise = n-1 print newword if iswordsolved newword then congrats else play n' newword congrats :: IO () congrats = putstrln "Congratulations! You won!" loss :: Word -> IO () loss word = do putstrln $ "You lost! The word was:" print word
41 Übungsblatt 12 Aufgabe 12.1 Partielle Funktionen Gegeben seien die drei partiellen Funktionen logarithmus :: Float -> Maybe Float logarithmus x x <= 0 = Nothing otherwise = Just (log x) quadratwurzel :: Float -> Maybe Float quadratwurzel x x < 0 = Nothing otherwise = Just (sqrt x) kehrwert :: Float -> Maybe Float kehrwert x x == 0 = Nothing otherwise = Just (1 / x) Schreiben Sie partielle Funktionen ergebnis1, ergebnis2, ergebnis3 :: Float -> Maybe Float, die den Kehrwert der Wurzel des Logarithmus von x berechnen. Formulieren Sie die Funktionen auf unterschiedliche Weise: (a) Benutzen Sie die case of Formulierung. (b) Schreiben Sie die Funktion als bind, also mit =. (c) Formulieren Sie in der do-notation.
42 Musterlösung 12 Aufgabe 12.1 Maybe-Monade module Loesung12 where logarithmus :: Float -> Maybe Float logarithmus x x <= 0 = Nothing x > 0 = Just $ log x wurzel :: Float -> Maybe Float wurzel x x < 0 = Nothing x>= 0 = Just $ sqrt x kehrwert :: Float -> Maybe Float kehrwert x x == 0 = Nothing x /= 0 = Just $ 1 / x ergebnis1 :: Float -> Maybe Float ergebnis1 x = case logarithmus x of Nothing -> Nothing Just y -> case wurzel y of Nothing -> Nothing Just z -> kehrwert z ergebnis2 :: Float -> Maybe Float ergebnis2 x = logarithmus x >>= \y -> wurzel y >>= \z -> kehrwert z ergebnis2_kurz x = logarithmus x >>= wurzel >>= kehrwert ergebnis3 :: Float -> Maybe Float ergebnis3 x = do y <- logarithmus x z <- wurzel y kehrwert z
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Programmieren in Haskell Einführung
 Programmieren in Haskell Einführung Peter Steffen Universität Bielefeld Technische Fakultät 16.10.2009 1 Programmieren in Haskell Veranstalter Dr. Peter Steffen Raum: M3-124 Tel.: 0521/106-2906 Email:
Programmieren in Haskell Einführung Peter Steffen Universität Bielefeld Technische Fakultät 16.10.2009 1 Programmieren in Haskell Veranstalter Dr. Peter Steffen Raum: M3-124 Tel.: 0521/106-2906 Email:
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Funktionale Programmierung ALP I. Funktionen höherer Ordnung. Teil 2 SS 2013. Prof. Dr. Margarita Esponda. Prof. Dr.
 ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
Einführung in die Programmierung
 : Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
: Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
Einführung in die Programmierung (EPR)
 Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Goethe-Center for Scientific Computing (G-CSC) Goethe-Universität Frankfurt am Main Einführung in die Programmierung (EPR) (Übung, Wintersemester 2014/2015) Dr. S. Reiter, M. Rupp, Dr. A. Vogel, Dr. K.
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Diana Lange. Generative Gestaltung Operatoren
 Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Erwin Grüner 09.02.2006
 FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
Informatik Grundlagen, WS04, Seminar 13
 Informatik Grundlagen, WS04, Seminar 13 Informatik Informatik Grundlagen, Seminar 13 WS04 1 Was wir heute besprechen Nachbesprechen von Übungsblatt 11 Rekursion Grundprinzipien Übung Besprechung Übungsblatt
Informatik Grundlagen, WS04, Seminar 13 Informatik Informatik Grundlagen, Seminar 13 WS04 1 Was wir heute besprechen Nachbesprechen von Übungsblatt 11 Rekursion Grundprinzipien Übung Besprechung Übungsblatt
Funktionale Programmierung
 Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 13 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 13 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Einführung in die Programmierung
 Technische Universität München WS 2003/2004 Institut für Informatik Prof. Dr. Christoph Zenger Testklausur Einführung in die Programmierung Probeklausur Java (Lösungsvorschlag) 1 Die Klasse ArrayList In
Technische Universität München WS 2003/2004 Institut für Informatik Prof. Dr. Christoph Zenger Testklausur Einführung in die Programmierung Probeklausur Java (Lösungsvorschlag) 1 Die Klasse ArrayList In
Der Aufruf von DM_in_Euro 1.40 sollte die Ausgabe 1.40 DM = 0.51129 Euro ergeben.
 Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Projekt Vorlesung: praktische Implementierung üben Ein und
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Projekt Vorlesung: praktische Implementierung üben Ein und
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
1 Vom Problem zum Programm
 Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Paradigmen der Programmierung
 SS 11 Prüfungsklausur 25.07.2011 Aufgabe 5 (6+9 = 15 Punkte) a) Bestimmen Sie jeweils den Typ der folgenden Haskell-Ausdrücke: ( 1, 2 :"3", 4 < 5) :: (Char, String, Bool) [(last, tail), (head, take 5)]
SS 11 Prüfungsklausur 25.07.2011 Aufgabe 5 (6+9 = 15 Punkte) a) Bestimmen Sie jeweils den Typ der folgenden Haskell-Ausdrücke: ( 1, 2 :"3", 4 < 5) :: (Char, String, Bool) [(last, tail), (head, take 5)]
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Java Kurs für Anfänger Einheit 4 Klassen und Objekte
 Java Kurs für Anfänger Einheit 4 Klassen und Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 13. Juni 2009 Inhaltsverzeichnis klasse
Java Kurs für Anfänger Einheit 4 Klassen und Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 13. Juni 2009 Inhaltsverzeichnis klasse
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Downloadfehler in DEHSt-VPSMail. Workaround zum Umgang mit einem Downloadfehler
 Downloadfehler in DEHSt-VPSMail Workaround zum Umgang mit einem Downloadfehler Downloadfehler bremen online services GmbH & Co. KG Seite 2 Inhaltsverzeichnis Vorwort...3 1 Fehlermeldung...4 2 Fehlerbeseitigung...5
Downloadfehler in DEHSt-VPSMail Workaround zum Umgang mit einem Downloadfehler Downloadfehler bremen online services GmbH & Co. KG Seite 2 Inhaltsverzeichnis Vorwort...3 1 Fehlermeldung...4 2 Fehlerbeseitigung...5
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Enigmail Konfiguration
 Enigmail Konfiguration 11.06.2006 Steffen.Teubner@Arcor.de Enigmail ist in der Grundkonfiguration so eingestellt, dass alles funktioniert ohne weitere Einstellungen vornehmen zu müssen. Für alle, die es
Enigmail Konfiguration 11.06.2006 Steffen.Teubner@Arcor.de Enigmail ist in der Grundkonfiguration so eingestellt, dass alles funktioniert ohne weitere Einstellungen vornehmen zu müssen. Für alle, die es
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Was bisher geschah. deklarative Programmierung. funktionale Programmierung (Haskell):
 Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
Was bisher geschah deklarative Programmierung funktional: Programm: Menge von Termgleichungen, Term Auswertung: Pattern matsching, Termumformungen logisch: Programm: Menge von Regeln (Horn-Formeln), Formel
OP-LOG www.op-log.de
 Verwendung von Microsoft SQL Server, Seite 1/18 OP-LOG www.op-log.de Anleitung: Verwendung von Microsoft SQL Server 2005 Stand Mai 2010 1 Ich-lese-keine-Anleitungen 'Verwendung von Microsoft SQL Server
Verwendung von Microsoft SQL Server, Seite 1/18 OP-LOG www.op-log.de Anleitung: Verwendung von Microsoft SQL Server 2005 Stand Mai 2010 1 Ich-lese-keine-Anleitungen 'Verwendung von Microsoft SQL Server
Kontrollstrukturen und Funktionen in C
 Kontrollstrukturen und Funktionen in C Lernziele: Vertiefen der Kenntnisse über Operatoren, Kontrollstrukturen und die Verwendung von Funktionen. Aufgabe 1: Quickies: Datentypen in C a) Was sind die elementaren
Kontrollstrukturen und Funktionen in C Lernziele: Vertiefen der Kenntnisse über Operatoren, Kontrollstrukturen und die Verwendung von Funktionen. Aufgabe 1: Quickies: Datentypen in C a) Was sind die elementaren
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Programmierung 2. Übersetzer: Code-Erzeugung. Sebastian Hack. Klaas Boesche. Sommersemester 2012. hack@cs.uni-saarland.de. boesche@cs.uni-saarland.
 1 Programmierung 2 Übersetzer: Code-Erzeugung Sebastian Hack hack@cs.uni-saarland.de Klaas Boesche boesche@cs.uni-saarland.de Sommersemester 2012 Bytecodes Der Java Übersetzer erzeugt keine Maschinensprache
1 Programmierung 2 Übersetzer: Code-Erzeugung Sebastian Hack hack@cs.uni-saarland.de Klaas Boesche boesche@cs.uni-saarland.de Sommersemester 2012 Bytecodes Der Java Übersetzer erzeugt keine Maschinensprache
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Stift-Karussell in M-Plot einrichten
 Einsteiger Fortgeschrittene Profis markus.meinl@m-quest.ch Version 1.0 Voraussetzungen für diesen Workshop Die M-Quest Suite 2005 oder höher ist auf einem Rechner installiert Das Produkt M-Plot Suite ist
Einsteiger Fortgeschrittene Profis markus.meinl@m-quest.ch Version 1.0 Voraussetzungen für diesen Workshop Die M-Quest Suite 2005 oder höher ist auf einem Rechner installiert Das Produkt M-Plot Suite ist
Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T:
 Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Graphic Coding. Klausur. 9. Februar 2007. Kurs A
 Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Fachgebiet Informationssysteme Prof. Dr.-Ing. N. Fuhr. Programmierung Prof. Dr.-Ing. Nobert Fuhr. Übungsblatt Nr. 6
 Gudrun Fischer Sascha Kriewel programmierung@is.informatik.uni-duisburg.de Anmeldung zur Klausur! Übungsblatt Nr. 6 Um an der Klausur teilzunehmen, müssen sich Studierende der angewandten Informatik in
Gudrun Fischer Sascha Kriewel programmierung@is.informatik.uni-duisburg.de Anmeldung zur Klausur! Übungsblatt Nr. 6 Um an der Klausur teilzunehmen, müssen sich Studierende der angewandten Informatik in
Programmierung in C. Grundlagen. Stefan Kallerhoff
 Programmierung in C Grundlagen Stefan Kallerhoff Vorstellungsrunde Name Hobby/Beruf Schon mal was programmiert? Erwartungen an den Kurs Lieblingstier Für zu Hause C-Buch online: http://openbook.rheinwerk-verlag.de/c_von_a_bis_z/
Programmierung in C Grundlagen Stefan Kallerhoff Vorstellungsrunde Name Hobby/Beruf Schon mal was programmiert? Erwartungen an den Kurs Lieblingstier Für zu Hause C-Buch online: http://openbook.rheinwerk-verlag.de/c_von_a_bis_z/
Klausur in Programmieren
 Studiengang Sensorik/Sensorsystemtechnik Note / normierte Punkte Klausur in Programmieren Wintersemester 2010/11, 17. Februar 2011 Dauer: 1,5h Hilfsmittel: Keine (Wörterbücher sind auf Nachfrage erlaubt)
Studiengang Sensorik/Sensorsystemtechnik Note / normierte Punkte Klausur in Programmieren Wintersemester 2010/11, 17. Februar 2011 Dauer: 1,5h Hilfsmittel: Keine (Wörterbücher sind auf Nachfrage erlaubt)
Datentypen. Agenda für heute, 4. März, 2010. Pascal ist eine streng typisierte Programmiersprache
 Agenda für heute, 4. März, 2010 Zusammengesetzte if-then-else-anweisungen Datentypen Pascal ist eine streng typisierte Programmiersprache Für jeden Speicherplatz muss ein Datentyp t (Datenformat) t) definiert
Agenda für heute, 4. März, 2010 Zusammengesetzte if-then-else-anweisungen Datentypen Pascal ist eine streng typisierte Programmiersprache Für jeden Speicherplatz muss ein Datentyp t (Datenformat) t) definiert
Das Typsystem von Scala. L. Piepmeyer: Funktionale Programmierung - Das Typsystem von Scala
 Das Typsystem von Scala 1 Eigenschaften Das Typsystem von Scala ist statisch, implizit und sicher 2 Nichts Primitives Alles ist ein Objekt, es gibt keine primitiven Datentypen scala> 42.hashCode() res0:
Das Typsystem von Scala 1 Eigenschaften Das Typsystem von Scala ist statisch, implizit und sicher 2 Nichts Primitives Alles ist ein Objekt, es gibt keine primitiven Datentypen scala> 42.hashCode() res0:
Quadratische Gleichungen
 Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen:
 Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen: Peano-Zahlen, Listen, Bäume Rekursive Funktionen strukturelle
Was bisher geschah Funktionale Programmierung in Haskell: Algebraische Datentypen Pattern Matching Polymorphie Typklassen Rekursive Datentypen: Peano-Zahlen, Listen, Bäume Rekursive Funktionen strukturelle
Programmentwicklungen, Webseitenerstellung, Zeiterfassung, Zutrittskontrolle
 Version LG-TIME /Office A 8.3 und höher Inhalt 1. Allgemeines S. 1 2. Installation S. 1 3. Erweiterungen bei den Zeitplänen S. 1;2 4. Einrichtung eines Schichtplanes S. 2 5. Einrichtung einer Wechselschicht
Version LG-TIME /Office A 8.3 und höher Inhalt 1. Allgemeines S. 1 2. Installation S. 1 3. Erweiterungen bei den Zeitplänen S. 1;2 4. Einrichtung eines Schichtplanes S. 2 5. Einrichtung einer Wechselschicht
Praktikum Ingenieurinformatik. Termin 2. Verzweigungen (if-else), printf und scanf, while-schleife
 Praktikum Ingenieurinformatik Termin 2 Verzweigungen (if-else), printf und scanf, while-schleife 1 1. Import/Export von Eclipse-Projekten 2. Verzweigungen (if-else-anweisung) 3. printf und scanf 4. Übungsaufgaben
Praktikum Ingenieurinformatik Termin 2 Verzweigungen (if-else), printf und scanf, while-schleife 1 1. Import/Export von Eclipse-Projekten 2. Verzweigungen (if-else-anweisung) 3. printf und scanf 4. Übungsaufgaben
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Erstellen der Barcode-Etiketten:
 Erstellen der Barcode-Etiketten: 1.) Zuerst muss die Schriftart Code-39-Logitogo installiert werden! Das ist eine einmalige Sache und muss nicht zu jeder Börse gemacht werden! Dazu speichert man zunächst
Erstellen der Barcode-Etiketten: 1.) Zuerst muss die Schriftart Code-39-Logitogo installiert werden! Das ist eine einmalige Sache und muss nicht zu jeder Börse gemacht werden! Dazu speichert man zunächst
Einführung in die C++ Programmierung für Ingenieure
 Einführung in die C++ Programmierung für Ingenieure MATTHIAS WALTER / JENS KLUNKER Universität Rostock, Lehrstuhl für Modellierung und Simulation 14. November 2012 c 2012 UNIVERSITÄT ROSTOCK FACULTY OF
Einführung in die C++ Programmierung für Ingenieure MATTHIAS WALTER / JENS KLUNKER Universität Rostock, Lehrstuhl für Modellierung und Simulation 14. November 2012 c 2012 UNIVERSITÄT ROSTOCK FACULTY OF
Grundlagen der Programmierung Prof. H. Mössenböck. 14. Schrittweise Verfeinerung
 Grundlagen der Programmierung Prof. H. Mössenböck 14. Schrittweise Verfeinerung Entwurfsmethode für Algorithmen Wie kommt man von der Aufgabenstellung zum Programm? Beispiel geg.: Text aus Wörtern ges.:
Grundlagen der Programmierung Prof. H. Mössenböck 14. Schrittweise Verfeinerung Entwurfsmethode für Algorithmen Wie kommt man von der Aufgabenstellung zum Programm? Beispiel geg.: Text aus Wörtern ges.:
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
AutoCAD 2007 - Dienstprogramm zur Lizenzübertragung
 AutoCAD 2007 - Dienstprogramm zur Lizenzübertragung Problem: Um AutoCAD abwechselnd auf mehreren Rechnern einsetzen zu können konnte man bis AutoCAD 2000 einfach den Dongle umstecken. Seit AutoCAD 2000i
AutoCAD 2007 - Dienstprogramm zur Lizenzübertragung Problem: Um AutoCAD abwechselnd auf mehreren Rechnern einsetzen zu können konnte man bis AutoCAD 2000 einfach den Dongle umstecken. Seit AutoCAD 2000i
Algorithmen und Programmieren 1 Funktionale Programmierung - Musterlösung zur Übungsklausur -
 Algorithmen und Programmieren 1 Funktionale Programmierung - Musterlösung zur Übungsklausur - Punkte: A1: 30, A2: 20, A3: 20, A4: 20, A5: 10, A6: 20 Punkte: /120 12.02.2012 Hinweis: Geben Sie bei allen
Algorithmen und Programmieren 1 Funktionale Programmierung - Musterlösung zur Übungsklausur - Punkte: A1: 30, A2: 20, A3: 20, A4: 20, A5: 10, A6: 20 Punkte: /120 12.02.2012 Hinweis: Geben Sie bei allen
Einfache Arrays. Annabelle Klarl. Einführung in die Informatik Programmierung und Softwareentwicklung
 Annabelle Klarl Zentralübung zur Vorlesung Einführung in die Informatik: http://www.pst.ifi.lmu.de/lehre/wise-13-14/infoeinf WS13/14 Action required now 1. Smartphone: installiere die App "socrative student"
Annabelle Klarl Zentralübung zur Vorlesung Einführung in die Informatik: http://www.pst.ifi.lmu.de/lehre/wise-13-14/infoeinf WS13/14 Action required now 1. Smartphone: installiere die App "socrative student"
Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?
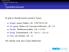
![Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?](/thumbs/24/4200701.jpg) Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Starten Sie Eclipse: Hier tragen sie Ihr Arbeitsverzeichnis ein. Zu Hause z.b. c:\workspace.
 Starten Sie Eclipse: Abgesehen vom Kommandozeilenfenster, auf welches wir später eingehen, öffnet sich ein Dialog (in der FH vermutlich nicht, überspringen Sie in diesem Fall): Hier tragen sie Ihr Arbeitsverzeichnis
Starten Sie Eclipse: Abgesehen vom Kommandozeilenfenster, auf welches wir später eingehen, öffnet sich ein Dialog (in der FH vermutlich nicht, überspringen Sie in diesem Fall): Hier tragen sie Ihr Arbeitsverzeichnis
Anleitung zur Erstellung von Serienbriefen (Word 2003) unter Berücksichtigung von Titeln (wie Dr., Dr. med. usw.)
 Seite 1/7 Anleitung zur Erstellung von Serienbriefen (Word 2003) unter Berücksichtigung von Titeln (wie Dr., Dr. med. usw.) Hier sehen Sie eine Anleitung wie man einen Serienbrief erstellt. Die Anleitung
Seite 1/7 Anleitung zur Erstellung von Serienbriefen (Word 2003) unter Berücksichtigung von Titeln (wie Dr., Dr. med. usw.) Hier sehen Sie eine Anleitung wie man einen Serienbrief erstellt. Die Anleitung
4. Lernen von Entscheidungsbäumen. Klassifikation mit Entscheidungsbäumen. Entscheidungsbaum
 4. Lernen von Entscheidungsbäumen Klassifikation mit Entscheidungsbäumen Gegeben sei eine Menge von Objekten, die durch /Wert- Paare beschrieben sind. Jedes Objekt kann einer Klasse zugeordnet werden.
4. Lernen von Entscheidungsbäumen Klassifikation mit Entscheidungsbäumen Gegeben sei eine Menge von Objekten, die durch /Wert- Paare beschrieben sind. Jedes Objekt kann einer Klasse zugeordnet werden.
Binäre Bäume Darstellung und Traversierung
 Binäre Bäume Darstellung und Traversierung Name Frank Bollwig Matrikel-Nr. 2770085 E-Mail fb641378@inf.tu-dresden.de Datum 15. November 2001 0. Vorbemerkungen... 3 1. Terminologie binärer Bäume... 4 2.
Binäre Bäume Darstellung und Traversierung Name Frank Bollwig Matrikel-Nr. 2770085 E-Mail fb641378@inf.tu-dresden.de Datum 15. November 2001 0. Vorbemerkungen... 3 1. Terminologie binärer Bäume... 4 2.
Zwischenablage (Bilder, Texte,...)
 Zwischenablage was ist das? Informationen über. die Bedeutung der Windows-Zwischenablage Kopieren und Einfügen mit der Zwischenablage Vermeiden von Fehlern beim Arbeiten mit der Zwischenablage Bei diesen
Zwischenablage was ist das? Informationen über. die Bedeutung der Windows-Zwischenablage Kopieren und Einfügen mit der Zwischenablage Vermeiden von Fehlern beim Arbeiten mit der Zwischenablage Bei diesen
Informatik Repetitorium SS 2009. Volker Jaedicke Volker.Jaedicke@web.de 0179 1322692
 Informatik Repetitorium SS 2009 Volker Jaedicke Volker.Jaedicke@web.de 0179 1322692 Operatoren und Datentypen Beispiel: Anweisungen Variable int a float b int c a= a % (int) (++b-1/4) Vorher 36 3.5 c=b
Informatik Repetitorium SS 2009 Volker Jaedicke Volker.Jaedicke@web.de 0179 1322692 Operatoren und Datentypen Beispiel: Anweisungen Variable int a float b int c a= a % (int) (++b-1/4) Vorher 36 3.5 c=b
Artikel Schnittstelle über CSV
 Artikel Schnittstelle über CSV Sie können Artikeldaten aus Ihrem EDV System in das NCFOX importieren, dies geschieht durch eine CSV Schnittstelle. Dies hat mehrere Vorteile: Zeitersparnis, die Karteikarte
Artikel Schnittstelle über CSV Sie können Artikeldaten aus Ihrem EDV System in das NCFOX importieren, dies geschieht durch eine CSV Schnittstelle. Dies hat mehrere Vorteile: Zeitersparnis, die Karteikarte
Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x),
![Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x), Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x),](/thumbs/29/13862323.jpg) Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 25. August 2014 Programmier-Labor 04. + 05. Übungsblatt Aufgabe 21: a) Schreiben Sie eine Methode
Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 25. August 2014 Programmier-Labor 04. + 05. Übungsblatt Aufgabe 21: a) Schreiben Sie eine Methode
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Funktionale Programmierung mit Haskell Prof. Dr. Hans J. Schneider Lehrstuhl für Programmiersprachen und Programmiermethodik Friedrich-Alexander-Universität Erlangen-Nürnberg Sommersemester 2011 I. Die
Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen:
 Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Dokumentation IBIS Monitor
 Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Grundlagen der Programmierung Prof. H. Mössenböck. 3. Verzweigungen
 Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Scala kann auch faul sein
 Scala kann auch faul sein Kapitel 19 des Buches 1 Faulheit Faulheit ( lazy evaluation ) ist auch in C oder Java nicht unbekannt int x=0; if(x!=0 && 10/x>3){ System.out.println("In if"); } Nutzen der Faulheit?
Scala kann auch faul sein Kapitel 19 des Buches 1 Faulheit Faulheit ( lazy evaluation ) ist auch in C oder Java nicht unbekannt int x=0; if(x!=0 && 10/x>3){ System.out.println("In if"); } Nutzen der Faulheit?
Wir arbeiten mit Zufallszahlen
 Abb. 1: Bei Kartenspielen müssen zu Beginn die Karten zufällig ausgeteilt werden. Wir arbeiten mit Zufallszahlen Jedesmal wenn ein neues Patience-Spiel gestartet wird, muss das Computerprogramm die Karten
Abb. 1: Bei Kartenspielen müssen zu Beginn die Karten zufällig ausgeteilt werden. Wir arbeiten mit Zufallszahlen Jedesmal wenn ein neues Patience-Spiel gestartet wird, muss das Computerprogramm die Karten
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Menü auf zwei Module verteilt (Joomla 3.4.0)
 Menü auf zwei Module verteilt (Joomla 3.4.0) Oft wird bei Joomla das Menü in einem Modul dargestellt, wenn Sie aber z.b. ein horizontales Hauptmenü mit einem vertikalen Untermenü machen möchten, dann finden
Menü auf zwei Module verteilt (Joomla 3.4.0) Oft wird bei Joomla das Menü in einem Modul dargestellt, wenn Sie aber z.b. ein horizontales Hauptmenü mit einem vertikalen Untermenü machen möchten, dann finden
Matrix42. Use Case - Sicherung und Rücksicherung persönlicher Einstellungen über Personal Backup. Version 1.0.0. 23. September 2015 - 1 -
 Matrix42 Use Case - Sicherung und Rücksicherung persönlicher Version 1.0.0 23. September 2015-1 - Inhaltsverzeichnis 1 Einleitung 3 1.1 Beschreibung 3 1.2 Vorbereitung 3 1.3 Ziel 3 2 Use Case 4-2 - 1 Einleitung
Matrix42 Use Case - Sicherung und Rücksicherung persönlicher Version 1.0.0 23. September 2015-1 - Inhaltsverzeichnis 1 Einleitung 3 1.1 Beschreibung 3 1.2 Vorbereitung 3 1.3 Ziel 3 2 Use Case 4-2 - 1 Einleitung
Suchmaschinen. Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6
 Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6 Aufgabe 1: Pareto mit SV-Semantik Suchmaschinen Pareto Definition: x < P
Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6 Aufgabe 1: Pareto mit SV-Semantik Suchmaschinen Pareto Definition: x < P
Praktikum zu Einführung in die Informatik für LogWiIngs und WiMas Wintersemester 2015/16. Vorbereitende Aufgaben
 Praktikum zu Einführung in die Informatik für LogWiIngs und WiMas Wintersemester 2015/16 Fakultät für Informatik Lehrstuhl 14 Lars Hildebrand, Marcel Preuß, Iman Kamehkhosh, Marc Bury, Diana Howey Übungsblatt
Praktikum zu Einführung in die Informatik für LogWiIngs und WiMas Wintersemester 2015/16 Fakultät für Informatik Lehrstuhl 14 Lars Hildebrand, Marcel Preuß, Iman Kamehkhosh, Marc Bury, Diana Howey Übungsblatt
Übungen 19.01.2012 Programmieren 1 Felix Rohrer. Übungen
 Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
Modellierung und Programmierung 1
 Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Modellierung und Programmierung 1 Prof. Dr. Sonja Prohaska Computational EvoDevo Group Institut für Informatik Universität Leipzig 19. November 2015 Gültigkeitsbereich (Scope) von Variablen { int m; {
Folge 19 - Bäume. 19.1 Binärbäume - Allgemeines. Grundlagen: Ulrich Helmich: Informatik 2 mit BlueJ - Ein Kurs für die Stufe 12
 Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Einrichten einer mehrsprachigen Webseite mit Joomla (3.3.6)
 Einrichten einer mehrsprachigen Webseite mit Joomla (3.3.6) 1. Loggen Sie sich im Administratorbereich ein und gehen Sie auf Extension > Extension Manager 2. Wählen Sie Install languages 3. Klicken Sie
Einrichten einer mehrsprachigen Webseite mit Joomla (3.3.6) 1. Loggen Sie sich im Administratorbereich ein und gehen Sie auf Extension > Extension Manager 2. Wählen Sie Install languages 3. Klicken Sie
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Arbeiten mit UMLed und Delphi
 Arbeiten mit UMLed und Delphi Diese Anleitung soll zeigen, wie man Klassen mit dem UML ( Unified Modeling Language ) Editor UMLed erstellt, in Delphi exportiert und dort so einbindet, dass diese (bis auf
Arbeiten mit UMLed und Delphi Diese Anleitung soll zeigen, wie man Klassen mit dem UML ( Unified Modeling Language ) Editor UMLed erstellt, in Delphi exportiert und dort so einbindet, dass diese (bis auf
Felder. November 5, 2014
 Felder Universität Bielefeld AG Praktische Informatik November 5, 2014 Felder: Datenstrukturen mit konstantem Zugriff Felder nennt man auch, Vektoren, Matrizen,... Konstanter Zugriff heisst: Zugriff auf
Felder Universität Bielefeld AG Praktische Informatik November 5, 2014 Felder: Datenstrukturen mit konstantem Zugriff Felder nennt man auch, Vektoren, Matrizen,... Konstanter Zugriff heisst: Zugriff auf
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
5. Übung: PHP-Grundlagen
 5.1. Erstes PHP-Programm 1. Schreiben Sie PHP-Programm innerhalb einer Webseite, d.h. innerhalb eines HTML-Dokument. Ihr PHP-Programm soll einen kurzen Text ausgeben und Komentare enthalten. Speichern
5.1. Erstes PHP-Programm 1. Schreiben Sie PHP-Programm innerhalb einer Webseite, d.h. innerhalb eines HTML-Dokument. Ihr PHP-Programm soll einen kurzen Text ausgeben und Komentare enthalten. Speichern
Kapitel MK:IV. IV. Modellieren mit Constraints
 Kapitel MK:IV IV. Modellieren mit Constraints Einführung und frühe Systeme Konsistenz I Binarization Generate-and-Test Backtracking-basierte Verfahren Konsistenz II Konsistenzanalyse Weitere Analyseverfahren
Kapitel MK:IV IV. Modellieren mit Constraints Einführung und frühe Systeme Konsistenz I Binarization Generate-and-Test Backtracking-basierte Verfahren Konsistenz II Konsistenzanalyse Weitere Analyseverfahren
Windows. Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1
 Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Import und Export von Übergängern
 Import und Export von Übergängern SibankPLUS bietet Ihnen eine komfortable Schnittstelle, um den Wechsel der Schüler nach der Stufe 4 von der Grundschule auf eine weiterführende Schule zu verarbeiten.
Import und Export von Übergängern SibankPLUS bietet Ihnen eine komfortable Schnittstelle, um den Wechsel der Schüler nach der Stufe 4 von der Grundschule auf eine weiterführende Schule zu verarbeiten.
CMS.R. Bedienungsanleitung. Modul Cron. Copyright 10.09.2009. www.sruttloff.de CMS.R. - 1 - Revision 1
 CMS.R. Bedienungsanleitung Modul Cron Revision 1 Copyright 10.09.2009 www.sruttloff.de CMS.R. - 1 - WOZU CRON...3 VERWENDUNG...3 EINSTELLUNGEN...5 TASK ERSTELLEN / BEARBEITEN...6 RECHTE...7 EREIGNISSE...7
CMS.R. Bedienungsanleitung Modul Cron Revision 1 Copyright 10.09.2009 www.sruttloff.de CMS.R. - 1 - WOZU CRON...3 VERWENDUNG...3 EINSTELLUNGEN...5 TASK ERSTELLEN / BEARBEITEN...6 RECHTE...7 EREIGNISSE...7
Menü Macro. WinIBW2-Macros unter Windows7? Macros aufnehmen
 Menü Macro WinIBW2-Macros unter Windows7?... 1 Macros aufnehmen... 1 Menübefehle und Schaltflächen in Macros verwenden... 4 Macros bearbeiten... 4 Macros löschen... 5 Macro-Dateien... 5 Macros importieren...
Menü Macro WinIBW2-Macros unter Windows7?... 1 Macros aufnehmen... 1 Menübefehle und Schaltflächen in Macros verwenden... 4 Macros bearbeiten... 4 Macros löschen... 5 Macro-Dateien... 5 Macros importieren...
Studentische Lösung zum Übungsblatt Nr. 7
 Studentische Lösung zum Übungsblatt Nr. 7 Aufgabe 1) Dynamische Warteschlange public class UltimateOrderQueue private Order[] inhalt; private int hinten; // zeigt auf erstes freies Element private int
Studentische Lösung zum Übungsblatt Nr. 7 Aufgabe 1) Dynamische Warteschlange public class UltimateOrderQueue private Order[] inhalt; private int hinten; // zeigt auf erstes freies Element private int
