EINMALEINS BEZIEHUNGSREICH
|
|
|
- Helga Schneider
- vor 8 Jahren
- Abrufe
Transkript
1 EINMALEINS BEZIEHUNGSREICH Thema: Übung des kleinen Einmaleins; operative Beziehungen erkunden Stufe: ab 2. Schuljahr Dauer: 2 bis 3 Lektionen Materialien: Kleine Einmaleinstafeln (ohne Farben), Punktefelder Quelle: Wittmann, E.Ch. und Müller, G.N.: Muster und Strukturen als fachliches Grundkonzept des Mathematikunterrichts der Grundschule. In: Walther, G. u.a. (Hg.), Bildungsstandards für die Grundschule: Mathematik konkret. Berlin: Cornelsen Scriptor 2007 Bearbeitung: Salome Tschopp und Elmar Hengartner Aufgabe A: Folgen von Aufgabenpaaren (waagrecht in der Maltafel) 1 Starte mit den Malaufgaben 2x5 und 1x6. Sie liegen in der Maltafel untereinander. Berechne die Ergebnisse. Gehe dann waagrecht nach rechts zu den nächsten Aufgabenpaaren und berechne die Ergebnisse: 2 x 5 = 3 x 6 = 4 x 7 = 5 x 8 =... 1 x 6 = 2 x 7 = 3 x 8 = 4 x 9 =... Beschreibe die Päckchen. Vergleiche die Ergebnisse. 2 Wähle selber Paare von untereinander liegenden Einmaleinsaufgaben. Setze in gleicher Weise wagrecht nach rechts fort und notiere die Rechnungen wie oben. 1
2 Aufgabe B: Folgen von Aufgabenpaaren (senkrecht in der Maltafel) 3 Starte mit den beiden Malaufgaben 1 x 8 und 2 x 9. Sie liegen in der Maltafel nebeneinander. Gehe senkrecht nach oben zu den nächsten Aufgabenpaaren und rechne die Ergebnisse: 1 x 8 =... 2 x 9 =... 2 x 7 =... 3 x 8 =... 3 x 6 =... 4 x 7 =... 4 x 5 =... 5 x 6 = Beschreibe die Päckchen. Vergleiche die Ergebnisse. 4 Wähle selber Paare von nebeneinander liegenden Einmaleinsaufgaben, rechne sie aus und setze sie in gleicher Art senkrecht nach oben oder nach unten fort:... x... = x... = x... = x... =... 2
3 Worum es geht? Die Idee zu dieser Lernumgebung verdanken wir Erich Ch. Wittmann: Wir folgen seiner Beschreibung im Aufsatz: Wittmann, E.Ch./ Müller, G.N.: Muster und Strukturen als fachliche Grundkonzepte des Mathematikunterrichts der Grundschule. Aufgabe A: Folgen von Aufgabenpaaren (waagrecht in der Maltafel) Die Übung des Einmaleins wird in dieser Lernumgebung mit der Maltafel so strukturiert, dass operative Beziehungen zwischen den Einmaleinsaufgaben unmittelbar sichtbar werden und der Kontrolle der Ergebnisse dienen können. Man startet mit einer Malaufgabe, zum Beispiel 2 x 5 und entwickelt daraus ein Päckchen nach folgender Regel: 2 x 5 = 3 x 6 = 4 x 7 = 5 x 8 =... 1 x 6 = 2 x 7 = 3 x 8 = 4 x 9 =... Jede Aufgabe in der zweiten Zeile entsteht aus der darüber stehenden dadurch, dass der erste Faktor um 1 erniedrigt und der zweite um 1 erhöht wird. In jeder Zeile nehmen die Faktoren von einem Feld zum nächsten um je 1 zu. Die Pünktchen am Schluss deuten an, dass das Päckchen fortgesetzt werden kann, wenn und so weit ein Kind das möchte. (ebd. S. XX). Dass die Kinder dies taten, zeigen ihre Dokumente. In ihnen wird auch deutlich, dass sie ein Muster entdeckt haben, dass nämlich die Ergebnisse der zweiten Zeile durchgehend um 4 kleiner sind als die Ergebnisse der darüber stehenden Aufgaben. Und einzelne Kinder konnten dies anhand von Punktfeldern (Kopiervorlage 2) auch begründen (siehe das Dokument von Melanie im Abschnitt Kinderdokumente aus der Erprobung). Aufgabe B: Folgen von Aufgabenpaaren (senkrecht in der Maltafel) Die Regel für die Bildung der Päckchen wird abgewandelt: Man startet zum Beispiel mit 1 x 8 und entwickelt folgendes Päckchen: 1 x 8 =... 2 x 9 =... 2 x 7 =... 3 x 8 =... 3 x 6 =... 4 x 7 =... 4 x 5 =... 5 x 6 = In beiden Päcken rechts wie links wird der erste Faktor um 1 erhöht, während der zweite Faktor um 1 erniedrigt wird. Von links nach rechts werden beide Faktoren der ersten Aufgabe um 1 erhöht. Wiederum bleiben die Ergebnisunterschiede konstant. Und wiederum haben die Kinder die Päckchen teils fortgesetzt, und einzelne versuchten die Konstanz der Ergebnisunterschiede an Punktefeldern zu begründen (siehe das Dokument von Tim). 3
4 Kinderdokumente aus der Erprobung Aufgabe A: Folgen von Aufgabenpaaren (waagrecht in der Maltafel) Simone hat drei Päckchen von Aufgabenpaaren waagrecht in der Maltafel fortgesetzt: - die vorgegebene mit Start bei 2 x 5 und 1 x 6 (über die Maltafelgrenze hinaus!), - die mittlere mit vertauschten Faktoren beginnend mit 2 x 1 und 1 x 2 und - eine dritte beginnend mit 6 x 1 und 5 x 2. Simone stellt fest, dass die Ergebnisunterschiede der Aufgabenpaare immer gleich bleiben. Sie begründet zudem, weshalb die Ergebnisunterschiede in der ersten und der dritten Folge gleich sind, nämlich 4, weil sie gleich weit von der Mitte, das heisst gleich weit von den Aufgaben der Quadratzahlen entfernt sind. 4
5 Melanie gibt anhand von Punktfeldern, in denen sie die Aufgaben anmalt, eine Begründung, weshalb der Ergebnisunterschied übereinander liegender Aufgabenpaare immer 4 bleibt: Von 2 x 5 zu 1 x 6 fällt 1 x 5 weg, dafür kommt 1 hinzu, der Unterschied ist also 4. Von 3 x 6 zu 2 x 7 fällt 1 x 6 weg, dafür kommen 2 dazu, der Unterschied bleibt 4. Von 4 x 7 zu 3 x 8 fällt 1 x 7 weg, dafür kommen 3 hinzu, der Unterschied bleibt 4. Und das gilt auch für die weiteren Beispiele. 5
6 Aufgabe B: Folgen von Aufgabenpaaren (senkrecht in der Maltafel) Daniela hat drei Folgen von Aufgabenpaaren senkrecht in der Maltafel fortgesetzt: - die vorgegebene Folge, begonnen mit 1 x 8 und 2 x 9 (siehe die Pfeile), - eine zweite begonnen von oben mit 6 x 1 und 7 x 3 und - eine dritte Folge begonnen von oben mit 7 x 6 und 8 x 7. Sie stellt fest, dass die Ergebnisunterschiede zwischen Aufgabenpaaren nebeneinander in allen drei Folgen jeweils gleich bleiben. In der ersten Folge ist der Unterschied immer 10, in der zweiten immer 8 und in der dritten immer 14. 6
7 Simone gibt keinerlei Erläuterungen weder Feststellungen zu gleichen Abständen der Ergebnisse noch Begründungen. Aber sie hat entlang der strukturierten Aufgabenpäckchen fast die gesamte Einmaleinstafel gerechnet, insgesamt 80 Aufgaben. Und sie hat alle richtig gerechnet und nur eine einzige nicht der Struktur entsprechend bestimmt (2 x 4 = 8 statt 2 x 5 = 10). Es ist anzunehmen, dass auch sie auf die gleichen Abstände zwischen den Ergebnissen aufmerksam wurde. Ohne dieses Muster hätte sie kaum so viele Aufgaben gerechnet. 7
8 David hat ähnlich viele Aufgaben wie Simone gerechnet.. Von Anfang an gilt seine Aufmerksamkeit aber den gleich bleibenden Unterschieden zwischen den Aufgabenpaaren, die er vertikal fortsetzt: Von der 1. Reihe zur 2. Reihe ist immer ein gewisser Unterschied, z.b. 10, 17, 14, 18, 13, 11 und 11, schreibt er nach den ersten Erkundungen, welche er dann weiter fortsetzt mit Aufgabenpaaren mit Unterschied 4, 5 und 8. Er macht eine interessante Feststellung: : Desto weiter ich nach links gehe (gemeint: bei der Wahl der vertikal fortgesetzten Aufgabenpaare in der Maltafel), desto kleiner werden die Ergebnisse (gemeint: Ergebnisunterschiede). 1
9 Timo rechnet nach dem vorgegebenen Päckchen, von unten beginnend mit 1 x 8 und 2 x 9, zwei weitere Folgen (Päckchen) von Aufgabenpaaren, die er unmittelbar nach rechts anschliesst. Wie andere Kinder auch geht er über die Grenze der Maltafel hinaus und setzt die Struktur der Aufgabenfolge fort. Interessant ist Timos neue Fragestellung, wie sich denn die Aufgaben waagrecht auf jeder Zeile entwickeln. Er untersucht das an der obersten Zeile von 5 x 4, 6 x 5, 7 x 6, 8 x 7, 9 x 8 und 10 x 9 und schreibt dazu, dass beide Faktoren jeweils um 1 grösser werden: Von Rechnung zu Rechnung wächst die vordere Zahl und die hintere Zahl um eins. Und zu den Ergebnissen schreibt er: Von Resultat zu Resultat wachsen die Abstände immer um zwei in einer geraden Reihe. Gemeint ist: Sie wachsen immer um die nächste gerade Zahl, was der Bildungsregel der Fast-Quadratzahlen entspricht. 2
10 Robin begründet anhand von Punktefeldern, in denen er die Aufgaben des ersten vorgegebenen Päckchens anmalt, weshalb der Ergebnisunterschied nebeneinander liegender Aufgabenpaare immer 10 bleibt : Von 1 x 8 zu 2 x 9 kommen 8 hinzu plus 2 rechts vertikal. Von 2 x 7 zu 3 x 8 kommen 7 hinzu plus 3 rechts vertikal. Von 3 x 6 zu 4 x 7 kommen 6 hinzu plus 4 rechts vertikal. Von 4 x 5 zu 5 x 6 kommen 5 hinzu plus 5 rechts vertikal usw. 3
11 Kopiervorlage 2: Punktefelder zum Anmalen von Aufgabenpaaren 4
12 5
GLEICH WEIT WEG. Aufgabe. Das ist ein Ausschnitt aus der Tausenderreihe:
 GLEICH WEIT WEG Thema: Sich orientieren und operieren an der Tausenderreihe Klasse: 3. Klasse (Zahlenbuch nach S. 26-27) Dauer: 3-4 Lektionen Material: Tausenderreihe, Arbeitsblatt, evt. Plättchen Bearbeitung:
GLEICH WEIT WEG Thema: Sich orientieren und operieren an der Tausenderreihe Klasse: 3. Klasse (Zahlenbuch nach S. 26-27) Dauer: 3-4 Lektionen Material: Tausenderreihe, Arbeitsblatt, evt. Plättchen Bearbeitung:
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Durch Wissen Millionär WerDen... Wer hat zuerst die Million erreicht? spielanleitung Zahl der spieler: alter: redaktion / autor: inhalt:
 Spielanleitung Durch Wissen Millionär werden... Diesen Traum kann man sich in diesem beliebten Quiz-Spiel erfüllen. Ob allein oder in der geselligen Runde dieses Quiz enthält 330 Fragen und 1.320 Multiple-Choice-Antworten.
Spielanleitung Durch Wissen Millionär werden... Diesen Traum kann man sich in diesem beliebten Quiz-Spiel erfüllen. Ob allein oder in der geselligen Runde dieses Quiz enthält 330 Fragen und 1.320 Multiple-Choice-Antworten.
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Sowohl die Malstreifen als auch die Neperschen Streifen können auch in anderen Stellenwertsystemen verwendet werden.
 Multiplikation Die schriftliche Multiplikation ist etwas schwieriger als die Addition. Zum einen setzt sie das kleine Einmaleins voraus, zum anderen sind die Überträge, die zu merken sind und häufig in
Multiplikation Die schriftliche Multiplikation ist etwas schwieriger als die Addition. Zum einen setzt sie das kleine Einmaleins voraus, zum anderen sind die Überträge, die zu merken sind und häufig in
Daten sammeln, darstellen, auswerten
 Vertiefen 1 Daten sammeln, darstellen, auswerten zu Aufgabe 1 Schulbuch, Seite 22 1 Haustiere zählen In der Tabelle rechts stehen die Haustiere der Kinder aus der Klasse 5b. a) Wie oft wurden die Haustiere
Vertiefen 1 Daten sammeln, darstellen, auswerten zu Aufgabe 1 Schulbuch, Seite 22 1 Haustiere zählen In der Tabelle rechts stehen die Haustiere der Kinder aus der Klasse 5b. a) Wie oft wurden die Haustiere
Zahlenwinkel: Forscherkarte 1. alleine. Zahlenwinkel: Forschertipp 1
 Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Zahlenwinkel: Forscherkarte 1 alleine Tipp 1 Lege die Ziffern von 1 bis 9 so in den Zahlenwinkel, dass jeder Arm des Zahlenwinkels zusammengezählt das gleiche Ergebnis ergibt! Finde möglichst viele verschiedene
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Das Leitbild vom Verein WIR
 Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Tipp III: Leiten Sie eine immer direkt anwendbare Formel her zur Berechnung der sogenannten "bedingten Wahrscheinlichkeit".
 Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
Mathematik- Unterrichts- Einheiten- Datei e. V. Klasse 9 12 04/2015 Diabetes-Test Infos: www.mued.de Blutspenden werden auf Diabetes untersucht, das mit 8 % in der Bevölkerung verbreitet ist. Dabei werden
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
10.1 Auflösung, Drucken und Scannen
 Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Alle gehören dazu. Vorwort
 Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
Alle gehören dazu Alle sollen zusammen Sport machen können. In diesem Text steht: Wie wir dafür sorgen wollen. Wir sind: Der Deutsche Olympische Sport-Bund und die Deutsche Sport-Jugend. Zu uns gehören
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
Das Schulsystem in Deutschland (Band 2, Lektion 1)
 Pluspunkt Deutsch Das Schulsystem in Deutschland (Band 2, Lektion 1) Übung 1 Lesen Sie den Text und kreuzen Sie an: Richtig oder falsch? In Deutschland können die Kinder mit 3 Jahren in den Kindergarten
Pluspunkt Deutsch Das Schulsystem in Deutschland (Band 2, Lektion 1) Übung 1 Lesen Sie den Text und kreuzen Sie an: Richtig oder falsch? In Deutschland können die Kinder mit 3 Jahren in den Kindergarten
Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book
 Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book Wir wollen wissen wieviel Umsatz Vertreter Müller im Juni gemacht hat? Dazu klicken wir irgendwo in ein Feld und geben ein: =SVERWEIS
Gratis Excel SVERWEIS Funktions-Anleitung, Tutorial, ebook, PDF-E-Book Wir wollen wissen wieviel Umsatz Vertreter Müller im Juni gemacht hat? Dazu klicken wir irgendwo in ein Feld und geben ein: =SVERWEIS
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Lichtbrechung an Linsen
 Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Anspruchsvolle Dreierausdrücke zum selbstständigen Lernen
 Anspruchsvolle Dreierausdrücke zum selbstständigen Lernen von Frank Rothe Das vorliegende Übungsblatt ist als Anregung gedacht, die Sie in Ihrer Klasse in unterschiedlicher Weise umsetzen können. Entwickelt
Anspruchsvolle Dreierausdrücke zum selbstständigen Lernen von Frank Rothe Das vorliegende Übungsblatt ist als Anregung gedacht, die Sie in Ihrer Klasse in unterschiedlicher Weise umsetzen können. Entwickelt
Binnendifferenzierte Aufgaben: Subtrahieren von negativen Zahlen
 Binnendifferenzierte Subtrahieren von negativen Zahlen Mit Hilfe der von uns erstellten Arbeitsblätter sollen die Schülerinnen und Schüler selbstständig erarbeiten, wie man negative Zahlen subtrahiert.
Binnendifferenzierte Subtrahieren von negativen Zahlen Mit Hilfe der von uns erstellten Arbeitsblätter sollen die Schülerinnen und Schüler selbstständig erarbeiten, wie man negative Zahlen subtrahiert.
Statuten in leichter Sprache
 Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
40-Tage-Wunder- Kurs. Umarme, was Du nicht ändern kannst.
 40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
40-Tage-Wunder- Kurs Umarme, was Du nicht ändern kannst. Das sagt Wikipedia: Als Wunder (griechisch thauma) gilt umgangssprachlich ein Ereignis, dessen Zustandekommen man sich nicht erklären kann, so dass
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Zahlenmauern. Dr. Maria Koth. Ausgehend von dieser einfachen Bauvorschrift ergibt sich eine Vielzahl an möglichen Aufgabenstellungen.
 Zahlenmauern Dr. Maria Koth Zahlenmauern sind nach einer einfachen Regel gebaut: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Ausgehend von dieser einfachen Bauvorschrift ergibt
Zahlenmauern Dr. Maria Koth Zahlenmauern sind nach einer einfachen Regel gebaut: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Ausgehend von dieser einfachen Bauvorschrift ergibt
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor
 Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
 Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009)
 Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
Zahlen und das Hüten von Geheimnissen (G. Wiese, 23. April 2009) Probleme unseres Alltags E-Mails lesen: Niemand außer mir soll meine Mails lesen! Geld abheben mit der EC-Karte: Niemand außer mir soll
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
CTI SYSTEMS S.A. CTI SYSTEMS S.A. 12, op der Sang. Fax: +352/2685-3000 L- 9779 Lentzweiler. Email: cti@ctisystems.com G.D.
 Z.I. Eselborn - Lentzweiler Phone: +352/2685-2000 12, op der Sang Fax: +352/2685-3000 L- 9779 Lentzweiler Email: cti@ctisystems.com G.D. Luxembourg URL: www.ctisystems.com Benutzung von Höhensicherungsgeräten
Z.I. Eselborn - Lentzweiler Phone: +352/2685-2000 12, op der Sang Fax: +352/2685-3000 L- 9779 Lentzweiler Email: cti@ctisystems.com G.D. Luxembourg URL: www.ctisystems.com Benutzung von Höhensicherungsgeräten
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
e LEARNING Kurz-Anleitung zum Erstellen eines Wikis 1. Wiki erstellen
 Kurz-Anleitung zum Erstellen eines Wikis Die Aktivität Wiki verschafft Ihnen die Möglichkeit, Wissen zu sammeln und zu strukturieren. Dabei können Sie die Teilnehmer Ihres Kurses an der Erstellung des
Kurz-Anleitung zum Erstellen eines Wikis Die Aktivität Wiki verschafft Ihnen die Möglichkeit, Wissen zu sammeln und zu strukturieren. Dabei können Sie die Teilnehmer Ihres Kurses an der Erstellung des
Simplex-Umformung für Dummies
 Simplex-Umformung für Dummies Enthält die Zielfunktion einen negativen Koeffizienten? NEIN Optimale Lösung bereits gefunden JA Finde die Optimale Lösung mit dem Simplex-Verfahren! Wähle die Spalte mit
Simplex-Umformung für Dummies Enthält die Zielfunktion einen negativen Koeffizienten? NEIN Optimale Lösung bereits gefunden JA Finde die Optimale Lösung mit dem Simplex-Verfahren! Wähle die Spalte mit
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Portfolio: "Die Ratten" von Gerhart Hauptmann
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Portfolio: "Die Ratten" von Gerhart Hauptmann Das komplette Material finden Sie hier: Download bei School-Scout.de Titel: man zum
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Portfolio: "Die Ratten" von Gerhart Hauptmann Das komplette Material finden Sie hier: Download bei School-Scout.de Titel: man zum
ist die Vergütung für die leihweise Überlassung von Kapital ist die leihweise überlassenen Geldsumme
 Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
Serienbrieferstellung in Word mit Kunden-Datenimport aus Excel
 Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
FAQs für beglaubigte Übersetzungen. 2015 Francesca Tinnirello
 FAQs für beglaubigte Übersetzungen Die am häufigsten gestellten Fragen für beglaubigte Übersetzungen 1) Was sind beglaubigte Übersetzungen? 2) Was kostet eine beglaubigte Übersetzung? 3) Muss ich das Original
FAQs für beglaubigte Übersetzungen Die am häufigsten gestellten Fragen für beglaubigte Übersetzungen 1) Was sind beglaubigte Übersetzungen? 2) Was kostet eine beglaubigte Übersetzung? 3) Muss ich das Original
Einen Wiederherstellungspunktes erstellen & Rechner mit Hilfe eines Wiederherstellungspunktes zu einem früheren Zeitpunkt wieder herstellen
 Einen Wiederherstellungspunktes erstellen & Rechner mit Hilfe eines Wiederherstellungspunktes zu einem früheren Zeitpunkt wieder herstellen 1 Hier einige Links zu Dokumentationen im WEB Windows XP: http://www.verbraucher-sicher-online.de/node/18
Einen Wiederherstellungspunktes erstellen & Rechner mit Hilfe eines Wiederherstellungspunktes zu einem früheren Zeitpunkt wieder herstellen 1 Hier einige Links zu Dokumentationen im WEB Windows XP: http://www.verbraucher-sicher-online.de/node/18
Professionelle Seminare im Bereich MS-Office
 Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Sich einen eigenen Blog anzulegen, ist gar nicht so schwer. Es gibt verschiedene Anbieter. www.blogger.com ist einer davon.
 www.blogger.com Sich einen eigenen Blog anzulegen, ist gar nicht so schwer. Es gibt verschiedene Anbieter. www.blogger.com ist einer davon. Sie müssen sich dort nur ein Konto anlegen. Dafür gehen Sie auf
www.blogger.com Sich einen eigenen Blog anzulegen, ist gar nicht so schwer. Es gibt verschiedene Anbieter. www.blogger.com ist einer davon. Sie müssen sich dort nur ein Konto anlegen. Dafür gehen Sie auf
Systemwette. Sporttip set
 Systemwette Sporttip set Swisslos Interkantonale Landeslotterie Lange Gasse 20, Postfach, CH-4002 Basel Telefon +41 (0)61 284 11 11, Fax +41 (0)61 284 13 33, info@sporttip.ch, www.sporttip.ch Einfacher,
Systemwette Sporttip set Swisslos Interkantonale Landeslotterie Lange Gasse 20, Postfach, CH-4002 Basel Telefon +41 (0)61 284 11 11, Fax +41 (0)61 284 13 33, info@sporttip.ch, www.sporttip.ch Einfacher,
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer
 Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
Das RSA-Verschlüsselungsverfahren 1 Christian Vollmer Allgemein: Das RSA-Verschlüsselungsverfahren ist ein häufig benutztes Verschlüsselungsverfahren, weil es sehr sicher ist. Es gehört zu der Klasse der
M03a Lernstraße für den Unterricht in Sekundarstufe I
 M03a Lernstraße für den Unterricht in Sekundarstufe I 1. Station: Der Taufspruch Jedem Täufling wird bei der Taufe ein Taufspruch mit auf den Weg gegeben. Dabei handelt es sich um einen Vers aus der Bibel.
M03a Lernstraße für den Unterricht in Sekundarstufe I 1. Station: Der Taufspruch Jedem Täufling wird bei der Taufe ein Taufspruch mit auf den Weg gegeben. Dabei handelt es sich um einen Vers aus der Bibel.
Die Bundes-Zentrale für politische Bildung stellt sich vor
 Die Bundes-Zentrale für politische Bildung stellt sich vor Die Bundes-Zentrale für politische Bildung stellt sich vor Deutschland ist ein demokratisches Land. Das heißt: Die Menschen in Deutschland können
Die Bundes-Zentrale für politische Bildung stellt sich vor Die Bundes-Zentrale für politische Bildung stellt sich vor Deutschland ist ein demokratisches Land. Das heißt: Die Menschen in Deutschland können
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Vorgestellt von Hans-Dieter Stubben
 Neue Lösungen in der GGf-Versorgung Vorgestellt von Hans-Dieter Stubben Geschäftsführer der Bundes-Versorgungs-Werk BVW GmbH Verbesserungen in der bav In 2007 ist eine wichtige Entscheidung für die betriebliche
Neue Lösungen in der GGf-Versorgung Vorgestellt von Hans-Dieter Stubben Geschäftsführer der Bundes-Versorgungs-Werk BVW GmbH Verbesserungen in der bav In 2007 ist eine wichtige Entscheidung für die betriebliche
Erstellen einer E-Mail in OWA (Outlook Web App)
 Erstellen einer E-Mail in OWA (Outlook Web App) Partner: 2/12 Versionshistorie: Datum Version Name Status 13.09.2011 1.1 J. Bodeit Punkte 7 hinzugefügt, alle Mailempfänger unkenntlich gemacht 09.09.2011
Erstellen einer E-Mail in OWA (Outlook Web App) Partner: 2/12 Versionshistorie: Datum Version Name Status 13.09.2011 1.1 J. Bodeit Punkte 7 hinzugefügt, alle Mailempfänger unkenntlich gemacht 09.09.2011
Mathematischer Spaziergang für die 1. Primarstufe
 . Lehre Weiterbildung Forschung Studierendenarbeit Florjana Imeri Angela Pfiffner Silvana Zürcher Matheliebe an der PHTG Mathematischer Spaziergang für die 1. Primarstufe Ort Sportplatz PMS sowie Gelände
. Lehre Weiterbildung Forschung Studierendenarbeit Florjana Imeri Angela Pfiffner Silvana Zürcher Matheliebe an der PHTG Mathematischer Spaziergang für die 1. Primarstufe Ort Sportplatz PMS sowie Gelände
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
DAUERHAFTE ÄNDERUNG VON SCHRIFTART, SCHRIFTGRÖßE
 DAUERHAFTE ÄNDERUNG VON SCHRIFTART, SCHRIFTGRÖßE UND ZEILENABSTAND Word 2010 und 2007 Jedes neue leere Dokument, das mit Word 2010 erstellt wird, basiert auf einer Dokumentvorlage mit dem Namen Normal.dotx.
DAUERHAFTE ÄNDERUNG VON SCHRIFTART, SCHRIFTGRÖßE UND ZEILENABSTAND Word 2010 und 2007 Jedes neue leere Dokument, das mit Word 2010 erstellt wird, basiert auf einer Dokumentvorlage mit dem Namen Normal.dotx.
Ebenenmasken Grundlagen
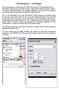 Ebenenmasken Grundlagen Was sind Ebenmasken? Was machen sie? Wofür braucht man sie? Wie funktionieren sie? Ebenmasken sind eines der sinnvollsten Tools in anspruchvollen EBV Programmen (EBV = elektronische
Ebenenmasken Grundlagen Was sind Ebenmasken? Was machen sie? Wofür braucht man sie? Wie funktionieren sie? Ebenmasken sind eines der sinnvollsten Tools in anspruchvollen EBV Programmen (EBV = elektronische
Das Persönliche Budget in verständlicher Sprache
 Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Manager. von Peter Pfeifer, Waltraud Pfeifer, Burkhard Münchhagen. Spielanleitung
 Manager von Peter Pfeifer, Waltraud Pfeifer, Burkhard Münchhagen Spielanleitung Manager Ein rasantes Wirtschaftsspiel für 3 bis 6 Spieler. Das Glück Ihrer Firma liegt in Ihren Händen! Bestehen Sie gegen
Manager von Peter Pfeifer, Waltraud Pfeifer, Burkhard Münchhagen Spielanleitung Manager Ein rasantes Wirtschaftsspiel für 3 bis 6 Spieler. Das Glück Ihrer Firma liegt in Ihren Händen! Bestehen Sie gegen
Kurzleitfaden für Schüler
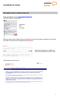 Wie melde ich mich in Schüler Online an? Geben Sie folgenden Link ein: www.schueleranmeldung.de Sie erhalten folgende Anmeldemaske: Mustermann Frank 31.05.1994 Nimmt Ihre Schule nicht an Schüler Online
Wie melde ich mich in Schüler Online an? Geben Sie folgenden Link ein: www.schueleranmeldung.de Sie erhalten folgende Anmeldemaske: Mustermann Frank 31.05.1994 Nimmt Ihre Schule nicht an Schüler Online
Animationen erstellen
 Animationen erstellen Unter Animation wird hier das Erscheinen oder Bewegen von Objekten Texten und Bildern verstanden Dazu wird zunächst eine neue Folie erstellt : Einfügen/ Neue Folie... Das Layout Aufzählung
Animationen erstellen Unter Animation wird hier das Erscheinen oder Bewegen von Objekten Texten und Bildern verstanden Dazu wird zunächst eine neue Folie erstellt : Einfügen/ Neue Folie... Das Layout Aufzählung
Festigkeit von FDM-3D-Druckteilen
 Festigkeit von FDM-3D-Druckteilen Häufig werden bei 3D-Druck-Filamenten die Kunststoff-Festigkeit und physikalischen Eigenschaften diskutiert ohne die Einflüsse der Geometrie und der Verschweißung der
Festigkeit von FDM-3D-Druckteilen Häufig werden bei 3D-Druck-Filamenten die Kunststoff-Festigkeit und physikalischen Eigenschaften diskutiert ohne die Einflüsse der Geometrie und der Verschweißung der
Gefahr erkannt Gefahr gebannt
 Ihre Unfallversicherung informiert Toter Winkel Gefahr erkannt Gefahr gebannt Gesetzliche Unfallversicherung Die Situation Liebe Eltern! Immer wieder kommt es zu schweren Verkehrsunfällen, weil LKW-Fahrer
Ihre Unfallversicherung informiert Toter Winkel Gefahr erkannt Gefahr gebannt Gesetzliche Unfallversicherung Die Situation Liebe Eltern! Immer wieder kommt es zu schweren Verkehrsunfällen, weil LKW-Fahrer
Dossier: Rechnungen und Lieferscheine in Word
 www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Viele Bilder auf der FA-Homepage
 Viele Bilder auf der FA-Homepage Standardmäßig lassen sich auf einer FA-Homepage nur 2 Bilder mit zugehörigem Text unterbringen. Sollen es mehr Bilder sein, muss man diese als von einer im Internet
Viele Bilder auf der FA-Homepage Standardmäßig lassen sich auf einer FA-Homepage nur 2 Bilder mit zugehörigem Text unterbringen. Sollen es mehr Bilder sein, muss man diese als von einer im Internet
Strom in unserem Alltag
 Strom in unserem Alltag Kannst du dir ein Leben ohne Strom vorstellen? Wir verbrauchen jeden Tag eine Menge Energie: Noch vor dem Aufstehen klingelt der Radiowecker, dann schalten wir das Licht ein, wir
Strom in unserem Alltag Kannst du dir ein Leben ohne Strom vorstellen? Wir verbrauchen jeden Tag eine Menge Energie: Noch vor dem Aufstehen klingelt der Radiowecker, dann schalten wir das Licht ein, wir
Informationen zum Ambulant Betreuten Wohnen in leichter Sprache
 Informationen zum Ambulant Betreuten Wohnen in leichter Sprache Arbeiterwohlfahrt Kreisverband Siegen - Wittgenstein/ Olpe 1 Diese Information hat geschrieben: Arbeiterwohlfahrt Stephanie Schür Koblenzer
Informationen zum Ambulant Betreuten Wohnen in leichter Sprache Arbeiterwohlfahrt Kreisverband Siegen - Wittgenstein/ Olpe 1 Diese Information hat geschrieben: Arbeiterwohlfahrt Stephanie Schür Koblenzer
L10N-Manager 3. Netzwerktreffen der Hochschulübersetzer/i nnen Mannheim 10. Mai 2016
 L10N-Manager 3. Netzwerktreffen der Hochschulübersetzer/i nnen Mannheim 10. Mai 2016 Referentin: Dr. Kelly Neudorfer Universität Hohenheim Was wir jetzt besprechen werden ist eine Frage, mit denen viele
L10N-Manager 3. Netzwerktreffen der Hochschulübersetzer/i nnen Mannheim 10. Mai 2016 Referentin: Dr. Kelly Neudorfer Universität Hohenheim Was wir jetzt besprechen werden ist eine Frage, mit denen viele
= i (V) = d 2. v = d! p! n da v 1 = v 2 gilt auch d 1 ÿ p ÿ n 1 = d 2 ÿ p ÿ n 2 (III) p kürzen (Division durch p) d 1 ÿ n 1 = d 2 ÿ n 2 (IV) oder
 v = d! p! n da v 1 = v 2 (I) (II) gilt auch d 1 ÿ p ÿ n 1 = d 2 ÿ p ÿ n 2 (III) p kürzen (Division durch p) d 1 ÿ n 1 = d 2 ÿ n 2 (IV) oder i = Übersetzungsverhältnis n 1 n 2 = d 2 d 1 = i (V) Beispiel
v = d! p! n da v 1 = v 2 (I) (II) gilt auch d 1 ÿ p ÿ n 1 = d 2 ÿ p ÿ n 2 (III) p kürzen (Division durch p) d 1 ÿ n 1 = d 2 ÿ n 2 (IV) oder i = Übersetzungsverhältnis n 1 n 2 = d 2 d 1 = i (V) Beispiel
Rechnung wählen Lernstandserfassung
 Rechnungen verstehen Richtige F1 Rechnung wählen Lernstandserfassung 1. Wie rechnen Sie? Höhe eines Personenwagens Schätzen Sie die Höhe des Gebäudes. Schätzen Sie die Grundfläche des Gebäudes. Schätzen
Rechnungen verstehen Richtige F1 Rechnung wählen Lernstandserfassung 1. Wie rechnen Sie? Höhe eines Personenwagens Schätzen Sie die Höhe des Gebäudes. Schätzen Sie die Grundfläche des Gebäudes. Schätzen
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
9 Auto. Rund um das Auto. Welche Wörter zum Thema Auto kennst du? Welches Wort passt? Lies die Definitionen und ordne zu.
 1 Rund um das Auto Welche Wörter zum Thema Auto kennst du? Welches Wort passt? Lies die Definitionen und ordne zu. 1. Zu diesem Fahrzeug sagt man auch Pkw oder Wagen. 2. kein neues Auto, aber viel billiger
1 Rund um das Auto Welche Wörter zum Thema Auto kennst du? Welches Wort passt? Lies die Definitionen und ordne zu. 1. Zu diesem Fahrzeug sagt man auch Pkw oder Wagen. 2. kein neues Auto, aber viel billiger
Nicht über uns ohne uns
 Nicht über uns ohne uns Das bedeutet: Es soll nichts über Menschen mit Behinderung entschieden werden, wenn sie nicht mit dabei sind. Dieser Text ist in leicht verständlicher Sprache geschrieben. Die Parteien
Nicht über uns ohne uns Das bedeutet: Es soll nichts über Menschen mit Behinderung entschieden werden, wenn sie nicht mit dabei sind. Dieser Text ist in leicht verständlicher Sprache geschrieben. Die Parteien
Es gibt einige Kardinalstellen, an denen sich auf der Festplatte Müll ansammelt: Um einen Großteil davon zu bereinigen.
 Windows Säubern: Es gibt einige Kardinalstellen, an denen sich auf der Festplatte Müll ansammelt: Um einen Großteil davon zu bereinigen. Internetdateien: Öffnen Sie den Internet Explorer (blaues e ). Öffnen
Windows Säubern: Es gibt einige Kardinalstellen, an denen sich auf der Festplatte Müll ansammelt: Um einen Großteil davon zu bereinigen. Internetdateien: Öffnen Sie den Internet Explorer (blaues e ). Öffnen
2. Speichern und öffnen
 2. Speichern und öffnen In diesem Modul lernen Sie, ein Dokument zum ersten Mal zu speichern, zu öffnen, nochmals zu speichern unter demselben Namen, nachdem Sie etwas geändert haben, zu speichern als
2. Speichern und öffnen In diesem Modul lernen Sie, ein Dokument zum ersten Mal zu speichern, zu öffnen, nochmals zu speichern unter demselben Namen, nachdem Sie etwas geändert haben, zu speichern als
Dreiecke. Worum geht es? Das Material
 Dreiecke Worum geht es? Das Es handelt sich um gleichseitige Dreiecke aus Holz mit einer Kantenlänge von 5 cm in drei verschiedenen Farben: orange, rot und grün. Die Dreiecke regen zum Legen von flächigen
Dreiecke Worum geht es? Das Es handelt sich um gleichseitige Dreiecke aus Holz mit einer Kantenlänge von 5 cm in drei verschiedenen Farben: orange, rot und grün. Die Dreiecke regen zum Legen von flächigen
Wie der Shop funktioniert!
 Wie der Shop funktioniert! 1. Einkaufen als Neukunde? Als erstes sollten Sie sich anmelden. Klicken Sie auf die Schrift "Neukunde? Jetzt registrieren" auf der rechten Seite. Dann geben Sie Ihre Daten ein
Wie der Shop funktioniert! 1. Einkaufen als Neukunde? Als erstes sollten Sie sich anmelden. Klicken Sie auf die Schrift "Neukunde? Jetzt registrieren" auf der rechten Seite. Dann geben Sie Ihre Daten ein
1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden.
 Der Serienversand Was kann man mit der Maske Serienversand machen? 1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden. 2. Adressen auswählen,
Der Serienversand Was kann man mit der Maske Serienversand machen? 1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden. 2. Adressen auswählen,
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Bedienungsanleitung KSG-Forum
 Bedienungsanleitung KSG-Forum Liebe Paddelfreunde, gemeinsam mit unserer neuen Seite geht jetzt auch das Forum richtig online. Hier können wir uns über alles rund um Verein & Hobby austauschen, sowie kleine
Bedienungsanleitung KSG-Forum Liebe Paddelfreunde, gemeinsam mit unserer neuen Seite geht jetzt auch das Forum richtig online. Hier können wir uns über alles rund um Verein & Hobby austauschen, sowie kleine
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: If-clauses - conditional sentences - Nie mehr Probleme mit Satzbau im Englischen! Das komplette Material finden Sie hier: School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: If-clauses - conditional sentences - Nie mehr Probleme mit Satzbau im Englischen! Das komplette Material finden Sie hier: School-Scout.de
WAS finde ich WO im Beipackzettel
 WAS finde ich WO im Beipackzettel Sie haben eine Frage zu Ihrem? Meist finden Sie die Antwort im Beipackzettel (offiziell "Gebrauchsinformation" genannt). Der Aufbau der Beipackzettel ist von den Behörden
WAS finde ich WO im Beipackzettel Sie haben eine Frage zu Ihrem? Meist finden Sie die Antwort im Beipackzettel (offiziell "Gebrauchsinformation" genannt). Der Aufbau der Beipackzettel ist von den Behörden
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Die Invaliden-Versicherung ändert sich
 Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Die Invaliden-Versicherung ändert sich 1 Erklärung Die Invaliden-Versicherung ist für invalide Personen. Invalid bedeutet: Eine Person kann einige Sachen nicht machen. Wegen einer Krankheit. Wegen einem
Geld Verdienen im Internet leicht gemacht
 Geld Verdienen im Internet leicht gemacht Hallo, Sie haben sich dieses E-book wahrscheinlich herunter geladen, weil Sie gerne lernen würden wie sie im Internet Geld verdienen können, oder? Denn genau das
Geld Verdienen im Internet leicht gemacht Hallo, Sie haben sich dieses E-book wahrscheinlich herunter geladen, weil Sie gerne lernen würden wie sie im Internet Geld verdienen können, oder? Denn genau das
Leitfaden zur ersten Nutzung der R FOM Portable-Version für Windows (Version 1.0)
 Leitfaden zur ersten Nutzung der R FOM Portable-Version für Windows (Version 1.0) Peter Koos 03. Dezember 2015 0 Inhaltsverzeichnis 1 Voraussetzung... 3 2 Hintergrundinformationen... 3 2.1 Installationsarten...
Leitfaden zur ersten Nutzung der R FOM Portable-Version für Windows (Version 1.0) Peter Koos 03. Dezember 2015 0 Inhaltsverzeichnis 1 Voraussetzung... 3 2 Hintergrundinformationen... 3 2.1 Installationsarten...
Adobe Photoshop. Lightroom 5 für Einsteiger Bilder verwalten und entwickeln. Sam Jost
 Adobe Photoshop Lightroom 5 für Einsteiger Bilder verwalten und entwickeln Sam Jost Kapitel 2 Der erste Start 2.1 Mitmachen beim Lesen....................... 22 2.2 Für Apple-Anwender.........................
Adobe Photoshop Lightroom 5 für Einsteiger Bilder verwalten und entwickeln Sam Jost Kapitel 2 Der erste Start 2.1 Mitmachen beim Lesen....................... 22 2.2 Für Apple-Anwender.........................
HALLO UND WILLKOMMEN!
 HALLO UND WILLKOMMEN! DRUCKEN: Am besten weisses Papier verwenden, Papierformat Din A4, Hochformat, Farbdruck. (Bei schwarz/weiss Druck: 4 Spielfiguren und 84 Elementsteine anmalen). Das Spiel ist natürlich
HALLO UND WILLKOMMEN! DRUCKEN: Am besten weisses Papier verwenden, Papierformat Din A4, Hochformat, Farbdruck. (Bei schwarz/weiss Druck: 4 Spielfiguren und 84 Elementsteine anmalen). Das Spiel ist natürlich
teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep
 teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
teischl.com Software Design & Services e.u. office@teischl.com www.teischl.com/booknkeep www.facebook.com/booknkeep 1. Erstellen Sie ein neues Rechnungsformular Mit book n keep können Sie nun Ihre eigenen
Woche 1: Was ist NLP? Die Geschichte des NLP.
 Woche 1: Was ist NLP? Die Geschichte des NLP. Liebe(r) Kursteilnehmer(in)! Im ersten Theorieteil der heutigen Woche beschäftigen wir uns mit der Entstehungsgeschichte des NLP. Zuerst aber eine Frage: Wissen
Woche 1: Was ist NLP? Die Geschichte des NLP. Liebe(r) Kursteilnehmer(in)! Im ersten Theorieteil der heutigen Woche beschäftigen wir uns mit der Entstehungsgeschichte des NLP. Zuerst aber eine Frage: Wissen
1. Weniger Steuern zahlen
 1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
1. Weniger Steuern zahlen Wenn man arbeitet, zahlt man Geld an den Staat. Dieses Geld heißt Steuern. Viele Menschen zahlen zu viel Steuern. Sie haben daher wenig Geld für Wohnung, Gewand oder Essen. Wenn
Hinweise zum Übungsblatt Formatierung von Text:
 Hinweise zum Übungsblatt Formatierung von Text: Zu den Aufgaben 1 und 2: Als erstes markieren wir den Text den wir verändern wollen. Dazu benutzen wir die linke Maustaste. Wir positionieren den Mauszeiger
Hinweise zum Übungsblatt Formatierung von Text: Zu den Aufgaben 1 und 2: Als erstes markieren wir den Text den wir verändern wollen. Dazu benutzen wir die linke Maustaste. Wir positionieren den Mauszeiger
Die Größe von Flächen vergleichen
 Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
mal an Ihre Karriere! glaub, ich werd verrückt!
 Dass wir Deutschen Gummibärchen lieben, ist ja bekannt. Wenn Sie die leckeren Süßigkeiten aus Zucker, Gelatine und Fruchtsaft zum ersten Mal probieren, verstehen Sie sofort, dass manche Menschen nicht
Dass wir Deutschen Gummibärchen lieben, ist ja bekannt. Wenn Sie die leckeren Süßigkeiten aus Zucker, Gelatine und Fruchtsaft zum ersten Mal probieren, verstehen Sie sofort, dass manche Menschen nicht
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Platinen mit dem HP CLJ 1600 direkt bedrucken ohne Tonertransferverfahren
 Platinen mit dem HP CLJ 1600 direkt bedrucken ohne Tonertransferverfahren Um die Platinen zu bedrucken, muß der Drucker als allererstes ein wenig zerlegt werden. Obere und seitliche Abdeckungen entfernen:
Platinen mit dem HP CLJ 1600 direkt bedrucken ohne Tonertransferverfahren Um die Platinen zu bedrucken, muß der Drucker als allererstes ein wenig zerlegt werden. Obere und seitliche Abdeckungen entfernen:
