Kapitel 9 Die Fermat-Vermutung für Zahlen und für Polynome
|
|
|
- Lioba Seidel
- vor 7 Jahren
- Abrufe
Transkript
1 Kapitel 9 Die Fermat-Vermutung für Zahlen und für Polynome 1: Zahlen und Funktionen Zum Beweis der eindeutigen Primzerlegung in der Hauptordnung eines Zahlkörpers mußten wir nur nachweisen, daß diese ein EUKLIDischer Ring ist, denn wie wir aus Kapitel 6, 5 wissen, ist jeder EUKLIDische Ring faktoriell. Da der Polynomring in einer Veränderlichen über einem Körper EUKLIDisch ist, gilt also auch dort das Gesetz von der eindeutigen Primzerlegung, wobei die irreduziblen Polynome die Rolle der Primzahlen einnehmen. Besonders einfach ist die Situation, wenn der Grundkörper k algebraisch abgeschlossen ist: Dann hat jedes nichtkonstante Polynom f k[x] eine Nullstelle a und ist damit durch x a teilbar. In diesem Fall sind also alle irreduziblen Polynome linear. Die Zerlegung in irreduzible Elemente ist bekanntlich nur eindeutig bis auf Einheiten, und die Einheiten eines Polynomrings sind nach 1 aus Kapitel 6 gerade die des Koeffizientenrings, hier also die von Null verschiedenen Elemente von k. Durch Multiplikation mit einem solchen Element kann man den höchsten Koeffizienten eines jeden Polynoms zu eins machen; die irreduziblen Polynome über einem algebraisch abgeschlossenen Körper sind also bis auf Assoziiertheit genau die Polynome der Form x a mit a k und sie entsprechen eindeutig den Elementen von k.
2 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 252 Den Primzahlen von Z entsprechen daher im Polynomring über einem algebraisch abgeschlossenen Körper die Punkte der affinen Geraden über k, wir können also geometrisch argumentieren. Natürlich gibt es zum Teil beträchtliche Unterschiede zwischen Z und dem Polynomring über einem Körper, aber gerade das macht die Analogie so interessant: Da es für jeden der beiden Ringe ein eigenes Instrumentarium gibt, kann man versuchen die damit bewiesenen Resultate auf den jeweils anderen Fall zu übertragen, was idealerweise zu neuen Sätzen und sonst zumindest zu interessanten Vermutungen führt. Als Beispiel für Parallelen und Unterschiede zwischen den beiden Situationen wollen wir die FERMAT-Vermutung betrachten. FERMAT schrieb bekanntlich um 1637 an den Rand seiner Arithmetik des DIOPHANTOS von Alexandrien, daß die Gleichung x n + y n = z n für n 3 keine Lösung in ganzen Zahlen habe außer natürlich den trivialen Lösungen, bei denen eine der beiden Variablen verschwindet. (Die französische Übersetzung der Arithmetik, die er dabei benutzte, stammt übrigens von BACHET DE MÉZIRIAC, denn wir bereits als Entdecker des erweiterten EUKLIDischen Algorithmus kennen. Bekannt wurde FER- MATs Randbemerkung erst, als dessen Sohn CLÉMENT-SAMUEL DE FER- MAT 1670 die Arithmetik mit den Randbemerkungen seines fünf Jahre zuvor gestorbenen Vaters veröffentlichte.) Die direkte Verallgemeinerung auf Polynomringe ist sicherlich falsch: Die Gleichung f n + g n = h n ist zumindest für konstante Polynome über einem algebraisch abgeschlossenen Körper immer lösbar: Für beliebig vorgegebene Konstanten f, g k muß man einfach h = n f n + g n setzen. Das sind allerdings, wenn wir uns wirklich für Polynome interessieren, uninteressante Lösungen, vergleichbar den Lösungen x n + 0 n = x n der klassischen FERMAT-Gleichung. Auch wenn wir verlangen, daß die Grade aller beteiligter Polynome positiv sein sollen, gibt es triviale Lösungen: Ist f irgendein beliebiges Polynom und sind a,b,c k so, daß gilt a n +b n = c n, ist natürlich auch (af) n + (bf) n = (cf) n. Was wir höchstens erwarten können ist also das folgende Analogon zur klassischen FERMAT-Vermutung: Es ist nicht möglich, einen Kubus in zwei Kuben oder ein Biquadrat in zwei Biquadrate und ganz allgemein irgendeine der unendlich vielen Potenzen jenseits des Quadrats in zwei ebensolche zu teilen. Ich habe einen wunderbaren Beweis hierfür gefunden, aber der Rand ist zu schmal, um ihn zu fassen.
3 253 Zahlentheorie Für n 3 gibt es keine paarweise teilerfremden Polynome f,g,h mit positivem Grad, so daß f n + g n = h n ist. Für Körper positiver Charakteristik ist selbst das noch falsch: Über einen Körper der Charakteristik p ist schließlich f p + g p = (f + g) p für beliebige Polynome f und g, und dasselbe gilt auch wenn man den Exponenten p durch eine seiner Potenzen ersetzt. Wir können also höchstens für Körper der Charakteristik null erwarten, daß diese Vermutung für alle Exponenten n 3 richtig ist, und genau das werden wir im übernächsten Paragraphen (zumindest für den Körper der komplexen Zahlen) auch beweisen. Zunächst aber wollen wir schauen, was im bei FERMAT ausgeschlossenen Fall des Exponenten zwei passiert. 2: Pythagoräische Tripel Betrachten wir zunächst den Fall der Polynome, wobei wir uns der Einfachheit halber gleich auf Polynome mit komplexen Koeffizienten beschränken wollen. Ist f 2 + g 2 = h 2, so ist f 2 = h 2 g 2 = (h + g)(h g). Wenn wir f und g als teilerfremd voraussetzen, sind auch g und h teilerfremd und somit auch h + g und h g, denn jeder gemeinsame Teiler dieser beiden Polynome wäre auch ein Teiler ihrer Summe 2h sowie ihrer Differenz 2g. Wenn wir die Zerlegung von f 2 in irreduzible Faktoren vergleichen mit der von h + g und h g folgt somit, daß jeder irreduzible Faktor von f entweder in h + g oder in h g in gerader Potenz auftreten muß. Da jede komplexe Zahl ein Quadrat ist, können wir auch eine eventuell auftretende Einheit als Quadrat schreiben; somit gibt es zwei Polynome u,v C[x] derart, daß u 2 = h + g, v 2 = h g und uv = f ist, d.h. f = uv, g = u2 v 2 2 und h = u2 + v 2. 2
4 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 254 Starten wir umgekehrt mit zwei beliebigen teilerfremden Polynomen u, v C[x], erhalten mit Hilfe dieser Formeln Lösungen der Gleichung f 2 + g 2 = h 2. Damit kennen wir alle teilerfremden Lösungen, und die restlichen erhalten wir, indem wir alle drei Polynome mit einem gemeinsamen Faktor multiplizieren. Nehmen wir als ein einfaches Beispiel u = 2x und v = 2, ist also in der Tat ist f = 4x, g = x 2 1 und h = x ; (2x) 2 + ( x 2 1 ) 2 = ( x ) 2. Hier erhalten wir also mit geringem Aufwand eine vollständige Übersicht über alle Lösungen. Versuchen wir das gleiche auch für den klassischen Fall! Wegen des Satzes von PYTHAGORAS bezeichnet man ein Tripel (x, y, z) ganzer Zahlen mit x 2 + y 2 = z 2 als pythagoräisches Tripel; für jedes solche Tripel gibt es ein rechtwinkliges Dreieck mit Seitenlängen x, y und z. Wir bezeichnen das Tripel (x,y,z) als primitiv, wenn sie sich nicht als Vielfaches eines anderen schreiben läßt, wenn also die Zahlen x, y, z keinen gemeinsamen Teiler haben. Sobald wir alle primitiven Lösungen kennen, können wir daraus die gesamte Lösungsmenge konstruieren, denn jede nichtprimitive Lösung ist Vielfaches einer primitiven. Wie im Fall der Polynome gehen wir aus von einem primitiven Tripel (x,y,z) und wenden die dritte binomische Formel an: x 2 = z 2 y 2 = (z + y)(z y). Hier können wir leider nicht mehr ohne weiteres folgern, daß z + y und z y teilerfremd und damit Quadrate sind: Sind y und z beide ungerade, so sind ihre Summe und ihre Differenz beide gerade, also durch zwei teilbar. Wir müssen uns also zunächst über die Paritäten von y und z klarwerden. Für eine primitive Lösung (x, y, z) müssen bereits x und y teilerfremd sein, denn ist d ein gemeinsamer Teiler von x und y, so sind x 2 und y 2
5 255 Zahlentheorie beide durch d 2 teilbar, also auch ihre Summe z 2. Wegen der eindeutigen Zerlegbarkeit einer natürlichen Zahl in Primfaktoren ist dann auch z durch d teilbar, d.h. d ist ein gemeinsamer Teiler von x,y und z. Insbesondere können daher x und y nicht beide gerade sein; mindestens eine der beiden Zahlen muß ungerade sein. Andererseits können aber auch nicht beide Zahlen ungerade sein: Wäre nämlich x = 2u + 1 und y = 2v + 1, so wäre z 2 = (2u + 1) 2 + (2v + 1) 2 = 4u 2 + 4u v 2 + 4v mod 4, was unmöglich ist, da modulo vier nur null und eins Quadrate sind. Somit muß in einem primitiven pythagoräischen Tripel (x, y, z) eine der beiden Zahlen x,y gerade sein und die andere ungerade. Da mit (x,y,z) auch (y, x, z) ein primitives pythagoräisches Tripel ist, genügt es, wenn wir diejenigen Tripel betrachten, in denen x gerade ist und y ungerade. Offensichtlich ist dann auch z ungerade. Für so ein Tripel steht in der Gleichung x 2 = z 2 y 2 = (z + y)(z y) rechts das Produkt zweier gerader Zahlen. Im Gegensatz zur Situation bei den Polynomen haben wir hier also keine teilerfremden Faktoren. Dividieren wir aber durch zwei, so können wir wie oben argumentieren, daß 1 2 (z+y) und 1 2 (z y) teilerfremd sind, denn jeder gemeinsame Teiler wäre Teiler ihrer Summe z und ihrer Differenz y. Jetzt können wir wieder die eindeutige Primzerlegung anwenden: Da ( z + y ) ( ) z y x 2 = 2 2, 2 2 wobei die beiden Klammern teilerfremd sind, gibt es ganze Zahlen u, v, so daß ( z + y ) ( z + y ) u 2 =, v 2 = und 2uv = x 2 2 ist, also x = 2uv, y = u 2 v 2 und z = u 2 v 2.
6 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 256 Umgekehrt definieren diese Formeln für beliebige ganze Zahlen u und v ein primitives pythagoräisches Tripel, und bis auf die Reihenfolge von x und y erhalten wir so auch jedes dieser Tripel, für u = 2 und v = 1 etwa das seit Jahrtausenden bekannte Tripel (4, 3, 5). Da sich in alten Sakralbauten und -anlagen auch deutlich kompliziertere pythagoräische Tripel nachweisen lassen, steht zu vermuten, daß die obige Konstruktion möglicherweise bereits in einigen steinzeitlichen Kulturen zumindest teilweise bekannt waren; entsprechende Thesen vertritt beispielsweise bekannte algebraische Geometer B.L. VAN DER WAERDEN ( ), der nach seiner Emeritierung auch mehrere Bücher über die Geschichte der Mathematik veröffentlichte. Mit pythagoräischen Tripel beschäftigt er sich ausführlich in B.L. VAN DER WAERDEN: Geometry and algebra in ancient civilizations, Springer, : Der Satz von Mason In diesem Abschnitt wollen wir, wie bereits angekündigt, sehen, daß es für n 3 keine zueinander teilerfremden Polynome positiven Grades f,g,h C[x] gibt mit f n + g n = h n. Der Beweis beruht darauf, daß die Polynome f n und g n dieselben Nullstellen wie f und g haben, aber mit n-facher Vielfachheit. Ist f n + g n = h n, so hat auch die Summe dieser beiden Potenzen im Vergleich zum Grad relativ wenige Nullstellen, diese aber mit mindestens n-facher Vielfachheit. Nach einem 1983 von R.C. MASON bewiesenen Satz können in einer solchen Situation aber f n,g n und h n nicht zu wenige verschiedene Nullstellen haben: Satz: Bezeichnet n 0 (f) die Anzahl verschiedener (komplexer) Nullstellen eines Polynoms f, so gilt für drei nichtkonstante, teilerfremde Polynome f,g,h mit f + g = h n 0 (fgh) max(deg f, degg, deg h) + 1. Bevor wir diesen Satz beweisen, wollen wir uns zunächst überlegen, daß daraus wirklich die FERMAT-Vermutung für Polynome folgt:
7 257 Zahlentheorie Für drei nichtkonstante teilerfremde Polynome f,g,h mit f n +g n = h n ist nach dem Satz von MASON Andererseits ist aber n 0 ( f n g n h n) max ( degf n, deg g n, deg h n) + 1 = n max ( deg f, degg, deg h ) + 1. n 0 ( f n g n h n) = n 0 ( fgh ) deg f + deg g + deg h 3 max ( degu(x), deg v(x), deg w(x) ), denn die Anzahl verschiedener Nullstellen einer Potenz eines Polynoms ist gleich der Anzahl verschiedener Nullstellen des Polynoms selbst, und die Nullstellenanzahl eines Polynom kann nicht größer sein als der Grad. Damit haben wir insgesamt die Ungleichung 3 max ( deg f, degg, deg h ) n 0 ( f n g n h n) n max ( deg f, degg, deg h ) + 1, die bei nichtkonstanten Polynomen nur für n 2 gelten kann. Somit gibt es für n 3 keine nichtkonstanten teilerfremden Polynome, für die f n + g n = h n ist. Zu einem vollständigen Beweis der FERMAT-Vermutung für Polynome fehlt nun nur noch der Beweis des Satzes von MASON. Die Idee dazu ist folgende: Ist f + g = h, so betrachten wir den Quotienten g/f im rationalen Funktionenkörper C(x). Da f und g teilerfremd sind, ist das ein gekürzter Bruch. Falls wir diesen auch in der Form g/f = G/F schreiben können mit Polynomen F,Gvom Grad höchstens n 0 (fgh) 1 schreiben können, so haben auch f und g höchstens den Grad n 0 (fgh) 1. Wegen f + g = h gilt dasselbe auch für h, und damit wäre der Satz bewiesen. Um g/f als Quotienten zweier neuer Polynome auszudrücken, schreiben wir zunächst g f = S R mit R = f h und S = g h.
8 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 258 Dabei ist R + S = 1, die Summe R + S der Ableitungen verschwindet also. Aus der Gleichung folgt die neue Darstellung R + S = R R R + S S S g f = S R = R /R S /S. Rechts stehen die logarithmischen Ableitungen von R und S im Zähler und Nenner, und damit lassen sich gut die Nullstellen von f,g und h ins Spiel bringen: Nach der LEIBNIZ-Regel ist bekanntlich (uv) = u v + uv, also (uv) uv = u u + v v, die logarithmische Ableitung eines Produkts ist also einfach die Summe der logarithmischen Ableitungen der Faktoren. Daraus folgt sofort, daß die logarithmische Ableitung eines Quotienten gleich der Differenz aus logarithmischer Ableitung des Zählers und logarithmischer Ableitung des Nenners ist. Schreiben wir r s t f = f 0 (x a i ) n i, g = g 0 (x b j ) s j und h = h 0 (x c k ) p k, i=1 so ist also und R R = f f h h = S S = g g h h = j=1 r i=1 r j=1 g f = R /R S /S = n i x a i m j x b j r i=1 s j=1 t k=1 t k=1 n i x a i m j x b j p k x c k, p k x c k t k=1 t k=1 p k x c k p k x c k k=1.
9 259 Zahlentheorie Erweitern wir Zähler und Nenner mit dem Hauptnenner aller Summanden erweitern, d.h. mit dem Polynom vom Grad r + s + t = n 0 (fgh) H = r (x a i ) i=1 s (x b j ) j=1 t (x c k ), so erhalten wir im Zähler wie auch im Nenner Summen von Polynomen vom Grad n 0 (fgh) 1, als Polynome vom Grad höchstens n 0 (fgh) 1, wie gewünscht. Damit ist der Satz von MASON bewiesen. 4: Die abc-vermutung Der Erfolg des Satzes von MASON beim Beweis der FERMAT-Vermutung für Polynome legt es nahe, etwas ähnliches auch im klassischen Fall zu versuchen. Da natürliche Zahlen weder Grade noch Nullstellen haben, müssen wir dazu den Satz von MASON zunächst einmal so umformulieren, daß wir eine Aussage bekommen, die ein sinnvolles Analogon für natürliche Zahlen hat. Dazu ordnen wir einem Polynom f anstelle der Anzahl n 0 (f) seiner (verschiedenen) Nullstellen ein Polynom N 0 (f) dazu, das genau diese Nullstellen mit jeweils der Vielfachheit eins haben soll: Für f = f 0 r i=1 k=1 (x a i ) n i sei N 0 (f) = def r (x a i ), so daß der Grad von N 0 (f) gerade die im vorigen Paragraphen definierte Zahl n 0 (f) ist. Der Vorteil des Polynoms N 0 (f) besteht darin, daß wir eine analoge Definition leicht auch für natürliche Zahlen hinschreiben können: Für r r n = p e i i setzen wir N 0 (n) = p i. def i=1 Mit Hilfe der Polynome N 0 (f) läßt sich der Satz von MASON folgendermaßen umformulieren: i=1 i=1
10 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 260 Gilt für drei teilerfremde Polynome f, g und h die Gleichung f + g = h, so hat jedes der drei Polynome einen kleineren Grad als das Polynom N 0 (fgh). In dieser Formulierung kommt immer noch der Grad vor, für den wir bei natürlichen Zahlen keine Verwendung haben. Betrachten wir aber den Grad lediglich als eine Methode, einem Polynom eine Zahl aus N 0 zuzuordnen, so können wir, wenn wir bereits natürliche Zahlen haben, einfach ganz auf ihn verzichten; falls wir ganze Zahlen betrachten, liegt es nahe, ihn durch den Betrag zu ersetzen. Gemäß dieser Philosophie können wir nun probeweise die folgende Aussage formulieren: A1: Istc = a+b für drei zueinander teilerfremde natürliche Zahlena,b,c, so ist jede der drei Zahlen kleiner als N 0 (abc). Damit haben wir eine sinnvolle Aussage über natürliche Zahlen gefunden, die falls sie korrekt ist sofort die FERMAT-Vermutung impliziert: Gibt es nämlich drei natürliche Zahlen x, y, z mit der Eigenschaft, daß x n + y n = z n für ein n 3, so gibt es auch drei zueinander teilerfremde Zahlen x,y,z mit dieser Eigenschaft: Wir müssen einfach die drei Zahlen durch ihren größten gemeinsamen Teiler kürzen. Alsdann muß, falls obige Aussage richtig ist, jede der drei Potenzen x n,y n,z n kleiner sein als N 0 (x n y n z n ). Nun ist aber N 0 (x n y n z n ) = N 0 (xyz) xyz, d.h. jede der drei Zahlen x n,y n,z n wäre kleiner als xyz. Damit wäre (xyz) n = x n y n z n < (xyz) 3, was für n 3 offensichtlich nicht möglich ist. Angesichts der Komplexität des WILESschen Beweises fällt es schwer, an einen so einfachen Beweis zu glauben, und in der Tat ist die obige Aussage in dieser Form falsch: Betrachten wir etwa die Gleichung = 9. Offensichtlich sind die drei Summanden teilerfremd zueinander, aber sowohl 8 als auch 9 sind größer als N 0 (8 1 9) = 2 3 = 6. Ganz so einfach geht es also nicht.
11 261 Zahlentheorie Da der Grad eines Polynoms nicht durch konstante Faktoren beeinflußt wird, könnte man versuchen, als richtiges Analogon zum Satz von MA- SON eine abgeschwächte Aussage zu nehmen, die nur eine Abschätzung bis auf einen konstanten Faktor enthält, etwa A2: Istc = a+b für drei zueinander teilerfremde natürliche Zahlena,b,c, so gibt es eine Konstante K derart, daß jede der drei Zahlen kleiner ist als K N 0 (abc). Diese Aussage ist trivialerweise richtig: Wir müssen nur eine Konstante K wählen, die größer ist als das Maximum von a,b und c. Leider ist sie auch völlig nutzlos, denn solange die Konstante von a,b und c abhängen darf, haben wir keine Chance, damit die FERMAT-Vermutung zu beweisen. Wir müssen die Aussage also noch einmal umformulieren: A3: Es gibt eine KonstanteK, so daß gilt: Ist c = a+b für drei zueinander teilerfremde natürliche Zahlen a, b, c, so ist jede der drei Zahlen kleiner als K N 0 (abc). Wie wir gleich sehen werden, würde hieraus die FERMAT-Vermutung zumindest für alle hinreichend großen Exponenten n folgen, allerdings ist die Aussage, so wie sie dasteht, leider immer noch falsch: Betrachten wir die Gleichung a n + b n = c n mit a n = 3 2n 1, b n = 1 und c n = 3 2n. ( ) Wäre sie richtig, müßte für jedes n gelten: 3 2n KN 0 ( (3 2 n 1)3 2n ) = K 3 N0 (3 2n 1). Um N 0 (3 2n 1) abzuschätzen, beachten wir, daß gilt 3 2n = ( 3 2n 1 ) 2 und 3 2n 1 = ( 3 2n )( 3 2n 1 1 ) nach der dritten binomischen Formel. Wenden wir dies mehrfach an,
12 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 262 erhalten wir 3 2n 1 = ( 3 2n )( 3 2n 1 1 ) = ( 3 2n )( 3 2n )( 3 2n 2 1 ) = ( 3 2n )( 3 2n )( 3 2n )( 3 2n 3 1 ) = = ( 3 2n )( 3 2n )... ( )( )( ). In der letzten Zeile steht ein Produkt aus n + 1 geraden Zahlen; somit ist 3 2n 1 durch 2 n+1 teilbar. Das Produkt N 0 (3 2n 1) aller verschiedener Primteiler von 3 2n 1 erfüllt daher die Ungleichung N 0 (3 2n 1) 2 32n 1 n = 32 2 n n, denn das Produkt aller ungerader Primteiler kann höchstens gleich (3 2n 1)/2 n sein. Falls A3 korrekt wäre, müßte nach Gleichung ( ) also gelten 3 2n 3K 2 n 1) für alle n. (32n Das kann aber unmöglich der Fall sein, denn für hinreichend große n ist der Faktor 3K 2 kleiner als eins, so daß 3 2n echt kleiner als sich selbst n sein müßte. Auf der Suche nach einem Analogon für den Satz von MASON müssen wir daher noch weiter abschwächen. Eine Möglichkeit dazu ist die 1986 aufgestellte abc-vermutung von MASSER und OESTERLÉ: Zu jedem ε > 0 gibt es eine Konstante K(ε), so daß für alle teilerfremden natürlichen Zahlen a,b,c mit a+b = c gilt: Jede der drei Zahlen a,b,c ist kleiner oder gleich K(ε) N 0 (abc) 1+ε. Diese Vermutung ist, im Gegensatz zur FERMAT-Vermutung, bis heute offen. Wir wollen uns überlegen, daß sie zumindest für große Exponenten n die FERMAT-Vermutung impliziert.
13 263 Zahlentheorie Dazu betrachten wir eine Lösung x n + y n = z n mit o.b.d.a. teilerfremden natürlichen Zahlen x,y,z und wählen uns irgendein ε > 0. Nach der abc-vermutung gibt es dazu eine Konstante K(ε), so daß x n,y n und z n allesamt höchstens gleich K(ε)N 0 (x n y n z n ) 1+ε = K(ε)N 0 (xyz) 1+ε K(ε)(xyz) 1+ε sind. Für ihr Produkt gilt daher x n y n z n K(ε) 3 (xyz) 3(1+ε) oder (xyz) n 3 3ε K(ε) 3. K(ε) 3 ist eine feste Zahl; es gibt daher einen Exponenten m derart, daß 2 m > K(ε) 3 ist. Da das Produkt xyz auf jeden Fall nicht kleiner als zwei sein kann, ist dann für n 3 3ε > m oder n > m ε insbesondere (xyz) n 3 3ε > K(ε) 3. Für Exponenten n > m ε kann daher die FERMAT-Gleichung keine Lösung in natürlichen Zahlen haben. Ob und gegebenenfalls welche konkreten Schranken für n man damit erreichen kann, hängt natürlich davon ab, wie K(ε) von ε abhängt. Dazu gibt es im Augenblick nicht einmal Vermutungen. Für weitere Informationen zu 3 und 4 sei auf einen Vortrag verwiesen, den SERGE LANG in Zürich vor einem allgemeinen Publikum hielt und dem ich hier im wesentlichen gefolgt bin: SERGE LANG: Die abc-vermutung, Elemente der Mathematik 48 (1993), Der Artikel ist (wie die gesamte Zeitschrift Elemente der Mathematik) unter frei zugänglich. 5: Die Frey-Kurve Da die FERMAT-Vermutung seit 1994 bewiesen ist, die abc-vermutung aber immer noch offen, mußte der Beweis der FERMAT-Vermutung
14 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 264 natürlich andere Wege gehen. Die meisten dieser Wege führen in Gebiete, die weit jenseits dessen liegen, was selbst ein guter auf Zahlentheorie spezialisierter Diplom-Mathematiker im Laufe seines Studiums lernen kann, aber zumindest die Grundidee der abc-vermutung, daß man nämlich Summenbeziehungen zwischen großen Zahlen nicht ohne ein gewisses Minimum an verschiedenen Primfaktoren realisieren kann, spielt in modifizierter Weise in der Tat eine große Rolle. Der Anstoß kam 1984 von GERHARD FREY, damals Professor an der Universität Saarbrücken, wo er auf dem Gebiet der Arithmetik elliptischer Kurven arbeitete. Heute leitet er die Arbeitsgruppe Zahlentheorie am Institut für experimentelle Mathematik der (inzwischen mit Duisburg vereinigten) Universität Essen und beschäftigt sich mit der Anwendung elliptischer (und anderer) Kurven in der Kryptologie. Elliptische Kurven sind ebene Kurven, die durch eine Gleichung der Form y 2 = f 3 (x) beschrieben werden mit einem Polynom f 3 (x) vom Grad drei mit drei verschiedenen Nullstellen. Da das Quadrat einer reellen Zahl nicht negativ sein kann, gibt es im Reellen nur Punkte mit x-koordinaten, für die f 3 (x) 0 ist. Im Falle f 3 (x) > 0 erfüllt mit y auch y die obige Gleichung, die Kurve ist also symmetrisch zur x-achse. Falls f 3 (x) nur zwei verschiedene Nullstellen hat, muß eine der Nullstellen doppelt sein, und bei diesem x-wert überkreuzt sich die Kurve; wir reden dann von einer Knotenkurve. Hat schließlich f 3 (x) nur eine, dafür aber dreifache Nullstelle, entsteht eine Spitzenkurve. FREY betrachtete eine (hypothetische) Lösung x n + y n = z n der FERMAT-Gleichung mit teilerfremden natürlichen Zahlen x, y, z und n 5. (Den Falln = 4 hat, wie wir gesehen haben, bereits FERMAT selbst gelöst, den Fall n = 3 nicht viel später EULER.) Wenn es eine solche Lösung gibt, dann gibt es auch eine Lösung für einen Primzahlexponenten l, denn ist l ein Primteiler von n und n = lm, so ist auch a l + b l = c l mit a = x m, b = y m und c = z m
15 265 Zahlentheorie 2 Elliptische Kurve y 2 = x(x-2)(x-3) 2 Knotenkurve y 2 2 = x(x-2) 2 Spitzenkurve y 2 = x 3
16 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 266 eine Lösung, und auch a,b,c sind teilerfremd. Auch für l genügt es, den Fall l 5 zu betrachten, denn wenn wir für l den größten Primteiler von n nehmen, bedeutet l = 2, daß n eine Zweierpotenz sein muß, was für n = 2 kein Widerspruch zur FERMAT-Vermutung ist und für n = 4 und damit auch jede höhere Zweierpotenz nach FERMATs Beweis ausgeschlossen ist. Für den Fall l = 3 kann wieder auf EULER verwiesen werden. Zur obigen Lösung definiert FREY die elliptische Kurve y 2 = x(x a l )(x + b l ) zu, die er aber nicht nur über den reellen oder komplexen Zahlen betrachtet, sondern auch über den ganzen Zahlen modulo einer Primzahl p: Ist allgemein y 2 = (x x 1 )(x x 2 )(x x 3 ) eine Kurvengleichung mit ganzen Zahlen x 1,x 2,x 3, so können wir für x und y auch ganze Zahlen einsetzen und diese Gleichung modulo p betrachten. Wir sprechen wieder von einer elliptischen Kurve, einer Knotenkurve oder einer Spitzenkurve je nachdem wie viele der Nullstellen x 1,x 2 und x 3 modulo p noch verschieden sind. Die obige Gleichung definiert genau dann eine elliptische Kurve, wenn alle drei Nullstellen verschieden sind, wenn also die sogenannte Diskriminante = (x 1 x 2 )(x 1 x 3 )(x 2 x 3 ) von Null verschieden ist. Modulo p definiert sie eine elliptische Kurve, wenn auch modulo p noch von Null verschieden ist, wenn also p kein Teiler von ist. Speziell für die FREY-Kurve y 2 = x(x a l )(x+b l ) ist die Diskriminante = (0 a l )(0 b l ) ( a l ( b) l) = a l b l (a l + b l ) = a l b l c l = (abc) l stets von Null verschieden; modulo p verschwindet sie genau dann, wenn p ein Teiler von ist, d.h., wenn p eine der drei Zahlen a,b,c teilt. Da die Diskriminante als l-te Potenz von abc verglichen mit a,b,c ziemlich groß ist, heißt das, daß es im Verhältnis zur Größe der Diskriminante
17 267 Zahlentheorie erstaunlich wenige Primzahlen gibt, modulo derer wir keine elliptische Kurve erhalten; wir sind also wieder einer ähnlichen Situation wie bei der abc-vermutung. Die FREYsche Kurve sieht damit so aus, als sei sie fast zu schön, um wirklich zu existieren. Einen Anhaltspunkt zum Beweis dieser Nichtexistenz liefert eine Vermutung, die auf um 1955 durchgeführte Rechnungen und Spekulationen des japanischen Mathematikers TANIYAMA zurückgeht und heute je nach Autor mit irgendeiner Kombination der drei Namen TANIYA- MA, SHIMURA und WEIL bezeichnet wird. Danach sollte es zu einer elliptischen Kurve E mit ganzzahligen Koeffizienten eine surjektive Abbildung X 0 (N) E von einer sogenannten Modulkurve X 0 (N) auf E geben, wobei N im wesentlichen das Produkt aller Primzahlen p ist, modulo derer E keine elliptische Kurve mehr ist. Wie FREYs Rechnungen zeigen, hat seine Kurve vor diesem Hintergrund sehr seltsame Eigenschaften. Als er damals hier in Mannheim über seine Resultate vortrug, meinte er noch, er glaube nicht, daß die FERMAT-Vermutung so bewiesen werde; er veröffentlichte sein Ergebnis auch nicht in einer der großen internationalen Fachzeitschriften, sondern als Band 1, Heft 1 einer gerade neu gestarteten Schriftenreihe der Universität Saarbrücken, in einfachster Aufmachung xerographiert mit einem nur schwarz-weiß gestalteten Karton als Umschlag: GERHARD FREY: Links between stable elliptic curves and certain diophantine equations, Annales Universitatis Saraviensis, Series Mathematicae, 1 (1), verschärfte der französische Mathematiker JEAN-PIERRE SERRE die TANIYAMA-Vermutung, und aus dieser stärkeren Vermutung folgt in der Tat, daß die FREY-Kurve nicht existieren kann. Leider ist die SERREsche Vermutung bis heute noch nicht bewiesen. SERRE erhielt übrigens 2002 den ersten der vom norwegischen Parlament gestifteten ABEL- Preise, die seither zur Erinnerung an den norwegischen Mathematiker NIELS HENRIK ABEL ( ) jedes Jahr in gleicher Weise und gleicher Ausstattung wie die Nobel-Preise für hervorragende Leistungen auf dem Gebiet der Mathematik vergeben werden. SERRE stellte jedoch noch zusätzlich seine sogenannte ε-vermutung auf,
18 Kap. 9: Die Fermat-Vermutung für Zahlen und für Polynome 268 und auch aus der TANIYAMA-Vermutung zusammen mit der ε-vermutung folgt die Nichtexistenz der FREY-Kurve und damit die FERMAT-Vermutung. Diese ε-vermutung bewies KENNETH RIBET von der Universität Berkeley Die Grundidee seines Beweises läßt sich interpretieren als eine Art zweidimensionale Version eines Beweises von ERNST EDU- ARD KUMMER ( ), der die FERMAT-Vermutung 1846 für sogenannte reguläre Primzahlen als Exponenten bewies. (Eine Primzahl p heißt regulär, wenn die Hauptordnung des Körpers Q[ζ p ] der p-ten Einheitswurzeln faktoriell ist.) Der Beweis von RIBET ist allerdings erheblich aufwendiger. Damit war also die FERMAT-Vermutung zurückgeführt auf die TANI- YAMA-Vermutung. Diese Vermutung schließlich (die für die weitere mathematische Forschung erheblich wichtiger ist als die FERMAT- Vermutung) bewies WILES 1994.
Pythagoreische Tripel
 Pythagoreische Tripel Ingolf Giese Mai 2018 Pythagoreische Tripel - oder Pythagoreische Zahlentripel - sind drei (positive) ganze Zahlen, bei denen die Summe der Quadrate der beiden kleineren Zahlen gleich
Pythagoreische Tripel Ingolf Giese Mai 2018 Pythagoreische Tripel - oder Pythagoreische Zahlentripel - sind drei (positive) ganze Zahlen, bei denen die Summe der Quadrate der beiden kleineren Zahlen gleich
Algebra. 0 = (f g)(x) = f(x) g(x).
 Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 25. November 2008 Algebra 7. Übung mit Lösungshinweisen Aufgabe 31 Sei R ein Integritätsbereich,
Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 25. November 2008 Algebra 7. Übung mit Lösungshinweisen Aufgabe 31 Sei R ein Integritätsbereich,
Seminararbeit zur Zahlentheorie. Die Gaußschen Zahlen
 Universität Paderborn WS 2007/2008 Warburger Str. 100 33098 Paderborn Seminararbeit zur Zahlentheorie Die Gaußschen Zahlen Tatjana Linkin, Svetlana Krez 20. November 2007 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis
Universität Paderborn WS 2007/2008 Warburger Str. 100 33098 Paderborn Seminararbeit zur Zahlentheorie Die Gaußschen Zahlen Tatjana Linkin, Svetlana Krez 20. November 2007 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis
Kapitel 3: Die Sätze von Euler, Fermat und Wilson. 8 Der Satz von Euler
 Kapitel 3: Die Sätze von Euler, Fermat und Wilson In diesem Kapitel wollen wir nun die eulersche -Funktion verwenden, um einen berühmten Satz von Euler zu formulieren, aus dem wir dann mehrere interessante
Kapitel 3: Die Sätze von Euler, Fermat und Wilson In diesem Kapitel wollen wir nun die eulersche -Funktion verwenden, um einen berühmten Satz von Euler zu formulieren, aus dem wir dann mehrere interessante
Karlsruher Institut für Technologie Institut für Algebra und Geometrie
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. Jochen Schröder Einführung in Algebra und Zahlentheorie Übungsblatt 9 Aufgabe 1 (4 Punkte +) Sei
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. Jochen Schröder Einführung in Algebra und Zahlentheorie Übungsblatt 9 Aufgabe 1 (4 Punkte +) Sei
schreiben, wobei p und q ganze Zahlen sind.
 Schülerinfotag 1. Man zeige, dass keine rationale Zahl ist. Das heißt lässt sich nicht als p q schreiben, wobei p und q ganze Zahlen sind. Proof. Wir werden das Prinzip Beweis durch Widerspruch verwenden.
Schülerinfotag 1. Man zeige, dass keine rationale Zahl ist. Das heißt lässt sich nicht als p q schreiben, wobei p und q ganze Zahlen sind. Proof. Wir werden das Prinzip Beweis durch Widerspruch verwenden.
31 Polynomringe Motivation Definition: Polynomringe
 31 Polynomringe 31.1 Motivation Polynome spielen eine wichtige Rolle in vielen Berechnungen, einerseits weil oftmals funktionale Zusammenhänge durch Polynome beschrieben werden, andererseits weil Polynome
31 Polynomringe 31.1 Motivation Polynome spielen eine wichtige Rolle in vielen Berechnungen, einerseits weil oftmals funktionale Zusammenhänge durch Polynome beschrieben werden, andererseits weil Polynome
Einführung in die algebraische Zahlentheorie
 Alexander Schmidt Einführung in die algebraische Zahlentheorie Springer-Lehrbuch Springer Berlin Heidelberg New York ISBN 978-3-540-45973-6 Kapitel 7 Der Große Fermatsche Satz Die folgende Behauptung wurde
Alexander Schmidt Einführung in die algebraische Zahlentheorie Springer-Lehrbuch Springer Berlin Heidelberg New York ISBN 978-3-540-45973-6 Kapitel 7 Der Große Fermatsche Satz Die folgende Behauptung wurde
Zahlentheorie I - Tipps & Lösungen. Aktualisiert: 15. Oktober 2016 vers Teilbarkeit
 Schweizer Mathematik-Olympiade smo osm Zahlentheorie I - Tipps & Lösungen Aktualisiert: 15. Oktober 2016 vers. 1.2.0 1 Teilbarkeit Einstieg 1.1 Zeige, dass 900 ein Teiler von 10! ist. Tipp: Schreibe 900
Schweizer Mathematik-Olympiade smo osm Zahlentheorie I - Tipps & Lösungen Aktualisiert: 15. Oktober 2016 vers. 1.2.0 1 Teilbarkeit Einstieg 1.1 Zeige, dass 900 ein Teiler von 10! ist. Tipp: Schreibe 900
Diagonalisierbarkeit symmetrischer Matrizen
 ¾ Diagonalisierbarkeit symmetrischer Matrizen a) Eigenwerte und Eigenvektoren Die Matrix einer linearen Abbildung ³: Î Î bezüglich einer Basis ( Ò ) ist genau dann eine Diagonalmatrix wenn jeder der Basisvektoren
¾ Diagonalisierbarkeit symmetrischer Matrizen a) Eigenwerte und Eigenvektoren Die Matrix einer linearen Abbildung ³: Î Î bezüglich einer Basis ( Ò ) ist genau dann eine Diagonalmatrix wenn jeder der Basisvektoren
Übungsblatt 7. Hausübungen
 Übungsblatt 7 Hausübungen Die Hausübungen müssen bis Mittwoch, den 06.1.17, um 18:00 Uhr in den Briefkasten Algebra mit Ihrer Übungsgruppennummer im Mathematischen Institut, Raum 301 abgegeben werden.
Übungsblatt 7 Hausübungen Die Hausübungen müssen bis Mittwoch, den 06.1.17, um 18:00 Uhr in den Briefkasten Algebra mit Ihrer Übungsgruppennummer im Mathematischen Institut, Raum 301 abgegeben werden.
Algebra. 1 = a u + b,
 Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 11. November 2008 Algebra 5. Übung mit Lösungshinweisen Aufgabe 23 Es sei R ein euklidischer Integritätsbereich.
Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 11. November 2008 Algebra 5. Übung mit Lösungshinweisen Aufgabe 23 Es sei R ein euklidischer Integritätsbereich.
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 11 Zerfällungskörper Wir wollen zu einem Polynom F K[X] einen Körper konstruieren, über dem F in Linearfaktoren zerfällt. Dies
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 11 Zerfällungskörper Wir wollen zu einem Polynom F K[X] einen Körper konstruieren, über dem F in Linearfaktoren zerfällt. Dies
9. Polynom- und Potenzreihenringe
 64 Andreas Gathmann 9. Polynom- und Potenzreihenringe Bevor wir mit der allgemeinen Untersuchung von Ringen fortfahren, wollen wir in diesem Kapitel kurz zwei sehr wichtige weitere Beispiele von Ringen
64 Andreas Gathmann 9. Polynom- und Potenzreihenringe Bevor wir mit der allgemeinen Untersuchung von Ringen fortfahren, wollen wir in diesem Kapitel kurz zwei sehr wichtige weitere Beispiele von Ringen
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Einführung in Algebra und Zahlentheorie Lösungsvorschläge zur Klausur vom Aufgabe 1 (6 Punkte)
 Aufgabe 1 (6 Punkte) Einführung in Algebra und Zahlentheorie svorschläge zur Klausur vom 23.09.2016 a) Bestimmen Sie das multiplikativ inverse Element zu 22 in Z/61Z. b) Finden Sie ein x Z mit folgenden
Aufgabe 1 (6 Punkte) Einführung in Algebra und Zahlentheorie svorschläge zur Klausur vom 23.09.2016 a) Bestimmen Sie das multiplikativ inverse Element zu 22 in Z/61Z. b) Finden Sie ein x Z mit folgenden
Algebraische Kurven - Vorlesung 29. Projektion weg von einem Punkt
 Algebraische Kurven - Vorlesung 29 Definition 1. Die Abbildung P n K Projektion weg von einem Punkt {(1, 0,..., 0)} Pn 1 K, (x 0, x 1...,x n ) (x 1,..., x n ), heißt die Projektion weg vom Punkt (1, 0,...,
Algebraische Kurven - Vorlesung 29 Definition 1. Die Abbildung P n K Projektion weg von einem Punkt {(1, 0,..., 0)} Pn 1 K, (x 0, x 1...,x n ) (x 1,..., x n ), heißt die Projektion weg vom Punkt (1, 0,...,
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 23 Die Gradformel Satz 1. Seien K L und L M endliche Körperweiterungen. Dann ist auch K M eine endliche Körpererweiterung und
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 23 Die Gradformel Satz 1. Seien K L und L M endliche Körperweiterungen. Dann ist auch K M eine endliche Körpererweiterung und
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Algebra. (b) Der Beweis funktioniert analog zu Teil (a), nur daß wir in der Argumentation Z durch R und 2 durch c ersetzen müssen.
 Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 2. Dezember 2008 Algebra 8. Übung mit Lösungshinweisen Aufgabe 36 (a) Zeige, daß Z[X] kein Hauptidealring
Fachbereich Mathematik Prof. Dr. Nils Scheithauer Walter Reußwig TECHNISCHE UNIVERSITÄT DARMSTADT WS 08/09 2. Dezember 2008 Algebra 8. Übung mit Lösungshinweisen Aufgabe 36 (a) Zeige, daß Z[X] kein Hauptidealring
a i x i, (1) Ein Teil der folgenden Betrachtungen gilt auch, wenn man den Körper durch einen Ring ersetzt.
 Polynome Definition 1. Ein Polynom f über einem Körper K mit der Unbestimmten x ist eine formale Summe f(x) = i 0 a i x i, (1) wobei nur endlich viele der Koeffizienten a i K von Null verschieden sind.
Polynome Definition 1. Ein Polynom f über einem Körper K mit der Unbestimmten x ist eine formale Summe f(x) = i 0 a i x i, (1) wobei nur endlich viele der Koeffizienten a i K von Null verschieden sind.
Eine kurze Tabelle soll uns erste Einsichten erleichtern. Der Strich heißt, dass es eine solche Darstellung nicht gibt.
 Summen von Quadraten 1 Physikalische Motivation Eine schwingende Saite hat eine Grundfrequenz F, die von Länge, Dicke, Beschaffenheit der Saite und so fort abhängt Neben dieser Grundfrequenz gibt es auch
Summen von Quadraten 1 Physikalische Motivation Eine schwingende Saite hat eine Grundfrequenz F, die von Länge, Dicke, Beschaffenheit der Saite und so fort abhängt Neben dieser Grundfrequenz gibt es auch
Mathematisches Institut II Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg
 1 Mathematisches Institut II 06.07.004 Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg SS 05 Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung Vorlesung 5: Elementare Zahlentheorie: Teilbarkeit Primfaktorzerlegung
1 Mathematisches Institut II 06.07.004 Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg SS 05 Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung Vorlesung 5: Elementare Zahlentheorie: Teilbarkeit Primfaktorzerlegung
Sätze über ganzrationale Funktionen
 Sätze über ganzrationale Funktionen 1. Sind alle Koeffizienten a i ganzzahlig und ist x 0 eine ganzzahlige Nullstelle, so ist x 0 ein Teiler von a 0. 2. Haben alle Koeffizienten dasselbe Vorzeichen, so
Sätze über ganzrationale Funktionen 1. Sind alle Koeffizienten a i ganzzahlig und ist x 0 eine ganzzahlige Nullstelle, so ist x 0 ein Teiler von a 0. 2. Haben alle Koeffizienten dasselbe Vorzeichen, so
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 20 Multiplikative Systeme Wir wollen zeigen, dass es zu jedem Integritätsbereich R einen Körper K gibt derart, dass R ein Unterring
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 20 Multiplikative Systeme Wir wollen zeigen, dass es zu jedem Integritätsbereich R einen Körper K gibt derart, dass R ein Unterring
Grundlagen der Arithmetik und Zahlentheorie
 Grundlagen der Arithmetik und Zahlentheorie 1.0 Teilbarkeit In diesem Abschnitt werden wir einerseits die ganzen Zahlen an sich studieren und dabei besonders wichtige Zahlen, die Primzahlen, entsprechend
Grundlagen der Arithmetik und Zahlentheorie 1.0 Teilbarkeit In diesem Abschnitt werden wir einerseits die ganzen Zahlen an sich studieren und dabei besonders wichtige Zahlen, die Primzahlen, entsprechend
Mathematik für Anwender I
 Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 4 Injektive und surjektive Abbildungen Definition 4.1. Es seien L und M Mengen und es sei eine Abbildung. Dann heißt F F
Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 4 Injektive und surjektive Abbildungen Definition 4.1. Es seien L und M Mengen und es sei eine Abbildung. Dann heißt F F
Geometrie kubischer Kurven
 Geometrie kubischer Kurven Werner Hoffmann Wir wollen die Theorie nur soweit entwickeln, wie es zum Verständnis der Gruppenoperation auf einer irreduziblen kubischen Kurve nötig ist. Satz 1 In der affinen
Geometrie kubischer Kurven Werner Hoffmann Wir wollen die Theorie nur soweit entwickeln, wie es zum Verständnis der Gruppenoperation auf einer irreduziblen kubischen Kurve nötig ist. Satz 1 In der affinen
1 Vorbereitung: Potenzen 2. 2 Einstieg und typische Probleme 3
 Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 26 Einheitswurzeln Definition 26.1. Es sei K ein Körper und n N +. Dann heißen die Nullstellen des Polynoms X n 1 in K die n-ten
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 26 Einheitswurzeln Definition 26.1. Es sei K ein Körper und n N +. Dann heißen die Nullstellen des Polynoms X n 1 in K die n-ten
Mathematik macht Freu(n)de im Wintersemester 2018/19
 Mathematik macht Freu(n)de im Wintersemester 08/9 Markus Fulmek 08 06 9 Im folgenden wird zunächst ein kombinatorischer Gedankengang entwickelt, der mit wenigen einfachen Definitionen (samt erläuternden
Mathematik macht Freu(n)de im Wintersemester 08/9 Markus Fulmek 08 06 9 Im folgenden wird zunächst ein kombinatorischer Gedankengang entwickelt, der mit wenigen einfachen Definitionen (samt erläuternden
$Id: integral.tex,v /05/05 13:36:42 hk Exp $
 $Id: integral.tex,v.5 07/05/05 3:36:4 hk Exp $ Integralrechnung.4 Integration rationaler Funktionen In diesem Abschnitt wollen wir die Integration rationaler Funktionen diskutieren. Es wird sich herausstellen
$Id: integral.tex,v.5 07/05/05 3:36:4 hk Exp $ Integralrechnung.4 Integration rationaler Funktionen In diesem Abschnitt wollen wir die Integration rationaler Funktionen diskutieren. Es wird sich herausstellen
Polynomiale Gleichungen
 Vorlesung 5 Polynomiale Gleichungen Definition 5.0.3. Ein polynomiale Funktion p(x) in der Variablen x R ist eine endliche Summe von Potenzen von x, die Exponenten sind hierbei natürliche Zahlen. Wir haben
Vorlesung 5 Polynomiale Gleichungen Definition 5.0.3. Ein polynomiale Funktion p(x) in der Variablen x R ist eine endliche Summe von Potenzen von x, die Exponenten sind hierbei natürliche Zahlen. Wir haben
3. Diskrete Mathematik
 Diophantos von Alexandria um 250 Georg Cantor 1845-1918 Pythagoras um 570 v. Chr Pierre de Fermat 1607/8-1665 Seite 1 Inhalt der Vorlesung Teil 3: Diskrete Mathematik 3.1 Zahlentheorie: Abzählbarkeit,
Diophantos von Alexandria um 250 Georg Cantor 1845-1918 Pythagoras um 570 v. Chr Pierre de Fermat 1607/8-1665 Seite 1 Inhalt der Vorlesung Teil 3: Diskrete Mathematik 3.1 Zahlentheorie: Abzählbarkeit,
Ringe. Kapitel Einheiten
 Kapitel 8 Ringe Die zahlreichen Analogien zwischen Matrizenringen und Endomorphismenringen (beides sind zugleich auch Vektorräume) legen es nahe, allgemeinere ringtheoretische Grundlagen bereitzustellen,
Kapitel 8 Ringe Die zahlreichen Analogien zwischen Matrizenringen und Endomorphismenringen (beides sind zugleich auch Vektorräume) legen es nahe, allgemeinere ringtheoretische Grundlagen bereitzustellen,
Endliche Körper und Codierung SS Übungsblatt. 9. Bestimmen Sie alle primitiven Elemente (Erzeuger der multiplikativen Gruppe) von
 Endliche Körper und Codierung SS 2007 1. Übungsblatt 1. Sei p eine Primzahl und 0 j p 1. Zeigen Sie, dass ( ) p 1 j ( 1) j (mod p). 2. Sei R ein kommutativer Ring der Charakteristik p > 0 (prim). Zeigen
Endliche Körper und Codierung SS 2007 1. Übungsblatt 1. Sei p eine Primzahl und 0 j p 1. Zeigen Sie, dass ( ) p 1 j ( 1) j (mod p). 2. Sei R ein kommutativer Ring der Charakteristik p > 0 (prim). Zeigen
Beispiellösungen zu Blatt 77
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
Lösungen der Aufgaben
 Lösungen der Aufgaben Aufgabe 1.3.1 Es gibt 42 mögliche Verschlüsselungen. Aufgabe 2.3.4 Ergebnisse sind 0, 4 und 4 1 = 4. Aufgabe 2.3.6 Da in Z 9 10 = 1 ist, erhalten wir x = c 0 + + c m = c 0 + + c m.
Lösungen der Aufgaben Aufgabe 1.3.1 Es gibt 42 mögliche Verschlüsselungen. Aufgabe 2.3.4 Ergebnisse sind 0, 4 und 4 1 = 4. Aufgabe 2.3.6 Da in Z 9 10 = 1 ist, erhalten wir x = c 0 + + c m = c 0 + + c m.
2 Polynome und rationale Funktionen
 Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Prof. S. Krauter Dezimalbruchdarstellung rationaler Zahlen DezDarst.doc. Über die Darstellung von rationalen Zahlen als Dezimalbrüche.
 1 Prof. S. Krauter Dezimalbruchdarstellung rationaler Zahlen DezDarst.doc Über die Darstellung von rationalen Zahlen als Dezimalbrüche. Anmerkung: Die Beschränkung auf die Dezimaldarstellung ist unnötig.
1 Prof. S. Krauter Dezimalbruchdarstellung rationaler Zahlen DezDarst.doc Über die Darstellung von rationalen Zahlen als Dezimalbrüche. Anmerkung: Die Beschränkung auf die Dezimaldarstellung ist unnötig.
Lösung zur 13. Hausübung Algebraische Strukturen (keine Abgabe)
 TU Kaiserslautern Fachbereich Mathematik Prof. Dr. Andreas Gathmann Inga Schwabrow Lösung zur 13. Hausübung Algebraische Strukturen (keine Abgabe) Aufgabe 1. Wintersemester 2016/17 (1 + i) (1 i) 3 (2 +
TU Kaiserslautern Fachbereich Mathematik Prof. Dr. Andreas Gathmann Inga Schwabrow Lösung zur 13. Hausübung Algebraische Strukturen (keine Abgabe) Aufgabe 1. Wintersemester 2016/17 (1 + i) (1 i) 3 (2 +
Zahlen und elementares Rechnen
 und elementares Rechnen Christian Serpé Universität Münster 7. September 2011 Christian Serpé (Universität Münster) und elementares Rechnen 7. September 2011 1 / 51 Gliederung 1 2 Elementares Rechnen 3
und elementares Rechnen Christian Serpé Universität Münster 7. September 2011 Christian Serpé (Universität Münster) und elementares Rechnen 7. September 2011 1 / 51 Gliederung 1 2 Elementares Rechnen 3
14 Kreisteilungskörper
 14 Kreisteilungskörper Wir wenden unsere Ergebnisse auf einen Fall an, mit dem die Algebraische Zahlentheorie begann und der bis heute im Zentrum der Forschung steht. 14.1 Erweiterungen mit Einheitswurzeln
14 Kreisteilungskörper Wir wenden unsere Ergebnisse auf einen Fall an, mit dem die Algebraische Zahlentheorie begann und der bis heute im Zentrum der Forschung steht. 14.1 Erweiterungen mit Einheitswurzeln
8. Musterlösung zu Mathematik für Informatiker II, SS 2004
 8. Musterlösung zu Mathematik für Informatiker II, SS 2004 MARTIN LOTZ &MICHAEL NÜSKEN Aufgabe 8.1 (Polynomdivision). (8 Punkte) Dividiere a mit Rest durch b für (i) a = x 7 5x 6 +3x 2 +1, b = x 2 +1in
8. Musterlösung zu Mathematik für Informatiker II, SS 2004 MARTIN LOTZ &MICHAEL NÜSKEN Aufgabe 8.1 (Polynomdivision). (8 Punkte) Dividiere a mit Rest durch b für (i) a = x 7 5x 6 +3x 2 +1, b = x 2 +1in
6.2. Ringe und Körper
 62 RINGE UND K ÖRPER 62 Ringe und Körper Wir betrachten nun Mengen (endlich oder unendlich) mit zwei Operationen Diese werden meist als Addition und Multiplikation geschrieben Meist ist dabei die additiv
62 RINGE UND K ÖRPER 62 Ringe und Körper Wir betrachten nun Mengen (endlich oder unendlich) mit zwei Operationen Diese werden meist als Addition und Multiplikation geschrieben Meist ist dabei die additiv
Analytische Lösung algebraischer Gleichungen dritten und vierten Grades
 Analytische Lösung algebraischer Gleichungen dritten und vierten Grades Inhaltsverzeichnis 1 Einführung 1 2 Gleichungen dritten Grades 3 3 Gleichungen vierten Grades 7 1 Einführung In diesem Skript werden
Analytische Lösung algebraischer Gleichungen dritten und vierten Grades Inhaltsverzeichnis 1 Einführung 1 2 Gleichungen dritten Grades 3 3 Gleichungen vierten Grades 7 1 Einführung In diesem Skript werden
Diophantische Gleichungen
 Diophantische Gleichungen Pythagoras, Fermat und Homer Simpson Tag der Mathematik 2013 Lars Kindler, Freie Universität Berlin Benannt nach Diophant von Alexandrien (~ 250 v.chr) Sein wichtigstes Werk war
Diophantische Gleichungen Pythagoras, Fermat und Homer Simpson Tag der Mathematik 2013 Lars Kindler, Freie Universität Berlin Benannt nach Diophant von Alexandrien (~ 250 v.chr) Sein wichtigstes Werk war
11. Primfaktorzerlegungen
 80 Andreas Gathmann 11. Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als ein Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
80 Andreas Gathmann 11. Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als ein Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
Prüfungsfragen zur Vorlesung Algebra und Diskrete Mathematik. Sommersemester 2018
 Prüfungsfragen zur Vorlesung Algebra und Diskrete Mathematik Sommersemester 2018 Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper).
Prüfungsfragen zur Vorlesung Algebra und Diskrete Mathematik Sommersemester 2018 Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper).
Die Gleichung x 2 + y 3 = z 7
 Die Gleichung x 2 + y 3 = z 7 Michael Stoll International University Bremen In Zusammenarbeit mit Bjorn Poonen, UC Berkeley und Ed Schaefer, University of Santa Clara Verallgemeinerung der Fermatschen
Die Gleichung x 2 + y 3 = z 7 Michael Stoll International University Bremen In Zusammenarbeit mit Bjorn Poonen, UC Berkeley und Ed Schaefer, University of Santa Clara Verallgemeinerung der Fermatschen
Übungen zum Vorkurs Mathematik für Studienanfänger Ein leeres Produkt ist gleich 1, eine leere Summe 0. ***
 Universität Bonn Mathematisches Institut Dr. Michael Welter Übungen zum Vorkurs Mathematik für Studienanfänger 2013 Einige Zeichen und Konventionen: IN := {1, 2, 3, 4,...} Die Menge der natürlichen Zahlen
Universität Bonn Mathematisches Institut Dr. Michael Welter Übungen zum Vorkurs Mathematik für Studienanfänger 2013 Einige Zeichen und Konventionen: IN := {1, 2, 3, 4,...} Die Menge der natürlichen Zahlen
Ganze algebraische Zahlen
 Seminarvortrag Ganze algebraische Zahlen gehalten von Johannes Hölken an der Universität Duisburg-Essen im Sommersemester 2012 im Rahmen des Seminars über Elementrare Zahlentheorie. Kontakt: johannes.hoelken@stud.uni-due.de
Seminarvortrag Ganze algebraische Zahlen gehalten von Johannes Hölken an der Universität Duisburg-Essen im Sommersemester 2012 im Rahmen des Seminars über Elementrare Zahlentheorie. Kontakt: johannes.hoelken@stud.uni-due.de
Quadrate und Wurzelziehen modulo p
 Quadrate und Wurzelziehen modulo p Sei im Folgenden p eine Primzahl größer als. Wir möchten im Körper Z p Quadratwurzeln ziehen. Die Quadrierabbildung Q :Z p Z p ist aber nicht surjektiv, daher gibt es
Quadrate und Wurzelziehen modulo p Sei im Folgenden p eine Primzahl größer als. Wir möchten im Körper Z p Quadratwurzeln ziehen. Die Quadrierabbildung Q :Z p Z p ist aber nicht surjektiv, daher gibt es
Gleichungen und Ungleichungen
 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme. Kapitel 3 Gleichungen und Ungleichungen linke Seite = rechte Seite Grundmenge: Menge aller Zahlen, die wir als Lösung der Gleichung
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Gleichungen und Ungleichungen
 Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
Kapitel 3 Gleichungen und Ungleichungen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 3 Gleichungen und Ungleichungen 1 / 58 Gleichung Eine Gleichung erhalten wir durch Gleichsetzen zweier Terme.
13 Polynome und Nullstellen
 60 II. Differentialrechnung 13 Polynome und Nullstellen Lernziele: Resultat: Zwischenwertsatz Methoden: Raten von Nullstellen, Euklidischer Algorithmus, Horner-Schema Kompetenzen: Bestimmung von Nullstellen
60 II. Differentialrechnung 13 Polynome und Nullstellen Lernziele: Resultat: Zwischenwertsatz Methoden: Raten von Nullstellen, Euklidischer Algorithmus, Horner-Schema Kompetenzen: Bestimmung von Nullstellen
Der Zwei-Quadrate-Satz von Fermat. Hauptseminar: Eine Einladung in die Mathematik Leitung: Prof. Dr. Lukacova Referent: Julia Breit Datum:
 Der Zwei-Quadrate-Satz von Fermat Hauptseminar: Eine Einladung in die Mathematik Leitung: Prof. Dr. Lukacova Referent: Julia Breit Datum: 09.11.2015 GLIEDERUNG Einleitung Der Zwei-Quadrate-Satz Vorwissen
Der Zwei-Quadrate-Satz von Fermat Hauptseminar: Eine Einladung in die Mathematik Leitung: Prof. Dr. Lukacova Referent: Julia Breit Datum: 09.11.2015 GLIEDERUNG Einleitung Der Zwei-Quadrate-Satz Vorwissen
UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN
 UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN VORLESUNG KOMMUTATIVE ALGEBRA, SOMMERSEMESTER 2007 1. Definitionen Ein kommutativer Ring mit Eins R ist ein Integritätsbereich, wenn er zumindest zwei
UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN VORLESUNG KOMMUTATIVE ALGEBRA, SOMMERSEMESTER 2007 1. Definitionen Ein kommutativer Ring mit Eins R ist ein Integritätsbereich, wenn er zumindest zwei
Algebra und Zahlentheorie WS 13/14
 Algebra und Zahlentheorie WS 13/14 FU Berlin David Müßig http://page.mi.fu-berlin.de/def/auz14/ muessig@mi.fu-berlin.de 21.01.2014 1 Hintergrund: Basen & Vektorräume 1.1 Grundlegende Begriffe Da einige
Algebra und Zahlentheorie WS 13/14 FU Berlin David Müßig http://page.mi.fu-berlin.de/def/auz14/ muessig@mi.fu-berlin.de 21.01.2014 1 Hintergrund: Basen & Vektorräume 1.1 Grundlegende Begriffe Da einige
5-1 Elementare Zahlentheorie
 5-1 Elementare Zahlentheorie 5 Summen von Quadraten Wir interessieren uns hier für die Frage, ob sich eine (natürlich positive) Zahl n als Summe von sagen wir t Quadraten ganzer Zahlen schreiben lässt,
5-1 Elementare Zahlentheorie 5 Summen von Quadraten Wir interessieren uns hier für die Frage, ob sich eine (natürlich positive) Zahl n als Summe von sagen wir t Quadraten ganzer Zahlen schreiben lässt,
5 Grundlagen der Zahlentheorie
 5 Grundlagen der Zahlentheorie 1 Primfaktorzerlegung Seienm, n N + := {k N k > 0} Man schreibt n n, gesprochen m teilt n oder m ist ein Teiler von n, wenn es eine positive natürliche Zahl k gibt mit mk
5 Grundlagen der Zahlentheorie 1 Primfaktorzerlegung Seienm, n N + := {k N k > 0} Man schreibt n n, gesprochen m teilt n oder m ist ein Teiler von n, wenn es eine positive natürliche Zahl k gibt mit mk
für alle a, b, x, y R.
 Algebra I 13. April 2008 c Rudolf Scharlau, 2002 2008 33 1.5 Ringe Definition 1.5.1 Ein Ring ist eine Menge R zusammen mit zwei Verknüpfungen + und, genannt Addition und Multiplikation, für die folgendes
Algebra I 13. April 2008 c Rudolf Scharlau, 2002 2008 33 1.5 Ringe Definition 1.5.1 Ein Ring ist eine Menge R zusammen mit zwei Verknüpfungen + und, genannt Addition und Multiplikation, für die folgendes
Der Satz von Eichler. Paul Breiding. 29. Januar Fakultat fur Mathematik und Informatik Georg-August-Universitat Gottingen
 Fakultat fur Mathematik und Informatik Georg-August-Universitat Gottingen 29. Januar 2013 Im Jahr 1637 schrieb der franzosiche Jurist Pierre Fermat an den Rand, neben das Problem 8, seiner Ausgabe der
Fakultat fur Mathematik und Informatik Georg-August-Universitat Gottingen 29. Januar 2013 Im Jahr 1637 schrieb der franzosiche Jurist Pierre Fermat an den Rand, neben das Problem 8, seiner Ausgabe der
KAPITEL 13. Polynome. 1. Primfaktorzerlegung in den ganzen Zahlen. ,, p r
 KAPITEL 13 Polynome 1. Primfaktorzerlegung in den ganzen Zahlen DEFINITION 13.1 (Primzahl). Eine Zahl p ist genau dann eine Primzahl, wenn folgende beiden Bedingungen gelten: (1) Es gilt p > 1. (2) Für
KAPITEL 13 Polynome 1. Primfaktorzerlegung in den ganzen Zahlen DEFINITION 13.1 (Primzahl). Eine Zahl p ist genau dann eine Primzahl, wenn folgende beiden Bedingungen gelten: (1) Es gilt p > 1. (2) Für
6 Polynomielle Gleichungen und Polynomfunktionen
 6 Polynomielle Gleichungen und Polynomfunktionen Lineare Gleichungen Eine lineare Gleichung in einer Variablen ist eine Gleichung der Form ax + b = cx + d mit festen Zahlen a und c mit a c. Dies kann man
6 Polynomielle Gleichungen und Polynomfunktionen Lineare Gleichungen Eine lineare Gleichung in einer Variablen ist eine Gleichung der Form ax + b = cx + d mit festen Zahlen a und c mit a c. Dies kann man
Algebra II, SS September 2011 Aufgaben zur Körpertheorie. (+1 + i), x 2 = 1 2. ( 1 + i), x 4 = 1 2
 1. Zeige, dass Q(, i) Zerfällungskörper von X 4 + 1 Q[X] ist. Lösung: Die vier Nullstellen von X 4 + 1 über Q sind x 1 = 1 (+1 + i), x = 1 (+1 i), x 3 = 1 ( 1 + i), x 4 = 1 ( 1 i). Damit ist ein Zerfällungskörper
1. Zeige, dass Q(, i) Zerfällungskörper von X 4 + 1 Q[X] ist. Lösung: Die vier Nullstellen von X 4 + 1 über Q sind x 1 = 1 (+1 + i), x = 1 (+1 i), x 3 = 1 ( 1 + i), x 4 = 1 ( 1 i). Damit ist ein Zerfällungskörper
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 3 Es sei K L eine endliche Körpererweiterung und x L ein Element. Dann sind die Potenzen x i, i N, linear abhängig, und das bedeutet,
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 3 Es sei K L eine endliche Körpererweiterung und x L ein Element. Dann sind die Potenzen x i, i N, linear abhängig, und das bedeutet,
Einführung in Algebra und Zahlentheorie
 Institut für Algebra und Geometrie 05. September 2013 Klausur zur Vorlesung Einführung in Algebra und Zahlentheorie Name, Vorname: Matrikelnummer: Fachrichtung: Semester: Zur Bearbeitung: Verwenden Sie
Institut für Algebra und Geometrie 05. September 2013 Klausur zur Vorlesung Einführung in Algebra und Zahlentheorie Name, Vorname: Matrikelnummer: Fachrichtung: Semester: Zur Bearbeitung: Verwenden Sie
2. Primzahlen. 2.1 Definition, Eigenschaften. Definition: Eine natürliche Zahl p heisst Primzahl, wenn p genau zwei Teiler hat.
 1 2. Primzahlen 2.1 Definition, Eigenschaften Definition: Eine natürliche Zahl p heisst Primzahl, wenn p genau zwei Teiler hat. Die Folge der Primzahlen: 2, 3, 5, 7, 11,13, 17, 19, 23, 29,... Die Suche
1 2. Primzahlen 2.1 Definition, Eigenschaften Definition: Eine natürliche Zahl p heisst Primzahl, wenn p genau zwei Teiler hat. Die Folge der Primzahlen: 2, 3, 5, 7, 11,13, 17, 19, 23, 29,... Die Suche
Gelöste und ungelöste Probleme in der Zahlentheorie
 Gelöste und ungelöste Probleme in der Zahlentheorie Teilnehmer: Kristin Emmrich Loryn Fechner Felix Neumann Alexandra Stepanova Roman Stolzenburg Walter Unger Gruppenleiter: Jürg Kramer Anna v. Pippich
Gelöste und ungelöste Probleme in der Zahlentheorie Teilnehmer: Kristin Emmrich Loryn Fechner Felix Neumann Alexandra Stepanova Roman Stolzenburg Walter Unger Gruppenleiter: Jürg Kramer Anna v. Pippich
15 Auflösbarkeit durch Radikale
 Chr.Nelius: Algebra (SS 2006) 1 15 Auflösbarkeit durch Radikale f [T] sei ein normiertes Polynom vom Grade 1. Wir wollen die Frage untersuchen, ob sich die Nullstellen von f formelmäßig berechnen lassen.
Chr.Nelius: Algebra (SS 2006) 1 15 Auflösbarkeit durch Radikale f [T] sei ein normiertes Polynom vom Grade 1. Wir wollen die Frage untersuchen, ob sich die Nullstellen von f formelmäßig berechnen lassen.
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Arbeitsblatt 19 Die Pausenaufgabe Aufgabe 19.1. Sei K ein Körper und sei K[X] der Polynomring über K. Wie lautet
Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Arbeitsblatt 19 Die Pausenaufgabe Aufgabe 19.1. Sei K ein Körper und sei K[X] der Polynomring über K. Wie lautet
Übungen zur Vorlesung Einführung in die Mathematik
 Übungen zur Vorlesung Einführung in die Mathematik von G. Greschonig und L. Summerer, WS 2017/18 Aufgabe 1. Zeige, dass das Quadrat einer ungeraden Zahl, vermindert um 1, stets durch 4 teilbar ist. Folgere
Übungen zur Vorlesung Einführung in die Mathematik von G. Greschonig und L. Summerer, WS 2017/18 Aufgabe 1. Zeige, dass das Quadrat einer ungeraden Zahl, vermindert um 1, stets durch 4 teilbar ist. Folgere
Kapitel 3 Der Fundamentalsatz der Algebra
 Kapitel 3 Der Fundamentalsatz der Algebra Dieser berühmte Satz wurde erstmals von C.F. Gauß 1801 in seiner Disseration bewiesen. Satz 3.1. Jedes nichtkonstante, komplexe Polynom n-ten Grades p(z) = n a
Kapitel 3 Der Fundamentalsatz der Algebra Dieser berühmte Satz wurde erstmals von C.F. Gauß 1801 in seiner Disseration bewiesen. Satz 3.1. Jedes nichtkonstante, komplexe Polynom n-ten Grades p(z) = n a
Die Menge C der komplexen Zahlen wird im Kapitel Weitere Themen behandelt.
 1 1 Funktionen 1.1 Grundlegende Zahlenmengen Georg Cantor (1845-1918) hat den Begriff der Menge eingeführt. Man versteht darunter die Zusammenfassung einzelner Dinge, welche Elemente genannt werden, zu
1 1 Funktionen 1.1 Grundlegende Zahlenmengen Georg Cantor (1845-1918) hat den Begriff der Menge eingeführt. Man versteht darunter die Zusammenfassung einzelner Dinge, welche Elemente genannt werden, zu
Prof. M. Eisermann Algebra SoSe 2010
 Übungsblatt 4: Teilbarkeitslehre Lassen Sie sich nicht durch die Menge der Aufgaben einschüchtern. Es gibt nur wenig schriftliche Aufgaben und wir halten die Menge der Votieraufgaben überschaubar. Alle
Übungsblatt 4: Teilbarkeitslehre Lassen Sie sich nicht durch die Menge der Aufgaben einschüchtern. Es gibt nur wenig schriftliche Aufgaben und wir halten die Menge der Votieraufgaben überschaubar. Alle
$Id: integral.tex,v /05/05 14:57:29 hk Exp hk $ ln(1 + t) 2 = ln 2 ln 3 + ln 2 = ln
 $Id: integral.tex,v.5 2009/05/05 4:57:29 hk Exp hk $ 2 Integralrechnung 2.3 Die Integrationsregeln Wir wollen noch eine letzte kleine Anmerkung zur Substitutionsregel machen. Der letzte Schritt bei der
$Id: integral.tex,v.5 2009/05/05 4:57:29 hk Exp hk $ 2 Integralrechnung 2.3 Die Integrationsregeln Wir wollen noch eine letzte kleine Anmerkung zur Substitutionsregel machen. Der letzte Schritt bei der
Probestudium Übungsblatt 1 -
 Probestudium 018 - Übungsblatt 1 - Prof Dr Werner Bley Dominik Bullach Martin Hofer Pascal Stucky Aufgabe 1 (mittel) Sei m Z Wir definieren für zwei ganze Zahlen a und b a b mod m : m ( a b) Seien a, b,
Probestudium 018 - Übungsblatt 1 - Prof Dr Werner Bley Dominik Bullach Martin Hofer Pascal Stucky Aufgabe 1 (mittel) Sei m Z Wir definieren für zwei ganze Zahlen a und b a b mod m : m ( a b) Seien a, b,
Musterlösung zur Probeklausur zur Angewandten Diskreten Mathematik
 UNIVERSITÄT ULM Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Musterlösung zur Probeklausur zur Angewandten Diskreten Mathematik Prof. Dr. Helmut Maier, Hans- Peter Reck Gesamtpunktzahl: 100
UNIVERSITÄT ULM Institut für Zahlentheorie und Wahrscheinlichkeitstheorie Musterlösung zur Probeklausur zur Angewandten Diskreten Mathematik Prof. Dr. Helmut Maier, Hans- Peter Reck Gesamtpunktzahl: 100
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Inhaltsverzeichnis Teil 1 Teil
Die Unlösbarkeit der Gleichung fünften Grades durch Radikale. Teilnehmer: Gruppenleiter:
 Die Unlösbarkeit der Gleichung fünften Grades durch adikale Teilnehmer: Max Bender Marcus Gawlik Anton Milge Leonard Poetzsch Gabor adtke Miao Zhang Gruppenleiter: Jürg Kramer Andreas-Oberschule Georg-Forster-Oberschule
Die Unlösbarkeit der Gleichung fünften Grades durch adikale Teilnehmer: Max Bender Marcus Gawlik Anton Milge Leonard Poetzsch Gabor adtke Miao Zhang Gruppenleiter: Jürg Kramer Andreas-Oberschule Georg-Forster-Oberschule
Zahlentheorie I. smo osm. Thomas Huber. Inhaltsverzeichnis. Aktualisiert: 1. August 2016 vers Teilbarkeit 2.
 Schweizer Mathematik-Olympiade smo osm Zahlentheorie I Thomas Huber Aktualisiert: 1. August 2016 vers. 1.0.0 Inhaltsverzeichnis 1 Teilbarkeit 2 2 ggt und kgv 3 3 Abschätzungen 6 1 Teilbarkeit Im Folgenden
Schweizer Mathematik-Olympiade smo osm Zahlentheorie I Thomas Huber Aktualisiert: 1. August 2016 vers. 1.0.0 Inhaltsverzeichnis 1 Teilbarkeit 2 2 ggt und kgv 3 3 Abschätzungen 6 1 Teilbarkeit Im Folgenden
Kapitel 6: Das quadratische Reziprozitätsgesetz
 Kapitel 6: Das quadratische Reziprozitätsgesetz Ziel dieses Kapitels: die Untersuchung der Lösbarkeit der Kongruenzgleichung X also die Frage, ob die ganze Zahl Z eine Quadratwurzel modulo P besitzt. Im
Kapitel 6: Das quadratische Reziprozitätsgesetz Ziel dieses Kapitels: die Untersuchung der Lösbarkeit der Kongruenzgleichung X also die Frage, ob die ganze Zahl Z eine Quadratwurzel modulo P besitzt. Im
1 Der Ring der ganzen Zahlen
 1 Der Ring der ganzen Zahlen Letztendlich wird die Addition und Multiplikation in endlichen Körpern auf die Addition und Multiplikation von ganzen Zahlen zurückgeführt. Deswegen müssen wir die an sich
1 Der Ring der ganzen Zahlen Letztendlich wird die Addition und Multiplikation in endlichen Körpern auf die Addition und Multiplikation von ganzen Zahlen zurückgeführt. Deswegen müssen wir die an sich
Algebra und Diskrete Mathematik, PS3. Sommersemester Prüfungsfragen
 Algebra und Diskrete Mathematik, PS3 Sommersemester 2016 Prüfungsfragen Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper). Wodurch
Algebra und Diskrete Mathematik, PS3 Sommersemester 2016 Prüfungsfragen Erläutern Sie die Sätze über die Division mit Rest für ganze Zahlen und für Polynome (mit Koeffizienten in einem Körper). Wodurch
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 10 Endliche Untergruppen der Einheitengruppe eines Körpers Wir wollen zeigen, dass die Einheitengruppe Z/(p), p Primzahl, zyklisch
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 10 Endliche Untergruppen der Einheitengruppe eines Körpers Wir wollen zeigen, dass die Einheitengruppe Z/(p), p Primzahl, zyklisch
Ältere Aufgaben (bis 1998)
 Ältere Aufgaben (bis 1998) Es waren in den 4 Stunden jeweils nur 2 Aufgaben zu bearbeiten, die einzelnen Aufgaben waren umfangreicher. September 1998, Aufgabe 1 Sei p eine ungerade Primzahl. a) Beweise:
Ältere Aufgaben (bis 1998) Es waren in den 4 Stunden jeweils nur 2 Aufgaben zu bearbeiten, die einzelnen Aufgaben waren umfangreicher. September 1998, Aufgabe 1 Sei p eine ungerade Primzahl. a) Beweise:
. Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z )
![. Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z ) . Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z )](/thumbs/62/46609231.jpg) Aufgabe 57 a) Seien p Primzahl, p 2, k N und [a] p k ( Z/p k Z ). Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z ) genau zwei oder gar keine Lösung. Beweis: Sei [x] p k ( Z/p k Z ) eine Lösung
Aufgabe 57 a) Seien p Primzahl, p 2, k N und [a] p k ( Z/p k Z ). Dann hat die Gleichung [X 2 ] p k = [a] p k in ( Z/p k Z ) genau zwei oder gar keine Lösung. Beweis: Sei [x] p k ( Z/p k Z ) eine Lösung
ist (oder besser Abspalten von Linearfaktoren beschäftigen. Zu einem beliebigen Körper K betrachten wir die Menge (j,k) N N j+k=n
 8. Polynomringe Das Umgehen mit Polynomen, d.h. mit Ausdrücken der Form a 0 + a 1 x + a 2 x 2 +... + a n x n ist aus der Schule vertraut, falls die Koeffizienten a 0,..., a n ganze oder rationale oder
8. Polynomringe Das Umgehen mit Polynomen, d.h. mit Ausdrücken der Form a 0 + a 1 x + a 2 x 2 +... + a n x n ist aus der Schule vertraut, falls die Koeffizienten a 0,..., a n ganze oder rationale oder
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 18 Kreisteilungskörper Definition 18.1. Der n-te Kreisteilungskörper ist der Zerfällungskörper des Polynoms X n 1 über Q. Offenbar
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 18 Kreisteilungskörper Definition 18.1. Der n-te Kreisteilungskörper ist der Zerfällungskörper des Polynoms X n 1 über Q. Offenbar
Das Gruppengesetz auf elliptischen Kurven: Assoziativität
 Ausarbeitung des Seminarvortrags Das Gruppengesetz auf elliptischen Kurven: Assoziativität Seminar Kryptographie, TU Kaiserslautern Sommersemester 2011 Pablo Luka Version vom 14. 05. 2011 Inhaltsverzeichnis
Ausarbeitung des Seminarvortrags Das Gruppengesetz auf elliptischen Kurven: Assoziativität Seminar Kryptographie, TU Kaiserslautern Sommersemester 2011 Pablo Luka Version vom 14. 05. 2011 Inhaltsverzeichnis
Körper- und Galoistheorie
 Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 8 Erzeugte Algebra und erzeugter Körper Satz 8.1. Sei K L eine Körpererweiterung und sei f L ein algebraisches Element. Dann ist
Prof. Dr. H. Brenner Osnabrück SS 2011 Körper- und Galoistheorie Vorlesung 8 Erzeugte Algebra und erzeugter Körper Satz 8.1. Sei K L eine Körpererweiterung und sei f L ein algebraisches Element. Dann ist
Algebra und Zahlentheorie I (WS03/04), Lösungen zu Blatt 12
 Algebra und Zahlentheorie I (WS03/04), Lösungen zu Blatt 12 Aufgabe 1. (Division mit Rest in Polynomringen) Es sei R ein kommutativer Ring {0} und R[X] ein Polynomring in der Unbestimmten X über R. Ferner
Algebra und Zahlentheorie I (WS03/04), Lösungen zu Blatt 12 Aufgabe 1. (Division mit Rest in Polynomringen) Es sei R ein kommutativer Ring {0} und R[X] ein Polynomring in der Unbestimmten X über R. Ferner
Seminar zur. Zahlentheorie. Prof. Dr. T. Wedhorn. Vortrag zum Thema. Euklidische und faktorielle Ringe Peter Picht. und.
 Seminar zur Zahlentheorie Prof. Dr. T. Wedhorn Vortrag zum Thema Euklidische und faktorielle Ringe 13.11.2007 Peter Picht und Stephan Schmidt 4 Euklidische und faktorielle Ringe (A) Assoziierheit, Irreduziblität,
Seminar zur Zahlentheorie Prof. Dr. T. Wedhorn Vortrag zum Thema Euklidische und faktorielle Ringe 13.11.2007 Peter Picht und Stephan Schmidt 4 Euklidische und faktorielle Ringe (A) Assoziierheit, Irreduziblität,
Irrationale Zahlen. Ausarbeitung zum Proseminar Modul 4c Unendlichkeit. angefertigt von. Felix Schultes. Dozentin: Fr.
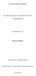 Irrationale Zahlen Ausarbeitung zum Proseminar Modul 4c Unendlichkeit angefertigt von Felix Schultes Dozentin: Fr. Regula Krapf Fachbereich 3 Universität Koblenz-Landau 24..207 INHALTSVERZEICHNIS Inhaltsverzeichnis
Irrationale Zahlen Ausarbeitung zum Proseminar Modul 4c Unendlichkeit angefertigt von Felix Schultes Dozentin: Fr. Regula Krapf Fachbereich 3 Universität Koblenz-Landau 24..207 INHALTSVERZEICHNIS Inhaltsverzeichnis
Prof. Dr. H. Brenner Osnabrück SS Zahlentheorie
 Prof. Dr. H. Brenner Osnabrüc SS 2008 Zahlentheorie Vorlesung 5 In diesem Abschnitt beschäftigen wir uns mit der Einheitengruppe der Restlassenringe Z/(n), also mit (Z/(n)). Ihre Anzahl wird durch die
Prof. Dr. H. Brenner Osnabrüc SS 2008 Zahlentheorie Vorlesung 5 In diesem Abschnitt beschäftigen wir uns mit der Einheitengruppe der Restlassenringe Z/(n), also mit (Z/(n)). Ihre Anzahl wird durch die
