Theoretische Informatik II
|
|
|
- Berthold Schuster
- vor 5 Jahren
- Abrufe
Transkript
1 Theoretische Informatik II Dr. Eva Richter / Holger Arnold Universität Potsdam, Theoretische Informatik, Sommersemester 2008 Übungsblatt 3 (Version 4) Abgabetermin: , Uhr Der λ-kalkül Da verschiedene Quellen zum λ-kalkül unterschiedliche Notationen verwenden, sind hier noch einmal die wichtigsten Definitionen zusammengefasst. Definition 1 (λ-terme). Sei V eine abzählbar unendliche Menge von Variablen und sei C eine abzählbare Menge von Konstanten. Die Menge Λ(V, C) der λ-terme über V und C ist die Menge von Ausdrücken, die auf folgende Weise gebildet werden können: 1. Variablen und Konstanten: Jede Variable x V und jede Konstante c C ist ein λ-term. 2. Abstraktion: Für alle Variablen x und alle λ-terme s ist λx s ein λ-term. 3. Applikation: Für alle λ-terme s und t ist s t ein λ-term. 4. Klammerung: Für alle λ-terme s ist (s) ein λ-term. Meist nimmt man V und C als gegeben an und spricht allgemein von λ-termen. Wenn nicht anders angegeben, bezeichnen x, y, z Variablen, c Konstanten und s, t, u, v beliebige λ-terme. Applikation ist linksassoziativ: s t u entspricht (s t) u. Abstraktion ist rechtsassoziativ: λx λy s entspricht λx (λy s). Applikation bindet stärker als Abstraktion: λx s t entspricht λx (s t). Für λx λy s schreibt man kurz λx y s. Definition 2 (Freie und gebundene Variablen). Für einen λ-term s sind die Menge fv(s) der freien Variablen in s und die Menge bv(s) der gebundenen Variablen in s definiert durch fv(x) = {x} fv(c) = fv(t u) = fv(t) fv(u) fv(λx t) = fv(t) {x} bv(x) = bv(c) = bv(t u) = bv(t) bv(u) bv(λx t) = bv(t) {x}. Ein λ-term heißt geschlossen oder Kombinator, wenn er keine freien Variablen enthält. Terme s und t, die sich nur in den Namen gebundener Variablen unterscheiden, werden als äquivalent betrachtet. Man bezeichnet solche Terme als α-konvertierbar und schreibt s t. Definition 3 (Substitutionen). Sei x eine Variable und t ein λ-term. Die Substitution von t für x, geschrieben [t/x], ist die wie folgt definierte Abbildung auf λ-termen: x[t/x] = t y[t/x] = y c[t/x] = c (s 1 s 2 )[t/x] = s 1 [t/x] s 2 [t/x] (λy s)[t/x] = λy s (λy s)[t/x] = λy (s[t/x]) (λy s)[t/x] = λz (s[z/y][t/x]) falls x y falls x = y oder x / fv(s) falls x y und y / fv(t) sonst, für ein z / fv(s) fv(t). 1
2 Definition 4 (Reduktion von λ-termen, Normalform). Auf den λ-termen ist eine Ableitungsrelation definiert. Die wichtigste Ableitungsregel des λ-kalküls ist die β-reduktion 1, die gegeben ist durch: (λx s) t s[t/x]. Einen Teilterm eines λ-terms, an dem eine Reduktion möglich ist, bezeichnet man als Redex. Ist für einen λ-term t keine β-reduktion mehr möglich, dann heißt t in Normalform. Gilt s t für zwei λ-terme s und t, wobei der reflexive, transitive und substitutive Abschluss der β-reduktion ist, dann heißt s reduzierbar zu t. Nicht jeder λ-term besitzt eine Normalform, aber wenn eine Normalform existiert, dann ist diese (bis auf α-konversion) eindeutig. Sie kann dann dadurch erhalten werden, dass stets das Redex reduziert wird, dessen λ am weitesten links steht. Definition 5 (λ-gleichheit). Die von α-konversion und β-reduktion erzeugte Kongruenzrelation bezeichnet man als λ-gleichheit. Das heißt, ist der reflexive, symmetrische, transitive und substitutive Abschluss von α-konversion und β-reduktion. Für zwei λ-terme s und t gilt genau dann, wenn es eine Folge u 1,..., u k von Termen und einen Term t t gibt, so dass s u 1 u 2... u k 1 u k t gilt. Die Relation kann auch durch folgende Ableitungsregeln charakterisiert werden: α-konversion s t β-reduktion s t Reflexivität t t Symmetrie t s Transitivität t u s u Substitution 1 u s u t Substitution 2 λx s λx t Der folgende Satz beschreibt eine wichtige Eigenschaft des λ-kalküls: Satz 6 (Satz von Church-Rosser). 1. Wenn s t 1 und s t 2 für Terme s, t 1 und t 2 gelten, dann gibt es Terme u und u mit t 1 u, t 2 u und u u. 2. Wenn s 1 s 2 für Terme s 1 und s 2 gilt, dann gibt es Terme t und t mit s 1 t, s 2 t und t t. 3. Wenn 1 und 2 für Terme s, t 1 und t 2 gelten, wobei t 1 und t 2 in Normalform sind, dann ist t 1 t 2. 1 Es gibt je nach Variation des Kalküls noch weitere Ableitungsregeln, unter Anderem die weiter oben erwähnte α-konversion und die η-reduktion, die sicherstellt, dass sich gleich verhaltende Funktionsterme auf einen gemeinsamen Term reduzierbar sind. Für unsere Zwecke genügt es aber, die β-reduktion zu betrachten. Die Bezeichnung Reduktion ist dabei etwas irreführend, denn s t bedeutet nicht, dass t in irgendeiner Weise kleiner als s sein muss. 2
3 Rekursiv definierte Funktionen im λ-kalkül Da Funktionen im λ-kalkül keine Namen besitzen, benötigt man zur Konstruktion rekursiv definierter Funktionen spezielle Kombinatoren: Definition 7. Ein λ-term F heißt Fixpunktkombinator, wenn für alle λ-terme t gilt: F t t (F t). Der bekannteste Fixpunktkombinator ist der Y-Kombinator, der definiert ist als Y = λf (λx f (x x)) (λx f (x x)). Eine rekursive Funktion f lässt sich durch eine Rekursionsgleichung der Form f x = t[f, x] spezifizieren, wobei t[f, x] ein λ-term ist, der f und x als freie Variablen enthalten kann. Mit einem Fixpunktkombinator wie Y lässt sich ein λ-term f definieren, der diese Rekursionsgleichung erfüllt: f = Y (λf x t[f, x]). Für diese Definition ist auch die Schreibweise let rec f x = t[f, x] üblich. Darstellung von Wahrheitswerten, Paaren und Zahlen im λ-kalkül Wahrheitswerte ist gegeben durch Die übliche Darstellung für die Wahrheitswerte true und false im λ-kalkül true = λx y x und false = λx y y. Damit lässt sich ein Kombinator für bedingte Ausdrücke wie folgt definieren: if then else = λs t 1 t 2 s t 1 t 2. Paare Geordnete Paare lassen sich im λ-kalkül wie folgt repräsentieren:, = λs t f f s t, fst = λp p true, snd = λp p false. Für n-tupel mit n > 2 gelte s 1,..., s n = s 1, s 2,..., s n. Natürliche Zahlen Die natürliche Zahl n kann im λ-kalkül als die n-fache Anwendung einer Funktion auf ein Argument dargestellt werden; n wird dann dargestellt durch n = λf x f n x mit f 0 x = x und f n+1 x = f (f n x). Man bezeichnet Zahlen in dieser Darstellung als Church- Numerale. Die arithmetischen Funktionen succ, iszero, add und mult sind auf Church-Numeralen durch folgende λ-terme definiert: succ = λn f x f (n f x), iszero = λn n (λx false) true, add = λm n f x m f (n f x), mult = λm n f x m (n f) x. Für diese Terme können auch die üblichen Infix-Schreibweisen verwendet werden, also +1 für succ, = 0 für iszero, + für add und für mult. 3
4 Mit den folgenden Aufgaben können Sie überprüfen, ob Sie die Darstellung von Wahrheitswerten, Paaren und Zahlen im λ-kalkül verstanden haben. 1. Zeigen Sie, dass gilt: if true then t 1 else t 2 t 1 und if false then t 1 else t 2 t 2 2. Geben Sie λ-terme für die logischen Operatoren and, or und not an. 3. Zeigen Sie, dass gilt: fst s, t s und snd s, t t. 4. Zeigen Sie, dass gilt: mult 0 n 0, mult 1 n n und succ add Prüfen Sie nach, dass die λ-terme succ, iszero, add und mult tatsächlich die entsprechenden Funktionen berechnen. 6. Welche arithmetischen Funktionen auf Church-Numeralen werden durch die folgenden λ- Terme repräsentiert? (a) λn f x n f (f x), (b) λm n n m. 4
5 Aufgabe Bestimmen Sie die Normalform des λ-terms (λf x f (f x)) (λy y) x. 2. Zeigen Sie, dass (λf x f (f x)) (λy x y) λw x (x w) gilt. 3. Zeigen Sie, dass die λ-terme (λx x x) (λx x x) und (λx x x x) (λx x x x) keine Normalform besitzen. Besitzt (λx y) ((λx x x) (λx x x)) eine Normalform? Aufgabe 3.2 Sei f folgender λ-term: f = Y(λf g x y if iszero y then x else f g (g x y) (pred y)). Dabei steht pred für die weiter unten definierte Vorgängerfunktion, für die gilt: pred 0 0 und pred n + 1 n. 1. Erklären Sie, warum die Definition von f keine rekursive Gleichung ist, obwohl f auf beiden Seiten des Gleichheitszeichens steht. 2. Beschreiben Sie die Funktion, die durch den λ-term f repräsentiert wird. Welche Funktionen berechnen die λ-terme f add 0 und f mult 1? In der funktionalen Programmierung ist der Kombinator f als fold bekannt. Aufgabe Erklären Sie die Funktionsweise der durch den folgenden λ-term definierten Vorgängerfunktion: pred = λn fst (n (λp snd p, succ (snd p) ) 0, 0 ) 2. Geben Sie mit Hilfe von pred einen λ-term sub an, für den gilt: { 0 falls m n, sub m n m n sonst. Aufgabe 3.4 Welche Bedingung muss ein Fixpunktkombinator erfüllen? Beweisen Sie, dass der λ-term T = (λx y y (x x y)) (λx y y (x x y)) ein Fixpunktkombinator ist. 5
6 Hausaufgabe 3.5 Beweisen oder widerlegen Sie folgende Aussage: Für jeden λ-term s, der eine Normalform besitzt, gilt: wenn s t 1 t 2... eine von s ausgehende Folge von β-reduktionen ist, dann sind höchstens endlich viele Terme in {t 1, t 2,... } nicht α-konvertierbar, d.h. die Menge der Äquivalenzklassen {t 1, t 2,... }/ ist endlich. Hausaufgabe 3.6 Beschreiben Sie die Funktion, die durch den folgenden λ-term f repräsentiert wird: Hausaufgabe 3.7 f = Y(λf x y if iszero y then 1 else mult x (f x (pred y))). Um den ganzzahligen Anteil der Quadratwurzel einer natürlichen Zahl n zu bestimmen, genügt es, zu zählen, wie viele Elemente der Folge der ungeraden Zahlen sich von n subtrahieren lassen, ohne dass das Ergebnis negativ wird (dieser Algorithmus basiert auf der sogenannten Pell-Gleichung). Zum Beispiel ist = 11, d.h. von 47 lassen sich 6 Elemente der Folge subtrahieren, 47 ist also 6 ( 47 = ). Geben Sie einen λ-ausdruck sqrt an, für den sqrt n n gilt und der diesen Algorithmus implementiert. Sie können alle λ-terme verwenden, die in diesem Übungsblatt gegeben sind. Hausaufgaben Für jede Hausaufgabe können Sie maximal 3 Punkte bekommen. Die Punkte werden nach folgenden Regeln vergeben: 3 Punkte = die Aufgabe wurde im Wesentlichen korrekt gelöst 2 Punkte = die Aufgabe wurde nur teilweise gelöst 1 Punkt = die Lösung der Aufgabe enthielt größere Fehler oder Lücken 0 Punkte = die Aufgabe wurde nicht gelöst oder enthielt sehr viele Fehler oder Lücken Sprechzeiten Haben Sie Fragen, Anregungen oder Probleme? Lassen Sie es uns wissen! Sprechen Sie in den Übungen Ihre Tutorin bzw. Ihren Tutor an. Holger Arnold, Raum 1.21, holger@cs.uni-potsdam.de Sprechzeiten: mittwochs Uhr und nach Vereinbarung Dr. Eva Richter, Raum 1.25, erichter@cs.uni-potsdam.de Sprechzeiten: dienstags Uhr und nach Vereinbarung 6
Funktionale Programmierung - Grundlagen -
 Funktionale Programmierung - Grundlagen - λ Logische und funktionale Programmierung - Universität Potsdam - M. Thomas - Funkt. Programmierung Gundlagen - IX.1 λ-ausdrücke 1) Variablen: x, y, z,...v,v 1,...
Funktionale Programmierung - Grundlagen - λ Logische und funktionale Programmierung - Universität Potsdam - M. Thomas - Funkt. Programmierung Gundlagen - IX.1 λ-ausdrücke 1) Variablen: x, y, z,...v,v 1,...
Der untypisierte Lambda-Kalkül als Programmiersprache
 Der untypisierte Lambda-Kalkül als Programmiersprache November 29, 2006 betreut von Prof. Tobias Nipkow Einführung In den 1930er Jahren von Alonzo Church und Stephen Kleene eingeführt Der Lambda-Kalkül
Der untypisierte Lambda-Kalkül als Programmiersprache November 29, 2006 betreut von Prof. Tobias Nipkow Einführung In den 1930er Jahren von Alonzo Church und Stephen Kleene eingeführt Der Lambda-Kalkül
Einführung in das λ-kalkül
 Einführung in das λ-kalkül Max Wagner IPD Snelting 1 3.11.2017 Max Wagner - Einführung in das λ-kalkül IPD KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Syntax Abstrakte Syntax:
Einführung in das λ-kalkül Max Wagner IPD Snelting 1 3.11.2017 Max Wagner - Einführung in das λ-kalkül IPD KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft www.kit.edu Syntax Abstrakte Syntax:
Übung zur Vorlesung Automatisierte Logik und Programmierung I
 Übung zur Vorlesung Automatisierte Logik und Programmierung I Prof. Chr. Kreitz Universität Potsdam, Theoretische Informatik Wintersemester 2008/09 Blatt 3 Abgabetermin: 26.11.08 nach der Übung Das dritte
Übung zur Vorlesung Automatisierte Logik und Programmierung I Prof. Chr. Kreitz Universität Potsdam, Theoretische Informatik Wintersemester 2008/09 Blatt 3 Abgabetermin: 26.11.08 nach der Übung Das dritte
1 Geschichte. 2 Syntax und Konzepte. Lamdba-Kalkül
 1 Geschichte 1673 Gottfried Wilhelm Leibniz entwickelt eine mechanische Rechenmaschine, beginnt zu träumen: Gibt es eine universelle Sprache, in der alle Probleme dargestellt werden können? Gibt es eine
1 Geschichte 1673 Gottfried Wilhelm Leibniz entwickelt eine mechanische Rechenmaschine, beginnt zu träumen: Gibt es eine universelle Sprache, in der alle Probleme dargestellt werden können? Gibt es eine
Lambda-Kalkül. Philipp Meyer. 28. April 2009
 Lambda-Kalkül Philipp Meyer 28. April 2009 1 Einleitung Der λ-kalkül ist eine von Alonzo Church und Stephen Kleene in den 1930er Jahren eingeführtes Modell zur Beschreibung berechenbarer Funktionen. Es
Lambda-Kalkül Philipp Meyer 28. April 2009 1 Einleitung Der λ-kalkül ist eine von Alonzo Church und Stephen Kleene in den 1930er Jahren eingeführtes Modell zur Beschreibung berechenbarer Funktionen. Es
Funktionale Programmierung ALP I. λ Kalkül WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
Inferenzmethoden. Einheit 18. Logik höherer Stufe
 Inferenzmethoden Einheit 18 Logik höherer Stufe 1. Syntax und Semantik 2. Simulation mathematischer Konstrukte 3. Beweisführung in Logik höherer Stufe Logik höherer Stufe Logik erster Stufe hat nur einfache
Inferenzmethoden Einheit 18 Logik höherer Stufe 1. Syntax und Semantik 2. Simulation mathematischer Konstrukte 3. Beweisführung in Logik höherer Stufe Logik höherer Stufe Logik erster Stufe hat nur einfache
Funktionale Programmierung ALP I. λ Kalkül. Teil 2 WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül Teil 2 WS 2012/2013 Lokale Variablennamen Haskell: let x = exp1 in exp2 Lambda: λ exp1. exp2 Einfache Regel: Der Geltungsbereich eines Lambda-Ausdrucks erstreckt sich soweit wie möglich
ALP I λ Kalkül Teil 2 WS 2012/2013 Lokale Variablennamen Haskell: let x = exp1 in exp2 Lambda: λ exp1. exp2 Einfache Regel: Der Geltungsbereich eines Lambda-Ausdrucks erstreckt sich soweit wie möglich
Der untypisierte Lambda-Kalkül
 Der untypisierte Lambda-Kalkül Fabian Immler 08.05.2008 1 Motivation und Einführung Der Lambda-Kalkül ist ein formales System zur Beschreibung von Funktionen, welches Funktionsdefinition sowie das Auswerten
Der untypisierte Lambda-Kalkül Fabian Immler 08.05.2008 1 Motivation und Einführung Der Lambda-Kalkül ist ein formales System zur Beschreibung von Funktionen, welches Funktionsdefinition sowie das Auswerten
Der untypisierte Lambda-Kalkül als Programmiersprache
 Proseminar: Programmiersprachen bei Prof. Tobias Nipkow Der untypisierte Lambda-Kalkül als Programmiersprache von Benjamin Peherstorfer betreut von Prof. Tobias Nipkow 23. November 2006 Inhaltsverzeichnis
Proseminar: Programmiersprachen bei Prof. Tobias Nipkow Der untypisierte Lambda-Kalkül als Programmiersprache von Benjamin Peherstorfer betreut von Prof. Tobias Nipkow 23. November 2006 Inhaltsverzeichnis
3 Exkurs: Der λ-kalkül
 3 Exkurs: Der λ-kalkül Alonso Churchs λ-kalkül (ca. 1940) ist der formale Kern jeder funktionalen Programmiersprache. Der λ-kalkül ist eine einfache Sprache, mit nur wenigen syntaktischen Konstrukten und
3 Exkurs: Der λ-kalkül Alonso Churchs λ-kalkül (ca. 1940) ist der formale Kern jeder funktionalen Programmiersprache. Der λ-kalkül ist eine einfache Sprache, mit nur wenigen syntaktischen Konstrukten und
Reduktion. 2.1 Abstrakte Reduktion
 2 Reduktion In diesem Kapitel studieren wir abstrakte Eigenschaften von Regeln. In den ersten beiden Abschnitten betrachten wir nicht einmal die Regeln selbst, sondern nur abstrakte Reduktionssysteme,
2 Reduktion In diesem Kapitel studieren wir abstrakte Eigenschaften von Regeln. In den ersten beiden Abschnitten betrachten wir nicht einmal die Regeln selbst, sondern nur abstrakte Reduktionssysteme,
Der einfach getypter Lambda-Kalkül
 Der einfach getypter Lambda-Kalkül Typprüfung und Typinferenz Tobias Nipkow und Steffen Smolka Technische Universität München 1 Einleitung 2 Explizit getypter λ-kalkül 3 Implizit getypter λ-kalkül Statische
Der einfach getypter Lambda-Kalkül Typprüfung und Typinferenz Tobias Nipkow und Steffen Smolka Technische Universität München 1 Einleitung 2 Explizit getypter λ-kalkül 3 Implizit getypter λ-kalkül Statische
Mathematische Strukturen
 Mathematische Strukturen Lineare Algebra I Kapitel 3 16. April 2013 Kartesisches Produkt Das kartesische Produkt (benannt nach René Descartes) von n Mengen M 1,..., M n ist M 1 M n := {(x 1,..., x n )
Mathematische Strukturen Lineare Algebra I Kapitel 3 16. April 2013 Kartesisches Produkt Das kartesische Produkt (benannt nach René Descartes) von n Mengen M 1,..., M n ist M 1 M n := {(x 1,..., x n )
Programmierparadigmen
 Programmierparadigmen Teil 1: Funktionale Programmierung Kapitel 3 Lambda Kalkül (Dieses Kapitel orientiert sich an Material von Prof. Dr.-Ing. Snelting, KIT) http://www.tu-ilmenau.de/fakia/functional.html
Programmierparadigmen Teil 1: Funktionale Programmierung Kapitel 3 Lambda Kalkül (Dieses Kapitel orientiert sich an Material von Prof. Dr.-Ing. Snelting, KIT) http://www.tu-ilmenau.de/fakia/functional.html
Software Entwicklung 1
 Software Entwicklung 1 Annette Bieniusa AG Softech FB Informatik TU Kaiserslautern Überblick für heute Programmierparadigmen Imperative vs. deklarative Programmierung Beispiele Funktionale Programmierung
Software Entwicklung 1 Annette Bieniusa AG Softech FB Informatik TU Kaiserslautern Überblick für heute Programmierparadigmen Imperative vs. deklarative Programmierung Beispiele Funktionale Programmierung
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
(1.18) Def.: Eine Abbildung f : M N heißt
 Zurück zur Mengenlehre: Abbildungen zwischen Mengen (1.17) Def.: Es seien M, N Mengen. Eine Abbildung f : M N von M nach N ist eine Vorschrift, die jedem x M genau ein Element f(x) N zuordnet. a) M = N
Zurück zur Mengenlehre: Abbildungen zwischen Mengen (1.17) Def.: Es seien M, N Mengen. Eine Abbildung f : M N von M nach N ist eine Vorschrift, die jedem x M genau ein Element f(x) N zuordnet. a) M = N
- Theorie der uninterpretierten
 Theorie der uninterpretierten Funktionen Entscheidungsverfahren mit Anwendungen in der Softwareverifikation STEPHAN FALKE INSTITUT FÜR THEORETISCHE INFORMATIK (ITI) 0 KIT 13. Universität Mai 2013 des S.
Theorie der uninterpretierten Funktionen Entscheidungsverfahren mit Anwendungen in der Softwareverifikation STEPHAN FALKE INSTITUT FÜR THEORETISCHE INFORMATIK (ITI) 0 KIT 13. Universität Mai 2013 des S.
Einführung in die funktionale Programmierung
 Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 17. Oktober 2006 Einführung in Haskell: Syntax, Reduktionen, Kernsprachen Haskell,
Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 17. Oktober 2006 Einführung in Haskell: Syntax, Reduktionen, Kernsprachen Haskell,
Funktionale Programmierung Einführung
 Einführung Prof. Dr. Oliver Braun Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 13.09.2017 15:29 Inhaltsverzeichnis Was ist imperative Programmierung.......................
Einführung Prof. Dr. Oliver Braun Fakultät für Informatik und Mathematik Hochschule München Letzte Änderung: 13.09.2017 15:29 Inhaltsverzeichnis Was ist imperative Programmierung.......................
Funktionen und sprachliche Bedeutungen
 Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Einführung in die Semantik,4. Sitzung Mehr zu Funktionen / Mengen, Relationen, Göttingen 1. November 2006 Mengen und sprachliche Bedeutungen Abstraktion und Konversion Rekursion Charakteristische Funktionen
Operationale Semantik 1
 Operationae Semantik 1 Side 1 Zie: Geschossene Terme t ι ι sind Programme, die auf Eingabe n die Ausgabe [t] n erzeugen. Ein-/Ausgabekonvention: Eingaben und Ausgaben sind Numerae! Def. Ein Numera ist
Operationae Semantik 1 Side 1 Zie: Geschossene Terme t ι ι sind Programme, die auf Eingabe n die Ausgabe [t] n erzeugen. Ein-/Ausgabekonvention: Eingaben und Ausgaben sind Numerae! Def. Ein Numera ist
Universität Hannover Fakultät für Elektrotechnik und Informatik Institut für Theoretische Informatik. Thema: von. Paul Krüger
 1 Universität Hannover Fakultät für Elektrotechnik und Informatik Institut für Theoretische Informatik Thema: - Kalkül von Paul Krüger Betreuer: Prof. Dr. Heribert Vollmer Das Rahmenthema ist " Berechenbarkeit
1 Universität Hannover Fakultät für Elektrotechnik und Informatik Institut für Theoretische Informatik Thema: - Kalkül von Paul Krüger Betreuer: Prof. Dr. Heribert Vollmer Das Rahmenthema ist " Berechenbarkeit
Mathematik für Informatiker I Mitschrift zur Vorlesung vom
 Mathematik für Informatiker I Mitschrift zur Vorlesung vom 18.11.2004 Zur Wiederholung: Das Kartesische Produkt dient dem Ordnen von Mengen. A B = {(a, b) : a A, b B)} Spezialfall A = Äquivalenzrelation
Mathematik für Informatiker I Mitschrift zur Vorlesung vom 18.11.2004 Zur Wiederholung: Das Kartesische Produkt dient dem Ordnen von Mengen. A B = {(a, b) : a A, b B)} Spezialfall A = Äquivalenzrelation
Übersicht. Nebenläufige Programmierung: Praxis und Semantik. Semantische Modelle nebenläufiger Programmiersprachen. Einleitung
 Stand der Folien: 24. Januar 2012 Übersicht Aktuelle Themen zu Informatik der Systeme: Nebenläufige Programmierung: Praxis und Semantik Semantische Modelle nebenläufiger Programmiersprachen 1 2 Call-by-Name
Stand der Folien: 24. Januar 2012 Übersicht Aktuelle Themen zu Informatik der Systeme: Nebenläufige Programmierung: Praxis und Semantik Semantische Modelle nebenläufiger Programmiersprachen 1 2 Call-by-Name
2 Mengen, Abbildungen und Relationen
 Vorlesung WS 08 09 Analysis 1 Dr. Siegfried Echterhoff 2 Mengen, Abbildungen und Relationen Definition 2.1 (Mengen von Cantor, 1845 1918) Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohl
Vorlesung WS 08 09 Analysis 1 Dr. Siegfried Echterhoff 2 Mengen, Abbildungen und Relationen Definition 2.1 (Mengen von Cantor, 1845 1918) Eine Menge M ist eine Zusammenfassung von wohlbestimmten und wohl
1. Typen 1.1 Typsicherheit 1.2 Typprüfung
 1. Typen 1.1 Typsicherheit 1.2 Typprüfung Ein Typsystem ist ein praktikables, syntaktisches Verfahren, mit dem man die Abwesenheit gewisser Laufzeit-Eigenschaften eines Programms beweisen kann, indem man
1. Typen 1.1 Typsicherheit 1.2 Typprüfung Ein Typsystem ist ein praktikables, syntaktisches Verfahren, mit dem man die Abwesenheit gewisser Laufzeit-Eigenschaften eines Programms beweisen kann, indem man
Einführung in die Informatik 2
 Einführung in die Informatik 2 Mathematische Grundbegriffe Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr,
Einführung in die Informatik 2 Mathematische Grundbegriffe Sven Kosub AG Algorithmik/Theorie komplexer Systeme Universität Konstanz E 202 Sven.Kosub@uni-konstanz.de Sprechstunde: Freitag, 12:30-14:00 Uhr,
6. Einführung 43. gilt. Dann soll also A B x B = b eindeutig lösbar sein, also A B vollen Rang haben, d. h. invertierbar (regulär) sein.
 6. Einführung 43 und aus der linearen Unabhängigkeit der (a i ) i I(x) folgt y i = z i auch für i I(x). Insgesamt gilt also y = z, d. h., nach Definition 6.9 ist x eine Ecke von P. Beachte: Der Koordinatenvektor
6. Einführung 43 und aus der linearen Unabhängigkeit der (a i ) i I(x) folgt y i = z i auch für i I(x). Insgesamt gilt also y = z, d. h., nach Definition 6.9 ist x eine Ecke von P. Beachte: Der Koordinatenvektor
Grundlagen der Programmierung 2. Operationale Semantik
 Grundlagen der Programmierung 2 Operationale Semantik Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 29. April 2009 Semantik von Programmiersprachen Semantik = Bedeutung
Grundlagen der Programmierung 2 Operationale Semantik Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 29. April 2009 Semantik von Programmiersprachen Semantik = Bedeutung
Grundbegriffe für dreiwertige Logik
 Grundbegriffe für dreiwertige Logik Hans Kleine Büning Universität Paderborn 1.11.2011 1 Syntax und Semantik Die klassische Aussagenlogik mit den Wahrheitswerten falsch und wahr bezeichnen wir im weiteren
Grundbegriffe für dreiwertige Logik Hans Kleine Büning Universität Paderborn 1.11.2011 1 Syntax und Semantik Die klassische Aussagenlogik mit den Wahrheitswerten falsch und wahr bezeichnen wir im weiteren
Formale Methoden 2. Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016
 Formale Methoden 2 Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016 Teil 1: Wiederholung 1 Mengen 2 Abbildungen 3 Exkurs Beweistechniken 4 Relationen Definition Operationen Eigenschaften Äquivalenzrelationen
Formale Methoden 2 Gaetano Geck Lehrstuhl I Logik in der Informatik WS 2015/2016 Teil 1: Wiederholung 1 Mengen 2 Abbildungen 3 Exkurs Beweistechniken 4 Relationen Definition Operationen Eigenschaften Äquivalenzrelationen
Programmierparadigmen Software Entwicklung 1
 Programmierparadigmen Software Entwicklung 1 Annette Bieniusa, Mathias Weber, Peter Zeller 1 Imperative vs. Deklarative Programmierung Wir haben in SE1 bisher zwei Programmiersprachen näher betrachtet:
Programmierparadigmen Software Entwicklung 1 Annette Bieniusa, Mathias Weber, Peter Zeller 1 Imperative vs. Deklarative Programmierung Wir haben in SE1 bisher zwei Programmiersprachen näher betrachtet:
Der untypisierte Lambda-Kalkül
 Der untypisierte Lambda-Kalkül Kern einer minimalen Programmiersprache Sabine Rieder Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen des Lambda-Kalküls 2 2.1 Syntax.....................................
Der untypisierte Lambda-Kalkül Kern einer minimalen Programmiersprache Sabine Rieder Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen des Lambda-Kalküls 2 2.1 Syntax.....................................
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2013/2014 1/61 Anmerkung Änderung im Wintersemester 2013/2014:
Grundbegriffe der Informatik Einheit 17: Relationen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2013/2014 1/61 Anmerkung Änderung im Wintersemester 2013/2014:
Seminar Mathematische Logik L-Strukturen und Syntax der Prädikatenlogik
 Seminar Mathematische Logik L-Strukturen und Syntax der Prädikatenlogik Linda Raabe 7. März 2012 1 L-Strukturen Definition 1.1 (Struktur) Eine Struktur A ist eine nichtleere Trägermenge A zusammen mit
Seminar Mathematische Logik L-Strukturen und Syntax der Prädikatenlogik Linda Raabe 7. März 2012 1 L-Strukturen Definition 1.1 (Struktur) Eine Struktur A ist eine nichtleere Trägermenge A zusammen mit
Lösungen zur Übungsserie 1
 Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag, 24. September Lösungen zur Übungsserie 1 Aufgaben 1, 3, 4, 5, 6, 8 Aufgabe 1. Sei X eine endliche Menge mit n Elementen, und sei Y eine endliche
Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag, 24. September Lösungen zur Übungsserie 1 Aufgaben 1, 3, 4, 5, 6, 8 Aufgabe 1. Sei X eine endliche Menge mit n Elementen, und sei Y eine endliche
Vor(schau)kurs für Studienanfänger Mathematik: Aussagen und Mengen
 Vor(schau)kurs für Studienanfänger Mathematik: Aussagen und Mengen 09.10.2014 Herzlich Willkommen zum 2. Teil des Vorschaukurses für Mathematik! Organisatorisches Der Vorkurs besteht aus sechs Blöcken
Vor(schau)kurs für Studienanfänger Mathematik: Aussagen und Mengen 09.10.2014 Herzlich Willkommen zum 2. Teil des Vorschaukurses für Mathematik! Organisatorisches Der Vorkurs besteht aus sechs Blöcken
Analysis für Informatiker
 Analysis für Informatiker Wintersemester 2017/2018 Carsten.Schneider@risc.jku.at 1 Bemerkung: Dies ist kein Skript, welches den gesamten Inhalt der Vorlesung abdeckt. Es soll den Studierenden aber während
Analysis für Informatiker Wintersemester 2017/2018 Carsten.Schneider@risc.jku.at 1 Bemerkung: Dies ist kein Skript, welches den gesamten Inhalt der Vorlesung abdeckt. Es soll den Studierenden aber während
Theoretische Informatik II
 Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Wintersemester 2007/2008 B. Beckert Theoretischen Informatik II: WS 2007/08 1 / 179 Dank Diese Vorlesungsmaterialien basieren
Vorlesung Theoretische Informatik II Bernhard Beckert Institut für Informatik Wintersemester 2007/2008 B. Beckert Theoretischen Informatik II: WS 2007/08 1 / 179 Dank Diese Vorlesungsmaterialien basieren
Mengen. (Nicht-) Elemente einer Menge { 3, 4 } { 1, { 2 }, { 3, 4 }, { 5 } } 3 { 1, { 2 }, { 3, 4 }, { 5 } }
 Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1,
Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1,
Einführung in die Semantik, 2./3. Sitzung Mengen / Relatione
 Eigenschaften von Einführung in die Semantik, 2./3. Sitzung Mengen / / Göttingen 2. November 2006 Eigenschaften von Mengenlehre Eigenschaften von Eigenschaften von Das Konzept Menge Eine Menge ist eine
Eigenschaften von Einführung in die Semantik, 2./3. Sitzung Mengen / / Göttingen 2. November 2006 Eigenschaften von Mengenlehre Eigenschaften von Eigenschaften von Das Konzept Menge Eine Menge ist eine
Die Prädikatenlogik erster Stufe: Syntax und Semantik
 Die Prädikatenlogik erster Stufe: Syntax und Semantik 1 Mathematische Strukturen und deren Typen Definition 1.1 Eine Struktur A ist ein 4-Tupel A = (A; (R A i i I); (f A j j J); (c A k k K)) wobei I, J,
Die Prädikatenlogik erster Stufe: Syntax und Semantik 1 Mathematische Strukturen und deren Typen Definition 1.1 Eine Struktur A ist ein 4-Tupel A = (A; (R A i i I); (f A j j J); (c A k k K)) wobei I, J,
Konstruktion reeller Zahlen aus rationalen Zahlen
 Konstruktion reeller Zahlen aus rationalen Zahlen Wir nehmen an, daß der Körper der rationalen Zahlen bekannt ist. Genauer wollen wir annehmen: Gegeben ist eine Menge Q zusammen mit zwei Verknüpfungen
Konstruktion reeller Zahlen aus rationalen Zahlen Wir nehmen an, daß der Körper der rationalen Zahlen bekannt ist. Genauer wollen wir annehmen: Gegeben ist eine Menge Q zusammen mit zwei Verknüpfungen
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 15. April 2018 1/46 Die Dimension eines Vektorraums Satz 2.27 (Basisergänzungssatz) Sei V ein Vektorraum über einem Körper K. Weiter seien v 1,...,
(Analysis und lineare Algebra) im Sommersemester 2018 15. April 2018 1/46 Die Dimension eines Vektorraums Satz 2.27 (Basisergänzungssatz) Sei V ein Vektorraum über einem Körper K. Weiter seien v 1,...,
Interpreter (Hilfsfunktionen)
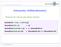 Interpreter (Hilfsfunktionen) -- Berechnet die Liste der gebundenen Variablen boundlist :: Expr -> [String] boundlist (Var x) = [] boundlist (Lambda x e) = x : (boundlist e) boundlist (App e1 e2) = (boundlist
Interpreter (Hilfsfunktionen) -- Berechnet die Liste der gebundenen Variablen boundlist :: Expr -> [String] boundlist (Var x) = [] boundlist (Lambda x e) = x : (boundlist e) boundlist (App e1 e2) = (boundlist
3 Werkzeuge der Mathematik
 3.1 Mengen (18.11.2011) Definition 3.1 Die Menge heißt leere Menge. :=»x M x x Definition 3.2 Es seien N und M Mengen. Wir definieren: und analog M N : (x M x N). N M : (x N x M). Wir sagen M ist Teilmenge
3.1 Mengen (18.11.2011) Definition 3.1 Die Menge heißt leere Menge. :=»x M x x Definition 3.2 Es seien N und M Mengen. Wir definieren: und analog M N : (x M x N). N M : (x N x M). Wir sagen M ist Teilmenge
Kapitel 5: λ-kalkül und Laziness
 Funktionale Programmierung (WS2005/2006) 5/1 Kapitel 5: λ-kalkül und Laziness Lernziele dieses Kapitels 1. Syntax des einfachen, ungetypten λ-kalküls Symbolische Manipulation von λ-ausdrücken in Haskell,
Funktionale Programmierung (WS2005/2006) 5/1 Kapitel 5: λ-kalkül und Laziness Lernziele dieses Kapitels 1. Syntax des einfachen, ungetypten λ-kalküls Symbolische Manipulation von λ-ausdrücken in Haskell,
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018 23. November 2017 1/40 Satz 4.27 (Multinomialsatz) Seien r, n N 0. Dann gilt für
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2017/2018 23. November 2017 1/40 Satz 4.27 (Multinomialsatz) Seien r, n N 0. Dann gilt für
Übersichtsblatt Hertrampf/Bahrdt. 1 Mathematische Aussagen. Theoretische Informatik I WS2018/19
 Theoretische Informatik I WS2018/19 Übersichtsblatt Hertrampf/Bahrdt Institut für Formale Methoden der Informatik Theoretische Informatik Universität Stuttgart 1 Mathematische Aussagen Um mathematische
Theoretische Informatik I WS2018/19 Übersichtsblatt Hertrampf/Bahrdt Institut für Formale Methoden der Informatik Theoretische Informatik Universität Stuttgart 1 Mathematische Aussagen Um mathematische
Überblick. Ausdrücke. 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke
 Überblick 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke 3 Mathematische Grundlagen 3 Ausdrücke Einf. Progr. (WS 08/09) 148 Ausdrücke Betrachten wir folgende
Überblick 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke 3 Mathematische Grundlagen 3 Ausdrücke Einf. Progr. (WS 08/09) 148 Ausdrücke Betrachten wir folgende
R = {(1, 1), (2, 2), (3, 3)} K 1 = {1} K 2 = {2} K 3 = {3}
 Äquivalenzrelationen Aufgabe 1. Lesen Sie im Skript nach was eine Äquivalenzrelation und eine Äquivalenzklasse ist. Gegeben ist die Menge A = {1, 2, 3. Finden Sie 3 Äquivalenzrelationen auf A und geben
Äquivalenzrelationen Aufgabe 1. Lesen Sie im Skript nach was eine Äquivalenzrelation und eine Äquivalenzklasse ist. Gegeben ist die Menge A = {1, 2, 3. Finden Sie 3 Äquivalenzrelationen auf A und geben
Logik und Künstliche Intelligenz
 Logik und Künstliche Intelligenz Kurze Zusammenfassung (Stand: 14. Januar 2010) Prof. Dr. V. Stahl Copyright 2007 by Volker Stahl. All rights reserved. V. Stahl Logik und Künstliche Intelligenz Zusammenfassung
Logik und Künstliche Intelligenz Kurze Zusammenfassung (Stand: 14. Januar 2010) Prof. Dr. V. Stahl Copyright 2007 by Volker Stahl. All rights reserved. V. Stahl Logik und Künstliche Intelligenz Zusammenfassung
Kapitel 1. Grundlagen Mengen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Mengen. Eigenschaften. Spezielle Mengen (1) Prominente Mengen. ! Mengenzugehörigkeit
 Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Mengen! Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor)! Notation 1. Aufzählung aller Elemente: {
Logische Grundlagen der Mathematik, WS 2014/15
 Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 26. November 2014 Was kommt nach den natürlichen Zahlen? Mehr als die natürlichen Zahlen braucht man nicht, um einige der schwierigsten
Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 26. November 2014 Was kommt nach den natürlichen Zahlen? Mehr als die natürlichen Zahlen braucht man nicht, um einige der schwierigsten
Relationen und DAGs, starker Zusammenhang
 Relationen und DAGs, starker Zusammenhang Anmerkung: Sei D = (V, E). Dann ist A V V eine Relation auf V. Sei andererseits R S S eine Relation auf S. Dann definiert D = (S, R) einen DAG. D.h. DAGs sind
Relationen und DAGs, starker Zusammenhang Anmerkung: Sei D = (V, E). Dann ist A V V eine Relation auf V. Sei andererseits R S S eine Relation auf S. Dann definiert D = (S, R) einen DAG. D.h. DAGs sind
Aufgabe 3. Sei A eine Menge von Zahlen und neg das Tripel. neg = (A, A, R) A = N A = Z A = R A = R \ {0} mod : N 0 N N 0
 Funktionen Aufgabe 1. Finden Sie 3 Beispiele von Funktionen und 3 Beispiele von partiellen Funktionen, die nicht total sind. Es sollten auch mehrstellige Funktionen darunter sein. Aufgabe 2. Zeigen Sie,
Funktionen Aufgabe 1. Finden Sie 3 Beispiele von Funktionen und 3 Beispiele von partiellen Funktionen, die nicht total sind. Es sollten auch mehrstellige Funktionen darunter sein. Aufgabe 2. Zeigen Sie,
modulo s auf Z, s. Def
 16. Januar 2007 Arbeitsblatt 5 Übungen zu Mathematik I für das Lehramt an der Grund- und Mittelstufe sowie an Sonderschulen I. Gasser, H. Strade, B. Werner WiSe 06/07 21.11.06 Präsenzaufgaben: 1) Seien
16. Januar 2007 Arbeitsblatt 5 Übungen zu Mathematik I für das Lehramt an der Grund- und Mittelstufe sowie an Sonderschulen I. Gasser, H. Strade, B. Werner WiSe 06/07 21.11.06 Präsenzaufgaben: 1) Seien
2 Lösungen zu Kapitel 2
 2 Lösungen zu Kapitel 2 2. Lösung. Die Funktion f ist nicht injektiv. So gibt es (unendlich) viele Paare (x, y) mit f(x, y) = 0, etwa (0, 0) und (/2, ). Die Funktion f ist surjektiv. Zum Beispiel gilt
2 Lösungen zu Kapitel 2 2. Lösung. Die Funktion f ist nicht injektiv. So gibt es (unendlich) viele Paare (x, y) mit f(x, y) = 0, etwa (0, 0) und (/2, ). Die Funktion f ist surjektiv. Zum Beispiel gilt
Fortgeschrittene Funktionale Programmierung
 Fortgeschrittene Funktionale Programmierung 13. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Erweiterung um Datentypen Typen: τ := Bool [τ] Terme: t := False True [ ] τ t : t case
Fortgeschrittene Funktionale Programmierung 13. Vorlesung Janis Voigtländer Universität Bonn Wintersemester 2015/16 Erweiterung um Datentypen Typen: τ := Bool [τ] Terme: t := False True [ ] τ t : t case
Mathematik-Vorkurs für Informatiker (Wintersemester 2012/13) Übungsblatt 8 (Relationen und Funktionen)
 DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6. Informatik Universität des Saarlandes Christian Eisentraut, M.Sc. Julia Krämer Mathematik-Vorkurs für Informatiker (Wintersemester 0/3) Übungsblatt 8 (Relationen
DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6. Informatik Universität des Saarlandes Christian Eisentraut, M.Sc. Julia Krämer Mathematik-Vorkurs für Informatiker (Wintersemester 0/3) Übungsblatt 8 (Relationen
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 30.04.2013 Grenzen regulärer Sprachen Wie beweist man, dass eine Sprache nicht regulär
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 30.04.2013 Grenzen regulärer Sprachen Wie beweist man, dass eine Sprache nicht regulär
1 Euklidische und unitäre Vektorräume
 1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
Kapitel 2. Mathematische Grundlagen. Skript zur Vorlesung Einführung in die Programmierung
 LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 2 Mathematische Grundlagen Skript zur Vorlesung Einführung in die Programmierung im Wintersemester 2012/13 Ludwig-Maximilians-Universität
LUDWIG- MAXIMILIANS- UNIVERSITY MUNICH DEPARTMENT INSTITUTE FOR INFORMATICS DATABASE Kapitel 2 Mathematische Grundlagen Skript zur Vorlesung Einführung in die Programmierung im Wintersemester 2012/13 Ludwig-Maximilians-Universität
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 3.2 Induktion und Rekursion 3.3 Boolsche Algebra Peer Kröger (LMU München) Einführung in die Programmierung WS 14/15 48 / 155 Überblick
4 Affine Koordinatensysteme
 4 Affine Koordinatensysteme Sei X φ ein affiner Raum und seien p,, p r X Definition: Nach ( c ist der Durchschnitt aller affinen Unterräume Z X, welche die Menge {p,,p r } umfassen, selbst ein affiner
4 Affine Koordinatensysteme Sei X φ ein affiner Raum und seien p,, p r X Definition: Nach ( c ist der Durchschnitt aller affinen Unterräume Z X, welche die Menge {p,,p r } umfassen, selbst ein affiner
Gerade, ungerade oder weder noch? Algebraische und graphische Beweise. 4-E1 Vorkurs, Mathematik
 Gerade, ungerade oder weder noch? Algebraische und graphische Beweise 4-E1 Symmetrie einer Funktion: Aufgabe 3 Bestimmen Sie algebraisch und graphisch, ob die Funktionen gerade oder ungerade sind, oder
Gerade, ungerade oder weder noch? Algebraische und graphische Beweise 4-E1 Symmetrie einer Funktion: Aufgabe 3 Bestimmen Sie algebraisch und graphisch, ob die Funktionen gerade oder ungerade sind, oder
4. ggt und kgv. Chr.Nelius: Zahlentheorie (SS 2007) 9
 Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
THEORETISCHE INFORMATIK UND LOGIK
 Prädikatenlogik als Universalsprache Die Entwicklung der Logik hat ein zentrales Motiv: Logik als eine universelle, präzise Sprache THEORETISCHE INFORMATIK UND LOGIK 15. Vorlesung: Logisches Schließen
Prädikatenlogik als Universalsprache Die Entwicklung der Logik hat ein zentrales Motiv: Logik als eine universelle, präzise Sprache THEORETISCHE INFORMATIK UND LOGIK 15. Vorlesung: Logisches Schließen
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 5. April 2018 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
(Analysis und lineare Algebra) im Sommersemester 2018 5. April 2018 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
Formale Methoden der Softwaretechnik 1 Vorlesung vom : Grundlage von Isabelle
 1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
Haskell, Typen, und Typberechnung. Grundlagen der Programmierung 3 A. Überladung und Konversion in Haskell. Typisierung in Haskell
 Haskell, Typen, und Typberechnung Grundlagen der Programmierung 3 A Typen, Typberechnung und Typcheck Prof. Dr Manfred Schmidt-Schauß Ziele: Haskells Typisierung Typisierungs-Regeln Typ-Berechnung Sommersemester
Haskell, Typen, und Typberechnung Grundlagen der Programmierung 3 A Typen, Typberechnung und Typcheck Prof. Dr Manfred Schmidt-Schauß Ziele: Haskells Typisierung Typisierungs-Regeln Typ-Berechnung Sommersemester
Abschnitt 3: Mathematische Grundlagen
 Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke 3 Mathematische Grundlagen Einf. Progr. (WS 08/09) 102 Überblick 3.
Abschnitt 3: Mathematische Grundlagen 3. Mathematische Grundlagen 3.1 Mengen und Abbildungen 3.2 Induktion und Rekursion 3.3 Ausdrücke 3 Mathematische Grundlagen Einf. Progr. (WS 08/09) 102 Überblick 3.
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 8 18. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 8 18. Juli 2011 Einführung in die Theoretische Informatik
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 015/016 30.10.015 Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 1. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 015/016 30.10.015 Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 1. Übungsblatt
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Woche 5 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Jede binäre Operation hat maximal ein
Einführung in die Theoretische Informatik Woche 5 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Jede binäre Operation hat maximal ein
Logik für Informatiker
 Vorlesung Logik für Informatiker 4. Aussagenlogik Syntax und Semantik der Aussagenlogik Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Syntax der Aussagenlogik:
Vorlesung Logik für Informatiker 4. Aussagenlogik Syntax und Semantik der Aussagenlogik Bernhard Beckert Universität Koblenz-Landau Sommersemester 2006 Logik für Informatiker, SS 06 p.1 Syntax der Aussagenlogik:
Einführung in die funktionale Programmierung
 Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 26. Oktober 2006 Haskell - Einführung Syntax Typen Auswertung Programmierung
Einführung in die funktionale Programmierung Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 26. Oktober 2006 Haskell - Einführung Syntax Typen Auswertung Programmierung
Die Definition eines Typen kann rekursiv sein, d.h. Typ-Konstruktoren dürfen Elemente des zu definierenden Typ erhalten.
 4.5.5 Rekursive Typen Die Definition eines Typen kann rekursiv sein, d.h. Typ-Konstruktoren dürfen Elemente des zu definierenden Typ erhalten. datatype IntList = Nil Cons o f ( i n t IntList ) ; Damit
4.5.5 Rekursive Typen Die Definition eines Typen kann rekursiv sein, d.h. Typ-Konstruktoren dürfen Elemente des zu definierenden Typ erhalten. datatype IntList = Nil Cons o f ( i n t IntList ) ; Damit
Beispiele: Funktionsabstraktion (3) Funktionsdeklaration. Funktionsdeklaration (2) Funktionsdeklaration (3) 3. Abstraktion über Funktionsbezeichner:
 Beispiele: Funktionsabstraktion (3) Funktionsdeklaration 3. Abstraktion über Funktionsbezeichner: Ausdruck: f (f x) Abstraktion: \ f x -> f (f x) Mit Bezeichnervereinbarung: twice = \ f x -> f (f x) erg
Beispiele: Funktionsabstraktion (3) Funktionsdeklaration 3. Abstraktion über Funktionsbezeichner: Ausdruck: f (f x) Abstraktion: \ f x -> f (f x) Mit Bezeichnervereinbarung: twice = \ f x -> f (f x) erg
Mathematische Grundlagen
 Prof. Dr. Peter Becker Fachbereich Informatik Mathematische Grundlagen Klausur Sommersemester 2016 16. September 2016, 1:00 14:0 Uhr Name: Vorname: Matrikelnr.: Unterschrift: Aufgabe 1 2 4 5 6 Summe Punkte
Prof. Dr. Peter Becker Fachbereich Informatik Mathematische Grundlagen Klausur Sommersemester 2016 16. September 2016, 1:00 14:0 Uhr Name: Vorname: Matrikelnr.: Unterschrift: Aufgabe 1 2 4 5 6 Summe Punkte
Behauptung: Wenn f : A -> W und g: W -> V Funktionen sind, dann ist g. f: A->V eine Funktion
 Algorithmen und Programmierung 2. Aufgabenblatt Aufgabe 2.1 a) Jedes Konto besitzt einen Betrag: total Es gibt Konten mit dem gleichen Betrag, aber nicht alle Beträge kommen vor: nicht injektiv und nicht
Algorithmen und Programmierung 2. Aufgabenblatt Aufgabe 2.1 a) Jedes Konto besitzt einen Betrag: total Es gibt Konten mit dem gleichen Betrag, aber nicht alle Beträge kommen vor: nicht injektiv und nicht
5. Äquivalenzrelationen
 36 Andreas Gathmann 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will so kann es sinnvoll sein zunächst kleinere einfachere Mengen (bzw. Gruppen) zu betrachten
36 Andreas Gathmann 5. Äquivalenzrelationen Wenn man eine große und komplizierte Menge (bzw. Gruppe) untersuchen will so kann es sinnvoll sein zunächst kleinere einfachere Mengen (bzw. Gruppen) zu betrachten
Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 3
 Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 3 Die Lösungshinweise dienen
Dipl.Inf. Malte Isberner Dr. Oliver Rüthing Dipl.Inf. Melanie Schmidt Dr. Hubert Wagner Übungen zur Vorlesung Mathematik für Informatiker 1 Wintersemester 2013/14 Übungsblatt 3 Die Lösungshinweise dienen
Grundlagen und Diskrete Strukturen Aufgaben zur Vorbereitung der Klausur
 Technische Universität Ilmenau WS 2008/2009 Institut für Mathematik Informatik, 1.FS Dr. Thomas Böhme Aufgabe 1 : Grundlagen und Diskrete Strukturen Aufgaben zur Vorbereitung der Klausur Gegeben sind die
Technische Universität Ilmenau WS 2008/2009 Institut für Mathematik Informatik, 1.FS Dr. Thomas Böhme Aufgabe 1 : Grundlagen und Diskrete Strukturen Aufgaben zur Vorbereitung der Klausur Gegeben sind die
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16
 Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Mathematik I für Studierende der Informatik und Wirtschaftsinformatik (Diskrete Mathematik) im Wintersemester 2015/16 21. Januar 2016 Definition 8.1 Eine Menge R zusammen mit zwei binären Operationen
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 1-14. Sitzung Dennis Felsing dennis.felsing@student.kit.edu http://www.stud.uni-karlsruhe.de/~ubcqr/2010w/tut gbi/ 2011-02-07 Äquivalenzrelationen 1 Äquivalenzrelationen
Grundbegriffe der Informatik Tutorium 1-14. Sitzung Dennis Felsing dennis.felsing@student.kit.edu http://www.stud.uni-karlsruhe.de/~ubcqr/2010w/tut gbi/ 2011-02-07 Äquivalenzrelationen 1 Äquivalenzrelationen
, 5;8 7,6 8;15;21 4/2,3/1,4 2; 4 3;15 7;7 3,2;3; 32 5,6,7 ; 8,2,1
 Mathematik (BG27) 2 3 { Objekt} { Menge } { Element } { } Reihenfolge spielt keine Rolle Unterscheidbarkeit der Objekte (redundanzfrei) 4 Objekt, 58 7,6 Beschreibung 81521 4/2,3/1,4 2 4 315 77 3,23 32
Mathematik (BG27) 2 3 { Objekt} { Menge } { Element } { } Reihenfolge spielt keine Rolle Unterscheidbarkeit der Objekte (redundanzfrei) 4 Objekt, 58 7,6 Beschreibung 81521 4/2,3/1,4 2 4 315 77 3,23 32
3 Terme und Algebren 3.1 Terme
 3 Terme und Algebren 3.1 Terme Mod - 3.1 In allen formalen Kalkülen benutzt man Formeln als Ausdrucksmittel. Hier betrachten wir nur ihre Struktur - nicht ihre Bedeutung. Wir nennen sie Terme. Terme bestehen
3 Terme und Algebren 3.1 Terme Mod - 3.1 In allen formalen Kalkülen benutzt man Formeln als Ausdrucksmittel. Hier betrachten wir nur ihre Struktur - nicht ihre Bedeutung. Wir nennen sie Terme. Terme bestehen
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 21: Relationen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 21: Relationen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Kontextfreie Sprachen. Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kontextfreie Sprachen
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2012 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Wortproblem: der CYK-Algorithmus Pumping Lemma für kontextfreie Sprachen
Logik I. Symbole, Terme, Formeln
 Logik I Symbole, Terme, Formeln Wie jede geschriebene Sprache basiert die Prädikatenlogik erster Stufe auf einem Alphabet, welches aus den folgenden Symbolen besteht: (a) Variabeln wie zum Beispiel v 0,v
Logik I Symbole, Terme, Formeln Wie jede geschriebene Sprache basiert die Prädikatenlogik erster Stufe auf einem Alphabet, welches aus den folgenden Symbolen besteht: (a) Variabeln wie zum Beispiel v 0,v
Lineare Algebra I 5. Tutorium Die Restklassenringe /n
 Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2011 Lösungsblatt 9 25. Juli 2011 Einführung in die Theoretische Informatik
Ordinalzahlen. Sei (X, ) eine total geordnete Menge und a X. Dann
 Ordinalzahlen Im Rahmen der Ordnungsrelationen wurden bisher die Begriffe Partialordnung und Totalordnung (lineare Ordnung) erwähnt. Ein weiterer wichtiger Ordnungsbegriff ist die Wohlordnung. Wohlgeordnete
Ordinalzahlen Im Rahmen der Ordnungsrelationen wurden bisher die Begriffe Partialordnung und Totalordnung (lineare Ordnung) erwähnt. Ein weiterer wichtiger Ordnungsbegriff ist die Wohlordnung. Wohlgeordnete
Bemerkungen zur Notation
 Bemerkungen zur Notation Wir haben gerade die Symbole für alle und es gibt gebraucht. Dies sind so genannte logische Quantoren, und zwar der All- und der Existenzquantor. Die Formel {a A; ( b B)[(a, b)
Bemerkungen zur Notation Wir haben gerade die Symbole für alle und es gibt gebraucht. Dies sind so genannte logische Quantoren, und zwar der All- und der Existenzquantor. Die Formel {a A; ( b B)[(a, b)
