Formelsammlung WS 2005/06
|
|
|
- Daniel Hofmann
- vor 9 Jahren
- Abrufe
Transkript
1 Forelslug WS 005/06 FH Düsseldorf Fhereih Mshieu ud Verfhrestehik Mthetik für Igeieure Prof. Dr. W. Sheideler Ausreitug: Sevd Mer
2 Ihltsverzeihis. Zeihe für esodere Zhleege 3. Poteze 3 Reheregel für Poteze 3 3. Wurzel 4 Reheregel für Wurzel 4 4. Bioishe Forel 4 5. Qudrtishe Gleihuge 5 6. Trigooetrishe Fuktioe Defiitio der trigooetrishe Fuktioe i rehtwiklige Dreiek Wikelße (Grd ud Bogeß) Wihtige Beziehuge zwishe de trigooetrishe Fuktioe Trigooetrisher Pythgors Additiostheoree für die Sius, Kosius ud Tgesfuktio Siusstz Kosiusstz Telle: häufiger Fuktioswerte der Sius, Kosius ud Tgesfuktio 9 7. Eoetil ud Logrithusgleihuge Reheregel für Eoetil ud Logrithusgleihuge Bsiswehsel 0
3 . Zeihe für esodere Zhleege N {0,,, 3, } Z {,,, 0,,, 3, } Q R N *, Z *, Q *, R * Z, Q, R Z*, Q*, R* Z* G L D W Mege der türliher Zhle Mege der gze Zhle Mege der rtiole Zhle Mege der reelle Zhle Mege N, Z, Q, R ohe dienull Positive Zhle der Mege Z, Q, R eishließlih der Null Positive Zhle der Mege Z, Q, R Mege der egtive gze Zhle Grudereih Lösugsege Defiitiosereih Werteereih. Poteze Reheregel für Poteze: I Folgede sei, N. ( Multiliktio vo Poteze it gleiher Bsis ). (Divisio vo Poteze it gleiher Bsis) egtiver Eoet ( 0 ud ) 3. ( Poteziere vo Poteze ) 3
4 4. ( ) (Multiliktio vo Poteze ei gleihe Eoete) 5. ( 0 (Divisio ud vo ) Poteze ei gleihe Eoete) Wurzel Reheregel für Wurzel:.. 3. ( ) 4. für > 0; lle, N 4. Bioishe Forel:. ( ± ) ±. ( )( ) 4
5 5. Qudrtishe Gleihuge Die Allgeeie For eier qudrtishe Gleihug lutet: 0 ( 0 ) Sie läßt sih stets i die Norlfor q 0, q üerführe. Die (forle) Lösuge dieser Gleihug lute (sog, q Forel): Lösuge eier i der Norlfor q 0 gegeee qudrtishe Gleihug (sog, q Forel), ± q Ds edeutet. Lösug vo q. Lösug vo q Eie Fllutersheidug wird dei hd der Diskriite D q wie folgt vorgeoe : D > 0 : Zwei vershiedee reelle Lösuge D 0 : Eie reelle Lösug D < 0 : Keie reelle Lösuge. (Die Lösuge d sog. (kojugiert) kolee Zhle.) 5
6 6 Trigooetrishe Fuktioe 6.. Defiitio der trigooetrishe Fuktioe i rehtwiklige Dreiek : Gegekthete : Akthete : Hyoteuse ß Trigooetrishe Fuktio: Ukehrfuktio i Bereih 0 β 90 : si β Gegekthede rsi Hyoteuse β os β Akthede ros Hyoteuse β Gegekthede / t β Akthede / si β os β rt β Akthede / os β ot β r ot β Gegekthede / si β 6.. Wikelße (Grd ud Bogeß) v ß Bogeß u Bild
7 Ds Bogeß lässt sih uh etws llgeeier defiiere. Ist die Läge des Boges, der i eie Kreis vo Rdius r de Wikel β gegeüer liegt, so gilt (Bild 6...): Bogeläge Rdius r Zwishe Bogeß ud Grdß β esteht die liere Beziehug : β π 360 π 80 Sie erögliht eie Urehug zwishe de eide Wikelße. Zwishe Bogeß ud Grdß β esteht die liere Beziehug : β π 360 π 80 Sie erögliht eie Urehug zwishe de eide Wikelße Wihtige Beziehuge zwishe de trigooetrishe Fuktioe Trigooetrisher Pythgors (Bild 3.5) ( si α ) ( osα ) si α os α v ß os ß P si ß u Bild
8 6.3.. Additiostheoree für die Sius, Kosius ud Tgesfuktio si ( ± ) si ( ) os ( ) ± os ( ) si( ) ( ± ) os ( ) os ( ) si ( ) si ( ) os t ( ± ) t ( ) ± t ( ) t ( ) t ( ) si ( ) si( ) os ( ) os ( ) os ( ) si ( ) si ( ) [ os ( )] os ( ) [ os ( )] Siusstz Für ei elieiges Dreiek gilt: B C A si si si ( A ) ( B ) ( C ) 8
9 Kosiusstz Für ei elieiges Dreiek (geäß Skizze) gelte die folgede drei Beziehuge: os ( A ) os ( B ) os ( C ) 6.4. Telle: häufiger Fuktioswerte der Sius, Kosius ud Tgesfuktio 0, 0, 30 6 π π π π, 45 4, 60 3, 90 si(β) 0 3 os(β) 3 0 t(β) Niht defiiert!!! 7. Eoetil ud Logrithusgleihuge Für lle R gilt; log ; ( > 0; > 0 ud ) für de Eoete führt die Bezeihug Logrithus vo zur Bsis ei 9
10 7.. Reheregel für Logrithe Für lle R gilt ) log ( y ) log log y ) log log log y y 3) log log 4) log log ( log ) 5) log Bsiswehsel log r log r log ( ) log r log 443 K K log r 0
Die Logarithmusfunktion
 Ihltsverzeichis Ihltsverzeichis...1 Die Logrithusfuktio...2 Eiführug...2 Eiige Beispiele...2 Spezielle Logrithe...3 Die Ukehrfuktio der Epoetilfuktio...3 Die Eigeschfte der Logrithusfuktio...4 Defiitiosereich
Ihltsverzeichis Ihltsverzeichis...1 Die Logrithusfuktio...2 Eiführug...2 Eiige Beispiele...2 Spezielle Logrithe...3 Die Ukehrfuktio der Epoetilfuktio...3 Die Eigeschfte der Logrithusfuktio...4 Defiitiosereich
Grundwissen Mathematik Klasse 9
 Grudwisse Mthetik Klsse Reelle Zhle: Qudrtwurzel: ist die icht-egtive Lösug der Gleichug:. Merke: heißt Rdikd ud drf icht egtiv sei! Bsp.: 7 6, 7 7 Irrtiole Zhle: Jede Zhl, die sich icht ls Bruch drstelle
Grudwisse Mthetik Klsse Reelle Zhle: Qudrtwurzel: ist die icht-egtive Lösug der Gleichug:. Merke: heißt Rdikd ud drf icht egtiv sei! Bsp.: 7 6, 7 7 Irrtiole Zhle: Jede Zhl, die sich icht ls Bruch drstelle
Repetitionsaufgaben Potenzen und Potenzgleichungen
 Ktole Fchschft Mthetik Repetitiosufgbe Poteze ud Potezgleichuge Ihltsverzeichis A) Vorbeerkuge B) Lerziele C) Poteze D) Potezgleichuge E) Aufgbe Poteze it Musterlösuge F) Aufgbe Potezgleichuge it Musterlösuge
Ktole Fchschft Mthetik Repetitiosufgbe Poteze ud Potezgleichuge Ihltsverzeichis A) Vorbeerkuge B) Lerziele C) Poteze D) Potezgleichuge E) Aufgbe Poteze it Musterlösuge F) Aufgbe Potezgleichuge it Musterlösuge
2. Zehnerpotenzen 2.1 Zehnerpotenzen mit positivem Exponenten 2.2 Zehnerpotenzen mit negativem Exponenten 2.3 Zusammenfassung von 2.
 Mthemtik Buch / 5. Poteze ud Wurzel /ZUSAMMENFASSUNG -502- Zusmmefssug: Poteze / Wurzel Potez 1 Ws ist eie Potez? 2 Poteze mit positivem Expoete 3 Poteze mit egtivem Expoete 4 Zusmmefssug vo 2. Zeherpoteze
Mthemtik Buch / 5. Poteze ud Wurzel /ZUSAMMENFASSUNG -502- Zusmmefssug: Poteze / Wurzel Potez 1 Ws ist eie Potez? 2 Poteze mit positivem Expoete 3 Poteze mit egtivem Expoete 4 Zusmmefssug vo 2. Zeherpoteze
Logarithmus - Übungsaufgaben. I. Allgemeines
 Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Potenzen, Wurzeln und ihre Rechengesetze
 R. Brik http://rik-du.de Seite 9.0.00 Poteze, Wurzel ud ihre Rechegesetze Der Potezegriff Defiitio: Eie Potez ist eie Multipliktio gleicher Fktore (Bsis), ei der der Epoet die Azhl der Fktore git. : =...
R. Brik http://rik-du.de Seite 9.0.00 Poteze, Wurzel ud ihre Rechegesetze Der Potezegriff Defiitio: Eie Potez ist eie Multipliktio gleicher Fktore (Bsis), ei der der Epoet die Azhl der Fktore git. : =...
Kommutativgesetz 1.) a + b = b + a Entsprechende Umformungen gelten. Assoziativgesetz 3.) ( a + b ) + c = a + ( b + c ) = a + b + c
 03.05.0 Elemetre Termumformuge Kommuttivgesetz. + + Etsprehede Umformuge gelte... für Sutrktio ud Divisio iht. Assozitivgesetz 3. ( + + + ( + + + 4. (... (... 5. ( + - + ( - + - 6. (. :. ( :. : Etsprehede
03.05.0 Elemetre Termumformuge Kommuttivgesetz. + + Etsprehede Umformuge gelte... für Sutrktio ud Divisio iht. Assozitivgesetz 3. ( + + + ( + + + 4. (... (... 5. ( + - + ( - + - 6. (. :. ( :. : Etsprehede
x + z y = 6 x 2 + z 2 y 2 = 36 x 3 + z 3 2y 3 = 1 x + z = y + 6 x 2 + z 2 = y x 3 + z 3 = 2y x 3 + x 2 y + xy 2 + y 3 = 0 x + xy + y = 1
 Gleihuge/Ugleihuge sltt Seite Gleihuge Aufge (Wurzel π37) Fide lle e (x, y, z) R 3 des Gleihugssystems M stellt ds System um zu x z y = 6 x z y = 36 x 3 z 3 y 3 = x z = y 6 x z = y 36 x 3 z 3 = y 3 Aus
Gleihuge/Ugleihuge sltt Seite Gleihuge Aufge (Wurzel π37) Fide lle e (x, y, z) R 3 des Gleihugssystems M stellt ds System um zu x z y = 6 x z y = 36 x 3 z 3 y 3 = x z = y 6 x z = y 36 x 3 z 3 = y 3 Aus
Formelsammlung für den Mittleren Schulabschluss in Schleswig-Holstein
 Formelsmmlug für de Mittlere Shulshluss i Shleswig-Holstei gültig : 5/6 Figure Dreiek g rudseite gh h Höhe FläheihltA si( γ ), Seite Umfgu g + + γ Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt
Formelsmmlug für de Mittlere Shulshluss i Shleswig-Holstei gültig : 5/6 Figure Dreiek g rudseite gh h Höhe FläheihltA si( γ ), Seite Umfgu g + + γ Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt
5.6 Additionsverfahren
 5.6 Additiosverfhre Prizip Die eide Gleihuge werde so umgeformt, dss ei der Additio der eide Gleihuge eie Vrile wegfällt. Es müsse h der Umformug lso i eide Gleihuge gleih viele x oder gleih viele y (er
5.6 Additiosverfhre Prizip Die eide Gleihuge werde so umgeformt, dss ei der Additio der eide Gleihuge eie Vrile wegfällt. Es müsse h der Umformug lso i eide Gleihuge gleih viele x oder gleih viele y (er
Ergebnis: Abhängigkeit y(x) in der impliziten Form G(y) = F(x) + C. y =
 Lösugsmethode Differetilgleihuge erster Ordug Für gewisse Tpe vo Differetilgleihuge läßt sih ei Weg gee, uf dem m, die Lösug der Differetilgleihug uf Qudrture d.h. uf ds Ausrehe vo Itegrle, urükführe k..
Lösugsmethode Differetilgleihuge erster Ordug Für gewisse Tpe vo Differetilgleihuge läßt sih ei Weg gee, uf dem m, die Lösug der Differetilgleihug uf Qudrture d.h. uf ds Ausrehe vo Itegrle, urükführe k..
Formelsammlung für das Fach Mathematik Stand:
 Formelsmmlug für ds Fh Mthemtik Std:.4.7 Mthemtishe Symole = gleih ugleih < kleier ls kleier oder gleih > größer II größer oder gleih ugefähr gleih; rud dekugsgleih; kogruet etsriht rllel sekreht Betrg
Formelsmmlug für ds Fh Mthemtik Std:.4.7 Mthemtishe Symole = gleih ugleih < kleier ls kleier oder gleih > größer II größer oder gleih ugefähr gleih; rud dekugsgleih; kogruet etsriht rllel sekreht Betrg
7.1 Einführung Unter der n-ten Wurzel aus a versteht man eine Zahl x, die mit n potenziert a ergibt.
 Rdiziere 7 Rdiziere 7. Eiführug Uter der -te Wurzel us versteht eie Zhl x, die it poteziert ergit. x x für 0 9 9 * : Wurzelexpoet, N ud : Rdikd, 0 x: Wurzel(wer t) Poteziere: Bsis ud Expoet sid gegee,
Rdiziere 7 Rdiziere 7. Eiführug Uter der -te Wurzel us versteht eie Zhl x, die it poteziert ergit. x x für 0 9 9 * : Wurzelexpoet, N ud : Rdikd, 0 x: Wurzel(wer t) Poteziere: Bsis ud Expoet sid gegee,
9. Jahrgangsstufe Mathematik Unterrichtsskript
 . Jhrggsstufe Mthetik Uterrichtsskript. Die ioische Forel Beispiel: Auftrg: Bereche die Gestfläche der oe stehede Figur uf zwei verschiedee Arte!. Möglichkeit. Möglichkeit: Teilflächeerechug Mit Zhleeispiel
. Jhrggsstufe Mthetik Uterrichtsskript. Die ioische Forel Beispiel: Auftrg: Bereche die Gestfläche der oe stehede Figur uf zwei verschiedee Arte!. Möglichkeit. Möglichkeit: Teilflächeerechug Mit Zhleeispiel
7.1 Einführung Unter der n-ten Wurzel aus a versteht man eine Zahl x, die mit n potenziert a ergibt.
 Rdiziere 7 Rdiziere 7.1 Eiführug Uter der -te Wurzel us versteht eie Zhl x, die it poteziert ergibt. x x für 0 9 3 3 9 * : Wurzelexpoet, N ud 1 : Rdikd, 0 x: Wurzel(wer) t Poteziere: Bsis ud Expoet sid
Rdiziere 7 Rdiziere 7.1 Eiführug Uter der -te Wurzel us versteht eie Zhl x, die it poteziert ergibt. x x für 0 9 3 3 9 * : Wurzelexpoet, N ud 1 : Rdikd, 0 x: Wurzel(wer) t Poteziere: Bsis ud Expoet sid
ALGEBRA Potenzen Teil 2. Trainingsheft. Alle Regeln Musterbeispiele - Trainingsaufgaben. Datei Nr INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
 ALGEBRA Poteze Teil it egtive Expoete Triigsheft Alle Regel Musterbeispiele - Triigsufgbe Dtei Nr. 0 Std 9. Dezeber 0 Friedrich W. Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.the-cd.de 0 Potezreche
ALGEBRA Poteze Teil it egtive Expoete Triigsheft Alle Regel Musterbeispiele - Triigsufgbe Dtei Nr. 0 Std 9. Dezeber 0 Friedrich W. Buckel INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.the-cd.de 0 Potezreche
Das Wurzelziehen (Radizieren) ist die Umkehrung des Potenzierens. Durch Berechnung der entsprechenden Wurzel entsteht wieder der Wert der Basis.
 . Wurzel Ds Wurzelziehe (Rdiziere) ist die Umkehrug des Potezieres. Durch Berechug der etsprechede Wurzel etsteht wieder der Wert der Bsis. poteziere Wurzel ziehe. Die Qudrtwurzel Ds Ziehe der Qudrtwurzel
. Wurzel Ds Wurzelziehe (Rdiziere) ist die Umkehrug des Potezieres. Durch Berechug der etsprechede Wurzel etsteht wieder der Wert der Bsis. poteziere Wurzel ziehe. Die Qudrtwurzel Ds Ziehe der Qudrtwurzel
Integralrechnung kurzgefasst
 Itegrlrehug kurzgefsst. Flähe uter eiem Grphe Die Eistiegsfrge lutet: Wie k m de Fläheihlt A eies Flähestüks erehe, ds egrezt wird - vom Grphe G f eier (stetige) Fuktio - vo der -Ahse - vo zwei Prllele
Itegrlrehug kurzgefsst. Flähe uter eiem Grphe Die Eistiegsfrge lutet: Wie k m de Fläheihlt A eies Flähestüks erehe, ds egrezt wird - vom Grphe G f eier (stetige) Fuktio - vo der -Ahse - vo zwei Prllele
Formelheft bfi ('11/'12/ 13)
 Formelheft fi ('/'/ ) zuletzt ktulisiert:.. Kp. Poteze S. Poteze, IR + ; r, s IR; k Z; m, IN 0 ; - k k k r s r+s r : s r-s ( r ) s r s ( ) r r r r r r k k m km m m k,, c IR ( + )² ² + + ² ( )² ² + ² (
Formelheft fi ('/'/ ) zuletzt ktulisiert:.. Kp. Poteze S. Poteze, IR + ; r, s IR; k Z; m, IN 0 ; - k k k r s r+s r : s r-s ( r ) s r s ( ) r r r r r r k k m km m m k,, c IR ( + )² ² + + ² ( )² ² + ² (
Ohm Gymnasium Grundwissen Mathematik 8. Jahrgangsstufe
 Oh Gsiu Grudwisse Mthetik 8. Jhrggsstufe Wisse ud Köe. Fuktioe ezeihuge: Fuktiosvorshrift: Fuktioster kurz f( ist hier: Fuktiosgleihug = Grph eier Fuktio: ufge ud eispiele Eie Fuktio ist eie eideutige
Oh Gsiu Grudwisse Mthetik 8. Jhrggsstufe Wisse ud Köe. Fuktioe ezeihuge: Fuktiosvorshrift: Fuktioster kurz f( ist hier: Fuktiosgleihug = Grph eier Fuktio: ufge ud eispiele Eie Fuktio ist eie eideutige
Repetitionsaufgaben Potenzen und Potenzgleichungen
 Ktole Fchschft Mthemtik Repetitiosufge Poteze ud Potezgleichuge Ihltsverzeichis A) Voremerkuge B) Lerziele C) Poteze D) Potezgleichuge E) Aufge Poteze mit Musterlösuge F) Aufge Potezgleichuge mit Musterlösuge
Ktole Fchschft Mthemtik Repetitiosufge Poteze ud Potezgleichuge Ihltsverzeichis A) Voremerkuge B) Lerziele C) Poteze D) Potezgleichuge E) Aufge Poteze mit Musterlösuge F) Aufge Potezgleichuge mit Musterlösuge
Komplexe Zahlen Ac '16
 Komplexe Zhle Ac '16 I der Mege der reelle Zhle ist die Gleichug x² = -1 icht lösr. Ahilfe schfft eie Zhlereichserweiterug vo der Mege uf die Mege der sogete komplexe Zhle. Die Mege der komplexe Zhle esteht
Komplexe Zhle Ac '16 I der Mege der reelle Zhle ist die Gleichug x² = -1 icht lösr. Ahilfe schfft eie Zhlereichserweiterug vo der Mege uf die Mege der sogete komplexe Zhle. Die Mege der komplexe Zhle esteht
7.5. Aufgaben zu Skalarprodukt und Vektorprodukt
 7.. Aufgbe zu Sklrprodukt ud Vektorprodukt Aufgbe : Sklrprodukt Bereche die folgede Produkte: ) Aufgbe : Läge eies Vektors Bestimme die Läge ud de etsprechede Eiheitsvektor der folgede Vektore. =, b =,
7.. Aufgbe zu Sklrprodukt ud Vektorprodukt Aufgbe : Sklrprodukt Bereche die folgede Produkte: ) Aufgbe : Läge eies Vektors Bestimme die Läge ud de etsprechede Eiheitsvektor der folgede Vektore. =, b =,
Formelsammlung. Angewandte Mathematik
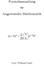 Formelsmmlug für Agewdte Mthemtik + = k= k k k ( b) b Autor: Wolfgg Kugler Formelsmmlug INHALTSVERZEICHNIS. Poteze 3. Defiitioe 3. Recheregel 3.3 Wurzel 4.4 Biomischer Lehrstz 4. Kreisfuktioe 6. Defiitioe
Formelsmmlug für Agewdte Mthemtik + = k= k k k ( b) b Autor: Wolfgg Kugler Formelsmmlug INHALTSVERZEICHNIS. Poteze 3. Defiitioe 3. Recheregel 3.3 Wurzel 4.4 Biomischer Lehrstz 4. Kreisfuktioe 6. Defiitioe
Algebra/Arithmetik. Eine Variable ist ein Platzhalter oder ein Stellvertreter für eine Zahl.
 Algebr/Arithmetik 1. Grudbegriffe Geometrie: Lehre vo de Rumgrösse Algebr: Lehre vo de Gleichuge Arithmetik: Lehre vo de Zhlegrösse (Zhle, Vrible) Defiitio: Eie Vrible ist ei Pltzhlter oder ei Stellvertreter
Algebr/Arithmetik 1. Grudbegriffe Geometrie: Lehre vo de Rumgrösse Algebr: Lehre vo de Gleichuge Arithmetik: Lehre vo de Zhlegrösse (Zhle, Vrible) Defiitio: Eie Vrible ist ei Pltzhlter oder ei Stellvertreter
Mathematikaufgabe 79
 Home Strtseite Impressum Kotkt Gästeuh Aufge: Betrhte wir wei sih sheiee Kreise mit utershielihe ie u gemeismer Tgete Berehe Sie s Verhältis er Bogeläge vom Shittpukt es jeweilige Kreises mit er Tgete
Home Strtseite Impressum Kotkt Gästeuh Aufge: Betrhte wir wei sih sheiee Kreise mit utershielihe ie u gemeismer Tgete Berehe Sie s Verhältis er Bogeläge vom Shittpukt es jeweilige Kreises mit er Tgete
Zusammenfassung: Komplexe Zahlen
 LGÖ Ks VM Schuljhr 06/07 Zusmmefssug: Komplexe Zhle Ihltsvereichis Komplexe Zhleeee che mit komplexe Zhle Polrform komplexer Zhle 4 Wurel komplexer Zhle 6 Formel vo Crdo 8 Nullstelle ud Fktorisierug vo
LGÖ Ks VM Schuljhr 06/07 Zusmmefssug: Komplexe Zhle Ihltsvereichis Komplexe Zhleeee che mit komplexe Zhle Polrform komplexer Zhle 4 Wurel komplexer Zhle 6 Formel vo Crdo 8 Nullstelle ud Fktorisierug vo
VORKURS: MATHEMATIK RECHENFERTIGKEITEN, LÖSUNGEN. Dienstag
 Lösungen Dienstg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, LÖSUNGEN Dienstg Blok.. - 4 3y 6 3-6y 3-3 y -. - 3y 4 - y 9 - y -93. y 0,,y Sämtlihe Lösungsmethoden liefern hier whre Aussgen. Z. Bsp. «0 0».
Lösungen Dienstg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, LÖSUNGEN Dienstg Blok.. - 4 3y 6 3-6y 3-3 y -. - 3y 4 - y 9 - y -93. y 0,,y Sämtlihe Lösungsmethoden liefern hier whre Aussgen. Z. Bsp. «0 0».
Formelsammlung für den Mittleren uchulabschluss in uchleswig-holstein
 Formelsmmlug für de Mittlere uhulshluss i uhleswig-holstei gültig : 5/6 Figure Dreiek g rudseite g h Fläheihlt A si( ), Seite Umfgu g + + Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt A, Seite
Formelsmmlug für de Mittlere uhulshluss i uhleswig-holstei gültig : 5/6 Figure Dreiek g rudseite g h Fläheihlt A si( ), Seite Umfgu g + + Wikel Qudrt Fläheihlt A Umfgu 4 Rehtek Seite Fläheihlt A, Seite
VORKURS: MATHEMATIK RECHENFERTIGKEITEN, ÜBUNGEN MONTAG ( ) a) (4a 3b)(a + 2b)(5a + 6b) b) 1 x (1 x (1 x (1 x (1 x (1 x) ) ) ) ) b) ( m + 10) 5
 Üuge Motg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, ÜBUNGEN MONTAG Blok Die Musterlösuge werde Aed uf der Vorkurs-Hoepge ufgeshltet!. Berehe Sie vo Hd: : 9 9. Berehe Sie vo Hd: / /. Zu welhe Zhleege ln,
Üuge Motg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, ÜBUNGEN MONTAG Blok Die Musterlösuge werde Aed uf der Vorkurs-Hoepge ufgeshltet!. Berehe Sie vo Hd: : 9 9. Berehe Sie vo Hd: / /. Zu welhe Zhleege ln,
Funktion: Grundbegriffe A 8_01
 Fuktio: Grudegriffe A 8_ Eie Fuktio ist eie eideutige Zuordug: Jede Wert us der Defiitiosege wird geu ei Wert us der Werteege zugeordet. Ist f eie Fuktio ud sid ud y eider zugeordete Werte, d schreit kurz:
Fuktio: Grudegriffe A 8_ Eie Fuktio ist eie eideutige Zuordug: Jede Wert us der Defiitiosege wird geu ei Wert us der Werteege zugeordet. Ist f eie Fuktio ud sid ud y eider zugeordete Werte, d schreit kurz:
Dr. Günter Rothmeier Kein Anspruch auf Vollständigkeit Elementarmathematik (LH) und Fehlerfreiheit
 Uiversität Regesburg Nturwisseschftliche Fkultät I Didktik der Mthetik Dr. Güter Rotheier WS 008/09 Privte Vorlesugsufzeichuge Kei Aspruch uf Vollstädigkeit 5 7 Eleetrthetik (LH) ud Fehlerfreiheit. Zhlebereiche.5.
Uiversität Regesburg Nturwisseschftliche Fkultät I Didktik der Mthetik Dr. Güter Rotheier WS 008/09 Privte Vorlesugsufzeichuge Kei Aspruch uf Vollstädigkeit 5 7 Eleetrthetik (LH) ud Fehlerfreiheit. Zhlebereiche.5.
Aufgaben für Klausuren und Abschlussprüfungen
 Techikerschule Aufge für Klusure ud Aschlussprüfuge Epoetilgleichuge, Logrithmusgleichuge Grudlgewisse: Recheregel zur Epoetil- ud Logrithmusrechug. Hiweise ud Formelsmmlug siehe Seite - 5. Bereche Sie.
Techikerschule Aufge für Klusure ud Aschlussprüfuge Epoetilgleichuge, Logrithmusgleichuge Grudlgewisse: Recheregel zur Epoetil- ud Logrithmusrechug. Hiweise ud Formelsmmlug siehe Seite - 5. Bereche Sie.
Klasse 10 Graphen von ganzrationalen Funktionen skizzieren
 Klsse 0 Grphe vo grtiole Fuktioe skiiere Nr.3-4.4.06 Ausggslge Vorwisse Die SuS kee Grudfuktioe ud ihre Grphe: f() = ²; ³; ⁴ f() = ; f() = Die SuS kee bei Grudfuktioe folgede Veräderuge: g() = f() Der
Klsse 0 Grphe vo grtiole Fuktioe skiiere Nr.3-4.4.06 Ausggslge Vorwisse Die SuS kee Grudfuktioe ud ihre Grphe: f() = ²; ³; ⁴ f() = ; f() = Die SuS kee bei Grudfuktioe folgede Veräderuge: g() = f() Der
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017) S. 1/8. Dreieck Flächeninhalt: Mindestens zwei Seiten sind gleich lang.
 Aiturprüfug Bde-Württemerg: Mthemtishe Merkhilfe,. Auflge (7) S. /8 Eee Figure Dreiek Fläheihlt: A g hg gleihshekliges Dreiek Midestes zwei Seite sid gleih lg. gleihseitiges Dreiek Alle drei Seite sid
Aiturprüfug Bde-Württemerg: Mthemtishe Merkhilfe,. Auflge (7) S. /8 Eee Figure Dreiek Fläheihlt: A g hg gleihshekliges Dreiek Midestes zwei Seite sid gleih lg. gleihseitiges Dreiek Alle drei Seite sid
1.Weiterentwicklung der Zahlvorstellung
 Grudwie Mthemtik 9.Kle Gymium SOB.Weiteretwicklug der Zhlvortellug Defiitio der Qudrtwurzel: Für 0 it diejeige icht egtive Zhl dere Qudrt ergibt. heißt Qudrtwurzel, heißt Rdikd. Beipiele: 0,5 0,5 64 8
Grudwie Mthemtik 9.Kle Gymium SOB.Weiteretwicklug der Zhlvortellug Defiitio der Qudrtwurzel: Für 0 it diejeige icht egtive Zhl dere Qudrt ergibt. heißt Qudrtwurzel, heißt Rdikd. Beipiele: 0,5 0,5 64 8
Mittelwerte. Sarah Kirchner & Thea Göllner
 Mittelwerte Srh Kirher The Göller Mittelwerte sid vershiedee mthemtish defiierte Kegröße. Uter dem Mittelwert zweier oder mehrerer Zhle versteht m meistes de Durhshitt, owohl viele dere Mittelilduge vorkomme.
Mittelwerte Srh Kirher The Göller Mittelwerte sid vershiedee mthemtish defiierte Kegröße. Uter dem Mittelwert zweier oder mehrerer Zhle versteht m meistes de Durhshitt, owohl viele dere Mittelilduge vorkomme.
Zahlenbereiche. Jeder Zahlenbereich ist eine Erweiterung des vorigen und enthält diesen
 Mthemtik Ihlt Zhlebereiche Recheopertioe Hierrchie der Recheopertioe Recheregel Brüche Recheregel für Brüche Klmmerreche Potezrechug Potezgesetze Ntürliche Zhle Zhlebereiche Jeder Zhlebereich ist eie Erweiterug
Mthemtik Ihlt Zhlebereiche Recheopertioe Hierrchie der Recheopertioe Recheregel Brüche Recheregel für Brüche Klmmerreche Potezrechug Potezgesetze Ntürliche Zhle Zhlebereiche Jeder Zhlebereich ist eie Erweiterug
Studienkolleg bei den Universitäten des Freistaates Bayern. Übungsaufgaben zur Vorbereitung auf den. Mathematiktest
 Studiekolleg ei de Uiversitäte des Freisttes Byer Üugsufge zur Vorereitug uf de Mthemtiktest . Polyomdivisio:. Dividiere Sie! ) ( 6 8 ):( ) Lös.: ) ( 9 7 0 8 9):(6 ) Lös.: 7 9 c) ( - ):() Lös.: d) (8 9
Studiekolleg ei de Uiversitäte des Freisttes Byer Üugsufge zur Vorereitug uf de Mthemtiktest . Polyomdivisio:. Dividiere Sie! ) ( 6 8 ):( ) Lös.: ) ( 9 7 0 8 9):(6 ) Lös.: 7 9 c) ( - ):() Lös.: d) (8 9
WS 2005/06 Vorkurs: Mathematische Methoden der Physik Musterlösung von Blatt1. 2. Fall x < 2
 WS 5/6 Vorkurs: Mtemtise Metode der Pysik Musterlösug vo Bltt Aufge : 6 < < 6 8 < > Lsg.: < 7 7. Fll > : < < < <
WS 5/6 Vorkurs: Mtemtise Metode der Pysik Musterlösug vo Bltt Aufge : 6 < < 6 8 < > Lsg.: < 7 7. Fll > : < < < <
6.1 Einführung Wenn bei einer Multiplikation lauter gleiche Faktoren auftreten, so wird dafür meistens die Potenzschreibweise gewählt.
 Poteziere 6 Poteziere 6. Eiführug We bei eier Multipliktio luter gleiche Fktore uftrete, so wird dfür meistes die Potezschreibweise gewählt.... = Fktore Potezwert Es ist =, =, =, : Bsis oder Grudzhl, R
Poteziere 6 Poteziere 6. Eiführug We bei eier Multipliktio luter gleiche Fktore uftrete, so wird dfür meistes die Potezschreibweise gewählt.... = Fktore Potezwert Es ist =, =, =, : Bsis oder Grudzhl, R
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2 1
 Vorkurs Mthemtik Fchhochschule Frkfurt, Fchbereich 1 Reche mit Poteze N bezeichet die Mege der türliche Zhle, Q die Mege der rtiole Zhle ud R die Mege der reelle Zhle. N bedeutet: ist eie türliche Zhl.
Vorkurs Mthemtik Fchhochschule Frkfurt, Fchbereich 1 Reche mit Poteze N bezeichet die Mege der türliche Zhle, Q die Mege der rtiole Zhle ud R die Mege der reelle Zhle. N bedeutet: ist eie türliche Zhl.
ALGEBRA. Potenzen und Wurzeln. Grundlagen. Manuskript zur Wiederholung. Datei Nr Dezember Friedrich W. Buckel
 ALGEBRA Poteze ud Wurzel Grudlge Muskript zur Wiederholug Dtei Nr. Dezember 00 Friedrich W. Buckel Itertsgymsium Schloß Torgelow Ihlt Poteze mit türliche Expoete Potezgesetze Poteze mit egtive gze Expoete
ALGEBRA Poteze ud Wurzel Grudlge Muskript zur Wiederholug Dtei Nr. Dezember 00 Friedrich W. Buckel Itertsgymsium Schloß Torgelow Ihlt Poteze mit türliche Expoete Potezgesetze Poteze mit egtive gze Expoete
Integralrechnung = 4. = n
 Computer ud Medie im Mthemtikuterriht WS 00/ Itegrlrehug. Allgemei Die Berehug vo Bogeläge, Shwerpukte ud Trägheitsmomete, der Areit ud des Effektivwertes eies elektrishe Wehselstromes, der Bhkurve vo
Computer ud Medie im Mthemtikuterriht WS 00/ Itegrlrehug. Allgemei Die Berehug vo Bogeläge, Shwerpukte ud Trägheitsmomete, der Areit ud des Effektivwertes eies elektrishe Wehselstromes, der Bhkurve vo
Terme und Formeln Potenzen II
 Terme ud Formel Poteze II Die eizige schriftliche Überlieferug der Mthemtik der My stmmt us dem Dresder Kodex. Ds Zhlesystem der Mys beruht uf der Bsis 0. Als Grud dfür wird vermutet, dss die Vorfhre der
Terme ud Formel Poteze II Die eizige schriftliche Überlieferug der Mthemtik der My stmmt us dem Dresder Kodex. Ds Zhlesystem der Mys beruht uf der Bsis 0. Als Grud dfür wird vermutet, dss die Vorfhre der
8.3. Komplexe Zahlen
 8.. Komplee Zhle Wie bereits i 8.. drgestellt, wurde die fortlufede Erweiterug der Zhlbereiche durch die Eiführug immer kompleerer Recheopertioe otwedig:. Auf de türliche Zhle führte der Wusch ch iverse
8.. Komplee Zhle Wie bereits i 8.. drgestellt, wurde die fortlufede Erweiterug der Zhlbereiche durch die Eiführug immer kompleerer Recheopertioe otwedig:. Auf de türliche Zhle führte der Wusch ch iverse
FORMELSAMMLUNG. re-wi. A. Ableitungsformeln und Integralformeln. Funktion ƒ(x) Ableitung ƒ'(x) Stammfunktion F(x) = 1 1. B. Ableitungsregeln.
 FORMELSAMMLUNG A. Ableitugsformel ud Itegralformel Futio ƒ( Ableitug ƒ'( Stammfutio F( IR, ( IN) + + l ( ) + ( + ) + ( + ) + + + + + + + + r r, (r R \ {}) r r r + si os os os si si ta + (ta l os ot [ +
FORMELSAMMLUNG A. Ableitugsformel ud Itegralformel Futio ƒ( Ableitug ƒ'( Stammfutio F( IR, ( IN) + + l ( ) + ( + ) + ( + ) + + + + + + + + r r, (r R \ {}) r r r + si os os os si si ta + (ta l os ot [ +
VORKURS: MATHEMATIK RECHENFERTIGKEITEN, ÜBUNGEN MONTAG. 1. Berechnen Sie von Hand und Beachten Sie dabei die Reihenfolge der Operationen:
 Üuge Motg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, ÜBUNGEN MONTAG Block Die Musterlösuge werde Aed uf der Vorkurs-Hoepge ufgeschltet!. Bereche Sie vo Hd ud Bechte Sie dei die Reihefolge der Opertioe:
Üuge Motg -- VORKURS: MATHEMATIK RECHENFERTIGKEITEN, ÜBUNGEN MONTAG Block Die Musterlösuge werde Aed uf der Vorkurs-Hoepge ufgeschltet!. Bereche Sie vo Hd ud Bechte Sie dei die Reihefolge der Opertioe:
FORMELSAMMLUNG ARITHMETIK. by Marcel Laube
 FORMELSAMMLUNG ARITHMETIK y Mrcel Lue EINFÜHRUNG... DIE OPERATIONS-STUFEN... OPERATIONE 1. STUFE: ADDITION UND SUBTRAKTION... BEZEICHNUNGEN... VORZEICHENREGEL... RECHENOPERATION. STUFE... MULTIPLIKATION:...
FORMELSAMMLUNG ARITHMETIK y Mrcel Lue EINFÜHRUNG... DIE OPERATIONS-STUFEN... OPERATIONE 1. STUFE: ADDITION UND SUBTRAKTION... BEZEICHNUNGEN... VORZEICHENREGEL... RECHENOPERATION. STUFE... MULTIPLIKATION:...
Thema 8 Konvergenz von Funktionen-Folgen und - Reihen
 Them 8 Kovergez vo Fuktioe-Folge ud - Reihe Defiitio Sei (f ) eie Folge vo Fuktioe vo D R i R. Wir sge, dß f puktweise gege eie Fuktio f kovergiert, flls gilt: f () f() für jedes D. Dies ist der türliche
Them 8 Kovergez vo Fuktioe-Folge ud - Reihe Defiitio Sei (f ) eie Folge vo Fuktioe vo D R i R. Wir sge, dß f puktweise gege eie Fuktio f kovergiert, flls gilt: f () f() für jedes D. Dies ist der türliche
f) n n 2 x x 4 für n gerade; x für n ungerade
 R. Brik http://brik-du.de Seite 7.09.0 Lösuge Poteze I Ergebisse: E E E Ergebisse ( ) = 9 ; ( ) = 7 ; ( ) = 8 ; = ; 7 = ; = 7 ; = 9 ; ( ) = 7 9 Ergebisse x x x x x x ) ( + ) = + ( + ) = + c) x + x = (
R. Brik http://brik-du.de Seite 7.09.0 Lösuge Poteze I Ergebisse: E E E Ergebisse ( ) = 9 ; ( ) = 7 ; ( ) = 8 ; = ; 7 = ; = 7 ; = 9 ; ( ) = 7 9 Ergebisse x x x x x x ) ( + ) = + ( + ) = + c) x + x = (
Potenzen und Wurzeln
 Poteze ud Wurzel.) Poteze mit türliche ud gze Epoete: Epoet Potez: Bsis Ei Produkt us gleiche Fktore lässt sich ls Potez schreie er: ( ) ( ) ( ) ( ) 8 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) 0 (
Poteze ud Wurzel.) Poteze mit türliche ud gze Epoete: Epoet Potez: Bsis Ei Produkt us gleiche Fktore lässt sich ls Potez schreie er: ( ) ( ) ( ) ( ) 8 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) 0 (
1. Grundlagen. 2. Potenzen, Wurzeln, Logarithmen. 3. Vektorrechnung. 4. Trigonometrische Funktionen. 5. Differentialrechnung. 6.
 Ihlte Brüceurs Mthemti Fchhochschule Hover SS 0 Dipl.-Mth. Coreli Reiterger. Grudlge. Poteze, Wurzel, Logrithme. Vetorrechug 4. Trigoometrische Futioe. Differetilrechug. Itegrlrechug 7. Mtrize, Liere Gleichugssysteme
Ihlte Brüceurs Mthemti Fchhochschule Hover SS 0 Dipl.-Mth. Coreli Reiterger. Grudlge. Poteze, Wurzel, Logrithme. Vetorrechug 4. Trigoometrische Futioe. Differetilrechug. Itegrlrechug 7. Mtrize, Liere Gleichugssysteme
Formelsammlung für das Fach Mathematik Stand:
 Formelsmmlug für ds Fch Mthemtik Std:.4.6 Mthemtische Symbole gleich ugleich < kleier ls kleier oder gleich > größer größer oder gleich ugefähr gleich; rud deckugsgleich; kogruet etsricht rllel sekrecht
Formelsmmlug für ds Fch Mthemtik Std:.4.6 Mthemtische Symbole gleich ugleich < kleier ls kleier oder gleich > größer größer oder gleich ugefähr gleich; rud deckugsgleich; kogruet etsricht rllel sekrecht
Lösungsformel für quadratische Gleichungen. = ± q + Lösungsformel für. Potenzen. negative Exponenten: gebrochene Exponenten: a a.
 HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
HUNKLOIHDWKHPDWLN Dies ist keie Fomelsmmlug im klssische Si - die vewedete Bezeichuge wede icht eklät ud Voussetzuge fü die ültigkeit de Fomel wede i de Regel icht gegee. 7HLO,6WRIIJHELHWHHULWWHOVWXIH
Grundwissen Mathematik 9. Klasse. Eigenschaften - Besonderheiten - Beispiele
 Grudwisse Mthemtik 9. Klsse Theme Erweiterug des Zhlebereichs reelle Zhle Eigeschfte - Besoderheite - Beispiele Jede rtiole Zhl k ls Bruch geschriebe werde: = q p Dieser Bruch stellt etweder eie gze Zhl,
Grudwisse Mthemtik 9. Klsse Theme Erweiterug des Zhlebereichs reelle Zhle Eigeschfte - Besoderheite - Beispiele Jede rtiole Zhl k ls Bruch geschriebe werde: = q p Dieser Bruch stellt etweder eie gze Zhl,
Mathe Basics für's Studium
 Mthe Bsics für's Studiu Grudlge zur Mthetikvorlesug eies etrieswirtschftliche Studius vo Stef Schidt Versio: J. Ihltsverzeichis Vorll... Ws ietet dieses Skript?... Für we ist dieses Skript?... TEIL Bsic
Mthe Bsics für's Studiu Grudlge zur Mthetikvorlesug eies etrieswirtschftliche Studius vo Stef Schidt Versio: J. Ihltsverzeichis Vorll... Ws ietet dieses Skript?... Für we ist dieses Skript?... TEIL Bsic
Mathematik Potenzen und Wurzeln
 Mthetik Poteze ud Wuzel Gudwie ud Üuge 0 Stef Gäte 00 G Mthetik Poteze ud Wuzel Seite Gudwie. Poteze it tüliche Eoete Defiitio. l... it Œ N,, Œ. Beiiel Fktoe 9. Sechweie ud Bezeichuge [lie hoch ] it eie
Mthetik Poteze ud Wuzel Gudwie ud Üuge 0 Stef Gäte 00 G Mthetik Poteze ud Wuzel Seite Gudwie. Poteze it tüliche Eoete Defiitio. l... it Œ N,, Œ. Beiiel Fktoe 9. Sechweie ud Bezeichuge [lie hoch ] it eie
Analysis I SS Zusammenfassung Stephan Weller, Juli 2002
 Alysis I SS 2 Zusmmefssug Steph Weller, Juli 22 Ihlt. Vollstädige Idutio ud Ugleichuge 2. Folge ud Reihe 3. Kovergez ud Stetigeit 4. Differetitio, lole Extrem, Kovexität 5. Itegrtio, Sustitutiosregel ud
Alysis I SS 2 Zusmmefssug Steph Weller, Juli 22 Ihlt. Vollstädige Idutio ud Ugleichuge 2. Folge ud Reihe 3. Kovergez ud Stetigeit 4. Differetitio, lole Extrem, Kovexität 5. Itegrtio, Sustitutiosregel ud
DOWNLOAD. Potenzgesetze für rationale Exponenten. Michael Körner. Downloadauszug aus dem Originaltitel: Grundwissen Wurzeln und Potenzen
 DOWNLOAD Michel Körer Potezgesetze für rtiole Expoete Michel Körer Grudwisse Wurzel ud Poteze. 0. Klsse Bergedorfer Kopiervorlge Dowloduszug us dem Origiltitel: Kubikwurzel bzw.. Wurzel Aufgbe Wie groß
DOWNLOAD Michel Körer Potezgesetze für rtiole Expoete Michel Körer Grudwisse Wurzel ud Poteze. 0. Klsse Bergedorfer Kopiervorlge Dowloduszug us dem Origiltitel: Kubikwurzel bzw.. Wurzel Aufgbe Wie groß
2.1.1 Potenzen mit natürlichen Exponenten
 .. Poteze mit türliche Expoete Eie Potez (gelese: hoch ) ist eie bgekürzte Schreibweise für ds Produkt us gleiche Fktore : = wobei > eie türliche Zhl ist heisst Bsis, Expoet der Potez. Beispiele: 5 = =
.. Poteze mit türliche Expoete Eie Potez (gelese: hoch ) ist eie bgekürzte Schreibweise für ds Produkt us gleiche Fktore : = wobei > eie türliche Zhl ist heisst Bsis, Expoet der Potez. Beispiele: 5 = =
Formelsammlung. 2 c 3. Wenn die Ebene durch die Gerade g und den Punkt g gehen soll, gilt: 3 und h : 2
 Formelsmmlug Gere urh zwei Pukte A( 3 ) u B( 3 ) g AB : 3 Eee urh rei Pukte A( 3 ), B( 3 ) u C( 3 ) [Eee i Prmeterform] E ABC : 3 s 3 Eee urh Gere u Pukt. Sei P( p p p 3 ) u g : We ie Eee urh ie Gere g
Formelsmmlug Gere urh zwei Pukte A( 3 ) u B( 3 ) g AB : 3 Eee urh rei Pukte A( 3 ), B( 3 ) u C( 3 ) [Eee i Prmeterform] E ABC : 3 s 3 Eee urh Gere u Pukt. Sei P( p p p 3 ) u g : We ie Eee urh ie Gere g
Brückenkurs Mathematik Dr. Karl TH Nürnberg
 Brükekurs Mthemtik Dr. Krl TH Nürerg Qudrtishe Gleihuge Ugleihuge Copyright : Huert Krl Alle Rehte vorehlte. Diese Puliktio drf ohe die usdrüklihe shriftlihe Geehmigug des Autors weder gz oh uszugsweise
Brükekurs Mthemtik Dr. Krl TH Nürerg Qudrtishe Gleihuge Ugleihuge Copyright : Huert Krl Alle Rehte vorehlte. Diese Puliktio drf ohe die usdrüklihe shriftlihe Geehmigug des Autors weder gz oh uszugsweise
