Inhaltsverzeichnis Thermodynamik
|
|
|
- Bella Schulze
- vor 9 Jahren
- Abrufe
Transkript
1 Inhaltsverzeichnis 1 Thermodynamik Temperatur und Wärme, Arbeit Grundbegriffe Erster Hauptsatz der Thermodynamik Wärmeübertragung Kinetische Gastheorie Grundbegriffe, Definitionen Statistische Mechanik Zusammenfassung der Prozesse Reale Gase Entropie und der zweite Hauptsatz der Thermodynamik Zur Berechnung von S Kreisprozesse
2 1 Thermodynamik 1.1 Temperatur und Wärme, Arbeit Grundbegriffe Kelvin-Skala: Absolute Skala, definiert über Helium-Druck. 0 K ˆ= C Celsius-Skala: An alltägliche Bedürfnisse, über Schmelz- und Siedepunkt von Wasser angepasste Skala. 0 C: Schmelzpunkt von Wasser 100 C: Siedepunkt von Wasser Definition 1 (Thermische Ausdehnung) Aufgrund der Molekularbewegung stoßen sich Atome bei größeren Temperaturen stärker ab = Material dehnt sich aus nach: L = α L T α : Längenausdehnungskoeff. (1.1) Analog: V = β V T β : Volumenausdehnungskoeff. (1.) wobei, i.a. β = 3α gilt. Bemerkung 1 α und β müssen nicht konstant sein, siehe Wasser: β < 0 für 0 C < T < 4 C. Definition (Wärme) ist thermische Energie, oder genauer Wärme ist die aufgrund einer Temperaturdifferenz zweier Körper zwischen Ihnen übertragene Energie. Konvention: Q > 0, wenn dem System Energie zugeführt wird. Q < 0, wenn dem System Energie entzogen wird. Definition 3 (Wärmekapazität) (Abstrakte) Definition über Q = C T, [C] = J/K. Praktischer: Materialspezifische Wärmekapazität: Q = m c T, c = J kg K (1.3) Molare Wärmekapazität: Q = n c mol T, c mol = J mol K (1.4) Definition 4 (Latente Wärme) Bei Phasenübergängen nimmt ein Stoff Wärme auf bzw. gibt sie ab, ohne seine Temperatur zu ändern. Die Energie wird z.b. aufgewendet, um den Stoff nach und nach verdampfen zu lassen (Verdampfungsenergie) oder die Energie wird der gasförmigen Phase nach und nach entzogen, woraufhin diese kondensiert. Diese Energie nennt man latente Wärme. 1
3 1 Thermodynamik Deswegen kann Wasser in einem normalen Topf nicht über 100 C erwärmt werden. Alle Moleküle über 100 C verdampfen und verlassen den Topf. Definition 5 (Wärme) Ein Gas kann bei einer Volumenänderung Arbeit verrichten, bspw.: hebt ein Gas durch Ausdehnung einen Behälter an, wird für einen infinitesimalen Weg die Arbeit: dw = F ds = p A ds = p dv (1.5) verrichtet, woraus folgt: W = dw = V V 1 p dv. (1.6) Dies gilt immer es muss nur eine Druckfunktion bekannt sein Erster Hauptsatz der Thermodynamik Wärme und Arbeit, W und Q, genauer W und Q, hängen vom jeweiligen Prozess ab, jedoch ist die Änderung der inneren Energie U wegunabhängig: HIER: U = Q + W. Wichtige Spezialfälle: U = Q ± W, (bzw. du = dq ± dw ). (1.7) ± hängt von der Definition der Richtung der Wärme ab. + : Arbeit ist bei Zufuhr (dem System) positiv (Meyer-Skript). : Arbeit ist bei Abfuhr (aus dem System) negativ (Halliday). Adiabatische Expansion: Prozess wird so schnell oder so isoliert ausgeführt, dass keine Wärme mit der Umgebung ausgetauscht wird: Q = 0 U = W. Isochore Zustandsänderung(V = const.): pdv = 0 U = Q. Kreisprozess: Der Ausgangspunkt wird immer wieder hergestellt, also U = 0 Q = W Freie Expansion: Ein isoliertes Gas dehnt sich in einen isolierten Freiraum aus: adiabatischer Prozess = Q = 0 kein Gegendruck = W = 0 Ein solcher Prozess kann nicht langsam oder kontrolliert ausgeführt werden Wärmeübertragung Definition 6 (Wärmeleitung) Zwei Materiale sind über einen Wärmeleiter der Dicke L, Kontaktfläche A und Wärmeleitkoeff. λ verbunden. Dann gilt für die übertragene Wärmeleistung: P = dq dt = λ AT heiss T kalt, [P ] = J/sec, [λ] = W L m K, (1.8) bzw. dq dt = λa dt dx.
4 1. Kinetische Gastheorie Bemerkung Wärmewiderstand: R Q = L λa T = R Q dq dt (analog zu U = R I ) Definition 7 (Konvektion) Wärmetransport durch Auftrieb aufgrund unterschiedlich dichter Gasschichten resultierend in einen Temperaturgradienten. Definition 8 (Wärmestrahlung) Jeder Körper mit T Strahlung aus. > 0K strahlt Energie in Form von EM- Das Spektrum dieser Strahlung ist gegeben durch das Planck sche Strahlungsgesetz. Integriert man über das gesamte Frequenzspektrum, so findet man: P rad = σ ɛ A T 4 K Stefan-Boltzmann-Gesetz (1.9) mit der Stefan-Boltzmann-Konstante σ = W m K 4, der Fläche A des strahlenden Körper, dessen Temperatur T K und dem Emissionsgrad ɛ [0, 1]. Für ɛ = 1 liegt ein Schwarzer Körper vor. Nach dem Kirchhoff schen Strahlungsgesetz sind Emissions- und Absorptionsgrad gleich. Ein schwarzer Körper ist also ein perfekter Strahler und Absorber. Analog: Ein Körper absorbiert Strahlung aus seiner Umgebung mit der Temperatur T gemäß: Die Differenz der abgestrahlten und absorbierten Leistung ist also: P abs = σ ɛ A T 4 Umg. (1.10) P = σ ɛ A (T 4 K T 4 Umg). (1.11) Das Maximum der Strahlungskurve verschiebt sich mit der Temperatur gemäß λ max = 898.7µmK T Wien sches Verschiebungsgesetz (1.1) 1. Kinetische Gastheorie 1..1 Grundbegriffe, Definitionen Definition 9 (Avogadro-Zahl) Anzahl der Teilchen pro mol N A = mol 1 (1.13) Definition 10 (Stoffmenge) n = N N A = m M (1.14) Definition 11 (Ideales Gas) durch folgende Eigenschaften: 3
5 1 Thermodynamik punktförmige Moleküle keine Anziehung der Teilchen untereinander nur elastische Stöße Aus den Beobachtungen pv = const. (Boyle Marriotte) und p/t = const. (Gay-Lussac) folgt p V = n R T Ideales Gasgesetz (für geringe Dichte), (1.15a) oder alternativ: p V = N k B T (1.15b) mit R = 8.31J(mol K) 1 allgemeine Gaskonstante, (1.16a) k B = R = J K 1 N A Boltzmann-Konstante (1.16b) Folgerungen: Arbeit bei isothermen Prozessen (mit p = nrt 1 V ): W = V V 1 p dv = V Arbeit bei isochoren Prozessen (V = const.) Arbeit bei isobaren Prozessen (p = const.) V 1 nrt V dv = nrt [ln V ]V V 1 = nrt ln V V 1 (1.17) W = 0 (1.18) W = p V (1.19) 1.. Statistische Mechanik Die Stöße der Teilchen untereinander führen zu einem breiten Geschwindigkeitsspektrum, das als Wahrscheinlichkeitsverteilung aufgefasst werden kann: P (v) = entspricht Gauß-Verteilung mit Vorfaktor, daher auch: ( ) 3/ m v e mv k B T Maxwell-Verteilung. (1.0) π k b T Man sieht: P (v) dv ist der Anteil der Moleküle im Intervall dv um v. Für den Anteil der Moleküle in [v 1, v ] ergibt sich: 0 P (v) dv = 1. (1.1) 4
6 1. Kinetische Gastheorie v v 1 P (v) dv. (1.) Die absolute Teilchenzahl der Teilchen mit Geschwindigkeit in diesem Intervall erhält man durch Multiplikation mit der Gesamtteilchenzahl N: N [v1,v ] = N v v 1 P (v) dv, da dn = N P (v) dv. (1.3) Mit dieser Verteilung kann man einige nützliche Größen einfach ausrechnen: Durchschnittliche Geschwindigkeit v = 0 v P (v) dv = 8RT πm = 8kB T πm. (1.4) Jede Geschwindigkeit wird also mit ihrem Anteil an der Verteilung gewichtet. RMS-Geschwindigkeit bzw. Mittleres Geschwindigkeitsquadrat (RMS - Root Mean Square) v = 0 = v rms = v P (v) dv = 3RT M, 3RT M = 3kB T m. (1.5) Wichtiger als die Durchschnittsgeschwindigkeit, da in der kinetischen Energie das Geschwindigkeitsquadrat auftritt. Wahrscheinlichste Geschwindigkeit d findet sich im Maximum von P (v), d.h. P (v) =! 0: dv v max = RT M = kb T m. (1.6) Innere Energie Das mittlere Geschwindigkeitsquadrat v rms kann zur Berechnung der mittleren kinetischen Energie eines Gasteilchens benutzt werden: E kin = 1 mv rms = 3 k BT. (1.7) Die innere Energie ist nun die Summe aller kinetischen Energien: U = N E kin = 3 n R T = 3 N k B T. (1.8) Wichtige Folgerung: = Die innere Energie eines Gases hängt nur von seiner Temperatur ab! Spezifische molare Wärme Für ein in festes Volumen eingeschlossenes Gas (kann also keine Arbeit verrichten) findet man 5
7 1 Thermodynamik Freiheitsgrade Bsp. Translatorisch Rotatorisch Gesamt He O 3 5 CH Tabelle 1.1: Beispiele zu Molekülen mit unterschiedlicher Anzahl Freiheitsgrade. bei Temperaturänderung Q W =0 = U = 3 Def. nr T = nc V T = C V = 3 R Molare Wärmekapazität bei konstantem Volumen für einatomige Gase (1.9) Bei konstantem Druck ist die Arbeit W = p V : U = nc V T = Q + W = nc p T p V = nc p T nr T Wichtig: = C p = C V + R = 5 R Molare Wärmekapazität bei konstantem Druck für einatomige Gase (1.30) Die Änderung der inneren Energie ist immer U = nc V T (nur abhängig von C V!), da bei nicht-konstantem Volumen die überschüssige Energie in Arbeit geht. Freiheitsgrade Bisher wurden ideale, einatomige Gase behandelt. Bei zwei- oder mehratomigen Gasen mit rotatorischen Freiheitsgraden kommen Energien für Rotationen und Schwingungen hinzu, wobei diese erst bei höheren Temperaturen freigeschaltet werden (siehe Tab.1.1). Dadurch erhöht sich die Wärmekapazität. Dazu fand Maxwell den Gleichverteilungssatz: = Jeder Freiheitsgrad trägt im Mittel 1/k B T an Energie bei! Beispiel ideales Gas: punktförmig, 3 translatorische Freiheitsgrade = C V = 3 R bekannt. (1.31) Adiabatische Expansion Diese Betrachtungen gelten für ein ideales Gas. Für sehr schnelle Zustandsänderungen oder für solche, die komplett thermisch isoliert von der Umgebung ablaufen, kann man Q = 0 setzen. Man findet dann mit pv = nrt : pv γ = const. pt γ 1 = const. bzw. p 1 V γ 1 = p V γ p 1 T γ 1 1 = p T γ 1 (1.3) 6
8 mit dem Adiabatenkoeffizienten γ C p /C V. Die Arbeit bei adiabatischen Prozessen kann nur aus der inneren Energie stammen! 1. Kinetische Gastheorie Bsp.: explodierende Cola-Flasche - Woher stammt der weisse Nebel, wenn bei einer Cola-Flasche der Deckel schlagartig wegfliegt? 1..3 Zusammenfassung der Prozesse Für alle Prozesse gilt: du = dq + dw du = n C V dt Abbildung 1.1: Zustandsänderungen im p V -Diagramm. Zustandsänderungen Pfad const. Bezeichnung Relationen 1 p isobar dq = nc p dt dw = pdv T isotherm du = 0 dw = nrt V 3 pv γ, pt γ 1 adiabatisch du = dw dq = 0 4 V isochor du = dq dq = nc V dt Tabelle 1.: Eigenschaften der in Abb.1.1 gezeichneten Zustandsänderungen Reale Gase Definition 1 (Reales Gas) In realen Gasen haben die Gasteilchen eine endliche Ausdehnung sowie eine anziehende bzw. abstoßende Wechselwirkung. 7
9 1 Thermodynamik Das Verhalten dieser Gase lässt sich in guter Näherung durch die Van-der-Waals-Gleichung für reale Gase beschreiben: ) (p + n V a (V b n) = nrt (1.33) Dies entspricht der idealen Gasgleichung mit Korrekturfaktoren a und b. a beschreibt den Binnendruck, also die Wechselwirkung der Teilchen untereinander; b beschreibt das Eigenvolumen der Teilchen. Abbildung 1.: p V -Diagramm des realen Gases. Für Drücke, Volumina und Temperaturen unterhalb des sog. kritischen Punktes sagt diese Gleichung unphysikalisches Verhalten voraus (Volumenzunahme bei Druckerhöhung, siehe Abb.1.). Tatsächlich koexistieren in diesem Bereich gasförmige und flüssige Phase und der Druck bleibt konstant, da der Stoff verflüssigt wird. 1.3 Entropie und der zweite Hauptsatz der Thermodynamik Kaffee wird immer kälter, nie wärmer; Popcorn schrumpft nicht zum Maiskorn zurück und Gebäude bewegen sich nicht wieder von alleine auf: Die Zeit hat eine Richtung. Also muss es eine Größe geben, die nicht erhalten ist und mit der Zeit immer größer wird - die Entropie S. Definition 13 (Entropie (klassische Definition)) Es ist sinnlos, die abstrakte Größe der Entropie absolut zu betrachten, weshalb immer Entropieänderungen betrachtet werden. S = f i dq T = S f S i Entropieänderung. (1.34) Dies führt auf den Zweiten Hauptsatz der Thermodynamik: Oder verbal: S 0. (1.35) 8
10 1.3 Entropie und der zweite Hauptsatz der Thermodynamik = Die Entropieänderung in einem geschlossenen System ist niemals negativ! = Der Saustall nimmt von alleine zu! Zur Berechnung von S Bei irreversiblen Prozessen ist die Verbindungslinie von Anfangs- und Endzustand im p V - Diagramm nicht bekannt. Da S aber nur von Anfangs- und Endpunkt abhängt, kann man den Prozess durch einen reversiblen Prozess ersetzen, der dieselben beiden Punkte im p V -Diagramm verbindet und für den die Zustandsfunktionen bekannt sind. Beispiel 1 Zwei Kupferbleche (c c Kupfer = 386J (kg K) 1 ) mit T = 0 C bzw. T = 60 C und jeweils einer Masse von m = 1.5kg werden zusammengebracht, sodass sich der Gleichgewichtszustand räumlich konstanter Temperatur einstellt (siehe Abb.1.3). Abbildung 1.3: (siehe Text) Abbildung 1.4: (siehe Text) = Ersetze diesen Prozess durch die beiden reversiblen Prozesse dargestellt in Abb.1.4 Für beide Prozesse gilt: dq = mcdt = S = woraus für die Gesamtentropieänderung folgt T T 1 mc dt T = mc ln T T 1, (1.36) ds = S L + S R = mc ( ) ln 313K 313K + ln 333K 93K = 35.86J K J K 1 =.4 J K 1 (> 0) Die Entropie ist also im Gegensatz zur Energie nicht erhalten! Wichtig: Prozesse, bei denen keine Wärmeenergie übertragen wird (dq = 0), haben auch Entropieänderung = 0. 9
11 1 Thermodynamik und: Reversible Prozesse in einem geschlossenen System haben Entropieänderung = 0 (Kreisprozess). Für reversible Prozesse in einem geschlossenen System ist auch die Entropie eines idealen Gases eine Zustandsfunktion und nur abhängig von Anfangs- und Endpunkt; somit berechenbar durch: dq = du dw = nc V dt + p dv = nc V dt + nrt dv V (1.37) = S = dq = dt nc T V + nr dv T V = nc V ln T T 1 + nr ln V V 1 (1.38) 1.3. Kreisprozesse Bei Kreisprozessen wird immer derselbe Weg im p V -Diagramm abgelaufen. Die eingeschlossene Fläche entspricht der verrichteten Arbeit. Der Carnot-Prozess ist solch ein Prozess und hier (Abb.1.5) zur Veranschaulichung und Untersuchung von Kreisprozessen gedacht. Er ist ein idealer Kreisprozess und hat als solcher keine Verluste, z.b. durch Reibung. Abbildung 1.5: Carnot-Prozess: a b isotherme Expansion, b c adiabatische Expansion, c d isotherme Kompression, d a adiabatische Kompression Dieser Prozess ist charakterisiert durch zwei Wärmebäder mit Temperatur T w und T k, bei denen die zwei isothermen Prozesse (unter Austausch der Wärmemengen Q w > 0 und Q k < 0) ablaufen, und zwei Adiabaten. Daraus lassen sich berechnen: Arbeit: Da ein Kreisprozess vorliegt, ist du = 0 für einen vollen Durchlauf und somit Entropie: Hier tragen nur die isothermen Prozesse bei mit dw = dq = Q w Q k. (1.39) S = S w + S k = Q w T w Q k T k. (1.40) 10
12 1.3 Entropie und der zweite Hauptsatz der Thermodynamik Da ein Kreisprozess vorliegt, muss S = 0 gelten und wir erhalten: Q w T w = Q k T k. (1.41) Definition 14 (Effizienz) Ganz allgemein lässt sich die thermische Effizienz definieren als ɛ = Energie bekommen Energie bezahlt = W gesamt Q w. (1.4) Für den Carnot-Zyklus ergibt sich: ɛ = Q w Q k Q w = 1 Q k Q w = 1 T k T w. (1.43) Mit Hilfe der letzten Definition lässt sich der zweite Hauptsatz auch anders formulieren: Es gibt keine periodisch zwischen den Temperaturen T w und T k arbeitende Maschine, die einen höheren Wirkungsgrad hat als eine Carnot-Maschine mit diesen Temperaturen. Der Stirling-Motor Ähnlich dem Carnot-Zyklus, aber dq 0 für alle vier Teilprozesse (siehe Abb.1.6), weswegen die Effizienz i.a. niedriger ist als beim Carnot-Prozess. Im Idealfall, d.h. bei Vorhandensein eines Wärmespeichers, der Q aufnimmt und als Q 4 wieder in das System einbringt, ist die Effizienz gleich dem Carnot-Prozess ɛ Ideal St. = 1 T k T w. (1.44) Abbildung 1.6: Stirling-Prozess: a b isotherme Expansion (Arbeitstakt), b c isochore Expansion, c d isotherme Kompression, d a isochore Kompression 11
Ferienkurs Experimentalphysik 2
 Ferienkurs Experimentalphysik 2 Vorlesung 1 Thermodynamik Andreas Brenneis, Marcus Jung, Ann-Kathrin Straub 13.09.2010 1 Allgemeines und Grundbegriffe Grundlegend für das nun folgende Kapitel Thermodynamik
Ferienkurs Experimentalphysik 2 Vorlesung 1 Thermodynamik Andreas Brenneis, Marcus Jung, Ann-Kathrin Straub 13.09.2010 1 Allgemeines und Grundbegriffe Grundlegend für das nun folgende Kapitel Thermodynamik
1 Thermodynamik allgemein
 Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Aufgaben zur Experimentalphysik II: Thermodynamik
 Aufgaben zur Experimentalphysik II: Thermodynamik Lösungen William Hefter - 5//8 1. 1. Durchmesser der Stahlstange nach T : D s D s (1 + α Stahl T) Durchmesser der Bohrung im Ring nach T : D m D m (1 +
Aufgaben zur Experimentalphysik II: Thermodynamik Lösungen William Hefter - 5//8 1. 1. Durchmesser der Stahlstange nach T : D s D s (1 + α Stahl T) Durchmesser der Bohrung im Ring nach T : D m D m (1 +
Der 1. Hauptsatz. Energieerhaltung:
 Der 1. Hauptsatz Energieerhaltung: Bei einer Zustandsänderung tauscht das betrachtete System Energie ( W, Q mit seiner Umgebung aus (oft ein Wärmereservoir bei konstantem. Für die Energiebilanz gilt: U
Der 1. Hauptsatz Energieerhaltung: Bei einer Zustandsänderung tauscht das betrachtete System Energie ( W, Q mit seiner Umgebung aus (oft ein Wärmereservoir bei konstantem. Für die Energiebilanz gilt: U
Musterlösung zu Übung 7
 PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
(b) Schritt I: freie adiabatische Expansion, also ist δw = 0, δq = 0 und damit T 2 = T 1. Folglich ist nach 1. Hauptsatz auch U = 0.
 3 Lösungen Lösung zu 65. (a) Siehe Abbildung 1. (b) Schritt I: freie adiabatische Expansion, also ist δw 0, δq 0 und damit. Folglich ist nach 1. Hauptsatz auch U 0. Schritt II: isobare Kompression, also
3 Lösungen Lösung zu 65. (a) Siehe Abbildung 1. (b) Schritt I: freie adiabatische Expansion, also ist δw 0, δq 0 und damit. Folglich ist nach 1. Hauptsatz auch U 0. Schritt II: isobare Kompression, also
Der Zustand eines Systems ist durch Zustandsgrößen charakterisiert.
 Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Experimentalphysik II: Thermodynamik
 Exerimentalhysik II: Thermodynamik Zweitversuch-Ferienkurs Sommersemester 09 William Hefter 11/09/2009 Inhaltsverzeichnis 1 Temeratur, Wärme und Arbeit 2 1.1 Einschub zur mathematischen Schreibweise.........................
Exerimentalhysik II: Thermodynamik Zweitversuch-Ferienkurs Sommersemester 09 William Hefter 11/09/2009 Inhaltsverzeichnis 1 Temeratur, Wärme und Arbeit 2 1.1 Einschub zur mathematischen Schreibweise.........................
Vorlesung Physik für Pharmazeuten PPh Wärmelehre
 Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
Vorlesung Physik für Pharmazeuten PPh - 07 Wärmelehre Aggregatzustände der Materie im atomistischen Bild Beispiel Wasser Eis Wasser Wasserdampf Dynamik an der Wasser-Luft Grenzfläche im atomistischen Bild
O. Sternal, V. Hankele. 5. Thermodynamik
 5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
5. Thermodynamik 5. Thermodynamik 5.1 Temperatur und Wärme Systeme aus vielen Teilchen Quelle: Wikimedia Commons Datei: Translational_motion.gif Versuch: Beschreibe 1 m 3 Luft mit Newton-Mechanik Beschreibe
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 ladimir Dyakonov # am 25.0.2007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 ladimir Dyakonov # am 25.0.2007 Folien im PDF Format unter: http://www.physik.uni-wuerzburg.de/ep6/teaching.html Raum E43, Tel. 888-5875,
Allgemeines Gasgesetz. PV = K o T
 Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
4 Thermodynamik mikroskopisch: kinetische Gastheorie makroskopisch: System:
 Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Theorie der Wärme kann auf zwei verschiedene Arten behandelt werden. mikroskopisch: Bewegung von Gasatomen oder -molekülen. Vielzahl von Teilchen ( 10 23 ) im Allgemeinen nicht vollständig beschreibbar
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 4.09.00 Inhaltsverzeichnis Inhaltsverzeichnis Thermodynamische Hauptsätze. Aufgabe :..................................... Aufgabe :.....................................
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 4.09.00 Inhaltsverzeichnis Inhaltsverzeichnis Thermodynamische Hauptsätze. Aufgabe :..................................... Aufgabe :.....................................
3 Der 1. Hauptsatz der Thermodynamik
 3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester
 Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 8 Lösungsvorschlag
 T4p: Thermodynamik und Statistische Physik Pro Dr H Ruhl Übungsblatt 8 Lösungsvorschlag 1 Adiabatengleichung Als adiabatische Zustandssänderung bezeichnet man einen thermodynamischen organg, bei dem ein
T4p: Thermodynamik und Statistische Physik Pro Dr H Ruhl Übungsblatt 8 Lösungsvorschlag 1 Adiabatengleichung Als adiabatische Zustandssänderung bezeichnet man einen thermodynamischen organg, bei dem ein
im 1. Fachsemester Vladimir Dyakonov / Volker Drach Professor Dr. Vladimir Dyakonov, Experimentelle Physik VI
 Physik für Mediziner im 1. Fachsemester #9 02/11/2010 Vladimir Dyakonov / Volker Drach [email protected] Wärmelehre Teil 1 - Energie, Wärmekapazität Def. 1: Lehre der Energie, ihrer Erscheinungsform
Physik für Mediziner im 1. Fachsemester #9 02/11/2010 Vladimir Dyakonov / Volker Drach [email protected] Wärmelehre Teil 1 - Energie, Wärmekapazität Def. 1: Lehre der Energie, ihrer Erscheinungsform
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
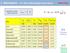 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas. Thermodynamik
 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Temperatur. Temperaturmessung. Grundgleichung der Kalorik. 2 ² 3 2 T - absolute Temperatur / ºC T / K
 Temperatur Temperatur ist ein Maß für die mittlere kinetische Energie der Teilchen 2 ² 3 2 T - absolute Temperatur [ T ] = 1 K = 1 Kelvin k- Boltzmann-Konst. k = 1,38 10-23 J/K Kelvin- und Celsiusskala
Temperatur Temperatur ist ein Maß für die mittlere kinetische Energie der Teilchen 2 ² 3 2 T - absolute Temperatur [ T ] = 1 K = 1 Kelvin k- Boltzmann-Konst. k = 1,38 10-23 J/K Kelvin- und Celsiusskala
1. Wärmelehre 1.1. Temperatur. Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités)
 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für die Temperatur Prinzip
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Übungsblatt 2 ( )
 Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung
Experimentalphysik für Naturwissenschaftler Universität Erlangen Nürnberg SS 01 Übungsblatt (11.05.01) 1) Geschwindigkeitsverteilung eines idealen Gases (a) Durch welche Verteilung lässt sich die Geschwindigkeitsverteilung
Gesetz von Boyle. Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V.
 Gesetz von Boyle Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V Isothermen Gesetz von Gay-Lussac Jacques Charles und Joseph-Louis Gay-Lussac fanden
Gesetz von Boyle Empirisch wurde beobachtet, dass bei konstanter Temperatur gilt: p.v = Konstant bzw V 1 / p bzw p 1 / V Isothermen Gesetz von Gay-Lussac Jacques Charles und Joseph-Louis Gay-Lussac fanden
Hochschule Düsseldorf University of Applied Sciences. 13. April 2016 HSD. Energiespeicher. Thermodynamik
 13. April 2016 Energiespeicher Thermodynamik Prof. Dr. Alexander Braun // Energiespeicher // SS 2016 26. April 2017 Thermodynamik Grundbegriffe Prof. Dr. Alexander Braun // Energiespeicher // SS 2017 26.
13. April 2016 Energiespeicher Thermodynamik Prof. Dr. Alexander Braun // Energiespeicher // SS 2016 26. April 2017 Thermodynamik Grundbegriffe Prof. Dr. Alexander Braun // Energiespeicher // SS 2017 26.
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
 Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Allgemeine Gasgleichung und technische Anwendungen
 Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
Allgemeine Gasgleichung und technische Anwendungen Ziele i.allgemeine Gasgleichung: Darstellung in Diagrammen: Begriffsdefinitionen : Iso bar chor them Adiabatische Zustandsänderung Kreisprozess prinzipiell:
6.7 Die Entropie und der Zweite Hauptsatz
 6.7. DIE ENROPIE UND DER ZWEIE HAUPSAZ 261 6.7 Die Entropie und der Zweite Hauptsatz 6.7.1 Definition der Entropie Im vorhergehenden Abschnitt haben wir im ersten Hauptsatz der hermodynamik die Änderung
6.7. DIE ENROPIE UND DER ZWEIE HAUPSAZ 261 6.7 Die Entropie und der Zweite Hauptsatz 6.7.1 Definition der Entropie Im vorhergehenden Abschnitt haben wir im ersten Hauptsatz der hermodynamik die Änderung
Musterlösung zur Abschlussklausur PC I Übungen (27. Juni 2018)
 1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
Grundlagen der statistischen Physik und Thermodynamik
 Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
Wärmelehre Wärme als Energie-Form
 Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
TU-München, Musterlösung. Experimentalphysik II - Ferienkurs Andreas Schindewolf
 TU-München, 18.08.2009 Musterlösung Experimentalphysik II - Ferienkurs Andreas Schindewolf 1 Random Kreisprozess a Wärme wird nur im isochoren Prozess ab zugeführt. Hier ist W = 0 und Q ab = nc V t b T
TU-München, 18.08.2009 Musterlösung Experimentalphysik II - Ferienkurs Andreas Schindewolf 1 Random Kreisprozess a Wärme wird nur im isochoren Prozess ab zugeführt. Hier ist W = 0 und Q ab = nc V t b T
d) Das ideale Gas makroskopisch
 d) Das ideale Gas makroskopisch Beschreibung mit Zustandsgrößen p, V, T Brauchen trotzdem n, R dazu Immer auch Mikroskopische Argumente dazunehmen Annahmen aus mikroskopischer Betrachtung: Moleküle sind
d) Das ideale Gas makroskopisch Beschreibung mit Zustandsgrößen p, V, T Brauchen trotzdem n, R dazu Immer auch Mikroskopische Argumente dazunehmen Annahmen aus mikroskopischer Betrachtung: Moleküle sind
Ferienkurs Experimentalphysik IV
 Ferienkurs Experimentalphysik IV Michael Mittermair, Daniel Jost 04.09.14 Inhaltsverzeichnis 1 Moleküle 2 1.1 Das H + 2 Molekül-Ion....................... 2 1.2 Näherungen............................ 3
Ferienkurs Experimentalphysik IV Michael Mittermair, Daniel Jost 04.09.14 Inhaltsverzeichnis 1 Moleküle 2 1.1 Das H + 2 Molekül-Ion....................... 2 1.2 Näherungen............................ 3
Hochschule Düsseldorf University of Applied Sciences. 20. April 2016 HSD. Energiespeicher Wärme
 Energiespeicher 02 - Wärme Wiederholung Energiearten Primärenergie Physikalische Energie Kernenergie Chemische Energie Potentielle Energie Kinetische Energie Innere Energie Quelle: Innere Energie Innere
Energiespeicher 02 - Wärme Wiederholung Energiearten Primärenergie Physikalische Energie Kernenergie Chemische Energie Potentielle Energie Kinetische Energie Innere Energie Quelle: Innere Energie Innere
Kapitel IV Wärmelehre und Thermodynamik
 Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Thermodynamik. Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur
 Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Thermodynamik Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur kann voraussagen, ob eine chemische Reaktion abläuft oder nicht kann nichts über den zeitlichen
Thermodynamik (Wärmelehre) III kinetische Gastheorie
 Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
Experimentalphysik. Vorlesungsergänzung (VE), Wintersemester 2017 Modulnummer PTI 301
 Experimentalphysik Vorlesungsergänzung (VE), Wintersemester 2017 Modulnummer PTI 301 Experimentalphysik, Inhalt VE 2.1: Temperatur und Wärmeausdehnung VE 2.2: Zustandsgleichung idealer Gase VE 2.3: Erster
Experimentalphysik Vorlesungsergänzung (VE), Wintersemester 2017 Modulnummer PTI 301 Experimentalphysik, Inhalt VE 2.1: Temperatur und Wärmeausdehnung VE 2.2: Zustandsgleichung idealer Gase VE 2.3: Erster
Ferienkurs Experimentalphysik II Elektro- und Thermodynamik. Thermodynamik Teil II. 12. September 2011 Michael Mittermair
 Ferienkurs Experimentalphysik II Elektro- und Thermodynamik Thermodynamik Teil II 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Allgemeines 3 1.1 Kategorisierung von Systemen..................
Ferienkurs Experimentalphysik II Elektro- und Thermodynamik Thermodynamik Teil II 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Allgemeines 3 1.1 Kategorisierung von Systemen..................
Musterlösung Übung 3
 Musterlösung Übung 3 Aufgabe 1: Der 1. Hautsatz der Thermodynamik a) Für ein geschlossenes System folgt aus der Energieerhaltung (Gleichung (94) im Skrit) du = dw + dq, (1.1) da ausser Arbeit und Wärme
Musterlösung Übung 3 Aufgabe 1: Der 1. Hautsatz der Thermodynamik a) Für ein geschlossenes System folgt aus der Energieerhaltung (Gleichung (94) im Skrit) du = dw + dq, (1.1) da ausser Arbeit und Wärme
1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen
 IV. Wärmelehre 1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen Historisch: Wärme als Stoff, der übertragen und in beliebiger Menge erzeugt werden kann. Übertragung: Wärmezufuhr Joulesche
IV. Wärmelehre 1. Wärme und der 1. Hauptsatz der Thermodynamik 1.1. Grundlagen Historisch: Wärme als Stoff, der übertragen und in beliebiger Menge erzeugt werden kann. Übertragung: Wärmezufuhr Joulesche
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene)
 Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti [email protected] Institut für Experimentelle Physik 25. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 25. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti [email protected] Institut für Experimentelle Physik 25. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 25. 06.
Physik für Mediziner und Zahnmediziner
 Physik für Mediziner und Zahnmediziner Vorlesung 21 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1 Gase (insbesondere: im Körper) aus: Klinke/Silbernagel: Lehrbuch der Physiologie
Physik für Mediziner und Zahnmediziner Vorlesung 21 Prof. F. Wörgötter (nach M. Seibt) -- Physik für Mediziner und Zahnmediziner 1 Gase (insbesondere: im Körper) aus: Klinke/Silbernagel: Lehrbuch der Physiologie
Physikalische Chemie 1
 Physikalische Chemie 1 Christian Lehmann 31. Januar 2004 Inhaltsverzeichnis 1 Einführung 2 1.1 Teilgebiete der Physikalischen Chemie............... 2 1.1.1 Thermodynamik (Wärmelehre)............... 2 1.1.2
Physikalische Chemie 1 Christian Lehmann 31. Januar 2004 Inhaltsverzeichnis 1 Einführung 2 1.1 Teilgebiete der Physikalischen Chemie............... 2 1.1.1 Thermodynamik (Wärmelehre)............... 2 1.1.2
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Allgemeine Vorgehensweise
 Allgemeine Vorgehensweise 1. Skizze zeichnen und Systemgrenze ziehen 2. Art des Systems festlegen (offen, geschlossen, abgeschlossen) und Eigenschaften charakterisieren (z.b. adiabat, stationär, ruhend...)
Allgemeine Vorgehensweise 1. Skizze zeichnen und Systemgrenze ziehen 2. Art des Systems festlegen (offen, geschlossen, abgeschlossen) und Eigenschaften charakterisieren (z.b. adiabat, stationär, ruhend...)
ST Der Stirling-Motor als Wärmekraftmaschine
 ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
Übungen zur Theoretischen Physik F SS Ideales Boltzmann-Gas: ( =25 Punkte, schriftlich)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS 2016 Prof. Dr. A. Shnirman Blatt 2 Dr. B. Narozhny, Dipl.-Phys. P. Schad Lösungsvorschlag
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS 2016 Prof. Dr. A. Shnirman Blatt 2 Dr. B. Narozhny, Dipl.-Phys. P. Schad Lösungsvorschlag
Hauptsatz der Thermodynamik
 0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
Die innere Energie eines geschlossenen Systems ist konstant
 Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Auswahl von Prüfungsfragen für die Prüfungen im September 2011
 Auswahl von Prüfungsfragen für die Prüfungen im September 2011 Was ist / sind / bedeutet / verstehen Sie unter... Wie nennt man / lautet / Wann spricht man von / Definieren Sie... Die anschließenden Fragen
Auswahl von Prüfungsfragen für die Prüfungen im September 2011 Was ist / sind / bedeutet / verstehen Sie unter... Wie nennt man / lautet / Wann spricht man von / Definieren Sie... Die anschließenden Fragen
Die Carnot-Maschine SCHRITT III. Isotherme Kompression bei einer Temperatur T 2 T 2. Wärmesenke T 2 = konstant. Nicolas Thomas
 Die Carnot-Maschine SCHRITT III Isotherme Kompression bei einer Temperatur T 2 T 2 Wärmesenke T 2 = konstant Die Carnot-Maschine SCHRITT IV Man isoliert das Gas wieder thermisch und drückt den Kolben noch
Die Carnot-Maschine SCHRITT III Isotherme Kompression bei einer Temperatur T 2 T 2 Wärmesenke T 2 = konstant Die Carnot-Maschine SCHRITT IV Man isoliert das Gas wieder thermisch und drückt den Kolben noch
2 Grundbegriffe der Thermodynamik
 2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
2 Grundbegriffe der Thermodynamik 2.1 Thermodynamische Systeme (TDS) Aufteilung zwischen System und Umgebung (= Rest der Welt) führt zu einer Klassifikation der Systeme nach Art der Aufteilung: Dazu: adiabatisch
Skript zur Vorlesung
 Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
Skript zur Vorlesung 1. Wärmelehre 1.1. Temperatur Physikalische Grundeinheiten : Die Internationalen Basiseinheiten SI (frz. Système international d unités) 1. Wärmelehre 1.1. Temperatur Ein Maß für
Einführung in die Physik
 Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Einführung in die Physik für Pharmazeuten und Biologen (PPh) Mechanik, Elektrizitätslehre, Optik Übung : Vorlesung: Tutorials: Montags 13:15 bis 14 Uhr, Liebig-HS Montags 14:15 bis 15:45, Liebig HS Montags
Die innere Energie and die Entropie
 Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
f) Ideales Gas - mikroskopisch
 f) Ideales Gas - mikroskopisch i) Annahmen Schon gehabt: Massenpunkte ohne Eigenvolumen Nur elastische Stöße, keine Wechselwirkungen Jetzt dazu: Wände vollkommen elastisch, perfekte Reflektoren Zeitliches
f) Ideales Gas - mikroskopisch i) Annahmen Schon gehabt: Massenpunkte ohne Eigenvolumen Nur elastische Stöße, keine Wechselwirkungen Jetzt dazu: Wände vollkommen elastisch, perfekte Reflektoren Zeitliches
Physikdepartment. Ferienkurs zur Experimentalphysik 4. Daniel Jost 10/09/15
 Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
4.6 Hauptsätze der Thermodynamik
 Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
11.2 Die absolute Temperatur und die Kelvin-Skala
 11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
11. Die absolute Temperatur und die Kelvin-Skala p p 0 Druck p = p(t ) bei konstantem olumen 1,0 0,5 100 50 0-50 -100-150 -00-73 T/ C Tripelpunkt des Wassers: T 3 = 73,16 K = 0,01 C T = 73,16 K p 3 p Windchill-Faktor
Musterlösung zu Übung 7
 PCI Thermodynamik G. eschke FS 011 Musterlösung zu Übung 7 (8. April 011) Aufgabe 1 (a) Die Shomate-Gleichung (Script (153)) lautet: C p (gas, T ) A + BT + CT + DT 3 + E T (1) Für das Kohlenstoffmonooxid
PCI Thermodynamik G. eschke FS 011 Musterlösung zu Übung 7 (8. April 011) Aufgabe 1 (a) Die Shomate-Gleichung (Script (153)) lautet: C p (gas, T ) A + BT + CT + DT 3 + E T (1) Für das Kohlenstoffmonooxid
Thermodynamik. Thermodynamics. Markus Arndt. Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008
 Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
Thermodynamik Thermodynamics Markus Arndt Quantenoptik, Quantennanophysik und Quanteninformation Universität Wien January 2008 Die Hauptsätze der Thermodynamik & Anwendungen in Wärmekraft und Kältemaschinen
2 Wärmelehre. Reibungswärme Reaktionswärme Stromwärme
 2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
Wärmelehre Zustandsänderungen ideales Gases
 Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt
 1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
4.6.5 Dritter Hauptsatz der Thermodynamik
 4.6 Hauptsätze der Thermodynamik Entropie S: ds = dq rev T (4.97) Zustandsgröße, die den Grad der Irreversibilität eines Vorgangs angibt. Sie ist ein Maß für die Unordnung eines Systems. Vorgänge finden
4.6 Hauptsätze der Thermodynamik Entropie S: ds = dq rev T (4.97) Zustandsgröße, die den Grad der Irreversibilität eines Vorgangs angibt. Sie ist ein Maß für die Unordnung eines Systems. Vorgänge finden
Physik I TU Dortmund WS2017/18 Gudrun Hiller Shaukat Khan Kapitel 6
 Physik I U Dortmund WS7/8 Gudrun Hiller Shaukat Khan Kapitel Carnotscher Kreisprozess Modell eines Kreisprozesses (Gedankenexperiment). Nicht nur von historischem Interesse (Carnot 84), sondern auch Prozess
Physik I U Dortmund WS7/8 Gudrun Hiller Shaukat Khan Kapitel Carnotscher Kreisprozess Modell eines Kreisprozesses (Gedankenexperiment). Nicht nur von historischem Interesse (Carnot 84), sondern auch Prozess
Versuch: Sieden durch Abkühlen
 ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
ersuch: Sieden durch Abkühlen Ein Rundkolben wird zur Hälfte mit Wasser gefüllt und auf ein Dreibein mit Netz gestellt. Mit dem Bunsenbrenner bringt man das Wasser zum Sieden, nimmt dann die Flamme weg
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 12: Wärmelehre Dr. Daniel Bick 09. Dezember 2016 Daniel Bick Physik für Biologen und Zahnmediziner 09. Dezember 2016 1 / 35 Übersicht 1 Wellen 2 Wärmelehre
Physik für Biologen und Zahnmediziner Kapitel 12: Wärmelehre Dr. Daniel Bick 09. Dezember 2016 Daniel Bick Physik für Biologen und Zahnmediziner 09. Dezember 2016 1 / 35 Übersicht 1 Wellen 2 Wärmelehre
Modelle zur Beschreibung von Gasen und deren Eigenschaften
 Prof. Dr. Norbert Hampp 1/7 1. Das Ideale Gas Modelle zur Beschreibung von Gasen und deren Eigenschaften Modelle = vereinfachende mathematische Darstellungen der Realität Für Gase wollen wir drei Modelle
Prof. Dr. Norbert Hampp 1/7 1. Das Ideale Gas Modelle zur Beschreibung von Gasen und deren Eigenschaften Modelle = vereinfachende mathematische Darstellungen der Realität Für Gase wollen wir drei Modelle
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti.
 (c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti [email protected] Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
(c) Ulm University p. 1/1 Grundlagen der Physik 2 Schwingungen und Wärmelehre 14. 05. 2007 Othmar Marti [email protected] Institut für Experimentelle Physik Universität Ulm (c) Ulm University p.
Physik I Mechanik der Kontinua und Wärmelehre Thomas Schörner-Sadenius
 Physik I Mechanik der Kontinua und Wärmelehre Thomas Universität Hamburg Wintersemester 2014/15 ORGANISATORISCHES Thomas : Wissenschaftler (Teilchenphysik) am Deutschen Elektronen-Synchrotron (DESY) Kontakt:
Physik I Mechanik der Kontinua und Wärmelehre Thomas Universität Hamburg Wintersemester 2014/15 ORGANISATORISCHES Thomas : Wissenschaftler (Teilchenphysik) am Deutschen Elektronen-Synchrotron (DESY) Kontakt:
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti [email protected] Institut für Experimentelle Physik 21. 05. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 21. 05.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti [email protected] Institut für Experimentelle Physik 21. 05. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 21. 05.
6.2 Zweiter HS der Thermodynamik
 Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
1. Klausur zur Vorlesung Physikalische Chemie I
 1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal
 Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal 7.2 Die Enthalpie Die Enthalpie H ist definiert als H = U + pv, womit wir für die Änderung erhalten dh = pdv + TdS +
Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal 7.2 Die Enthalpie Die Enthalpie H ist definiert als H = U + pv, womit wir für die Änderung erhalten dh = pdv + TdS +
PC-Übung Nr.3 vom
 PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Kapitel 8: Thermodynamik
 Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Festkörper - System steht unter Atmosphärendruck gemessenen Wärmen erhalten Index p : - isoliert
 Kalorimetrie Mit Hilfe der Kalorimetrie können die spezifischen Wärmekapazitäten für Festkörper, Flüssigkeiten und Gase bestimmt werden. Kalorische Grundgleichung: ΔQ = c m ΔT Festkörper - System steht
Kalorimetrie Mit Hilfe der Kalorimetrie können die spezifischen Wärmekapazitäten für Festkörper, Flüssigkeiten und Gase bestimmt werden. Kalorische Grundgleichung: ΔQ = c m ΔT Festkörper - System steht
ELEMENTE DER WÄRMELEHRE
 ELEMENTE DER WÄRMELEHRE 3. Elemente der Wärmelehre 3.1 Grundlagen 3.2 Die kinetische Gastheorie 3.3 Energieumwandlungen 3.4 Hauptsätze der Thermodynamik 2 t =? 85 ºC t =? 61.7 ºC Warum wird der Kaffe eigentlich
ELEMENTE DER WÄRMELEHRE 3. Elemente der Wärmelehre 3.1 Grundlagen 3.2 Die kinetische Gastheorie 3.3 Energieumwandlungen 3.4 Hauptsätze der Thermodynamik 2 t =? 85 ºC t =? 61.7 ºC Warum wird der Kaffe eigentlich
Thermodynamik I Formeln
 Thermodynamik I Formeln Tobi 4. September 2006 Inhaltsverzeichnis Thermodynamische Systeme 3. Auftriebskraft........................................ 3 2 Erster Hauptsatz der Thermodynamik 3 2. Systemenergie........................................
Thermodynamik I Formeln Tobi 4. September 2006 Inhaltsverzeichnis Thermodynamische Systeme 3. Auftriebskraft........................................ 3 2 Erster Hauptsatz der Thermodynamik 3 2. Systemenergie........................................
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 11: Wärmelehre Dr. Daniel Bick 13. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 13. Dezember 2017 1 / 36 Übersicht 1 Wellen 2 Wärmelehre
Physik für Biologen und Zahnmediziner Kapitel 11: Wärmelehre Dr. Daniel Bick 13. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 13. Dezember 2017 1 / 36 Übersicht 1 Wellen 2 Wärmelehre
II. Wärmelehre. II.2. Die Hauptsätze der Wärmelehre. Physik für Mediziner 1
 II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
II. Wärmelehre II.2. Die auptsätze der Wärmelehre Physik für Mediziner 1 1. auptsatz der Wärmelehre Formulierung des Energieerhaltungssatzes unter Einschluss der Wärmenergie: die Zunahme der Inneren Energie
10. Thermodynamik. 10.1 Temperatur und thermisches Gleichgewicht 10.2 Thermometer und Temperaturskala 10.3 Thermische Ausdehnung 10.
 Inhalt 10.1 Temperatur und thermisches Gleichgewicht 10.2 Thermometer und Temperaturskala 10.3 Thermische Ausdehnung 10.4 Wärmekapazität Aufgabe: - Temperaturverhalten von Gasen, Flüssigkeiten, Festkörpern
Inhalt 10.1 Temperatur und thermisches Gleichgewicht 10.2 Thermometer und Temperaturskala 10.3 Thermische Ausdehnung 10.4 Wärmekapazität Aufgabe: - Temperaturverhalten von Gasen, Flüssigkeiten, Festkörpern
Thermodynamik. Kapitel 4. Nicolas Thomas
 Thermodynamik Kapitel 4 Arbeit und Wärme Länge, x F Kolben Länge, x F Der Kolben wird sehr langsam um die Distanz -dx verschoben. dx Kolben Wieviel Arbeit mussten wir leisten, um den Kolben zu bewegen?
Thermodynamik Kapitel 4 Arbeit und Wärme Länge, x F Kolben Länge, x F Der Kolben wird sehr langsam um die Distanz -dx verschoben. dx Kolben Wieviel Arbeit mussten wir leisten, um den Kolben zu bewegen?
9.4 Der 2. Hautsatz: spontane Prozesse und Entropie
 9.4 Der 2. Hautsatz: spontane Prozesse und Entropie Beispiele für spontane Prozesse: Ein heisser Körper kühlt sich auf Umgebungstemperatur ab. Ein kalter Köper erwärmt sich auf Umgebungstemperatur. Die
9.4 Der 2. Hautsatz: spontane Prozesse und Entropie Beispiele für spontane Prozesse: Ein heisser Körper kühlt sich auf Umgebungstemperatur ab. Ein kalter Köper erwärmt sich auf Umgebungstemperatur. Die
Physikalische Chemie: Kreisprozesse
 Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
