Musterlösung zu Übung 7
|
|
|
- Martin Baumhauer
- vor 6 Jahren
- Abrufe
Transkript
1 PCI Thermodynamik G. eschke FS 011 Musterlösung zu Übung 7 (8. April 011) Aufgabe 1 (a) Die Shomate-Gleichung (Script (153)) lautet: C p (gas, T ) A + BT + CT + DT 3 + E T (1) Für das Kohlenstoffmonooxid gilt dann: C p,co (gas, T ) T T T K 1 4 T (b) Für T 500 K, ist die Wärmekapazität C p (500 K) Man sieht, dass die letzten drei Terme weniger als 5 % Korrektur für C p (CO) bringen. Der grösste Anteil in dieser Korrektur kommt vom quadratischen Term CT, der bei 500 K etwa 3.4 % von der ganze Wärmekapazität ist. Deswegen reicht in dem Fall die vereinfachte Gleichung C p A + B T ( 8.6 K ). Für T 1000 K, analog, wie oben: C p (1000 K) In dem Fall darf man nur den letzten Term vernachlässigen. Die Gleichung für die Wärmekapazität wäre dann C p A + B T + C T + D T 3 ( K ). 1
2 (c) Für die Bildungsenthalpie gilt die Gleichung (vergl. mit Script (151)): B H 0 (T ) B H 0 ( ) + C p (T ) dt. () Wenn man die Shomate-Gleichung für die Wärmekapazität einsetzt, dann C p (T ) dt (A + BT + CT + DT 3 + ET ) dt [AT + BT + CT DT 4 4 E T ] T (3) Hier nehmen wir wieder die zwei Temperaturen T 500 K und T 1000 K. Für T 500 K: B H 0 (500 K) k k k k k k k Man sieht, dass für die Präzision von 5 % es reicht die Wärmekapazität temperaturunabhängig zu betrachten. Die Termen B bis E bringen maximal 0.8 % ( ) k Korrektur für B H 0 (500 K). Für T 1000 K: B H 0 (1000 K) k k 0.66 k +.78 k k k k Hier wenn wir die Temperaturabhängigkeit der Wärmekapazität vernachlässigen, dann bekommen wir einen Fehler von etwa 4 % ( ) k. Allgemein, wenn man die Bildungsenthalpie berechnet, darf man oft (aber nicht immer!) die Wärmekapazität eines Gases als temperaturunabhängig zu betrachten. In Gegensatz dazu, wenn die Wärmekapazität selber zu bestimmen ist, dann braucht man mindestens den linearen und den quadratischen Term zu beachten.
3 Aufgabe Hier um eine Präzision von 0.1 k/ zu erreichen braucht man die quadratische Terme in Wärmekapazität. Für die Referenztemperatur reicht aber die Annäherung 98 K. Nach dem Skript Gleichung (151) gilt der Kirchoff sche Satz, mit dem sich die Reaktionsenthalpie für eine beliebige Temperatur berechnen lässt zu R H 0 (T ) R H 0 ( ) + R C p dt. (4) Mit 98 K und T 700 K, wobei nach Skript Gleichungen (149) gilt R H 0 ( ) i ν i B H 0 ( i ) (5) B H 0 (C H 6 ) + B H 0 (H O) B H 0 (CO) 5 B H 0 (H ) (6) 84.0 k k k k 1 (7) k 1. Der Wert entspricht zugleich der Reaktionsenthalpie bei 10 5 P a und K. Die in Gleichung (4) enthaltene Wärmekapazität erhält man nach Skript Gleichung (15) mit (8) R C p i ν i C p ( i ) C p,c H 6 + C p,h O C p,co 5 C p,h (9) ( T K T K ) K ( T K T K ) K 1 1 ( T K T K ) K ( T K T K ) K 1 1 (10) ( T K T K ) K 1 1. (11) Gleichung (11) integriert über die Temperatur ergibt 700 K R C p dt 700 K dt ( T K T K ) K K 98 K [ T T K ] 700 K T 3 K K K (1) (13) k 1. (14) etzt besitzen wir alle Werte, um Gleichung (4) zu lösen. Durch Einsetzen von (8) und (14) erhält man eine Reaktionsenthalpie von R H 0 (700 K) k k k 1. (15) 3
4 Aufgabe 3 (a) Wenn jede Wärmemaschine die gleiche Wärmemenge pro Stunde benutzt, dann kann man schreiben: q in,1 q in, q Die Arbeiten lassen sich dann berechnen nach: w 1 ɛ 1 q w ɛ q Der gesammte Wirkungsgrad ist in dem Fall gleich ɛ ges w 1 + w ɛ 1 q + ɛ q q in,1 + q in, q ɛ 1 + ɛ (b) In diesem Fall w 1 w w und daraus folgt, dass q 1 w ɛ 1 q w ɛ Der gesammte Wirkungsgrad ist dann gleich ɛ ges w 1 + w q in,1 + q in, w w ɛ 1 + w ɛ 1 ɛ ɛ ɛ 1 ɛ ɛ 1 + ɛ etzt ordnen wir die zwei Fälle nach der Effizienz. Wenn wir den Fall (a) betrachten, dann produziert die Maschine mit dem besseren Wirkungsgad mehr Arbeit, als die jenige mit dem schlimmeren Wirkungsgad. Wenn wir den Fall (b) betrachten, und nehmen an, dass die gesammte Wärme gleich wie im (a) bleibt, dann wird mehr Wärme bei der Maschine mit dem geringsten Wirkungsgrad in Arbeit transformiert. Man kann die ganze Wärme dann teilen. Ein Teil wird in der beiden Fälle (a) und (b) bei der besseren Maschine in die Arbeit transformiert, der zweite Teil wird in der beiden Fälle bei der shlechteren Maschine in die Arbeit transformiert. Die Reste kommt im Fall (a) in die bessere Maschine und im Fall (b) in die schlechtere Maschine. D.h. in dem Fall (b) wird von der gleiche Wärmemenge etwas weniger Arbeit produziert im Vergleich mit dem Fall (a). Die gesammte Effizienz ist dann in (b) ungünstiger und der gesammte Wirkungsgrad ist deswegen kleiner. Um dasselbe mathematisch zu zeigen muss man das Verhältnis ɛ a /ɛ b analysieren: 4
5 ɛ a ɛ 1 + ɛ 1 ɛ b ɛ1 + ɛ 1 ɛ 1 ɛ 4 ɛ 1 + ɛ 1 ɛ + ɛ 1 ( ɛ 1 ɛ 4 ɛ1 + + ɛ ) ɛ ɛ 1 1 ( 4 x ) x Die Funktion f(x) 1 (x x), (mit x ɛ 1 ɛ ) hat ein Minimum bei x 1.0 und ist überall grösser als 1 mit der Ausnahme auf dem Minimumpunkt, wo f(1) 1. Das folgt daraus, dass bei x 1 gilt df 0 und d f 1 > 0. Die Ableitungen dieser Funktion sind dx dx df 1 (1 ) 1 dx 4 x ; d f 1. dx x 3 Das bedeutet wieder, dass der Fall (a) einen effizienteren Aufbau beschreibt. Die Effizienz in (a) und (b) ist gleich, wenn ɛ a ɛ b. Aufgabe 4 Hier, obwohl die Prozesse, die das System von dem Zustand 1 in Zustand führen, irreversibel sind, entsprechen die beide Zustände 1 und einem termodynamischen Gleichgewicht. Die Entropie ist eine Zustandsgrösse. Man kann, deswegen, die Entropieänderung zwischen den Zuständen 1 und entlang einen beliebigen reversiblen Weg berechnen. (a) Hier V 1 V 10 L. Die beide Zustände liegen also auf einer Isochore. Für so einen Prozess (dv 0, dw pdv 0) gilt dq du c v dt, mit c v 1 C V. Die Wärmekapazität kann man wie folgt berechnen: C v R γ K c v 1 C v C p C v R C p C v + R γ C p C v + R C v C v γc v C v + R C v (γ 1) R K (16) Die Entropiedifferenz ist dann s ds dq T c v dt T c v ln T 0.79 K ln 00 K 400 K K (17) 5
6 (b) Das ist ein allgemeiner Fall. Die Zustände 1 und liegen auf keiner speziellen Kurve (wie z.b. Isobare oder Isoterme). Hier ist es günstig das Resultat von (a) zu benutzen. Der Weg von Zustand 1 nach Zustand kann man dann in zwei Schritten machen. Erst nehmen wir eine Isochore bis Zustand (*) mit T T 00 K und V 1 10 L, wie in (a). Die Entropieänderung für den Schritt ist uns bereits bekannt. Als zweiter Schritt nehmen wir eine Isoterme von T 00 K, 10 L bis T 00 K, V 7 L. Da gilt dt 0, und du dq + dw 0 (ideales Gas, T Const) ; dq dw pdv, s (( ) ) V nr ln V dq T V dq pv/nr nr V pdv pv nr V dv V ln m m K ln K. (18) Die gesammte Entropieänderung ist dann s (1 ) s (1 ( )) + s (( ) ) K.97 K K 6
(b) Schritt I: freie adiabatische Expansion, also ist δw = 0, δq = 0 und damit T 2 = T 1. Folglich ist nach 1. Hauptsatz auch U = 0.
 3 Lösungen Lösung zu 65. (a) Siehe Abbildung 1. (b) Schritt I: freie adiabatische Expansion, also ist δw 0, δq 0 und damit. Folglich ist nach 1. Hauptsatz auch U 0. Schritt II: isobare Kompression, also
3 Lösungen Lösung zu 65. (a) Siehe Abbildung 1. (b) Schritt I: freie adiabatische Expansion, also ist δw 0, δq 0 und damit. Folglich ist nach 1. Hauptsatz auch U 0. Schritt II: isobare Kompression, also
1 Thermodynamik allgemein
 Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Einführung in die Energietechnik Tutorium II: Thermodynamik Thermodynamik allgemein. offenes System: kann Materie und Energie mit der Umgebung austauschen. geschlossenes System: kann nur Energie mit der
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 4.09.00 Inhaltsverzeichnis Inhaltsverzeichnis Thermodynamische Hauptsätze. Aufgabe :..................................... Aufgabe :.....................................
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 4.09.00 Inhaltsverzeichnis Inhaltsverzeichnis Thermodynamische Hauptsätze. Aufgabe :..................................... Aufgabe :.....................................
Ferienkurs Experimentalphysik II Elektro- und Thermodynamik. Thermodynamik Teil II. 12. September 2011 Michael Mittermair
 Ferienkurs Experimentalphysik II Elektro- und Thermodynamik Thermodynamik Teil II 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Allgemeines 3 1.1 Kategorisierung von Systemen..................
Ferienkurs Experimentalphysik II Elektro- und Thermodynamik Thermodynamik Teil II 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Allgemeines 3 1.1 Kategorisierung von Systemen..................
10. Thermodynamik Der erste Hauptsatz Der zweite Hauptsatz Thermodynamischer Wirkungsgrad Der Carnotsche Kreisprozess
 Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Inhalt 10.10 Der zweite Hauptsatz 10.10.1 Thermodynamischer Wirkungsgrad 10.10.2 Der Carnotsche Kreisprozess Für kinetische Energie der ungeordneten Bewegung gilt: Frage: Frage: Wie kann man mit U Arbeit
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
 Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Übungen zur Theoretischen Physik F SS Ideales Boltzmann-Gas: ( =25 Punkte, schriftlich)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS 2016 Prof. Dr. A. Shnirman Blatt 2 Dr. B. Narozhny, Dipl.-Phys. P. Schad Lösungsvorschlag
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS 2016 Prof. Dr. A. Shnirman Blatt 2 Dr. B. Narozhny, Dipl.-Phys. P. Schad Lösungsvorschlag
Kompressible Gasdynamik
 Hauptseminar Lineare und Nichtlineare Wellenphänomene 14. Januar 2013 Inhaltsverzeichnis 1 Thermodynamische Grundlagen 2 Bewegungsgleichungen 3 Konstruktion der Charakteristiken Allgemeine Konstruktion
Hauptseminar Lineare und Nichtlineare Wellenphänomene 14. Januar 2013 Inhaltsverzeichnis 1 Thermodynamische Grundlagen 2 Bewegungsgleichungen 3 Konstruktion der Charakteristiken Allgemeine Konstruktion
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Die innere Energie and die Entropie
 Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Die innere Energie and die Entropie Aber fangen wir mit der Entropie an... Stellen Sie sich ein System vor, das durch die Entropie S, das Volumen V und die Stoffmenge n beschrieben wird. U ' U(S,V,n) Wir
Thermodynamische Hauptsätze, Kreisprozesse Übung
 Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
Thermodynamische Hauptsätze, Kreisprozesse Übung Marcus Jung 14.09.2010 Inhaltsverzeichnis Inhaltsverzeichnis 1 Thermodynamische Hauptsätze 3 1.1 Aufgabe 1:.................................... 3 1.2 Aufgabe
TU-München, Musterlösung. Experimentalphysik II - Ferienkurs Andreas Schindewolf
 TU-München, 18.08.2009 Musterlösung Experimentalphysik II - Ferienkurs Andreas Schindewolf 1 Random Kreisprozess a Wärme wird nur im isochoren Prozess ab zugeführt. Hier ist W = 0 und Q ab = nc V t b T
TU-München, 18.08.2009 Musterlösung Experimentalphysik II - Ferienkurs Andreas Schindewolf 1 Random Kreisprozess a Wärme wird nur im isochoren Prozess ab zugeführt. Hier ist W = 0 und Q ab = nc V t b T
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Aufgaben zur Experimentalphysik II: Thermodynamik
 Aufgaben zur Experimentalphysik II: Thermodynamik Lösungen William Hefter - 5//8 1. 1. Durchmesser der Stahlstange nach T : D s D s (1 + α Stahl T) Durchmesser der Bohrung im Ring nach T : D m D m (1 +
Aufgaben zur Experimentalphysik II: Thermodynamik Lösungen William Hefter - 5//8 1. 1. Durchmesser der Stahlstange nach T : D s D s (1 + α Stahl T) Durchmesser der Bohrung im Ring nach T : D m D m (1 +
Thermodynamik I - Übung 7. Nicolas Lanzetti
 Thermodynamik I - Übung 7 Nicolas Lanzetti Nicolas Lanzetti 13.11.2015 1 Heutige Themen Zusammenfassung letzter Woche; Die Entropie; Die T ds-gleichungen; Die erzeugte Entropie; Isentroper Wirkungsgrad;
Thermodynamik I - Übung 7 Nicolas Lanzetti Nicolas Lanzetti 13.11.2015 1 Heutige Themen Zusammenfassung letzter Woche; Die Entropie; Die T ds-gleichungen; Die erzeugte Entropie; Isentroper Wirkungsgrad;
Thermodynamik I Formeln
 Thermodynamik I Formeln Tobi 4. September 2006 Inhaltsverzeichnis Thermodynamische Systeme 3. Auftriebskraft........................................ 3 2 Erster Hauptsatz der Thermodynamik 3 2. Systemenergie........................................
Thermodynamik I Formeln Tobi 4. September 2006 Inhaltsverzeichnis Thermodynamische Systeme 3. Auftriebskraft........................................ 3 2 Erster Hauptsatz der Thermodynamik 3 2. Systemenergie........................................
22. Entropie; Zweiter Hauptsatz der Wärmelehre
 22. Entropie; Zweiter Hauptsatz der Wärmelehre Nicht alle Prozesse, die dem Energiesatz genügen, finden auch wirklich statt Beispiel: Um alle Energieprobleme zu lösen, brauchte man keine Energie aus dem
22. Entropie; Zweiter Hauptsatz der Wärmelehre Nicht alle Prozesse, die dem Energiesatz genügen, finden auch wirklich statt Beispiel: Um alle Energieprobleme zu lösen, brauchte man keine Energie aus dem
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Der Zustand eines Systems ist durch Zustandsgrößen charakterisiert.
 Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Grundbegriffe der Thermodynamik Die Thermodynamik beschäftigt sich mit der Interpretation gegenseitiger Abhängigkeit von stofflichen und energetischen Phänomenen in der Natur. Die Thermodynamik kann voraussagen,
Musterlösung zur Abschlussklausur PC I Übungen (27. Juni 2018)
 1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
1. Abkühlung (100 Punkte) Ein ideales Gas (genau 3 mol) durchläuft hintereinander zwei (reversible) Zustandsänderungen: Zuerst expandiert es isobar, wobei die Temperatur von 50 K auf 500 K steigt und sich
Theorie der Wärme Musterlösung 11.
 Theorie der Wärme Musterlösung. FS 05 Prof. Thomas Gehrmann Übung. Edelgas im Schwerefeld Berechne den Erwartungswert der Energie eines monoatomaren idealen Gases z. B. eines Edelgases in einem zylindrischen
Theorie der Wärme Musterlösung. FS 05 Prof. Thomas Gehrmann Übung. Edelgas im Schwerefeld Berechne den Erwartungswert der Energie eines monoatomaren idealen Gases z. B. eines Edelgases in einem zylindrischen
Der 1. Hauptsatz. Energieerhaltung:
 Der 1. Hauptsatz Energieerhaltung: Bei einer Zustandsänderung tauscht das betrachtete System Energie ( W, Q mit seiner Umgebung aus (oft ein Wärmereservoir bei konstantem. Für die Energiebilanz gilt: U
Der 1. Hauptsatz Energieerhaltung: Bei einer Zustandsänderung tauscht das betrachtete System Energie ( W, Q mit seiner Umgebung aus (oft ein Wärmereservoir bei konstantem. Für die Energiebilanz gilt: U
Musterlösung Aufgabe 1: Zweikammermesssysatem
 Klausur Thermodynamik I (08.09.2016) 1 Musterlösung Aufgabe 1: Zweikammermesssysatem Teilaufgabe a) Da die Membrane zunächst für Wärme undurchlässig ist, handelt es sich um eine adiabate Zustandsänderung
Klausur Thermodynamik I (08.09.2016) 1 Musterlösung Aufgabe 1: Zweikammermesssysatem Teilaufgabe a) Da die Membrane zunächst für Wärme undurchlässig ist, handelt es sich um eine adiabate Zustandsänderung
Übungen zu Theoretische Physik IV
 Physikalisches Institut Übungsblatt 4 Universität Bonn 02. November 2012 Theoretische Physik WS 12/13 Übungen zu Theoretische Physik IV Priv.-Doz. Dr. Stefan Förste http://www.th.physik.uni-bonn.de/people/forste/exercises/ws1213/tp4
Physikalisches Institut Übungsblatt 4 Universität Bonn 02. November 2012 Theoretische Physik WS 12/13 Übungen zu Theoretische Physik IV Priv.-Doz. Dr. Stefan Förste http://www.th.physik.uni-bonn.de/people/forste/exercises/ws1213/tp4
Probeklausur STATISTISCHE PHYSIK PLUS
 DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
Hauptsatz der Thermodynamik
 0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
0.7. Hauptsatz der Thermodynamik Die einem System von außen zugeführte Wärmemenge Q führt zu Erhöhung U der inneren Energie U und damit Erhöhung T der Temperatur T Expansion des olumens gegen den äußeren
Formelsammlung. Experimentalphysik II. Zur Vorlesung bei Prof. Dr. M. Wuttig, Sommersemester Pascal Del Haye 27.
 Formelsammlung Experimentalphysik II Zur Vorlesung bei Prof. Dr. M. Wuttig, Sommersemester 2003 Pascal Del Haye www.delhaye.de 27. Juli 2003 Inhaltsverzeichnis Thermodynamik 3. Ideale Gasgleichung........................
Formelsammlung Experimentalphysik II Zur Vorlesung bei Prof. Dr. M. Wuttig, Sommersemester 2003 Pascal Del Haye www.delhaye.de 27. Juli 2003 Inhaltsverzeichnis Thermodynamik 3. Ideale Gasgleichung........................
Thermodynamik I PVK - Tag 2. Nicolas Lanzetti
 Thermodynamik I PVK - Tag 2 Nicolas Lanzetti Nicolas Lanzetti 05.01.2016 1 Heutige Themen Carnot; Wirkungsgrad/Leistungsziffer; Entropie; Erzeugte Entropie; Isentroper Wirkungsgrad; Isentrope Prozesse
Thermodynamik I PVK - Tag 2 Nicolas Lanzetti Nicolas Lanzetti 05.01.2016 1 Heutige Themen Carnot; Wirkungsgrad/Leistungsziffer; Entropie; Erzeugte Entropie; Isentroper Wirkungsgrad; Isentrope Prozesse
Thermodynamik Hauptsatz
 Thermodynamik. Hauptsatz Inhalt Wärmekraftmaschinen / Kälteprozesse. Hauptsatz der Thermodynamik Reversibilität Carnot Prozess Thermodynamische Temperatur Entropie Entropiebilanzen Anergie und Exergie
Thermodynamik. Hauptsatz Inhalt Wärmekraftmaschinen / Kälteprozesse. Hauptsatz der Thermodynamik Reversibilität Carnot Prozess Thermodynamische Temperatur Entropie Entropiebilanzen Anergie und Exergie
Die Innere Energie U
 Die Innere Energie U U ist die Summe aller einem System innewohnenden Energien. Es ist unmöglich, diese zu berechnen. U kann nicht absolut angegeben werden! Differenzen in U ( U) können gemessen werden.
Die Innere Energie U U ist die Summe aller einem System innewohnenden Energien. Es ist unmöglich, diese zu berechnen. U kann nicht absolut angegeben werden! Differenzen in U ( U) können gemessen werden.
Moderne Theoretische Physik IIIa WS 18/19
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik IIIa WS 18/19 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 2 Dr. Stefan Rex Besprechung: 06.11.2018
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik IIIa WS 18/19 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 2 Dr. Stefan Rex Besprechung: 06.11.2018
Kapitel IV Wärmelehre und Thermodynamik
 Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
Kapitel IV Wärmelehre und Thermodynamik a) Definitionen b) Temperatur c) Wärme und Wärmekapazität d) Das ideale Gas - makroskopisch e) Das reale Gas / Phasenübergänge f) Das ideale Gas mikroskopisch g)
PC-Übung Nr.3 vom
 PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Institut für Thermodynamik Prof. Dr. rer. nat. M. Pfitzner Thermodynamik II - Lösung 04. Aufgabe 6: (1): p 1 = 1 bar, t 1 = 15 C.
 Aufgabe 6: 2) 3) ): p = bar, t = 5 C 2): p 2 = 5 bar ) 3): p 3 = p 2 = 5 bar, t 3 = 5 C Die skizzierte Druckluftanlage soll V3 = 80 m 3 /h Luft vom Zustand 3) liefern. Dazu wird Luft vom Zustand ) Umgebungszustand)
Aufgabe 6: 2) 3) ): p = bar, t = 5 C 2): p 2 = 5 bar ) 3): p 3 = p 2 = 5 bar, t 3 = 5 C Die skizzierte Druckluftanlage soll V3 = 80 m 3 /h Luft vom Zustand 3) liefern. Dazu wird Luft vom Zustand ) Umgebungszustand)
Analysis III Gewöhnliche Differentialgleichungen 3. Übungsblatt (mit Lösungshinweisen)
 Analysis III Gewöhnliche Differentialgleichungen 3. Übungsblatt (mit Lösungshinweisen) Fachbereich Mathematik Wintersemester 0/0 Prof. Dr. Burkhard Kümmerer./3. November 0 Andreas Gärtner Walter Reußwig
Analysis III Gewöhnliche Differentialgleichungen 3. Übungsblatt (mit Lösungshinweisen) Fachbereich Mathematik Wintersemester 0/0 Prof. Dr. Burkhard Kümmerer./3. November 0 Andreas Gärtner Walter Reußwig
Klausur Thermodynamik E2/E2p SoSe 2019 Braun. Formelsammlung Thermodynamik
 Klausur Thermodynamik E2/E2p SoSe 2019 Braun Name: Matrikelnummer: O E2 O E2p (bitte ankreuzen) Die mit Stern (*) gekennzeichneten Aufgaben sind für E2-Kandidaten vorgesehen - E2p-Kandidaten dürfen diese
Klausur Thermodynamik E2/E2p SoSe 2019 Braun Name: Matrikelnummer: O E2 O E2p (bitte ankreuzen) Die mit Stern (*) gekennzeichneten Aufgaben sind für E2-Kandidaten vorgesehen - E2p-Kandidaten dürfen diese
Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt
 1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1 Aufgabe: Entropieänderung Ferienkurs Experimentalphysik 2 - Donnerstag-Übungsblatt 1 Aufgabe: Entropieänderung a) Ein Kilogramm Wasser bei = C wird in thermischen Kontakt mit einem Wärmereservoir bei
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases. f=5 Translation + Rotation. f=7 Translation + Rotation +Vibration. Wiederholung
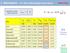 1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
1. Wärmelehre 2.4. Die Freiheitsgrade eines Gases Wiederholung Speziische molare Wärmekapazität c m,v = 2 R R = N A k B = 8.315 J mol K =5 Translation + Rotation =7 Translation + Rotation +ibration 1.
Thermodynamik I PVK - Tag 1. Nicolas Lanzetti
 Thermodynamik I PVK - Tag 1 Nicolas Lanzetti Nicolas Lanzetti 04.01.2016 1 Hinweise zu dem PVK Name: Nicolas Lanzetti; 5. Semester Maschinenbau; Mail: [email protected]; Raum: ML F34; Zeit: Montag-Mittwoch,
Thermodynamik I PVK - Tag 1 Nicolas Lanzetti Nicolas Lanzetti 04.01.2016 1 Hinweise zu dem PVK Name: Nicolas Lanzetti; 5. Semester Maschinenbau; Mail: [email protected]; Raum: ML F34; Zeit: Montag-Mittwoch,
Ferienkurs Experimentalphysik 2
 Ferienkurs Experimentalphysik 2 Vorlesung 1 Thermodynamik Andreas Brenneis, Marcus Jung, Ann-Kathrin Straub 13.09.2010 1 Allgemeines und Grundbegriffe Grundlegend für das nun folgende Kapitel Thermodynamik
Ferienkurs Experimentalphysik 2 Vorlesung 1 Thermodynamik Andreas Brenneis, Marcus Jung, Ann-Kathrin Straub 13.09.2010 1 Allgemeines und Grundbegriffe Grundlegend für das nun folgende Kapitel Thermodynamik
ST Der Stirling-Motor als Wärmekraftmaschine
 ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
ST Der Stirling-Motor als Wärmekraftmaschine Blockpraktikum Herbst 2007 Gruppe 2b 24. Oktober 2007 Inhaltsverzeichnis 1 Grundlagen 2 1.1 Stirling-Kreisprozess............................. 2 1.2 Technische
Musterlösung Übung 3
 Musterlösung Übung 3 Aufgabe 1: Der 1. Hautsatz der Thermodynamik a) Für ein geschlossenes System folgt aus der Energieerhaltung (Gleichung (94) im Skrit) du = dw + dq, (1.1) da ausser Arbeit und Wärme
Musterlösung Übung 3 Aufgabe 1: Der 1. Hautsatz der Thermodynamik a) Für ein geschlossenes System folgt aus der Energieerhaltung (Gleichung (94) im Skrit) du = dw + dq, (1.1) da ausser Arbeit und Wärme
Ferienkurs Experimentalphysik IV
 Ferienkurs Experimentalphysik IV Michael Mittermair, Daniel Jost 04.09.14 Inhaltsverzeichnis 1 Moleküle 2 1.1 Das H + 2 Molekül-Ion....................... 2 1.2 Näherungen............................ 3
Ferienkurs Experimentalphysik IV Michael Mittermair, Daniel Jost 04.09.14 Inhaltsverzeichnis 1 Moleküle 2 1.1 Das H + 2 Molekül-Ion....................... 2 1.2 Näherungen............................ 3
Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie
 Sommer-Semester 2011 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-11:15, Lehmann HS 022, Geb 30.22 Do 09:45-11:15,
Sommer-Semester 2011 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-11:15, Lehmann HS 022, Geb 30.22 Do 09:45-11:15,
Physikalische Chemie I
 M.Bredol / MP Physikalische Chemie I / 10.3.16 1 Physikalische Chemie I Nachname orname Matrikel Aufgabe Punkte erreicht Note 1 20 2 20 3 20 4 22 5 18 Summe: 100 1. Gegeben seien 20 g Kohlendioxid, die
M.Bredol / MP Physikalische Chemie I / 10.3.16 1 Physikalische Chemie I Nachname orname Matrikel Aufgabe Punkte erreicht Note 1 20 2 20 3 20 4 22 5 18 Summe: 100 1. Gegeben seien 20 g Kohlendioxid, die
Thermodynamik I. Sommersemester 2012 Kapitel 3, Teil 2. Prof. Dr. Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3Bilanzgleichungen 3.3.1Massenbilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3Bilanzgleichungen 3.3.1Massenbilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene)
 Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Das Ideale Gas Kinetische Gastheorie (auf atomarer Ebene) Wir haben gesehen, dass ein sogenanntes 'ideales Gas' durch die Zustandsgleichung pv = νr T [1] beschrieben wird; wir wollen nun verstehen, welchen
Wärmelehre Zustandsänderungen ideales Gases
 Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Wärmelehre Zustandsänderungen ideales Gases p Gas-Gleichung 1.Hauptsatz p V = N k B T U Q W p 1 400 1 isobar 300 200 isochor isotherm 100 p 2 0 2 adiabatisch 0 1 2 3 4 5 V V 2 1 V Bemerkung: Mischung verschiedener
Repetitorium QM 1 - Tag 5
 Thermodynamik und 4. März 2016 Inhaltsverzeichnis 1 Thermodynamik Hauptsätze der Thermodynamik 2 Zustandsgrößen Thermodynamik Hauptsätze der Thermodynamik Ziel: Beschreibung des makroskopischen Gleichgewichtszustandes
Thermodynamik und 4. März 2016 Inhaltsverzeichnis 1 Thermodynamik Hauptsätze der Thermodynamik 2 Zustandsgrößen Thermodynamik Hauptsätze der Thermodynamik Ziel: Beschreibung des makroskopischen Gleichgewichtszustandes
Thermodynamik. Kapitel 4. Nicolas Thomas
 Thermodynamik Kapitel 4 Arbeit und Wärme Länge, x F Kolben Länge, x F Der Kolben wird sehr langsam um die Distanz -dx verschoben. dx Kolben Wieviel Arbeit mussten wir leisten, um den Kolben zu bewegen?
Thermodynamik Kapitel 4 Arbeit und Wärme Länge, x F Kolben Länge, x F Der Kolben wird sehr langsam um die Distanz -dx verschoben. dx Kolben Wieviel Arbeit mussten wir leisten, um den Kolben zu bewegen?
Lehrbuch der Thermodynamik
 Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung Ж HANSER Carl Hanser Verlag München Wien VII Inhaltsverzeichnis 1 GRUNDBEGRIFFE DER THERMODYNAMIK 1 Einführung 1 Systeme 3 offene
Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung Ж HANSER Carl Hanser Verlag München Wien VII Inhaltsverzeichnis 1 GRUNDBEGRIFFE DER THERMODYNAMIK 1 Einführung 1 Systeme 3 offene
Physikalische Chemie: Kreisprozesse
 Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
Physikalische Chemie: Kreisprozesse Version vom 29. Mai 2006 Inhaltsverzeichnis 1 Diesel Kreisprozess 2 1.1 Wärmemenge Q.................................. 2 1.2 Arbeit W.....................................
Musterlösung zu Übung 7
 PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
PCI hermodynamik G. Jeschke FS 05 Musterlösung zu Übung 7 08.04.05 a Der Goldbarren wird beim Einbringen in das Reservoir sprunghaft erwärmt. Der Wärmeaustausch erfolgt daher auf irreversiblem Weg. Um
6.2 Zweiter HS der Thermodynamik
 Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
Die Änderung des Energieinhaltes eines Systems ohne Stoffaustausch kann durch Zu-/Abfuhr von Wärme Q bzw. mechanischer Arbeit W erfolgen Wird die Arbeit reversibel geleistet (Volumenarbeit), so gilt W
ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14,
 ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14, 12.02.2016 Aufgabe 1 Kreisprozesse Mit einem Mol eines idealen, monoatomaren Gases (cv = 3/2 R) wird, ausgehend
ÜBUNGEN ZUR VORLESUNG Physikalische Chemie I (PC I) (Prof. Meerholz, Hertel, Klemmer) Blatt 14, 12.02.2016 Aufgabe 1 Kreisprozesse Mit einem Mol eines idealen, monoatomaren Gases (cv = 3/2 R) wird, ausgehend
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
16 Vektorfelder und 1-Formen
 45 16 Vektorfelder und 1-Formen 16.1 Vektorfelder Ein Vektorfeld v auf D R n ist eine Abbildung v : D R n, x v(x). Beispiele. Elektrisches und Magnetisches Feld E(x), B(x), Geschwindigkeitsfeld einer Strömung
45 16 Vektorfelder und 1-Formen 16.1 Vektorfelder Ein Vektorfeld v auf D R n ist eine Abbildung v : D R n, x v(x). Beispiele. Elektrisches und Magnetisches Feld E(x), B(x), Geschwindigkeitsfeld einer Strömung
Die Carnot-Maschine SCHRITT III. Isotherme Kompression bei einer Temperatur T 2 T 2. Wärmesenke T 2 = konstant. Nicolas Thomas
 Die Carnot-Maschine SCHRITT III Isotherme Kompression bei einer Temperatur T 2 T 2 Wärmesenke T 2 = konstant Die Carnot-Maschine SCHRITT IV Man isoliert das Gas wieder thermisch und drückt den Kolben noch
Die Carnot-Maschine SCHRITT III Isotherme Kompression bei einer Temperatur T 2 T 2 Wärmesenke T 2 = konstant Die Carnot-Maschine SCHRITT IV Man isoliert das Gas wieder thermisch und drückt den Kolben noch
Lösungsvorschlag zu Übung 11
 PCI Thermodynamik G. Jeschke FS 2015 Lösungsvorschlag zu Übung 11 (Version vom 28.04.2015) Aufgabe 1 Alle Reaktionsgleichgewichte stellen sich bei 1000 K ein, damit sind alle Komponenten stets gasförmig.
PCI Thermodynamik G. Jeschke FS 2015 Lösungsvorschlag zu Übung 11 (Version vom 28.04.2015) Aufgabe 1 Alle Reaktionsgleichgewichte stellen sich bei 1000 K ein, damit sind alle Komponenten stets gasförmig.
Kapitel 8: Thermodynamik
 Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Kapitel 8: Thermodynamik 8.1 Der erste Hauptsatz der Thermodynamik 8.2 Mechanische Arbeit eines expandierenden Gases 8.3 Thermische Prozesse des idealen Gases 8.4 Wärmemaschine 8.5 Der zweite Hauptsatz
Physikdepartment. Ferienkurs zur Experimentalphysik 4. Daniel Jost 10/09/15
 Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Berechnung von Zustandsgrößen für ideale Gas im geschlossenen und offenen System
 Was Sie im letzten Lehrabschnitt gelernt haben 1 Einordnen von thermodynamischen Prozessen Berechnung von Zustandsgrößen für ideale Gas im geschlossenen und offenen System Aussage und mathematische Formulierung
Was Sie im letzten Lehrabschnitt gelernt haben 1 Einordnen von thermodynamischen Prozessen Berechnung von Zustandsgrößen für ideale Gas im geschlossenen und offenen System Aussage und mathematische Formulierung
Musterlösung Übung 7
 Musterlösung Übung 7 Aufgabe : Kühlschränke Das Prinzip eines Kühlschrankes ist schematisch in Abbildung - dargestellt. Überträgt man Wärme von der Region mit der tieferen emperatur zur Region mit der
Musterlösung Übung 7 Aufgabe : Kühlschränke Das Prinzip eines Kühlschrankes ist schematisch in Abbildung - dargestellt. Überträgt man Wärme von der Region mit der tieferen emperatur zur Region mit der
Physikalische Chemie I
 M.Bredol / M hysikalische Chemie I / 6.7.2017 1 hysikalische Chemie I Nachname orname Matrikel Aufgabe unkte erreicht Note 1 20 2 20 3 20 4 22 5 18 Summe: 100 1. Wasser besitzt die folgenden charakteristischen
M.Bredol / M hysikalische Chemie I / 6.7.2017 1 hysikalische Chemie I Nachname orname Matrikel Aufgabe unkte erreicht Note 1 20 2 20 3 20 4 22 5 18 Summe: 100 1. Wasser besitzt die folgenden charakteristischen
Thermodynamik (Wärmelehre) IV Kreisprozesse und Entropie
 Physik A VL7 (..0) hermodynamik (Wärmelehre) IV Kreisprozesse und Entropie Kreisprozesse Carnot scher Kreisprozess Reale Wärmemaschinen (tirling-motor, Dampfmaschine, Otto- und Dieselmotor) Entropie Der.
Physik A VL7 (..0) hermodynamik (Wärmelehre) IV Kreisprozesse und Entropie Kreisprozesse Carnot scher Kreisprozess Reale Wärmemaschinen (tirling-motor, Dampfmaschine, Otto- und Dieselmotor) Entropie Der.
2 Wärmelehre. Reibungswärme Reaktionswärme Stromwärme
 2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
2 Wärmelehre Die Thermodynamik ist ein Musterbeispiel an axiomatisch aufgebauten Wissenschaft. Im Gegensatz zur klassischen Mechanik hat sie die Quantenrevolution überstanden, ohne in ihren Grundlagen
4.6 Hauptsätze der Thermodynamik
 Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Thermodynamik.6 Hautsätze der Thermodynamik.6. Erster Hautsatz: Energieerhaltungssatz In einem abgeschlossenen System bleibt der gesamte Energievorrat, also die Summe aus Wärmeenergie, mechanischer Energie
Aufgabe 1: Theorie Punkte
 Aufgabe 1: Theorie.......................................... 30 Punkte (a) (2 Punkte) In einen Mischer treten drei Ströme ein. Diese haben die Massenströme ṁ 1 = 1 kg/s, ṁ 2 = 2 kg/s und ṁ 3 = 2 kg/s.
Aufgabe 1: Theorie.......................................... 30 Punkte (a) (2 Punkte) In einen Mischer treten drei Ströme ein. Diese haben die Massenströme ṁ 1 = 1 kg/s, ṁ 2 = 2 kg/s und ṁ 3 = 2 kg/s.
Prof. Dr. Peter Vogl, Thomas Eissfeller, Peter Greck. Übung in Thermodynamik und Statistik 4B Blatt 4 Lösung. P + a )
 U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
2. Thermodynamik Grundbegriffe Hauptsätze Thermodynamische Potentiale response -Funktionen
 2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & B.M. Mladek (E136) Statistische Physik I Kapitel 2 5. März 2012 1 / 25 2.1 Grundbegriffe
2. Thermodynamik 1 2.1 Grundbegriffe 2 2.2 Hauptsätze 3 2.3 Thermodynamische Potentiale 4 2.4 response -Funktionen G. Kahl & B.M. Mladek (E136) Statistische Physik I Kapitel 2 5. März 2012 1 / 25 2.1 Grundbegriffe
Thermo Dynamik. Mechanische Bewegung (= Arbeit) Wärme (aus Reaktion) maximale Umsetzung
 Thermo Dynamik Wärme (aus Reaktion) Mechanische Bewegung (= Arbeit) maximale Umsetzung Aussagen der Thermodynamik: Quantifizieren von: Enthalpie-Änderungen Entropie-Änderungen Arbeit, maximale (Gibbs Energie)
Thermo Dynamik Wärme (aus Reaktion) Mechanische Bewegung (= Arbeit) maximale Umsetzung Aussagen der Thermodynamik: Quantifizieren von: Enthalpie-Änderungen Entropie-Änderungen Arbeit, maximale (Gibbs Energie)
Allgemeines Gasgesetz. PV = K o T
 Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Allgemeines Gasgesetz Die Kombination der beiden Gesetze von Gay-Lussac mit dem Gesetz von Boyle-Mariotte gibt den Zusammenhang der drei Zustandsgrößen Druck, Volumen, und Temperatur eines idealen Gases,
Die innere Energie eines geschlossenen Systems ist konstant
 Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Rückblick auf vorherige Vorlesung Grundsätzlich sind alle möglichen Formen von Arbeit denkbar hier diskutiert: Mechanische Arbeit: Arbeit, die nötig ist um einen Massepunkt von A nach B zu bewegen Konservative
Übungen zu Experimentalphysik 2 für MSE
 Physik-Department LS für Funktionelle Materialien SS 208 Übungen zu Experimentalphysik 2 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. olker Körstgens, Sebastian Grott, Julian Heger, Dr. Neelima Paul,
Physik-Department LS für Funktionelle Materialien SS 208 Übungen zu Experimentalphysik 2 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. olker Körstgens, Sebastian Grott, Julian Heger, Dr. Neelima Paul,
Moderne Theoretische Physik IIIa WS 18/19
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik IIIa WS 8/9 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 7 Dr. Stefan Rex Besprechung: 9..9.
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik IIIa WS 8/9 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 7 Dr. Stefan Rex Besprechung: 9..9.
Grundlagen der Physik II
 Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Grundlagen der Physik II Othmar Marti 05. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 05. 07. 2007 Klausur Die Klausur
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik III im Studiengang Elektrotechnik -. Hauptsatz der Thermodynamik - Prof. Dr. Ulrich Hahn WS 2008/09 Energieerhaltung Erweiterung des Energieerhaltungssatzes der Mechanik Erfahrung: verschiedene
Physik 2 Hydrologen et al., SoSe 2013 Lösungen 3. Übung (KW 19/20) Carnot-Wärmekraftmaschine )
 3. Übung KW 19/20) Aufgabe 1 T 4.5 Carnot-Wärmekraftmaschine ) Eine Carnot-Wärmekraftmaschine arbeitet zwischen den Temperaturen und. Während der isothermen Expansion vergrößert sich das Volumen von auf
3. Übung KW 19/20) Aufgabe 1 T 4.5 Carnot-Wärmekraftmaschine ) Eine Carnot-Wärmekraftmaschine arbeitet zwischen den Temperaturen und. Während der isothermen Expansion vergrößert sich das Volumen von auf
Analysis von singulären Differentialgleichungen erster und zweiter Ordnung - Skalare Probleme
 Analysis von singulären Differentialgleichungen erster und zweiter Ordnung - Skalare Probleme Jonathan Mosser 3. Juni 27 / 38 Vorbemerkungen Singularität Singuläre Probleme können auf zwei Arten formuliert
Analysis von singulären Differentialgleichungen erster und zweiter Ordnung - Skalare Probleme Jonathan Mosser 3. Juni 27 / 38 Vorbemerkungen Singularität Singuläre Probleme können auf zwei Arten formuliert
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
TU München Reinhard Scholz Physik Department, T33 Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler http://www.wsi.tum.de/t33/teaching/teaching.htm Übung in Theoretischer Physik B (Thermodynamik)
Wärmelehre Wärme als Energie-Form
 Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
Wärmelehre Wärme als Energie-Form Joule's Vorrichtung zur Messung des mechanischen Wärme-Äquivalents alte Einheit: 1 cal = 4.184 J 1 kcal Wärme erwärmt 1 kg H 2 O um 1 K Wird einem Körper mit der Masse
Thermodynamik I. Sommersemester 2012 Kapitel 3, Teil 2. Prof. Dr.-Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr.-Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3 Bilanzgleichungen 3.3.1 Massebilanz 3.3.2 Energiebilanz und 1. Hauptsatz
Thermodynamik I Sommersemester 2012 Kapitel 3, Teil 2 Prof. Dr.-Ing. Heinz Pitsch Kapitel 3, Teil 2: Übersicht 3 Energiebilanz 3.3 Bilanzgleichungen 3.3.1 Massebilanz 3.3.2 Energiebilanz und 1. Hauptsatz
1. Klausur zur Vorlesung Physikalische Chemie I
 1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
1. Klausur zur Vorlesung Physikalische Chemie I Sommersemester 2006 8. Juni 2006 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort... Matrikelnummer...
Klausur zur Vorlesung Thermodynamik
 Institut für Thermodynamik 8. September 2012 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
Institut für Thermodynamik 8. September 2012 Technische Universität Braunschweig Prof. Dr. Jürgen Köhler Klausur zur Vorlesung Thermodynamik Für alle Aufgaben gilt: Der Rechen- bzw. Gedankengang muss stets
a) Wie nennt man den oben beschriebenen Vergleichsprozess in Bezug auf die Klassifizierung der Idealprozesse?
 Aufgabe 11: Das Betriebsverhalten eines Viertakt- Dieselmotors kann durch folgenden reversiblen Kreisprozess näherungsweise beschrieben werden, wobei kinetische und potenzielle Energien zu vernachlässigen
Aufgabe 11: Das Betriebsverhalten eines Viertakt- Dieselmotors kann durch folgenden reversiblen Kreisprozess näherungsweise beschrieben werden, wobei kinetische und potenzielle Energien zu vernachlässigen
12 Der erste Hauptsatz der Thermodynamik für geschlossene Systeme
 Der erste Hauptsatz der Thermodynamik für geschlossene Systeme Der erste Hauptsatz ist die thermodynamische Formulierung des Satzes von der Erhaltung der Energie. Er besagt, daß Energie weder erzeugt noch
Der erste Hauptsatz der Thermodynamik für geschlossene Systeme Der erste Hauptsatz ist die thermodynamische Formulierung des Satzes von der Erhaltung der Energie. Er besagt, daß Energie weder erzeugt noch
Q i + j. dτ = i. - keine pot. und kin. Energien: depot. - adiabate ZÄ: Q i = 0 - keine technische Arbeit: Ẇ t,j = 0
 Institut für hermodynamik hermodynamik - Formelsammlung. Hauptsätze der hermodynamik (a. Hauptsatz der hermodynamik i. Offenes System de = de pot + de kin + du = i Q i + j Ẇ t,j + ein ṁ ein h tot,ein aus
Institut für hermodynamik hermodynamik - Formelsammlung. Hauptsätze der hermodynamik (a. Hauptsatz der hermodynamik i. Offenes System de = de pot + de kin + du = i Q i + j Ẇ t,j + ein ṁ ein h tot,ein aus
4.1.2 Quantitative Definition durch Wärmekapazitäten
 4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
4 Energie Aus moderner (mikroskopischer Sicht ist klar, daß die Summe U der kinetischen Energien der Moleküle eines Gases (und ggf. ihrer Wechselwirkungsenergien eine thd. Zustandsgröße des Gases ist,
3 Grundlegende strömungstechnische und thermodynamische Voraussetzungen
 3 Grundlegende strömungstechnische und thermodynamische Voraussetzungen 3.1 Stationär durchströmte offene Systeme - Grundlegende Beziehungen - nergiesatz stationär durchströmter offener Systeme - nwendung
3 Grundlegende strömungstechnische und thermodynamische Voraussetzungen 3.1 Stationär durchströmte offene Systeme - Grundlegende Beziehungen - nergiesatz stationär durchströmter offener Systeme - nwendung
3 Der 1. Hauptsatz der Thermodynamik
 3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
3 Der 1. Hauptsatz der Thermodynamik 3.1 Der Begriff der inneren Energie Wir betrachten zunächst ein isoliertes System, d. h. es können weder Teilchen noch Energie mit der Umgebung ausgetauscht werden.
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester
 Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
Verbundstudium TBW Teil 1 Wärmelehre 1 3. Semester 1. Temperaturmessung Definition der Temperaturskala durch ein reproduzierbares thermodynam. Phänomen, dem Thermometer Tripelpunkt: Eis Wasser - Dampf
Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Wa
 103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
1 I. Thermodynamik. 1.1 Ideales Gasgesetz. 1.2 Vereinfachte kinetische Gastheorie. 1.3 Erster Hauptsatz der Thermodynamik.
 1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
1 I. hermodynamik 1.1 Ideales Gasgesetz eilchenzahl N Stoffmenge: n [mol], N A = 6.022 10 23 mol 1 ; N = nn A molare Größen: X m = X/n ideales Gasgesetz: V = nr, R = 8.314JK 1 mol 1 Zustandsgrößen:, V,,
