Das geteilte Quadrat
|
|
|
- Maja Breiner
- vor 8 Jahren
- Abrufe
Transkript
1 1 Ds geteilte Qudrt Puzzles from round the world by Dik Hess 19. Juli 001 Gegeben sei ein Qudrt mit der Seitenlänge. Ds Qudrt soll in zwei untershiedlihe Rehteke geteilt werden, wobei ds kleine Rehtek genu in ds große Rehtek pssen soll, wie in Abbildung 1 drgestellt. In welhen Verhältnis : muß ds Qudrt geteilt werden? Abbildung 1: Bild zur Aufgbenstellung
2 ? O Lösungsorshlg I on Feli Wolfheimer, Rosbh Wir werden die Aufgbe lgebrish mittels dreier Gleihungen lösen. Die Hilfsgrößen y und z, die bei der Berehnung uftreten, sind in der folgenden Skizze des Problems eingezeihnet., H A E A?, H A E A? Abbildung : Skizze des Problems mit den Hilfsgrößen y und z Ohne Einshränkung der Allgemeinheit werden wir im folgenden den Wert 1 [Längeneinheit] zuweisen. Es seih druf hingewiesen, dß sih ds Verhältnis : niht ändert, wenn ds Qudrt ergrößert oder erkleinert wird. Wir werden nun drei Gleihungen ufstellen, die den Zusmmenhng zwishen den Größen, z und y beshreiben. Dieses nihtlinere Gleihungssystem wird sodnn nh der Größe ufgelöst und drus ds gesuhte Verhältnis berehnet. Die erste Gleihung, die wir ufstellen können beshreibt den Zusmmenhng zwishen y und z. Mit dem Stz des Pythgors folgt z y Mit 1 gilt folglih z 1 y (1) Die zweite Gleihung folgt us der Ähnlihkeit der zwei rehtwinkligen Dreieke, die in der Skizze mrkiert sind. D die Dreieke ähnlih zueinnder sind, müssen die Verhältnisse der Seitenlägen in Dreiek 1 und Dreiek gleih sein. Dmit folgt y {{{{ z Dreiek1 Dreiek
3 3 Setzt mn für 1 und für z den Wert us Gleihung 1, so erhält mn 1 y 1 1 y () Die nähste Gleihung ergibt sih wie shon die orherige us den Ähnlihkeitssätzen. Nur setzen wir dieses Ml ndere Seiten der beiden Dreieke ins Verhältnis. Es folgt {{ z y {{ Dreiek1 Dreiek Setzt mn wieder 1 ein, so folgt, wenn mn ußerdem noh für z den Wert us Gleihung (1) einsetzt 1 1 y 1 y Löst mn Gleihung (3) nh y uf, so ergibt sih (3) y (4) Nun eliminieren wir ls letztes y us Gleihung (), indem wir den unter (4) gefundenen Ausdruk einsetzen. Es folgt 1 1 ( 1 1+ ) Dies ist die Bestimmungsgleihung für, die es nun zu lösen gilt. Der Lösungsweg soll mit den unten orgeführten Shritten grob skizziert werden T (1+ ) : (1 + ) ( ) (1 ) , ± 3 D ntürlih < 1 gelten muß, ist die Lösung 3 die einzig sinnolle Lösung. Ds gesuhte Verhältnis ist dher 1 3
4 4 Lösungsorshlg II Wir bezeihnen die Abshnitte uf den Rehtekseiten wie folgt: y u u y Abbildung 3: Bild zur Aufgbenstellung Vier Gleihungen lssen sih unmittelbr us Abbildung blesen: u + y (1) + () + y (3) u + (4) Bei gegebenen enthlten diese ier Gleihungen fünf Unbeknnte. Um eine eindeutige Lösung zu erzielen, wird noh ein fünfte Bedingung benötigt. Betrhtet mn ds goße Dreik mit den Seiten y, u, und ds kleine Dreiek mit den Seiten,,, so stellt mn fest, ds es sih um ähnlihe Dreiek hndelt (gleih große Innenwinkel!). Sie sind um 90 zueinder gedreht. Dmit ergibt sih ls fünfte Gleihung:
5 5 u y u y (5) Weiterhin knn us dem Flähenäquilent on Qudrt, den Dreieken und den beiden Rehtekstreifen eine Beziehung bgeleitet werden: + + u y (6) Zur Auflösung des Gleihungssystems wird ein Computerlgebrprogrmm wie Derie, MpleV oder Mthemti benutzt. In Mthemti erhält mn ls Lösungsmenge für Gleihung... 6 : Sole[{gl, gl3, gl4, gl5, gl6, {, y, u,, ] {{ y 0, u,, 0, {, y, u 3, + 3, 1 ) ) ( + 3, 1 ( 3 3, { y, u 3, 3, 1 ) ( 3, 1 ( ), { y i ), u + i ), 0, i ), + i ), { y + i ), u i ), 0, + i ), i ), {y, u, 0, 0, 0, Der erste Fll mit bedeutet, ds ds Qudrt im Verhältnis 1 1 geteilt wird. Lut Aufgbenstellung soll ds Qudrt in zwei untershiedlih große Rehteke zerlegt werden. Die Lösung mit + 3 und u 3 kommt niht in Betrht, d < sein muß und lle Streken größer Null sein müssen. Die kompleen Lösungsnteile sind nur im Bereih der theoretishen Mthemtik on Bedeutung. Die letzte Teillösung mit y und 0 heißt, dss ds Rehtek zur Linie entrtet. Als einzige sinnolle Lösung erbleibt dmit: ( 3) (7) ( 3 3) (8) ( 3) (9) u 3 y (10) (11) In Abbildung 3 ist ds Qudrt mit einer Seitenlänge on 6 m und dem Teilungserhältnis 1 3 drgestellt.
6 6 Lösungsorshlg III Während der orn gezeigte Lösungsweg uf ein kompliziertes Gleihungssystem führt soll nun eine Lösung gezeigt werden, die mit elementren Geometriekenntnissen uskommt. Als Lösungsskizze dient Abbildung 4. Es lssen sih folgende Beziehungen blesen: G D A d d H K F E C B Abbildung 4: Skizze zur zweiten Lösung ABC DEF F E (1) + () Ds HGD ist dem HKF ähnlih (gleihe Innenwinkel). Ds Verhältnis der Dreieksseiten muß dher gleih sein. GD, HD HK 1 HF (3) Der Stz des Pythgors im HKF liefert shließlih die Lösung: + ( ) + ( ) (4) ( 3) (5)
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Chemisches Gleichgewicht
 TU Ilmenu Chemishes Prktikum Versuh Fhgebiet Chemie 1. Aufgbe Chemishes Gleihgewiht Stellen Sie 500 ml einer 0,1m N her! estimmen Sie die genue onzentrtion der hergestellten N mit zwei vershiedenen Anlysenmethoden
TU Ilmenu Chemishes Prktikum Versuh Fhgebiet Chemie 1. Aufgbe Chemishes Gleihgewiht Stellen Sie 500 ml einer 0,1m N her! estimmen Sie die genue onzentrtion der hergestellten N mit zwei vershiedenen Anlysenmethoden
750 + 142,50 = 892,50 Nettopreis Umsatzsteuer Bruttopreis
 2.7 Verminderter und vermehrter Grundwert 41 Beispiel: Bruttobetrg, Nettobetrg, Umstzsteuer Profirdfhrer Klus kuft sih ein Mountinbike. Ds Fhrrd kostet einshließlih 19 % Umstzsteuer 892,50. Ds Finnzmt
2.7 Verminderter und vermehrter Grundwert 41 Beispiel: Bruttobetrg, Nettobetrg, Umstzsteuer Profirdfhrer Klus kuft sih ein Mountinbike. Ds Fhrrd kostet einshließlih 19 % Umstzsteuer 892,50. Ds Finnzmt
Spannung galvanischer Zellen (Zellspannungen)
 Spnnung glvnisher Zellen (Zellspnnungen) Ziel des Versuhes Kennenlernen der Abhängigkeit der Zellspnnung von den Konzentrtionen der potenzilbestimmenden Ionen (Nernst-Gleihung). Anwendung der Zellspnnungsmessung
Spnnung glvnisher Zellen (Zellspnnungen) Ziel des Versuhes Kennenlernen der Abhängigkeit der Zellspnnung von den Konzentrtionen der potenzilbestimmenden Ionen (Nernst-Gleihung). Anwendung der Zellspnnungsmessung
1. Elektrostatische Felder E
 1. Elektrosttishe Felder E Zusmmenfssung wihtiger Formeln Die Elektrosttik beshäftigt sih mit den Feldern zeitlih konstnter Ldungsverteilungen. Grundlge dfür ist die Coulomb-Krft uf eine infinitesimle
1. Elektrosttishe Felder E Zusmmenfssung wihtiger Formeln Die Elektrosttik beshäftigt sih mit den Feldern zeitlih konstnter Ldungsverteilungen. Grundlge dfür ist die Coulomb-Krft uf eine infinitesimle
AT = λ TB. Kapitel 5: Teilverhältnisse und Ähnlichkeit. Definition Teilverhältnis λ. Allgemeiner
 Definition Teilverhältnis Definition Teilverhältnis Üung Kpitel 5: Teilverhältnisse und Ähnlihkeit Definition Teilverhältnis λ λ T T llgemeiner T λ T T T T T ist innerer Teilpunkt, flls λ > 0 T ist äußerer
Definition Teilverhältnis Definition Teilverhältnis Üung Kpitel 5: Teilverhältnisse und Ähnlihkeit Definition Teilverhältnis λ λ T T llgemeiner T λ T T T T T ist innerer Teilpunkt, flls λ > 0 T ist äußerer
Kapitel 6 E-Mails schreiben und organisieren
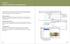 Kpitel 6 E-Mils shreien und orgnisieren Die Kommuniktion vi E-Mil ist heute essenziell. Und Ihr M ist estens gerüstet für den Empfng, ds Verfssen und die Orgnistion von E-Mils. Wie Sie effektiv mit dem
Kpitel 6 E-Mils shreien und orgnisieren Die Kommuniktion vi E-Mil ist heute essenziell. Und Ihr M ist estens gerüstet für den Empfng, ds Verfssen und die Orgnistion von E-Mils. Wie Sie effektiv mit dem
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Musterlösung zu Aufgabe 1 (Klassenstufe 9/10)
 Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Grundwissen Abitur Analysis
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
2 Kinobesuch GRAMMATIK. perfekt. Im September LEICHT. wann die Vorstellung beginnt. Schreiben Sie Sätze! Beginnen Sie mit den grün markierten Wörtern!
 DEUTSCH GRAMMATIK VERBPOSITION S. 0 Im Septemer LEICHT Shreien Sie Sätze! Beginnen Sie mit den grün mrkierten Wörtern! der Herst / m. Septemer / eginnt ds Oktoerfest / in Münhen / findet sttt die Österreiher
DEUTSCH GRAMMATIK VERBPOSITION S. 0 Im Septemer LEICHT Shreien Sie Sätze! Beginnen Sie mit den grün mrkierten Wörtern! der Herst / m. Septemer / eginnt ds Oktoerfest / in Münhen / findet sttt die Österreiher
Mathematik Thema Vielecke
 Them Vielecke Im Jnur 2006 Florin Vetter, Klsse 8, Riegelhof Relschule Seite 1 von 15 INHALTSVERZEICHNES 1. EINLEITUNG 3 2. ARTEN VON VIELECKEN 4 2.1. DREIECK 4 2.2. VIERECK 4 2.2.1. RECHTECK 4 2.2.2.
Them Vielecke Im Jnur 2006 Florin Vetter, Klsse 8, Riegelhof Relschule Seite 1 von 15 INHALTSVERZEICHNES 1. EINLEITUNG 3 2. ARTEN VON VIELECKEN 4 2.1. DREIECK 4 2.2. VIERECK 4 2.2.1. RECHTECK 4 2.2.2.
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Musterlösung zur Musterprüfung 2 in Mathematik
 Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
Brückenkurs Mathematik Dr. Karl TH Nürnberg
 Brükekurs Mthemtik Dr. Krl TH Nürerg Qudrtishe Gleihuge Ugleihuge Copyright : Huert Krl Alle Rehte vorehlte. Diese Puliktio drf ohe die usdrüklihe shriftlihe Geehmigug des Autors weder gz oh uszugsweise
Brükekurs Mthemtik Dr. Krl TH Nürerg Qudrtishe Gleihuge Ugleihuge Copyright : Huert Krl Alle Rehte vorehlte. Diese Puliktio drf ohe die usdrüklihe shriftlihe Geehmigug des Autors weder gz oh uszugsweise
Orientierungshilfe zu Auswahltests Training, Tipps und Taktik Bundesagentur für Arbeit
 Informtionen für Jugendlihe Orientierungshilfe zu Auswhltests Trining, Tipps und Tktik Bundesgentur für Areit Bundesgentur für Areit I N H A LT Orientierungshilfe zu Auswhltests Inhlt Seite 3 Vorwort
Informtionen für Jugendlihe Orientierungshilfe zu Auswhltests Trining, Tipps und Tktik Bundesgentur für Areit Bundesgentur für Areit I N H A LT Orientierungshilfe zu Auswhltests Inhlt Seite 3 Vorwort
Keil Telecom Homepage - Hersteller von Isdn Tk Anlagen und Türsprechsystemen für Heim und Bü...
 Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
ÜBUNGSSATZ 01 ZERTIFIKAT DEUTSCH FÜR DEN BERUF. Kandidatenblätter STRUKTUREN UND WORTSCHATZ ZEIT: 30 MINUTEN. ZDfB_Ü01_SW_06 120206
 Felix Brndl Münhen ZDfB_Ü01_SW_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 30 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Lesen Sie den folgenden Text zuerst
Felix Brndl Münhen ZDfB_Ü01_SW_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 30 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Lesen Sie den folgenden Text zuerst
Musterlösungen (ohne Gewähr) Aufgabe 1 ( 7 Punkte) Geben Sie die Koordinaten des Flächenschwerpunktes des dargestellten Querschnitts an!
 Seite 1/15 Aufgbe 1 ( 7 Punkte) Geben Sie die Koordinten des lächenschwerpunktes des drgestellten Querschnitts n! 2 Gegeben:. 4 ΣA i = y 2 x Σx i A i = x s = Σy i A i = y s = ΣA i = 8 2 Σx i A i = 13 3
Seite 1/15 Aufgbe 1 ( 7 Punkte) Geben Sie die Koordinten des lächenschwerpunktes des drgestellten Querschnitts n! 2 Gegeben:. 4 ΣA i = y 2 x Σx i A i = x s = Σy i A i = y s = ΣA i = 8 2 Σx i A i = 13 3
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Das customized Alignersystem
 Inwieweit durh Einstz modernster Computertehnologie die Aktivierung von Korrekturshienen noh präziser relisiert werden knn, demonstriert Dr. Wjeeh Khn nhnd des von ihm entwikelten orthops -Alignersystems*.
Inwieweit durh Einstz modernster Computertehnologie die Aktivierung von Korrekturshienen noh präziser relisiert werden knn, demonstriert Dr. Wjeeh Khn nhnd des von ihm entwikelten orthops -Alignersystems*.
Stabile Hochzeiten wie und warum?
 Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik [email protected] Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik [email protected] Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Deutsch. Installationsanleitung. Italiano. Guida di installazione. Português. Manual de instalação
 Instlltionsnleitung Deutsh Guid di instllzione Itlino Mnul de instlção Português Sihere Verwendung des Produktes Siherheitsnweisungen Zu Ihrer Siherheit sollten Sie lle Anweisungen in dieser Anleitung
Instlltionsnleitung Deutsh Guid di instllzione Itlino Mnul de instlção Português Sihere Verwendung des Produktes Siherheitsnweisungen Zu Ihrer Siherheit sollten Sie lle Anweisungen in dieser Anleitung
1 152.17. 1. Gegenstand und Zweck
 5.7. März 0 Verordnung üer die Klssifizierung, die Veröffentlihung und die Arhivierung von Dokumenten zu Regierungsrtsgeshäften (Klssifizierungsverordnung, KRGV) Der Regierungsrt des Kntons Bern, gestützt
5.7. März 0 Verordnung üer die Klssifizierung, die Veröffentlihung und die Arhivierung von Dokumenten zu Regierungsrtsgeshäften (Klssifizierungsverordnung, KRGV) Der Regierungsrt des Kntons Bern, gestützt
8.3. Komplexe Zahlen
 8.. Komplee Zhle Wie bereits i 8.. drgestellt, wurde die fortlufede Erweiterug der Zhlbereiche durch die Eiführug immer kompleerer Recheopertioe otwedig:. Auf de türliche Zhle führte der Wusch ch iverse
8.. Komplee Zhle Wie bereits i 8.. drgestellt, wurde die fortlufede Erweiterug der Zhlbereiche durch die Eiführug immer kompleerer Recheopertioe otwedig:. Auf de türliche Zhle führte der Wusch ch iverse
Solatube Brighten Up -Serie
 Soltue Brighten Up -Serie Soltue 60 DS DS-Tgeslihteleuhtungssystem Soltue 290 DS DS-Tgeslihteleuhtungssystem Montgenleitung 8 Teileliste * Anzhl Kuppel mit Ryender 3000-Tehnologie (). Kuppelstoßdämpfer*
Soltue Brighten Up -Serie Soltue 60 DS DS-Tgeslihteleuhtungssystem Soltue 290 DS DS-Tgeslihteleuhtungssystem Montgenleitung 8 Teileliste * Anzhl Kuppel mit Ryender 3000-Tehnologie (). Kuppelstoßdämpfer*
FernUniversität Gesamthochschule in Hagen
 FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
SPRACHFERIEN KÜNZELSAU 2008
 SPRACHFERIEN KÜNZELSAU 2008 (Mittelstufe) CODENUMMER: I. Lesen Sie den Text. Entsheiden Sie, welhe der Antworten ( ) psst. Es git jeweils nur eine rihtige Lösung. GEMEINSAM FÚR SPRACHE UND KULTUR Ashenputtel,
SPRACHFERIEN KÜNZELSAU 2008 (Mittelstufe) CODENUMMER: I. Lesen Sie den Text. Entsheiden Sie, welhe der Antworten ( ) psst. Es git jeweils nur eine rihtige Lösung. GEMEINSAM FÚR SPRACHE UND KULTUR Ashenputtel,
Z R Z R Z R Z = 50. mit. aus a) Z L R. Wie groß ist der Leistungsfaktor cos der gesamten Schaltung?
 Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Internationale Ökonomie I Vorlesung 3: Das Riccardo-Modell: Komparative Vorteile und Produktivität (Master)
 Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Beispiel-Abiturprüfung
 Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Matrizen und Determinanten
 Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Übungsheft Mittlerer Schulabschluss Mathematik
 Ministerium für Bildung und Kultur des Lndes Schleswig-Holstein Zentrle Abschlussrbeit 011 Übungsheft Mittlerer Schulbschluss Mthemtik Korrekturnweisung Impressum Herusgeber Ministerium für Bildung und
Ministerium für Bildung und Kultur des Lndes Schleswig-Holstein Zentrle Abschlussrbeit 011 Übungsheft Mittlerer Schulbschluss Mthemtik Korrekturnweisung Impressum Herusgeber Ministerium für Bildung und
Sie das Gerät aus und überprüfen Sie den Lieferumfang. Netzkabel. Trägerbogen/Plastikkarten-Trägerbogen DVD-ROM
 Instlltionsnleitung Hier eginnen ADS-2100 Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät einrihten. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Instlltionsnleitung Hier eginnen ADS-2100 Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät einrihten. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
ZDfB_Ü01_LV_06 120206. Felix Brandl München ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01. Kandidatenblätter LESEVERSTEHEN ZEIT: 40 MINUTEN
 Felix Brndl Münhen ZDfB_Ü01_LV_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 40 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Bitte lesen Sie den folgenden
Felix Brndl Münhen ZDfB_Ü01_LV_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 40 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Bitte lesen Sie den folgenden
TE- und TM-Moden im Wellenleiter. Bachelorarbeit
 TE- und TM-Moden im Wellenleiter Sebstin Rubitzek 30. September 2014 in Grz Bchelorrbeit betreut von Ao.Univ.-Prof. Mg. Dr.rer.nt. Ulrich Hohenester 1 Inhltsverzeichnis 1 Einleitung 3 1.1 Ws ist ein Wellenleiter?......................
TE- und TM-Moden im Wellenleiter Sebstin Rubitzek 30. September 2014 in Grz Bchelorrbeit betreut von Ao.Univ.-Prof. Mg. Dr.rer.nt. Ulrich Hohenester 1 Inhltsverzeichnis 1 Einleitung 3 1.1 Ws ist ein Wellenleiter?......................
Grundlagen der Technischen Informatik. Bausteine der Digitaltechnik - Binäre Schalter und Gatter. Kapitel 7.1
 Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Übungssatz 01 FIT IN DEUTSCH 1. Kandidatenblätter/Prüferblätter ISBN: 3-938744-76-6. FIT1_ÜS01_Kandidaten-/Prueferblaetter_Oktober_2005
 KASTNER AG ds medienhus FIT_ÜS_Kndidten-/Prueferletter_Oktoer_5 FIT IN DEUTSCH Üungsstz Kndidtenlätter/Prüferlätter ISBN: 3-938744-76-6 Fit in Deutsh. Üungsstz Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen
KASTNER AG ds medienhus FIT_ÜS_Kndidten-/Prueferletter_Oktoer_5 FIT IN DEUTSCH Üungsstz Kndidtenlätter/Prüferlätter ISBN: 3-938744-76-6 Fit in Deutsh. Üungsstz Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen
Besprechung der thermodynamischen Grundlagen von Wärmekraftmaschinen und Wärmepumpen
 3.5 Zustandsänderung nderung von Gasen Ziel: Besrehung der thermodynamishen Grundlagen von Wärmekraftmashinen und Wärmeumen Zustand von Gasen wird durh Druk, olumen, und emeratur beshrieben thermodyn.
3.5 Zustandsänderung nderung von Gasen Ziel: Besrehung der thermodynamishen Grundlagen von Wärmekraftmashinen und Wärmeumen Zustand von Gasen wird durh Druk, olumen, und emeratur beshrieben thermodyn.
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
2008-06-11 Klassenarbeit 5 Klasse 10c Mathematik
 2008-06- Klssenrbeit 5 Klsse 0c Mtemtik Lösung Version 2008-06-4 Cindy t 3000 geerbt. ) Den Betrg will sie so nlegen, dss sie in 20 Jren doppelt so viel Geld t. Berecne, zu welcem Zinsstz sie ds Geld nlegen
2008-06- Klssenrbeit 5 Klsse 0c Mtemtik Lösung Version 2008-06-4 Cindy t 3000 geerbt. ) Den Betrg will sie so nlegen, dss sie in 20 Jren doppelt so viel Geld t. Berecne, zu welcem Zinsstz sie ds Geld nlegen
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Shortest Path Algorithmus von Edsger Dijkstra
 Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Mäxchen ein Würfelspiel
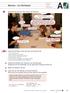 Mäxhen ein Würfelspiel A A1 Betrhten Sie ds Foto. Ws mhen die Personen? 2 + 5 Fünfundzwnzig..., hlt, nein: zweiundfünfzig. 3 + 2 Dreier Psh Ds glue ih niht. Ds will ih sehen. Ertppt! Du hst j nur eine
Mäxhen ein Würfelspiel A A1 Betrhten Sie ds Foto. Ws mhen die Personen? 2 + 5 Fünfundzwnzig..., hlt, nein: zweiundfünfzig. 3 + 2 Dreier Psh Ds glue ih niht. Ds will ih sehen. Ertppt! Du hst j nur eine
17 Doppelbündel-Rekonstruktion mit Semitendinosussehne
 Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Licht- und rasterelektronenmikroskopischen Aufnahmen zur prae- und perinatalen Entwicklung der Hundekralle
 ABBILDUNGEN 207 8. ABBILDUNGEN Liht- und rsterelektronenmikroskopishen Aufnhmen zur pre- und perintlen Entwiklung der Hundekrlle Wenn niht nders ngegeen, sind Längsshnitte uf den Aildungen mit der Krllensis
ABBILDUNGEN 207 8. ABBILDUNGEN Liht- und rsterelektronenmikroskopishen Aufnhmen zur pre- und perintlen Entwiklung der Hundekrlle Wenn niht nders ngegeen, sind Längsshnitte uf den Aildungen mit der Krllensis
Controlling als strategisches Mittel im Multiprojektmanagement von Rudolf Fiedler
 von udolf Fiedler Zusmmenfssung: Der Beitrg eshreit die Aufgen des Projektontrollings, insesondere des strtegishen Projektontrollings. Für die wesentlihen Aufgenereihe werden prktikle Instrumente vorgestellt.
von udolf Fiedler Zusmmenfssung: Der Beitrg eshreit die Aufgen des Projektontrollings, insesondere des strtegishen Projektontrollings. Für die wesentlihen Aufgenereihe werden prktikle Instrumente vorgestellt.
Brückenkurs Mathematik
 Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
1 Fairer Handel Hintergrund zur Aktion. 2 Konzeption
 1 Firer Hndel Hintergrund zur Aktion 1.1 Problemstellung Shokolde, Bnnen, Orngensft und Tee Lebensmittel us den Entwiklungsländern wndern ls Pusenverpflegung regelmäßig in die Shultshen. Doh nur wenige
1 Firer Hndel Hintergrund zur Aktion 1.1 Problemstellung Shokolde, Bnnen, Orngensft und Tee Lebensmittel us den Entwiklungsländern wndern ls Pusenverpflegung regelmäßig in die Shultshen. Doh nur wenige
DV1_Kapitel_5.doc Seite 5-1 von 36 Rüdiger Siol 12.09.2009 16:31
 Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Regressionsverfahren haben viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der folgenden beiden Kategorien:
 Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet
Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet
Ja, klar! Das weiß ich.
 J, klr! Ds weiß ih. Einstieg ins Modul 1: Wir und die nderen Areit mit den Aildungen S. XXX Lösung: 1G; 2K; 3C; 4E; 5F; 6H; 7B; 8D; 9I; 10J; 11L; 12A Einführung der Begriffe Sprehen, Shreien, Lesen und
J, klr! Ds weiß ih. Einstieg ins Modul 1: Wir und die nderen Areit mit den Aildungen S. XXX Lösung: 1G; 2K; 3C; 4E; 5F; 6H; 7B; 8D; 9I; 10J; 11L; 12A Einführung der Begriffe Sprehen, Shreien, Lesen und
( 3) k ) = 3) k 2 3 für k gerade
 Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3
Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3
Installation und Einsatz von ImageShare
 Instlltion und Einstz von ImgeShre Copyright 2000-2002: Polycom, Inc. Polycom, Inc., 4750 Willow Rod, Plesnton, CA 94588 www.polycom.com Polycom und ds Polycom-Logo sind eingetrgene Mrken der Polycom,
Instlltion und Einstz von ImgeShre Copyright 2000-2002: Polycom, Inc. Polycom, Inc., 4750 Willow Rod, Plesnton, CA 94588 www.polycom.com Polycom und ds Polycom-Logo sind eingetrgene Mrken der Polycom,
Teilfachprüfung Mathematik Studiengang: Wirtschaft Neue Diplomprüfungsordnung (NPO)
 Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
Fchhochschule Düsseldorf SS 2007 Teilfchprüfung Mthemtik Studiengng: Wirtschft Neue Diplomprüfungsordnung (NPO) Prüfungsdtum: 29..2007 Prüfer: Prof. Dr. Horst Peters / Dipl. Volkswirt Lothr Schmeink Prüfungsform:
VIESMANN. VITODENS Abgassysteme für Gas-Brennwertkessel 3,8 bis 105,0 kw. Planungsanleitung ABGASSYSTEME VITODENS
 VIESMANN VITODENS Agssysteme für Gs-Brennwertkessel 3,8 is 105,0 kw Plnungsnleitung ABGASSYSTEME VITODENS 5369 08 5/011 Inhltsverzeihnis Inhltsverzeihnis 1. Agssysteme 1.1... 4 Butehnishe Einheit... 4
VIESMANN VITODENS Agssysteme für Gs-Brennwertkessel 3,8 is 105,0 kw Plnungsnleitung ABGASSYSTEME VITODENS 5369 08 5/011 Inhltsverzeihnis Inhltsverzeihnis 1. Agssysteme 1.1... 4 Butehnishe Einheit... 4
Satzung Elephants Club e.v. Stand Dezember 2010. ELEPHANTS CLUB e. V. Vereinsregister-Nr.: 10751, Amtsgericht Frankfurt/Main
 Stzung Elephnts Clu e.v. Stnd Dezemer 2010 ELEPHANTS CLUB e. V. Vereinsregister-Nr.: 10751, Amtsgeriht Frnkfurt/Min 1 Nme, Sitz und Geshäftsjhr 1.1 Der Nme der Vereines lutet: Elephnts Clu e.v. 1.2 Der
Stzung Elephnts Clu e.v. Stnd Dezemer 2010 ELEPHANTS CLUB e. V. Vereinsregister-Nr.: 10751, Amtsgeriht Frnkfurt/Min 1 Nme, Sitz und Geshäftsjhr 1.1 Der Nme der Vereines lutet: Elephnts Clu e.v. 1.2 Der
3 Exzisionstechniken und Defektdeckungen in speziellen Lokalisationen
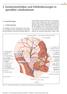 95 3 Exzisionstehniken und Defektdekungen in speziellen Loklistionen 3.1 Kopf-Hls-Region Voremerkungen Die Häufigkeit störender Veränderungen sowie enigner und mligner kutner Neuildungen im Kopf-Hls- Bereih
95 3 Exzisionstehniken und Defektdekungen in speziellen Loklistionen 3.1 Kopf-Hls-Region Voremerkungen Die Häufigkeit störender Veränderungen sowie enigner und mligner kutner Neuildungen im Kopf-Hls- Bereih
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Hier beginnen DCP-J140W
 Instlltionsnleitung Hier eginnen DCP-J140W Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät in Betrie nehmen. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Instlltionsnleitung Hier eginnen DCP-J140W Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät in Betrie nehmen. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Die nächste Übung ist vom 12.1. auf den 19.1.2012 verlegt worden.
 Allgemeines Einige Hinweise: Die nähste Üung ist vom.. auf den 9..0 verlegt worden. Die alten Klausuren findet Ihr unter folgendem Link: http://www.wiwi.uni muenster.de/vwt/studieren/pruefungen_marktpreis.htm
Allgemeines Einige Hinweise: Die nähste Üung ist vom.. auf den 9..0 verlegt worden. Die alten Klausuren findet Ihr unter folgendem Link: http://www.wiwi.uni muenster.de/vwt/studieren/pruefungen_marktpreis.htm
80 Isolation 0.0. Das Diagramm zeigt den Temperaturverlauf im Stab.
 Wäreleiung in ruhenden Soffen 45 x x C 0,00 50,00 0,0 05,07 0,3 9,76 0,6 8,53 0,9 74, 0, 67,5 0,5 6,74 0,8 57,44 0,3 54, 0,34 5,98 0,37 50,66 0,40 50,3 Teeraur in C 40 W 0 00 80 Isolaion 60 40 0 0.0 0
Wäreleiung in ruhenden Soffen 45 x x C 0,00 50,00 0,0 05,07 0,3 9,76 0,6 8,53 0,9 74, 0, 67,5 0,5 6,74 0,8 57,44 0,3 54, 0,34 5,98 0,37 50,66 0,40 50,3 Teeraur in C 40 W 0 00 80 Isolaion 60 40 0 0.0 0
Brückenkurs MATHEMATIK
 Brückenkurs MATHEMATIK Professor Dr. rer. nt. Bernd Bumnn Professor Dr. rer. nt. Ulrich Stein Hochschule für Angewndte Wissenschften Hmburg 5. März 008 VO R B E M E R K U N G E N Liebe Studentin, lieber
Brückenkurs MATHEMATIK Professor Dr. rer. nt. Bernd Bumnn Professor Dr. rer. nt. Ulrich Stein Hochschule für Angewndte Wissenschften Hmburg 5. März 008 VO R B E M E R K U N G E N Liebe Studentin, lieber
Grundwissen Mathematik 7I
 Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
Gerd Wöstenkühler. Grundlagen der Digitaltechnik Elementare Komponenten, Funktionen und Steuerungen
 Gerd Wöstenkühler Grundlgen der Digitltehnik Elementre Komponenten, Funktionen und Steuerungen Inhlt 1 Einleitung... 11 1.1 Anloge unddigitledrstellungsformen... 11 1.1.1 AnlogeGrößendrstellung... 11 1.1.2
Gerd Wöstenkühler Grundlgen der Digitltehnik Elementre Komponenten, Funktionen und Steuerungen Inhlt 1 Einleitung... 11 1.1 Anloge unddigitledrstellungsformen... 11 1.1.1 AnlogeGrößendrstellung... 11 1.1.2
Hier beginnen DCP-J152W
 Instlltionsnleitung Hier eginnen DCP-J152W Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät in Betrie nehmen. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Instlltionsnleitung Hier eginnen DCP-J152W Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät in Betrie nehmen. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Elektrischer Widerstand und Strom-Spannungs-Kennlinien
 Versuch 6 Elektrischer Widerstnd und Strom-Spnnungs-Kennlinien Versuchsziel: Durch biochemische ektionen ufgebute Potentildifferenzen (Spnnungen) bewirken elektrische Ströme im Orgnismus, die n einer Vielzhl
Versuch 6 Elektrischer Widerstnd und Strom-Spnnungs-Kennlinien Versuchsziel: Durch biochemische ektionen ufgebute Potentildifferenzen (Spnnungen) bewirken elektrische Ströme im Orgnismus, die n einer Vielzhl
DIN 41612/60603-2 Steckverbinder und ergänzende Komponenten. www.erni.com. Katalog D 074559 11/09 Ausgabe 2
 DIN /00- tekverinder und ergänzende Komponenten www.erni.om Ktlog D 09 /09 Ausge www.erni.om Ctlog E 0 Ktlog 0/0 D 09 /09 Edition Ausge www.erni.om DIN /IEC 00- tekverinder Inhltsverzeihnis DIN /IEC 00-
DIN /00- tekverinder und ergänzende Komponenten www.erni.om Ktlog D 09 /09 Ausge www.erni.om Ctlog E 0 Ktlog 0/0 D 09 /09 Edition Ausge www.erni.om DIN /IEC 00- tekverinder Inhltsverzeihnis DIN /IEC 00-
Aussichten A1. Einstufungstest. Autorin: Sanja Mazuranic Redaktion: Renate Weber Layout: Claudia Stumpfe Satz: Regina Krawatzki, Stuttgart
 Aussihten A1 Autorin: Snj Mzurni Rektion: Rente Weer Lyout: Clui Stumpfe Stz: Regin Krwtzki, Stuttgrt Ernst Klett Sprhen GmH, Stuttgrt 2010 www.klett.e Alle Rehte vorehlten. Aussihten A1 Aussihten A1 Aufgenltt
Aussihten A1 Autorin: Snj Mzurni Rektion: Rente Weer Lyout: Clui Stumpfe Stz: Regin Krwtzki, Stuttgrt Ernst Klett Sprhen GmH, Stuttgrt 2010 www.klett.e Alle Rehte vorehlten. Aussihten A1 Aussihten A1 Aufgenltt
Laser und Wellenoptik, Teil B
 Physikalishes Anfängerpraktikum Gruppe Mo-16 Sommersemester 006 Jens Kühenmeister (153810) Julian Merkert (1999) Versuh: P-4 Laser und Wellenoptik, Teil B - Vorbereitung - Vorbemerkung Bereits 1917 erkannte
Physikalishes Anfängerpraktikum Gruppe Mo-16 Sommersemester 006 Jens Kühenmeister (153810) Julian Merkert (1999) Versuh: P-4 Laser und Wellenoptik, Teil B - Vorbereitung - Vorbemerkung Bereits 1917 erkannte
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
Krankheitskostenversicherung
 Brmeni Krnkenversiherung. G. Huptverwltung Brmeni-Allee 1 42119 Wuppertl Krnkheitskostenversiherung Trif B-Smrt+ Ergänzungstrif für Personen, die in der deutshen gesetzlihen Krnkenversiherung versihert
Brmeni Krnkenversiherung. G. Huptverwltung Brmeni-Allee 1 42119 Wuppertl Krnkheitskostenversiherung Trif B-Smrt+ Ergänzungstrif für Personen, die in der deutshen gesetzlihen Krnkenversiherung versihert
McAfee Firewall Enterprise Control Center
 Shnellstrt Hnuh Revision A MAfee Firewll Enterprise Control Center Version 5.3.x In iesem Hnuh für en Shnellstrt finen Sie llgemeine Anweisungen zum Einrihten von MAfee Firewll Enterprise Control Center
Shnellstrt Hnuh Revision A MAfee Firewll Enterprise Control Center Version 5.3.x In iesem Hnuh für en Shnellstrt finen Sie llgemeine Anweisungen zum Einrihten von MAfee Firewll Enterprise Control Center
Verkürzungsfaktor bei Antennen und Koax-Leitungen
 071111 [email protected] Verkürzungsaktor bei Antennen und Koax-Leitungen Vielleiht haben Sie sih beim Bau von Antennen oder Umwegleitungen auh shon geragt, woher eigentlih der Verkürzungsaktor stammt.
071111 [email protected] Verkürzungsaktor bei Antennen und Koax-Leitungen Vielleiht haben Sie sih beim Bau von Antennen oder Umwegleitungen auh shon geragt, woher eigentlih der Verkürzungsaktor stammt.
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschftsmthemtik für Interntionl Mngement (BA) und Betriebswirtschft (BA) Wintersemester 2013/14 Stefn Etschberger Hochschule Augsburg Mthemtik: Gliederung 1 Aussgenlogik 2 Linere Algebr 3 Linere
Wirtschftsmthemtik für Interntionl Mngement (BA) und Betriebswirtschft (BA) Wintersemester 2013/14 Stefn Etschberger Hochschule Augsburg Mthemtik: Gliederung 1 Aussgenlogik 2 Linere Algebr 3 Linere
16.3 Unterrichtsmaterialien
 16.3 Unterrichtsmterilien Vness D.l. Pfeiffer, Christine Glöggler, Stephnie Hhn und Sven Gembll Mteril 1: Alignieren von Nukleotidsequenzen für die Verwndtschftsnlyse Für eine Verwndtschftsnlyse vergleicht
16.3 Unterrichtsmterilien Vness D.l. Pfeiffer, Christine Glöggler, Stephnie Hhn und Sven Gembll Mteril 1: Alignieren von Nukleotidsequenzen für die Verwndtschftsnlyse Für eine Verwndtschftsnlyse vergleicht
Übungssatz 02 FIT IN DEUTSCH 2. Kandidatenblätter/Prüferblätter ISBN: 3-938744-85-5. FIT2_ÜS02_Kandidaten-/Prueferblaetter_April_2006
 KASTNER AG ds medienhus FIT2_ÜS02_Kndidten-/Prueferletter_April_2006 FIT IN DEUTSCH 2 Üungsstz 02 Kndidtenlätter/Prüferlätter ISBN: 3-938744-85-5 Üungsstz 02 Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen
KASTNER AG ds medienhus FIT2_ÜS02_Kndidten-/Prueferletter_April_2006 FIT IN DEUTSCH 2 Üungsstz 02 Kndidtenlätter/Prüferlätter ISBN: 3-938744-85-5 Üungsstz 02 Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen
Haus B Außenwand, Sockel
 Hus B 18 Außenwnd, Sokel 19 Innenwnd, Bodenpltte 20 Außenwnd, Fundment 21 Innenwnd, Fundment 22 Außenwnd, Deke, Fenster 23 Innenwnd, Deke, Tür 24 Außenwnd, Trufe 25 Außenwnd, Ortgng 26 Außenwnd, Eke 27
Hus B 18 Außenwnd, Sokel 19 Innenwnd, Bodenpltte 20 Außenwnd, Fundment 21 Innenwnd, Fundment 22 Außenwnd, Deke, Fenster 23 Innenwnd, Deke, Tür 24 Außenwnd, Trufe 25 Außenwnd, Ortgng 26 Außenwnd, Eke 27
