Mathematik für Wirtschaftsinformatiker
|
|
|
- Carl Krämer
- vor 5 Jahren
- Abrufe
Transkript
1 UNIVERSITÄT SIEGEN Prof. Dr. Alfred Müller 12. Februar 2009 Klausuraufgaben Mathematik für Wirtschaftsinformatiker Beachten Sie folgende Hinweise: (1) Überprüfen Sie Ihr Exemplar auf Vollständigkeit! Die Klausur besteht aus 6 Aufgaben und 18 Seiten. Das letzte Blatt ist Konzeptpapier und darf herausgetrennt werden. Der Inhalt dieser Seite wird nicht gewertet. Abgesehen davon darf die Klausur nicht auseinandergenommen werden! (2) Tragen Sie die Lösungen und den Rechenweg, soweit verlangt, direkt bei den Aufgaben ein. Benützen Sie falls nötig die am Ende eingefügten leeren Seiten für weitere Nebenrechnungen. (3) Es werden nur Ergebnisse mit nachvollziehbarem Lösungsweg gewertet! (4) Erlaubte Hilfsmittel: - 4 handgeschriebene Seiten DIN A4 einseitig oder 2 handgeschriebene Blätter DIN A4 zweiseitig mit eigenen Notizen, - ein nicht-graphikfähiger Taschenrechner. Maximal zu erreichende Punktzahl: 60 Erreichte Punktzahl: 60 Zur Benotung: Als 100% galten 50 Punkte; 23 Punkte genügten zum Bestehen. Aufgabe Mögliche Punkte Erreichte Punkte
2 Aufgabe 1 ( Punkte). Kreuzen Sie an, ob die folgenden Aussagen wahr oder falsch sind. Richtige Antwort: 2 Pluspunkte; falsche Antwort: 2 Minuspunkte; keine Antwort: 0 Punkte. Ist die Gesamtpunktzahl negativ, wird die Aufgabe mit 0 Punkten bewertet. Aussage wahr falsch Jedes Polynom 2-ten Grades hat eine Extremstelle. X Jede differenzierbare Funktion f : R + R ist stetig. X Jede monoton wachsende Funktion f : R R + hat eine Nullstelle. Für jede reelle Zahl x gilt X X n=1 x n = 1 1 x. Es gilt die Gleichung k 2 = 5 n. k=3 n=1 X Es wird nur das Ergebnis gewertet! Zu 1: Dass die Behauptung wahr ist, ist an der Scheitelgleichungsformel abzulesen bzw. lässt sich damit begründen, dass die Ableitung (ein Polynom ersten Grades) eine Nullstelle besitzt. Kanonischerweise ist R sowohl als Definitionsmenge als auch als Bildbereich zu verstehen. Zu 2: Die Behauptung ist wahr, denn der Differentialquotient (die Ableitung) existiert nur, falls beim Grenzübergang von h mit dem Nenner des Differenzenquotienten auch der Zähler gegen 0 konvergiert; das ist die Stetigkeit der Funktion. Zu 3: Die Behauptung ist falsch und zwar schlechthin, weil 0 im Bildbereich R + von f nicht enthalten ist. Speziell kann man die e-funktion betrachten und hat auch dann die Behauptung einzusehen. Zu 4: Die Behauptung ist falsch, weil für reelle x die Konvergenz nur für x mit 1 < x < 1 vorliegt. Im Besonderen erfolgt die Summation von 1 ab, statt von 0. Zu 5: Diese Behauptung ist wahr, denn die Formel ist korrekt: Der Laufindex kann umbenannt werden und ist auch korrekt geshiftet worden. 2
3 3
4 Aufgabe 2 (3 + 5 Punkte). Zeigen Sie mittels vollständiger Induktion, dass für alle n N gilt: n 2 k = 2 (2 n 1). k=1 Hinweis: Gliedern Sie explizit nach Induktionsanfang und Induktionsschritt. Markieren Sie jede Verwendung der Induktionshypothese. Beweis: Induktionsanfang: (n = 1) l.s.: 1 k=1 2k = 2 1 = 2 r.s.: 2 (2 1 1) = 2 also: l.s. = r.s. Alternativ: 1 k=1 2k = 2 1 = 2 = 2 (2 1 1) (w) Induktionshypothese: Die behauptete Gleichung gilt für ein n N n 2 k = 2 (2 n 1). k=1 Unter Verwendung der Induktionshypothese ist im Induktionsschritt die behauptete Gleichung für dessen Nachfolger zu zeigen. Induktionsschritt: (n n + 1) n+1 2 k = 2 n+1 + n k=1 k=1 2 k IH = 2 n (2 n 1) = 2 n n+1 2 = (1 + 1) 2 n+1 2 = 2 2 n = 2 (2 n+1 1) q.e.d. 4
5 5
6 Aufgabe 3 ( Punkte). Sie wollen Euro für 10 Jahre anlegen, und haben die Auswahl zwischen den beiden folgenden Angeboten: Angebot A: Ihre Hausbank bietet Ihnen einen 10-jährigen Sparbrief an, bei dem das Guthaben in den ersten 4 Jahren jeweils mit 2 % und in den letzten 6 Jahren jeweils mit 4 % verzinst wird. Angebot B: Eine Online-Bank garantiert Ihnen bei beliebiger Laufzeit eine jährliche Verzinsung von 3.5 %. (a) Berechnen Sie für beide Angebote Ihren Kapitalstand K in Euro nach Ablauf der 10 Jahre. Kapitalstand K in Euro bei Angebot A: Kapitalstand K in Euro bei Angebot B: (b) Welcher konstante Zinssatz p liefert nach 5 Jahren den Kapitalstand von Euro? Zinssatz p: = 8.4% (c) Wieviele Jahre n müssen Sie bei der Online-Bank Ihr Geld mindestens anlegen, um einen Kapitalstand von Euro zu überschreiten? Anlagedauer (in Jahren) n: 21 (mindestens) Rechnungen: Zu a): K A (10) = ( ) 4 ( ) K B (10) = ( )
7 Zu b): K p (5) = (1 + p) 5! = p = (1.5) 1/ Zu c): K B (n) = ( ) n! n ln(2) ln(1.035) (20, 21] N 0. 7
8 Aufgabe 4 ( Punkte). Gegeben sei die Funktion f : R R mit f(x) = e x + x. (a) Begründen Sie die Behauptung: Im Intervall [ 1, 0] liegt eine Nullstelle von f. Es gibt ein x [ 1, 0] mit f(x) = 0 nach dem Zwischenwertsatz, weil f stetig, f( 1) = e 1 + ( 1) negativ und f(0) = e = 1 positiv ist. (b) Berechnen Sie eine verbesserte Näherung [x l, x r ] [ 1, 0] für diese Nullstelle. Führen Sie dazu einen Schritt des Regula-falsi-Verfahrens durch. x l = x r = 0 (c) Bestimmen Sie den Funktionsausdruck S(x) der Sekante S : R R, die den Graphen G f in den beiden Punkten ( 1, f( 1)), (0, f(0)) schneidet. S(x) = (2 e 1 )x + 1 (d) Bestimmen Sie den Funktionsausdruck T (x) einer Tangente T : R R an G f Steigung 2. mit T (x) = 2x + 1 Rechnungen: Zu a): Es gibt ein x [ 1, 0] mit f(x) = 0 nach dem Zwischenwertsatz (ZWS), weil f stetig, f( 1) = e 1 + ( 1) negativ und f(0) = e = 1 positiv ist. Zu b): Sei also x 1 = 1 und x 2 = 0. Dann ist x 3 nach der Iterationsformel des Regula-falsi- Verfahrens folgendermaßen zu berechnen x 3 = x 2 x 2 x 1 f(x f(x 2 ) f(x 1 ) 2) x 3 = x 1f(x 2 ) f(x 1 )x 2 f(x 2 ) f(x 1 ) = 0 0 ( 1) f(0) f( 1) f(0) = ( 1)f(0) f( 1)(0) f(0) f( 1) (e 0 +0) 0 (e 0 +0) (e 1 +( 1)) 1 = (e 0 +0) (e 1 +( 1)) (e0 + 0) = = 1 = 1 2 e 1 2 e 1 = =
9 und damit weiter f(x 3 ) = e x 3 + x 3 = e 1 2 e e 1 = < 0. Demnach ist x 1 = 1 zu ersetzen durch x 3 = ; es gilt x l := x 3 und x r := x 2. Zu c): Es ist ( 1, f( 1)) = ( 1, e 1 1) und (0, f(0)) = (0, 1). Die Zweipunkteformel für Geraden liefert für die Sekante S den Funktionsausdruck Zu d): Es ist f (x)! = 2 nach x aufzulösen. f(0) f( 1) S(x) = (x 0) + f(0) 0 ( 1) = 1 (e 1 1) x = (2 e 1 )x + 1. f (x) = e x + 1 = 2 gdw. e x = 1 gdw. x = 0 Die Einpunkteformel für Geraden liefert für die Tangente T den Funktionsausdruck f T (x) = 2(x 0) + f(0) = 2x
10 Aufgabe 5 ( Punkte). Gegeben sei die Funktion f : R + 0 R mit f(x) = ln (e x + x) (a) Berechnen Sie die ersten beiden Ableitungen der Funktion f. f (x) = ex +1 e x +x f (x) = xex 2e x 1 (e x +x) 2 (b) Was folgt aus (a) über stationäre Punkte und Monotonieverhalten von f? Stationäre Punkte: keine Monotonieverhalten: streng monoton wachsend (c) Bestimmen Sie die Wertemenge W f = f(r + 0 ) der Funktion. W f = [42, ) Rechnungen: Zu a): f(x) = ln (e x + x) + 42 f (x) = 1 e x + x (ex + 1) + 0 = ex + 1 e x + x f (x) = (ex + x)(e x ) (e x + 1)(e x + 1) (e x + x) 2 = e2x + xe x e 2x 2e x 1 (e x + x) 2 = xex 2e x 1 (e x + x) 2 [Es sind f, f und f stetig (auf D f ) und differenzierbar (auf D f \ {0}).] Zu b): Es ist e x + 1, e x + x > 0 und damit auch f (x) positiv für jedes x R + ; der Fall x = 0 ist hier 10
11 irrelevant. Also wächst f auf ganz D f streng monoton und besitzt keine stationären Punkte (keine lokalen Extrema). Zu c): Es ist W f = [42, ). Denn zunächst gilt: lim f(x) = x 0 ln(e0 + 0) + 42 = ln(1) + 42 = = 42 lim f(x) = lim ln(x) + 42 = + 42 =. x x und Weil f stetig ist, gibt es nach dem Zwischenwertsatz für jedes y [42, ) ein x [0, ) mit f(x) = y; also ist [42, ) W f ; wegen der Monotonie von f und [0, ) = R + 0 = D f gilt also die Gleichheit. 11
12 Aufgabe 6 ( Punkte). Bestimmen Sie die folgenden vier Grenzwerte: ln(x) + x (a) lim x x 2 + 1, 2x x (c) lim x 0 x x 3 1 (b) lim x 1 x 1, e x, (d) lim x 4. x lim x ln(x)+x x 2 +1 = 0 lim x 1 x 3 1 x 1 = 3 lim x 0 2x x x = lim x e x 4 x = 0 Rechnungen: Zu a): mit L H: ln(x) + x lim x x = lim x x 2x = 0 Zu b): mit L H: 0 0 x 3 1 lim x 1 x 1 = lim 3x 2 x 1 1 = 3 alternativ: mit geometrischer Summenformel Zu c): mit Kürzen und ( 2 1) positiv x 3 1 lim x 1 x 1 = lim x 1 (x2 + x + 1) = 3 lim x 0 Zu d): mit 1 < e 4 < 1 2x x alternativ: mit (ln(4) 1) > 0 x x( 2 1) = lim x 0 x = lim x 0 e x ( e ) x lim x 4 = lim = 0 x x x = + e x lim x 4 = lim x x e(1 ln(4))x = lim e (ln(4) 1)x = 0 x 12
13 13
14 Weitere Nebenrechnungen: (Geben Sie eindeutig an, auf welche Aufgaben sich die Nebenrechnungen beziehen, und geben Sie bei den entsprechenden Aufgaben einen Hinweis auf die weiteren Nebenrechnungen hier!) 14
15 15
16 16
17 Konzeptpapier, das nicht gewertet werden soll: 17
18 18
Höhere Mathematik I. Variante A
 Prof. Dr. E. Triesch Höhere Mathematik I SoSe 06 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die
Prof. Dr. E. Triesch Höhere Mathematik I SoSe 06 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die
Teil I Auswahlfragen
 UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Dominik Faas Grundlagen der Analysis Sommersemester 010 Klausur vom 07.09.010 Teil I Auswahlfragen Name: Hinweise: Bei den folgenden Auswahlfragen
UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Dominik Faas Grundlagen der Analysis Sommersemester 010 Klausur vom 07.09.010 Teil I Auswahlfragen Name: Hinweise: Bei den folgenden Auswahlfragen
Mathematik I HM I A. SoSe Variante A
 Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
Prof. Dr. E. Triesch Mathematik I SoSe 08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur die Antworten
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
Mathematik für Sicherheitsingenieure I A
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 9.0.08 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+6+4 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH
Höhere Mathematik II. Variante C
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante C Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante C Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 01 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA-Blätter Vorder- und Rückseite
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
2004, x 0 (e 2x + x) x 1, x > 0. Untersuchen Sie die Funktion auf Stetigkeit an der Stelle x 0 = 0!
 Klausur 25.02.2004 Aufgabe 5 Gegeben ist die Funktion f(x) = 2004, x 0 (e 2x + x) x 1, x > 0. Untersuchen Sie die Funktion auf Stetigkeit an der Stelle x 0 = 0! Klausur 06.08.2003 Aufgabe 5 Gegeben ist
Klausur 25.02.2004 Aufgabe 5 Gegeben ist die Funktion f(x) = 2004, x 0 (e 2x + x) x 1, x > 0. Untersuchen Sie die Funktion auf Stetigkeit an der Stelle x 0 = 0! Klausur 06.08.2003 Aufgabe 5 Gegeben ist
Klausur zur Vorlesung Analysis I für Lehramtskandidaten. (Sommersemester 2008) Dr. C. Lange, J. Schütz
 Klausur zur Vorlesung Analysis I für Lehramtskandidaten (Sommersemester 008) Dr. C. Lange, J. Schütz Beginn: 17. Juli 008, 10:00 Uhr Ende: 17. Juli 008, 11:30 Uhr Name: Matrikelnummer: Ich studiere: Bachelor
Klausur zur Vorlesung Analysis I für Lehramtskandidaten (Sommersemester 008) Dr. C. Lange, J. Schütz Beginn: 17. Juli 008, 10:00 Uhr Ende: 17. Juli 008, 11:30 Uhr Name: Matrikelnummer: Ich studiere: Bachelor
Mathematik I. Variante A
 Prof. Dr. E. Triesch Prof. Dr. Y. Guo Mathematik I WiSe 07/08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es
Prof. Dr. E. Triesch Prof. Dr. Y. Guo Mathematik I WiSe 07/08 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es
1. Aufgabe 8 Punkte. f (x) = (x 2 + 1) e x2. Es gilt. f (x) = 2xe x2 + ( x ) e x2 ( 2x) = 2x 3 e x2.
 1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
KLAUSURARBEIT IM BACHELOR-STUDIENGANG MATHEMATIK
 HOCHSCHULE FÜR TECHNIK STUTTGART SS 07 KLAUSURARBEIT IM BACHELOR-STUDIENGANG MATHEMATIK MODUL: Analysis FACH: Analysis A DATUM:. Juli 07 ZEIT: 8:0 0:0 PRÜFER: Wolfgang Erben SEMESTER: MB HILFSMITTEL: ein
HOCHSCHULE FÜR TECHNIK STUTTGART SS 07 KLAUSURARBEIT IM BACHELOR-STUDIENGANG MATHEMATIK MODUL: Analysis FACH: Analysis A DATUM:. Juli 07 ZEIT: 8:0 0:0 PRÜFER: Wolfgang Erben SEMESTER: MB HILFSMITTEL: ein
Mathematik für Sicherheitsingenieure I A
 Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Prof. Dr. J. Ruppenthal Wuppertal, 3.8.8 Dr. T. Pawlaschyk Mathematik für Sicherheitsingenieure I A Aufgabe. (5+5+5+5 Punkte) a) Geben Sie für jede der folgenden Aussagen an, ob sie WAHR oder FALSCH ist.
Technische Universität Berlin Fakultät II Institut für Mathematik SS 14
 Technische Universität Berlin Fakultät II Institut für Mathematik SS 4 Doz.: Blath, Gündel vom Hofe Ass.: Altmann, Fackeldey, Hammer 8. Okt 4 Oktober Klausur Analysis I für Ingenieure Name:....................................
Technische Universität Berlin Fakultät II Institut für Mathematik SS 4 Doz.: Blath, Gündel vom Hofe Ass.: Altmann, Fackeldey, Hammer 8. Okt 4 Oktober Klausur Analysis I für Ingenieure Name:....................................
Analysis I. Vorlesung 19
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 19 In dieser Vorlesung untersuchen wir mit Mitteln der Differentialrechnung, wann eine Funktion f: I R, wobei I R ein Intervall ist, (lokale)
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 19 In dieser Vorlesung untersuchen wir mit Mitteln der Differentialrechnung, wann eine Funktion f: I R, wobei I R ein Intervall ist, (lokale)
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Didaktik der Mathematik der Sekundarstufe II
 Didaktik der Mathematik der Sekundarstufe II Teil 8: Satz von Rolle - Mittelwertsatz - Monotoniekriterium Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur
Didaktik der Mathematik der Sekundarstufe II Teil 8: Satz von Rolle - Mittelwertsatz - Monotoniekriterium Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
KLAUSUR. Analysis (E-Technik/Mechatronik/W-Ing) Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf
 KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
KLAUSUR Analysis (E-Technik/Mechatronik/W-Ing).9.7 Prof. Dr. Werner Seiler Dr. Matthias Fetzer, Dominik Wulf Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Unterschrift: In der Klausur können Sie insgesamt
Modulprüfung Analysis I für Ingenieurwissenschaften
 Technische Universität Berlin WiSe 4/5 Fakultät II Institut für Mathematik 20. Februar 205 Doz.: Fackeldey, Guillemard, Penn-Karras Ass.: Beßlich, Winkert Modulprüfung Analysis I für Ingenieurwissenschaften
Technische Universität Berlin WiSe 4/5 Fakultät II Institut für Mathematik 20. Februar 205 Doz.: Fackeldey, Guillemard, Penn-Karras Ass.: Beßlich, Winkert Modulprüfung Analysis I für Ingenieurwissenschaften
Klausur. Wir wünschen Ihnen viel Erfolg! Klausur Mathematik für Informatiker und Softwaretechniker
 Apl. Prof. Dr. W.-P. Düll Fachbereich Mathematik Universität Stuttgart Klausur für Studierende der Fachrichtungen inf, swt Bitte unbedingt beachten: Bitte beschriften Sie jeden Ihrer Zettel mit Namen und
Apl. Prof. Dr. W.-P. Düll Fachbereich Mathematik Universität Stuttgart Klausur für Studierende der Fachrichtungen inf, swt Bitte unbedingt beachten: Bitte beschriften Sie jeden Ihrer Zettel mit Namen und
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Wiederholungsklausur zur Analysis I
 Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Wiederholungsklausur zur Analysis I Prof. Dr. C. Löh/M. Blank 5. Oktober 2011 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
23 Konvexe Funktionen und Ungleichungen
 23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
Technische Universität Berlin Fakultät II Institut für Mathematik SS 2013 Doz.: Gündel-vom Hofe, Hömberg, Ortgiese Ass.
 Technische Uniersität Berlin Fakultät II Institut für Mathematik SS 3 Doz.: Gündel-om Hofe, Hömberg, Ortgiese 5.7.3 Ass.: Böttle, Meiner Juli Klausur Analysis I für Ingenieure Name:... Vorname:... Matr.
Technische Uniersität Berlin Fakultät II Institut für Mathematik SS 3 Doz.: Gündel-om Hofe, Hömberg, Ortgiese 5.7.3 Ass.: Böttle, Meiner Juli Klausur Analysis I für Ingenieure Name:... Vorname:... Matr.
Mathematik für Studierende der Biologie Wintersemester 2017/18. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Nachklausur Analysis I
 SS 008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Nachklausur Analysis I 07.0.008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
SS 008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Nachklausur Analysis I 07.0.008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
(b) Bestimmen Sie mit Hilfe des Newton-Verfahrens eine Nullstelle von f auf 6 Nachkommastellen
 Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Mathematik I für Naturwissenschaften Dr. Christine Zehrt 5.10.18 Übung 6 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 9. Oktober 018 in den Übungsstunden Aufgabe 1 GebenSieohneTaschenrechnereineNäherungvon
Höhere Mathematik II. Variante B
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 202 Variante B Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind handschriftliche Aufzeichnungen von maximal 0 DinA4-Blättern.
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik II SoSe 202 Variante B Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind handschriftliche Aufzeichnungen von maximal 0 DinA4-Blättern.
Serie 4 2 = 10. ) ist). Dann gilt für alle n n 0
 Serie 4. Aufgabe 336 Punkte) Gegeben seien zwei reelle Zahlenfolgen durch a n : 0 n, n N b n : n n, n N Bestimmen Sie die Grenzwerte a bzw. b der Folgen a n ) n N bzw. b n ) n N. Geben Sie jeweils zu gegebenem
Serie 4. Aufgabe 336 Punkte) Gegeben seien zwei reelle Zahlenfolgen durch a n : 0 n, n N b n : n n, n N Bestimmen Sie die Grenzwerte a bzw. b der Folgen a n ) n N bzw. b n ) n N. Geben Sie jeweils zu gegebenem
Mathematik für Anwender I. Klausur
 Fachbereich Mathematik/Informatik 27. März 2012 Prof. Dr. H. Brenner Mathematik für Anwender I Klausur Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
Fachbereich Mathematik/Informatik 27. März 2012 Prof. Dr. H. Brenner Mathematik für Anwender I Klausur Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
V.1 Konvergenz, Grenzwert und Häufungspunkte
 V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
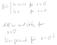 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Zulassungsprüfung in Mathematik
 der Deutschen Aktuarvereinigung e V Hinweise: Als Hilfsmittel sind ein Taschenrechner, eine mathematische Formelsammlung sowie entsprechende Literatur zugelassen Die Gesamtpunktzahl beträgt 9 Punkte Die
der Deutschen Aktuarvereinigung e V Hinweise: Als Hilfsmittel sind ein Taschenrechner, eine mathematische Formelsammlung sowie entsprechende Literatur zugelassen Die Gesamtpunktzahl beträgt 9 Punkte Die
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
dx nf(x 0). dx f(n 1) (x 0 ) = dn
 4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
Mathematische Grundlagen (01141) SoSe 2009
 Mathematische Grundlagen (04) SoSe 2009 Klausur am 29.08.2009: Musterlösungen Aufgabe Im Induktionsanfang sei n 0 = 0. Dann gilt Somit gilt der Induktionsanfang. 0 Die Induktionsvoraussetzung ist, dass
Mathematische Grundlagen (04) SoSe 2009 Klausur am 29.08.2009: Musterlösungen Aufgabe Im Induktionsanfang sei n 0 = 0. Dann gilt Somit gilt der Induktionsanfang. 0 Die Induktionsvoraussetzung ist, dass
Übungen zur Vorlesung MATHEMATIK II
 Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
Serie 4: Flächeninhalt und Integration
 D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
Modul Grundbildung Analysis WiSe 10/11. A.: Wurde in diesem Kapitel behandelt. C.: Weitere Fragen (Nicht nur für die Klausur interessant)
 Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
streng monoton steigend. streng monoton fallend. Ist f eine in einem Intervall stetige und im Innern des Intervalls differenzierbare Funktion mit
 3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
Musterlösung. TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik. Klausur Mathematik für Physiker 3 (Analysis 2) I... II...
 ................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Eigenschaften stetiger Funktionen Buch Kap. 2.5
 Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
Univariate Analysis. Analysis und nichtlineare Modelle Sommersemester
 Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
LMU MÜNCHEN. Mathematik für Studierende der Biologie Wintersemester 2016/17. GRUNDLAGENTUTORIUM 5 - Lösungen. Anmerkung
 LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Meine persönliche Einschätzung der Aufgaben der Klausur vom :
 Meine persönliche Einschätzung der Aufgaben der Klausur vom.9.: a) h) Einige leicht, andere Standard, einige zum (kurzen) Nachdenken. ) Standard. Vergleiche Aufgabe 9, Bonusaufgabe a) Standard. Vergleiche
Meine persönliche Einschätzung der Aufgaben der Klausur vom.9.: a) h) Einige leicht, andere Standard, einige zum (kurzen) Nachdenken. ) Standard. Vergleiche Aufgabe 9, Bonusaufgabe a) Standard. Vergleiche
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar 0 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 3 6 Total Vollständigkeit Bitte
Dr. A. Caspar ETH Zürich, Januar 0 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 3 6 Total Vollständigkeit Bitte
Lösungen zur Klausur A Grundkurs Mathematik für Wirtschaftswissenschaft
 Lösungen zur Klausur A Grundkurs Mathematik für Wirtschaftswissenschaft Wintersemester 29/21 16.2.21 Aufgabe A.1. Betrachten Sie die Polynomfunktion p : R R, welche durch die Abbildungsvorschrift p(x)
Lösungen zur Klausur A Grundkurs Mathematik für Wirtschaftswissenschaft Wintersemester 29/21 16.2.21 Aufgabe A.1. Betrachten Sie die Polynomfunktion p : R R, welche durch die Abbildungsvorschrift p(x)
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
9. Übungsblatt zur Vorlesung Mathematik I für Informatik
 Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Ferienkurs Stetigkeit und Konvergenz Seite 1. Technische Universität München Ferienkurs Analysis 1. Musterlösung = lim.
 Ferienkurs Stetigkeit und Konvergenz Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit und Konvergenz Musterlösung 6.03.20. Grenzwerte I Berechnen Sie lim f(), lim f()
Ferienkurs Stetigkeit und Konvergenz Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit und Konvergenz Musterlösung 6.03.20. Grenzwerte I Berechnen Sie lim f(), lim f()
differenzierbare Funktionen
 Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
13. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 3. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 00/ 07.0.-.0. Aufgabe G Stetigkeit) a) Gegeben
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 3. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 00/ 07.0.-.0. Aufgabe G Stetigkeit) a) Gegeben
)e2 (3 x2 ) a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen Sie das Verhalten von f für x.
 Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Mathematik 1 für Bauingenieure
 Mathematik 1 für Bauingenieure Name (bitte ausfüllen): Prüfung am 5.12.2014 Reinhard Winkler Matrikelnummer (bitte ausfüllen): Wichtige Hinweise bevor Sie beginnen: Die Prüfung besteht aus vier Aufgaben
Mathematik 1 für Bauingenieure Name (bitte ausfüllen): Prüfung am 5.12.2014 Reinhard Winkler Matrikelnummer (bitte ausfüllen): Wichtige Hinweise bevor Sie beginnen: Die Prüfung besteht aus vier Aufgaben
Mathematik für Anwender. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 4. Januar 0 Prof. Dr. H. Brenner Mathematik für Anwender Testklausur mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden
Fachbereich Mathematik/Informatik 4. Januar 0 Prof. Dr. H. Brenner Mathematik für Anwender Testklausur mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Mathematik für Wirtschaftswissenschaftler II (Analysis) 2. Klausur SoSe 2010 Hamburg,
 Mathematik für Wirtschaftswissenschaftler II (Analysis) 2. Klausur SoSe 2010 Hamburg, 08.10.2010 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN Nachname:...................................................................
Mathematik für Wirtschaftswissenschaftler II (Analysis) 2. Klausur SoSe 2010 Hamburg, 08.10.2010 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN Nachname:...................................................................
Mathematische Grundlagen der Ökonomie Übungsblatt 8
 Mathematische Grundlagen der Ökonomie Übungsblatt 8 Abgabe Donnerstag 7. Dezember, 0:5 in H 5+7+8 = 20 Punkte Mit Lösungshinweisen zu einigen Aufgaben 29. Das Bisektionsverfahren sucht eine Nullstelle
Mathematische Grundlagen der Ökonomie Übungsblatt 8 Abgabe Donnerstag 7. Dezember, 0:5 in H 5+7+8 = 20 Punkte Mit Lösungshinweisen zu einigen Aufgaben 29. Das Bisektionsverfahren sucht eine Nullstelle
Das Newton-Verfahren
 1/14 Das Newton-Verfahren 11./12. Jgst. Bayern Doris Behrendt Gymnasium Marktbreit Stand: 12. März 2016 2/14 Formelsammlung Seite 72 oben, vierter Punkt: Newton-Iterationsformel: x n+1 = x n f(x n) f (x
1/14 Das Newton-Verfahren 11./12. Jgst. Bayern Doris Behrendt Gymnasium Marktbreit Stand: 12. März 2016 2/14 Formelsammlung Seite 72 oben, vierter Punkt: Newton-Iterationsformel: x n+1 = x n f(x n) f (x
Karlsruher Institut für Technologie (KIT) WS 2012/13 Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning
 Karlsruher Institut für Technologie (KIT) WS 202/3 Institut für Analysis 26..202 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 7. Übungsblatt Aufgabe Untersuchen
Karlsruher Institut für Technologie (KIT) WS 202/3 Institut für Analysis 26..202 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 7. Übungsblatt Aufgabe Untersuchen
Σ / 100 P
 0. Klausur zur Vorlesung Mathematik für Naturwissenschaftler I Probeklausur Prof. Andreas Dreuw, Manuel Hodecker, Michael F. Herbst ungef. Beginn: ungef. Ende: Bitte beachten Sie die folgenden Hinweise
0. Klausur zur Vorlesung Mathematik für Naturwissenschaftler I Probeklausur Prof. Andreas Dreuw, Manuel Hodecker, Michael F. Herbst ungef. Beginn: ungef. Ende: Bitte beachten Sie die folgenden Hinweise
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 203/4 Prof Dr Armin Iske Dr Hanna Peywand Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungen zu Blatt 5 Aufgabe :je 2 Punkte Untersuchen
Fachbereich Mathematik der Universität Hamburg WiSe 203/4 Prof Dr Armin Iske Dr Hanna Peywand Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungen zu Blatt 5 Aufgabe :je 2 Punkte Untersuchen
Übungen Mathematik I, M
 Übungen Mathematik I, M Übungsblatt, Lösungen (Stoff aus Mathematik 0) 09.0.0. Kommissar K hat 3 Tatverdächtige P, Q und R. Er weiß: (a) Wenn sich Q oder R als Täter herausstellen, dann ist P unschuldig.
Übungen Mathematik I, M Übungsblatt, Lösungen (Stoff aus Mathematik 0) 09.0.0. Kommissar K hat 3 Tatverdächtige P, Q und R. Er weiß: (a) Wenn sich Q oder R als Täter herausstellen, dann ist P unschuldig.
Höhere Mathematik III. Variante A
 Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik III WiSe 04/05 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof. Dr. E. Triesch Höhere Mathematik III WiSe 04/05 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter Vorder- und Rückseite
Musterlösung zur Probeklausur zur Mathematik für Biologen
 Lehrstuhl A für Mathematik Aachen, den 15.01.04 Prof. Dr. R. Stens P. - M. Küpper Musterlösung zur Probeklausur zur Mathematik für Biologen Aufgabe 1: a) Vereinfachen Sie die folgenden Terme so weit wie
Lehrstuhl A für Mathematik Aachen, den 15.01.04 Prof. Dr. R. Stens P. - M. Küpper Musterlösung zur Probeklausur zur Mathematik für Biologen Aufgabe 1: a) Vereinfachen Sie die folgenden Terme so weit wie
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Klausur zur Mathematik III. Variante A
 Lehrstuhl C für Mathematik (Analysis) Prof. Dr. Oliver Schaudt Aachen, den 21.02.2018 Klausur zur Mathematik III WS 2017/18 Variante A Name Matrikelnr. Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel
Lehrstuhl C für Mathematik (Analysis) Prof. Dr. Oliver Schaudt Aachen, den 21.02.2018 Klausur zur Mathematik III WS 2017/18 Variante A Name Matrikelnr. Hinweise Zugelassene Hilfsmittel: Als Hilfsmittel
Nachholklausur Wirtschafts- und Finanzmathematik
 Vorname: Nachname: Matrikel-Nr.: Nachholklausur Wirtschafts- und Finanzmathematik Prüfer Burkart, Etschberger, Jansen Prüfungsdatum 7. Juli 2016 Prüfungsort Augsburg Studiengang IM und BW Bearbeitungszeit:
Vorname: Nachname: Matrikel-Nr.: Nachholklausur Wirtschafts- und Finanzmathematik Prüfer Burkart, Etschberger, Jansen Prüfungsdatum 7. Juli 2016 Prüfungsort Augsburg Studiengang IM und BW Bearbeitungszeit:
Höhere Mathematik I für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt. < 0 für alle t > 1. tan(x) tan(0) x 0
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i
![C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i](/thumbs/96/129296716.jpg) ETH-Aufnahmeprüfung Herbst 18 Mathematik I (Analysis) D C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5 α. A 1 Aufgabe [1 Punkte] Geben Sie die Lösungsmenge folgender Gleichungen in!
ETH-Aufnahmeprüfung Herbst 18 Mathematik I (Analysis) D C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5 α. A 1 Aufgabe [1 Punkte] Geben Sie die Lösungsmenge folgender Gleichungen in!
2.6 Lokale Extrema und Mittelwertsatz
 2.6. Lokale Etrema und Mittelwertsatz 49 2.6 Lokale Etrema und Mittelwertsatz In diesem Kapitel bezeichne f stets eine reellwertige Funktion, definiert auf einem abgeschlossenen Intervall [a, b]. Unter
2.6. Lokale Etrema und Mittelwertsatz 49 2.6 Lokale Etrema und Mittelwertsatz In diesem Kapitel bezeichne f stets eine reellwertige Funktion, definiert auf einem abgeschlossenen Intervall [a, b]. Unter
Analysis I. 7. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Analysis. Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente. Gymnasium Klasse 10
 Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Standards Differentialrechnung (Vorschlag erarbeitet von Melanie Schönauer im Rahmen einer FBA/ 0809; Betreuung der FBA durch Dr.
 Standards Differentialrechnung (Vorschlag erarbeitet von Melanie Schönauer im Rahmen einer FBA/ 0809; Betreuung der FBA durch Dr. Walter Mayer) 1. Der Punkt P(1/y) liegt auf dem Graphen der Funktion f(x)
Standards Differentialrechnung (Vorschlag erarbeitet von Melanie Schönauer im Rahmen einer FBA/ 0809; Betreuung der FBA durch Dr. Walter Mayer) 1. Der Punkt P(1/y) liegt auf dem Graphen der Funktion f(x)
19.2 Mittelwertsatz der Differentialrechnung
 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
Wir halten in einem s t Diagramm das Anfahren eines Autos fest. Wir nehmen an, dass zwischen Weg und Zeit der einfache Zusammenhang
 . Die Momentangeschwindigkeit eines Autos Wir halten in einem s t Diagramm das Anfahren eines Autos fest. Wir nehmen an, dass zwischen Weg und Zeit der einfache Zusammenhang s(t) = t gilt. Im s t Diagramm
. Die Momentangeschwindigkeit eines Autos Wir halten in einem s t Diagramm das Anfahren eines Autos fest. Wir nehmen an, dass zwischen Weg und Zeit der einfache Zusammenhang s(t) = t gilt. Im s t Diagramm
Institut für Analysis WiSe 2018/2019 Prof. Dr. Dirk Hundertmark Dr. Markus Lange. Analysis 1. Aufgabenzettel 14
 Institut für Analysis WiSe 2018/2019 Prof. Dr. Dirk Hundertmark 03.02.2019 Dr. Markus Lange Analysis 1 Aufgabenzettel 14 Dieser Zettel wird in der letzten Übung des Semesters am 08.02.2019 besprochen Aufgabe
Institut für Analysis WiSe 2018/2019 Prof. Dr. Dirk Hundertmark 03.02.2019 Dr. Markus Lange Analysis 1 Aufgabenzettel 14 Dieser Zettel wird in der letzten Übung des Semesters am 08.02.2019 besprochen Aufgabe
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Mathematik 1 für Bauingenieurwesen
 Mathematik 1 für Bauingenieurwesen Name (bitte ausfüllen): Prüfung am 20.1.2017 Reinhard Winkler Matrikelnummer (bitte ausfüllen): Wichtige Hinweise bevor Sie beginnen: Die Prüfung besteht aus vier Aufgaben
Mathematik 1 für Bauingenieurwesen Name (bitte ausfüllen): Prüfung am 20.1.2017 Reinhard Winkler Matrikelnummer (bitte ausfüllen): Wichtige Hinweise bevor Sie beginnen: Die Prüfung besteht aus vier Aufgaben
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mathematik-Vorkurs. Übungsaufgaben. im Sommersemester 2012
 Mathematik-Vorkurs Übungsaufgaben im Sommersemester 2012 Goethe Universität-Frankfurt am Main Prof. Dr. Heinz D. Mathes Professur für Produktionswirtschaft 1 Aufgaben zu Thema 1 Aufgabe 1.1: Lesen Sie
Mathematik-Vorkurs Übungsaufgaben im Sommersemester 2012 Goethe Universität-Frankfurt am Main Prof. Dr. Heinz D. Mathes Professur für Produktionswirtschaft 1 Aufgaben zu Thema 1 Aufgabe 1.1: Lesen Sie
Ferienkurs Seite 1. Technische Universität München Ferienkurs Analysis 1 Stetigkeit, Konvergenz, Topologie
 Ferienkurs Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit, Konvergenz, Topologie Lösung 2.03.202. Gleichmäßige Konvergenz Entscheiden Sie, ob die folgenden auf (0,
Ferienkurs Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit, Konvergenz, Topologie Lösung 2.03.202. Gleichmäßige Konvergenz Entscheiden Sie, ob die folgenden auf (0,
Grundlagen der Mathematik (BSc Maschinenbau)
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 5.9.7 Grundlagen der Mathematik (BSc Maschinenbau) Aufgabe. (6+8+6 Punkte) a) Zeigen Sie durch Induktion nach n N: n (k ) = n k= b) Stellen Sie die folgenden Mengen
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 5.9.7 Grundlagen der Mathematik (BSc Maschinenbau) Aufgabe. (6+8+6 Punkte) a) Zeigen Sie durch Induktion nach n N: n (k ) = n k= b) Stellen Sie die folgenden Mengen
Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 1
 Studiengang: Matrikelnummer: 3 4 5 6 Z Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 8. 7. 6, 8. -. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
Studiengang: Matrikelnummer: 3 4 5 6 Z Punkte Note Prüfungsklausur zum Modul Höhere Mathematik für Ingenieure 8. 7. 6, 8. -. Uhr Zugelassene Hilfsmittel: A4-Blätter eigene, handschriftliche Ausarbeitungen
(1 + z 2j ) = 1 z2n+2. 1 z. (1 + z)(1 z) 1 z. 1 z. (1 + z 2j ) = 1 z. 1 z 1 z
 Aufgabe Zeigen Sie mit vollständiger Induktion: Für alle n N gilt (8 Punkte) n ( + z 2j ) = 2n+, wobei z C, z, eine komplexe Zahl ist Lösung [8 Punkte] Induktionsanfang: n = : ( + z 2j ) = ( + z 2 ) =
Aufgabe Zeigen Sie mit vollständiger Induktion: Für alle n N gilt (8 Punkte) n ( + z 2j ) = 2n+, wobei z C, z, eine komplexe Zahl ist Lösung [8 Punkte] Induktionsanfang: n = : ( + z 2j ) = ( + z 2 ) =
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
