7 Das lokale Ito-Integral
|
|
|
- Stephanie Kaiser
- vor 7 Jahren
- Abrufe
Transkript
1 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale sind lokale L p -Maringale 7.7 Λ(M) enhäl die seigen, adapieren Prozesse für seiges M 7.8 Geeignee Folgen von Soppzeien für lokale Maringale ]0,τ] X dm = 1 ]0,τ] X dm τ 7.12 Gleichhei von Inegralprozessen bzgl. M τ und M σ 7.14 τ n σ n is eine lokalisierende Folge für (X, M) und (Y, N) 7.16 Einfache Eigenschafen des lokalen Io-Inegrals 7.17 Subsiuion beim lokalen Io-Inegral 7.18 Lokalbeschränke, previsible Prozesse sind lokal Io-inegrierbar 7.23 Das sochasische Inegral als Limes von Zwischensummen 7.24 Lokale Io-Inegrale bzgl. αm + βn In diesem Paragrafen werden wir das Io-Inegral von Λ 2 (µ M ) auf eine größere Klasse von Sochasischen Prozessen ausdehnen. Gleichzeiig werden wir die Voraussezung, dass (M ) 0 ein rechsseiig seiges L 2 (P )-Maringal is, abschwächen können. Wir benöigen nur ein rechsseiig seiges, lokales L 2 (P )-Maringal. Hierzu definieren wir 7.1 Lokalisierende Folge von Soppzeien Eine aufseigende Folge von Soppzeien (τ n ) n N heiß eine lokalisierende Folge von Soppzeien, wenn τ n (ω) n für ω Ω. Sind (τ n ) n N und(σ n ) n N zwei lokalisierende Folgen, so is auch (τ n σ n ) n N eine lokalisierende Folge. Wir kommen nun zum Begriff des lokalen Maringals. C3NEU 1
2 Finanzmahemaik II 7.2 Lokale L p -Maringale Sei (Ω, A, P ) ein W-Raum, p 1 und (A ) 0 eine Filraion. Ein reellweriger Prozess (M ) 0 heiß ein lokales L p -Maringal bzgl. (A ) 0, wenn gil: M 0 is A 0 -messbar. (ii) Es exisier eine lokalisierende Folge von Soppzeien (τ n ) n N, so dass M (τn) := (M τn M 0 ) 0 ein L p -Maringal bzgl. (A ) 0 für jedes n N is. Hierbei is M τn := M τn. Eine solche lokalisierende Folge von Soppzeien, nennen wir eine für das lokale L p -Maringal (M ) 0, geeignee Folge von Soppzeien. Ein lokales L 1 -Maringal, nenn man auch einfach lokales Maringal. Is 1 q < p, so is jedes lokale L p -Maringal ein lokales L q -Maringal, insbesondere also ein lokales Maringal. Man beache, dass ein lokales L p -Maringal (M ) 0 ein bzgl. (A ) 0 adapierer Prozess is. Zunächs is M 0 A 0 -messbar nach 7.2. Is > 0, so gil wegen τ n (ω) für n ω Ω M M 0 = lim τ n n M 0 ]. Da M τn M 0 A -messbar is, is auch M M 0 und somi M A -messbar. Es is nach Definiion M (τn) = (M τn M 0 ) 0 = (M τn M 0 ) 0. Is M 0 A 0 -messbar und M M 0 für > 0, so is nach Definiion (M ) 0 ein lokales L p -Maringal für jedes p 1. Die obige Definiion mi M (τn) an Selle von M τn = (M τn ) 0 is dadurch moivier, dass man z.b. bei sochasischen Differenialgleichungen keine Inegrierbarkeisvoraussezung an die Variable M 0 sellen möche. Außerdem zeig Saz 6.22 (iii), dass es für die sochasische Inegraion sowieso nur auf (M M 0 ) 0 ankomm. Is (M ) 0 ein L p -Maringal bzw. (A ) 0, so is (M M 0 ) 0 ein L p -Maringal bzgl. (A ) 0 und M 0 A 0 -messbar. Durch Wahl der lokalisierenden Folge τ n n erkenn man, dass somi (M ) 0 auch ein lokales L p -Maringal bzgl. (A ) 0 is. Bei der Definiion eines lokalen L 1 -Maringals darf man auch fordern, es gib eine lokalisierende Folge von Soppzeien, so dass M (τn) für jedes n ein gleichgradig inegrierbares Maringal bzgl. (A ) 0 is: Sei nämlich (τ n ) n N eine lokalisierende Folge, so dass für jedes n N (M τn M 0 ) 0 ein L 1 -Maringal bzgl. (A ) 0 is. Man berache nun die lokalisierende Folge σ n := τ n n, dann is (M σn M 0 ) 0 ein L 1 - Maringal bzgl. (A ) 0 für jedes n N. Es gil nämlich M σn M 0 = M τ n n M 0 L 1 und (1) M σn M 0 = E(M σn M 0 A ). Zu (1): Is n, so is wegen σ n = τ n, σ n = τ n n und der Maringalgeigenschaf von (M τn M 0 ) 0 2 C3NEU
3 Die Brownsche Bewegung M σn M 0 = M τn M 0 = E(Mn τn M 0 A ) = E(M σn M 0 A ). Is > n, so is σ n = (τ n n) = τ n n = σ n und daher is M σn M 0 = Mn τn M 0 A n messbar und daher auch A -messbar. Also is M σn M 0 = E(M σn M 0 A ) = E(M σn M 0 A ). Nach 4.5 is daher (M σn M 0 ) 0 wegen (1) auch gleichgradig inegrierbar. 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal (ii) (iii) Sei (M ) 0 ein lokales L p -Maringal bzgl. (A ) 0 mi geeigneer lokalisierender Folge (τ n ) n N. Is dann für jedes 0 (G) { M τn p : n N} gleichgradig inegrierbar, so is (M ) 0 ein L p - Maringal bzgl. (A ) 0. Is (M ) 0 ein rechsseiig seiges L p -Maringal bzgl. (A ) 0, so is für jedes 0 und jede lokalisierende Folge(τ n ) n N { M τn p : n N} gleichgradig inegrierbar. Is (M ) 0 ein rechsseiig seiges, lokales L p -Maringal bzgl. (A ) 0, so is für jede Soppzei τ auch (M τ ) 0 (und dami auch (M τ M 0) 0 ) ein rechsseiig seiges, lokales L p -Maringal bzgl. (A ) 0. Beweis. Für = 0, erhalen wir aus (G), dass M 0 L p is. Da (M τn M 0 ) 0 ein L p -Maringal bzgl. (A ) 0 is, is wegen M 0 L p somi auch (M τn ) 0 ein L p -Maringal bzgl. (A ) 0. Nun gil für jedes 0 (1) M τn n M, da τ n (ω) = für genügend große n is. Aus (1) und (G) folg daher nach 4.20 (2) M L p, E( M τn M p ) n 0. Sei nun A A s und s <, dann gil, da (M τn ) 0 ein Maringal bzgl. (A ) 0 is: (3) A M τ n dp = A M τ n sdp. Aus (2) folg (4) 1 A (M τn M ) 1 1 A (M τn M ) p (2) n 0, (2) (5) 1 A (M τn s M s ) 1 1 A (M τn s M s ) p 0. n Aus (4) und (5) folgen A M τ n τ dp n A M dp und A M τ n sdp n A M sdp. Zusammen mi (3) ergib sich (6) A M dp = A M sdp für A A s. Da M A -messbar und M L p nach (2) is, folg mi (6), dass (M ) 0 ein L p - Maringal bzgl. (A ) 0 is. C3NEU 3
4 Finanzmahemaik II (ii) Berache für feses das Sysem {τ i : i N} der aufseigenden Soppzeien. Dann is { M τi p : i N} nach 4.39 gleichgradig inegrierbar. (iii) Sei (τ n ) n N eine lokalisierende Folge für das lokale L p -Maringal M. Wir zeigen (τ n ) n N is auch eine lokalisierende Folge für M τ. Hierzu bleib nach Definiion 7.2 (wegen (M τ ) (τn) = [M (τn) ] τ ) zu zeigen: Is M ein rechsseiig seiges L p -Maringal bzgl. (A ) 0, so is auch M τ = (M τ ) 0 ein L p -Maringal bzgl. (A ) 0. Dies folg nach 4.39 (ii). In 7.3 (iii) haen wir schon den folgenden Begriff benuz 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal Ein lokales L p -Maringal heiß rechsseiig seig (seig), wenn für alle ω Ω [0, [ M (ω) rechsseiig seig (seig) is. Is (M ) 0 ein seiges, lokales Maringal, dann gib es eine lokalisierende Folge für M = (M ) 0, so dass M ein lokales L p -Maringal für jedes p 1 is. Genauer gil 7.5 Seige, lokale Maringale sind lokale L p -Maringale Es sei (M ) 0 ein seiges, lokales Maringal bzgl. (A ) 0. Seze τ n := inf{ 0 : M M 0 n} für n N. Dann is (τ n ) n N eine geeignee, lokalisierende Folge für das lokale Maringal (M ) 0 und (M τn M 0 ) 0 is für jedes n N gleichmäßig beschränk und insbesondere also ein seiges L p -Maringal für jedes p 1. Daher is (M ) 0 ein seiges, lokales L p -Maringal bzgl. (A ) 0 für jedes p 1. Beweis. Nach 4.27, angewand auf die abgeschlossene Menge A := [n, [ undx := M M 0, sind τ n für alle n N Soppzeien mi τ n (ω) τ n+1 (ω). Da [0, [ M (ω) M 0 (ω) seig is, und daher auf beschränken Inervallen beschränk is, gil τ n (ω). Die gleichmäßige Beschränkhei folg, da wegen der linksseiigen Seigkei von M gil (1) M (ω) M 0 (ω) n für alle τ n (ω). Zu zeigen bleib wegen (1), für jedes n N gil: (2) (M τn M 0 ) 0 is ein Maringal bzgl. (A ) 0. Nach 4.29 is M τn A τn -messbar, und daher, wegen A τn A, auch A -messbar. Somi is (M τn M 0 ) 0 bzgl. (A ) 0 adapier und wegen (1) auch inegrierbar. Nach 4.30 reich es für jede beschränke Soppzei τ zu zeigen (3) E(M τn τ M 0 ) = 0. Sei nun (σ n ) n N eine geeignee lokalisierende Folge für (M ) 0. Es is also nach Definiion (M σk M 0 ) 0 ein (seiges) Maringal bzgl. (A ) 0, und nach 4.30 gil daher, da τ n τ eine beschränke Soppzei bzgl. (A ) 0 is: 4 C3NEU
5 (4) E(M σk τ n τ M 0 ) = 0. Die Brownsche Bewegung Nun gil M σk τ n τ M 0 k M τn τ M 0, und wegen (1) is auch M σk τ n τ M 0 n. Hieraus folg mi (4) und dem Saz von der beschränken Konvergenz (3). Das sochasische Inegral soll nun bzgl. rechsseiig seiger, lokaler L 2 -Maringale eingeführ werden; nach 7.5 können wir dami insbesondere bzgl. seiger, lokaler Maringale inegrieren. Genauer gesag, haben wir bisher sochasische Inegrale der Form 0 X dm berache, wobei der Inegraor M ein rechsseiig seiges L 2 -Maringal und X Λ 2 (µ M ) is. Als abschließende Ausdehnung berachen wir ein sochasisches Inegral für den Fall wo Inegraor und Inegral diese Eigenschaf nur lokal besizen. Sa also (M ) 0 als rechsseiig seiges, L 2 -Maringal voraussezen, nehmen wir nun ab jez nur an, dass (M ) 0 ein rechsseiig seiges, lokales L 2 -Maringal is. Is (τ n ) n N eine geeignee, lokalisierende Folge für M, so schreiben wir wieder M (τn) := (M τn M 0 ) 0. Wir definieren nun die zu M gehörige Klasse der Inegranden: 7.6 Die Klasse Λ(M) Sei (M ) 0 rechsseiig seig. Es bezeichne Λ(M) die Klasse aller (X ) >0 für die es eine lokalisierende Folge (τ n ) n N von Soppzeien gib, so dass für jedes n N gil: M (τn) = (M τn M 0 ) 0 is ein L 2 -Maringal bzgl. (A ) 0 ; 1 ]0,τn]X Λ 2 (µ M (τn)). Eine solche Folge von Soppzeien, heiß eine lokalisierende Folge für (X, M). Is X Λ(M), so is wegen τ n (ω) und 1 ]0,τn]X P 0 -messbar, auch X = lim 1 ]0,τ n n]x P 0 -messbar. Ferner is in 7.6 nach Definiion (M ) 0 ein rechsseiig seiges lokales L 2 -Maringal. Im Folgenden zeigen wir, dass seige, adapiere Prozesse zu Λ(M) gehören, wenn M ein seiges, lokales Maringal is. 7.7 Λ(M) enhäl die seigen, adapieren Prozesse für seiges M Sei (M ) 0 ein seiges, lokales Maringal bzgl. (A ) 0 und (X ) 0 ein seiger, adapierer Prozess. Dann gil (X ) >0 Λ(M). Beweis. Nach 6.4 is (X ) >0 previsibel. Also is für jede Soppzei τ insbesondere 1 ]0,τ] X P 0 -messbar nach 6.5. Analog zu 7.5 sezen wir τ n := inf{ 0 : max{ X, M M 0 } n}. C3NEU 5
6 Finanzmahemaik II Dann sind τ n nach 4.27 Soppzeien mi τ n (ω) τ n+1 (ω). Wegen der Seigkei von [0, [ max{ X (ω), M (ω) M 0 (ω) } gil τ n (ω) n. Bezeichnen wir die Soppzeien in 7.5 mi σ n, so is nach 7.5 (M σn M 0 ) 0 ein (rechsseiig) seiges L 2 Maringal bzgl. (A ) 0. Nach 4.39 (ii) folg daher wegen τ n σ n, dass (1) M (τn) = (M τn M 0 ) 0 ein seiges L 2 -Maringal bzgl. (A ) 0 is. Nun gil für feses n (2) X s (ω) n für 0 < s τ n (ω). Ferner gil M τn M 0 n und somi (3) 1]0,] dµ M (τn) = 6.10 Ω (M (τn) M (τn) 0 ) 2 dp = Ω(M τn M 0 ) 2 dp n 2. Aus (2) und (3) folgen nun 1]0,] 1 ]0,τn]X 2 dµ M (τn) n 2 1 ]0,] dµ M (τn) n 4. (2) (3) Somi is 1 ]0,τn]X Λ 2 (µ M (τn)). Zusammen mi (1) folg (X ) >0 Λ(M) nach Definiion. Is also (M ) 0 ein seiges, lokales Maringal, so is insbesondere (M ) >0 Λ(M). Als echnisch nüzlich erweis sich 7.8 Geeignee Folgen von Soppzeien für lokale Maringale Sei (τ n ) n N eine geeignee lokalisierende Folge für das rechsseiig seige, lokale L p -Maringal (M ) 0 bzgl. (A ) 0. Sei (σ n ) n N eine beliebige lokalisierende Folge. Dann is (τ n σ n ) n N ebenfalls eine geeignee lokalisierende Folge von Soppzeien für das lokale L p -Maringal (M ) 0. Beweis. Es is (τ n σ n ) n N eine lokalisierende Folge von Soppzeien. Es is für feses n N zu zeigen (1) (M τn σ n M 0 ) 0 is ein L p -Maringal bzgl. (A ) 0. Nach Voraussezung is für jedes n N (2) (M τn M 0 ) 0 ein rechsseiig seiges, L p -Maringal bzgl. (A ) 0. Nach 4.39 (ii) angewand auf τ := σ n, folg (1). Hieraus folg insbesondere, dass eine Linearkombinaion von rechsseiig seigen, lokalen L p -Maringalen ein rechsseiig seiges, lokales L p -Maringal is. Wir wollen nun das lokale sochasische Inegral einführen. Wir erinnern, dass wir annehmen (siehe 6.32) (A ) 0 is eine augmeniere Filraion; (M ) 0 is ein rechsseiig seiges, lokales L 2 -Maringal bzgl. (A ) 0. 6 C3NEU
7 Die Brownsche Bewegung Sei (X ) >0 Λ(M) gegeben, und wähle eine lokalisierende Folge (τ n ) n N für (X, M). Dann is also M (τn) ein rechsseiig seiges L 2 -Maringal bzgl. (A ) und 1 ]0,τn]X Λ 2 (µ M (τn)), und daher is für jedes n N Y [τn] := ( 0 1 ]0,τ n]x dm (τn) ) 0 als rechsseiig seiges (bzw. seiges, wenn (M ) 0 seig is) L 2 -Maringal bzgl. (A ) 0 wählbar. (Benuze 6.28 und 6.29, (iii) sowie 5.11 (ii) und beache, dass die Filraion augmenier is). Das lokale sochasische Inegral Y = ( X dm) 0 0 werden wir als den P -f.s. exisierenden Grenzwer von lim n Y [τn] (ω) einführen. Hierzu zeigen wir (7.9) Für jedes n und m n gil für P -f.a. ω, dass Y [τm] (ω) = Y [τn] (ω) für 0 τ n (ω). (7.10) Die Definiion von Y is bis auf Ununerscheidbarkei unabhängig von der lokaliserenden Folge (τ n ) n N für (X, M). Wir beweisen zunächs zwei Hilfssäze ]0,τ ] X dm = 1 ]0,τ ] X dm τ Sei (M ) 0 ein rechsseiig seiges L 2 -Maringal und τ eine Soppzei bzgl. (A ) 0. Is X L 2 (µ M ), so is 1 ]0,τ] X L 2 (µ M τ ), und es gil: 1]0,τ] X dm = 1 ]0,τ] X dm τ. (ii) Is X Λ 2 (µ M ), so is 1 ]0,τ] X Λ 2 (µ M τ ), und es gil: 1]0,] 1 ]0,τ] X dm = 1 ]0,] 1 ]0,τ] X dm τ für jedes 0. Beweis. (ii) folg aus, da X Λ 2 (µ M ) nach Definiion bedeue 1 ]0,] X L 2 (µ M ) für alle 0. Übungsaufgabe Gleichhei von Inegralprozessen bzgl. M (τ ) und M (σ) Es seien τ und σ zwei Soppzeien, so dass M (τ) = (M τ M 0 ) 0 und M (σ) = (M σ M 0 ) 0 zwei rechsseiig seige (bzw. seige) L 2 -Maringale sind, mi 1 ]0,τ] X Λ 2 (M (τ) ) und 1 ]0,σ] X Λ 2 (M (σ) ). Es bezeichne Y [τ] bzw. Y [σ] die rechsseiig seigen (bzw. seigen) L 2 -Maringale ( 0 1 ]0,τ]XdM (τ) ) 0 bzw. ( 0 1 ]0,σ]X dm (σ) ) 0. Dann gil P {ω : Y [τ] (ω) = Y [σ] (ω) für 0 τ(ω) σ(ω)} = 1. C3NEU 7
8 Finanzmahemaik II Beweis. Da Y [τ] τ = 6.31 Übungsaufgabe 8. (1]0, τ] 1 ]0,τ] X) dm (τ) = Y [τ] P -f.s. für jedes 0 is, folg aus der rechsseiigen Seigkei von Y [τ] und Y [τ] τ (7.13) (Y [τ] τ ) 0 = P (Y [τ] ) 0. Aus 7.11 folg ferner 7.14 τ n σ n is eine lokalisierende Folge von (X, M) und (Y, N) Sei (τ n ) n N eine lokalisierende Folge für (X, M) und (σ n ) n N eine lokalisierende Folge für (Y, N). Dann is (τ n σ n ) n N eine gemeinsame lokalisierende Folge für(x, M) und(y, N). Beweis. Es is (τ n σ n ) n N eine lokalisierende Folge von Soppzeien. Nach 7.8 angewand auf τ n, σ n und (M ) 0 bzw. σ n, τ n und (N ) 0 folg: (1) (M (τn) ) σn = (M τn σ n M 0 ) 0 is ein L 2 -Maringal bzgl. (A ) 0, (2) (N (σn) ) τn = (N σn τ n N 0 ) 0 is ein L 2 -Maringal bzgl. (A ) 0. Ferner gil, da τ n eine lokalisierende Folge für (X, M) und σ n für (Y, N) is (3) 1 ]0,τn]X Λ 2 (µ M (τn)), (4) 1 ]0,σn]Y Λ 2 (µ N (σn)). Nach 7.11 (ii) angewand auf das rechsseiig seige L 2 -Maringal M (τn) bzw. N (σn) folg daher aus (3) und (4) (5) 1 ]0,σn τ n]x = 1 ]0,σn]1 ]0,τn]X Λ 2 (µ (M (τn) ) σn ), (6) 1 ]0,σn τ n]y = 1 ]0,τn]1 ]0,σn]Y Λ 2 (µ (N (σn) ) τn ). Aus (1) und (5) sowie (2) und (6) folg die Behaupung. Zur Definiion des lokalen Io-Inegrals Sei X Λ(M) und (τ n ) n N eine lokalisierende Folge für (X, M). Wenden wir nun 7.12 an auf τ := τ n und σ := τ m für m n, so folg 7.9. Somi gib es eine Menge Ω 1, vom Maße 1, so dass lim (ω) für ω Ω 1 exisier und endlich für jedes 0 is, wobei Y [τm] m Y [τn] (ω) = Y [τm] (ω) für 0 τ n (ω) und m n gil. Wir bezeichnen diesen Grenzwer mi Y (ω). Es gil für ω Ω 1 : (L) Y (ω) = Y [τn] (ω) für alle τ n (ω). Wegen τ n (ω) und (L) is Y (, ω) rechsseiig seig (seig) für ω Ω 1. Sezen wir Y (, ω) 0 für 0 und ω Ω 1, so is Y (, ω) für alle ω Ω rechsseiig seig (seig). Somi gil wegen (L) und 7.13 Y τn = Y [τn] für alle 0 P -f.s.. 8 C3NEU
9 Die Brownsche Bewegung Also is (Y ) 0 ein rechsseiig seiges (seiges), lokales L 2 -Maringal, mi lokalisierender Folge (τ n ) n N (beache, dass die Filraion augmenier is, und benuze 5.11). Für diesen Prozess (Y ) 0 schreiben wir (Y ) 0 = ( 0 X dm) 0. Die Definiion von Y = (Y ) 0 is bis auf die Ununerscheidbarkei der ensprechenden Sochasischen Prozesse von der Wahl der lokalisierenden Folge für (X, M) unabhängig: Zum Nachweis dieser Aussage, wähle eine weiere lokalisierende Folge(σ n ) n N für (X, M). Nach Definiion des sochasischen Inegrals reich es zu zeigen, es gil P -f.s. für jedes n N und für τ n (ω) σ n (ω) : (G) mi Y [τn] = Y [σn] := 0 1 ]0,σ n]x dm (σn), Y [τn] = 0 1 ]0,τ n]x dm (τn). Es folg (G) mi 7.12 angewand auf τ := τ n und σ := σ n. Zusammenfassend erhalen wir 7.15 Das lokale Io-Inegral Es sei(m ) 0 ein rechsseiig seiges, lokales L 2 -Maringal bzgl. der augmenieren Filraion (A ) 0. Es sei X Λ(M) und (τ n ) n N eine beliebige lokalisierende Folge für (X, M). Dann heiß (Y ) 0 = ( 0 X dm) 0das lokale Io-Inegral von X bzgl. M. Das lokale Io-Inegral is ein rechsseiig seiges, lokales L 2 -Maringal bzgl. (A ) 0 mi lokalisierender Folge (τ n ) n N. Hierbei gil 0 X dm = 0 1 ]0,τ n]x dm (τn) für τ n (ω) P -f.s. Is (M ) 0 sogar ein seiges, lokales Maringal, so is das lokale Inegral ( 0 X dm) 0 ebenfalls seig. Für 0 s < sez man s X dm := Y Y s. Ferner is Y τn = 0 1 ]0,τ n]xdm (τn) für alle 0 P -f.s. Wegen Y 0 = 0 is die Definiion von s XdM für s = 0 widerspruchsfrei, und es gil s 0 X dm + s X dm = 0 X dm. Mi X Λ(M) is αx Λ(M) mi ( 0 αxdm) 0 = P α( 0 XdM) 0. Sind X, Y Λ(M), so folg nach 7.14 (N := M), dass es eine gemeinsame lokalisiernde Folge (τ n ) n N für (X, M) und (Y, M) gib. Dann is (τ n ) n N auch eine lokalisierende Folge für (X + Y, M). Also is X + Y Λ(M) und es gil 0 1 ]0,τ n](x + Y )dm (τn) = 0 1 ]0,τ n]x dm (τn) ]0,τ n]y dm (τn) und daher is auch bis auf Ununerscheidbarkei 0 (X + Y )dm = 0 X dm + 0 Y dm. C3NEU 9
10 Finanzmahemaik II 7.16 Einfache Eigenschafen des lokalen Io-Inegrals (ii) Es sei (M ) 0 ein rechsseiig seiges, lokales L 2 -Maringal. Dann is α) Λ(M) ein R-linearer Raum; β) Λ(M) X Y = ( 0 X dm) 0 eine R-lineare Abbildung in die rechsseiig seigen, lokalen L 2 -Maringale bzgl. (A ) 0. γ) Für 0 s < gil 0 X dm = s 0 X dm + s X dm. Sei (M ) 0 ein seiges, lokales Maringal. α) Dann is für X Λ(M) Y = ( 0 X dm) 0 ein seiges, lokales Maringal. β) Is(X ) 0 ein seiger, adapierer Prozess, dann is (X ) >0 Λ(M), und somi Y = ( 0 X dm) 0 ein seiges, lokales Maringal. Insbesondere is also ( 0 M dm) 0 ein seiges, lokales Maringal. (iii) Is M ein rechsseiig seiges, L 2 -Maringal bzgl. (A ) 0, dann is Λ 2 (µ M ) Λ(µ M ) und für X Λ 2 (µ M ) is das in 6.28 und 6.29 definiere ( 0 X dm) 0 gleich dem lokalen Io-Inegral. (iv) Seien (M ) 0 und (M ) 0 zwei rechsseiig seige, lokale L 2 -Maringale mi M M 0 = M M 0 P -f.s. für jedes 0. Dann gil Λ(M) = Λ(M ) und für X Λ(M) is ( 0 X dm) 0 = P ( 0 X dm ) 0. Beweis. α), β) und γ) sind schon bewiesen. (ii) α) is in 7.15 noier. Beache, dass ein seiges, lokales Maringal auch ein lokales L 2 -Maringal is (siehe 7.5). β) folg aus 7.7 und α). (iii) τ n für alle n liefer eine lokalisierende Folge für (X, M), denn es is (M (τn) ) 0 mi M (τn) = M M 0 ein L 2 -Maringal bzgl. (A ) 0 und für X Λ 2 (µ M ) gil 1 ]0,τn]X = X Λ 2 (µ M ) = Λ 2 (µ (τn) 6.22 (M ). ) 0 Also is X Λ(M). Das lokale Io-Inegral is nach 7.15 gegeben durch 0 1 ]0,τ n]xdm (τn) = 0 X dm. 6.22(iii) (iv) Wegen der rechsseiigen Seigkei sind (M M 0 ) 0 und (M M 0 ) 0 ununerscheidbar. Für eine lokalisierende Folge τ n sind M (τn) und M (τn) gleichzeiig L 2 - Maringale mi µ M (τn) = µ M (τn) nach Also gil auch L 2 (µ M (τn)) = L 2 (µ M (τn)) und somi Λ 2 (µ M (τn)) = Λ 2 (µ M (τn)). Daher is Λ(M) = Λ(M ) nach Definiion 7.6. Wegen der rechsseiigen Seigkei des lokalen Io-Inegrals bleib noch zu zeigen 1]0,] X dm = 1 ]0,] X dm P -f.s.. 10 C3NEU
11 Die Brownsche Bewegung Dies folg aus der Definiion des lokalen Io-Inegrals, und da nach 6.22(ii) P -f.s. für jedes 0 gil wegen 1 ]0,] 1 ]0,τn]X L 2 (µ M (τn) ) 1]0,] 1 ]0,τn]X dm (τn) = 1 ]0,] 1 ]0,τn] X dm (τn) Subsiuion beim lokalen Io-Inegral Es sei (M ) 0 ein rechsseiig seiges, lokales L 2 -Maringal bzgl. (A ) 0. Es sei X = (X ) >0 Λ(M) und Y = (Y ) 0 = ( 0 X dm) 0 das lokale Io-Inegral von X bzgl. M. Also is (Y ) 0 ein rechsseiig seiges, lokales L 2 -Maringal bzgl. (A ) 0. Sei nun Z = (Z ) >0 P 0 -messbar. Dann gil (ii) Z Λ(Y ) ZX Λ(M); ( 0 Z dy ) 0 = P ( 0 ZX dm) 0 für Z Λ(Y ). Beweis. und (ii) Nach 7.14 gib es eine gemeinsame lokalisierende Folge (τ n ) n N für (X, M) und (Z, Y ). Dann gil für alle n 1 ]0,τn]X Λ 2 (µ M (τn)) 1 ]0,τn]Z Λ 2 (µ Y (τn)). Wegen Y 0 = 0 is Y (τn) = Y τn = ( ]0,τ n]x dm (τn) ) 0. Somi folg für alle n nach 6.33 (iii), dass 1 ]0,τn]X Z Λ 2 (µ M (τn)) is, und 0 1 ]0,τ n]z dy (τn) = 0 1 ]0,τ n]zx dm (τn). Aus Erserem folg, aus der Gleichung folg (ii) nach Definiion des lokalen Io- Inegrals, da (τ n ) n N eine lokalisierende Folge für (Z, Y ) und (XZ, M) is. Zu : mi Da X, ZX Λ(M) sind, gib es nach 7.14 eine lokalisierende Folge (τ n) n N M (τn) is ein rechsseiig seiges L 2 -Maringal für jedes n N 1 ]0,τn]X, (1 ]0,τn]Z)(1 ]0,τn]X) Λ 2 (µ M (τn)). Wegen Y 0 = 0 is für feses n nun Y (τn) = Y τn = ( 0 (1 ]0,τ n]x)dm (τn) ) 0. Nach 6.33 (iii) folg dann 1 ]0,τn]Z Λ 2 (µ Y (τn)). Somi is Z Λ(Y ), da τ n auch eine lokalisierende Folge für das lokale L 2 -Maringal Y is Lokalbeschränke, previsible Prozesse sind lokal Io-inegrierbar Sei (X ) >0 previsibel, (M ) 0 ein rechsseiig seiges, lokales L 2 -Maringal. Is (X ) >0 lokal beschränk, d.h. gib es eine lokalisierende Folge (σ n ) n N und K n R + mi X (ω) K n für 0 < σ n (ω), dann is X Λ(M). C3NEU 11
12 Finanzmahemaik II Beweis. Sei (τ n ) n N eine lokalisierende Folge für (M ) 0. Nach 7.8 is dann (τ n σ n n) n N eine lokalisierende Folge für das rechsseiig seige, lokale L 2 -Maringal (M ) 0. Nun is 1 ]0,τn σ n n]x P 0 -messbar und 1 ]0,τn σ n n]x 2 K 2 n 1 ]0,n] Ω. Also is 1 ]0,τn σ n n]x L 2 (µ (M τn σn n M 0 )), und daher is X Λ(M) nach Definiion 7.6. Is M ein rechsseiig seiges, lokales L 2 -Maringal so is offenbar M M 0 ebenfalls ein rechsseiig seiges, lokales L 2 -Maringal mi Λ(M) = Λ(M M 0 ) und 0 X dm = 0 X d(m M 0) für X Λ(M) nach 7.16 (iv). Is nun M sogar ein seiges, lokales Maringal so zeigen wir (7.19) 0 M dm = 0 (M M 0)dM + M 0 (M M 0 ) = 0 (M M 0)d(M M 0 ) + M 0 (M M 0 ) Da wir die zweie Gleichhei schon nachgewiesen haben, reich es die erse Gleichhei zu beweisen. Nach 7.16 (ii) β) exisier sowohl 0 M dm als auch 0 (M M 0)dM. Nach 7.16 gil dann 0 M dm 0 (M M 0)dM = 0 M 0dM. Es bleib also 0 M 0dM = M 0 (M M 0 ) zu zeigen. Wir zeigen in Übungsaufgabe 9 ewas allgemeiner: is X 0 A 0 -messbar, so gil (7.19) B X 0 Λ(M) und 0 X 0dM = X 0 (M M 0 ) Andere Definiion von Λ(M) In der Definiion 7.6 von Λ(M) kann die Bedingung 1 ]0,τn]X Λ 2 (µ M (τn)) zu 1 ]0,τn]X L 2 (µ M (τn)) verschärf werden. Beweis. Sei τ n die lokalisierende Folge die in 7.6 vorkomm. Nach 7.8 is dann (τ n) n N := (τ n n) n N ebenfalls eine geeignee lokalisierende Folge von Soppzeien für (M ) 0. Da 1 ]0,τn]X Λ 2 (µ M (τn)) is, is 1 ]0,τn n]x = 1 ]0,n] 1 ]0,τn]X L 2 (µ M (τn)). Wende man nun 7.11 an auf M := M (τn), τ n und X := 1 ]0,τn n], X dann is wegen (M (τn) ) n = M (τn n) dann 1 ]0,τn n]x L 2 (µ M (τn n)). Also is 1 ]0,τ n ]X L 2 (µ M (τ n ) ) für alle n N und (τ n) n N is die geeignee lokalisierende Folge Lokalisierende Folgen für (X, M) Sei (τ n ) n N eine lokalisierende Folge für (X, M) und (σ n ) n N eine beliebige lokalisierende Folge. Dann is (τ n σ n ) n N eine lokalisierende Folge für (X, M). Beweis. Wende Saz 7.14 an auf die (0, 0) lokalisierende Folge (σ n ) n N. 12 C3NEU
13 Die Brownsche Bewegung 7.22 Definiionsmöglichkei von Λ(M) für seige, lokale Maringale Sei M ein seiges, lokales Maringal und X Λ(M), dann gib es eine lokalisierende Folge von Soppzeien (τ n ) n N, so dass M (τn) für jedes n N ein seiges, beschränkes Maringal is, und 1 ]0,τn]X L 2 (µ M (τn)) für jedes n N is. Beweis. Wähle nach 7.20 eine lokalisierende Folge (τ n ) n N, so dass M (τn) für jedes n N ein seiges L 2 -Maringal mi 1 ]0,τn]X L 2 (µ M (τn)) is. Sei nun σ n die lokalisierende Folge aus 7.5, so dass also M (σn) für feses n N ein beschränkes Maringal is. Nach 7.8 is dann (τ n σ n ) n N ebenfalls eine lokalisierende Folge für M, so dass auch M (τn σn) = (M (τn) ) σn ein seiges, beschränkes Maringal is. Da 1 ]0,τn]X L 2 (µ M (τn)) is, is nach 7.11 auch 1 ]0,τn σ n]x = 1 ]0,σn]1 ]0,τn]X L 2 (µ [M (τn) ] σn ) = L 2 (µ M (τn σn)). Die Aussage folg daher mi der lokalisierenden Folge (τ n σ n ) n N Das sochasische Inegral als Limes von Zwischensummen Es sei (M ) 0 ein seiges, lokales Maringal und (X ) 0 ein seiger, adapierer Prozess. Sei > 0, dann gil für jede reguläre Zerlegungsfolge Z n = ( n 0,..., n k n ) von [0, ], dass (ii) k n ν=1 X n (M n ν M n ) für n sochasisch gegen 0 X dm konvergier. Sind X und M beschränk, so konvergier kn X n (M n ν M n ) für n sogar im L 2 (P ) gegen 0 X dm. ν=1 Wir zeigen zunächs (ii) : Nach Saz 6.4 is (X ) >0 P 0 -messbar. Seze X n (s, ω) := kn X n (ω)1 ] n, n ν ](s). ν=1 Dann gil nach 6.35 (iii) angewand auf τ := (1) X n dm = kn X n (M n ν M n ), ν=1 da M ein seiges L 2 -Maringal nach 7.3 is. Da X linksseiig seig is, konvergier X n für n punkweise gegen 1 ]0,] X. Wegen µ M (]0, [ Ω) = lim (Mn M 0 ) 2 dp < n is X L 2 (µ M ), und die Konvergenz von X n gegen 1 ]0,] X finde auch im L 2 (µ M ) sa. Auf Grund der Io-Isomerie gil somi X n dm n 0 X dm. L 2 (P ) C3NEU 13
14 Finanzmahemaik II Zusammen mi (1) folg hieraus (ii). Wir berachen nun den Fall eines seigen, lokalen Maringals. Nach 7.16 (iv) dürfen wir M 0 = 0 annehmen. Nach 7.19 (B) gil 0 X 0dM = X 0 (M M 0 ) = kn X 0 (M n ν M n ). Wir dürfen daher auch X 0 = 0 annehmen. Dieser Fall folg nun mi Hilfe des Lokalisaionsprinzips aus. Siehe Übungsaufgabe 10. Wegen P {τ k < } k 0 und (5) folg die Behaupung. Wir erhalen nun aus 6.37 mi 7.14 nach Definiion des lokalen Io-Inegrals ν= Lokale Io-Inegrale bzgl. αm + βn Seien M, N rechsseiig seige, lokale L 2 -Maringale. Dann sind αm und M + N rechsseiig seige, lokale L 2 -Maringale. (ii) Is X Λ(M) und α R so is X Λ(αM), und es gil ( 0 Xd(αM)) 0 = P (α 0 XdM) 0. Is X Λ(M) und X Λ(N), so is X Λ(M + N), und es gil ( 0 Xd(M + N)) 0 = P ( 0 XdM) 0 + ( 0 XdN) 0. Beweis. Übungsaufgabe 11. In der Regel wird schon bei der Einführung von lokalisierenden Folgen eine augmeniere Filraion vorausgesez. Is dann (τ n ) n N eine Folge von Soppzeien mi τ n τ n+1 und τ n (ω) P -f.s., so is τ n := τ n 1 {lim τn= } + n1 {lim τn< } eine lokalisierende Folge von Soppzeien mi τ n : τ n is nämlich eine Soppzei wegen der Augmenierhei der Filraion und τ n = τ n P -f.s.. Hieraus folg X Λ(M) genau dann, wenn X previsibel is, und es eine Folge τ n von Soppzeien gib mi τ n τ n+1 sowie τ n P -f.s., so dass gil (M τn M 0 ) 0 is ein L 2 (P )-Maringal bzgl. (A ) 0, 1 ]0,τn]X L 2 (µ M (τn)). Is X Λ(M), so is X previsibel und die Eigenschafen sind nach 7.20 sogar für eine Folge von Soppzeien mi τ n erfüll. Sind die Eigenschafen gegeben, so bilde τ n gemäß obiger Konsrukion. Wegen τ n = τ n P -f.s. und der Augmenierhei is zunächs auch (M τ n M 0 ) 0 ein L 2 (P )-Maringal bzgl. (A ) 0. Da 1 ]0,τ n ]X mi X auch P 0 -messbar is, und 1 ]0,τ n ]X = 1 ]0,τn]X P -f.s. gil, is 1 ]0,τ n ]X L 2 (µ M (τn)) = L 2(µ 6.22 (iii) M (τ n ). Also ) is X Λ(M) nach Definiion 7.8. Nach Saz 7.7 gil X Λ(M) für seiges X und M. Saz 7.18 leg nahe, dass die Voraussezungen an X und M abschwächbar sind. Allerdings benöigen wir dann, dass die augmeniere Filraion rechsseiig seig is. 14 C3NEU
15 Die Brownsche Bewegung 7.25 Adapiere Prozesse die linksseiig seig sind und rechsseiige Grenzwere besizen, sind lokal Io-inegrierbar Sei (X ) 0 ein adapierer Prozess, der linksseiig seig is, und rechsseiige Grenzwere besiz. Es sei (M ) 0 ein rechsseiig seiges, lokales L 2 -Maringal bzgl. einer augmenieren, rechsseiig seigen Filraion. Dann gil X Λ(M). Beweis. Es is (X ) >0 previsibel nach 6.4. Wir zeigen nun, dass die Voraussezungen von 7.18 erfüll sind. Da X linksseiig seig is, erhäl man wie in 4.23, dass σ n (ω) := inf{ 0 X (ω) > n} eine schwache Soppzei und somi nach 4.25, da die Filraion auch rechsseiig seig is, eine Soppzei is. Nun gil wegen der linksseiigen Seigkei von X X (ω) n für 0 < σ n (ω). Es is σ n eine lokalisierende Folge von Soppzeien, da eine linksseiige seige Funkion mi rechsseiigen Grenzweren über [0, [ auf jedem beschränken Inervall beschränk is. Somi folg X Λ(M) nach Für eine rechsseiige seige, augmeniere Filraion sind also die Komponenen jeder elemenaren Handelssraegie nach 7.25 lokal Io-inegrierbar (zur Definiion der elemenaren Handelssraegie siehe 2.3). C3NEU 15
8 Die quadratische Variation, und die Integration bzgl. stetiger Semimartingale
 8 Die quadratische Variation, und die Integration bzgl. stetiger Semimartingale 8.1 Der quadratische Variationsprozess eines stetigen, lokalen Martingals 8.3 Die quadratische Variation einer reellen Brownschen
8 Die quadratische Variation, und die Integration bzgl. stetiger Semimartingale 8.1 Der quadratische Variationsprozess eines stetigen, lokalen Martingals 8.3 Die quadratische Variation einer reellen Brownschen
Stochastische Analysis
 Skrip Sochasische Analysis Seffen Schwarz 17. April 216 Dozen: PD Dr. Volker Paulsen Fakulä für Mahemaik Wesfälische Wilhelms-Universiä Münser Inhalsverzeichnis Einleiung 1 I Sochasische Inegraion 1 1
Skrip Sochasische Analysis Seffen Schwarz 17. April 216 Dozen: PD Dr. Volker Paulsen Fakulä für Mahemaik Wesfälische Wilhelms-Universiä Münser Inhalsverzeichnis Einleiung 1 I Sochasische Inegraion 1 1
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Stochastische Analysis und Finanzmathematik
 Sochasische Analysis und Finanzmahemaik Vorlesung im Winersemeser 211/212 von Dr. Markus Schulz Inhalsverzeichnis 1 Sochasische Prozesse 1 1.1 Grundlagen................................ 1 1.2 Die Brownsche
Sochasische Analysis und Finanzmahemaik Vorlesung im Winersemeser 211/212 von Dr. Markus Schulz Inhalsverzeichnis 1 Sochasische Prozesse 1 1.1 Grundlagen................................ 1 1.2 Die Brownsche
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
7. Funktionalgleichung der Zeta-Funktion
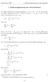 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Stochastik III. Skript zu einer Vorlesung an der Johannes-Gutenberg-Universität Mainz, Sommer Matthias Birkner. Vorläufige Version, 23.7.
 Sochasik III Skrip zu einer Vorlesung an der Johannes-Guenberg-Universiä Mainz, Sommer 215 Mahias Birkner Vorläufige Version, 23.7.215 Kommenare, Korrekurvorschläge, Hinweise auf (Tipp-)fehler gerne per
Sochasik III Skrip zu einer Vorlesung an der Johannes-Guenberg-Universiä Mainz, Sommer 215 Mahias Birkner Vorläufige Version, 23.7.215 Kommenare, Korrekurvorschläge, Hinweise auf (Tipp-)fehler gerne per
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
No-Arbitrage Modelle
 No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
3 Bedingte Erwartungswerte
 3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
3 Bedingte Erwartungswerte 3.3 Existenz und Eindeutigkeit des bedingten Erwartungswertes E A 0(X) 3.6 Konvexitätsungleichung für bedingte Erwartungswerte 3.9 Konvergenzsätze von Levi, Fatou und Lebesgue
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Motivation. Finanzmathematik in diskreter Zeit
 Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
Schwache Konvergenz von Wahrscheinlichkeitsmaßen
 Schwache Konvergenz von Wahrscheinlichkeitsmaßen 6. Juli 2010 Inhaltsverzeichnis 1 Definition 2 3 Lindeberg-Bedingung Interpretation Definition Motivation (Konvergenz von Wahrscheinlichkeitsmaßen) Sind
Schwache Konvergenz von Wahrscheinlichkeitsmaßen 6. Juli 2010 Inhaltsverzeichnis 1 Definition 2 3 Lindeberg-Bedingung Interpretation Definition Motivation (Konvergenz von Wahrscheinlichkeitsmaßen) Sind
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
9 Die Ito-Formel und ihre Anwendungen
 9 Die Ito-Formel und ihre Anwendungen 9.1 Die eindimensionale Ito-Formel 9. Die Formel der partiellen Integration 9.3 Die quadratische Variaton eines stetigen Semimartingals 9.4 Die eindimensionale Ito-Formel
9 Die Ito-Formel und ihre Anwendungen 9.1 Die eindimensionale Ito-Formel 9. Die Formel der partiellen Integration 9.3 Die quadratische Variaton eines stetigen Semimartingals 9.4 Die eindimensionale Ito-Formel
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
4 Gleichgradige Integrierbarkeit, Stoppzeiten und Martingale
 4 Gleichgradige Integrierbarkeit, Stoppzeiten und Martingale 4.2 Filtrationen und kanonische Filtrationen 4.3 Supermartingale, Martingale bzw. Submartingale bzgl. der Filtrationen (A t ) t I 4.4 Gleichgradig
4 Gleichgradige Integrierbarkeit, Stoppzeiten und Martingale 4.2 Filtrationen und kanonische Filtrationen 4.3 Supermartingale, Martingale bzw. Submartingale bzgl. der Filtrationen (A t ) t I 4.4 Gleichgradig
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
2 Martingale in stetiger Zeit
 2 Martingale in stetiger Zeit Ziel dieses Abschnitts ist es die wichtigsten Resultate für Martingale aus diskreter Zeit in stetige Zeit zu übertragen. Wie zu erwarten ist treten in stetiger Zeit einige
2 Martingale in stetiger Zeit Ziel dieses Abschnitts ist es die wichtigsten Resultate für Martingale aus diskreter Zeit in stetige Zeit zu übertragen. Wie zu erwarten ist treten in stetiger Zeit einige
Portfoliooptimierung in HJM-Modellen
 Porfolioopimierung in HJM-Modellen Maserarbei von Eugenia Kiefel Bereuer: Privadozen Dr. V. Paulsen Mahemaisches Insiu für Saisik Fachbereich - Mahemaik und Informaik Wesfälische Wilhelms-Universiä Münser
Porfolioopimierung in HJM-Modellen Maserarbei von Eugenia Kiefel Bereuer: Privadozen Dr. V. Paulsen Mahemaisches Insiu für Saisik Fachbereich - Mahemaik und Informaik Wesfälische Wilhelms-Universiä Münser
Klausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 003/004 Universität Karlsruhe 05. 04. 004 Prof. Dr. G. Last Klausur zur Vorlesung Stochastik II Dauer: 90 Minuten Name: Vorname: Matrikelnummer: Diese Klausur hat
Institut für Mathematische Stochastik WS 003/004 Universität Karlsruhe 05. 04. 004 Prof. Dr. G. Last Klausur zur Vorlesung Stochastik II Dauer: 90 Minuten Name: Vorname: Matrikelnummer: Diese Klausur hat
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
mittlere bremsende Kraft auf das Teilchen um diesen Mittelwert fluktuierende stochastische Kraft f(t) stochastischer Prozess
 Brownsche Bewegung schweres Teilchen mi Masse m und Geschwindigkei v beweg sich in Flüssigkei von leichen Teilchen. Dieses Brownsche Teilchen wird von den Molekülen der Flüssigkei gesoßen. Söße bewirken:
Brownsche Bewegung schweres Teilchen mi Masse m und Geschwindigkei v beweg sich in Flüssigkei von leichen Teilchen. Dieses Brownsche Teilchen wird von den Molekülen der Flüssigkei gesoßen. Söße bewirken:
Satz von Rademacher und weiterführende Resultate
 S E M I N R R B E I T Saz von Rademacher und weierführende Resulae ausgeführ am Insiu für nalysis und Scienific Compuing TU Wien uner der nleiung von o.univ.prof. Dipl.-Ing. Dr.echn. Michael Kalenbäck
S E M I N R R B E I T Saz von Rademacher und weierführende Resulae ausgeführ am Insiu für nalysis und Scienific Compuing TU Wien uner der nleiung von o.univ.prof. Dipl.-Ing. Dr.echn. Michael Kalenbäck
Kapitel : Exponentielles Wachstum
 Wachsumsprozesse Kapiel : Exponenielles Wachsum Die Grundbegriffe aus wachsum 1.xmcd werden auch hier verwende! Wir verwenden im Beispiel 2 auch fas die gleiche Angabe wie in Beispiel 1 - lediglich eine
Wachsumsprozesse Kapiel : Exponenielles Wachsum Die Grundbegriffe aus wachsum 1.xmcd werden auch hier verwende! Wir verwenden im Beispiel 2 auch fas die gleiche Angabe wie in Beispiel 1 - lediglich eine
Finanzmathematik. Wolfgang Müller. Institut für Statistik Technische Universität Graz
 Finanzmahemaik Wolfgang Müller 213 Insiu für Saisik Technische Universiä Graz Inhalsverzeichnis 1. Markmodelle in diskreer Zei 1 1.1. Das Binomialmodell................................ 1 1.2. Das allgemeine
Finanzmahemaik Wolfgang Müller 213 Insiu für Saisik Technische Universiä Graz Inhalsverzeichnis 1. Markmodelle in diskreer Zei 1 1.1. Das Binomialmodell................................ 1 1.2. Das allgemeine
Arbitragefreie Preise
 Arbiragefreie Preise Maren Schmeck 24. Okober 2006 1 Einleiung P i () Preis von Anleihe i zur Zei, i = 1,..., n x i Anzahl an Einheien der Anleihe i V () = n i=1 x ip i () Wer eines Porfolios mi x i Einheien
Arbiragefreie Preise Maren Schmeck 24. Okober 2006 1 Einleiung P i () Preis von Anleihe i zur Zei, i = 1,..., n x i Anzahl an Einheien der Anleihe i V () = n i=1 x ip i () Wer eines Porfolios mi x i Einheien
