Stochastische Analysis
|
|
|
- Krista Schulz
- vor 6 Jahren
- Abrufe
Transkript
1 Skrip Sochasische Analysis Seffen Schwarz 17. April 216 Dozen: PD Dr. Volker Paulsen Fakulä für Mahemaik Wesfälische Wilhelms-Universiä Münser
2 Inhalsverzeichnis Einleiung 1 I Sochasische Inegraion 1 1 Zeiseige Maringalheorie Pfadeigenschafen Äquivalenzklassen Zwei unerschiedliche Äquivalenzbegriffe Maringalkonvergenzsaz Soppzeien Opional Sampling Charakerisierung eines Maringals Anwendungen von Opional Sampling Weiere Anwendungen von Opional Sampling Doob sche Maximalungleichungen Usual condiions H p -Räume Das sochasische Inegral Elemenare Sraegien Progressiv messbare Prozesse Previsible σ-algebra Beispiele für previsible Prozesse Das Doléans-Maß Das sochassische Inegral für elemenar previsible Prozesse Das sochasische Inegral für H L 2 (µ M ) Der sochasische Inegralprozess Der sochasische Inegralprozess für elemenar previsible H... 5 Weiere Eigenschafen des Inegralprozesses Soppen und Abschneiden Der quadraische Variaionsprozess Die Variaion Lebesgue-Sieljes Inegraion Die quadraische Variaion Der quadraische Variaionsprozess für beschränke, seige Maringale Eigenschafen Der quadraische Variaionsprozess für seige L 2 -Maringale... 7 Der quadraische Variaionsprozess für sochasische Inegralprozesse Die quadraische Kovariaion Eigenschafen der quadraische Kovariaion Lokalisaion Lokalisierung des Inegraors
3 II Der Iō-Kalkül 13 1 Iō-Formel Parielle Inegraionsformel für F V -Funionen Die Iō-Formel Mehrdimensionale Iō-Formel Doléans Exponenialsemimaringal Lineare sochasische Differenialgleichungen Die allgemeine Black-Scholes Modellierung der Preisenwicklung einer Akie Das klassische Black-Scholes Modell Der Ornsein-Uhlenbeck-Prozess Der Vasicek-Prozess Die allgemeine 1-dimensionale lineare sochasische Differenialgleichung Haupsäze der sochasischen Analysis Komplexe Semimaringale Das komplexe Doléans Exponenial Saz von Lévy Maringaldarsellungssaz, Teil I (Maringale) Maringaldarsellungssaz, Teil II (lokale Maringale) Allgemeine Bayes-Formel Saz von Girsanov, Teil I Saz von Girsanov, Teil II Saz von Girsanov, Teil III Anwendung 1: Maßwechsel Anwendung 2: Zum Saz von Lévy III Sochasische Differenialgleichungen Sarke Lösbarkei
4 Einleiung Inhal der Vorlesung I Sochasische Inegraion 1. zeiseige Maringalheorie 2. Definiion des sochasischen Inegralprozesses 3. Definiion der quadraischen Variaion 4. Lokalisaion II Iō-Kalkül 1. Iō-Formel 2. lineare sochasische Differenialgleichungen 3. Haupsäze der sochasischen Analysis III Sochasische Differenialgleichungen 1. sarke Lösbarkei I Sochasische Inegraion 1 Zeiseige Maringalheorie Ziel: Bereisellung der Hilfsmiel für die sochasische Inegraion Seup 1.1. Wir haben einen Wahrscheinlichkeisraum (Ω, F, P). Definiion Eine Filraion (F ) is eine aufseigende Familie von σ-algebren mi F F. F = σ ( F ) Definiion Ein sochasischer Prozess X is eine Familie (X ) von Zufallsvariablen mi Weren in (R, B) Definiion X is adapier bzgl. der Filraion (F ), wenn X messbar is bzgl. F für alle. 1
5 Definiion Durch F X = σ (X s s ) für alle wird die zu X gehörige kanonische Filraion definier. X is bzgl. (F X ) adapier. Genauer: F X = σ ( s σ(x s )) = σ ( s Xs 1 (B)) Pfadeigenschafen Definiion X ha seige Pfade, wenn seig is für alle und ω Ω X (ω) Definiion X ha rechsseiig seige Pfade, wenn X (ω) rechsseiig seig is für alle und ω Ω Definiion X is linksseiig limiierbar, wenn für jedes > der Limes lim s X s (ω) exisier für alle ω Ω Definiion X ha cadlag-pfade, wenn X rechsseiig seig und linksseiig limiierbar is. Äquivalenzklassen Definiion Ein A Ω heiß vernachlässigbar, falls es ein N F gib, mi P(N) = und A N. Definiion Wir sagen, dass eine Eigenschaf E P-fas sicher erfüll is, wenn vernachlässigbar is. {ω ω erfüll nich E} Zwei unerschiedliche Äquivalenzbegriffe 2
6 Definiion X heiß Modifikaion von Y, falls vernachlässigbar is für alle. {ω X (ω) Y (ω)} Definiion X heiß nich unerscheidbar von Y, falls vernachlässigbar is. {ω X (ω) Y (ω)} = {ω X (ω) Y (ω)} Bemerkung. (i) Is X nich unerscheidbar von Y, so sind X und Y Modifikaionen. (ii) Haben X und Y P-f.s. rechsseiig seige Pfade und sind X und Y Modifikaionen, so sind X und Y auch nich unerscheidbar. Definiion 1.2. Ein (F ) adapierer sochasischer Prozess X heiß Maringal bzgl. (F ), falls gil: (i) E X < für alle (ii) E(X F s ) = X s für alle s Ensprechend Submaringal, falls (i) E X < für alle (ii) E(X F s ) X s für alle s und Supermaringal, falls (i) E X < für alle (ii) E(X F s ) X s für alle s Haupbeispiele sind die zum Wiener-Prozess gehörenden Maringale. Definiion 1.3. Ein bzgl. einer Filraion (F ) adapierer Prozess W heiß Wiener- Prozess, falls gil: (i) W = P-f.s. (ii) W W s is sochasisch unabhängig von F s für alle s (iii) W W s is vereil wie W s für alle s (iv) W N (, ) für alle 3
7 (v) W ha P-f.s. seige Pfade Der Wiener-Prozess sare aus der Null (i), ha unabhängige (ii) und saionäre (iii) Zuwächse, die normalvereil (iv) sind und ha seige Pfade (v). Der Wiener-Prozess is ein Beispiel für einen Lévy-Prozess (da er (ii) und (iii) erfüll). Konsruier werden kann ein Wiener-Prozess als Grenzwer einer Folge von skalieren zenrieren Irrfahren. Idee: Sei (Y k ) k N eine Folge von idenisch vereilen, unabhängigen Zufallsvariablen mi P(Y k = 1) = 1 2 = P(Y k = 1) Definiere W (n) ( k n ) = 1 n k j=1 Y j Seze W (1) () = k=1 Y k. Durch lineare Inerpolaion erhäl man (W (1) ()). Erhöhe dann die Frequenz um den Fakor n und sauche die Höhe um n (da die Varianz auf n seig). 1 n 2 n 3 n 4 n 1 k n 2 3 Durch lineare Inerpolaion erhäl man (W (n) ()). Durch W (n) wird eine Folge von sochasischen Prozessen mi seigen Pfaden konsruier, die gegen einen Grenzprozess (W ()) konvergier. W ha die definierenden Eigenschafen eines Wiener-Prozesses. (Präzisier wird dies durch das Donskersche Invarianzheorem, vgl. WT II). Bemerkung 1.4. Sei W ein Wiener-Prozess bzgl (F ). Dann gil: (i) (W ) is ein (F ) -Maringal, (ii) (W 2 ) is ein (F ) -Maringal, (iii) (exp(ϑw 1 2 ϑ2 )) is ein (F ) -Maringal für ϑ R Beweis. (i) W is N (, ) vereil E W <. E(W F s ) = E(W s + W W s F s ) 4
8 = E(W s F s ) + E(W W s F s ) = W s + E(W W s ) = W s + E(W s ) = W s (ii) + (iii) analog. Bei Maringalen ineressier man sich für das Verhalen im Unendlichen. Eine erse Anwor liefer der Maringalkonvergenzsaz Saz 1.5 (Maringalkonvergenzsaz). Sei (X ) ein rechsseiig seiges Submaringal mi sup EX + <. Dann exisier eine F -messbare Abbildung X mi X X P-f.s. und E X < Beweis. Rückführung auf den zeidiskreen Fall. Wichig is, dass man auf die rechsseiige Seigkei der Pfade nich verzichen kann. Vgl. Revuz, Yor: Coninuous Maringales and Brownian Moion Bemerkung. -Jedes rechsseiig seige posiive Maringal konvergier P-f.s. exp(ϑw 1 2 ϑ2 ) konvergier P-f.s.: Da W gil: - Die Prozesse ϑw 1 2 ϑ2 = (ϑ W - (W s+ W s ) für alle s, 1 2 ϑ2 ) falls ϑ - ( W ) und - (cw c 2 ) für alle c > sind Wiener-Prozesse. -Der Wiener-Prozess selber is nich konvergen, d.h. P(sup W = + ) = 1 = P(inf W = ) Beweis. Zeige zuers, dass M = sup W die gleiche Vereilung ha wie cm, für alle c >. Da sowohl (W ) also auch (cw ) Wiener-Prozesse sind, gil c 2 M = sup W = sup W c 2 = 1 c sup cw c 2 5
9 Also cm = sup cw c 2 M Sei nun a = P(M = ) und sei F die Vereilungsfunkion von M, d.h. F () = P(M ) Zeige, dass F konsan is. Berache dazu und a = P(M = ) = P(M ) = F () F () F () = P( < M ) = P( < cmleqc) = P( < M ) = F (c) F () wobei wir hier die gleiche Vereilung von M und cm genuz haben. Also is F () = F (c) für alle < c R Da auch >, is F konsan auf ganz (, ). Wegen der rechsseiigen Seigkei der Vereilungsfunkion gil Hieraus folg: und F () = F (+) = F () = a für alle > P(M < ) = lim P(M ) = lim F () = a = P(M = ) P(M = ) = 1 a Es bleib zu zeigen, dass a =. Denn dann is P(M = ) = 1. P(M = ) P(W 1, W W 1 W 1 für alle ) = P(W 1, sup(w 1+ W 1 ) W 1 ) = E [P(W 1, sup(w 1+ W 1 ) W 1 W 1 )] = E [1 W1 P(sup(W 1+ W 1 ) W 1 W 1 )] = M P(M x) dp W 1 (x) =P(M=) 6
10 = P(M = ) P(W 1 ) = 1 2 Da P ein Wahrscheinlichkeismaß is, muss = P(M = ) = a sein. Das bedeue, dass P(M = ) = 1 is. Da ( W ) ein Wiener-Prozess is, gil P(inf W = ) = P( sup W = ) = P(sup W = ) = 1 Sa P-f.s.-Konvergenz, kann man sich fragen, wann L 1 -Konvergenz vorlieg. Wann gil E X X? Dafür is es sinnvoll, den Begriff der gleichgradig Inegrierbarkei einzuführen: Definiion 1.6. Sei I eine Indexmenge, ewa I = [, ). Eine Familie von reellwerigen Zufallsvariablen (X ) I heiß gleichgradig inegrierbar, wenn gil a sup E X 1 { X >a} I Häufig nüzlich is die folgende Charakerisierung: Saz 1.7. Sei (X ) I eine Familie reeller Zufallsvariablen. Dann sind äquivalen: (i) (X ) I is gleichgradig inegrierbar. (ii) a) sup I E X < (L 1 -Beschränkhei) b) ɛ > δ > A F P(A) < δ sup I E X 1 A < ɛ (iii) Es exisier eine nich negaive, monoon wachsende konvexe Funkion G [, ) [, ) mi G(x) lim x x = + und sup EG( X ) < I (iv) Es exisier eine nich negaive, messbare Funkion G [, ) [, ) mi Beweis. vgl. Skrip Alsmeyer G(x) lim x x = + und sup EG( X ) < I Bemerkung. a) Jede endliche Familie von inegrierbaren Zufallsvariablen is gleichgradig inegrierbar. 7
11 b) Sind (X ) I und (X ) J gleichgradig inegrierbar, so auch (X ) I J. c) Exisier eine inegrierbare Zufallsvariable Y mi X Y für alle I, so is (X ) I gleichgradig inegrierbar. d) Aus sup I E X < folg im Allgemeinen nich gleichgradige Inegrierbarkei. e) Is sup I E X p < für ein p > 1, is is (X ) I gleichgradig inegrierbar. Wichiges Beispiel: Beispiel 1.8. Sei (Ω, F, P) ein Wahrscheinlichkeisraum und I eine Menge von Unerσ-Algebren von F. Dann is die Familie (E(Y G)) G I gleichgradig inegrierbar, sofern Y inegrierbar is. Beweis. Ein einfacher Beweis nuz die Jensensche Ungleichung für bedinge Erwarungswere, die besag: Is G R R konvex, so gil E(G(X) F) G(E(X F)). Y is gleichgradig inegrierbar. Es exisier also eine monoon wachsende konvexe Funkion G mi G(x) x x und EG( Y ) <. Jensen liefer: G( E(Y G) ) E(G( Y ) G) Also sup G I EG( E(Y G) ) < EG( E(Y G) ) EE(G( Y ) G) = EG( Y ) < Das Beispiel liefer, dass für Y L 1 (Ω, F, P) durch (E(Y F )) ein gleichgradig inegrierbares Maringal definier wird. Beweis. Die gleichgradige Inegrierbarkei folg aus dem Beispiel. Für die Maringaleigenschaf gil für alle s : E(E(Y F ) F s ) = E(Y F s ) mi Hilfe der Turmeigenschaf des bedingen Erwarungsweres. Miels gleichgradiger Inegrierbarkei kann auf L 1 -Konvergenz geschlossen werden Saz 1.9. Sei (X ) ein sochasischer Prozess mi E X < für alle und sei X eine weiere Zufallsvariable. Es gele: a) (X ) is gleichgradig inegrierbar, b) X X in Wahrscheinlichkei, das heiß, P( X X > ɛ) 8
12 Dann is X auch konvergen in L 1 gegen X, d.h. lim E X X = Beweis. Beh: X L 1, d.h. E X < Wegen (b) exisier eine Folge ( n ) n N mi n und X n X P-f.s. Lemma von Faou liefer E X = E lim inf n X n lim inf E X n n sup E X n n N sup E X < a) Zeige jez die L 1 -Konvergenz. Sei ɛ >. Wegen der gleichgradigen Inegrierbarkei exisier ein δ > mi P(A) < δ E X 1 A < ɛ 3 für alle und P(A) < δ E X 1 A < ɛ 3. Weier exisier ein T mi Für alle T gil also P( X X > ɛ ) < δ für alle T. 3 E X X = E X X 1 { X X ɛ 3 } + E X X 1 { X X > ɛ 3 } ɛ 3 P( X X ɛ 3 ) + E X 1 { X X > ɛ 3 } + E X 1 { X X > ɛ 3 } 3 ɛ 3 = ɛ Eine L p Formulierung von Saz 1.9 liefer: Saz 1.1. Sei p > 1 und (X ) ein sochasischer Prozess mi E X p < für alle. Sei ferner X eine weiere Zufallsvariable. Es gele: a) ( X p ) is gleichgradig inegrierbar, b) X X in Wahrscheinlichkei 9
13 Dann is X auch konvergen in L p gegen X, d.h. Beweis. lim E X X p = E X X p X X p in L p. Weier is X X p in Wahrscheinlichkei. Verbleib zu zeigen: ( X X p ) is gleichgradig inegrierbar. Wie in Saz 1.9 folg mi Faou E X p <. Wegen X X p 2 p 1 ( X p + X p ) folg die behaupee gleichgradige Inegrierbarkei, da ( X p ) { X p } gleichgradig inegrierbar is. Die gleichgradig inegrierbaren Maringale kann man mi L 1 (Ω, F, P) idenifizieren. Saz 1.11 (Isomerie I). Sei (F ) eine Filraion und M die Menge der gleichgradig inegrierbaren (F ) -Maringale. Dann is J M L 1 (Ω, F, P) X X = lim X ein Vekorraumisomorphismus mi Umkehrabbildung I L 1 (Ω, F, P) M Y (E(Y F )) Beweis. 1. Schri: (I J)(X) = X Die Wohldefinierhei von I und J folgen aus dem Maringalkonvergenzsaz und Beispiel 1.8. Sei X M. Dann exisier genau ein X L 1 mi X X P-fas sicher wegen des Maringalkonvergenzsazes. Da (X ) gleichgradig inegrierbar is, gil X X in L 1. Dies implizier X = E(X F ) P-f.s. für alle, denn: Für beliebiges gil P( X E(X F ) > δ) = P( E(X T F ) E(X F ) > δ) = P( E(X T X F ) > δ) 1 δ E E( X T X F ) Markov- Ungl. 1 δ EE( X T X F ) 1
14 = 1 δ E X T X T. 2. Schri: Zur Surjekiviä von J. Für Y L 1 (Ω, F, P) is (E(Y F )) ein gleichgradig inegrierbares Maringal. Nach dem Maringalkonvergenzsaz exisier ein X L 1 (Ω, F, P) mi Mi dem 1. Schri folg X = E(Y F ) X P-fas sicher E(Y F ) = X = E(Y F ) für alle zu zeigen: Y = X P-f.s., denn dann is J(X) = Y. Zeige hierzu: EY 1 A = EX 1 A für alle A F, denn dann is Y = E(Y F ) = X P-fas sicher. Für A F gil: EY 1 A = E(Y F )1 A = EX 1 A = EE(X F )1 A = EX 1 A F bilde ein -sabiles Erzeugendensysem für F. Da {A F EY 1 A = EX 1 A } ein Dynkinsysem is, folg die Behaupung. Zu bemerken is, dass die Aussage und der Beweis an einer kleinen Selle ewas ungenau is. Die Frage is, was genau der Vekorraum der gleichgradig inegrierbaren Maringale is, denn diese sind ja nich eindeuig besimm. Wichig is, wie späer noch bemerk wird, dass es zu einem Maringal X eine Modifikaion mi cadlag Pfaden gib, die bis auf Nichunerscheidbarkei eindeuig besimm is. Aus der Äquivalenzklasse der Modifikaionen von X wird deshalb als Repräsenan die bis auf Nichunerscheidbarkei eindeuige Version mi cadlag Pfaden gewähl. Deshalb kann man annehmen, dass jedes Maringal X cadlag Pfade ha. Ziel: Zusammenhang zu Glücksspielen. Soppzeien Definiion Sei (F ) eine Filraion. Eine Soppzei τ is eine Abbildung τ Ω [, ) {+ } mi {τ } F für alle Die Enscheidung vor zu soppen, häng nur von der Informaion bis ab. Durch F τ = {A F A {τ } F für alle } wird die σ-algebra der durch τ-beobachbaren Ereignissen definier. Eine Definiion der Form F τ = {A F A {τ } F für alle } liefer das Gleiche. 11
15 Bemerkung. Für σ, τ Soppzeien gil: (i) σ τ(= min(σ, τ)), σ τ(= max(σ, τ)), σ + τ sind Soppzeien (ii) Gil σ τ, so is F σ F τ. (iii) Is X ein cadlag-prozess, so is X τ 1 {τ< } F τ messbar. (iv) Es gil: F τ σ = F τ F σ. (v) Is (τ n ) n N eine Folge von Soppzeien, so is sup τ n n eine (F ) Soppzei und eine (F + ) Soppzei. inf n τ n (vi) Eine Zufallsvariable X is F τ messbar genau dann, wenn X1 {τ } messbar is bezüglich F für alle. Dies wird späer noch im Zusammenhang mi progressiv messbaren Prozessen genauer beleuche. Opional Sampling Saz 1.13 (Opional Sampling I). Sei X ein (F ) -Maringal mi cadlag Pfaden und τ eine beschränke Soppzei, d.h. es exisier ein T > mi τ T P-f.s. Dann gil: (i) E(X T F τ ) = X τ P-f.s. (ii) EX τ = EX Bemerkung. Dieser Saz gil auch für Submaringale: Is (X ) ein cadlag Submaringal bezüglich einer Filraion (F ) und is τ eine, durch T > beschränke, Soppzei, so gil: (i) E(X T F τ ) X τ (ii) EX T EX τ Beweis von Saz (i) 1. Schri: τ habe nur endlich viele Were N T 12
16 Für A F τ und k {1,..., N} A {τ = k } = (A {τ k })/(A {τ k 1} ) F k F k F k 1 Dann is Also für alle A F τ : A {τ= k } X τ dp = X dp = k F k A {τ= k } A {τ= k } X T dp A X τ dp = N k=1 A {τ= k } X τ dp = N k=1 A {τ= k } X T dp = A X T dp E(X T F τ ) = X τ 2. Schri: Approximiere τ durch (τ n ) n N mi τ 1 τ 2... τ und τ n habe endlich viele Were. Das geschieh durch: τ τ n T τ T Wähle hierzu eine geschachele Folge von Zerlegungen (n) < (n) 1 <... < (n) l(n) = T mi l(n) die maximale Anzahl der Zerlegungspunke und mi max i (n) i 1 (n) n i. Definiere τ n (ω) = inf{ (n) i Dann is τ 1 τ 2... lim n τ n (ω) = τ(ω). Wegen Schri 1 gil dann (n) i τ(ω)} X τn = E(X T F τn ) für alle n N (X τn ) n N is gleichgradig inegrierbar. Zusäzlich is n X τn X τ P-fas sicher (cadlag-pfade) Also X τn n X τ in L 1. Für A F τ gil deshalb: Also is EX T 1 A = EX τ 1 A für alle A F τ. X τ = E(X T F τ ). (ii) folg aus (i) durch EX T 1 A = EX τn 1 A n EX τ 1 A EX = EE(X T F ) = EX T = EE(X T F τ ) = EX τ 13
17 Beschränke Soppzeien kann man als Sraegien inerpreieren, die ein Spieler für einen Auszahlungsprozess X realisieren kann. Lieg ein Maringal vor, kann ein Spieler sich im Miel nich durch eine Sraegie verbessern. Insofern is das Maringal ein faires Glücksspiel. Umgekehr is in diesem Sinne auch der Auszahlungsprozess eines fairen Glücksspieles ein Maringal. Charakerisierung eines Maringals Saz Sei X ein (F ) adapierer Prozess mi cadlag Pfaden und E X < für alle. Dann sind äquivalen: (i) X is ein Maringal (ii) Für jede beschränke Soppzei τ gil Beweis. siehe Saz 1.13 Zeige E(X F s ) = X s für alle s. zu zeigen: EX 1 A = EX s 1 A für alle A F s. Zu A F s definiere eine Soppzei τ durch EX τ = EX s τ(ω) = falls ω A falls ω A Dann gil: EX 1 A = EX EX 1 A C = EX EX τ 1 A C = EX (EX τ E τ 1 A ) (ii) = EX EX +EX τ 1 A = = EX s 1 A Beache: (ii) liefer für τ : EX = EX τ = EX Die Aussage kann verbesser werden, wenn man gleichgradig inegrierbare Maringale berache, denn dann kann auf die Beschränkhei der Soppzei verziche werden. 14
18 Saz 1.15 (Opional Sampling II). Sei X ein (F ) adapieres gleichgradig inegrierbares Maringal mi cadlag Pfaden. Dann gil: (i) Es exisier eine F -messbare Abbildung X mi E(X F τ ) = X τ P-fas sicher für jede Soppzei τ. (ii) EX τ = EX für jede Soppzei τ. Bemerkung. Auch dieser Saz gil für Submaringale: Sei (X ) ein gleichgradig inegrierbares Submaringal bezüglich einer Filraion (F ) mi cadlag Pfaden, so gil: (i) Es exisier eine F messbare Abbildung X mi E(X F τ ) X τ P-fas sicher für jede Soppzei τ. (ii) EX τ EX für jede Soppzei τ. Beweis von Saz (i) Wegen Saz 1.11 exisier ein X L 1 mi X = E(X F ) für alle. Sei τ eine beliebige Soppzei. Für A F τ gil: A {τ T } F τ F T = F τ T τ T is eine beschränke Soppzei. Also gil: A {τ T } X τ dp = A {τ T } F τ T X τ T dp = A {τ T } = A {τ T } = A {τ T } E(X T F τ T )dp X T dp X dp Weier gil: E(X F τ T ) = X τ T für alle T 15
19 denn E(X F τ T ) = E(E(X F T ) F τ T ) = E(X T F τ T ) = X τ T Dies liefer die gleichgradige Inegrierbarkei von (X τ T ) T. Zusammen mi der punkweisen Konvergenz gegen X τ folg die Inegrierbarkei von X τ und die L 1 -Konvergenz von X τ T T X τ Somi folg mi der majorisieren Konvergenz A {τ< } X τ dp = lim T A {τ T } = lim T A {τ T } = X dp A {τ< } X τ dp X dp Zusammen mi folg (ii) A X τ dp = X dp A {τ= } A {τ= } X τ dp = X dp für alle A F τ A EX τ = EE(X F τ ) = EX = EX Man erhäl folgende Charakerisierung: Saz Sei (X ) ein bzgl (F ) adapierer Prozess mi cadlag Pfaden und sei X eine F -messbare Zufallsvariable. Genau dann is (X ) ein gleichgradig inegrierbares Maringal mi lim X = X, wenn für jede Soppzei τ X τ inegrierbar is und EX τ = EX 16
20 erfüll. Beweis. siehe Saz 1.14 Zeige: X = E(X F ) für alle. Für τ is X = X τ inegrierbar und Für τ is X = X τ inegrierbar und Definiere für A F eine Soppzei τ durch EX = EX τ = EX EX = EX τ = EX τ(ω) = falls ω A falls ω A Dann gil Also folg EX = EX = EX τ = EX 1 A + EX 1 A C EX 1 A = EX 1 A Man kann dies auf gesoppe Prozesse anwenden. Saz Sei X ein (F ) -Maringal mi cadlag Pfaden und τ eine Soppzei. Dann is der durch τ gesoppe Prozess X τ, definier durch ein (F ) -Maringal. X τ = X τ = X 1 { τ} + X τ 1 {>τ} Beweis. X τ is ein Prozess mi cadlag Pfaden und adapier bzgl (F ), da F τ F. Für jede beschränke Soppzei σ gil: EX τ σ = EX τ σ = EX = EX τ Wichige Beispiele von Soppzeien sind Erseinriszeien. Beispiel Sei (X ) ein adapierer Prozess bzgl einer Filraion (F ). Für eine Borelmenge B is τ B = inf{ X B} die Erseinriszei in B. Behaupung: Ha X seige Pfade und is B abgeschlossen, so is τ B eine Soppzei bzgl. (F ). 17
21 Beweis. Definiere offene Mengen B n = {x R d(x, B) < 1 n } für alle n N Erreich X die Menge B vor, so erreich X auch jedes B n vor. Wegen der Seigkei der Pfade ri X vor in B n auch zu einem raionalen Zeipunk ein. Genauer: {τ B } = {X B} {X q B n } F So haben wir nur noch abzählbare Vereinigungen und Durchschnie, können dami also die Messbarkei folgern. klar, wegen Offenhei der B n und Seigkei der Pfade {X B} {τ B } Is ω n N q Q{X q B n } (q n ) n Q [, ) mi X qn B n. q< Is B offen, so is τ B im Allgemeinen keine Soppzei. Die Informaion muss infiniesimal vergrößer werden. Seze dazu n N q Q q< F + = F +ɛ ɛ> Behaupung: Ha X rechsseiig seige Pfade, so is τ B eine (F + ) -Soppzei für jedes offene B. Beweis. Es gil: τ B is eine (F + ) -Soppzei {τ B } F + für alle {τ B < } F für alle Es gil {τ B < } = {X q B} F q Q q< Anwendungen von Opional Sampling Beispiel Sei (W ) ein Wiener-Prozess bezüglich einer Filraion (F ). Dann erreich der Wiener-Prozess mi Wahrscheinlichkei 1 jedes a R. Genauer: Sei a R und τ a = inf{ W = a} inf =. Dann is P(τ a < ) = 1 18
22 Beweis. OEdA is a >, da ( W ) auch ein Wiener-Prozess is. Für λ > berache das Maringal Dann gil: M λ () = exp(λw 1 2 λ2 ). M λ ( τ a ) e λa (M τa λ ()) is ein beschränkes Maringal und dami gleichgradig inegrierbar. Also konvergier M τa λ () für gegen exp(λa 1 2 λ2 τ a )1 {τa< }, da auf {τ a = } Es gil mi Opional Sampling M τa λ () = M λ(). Also folg 1 = EM τa τa λ () = EMλ ( ) = E exp(λa 1 2 λ2 τ a )1 {τa< } = e λa Ee 1 2 λ2 τ a 1 {τa< } Monoone Konvergenz liefer Ee 1 2 λ2 τ a 1 {τa< } = e λa für alle λ > P(τ a < ) = lim λ Ee 1 2 λ2 τ a 1 {τa< } = lim λ e λa = 1 Eigenlich is die Laplaceransformiere von τ a besimm worden: Es gil: L τa [, ) [, ) ν Ee ντa L τa (ν) = Ee ντa = ν= 1 2 λ2 2ν=λ e 2νa Die Laplaceransformiere besimm die Vereilung von τ a. Man erhäl, dass τ a die Diche ha, denn Es gil: Ee ντa = g a () = 1 exp( 1 a 2 2π 3 2 )1 (, )() e ν g a ()d = e 2νa für alle ν > Eτ a = g a ()d = Das bedeue, dass man im Miel unendlich lange brauch, um ein beliebiges a R zu erreichen. Und doch erreich man jedes a R. 19
23 Weiere Anwendungen von Opional Sampling Beispiel 1.2. Sei W ein Wiener-Prozess bezüglich einer Filraion (F ) und definiere τ durch τ = inf{ W = a oder W = b} für a, b >. Dann is P(τ < ) = 1 und W τ ein beschränkes Maringal, was die gleichgradige Inegrierbarkei implizier. Deshalb gil: Zusammen mi folg = EW τ = EW τ = EW τ = ap(w τ = a) + bp(w τ = b) P(W τ = a) = P(W τ = a) + P(W τ = b) = 1 b a + b und P(W τ = b) = a a + b Weier is (W 2 ) ein Maringal. Mi Opional Sampling folg Wegen monooner Konvergenz gil E(W 2 τ T τ T ) = EW 2 τ T = Eτ T E(τ T ) E(τ) (W 2 τ T ) is ein beschränker Prozess, also folg mi majorisierer Konvergenz: Andererseis gil aber auch EW 2 τ = lim T E(W 2 τ T ) = lim T E(τ T ) = Eτ EWτ 2 = a 2 P(W τ = a) +b 2 P(W τ = b) = ab b a a+b a+b Also gil Eτ = ab Beispiel. Definiere, für (W ) ein Wiener-Prozess, die Soppzei τ durch Definiere τ = inf{ W = b oder W = b} M = W 4 6W für alle ( ) Dann is (M ) ein Maringal (überprüfen durch Nachrechnen) und es gil = EM τ = E(W 4 τ 6(τ )W 2 τ + 3(τ ) 2 ) 2
24 Wegen monooner Konvergenz konvergier und es gil E(τ ) 2 Eτ 2 (τ )W 2 τ τb 2 Da τ inegrierbar is, liefer die majorisiere Konvergenz: E((τ )W 2 τ ) E(τW 2 τ ) = b 2 E(τ) = b 4 (W 4 τ ) is beschränk, also liefer majorisiere Konvergenz: b 4 = W 4 τ = lim EW 4 τ Insgesam ergib das Wegen E(τ) = b 2 is also 3E(τ 2 ) = 6b 4 b 4 = 5b 4 Var(τ) = 2 3 b4 Ziel: Einführung der H p -Räume. Hierzu dienen die Doob schen Maximalungleichungen: Saz Sei E eine konvexe Teilmenge von R (i) Is X ein Maringal mi Weren in E und is f E R konvex, so dass E f(x ) < für alle, so is (f(x )) ein Submaringal. (ii) Is X ein Submaringal in E und f E R konvex und monoon wachsend mi E f(x ) < für alle, so is (f(x )) ein Submaringal. Beweis. Dies folg aus der Jensenschen Ungleichung für bedinge Erwarungswere: (i) E(f(X ) F s ) f(e(x F s )) = f(x s ) für s (ii) E(f(X ) F s ) f(e(x F s )) f(x s ) für s Anwendung finde dies in 21
25 (i) X Maringal X Submaringal (ii) X Maringal und E X p < für alle ( X p ) Submaringal (iii) X Maringal X + Submaringal Die Maringaleigenschaf kann von (F ) auf (F + ) ausgeweie werden. (Erinnerung: F + = ɛ> F +ɛ ) Saz Sei (X ) ein rechsseiig seiges Maringal bezüglich einer Filraion (F ). Dann is X auch ein Maringal bezüglich (F + ). Beweis. Sei fes gewähl und T >, sowie ( n ) n N mi n. Wegen der rechsseiigen Seigkei konvergier X n X. Da X n = E(X T F n ) für alle n N, is (X n ) n N gleichgradig inegrierbar. Aus der punkweisen Konvergenz und der gleichgradigen Inegrierbarkei folg die Konvergenz von X n X in L 1. Dami folg für alle A F + EX 1 A = EX T 1 A denn Beache EX T 1 A = EX n 1 A n EX 1 A EX n 1 A EX 1 A E X n X 1 A E X n X n Saz 1.23 (Doob sche Maximalungleichungen). Sei (X ) ein rechsseiig seiges Maringal oder ein posiives Submaringal bezüglich einer Filraion (F ). Dann gil für XT = sup T X : (i) λ p P(X T λ) E X T p 1 {X λ} E X T p für alle p 1 (ii) λ p P(X > λ) sup E X p für alle p 1 (iii) X T p p p 1 sup T X p für alle p > 1 (iv) X p p p 1 sup X p für alle p > 1 Bemerkung. Die Aussagen (iii) und (iv) bezeichne man auch als Doob sche L p Ungleichung. Diese sind äquivalen mi E XT p ( p p p 1 ) sup E X p T für alle p > 1, < T 22
26 Beweis. (i) Sei p 1, T >. O.E.d.A. is E X p < für alle. Dann is ( X p ) ein Submaringal und wegen der Version für Submaringale des Opional Sampling Sazes 1.13 gil E X τ p E X T p für jede durch T beschränke Soppzei τ. Berache für λ > die Soppzei Dann gil: τ = inf{ X λ} (ii) E X T p 1 {τ T } = E X T p E X T p 1 {τ>t } E X τ T p E X T p 1 {τ>t } = E X τ p 1 {τ T } λ p P(τ T ) = λ p P(X T λ) P(X > λ) = P(sup X > λ) P(τ < ) = lim T P(τ T ) (i) 1 lim T λ E X p T p = 1 λ sup E X p p (iii) erhäl man aus (i) und der Hölderungleichung: Für jedes K > gil: X L p, X L q, 1 p + 1 q = 1 E XY X p Y q E(X T K) p = E = E Fubini = X T K K K py p 1 dy py p 1 1 {X T y}dy py p 1 P(X T y)dy 23
27 Also Und somi Dami folg: (i) mi = p=1 Fubini = E K py p 2 E X T 1 {X T y}dy K = E X T p = pe X T py p 1 X T 1 {X T y}dy K X T K y p 2 1 {X T y}dy y p 2 dy p = p 1 E X T (XT K) p 1 Hölder p p 1 (E X T p ) 1 p (E(X T K) (p 1)q ) 1 q 1 p + 1 q = 1 1 q = 1 1 p = p 1 p q = p p 1 p = p 1 (E X T p ) 1 p (E(X T K) p ) p 1 p (E(XT K) p ) p ( p p p 1 ) E X T p (E(XT K) p ) p 1 E(XT K) p ( p p p 1 ) E X T p E(XT ) p = lim E(XT K) ( p p T p 1 ) E X T p (iv) X T konvergier monoon gegen X. Also gil: E(X ) p mon. = Konv. lim T E(X T ) p p p 1 lim T E(X T ) p = p p 1 sup E X p Usual condiions Sei (F ) eine Filraion. Definiion (F ) erfüll die usual condiions, falls gil: (i) (F ) is rechsseiig seig, d.h. F = F + für alle, 24
28 Voreile: (ii) F enhäl alle vernachlässigbaren Mengen. 1. Modifikaionen von adapieren Prozessen sind wieder adapier, 2. Einriszeien in Borelsche Mengen sind Soppzeien, 3. Maringale lassen eine Pfadregulierung zu. Genauer: Erfüll (F ) die usual condiions, so gib es zu jedem (F ) -Maringal X eine Modifikaion mi cadlag Pfaden. Diese cadlag Version is bis aus Nichunerscheidbarkei eindeuig besimm. Deshalb kann bei Vorhandensein der usual condiions o.e.d.a. angenommen werden, dass X cadlag Pfaden ha P-fas sicher. Konsrukion einer Filraion, die die usual condiions erfüll: Sei (F () ) eine Filraion. Sei N die Menge der vernachlässigbaren Mengen. Definiere: F (1) = σ(f () N ) für alle F (1) enhäl alle vernachlässigbaren Mengen. Seze F = F (1) + = F (1) +ɛ für alle ɛ> Dann erfüll (F ) die usual condiions per Konsrukion. Die so definiere Filraion nenn man die Vervollsändigung von (F () ). Bemerkung. Is X ein Maringal bzgl (F () ), so is X auch ein Maringal bezüglich der vervollsändigen Filraion (F ) und es gib eine Modifikaion mi rechsseiig seigen Pfaden. Bemerkung. Is W ein Wiener-Prozess bzgl (F () ), so is W auch ein Wiener Prozess bezüglich der vervollsändigen Filraion (F ). Die Annahme, dass eine Filraion die usual condiions erfüll, is also keine wirklich einschränkende Annahme. H p -Räume Definiion Für p > 1 kann der Raum H p definier werden durch H p = {X X is ein cadlag Maringal bzgl (F ) mi sup E X p < } 25
29 ( Menge der L p -beschränken Maringale) Dabei is (F ) eine Filraion, die die usual condiions erfüll. Jedes X H p is in L p beschränk und dami gleichgradig inegrierbar. Also is H p M = {X X gleichgradig inegrierbares cadlag Maringal} Auf H p kann man eine Norm definieren durch X Hp = sup(e X p ) 1 p = sup X p = (sup 1 E X p p ) Saz (Isomerie II). Durch J H p L p (Ω, F, P) X X = lim X wird eine Isomerie zwischen Banach-Räumen definier mi der Umkehrabbildung Dabei bedeue Isomerie, dass gil: I L p (Ω, F, P) H p X (E(X F ) J(X) p = X p = X Hp für alle X H p Beweis. Gezeig worden is in Saz 1.11, dass J und I zueinander inverse Isomorphismen zwischen M und L 1 sind. Zu zeigen verbleib, dass die Teilräume ensprechend abgebilde werden und die Isomerieeigenschaf erfüll is: Behaupung: Is X H p, so is J(X) = X L p und X Hp = J(X) p = X p Beweis. Nuze die Doob sche Maximalungleichung: Weier is X p X p p p 1 sup X p = eine inegrierbare Majorane von ( X p ). Also liefer die majorisiere Konvergenz: X p = X Hp X p = (sup X p ) 1 p p p 1 X H p < E X p = lim E X p = sup E X p = X Hp 26
30 Behaupung: Is X L p, so is I(X ) H p. Beweis. I(X ) = (E(X F )) Weier is E( E(X F ) p ) EE( X p F ) = E X p < I(X ) H p Insbesondere is für p = 2 der H 2 Raum ein Hilber-Raum, isomerisch isomorph zu L 2 (Ω, F, P). Definiere H 2,c = {X H 2 X ha seige Pfade} Saz Sei (F ) eine Filraion, die die usual condiions erfüll. Dann is H 2,c ein abgeschlossener Teilraum von H 2. Beweis. Klar is, dass H 2,c ein Teilraum von H 2 is. zur Abgeschlossenhei: Sei (X (n) ) n N eine Folge in H 2,c mi Grenzwer X H 2 (, da H 2 Hilber-Raum). Das heiß: X (n) n X H2 also sup Doob sche L 2 -Ungleichung liefer: E(sup X (n) Also sup X (n) X 2 in L 1. Also exisier eine Teilfolge (n k ) k N mi Also auch Da X (n k) Pfade. E(X (n) X) 2 n. X ) 2 4 sup E X (n) X 2 n sup X (n k) X 2 P-fas sicher sup X (n k) X P-fas sicher P-fas sicher seige Pfade ha, ha X als gleichmäßiger Limes auch seige 2 Das sochasische Inegral Ziel: Wir wollen eine sinnvolle Definiion für T H()dS() = [,T ] geben, wobei H und S sochasische Prozesse sind. Inerpreaion in der Finanzmahemaik: H()dS() 27
31 (H()) T Handelssraegie eines Händlers. Dabei ensprich H() der Anzahl an Akien, die zum Zeipunk gehalen werden. (S()) T Preisenwicklung der Akie, S() ensprich dem Preis der Akie zum Zeipunk. H()dS() Gewinn, den ein Händler durch die Sraegie H über den Zeiraum [,T ] [, T ] erziel. Präzisieren kann man dies für elemenare Sraegieren. Elemenare Sraegien Definiion 2.1. Eine elemenare Sraegie lieg dann vor, wenn nur zu endlich vielen Zeipunken < 1 <... < n = T eine Umschichung in der Porfoliozusammensezung vorgenommen werden kann. Das bedeue, in k 1 wird das Porfolio zufällig gemäß einer F k 1 -messbaren Zufallsvariable h k gebilde und bis k gehalen. Formal bedeue das: T h 1 h 2 h k H(, ω) = h k (ω)1 (k 1, k ]() k=1 1 2 k 1 k Der Händler erziel in [, T ] einen Gewinn von Fragen: [,T ] H()dS() = T k=1 h k (S( k ) S( k 1 )) = = S( k ) T k=1 h k S( k ) - Wie kann man die elemenaren Sraegieren verallgemeinern? - Welche Prozesse kann man inegrieren? 1. Anwor: Ha S Pfade mi beschränker Variaion, so können progressiv messbare Prozesse H inegrier werden, deren Pfade Lebesgue Sieljes-inegrierbar sind. Zum Beispiel können adapiere Prozesse mi seigen Pfaden inegrier werden. 2. Anwor: Die wichigsen Preisprozesse in der Finanzmahemaik haben keine Pfade von beschränker Variaion. Deshalb is eine Ausdehnung nowendig. Progressiv messbare Prozesse Definiion 2.2. Bezeichne mi B [,] die Borelsche-σ-Algebra auf [, ] für alle. Sei weier eine Filraion (F ) gegeben. Eine Abbildung X [, ] Ω R 28
32 heiß progressiv messbar, falls für jedes > X [, ] Ω R messbar is bezüglich B [,] F. Das heiß, dass für alle B B gil: {(s, ω) [, ] Ω X s (ω) B} B [,] F Bemerkung 2.3. Jeder adapiere Prozess mi rechsseiig seigen Pfaden is progressiv messbar. Beweis. Sei >. Zerlege [, ] in = (n) < (n) 1 <... < (n) = und seze l(n) auf [, ] Ω und X (n) = l(n) 1 k= X (n) X (n) k = X 1 (n) [ k,(n) k+1 ) Wegen der Adapierhei is X (n) messbar bezüglich B [,] F und wegen der rechsseiigen Seigkei konvergier X (n) gegen X auf [, ] Ω, was die Messbarkei von X [,] Ω bezüglich B [,] F implizier. Bemerkung 2.4. Is X ein progressiv messbarer Prozess und τ eine Soppzei, so is X τ 1 {τ< } eine F τ -messbare Abbildung. Beweis. Es gil: X τ 1 {τ< } is F τ -messbar genau dann, wenn X τ 1 {τ } F -messbar is, für alle : Für B B gil: - Is B, so is (X τ 1 {τ } ) 1 (B) = X 1 τ (B) {τ } - Is B, so is (X τ 1 {τ } ) 1 (B) = (X 1 τ (B) {τ }) {τ > } Sei X τ 1 {τ< } F τ messbar. Dann is in beiden obigen Fällen (X τ 1 {τ } ) 1 (B) F. Also is X τ 1 {τ } F messbar für alle. Sei nun X 1 {τ } F messbar für alle. Dann is X 1 τ (B) {τ } = (X τ 1 {τ } ) 1 (B) B (X τ 1 {τ } ) 1 F (B) {τ } B. Also is X τ 1 τ< messbar bezüglich F τ. Sei nun >. Dann is τ = τ eine messbare Abbildung von (Ω, F ) ([, ] B [,] ), denn {τ s} = {τ s} F s F für alle s < und {τ = } = {τ = } = {τ } = {τ < } C F 29
33 Weier is ω (τ (ω), ω) eine messbare Abbildung von (Ω, F ) nach ([, ] Ω, B [,] F ). Also is X τ 1 {τ } (ω) = X(τ (ω), ω)1 {τ } (ω) als Hinereinanderausführung von messbaren Abbildungen wieder eine F -messbare Abbildung. Bemerkung 2.5. Es seien alle Nullmengen schon in F enhalen, d. h. N F. Is X dann ein progressiv messbarer Prozess mi X s (ω) ds < P-fas sicher für alle so wird durch Y = X s ds ein adapierer Prozess mi P-fas sicheren seigen Pfaden definier. Beweis. Sei (T n ) Folge mi T 1 < T 2 <..., T n. Für jedes n N is eine B [,Tn] F Tn messbare Abbildung. Es gib eine Nullmenge N Tn mi X [, T n ] Ω R T n X s (ω) ds < für alle ω N Tn Für ω N Tn is X s(ω)ds wohldefinier, seig und F Tn -messbar in ω. Seze N = n N N Tn. Dann is N vernachlässigbar und für alle ω N is Y (ω) = X s (ω)ds wohldefinier für alle. Weier is Y (ω) seig und adapier, da X progressiv messbar is. Previsible σ-algebra Auf [, ) Ω soll die σ-algebra der previsiblen Mengen eingeführ werden. Sei (F ) eine Filraion, die die usual condiions erfüll. 1. Schri: Das Sysem der previsiblen Rechecke is definier durch R = {{} F F F } {(s, ] F s s,, F s F s } 3
34 R is ein Halbring denn (i) R R 1 R 1 R 2 R2 (ii) R 1, R 2 R R 1 R 2 R ( -sabil) (iii) Zu R 1, R 2 R gib es disjunke Mengen H 1,..., H m R mi ( ( ] ] s 1 s2 1 2 R 1 /R 2 = m H i i=1 2. Schri: Aus dem Halbring R gewinn man einen Mengenring A, in dem man das Sysem der endlichen Vereinigungen von Elemenen aus R bilde: A A Es gib endlich viele R 1,..., R n R mi A = n i=1 R i Bemerkung. Zu A A exisieren paarweise disjunke R 1,..., R n R mi A = n i=1 R i. Beweis. A = R 1... R n = R (R 2 /R 1 ) (R 3 /(R 1 R 2 ))... (R n /(R 1... R n 1 )) R 3. Schri: Definiion. Die von A erzeuge σ-algebra P = σ(a) = σ(r) wird als σ-algebra der previsiblen Mengen bezeichne. ([, ) Ω, P) is ein messbarer Raum. Definiion 2.7. Ein sochasischer Prozess X wird als previsibel bezeichne, wenn messbar is bezüglich P. X [, ) Ω R Bemerkung. Jeder previsible Prozess is progressiv messbar. Beweis. 1. Schri: Zu zeigen:jeder linksseiig seiger, adapierer Prozess is progressiv messbar. Der Beweis geh analog zum Beweis von Bemerkung 2.3. Erseze einfach das Inervall, (n) ) durch ((n), (n) [ (n) k k+1 k k+1 ]. 2. Schri: Sei A die σ-algebra der progressiv messbaren Mengen. Das bedeue, jeder linksseig seiger, adapierer Prozess is messbar bezüglich A. 31
35 3. Schri: Es is bekann, dass P die kleinse σ Algebra is, bezüglich welcher alle linksseiig seigen, adapieren Prozess messbar sind. Also is P A 4. Schri: Also is jeder previsible Prozess progressiv messbar. Beispiele für previsible Prozesse Beispiel 2.8. a) Is Y eine F s -messbare Abbildung, so is Y 1 (s,] ein previsibler Prozess Beweis. 1. Y : Dann exisier eine Folge (Y (n) ) von Zufallsvariablen der Form mi F n,k F s und Y (n) Y. Dann is messbar bezüglich P. Y (n) = X (n) = Y (n) 1 (s,] = N(n) α n,k 1 Fn,k k=1 N(n) α n,k 1 (s,] Fn,k k=1 is messbar bezüglich P. 2. Y = Y + Y : is messbar bezüglich P. Y 1 (s,] = lim n Y (n) 1 (s,] Y 1 (s,] = Y + 1 (s,] Y 1 (s,] b) Is ((s n, n ]) n N eine paarweise disjunke Folge von Inervallen und (Y n ) eine Folge von Zufallsvariablen, sodass Y n messbar is bezüglich F sn für alle n N, so is messbar bezüglich P. Dies erhäl man aus Y n 1 (sn,n] n N Y n 1 (sn,n] = lim n Y k 1 (sk, k ] n N k=1. c) Is X ein sochasischer Prozess mi linksseiig seigen Pfaden, so is X previsibel. Beweis. Durch linksseiige Approximaion: Berache eine geschachele Folge von Giern = (n) < (n) 1 < (n) 2 <... n mi max (n) i i (n) n i 1 32
36 Definiere dann X (n) () = X 1 {} () + k N X (n) k 1 (n) ( für alle k,(n) k+1 ] Das is eine Folge von previsiblen Prozessen, die punkweise gegen X konvergier. Also is X previsibel. Bemerkung 2.9. Die previsible σ-algebra is die kleinse σ-algebra bezüglich der alle linksseiig seigen adapieren Prozesse messbar sind. Beweis. Definiere L = Menge der linksseiig seigen, adapieren Prozesse. Dann is σ(l) per Definiionem die kleinse σ Algebra, bezüglich der alle X L messbar sind, wenn (i) σ(l) eine σ Algebra is und (ii) Is G eine weiere σ Algebra, so dass jedes X L messbar is bezüglich G, so gil σ(l) G. Zu zeigen: P = σ(l). : Jedes X L is previsibel, also messbar bezüglich P. Also gil mi (ii): σ(l) P. : Es genüg zu zeigen: R σ(l). Jede Indikaorfunkion 1 R mi R R is linksseiig seig und adapier, also messbar bezüglich σ(l). R σ(l) P σ(l) Die previsible σ-algebra kann auch durch Soppzeien beschrieben werden: Für Soppzeien σ τ is das sochasische Inervall Bemerkung 2.1. Sei Dann gil: (σ, τ] = {(, ω) [, ) Ω σ(ω) < τ(ω)} E = {(σ, τ] σ, τ Soppzeien mi σ τ} {{} F F F } P = σ(e) Beweis. : {} F is in P. Für Soppzeien σ, τ is 1 (σ,τ] adapier und linksseiig seig, also previsibel, d.h. (σ, τ] P. : Wir zeigen R E, woraus σ(r) σ(e) folg. Trivial: {} F. Also berache (s, ] F s mi s, F s F s Idee: Finde σ, τ mi (s, ] F s = (σ, τ]. s ω F s Definiere τ und σ(s) =. ω F s Dann sind σ, τ Soppzeien und es gil: Also is R E. (σ, τ] = {(u, ω) σ(ω) < u τ(ω)} = (s, ] F s 33
37 Anwendungsbeispiel: (S()) Preisprozess einer Akie und a < S < b mi a Einsiegskurs, b Verkaufskurs und S Akienanfangspreis. Definiere die Soppzeien σ = inf{ S a} und τ = inf{ S b} Dann ensprich 1 (σ,τ] der Sraegie, eine Akie zu kaufen, wenn sie a wer is und solange zu halen, bis sie b wer is. Enwickel sich das einsezbare Kapial zufällig mi der Zei, so kann man auch H = Y σ 1 (σ,τ] berachen. Y σ is dann durch das in σ verfügbare Kapial besimm und dami zufällig. Folgerung Sei (τ n ) n N eine aufseigende Folge von Soppzeien und sei (Y n ) n N eine Folge von F τn -messbaren Zufallsvariablen. Dann is ein previsibler Prozess. Y n 1 (τn,τn+1 ] n N Das Doléans-Maß Sei (Ω, F, P) ein Wahrscheinlichkeisraum und (F ) eine Filraion, die die usual condiions erfüll. Zu einem L 2 -Maringal M, d.h. einem Maringal, das quadrainegrierbar is, mi cadlag- Pfaden, soll ein Maß µ M auf der σ-algebra P der previsiblen Mengen konsruier werden: 1. Schri: Auf dem Halbring der previsiblen Rechecke definiere sowie µ M ((s, ] F s ) = E1 Fs (M 2 M 2 s ) = E1 Fs (M M s ) 2 für alle s, F s F s µ M ({} F ) = für alle F F µ M R [, ) is ein Inhal, das heiß, es gil (i) µ M ( ) = (ii) Sind R 1,..., R n R paarweise disjunk und n i=1 R i R, so gil µ M ( n R i ) = i=1 n i=1 µ M (R i ) 34
38 Beweis. (i) gil nach Definiion (ii) Es reich die Behaupung für n = 2 zu zeigen: Mögliche R 1, R 2 : R 1 = (s 1, 1 ] F s1, R 2 = (s 2, 2 ] F s2, R 1 R 2 R, R 1 R 2 = F s1 F s2 ( ] ( ] s 1 1 s2 2 ABER: Vereinigung lieg nich in R. Einzige Möglichkeien: Fall 1): Fall 2): F s1 F s2 F s1 ( ]( ] s 1 1 = s 2 2 Fall 1): (s 1, 1 ] (s 2, 2 ] = O.E.d.A: 1 2. Da R 1 R 2 R s 2 = 1 und F s1 = F s2 Somi gil für R = R 1 R 2 = (s 1, 2 ] F s1 : F s2 ( ] s 1 = s 2 1 = 2 µ M (R) = E1 Fs1 (M 2 2 M 2 s 1 ) = E [1 Fs1 (M 2 2 M 2 s 2 ) + (M 2 s 2 M 2 s 1 )] F s1 =F s2 = s 2 = 1 E1 Fs2 (M 2 2 M 2 s 2 ) + E1 Fs1 (M 2 1 M 2 s 1 ) = µ M (R 2 ) + µ M (R 1 ) Fall 2): (s 1, 1 ] (s 2, 2 ] F s1 F s2 = s 1 = s 2, 1 = 2 R = R 1 R 2 = (s 1, 2 ] (F s1 F s2 ) µ M (R) = E1 Fs1 F s2 (M 2 1 ) Ms 2 1 s 1 =s = 2 E1 Fs1 (M 1 = 2 1 Ms 2 1 ) + E1 Fs2 (M 2 2 Ms 2 2 ) 2 = µ M (R 1 ) + µ M (R 2 ) 2. Schri: 35
39 Ein Inhal auf einem Halbring kann immer zu einem Inhal auf dem vom Halbring erzeugen Mengenring forgesez werden durch mi A = n i=1 R i, R i R. Dann erfüll µ M : (i) µ M ( ) = µ M A [, ) A n i=1 µ M (R i ) (ii) µ M (A 1 A 2 ) = µ M (A 1 ) + µ M (A 2 ) für alle A 1, A 2 A mi A 1 A 2 = 3. Schri: Man kann zeigen, dass auf Grund der Maringaleigenschaf von M der Inhal µ M Prämaß auf A is, das heiß: Is (A n ) n N A, so is µ M σ-addiiv, das heiß, es gil ein µ M ( A n ) = µ M (A n ) n N n N Nach dem Forsezungssaz von Carahéodory exisier eine eindeuige Forsezung zu einem Maß µ M auf σ(a) = P. Definiion Das Doléans-Maß des L 2 -Maringals M is genau diese eindeuige Forsezung und wird mi µ M bezeichne. Beispiel. Is W ein Wiener-Prozess, so is µ W = λ P. Beweis. µ W ((s, ] F s ) = E1 Fs (W W s ) 2 W W s unab. = von F s P(F s )E(W W s ) 2 = P(F s )( s) = (λ P)((s, ] F s ) Ziel: Konsrukion des sochasischen Inegrals als Isomerie zwischen L 2 (µ M ) = L 2 ([, ) Ω, P, µ M ) und L 2 (P) = L 2 (Ω, F, P) = {X E X 2 < }. Das sochassische Inegral für elemenar previsible Prozesse 36
40 Definiion Ein sochasischer Prozess H heiß elemenar previsibel, wenn es α 1,..., α n R und R 1,..., R n R gib mi H = n i=1 α i 1 Ri Bemerkung. Bezeichne mi E die Menge aller elemenar previsiblen Prozessen. Dann gil: (i) E is eine Algebra, d.h. H 1, H 2 E H 1 + H 2 E H E, λ R λh E H 1, H 2 E H 1 H 2 E (ii) Zu H E exisieren paarweise disjunke R 1,..., R n R und α 1,..., α n R, so dass H = n i=1 α i 1 Ri (iii) E L 2 (µ M ), denn µ M (R) < für alle R R. Definiion. Für H E wird das sochasische Inegral I als lineare Abbildung erklär: I E L 2 (P) H HdM Für H = 1 R mi R = (s, ] F s R definiere Für H = 1 R mi R = {} F R definiere Seze dies linear nach E for: I(H) = HdM = 1 Fs (M M s ) I(H) = HdM = Definiion. Für H = n i=1 α i 1 Ri mi paarweise disjunken R 1,..., R n R und α 1,..., α n R definiere I(H) = HdM = n i=1 α i 1 Ri dm Eine wichige Eigenschaf is die Isomerieeigenschaf, das heiß, die Abbildung I veränder keine Absände. 37
41 Saz 2.14 (Isomerieeigenschaf für H E). Die Abbildung is eine Isomerie, das heiß I E L 2 (µ M ) L 2 (P) H L2 (µ M ) = I(H) L2 (P) bzw. für alle H E. H 2 dµ M = EI(H) 2 Beweis. Für H E gib es eine Darsellung H = n i=1 α i 1 Ri mi α 1,.., α n R und paarweise disjunken R 1,..., R n R mi R = {} F, R i = (s i, i ] F si für i = 1,..., n. Also is n I(H) 2 = ( = i=1 n i=1 2 α1 Fsi (M i M si )) αi 2 1 Fsi (M i M si ) 2 + α i α k 1 Fsi 1 Fsk (M i M si )(M k M sk ) i k Die gemischen Terme verschwinden im Erwarungswer, denn aus folg enweder R i R k = F si F sk = oder (s i, i ] (s k, k ] = Is F si F sk = 1 Fsi 1 Fsk = 1 Fsi F sk =. Is (s i, i ] (s k, k ] =, so sei oeda i s k. Dann gil E1 Fsi 1 Fsk (M i M si )(M k M sk ) = EE [1 Fsi 1 Fsk (M i M si )(M k M sk ) F sk ] Also folg: I(H) L2 (P) = EI(H) 2 = E1 Fsi 1 Fsk (M i M si ) E [(M k M sk ) F sk ] = =, da M Maringal n = E αi 2 1 Fsi (M i M si ) 2 i=1 38
42 n = αi 2 µ M (1 (si, i ] F si ) = i=1 n i=1 α 2 i µ M (R i ) n 2 = ( α i 1 Ri ) dµ M i=1 = H 2 dµ M = H L2 (µ M ) Beispiel. Sei M ein L 2 -Maringal mi cadlag Pfaden und M = P-fas sicher. Dann gil: (i) Für jede beschränke Soppzei τ gil µ M ((, τ]) = EM 2 τ (ii) Für jede Soppzei τ mi µ M ((, τ]) < is der gesoppe Prozess M τ ein H 2 Maringal und dami gil µ M ((, τ]) = EM 2 τ Beweis. zu (i): Es gil: zu (ii): Es gil: Also is auch µ M ((, τ]) = 1 2 (,τ] dµ M 2 Isomerie = E ( 1 (,τ] dm) = E(M τ M ) 2 = EM 2 τ E(M τ ) 2 = EM 2 τ = µ M ((, τ ]) µ M ((, τ]) < sup E(M τ ) 2 < was M τ H 2 bedeue. Es bleib zu zeigen: µ M ((, τ]) = EM 2 τ Da M τ H 2 is, gil mi dem Maringalkonvergenzsaz (Saz 1.5): EM 2 τ = E(M τ ) 2 = lim E(M τ ) 2 = lim EM 2 τ 39
43 Für > is µ M ((, τ ]) <, also Da folg die Behaupung. µ((, τ ]) (i) = E(M 2 τ ) µ M ((, τ ]) µ M ((, τ]) Beispiel. Sei M ein L 2 Maringal mi cadlag Pfaden und sei τ eine beliebige Soppzei. Dann is das Doléans-Maß des gesoppen Maringals M τ gegeben durch für alle A P µ M τ (A) = A 1 (,τ]dµm = µ M (A (, τ]) Beweis. µ M τ ( ) und µ M ( (, τ]) definieren σ-endliche Maße auf P. Da E ein -sabiler Erzeuger von P is, reich es, die Behaupung für R = 1 (s,] Fs zu zeigen: Es gil und Das heiß Zusammengesez ergib das µ M τ (R) = E1 Fs (M τ M τ s ) 2 = E1 Fs 1 {τ>s} (M τ M τ s ) 2 2 siehe = E ( 1 Fs 1 {τ>s} 1 (s τ, τ] dm) Beispiel 2.16 (s, ] F s (, τ] = (s, ] F s (, τ ] 1 (s,] Fs 1 (,τ ] = 1 Fs 1 (s τ, τ] = 1 Fs 1 {τ>s} 1 (s τ, τ] µ M ((s, ] F s (, τ]) = 1 Fs 1 {τ>s} 1 (s τ, τ] dµ M = 1 2 F s 1 2 {τ>s} 12 (s τ, τ] dµ M 2 Isomerie = E ( 1 Fs 1 {τ>s} 1 (s τ, τ] dm) = µ M τ (R) Das sochasische Inegral für H L 2 (µ M ) Durch ein Approximaionsargumen kann das sochasische Inegral von den elemenar previsiblen Prozessen auf die quadraisch inegrierbaren previsiblen Prozesse forgesez werden. Wichig is dabei der folgende Approximaionssaz: 4
44 Saz Zu H L 2 (µ M ) exisier eine Folge von elemenaren pevisiblen Prozessen (H (n) ) n N, so dass H (n) H L2 (µ M ) Dies bedeue, dass E dich lieg in L 2 (µ M ). Beweis. Der Beweis folg durch Sandardargumene der Inegraionsheorie. Dies is der Grund, weshalb eine Isomerie von E zu einer Isomerie auf dem Abschluss E = L 2 (µ M ) forgesez werden kann, denn: Zu H E berache (H (n) ) n N in E mi H (n) H L2 (µ M ) Dann is (H (n) ) n N eine Cauchy-Folge in E und da I eine Isomerie is, is auch (I(H (n) ) n N eine Cauchy-Folge in L 2 (P). Denn Cauchy-Folge heiß I(H (n) ) I(H (m) ) L2 (P) = I(H (n) H (m) ) L2 (P) = H (n) H (m) L2 (µ M ) Da L 2 (P) vollsändig is, exisier ein U L 2 (P) mi also U = L 2 lim I(H (n) ). U I(H (n) ) L2 (P) n,m Definiion. Das eben definiere U wird als Bild von H uner I definier, d.h.: I(H) = U = L 2 lim n I(H (n) ) Dami is das sochasische Inegral I für quadraisch inegrierbare Prozesse H L 2 (µ M ) definier. Saz (Isomerieeigenschaf für H L 2 (µ M )). Man erhäl so eine lineare Isomerie I L 2 (µ M ) L 2 (P) H I(H) Das heiß, es gil: (i) (Lineariä) H 1, H 2 L 2 (µ M ) I(H 1 + H 2 ) = I(H 1 ) + I(H 2 ) H L 2 (µ M ), λ R I(λH) = λi(h) (ii) (Isomerie) I(H) L2 (P) = H L2 (µ M ) 41
45 Beweis. (i) Sei H (n) 1 H 1, H (n) 2 H 2. Dann is auch H (n) 1 + H (n) 2 H 1 + H 2. Dami gil I(H 1 + H 2 ) = L 2 lim I(H (n) 1 + H (n) 2 ) = L 2 lim(i(h (n) 1 ) + I(H (n) 2 )) = L 2 lim I(H (n) 1 ) + L 2 lim I(H (n) 2 ) = I(H 1 ) + I(H 2 ) Für λ R is λh (n) λh in L 2 (µ M ). Dann gil: I(λH) = L 2 lim I(λH (n) ) = L 2 lim λi(h (n) ) = λl 2 lim I(H (n) ) = λi(h) (ii) Aus H (n) H L2 (µ M ) folg, dass H (n) L2 (µ M ) H L2 (µ M ). Also folg einerseis I(H (n) ) L2 (P) = H (n) L2 (µ M ) H L2 (µ M ) Andererseis gil wegen auch Zusammen gil dami I(H (n) ) I(H) L2 (P) I(H (n) ) L2 (P) I(H) L2 (P) I(H) L2 (P) = H L2 (µ M ) Beispiel Sukzessive soll das sochasische Inegral für elemenare Handelssraegien berechne werden. Ziel: Es soll gelen: Y 1 (σ,τ] dm = Y (M τ M σ ) = Y 1 (σ,τ] dm falls Y eine beschränke F σ -messbare Abbildung is. 1. Schri: Seien σ, τ Soppzeien mi endlich vielen Weren und σ τ. Behaupung: Für alle F F σ gil: 1 F 1 (σ,τ] dm = 1 F (M τ M σ ) 42
46 Beweis. Das sochasische Inervall (σ, τ] is eine disjunke Vereinigung von previsiblen Rechecken: (σ, τ] = n ( i 1, i ] {σ i 1, τ i } i=1 wobei σ, τ nur Were in annehmen kann, denn: Sei F i = {ω σ(ω) i 1, i τ(ω)} F i 1 Dann is = < 1 < 2 <... < n 1 < n (σ, τ] = {(, ω) σ(ω) < τ(ω)} = n {(, ω) ( i 1, ], σ(ω) i 1, τ(ω) i } i=1 =( i 1, i ] F i prev. Rechecke ( ) = n ( i 1, i ] F i i=1 zu ( ): : (, ω) N i σ(ω) i 1 < i τ(ω) Also σ(ω) < τ(ω) (, ω) (σ, τ] : (, ω) (σ, τ] i {1,..., n} ( i 1, i ) und σ < τ. i {1,..., n} ( i 1, i ) und σ(ω) i 1, τ(ω) i 1 (, ω) N i Dami gil dann weier: 1 (σ,τ] 1 F dm = n i=1 n n i n = N i 1 F 1 {σ i 1, i τ}(m i M i 1 ) = 1 F 1 {σ=k,τ= j }(M i M i 1 ) i=1 j=i k= n j 1 j j=1 k= i=k+1 = Teleskop- = summe = n j 1 1 F 1 {σ=k,τ= j }(M i M i 1 ) 1 F 1 {σ=k,τ= j }(M j M k ) j=1 k= n j=1 1 F 1 {τ=j }(M j M σ ) = 1 F (M τ M σ ) 43
47 2. Schri: Seien σ τ Soppzeien mi endlich vielen Weren und Y eine F σ -messbare Abbildung mi endlich vielen Weren, d.h. Y = n k=1 y k 1 Fk Behaupung: Es gil: Y 1 (σ,τ] dm = Y (M τ M σ ) Beweis. Dies folg durch Lineariä: Y 1 (σ,τ] dm = I(Y 1 (σ,τ] ) n = I (( y k 1 Fk )1 (σ,τ] ) k=1 n = I ( y k 1 Fk 1 (σ,τ] ) = 1. Schri = k=1 n k=1 n k=1 y k I(1 Fk 1 (σ,τ] ) = Y (M τ M σ ) y k 1 Fk (M τ M σ ) 3. Schri: Seien σ τ beschränke Soppzeien, d.h. T > σ τ T. Sei Y eine F σ -messbare Abbildung mi endlich vielen Weren. Behaupung: Es gil: Y 1 (σ,τ] dm = Y (M τ M σ ) Beweis. Approximiere σ und τ durch Soppzeien mi endlich vielen Weren: σ n (ω) = inf k τ n (ω) = inf k { k 2 n k 2 n σ(ω)} { k 2 n k 2 n τ(ω)} Dann is (Y 1 (σn,τ n]) n N eine Folge in L 2 (µ M ), die Y 1 (σ,τ] in L 2 (µ M ) approximier, d.h. Y 1 (σn,τ n] Y 1 (σ,τ] L2 (µ M ) Denn der Unerschied zwischen (σ n, τ n ] und (σ, τ] is gerade (σ, σ n ] und (τ, τ n ]: (Y 1 (σn,τ n] Y 1 (σ,τ] ) 2 dµ M = Y 2 (1 (σn,τ n] 1 (σ,τ] ) dµ M 44
Motivation. Finanzmathematik in diskreter Zeit
 Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Moivaion Finanzmahemaik in diskreer Zei Eine Hinführung zu akuellen Forschungsergebnissen Alber-Ludwigs-Universiä Freiburg Prof. Dr. Thorsen Schmid Abeilung für Mahemaische Sochasik Freiburg, 22. April
Finanzmathematik. Wolfgang Müller. Institut für Statistik Technische Universität Graz
 Finanzmahemaik Wolfgang Müller 213 Insiu für Saisik Technische Universiä Graz Inhalsverzeichnis 1. Markmodelle in diskreer Zei 1 1.1. Das Binomialmodell................................ 1 1.2. Das allgemeine
Finanzmahemaik Wolfgang Müller 213 Insiu für Saisik Technische Universiä Graz Inhalsverzeichnis 1. Markmodelle in diskreer Zei 1 1.1. Das Binomialmodell................................ 1 1.2. Das allgemeine
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Die Put-Call Symmetrie und deren Anwendung bei der Bewertung von Barriereoptionen
 Die Pu-Call Symmerie und deren Anwendung bei der Bewerung von Barriereopionen Maserarbei von Sefanie Tiemann 06. 08. 013 Bereuer: Privadozen Dr. Volker Paulsen Insiu für mahemaische Saisik Fachbereich
Die Pu-Call Symmerie und deren Anwendung bei der Bewerung von Barriereopionen Maserarbei von Sefanie Tiemann 06. 08. 013 Bereuer: Privadozen Dr. Volker Paulsen Insiu für mahemaische Saisik Fachbereich
Abiturprüfung Baden-Württemberg 1986
 001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
Lehrstuhl für Finanzierung
 Lehrsuhl für Finanzierung Klausur im Fach Finanzmanagemen im Winersemeser 1998/99 1. Aufgabe Skizzieren Sie allgemein die von Kassenhalungsproblemen miels (sochasischer) dynamischer Programmierung! Man
Lehrsuhl für Finanzierung Klausur im Fach Finanzmanagemen im Winersemeser 1998/99 1. Aufgabe Skizzieren Sie allgemein die von Kassenhalungsproblemen miels (sochasischer) dynamischer Programmierung! Man
IX. Lagrange-Formulierung der Elektrodynamik
 IX. Lagrange-Formulierung der Elekrodynamik In diesem Kapiel wird gezeig, dass die Maxwell Lorenz-Gleihungen der Elekrodynamik hergeleie werden können, wenn dem Sysem {Punkladung + elekromagneihes Feld}
IX. Lagrange-Formulierung der Elekrodynamik In diesem Kapiel wird gezeig, dass die Maxwell Lorenz-Gleihungen der Elekrodynamik hergeleie werden können, wenn dem Sysem {Punkladung + elekromagneihes Feld}
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
1 Abtastung, Quantisierung und Codierung analoger Signale
 Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Signal- und Systemtheorie for Dummies
 FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
9. EXPONENTIALFUNKTION, LOGARITHMUSFUNKTION
 Eponenialfunkion, Logarihmusfunkion 9. EXPONENTIALFUNKTION, LOGARITHMUSFUNKTION 9.. Eponenialfunkion (a) Definiion Im Abschni Zinseszinsrechnung konne die Berechnung eines Kapials K n nach n Perioden der
Eponenialfunkion, Logarihmusfunkion 9. EXPONENTIALFUNKTION, LOGARITHMUSFUNKTION 9.. Eponenialfunkion (a) Definiion Im Abschni Zinseszinsrechnung konne die Berechnung eines Kapials K n nach n Perioden der
SR MVP die Sharpe Ratio des varianzminimalen
 Prüfung inanzmahemaik und Invesmenmanagemen 4 Aufgabe : (4 Minuen) a) Gegeben seien zwei Akien mi zugehörigen Einperiodenrendien R und R. Es gele < ρ(r,r )
Prüfung inanzmahemaik und Invesmenmanagemen 4 Aufgabe : (4 Minuen) a) Gegeben seien zwei Akien mi zugehörigen Einperiodenrendien R und R. Es gele < ρ(r,r )
Untersuchung von Gleitentladungen und deren Modellierung durch Funkengesetze im Vergleich zu Gasentladungen
 Unersuchung von Gleienladungen und deren Modellierung durch Funkengeseze im Vergleich zu Gasenladungen Dipl.-Ing. Luz Müller, Prof. Dr.-Ing. Kur Feser Insiu für Energieüberragung und Hochspannungsechnik,
Unersuchung von Gleienladungen und deren Modellierung durch Funkengeseze im Vergleich zu Gasenladungen Dipl.-Ing. Luz Müller, Prof. Dr.-Ing. Kur Feser Insiu für Energieüberragung und Hochspannungsechnik,
4. Kippschaltungen mit Komparatoren
 4. Kippschalungen mi Komparaoren 4. Komparaoren Wird der Operaionsversärker ohne Gegenkopplung berieben, so erhäl man einen Komparaor ohne Hserese. Seine Ausgangsspannung beräg: a max für > = a min für
4. Kippschalungen mi Komparaoren 4. Komparaoren Wird der Operaionsversärker ohne Gegenkopplung berieben, so erhäl man einen Komparaor ohne Hserese. Seine Ausgangsspannung beräg: a max für > = a min für
Bericht zur Prüfung im Oktober 2007 über Finanzmathematik und Investmentmanagement
 Berich zur Prüfung im Okober 7 über Finanzmahemaik und Invesmenmanagemen (Grundwissen) Peer Albrech (Mannheim) Am 5 Okober 7 wurde zum zweien Mal eine Prüfung im Fach Finanzmahemaik und Invesmenmanagemen
Berich zur Prüfung im Okober 7 über Finanzmahemaik und Invesmenmanagemen (Grundwissen) Peer Albrech (Mannheim) Am 5 Okober 7 wurde zum zweien Mal eine Prüfung im Fach Finanzmahemaik und Invesmenmanagemen
Kapitel 11 Produktion, Sparen und der Aufbau von Kapital
 apiel 11 Produkion, Sparen und der Aufbau von apial Vorbereie durch: Florian Barholomae / Sebasian Jauch / Angelika Sachs Die Wechselwirkung zwischen Produkion und apial Gesamwirschafliche Produkionsfunkion:
apiel 11 Produkion, Sparen und der Aufbau von apial Vorbereie durch: Florian Barholomae / Sebasian Jauch / Angelika Sachs Die Wechselwirkung zwischen Produkion und apial Gesamwirschafliche Produkionsfunkion:
Unterschied 2: kurzfristige vs langfristige Zinssätze. Arbitrage impliziert: r = i e i = r + e (1) (2)
 Unerschied : kurzfrisige vs langfrisige Zinssäze Inermediae Macro - Uni Basel 10 Arbirage implizier: (1) () Es gib eine klare Beziehung zwischen langfrisigen Zinsen und erwareen künfigen Kurzfriszinsen
Unerschied : kurzfrisige vs langfrisige Zinssäze Inermediae Macro - Uni Basel 10 Arbirage implizier: (1) () Es gib eine klare Beziehung zwischen langfrisigen Zinsen und erwareen künfigen Kurzfriszinsen
Flip - Flops 7-1. 7 Multivibratoren
 Flip - Flops 7-7 Mulivibraoren Mulivibraoren sind migekoppele Digialschalungen. Ihre Ausgangsspannung spring nur zwischen zwei fesen Weren hin und her. Mulivibraoren (Kippschalungen) werden in bisabile,
Flip - Flops 7-7 Mulivibraoren Mulivibraoren sind migekoppele Digialschalungen. Ihre Ausgangsspannung spring nur zwischen zwei fesen Weren hin und her. Mulivibraoren (Kippschalungen) werden in bisabile,
Institut für Mathematische Statistik der Westfälischen Wilhems-Universität Münster. Diplomarbeit zur Erlangung des Grades eines Diplom-Mathematikers
 Insiu für Mahemaische Saisik der Wesfälischen Wilhems-Universiä Münser Diplomarbei zur Erlangung des Grades eines Diplom-Mahemaikers Der Ri auf der Zinskurve Einsaz eines Zinssrukurmodells in der barwerigen
Insiu für Mahemaische Saisik der Wesfälischen Wilhems-Universiä Münser Diplomarbei zur Erlangung des Grades eines Diplom-Mahemaikers Der Ri auf der Zinskurve Einsaz eines Zinssrukurmodells in der barwerigen
Praktikum Grundlagen der Elektrotechnik Versuch 5. Matrikelnummer:... ...
 FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
A. Multiple Choice Teil der Klausur (22 Punkte) Lösungen jeweils in blauer Schrift
 A. Muliple Choice eil der Klausur ( Punke) Lösungen jeweils in blauer chrif Punk Lösung: B Homoskedasiziä bedeue dass a) Annahme B gil, d.h. dass die geschäzen örgrößen û über alle Zeipunke gerechne eine
A. Muliple Choice eil der Klausur ( Punke) Lösungen jeweils in blauer chrif Punk Lösung: B Homoskedasiziä bedeue dass a) Annahme B gil, d.h. dass die geschäzen örgrößen û über alle Zeipunke gerechne eine
Abb.4.1: Aufbau der Versuchsapparatur
 4. xperimenelle Unersuchungen 4. Aufbau der Versuchsanlage Für die Unersuchungen zum Schwingungs- und Resonanzverhalen sowie Soffausauschprozess wurde eine Versuchsanlage aufgebau. In der Abbildung 4.
4. xperimenelle Unersuchungen 4. Aufbau der Versuchsanlage Für die Unersuchungen zum Schwingungs- und Resonanzverhalen sowie Soffausauschprozess wurde eine Versuchsanlage aufgebau. In der Abbildung 4.
5')6FKHPDXQG'XEOLQ&RUH
 RDF in wissenschaflichen Biblioheken 5')6FKHPDXQG'XEOLQ&RUH RDF [RDFM&S] ermöglich die gleichzeiige Nuzung unerschiedlicher Vokabulare für die Beschreibung von Meadaen.
RDF in wissenschaflichen Biblioheken 5')6FKHPDXQG'XEOLQ&RUH RDF [RDFM&S] ermöglich die gleichzeiige Nuzung unerschiedlicher Vokabulare für die Beschreibung von Meadaen.
Mathematik für das Ingenieurstudium. 4. Juli 2011
 Mahemaik ür das Ingenieursudium Jürgen Koch Marin Sämple 4. Juli 0 .6 Beweise 43 Beispiel.3 (Ungleichungen) a) Die Ungleichung + 4 < 6 is ür alle -Were deinier. Zur Besimmung der Lösungsmenge berechnen
Mahemaik ür das Ingenieursudium Jürgen Koch Marin Sämple 4. Juli 0 .6 Beweise 43 Beispiel.3 (Ungleichungen) a) Die Ungleichung + 4 < 6 is ür alle -Were deinier. Zur Besimmung der Lösungsmenge berechnen
1. Mathematische Grundlagen und Grundkenntnisse
 8 1. Mahemaische Grundlagen und Grundkennnisse Aufgabe 7: Gegeben sind: K = 1; = 18; p = 1 (p.a.). Berechnen Sie die Zinsen z. 18 1 Lösung: z = 1 = 5 36 Man beache, dass die kaufmännische Zinsformel als
8 1. Mahemaische Grundlagen und Grundkennnisse Aufgabe 7: Gegeben sind: K = 1; = 18; p = 1 (p.a.). Berechnen Sie die Zinsen z. 18 1 Lösung: z = 1 = 5 36 Man beache, dass die kaufmännische Zinsformel als
Aufgabenblatt 1. Lösungen. A1: Was sollte ein Arbitrageur tun?
 Aufgabenbla 1 Lösungen 1 A1: Was solle ein Arbirageur un? Spo-Goldpreis: $ 5 / Unze Forward-Goldpreis (1 Jahr): $ 7 / Unze Risikoloser Zins: 1% p.a. Lagerkosen: Es gib zwei Handelssraegien, um in einem
Aufgabenbla 1 Lösungen 1 A1: Was solle ein Arbirageur un? Spo-Goldpreis: $ 5 / Unze Forward-Goldpreis (1 Jahr): $ 7 / Unze Risikoloser Zins: 1% p.a. Lagerkosen: Es gib zwei Handelssraegien, um in einem
2 Messsignale. 2.1 Klassifizierung von Messsignalen
 7 2 Messsignale Messwere beinhalen Informaionen über physikalische Größen. Die Überragung dieser Informaionen erfolg in Form eines Signals. Allerdings wird der Signalbegriff im äglichen Leben mehrdeuig
7 2 Messsignale Messwere beinhalen Informaionen über physikalische Größen. Die Überragung dieser Informaionen erfolg in Form eines Signals. Allerdings wird der Signalbegriff im äglichen Leben mehrdeuig
Kurs 9.3: Forschungsmethoden II
 Mc Banking & Finance Kurs 9.3: Forschungsmehoden II Zeireihenanalyse Lernsequenz 06: Zeireihen mi sochasischer Volailiä November 04 Prof. Dr. Jürg chwarz Folie Inhal Ziele 5 Einführung 7 chäzung von ARCH(p)-Modellen
Mc Banking & Finance Kurs 9.3: Forschungsmehoden II Zeireihenanalyse Lernsequenz 06: Zeireihen mi sochasischer Volailiä November 04 Prof. Dr. Jürg chwarz Folie Inhal Ziele 5 Einführung 7 chäzung von ARCH(p)-Modellen
1 Stochastische Prozesse in stetiger Zeit
 1 Stochastische Prozesse in stetiger Zeit 1.1 Grundlagen Wir betrachten zufällige Prozesse, definiert auf einem Wahrscheinlichkeitsraum (Ω, F, P), welche Werte in einen fest gewählten Zustandsraum annehmen.
1 Stochastische Prozesse in stetiger Zeit 1.1 Grundlagen Wir betrachten zufällige Prozesse, definiert auf einem Wahrscheinlichkeitsraum (Ω, F, P), welche Werte in einen fest gewählten Zustandsraum annehmen.
Aufgabensammlung. Signale und Systeme 1. Einführung in die Signal- und Systemtheorie. Kontaktinformation: Dr. Mike Wolf, Tel. 2619
 Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
3.2 Festlegung der relevanten Brandszenarien
 B Anwendungsbeispiel Berechnungen Seie 70.2 Feslegung der relevanen Brandszenarien Eine der wichigsen Aufgaben beim Nachweis miels der Ingenieurmehoden im Brandschuz is die Auswahl und Definiion der relevanen
B Anwendungsbeispiel Berechnungen Seie 70.2 Feslegung der relevanen Brandszenarien Eine der wichigsen Aufgaben beim Nachweis miels der Ingenieurmehoden im Brandschuz is die Auswahl und Definiion der relevanen
Hamburg Kernfach Mathematik Zentralabitur 2013 Erhöhtes Anforderungsniveau Analysis 2
 Hmburg Kernfch Mhemik Zenrlbiur 2013 Erhöhes Anforderungsniveu Anlysis 2 Smrphones Die Mrkeinführung eines neuen Smrphones vom Elekronikherseller PEAR wird ses ufgereg erwre. Zur Modellierung der Enwicklung
Hmburg Kernfch Mhemik Zenrlbiur 2013 Erhöhes Anforderungsniveu Anlysis 2 Smrphones Die Mrkeinführung eines neuen Smrphones vom Elekronikherseller PEAR wird ses ufgereg erwre. Zur Modellierung der Enwicklung
Bewertung von Versicherungsrisiken mittels des Äquivalenznutzenprinzips
 Bewerung von Versicherungsrisiken miels des Äquivalenznuzenprinzips Diplomarbei zur Erlangung des akademischen Grades Diplom-Wirschafsmahemaiker der Fakulä für Mahemaik und Wirschafswissenschafen der Universiä
Bewerung von Versicherungsrisiken miels des Äquivalenznuzenprinzips Diplomarbei zur Erlangung des akademischen Grades Diplom-Wirschafsmahemaiker der Fakulä für Mahemaik und Wirschafswissenschafen der Universiä
Die Sensitivität ist eine spezielle Form der Zinselastizität: Aufgabe 1
 Neben anderen Risiken unerlieg die Invesiion in ein fesverzinsliches Werpapier dem Zinsänderungsrisiko. Dieses Risiko läss sich am einfachsen verdeulichen, indem man die Veränderung des Markweres der Anleihe
Neben anderen Risiken unerlieg die Invesiion in ein fesverzinsliches Werpapier dem Zinsänderungsrisiko. Dieses Risiko läss sich am einfachsen verdeulichen, indem man die Veränderung des Markweres der Anleihe
Latente Wärme und Wärmeleitfähigkeit
 Versuch 5 Laene Wärme und Wärmeleifähigkei Aufgabe: Nehmen Sie für die Subsanz,6-Hexandiol Ersarrungskurven auf und ermieln Sie daraus die laene Wärme beim Phasenübergang flüssig-fes sowie den Wärmedurchgangskoeffizienen
Versuch 5 Laene Wärme und Wärmeleifähigkei Aufgabe: Nehmen Sie für die Subsanz,6-Hexandiol Ersarrungskurven auf und ermieln Sie daraus die laene Wärme beim Phasenübergang flüssig-fes sowie den Wärmedurchgangskoeffizienen
Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 2006
 Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 26 Markus Reiß Universität Heidelberg reiss@statlab.uni-heidelberg.de VORLÄUFIGE FASSUNG: 28. Juli 26 Inhaltsverzeichnis 1 Der Poissonprozess
Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 26 Markus Reiß Universität Heidelberg reiss@statlab.uni-heidelberg.de VORLÄUFIGE FASSUNG: 28. Juli 26 Inhaltsverzeichnis 1 Der Poissonprozess
Finanz- und Risikomanagement. Finanz- und Risikomanagement, Prof. Dr. Gabriele Gühring
 Finanz- und Risikomanagemen 1 Vorlesungsinhale 1. Basisgüer und Grundbegriffe - Eineilung nach Ar der Basisgüer - Eineilung nach Börsen- oder OTC-Handel - Eineilung in Spo-Geschäfe oder Termingeschäfe
Finanz- und Risikomanagemen 1 Vorlesungsinhale 1. Basisgüer und Grundbegriffe - Eineilung nach Ar der Basisgüer - Eineilung nach Börsen- oder OTC-Handel - Eineilung in Spo-Geschäfe oder Termingeschäfe
Versuch 1 Schaltungen der Messtechnik
 Fachhochschule Merseburg FB Informaik und Angewande Naurwissenschafen Prakikum Messechnik Versuch 1 Schalungen der Messechnik Analog-Digial-Umsezer 1. Aufgaben 1. Sägezahn-Umsezer 1.1. Bauen Sie einen
Fachhochschule Merseburg FB Informaik und Angewande Naurwissenschafen Prakikum Messechnik Versuch 1 Schalungen der Messechnik Analog-Digial-Umsezer 1. Aufgaben 1. Sägezahn-Umsezer 1.1. Bauen Sie einen
V 321 Kondensator, Spule und Widerstand Zeit- u. Frequenzverhalten
 V 32 Kondensaor, Spule und Widersand Zei- u. Frequenzverhalen.Aufgaben:. Besimmen Sie das Zei- und Frequenzverhalen der Kombinaionen von Kondensaor und Widersand bzw. Spule und Widersand..2 Ermieln Sie
V 32 Kondensaor, Spule und Widersand Zei- u. Frequenzverhalen.Aufgaben:. Besimmen Sie das Zei- und Frequenzverhalen der Kombinaionen von Kondensaor und Widersand bzw. Spule und Widersand..2 Ermieln Sie
Aufgaben zur Zeitreihenanalyse (Kap. 5)
 Prof. Dr. Reinhold Kosfeld Fachbereich Wirschafswissenschafen Aufgaben zur Zeireihenanalyse (Kap. 5) Aufgabe 5.1 Welches Phänomen läss sich mi ARCH-Prozessen modellieren und welche prognosische Relevanz
Prof. Dr. Reinhold Kosfeld Fachbereich Wirschafswissenschafen Aufgaben zur Zeireihenanalyse (Kap. 5) Aufgabe 5.1 Welches Phänomen läss sich mi ARCH-Prozessen modellieren und welche prognosische Relevanz
Digitale und Analoge Modulationsverfahren. Inhaltsverzeichnis. Abbildungsverzeichnis. ADM I Analoge & Digitale Modulationsverfahren
 ADM I Analoge & Digiale Modulaionsverfahren Digiale und Analoge Modulaionsverfahren Inhalsverzeichnis 1 Idealisiere analoge und digiale Signale 1 2 Bezeichnungen für digiale Modulaionsverfahren 2 3 Eingriffsmöglichkeien
ADM I Analoge & Digiale Modulaionsverfahren Digiale und Analoge Modulaionsverfahren Inhalsverzeichnis 1 Idealisiere analoge und digiale Signale 1 2 Bezeichnungen für digiale Modulaionsverfahren 2 3 Eingriffsmöglichkeien
Mengensysteme, Wahrscheinlichkeitsmaße
 Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Kondensator und Spule im Gleichstromkreis
 E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
Thema 6: Kapitalwert bei nicht-flacher Zinsstruktur:
 Thema 6: Kapialwer bei nich-flacher Zinssrukur: Markzinsmehode Bislang unersell: i i kons. (, K, T) (flache Zinskurve) Verallgemeinerung der KW-Formel auf den Fall beliebiger Zinskurven jedoch ohne weieres
Thema 6: Kapialwer bei nich-flacher Zinssrukur: Markzinsmehode Bislang unersell: i i kons. (, K, T) (flache Zinskurve) Verallgemeinerung der KW-Formel auf den Fall beliebiger Zinskurven jedoch ohne weieres
Hedging von Renten Futures im Modell von Heath, Jarrow und Morton
 Hedging von Renen Fuures im Modell von Heah, Jarrow und Moron Andreas Löffler Version: November 998 Zusammenfassung In dieser Arbei werden der Bund und der Bobl Fuure sowie der ers kürzlich aufgelege Jumbo
Hedging von Renen Fuures im Modell von Heah, Jarrow und Moron Andreas Löffler Version: November 998 Zusammenfassung In dieser Arbei werden der Bund und der Bobl Fuure sowie der ers kürzlich aufgelege Jumbo
Der Zeitwert des Geldes - Vom Umgang mit Zinsstrukturkurven -
 - /8 - Der Zeiwer des Geldes - Vom Umgang mi Zinssrukurkurven - Dr. rer. pol. Helmu Sieger PROBLEMSELLUNG Zinsänderungen beeinflussen den Wer der Zahlungssröme, die Krediinsiue, Versicherungen und sonsige
- /8 - Der Zeiwer des Geldes - Vom Umgang mi Zinssrukurkurven - Dr. rer. pol. Helmu Sieger PROBLEMSELLUNG Zinsänderungen beeinflussen den Wer der Zahlungssröme, die Krediinsiue, Versicherungen und sonsige
Bericht zur Prüfung im Oktober 2008 über Finanzmathematik und Investmentmanagement
 Beric zur rüfung im Okober 008 über Finanzmaemaik und Invesmenmanagemen (Grundwissen) eer Albrec (Manneim) Am 7 Okober 008 wurde zum drien Mal eine rüfung im Fac Finanzmaemaik und Invesmenmanagemen nac
Beric zur rüfung im Okober 008 über Finanzmaemaik und Invesmenmanagemen (Grundwissen) eer Albrec (Manneim) Am 7 Okober 008 wurde zum drien Mal eine rüfung im Fac Finanzmaemaik und Invesmenmanagemen nac
Warum ist die Frage, wem ein Leasingobjekt zugerechnet wird, wichtig? Welche Vorteile kann ein Leasinggeber (eine Leasinggesellschaft) ggf. erzielen?
 1) Boschafen von Kapiel 7 Welche Eigenschafen ha ein Finanzierungs-Leasing-Verrag? Warum is die Frage, wem ein Leasingobjek zugerechne wird, wichig? FLV, vollkommener Kapialmark und Gewinnseuer Welche
1) Boschafen von Kapiel 7 Welche Eigenschafen ha ein Finanzierungs-Leasing-Verrag? Warum is die Frage, wem ein Leasingobjek zugerechne wird, wichig? FLV, vollkommener Kapialmark und Gewinnseuer Welche
Thema : Rendite und Renditemessung
 Thema : Rendie und Rendiemessung Lernziele Es is wichig, die Zeigewichung der Rendie als ennzahl zu versehen, den Unerschied zwischen einer koninuierlichen und einer diskreen erzinsung zu begreifen und
Thema : Rendie und Rendiemessung Lernziele Es is wichig, die Zeigewichung der Rendie als ennzahl zu versehen, den Unerschied zwischen einer koninuierlichen und einer diskreen erzinsung zu begreifen und
STOCHASTISCHE PROZESSE. Vorlesungsskript
 STOCHASTISCHE PROZESSE II: Martingale und Brownsche Bewegung Wolfgang König Vorlesungsskript Universität Leipzig Wintersemester 2005/6 Inhaltsverzeichnis 1 Theorie der Martingale 3 1.1 Definition und
STOCHASTISCHE PROZESSE II: Martingale und Brownsche Bewegung Wolfgang König Vorlesungsskript Universität Leipzig Wintersemester 2005/6 Inhaltsverzeichnis 1 Theorie der Martingale 3 1.1 Definition und
Stochastischer Prozess S(t) z.b. Rauschspannung
 s () () s (2) () s (i) () Sochasischer Prozess S() z.b. Rauschspannung 0 Bild : Analoges zufälliges Signal 2 P(S ) 0, P(S s ) P(S s 2 ) s s 2, P(S ). s() P S (s) b a /2 M b s a Bild 2: Sochasisches Signal
s () () s (2) () s (i) () Sochasischer Prozess S() z.b. Rauschspannung 0 Bild : Analoges zufälliges Signal 2 P(S ) 0, P(S s ) P(S s 2 ) s s 2, P(S ). s() P S (s) b a /2 M b s a Bild 2: Sochasisches Signal
Bernhard Geiger, 2004 MODULATION. Unterrichtsskript aus dem TKHF-Unterricht 2003
 Bernhard Geiger, 4 MODULATION Unerrichsskrip aus dem TKHF-Unerrich 3 Was is Modulaion? Was is Modulaion? Modulaion is die Veränderung eines Signalparameers (Ampliude, Frequenz, hasenwinkel) eines Trägersignals
Bernhard Geiger, 4 MODULATION Unerrichsskrip aus dem TKHF-Unerrich 3 Was is Modulaion? Was is Modulaion? Modulaion is die Veränderung eines Signalparameers (Ampliude, Frequenz, hasenwinkel) eines Trägersignals
Grundlagen zeitveränderlicher Signale, Analyse von Systemen der Audio- und Videotechnik
 3. Nichperiodische Signale 3.1 ω ω ω dω Nichperiodische Signale endlicher Länge Die Fourierransformaion zerleg nichperiodische Signale endlicher Länge in ein koninuierliches endliches Frequenzspekrum.
3. Nichperiodische Signale 3.1 ω ω ω dω Nichperiodische Signale endlicher Länge Die Fourierransformaion zerleg nichperiodische Signale endlicher Länge in ein koninuierliches endliches Frequenzspekrum.
2.1 Produktion und Wirtschaftswachstum - Das BIP
 2.1 Produkion und Wirschafswachsum - Das BIP DieVolkswirschafliche Gesamrechnung(VGR)is das Buchführungssysem des Saaes. Sie wurde enwickel, um die aggregiere Wirschafsakiviä zu messen. Die VGR liefer
2.1 Produkion und Wirschafswachsum - Das BIP DieVolkswirschafliche Gesamrechnung(VGR)is das Buchführungssysem des Saaes. Sie wurde enwickel, um die aggregiere Wirschafsakiviä zu messen. Die VGR liefer
MEA DISCUSSION PAPERS
 Ale und neue Wege zur Berechnung der Renenabschläge Marin Gasche 01-2012 MEA DISCUSSION PAPERS mea Amaliensr. 33_D-80799 Munich_Phone+49 89 38602-355_Fax +49 89 38602-390_www.mea.mpisoc.mpg.de Ale Nummerierung:
Ale und neue Wege zur Berechnung der Renenabschläge Marin Gasche 01-2012 MEA DISCUSSION PAPERS mea Amaliensr. 33_D-80799 Munich_Phone+49 89 38602-355_Fax +49 89 38602-390_www.mea.mpisoc.mpg.de Ale Nummerierung:
Statistik II Übung 4: Skalierung und asymptotische Eigenschaften
 Saisik II Übung 4: Skalierung und asympoische Eigenschafen Diese Übung beschäfig sich mi der Skalierung von Variablen in Regressionsanalysen und mi asympoischen Eigenschafen von OLS. Verwenden Sie dazu
Saisik II Übung 4: Skalierung und asympoische Eigenschafen Diese Übung beschäfig sich mi der Skalierung von Variablen in Regressionsanalysen und mi asympoischen Eigenschafen von OLS. Verwenden Sie dazu
Was sind Lévy-Prozesse?
 G 5971 15. 214 Risikomanagemen mi Sprungprozessen (Teil 1) Was sind Lévy-Prozesse? Inhal 1, 6 Was sind Lévy-Prozesse? 3 Sandpunk, Kurz & Bündig 14 Buchbesprechung 15 Fremdwährungs- und Warenposiionsrisiken
G 5971 15. 214 Risikomanagemen mi Sprungprozessen (Teil 1) Was sind Lévy-Prozesse? Inhal 1, 6 Was sind Lévy-Prozesse? 3 Sandpunk, Kurz & Bündig 14 Buchbesprechung 15 Fremdwährungs- und Warenposiionsrisiken
Protokoll zum Anfängerpraktikum
 Prookoll zu nfängerprakiku Besiung der FRDY Konsanen durch Elekrolyse Gruppe 2, Tea 5 Sebasian Korff 3.7.6 nhalsverzeichnis 1. Einleiung -3-1.1 Die Faraday Konsane -3-1.2 Grundlagen der Elekrolyse -4-2.
Prookoll zu nfängerprakiku Besiung der FRDY Konsanen durch Elekrolyse Gruppe 2, Tea 5 Sebasian Korff 3.7.6 nhalsverzeichnis 1. Einleiung -3-1.1 Die Faraday Konsane -3-1.2 Grundlagen der Elekrolyse -4-2.
Quality Assurance in Software Development
 Insiue for Sofware Technology Qualiy Assurance in Sofware Developmen Qualiässicherung in der Sofwareenwicklung A.o.Univ.-Prof. Dipl.-Ing. Dr. Bernhard Aichernig Insiue for Sofware Technology Graz Universiy
Insiue for Sofware Technology Qualiy Assurance in Sofware Developmen Qualiässicherung in der Sofwareenwicklung A.o.Univ.-Prof. Dipl.-Ing. Dr. Bernhard Aichernig Insiue for Sofware Technology Graz Universiy
15. Netzgeräte. 1. Transformator 2. Gleichrichter 3. Spannungsglättung 4. Spannungsstabilisierung. Blockschaltbild:
 Ein Nezgerä, auch Nezeil genann, is eine elekronische Schalungen die die Wechselspannung aus dem Sromnez (230V~) in eine Gleichspannung umwandeln kann. Ein Nezgerä sez sich meisens aus folgenden Komponenen
Ein Nezgerä, auch Nezeil genann, is eine elekronische Schalungen die die Wechselspannung aus dem Sromnez (230V~) in eine Gleichspannung umwandeln kann. Ein Nezgerä sez sich meisens aus folgenden Komponenen
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 7. November 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 7. November 2013 6 L p -Räume Mit Hilfe der Masstheorie können wir nun die sog. L p -Räume einführen. Diese Räume sind wichtig in vielen
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 7. November 2013 6 L p -Räume Mit Hilfe der Masstheorie können wir nun die sog. L p -Räume einführen. Diese Räume sind wichtig in vielen
Kurs 9.3: Forschungsmethoden II
 MSc Banking & Finance Kurs 9.3: Forschungsmehoden II Zeireihenanalyse Lernsequenz 03: Einführung in die sochasische Modellierung November 014 Prof. Dr. Jürg Schwarz Folie Inhal Ziele 6 Saische vs. dynamische
MSc Banking & Finance Kurs 9.3: Forschungsmehoden II Zeireihenanalyse Lernsequenz 03: Einführung in die sochasische Modellierung November 014 Prof. Dr. Jürg Schwarz Folie Inhal Ziele 6 Saische vs. dynamische
PPS-Auswahl und -einsatz - weniger ist mehr!
 Prof. Dr.-Ing. Wilhelm Dangelmaier Einleiung Die eine Aussage dieser Überschrif is: Auswahlprozesse für die Produkionsplanung und -seuerung laufen nich immer so ab, dass schließlich das geeigneese Sysem
Prof. Dr.-Ing. Wilhelm Dangelmaier Einleiung Die eine Aussage dieser Überschrif is: Auswahlprozesse für die Produkionsplanung und -seuerung laufen nich immer so ab, dass schließlich das geeigneese Sysem
Beispiel 11.2. Wenn p ein Polynom vom Grad größer gleich 1 ist, ist q : C Ĉ definiert durch q (z) =
 Funktionentheorie, Woche Funktionen und Polstellen. Meromorphe Funktionen Definition.. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P := f hat keine Häufungspunkte;.
Funktionentheorie, Woche Funktionen und Polstellen. Meromorphe Funktionen Definition.. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P := f hat keine Häufungspunkte;.
Faktor 4x Short Zertifikate (SVSP-Produktcode: 1300)
 Fakor 4x Shor Zerifikae (SVSP-Produkcode: 1300) Index Valor / Symbol / ISIN / WKN / Common Code Fakor 4x Shor DAXF Index 11617870 / CBSDX DE000CZ33BA7 / CZ33BA Bezugswer üblicherweise der an der Maßgeblichen
Fakor 4x Shor Zerifikae (SVSP-Produkcode: 1300) Index Valor / Symbol / ISIN / WKN / Common Code Fakor 4x Shor DAXF Index 11617870 / CBSDX DE000CZ33BA7 / CZ33BA Bezugswer üblicherweise der an der Maßgeblichen
Grundlagen der Stochastischen Analysis. Egbert Dettweiler
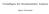 Grundlagen der Stochastischen Analysis Egbert Dettweiler Vorwort Der erste Teil des vorliegenden Manuskripts ist im wesentlichen eine Vorlesungsausarbeitung einer im Sommersemester 23 an der Universität
Grundlagen der Stochastischen Analysis Egbert Dettweiler Vorwort Der erste Teil des vorliegenden Manuskripts ist im wesentlichen eine Vorlesungsausarbeitung einer im Sommersemester 23 an der Universität
Zuverlässigkeitstechnik
 Zuverlässigkeisechnik Derzei gebräuchliche Begriffe, Modelle, Mehoden, und deren Anwendung Mache die Dinge so einfach wie möglich aber nich einfacher! 13. Dezember 2012 Dr. Andraes Hildebrand Alber Einsein
Zuverlässigkeisechnik Derzei gebräuchliche Begriffe, Modelle, Mehoden, und deren Anwendung Mache die Dinge so einfach wie möglich aber nich einfacher! 13. Dezember 2012 Dr. Andraes Hildebrand Alber Einsein
GRUNDLAGENLABOR CLASSIC RC-GLIED
 GUNDLAGNLABO LASSI -GLID Inhal: 1. inleing nd Zielsezng...2 2. Theoreische Afgaben - Vorbereing...2 3. Prakische Messafgaben...4 Anhang: in- nd Asschalvorgänge...5 Filename: Version: Ahor: _Glied_2_.doc
GUNDLAGNLABO LASSI -GLID Inhal: 1. inleing nd Zielsezng...2 2. Theoreische Afgaben - Vorbereing...2 3. Prakische Messafgaben...4 Anhang: in- nd Asschalvorgänge...5 Filename: Version: Ahor: _Glied_2_.doc
Investment under Uncertainty Princeton University Press, New Jersey, 1994
 Technische Universiä Dresden Fakulä Wirschafswissenschafen Lehrsuhl für Energiewirschaf (EE 2 ) Prof. Dr. C. v. Hirschhausen / Dipl.-Vw. A. Neumann Lesebeweis: Avinash K. Dixi und Rober S. Pindyck Invesmen
Technische Universiä Dresden Fakulä Wirschafswissenschafen Lehrsuhl für Energiewirschaf (EE 2 ) Prof. Dr. C. v. Hirschhausen / Dipl.-Vw. A. Neumann Lesebeweis: Avinash K. Dixi und Rober S. Pindyck Invesmen
Kosten der Verzögerung einer Reform der Sozialen Pflegeversicherung. Forschungszentrum Generationenverträge Albert-Ludwigs-Universität Freiburg
 Kosen der Verzögerung einer Reform der Sozialen Pflegeversicherung Forschungszenrum Generaionenverräge Alber-Ludwigs-Universiä Freiburg 1. Berechnungsmehode Die Berechnung der Kosen, die durch das Verschieben
Kosen der Verzögerung einer Reform der Sozialen Pflegeversicherung Forschungszenrum Generaionenverräge Alber-Ludwigs-Universiä Freiburg 1. Berechnungsmehode Die Berechnung der Kosen, die durch das Verschieben
Elementare RC- und RL-Glieder
 ANGEWANDTE ELEKTRONIK EINFÜHRNG WS 09/0 Elemenare RC- und RL-Glieder. Der Sromluß durch einen Kondensaor Abb.. veranschaulich einen Kondensaor, der durch Anschalen an eine Spannungsquelle geladen und anschließend
ANGEWANDTE ELEKTRONIK EINFÜHRNG WS 09/0 Elemenare RC- und RL-Glieder. Der Sromluß durch einen Kondensaor Abb.. veranschaulich einen Kondensaor, der durch Anschalen an eine Spannungsquelle geladen und anschließend
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
SERVICE NEWSLETTER. Einführung in die Mechanik Teil 2: Kinematik (2)
 Einührung in ie Mechanik Teil : Kinemaik Ausgabe: 9 / 4 In iesem Teil er Reihe wollen wir anhan eines Zahlenbeispiels en Deomaionsgraienen als zenrale Größe zur Beschreibung er Deormaion in er Kinemaik
Einührung in ie Mechanik Teil : Kinemaik Ausgabe: 9 / 4 In iesem Teil er Reihe wollen wir anhan eines Zahlenbeispiels en Deomaionsgraienen als zenrale Größe zur Beschreibung er Deormaion in er Kinemaik
Nachtrag Nr. 93 a. gemäß 10 Verkaufsprospektgesetz (in der vor dem 1. Juli 2005 geltenden Fassung) Unvollständiger Verkaufsprospekt
 Nachrag Nr. 93 a gemäß 10 Verkaufsprospekgesez (in der vor dem 1. Juli 2005 gelenden Fassung) vom 27. Okoer 2006 zum Unvollsändiger Verkaufsprospek vom 31. März 2005 üer Zerifikae auf * ezogen auf opzins
Nachrag Nr. 93 a gemäß 10 Verkaufsprospekgesez (in der vor dem 1. Juli 2005 gelenden Fassung) vom 27. Okoer 2006 zum Unvollsändiger Verkaufsprospek vom 31. März 2005 üer Zerifikae auf * ezogen auf opzins
Faktor 4x Long Zertifikate (SVSP-Produktcode: 1300)
 Fakor 4x Long Zerifikae (SVSP-Produkcode: 1300) Index Valor / Symbol / ISIN / WKN Bezugswer Fakor 4x Long Copper Index CBLKU4 / 12306935 / CZ33RK / DE000CZ33RK2 üblicherweise der an der Maßgeblichen erminbörse
Fakor 4x Long Zerifikae (SVSP-Produkcode: 1300) Index Valor / Symbol / ISIN / WKN Bezugswer Fakor 4x Long Copper Index CBLKU4 / 12306935 / CZ33RK / DE000CZ33RK2 üblicherweise der an der Maßgeblichen erminbörse
Werttheoretische Rekonstruktion der Konkurrenz als Ursache der Unterentwicklung
 Georg Quaas Werheoreische Rekonsrukion der Konkurrenz als Ursache der Unerenwicklung (Erschienen in: Friedrun & Georg Quaas (Hrsg.: Elemene zur Kriik der Werheorie. Peer Lang-Verlag, Frankfur a. M. 1997.
Georg Quaas Werheoreische Rekonsrukion der Konkurrenz als Ursache der Unerenwicklung (Erschienen in: Friedrun & Georg Quaas (Hrsg.: Elemene zur Kriik der Werheorie. Peer Lang-Verlag, Frankfur a. M. 1997.
Zwei Rechenbeispiele für die einfache lineare Regression
 Einfache Regression mi Ecel Prof. Dr. Peer von der Lippe Zwei Rechenbeispiele für die einfache lineare Regression 1.1. Daen 1. Mindeslöhne Beispiel 1 Ennommen aus Rolf Ackermann, pielball des Lobbyisen,
Einfache Regression mi Ecel Prof. Dr. Peer von der Lippe Zwei Rechenbeispiele für die einfache lineare Regression 1.1. Daen 1. Mindeslöhne Beispiel 1 Ennommen aus Rolf Ackermann, pielball des Lobbyisen,
Angewandte Versicherungsmathematik und Risikomanagement
 Angewande Versicherungsmahemaik und Risikomanagemen Vorlesung am Insiu für Mahemaik der Universiä Wien Winersemeser 6/7 Skripum Version. Dr. Huber Schickeanz Dr. Huber Schickeanz Angewande Versicherungsmahemaik
Angewande Versicherungsmahemaik und Risikomanagemen Vorlesung am Insiu für Mahemaik der Universiä Wien Winersemeser 6/7 Skripum Version. Dr. Huber Schickeanz Dr. Huber Schickeanz Angewande Versicherungsmahemaik
1 Kinematik der geradlinigen Bewegung eines Punktes 1.1 Freier Fall; Geschwindigkeit, Fallzeit, kinematische Diagramme
 Inhal / Übersich der Aufgaben mi Lösungen XI Aufgabe Erläuerung "Info"-Bild Seie 1 1 Kinemaik der geradlinigen Bewegung eines Punkes 1.1 Freier Fall; Geschwindigkei, Fallzei, kinemaische Diagramme 5 1.2
Inhal / Übersich der Aufgaben mi Lösungen XI Aufgabe Erläuerung "Info"-Bild Seie 1 1 Kinemaik der geradlinigen Bewegung eines Punkes 1.1 Freier Fall; Geschwindigkei, Fallzei, kinemaische Diagramme 5 1.2
Energietechnisches Praktikum I Versuch 11
 INSI FÜR HOCHSPANNNGSECHNIK Rheinisch-Wesfälische echnische Hochschule Aachen niv.-prof. Dr.-Ing. Armin Schneler INSI FÜR HOCHSPANNNGS ECHNIK RHEINISCH- WESFÄLISCHE ECHNISCHE HOCHSCHLE AACHEN Energieechnisches
INSI FÜR HOCHSPANNNGSECHNIK Rheinisch-Wesfälische echnische Hochschule Aachen niv.-prof. Dr.-Ing. Armin Schneler INSI FÜR HOCHSPANNNGS ECHNIK RHEINISCH- WESFÄLISCHE ECHNISCHE HOCHSCHLE AACHEN Energieechnisches
sammeln speichern C [F = As/V] Proportionalitätskonstante Q = CU I = dq/dt sammeln i - speichern u i (t)dt d t u c = 1 C i(t) dt
![sammeln speichern C [F = As/V] Proportionalitätskonstante Q = CU I = dq/dt sammeln i - speichern u i (t)dt d t u c = 1 C i(t) dt sammeln speichern C [F = As/V] Proportionalitätskonstante Q = CU I = dq/dt sammeln i - speichern u i (t)dt d t u c = 1 C i(t) dt](/thumbs/29/13357838.jpg) Elekronische Sseme - 3. Kapaziä und Indukiviä 1 -------------------------------------------------------------------------------------------------------------- G. Schaer 26. Mai 24 3. Kapaziä und Indukiviä
Elekronische Sseme - 3. Kapaziä und Indukiviä 1 -------------------------------------------------------------------------------------------------------------- G. Schaer 26. Mai 24 3. Kapaziä und Indukiviä
10 VORBEREITUNG AUF DAS ABITUR
 4 VORBEREITUNG AUF DAS ABITUR. Aufgaben zur Analysis 5 Golden-Gae-Bridge. Dadurch läss sichdie Symmerie der Brücke ausnuzen.. a) Anach B: Ansaz: y=m x+b liefer LGS: m ( 4) + b = 5 m ( 977) + b =. 5 Lösung:
4 VORBEREITUNG AUF DAS ABITUR. Aufgaben zur Analysis 5 Golden-Gae-Bridge. Dadurch läss sichdie Symmerie der Brücke ausnuzen.. a) Anach B: Ansaz: y=m x+b liefer LGS: m ( 4) + b = 5 m ( 977) + b =. 5 Lösung:
Seminararbeitspräsentation Risiko und Steuern. On the Effects of Redistribution on Growth and Entrepreneurial Risk-taking
 Seminararbeispräsenaion Risiko und Seuern On he Effecs of Redisribuion on Growh and Enrepreneurial Risk-aking aus der Vorlesung bekann: Posiionswahlmodell Selbssändigkei vs. abhängige Beschäfigung nun
Seminararbeispräsenaion Risiko und Seuern On he Effecs of Redisribuion on Growh and Enrepreneurial Risk-aking aus der Vorlesung bekann: Posiionswahlmodell Selbssändigkei vs. abhängige Beschäfigung nun
1 Physikalische Grundlagen
 Qaniaive Messng der spezifischen Wärmekapaziä nd der Schmelzwärme einer eekischen Legierng (SWE) Sichwore: Innere Energie, Schmelzenergie, hasenmwandlng hysikalische Grndlagen. Wärmekapaziä nd Schmelzkrve
Qaniaive Messng der spezifischen Wärmekapaziä nd der Schmelzwärme einer eekischen Legierng (SWE) Sichwore: Innere Energie, Schmelzenergie, hasenmwandlng hysikalische Grndlagen. Wärmekapaziä nd Schmelzkrve
Johann Wolfgang Goethe-Universität
 4. Asynchrone sequenielle chalungen 4. Asynchrone sequenielle chalungen 4.2 egiser 22 Technische Informaik 2 Asynchrone sequenielle chalungen 4. Asynchrone sequenielle chalungen Bei chalnezen exisier kein
4. Asynchrone sequenielle chalungen 4. Asynchrone sequenielle chalungen 4.2 egiser 22 Technische Informaik 2 Asynchrone sequenielle chalungen 4. Asynchrone sequenielle chalungen Bei chalnezen exisier kein
Ein Optimierungsansatz für ein fortlaufendes Datenqualitätsmanagement und seine praktische Anwendung bei Kundenkampagnen
 Universiä Augsburg Prof. Dr. Hans Ulrich Buhl Kernkompeenzzenrum Finanz- & Informaionsmanagemen Lehrsuhl für BWL, Wirschafsinformaik, Informaions- & Finanzmanagemen Diskussionspapier WI-74 Ein Opimierungsansaz
Universiä Augsburg Prof. Dr. Hans Ulrich Buhl Kernkompeenzzenrum Finanz- & Informaionsmanagemen Lehrsuhl für BWL, Wirschafsinformaik, Informaions- & Finanzmanagemen Diskussionspapier WI-74 Ein Opimierungsansaz
Saisonbereinigung ökonomischer Zeitreihen: Das Beispiel BIP
 Jürgen Kähler, Nicolas Pinkwar Saisonbereinigung ökonomischer Zeireihen: Das Beispiel BIP IWE Working Paper Nr. 01-2009 ISSN: 1862-0787 Erlangen, Dezember 2009 Insiu für Wirschafswissenschaf (Insiu of
Jürgen Kähler, Nicolas Pinkwar Saisonbereinigung ökonomischer Zeireihen: Das Beispiel BIP IWE Working Paper Nr. 01-2009 ISSN: 1862-0787 Erlangen, Dezember 2009 Insiu für Wirschafswissenschaf (Insiu of
HAW Hamburg Fakultät Life Sciences - Physiklabor Physikalisches Praktikum
 HAW Hamburg Fakulä Life Sciences - Physiklabor Physikalisches Prakikum Auf- und Enladungen von Kondensaoren in -Gliedern Messung von Kapaziäen Elekrische Schalungen mi -Gliedern finde man z. B. in Funkionsgeneraoren
HAW Hamburg Fakulä Life Sciences - Physiklabor Physikalisches Prakikum Auf- und Enladungen von Kondensaoren in -Gliedern Messung von Kapaziäen Elekrische Schalungen mi -Gliedern finde man z. B. in Funkionsgeneraoren
Value Based Management
 Value Based Managemen Vorlesung 5 Werorieniere Kennzahlen und Konzepe PD. Dr. Louis Velhuis 25.11.25 Wirschafswissenschafen PD. Dr. Louis Velhuis Seie 1 4 CVA Einführung CVA: Cash Value Added Spezifischer
Value Based Managemen Vorlesung 5 Werorieniere Kennzahlen und Konzepe PD. Dr. Louis Velhuis 25.11.25 Wirschafswissenschafen PD. Dr. Louis Velhuis Seie 1 4 CVA Einführung CVA: Cash Value Added Spezifischer
Bericht zur Prüfung im Oktober 2006 über Finanzmathematik und Investmentmanagement
 Berich zur Prüfung im Okober 006 über Finnzmhemik und Invesmenmngemen Grundwissen Peer Albrech Mnnheim Am 07. Okober 006 wurde zum ersen Ml eine Prüfung im Fch Finnzmhemik und Invesmenmngemen nch PO III
Berich zur Prüfung im Okober 006 über Finnzmhemik und Invesmenmngemen Grundwissen Peer Albrech Mnnheim Am 07. Okober 006 wurde zum ersen Ml eine Prüfung im Fch Finnzmhemik und Invesmenmngemen nch PO III
Von: Datum: Korrekturvorschlag: Anmerkung der Übersetzer:
 Marc Haunschild haunschild@mh is.de 05.06.09 09:16 maschinell besimmbar is keine eindeuige Formulierung, da es auch heißen kann, dass maschinell ewas fesgeleg (besimm) werden kann. Besser wäre "fessellbar"
Marc Haunschild haunschild@mh is.de 05.06.09 09:16 maschinell besimmbar is keine eindeuige Formulierung, da es auch heißen kann, dass maschinell ewas fesgeleg (besimm) werden kann. Besser wäre "fessellbar"
Seminar: Quantitatives Risikomanagement Grundlegende Konzepte des Risikomanagements. 2.1. Risikofaktoren und die Verlustverteilung.
 Prof: Hanspeer.Scmili Bereuung: Julia Eisenberg Sun,Fang Seminar: Quaniaives Risikomanagemen Grunlegene Konzepe es Risikomanagemens 2.. Risikofakoren un ie Verlusvereilung 2.. Allgemeine Definiion Wir
Prof: Hanspeer.Scmili Bereuung: Julia Eisenberg Sun,Fang Seminar: Quaniaives Risikomanagemen Grunlegene Konzepe es Risikomanagemens 2.. Risikofakoren un ie Verlusvereilung 2.. Allgemeine Definiion Wir
Finanzwirtschaftliche Analyse der schenkungsteuerlichen Zehnjahresregel
 Universiä Augsburg Prof. Dr. Hans Ulrich Buhl Kernkompeenzzenrum Finanz- & Informaionsmanagemen Lehrsuhl für BWL, Wirschafsinformaik, Informaions- & Finanzmanagemen Diskussionspapier WI-195 Finanzwirschafliche
Universiä Augsburg Prof. Dr. Hans Ulrich Buhl Kernkompeenzzenrum Finanz- & Informaionsmanagemen Lehrsuhl für BWL, Wirschafsinformaik, Informaions- & Finanzmanagemen Diskussionspapier WI-195 Finanzwirschafliche
Der Einfluss von Sozialkapital in der Asset Allocation von Privatanlegern
 Universiä Augsburg Prof. Dr. Hans Ulrich Buhl Kernkompeenzzenrum Finanz- & Informaionsmanagemen Lehrsuhl für BWL, Wirschafsinformaik, Informaions- & Finanzmanagemen Diskussionspapier WI-236 Der Einfluss
Universiä Augsburg Prof. Dr. Hans Ulrich Buhl Kernkompeenzzenrum Finanz- & Informaionsmanagemen Lehrsuhl für BWL, Wirschafsinformaik, Informaions- & Finanzmanagemen Diskussionspapier WI-236 Der Einfluss
Zuverlässigkeitsberechnung und vorbeugende Wartung von komplexen technischen Systemen mittels modifizierter Markov-Methode
 Disseraion Zuverlässigkeisberechnung und vorbeugende Warung von komplexen echnischen Sysemen miels modifizierer Markov-Mehode von Alexei Konnov Universiä Karlsruhe TH 7 Zuverlässigkeisberechnung und vorbeugende
Disseraion Zuverlässigkeisberechnung und vorbeugende Warung von komplexen echnischen Sysemen miels modifizierer Markov-Mehode von Alexei Konnov Universiä Karlsruhe TH 7 Zuverlässigkeisberechnung und vorbeugende
Ökonomische Potenziale einer Online-Kundenwertanalyse zur gezielten Kundenansprache im Internet
 Ökonomische Poenziale einer Online-Kundenweranalyse zur gezielen Kundenansprache im Inerne von Julia Heidemann, Mahias Klier, Andrea Landherr, Florian Probs Dezember 2011 in: D. C. Mafeld, S. Robra-Bissanz
Ökonomische Poenziale einer Online-Kundenweranalyse zur gezielen Kundenansprache im Inerne von Julia Heidemann, Mahias Klier, Andrea Landherr, Florian Probs Dezember 2011 in: D. C. Mafeld, S. Robra-Bissanz
Jan Kallsen. Mathematical Finance Eine Einführung in die zeitdiskrete Finanzmathematik
 Jan Kallsen Mathematical Finance Eine Einführung in die zeitdiskrete Finanzmathematik AU zu Kiel, WS 13/14, Stand 10. Februar 2014 Inhaltsverzeichnis 1 Mathematische Hilfsmittel 4 1.1 Absolutstetigkeit
Jan Kallsen Mathematical Finance Eine Einführung in die zeitdiskrete Finanzmathematik AU zu Kiel, WS 13/14, Stand 10. Februar 2014 Inhaltsverzeichnis 1 Mathematische Hilfsmittel 4 1.1 Absolutstetigkeit
Handelsstrategien mit Mindestgarantien
 Handelssraegien mi Mindesgaranien Eine analyische Beschreibung Inaugural-Disseraion zur Erlangung des Grades eines Dokors der Wirschafs- und Gesellschafswissenschafen durch die Rechs- und Saaswissenschafliche
Handelssraegien mi Mindesgaranien Eine analyische Beschreibung Inaugural-Disseraion zur Erlangung des Grades eines Dokors der Wirschafs- und Gesellschafswissenschafen durch die Rechs- und Saaswissenschafliche
Induktive Limiten. Arpad Pinter, Tobias Wöhrer. 30. Jänner 2010
 Induktive Limiten Arpad Pinter, Tobias Wöhrer 30. Jänner 2010 1 Inhaltsverzeichnis 1 Induktiver Limes von Mengen 2 2 Induktiver Limes von Vektorräumen 4 3 Lokalkonvexe topologische Vektorräumen 7 4 Induktiver
Induktive Limiten Arpad Pinter, Tobias Wöhrer 30. Jänner 2010 1 Inhaltsverzeichnis 1 Induktiver Limes von Mengen 2 2 Induktiver Limes von Vektorräumen 4 3 Lokalkonvexe topologische Vektorräumen 7 4 Induktiver
Asset Liability Management in einem selbstfinanzierenden Pensionsfonds
 Forschung am IVW Köln, 9/215 Insiu für Versicherungswesen Asse Liabiliy Managemen in einem selbsfinanzierenden Pensionsfonds Osar Goece Forschung am IVW Köln, 9/215 Wählen Sie ein Elemen aus. Osar Goece
Forschung am IVW Köln, 9/215 Insiu für Versicherungswesen Asse Liabiliy Managemen in einem selbsfinanzierenden Pensionsfonds Osar Goece Forschung am IVW Köln, 9/215 Wählen Sie ein Elemen aus. Osar Goece
