Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
|
|
|
- Waltraud Diefenbach
- vor 5 Jahren
- Abrufe
Transkript
1 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee Analysis und Inegralransformaionen Lösungsvorschläge zum 4. Übungsbla Aufgabe a) Den Graphen von f bzw. g ennehmen wir { { für [, ] für [, ] f) = und g) = Die Falung von f und g is nach Definiion gegeben durch fτ)g τ) dτ, R. R). Offenbar is für <. Zur Berechnung von f g)) für unerscheiden wir folgende Fälle:. Fall: Für [, ) ergib sich mi der Subsiuion r := τ, dr = dτ g τ) dτ = gr) dr = dr =.. Fall: Für [, 4) ergib sich abermals mi der Subsiuion r := τ, dr = dτ g τ) dτ +. Fall: Für 4 ergib sich g τ) dτ = g τ) }{{} dτ + =, da τ gr) dr = dr + g τ) dτ =. dr = 8. Insgesam haben wir für [, ) 8 für [, 4) = { 4 für [, 4), R. f g) 4 4
2 b) Hier sind { für [, ] f) = { für [, 4] und g) = R). Wiederum gil für <. Um die Falung fτ)g τ) dτ für zu berechnen, führen wir eine Fallunerscheidung durch:. Fall: Für [, ) gil fτ) g τ) }{{} dτ =. =, da τ <. Fall: Für [, 4) ergib sich mi der Subsiuion r := τ, dr = dτ g τ) dτ = gr) dr = dr =.. Fall: Für [4, 5) ergib sich erneu mi der Subsiuion r := τ, dr = dτ 4. Fall: Für 5 ergib sich g τ) dτ = gr) dr = 4 g τ) }{{} dτ =. =, da τ 4 dr = 5. Zusammenfassend haben wir für [, 4) 5 für [4, 5) f g) = { 4 für [, 5), R. 5 Aufgabe Um eine Funkion f Z mi f) = + fτ) sin τ) dτ für alle anzugeben, schreiben wir die reche Seie mi Hilfe der Falung f) = + f h sin)))
3 und wenden die Falungsregel. an. Für s C mi hinreichend großem Res) gil L f)s) = L h))s) + L f h sin))s) = L h))s) + L f)s) L h sin)s). Hieraus folg wegen h) bzw. äquivalen dazu! s + = 6 s 4 und sin)h) s + L f)s) = 6 s 4 + L f)s) s + L f)s) = s + s 6 s 4 = 6 s s 6. Schließlich erhalen wir mi 5 h) 5! s 6 für Res) > ) für Res) > ) L f)s) ) s = 6 + s 4 L f)s) h) + 6 5! 5 h) = + 5 /) h), also f) = + 5 ) h), R. Somi lös y) := + 5,, die gegebene Gleichung. Aufgabe a) i) Der Ansaz für eine Parialbruchzerlegung riche sich nach den Nullsellen des Nennerpolynoms = ) = + ) ). Diese sind,,. Jede dieser Nullsellen is einfach. Demzufolge laue der Ansaz der Parialbruchzerlegung + = + + ) ) = A + B + + C. Um die Koeffizienen A, B, C zu ermieln, haben wir verschiedene Möglichkeien.. Möglichkei: Wir muliplizieren obige Gleichung mi dem Haupnenner + ) ) + = A + ) ) + B ) + C + ) und sezen die Nullsellen des Nennerpolynoms ein = : = A A = / = : = B B = / = : 5 = 6C C = 5/6. Möglichkei: Um A, den Koeffizienen des zur Nullselle λ = gehörenden Terms, zu ermieln, muliplizier man + +) ) mi λ = und bilde dann den Grenzwer λ, also. Formal ausgedrück bedeue dies ) + A = lim + ) ) + = lim + ) ) = =. Ensprechend kann man für B und C verfahren ) + B = lim + ) + ) ) ) + C = lim ) + ) ) + = lim = ), + = lim = 5 + ) 6. Mi den Koeffizienen A = /, B = / sowie C = 5/6 ergib sich + = + + ) ) = + ) ).
4 ii) Wiederum müssen zunächs die Nullsellen des Nennerpolynoms besimm werden. Durch scharfes Hinsehen erkennen wir, dass eine solche is. Polynomdivision liefer + = ) + ), und wegen ) = ) + ) ergib sich + = ) + ). Dami is eine einfache Nullselle und eine doppele Nullselle des Nennerpolynoms. Der Ansaz für eine Parialbruchzerlegung is daher + = ) + ) = A + Nach Muliplikaion mi ) + ) is B + ) + C + ). = A + ) + B + ) ) + C ) = A + + ) + B ) + C ). Sezen wir die Nullsellen und hierin ein, erhalen wir = : = C C = / = : = 4A A = /4 Um B zu besimmen, können wir einen beliebigen anderen Wer für einsezen. Wir wählen =, weil dann die linke Seie der Gleichung verschwinde: = A B C = 4 B B = 4. Alernaiv können wir zur Besimmung von A, B, C auch einen Koeffizienenvergleich durchführen, der auf ein lineares Gleichungssysem führ : = A + B : = A + C : = A B C beziehungsweise geschrieben mi Hilfe der zugehörigen erweieren Mari /4... /4. / Jedenfalls liefern beide Alernaiven A = /4, B = /4, C = /. Folglich is + = ) + ) = 4 ) 4 + ) + + ). iii) Offenbar is eine Nullselle des Nennerpolynoms 8. Mi Hilfe der Polynomdivision + 8) : ) sehen wir 8 = ) + + 4). Das Polynom ha die beiden nichreellen Nullsellen + i und i. Dami laue der Ansaz für die komplee) Parialbruchzerlegung 8 = ) + i)) i)) = A + B + i) + C i). Nun müssen wir die Koeffizienen A, B, C besimmen. Hierzu muliplizieren wir obige Gleichung mi dem Haupnenner ) + i)) i)) durch = A + i)) i))+b ) i))+c ) + i)). 4
5 Einsezen der Nullsellen des Nennerpolynoms ergib Hieraus folg = : = A i) + i) = A, = + i : i = B + i) i) = 6B + i), = i : + i = C i) i) = 6C i). A = /6, B = 6 i + i = 6 i) + C = 6 + i i = 6 + i) + = + = i, i. Als Endergebnis für die komplee Parialbruchzerlegung erhalen wir 8 = 6 + i + i) + i i). + b) i) Wegen + ) + ) = + ) + ) = + ) + i ) i ) sind eine dreifache Nullselle und + i bzw. i jeweils eine einfache Nullselle des Nennerpolynoms. Deshalb laue der Ansaz für die komplee) Parialbruchzerlegung ii) Aufgabe 4 + ) + ) = A + + B + ) + C + ) + D + i Ergebnis: A = 9, B =, C =, D = 9, E = 9. + E i Es gil: 6 = 4 ) = ) +) = )+) i)+i). Also is eine doppele Nullselle, während die Nullsellen,, i, i jeweils einfach sind. Der Ansaz für die komplee) Parialbruchzerlegung is 6 = A + B + C + D + + E i + Ergebnis: A =, B =, C = 4, D = 4, E = 4 i, F = 4 i. a) Parialbruchzerlegung liefer s = s ). s + F + i. Wegen s = L h)s ) = L e h))s) für Res) > und s+ L e ) h))s) für Res) > erhalen wir für Res) > s e e )h) = sinh)h). Alernaiv: Nach der Falungsregel gil für Res) > s = s s + = L g )s) L g )s) = L g g )s) = L h)s + ) = wobei g ) := e h) und g ) := e h) gesez seien. Also fanden wir mi der Falung g g eine Funkion mi L g g )s) = s. Nun müssen wir nur noch g g berechnen. Für < is g g )) = und für is g g )) = g u)g u) du = = e e u) e u e u du = e e u du u= = e e ) = sinh). 5.
6 b) Mi Hilfe der Parialbruchzerlegung erkennen wir für Res) > s + s = ss + ) = / s / s + s + s = L h)s) L e h))s) = L )h)) e s). Alernaiv: Wir können den b)-teil auch lösen, indem wir die Dämpfungsregel auf das Resula des a)-teils anwenden. Es gil nämlich für alle s C mi Res) > s + s = = L s + ) e e e )h) a) = L sinh)h) ) s + ) = L e sinh)h) ) s) ) ) s) = L e )h) s). c) Der Ansaz s + s + 4s = s + s s + 4) = A s + B s + C s + 4 führ auf A = 6, B = 4, C = 6. Dami gil für alle s C mi Res) > s + s + 4s = 6 s + 4 s 6 s e 4 )h). d) Es sei a > fes gewähl. Der Ansaz einer kompleen) Parialbruchzerlegung laue s + a ss + a ) = s + a ss ia)s + ia) = A s + B s ia + C s + ia bzw. s + a = As ia)s + ia) + Bss + ia) + Css ia). Einsezen der Nullsellen des Nennerpolynoms liefer Demzufolge is für Res) > s = : a = Aa A = a, s = ia : ia + a = Ba B = +i a, s = ia : ia + a = Ca C = i a. s + a ss + a ) = a s + i a s ia i a s + ia = a L h)s) + i a L eia h))s) i a L e ia h))s) = L a h) + i a eia h) i ) a e ia h) s) = L a h) eia + e ia ) + i eia e ia ) )) s) = L a h) cosa) + sina) )) s). 6
7 Aufgabe 5 Wir verwenden Saz aus 9.: Sei f Z eine Funkion mi dem Wachsumskoeffizienen σ. Gil f) F s), dann is F in {s C Res) > σ } holomorph mi F s) = e s f) d, d.h. Deshalb is f) = L F )) für >. f) F s). a) Für s R mi s > a sei F s) := ln s+a s a+a s a ) = ln s a ) = ln + a s a ). Dann is F s) = + a s a Dami erhalen wir für a s a) = a s a) + as a) = a s a)s + a) = s a + s + a e a + e a ) h). f) = L F )) = ea e a ) h) = sinha) b) Für F s) := arcan a s ), s, ), ergib sich F s) = Hieraus folg f) = sina) h),. a + a/s) s = a s + a sina) h). h). c) Is F s) := ln a ) = ln a s s ) + a s )) = ln a s ) + ln + a s ) für s R mi s > a gesez, so erhäl man F s) = a s as a s + as = a ss a) a ss + a) = s + s a s + s + a = s + s a + s + a + e a + e a ) h) = + cosha)) h). Für f) := cosha) h),, gil somi f) ln a s ). Aufgabe 6 a) Aus der Vorlesung kennen wir die Ideniä L f n) )s) = s n L f)s) s n f+) s n f +)... f n ) +) ) = s n L f)s) s n f) s n f )... f n ) ) für eine n-mal seig differenzierbare Funkion f [Insbesondere sind dann f, f,..., f n ) rechsseiig seig in, woraus die Gleichhei in ) folg.], die höchsens von eponeniellem Wachsum is, und s C mi hinreichend großem Res). Speziell für n =, haben wir L f )s) = s L f)s) f) und L f )s) = s L f)s) sf) f ). ) Da die Anfangswere y) und y ) vorgegeben sind, können wir obiges Resula nich direk anwenden. Deshalb besimmen wir zunächs eine Funkion u mi u ) + 4u ) + u) =, u) = 7, u ) =. Dann gewinnen wir eine Lösung y des ursprünglichen Anfangswerproblems durch Verschieben von u, indem wir y) := u ) sezen. Für eine Lösung u des Problems u ) + 4u ) + u) = mi den Anfangsweren u) = 7 und u ) = bedeue ) L u )s) = s L u)s) 7 und L u )s) = s L u)s) 7s. 7
8 Somi ergib sich s = L h)s) = L u + 4u + u)s) = s L u)s) 7s ) + 4s L u)s) 7) + L u)s) = s + 4s + )L u)s) 7s 9, also L u)s) = s 7s ) = 7s + 9s + + 4s + s ss + )s + ). Um eine Funkion anzugeben, deren Laplaceransformiere gleich 7s +9s+ ss+)s+) eine Parialbruchzerlegung durch. Hierzu machen wir den Ansaz is, führen wir 7s + 9s + ss + )s + ) = A s + B s + + C s +. Muliplizieren wir diese Gleichung mi s und sezen s = ein, so folg A = = 4. Muliplikaion mi s + und Einsezen von s = liefer B = = 5, und ganz analog erhäl man schließlich noch C = 6 =. Dami gil und wir haben eine Lösung u gefunden: Es is L u)s) 4 + 5e e ) h), u) = 4 + 5e e,. Somi lös y) := u ) = 4 + 5e + e +9,, das ursprüngliche Problem. b) Wegen y) = y ) = erhäl man hier L y )s) = s L y)s) und L y )s) = s L y)s) für hinreichend große Res), und mi y ) = ergib sich Insgesam ha man also und dies führ auf L y )s) = s L y)s) s y) sy ) y ) = s L y)s). s = L h)s ) = L e h))s) = L y y + y y)s) = s L y)s) ) s L y)s) + s L y)s) L y)s) = s s + s )L y)s) = s ) L y)s), L y)s) = Für jedes n N {} gil bekannlich und mi der Dämpfungsregel folg s ) + ) = s s ) + s ) 4. L n h))s) = n! s n+ Res) > ), s ) n+ = n! L n h))s ) = n! L e n h))s) Res) > ). Hiermi bekommen wir L y)s) = L e h))s) + 6 L e h))s) = L e h) / + /6) ) s), d.h. eine Lösung des Anfangswerproblems is y) = e / + /6),. 8
9 c) Man erhäl mi c := y ) für s C mi hinreichend großem Res) Dami ergib sich L y )s) = s L y)s) 6 und L y )s) = s L y)s) 6s c. 6 s + ) = L 6e h))s) = L y + y + y)s) = s L y)s) 6s c) + s L y)s) 6) + L y)s) = s + s + )L y)s) 6s c. Für eine Lösung y der Differenialgleichung mi y) = 6 und y ) = c ha man also ) 6 6s + ) + c L y)s) = s 6s + c s + s + ) = s + ) + s + ) 4 Uner Verwendung von = 6 s + + c + 6 s + ) + 6 s + ) 4. s + ) n+ = n! L n h))s + ) = n! L e n h))s) Res) >, n N {}) schließ man L y)s) = 6 s + + c + 6 s + ) + 6 s + ) 4 6e + c + 6)e + e )h), d.h. y) = 6 + c + 6) + )e,. Bei dieser Funkion gil y) = + c)e, und für c = wird die Bedingung y) = /e erfüll. Eine Lösung des Problems is demzufolge Aufgabe 7 y) = )e,. Wende man auf die reche und linke Seie der Gleichung y ) 4y ) + 4y) = δ ) + δ ) die Laplaceransformaion an und berücksichig die Were y) =, y ) =, so bekomm man für s C mi hinreichend großem Res) s Y s) s 4sY s) ) + 4Y s) = e s + e s Dabei sei Y s) := L y)s) gesez. Nun is s 4s + 4)Y s) = s + e s + e s Y s) = s s ) + e s s ) + e s s ). s s ) = s s ) s ) e e )h) = )e h). Für f) := e h), R, gil nach der Dämpfungsregel L f)s) = L h))s ) = s ) alle s C mi Res) >. Mi der Verschiebungsregel ergib sich e s s ) = e s L f)s) = L f ))s) bzw. Daher is für e s s ) = e s L f)s) = L f ))s). e s s ) + e s s ) f ) + f ) = )e ) h ) + )e ) h ). Zusammen folg Y s) )e h) + )e ) h ) + )e ) h ). Nach einer Probe sieh man, dass y) := )e h)+ )e ) h )+ )e ) h ), R, das gegebene Problem im Sinne von 4. der Vorlesung lös. 9
Aufgabe 69 Wir wenden die Laplacetransformation auf das System von Differentialgleichungen an. Schreibe. Y 1, y 2. (1 s 2 )Y 2 (s) = 1.
 Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang Sommersemester 3 7.7.3 Höhere Mathematik II für die Fachrichtungen Elektrotechnik und Informationstechnik
Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang Sommersemester 3 7.7.3 Höhere Mathematik II für die Fachrichtungen Elektrotechnik und Informationstechnik
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Ganzrationale Funktionen (Polynomfunktionen) - Berechnung von Nullstellen, Gleichungen höheren Grades -
 GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
(10 Punkte) Gegeben ist die in Fig. 1 abgebildete in T periodische Zeitfunktion f(t). f(t)
 H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Fourier- und Laplace- Transformation
 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Fourier-Transformation Linearität, Symmetrie, Verschiebung, Skalierung, Faltung, Modulation
 Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Stammgruppe trifft sich zum Museumsrundgang Experte erklärt jeweils sein Plakat
 Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Abschlussprüfung an Fachoberschulen in Bayern Mathematik mit CAS 2015 Analysis A2 Ausbildungsrichtung Technik
 MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
Hauptachsentransformation
 Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Mathematikaufgaben > Analysis > Funktionenscharen
 Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Lösungen Test 2 Büro: Semester: 2
 Fachhochschule Nordwesschweiz (FHNW) Hochschule für Technik Insiu für Geises- und Naurwissenschaf Dozen: Roger Burkhard Klasse: Sudiengang ST Lösungen Tes Büro: 4.613 Semeser: Modul: MDS Daum: FS1 Bemerkungen:
Fachhochschule Nordwesschweiz (FHNW) Hochschule für Technik Insiu für Geises- und Naurwissenschaf Dozen: Roger Burkhard Klasse: Sudiengang ST Lösungen Tes Büro: 4.613 Semeser: Modul: MDS Daum: FS1 Bemerkungen:
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
7. Funktionalgleichung der Zeta-Funktion
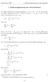 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
4.7. Exponential- und Logarithmusfunktionen
 ... Eonenialfunkionen Definiion:.. Eonenial- und Logarihmusfunkionen Die Funkion f() = c a mi D = R, c und a R + \{}heiß Eonenialfunkion zur Basis a. Die Eonenialfunkion zur Basis a = e mi der Eulerschen
... Eonenialfunkionen Definiion:.. Eonenial- und Logarihmusfunkionen Die Funkion f() = c a mi D = R, c und a R + \{}heiß Eonenialfunkion zur Basis a. Die Eonenialfunkion zur Basis a = e mi der Eulerschen
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 7. Übungsblatt
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
Analysis: Exponentialfunktionen Analysis
 www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Kapitel : Exponentielles Wachstum
 Wachsumsprozesse Kapiel : Exponenielles Wachsum Die Grundbegriffe aus wachsum 1.xmcd werden auch hier verwende! Wir verwenden im Beispiel 2 auch fas die gleiche Angabe wie in Beispiel 1 - lediglich eine
Wachsumsprozesse Kapiel : Exponenielles Wachsum Die Grundbegriffe aus wachsum 1.xmcd werden auch hier verwende! Wir verwenden im Beispiel 2 auch fas die gleiche Angabe wie in Beispiel 1 - lediglich eine
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
Ministerium für Schule und Weiterbildung NRW M LK HT 4 Seite 1 von 9. Unterlagen für die Lehrkraft. Abiturprüfung Mathematik, Leistungskurs
 Seie von 9 Unerlagen für die Lehrkraf Abiurprüfung 9 Mahemaik, Leisungskurs. Aufgabenar Lineare Algebra/Geomerie ohne Alernaive. Aufgabensellung siehe Prüfungsaufgabe. Maerialgrundlage 4. Bezüge zu den
Seie von 9 Unerlagen für die Lehrkraf Abiurprüfung 9 Mahemaik, Leisungskurs. Aufgabenar Lineare Algebra/Geomerie ohne Alernaive. Aufgabensellung siehe Prüfungsaufgabe. Maerialgrundlage 4. Bezüge zu den
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Institut für Analysis WS 2017/18 PD Dr. Peer Christian Kunstmann Dipl.-Math. Leonid Chaichenets Tobias Ried, M.Sc.
 Institut für Analysis WS 07/8 PD Dr. Peer Christian Kunstmann 0..07 Dipl.-Math. Leonid Chaichenets Tobias Ried, M.Sc. Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 0. Übungsblatt
Institut für Analysis WS 07/8 PD Dr. Peer Christian Kunstmann 0..07 Dipl.-Math. Leonid Chaichenets Tobias Ried, M.Sc. Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum 0. Übungsblatt
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Homogene Gleichungssysteme, Gausscher Algorithmus
 HTW Mhemik MST Prof.Dr.B.Grbowski e-mil: grbowski@hw-srlnd.de Tel.: 7- Lösungen zu Übung Homogene Gleichungssyseme, Gusscher lgorihmus u ufgbe Besimmen Sie mi Hilfe des Gusschen lgorihmus die jeweilige
HTW Mhemik MST Prof.Dr.B.Grbowski e-mil: grbowski@hw-srlnd.de Tel.: 7- Lösungen zu Übung Homogene Gleichungssyseme, Gusscher lgorihmus u ufgbe Besimmen Sie mi Hilfe des Gusschen lgorihmus die jeweilige
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Flugzeugaerodynamik I Lösungsblatt 3
 Flugzeugaerodynam I Lösungsbla 3 Lösung Aufgabe 5 geg: dünnes Profil a) ges: A 1 mi m (1) f 0.01 () Annahme Amosphärendaen: Abschäzung der Ansrömmachzahl U 1 50m/s (3) ρ 1 1.kg/m 3 (4) α 1 10 o (5) dc
Flugzeugaerodynam I Lösungsbla 3 Lösung Aufgabe 5 geg: dünnes Profil a) ges: A 1 mi m (1) f 0.01 () Annahme Amosphärendaen: Abschäzung der Ansrömmachzahl U 1 50m/s (3) ρ 1 1.kg/m 3 (4) α 1 10 o (5) dc
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Formelsammlung (Fundamentum, ohne zusätzliche Blätter) Grafikfähiger Taschenrechner CAS im Prüfungsmodus (zurückgesetzt)
 BM Mahemaik T Schwerpunk_6 / 0 - Serie Seie: /7 Abschlussprüfung BM Mahemaik Schwerpunk TAL Teil Prüfungsdauer 90 Minuen, ohne Hilfsmiel Formelsammlung (Fundamenum, ohne zusäzliche Bläer Grafikfähiger
BM Mahemaik T Schwerpunk_6 / 0 - Serie Seie: /7 Abschlussprüfung BM Mahemaik Schwerpunk TAL Teil Prüfungsdauer 90 Minuen, ohne Hilfsmiel Formelsammlung (Fundamenum, ohne zusäzliche Bläer Grafikfähiger
gegeben durch x 4 in dasselbe Koordinatensystem (Längeneinheit auf beiden Achsen: 1 cm). Zur Kontrolle: ft
 KA LK M2 13 18. 11. 05 I. ANALYSIS Leisungsfachanforderungen Für jedes > 0 is eine Funkion f gegeben durch f (x) = x + 1 e x ; x IR. Der Graph von f sei G. a) Unersuche G auf Asympoen, Nullsellen, Exrem-
KA LK M2 13 18. 11. 05 I. ANALYSIS Leisungsfachanforderungen Für jedes > 0 is eine Funkion f gegeben durch f (x) = x + 1 e x ; x IR. Der Graph von f sei G. a) Unersuche G auf Asympoen, Nullsellen, Exrem-
Übungsblatt 4 Lösungsvorschläge
 Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Übungen zur Einführung in die Physik II (Nebenfach)
 Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Analysis: Ganzrationale Funktionen Analysis Ganzrationale Funktionen Differenzialrechnung, Extrem- und Wendepunkte
 www.mahe-aufgaben.com Analysis: Ganzraionale Funkionen Analysis Ganzraionale Funkionen Differenzialrechnung, Exrem- und Wendepunke Gymnasium Klasse 0 Alexander Schwarz www.mahe-aufgaben.com Juni 0 www.mahe-aufgaben.com
www.mahe-aufgaben.com Analysis: Ganzraionale Funkionen Analysis Ganzraionale Funkionen Differenzialrechnung, Exrem- und Wendepunke Gymnasium Klasse 0 Alexander Schwarz www.mahe-aufgaben.com Juni 0 www.mahe-aufgaben.com
Abiturprüfung Mathematik 2010 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1 ( )( ) und der Normalen von K
 Abiurprüfung Mhemik (Bden-Würemberg) Berufliche Gymnsien Anlysis, Aufgbe. Für jedes * is die Funkion f gegeben durch f (x) = x x + x +, x Ds Schubild von f is K. ( )( ).. (4 Punke) Zeichnen Sie K und K
Abiurprüfung Mhemik (Bden-Würemberg) Berufliche Gymnsien Anlysis, Aufgbe. Für jedes * is die Funkion f gegeben durch f (x) = x x + x +, x Ds Schubild von f is K. ( )( ).. (4 Punke) Zeichnen Sie K und K
Kapitel 3. x, wobei x, y R + und t R.
 Lineare Geomerie Kapiel Homogene und inhomogene lineare Gleichungssyseme Täglich werden wir mi Gleichungssysemen konfronier Manche scheinen sehr komplizier zu sein und manchmal können sie nur numerisch
Lineare Geomerie Kapiel Homogene und inhomogene lineare Gleichungssyseme Täglich werden wir mi Gleichungssysemen konfronier Manche scheinen sehr komplizier zu sein und manchmal können sie nur numerisch
mathphys-online Abschlussprüfung Berufliche Oberschule 2009 Mathematik 12 Technik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die reelle Funktion f( x)
 Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Exponential- und Logarithmusfunktionen
 . ) Personen, Personen bzw. Personen ) Ewas weniger als Minuen. (Nach,... Minuen sind genau Personen informier.) ) Ja. Bereis um : Uhr sind (heoreisch) Personen informier. ) Informiere Miarbeierinnen und
. ) Personen, Personen bzw. Personen ) Ewas weniger als Minuen. (Nach,... Minuen sind genau Personen informier.) ) Ja. Bereis um : Uhr sind (heoreisch) Personen informier. ) Informiere Miarbeierinnen und
Flugzeugaerodynamik I Lösungsblatt 2
 Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Lösung - Serie 8. D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. MC-Aufgaben (Online-Abgabe) 1. Was für eine Kurve stellt die Parametrisierung
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
Aufgabe 1: Kontinuierliche und diskrete Signale
 Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
MATHEMATIK. Fachabituiprüfung 2013 zum Erwerb der Fachhochschulreife an. Fachoberschulen und Berufsoberschulen. Ausbildungsrichtung Technik
 Fachabiuiprüfung 2013 zum Erwerb der Fachhochschulreife an Fachoberschulen und Berufsoberschulen MATHEMATIK Ausbildungsrichung Technik Diensag, 4. Juni 2013, 9.00-12.00 Uhr Die Schülerinnen und Schüler
Fachabiuiprüfung 2013 zum Erwerb der Fachhochschulreife an Fachoberschulen und Berufsoberschulen MATHEMATIK Ausbildungsrichung Technik Diensag, 4. Juni 2013, 9.00-12.00 Uhr Die Schülerinnen und Schüler
