Fourier- und Laplace- Transformation
|
|
|
- Kornelius Raske
- vor 7 Jahren
- Abrufe
Transkript
1 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule Pforzheim FB-Ingenieurwissenschafen, Elekroechnik/Informaionsechnik
2 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion Inhal. Fourier- und Lalace-Transformaion. Fourier-Reihenenwicklung.. Zielsezung, Begründung und Vorgehensweise.. Ableiung der reellen Fourierreihe... Reelle Fourierreihe mi Sinus- und Kosinusschwingungen... Vereinfache Besimmung der reellen Fourierkoeffizienen...3 Reelle Fourierreihe in Sinusform...4 Reelle Fourierreihe in Cosinusform...5 Anschauliche Darsellung der verschiedenen Formen der reellen Fourierreihe..3 Ableiung der komlexen Fourierreihe..4 Rechenbeisiel..5 Grahische Darsellung eriodischer Zeifunkionen im Frequenzbereich..5. Amliudensekrum..5. Amliudenberags- und Phasensekrum..5.3 Komlexe Darsellung Übungsbla Fourierreihe. Fourier-Transformaion.. Herleiung des Fourier-Inegrals.. Rechenbeisiele... Recheckimuls... Zeibegrenze Cosinusschwingung...3 Dela-Imuls Übungsbla Fourier-Transformaion.3 Lalace-Transformaion.3. Einführung.3. Rechenregeln der Lalace-Transformaion.3.. Lineariässaz.3.. Änlichkeissaz.3..3 Verschiebungssaz.3..4 Dämfungssaz.3..5 Differeniaionssaz.3.3 Korresondenzabelle.3.4 Beisiele.3.5 Periodische Funkionen.3.6 Lalace-Rückransformaion.3.7 Anwendungsbeisiele Übungsbla Lalace-Transformaion Ergänzungsaufgaben Fourier-Reihen und Transformaion / Lösungen Ergänzungsaufgaben zur Lalace-Transformaion / Lösungen Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
3 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3 Lalace-Transformaion.3. Einführung Zweck: u.a. leicheres Lösen komlizierer Differenialgleichungen Einsaz in E-Technik / Maschinenbau / Regelungsechnik... Differenialgleichung: Vorgehensweise:. Die DGL (linear mi konsanen Koeffizienen, s. Ka. ) wird mi Lalace-Transformaion in eine algebraische Gleichung überführ.. Als Lösung dieser Gleichung erhäl man die Bildfunkion Y() der gesuchen Originalfunkion y(). 3. Die gesuche Lösung y() der DGL erhäl man durch Rückransformaion der Bildfunkion Y(). (Korresondenzabellen, Parialbruchzerlegung, Reihenenwicklung,...) Voreil: Rechenoeraionen im Bildbereich meis leicher ausführbar! Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
4 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion Definiionsgleichungen Transformaion: F( ) LT{ f ( ) } F( ) f ( ) e d bzw. F() ο f() (Korresondenzschreibweise n. DIN 5487) { } Inverse Transformaion: f ( ) LT F( ) σ + j o f ( ) F( ) e d π j σ j o bzw. f() ο F() Lalace-Oeraor: σ + jω (Lieraur auch s ) σ reel, osiiv Dämfung vgl. Fourier-Transformaion (σ ) Beisiel: Einheissrung σ() f() ( ) f ; < ; F f e d e d e ( ) ( ) ( ) "Praxis": Transformaion bzw. Rückransformaion miels Korresondenzabellen und Anwendung der Lalace-Rechenregeln (s.u.), evl. assende algebraische Umformungen nöig. Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 3
5 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3. Rechenregeln der Lalace-Transformaion Transformaion f f() F() f() σ + j o ( ) F( ) e d π j σ j o (*) F() F( ) f ( ) e d Lineariässaz a f () + a f () a F () + a F () Ähnlichkeissaz f(a) mi a > / a F( / a ) Verschiebungssaz f(-τ) mi τ > e -τ F() Dämfungssaz e -a f() F(+a). Differeniaion f () F() - f(+) (**) n. Differeniaion f (n) () n n n F( ) f ( ) f ( ) Inegraionssaz Falungssaz f( τ ) f ( τ ) dτ Anfangswersaz lim x( ) Endwersaz lim x( ) + + ( n ) ( n ( ) f ) ( ) K f + + f() τ dτ / F() F () F () F( ) lim( ) lim( F ) ( ) (*): Rückransformaion besser mi Parialbruchzerlegung bzw. Reihenenwicklung von F() und Korresondenzafel (**): +, da linksseiiger Grenzwer null Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 4
6 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.. Lineariässaz f() a f () + a f () { ( ) ( )} ( ) ( ) ( ) LT a f + a f a f + a f e d ( ) ( ) a f e d + a f e d { ( )} ( ) { } a LT f + a LT f { + } { ( )} + { ( )} LT a f a f a LT f a LT f ( ) ( ).3.. Ähnlichkeissaz LT{ f ( a) } f ( a) e d LT f ( a) LT{ f ( a) } u/ a f u e du a { } ( ) a F a Subsiuion: ua d /a du.3..3 Verschiebungssaz f f() f(-τ) f(<) τ τ Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 5
7 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion { ( τ )} ( τ ) LT f f e d τ Subsiuion: u-τ d du ( + τ ) τ { ( τ )} ( ) ( ) u u LT f f u e du e f u e du ( τ ) τ { } ( ) LT f e F.3..4 Dämfungssaz { ( )} ( ) ( + ) ( ) ( ) a a a ' LT e f f e e d f e d f e d mi ' + a { } ( + ) LT e f F a a ( ).3..5 Differeniaionssaz LT{ f& df ( ) } e d d In.regel: u dv u v v du df seze dv d u. u e d v f ( ) du e d { } ( ) ( ) LT f& ( ) f e + f e d {& ( )} ( ) + ( ) LT f f e F ( ) { & } ( ) + ( ) LT f f F Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 6
8 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion LT{ f&& ( ) } f&& ( ) e d seze dv f&& d u. u e ( ) {&& } & ( ) & ( ) LT f f e + f e d LT v f& ( ) du e d { f& ( ) } [ ] &f + f + F ( ) ( ) ( ) &f f + F ( ) ( ) ( ) bisher: LT f ( ) { } F( ) ( ) LT df F f d ( ) ( ) ( ) LT d f F f f d & ( ) ( ) ( ) analoges Weierführen der Rechnung führ auf: ( ) LT d n f n d F f f f f ( ( ) ( ) ( ) ) ( K ( ) ) ( ) n n n n n sind sämliche Anfangsbedingungen f (i) () i...(n-) gleich Null, so folg: ( n ) n LT{ f ( ) } F( ) Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 7
9 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.3 Korresondenzabelle Nr. F() f() 3 n 4 + a 5 ( + a) 6 + ω ( ) δ ( ) σ ; ; ; ; < n ( n )! a e a ( e a ) cos(ω) "Dela-Imuls" "Einheissrung" 7 ω + ω 8 9 (*) (*) 3 ( + a) ( + b) ( + a) n ; n > ( + a) n + a + b + a + b (*) ( + a + b ) b w e ω e sin(ω) b e a b n ( n ) a e! n ( a) n a i i! [ e e ] a für a i e a D a b sin( ω) für D < [ e e ] w a e cos a ω für D > a b > ( ω) sin( ω) für D < w e w e für D a + > b a a ( ) ( ) e für D b cos ω sin ω < < ω (*) Abkürzungen: w a b ; ω b a ;, a ± w a ± jω Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 8
10 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion Herleiung einiger Korresondenzen Nr. 4: Dämfungssaz mi f() σ() f. > (Einheissrung) LT{ σ ( ) } F( ) (s.o., Beisiel zum Einheissrung) a { σ( )} ( ) LT e F + a + a σ a a Nr. 5: f ( ) ( e ) ( ) f /a LT e a a { } a a ( ) ( ) LT{ ( ) } σ σ LT{ e σ ( ) } a a + a a + a + a ( ) ( ) Nr. 6: f ( ) cos( ω) σ ( ) f ( ) ( e j ω jω + e ) σ ( ) [ ] jω jω LT{ cos( ω) } LT{ e } + LT{ e } + jω + jω + ω { } LT cos( ω) + ω Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 9
11 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion Nr. 3: für n "Ramenfunkion" f() f ( ) σ ( ) LT{ σ ( ) } e d In.regel: u dv u v v du seze dv e d u. u e v du d e LT{ σ ( ) } + e d lim( e ) lim lim e L' Hosial e e LT{ σ ( ) } Übungsaufgabe: Bie leien Sie die allgemeine Form für n her! (Ti: sukzessive Anwendung der Inegraionsregel (u,v), vgl. Herleiung des Differeniaionssazes) Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
12 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.4 Beisiele.3.4. Verzögerer Srung f() A ( ) f A ; T ; < T T o a) Lösung mi Lalace-Inegral (l. Definiion): A LT{ f ( ) } f ( ) e d A e d e A + e { ( )} A LT A T e σ T T T T b) Lösung mi Rechenregeln / Korresondenzabelle: σ() ο / (Korr.ab. Nr. ) f(-t) ο e -T F() (Verschiebungssaz) A f() ο A F() (Lin.saz mi f ) T LT{ Aσ ( T )} e A Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
13 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.4. Exonenialfunkion f() e a a bel. komlexe Zahl a ( a ) ( a ) F( ) e e d e d a e ( a ) lime a a a ( ) für Re a < Übung: leien Sie bie das Ergebnis mi Hilfe d. Korresondenzabelle her! Poenzfunkion f() F( ) e d e ² ² e + ( )² ( )³ ² ³ Bronsein ² lim e + ² ³ ³ ³ , da e ' sär ker' als ² vgl. Korresondenzabelle Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
14 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.5 Periodische Funkionen Transformiere einer eriodischen Funkion f() mi Periodendauer T f() Definiion einer eriodischen Fk.: f(-kt) f() F( ) T f ( ) e e 4 34 Periodiziä T d mi f( < ) T vgl. nich eriodische Funkion: F( ) f ( ) e d Beisiel: Rechecksignal f() < < T / f ( ) T / < < T T/ T T/ T F( ) e d e d e e e T + T T/ T/ T/ ( ) e e T/ e T T/ ( e ) ( a ²) ( a)( + a) e T / T/ T / ( )( + ) e e / T/ e + e T ( + ) Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 3
15 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.6 Lalace-Rückransformaion { ( )} ( ) ( ) LT F f F e d jπ Inegraion um alle (i.a. komlexen) Pole von F() z.b. σ + j o f ( ) F( ) e d π j σ j o Inegraion of "schwer" durchzuführen Praxis: Korresondenzabelle Beisiel: F( ) + 5 ² + + umformen: ² ( )² 9 ( + )² + 3² 3 ( + )² + 3² Korresondenzen aus Tabelle: cos(ω) sin(ω) ² +ω ² ω ² + ω ² mi + ω 3 mi + ω 3 Dämfungssaz e -a f() F(+a) hier: + a f() [cos(3) + 4/3 sin(3)]e - Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 4
16 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.6. Parialbruchzerlegung sehr hilfreich, um gebrochen raionale Funkionen F() miels Korresondenzabelle rückzuransformieren auch hilfreich bei Inegraion gebr. ra. Funkion wird in Summe von kleineren Brüchen umgeform allgemein: Z( x) f ( x) N( x) n anx ax + a m x b x + b o o mi n < m ; m, n N ; a i, b i R ; a n (b m durch Kürzen) Prinzi (zunächs rückwärs) 3 3 x 5 x 5x x + x + 5 ( + ) + ( ) + ( x )( x + 5) x² + 3x < Parialbruchzerlegung Ziel: Fakorzerlegung Nenner N(x) (x - x )(x - x ) (bei quadraischem Nenner) Bem.: Parialbruchzerlegung grundsäzlich immer möglich! Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 5
17 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion Vorgehensweise: Z( x) f ( x) N( x). Besimme Nullsellen des Nennerolynoms N(x). Jeder Nullselle wird ein Parialbruch zugeordne. Ansaz: a) x einfache reelle Nullselle A x x b( x) b) x zweifache reelle Nullselle A x x A + ( x x )² b( x) c) x r-fache reelle Nullselle A A A r x x ( x x )² x x r ( ) b( x) d) komlexe Nullsellen relaiv komlizier A i unbekann zu besimmende Konsanen 3. f ( x) b ( x) N i i mi N: Anzahl der Nullsellen des Nennerolynoms 4. Besimmung der Konsanen A i : alle Brüche auf Haunenner bringen geeignee x-were einsezen, z.b. Nennernullsellen, ergib Lineares Gleichungssysem Lösung des LG mi Gauß oder Koeffizienenvergleich Anm.: f(x) mi Nennerolynomen der Form N(x) (x + ax + q) r können auch d. den Ansaz f ( x) B x + C B x C x + ax + q + + Br x + Cr + K + zerleg werden. ( x + ax + q) ( x + ax + q) r Besimmung der B i, C i über z.b. Koeffizienenvergleich. Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 6
18 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.6. Beisiele zur Parialbruchzerlegung a) einfache Nullsellen f ( x) 5x + Z( x) x² + 3x N ( x). Besimme Nullsellen N(x) x² + 3x - x 3 ± / ± x + x -5 N(x) (x-)(x+5) Probe: x² - x + 5x - x² + 3x -. Zuordnung Parialbruch x + : A A b ( x) x x x x -5 : b ( x) B x + 5 A B 3. Parialbrüche f ( x) bi ( x) + x x + 5 i 4. Besimmung der Konsanen f ( x)! A( x + 5) + B( x ) Ax + 5A + Bx B 5x + ( x )( x + 5) x² + 3x x² + 3x ( A + B) x + ( 5A B) 5x + (*)! Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 7
19 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion Mehode : Koeffizienenvergleich mi (*) A + B 5 (i) 5A - B (ii) A 5 - B (i ) (i ) in (ii) : 5(5-B) - B 5-5B - B -7B -4 B A 3 5x + 3 x² + 3x x + x + 5 Mehode : geeignee x-were einsezen x kann beliebig sein, z.b. Nullsellen von N(x) mi (*): x : (A+B) + (5A-B) + A + B + 5A - B 7A A 3 s.o. x -5 : (A+B)(-5) + (5A-B) A - 5B + 5A - B -4 B s.o. z.b. Anwendung Inegraion: 5x + dx x² + 3x 3 dx 3 x x 5 x + ln + ln + x + 5 Übung: x 9 3 x² x 4 ( x + 4) ( x 6) Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 8
20 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion b) zweifache Nullsellen f ( x) x 5 Z( x) x² 6x + 9 N ( x). Besimme Nullsellen N(x) x² - 6x x / + ± 3 x x 3 N(x) (x-3). Zuordnung Parialbruch A A x x 3 : b ( x) + x 3 ( x 3)² A A 3. Parialbrüche f ( x) b( x) + x 3 ( x 3)² 4. Besimmung der Konsanen A ( x 3) + A f ( x) ( x 3)² A x 3A + A x 5! (*) Mehode : Koeffizienenvgl. mi (*) A 3. - A 5 A - f ( x) x 5 x² x + x ( x 3)² Mehode : geeignee x-were mi (*) x 3 : 3A - 3A + A 3-5 A - s.o. A : A x - 3A - x - 5 A (x - 3) x - 3 A s.o. Übung: 5x² + 6x x³ + 3x² 4 x ( x + ) ( x + )² Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) 9
21 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.7 Anwendungsbeisiele.3.7. Differenialgleichung erser Ordnung Ein Körer beweg sich mi der Anfangsgeschwindigkei v horizonal in einer reibungsbehafeen Flüssigkei: k &v + m v Anfangsbedingung: v() v o mahemaisch: y + a y mi a k/m Anfangsbed.: y(x) y o. Lalace-Transformaion aus Rechenregeln: F() - y() + a F(). Lösen im Bildbereich F() ( + a) y() (Anfangsbed. bereis berücksichig!) F( ) y( ) + a 3. Rückransformaion aus Korresondenzabelle (Nr. 4) e -a / +a y y() e -a hysikalische Größen: v v v o e -(k/m) v o k/m Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
22 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion.3.7. Differenialgleichung. Ordnung RLC in Reihenschalung mi lözlich angeleger äußerer Sannung U (σ - Imuls, Einheissrung) L && R I & & ( ) L I C L I L U + + L U o δ Anfangsbedingung: ( ) ; I ( ) I & U o R C mahemaisch: y + d y + ω o ²y b o δ() Anf.bed.: y(x) y () mi y I ; d R/L ; ω /LC ; b U /L. Lalace-Transformaion aus Rechenregeln: ² F() - y() - y () + d F() - d y() + ω o ² F() b o. Lösen im Bildbereich mi Anf.bed.: ² F() + d F() + ω o ² F() b o F() {² + d + ω o ²} b o F( ) bo ² + d +ω o auch hier 3 Fälle im Nenner! (vgl. Ka..3.6) im weieren: gedämfer Schwingfall angenommen Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
23 Vorlesungsskri "Mahemaik : Fourier- und Lalace-Transformaion", Teil 3: Lalace-Transformaion 3. Rückransformaion Korresondenzabelle Nr. : ο + a + b w e ω [ e e ] a für D a b sin( ω) für D < > d R C hier: a d ; b ω gedämfe Schwingung: D < ω L b e sin mi ω ω ω R a LC L a f ( ) ( ω ) R U Lω e o L hysikalische Größen: I( ) sin( ω ) Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner)
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Fourier- und Laplace- Transformation
 Skriptum zur Vorlesung Mathematik für Ingenieure Fourier- und Laplace- Transformation Teil : Fourier-Transformation Prof. Dr.-Ing. Norbert Höptner (nach einer Vorlage von Prof. Dr.-Ing. Torsten Benkner)
Skriptum zur Vorlesung Mathematik für Ingenieure Fourier- und Laplace- Transformation Teil : Fourier-Transformation Prof. Dr.-Ing. Norbert Höptner (nach einer Vorlage von Prof. Dr.-Ing. Torsten Benkner)
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Fourier- und Laplace- Transformation
 Übungsaufgaben zur Vorlesung Mathematik für Ingenieure Fourier- und Lalace- Transformation Teil : Lalace-Transformation Prof. Dr.-Ing. Norbert Hötner (nach einer Vorlage von Prof. Dr.-Ing. Torsten Benkner)
Übungsaufgaben zur Vorlesung Mathematik für Ingenieure Fourier- und Lalace- Transformation Teil : Lalace-Transformation Prof. Dr.-Ing. Norbert Hötner (nach einer Vorlage von Prof. Dr.-Ing. Torsten Benkner)
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Der kinetische Ansatz zur Beschreibung von Selbstorganisationsprozessen. mögliche Variationen und Erweiterungen: diskrete Gleichungen (endliches t):
 Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
5. Signalverarbeitung
 5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Bildmaterial zur Vorlesung Regelungstechnik Teil I Die Regelstrecke. Wintersemester 2014 Prof. Dr.-Ing. habil. Klaus-Peter Döge
 Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
7. Funktionalgleichung der Zeta-Funktion
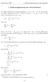 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
7. Gewöhnliche Differentialgleichungen
 1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
um (x + X) 4 auszurechnen verwenden wir den Binomischen Lehrsatz (a+b) n = a n + ( n 1 )a n-1* b 1 + + b n ( n k ) = in Gleichung einsetzen
 Mahemaik I Übungsaufgaben 8 Lösungsorschläge on T. Meyer Era-Mahemaik-Übung: 005--06 Aufgabe Berechnen Sie die Ableiung der Funkion f an einer beliebigen Selle 0 ohne Verwendung irgendwelcher Vorkennnisse
Mahemaik I Übungsaufgaben 8 Lösungsorschläge on T. Meyer Era-Mahemaik-Übung: 005--06 Aufgabe Berechnen Sie die Ableiung der Funkion f an einer beliebigen Selle 0 ohne Verwendung irgendwelcher Vorkennnisse
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
Grundlagen der Nachrichtentechnik 1 Communications 1
 Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Kapitel 2: Fourieranalyse. Analoge, nichtperiodische Signale
 ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
(10 Punkte) Gegeben ist die in Fig. 1 abgebildete in T periodische Zeitfunktion f(t). f(t)
 H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
mathphys-online Abschlussprüfung Berufliche Oberschule 2009 Mathematik 12 Technik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die reelle Funktion f( x)
 Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Aufgabe 1: Kontinuierliche und diskrete Signale
 Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
λ + ω 0 2 = 0, Lösung: λ 1,2
 SDOFs Der lineare Einassenschwinger Bewegungsgleichung!!x + c!x + k x = f () = p()...krafanregung!!x g ()...Weganregung!!x + ζω!x + ω x = f (), ω = k, ζ = c k... Lehr'sches Däpfungsaß AB : x( = ) = x,!x(
SDOFs Der lineare Einassenschwinger Bewegungsgleichung!!x + c!x + k x = f () = p()...krafanregung!!x g ()...Weganregung!!x + ζω!x + ω x = f (), ω = k, ζ = c k... Lehr'sches Däpfungsaß AB : x( = ) = x,!x(
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
4.2.5 Energie und Energiedichte im Magnetfeld
 4..5 Energie und Energiediche im Magnefeld - die magneische Energie W ui dψ ( ) i i d m ψ ψ Ψ d dw mag V dφ V V Φ Wmag V ( Φ ) dφ Tuorium jeweils Miwoch 3: Uhr Hu - die Energiediche im magneischen Feld
4..5 Energie und Energiediche im Magnefeld - die magneische Energie W ui dψ ( ) i i d m ψ ψ Ψ d dw mag V dφ V V Φ Wmag V ( Φ ) dφ Tuorium jeweils Miwoch 3: Uhr Hu - die Energiediche im magneischen Feld
Näherung einer Wechselspannung
 HL Seyr Wechselsromparabel Seie 1 von 1 Nieros Bernhard bernhard.nieros@hl-seyr.ac.a Näherung einer Wechselspannung Mahemaische / Fachliche Inhale in Sichworen: Polynomfunkion, allgemeine Sinusschwingung,
HL Seyr Wechselsromparabel Seie 1 von 1 Nieros Bernhard bernhard.nieros@hl-seyr.ac.a Näherung einer Wechselspannung Mahemaische / Fachliche Inhale in Sichworen: Polynomfunkion, allgemeine Sinusschwingung,
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Lösungen Test 2 Büro: Semester: 2
 Fachhochschule Nordwesschweiz (FHNW) Hochschule für Technik Insiu für Geises- und Naurwissenschaf Dozen: Roger Burkhard Klasse: Sudiengang ST Lösungen Tes Büro: 4.613 Semeser: Modul: MDS Daum: FS1 Bemerkungen:
Fachhochschule Nordwesschweiz (FHNW) Hochschule für Technik Insiu für Geises- und Naurwissenschaf Dozen: Roger Burkhard Klasse: Sudiengang ST Lösungen Tes Büro: 4.613 Semeser: Modul: MDS Daum: FS1 Bemerkungen:
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
3.1 Grundlagen. Grundbegriffe (Forts.) Grundbegriffe
 Beriebssyseme II - Analyse und Modellierung Sommersemeser 208 3. Grundlagen Moivaion 3. Grundlagen Beriebssyseme II - Analyse und Modellierung 3. Kapiel Grundlagen der Sochasik Prof. Mahias Werner Professur
Beriebssyseme II - Analyse und Modellierung Sommersemeser 208 3. Grundlagen Moivaion 3. Grundlagen Beriebssyseme II - Analyse und Modellierung 3. Kapiel Grundlagen der Sochasik Prof. Mahias Werner Professur
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
mathphys-online Abiturprüfung Mathematik 13 Technik Differentialgleichungen in Anwendungen - Lösung Aufgabe 1: Abi 1999 / AI
 mahphys-online Abiurprüfung Mahemai 3 Techni Differenialgleichungen in Anwendungen - ösung Aufgabe : Abi 999 / AI Ein erhizer Körper ühl sich im aufe der Zei allmählich auf die onsane Temperaur a (in C)
mahphys-online Abiurprüfung Mahemai 3 Techni Differenialgleichungen in Anwendungen - ösung Aufgabe : Abi 999 / AI Ein erhizer Körper ühl sich im aufe der Zei allmählich auf die onsane Temperaur a (in C)
2. Grundlagen Schwingungslehre
 Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Korrespondenzen der FOURIER - Transformation I
 Korresodee der FOURIER - rsormio I A: HEOREME s() S() F-rsormio s () jπ S( ) = s e d Iverse F- jπ rsormio s () = S e d S( ) 3 Zerlegug reeller Zeiukioe mi s () = s() + s() S( ) = Re{ S( )} + jim{ S( )}
Korresodee der FOURIER - rsormio I A: HEOREME s() S() F-rsormio s () jπ S( ) = s e d Iverse F- jπ rsormio s () = S e d S( ) 3 Zerlegug reeller Zeiukioe mi s () = s() + s() S( ) = Re{ S( )} + jim{ S( )}
Gewöhnliche Differentialgleichungen - Abiturprüfungsaufgaben mit Anwendungen -
 Aufgabe : Abi 999 / AI Gewöhnliche Differenialgleichungen - Abiurprüfungsaufgaben mi Anwendungen - Ein erhizer Körper ühl sich im aufe der Zei allmählich auf die onsane Temperaur a (in C) seiner Umgebung
Aufgabe : Abi 999 / AI Gewöhnliche Differenialgleichungen - Abiurprüfungsaufgaben mi Anwendungen - Ein erhizer Körper ühl sich im aufe der Zei allmählich auf die onsane Temperaur a (in C) seiner Umgebung
Physik 1 ET, WS 2012 Aufgaben mit Lösung 1. Übung (KW 43) Schwingender Körper ) Notbremse ) Stahlkugel )
 1. Übun KW 43) Aufabe 1 M 1. Schwinender Körper ) Ein schwinender Körper ha die Geschwindiei v x ) = v m cosπ ). Er befinde T sich zur Zei 0 = T am Or x 4 0. Geben Sie den Or x und die Beschleuniun a x
1. Übun KW 43) Aufabe 1 M 1. Schwinender Körper ) Ein schwinender Körper ha die Geschwindiei v x ) = v m cosπ ). Er befinde T sich zur Zei 0 = T am Or x 4 0. Geben Sie den Or x und die Beschleuniun a x
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Vorkurs Mathematik-Physik, Teil 6 c 2016 A. Kersch
 Vorkurs Mahemaik-Physik, Teil 6 c 6 A. Kersch Kinemaik In der Kinemaik geh es um die Frage: wie kann ich Bewegungen, also Bahnen von punkförmigen (Kinemaik der Translaion) oder ausgedehnen Körpern (Kinemaik
Vorkurs Mahemaik-Physik, Teil 6 c 6 A. Kersch Kinemaik In der Kinemaik geh es um die Frage: wie kann ich Bewegungen, also Bahnen von punkförmigen (Kinemaik der Translaion) oder ausgedehnen Körpern (Kinemaik
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Traktrix DEMO. Text Nr Stand 11. Mai 2016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Trkri Te Nr. 540 Snd. Mi 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mhe-cd.de 540 Trkri Vorwor Die Trkri is eine Kurve für gehobenemhemische Ansprüche. Ineressn is schon ihre mechnische
Trkri Te Nr. 540 Snd. Mi 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mhe-cd.de 540 Trkri Vorwor Die Trkri is eine Kurve für gehobenemhemische Ansprüche. Ineressn is schon ihre mechnische
Fokker-Planck-Gleichung
 Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Durch Modellierung beschreibt man Vorgänge aus der Natur sowie industrielle Prozesse
 Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Fourier-Transformation Linearität, Symmetrie, Verschiebung, Skalierung, Faltung, Modulation
 Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
Konjunkturtheorie (Stand: )
 Konjunkurheorie (Sand: 18.11.2009) Prof. Dr. Kai Carsensen, LMU und ifo Insiu Seffen Elsner, ifo Insiu Schwerpunk Dynamische Modelle in diskreer Zei mi konsanen Inpus Lösung linearer Differenzengleichungssyseme
Konjunkurheorie (Sand: 18.11.2009) Prof. Dr. Kai Carsensen, LMU und ifo Insiu Seffen Elsner, ifo Insiu Schwerpunk Dynamische Modelle in diskreer Zei mi konsanen Inpus Lösung linearer Differenzengleichungssyseme
Stammgruppe trifft sich zum Museumsrundgang Experte erklärt jeweils sein Plakat
 Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Ganzrationale Funktionen (Polynomfunktionen) - Berechnung von Nullstellen, Gleichungen höheren Grades -
 GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
4.7. Exponential- und Logarithmusfunktionen
 ... Eonenialfunkionen Definiion:.. Eonenial- und Logarihmusfunkionen Die Funkion f() = c a mi D = R, c und a R + \{}heiß Eonenialfunkion zur Basis a. Die Eonenialfunkion zur Basis a = e mi der Eulerschen
... Eonenialfunkionen Definiion:.. Eonenial- und Logarihmusfunkionen Die Funkion f() = c a mi D = R, c und a R + \{}heiß Eonenialfunkion zur Basis a. Die Eonenialfunkion zur Basis a = e mi der Eulerschen
Abschlussprüfung an Fachoberschulen in Bayern Mathematik mit CAS 2015 Analysis A2 Ausbildungsrichtung Technik
 MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
Mathematik für Physiker I
 Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Freie Schwingung - Lösungsfälle
 Freie Schwingungen Seie von 6 Peer Schüller peer.schueller@bbw.gv.a Freie Schwingung - Lösungsfälle Maheaische / Fachliche Inhale in Sichworen: Differenialgleichung.Ornung i onsanen Koeffizienen, Schwingung
Freie Schwingungen Seie von 6 Peer Schüller peer.schueller@bbw.gv.a Freie Schwingung - Lösungsfälle Maheaische / Fachliche Inhale in Sichworen: Differenialgleichung.Ornung i onsanen Koeffizienen, Schwingung
Vielseitige Darstellungen von Drehstromsignalen
 Vielseiige Darsellungen von Drehsromsignalen Die Leisungs- und Energie-Analysaoren Qualisar+ dienen zur soforigen Darsellung aller wesenlichen Eigenschafen eines Drehsromnezes. Zeiliche Darsellung Die
Vielseiige Darsellungen von Drehsromsignalen Die Leisungs- und Energie-Analysaoren Qualisar+ dienen zur soforigen Darsellung aller wesenlichen Eigenschafen eines Drehsromnezes. Zeiliche Darsellung Die
Lösung 05 Klassische Theoretische Physik I WS 15/16. y a 2 + r 2. A(r) =
 Karlsruher Institut für Technologie Institut für theoretische Festkörperphsik www.tfp.kit.edu Lösung Klassische Theoretische Phsik I WS / Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler Besprechung...
Karlsruher Institut für Technologie Institut für theoretische Festkörperphsik www.tfp.kit.edu Lösung Klassische Theoretische Phsik I WS / Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler Besprechung...
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
1. Schularbeit (6R) 24. Okt. 1997
 . Schularbei (6R). Ok. 997. Vereinfache und selle das Ergebnis mi posiiven Hochzahlen dar. Es sind dabei alle Rechenschrie anzugeben: 7 x x y 8 : x x y. Löse die folgende Wurzelgleichung ohne Verwendung
. Schularbei (6R). Ok. 997. Vereinfache und selle das Ergebnis mi posiiven Hochzahlen dar. Es sind dabei alle Rechenschrie anzugeben: 7 x x y 8 : x x y. Löse die folgende Wurzelgleichung ohne Verwendung
Anfangswertprobleme gewöhnlicher Differentialgleichungen
 13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Formelanhang Mathematik II
 Formelanhang Mathematik II Mechatronik 2. Sem. Prof. Dr. K. Blankenbach Wichtige Formeln: - Euler: e j = cos() + j sin() ; e -j = cos() - j sin() - Sinus mit Phase: Übersicht Differentialgleichungen (DGL)
Formelanhang Mathematik II Mechatronik 2. Sem. Prof. Dr. K. Blankenbach Wichtige Formeln: - Euler: e j = cos() + j sin() ; e -j = cos() - j sin() - Sinus mit Phase: Übersicht Differentialgleichungen (DGL)
HTW. Probe-Klausur (und klausurvorbereitende Übungsaufgaben) Angewandte Mathematik MST
 HTW Probe-Klausur (und klausurvorbereitende Übungsaufgaben) Angewandte Mathematik MST Dauer : 100 Minuten Prof. Dr. B. Grabowski Name: Matr.Nr.: Erreichte Punktzahl: Hinweise zur Bearbeitung der Aufgaben:
HTW Probe-Klausur (und klausurvorbereitende Übungsaufgaben) Angewandte Mathematik MST Dauer : 100 Minuten Prof. Dr. B. Grabowski Name: Matr.Nr.: Erreichte Punktzahl: Hinweise zur Bearbeitung der Aufgaben:
Flugzeugaerodynamik I Lösungsblatt 2
 Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Merkmale flexibler Fertigung
 FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Signale und Systeme I
 TECHNISCHE FAKULTÄT DER CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITALE SIGNALVERARBEITUNG UND SYSTEMTHEORIE DSS Signale und Systeme I Formelsammlung v.5 Inhaltsverzeichnis Mathematische Formeln. Trigonometrische
TECHNISCHE FAKULTÄT DER CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITALE SIGNALVERARBEITUNG UND SYSTEMTHEORIE DSS Signale und Systeme I Formelsammlung v.5 Inhaltsverzeichnis Mathematische Formeln. Trigonometrische
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Systemtheorie I WS 04/05 Prof. Dr.-Ing. habil. Hoffmann, TU Dresden Mitschrift. Fabian Kurz
 Sysemheorie I WS 4/5 Prof Dr-Ing habil Hoffmann, TU Dresden Mischrif Fabian Kurz hp://fkurzne/ Zulez akualisier: 5 Mai 25 Inhalsverzeichnis Einführung Inhal des Lehrgebiees 2 Soffeineilung 3 Lieraur Teil
Sysemheorie I WS 4/5 Prof Dr-Ing habil Hoffmann, TU Dresden Mischrif Fabian Kurz hp://fkurzne/ Zulez akualisier: 5 Mai 25 Inhalsverzeichnis Einführung Inhal des Lehrgebiees 2 Soffeineilung 3 Lieraur Teil
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
