e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
|
|
|
- Kevin Geiger
- vor 5 Jahren
- Abrufe
Transkript
1 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion L[y(x)] e x y(x)dx Mehoden zur Beimmung der Laplace Tranformieren Direk gemä der Definiion 2 Direk gemä der Definiion uner Verwendung der in der Vorleung angeführen Eigenchafen 3 Mehode der Reihenenwicklung: Durch Einezen der Poenzreihe von y(x), y(x) k a kx k, in da Inegral und gliedweier Inegraion erhäl man k!a k k+ k (Die gliedweie Inegraion i erlaub, wenn die Reihe der Tranformieren für > γ konvergier) Beipiel: J i die Beel Funkion der Ordnung Null, dh: Dann folg: n (2n)!( ) n 2 2n n!n! y(x) J (x) 2n+ n ( ) n x 2n 2 2n n!n! n (2n )(2n 3)3 ( ) n 2 n n! 2n ( ) ( ) n 2 n n 2 +
2 4 Verwendung der Differenialgleichung von y(x): I die Laplace Tranformiere von y(x) zu berechnen, o ha man alo eine Dgl mi Anfangweren, welche y(x) erfüll, zu beimmen und die Dgl nach Laplace zu ranformieren Beipiel: Beimme L[y(x)] für y(x) in( x) Mi y (x) 2 x co( x) und y (x) 4x x co( x) 4x in( x) erhäl man die Dgl 4xy + 2y + y Der AW i y() (iehe Angabe) Die Laplace Tranformaion der Dgl liefer: 4 d d ( 2 F () f() f () ) + 2 (F () f()) F + (6 )F Trennung der Variablen und Inegraion liefern C e /4 3/2 Um die Inegraionkonane zu beimmen, verwende man den verallgemeineren Anfangweraz ( L[f(x)] und G() L[g(x)]): f(x) lim x g(x) F () lim G() Dami der Lime von F einen konanen Wer ergib, mu G() C G / 3/2 Wir wählen alo g(x) x, womi man G() L[ x] 2 π 3/2 erhäl Darau folg: F () lim G() lim C 3/2 e /4 2 π 3/2 C 5 Differeniaion bzw Inegraion nach einem Parameer: π 2 L[in( x)] π 2 3/2 e /4 Wenn y(x, a) von einem Parameer a abhängig i, dann folg au F (, a) L[y(x, a)] durch Differeniaion nach a: [ ] y(x, a) F (, a) L a a bzw durch Inegraion nach a: [ a ] L y(x, ã)dã a a a F (, ã)dã Beipiel: Beimme die Laplace Tranformiere von y(x) x co( ax) Gemä dem lezen Beipiel gil nach dem Ähnlichkeiaz, dh L[y(x)] L[y(ax)] F ( ), a con: a a L[in( aπ ax)] 2 3/2 e a/4 Differeniaion nach dem Parameer a liefer: Darau folg: L[ x co( ax) 2 ] a π 4 a 3/2 e a/4 L[ x co( ax)] aπ 2 3/2 4 e a/4 π(2 a) 4 5/2 e a/4 π(2 a) 8 a 5/2 e a/4
3 Aufgabe: Berechne L[ co( ax) x ] durch Inegraion von L[in(a x)] nach a Löung: ( ) π exp a2 4 6 Verwendung von Tabellen und Compuerprogrammen Anfang- und Grenzweräze Dabei i: L[f(x)] und G() L[g(x)] Zunäch gil: lim Anfangweräze: x f(x) lim F () x f (x) lim ( 2 F () f()) x f (n) (x) lim ( n+ F () n f() n f () f (n ) () ) f(x) x g(x) Grenzweräze: F () lim G() x f(x) lim F () F () G() f(x) lim x g(x) verallgemeinerer Anfangweraz verallgemeinerer Grenzweraz BEISPIELE Beimme die Laplace Tranformiere der Funkion f() e co Löung: (a) Direk: L[f()] e (+) co d Für par die Inegraion mi u und v e (+) co und noch eine weiere par Inegraion benöig man da Inegral I e α [a co(β) + b in(β)]d eα [(αa βb) co(β) + (αb + βa) in(β)], α 2 + β2
4 welche durch zweimalige par Inegraion herleibar i Speziell mi folg dann α ( + ), β, a und b e (+) co d e (+) ( + ) 2 + Durchführung der par Inegraion im Inegral für F () liefer: [ ( + ) co() + in()] e (+) ( + ) 2 + [ ( + ) co + in ] ( + ) 2 + e (+) [ (+) co +in ]d Au I erhäl man mi den Parameern α ( + ), β, a ( + ) und b für da leze Inegral: { } e (+) ( + ) 2 + ( + ) 2 + [( + )2 ] co + [ ( + ) ( + ) in ] ( + )2 [( + ) 2 + ] 2 (b) Miel verchiedener Eigenchafen der Laplace Tranformaion: Mi g(), g() e co folg: G () Weier folg mi g() e co und h() co : G() H( + ) nach dem Dämpfungaz und wegen L[co ] /( 2 + ) erhäl man d d + ( + ) 2 + ( + )2 [( + ) 2 + ] 2 2 Beimme die Laplace Tranformiere der Funkion Löung: f() coh(a) + a 2 inh(a), a R Wegen der Lineariä der Laplace Tranformaion gil L[f()] L[coh(a)] + a L[ inh(a)] 2 und weier wegen L[g()] G (), owie wegen L[coh(a)] /( 2 a 2 ) und L[inh(a)] a/( 2 a 2 ): 2 a a ( ) d a d 2 a 2 ( 2 a 2 ) 2 3 Beimme die Laplace Tranformiere de Inegral-Sinu: Si() : in τ τ dτ
5 Löung: Wegen dem Inegralaz und wegen [ ] L f(τ)dτ F () [ ] g(τ) L τ G(σ)dσ (iehe Vorleung) folg dann mi g(τ) in τ und L[in τ] /(σ 2 + ): L[Si()] dσ σ 2 + ( π 2 arcan ) arcco 4 Beimme die Laplace Tranformiere der Funkion { c für a f() für > Löung: L[f()] e f() d a e c d c [ e a ] 5 Beimme die Laplace Tranformiere der Funkion Löung: f() e c, c < Mi der Subiuion τ 2 geh da Laplace Inegral in L[f()] 2 über Quadraiche Ergänzung im Exponenen liefer e c/ d e τ 2 c/τ 2 dτ 2e 2 c Da vorliegende Inegral i vom Typ e ( τ c/τ) 2 dτ I(a, b) e (ax b/x)2 dx
6 (Erlaube) Differeniaion nach b liefer I ( b ( 2) ax b ) ( ) x x e (ax b/x)2 dx 2 4aI 2 (a + bx 2 ) e (ax b/x)2 dx [ 2a (a + bx )] e (ax b/x)2 dx 2 Subiuion: ξ(x) ax b/x (dξ/dx a + b/x 2 (an den Grenzen: ξ() und ξ( ) ) (a + bx ) e (ax b/x)2 dx e ξ2 dξ π 2 Dami erhäl man für I die gew Dgl mi der allgemeinen Löung I b 4aI 2 π, I(a, b) C(a)e 4ab + π/(2a) Um die Inegraionkonane zu beimmen, ez man b und erhäl I(a, ) e a2 x 2 dx C(a) + π/(2a) Da da Inegral den Wer π/(2a) ha, i C(a), womi folg I(a, b) e (ax b/x)2 dx π 2a Dami erhäl man mi a und b c : π c e 2 6 Beimme Löung: [ ] f() L Die raionale Funkion F () wird in Parialbrüche zerleg: Wegen der Lineariä der Umkehrranformaion folg f() L [F ()] [ ] 2 L + 2 [ ] 3 L + 5 [ ] + 6 L e e2
7 7 Beimme f() o, da gil L[f()] + 2 e Löungweg : E gil: + e d e 2 d, worau wegen L[h()] H () mi H() e / zunäch f() h() folg Zur Beimmung von h() verwende man die Lineariä : [ ] [ ] [ ] [ ] e L e L e + L L + Verwende man Beipiel 4, o gil: [ ] e L { für für > Ingeam erhäl man f() { für für > Löungweg 2: Wegen der Lineariä gil L [ + 2 Für den eren Aneil gil (iehe oben): ] [ ] [ ] e L e + L 2 e L [ e ] { für für > Den zweien Aneil zerleg man muliplikaiv und verwende den Falungaz 2 e P ()Q(), P (), Q() [ ] e L 2 e p() q() : g() Dabei i p() L [/] und q() L [e /] (iehe oben) Nach dem Falungaz i dann g() q(τ)dτ Für [, ] i dann g() und für > gil dτ Ingeam folg dann: { für f() für >
8 8 Beimme jene Funkion f(), deren Laplace Tranformiere durch gegeben i Löungweg: Wegen a b, < a < b, a b 2 (iehe Vorleung) erhäl man dann: f() ( fa () 2 [ ] g() L f ) b() ( ) dσ σ a σ b G(σ)dσ [ ], f c () : L c Wegen L [/ ] / π folg dann ingeam uner Verwendung de Dämpfungaze: [ ] f() L a b 2 π 3 [ea e b ] 9 Beimme die Funkion f(), deren Laplace Tranformiere i ( a) 3, a R Löungweg: ( a) + a a + 2a d ( ) ( a) 3 a ( a) 3 a d a Wegen L[g()] G () erhäl man mi Verwendung de Dämpfungaze, owie wegen L [/ ] / π [ ] f() L ( + 2a) ea ( a) 3 π Beimme die Funkion f(), deren Laplace Tranformiere ( ) a ln, a, b R, b i Löungweg: ln ( ) a b ( σ b ) dσ σ a
9 Wegen folg worau man erhäl [ ] g() G(σ)dσ L [ g() L b ] e b e a, a f() eb e a Beimme jene Löung y() der Dgl y 2y 4y, < <, die den Anfangbedingungen y() 3, y () 2 und y () genüg mi Hilfe der Laplace Tranformaion Löungweg: Die Laplace Tranformiere der Dgl: L[y ()] 2L[y ()] 4L[y()] Sez man Y () : L[y()], o folg darau wegen der Relaionen L[y ()] 3 L[y()] 2 y() y () y () und L[y ()] L[y()] y() ( 3 4)Y () Y () ( + ) 2 + ( + ) 2 + Die Umkehrranformaion liefer uner Verwendung de Dämpfungaze und der Lineariä [ ] [ ] [ ] y() 2L + L + L 2e 2 + e co e in 2 ( + ) 2 + ( + ) Beimme jene Löung y() der Dgl y + y 2y in, < <, die den Anfangbedingungen y(), y () /2 genüg mi Hilfe der Laplace Tranformaion Löungweg: Seze: Y () : L[y()] Mi L[y ()] 2 L[y()] y() y () und L[y ()] L[y()] y() (uner Verwendung der Anfangwere) laue die Laplace Tranformiere der Dgl ( 2 + 2)Y () ( 2 + ) 2
10 Durch Vereinfachung und Parialbruchzerlegung folg darau Y () ( 2 + ) 2 Da die Umkehrranformaion linear i, ennimm man au der Tabelle der Laplace Tranformaion y() L [Y ()] e 2 + 2e in co + + co in 2 3 Auf einem harmonichen Ozillaor (zb ein Federpendel) mi der Mae m, der Kreifrequenz ω der Anfangaulenkung y owie der Anfanggechwindigkei v wirk ab eine äuere Kraf f() Die mahemaiche Modellierung ergib dann da AWP d 2 y d + 2 ω2 y f() m : g(), y() y, y () v Uner Verwendung der Laplace Tranformaion i die Löung diee AWP peziell für eine konane Kraf f zu beimmen Löungweg: Seze: Y () : L[y()], G() : L[g()] Weier gil: L[y ()] 2 L[y()] y() y () und L[y ()] L[y()] y() Wegen der Lineariä folg ( 2 + ω 2 )Y () y v + G() Y () x 2 + ω + v ω + G() ω 2 Verwende man die lineare Umkehrranformaion und den Falungaz, o folg bzw auführlich y() L [Y ()] x co(ω) + v ω in(ω) + ω y() x co(ω) + v ω in(ω) + ω I peziell f() f con, o folg mi g(τ) f /m: in(ω) g() in[ω( τ)]g()dτ y() x co(ω) + v ω in(ω) + f [ co(ω)] mω2 Bemerkung: Au der Löung ieh man, da e ich um eine harmoniche Schwingung um die neue Ruhelage handel Dabei bezeichne k die Federkonane, au der bekannlich ω k f f mω 2 k m folg
11 4 Beimme - uner Verwendung der Laplace Tranformaion - jene Löung x x(), y y() de Differenialgleichungyem ẋ x + y, ẏ 8x + 3y, da den Anfangbedingungen x() y() 2 genüg Löungweg: X() : L[x()], Y () : L[y()] Tranformier man die Dgln nach Laplace, o erhäl man Dh X 2 X + Y, Y 2 8X + 3Y ( )X Y 2, 8X + ( 3)Y 2 Al Löung diee algebraichen Gleichungyem erhäl man (nach Eliminaion bzw Gau- Algorihmu) X() Rückranformaion: und Y () x() e + e 5 und y() 2e + 4e 5
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Laplace Transformation
 Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
Prof. Dr. Michael Eiermann Höhere Mahemaik 3 (verief) Kapiel L Laplace Tranformaion Die Laplace Tranformaion verwandel Anfangwerprobleme für lineare Differenialgleichungen mi konanen Koeffizienen in algebraiche
Von der Fourier-Reihe zum Fourier-Integral
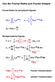 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
12.6 Aufgaben zur Laplace-Transformation
 292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
2.1 STURMSCHES ANFANGSWERTPROBLEM UND DGL 2. ORDNUNG
 . STURMSCHES ANANGSWERTPROBLEM UND DGL. ORDNUNG S o genanne Anfangwerprobleme reen ehr häufig bei naurwienchaflichen un echnichen Problemellungen auf. Hierbei hanel e ich in er Regel um DGL. Ornung oer.
. STURMSCHES ANANGSWERTPROBLEM UND DGL. ORDNUNG S o genanne Anfangwerprobleme reen ehr häufig bei naurwienchaflichen un echnichen Problemellungen auf. Hierbei hanel e ich in er Regel um DGL. Ornung oer.
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Fokker-Planck-Gleichung
 Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Fourier- und Laplace- Transformation
 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
Aufgabe 1: a) (i) und (ii) und (iv) 1 Punkt b) (i) 1 Punkt c) (i) 1 Punkt d) (iv) 1 Punkt e) (B) 1 Punkt f) (iv) 1 Punkt g) (i) und (ii) 2 Punkte h
 Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Aufgabe : a) i) un ii) un i) Punk b) i) Punk c) i) Punk ) i) Punk e) B) Punk f) i) Punk g) i) un ii) Punke i) un iii) un i) un ).5 lu.5 Punk Aufgabe : Venuri Ror Punke) a. Volumenrom Für ieen Aufgabeneil
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Eylert, Numerische Mathematik Kapitel 7
 Eyler, Numeriche Mahemaik Kapiel 7 7 aplace-tranformaion Moivaion Da öen linearer Differenialgleichungen i nich immer eine einfache Aufgabe. E gib viele öunganäze, die vor allem auch in der numerichen
Eyler, Numeriche Mahemaik Kapiel 7 7 aplace-tranformaion Moivaion Da öen linearer Differenialgleichungen i nich immer eine einfache Aufgabe. E gib viele öunganäze, die vor allem auch in der numerichen
7. Funktionalgleichung der Zeta-Funktion
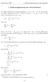 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
8.5 Uneigentliche Integrale Integrale über unbeschränkte Bereiche. f(x) dx. Integrale über unbeschränkte Funktionen mit Singularitäten am Rand
 8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Inhaltsübersicht. Funktionenraum Fouriertransformation Laplacetransformation Partialbruchzerlegung Faltung
 Inhalüberich Kapiel : Reihenenwicklungen und Tranformaionen: au x mach u und wieder zurück Funkionenraum Fourierranformaion Laplaceranformaion Parialbruchzerlegung Falung Noizen zur Vorleung Mahemaik für
Inhalüberich Kapiel : Reihenenwicklungen und Tranformaionen: au x mach u und wieder zurück Funkionenraum Fourierranformaion Laplaceranformaion Parialbruchzerlegung Falung Noizen zur Vorleung Mahemaik für
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
λ + ω 0 2 = 0, Lösung: λ 1,2
 SDOFs Der lineare Einassenschwinger Bewegungsgleichung!!x + c!x + k x = f () = p()...krafanregung!!x g ()...Weganregung!!x + ζω!x + ω x = f (), ω = k, ζ = c k... Lehr'sches Däpfungsaß AB : x( = ) = x,!x(
SDOFs Der lineare Einassenschwinger Bewegungsgleichung!!x + c!x + k x = f () = p()...krafanregung!!x g ()...Weganregung!!x + ζω!x + ω x = f (), ω = k, ζ = c k... Lehr'sches Däpfungsaß AB : x( = ) = x,!x(
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Partielle Differentialgleichungen
 Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
Partielle Differentialgleichungen Definition. Eine partielle Differentialgleichung ist eine Dgl., in der partielle Ableitungen einer gesuchten Funktion z = z(x 1, x 2,..., x n ) mehrerer unabhängiger Variabler
Zusammenfassung Analysis 3
 Zuammenfaung Analyi 3 Parik Rohner, rohnerpa@uden.ehz.ch 9. Januar 9 aplace - Tranformaion Die aplace Tranformaion i für folgendermaen definier: F () [f()] Originalfunkion f() n (n,,,...) n f() n f() f()
Zuammenfaung Analyi 3 Parik Rohner, rohnerpa@uden.ehz.ch 9. Januar 9 aplace - Tranformaion Die aplace Tranformaion i für folgendermaen definier: F () [f()] Originalfunkion f() n (n,,,...) n f() n f() f()
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Höhere Mathematik I für die Fachrichtung Physik
 Isiu für Aalysis SS7 Arbeisgruppe Agewade Aalysis 997 PD Dr Peer Chrisia Kusma Höhere Mahemaik I für die Fachrichug Physik Lösugsvorschläge zur Bachelor-Modulprüfug Aufgabe : (a) (i) Kurze Rechug liefer
Isiu für Aalysis SS7 Arbeisgruppe Agewade Aalysis 997 PD Dr Peer Chrisia Kusma Höhere Mahemaik I für die Fachrichug Physik Lösugsvorschläge zur Bachelor-Modulprüfug Aufgabe : (a) (i) Kurze Rechug liefer
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
D-HEST, Mathematik III HS 2017 Prof. Dr. E. W. Farkas M. Nitzschner. Lösung 7. Bitte wenden!
 D-HEST, Mathematik III HS 27 Prof. Dr. E. W. Farka M. Nitzchner Löung 7 Bitte wenden! . Wir betrachten ein Sytem linearer Differentialgleichungen erter Ordnung mit kontanten Koeffizienten der Form y (t)
D-HEST, Mathematik III HS 27 Prof. Dr. E. W. Farka M. Nitzchner Löung 7 Bitte wenden! . Wir betrachten ein Sytem linearer Differentialgleichungen erter Ordnung mit kontanten Koeffizienten der Form y (t)
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Übungen zum Ferienkurs Analysis II
 Übungen zum Ferienkurs Analysis II Implizite Funktionen und Differentialgleichungen 4.1 Umkehrbarkeit Man betrachte die durch g(s, t) = (e s cos(t), e s sin(t)) gegebene Funktion g : R 2 R 2. Zeigen Sie,
Übungen zum Ferienkurs Analysis II Implizite Funktionen und Differentialgleichungen 4.1 Umkehrbarkeit Man betrachte die durch g(s, t) = (e s cos(t), e s sin(t)) gegebene Funktion g : R 2 R 2. Zeigen Sie,
Laplace Transformation
 Department Mathematik der Univerität Hamburg SoSe 29 Dr. Hanna Peywand Kiani Laplace Tranformation Die in Netz getellten Kopien der Anleitungfolien ollen nur die Mitarbeit während der Verantaltung erleichtern.
Department Mathematik der Univerität Hamburg SoSe 29 Dr. Hanna Peywand Kiani Laplace Tranformation Die in Netz getellten Kopien der Anleitungfolien ollen nur die Mitarbeit während der Verantaltung erleichtern.
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
2.3 Schätzeigenschaften der OLS-Methode
 .3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
.3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
DIPLOMARBEIT. Titel der Diplomarbeit. Stochastische Differentialgleichungen: Erweiterung deterministischer Modelle um. Angestrebter akademischer Grad
 DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Lösungen zu Übungs-Blatt Differentialgleichungen 2. Ordnung und PBZ
 Prof.Dr. B.Grabowki Mathematik III/MST Übung Löungen Löungen zu Übung-Blatt Differentialgleichungen. Ordnung und PBZ Zu Aufgabe ) Geben Sie jeweil mindeten eine Löung folgender Differentialgleichung an
Prof.Dr. B.Grabowki Mathematik III/MST Übung Löungen Löungen zu Übung-Blatt Differentialgleichungen. Ordnung und PBZ Zu Aufgabe ) Geben Sie jeweil mindeten eine Löung folgender Differentialgleichung an
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Aufgaben GDGL SS 1998
 Aufgaben GDGL SS 1998 Frank Wübbeling 17. September 1998 Aufgabe 1: (4 Punkte) Stellen Sie eine Differentialgleichung 1. Ordnung auf für die Schar der Parabeln mit der x-achse als Achse und dem Ursprung
Aufgaben GDGL SS 1998 Frank Wübbeling 17. September 1998 Aufgabe 1: (4 Punkte) Stellen Sie eine Differentialgleichung 1. Ordnung auf für die Schar der Parabeln mit der x-achse als Achse und dem Ursprung
Induktionsgesetz. a = 4,0cm. m = 50g
 1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
Merkmale flexibler Fertigung
 FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
2.3 Theorie linearer Systeme
 2.3 Theorie linearer Syseme 2.3.1 Grundsäzliche Mehode Mehode: Berechnung durch Zerlegen in einfach berechenbare Teile (Superposiion) x() = x 1 ()+x 2 ()+x 3 ()+.. y() = y 1 ()+y 2 ()+y 3 ()+.. zerlegen
2.3 Theorie linearer Syseme 2.3.1 Grundsäzliche Mehode Mehode: Berechnung durch Zerlegen in einfach berechenbare Teile (Superposiion) x() = x 1 ()+x 2 ()+x 3 ()+.. y() = y 1 ()+y 2 ()+y 3 ()+.. zerlegen
Mess- und Regelungstechnik
 Skrip zur Vorleung Me- und egelungechnik Prof. Dr.-Ing. Chrioph Amen Sand: Juni 7 Gliederung und Lieraur Vorleung Me- und egelungechnik Seie - Gliederung Einführung: Worum oll e gehen?... -. Die Grundaufgabe...
Skrip zur Vorleung Me- und egelungechnik Prof. Dr.-Ing. Chrioph Amen Sand: Juni 7 Gliederung und Lieraur Vorleung Me- und egelungechnik Seie - Gliederung Einführung: Worum oll e gehen?... -. Die Grundaufgabe...
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Systemtheorie. System. Prof. Dr. August Reiner. Dipl. Ing. Manfred Schneider
 Syemheorie Eingang Syem Augang Prof. Dr. Augu Reiner Dipl. Ing. Manfred Schneider Einleiung Einleiung Die Syemheorie, wie ie in den Ingenieurwienchafen verwende wird, wurde um 9 konzipier. Einen encheidenden
Syemheorie Eingang Syem Augang Prof. Dr. Augu Reiner Dipl. Ing. Manfred Schneider Einleiung Einleiung Die Syemheorie, wie ie in den Ingenieurwienchafen verwende wird, wurde um 9 konzipier. Einen encheidenden
Übersicht Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 16: Maximaler Fluss
 Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Überich aenrukuren und lgorihmen Vorleung 16: Prof. r. Erika Ábrahám Theorie Hybrider Syeme Informaik 2 hp://h.rwh-aachen.de/eaching/-1/ daenrukuren-und-algorihmen/ iee Präenaion verwende in Teilen Folien
Übungen zur Vorlesung PN1 Lösung Übungsblatt 12 Besprechung am
 Übungen zur Vorleung PN1 Löung Übungblatt 12 Beprechung am 22.1.2013 Aufgabe 1: Gedämpfte Schwingung An einer Feder mit der Federhärte 20 N/m hängt eine Kugel der Mae 100g. Die Kugel wird um 10 cm nach
Übungen zur Vorleung PN1 Löung Übungblatt 12 Beprechung am 22.1.2013 Aufgabe 1: Gedämpfte Schwingung An einer Feder mit der Federhärte 20 N/m hängt eine Kugel der Mae 100g. Die Kugel wird um 10 cm nach
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Abiturprüfung Baden-Württemberg 1986
 c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
Prüfungsvorbereitungskurs Höhere Mathematik 3
 Prüfungsvorbereitungskurs Höhere Mathematik 3 Gewöhnliche Differentialgleichungen Marco Boßle Jörg Hörner Mathematik Online Frühjahr 2011 PV-Kurs HM 3 Gew. DGl 1-1 Zusammenfassung y (x) = F (x, y) Allgemeine
Prüfungsvorbereitungskurs Höhere Mathematik 3 Gewöhnliche Differentialgleichungen Marco Boßle Jörg Hörner Mathematik Online Frühjahr 2011 PV-Kurs HM 3 Gew. DGl 1-1 Zusammenfassung y (x) = F (x, y) Allgemeine
5. Laplace Transformation. 5.1 Definition und Korrespondenzen
 23 5. Laplac Tranformaion 5. Dfiniion und Korrpondnzn Di Laplac Tranformaion ha für di Analy und dn Endwurf linarr ziinvarianr dynamichr Sym mi konznrirn Elmnn in groß prakich Bduung rlang. Si ghör wi
23 5. Laplac Tranformaion 5. Dfiniion und Korrpondnzn Di Laplac Tranformaion ha für di Analy und dn Endwurf linarr ziinvarianr dynamichr Sym mi konznrirn Elmnn in groß prakich Bduung rlang. Si ghör wi
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
mittlere bremsende Kraft auf das Teilchen um diesen Mittelwert fluktuierende stochastische Kraft f(t) stochastischer Prozess
 Brownsche Bewegung schweres Teilchen mi Masse m und Geschwindigkei v beweg sich in Flüssigkei von leichen Teilchen. Dieses Brownsche Teilchen wird von den Molekülen der Flüssigkei gesoßen. Söße bewirken:
Brownsche Bewegung schweres Teilchen mi Masse m und Geschwindigkei v beweg sich in Flüssigkei von leichen Teilchen. Dieses Brownsche Teilchen wird von den Molekülen der Flüssigkei gesoßen. Söße bewirken:
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
Abiturprüfung Baden-Württemberg 1986
 001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Übungsmaterial. Lösen von Anfangswertproblemen mit Laplacetransformation
 Prof. Dr. W. Roenheinrich 30.06.2009 Fachbereich Grundlagenwienchaften Fachhochchule Jena Übungmaterial Löen von Anfangwertproblemen mit Laplacetranformation Nachtehend ind einige Anfangwertprobleme zu
Prof. Dr. W. Roenheinrich 30.06.2009 Fachbereich Grundlagenwienchaften Fachhochchule Jena Übungmaterial Löen von Anfangwertproblemen mit Laplacetranformation Nachtehend ind einige Anfangwertprobleme zu
4 Gewöhnliche Differentialgleichungen
 4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
4 Gewöhnliche Differentialgleichungen 4.1 Einleitung Definition 4.1 Gewöhnliche Differentialgleichung n-ter Ordnung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
