Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
|
|
|
- Mina Weber
- vor 5 Jahren
- Abrufe
Transkript
1 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35) ind lineare parielle Differenialgleichungen (PDn) 1. Ordnung. Aufgrund de Terme B *f ind die PDn inhomogen. Die unabhängigen Variablen ind L, und. Zur Löung dieer PDn wird ein Charakeriikenverfahren verwende [iehe z.b. Mey 91, S. 367]. Eine Löung der Populaionbilanzen kann mi zwei Randbedingungen, f(l,, ) und f(l,, ), owie der Anfangbedingung im dikoninuierlichen Fall erfolgen. Die Anfangbedingung i mi f(l,, ) gegeben, d.h. e lieg eine klare, kriallfreie Löung vor. Impfkrialle werden in dieem Abchni nich berückichig. Für die ere Randbedingung gil daher f(l,, ), d.h. e gib keine Krialle, deren Wachum völlig zum Silland gekommen i. Im Modell werden nur Krialle mi L > berache. Für die zweie Randbedingung gil daher f(l,, ). Bei L L N werden permanen Keime mi einer Anzahlvereilung *f (L,) gebilde. Die Anzahlvereilung i definier al *f (L,) j(l) y(), wobei j(l) eine Dirac-Dela- Funkion d(l-l N ) mi den Eigenchafen A-1 bi A-3 [Jäh 95, S. 69] i. Die Dirac- Dela-Funkion i folgendermaßen definier: E gil: ì, x ¹ x d( x - x ) : í und î, x x ò d( x - x ) dx : 1 (A-1) - ò f (x) d (x - x ) dx : f (x) und (A-) - n d(x - x d i ) ( f (x)) å. (A-3) ' f (x ) i 1 i In leichung A-3 ind x i die Nullellen der Funkion f(x) und e gil f (x ) ¹. A1.1 Koninuierliche Krialliaion Im aionären Zuand erfolg keine Änderung der Prozeßparameer Überäigung und Temperaur. Da bedeue, daß owohl die häufige Wachumgechwindigkei al auch die individuellen Wachumgechwindigkeien der Krialle und die Keimbildungrae B konan ind. Mi A vereinfach ich leichung 3-6 zu f (L,) f (L,) B * f(l,). (A-4) L ' i
2 118 ANAN leichung A-4 i eine gewöhnliche inhomogene DL 1. Ordnung und kann durch Variaion der Konanen [Mey 91, S. 16] gelö werden. Durch Einezen der Vereilungfunkion * f (L,) y() j(l) und j(l) d(l-l N ) erhäl man zunäch f 1 f L B y() d(l - L N ). (A-5) Die allgemeine Löung der zugeordneen homogenen DL laue - L f h (L,) c e. (A-6) Für die volländige allgemeine Löung kann man den Anaz y(x) c(x) y h (x) wählen. Dabei gil für c(x) x 1 c (x) ò f ( x) dx c. (A-7) y ( x) E ergib ich x h - L f (L,) c(l,)e mi L L N c B B (L,) e () (L LN )dl C e ò y d - y() C. (A-8) Für die Inegraionkonane in l. A-8 erhäl man mi der Randbedingung für f(l,, ) und dem oben erläueren Definiionbereich C. Aufgrund der Eigenchafen der Dirac-Dela-Funkion (l. A-1 bi A-3) gil für den eren Term in l. A-8 ein Definiionbereich L ³ L N. Für L < L N i dieer Term Null. Dami ergib ich für f(l,) folgende Löung B L-L - N f (L,) y()e. (A-9) In Abbildung A-1 i diee Löung al Funkion von L und für eine Verweilzei dargeell. Die Darellung der dazugehörenden Anzahldiche n owie eine Dikuion der Parameer und b erfolg im Abchni (iehe auch Abb. 3-5). A1. Dikoninuierliche Krialliaion Veränderliche Wachumgechwindigkei Für den Fall der veränderlichen Wachumgechwindigkei A ¹ wird bei dieer Berachung angenommen, daß die Änderung der häufigen Wachumgechwindigkei A konan i. Demzufolge änder ich die häufige Wachumgechwindigkei proporional zur Zei. E gil
3 A1 ANALYTISCE LÖSUNEN DER ERWEITERTEN ANZALBILANZ 119 Abb. A-1 Analyiche Löung der erweieren Populaionbilanz für die koninuierliche Beriebweie (l. A-9). Parameer: b 3, m/, B 1 1 # m -3-1, und L N 1µm () A. (A-1) Für die Änderung der individuellen Wachumgechwindigkei gil leichung 3-15: A(,) A / (). Die Keimbildungrae i für diee Berachung konan. Für die Populaionbilanz der dikoninuierlichen Beriebweie erhäl man mi leichung.-35: f (L,, ) f (L,, ) f (L,, ) A(, ) L A f (L,, ) () B *f (L,) (A-11) Die zugeordnee Rumpf-DL laue f f f A A f L. (A-1) Für leichung A-11 kann man da charakeriiche Differenialgleichungyem A & 1, L & und & A A (A-13)
4 1 ANAN aufellen. Dami lauen die Phaen-DLn: d L d & L & und d d & & A (A-14) mi den Löungen () ( A ) und (A-15) A L () ò () d L. (A-16) Au den Phaen-DLn A-15 und A-16 ergeben ich die Charakeriiken von A-1, läng derer die Löungen der Rumpf-DL konan ind. Die Charakeriiken L - - A z und h A (A-17) owie x werden al neue Koordinaen eingeführ, wodurch leichung A-11 auf eine gewöhnliche lineare DL reduzier werden kann. Die Anwendung von F ( z, h, x) f (L,, ) auf die PD A-11 führ zu F x A F - B x *f A. (A-18) leichung A-18 i eine gewöhnliche inhomogene DL 1. Ordnung und kann durch Variaion der Konanen gelö werden. Konane Wachumgechwindigkei Im folgenden wird eine Löung für den Spezialfall konane Wachumgechwindigkei geuch. Mi A vereinfach ich leichung A-11 zu f f L B * f. (A-19) Die Phaen-DL der Rumpf-DL der PD A-19 laue d L d L& &. (A-) Durch Anwendung der Koordinaen h L- und x auf l. A-19 erhäl man eine gewöhnliche lineare DL F B x * f (A-1)
5 A1 ANALYTISCE LÖSUNEN DER ERWEITERTEN ANZALBILANZ 11 Abb. A- Analyiche Löung der erweieren Populaionbilanz für die dikoninuierliche Beriebar (leichung A-3). Parameer: b 3, m/, A, B 1 1 # m -3-1, und L N 1µm mi der Vereilungfunkion * f (L,) y() j(l) y() j( h x). Die Längenvereilung j(hx) i hierbei wiederum eine Dirac-Dela-Funkion d ( h x - LN ). Die Löung der leichung A-1 erhäl man uner Verwendung der Eigenchafen der Dirac- Funkion (A-1 bi A-3) B x B ò*f( x)d x B y() ò j( h x)d x y() C. (A-) F leichung A- gil für h x - LN ³. Die Rückubiuion f (L,,) F( h, x ) liefer die allgemeine Löung der PD im Definiionbereich - (L - LN ) / ³. f (L,, ) B y() (A-3) Für die Inegraionkonane in l. A- ergib ich mi der Randbedingung f(l,,) zu C. In Abbildung A- i diee Löung al Funkion von L und für dargeell. Die öhenliniendarellung im uneren Teil von Abb. A- zeig deulich die renze de güligen Definiionbereiche bei -(L-L N )/. Zeiliche Enwicklung einer Kriallvereilung Im folgenden wird die zeiliche Enwicklung einer Kriallvereilung f(l,,) ohne Berückichigung der Keimbildung für die dikoninuierliche Beriebweie berache. ierfür i
6 1 ANAN die Änderung der häufigen Wachumgechwindigkei für da berachee Zeiinervall konan. Die Sarvereilung f(l,,) f (L,) N T *f (L,) ez ich au der Kriallgrößenvereilung j(l) und der Vereilung der Wachumgechwindigkei y() (l..-6) zuammen. Al Beipielvereilung der Kriallgröße wird eine au che Normalvereilung mi w 1 µm und L 5mm verwende. j(l) 1 w p e (L-L) - w (A-4) Der Verlauf der häufigen Wachumgechwindigkei in einen Zeiinervall mi A con i mi leichung A-1 fegeleg. Für die Anzahlvereilung gil die Bilanzgleichung A-11. Mi der Einführung der Variablen z und h (l. A-17) owie x und B gelang man analog leichung A-18 zu F A F x A x mi der Löung F F( x ). (A-5) ( x) Die Rückubiuion f (L,, ) F( z, h, x) liefer die Löung enlang der Charakeriiken in Abhängigkei de Parameer f (L,, ) A f (L - -, ), (A-6) A A wobei f die Sarvereilung für diee Berachung darell. Mi leichung.-31 erhäl man eine Verallgemeinerung für beliebige Wachumgechwindigkeien f f f. (A-7) () () In Abbildung A-3 i die zeiliche Enwicklung der Beipielvereilung II mi A (oben) dem zeilichen Verlauf für A con (unen) gegenübergeell. Für A bleib die Vereilung f(l,,) f (L,) unveränder und wird lediglich in Richung größerer Teilchendurchmeer enprechend der Wachumgechwindigkei verchoben. emäß l. A-6 bleib dabei die Vereilung enlang der Charakeriiken / und L- (mi A und con) konan. Diee Verchiebung von f (L,) bewirk eine analoge Verchiebung bei gleichzeiiger Aufweiung der Anzahlvereilung n(l) (vgl. Abb..-8, link). Im Fall A ¹ und A con verchieb ich die erweiere Anzahlvereilung jedoch auch parallel zur -Koordinae. In Abbildung A-3 unen i deulich da verzögere Wachum bei einer negaiven Wachumänderung von A m - zu erkennen. Dabei ändern ich auch die Funkionwere der Vereilung f(l,,) enprechend leichung A-7. Diee Wirkung der inkenden häufige Wachumgechwindigkei () führ zum Anwachen der Vereilungdiche in den kleineren echwindigkeiklaen
7 A1 ANALYTISCE LÖSUNEN DER ERWEITERTEN ANZALBILANZ 13 Abb. A-3 Beipielvereilung II (vgl. auch Abb. 3-6): Verlauf der zweidimenionalen Anzahldiche log(f [# m -1 (m/) -1 m -3 ]). In der oberen Bildfolge i die häufige Wachumgechwindigkei konan (A ). Zur Verdeulichung der Verchiebung und Sauchung der Vereilung für A < i die Ordinae logarihmich (milere Bildfolge) bzw. linear (unere Bildfolge) geeil dargeell. (Parameer: b1, N S 1 1 # m -3 ) (Abb. A-3 unen). Ingeam bewirk die Enwicklung von f (L,) eine verzögere Verchiebung und Aufweiung der Anzahlvereilung n(l) (vgl. Abb. 3-6, rech).
8 14 ANAN A Momene der zweidimenionalen Anzahlvereilung Die Bechreibung der Anzahlvereilungfunkion miel Momenen baier auf der Mehode nach ulber und Kaz für zwei inerne Koordinaen [ul 64, S. 566]. Die Keimbildung wird für die im folgenden dikuieren Beziehungen nich berückichig. Zunäch wird die Vereilung f(l,,) mi der Anzahl der Teilchen normier. Man erhäl *f(l,,). Da Momen m i j einer zweidimenionalen Vereilung i definier al m ij i L òò j *f(l,,) dld (A-8) Die Momene m i der eindimenionalen, normieren Anzahlvereilung *n(l,) ergeben ich au den Momenen m i j : i i L*f(L,,) dld òò ò m L*n(L,) dl m i i (A-9) Beondere Bedeuung für die Charakeriierung von Anzahlvereilungen beizen da ere Momen (Mielwer L m 1 m 1 ) owie da zweie zenrale Momen der Kriallgrößenvereilung (Varianz L m m 1 m m 1 ). Die Anwendung der Definiiongleichung A-8 auf die Populaionbilanz eine dikoninuierlich beriebenen Krialliaor (l. 3-18) mi B führ zu òò i jé *f L ê ë *f L *f A A ù * f d L d () ú û i, j,1,... (A-3) Die einzelnen Terme der linken Seie ergeben folgende Audrücke i L òò j é * f ê ë ù ú û mi d L d j, (A-31) i jé *fù L ê dld -imi-1j 1 L ú owie (A-3) òò ë û i òò jé *f A ù A L *f dld j êa - m () ú ë û () i j (A-33) mi A/ () A (l. 3-15). Für den Fall einer veränderlichen Wachumgechwindigkei mi A con gil für () leichung A-1 (analog Abchni A1.). Da o enandene Differenialgleichungyem für die Bechreibung der zeilichen Enwicklung
9 A MOMENTE DER ZWEIDIMENSIONALEN ANZALVERTEILUN 15 Tabelle A-1 Zeiliche Enwicklung der Momene für die dikoninuierlich beriebene Krialliaion Momen mi j Populaionbilanz m i j / Anfangbedingung m i j ( ) m 1 m1 m1 L m 1 A m 1 A m m 1 1 L L m 11 m m A A m A m 11 A L L der eren und zweien Momene i in Tabelle A-1 zuammengefaß. Mi den Anfangbedingungen in Spale 3 erhäl man folgende Löungen: A L () L () m 1 () ( A ) (A-34) (A-35) L () L A L 3 A A 4 L 4 (A-36) L () L A L A L (A-37)
10 16 ANAN () A A (A-38) Für den Spezialfall A erhäl man für L () bzw. L () au leichung A-34 bzw. A-35 L() L und (A-39) L L L ( ). (A-4)
11 A3 SIMULATIONSSCEMATA 17 A3 Simulaionchemaa A3.1 Digiale Bildverarbeiung Schleife über alle Meßpunke Mielung über alle Bilder eine Meßpunke BILD# Schleife über alle Bilder eine Meßpunke (Meßbereich I und II) Bildverarbeiung und Objekerkennung BILD#1 (Abb. 3.3-) Subrakion BILD# Inverieren Duplizieren Umwandlung in Binärbild Separierung der Objeke: Binary Morphology - Cloe BILD# Subrakion BILD# BILD#3 Umwandlung in Binärbild und Separierung der Objeke: Waerhedding BILD#4 Klaifizierung der Objeke: rößenvereilung eine Bilde (iehe Abb ) Maenbilanz Vereinigung von Meßbereich I und II eine Meßpunke Normierung der Anzahlvereilung (iehe Abb ) Augabe der Vereilungen
12 18 ANAN A3. Parameeropimierung Opimierungalgorihmu SIMPLEX Berechnung neuer Opimierungparameer Veruchar? enerierung von Simulaioneilchen für Impfkrialle nein Berechnung von. Lieg eine minimale Wachumoder Auflöunggechwindigkei vor? ja Schleife über alle Simulaioneilchen Berechnung von Teilchengröße und Wachumgechwindigkei > ja nein Keimbildung: enerierung von Simulaioneilchen nein Augabe? ja Berechnung der Vereilungen f(l,,) und n(l,) Berechnung de Zeichrie. I da Veruchende erreich? nein ja Berechnung de Opimierungkrierium nein Abbruch der Opimierung? ja
13 A4 VERSUCSEREBNISSE 19 A4 Veruchergebnie.6 Meung der Anzahlvereilung Impfkriallzugabe 8 7 Überäigung [-] Temperaur [ C] Veruchzei [min] Überäigung [-].6.4. Meung der Anzahlvereilung Impfkriallzugabe Temperaur [ C] Veruchzei [min] Abb. A-4 Verlauf von Überäigung und Temperaur Experimen #1 (oben) und Experimen # (unen)
14 13 ANAN Überäigung [-].4. Meung der Anzahlvereilung Impfkriallzugabe Temperaur [ C]. 4 6 Veruchzei [min] Überäigung [-].4. Meung der Anzahlvereilung Impfkriallzugabe Temperaur [ C] Veruchzei [min] Abb. A-5 Verlauf von Überäigung und Temperaur Experimen #3 (oben) und Experimen #4 (unen)
15 A4 VERSUCSEREBNISSE 131 Meung der Anzahlvereilung Impfkriallzugabe.6 8 Überäigung [-] Veruchzei [min] Temperaur [ C] Abb. A-6 Verlauf von Überäigung und Temperaur Experimen #5
16 13 ANAN Abb. A-7 Experimen #1
17 A4 VERSUCSEREBNISSE 133 Abb. A-8 Experimen #
18 134 ANAN Abb. A-9 Experimen #3
19 A4 VERSUCSEREBNISSE 135 Abb. A-1 Experimen #4
20 136 ANAN Abb. A-11 Experimen #5: bi 7 min
21 A4 VERSUCSEREBNISSE 137 Abb. A-1 Experimen #5: 7 bi 13 min
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Zusammenfassung Gleichmäßig beschleunigte Bewegung
 3c D-Kineaik Zuaenfaung a a a a a con con poii con negai Gleichäßig bechleunige Bewegung + a + + a + a( ) + ( - ) + - a Bechleunigungen Magnechwebebahn Erreich der Tranrapid auf der Srecke on Shanghai-Flughafen
3c D-Kineaik Zuaenfaung a a a a a con con poii con negai Gleichäßig bechleunige Bewegung + a + + a + a( ) + ( - ) + - a Bechleunigungen Magnechwebebahn Erreich der Tranrapid auf der Srecke on Shanghai-Flughafen
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
W. Stark; Berufliche Oberschule Freising
 9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
9.6 Aufellen der Bewegunggleichungen der haronichen Schwingung bei unerchiedlichen Anfangbedingungen i Hilfe eine Zeiger- und Liniendiagra 9.6. Der chwingende Körper durchläuf zu Zeinullpunk eine uhelage
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die wichtigsten Inhalte der einzelnen Kapitel zur schnellen Wiederholung
 Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Checklien Die wichigen Inhale der einzelnen Kapiel zur chnellen Wiederholung I Kenn du eigenlich die rbeiweie der Naurwienchafler? I 1 Nenne die einzelnen Schrie, die Naurwienchafler gehen, u zu neuen
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
Von der Fourier-Reihe zum Fourier-Integral
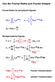 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Aufgabenblatt 10: Investitionstheoretische Kostenrechnung I
 Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Prof. Dr. Gunher Friedl Aufgabenbla 10: Inveiionheoreiche oenrechnung I Aufgabe 10.1: Inveiionheoreiche oenrechnung, Abchreibung (Aufg. 6.2.2 im Übungbuch) Die Gechäfleiung der Brauerei Benedikiner erwäg
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Nutzung der inhärenten sensorischen Eigenschaften von piezoelektrischen Aktoren
 Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Nuzung der inhärenen enorichen Eigenchafen von piezoelekrichen Akoren K. Kuhnen; H. Janocha Lehruhl für Prozeßauomaiierung (LPA), Univeriä de Saarlande Im Sadwald, Gebäude 13, 6641 Saarbrücken Tel: 681
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
reibungsgedämpfte Schwingung
 HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
HTL-LiTec reibunggedäpfe Schwingung Seie 1 von 7 Dipl.-Ing. Paul MOHR E-Brief: p.ohr@eduhi.a reibunggedäpfe Schwingung Maheaiche / Fachliche Inhale in Sichworen: reibunggedäpfe Schwingung; nueriche Löung
2 Torsion in dünnwandigen Querschnitten
 apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
apl oz r-ing hail G Georgi Tragwerkerechnung Torion in dünnwandigen Querchnien Theorien, Vorauezungen und Hpoheen Theorien: Reine Torion ( Grundufe) Begründer: Jean Claude de T VENANT (9-886) mol, Inde:
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Transport. Explizite und implizite Verfahren
 p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
p. 1/9 Tranpor Explizie und implizie Verfahren home/lehre/vl-mhs-1/inhalt/folien/vorlesung/10_transport_verf/decbla.ex Seie 1 von 9 p. /9 Inhalverzeichni 1. Explizie Verfahren Inabile Verfahren Lax Verfahren
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Fokker-Planck-Gleichung
 Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
1 Abtastung, Quantisierung und Codierung analoger Signale
 Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
10 Gleichspannungs-Schaltvorgänge RL-Reihenschaltung
 GleichspannungsSchalvorgänge eihenschalung Seie von 6 222 Prof. Dr.Ing. T. Harriehausen Wolfenbüel.9.2. Beziehung zwischen en lemmengrößen einer konsanen Inukiviä Die Abhängigkei zwischen en lemmengrößen
GleichspannungsSchalvorgänge eihenschalung Seie von 6 222 Prof. Dr.Ing. T. Harriehausen Wolfenbüel.9.2. Beziehung zwischen en lemmengrößen einer konsanen Inukiviä Die Abhängigkei zwischen en lemmengrößen
wird auch die Dehnung zz nach (3.12) gleich null. Die nicht verschwindenden Verzerrungen sind (mit (3.17a) ):
 Tragwerkberecnung apl Doz Dr-Ing abil G Georgi Reine Torion Offene Quercnie Uner der Vorauezung kon wird auc die Denung zz nac () gleic null Die nic vercwindenden Verzerrungen ind (i (7a) ):, ( z),, (
Tragwerkberecnung apl Doz Dr-Ing abil G Georgi Reine Torion Offene Quercnie Uner der Vorauezung kon wird auc die Denung zz nac () gleic null Die nic vercwindenden Verzerrungen ind (i (7a) ):, ( z),, (
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Bestimmung der Gasdichte mit dem Effusiometer
 mi dem Effuiomeer Sichwore: Bernoulliche Gleichung, aiiche Auwereverfahren, Reynoldche Zahl, laminare und urbulene Srömung, Koninuiägleichung Einführung und Themenellung Die Aurömgechwindigkei eine Gae
mi dem Effuiomeer Sichwore: Bernoulliche Gleichung, aiiche Auwereverfahren, Reynoldche Zahl, laminare und urbulene Srömung, Koninuiägleichung Einführung und Themenellung Die Aurömgechwindigkei eine Gae
Physik der sozio-ökonomischen Systeme mit dem Computer. 4. Vorlesung
 Physik der sozio-ökonomischen Syseme mi dem Compuer PC-POOL RAUM 0.0 JOHANN WOLFGANG GOETHE UNIVERSITÄT 0..07 4. Vorlesung MATTHIAS HANAUSKE FRANKFURT INSTITUTE FOR ADVANCED STUDIES JOHANN WOLFGANG GOETHE
Physik der sozio-ökonomischen Syseme mi dem Compuer PC-POOL RAUM 0.0 JOHANN WOLFGANG GOETHE UNIVERSITÄT 0..07 4. Vorlesung MATTHIAS HANAUSKE FRANKFURT INSTITUTE FOR ADVANCED STUDIES JOHANN WOLFGANG GOETHE
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
3.3 Moving-Average-Prozesse (MA-Modelle)
 . Moving-Average-Prozesse MA-Modelle Definiion: in sochasischer Prozess heiß Moving-Average-Prozess der Ordnng [MA-Prozess], wenn er die Form θ θ i i... θ i oder B mi ha. is dabei ein reiner Zfallsprozess
. Moving-Average-Prozesse MA-Modelle Definiion: in sochasischer Prozess heiß Moving-Average-Prozess der Ordnng [MA-Prozess], wenn er die Form θ θ i i... θ i oder B mi ha. is dabei ein reiner Zfallsprozess
6 Stochastische Differentialgleichungen
 6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Ermittlung von Leistungsgrenzen verschiedener Lagerstrategien unter Berücksichtigung zentraler Einflussgrößen
 Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Ermilung von Leiunggrenzen verchiedener Lagerraegien uner Berücichigung zenraler Einflugrößen Dipl.-Wir.-Ing. (FH) Anne Piepenburg, Prof. Dr.-Ing. Rainer Brun Helmu-Schmid-Univeriä, Hamburg Lehruhl für
Das lineare H-unendlich Problem
 Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
4. Quadratische Funktionen.
 4-1 Funkionen 4 Quadraische Funkionen 41 Skalierung, Nullsellen Eine quadraische Funkion is von der Form f() = c 2 + b + a mi reellen Zahlen a, b, c; is c 0, so sprechen wir von einer echen quadraischen
4-1 Funkionen 4 Quadraische Funkionen 41 Skalierung, Nullsellen Eine quadraische Funkion is von der Form f() = c 2 + b + a mi reellen Zahlen a, b, c; is c 0, so sprechen wir von einer echen quadraischen
Aufgabe 1: Kontinuierliche und diskrete Signale
 Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Strömung im Rohr. Versuch: Inhaltsverzeichnis. Fachrichtung Physik. Physikalisches Grundpraktikum. 1 Aufgabenstellung 2
 Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Induktionsgesetz. a = 4,0cm. m = 50g
 1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
1. Die neenehende Aildung (Blick von vorn) zeig eine Spule mi 5 Windungen von quadraichem uerchni mi Seienlänge a = 4,cm zum Zeipunk. DieSpuleeweg ich mider Gechwindigkei v vom Berag v = 2, cm nachrech.
Schätzungen und Hypothesenprüfungen. Hypothesenprüfungen. t Tests. Gibt es eine Wirkung einer Behandlung? Typische Entscheidungsfragen in der Medizin
 Hypoheenprüfungen. Te Schäzungen Wie gro i eine Gröe? Punkchäzungen Schäzungen und Hypoheenprüfungen ein Wer i gegeben und nich über die Sicherhei Parameer der Sichprobe Parameer der Populaion μ σ ( n
Hypoheenprüfungen. Te Schäzungen Wie gro i eine Gröe? Punkchäzungen Schäzungen und Hypoheenprüfungen ein Wer i gegeben und nich über die Sicherhei Parameer der Sichprobe Parameer der Populaion μ σ ( n
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
2. Übungsblatt zu Algorithmen II im WS 2011/2012
 Karlruher Iniu für Technologie Iniu für Theoreiche Informaik Prof. Dr. Peer Sander Moriz Kobizch, Denni Schieferdecker. Übungbla zu Algorihmen II im WS 0/0 hp://algo.ii.ki.edu/algorihmenii.php {kobizch,ander,chieferdecker}@ki.edu
Karlruher Iniu für Technologie Iniu für Theoreiche Informaik Prof. Dr. Peer Sander Moriz Kobizch, Denni Schieferdecker. Übungbla zu Algorihmen II im WS 0/0 hp://algo.ii.ki.edu/algorihmenii.php {kobizch,ander,chieferdecker}@ki.edu
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Prüfung Finanzmathematik und Investmentmanagement 2011
 Prüfung Finanzmahemaik und Invesmenmanagemen 0 Aufgabe : (0 Minuen) a) Auf der Grundlage einer Lagrange-Opimierung ergib sich die folgende funkionale Form für die (, ) -Koordinaen der (rein riskanen) Randporfolios
Prüfung Finanzmahemaik und Invesmenmanagemen 0 Aufgabe : (0 Minuen) a) Auf der Grundlage einer Lagrange-Opimierung ergib sich die folgende funkionale Form für die (, ) -Koordinaen der (rein riskanen) Randporfolios
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Der kinetische Ansatz zur Beschreibung von Selbstorganisationsprozessen. mögliche Variationen und Erweiterungen: diskrete Gleichungen (endliches t):
 Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Übung 5: BB-Datenübertragung
 ZHW, NM, 5/6, Rur Übung 5: BB-Daenüberragung Aufgabe Nichlineare Ampliudenquanisierung. Das Signal s() = S p?sin(pf ) wird über einen Kanal überragen, der das Signal mi dem Fakor a dämpf. Der Parameer
ZHW, NM, 5/6, Rur Übung 5: BB-Daenüberragung Aufgabe Nichlineare Ampliudenquanisierung. Das Signal s() = S p?sin(pf ) wird über einen Kanal überragen, der das Signal mi dem Fakor a dämpf. Der Parameer
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
3. Anlaufgesetze/Zeitgesetze
 3. Anlaufgeseze/Zeigeseze 24 3. Anlaufgeseze/Zeigeseze Die Anlaufgeseze (Zeigeseze) beschreiben den Verlauf der Schichdicenänderung bzw. der Gewichsänderung in Abhängigei von der Zei und gesaen in der
3. Anlaufgeseze/Zeigeseze 24 3. Anlaufgeseze/Zeigeseze Die Anlaufgeseze (Zeigeseze) beschreiben den Verlauf der Schichdicenänderung bzw. der Gewichsänderung in Abhängigei von der Zei und gesaen in der
7) Fertigung der Durchströmturbine
 oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
oku Verion 1.0 aum 04.10.2004 urchrömurbine elb gebau 7) Ferigung der urchrömurbine 7.1 Turbinendaen - Geamanich ie hier im eail bechriebene urchrömurbine mi einem Laufraddurchmeer von 200 mm kann Fallhöhen
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
BESCHREIBUNG VON ZERFALLSPROZESSEN
 BESCHREIBUNG VON ZERFALLSPROZESSEN ab Ende der 1. Schulsufe Kreuze zu jedem angeführen Beispiel das richige mahemaische Modell an, begründe deine Enscheidung und beschreibe die Bedeuung der in den Modellen
BESCHREIBUNG VON ZERFALLSPROZESSEN ab Ende der 1. Schulsufe Kreuze zu jedem angeführen Beispiel das richige mahemaische Modell an, begründe deine Enscheidung und beschreibe die Bedeuung der in den Modellen
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Ausgleichsrechnung - Lineare Regression
 ugleichrechnung - Lineare Regreion Die biher berachee Fehlerrechnung i gu verwendbar wenn ich die beracheen Größen dire een laen. Of ind phialiche Größen für eine diree Meung aber nur chwer zugänglich;
ugleichrechnung - Lineare Regreion Die biher berachee Fehlerrechnung i gu verwendbar wenn ich die beracheen Größen dire een laen. Of ind phialiche Größen für eine diree Meung aber nur chwer zugänglich;
Lösung - Serie 8. D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. MC-Aufgaben (Online-Abgabe) 1. Was für eine Kurve stellt die Parametrisierung
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
