Systemtheorie I WS 04/05 Prof. Dr.-Ing. habil. Hoffmann, TU Dresden Mitschrift. Fabian Kurz
|
|
|
- Käthe Richter
- vor 5 Jahren
- Abrufe
Transkript
1 Sysemheorie I WS 4/5 Prof Dr-Ing habil Hoffmann, TU Dresden Mischrif Fabian Kurz hp://fkurzne/ Zulez akualisier: 5 Mai 25
2 Inhalsverzeichnis Einführung Inhal des Lehrgebiees 2 Soffeineilung 3 Lieraur Teil : Digiale Syseme 2 Mahemaische Grundlagen 2 Algebraische Srukuren 2 Operaion und Srukur 2 2 Verallgemeinerungen 2 3 Isomorphe Srukuren 3 4 Boolesche Algebra 3 2 Schalalgebra 4 2 Rechenregeln 4 22 Gaerschalungen 5 23 Schalfunkionen 6 24 Vollsändiges Operaionensysem 6 3 Darsellung von Schalfunkionen 7 3 Wereabelle 7 32 Boolesche Terme 7 33 Kanonische disjunkive Normalfunkion 8 34 Kanonische konjunkive Normalform 8 35 Karnaugh Tafel 9 2 Saische digiale Syseme (kombinaorische Auomaen) 2 Alphabebildung 2 Alphabee 22 Syseme mi einem Ausgang 2 23 Syseme mi mehreren Ausgängen 2 22 Worabbildung 3 22 Buchsaben und Wörer Eigenschafen der Worabbildung 3 3 Dynamische digiale Syseme (sequenieller Auoma) 4 3 Zusandsbeschreibung 4 3 Speicher 4 32 Zusandsgleichungen 5 33 Auomaendarsellung 7 34 Spezielle Auomaen 8 32 Worabbildungen 9 32 Abbildungsfamilie Eigenschafen der Worabbildung Auonomer Auoma 2 I
3 Teil 2: Zeikoninuierliche Syseme 2 4 Zeikoninuierliche Signale und Syseme 2 4 Signalbeschreibung im Zeibereich 2 4 Zeikoninuierliche Signale 2 42 Signaloperaionen 2 43 Spezielle Signale Signale allgemeineren Typs Inerpolaion abgeaseer Signale Saische Syseme mi koninuierlicher Zei Elemenarsyseme Verallgemeinerung der Beispiele Kleinsignalverhalen Dynamische zeikoninuierliche Syseme 3 43 Zusandsbeschreibung Lineares zeikoninuierliches Sysem Ordnung Nichlineares zeikoninuierliches Sysem Ordnung 34 5 Lineare Syseme 35 5 Signalbeschreibung im Bildbereich (Fourier-Transformaion) 35 5 Die komplexe Fourier-Reihe Fourier-Inegral Fourier-Transformaion Rechenregeln der Fourier-Transformaion Signalbeschreibung im Bildbereich (Laplace-Transformaion) Laplace-Inegral Laplace-Transformaion Rechenregeln Grenzwersäze Die inverse Laplace-Transformaion Sysembeschreibung im Zeibereich Zusandsgleichungen Differenialgleichung und Realisierung 46 II
4 Einführung Inhal des Lehrgebiees Realiä Mahemaisches Modell Erregung (Ursache) Schalung Gerä, usw Reakion (Wirkung) Eingabe x() Sysem Ausgabe y() Aufgaben gegeben gesuch Gebie Eingabe, Sysem Ausgabe Sysemanalyse Eingabe, Ausgabe Sysem Sysemsynhese Sysem, Ausgabe Eingabe Messechnik Beache: Beispiel: Modell is anwendungsabhängig Drahwidersand Realiä Modell C C C R R L R L R L R L ω = NF HF UHF Eingabe und Ausgabe sind Zeifunkionen x() bzw y() oder sogenanne Signale 2 Soffeineilung (nach der Ar des verarbeieen Signals) Zeikoninuierliche Syseme Zeidiskree Syseme Digiale Syseme x() x(k) 2 3 k x(k) k reell k ganzzahlig k ganzzahlig x() reell x(k) reell x(k) ganzzahlig 3 Lieraur Wunsch/Schreiber, Digiale Syseme, Verlag Technik / Springer Wunsch/Schreiber, Analoge Syseme, Verlag Technik / Springer
5 Teil : Digiale Syseme Mahemaische Grundlagen Algebraische Srukuren Operaion und Srukur Beispiele: = 7 x x 2 = x 3 A Die Menge A mi der auf ihr definieren Operaion * bilde eine algebraische Srukur, in Zeichen (A, ) a 2 a 3 = a a a 2 Beispiele: (R, +) (Z, ) reelle Zahlen mi Addiion ganze Zahlen mi Muliplikaion 2 Verallgemeinerungen a) Träger der Srukur kann auch mehr als eine Menge enhalen b) Srukur kann auch mehrere Operaionen enhalen Beispiele: (R, +, ) reelle Zahlen mi Addiion und Muliplikaion (P (M),,, ) Poenzmenge von M mi Vereinigung, Durchschni und Komplemen c) Operaionen können n sellig sein d) Bisher: a A, a 2 A a 3 = a a 2 A innere Operaion Allgemein: a A, a 2 A a 3 = a a 2 B A a a 2 B a 3 äußere Operaion Beispiel: Skalarproduk zweier Vekoren x x 2 = c 2
6 3 Isomorphe Srukuren Gegeben seien die Srukuren (A, ) und (B, ) (A, ) (B, ) Definiion: Die Srukuren (A, ) und (B, ) heißen isomorph (gleichgesalig), in Zeichen (A, ) = (B, ), falls eine bijekive x x 2 y y 2 Abbildung ϕ : A B exisier, so daß gil: x y x2 y 2 ϕ(x x 2 ) = ϕ(x ) ϕ(x 2 ) = y y 2 Die Abbildung ϕ heiß dann Isomorphismus Beispiel: (A, ) = (R +, ) (B, ) = (R, +) posiive reelle Zahlen mi Muliplikaion reelle Zahlen mi Addiion Behaupung: (R +, ) = (R, +) Isomorphismus: ϕ : R + R, ϕ(x) = log x Dann gil: ϕ(x x 2 ) = ϕ(x ) + ϕ(x 2 ), denn log(x x 2 ) = log x + log x 2 Beache: Isomorphe Srukuren unerscheiden sich lediglich durch die Bezeichnung der Elemene des Trägers und der Operaionen Ansonsen sind sie formal gleich Bedeuung isomorpher Srukuren Originalsrukur (kompliziere Operaion) Transformaion (bij Abbildung) Bildsrukur (einfache Operaion) Lösung in der Originalsrukur Rückransformaion Lösung in der Bildsrukur Beispiele: ˆ Logarihmenrechnung ˆ komplexe Wechselsromrechnung ˆ Funkionalransformaion (Fourier, Laplace, Z) 4 Boolesche Algebra Definiion: Die Srukur (A,,,, e, e ) heiß Boolesche Algebra, falls gil: (a) und sind assoziaiv (b) und sind kommuaiv 3
7 (c) is adjunkiv bezüglich und umgekehr (d) is disribuiv bezüglich und umgekehr (e) neurale Elemene x e = x, x e = x, (x A) (f) einsellige Operaion: x x = e, x x = e Beispiel: Mengenalgebra (P (M),,,,, M) Für beliebige M, M 2, M 3 M gil: () M (M 2 M 3 ) = (M M 2 ) M 3 Assoziaivgesez M (M 2 M 3 ) = (M M 2 ) M 3 (2) M M 2 = M 2 M Kommuaivgesez M M 2 = M 2 M (3) M (M M 2 ) = M Adjunkivgesez M (M M 2 ) = M (4) M (M 2 M 3 ) = (M M 2 ) (M M 3 ) Disribuivgesez M (M 2 M 3 ) = (M M 2 ) (M M 3 ) (5) M = M neurale Elemene M M = M (6) M M = M Komplemenbildung M M = Jede endliche Boolesche Algebra is zu einer endlichen Mengenalgebra isomorph 2 Schalalgebra 2 Rechenregeln Einfachser Sonderfall einer Booleschen Algebra: A = {e, e } Neue Symbolik: (A,,, e,, e ) (B,,,,, ) : oder Verknüpfung (Disjunkion), : und Verknüpfung (Konjunkion), : Negaion Eine Boolesche Algebra mi zweielemenigem Träger heiß Schalalgebra Rechenregeln der Schalalgebra: x (y z) = (x y) z x (y z) = (x y) z 2 x y = y x x y = y x 3 x (x y) = x x (x y) = x 4 x (y z) = (x y) (x z) x (y z) = (x y) (x z) 5 x x = x x = 6 x = x x = x 7 = = 8 x y = x y x y = x y 9 x x = x x x = x x = x = x = x () (6) ensprechen der Booleschen Algebra, x y wird of als xy geschrieben 4
8 Anwendung: Vereinfachung Boolescher Terme Beispiel: y = (ax (a x))(b )c a, b, c, x, y B = {, } = (ax (a x))c mi Regeln und 6 = (ax ax)c mi Regeln 8 und = (a a)xc mi Regel 4 = xc mi Regeln 5 und 6 Operaionsabellen oder und nich 22 Gaerschalungen Tabelle der Schalsymbole: Bezeichnung DIN 47 (al) DIN 49 (neu) Oder Gaer Und Gaer & Negaions Gaer NOR Gaer NAND Gaer & Anivalenz Gaer *) = Äquivalenz Gaer *) = *) nich genorm Bemerkungen: ˆ Die Variablen x, x 2, B heißen Schalvariablen und bezeichnen die Eingangs und Ausgangsbelegung eines Gaers ˆ Jedem Booleschen Term kann eine Gaerschalung zugeordne werden 5
9 Beispiele Gaerschalung zum Term x x 2 x 3 : x x 2 x 3 & y 2 Gaerschalung zum Term x x 2 x 3 : x x 2 x 3 & y einfacher: x x 2 x 3 & y 3 x x 2 x x 2 = x x 2 (Anivalenz, Exklusiv Oder) 4 x x 2 x x 2 = x x 2 (Äquivalenz) 23 Schalfunkionen Definiion: Die Abbildung f : B n B; f(x, x 2,, x n ) = y heiß n sellige Schalfunkion Eigenschafen I) Definiionsbereich: enhäl 2 n Elemene Werebereich: B = {, } B n = {, } n = {(,,, ), (,,, ),, (,,, )} }{{} n Elemene II) Anzahl n selliger Schalfunkionen: 2 (2n) (Tabelle s Formelsammlung) III) In die Rechenregeln der Schalalgebra (2) können anselle der Variablen x, y, z auch Schalfunkionen f, f 2, f 3 eingesez werden 24 Vollsändiges Operaionensysem Das Operaionensysem (,, ) is vollsändig dh es is jede beliebige Schalfunkion dami darsellbar Frage: Gib es weiere vollsändige Operaionensyseme? Beispiel : (, ) is vollsändig, läß sich durch ausdrücken: x x x 2 = x x 2 = x x 2 x 2 x & y y x 2 6
10 Beispiel 2: ( ) is vollsändig, wobei x x 2 = x x 2 (NAND) x = xx = x x x & y & x & y x x 2 = x x 2 = x x 2 = (x x ) (x 2 x 2 ) x 2 & x & x x 2 = x x 2 = x x 2 = (x x 2 ) (x x 2 ) & x 2 y 3 Darsellung von Schalfunkionen 3 Wereabelle Beispiel: n = 3, f : B 3 B, y = f(x, x 2, x 3 ) i x x 2 x 3 y Boolesche Terme Bemerkungen: ˆ Tabelle beschreib Schalbild vollsändig ˆ Es genüg Angabe der Zeilen mi Funkionswer ˆ Einführung Zeilenenindex i aus Indexmenge I: I f = {i : f(x, x 2,, x n ) = } mi i = Bin(x, x 2, x n ) Für obiges Beispiel: I f = {3, 5, 6} Konsanen und und die Variablen x, x 2, x n sind Boolesche Terme 2 Is B ein Boolescher Term, so auch B 3 Sind B und B 2 Boolesche Terme, dann auch B B 2 sowie B B 2 Beispiel: B = ((x x 2 x 3 )x 3 ) (*) Darsellung einer Schalfunkion ensprechend (3): Wereabelle x x 2 x 3 y Verallgemeinerung: Jeder Boolesche Term mi n Variablen sell eine n sellige Srukur dar Umkehrung: Jede n Sellige Srukur f : B n B läß sich durch einen Booleschen Term darsellen, jedoch nich in eindeuiger Weise Beispiel: Der Term sell die gleiche Schalfunkion dar wie B = x x 2 x 3 Definiion: Boolesche Terme die die gleiche Schalfunkion darsellen heißen äquivalen Sandardisierung durch sogenanne Normalfunkion! 7
11 33 Kanonische disjunkive Normalfunkion Definiion: Ein Boolescher Term des Typs m i = x i x 2 i 2 x n i n mi x ν i ν = heiß Minerm in n Variablen Eigenschafen { xν falls i ν = x ν falls i ν = m i enhäl jede Variable genau einmal und zwar negier oder nich negier 2 Alle Variablen sind konjunkiv verknüpf 3 m i nimm für genau eine Belegung der Variablen den Wer and, sons 4 Die Bedeuung des Index von i von m i : Die Binärdarsellung Bin (i) ensprich der Belegung für die m i den Wer annimm { für x =, x Beispiel: n = 3, m 2 = x x 2 x 3 = 2 =, x 3 = sons Darsellungssaz I f(x, x 2,, x n ) = i I f m i heiß Darsellung von f in kanonischer disjunkiver Normalform (KDNF) Beispiel: Wereabelle aus (3), I f = {3, 5, 6} f(x, x 2, x 3 ) = m i = m 3 m 5 m 6 = x x 2 x 3 x x 2 x 3 x x 2 x 3 i I f = x x 2 x 3 x x 2 x 3 x x 2 x 3 34 Kanonische konjunkive Normalform Definiion: Ein Boolescher Term des Typs M i = x i x 2 i 2 x n i n mi x ν i ν = heiß Maxerm in n Variablen Eigenschafen M i enhäl jede Variable genau einmal, negier oder nich negier 2 Die Variablen sind disjunkiv verknüpf { xν falls i ν = x ν falls i ν = 3 M i nimm genau für eine Belegung der Variablen den Wer an, sons immer 4 Bedeuung des Index i von M i : Die Binärdarsellung Bin (i) ergib die Belegung der Variablen für die M i = is 8
12 { Beispiel: n = 3, M 5 = x x 2 x x =, x 3 = x x 2 x 3 = 2 =, x 3 = sons Darsellungssaz II f(x, x 2,, x n ) = i I f M i mi I f = I I f heiß Darsellung von f in kanonischer konjunkiver Normalform (KKNF) Beispiel: (zur Vereinfachung mi einer anderen Wereabelle) i x x 2 x 3 f(x, x 2, x 3 ) I f = {, 5} f(x, x 2, x 3 ) = M i = M M 2 i I f = (x x 2 x 3 ) (x x 2 x 3 ) = (x x 2 x 3 ) (x x 2 x 3 ) Bemerkungen KDNF und KNNF sind eindeuig bis auf die Reihenfolge der Maxerme bzw Minerme 2 Wann KDNF bzw KKNF? Werespale enhäl mehr als KKNF, sons KDNF 35 Karnaugh Tafel Ziel: Gewinnen eines minimalen Booleschen Terms Beispiel: n = 4 Wereabelle: x x 2 x 3 x 4 f(x, x 2, x 3, x 4 ) m i f(,,, ) m f(,,, ) m f(,,, ) m 2 f(,,, ) m 5 Karnaugh Tafel für n = 4: x 3,4 x,2 m m m 3 m 2 m 4 m 5 m 7 m 6 m 2 m 3 m 5 m 4 m 8 m 9 m m Eigenschafen: Jedem Käschen is genau ein Minerm zugeordne 2 Die Minerme in den benachbaren Käschen unerscheiden sich in der Negaion genau einer Variablen, zb m = x x 2 x 3 x 4 m = x x 2 x 3 x 4 m 4 = x x 2 x 3 x 4 (benachbar sind auch die Randkäschen) 9
13 Beispiele 3 Um Schalfunkionen anzugeben werden die bereffenden Minerme durch markier 4 Vereinfachung der Schalfunkionen geschieh durch Blockbildung benachbarer Minerme f(x, x 2, x 3, x 4 ) = x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x 3,4 x,2 = x x 2 unerer Viererblock x x 3 x 4 Zweierblock Beim uneren Viererblock sind x 3 x 3 und x 4 x 4 immer wahr Beim oberen Zweierblock is x 2 x 2 immer wahr Daher können diese Terme wegfallen f(x, x 2, x 3, x 4 ) = x x 2 x x 3 x 4 2 f(x, x 2, x 3, x 4 ) = x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x x 2 x 3 x 4 x 3,4 x,2 = x 3 x 4 Viererspale x x 3 Viererblock In diesem Falle is es einfacher mi zwei Viererblöcken als mi einem Vierer und einem Zweierblock zu arbeien Vereinfach ergib sich für die Schalfunkion: f(x, x 2, x 3, x 4 ) = x 3 (x 4 x ) 3 f(x, x 2, x 3, x 4 ) = x x 2 x 3 x 4 x x 2 x x 2 x 3 x 4 x x 2 x x 2 x 3 x 4 x 3,4 x,2 = x 2 Acherblock x 3 x 4 Viererspale x x 3 Viererblock f(x, x 2, x 3, x 4 ) = x 2 x 3 (x x 4 )
14 2 Saische digiale Syseme (kombinaorische Auomaen) 2 Alphabebildung 2 Alphabee x x x 2 x l Φ y y 2 y m y zb Gaerschalung Definiionen: Die Menge X = {, } l = B l heiß Eingabealphabe mi den Buchsaben x x = (x, x 2, x 3,, x l ) oder x 2 x = x l 2 Die Menge Y = {, } m = B m heiß Ausgabealphabe mi den Buchsaben y y = (y, y 2, y 3,, y m ) oder y 2 y = y m 3 Jede Abbildung Φ : X Y kurz Φ(x) = y heiß Alphabeabbildung Φ(x, x 2,, x l ) = (y, y 2, y m ) 4 Das Eingabealphabe X = B l und das Ausgabalphabe Y = B m zusammen mi der Alphabeabbildung Φ bilde ein (absrakes) saisches digiales Sysem (oder einen kombinaorischen Auomaen), in Zeichen: (X, Y, Φ) Beache: (X, Y, Φ) sell eine algebraische Srukur dar: X x Φ y Y
15 22 Syseme mi einem Ausgang Sonderfall: m =, X = B l, Y = B = {, } x x 2 x l Φ y y = Φ(x, x 2,, x l ) Ergebnis: Die Alphabeabbildung sell eine l sellige Schalfunkion dar 23 Syseme mi mehreren Ausgängen Beispiel: l = 3, m = 2 x x 2 x 3 & y Φ & y 2 y = x x 2 x 3 = f (x, x 2, x 3 ) y 2 = x x 2 x 3 = f(x, x 2, x 3 ) Verallgemeinerung: (l, m beliebig) Die Alphabeabbildung Φ läß sich durch m l sellige Schalfunkionen f i : B l B (i =,, n) darsellen f (x, x 2,, x l ) = y f 2 (x, x 2,, x l ) = y 2 f m (x, x 2,, x l )= y m Φ : B l B m x f x l f 2 y y 2 Φ f m y 3 2
16 22 Worabbildung 22 Buchsaben und Wörer Definiionen: Zeiskala T = {,,, k,, N}, Takzeipunke k T (äquidisan) Die Zei is normier (dimensionslos) 2 Die Abbildung x : T X heiß digiales Eingabesignal oder Eingabewor Schreibweise: x = (x(), x(), x(2),, x(k),, x(n)) x(k) X is Eingabebuchsabe im Takzeipunk k x () x () x (N) (x (), x (), x (2),, x (N)) x x 2 () x =, x 2 (),, x 2 (N) = (x 2 (), x 2 (), x 2 (2),, x 2 (N)) = x 2 x l () x l () x l (N) (x l (), x l (), x l (2),, x l (N)) x l 3 Die Abbildung y : T Y heiß digiales Ausgabesignal oder Ausgabwer Schreibweise: y = (y(), y(), y(2),, y(n)) y (k) y 2 (k) Mi y(k) = analog zu 2 y m (k) 4 Worlänge l(x) = T = N + 5 Eingabeworraum: X T = X Menge aller Eingabewörer Ausgabeworraum: Y T = Y Menge aller Ausgabewörer 6 Die Abbildung Φ : X Y, Φ(x) = y heiß Worabbildung 222 Eigenschafen der Worabbildung Offensichlich: Abbildung erfolg Buchsabe für Buchsabe Eingabewor: x : x() x() x(2) x(n) Φ Φ Φ Φ Ausgabewor: y : y() y() y(2) y(n) Grundgleichung des kombinaorischen Auomaen: y(k) = Φ(x(k)) Diskussion: l(y) = l(y) 2 Ausgabe y(k) im Tak k häng nur von Eingabe x(k) im gleichen Tak k ab, nich aber von x(k ), x(k 2), 3 gleiche Eingangsbuchsaben haben gleiche Ausgangsbuchsaben zur Folge 3
17 Gegenbeispiel: x? y x = (,,,,, ) y = (,,,,, ) Diese Worabbildung is durch einen kombinaorische Auomaen nich realisierbar 3 Dynamische digiale Syseme (sequenieller Auoma) 3 Zusandsbeschreibung 3 Speicher Zusäzlich zu den beracheen BE (Gaer) wird eingeführ: Speicher S x(k) = y(k + ) x S y Durch Hinzunahme von Speichern zu einem kombinaorischen Auomaen enseh ein sequenieller Auoma Beispiel: x (k) x 2 (k) & S z (k) y (k) z 2(k) S 2 x 3 (k) & z 2(k+) y 2 (k) z 3 (k) S 3 z 3 (k+) Regel: An den Ausgängen der Speicher werden Hilfswörer z i erzeug, da ein direker Zusammenhang zwischen y(k) und x(k) nich dargesell werden kann Aus Schalung ablesbar: Eingangswer x = x x 2 x 3 Gesuch: Ausgangswer y = = ( y z (k + ) = z 2 (k)(x (k) x 2 (k)) z 2 (k + ) = z 3 (k) z 3 (k + ) = z (k) x 3 (k)z 3 (k) y 2 y (k) = z (k) y 2 (k) = z (k) x 3 (k)z 3 (k) (,, ) (,, ) (,, ) ) =?, Anfangszusand z() = z () z 2 () z 3 () = 4
18 Lösung k 2 3 x (k) x 2 (k) x 3 (k) z (k) z 2 (k) z 3 (k) y (k) y 2 (k) Ergebnis: y = ( y y 2 ) = ( (,, ) (,, ) ) 32 Zusandsgleichungen Verallgemeinerung: x x 2 x l Gaer + n Speicher y y 2 y m z(k) x(k) {}}{{}}{ z (k + ) = f [ z (k),, z m (k), x (k),, x l (k)] z(k + ) z n (k + ) = f n [z (k),, z m (k), x (k),, x l (k)] y (k) = g [z (k),, z m (k), x (k),, x l (k)] y(k) z n (k + ) = f n [z (k),, z m (k), x (k),, x l (k)] Zusammenfassung des sequeniellen Auomaen: z(k + ) = f[z(k), x(k)] y(k) = g[z(k), x(k)] Definiionen: Die Menge Z = B n = {, } n heiß Zusandsalphabe (Zusandsraum) 2 Die Abbildung z T Z heiß Zusandswor (Zusandsrajekorie) z (k) z = (z(), z(),, z(n)) mi z(k) = z(k) heiß Zusand des Auomaen im Tak k z n (k) 5
19 3 z() = z () z n () Diskussion der Zusandsgleichungen f: Überführungsfunkion g: Ergebnisfunkion heiß Anfangszusand des Auomaen Definiion: Die Mengen X = B l (Eingabealphabe), Y = B m (Ausgabealphabe) und Z = B n (Zusandsalphabe) zusammen mi den Abbildungen f : Z X Z f[z(k), x(k)] = z(k + ) g : Z X Y g[z(k), x(k)] = y(k) bilden ein (absrakes) dynamisches digiales Sysem (oder einen absraken sequeniellen Auomaen oder Mealy Auomaen), in Zeichen (X, Y, Z, f, h) z(k) x(k) n Leiungen l Leiungen f S g z(k + ) m Leiungen y(k) Der sequenielle Auoma is durch zwei herkömmliche Auomaen (f und g) und n Speicher darsellbar Beispiel: (aus 3) z (k + ) = z 2 (k)(x (k) x 2 (k)) z 2 (k + ) = z 3 (k) z 3 (k + ) = z (k) x 3 (k)z 3 (k) y (k) = z (k) y 2 (k) = z (k) x 3 (k)z 3 (k) z (k) z 2 (k) z 3 (k) x (k) x 2 (k) x 3 (k) & S z (k+) z 2 (k+) S z 2 (k) & S z 3 (k+) & y (k) y 2 (k) 6
20 33 Auomaendarsellung x (k) x 2 (k) x(k) x l (k) Gaer + n Speicher y (k) y 2 (k) y(k) y m (k) z(k + ) y(k) = f[z(k), x(k)] = f[z(k), x(k)] (z (k), z 2 (k),, z 3 (k)) }{{} z(k) Der sequenielle Auoma läß sich wie folg darsellen: Auomaenabelle: Zusandsalphabe f z(k) Zusandsalphabe g z(k) Eingabealphabe x(k) z(k + ) Eingabealphabe x(k) z(k + ) Überführungsabelle Ergebnisabelle 2 Auomaengraph Bezeichnung Symbol Bedeuung Knoen O Zusand Zweige (Kanen) Zusandsübergänge Zusandsgleichungen dargesell durch: z(k) x(k) y(k) z(k+) Beispiel : X = {, }, Y = {, }, Z = {(, ), (, ), (, ), (, ) } }{{}}{{}}{{}}{{} 2 3 Auomaenabelle (gegeben): Auomaengraph: X Z {}}{ { f X Z {}}{ { g 2 3 Es sei x = (,,,, ) und z() = Ablesen: y = (,,,, ) und z(5) =
21 Beispiel 2: gegeben: Auomaengraph gesuch: Auomaenabelle, Zusandsgleichungen, Schalung Auomaenabelle: X Z {}}{ { f X Z {}}{ { g Wereabelle z(k) x(k) z(k + ) y(k) Dekodiere Wereabelle z (k) z 2 (k) x(k) z (k + ) z 2 (k + ) y (k) y 2 (k) Zusandsgleichungen (aus Karnaugh-Diagramm): Schalung: f : z (k + ) = z (k) z 2 (k) x(k) f 2 : z 2 (k + ) = z 2 (k) x(k) z (k) z 2 (k) x(k) g : y (k) = z (k) x(k) z (k) z 2 (k) x(k) g 2 : y 2 (k) = z 2 (k) x(k) z (k) z 2 (k) x(k) f f 2 g g 2 z (k+) S z (k) z 2 (k+) S z 2 (k) y 2 (k) y (k) 34 Spezielle Auomaen Allgemeiner Fall: Mealy-Auoma x(k) f z(k+) S z(k) g y(k) z(k + ) = f[z(k), x(k)] y(k) = g[z(k), x(k)] 8
22 Sonderfälle: (a) Moore-Auoma x(k) f S g z(k+) z(k) y(k) z(k + ) = f[z(k), x(k)] y(k) = g[z(k)] (b) Medwedjew-Auoma x(k) f z(k+) S y(k) z(k) z(k + ) = f[z(k), x(k)] y(k) = z(k) (c) Auonomer Auoma (Generaor) f S g z(k+) z(k) y(k) z(k + ) = f[z(k)] y(k) = g[z(k)] NB: Bei allen Auomaen muß der Zusand z() bekann sein 32 Worabbildungen 32 Abbildungsfamilie Zusandsgleichungen Schema der Worabbildung: Eingabewor x {}}{ x() x() x(n) z() f, g z() f, g z(2) z(n) f, g z(n + ) y() y() y(n) } {{ } Ausgabewor y Diskussion: Eingabewor und Ausgabewor haben die gleiche Länge, L(x) = L(y) 2 Der Ausgabebuchsabe y(k) häng von x(k), x(k ),, x() ab, nich aber von x(k + ), x(k + 2), (Kausaliä) 3 Das Ausgabewor y häng vom Anfangszusand z() ab 9
23 Definiionen: Die Abbildung Φ z : X Y, Φ z (x) = y heiß vom Anfangszusand z = z() Z erzeuge Worabbildung 2 Jedem Mealy-Auomaen is eine Abbildungsfamilie zugeordne 322 Eigenschafen der Worabbildung Φ = {Φ z z Z} Definiion: Sind x = (x (), x (),, x (r)) und x = (x (), x (),, x (s)) zwei Wörer aus X, so heiß das Wor x x = (x (), x (),, x (r), x (), x (),, x (s)) X Verkeungsproduk (Konkaenaionsproduk) von x und x Beache: Eine Worabbildung Φ z : X Y is durch einen Mealy-Auomaen realisierbar, falls gil: L(x) = L(y) 2 Φ z (x x ) = Φ z (x ) Φ z (x ) (z : Zusand nach Eingabe von x ) }{{}}{{} y y 323 Auonomer Auoma Wir berachen Mealy-Auomaen mi konsaner Eingabe Beispiel: Es sei z() = 2 3 Fall I: x = (,,,, ) z = (, 2,, 3, 2,, 3, 2,, ) y = (,,,,, }{{} Zyklus,,,, ) periodische Folge Fall II: x = (,,,, ) z = (,,,,,,,, ) y = (,,,,,, }{{} Fixpunk, ) konsane Folge Verhalensformen des endlichen auonomen Auomaen I) Da bei Z = 2 n nach späesens 2 n Taken alle Zusände ausgeschöpf sind, wird späesens im Tak 2 n ein bereis durchlaufener Zusand erreich s: Periodendauer z(k + s) = z(k), für < s < z n II) Nach r Taken wird ein konsaner Endzusand (Fixpunk) erreich: z(k + ) = z(k), (An Schlingen im Graphen erkennbar) für k > r 2
24 Teil 2: Zeikoninuierliche Syseme 4 Zeikoninuierliche Signale und Syseme 4 Signalbeschreibung im Zeibereich 4 Zeikoninuierliche Signale Feslegungen: Zeiskala: Sonderfälle: Alphabe: Sonderfall: R T = R T = R + = [, ) X = C X = R Definiion: Ein zeikoninuierliches Signal is eine Abbildung x : T X, durch die jedem Zeipunk T ein Signalwer x() X zugeordne is Sonderfall: x : T R reelles zeikoninuierliches Signal oder analoges Signal Beispiel: x() e a, < a < 42 Signaloperaionen Einsellige Operaionen a) Skalarmuliplikaion y() = α x() x() y() y() x() b) Translaion x() y() y = S τ (x) y() = x( τ) x() y() 2
25 c) Differeniaion d) Inegraion y = D(x) y() = dx() d y = D (x) y() = x(τ) dτ x() y() y() x() x() y() y() x() Zweisellige Operaionen a) Signaladdiion: y() = x () + x 2 () b) Signalmuliplikaion: y() = x () x 2 () c) Falung: y = x x 2 y() = (x x 2 )() = x (τ) x 2 ( τ) dτ = x 2 (τ) x ( τ) dτ = (x 2 x )() Falung is kommuaiv! Sonderfall: x () = für <, x 2 () = für < Veranschaulichung am Beispiel x (τ) y() = (x x 2 )() = x (τ) }{{} x 2 ( τ) dτ }{{} für τ< für τ> x 2 (τ) τ x 2 (τ ) x 2 (τ ) x (τ) x 2 (τ ) τ τ τ : x (τ) x 2 ( τ) : y() = x (τ) x 2 ( τ) dτ τ 22
26 43 Spezielle Signale (a) Sprungsignal () 2 (b) Rampensignal r() (c) Rechecksignal für > () = 2 für = für < r() = r = D () (τ) dτ = r() = () x() = a ( + τ) a ( τ) { für für < x() a τ a τ x() a τ τ (d) Impulssignal, Dirac-Impuls a für τ < < τ a x() = 2 für = ±τ sons Aus (c) erhäl man für τ = ε und a = 2ε das schmale Rechecksignal δ ε δ ε () 2ε τ τ δ ε () ε = δ() = { für für = mi δ() d = Impulssignal, Dirac-Impuls, Dela-Funkion Diskussion: ˆ lim ε δ ε = exisier nich 23
27 ˆ lim ε kurz: δ ε () f() d = f() exisiier (e) Harmonisches Signal x() δ() f() d = f() Ausblendeeigenschf der Dirac-Funkion x() = ˆX cos(ω + ϕ x ) 44 Signale allgemeineren Typs Definiionen: Ein Signal heiß sückweise seig, wenn in jedem endlichen Teilinervall gil: (a) x is seig für alle τ i (i =,, n) (b) lim ε x(τ i ± ε) exisieren (kurz x(τ ± )) τ i τ i τ i+ 2 Ein Signal heiß sückweise gla, wenn (a) und (b) auch für ẋ gelen 45 Inerpolaion abgeaseer Signale a) Inerpolaionsproblem Zeikoninuierliches Signal Äquidisane Abasung x() x() 2 k x(k) = x() =k k Aufgabe: Zwischenwere inerpolieren, Abaswere unveränder lassen 24
28 b) Ansaz: Lagrangesche Inerpolaionsformel x() x( ) x( 2 ) x( 3) 2 3 x() = x( ) + x( 2 ) + x( 3 ) ( 2 )( 3 ) ( 2 )( 3 ) ( )( 3 ) ( 2 )( 2 3 ) ( )( 2 ) ( 3 )( 3 2 ) bei =, 2 und 3 = bei 2 =, und 3 = bei 3 =, und 2 = Verallgemeinerung auf K Messwere: x() = K ( ) ( k )( k+ ) ( K ) x( k ) ( k + ) ( K k )( k k+ ) ( k K ) k= mi P K () = ( )( 2 ) ( K ): x() = K P K () x( k ) ( k ) P K ( k ) k= P K () = 2 K 2 }{{ K } Q K () x() = k= K Q K () x( k ) ( k ) Q K ( k ) c) Lagrange-Inerpolaion für äquidisane Abaswere k = k, (k ganz), K ( Q () = k = k= ( ) 2 k 2 2 Einsezen in das Ergebnis von b): ( ) ) = sin π ( ) ( ) k x() = = = k= k= k= x(k ) (Abasreihe, Samplingreihe) sin π ( k ) π cos π k }{{} x(k ) k sin π ( k ) π = x(k ) sin( π ( k )) π ( k k k= x(k ) sin( π k π) ( k ) π 25
29 d) Inerpreaion der Samplingreihe Aufbaufunkion vom Typ sin α α = si α si α 3π 2π π π 2π 3π α ( π ) x() = x(k ) si ( k ) k= Beispiel für k = 3, x() =, x() =,5, x(2) =,75: x() 2 3 k = 42 Saische Syseme mi koninuierlicher Zei 42 Elemenarsyseme Grundbauseine Signalabbildung Gleichung Schalsymbol Bezeichnung Skalarmuliplikaion y() = α x(), α R x() α y() Versärker x () Signaladdiion y() = x () + x 2 () + y() Versärker x 2 () Signalmuliplikaion y() = x () + x 2 () x () x 2 () y() Muliplizierglied Sonderfall y() = [x()] n x() () n y() Poenzierglied 26
30 Beispiel für Zusammenschalung x () x 2 () () 2 a + b y () y 2 () y 3 () y () = f (x (), x 2 ()) = a (x ()) 2 + b x () x 2 () y 2 () = f 2 (x (), x 2 ()) = b x () x 2 () y 3 () = f 3 (x (), x 2 ()) = x () x 2 () Schema x () x 2 () Φ y () y 2 () y 3 () Φ : R 2 R 3 Φ(x (), x 2 ()) = (y (), y 2 (), y(3) ) }{{}}{{} R 2 R 3 Wichiger Sonderfall: Resisives elekrisches Nezwerk (keine Energiespeicher) u 2 () u D () u R3 () i i 3 2() () R 3 u () i () Eingänge: u () x () u 2 () x 2 () Ausgang: i () y () i 2 () y 2 () i 3 () y 3 () Widersand: i 3 () = u R3() = u () R 3 ( ) Diode: i 2 () = a e b ud() R 3 Knoengleichung: i () = i 2 () + i 3 () Maschengleichung: u D () = u () + u 2 () i () = f (u (), u 2 ()) = u ( ) () + a e b(u ()+u 2 ()) R ( 3 ) i 2 () = f 2 (u (), u 2 ()) = a e b(u ()+u 2 ()) i 3 () = f 3 (u (), u 2 ()) = u () R 3 27
31 422 Verallgemeinerung der Beispiele x () x 2 () x() x l () Φ y () y 2 () y() y m () y () = f (x (),, x l ()) y m () = f m (x (),, x l ()) Definiionen: a) Die Menge X R l heiß Eingabealphabe mi den Buchsaben (Signalweren) x () x() = X x l () b) Die Menge Y R m heiß Ausgabealphabe mi den Buchsaben (Signalweren) y () y() = Y y m () c) Die Abbildung Φ : X Y Φ(x (), x l ()) = (y (),, y m ()), kurz Φ(x()) y() heiß Alphabeabbildung d) Das Eingabealphabe X, das Ausgabealphabe Y und die Alphabeabbildung Φ bilden ein (absrakes) saisches Sysem, in Zeichen: (X, Y, Φ) e) Die Abbildung x : T X, (X = R l ) heiß l dimensionales Eingabesignal: x l () xx () x 2 () x x 2 x l x f) Die Abbildung y : T Y, (Y = R m ) heiß n dimensionales Ausgabesignal g) Die Menge aller Eingangssignale X T = X heiß Eigangssignalraum, die Menge aller Ausgabesignale Y T = Y heiß Ausgabesignalraum h) Die Abbildung Φ : X Y, Φ(x) = y heiß Signalabbildung 28
32 423 Kleinsignalverhalen x i () Φ y j () x i () c i Für alle Eingänge soll gelen: Für die Ausgänge gil dann: Taylorreihe: x i () = c i + x i (), i =,, l, x i () max c i y j () = f j (x (),, x l ()) f(x + h) = f(x) +! f (x) h + 2! f (x) h 2 + für h x berachen wir als gue Näherung nur das erse Glied der Taylorreihe: y j () = f j (x (),, x l ()) f j (c,, c l ) + y j (), l f i f j (c,, c l ) + (c,, c l ) x i x i= i }{{} y j () y () y m () } {{ } y() = mi c i = c konsane Marix, Kurzform: f f x x l f m f m x x l }{{} Jacobi-Marix J(x) x i =c i j =,, m x () x l () } {{ } x() y() = J(c) x() Linearisierung bei Kleinsignalberieb! Beispiel: Sysem aus Abschni 42 y () = f (x (), x 2 ()) = a (x ()) 2 + b x () x 2 () y 2 () = f 2 (x (), x 2 ()) = b x () x 2 () y 3 () = f 3 (x (), x 2 ()) = x () x 2 () J(x) = f x f x 2 f 2 x f 2 x 2 f 3 x f 3 x 2 2ax + bx 2 bx = bx 2 bx x 2 x 29
33 Es seien: x () = c + x cos(ω + ϕ ) und x 2 () = c 2 + x 2 cos(ω 2 + ϕ 2 ) }{{}}{{} x mi x c, x 2 c 2 y () 2ax + bx 2 bx y 2 () = bx 2 bx y 3 () x 2 x x 2 ( x cos(ω + ϕ ) x 2 cos(ω 2 + ϕ 2 ) ) y () ac 2 + bc c 2 + (2ac + bc 2 ) x cos(ω + ϕ ) + bc x 2 cos(ω 2 + ϕ 2 ) y 2 () bc c 2 + bc 2 x cos(ω + ϕ ) + bc x 2 cos(ω 2 + ϕ 2 ) y 3 () c c 2 + c 2 x cos(ω + ϕ ) + c x 2 cos(ω 2 + ϕ 2 ) 43 Dynamische zeikoninuierliche Syseme 43 Zusandsbeschreibung Hinzunahme eines weieren Elemens: Inegrierglied x() y() y() = y + Beispiel aus der Elekroechnik: Kondensaor i() Q Q() = Q() + i(τ) dτ, Zusammenschalung mi Elemenarsysem (42): x(τ) dτ, Q() = i() ẏ() = x() x 2 () a ż() z () () 2 y () () 2 y 2 () z 2 () ż 2 () x 2 () + y 3 () ż () = a x () z 2 () = z () z 2 2 () y () = (z () z 2 2 ()) 2 = z 2 () z 2 4 () y 2 () = z 2 2 () y 3 () = z 2 () + x 2 () nichlineares gekoppeles DGL-Sysem Ordnung Es sei: x () = für z () = x 2 () = sin ω für z 2 () = 3
34 Lösung: ż () = ax () = a z () = a c mi z () = c = z () = a 2 2 ż 2 () = z () z 2 2 () = a2 2 z 2 2 () dz 2 z 2 = a2 2 2 d z 2 = a3 6 + c 2 mi z 2 () = c 2 = z 2 () = a 3 6 = 6 a Einsezen in Ergebnisfunkionen y (), y 2 (), y 3 () Ggf numerische Lösungsverfahren für kompliziere DGL-Syseme anwenden Schema für Beispiel x () x 2 () z (), z 2 () y 3 () y 2 () y () Wichigser Sonderfall: Nichlineares RLC-Nezwerk i C () i L () u C () u () u R () i R () Schema: x () z (), z 2 () u L () y 2 () y () Eingabe: u () x() Ausgabe: u L () y () u C () y 2 () Zusände: Φ() z () (Magnefluß) Q() z 2 () (Ladung) Schalelemene: i R () = ϕ R (u R ()) = u() R u C () = ϕ C (Q()) = Q() C i L () = ϕ L (Φ()) u L () = Φ() i C () = Q() = Φ() L 3
35 Maschengleichung: u () = u C () + u L () = ϕ C (Q()) + Φ() Knoengleichung: i C () = i R () + i L () = ϕ R (u R ()) + ϕ 2 (Φ()) = Q() Zusandsgleichungen: Φ() = u () ϕ C (Q()) Q() = ϕ L (Φ()) + ϕ R (u R ()) = ϕ L (Φ()) + ϕ R (u () ϕ C (Q())) u L () = u () ϕ C (Q()) u C () = ϕ C (Q()) allgemein: ż () = f (z (), z 2 (), x()) ż 2 () = f 2 (z (), z 2 (), x()) y () = g (z (), z 2 (), x()) y 2) = g 2 (z (), z 2 (), x()) Verallgemeinerung x () x 2 () x() x l () z (),, z n () }{{} z() y () y 2 () y() y m () ż () = f (z (),, z n (), x (),, x l ()) ż() = ż n () = f n (z (),, z n (), x (),, x l ()) y () = g (z (),, z n (), x (),, x l ()) y() = y m () = g m (z (),, z n (), x (),, x l ()) Kurzform: ż() = f(z(), x()) y() = g(z(), x()) Grundgleichung des zeikoninuierlichen dyn Sysems f: Überragungsfunkion g: Ergebnisfunkion 32
36 Definiionen: Die Menge Z = R n heiß Zusandsalphabe (auch Zusandsraum) z () z() = Z, (z i () R, i =,, n) z n () 2 z() heiß Zusand des Sysems zum Zeipunk z() heiß Anfangszusand des Sysems 3 Die Abbildung z : T Z (Z = R n ) heiß n-dimensionales Zusandssignal (oder Zusandsrajekorie) z l () z () z 2 () z z 2 z n z z() z 3 z 3 z() z 2 4 Die Mengen X = R l (Eingabealphabe), Y = R m (Ausgabealphabe) und Z = R n (Zusandsalphabe) sowie die Überführungsfunkion und die Ergebnisfunkion f : Z X Z, f(z(), x()) = ż() g : Z X Y, g(z(), x()) = y() bilden ein absrakes zeikoninuierliches dynamisches Sysem, in Zeichen (X, Y, Z, f, g) 432 Lineares zeikoninuierliches Sysem Ordnung ż() = a z() + b x() } Überführungsfunkion y() = c z() + d x() Ergebnisfunkion (f und g sind jez lineare Funkionen) Zusandsgleichungen Schalung a x() b c y() ż() z() d gegeben: x() für, z() gesuch: y() für 33
37 Lösung: ż() a z() = b x() lineare DGL (inhomogen) Ordnung z() = z() e a + y() = c z() e a + }{{} freie Ausgabe b e a( τ) x(τ) dτ b c e a ( τ) x(τ) dτ + d x() } {{ } erzwungene Ausgabe 433 Nichlineares zeikoninuierliches Sysem Ordnung Beispiel: u R () R u() C i() u C () Zuordnungen: u() x() i() y() u C () z() nichlinearer Widersand: i R () = α u R 3 () (Varisor-Typ) linearer Kapaziviä: u C () = C Q(), u C() = C Q() = C i() Maschengleichung: u() = u R () + u C () Knoengleichung: i() = i R () = i R () Zusandsgleichungen: u C () = C i R() = C α u R 3 () u C () = α C [u() u C()] 3 ż() = f[z(), x()] i() = α [u() u C ()] 3 y() = g[z(), x()] u() U Lösung für : du C () d u() = U () = α C [U u C ()] 3 Lösung durch Trennung der Veränderlichen ) C u C () = U ( 2α U 2 + C i C () = C du ( 2 C() C U = i() = α d 2α U 2 + C ) 3 2 i() 34
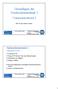
38 5 Lineare Syseme 5 Signalbeschreibung im Bildbereich (Fourier-Transformaion) 5 Die komplexe Fourier-Reihe x() ω = 2π T Grundfrequenz T T 3T T 2 7T 2 Saz: Für jedes mi T periodische sückweise glae Signal x gil: x() = c(ω k ) e jω k k= (ω k = k ω ) wobei c(ω k ) = T T 2 x() e jω k d komplexer Fourier-Koeffizien T 2 Beweisskizze: c(ω n ) = T T 2 x() e jωn d Einsezen von x() T 2 = T T 2 T 2 = T k= k= = T c(ω ) c(ω k ) T 2 T 2 c(ω k ) e jω k e jωn d ω k = k ω, ω n = n ω T 2 T 2 d e j(k n)ω d Inegral verschwinde, außer für k = n Komplexe Fourier-Koeffizienen: c(ω k ) = c k Die Folge c = (, c 2, c, c, c, c 2, ) heiß komplexes diskrees Fourier-Spekrum des periodischen Signals 35
39 Eigenschafen der Koeffizienen c k : c k = c k = c k z + z = 2 Re (z), c k = c k e j arg c k x() = c k e jωk = c + 2 Re (c k e jωk ) k= k= x() = c + 2 c k cos(ω k + arg c k ) reelle Fourierreihe k= Graphische Darsellung Ampliudenspekrum Phasenspekrum c k arg c k ω-3 ω-2 ω- ω ω ω 2 ω 3 ω k gerade Funkion, da c k = c k = c k k ungerade Funkion, da arg c k = arg c k = arg c k 2 k= c k 2 = T 2 T 2 x 2 () d Parsevalsche Formel (Leisungsbilanz) 3 c k für k 52 Fourier-Inegral Aperiodische Signale Ansaz: Fourier-Reihe mi T Definiion: Signalraum X : Es gil x X, falls (a) x is sückweise gla (b) x is absolu inegrierbar, dh x() d < Saz: Für jedes Elemen x X gil die Darsellung x() = 2π X(ω) e jω dω, wobei X(ω) = x() e jω d X heiß kompexes (koninuierliches) Fourier-Spekrum des Signals x 36
40 Eigenschafen X( ω) = X (ω) Ampliudendichespekrum X(ω) Phasenspekrum arg X(ω) ω ω 2 x 2 () d = 2π (X(ω)) 2 dω Parsevalsche Formel (Leisungsbilanz) 3 X(ω) für ω Beispiele: Korrespondenzabelle S 55 Erser Einrag: Dirac-Impuls X(ω) = δ() e jω d = 53 Fourier-Transformaion X Fourier-Inegral X x y Originalsignal Bild- funkion Originalbereich Fourier-Umkehrinegral Bildbereich Zusammenfassung: Zu jedem x X exisier eine bijekive Abbildung mi den Zuordnungen x X X x Diese Abbildung heiß Fourierransformaion bzw Fourierrückransformaion Schreibweise: F{x()} = X(ω), F {X(ω)} = x() X(ω) = x() e jω d = x()e j2πf d x() = 2π X(ω) e jω dω = X(f)e j2πf df 37
41 54 Rechenregeln der Fourier-Transformaion Hef S 54 F{α x () + β x 2 ()} = α F{x ()} + β F{x 2 ()} = α X (ω) + β X 2 (ω) (Linearkombinaion) 2 Verschiebungssaz x() x( τ) F{x()} bekann, F{x( τ)} gesuch τ F{x( τ)} = = e jωτ x( τ) e }{{}} jω {{} e jω( +τ) x( ) e jω d d }{{} d τ =, = + τ = e jωτ F{x()} e jωτ : Verschiebungsfakor 5 Differeniaionsregel: F{ẋ()} = jωf{x()} = jωx(ω) { } 7 Falungssaz: F{(x x2)()} = F x (τ)x 2 ( τ) dτ = X (ω) X 2 (ω) 52 Signalbeschreibung im Bildbereich (Laplace-Transformaion) 52 Laplace-Inegral Nacheil der Fourier-Transformaion: konvergier für wichige Signale nich, zb ˆ Sprungfunkion (()) ˆ periodische Funkionen Ansaz: (σ >, s = σ + jω: komplexe Frequenz) Definiion: Signalraum X γ Es gil: x X γ, falls (a) x is sückweise gla (b) für < is x() = F{x() e σ () } = }{{} X ( kausale Signale ) x() e (σ+jω) = X(σ + jω) }{{} s (c) für gil x() < M e γ ( < M <, γ < ) 38
42 Veranschaulichung: x() M e γ x M e γ Im s = ω ω s γ δ σ Re s = σ Konvergenzhalbebene C γ X(s) = x() e s d Laplace-Inegral Saz: Für jedes Inegral x X γ gil die Darsellung x() = 2πj δ+j δ j X(s) e s ds Laplace-Umkehrinegral Bemerkungen: Das Laplace-Inegral konvergier für alle s = σ + jω, für die Re (s) = σ > γ gil 2 X(s) sell im Inneren von C γ (Konvergenzhalbebene) eine reguläre (analyische, holomorphe) Funkion der komplexen Variablen s dar 3 Für das Umkehrinegral gil: δ > γ Beispiele x() = () x() 2 x() = () x() X(s) = X(s) = () e s d = }{{} = e s = s () e s d = }{{} e s d = e s s für Re (s) = σ > = s 2 für Re (s) = σ > e s d = [ ] 39
43 3 x() = e a () (a R) x() X(s) = = s a e a e s d = e (s a) d = e (s a) (s a) Bedingung: Re (s a) >, Re (s) = σ > a Korrespondenzen: Doesch, Anleiung zum prakischen Gebrauch der Laplaceransformaion, siehe auch Tabelle im Hef 522 Laplace-Transformaion X γ x Original-/Zeibereich Laplace-Transformaion y X γ inverse Laplace- Transformaion Bildbereich Für alle Signale x X γ exisier eine bijekive Abbildung mi den Zuordnungen x X X x Diese Abbildung heiß Laplace-Transformaion bzw inverse Laplace-Transformaion 523 Rechenregeln L(x()) = X(s) = L (X(s)) = x() = 2πj x() e s d δ+j δ j X(s) e s ds Nr x() X(s) Bemerkung αx () + βx 2 () αx (s) + βx 2 (s) Lineariä 2 x( τ), (τ > ) e sτ X(s) Verschiebungssaz x() x() τ ) 3 x(a ), (a > ) a X ( s a Ähnlichkeissaz a > : Sauchung a < : Sreckung 4 ẋ() s X(s) x(+) Differeniaionsregel x() x(+) 4
44 5 x(τ) dτ X(s) s Inegraionsregel 6 x() e a X(s + a) Dämpfungssaz 7 x (τ)x 2 ( τ) dτ X (s) X 2 (s) Falungssaz = (x x 2 )() Anwendungsbeispiele x() a τ L(x()) = = x() e s d = τ a τ e s d + τ a e s d Zerlegung Vereinfachung x() x a τ x 2 x() = x () + x 2 () x () = a τ () x 2 () = a ( τ) ( τ) τ X(s) = X (s) + X 2 (s) = a }{{} τ Regel s 2 a τ 2 gegeben: X(s) = e sτ, gesuch: x() =? s(s + 3) }{{} X (s) s 2 e sτ } {{ } Regel 2 Zunächs: L {X (s)}, danach Zeiverschiebung um τ X (s) = Aus der Korrespondenzabelle: Zeiverschiebung um τ (e sτ ): x () x() = a τs 2 ( e sτ ) s(s + 3) = A s + B s + 3, durch Parialbruchzerlegung: A = 3, B = 3 x () = 3 () 3 e 3 () = 3 x() = x ( τ) = 3 ( e 3 ) () ( e 3( τ)) ( τ) x x τ 4
45 3 gegeben (Q C () = ): gesuch: i() für > R L C = u() i() di() R i() + L + i(τ) dτ = u() d C Differenialgleichung L-Transformaion: R I(s) + L(s I(s) i(+) ) + }{{}}{{} C s I(s) = U(s) }{{} Regel 4 Regel 5 ( R + s L + ) I(s) = U(s) s C Beache: Einfacher Zusammenhang im Bildbereich 2 Gleichung kann mi Regeln der E-Technik sofor aus Schalung abgelesen werden verallgemeinere symbolische Mehode I(s) = U(s) R + sl + sc = U(s) L = s (s s )(s s 2 ) U(s) sc s 2 LC + src + = U(s) s L s 2 + s R L + LC s /2 = R 2L ± ( R 2L ) 2 LC, sei ( ) R 2 > 2L LC s, s 2 R I(s) = U(s) [ A + B ], A = s, B = s 2 }{{ L } s s s s 2 s s 2 s 2 s }{{} X 2 (s) X (s) Falungssaz (Regel 7): i() = = x (τ) x 2 ( τ) dτ [ mi x () = A e s + B e s 2 s e sτ + s ] 2 e s 2τ u( τ) dτ s s 2 s 2 s L 42
46 524 Grenzwersäze Es sei x, ẋ X γ Dann gil: Falls lim x() = A, dann gil auch lim s s X(s) = A 2 Falls lim x() = B, dann gil auch lim s X(s) = B + s Beispiel (aus 523) lim x() = 3 x() = 3 lim s X(s) = lim s s s+3 = 3 2 lim + x() = lim s X(s) = lim s s s+3 = ( e 3 ) (), X(s) = 525 Die inverse Laplace-Transformaion Es gil (s 522) für X X γ : Probleme Wann gil X X γ? x() = 2πj Teilanwor: Es gil X X γ, falls (a) X(s) is raional in s, dh δ+j δ j s(s + 3) X(s) e s ds () X(s) = Z a ν s ν ν N b ν s ν ν Z: Grad des Zählerpolynoms N: Grad des Nennerpolynoms (b) für s gil X(s), dh Z < N 2 Wie kann das Umkehrinegral () auf einfache Weise berechne werden? Teilanwor: Is X(s) raional in s und gil Z < N, so gil die Residuenformel x() = L {X(s)} = s=s i Res [X(s) e s ] ( > ) s i : Singuläre Sellen von X(s) 43
47 Berechnung der Residuen s i sei Pol Ordnung: [ Res X(s) e s ] [ = lim X(s) e s (s s i ) ] s=s i s=si s i sei Pol m-er Ordnung: Res s=s i [ X(s) e s ] = (m )! lim s=s i Beispiel: X(s) = 3s2 + 6s + 6 s 3 + 4s 2 3s 8 = 3s2 + 6s + 6 (s 2)(s + 3) 2 s = 2: einfacher Pol, (m = ) s 2 = 3: doppeler Pol, (m 2 = 2) [ Res X(s) e s ] [ 3s 2 + 6s + 6 = lim s=2 s 2 [ Res X(s) e s ] = s=2 (2 )! lim s 3 d (m ) ds (m ) [ X(s) e s (s s i ) m] ] (s 2)(s + 3) 2 es (s 2) = 2 e 2 [ d 3s 2 + 6s + 6 ds (s 2)(s + 3) 2 es (s + 3) 2 ] [] = (3 + ) e 3 Ergebnis: x() = 2 e 2 + (3 + ) e 3 ( > ) 2 Beispiel: X(s) = 2s s+3 hier Z = N! Wir bilden: X(s) = Rückransformaion mi Tabelle: 2s X( ) + X( ) = 2s s + 3 s = x() = 6e 3 () + 2δ() 53 Sysembeschreibung im Zeibereich 53 Zusandsgleichungen 6 s x () x 2 () x() x l () z (),, z n () }{{} z() y () y 2 () y() y m () Allgemein: ż () = f [z (),, z n (), x (),, x l ()] ż n () = f n [z (),, z n (), x (),, x l ()] Überführungsgleichungen y () = g [z (),, z n (), x (),, x l ()] y m () = g m [z (),, z n (), x (),, x l ()] 44 Ergebnisgleichungen
48 Für lineare Syseme gil: ż () = a z () + + a n z n () + b x () + + b l x l () ż n () = a n z () + + a nn z n () + b n x () + + b nl x l () y () = c z () + + c n z n () + d x () + + d l x l () y m () = c m z () + + c mn z m () + d m x () + + d ml x l () In Marizen-Form: ż () a a n z () b b l x () = + } ż n () {{} } a n {{ a nn } z n () }{{} } b n {{ b nl } x l () }{{} ż() A z() B x() Kurzform: ẏ () c c n z () d d l x () = + } ẏ m () {{} } c m {{ c mn } z n () }{{} } d m {{ d ml } x l () }{{} y() C z() D x() ż() = A z() + B x() ẏ() = C z() + D x() Zusandsgleichungen des linearen, zeikoninuierlichen, dynamischen Sysems Beispiel aus 43 i C () i L () u () x() Eingabe } u L () y () u C () Ausgabe u C () y 2 () u () u R () u L () } Φ() z () i R () Zusände Q() z 2 () Außerdem gil: (da lineares Sysem) i R () = ϕ R (u R ()) = R u() i L () = ϕ L (Φ()) = L Φ() u C () = ϕ C (Q()) = C Q() 45
49 Dami gil für die Zusandgleichungen aus 43: Φ() = u() ϕ C (Q()) = Q() +u() C Q() = ϕ L (Φ()) + ϕ R (u() ϕ C (Q())) = L Φ() RC Q() + R u() u L () = u() ϕ C (Q()) = Q() +u() C u C () = ϕ C (Q()) } {{ } allgemein = + C Q() }{{} linearer Fall Marizenform: Bemerkung: Bei linearen Bauelemenen gil ( ) ( ) ( ) ( ) Φ() C Φ() = Q() L + u() RC Q() R }{{}}{{} A B ( ) ( ) ( ) ( ) ul () C Φ() = u C () + u() C Q() }{{}}{{} C D Φ() = L i L () Q() = C u C () in der Regel i L () bzw u C () als Zusandssignale verwende 532 Differenialgleichung und Realisierung Sonderfall: Eingang, Ausgang (l = m = ) x() z() Es gil: Ein lineares, zeikoninuierliches, dynamisches Sysem mi l = m = (n beliebig) kann durch eine Differenialgleichung folgenden Typs beschrieben werden: y (n) () + b y (n ) () + b 2 y (n 2) () + + b n ẏ() + b n y() = (a i, b i R, b = ) y() a x (n) () + a x (n ) () + a 2 x (n 2) () + + a n ẋ() + a n x() Ansaz: Blockschalbild Differenialgleichungen, Zusandsgleichungen x() a n a n- a a ż n() + z n() + b n b n- + ż () b z + () y() 46
50 Beschreibung des Blockschalbildes ż () = z 2 () + a x() b y() () ż 2 () = z 3 () + a 2 x() b 2 y() (2) ż n () = z n () + a n x() b n y() (n ) ż n () = a n x() b n y() (n) y() = z () + a x() (n + ) Übergang zur Differenialgleichung: Ziel: Eliminaion der z,, z n ˆ Gleichung (n + ) differenzieren: ẏ() = ż () + a ẋ() ˆ Gleichung () einsezen: ẏ() = z 2 () + a x() b y() + a ẋ() (n + 2) ˆ Gleichung (n + 2) differenzieren: ÿ() = ż 2 () + a ẋ() b ẏ() + a ẍ() ˆ Gleichung (2) einsezen ˆ Nach n Schrien sind alle Zusandssignale eliminier DGL ferig Übergang zu den Zusandsgleichungen: Einsezen von (n + ) in Gleichungen () bis (n): ż () ż 2 () ż n () ż n () b b 2 = b n } b n {{ } A y() = ( ) }{{} C z () z 2 () z n () z n () z () z 2 () z n () z n () a b a a 2 b 2 a + x() a n b n a a n b n a } {{ } B + (a ) x() }{{} D 47
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Aufgabe 1: Kontinuierliche und diskrete Signale
 Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
5. Signalverarbeitung
 5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
5.2 Logische Schaltungen und bistabile Kippstufen (FF)
 Dipl.-Ing. G.Lebel Logische Schalungen und bisabile Kippsufen (FF) logik+ff- 5.2 Logische Schalungen und bisabile Kippsufen (FF) Sachwore: Logische Schalungen, Äquivalenz-Gaer, EXOR-Gaer, UND-Gaer, ODER-Gaer,
Dipl.-Ing. G.Lebel Logische Schalungen und bisabile Kippsufen (FF) logik+ff- 5.2 Logische Schalungen und bisabile Kippsufen (FF) Sachwore: Logische Schalungen, Äquivalenz-Gaer, EXOR-Gaer, UND-Gaer, ODER-Gaer,
Bildmaterial zur Vorlesung Regelungstechnik Teil I Die Regelstrecke. Wintersemester 2014 Prof. Dr.-Ing. habil. Klaus-Peter Döge
 Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Kapitel 2: Fourieranalyse. Analoge, nichtperiodische Signale
 ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
Konjunktion. Disjunktion. x 1 x 0 y 0 0 0
 Klausuren zurückliegender Jahre Digiale Syseme Konjunkion B (, V, _, 0, 1 ) UND ODER NICHT y 0 0 0 0 1 0 1 0 0 1 1 1 UND y 1 0 * 1 0 1 0 y CT05 ET05 George Boole * 2 Nov 1815 in Lincoln, Lincolnshire,
Klausuren zurückliegender Jahre Digiale Syseme Konjunkion B (, V, _, 0, 1 ) UND ODER NICHT y 0 0 0 0 1 0 1 0 0 1 1 1 UND y 1 0 * 1 0 1 0 y CT05 ET05 George Boole * 2 Nov 1815 in Lincoln, Lincolnshire,
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Der kinetische Ansatz zur Beschreibung von Selbstorganisationsprozessen. mögliche Variationen und Erweiterungen: diskrete Gleichungen (endliches t):
 Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Fourier- und Laplace- Transformation
 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Grundlagen der Nachrichtentechnik 1 Communications 1
 Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
Fourier-Transformation Linearität, Symmetrie, Verschiebung, Skalierung, Faltung, Modulation
 Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Formelsammlung. Formelsammlung Systemtheorie I (Blatt 1) Rechenregeln der Schaltalgebra: 2. x y = y x x y = y x
 F Formelsammlung Formelsammlung Systemtheorie I (Blatt ) Rechenregeln der Schaltalgebra: x (y ) =(x y) x (y ) =(x y) 2 x y = y x x y = y x 3 x (x y) =x x (x y) =x 4 x (y ) =(x y) (x ) x (y ) =(x y) (x
F Formelsammlung Formelsammlung Systemtheorie I (Blatt ) Rechenregeln der Schaltalgebra: x (y ) =(x y) x (y ) =(x y) 2 x y = y x x y = y x 3 x (x y) =x x (x y) =x 4 x (y ) =(x y) (x ) x (y ) =(x y) (x
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Leseprobe. Ines Rennert, Bernhard Bundschuh. Signale und Systeme. Einführung in die Systemtheorie. ISBN (Buch):
 Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
In einem linearen System können sich Schwingungen ungestört überlagern. Die Schwingungen beeinflussen sich dabei nicht gegenseitig.
 6_Superposiionsprinzip_B_W000.doc - /6. Sysee i ehreren Freiheisgraden. Das Superposiionsprinzip für Lineare Sysee Die Schwingungsdifferenialgleichung is eine lineare DGL. Lineare Sysee (Sysee die i linearen
6_Superposiionsprinzip_B_W000.doc - /6. Sysee i ehreren Freiheisgraden. Das Superposiionsprinzip für Lineare Sysee Die Schwingungsdifferenialgleichung is eine lineare DGL. Lineare Sysee (Sysee die i linearen
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Systemtheorie: Übertragungssystem: Beispiele
 Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Abstrakte Lineare Algebra
 Frank Fischer Insiu für Informaik frank.fischer@uni-mainz.de Mahemaische Modellierung am Rechner WINTERSEMESTER 08/9 *#$?!! Kapiel Absrake Lineare Algebra Vekorräume Algebraische Definiion Wiederholung:
Frank Fischer Insiu für Informaik frank.fischer@uni-mainz.de Mahemaische Modellierung am Rechner WINTERSEMESTER 08/9 *#$?!! Kapiel Absrake Lineare Algebra Vekorräume Algebraische Definiion Wiederholung:
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Systemeigenschaften, Nomenklatur und Modellbildung
 Fakulä Informaik Insiu für Angewande Informaik, Professur für Technische Informaionssyseme Sysemeigenschafen, Nomenklaur und Dresden, den 03.08.2011 Gliederung Vorbemerkungen Weiere Sysemeigenschafen Nomenklaur
Fakulä Informaik Insiu für Angewande Informaik, Professur für Technische Informaionssyseme Sysemeigenschafen, Nomenklaur und Dresden, den 03.08.2011 Gliederung Vorbemerkungen Weiere Sysemeigenschafen Nomenklaur
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
Inhalt Prof. Dr.-Ing. Barbara Hippauf Hochschule für Technik und Wirtschaft des Saarlandes; Physik, SS 2016
 Inhal.. 3. 4. 5. 6. 7. 8. Gekoppele Oszillaoren Gekoppele Oszillaoren, ifferenialgleichung Gekoppele Oszillaoren, Normalkoordinaen, Normalschwingungen Gekoppele Oszillaoren, Schwebungen Gekoppele Oszillaoren,
Inhal.. 3. 4. 5. 6. 7. 8. Gekoppele Oszillaoren Gekoppele Oszillaoren, ifferenialgleichung Gekoppele Oszillaoren, Normalkoordinaen, Normalschwingungen Gekoppele Oszillaoren, Schwebungen Gekoppele Oszillaoren,
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Musterlösungen. zu den Aufgaben der Klausur zum. Kurs 1701 Grundlagen der Technischen Informatik. und. Kurs 1707 Technische Informatik I
 Muserlösungen zu den Aufgaben der Klausur zum Kurs 7 Grundlagen der Technischen Informaik und Kurs 77 Technische Informaik I im Sommersemeser vom 5.8. Muserlösung zur Haupklausur der Kurse 7 und 77 im
Muserlösungen zu den Aufgaben der Klausur zum Kurs 7 Grundlagen der Technischen Informaik und Kurs 77 Technische Informaik I im Sommersemeser vom 5.8. Muserlösung zur Haupklausur der Kurse 7 und 77 im
(10 Punkte) Gegeben ist die in Fig. 1 abgebildete in T periodische Zeitfunktion f(t). f(t)
 H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
2. Grundlagen Schwingungslehre
 Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Note: FACH NR DIGITALTECHNIK. Fachbereich Elektrotechnik und Informationstechnik Prof. Dr.-Ing. H. Heuermann
 Name (Blockschrif) Unerschrif Marikel-Nr. Sudiengang FH Aachen Fachbereich Elekroechnik und Informaionsechnik Prof. Dr.-Ing. H. Heuermann FACH NR. 52107 - DIGITALTECHNIK 11. Februar 2014-8:30 bis 10:00
Name (Blockschrif) Unerschrif Marikel-Nr. Sudiengang FH Aachen Fachbereich Elekroechnik und Informaionsechnik Prof. Dr.-Ing. H. Heuermann FACH NR. 52107 - DIGITALTECHNIK 11. Februar 2014-8:30 bis 10:00
Kapitel 4. Versuch 415 T-Flipflop
 Kapiel 4 Versuch 415 T-Flipflop Flipflops, die mi jeder seigenden oder mi jeder fallenden Takflanke in den engegengesezen Zusand kippen, heissen T Flipflops ( Toggle Flipflops ). T-Flipflops können aus
Kapiel 4 Versuch 415 T-Flipflop Flipflops, die mi jeder seigenden oder mi jeder fallenden Takflanke in den engegengesezen Zusand kippen, heissen T Flipflops ( Toggle Flipflops ). T-Flipflops können aus
Diskrete Integratoren und Ihre Eigenschaften
 Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
7. Funktionalgleichung der Zeta-Funktion
 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Kennzeichnung stochastischer Prozesse
 . Kennzeichnung sochasischer Prozesse...1.0. Der Plaz der sochasischen Prozesse in der Regelungsechnik...1.1. Beschreibung sochasischer Prozesse im Zeibereich...3.1.1. Die Auokorrelaionsfunkion (AKF)...3.1..
. Kennzeichnung sochasischer Prozesse...1.0. Der Plaz der sochasischen Prozesse in der Regelungsechnik...1.1. Beschreibung sochasischer Prozesse im Zeibereich...3.1.1. Die Auokorrelaionsfunkion (AKF)...3.1..
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Schriftliche Prüfung aus Control Systems 1 (Information and Computer Engineering) am
 TU Graz, Insiu für Regelungs- und Auomaisierungsechnik Schrifliche Prüfung aus Conrol Sysems (Informaion and Compuer Engineering) am 04.07.06 Name / Vorname(n): Marikel-Nummer: Aufgabe A A A3 A4 A5 A6
TU Graz, Insiu für Regelungs- und Auomaisierungsechnik Schrifliche Prüfung aus Conrol Sysems (Informaion and Compuer Engineering) am 04.07.06 Name / Vorname(n): Marikel-Nummer: Aufgabe A A A3 A4 A5 A6
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
2.3 Theorie linearer Systeme
 2.3 Theorie linearer Syseme 2.3.1 Grundsäzliche Mehode Mehode: Berechnung durch Zerlegen in einfach berechenbare Teile (Superposiion) x() = x 1 ()+x 2 ()+x 3 ()+.. y() = y 1 ()+y 2 ()+y 3 ()+.. zerlegen
2.3 Theorie linearer Syseme 2.3.1 Grundsäzliche Mehode Mehode: Berechnung durch Zerlegen in einfach berechenbare Teile (Superposiion) x() = x 1 ()+x 2 ()+x 3 ()+.. y() = y 1 ()+y 2 ()+y 3 ()+.. zerlegen
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Durch Modellierung beschreibt man Vorgänge aus der Natur sowie industrielle Prozesse
 Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Nachrichtentechnik 2 5 Zwei Zufallsvariablen, Folgen von Zufallsvar.
 Nachrichenechnik 5 Zwei Zufallsvariablen, Folgen von Zufallsvar. Folgen von Zufallsvariablen Definiion 5.: Gemeinsame Wahrscheinlichkeisvereilung F x,x,x 3,...,x N (x,x,x 3,..., x N P({x x } {x x } {x
Nachrichenechnik 5 Zwei Zufallsvariablen, Folgen von Zufallsvar. Folgen von Zufallsvariablen Definiion 5.: Gemeinsame Wahrscheinlichkeisvereilung F x,x,x 3,...,x N (x,x,x 3,..., x N P({x x } {x x } {x
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
7. Gewöhnliche Differentialgleichungen
 1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
13.1 Charakterisierung von Schwingungen
 87 Schwingungen reen in allen Fachgebieen mi rückgekoppelen Prozessen auf. Im Maschinenbau ensehen Schwingungen durch elasische Radaufhängungen, Maschinenfundamene oder Maschineneile, in der Elekroechnik
87 Schwingungen reen in allen Fachgebieen mi rückgekoppelen Prozessen auf. Im Maschinenbau ensehen Schwingungen durch elasische Radaufhängungen, Maschinenfundamene oder Maschineneile, in der Elekroechnik
Das lineare H-unendlich Problem
 Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Die numerische Erzeugung eines durchstimmbaren Sinussignals
 Die numerische Erzeugung eines durchsimmbaren Sinussignals Jakob Fröhling Die Hersellung eines sinusförmigen Signals is eine Aufgabensellung aus der Messechnik. Für die Messung bei einer Frequenz soll
Die numerische Erzeugung eines durchsimmbaren Sinussignals Jakob Fröhling Die Hersellung eines sinusförmigen Signals is eine Aufgabensellung aus der Messechnik. Für die Messung bei einer Frequenz soll
Anfangswertprobleme gewöhnlicher Differentialgleichungen
 13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
Vielseitige Darstellungen von Drehstromsignalen
 Vielseiige Darsellungen von Drehsromsignalen Die Leisungs- und Energie-Analysaoren Qualisar+ dienen zur soforigen Darsellung aller wesenlichen Eigenschafen eines Drehsromnezes. Zeiliche Darsellung Die
Vielseiige Darsellungen von Drehsromsignalen Die Leisungs- und Energie-Analysaoren Qualisar+ dienen zur soforigen Darsellung aller wesenlichen Eigenschafen eines Drehsromnezes. Zeiliche Darsellung Die
Leseprobe. Daniel von Grünigen. Digitale Signalverarbeitung. mit einer Einführung in die kontinuierlichen Signale und Systeme
 Leseprobe Daniel von Grünigen Digiale Signalverarbeiung mi einer Einführung in die koninuierlichen Signale und Syseme ISBN (Buch: 978-3-446-4479- ISBN (E-Book: 978-3-446-4399-7 Weiere Informaionen oder
Leseprobe Daniel von Grünigen Digiale Signalverarbeiung mi einer Einführung in die koninuierlichen Signale und Syseme ISBN (Buch: 978-3-446-4479- ISBN (E-Book: 978-3-446-4399-7 Weiere Informaionen oder
3.1 Grundlagen. Grundbegriffe (Forts.) Grundbegriffe
 Beriebssyseme II - Analyse und Modellierung Sommersemeser 208 3. Grundlagen Moivaion 3. Grundlagen Beriebssyseme II - Analyse und Modellierung 3. Kapiel Grundlagen der Sochasik Prof. Mahias Werner Professur
Beriebssyseme II - Analyse und Modellierung Sommersemeser 208 3. Grundlagen Moivaion 3. Grundlagen Beriebssyseme II - Analyse und Modellierung 3. Kapiel Grundlagen der Sochasik Prof. Mahias Werner Professur
Numerische Behandlung von gewöhnlichen Differentialgleichungen Eine Einführung. Universität Hamburg SoSe07. K. Taubert
 Numerische Behandlung von gewöhnlichen Differenialgleichungen Eine Einführung Universiä Hamburg SoSe7 K. Tauber Besondere Aufgaben 6 UNSTETIGE-, SYMPLEKTISCHE- und ALGEBRO-DIFFERENTIALGLEICHUNGEN 6.1 Einführung
Numerische Behandlung von gewöhnlichen Differenialgleichungen Eine Einführung Universiä Hamburg SoSe7 K. Tauber Besondere Aufgaben 6 UNSTETIGE-, SYMPLEKTISCHE- und ALGEBRO-DIFFERENTIALGLEICHUNGEN 6.1 Einführung
Mathematik für Physiker I
 Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Leistungselektronik Grundlagen und Standardanwendungen. Übung 3: Kommutierung
 Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Von der Fourier-Reihe zum Fourier-Integral
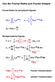 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Aufgabensammlung. Signale und Systeme 1. Einführung in die Signal- und Systemtheorie. Kontaktinformation: Dr. Mike Wolf, Tel. 2619
 Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Semantik. Semantik. Die Sprache der Typtheorie sieht für jeden Typ eine Menge nichtlogischer
 Universiy of Bielefeld Beispiele: Prädikaskonsanen (Suden, verheirae, arbeie): Typ ; sie nehmen einen Eigennamen/ein Referenzobjek und liefern einen Saz/einen Wahrheiswer ab. Zweisellige Relaionskonsanen
Universiy of Bielefeld Beispiele: Prädikaskonsanen (Suden, verheirae, arbeie): Typ ; sie nehmen einen Eigennamen/ein Referenzobjek und liefern einen Saz/einen Wahrheiswer ab. Zweisellige Relaionskonsanen
Prüfungsaufgaben Wiederholungsklausur
 NIVESITÄT LEIPZIG Insiu für Informaik Prüfungsaufgaben Wiederholungsklausur Ab. Technische Informaik Prof. Dr. do Kebschull Dr. Hans-Joachim Lieske 5. März / 9 - / H7 Winersemeser 999/ Aufgaben zur Wiederholungsklausur
NIVESITÄT LEIPZIG Insiu für Informaik Prüfungsaufgaben Wiederholungsklausur Ab. Technische Informaik Prof. Dr. do Kebschull Dr. Hans-Joachim Lieske 5. März / 9 - / H7 Winersemeser 999/ Aufgaben zur Wiederholungsklausur
Kryptologie. Bernd Borchert. Univ. Tübingen WS 15/16. Vorlesung. Teil 1b. Rechnen modulo n
 Krypologie Bernd Borcher Univ. Tübingen WS 15/16 Vorlesung Teil 1b Rechnen modulo n Modulo Rechnen a mod n is definier als Res von a bei Division durch n (a aus Z, n aus N) a + b mod n = a mod n + b mod
Krypologie Bernd Borcher Univ. Tübingen WS 15/16 Vorlesung Teil 1b Rechnen modulo n Modulo Rechnen a mod n is definier als Res von a bei Division durch n (a aus Z, n aus N) a + b mod n = a mod n + b mod
Note: FACH NR DIGITALTECHNIK. Fachbereich Elektrotechnik und Informationstechnik. Prof. Dr.-Ing. H. Heuermann
 Name (Blockschrif) Marikel-Nr. Unerschrif Sudiengang FH Aachen Prof. Dr.-Ing. H. Heuermann Fachbereich Elekroechnik und Informaionsechnik FACH NR. 527 - DIGITALTECHNIK 22. Sepember 24-8:3 bis : Uhr Die
Name (Blockschrif) Marikel-Nr. Unerschrif Sudiengang FH Aachen Prof. Dr.-Ing. H. Heuermann Fachbereich Elekroechnik und Informaionsechnik FACH NR. 527 - DIGITALTECHNIK 22. Sepember 24-8:3 bis : Uhr Die
