ALGEBRA II Serie 9. (c) Beweisen Sie, dass die Charaktertafel von G wie unten ist: Abgabetermin. Bis am Montag 11 Juni.
|
|
|
- Gundi Goldschmidt
- vor 5 Jahren
- Abrufe
Transkript
1 Sommersemester 2018 ALGEBRA II Serie 9 Prof. Dr. J.S. Wilson Aufgabe 9.1. Sei G endlich und g G. Zeigen Sie, dass g zu g 1 konjugiert ist, genau dann, wenn χ(g) reel für jeden Charakter χ von G ist. [Hinweis: siehe Übung 8.4.] Aufgabe 9.2. (a) Konstruieren Sie die Charaktertafel (a) der zylischen Gruppe t der Ordnung 3 und (b) der Gruppe A 4. [Die in (a) konstruierte Tafel ist ein Untermatrix der Tafel in (b).] Aufgabe 9.3. Eine Gruppe hat sieben Konjugiertenklassen C 1 = {1}, C 2,..., C 7, und die Werte von fünf der irreduzibeln Charaktere sind wie folgt. C 1 C 2 C 3 C 4 C 5 C 6 C Berechnen Sie die Größen der Konjugiertenklassen und die anderen irreduziblen Charaktere. Aufgabe 9.4. (a) Sei H eine Gruppe der Permutationen der endlichen Menge X und für h H sei σh = {x X hx x}. Also ist σ ein Charakter von H (der der Darstellung auf einem Vektorraum mit Basis X entspricht). Sei χ 1 der triviale Charakter von H. Beweisen Sie dass σ χ 1 ein Charakter von H ist. (b) Konstruieren Sie die Charaktertafel von A 5. [Ergebnisse von den Übungsblättern 7, 8 werden eventuell nützlich sein.] Aufgabe 9.5. Eine Gruppe G der Ordnung 21 wird durch Elemente a, b erzeugt die die Relationen a 7 = b 3 = 1, bab 1 = a 2 erfüllen. (a) Identifizieren Sie [G, G], und beweisen Sie, dass jedes Element eindeutig in der Form a α b β schreibbar ist mit 0 α < 7, 0 β < 3. (b) Verifizieren Sie, dass die Konjugiertenklassen wie folgt sind: C 1 = {1}, C 2 = {a, a 2, a 4 }, C 3 = {a 3, a 5, a 6 }, C 4 = {a α b 0 α < 7}, C 5 = {a α b 2 0 α < 7}. (c) Beweisen Sie, dass die Charaktertafel von G wie unten ist: C 1 C 2 C 3 C 4 C 5 C r χ (1) χ (2) ω ω 2 χ (3) ω 2 ω χ (4) 3 η η 0 0 χ (5) 3 η η 0 0 wobei ω, η die Gleichungen ω 2 + ω + 1 = η 2 + η + 2 = 0 erfüllen. Abgabetermin. Bis am Montag 11 Juni.
2 Serie 10 Aufgabe Seien G, H endliche Grupppen, und seien V ein CG-Modul und W ein CH-Modul. Das Tensorprodukt V W wird ein Modul für G H mit Wirkung (g, h)(v w) = gv hw. Beweisen Sie anhand der Charaktere, dass falls V, W irreduzibel sind, auch V W irreduzibel ist. Aufgabe Konstruieren Sie die Charaktertafel der Diedergruppe D 10 = a, b a 5 = b 2 = 1, bab = a 1. [Sie kennen schon eine Darstellung der Dimension 2.] Aufgabe Konstruieren Sie die Charaktertafel von S 4. [Sie können Ideen vom Beweis in der Vorlesung verwenden, oder auch eine Kombination von Methoden, aber Sie sollen deutlich zeigen, dass Sie den von Ihnen vorgeschlagen Beweis vollständig verstehen.] Aufgabe Sei G eine endliche Gruppe. (a) Geben Sie eine andere Beschreibung für Ind G 1 C. (b) Sei H G und seien W 1, W 2 CH-Moduln. Zeigen Sie, dass die CG- Moduln Ind G H(W 1 W 2 ) und Ind G HW 1 Ind G HW 2 isomorph sind. (c) Sei V ein irreduzibler CG-Modul und H G. Beweisen Sie, dass es einen irreduziblen CH-Modul W gibt derart, dass V isomorph zu einem Summanden von Ind G HW ist. (d) Beweisen Sie, dass falls A eine abelsche Untergruppe von G ist, dann hat jeden irreduziblen Charakter von G höchstens den Grad G : A. Aufgabe Berechnen Sie die Charaktere von S 5 die von den irreduziblen Charakteren von S 4 induziert werden, und konstruieren Sie die Charaktertafel von S 5. Aufgabe (a) Sei G eine transitive Permutationsgruppe auf einer Menge X mit X 2. Zeigen Sie, dass G genau dann 2-transitiv auf X ist, wenn für jedes x X die Gruppe stab G (x) transitiv auf X \ {x} wirkt. (b) Die gewöhnliche Wirkung der Gruppe SL 2 (F q ) auf F 2 q induziert eine Wirkung auf der Menge der 1-dimensionalen Unterräumen von F 2 q. Beweisen Sie, dass SL 2 (F q ) einen irreduziblen Charakter vom Grad q hat. Abgabetermin. Bis zum Uhr am Montag 18 Juni.
3 Serie 11 Unten ist G stets eine endliche Gruppe. Alle Darstellungen sind über C. Aufgabe (a) Sei χ der Charakter einer Wirkung von G auf einer endlichen Menge X. Beweisen Sie, dass g G χ(g) = G r ist, wobei r die Anzahl der Bahnen von G auf X ist. (b) Sei π die durch Konjugation definierte Wirkung von G auf der Menge G. Bestimmen Sie den Charakter von π. Aufgabe Sei x ein Element von G der Ordnung n und χ ein Charakter von G. Erklären Sie ohne zu viele Einzelheiten, warum die folgenden Aussagen gelten. (a) χ(x) ist eine Summe von nten Wurzeln von 1. (b) χ(x) χ(1). (c) K χ = {g χ(g) = χ(1)} G. (d) L χ = {g χ(g) = χ(1)} G. (e) grad χ = 1 genau dann, wenn χ ein Homomorphismus G C ist. (f) Für jedes g G \ {1} gibt es einen irreduziblen Charakter θ mit θ(g) θ(1). (g) Die Konjugiertenklassen von x, x 1 haben dieselbe Größe. (h) τ(x) R für jeden Charakter τ genau dann, wenn x, x 1 konjugiert sind. Aufgabe Seine G 1, G 2 Gruppen mit derselben Charaktertafel. Beweisen Sie, dass G 1 /[G 1, G 1 ] = G 2 /[G 2, G 2 ]. Beweisen Sie auch, dass Z(G 1 ) = Z(G 2 ). Aufgabe Sei M die Untergruppe (1, 4, 9, 8)(2, 5, 3, 6), (1, 6, 5, 2)(3, 7, 9, 8) von S 9. Die folgenden Fakten sind gegeben: g, g 1 sind konjugiert für alle g M. M hat sechs Konjugiertenklassen, C 1 = {1}, für 2 i 4 ist C i = 18, und C i enthält g i, mit g 1 = (2, 3, 8, 6)(4, 7, 5, 9), g 3 = (2, 4, 8, 5)(3, 9, 6, 7), g 4 = (2, 7, 8, 9)(3, 4, 6, 5): C 5 = 9 und C 5 enthält g 5 = (2, 8)(3, 6)(4, 5)(7, 9); C 6 = 8, und C 6 enthält g 6 = (1, 2, 8)(3, 9, 4)(5, 7, 6); Finden Sie die Charaktertafel von M. [Hinweis: g 2 2 = g 2 3 = g 2 4 = g 5.] Aufgabe Sei χ ein Charakter von G. Wir wissen schon, dass der Grad von χ ein Teiler von G ist. Ziel hier ist zu beweisen dass der Grad von χ ein Teiler von G/Z ist, wobei Z das Zentrum von G ist. (a) Sei V ein irreduzibler Modul für G und n 1. Beweisen Sie, dass n V ein irreduzibler Modul für das direkte Produkt D von n Kopien von G ist. Sei σ die entsprechende Darstellung von D. [Vgl. Übung 10.1.] (b) Was ist das Zentrum von D, und wie wirkt es auf n V? Beweisen Sie, dass D/ker σ Z G/Z n. (c) Beweisen Sie die Aussage oben. Abgabetermin. Bis zum am Montag 25 Juni.
4 .
5 Serie 12 Unten sind alle Darstellungen über C. Aufgabe Konstruieren Sie die Charaktertafel der Gruppe { ( ) } t a a F 0 1 5, t F 5 \ {0} der Ordnung 20. [Beweisen Sie zuerst, dass alle Elemente, die nicht im Normalteiler der Elemente mit t = 1 liegen, zu Diagonalelementen konjugiert sind.] Aufgabe Eine Gruppe G der Ordnung 24 hat sieben Konjugiertenklassen mit Vertretern g 1 = 1,..., g 7. Ausserdem gibt es einen CG-Modul V dessen Charakter χ die folgenden Werte hat: g i g 1 g 2 g 3 g 4 g 5 g 6 g 7 C G (g i ) χ ω 2 ω ω ω 2 wobei ω = e 2πi/3. Die Elemente g 2 1, g 2 2, g 2 3, g 2 4, g 2 5, g 2 6, g 2 7 sind konjugiert zu g 1,, g 1, g 2, g 5, g 4, g 4, g 5. Zeigen Sie, dass das s 2 (V ) und 2 (V ) irreduzibel sind, und bestimmen Sie die Charaktertafel von G. Aufgabe Eine Gruppe der Ordnung 168 hat sechs Konjugiertenklassen und drei Charaktere α, β, γ sind bekannt. In der Tafel unten sind die Größen der Konjugiertenklassen und die Werte von α, β, γ auf der Klassen gegeben α β γ Konstruieren Sie die Charaktertafel dieser Gruppe. [Hauptsache ist vielleicht zu beweisen, dass γ nicht eine Summe von vier Irreduziblen ist; Sie könnten z.b. den Fakt benutzen, dass χ(1) 168 für jedes irreduzible χ. Sie dürfen nicht annehmen, dass G mit einer in der Vorlesung behandelten Gruppe isomorph ist!] Aufgabe Ein Hauptfaktor einer endlichen Gruppe G ist ein Minimalnormalteiler einer Quotientengruppe von G. Sei G auflösbar. (a) Warum hat jeder Hauptfaktor von G Primzahlpotenzordnung? (b) (Galois) Sei M eine maximale Untergruppe von G. Beweisen Sie, dass G: M ist eine Primzahlpotenz ist. [Bitte wenden]
6 Aufgabe Sei { G = 1 a x 0 1 b a, b, x F p }; Also ist G eine nichtabelsche Gruppe der Ordnung p 3 ; sein Zentrum und seine Kommutatorgruppe bestehen aus den Elementen mit a = b = 0. (a) Zeigen Sie, dass G p Konjugiertenklassen mit einem Element und p 2 1 mit p Elementen hat. (b) Beschreiben Sie p 2 Charaktere vom Grad 1. (c) Sei H die Untergruppe der Elemente mit a = 0. Sei ψ: F p C ein nichttrivialer Homomorphismus und ρ die durch 1 0 x 0 1 b ψ(x) definierte 1-dimensionale Darstellung von H. Verifizieren Sie, dass V ψ = Ind G Hρ irreduzibel ist. [Benutzen Sie Reziprozität, oder finden Sie ein Widerspruch falls V ψ nicht irreduzibel ist: wie würde V ψ als Summe von Irreduziblen aussehen, was wäre der Kern der Wirkung von G auf den Summanden?] (d) Jetzt listen Sie alle irreduziblen Charaktere von G auf. Warum ist Ihre Liste vollständig? Abgabetermin. Bis zum Uhr am Montag 2 Juli.
7 Serie 13 Wie immer, wenn Sie eine Aussage nicht beweisen können, nehmen Sie die Aussage an und machen Sie weiter mit der nächsten Aussage. Aufgabe Sei R ein kommutative Ring, U eine Untergruppe seiner Einheitengruppe und n 2. Sei G die Untergruppe aller invertierbaren oberen n n Dreiecksmatrizen über R mit Einträgen aus U auf der Hauptdiagonale. (a) Zeigen Sie, dass G ein semidirektes Produkt von der Gruppe T der unipotenten Matrizen in G mit der Gruppe D der diagonalen Matrizen in G ist. (b) Im Falle dass R ein endlicher Körper mit Charakteristik p ist, identifizieren Sie eine Sylow p-untergruppe und ein p-komplement. (c) Wieder im allgemeinen Fall, was ist die Form der Matrizen in [T, T ]? Unter welchen Bedingungen ist T ab endlich erzeugbar? Aufgabe Sei jetzt R ein Körper, U = R \ {0} und n = 2. Beweisen Sie, dass die Untergruppe der unipotenten Matrizen ein Minimalnormalteiler von G ist. Folgern Sie, dass ein abelscher Minimalnormalteiler einer unendlichen auflösbaren Gruppe nicht notwendig elementar abelsch ist. Aufgabe (a) Sei K ein Normalteiler einer Gruppe G und H 1, H 2 Untergruppen von G mit H 1 H 2. Seien auch H 1 K = H 2 K und H 1 K = H 2 K. Beweisen Sie dass H 1 = H 2. In Aufgabe 13.1 sei jetzt R = Z[X 1 ±1,..., X±1 m ], U = X 1,..., X m und n = 2. Für x R und A eine Untergruppe von R schreibe ( ) 1 x x = und A = {x x A}. 0 1 (b) Zeigen Sie, dass die Normalteiler N G mit N T genau die A mit A ein Ideal von R sind. (c) (optionell ) Beweisen Sie, dass jede aufsteigende Kette von Untergruppen in Z m abbricht. (d) Zeigen Sie, dass jede aufsteigende Kette von Normalteilern in G abbricht. Aufgabe Sei G eine endliche auflösbare Gruppe, sei σ die Menge der Primzahlteiler von G und sei H p ein p-komplement für jedes p σ. Für jedes π σ sei P π = (H p p teilt G, p π ). (P wird als G interpretiert.) Beweisen Sie: (a) P π ist eine Hall π-untergruppe von G für jedes π σ; (b) die Abbildung π P π erhält Durchschnitte, und bildet Vereinigungen von Untermengen auf Erzeugnisse der Halluntergruppen; (c) P π1 P π2 = P π2 P π1 für alle π 1, π 2 σ. [Bitte wenden]
8 Aufgabe Seien R ein kommutativer Ring, G eine Gruppe. Ein RG- Modul M heißt überauflösbar falls es eine Kette 0 = M 0 M s = M von RG-Moduln derart gibt dass jedes M i /M i 1 zyklisch als R-Modul ist. (a) Zeigen Sie, dass falls M überauflösbar ist, dann ist auch M/P überauflösbar für jeden RG-Untermodul P. Für RG-Moduln M, N, ist wie gewöhnlich das Tensorprodukt M N auch ein RG-Modul mit Wirkung durch g(u v) = gu gv definiert. (b) Beweisen Sie, dass falls M, M überauflösbare RG-Modul sind, dann ist auch M N ein überauflösbarer RG-Modul. Aufgabe (optionell) Sei M ein abelscher Minimalnormalteiler einer (nicht notwendig endlichen) Gruppe G und sei M nicht elementar abelsch. Beweisen Sie die folgenden Aussagen. (a) {u M u hat endliche Ordnung} = {0}; also ist M torsions-frei. (b) Für p prim ist {u p u M} = M. (c) Für n Z \ {0} ist {u n u M} = M; also ist M divisibel. (d) Für r, s Z mit s 0 und u M gibt es ein eindeutiges Element v M mit v s = u r ; wir schreiben u r/s für dieses Element. (e) M wird ein Q-Modul; an dieser Stelle wird es besser, M additiv zu schreiben. (f) M wird durch Konjugation in G ein QG-Modul. (g) M ist ein irreduzibler QG-Modul. Abgabetermin. Bis zum Uhr am Montag 9 Juli.
Serie 4. Abgabetermin. Bis zum in meinem Briefkasten (Raum A 514). Bitte die Lösungen mit Namen, Matrikelnummer und Übungsgruppe versehen.
 Wintersemester 17/18 ALGEBRA I Serie 1 Prof. Dr. J.S. Wilson Aufgabe 1.1. (a) Seien H 1, H 2 Untergruppen einer Gruppe G und sei G = H 1 H 2. Zeigen Sie, daß entweder H 1 = G oder H 2 = G. (b) Geben Sie
Wintersemester 17/18 ALGEBRA I Serie 1 Prof. Dr. J.S. Wilson Aufgabe 1.1. (a) Seien H 1, H 2 Untergruppen einer Gruppe G und sei G = H 1 H 2. Zeigen Sie, daß entweder H 1 = G oder H 2 = G. (b) Geben Sie
ALGEBRA II Serie 1. Aufgabe 1.1. Sei f: M! N ein R-Modulhomomorphismus. (a) Zeigen Sie, dass Ker f ein Untermodul von M ist, und Bild f ein Untermodul
 Sommersemester 2018 ALGEBRA II Serie 1 Prof. Dr. J.S. Wilson Aufgabe 1.1. Sei f: M! N ein R-Modulhomomorphismus. (a) Zeigen Sie, dass Ker f ein Untermodul von M ist, und Bild f ein Untermodul von N. (b)
Sommersemester 2018 ALGEBRA II Serie 1 Prof. Dr. J.S. Wilson Aufgabe 1.1. Sei f: M! N ein R-Modulhomomorphismus. (a) Zeigen Sie, dass Ker f ein Untermodul von M ist, und Bild f ein Untermodul von N. (b)
Einführung in die Algebra Blatt 1
 Abgabefrist: Fr 03. 11. 2017 12:00 Uhr Blatt 1 Aufgabe 1 (2 Punkte). Lösen Sie die Gleichung x 3 3x 2 + x 1 = 0. Aufgabe 2 (2 + 2 + 2 + 2 Punkte). Sei G eine Gruppe und H G. Zeigen Sie, dass die folgenden
Abgabefrist: Fr 03. 11. 2017 12:00 Uhr Blatt 1 Aufgabe 1 (2 Punkte). Lösen Sie die Gleichung x 3 3x 2 + x 1 = 0. Aufgabe 2 (2 + 2 + 2 + 2 Punkte). Sei G eine Gruppe und H G. Zeigen Sie, dass die folgenden
ALGEBRA I Serie 7. z 2 z 1 mit z1, z 2 C. Zeigen Sie, daß
 Wintersemester 17/18 ALGEBRA I Serie 7 Prof. Dr. J.S. Wilson Aufgabe 7.1 [4 Punkte] (a) Seien R = {a + bi a, b Q}, S = {a + bi a, b Z}. Zeigen Sie, daß R, S Unterringe von C sind. Bestimmen Sie die Einheitengruppen
Wintersemester 17/18 ALGEBRA I Serie 7 Prof. Dr. J.S. Wilson Aufgabe 7.1 [4 Punkte] (a) Seien R = {a + bi a, b Q}, S = {a + bi a, b Z}. Zeigen Sie, daß R, S Unterringe von C sind. Bestimmen Sie die Einheitengruppen
(a) Welche der folgenden Gruppen hat 24 Elemente? D 6 GL 2 (F 2 ) X Die Tetraedergruppe. (b) Welche der folgenden Aussagen ist wahr?
 Aufgabe 1. (10 Punkte) Bei den folgenden Teilaufgaben ist jeweils genau eine Antwort richtig; diese ist anzukreuzen. Beweise oder Begründungen sind nicht erforderlich. Für jede richtige Antwort erhalten
Aufgabe 1. (10 Punkte) Bei den folgenden Teilaufgaben ist jeweils genau eine Antwort richtig; diese ist anzukreuzen. Beweise oder Begründungen sind nicht erforderlich. Für jede richtige Antwort erhalten
Algebra I Aufgaben. Aufgaben SS Aufgabe 1. Sei G eine Gruppe und g, h G. Man zeige, dass (gh) 1 = h 1 g 1 gilt.
 Universität Wien Prof. Dr. D. Burde Algebra I Aufgaben Aufgaben SS 2019 Aufgabe 1. Sei G eine Gruppe und g, h G. Man zeige, dass (gh) 1 = h 1 g 1 gilt. Aufgabe 2. Sei G eine Gruppe mit g 2 = e für alle
Universität Wien Prof. Dr. D. Burde Algebra I Aufgaben Aufgaben SS 2019 Aufgabe 1. Sei G eine Gruppe und g, h G. Man zeige, dass (gh) 1 = h 1 g 1 gilt. Aufgabe 2. Sei G eine Gruppe mit g 2 = e für alle
Proseminar: Darstellungstheorie von endlichen Gruppen. Vorläuges Programm
 Prof. Dr. S. Orlik WiSe 2011/12 MSc. Mark Kuschkowitz Proseminar: Darstellungstheorie von endlichen Gruppen Vorläuges Programm 27.10.: Wiederholung: Gruppen und Gruppenoperationen. (Literatur: Bücher über
Prof. Dr. S. Orlik WiSe 2011/12 MSc. Mark Kuschkowitz Proseminar: Darstellungstheorie von endlichen Gruppen Vorläuges Programm 27.10.: Wiederholung: Gruppen und Gruppenoperationen. (Literatur: Bücher über
Klausur zur Einführung in die Algebra, Lösungsvorschlag
 Universität Konstanz Christoph Hanselka Fachbereich Mathematik und Statistik Markus Schweighofer 16. März 2015 Wintersemester 2014/2015 Klausur zur Einführung in die Algebra, Lösungsvorschlag Aufgabe 1
Universität Konstanz Christoph Hanselka Fachbereich Mathematik und Statistik Markus Schweighofer 16. März 2015 Wintersemester 2014/2015 Klausur zur Einführung in die Algebra, Lösungsvorschlag Aufgabe 1
1 Gruppen. 1.1 Grundlagen. 1.2 Homomorphie- und Isomorphiesätze
 1 Gruppen 1.1 Grundlagen 1.2 Homomorphie- und Isomorphiesätze Sind G und G Gruppen und ϕ : G G ein Gruppenhomomorphismus. Dann gilt: G/Kern(ϕ) = Bild(ϕ) Beispiele 1.1 (a) G/Z(G) = Aut i (G) Satz 1 Sei
1 Gruppen 1.1 Grundlagen 1.2 Homomorphie- und Isomorphiesätze Sind G und G Gruppen und ϕ : G G ein Gruppenhomomorphismus. Dann gilt: G/Kern(ϕ) = Bild(ϕ) Beispiele 1.1 (a) G/Z(G) = Aut i (G) Satz 1 Sei
Darstellungstheorie. Manfred Hörz
 Darstellungstheorie Manfred Hörz Die (lineare) Darstellungstheorie versucht schwer zu durchschauende Eigenschaften von gewissen Gruppen (oder Algebren) durch strukturerhaltende Abbildungen auf Matrizen,
Darstellungstheorie Manfred Hörz Die (lineare) Darstellungstheorie versucht schwer zu durchschauende Eigenschaften von gewissen Gruppen (oder Algebren) durch strukturerhaltende Abbildungen auf Matrizen,
Algebra I - Wintersemester 05/06 - Zusammenfassung
 Algebra I - Wintersemester 05/06 - Zusammenfassung Die Autoren 28. September 2017 1 Gruppen 1.1 Grundlagen 1.2 Homomorphie- und Isomorphiesätze Sind G und G Gruppen und ϕ : G G ein Gruppenhomomorphismus.
Algebra I - Wintersemester 05/06 - Zusammenfassung Die Autoren 28. September 2017 1 Gruppen 1.1 Grundlagen 1.2 Homomorphie- und Isomorphiesätze Sind G und G Gruppen und ϕ : G G ein Gruppenhomomorphismus.
Ich benötige einen Schein. Ich habe bereits genug Scheine.
 1 Klausur 20.01.2003 Algebra I WS 2002/03 Dr. Elsholtz Name, Vorname Matr.nummer Fachrichtung Fachsemester Ich benötige einen Schein. Ich habe bereits genug Scheine. Die folgende Klausur hat mehr Aufgaben
1 Klausur 20.01.2003 Algebra I WS 2002/03 Dr. Elsholtz Name, Vorname Matr.nummer Fachrichtung Fachsemester Ich benötige einen Schein. Ich habe bereits genug Scheine. Die folgende Klausur hat mehr Aufgaben
Seminar über Darstellungstheorie endlicher Gruppen Berechnung einiger Charaktertafeln
 Seminar über Darstellungstheorie endlicher Gruppen Berechnung einiger Charaktertafeln Anna Bot, Georg Grützner 17. Mai 016 Der Inhalt der Präsentation und des Handouts entstammen den Kapiteln 5 und 8 von
Seminar über Darstellungstheorie endlicher Gruppen Berechnung einiger Charaktertafeln Anna Bot, Georg Grützner 17. Mai 016 Der Inhalt der Präsentation und des Handouts entstammen den Kapiteln 5 und 8 von
Klausur Grundlagen der Algebra und Computeralgebra
 Prof. Werner M. Seiler, Ph.D. FB 10 Mathematik und Naturwissenschaften Institut für Mathematik Klausur Grundlagen der Algebra und Computeralgebra 21.02.2012 Name: Vorname: Geburtsdatum: Matrikelnummer:
Prof. Werner M. Seiler, Ph.D. FB 10 Mathematik und Naturwissenschaften Institut für Mathematik Klausur Grundlagen der Algebra und Computeralgebra 21.02.2012 Name: Vorname: Geburtsdatum: Matrikelnummer:
Algebra und Zahlentheorie I, Blatt 10, Aufgabe 4
 Algebra und Zahlentheorie I, Blatt 10, Aufgabe 4 Aufgabe 4. (Die Gruppen der Ordnung 12) Beweisen Sie, dass jede Gruppe der Ordnung 12 sich als semidirektes Produkt einer 2-Sylowuntergruppe mit einer 3-Sylowuntergruppe
Algebra und Zahlentheorie I, Blatt 10, Aufgabe 4 Aufgabe 4. (Die Gruppen der Ordnung 12) Beweisen Sie, dass jede Gruppe der Ordnung 12 sich als semidirektes Produkt einer 2-Sylowuntergruppe mit einer 3-Sylowuntergruppe
Prof. M. Eisermann Algebra SoSe 2010
 Übungsblatt 9: Sylowsatz und semidirekte Produkte Die folgenden Lemmata könnten Ihnen bei einigen Aufgaben auf dem Blatt hilfreich sein. Sei im Folgenden G stets eine endliche Gruppe und p eine Primzahl.
Übungsblatt 9: Sylowsatz und semidirekte Produkte Die folgenden Lemmata könnten Ihnen bei einigen Aufgaben auf dem Blatt hilfreich sein. Sei im Folgenden G stets eine endliche Gruppe und p eine Primzahl.
Übungen zur Vorlesung Lineare Algebraische Gruppen im Wintersemester 2012/13
 Übung 1.1. (k = k). Es sei k die multiplikative Gruppe und k die additive Gruppe. Welche Homomorphismen gibt es von jeder der algebraischen Gruppen k, k zu jeder der algebraischen Gruppen k, k? Übung 1.2.
Übung 1.1. (k = k). Es sei k die multiplikative Gruppe und k die additive Gruppe. Welche Homomorphismen gibt es von jeder der algebraischen Gruppen k, k zu jeder der algebraischen Gruppen k, k? Übung 1.2.
Übungsblatt 11. Hausübungen
 Übungsblatt 11 Hausübungen Die Hausübungen müssen bis Mittwoch, den 09.01.19, um 18:00 Uhr in den Briefkasten Algebra mit Ihrer Übungsgruppennummer im Mathematischen Institut, Raum 301 abgegeben werden.
Übungsblatt 11 Hausübungen Die Hausübungen müssen bis Mittwoch, den 09.01.19, um 18:00 Uhr in den Briefkasten Algebra mit Ihrer Übungsgruppennummer im Mathematischen Institut, Raum 301 abgegeben werden.
ALGEBRA, WINTERSEMESTER 2014/15
 ALGEBRA, WINTERSEMESTER 2014/15 KARIN BAUR Zusammenfassung. Algebra, 4stündig, Wintersemester 2014/15, KFU Graz. Kurze Übersicht über den Inhalt der Vorlesung. Teil I: Gruppen Im ersten Teil geht es vor
ALGEBRA, WINTERSEMESTER 2014/15 KARIN BAUR Zusammenfassung. Algebra, 4stündig, Wintersemester 2014/15, KFU Graz. Kurze Übersicht über den Inhalt der Vorlesung. Teil I: Gruppen Im ersten Teil geht es vor
Übungen zur Einführung in die Algebra
 Blatt 1, 17.10.2013 Aufgabe 1.1. Bestimme alle Untergruppen und Normalteiler der symmetrischen Gruppe S 3. Aufgabe 1.2. Es seien E, I, J, K M(2 2; C) die folgenden Matrizen: ( ) ( ) ( ) ( ) 1 0 0 1 0 i
Blatt 1, 17.10.2013 Aufgabe 1.1. Bestimme alle Untergruppen und Normalteiler der symmetrischen Gruppe S 3. Aufgabe 1.2. Es seien E, I, J, K M(2 2; C) die folgenden Matrizen: ( ) ( ) ( ) ( ) 1 0 0 1 0 i
Einführung in die Algebra Blatt 1 Abgabe
 Blatt 1 Abgabe 2.5.2017 Begründen Sie, dass die folgende Menge mit der dazugehörigen Multiplikation eine Halbgruppe bildet. Entscheiden Sie, welche der Halbgruppen eine Gruppe ist. (i) G = Z 1 versehen
Blatt 1 Abgabe 2.5.2017 Begründen Sie, dass die folgende Menge mit der dazugehörigen Multiplikation eine Halbgruppe bildet. Entscheiden Sie, welche der Halbgruppen eine Gruppe ist. (i) G = Z 1 versehen
Übungen zu Algebra, WS 2015/16
 Übungen zu Algebra, WS 2015/16 Christoph Baxa 1) Es seien G 1,..., G n Gruppen. Beweisen Sie: Ist σ S n, so ist G σ(1) G σ(n) = G1 G n. 2) Beweisen Sie: Sind G 1,..., G n und H 1,..., H n Gruppen mit der
Übungen zu Algebra, WS 2015/16 Christoph Baxa 1) Es seien G 1,..., G n Gruppen. Beweisen Sie: Ist σ S n, so ist G σ(1) G σ(n) = G1 G n. 2) Beweisen Sie: Sind G 1,..., G n und H 1,..., H n Gruppen mit der
Lineare Darstellungen von Symmetrischen Gruppen
 Lineare Darstellungen von Symmetrischen Gruppen 150 232 (Holtkamp) 2st., Mi 12.00-14.00, NA 2/24 1 Beispiel 1. Freies Monoid über Alphabet X Beispiel 2. S 1, S 2, S 3,... Satz 1. (Bijektion zw. Partitionen
Lineare Darstellungen von Symmetrischen Gruppen 150 232 (Holtkamp) 2st., Mi 12.00-14.00, NA 2/24 1 Beispiel 1. Freies Monoid über Alphabet X Beispiel 2. S 1, S 2, S 3,... Satz 1. (Bijektion zw. Partitionen
Einführung in Algebra und Zahlentheorie Lösungsvorschlag zur Klausur am 16. Februar 2016
 Fakultät für Mathematik Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. oec. Anja Randecker Einführung in Algebra und Zahlentheorie Lösungsvorschlag zur Klausur am 16. Februar 016
Fakultät für Mathematik Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. oec. Anja Randecker Einführung in Algebra und Zahlentheorie Lösungsvorschlag zur Klausur am 16. Februar 016
Lösungen zur Algebra-Klausur vom Es sei G eine Gruppe, die von je einem Element der Ordnung 7, 11 und 13 erzeugt wird.
 Aufgabe 1 Lösungen zur Algebra-Klausur vom 3.4.9 Es sei G eine Gruppe, die von je einem Element der Ordnung 7, 11 und 13 erzeugt wird. a) Zeigen Sie, dass es keine transitive Operation von G auf einer
Aufgabe 1 Lösungen zur Algebra-Klausur vom 3.4.9 Es sei G eine Gruppe, die von je einem Element der Ordnung 7, 11 und 13 erzeugt wird. a) Zeigen Sie, dass es keine transitive Operation von G auf einer
Darstellungstheorie endlicher Gruppen Charaktere
 Darstellungstheorie endlicher Gruppen Charaktere Ramon Braunwarth, Georg Grützner. März 016 Die folgenden Ausführungen sind eine geringfügig veränderte Exposition des Kapitels 13 aus [1]. Sei F ein algebraisch
Darstellungstheorie endlicher Gruppen Charaktere Ramon Braunwarth, Georg Grützner. März 016 Die folgenden Ausführungen sind eine geringfügig veränderte Exposition des Kapitels 13 aus [1]. Sei F ein algebraisch
1 Grundlagen zur Darstellungstheorie
 Seminar Gruppen in der Physik SS 06 Vortrag 1 Gruppen und ihr Darstellung Matthias Nagl 1 Grundlagen zur Darstellungstheorie In diesem Vortrag wird es nur um lineare Darstellungen endlicher Gruppen in
Seminar Gruppen in der Physik SS 06 Vortrag 1 Gruppen und ihr Darstellung Matthias Nagl 1 Grundlagen zur Darstellungstheorie In diesem Vortrag wird es nur um lineare Darstellungen endlicher Gruppen in
Algebra I. Gal(K/Q), Gal(K/Q), a σa.
 WS 05/06 Priv.-Doz. Dr. S. Wewers Andreas Martin Algebra I 12. Übungsblatt Aufgabe 1: (6 1 P) Sei ζ = ζ 7 = exp(2πi/7) und K := Q[ζ]. Wir nehmen an, dass K/Q eine Galois-Erweiterung ist und dass es einen
WS 05/06 Priv.-Doz. Dr. S. Wewers Andreas Martin Algebra I 12. Übungsblatt Aufgabe 1: (6 1 P) Sei ζ = ζ 7 = exp(2πi/7) und K := Q[ζ]. Wir nehmen an, dass K/Q eine Galois-Erweiterung ist und dass es einen
Algebra I. Zwischenprüfung. 19. Februar 2016
 Name: Vorname: Studiengang: Legi-Nr.: Algebra I D-MATH, HS 2015 Prof. Richard Pink Algebra I Zwischenprüfung Wichtig: 19. Februar 2016 Die Prüfung dauert 120 Minuten. Bitte legen Sie Ihre Legi (Studierendenausweis)
Name: Vorname: Studiengang: Legi-Nr.: Algebra I D-MATH, HS 2015 Prof. Richard Pink Algebra I Zwischenprüfung Wichtig: 19. Februar 2016 Die Prüfung dauert 120 Minuten. Bitte legen Sie Ihre Legi (Studierendenausweis)
Zusatzkapitel Algebra Anton Deitmar
 Zusatzkapitel Algebra 1 Zusatzkapitel Algebra Anton Deitmar 1 Gruppen 1.9 Kommutatoren Definition 1.9.1. Sind a, b Elemente einer Gruppe G, so sei [a, b] = aba 1 b 1 der Kommutator von a und b. Sei [G,
Zusatzkapitel Algebra 1 Zusatzkapitel Algebra Anton Deitmar 1 Gruppen 1.9 Kommutatoren Definition 1.9.1. Sind a, b Elemente einer Gruppe G, so sei [a, b] = aba 1 b 1 der Kommutator von a und b. Sei [G,
1 Herangehensweise an eine Aufgabe
 Im Folgenden seien sofern nicht anders angegeben G eine Gruppe, R, S Ringe, I, J Ideale, K, L Körper, p Z eine Primzahl und m Z. 1 Herangehensweise an eine Aufgabe Soll man einen gewissen Sachverhalt A
Im Folgenden seien sofern nicht anders angegeben G eine Gruppe, R, S Ringe, I, J Ideale, K, L Körper, p Z eine Primzahl und m Z. 1 Herangehensweise an eine Aufgabe Soll man einen gewissen Sachverhalt A
1.8 Endlich erzeugte kommutative Gruppen
 1.8 Endlich erzeugte kommutative Gruppen 23 1.8 Endlich erzeugte kommutative Gruppen Im folgenden sei (G, +) stets eine endlich erzeugte kommutative Gruppe. G ist direkte Summe der Untergruppen H 1,...,H
1.8 Endlich erzeugte kommutative Gruppen 23 1.8 Endlich erzeugte kommutative Gruppen Im folgenden sei (G, +) stets eine endlich erzeugte kommutative Gruppe. G ist direkte Summe der Untergruppen H 1,...,H
Einführung in Algebra und Zahlentheorie Lösungsvorschläge zur Klausur vom Aufgabe 1 (6 Punkte)
 Aufgabe 1 (6 Punkte) Einführung in Algebra und Zahlentheorie svorschläge zur Klausur vom 23.09.2016 a) Bestimmen Sie das multiplikativ inverse Element zu 22 in Z/61Z. b) Finden Sie ein x Z mit folgenden
Aufgabe 1 (6 Punkte) Einführung in Algebra und Zahlentheorie svorschläge zur Klausur vom 23.09.2016 a) Bestimmen Sie das multiplikativ inverse Element zu 22 in Z/61Z. b) Finden Sie ein x Z mit folgenden
Übungsblatt 4. Hausübungen
 Übungsblatt 4 Hausübungen Die Hausübungen müssen bis Mittwoch, den 07.11.18, um 18:00 Uhr in den Briefkasten mit Ihrer Übungsgruppennummer im Mathematischen Institut, Raum 301 abgegeben werden. Bitte schreiben
Übungsblatt 4 Hausübungen Die Hausübungen müssen bis Mittwoch, den 07.11.18, um 18:00 Uhr in den Briefkasten mit Ihrer Übungsgruppennummer im Mathematischen Institut, Raum 301 abgegeben werden. Bitte schreiben
EINFÜHRUNG IN DIE GRUPPENTHEORIE BORIS BETZHOLZ UND TOBIAS SCHWARZ. Seminarvortrag im Rahmen des Seminars Gruppen und Codes bei Frau Dr.
 EINFÜHRUNG IN DIE GRUPPENTHEORIE BORIS BETZHOLZ UND TOBIAS SCHWARZ Seminarvortrag im Rahmen des Seminars Gruppen und Codes bei Frau Dr. Baumeister 1 2 1. Einleitung Definition 1.1. Gruppe Eine Menge M
EINFÜHRUNG IN DIE GRUPPENTHEORIE BORIS BETZHOLZ UND TOBIAS SCHWARZ Seminarvortrag im Rahmen des Seminars Gruppen und Codes bei Frau Dr. Baumeister 1 2 1. Einleitung Definition 1.1. Gruppe Eine Menge M
S n. C n. D n. A n. Automorphismengruppe. Definition: Gruppe. Eigenschaften: Äquivalenzrelation. Definition: Nebenklasse. Definition: Normalteiler
 S n C n D n A n Automorphismengruppe Definition: Gruppe Definition: Nebenklasse Eigenschaften: Äquivalenzrelation Satz: Lagrange Definition: Normalteiler Einheitswurzelgruppe C n = {ζ C; ζ n = 1} Permutationsgruppe
S n C n D n A n Automorphismengruppe Definition: Gruppe Definition: Nebenklasse Eigenschaften: Äquivalenzrelation Satz: Lagrange Definition: Normalteiler Einheitswurzelgruppe C n = {ζ C; ζ n = 1} Permutationsgruppe
EINFÜHRUNG IN DIE ALGEBRA Proseminar SS Übungsblatt für den
 1. Übungsblatt für den 11. 3. 2010 1. Es seien a, b Z. Beweisen Sie: a) a b T (a) T (b) b) Für jedes k Z gilt: T (a) T (b) = T (a) T (b + ka) c) Für jedes k Z gilt: ggt(a, b) = ggt(a, b + ka). 2. Für n
1. Übungsblatt für den 11. 3. 2010 1. Es seien a, b Z. Beweisen Sie: a) a b T (a) T (b) b) Für jedes k Z gilt: T (a) T (b) = T (a) T (b + ka) c) Für jedes k Z gilt: ggt(a, b) = ggt(a, b + ka). 2. Für n
Inhalt der Vorlesung Elemente der Algebra und Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS Grundlegende Definitionen (Wiederholung)
 Inhalt der Vorlesung Elemente der Algebra und Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel I. Gruppen 1 Grundlegende Definitionen (Wiederholung) 1.1 Definition. Eine Gruppe ist ein Paar
Inhalt der Vorlesung Elemente der Algebra und Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel I. Gruppen 1 Grundlegende Definitionen (Wiederholung) 1.1 Definition. Eine Gruppe ist ein Paar
Inhalt der Vorlesung Algebraische Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017
 Inhalt der Vorlesung Algebraische Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel II. Moduln 1 Moduln Sei R ein Ring (stets kommutativ und mit 1). 1.1 Definition. 1. Ein R-(links-)Modul ist
Inhalt der Vorlesung Algebraische Zahlentheorie Prof. Dr. Arno Fehm TU Dresden SS2017 Kapitel II. Moduln 1 Moduln Sei R ein Ring (stets kommutativ und mit 1). 1.1 Definition. 1. Ein R-(links-)Modul ist
Bilineare duale Hyperovale und elementar abelsche TI Gruppen
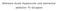 Bilineare duale Hyperovale und elementar abelsche TI Gruppen DEFINITION. Sei V ein endlich-dimensionaler Raum über F q und D eine Teilmenge n-dimensionaler Unterräume. D ist ein duales Hyperoval vom Rang
Bilineare duale Hyperovale und elementar abelsche TI Gruppen DEFINITION. Sei V ein endlich-dimensionaler Raum über F q und D eine Teilmenge n-dimensionaler Unterräume. D ist ein duales Hyperoval vom Rang
Klausur vom Algebra I. Rolf Farnsteiner
 Klausur vom 12.02.2010 Algebra I Rolf Farnsteiner Lösungen Daiva Pučinskaitė Aufgabe 1. Seien U 1, U 2 G Untergruppen einer Gruppe G. Zeigen Sie, dass folgende Aussagen äquivalent sind: (1) U 1 U 2 ist
Klausur vom 12.02.2010 Algebra I Rolf Farnsteiner Lösungen Daiva Pučinskaitė Aufgabe 1. Seien U 1, U 2 G Untergruppen einer Gruppe G. Zeigen Sie, dass folgende Aussagen äquivalent sind: (1) U 1 U 2 ist
MMP II FS 2017 PROF. DR. HORST KNÖRRER MUSTERLÖSUNG ZU SERIE 6
 MMP II FS 2017 PROF. DR. HORST KNÖRRER MUSTERLÖSUNG ZU SERIE 6 1. Aufgabe: Burnside Matrizen (1) Eine Gruppe zerfällt disjunkt in Konjugationsklassen, da konjugiert sein eine Äquivalenzrelation definiert.
MMP II FS 2017 PROF. DR. HORST KNÖRRER MUSTERLÖSUNG ZU SERIE 6 1. Aufgabe: Burnside Matrizen (1) Eine Gruppe zerfällt disjunkt in Konjugationsklassen, da konjugiert sein eine Äquivalenzrelation definiert.
Wiederholungsklausur zur Linearen Algebra II
 Wiederholungsklausur zur Linearen Algebra II Prof. Dr. C. Löh/D. Fauser/J. Witzig 5. Oktober 2017 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie,
Wiederholungsklausur zur Linearen Algebra II Prof. Dr. C. Löh/D. Fauser/J. Witzig 5. Oktober 2017 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie,
6.6 Normal- und Kompositionsreihen
 282 6.6 Normal- und Kompositionsreihen Es geht jetzt um die innere Struktur von Gruppen, soweit diese mit Ketten von ineinandergeschachtelten Normalteilern beschrieben werden kann. Erinnern wir uns deshalb
282 6.6 Normal- und Kompositionsreihen Es geht jetzt um die innere Struktur von Gruppen, soweit diese mit Ketten von ineinandergeschachtelten Normalteilern beschrieben werden kann. Erinnern wir uns deshalb
Klausur vom Algebra I. Rolf Farnsteiner
 Klausur vom 31.03.2010 Algebra I Rolf Farnsteiner Lösungen Daiva Pučinskaitė Aufgabe 1. Sei p R ein Primideal eines Integritätsbereichs R. Beweisen Sie folgende Aussagen: (1 S := R \ p ist eine multiplikativ
Klausur vom 31.03.2010 Algebra I Rolf Farnsteiner Lösungen Daiva Pučinskaitė Aufgabe 1. Sei p R ein Primideal eines Integritätsbereichs R. Beweisen Sie folgende Aussagen: (1 S := R \ p ist eine multiplikativ
Übungsblatt 12: Abschluss
 Übungsblatt 1: Abschluss 1. PRIMITIVE ELEMENTE V 1.1. (a) Sei E K eine endliche Galoiserweiterung. Zeigen Sie (mit Hilfe der Galoiskorrespondenz), dass für α E die beiden Aussagen äquivalent sind: (i)
Übungsblatt 1: Abschluss 1. PRIMITIVE ELEMENTE V 1.1. (a) Sei E K eine endliche Galoiserweiterung. Zeigen Sie (mit Hilfe der Galoiskorrespondenz), dass für α E die beiden Aussagen äquivalent sind: (i)
MUSTERLÖSUNG KLAUSUR ZUR ALGEBRA I. Prof. Dr. Daniel Plaumann Konstantinos Lentzos Wintersemester 2016/ Februar Nachname: Vorname:
 Prof. Dr. Daniel Plaumann Konstantinos Lentzos Wintersemester 2016/2017 KLAUSUR ZUR ALGEBRA I 15. Februar 2017 MUSTERLÖSUNG Nachname: Vorname: Studiengang: Aufgabe 1 2 3 4 5 6 7 8 9 Summe Punktzahl /60
Prof. Dr. Daniel Plaumann Konstantinos Lentzos Wintersemester 2016/2017 KLAUSUR ZUR ALGEBRA I 15. Februar 2017 MUSTERLÖSUNG Nachname: Vorname: Studiengang: Aufgabe 1 2 3 4 5 6 7 8 9 Summe Punktzahl /60
Mathematisches Institut SS 2010 Heinrich-Heine-Universität Prof. Dr. Stefan Schröer. Algebra. Blatt 1. ω = u + v,
 Blatt 1 Aufgabe 1. Sei z = re iϕ C eine komplexe Zahl mit r, ϕ R, und n 1. Geben Sie alle ω C mit ω n = z in Polarkoordinaten an. Aufgabe 2. Sei X 3 + px + q C[X] ein kubisches Polynom. Dessen drei Nullstellen
Blatt 1 Aufgabe 1. Sei z = re iϕ C eine komplexe Zahl mit r, ϕ R, und n 1. Geben Sie alle ω C mit ω n = z in Polarkoordinaten an. Aufgabe 2. Sei X 3 + px + q C[X] ein kubisches Polynom. Dessen drei Nullstellen
Algebra I. (c) Der Homomorphismus ϕ ist genau dann injektiv, wenn der Kern nur aus dem neutralen Element besteht. 2 ) = ϕ(g 1g 1.
 WS 05/06 Priv.-Doz. Dr. S. Wewers Andreas Martin Algebra I 1. Übungsblatt Aufgabe 1: (1+1+1=3 P Seien G und H Gruppen und ϕ : G H ein Gruppenhomomorphismus. Zeigen Sie: (a Das Bild ϕ(g von ϕ ist eine Untergruppe
WS 05/06 Priv.-Doz. Dr. S. Wewers Andreas Martin Algebra I 1. Übungsblatt Aufgabe 1: (1+1+1=3 P Seien G und H Gruppen und ϕ : G H ein Gruppenhomomorphismus. Zeigen Sie: (a Das Bild ϕ(g von ϕ ist eine Untergruppe
KLAUSUR ZUR ALGEBRA UND ZAHLENTHEORIE. 15. Februar 2017 MUSTERLÖSUNG. Aufgabe Summe. Allgemeine Hinweise
 Prof. Dr. Daniel Plaumann Konstantinos Lentzos Wintersemester 2016/2017 KLAUSUR ZUR ALGEBRA UND ZAHLENTHEORIE 15. Februar 2017 MUSTERLÖSUNG Nachname: Vorname: Studiengang: Aufgabe 1 2 3 4 5 6 7 8 9 Summe
Prof. Dr. Daniel Plaumann Konstantinos Lentzos Wintersemester 2016/2017 KLAUSUR ZUR ALGEBRA UND ZAHLENTHEORIE 15. Februar 2017 MUSTERLÖSUNG Nachname: Vorname: Studiengang: Aufgabe 1 2 3 4 5 6 7 8 9 Summe
15 Auflösbarkeit durch Radikale
 Chr.Nelius: Algebra (SS 2006) 1 15 Auflösbarkeit durch Radikale f [T] sei ein normiertes Polynom vom Grade 1. Wir wollen die Frage untersuchen, ob sich die Nullstellen von f formelmäßig berechnen lassen.
Chr.Nelius: Algebra (SS 2006) 1 15 Auflösbarkeit durch Radikale f [T] sei ein normiertes Polynom vom Grade 1. Wir wollen die Frage untersuchen, ob sich die Nullstellen von f formelmäßig berechnen lassen.
Multiple Choice Quiz: Lösungen
 D-MATH Algebra I HS 2015 Prof. Richard Pink Multiple Choice Quiz: Lösungen Jede Frage hat mindestens eine richtige Antwort, manchmal mehrere. 1. Eine nichtleere Teilmenge H G einer Gruppe G ist eine Untergruppe
D-MATH Algebra I HS 2015 Prof. Richard Pink Multiple Choice Quiz: Lösungen Jede Frage hat mindestens eine richtige Antwort, manchmal mehrere. 1. Eine nichtleere Teilmenge H G einer Gruppe G ist eine Untergruppe
KLAUSUR ZUR ALGEBRA (B3) 18. Februar 2009 MUSTERLÖSUNG
 KLAUSUR ZUR ALGEBRA (B3) 18. Februar 2009 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 7 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
KLAUSUR ZUR ALGEBRA (B3) 18. Februar 2009 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 7 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
Algebra I. keine Abgabe
 WS 05/06 Priv.-Doz. Dr. S. Wewers Andreas Martin Algebra I 13. Übungsblatt keine Abgabe Aufgabe 1: Sei G eine endliche abelsche Gruppe der Ordnung n. (a) Zeigen Sie: für jeden Teiler d von n existiert
WS 05/06 Priv.-Doz. Dr. S. Wewers Andreas Martin Algebra I 13. Übungsblatt keine Abgabe Aufgabe 1: Sei G eine endliche abelsche Gruppe der Ordnung n. (a) Zeigen Sie: für jeden Teiler d von n existiert
Serie 29. (Zusatzaufgaben ohne Musterlösung) Repetition 2. Semester
 D-MATH Algebra II FS 013 Prof. Richard Pink Serie 9 (Zusatzaufgaben ohne Musterlösung) Repetition. Semester 1. Sei R ein Hauptidealring und sei a R ein Ideal. Zeige, dass jedes Ideal in R/a ein Hauptideal
D-MATH Algebra II FS 013 Prof. Richard Pink Serie 9 (Zusatzaufgaben ohne Musterlösung) Repetition. Semester 1. Sei R ein Hauptidealring und sei a R ein Ideal. Zeige, dass jedes Ideal in R/a ein Hauptideal
Probeklausur - eine Lösung
 Probeklausur - eine Lösung Aufgabe 1 Sei p eine Primzahl, n N, q = p n und F q der Körper mit q Elementen. Sei G = GL 2 (F q ). a) Bestimmen Sie #G. 1 x b) Zeigen Sie, dass P = { : x F 1 q } eine p-sylowgruppe
Probeklausur - eine Lösung Aufgabe 1 Sei p eine Primzahl, n N, q = p n und F q der Körper mit q Elementen. Sei G = GL 2 (F q ). a) Bestimmen Sie #G. 1 x b) Zeigen Sie, dass P = { : x F 1 q } eine p-sylowgruppe
Algebra I, WS 04/05. i 0)
 G. Nebe, M. Künzer Algebra I, WS 04/05 Lösung 5 Aufgabe 20. 1 Wir haben einen Normalteiler C 3 = 1, 2, 3. Es ist mit C 2 := 1, 2 der Schnitt C 3 C 2 = 1, und folglich aus Ordnungsgründen S 3 = C 3 C 2.
G. Nebe, M. Künzer Algebra I, WS 04/05 Lösung 5 Aufgabe 20. 1 Wir haben einen Normalteiler C 3 = 1, 2, 3. Es ist mit C 2 := 1, 2 der Schnitt C 3 C 2 = 1, und folglich aus Ordnungsgründen S 3 = C 3 C 2.
Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II
 Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II Matrizen, lineare Gleichungssysteme Wie kommt man von einem linearen Gleichungssystem zu einer Matrix? Was ist die Zeilenstufenform?
Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II Matrizen, lineare Gleichungssysteme Wie kommt man von einem linearen Gleichungssystem zu einer Matrix? Was ist die Zeilenstufenform?
Algebra 2. Aufgabe 4: (3 P.) Sei R ein kommutativer Ring und M ein R-Modul. Zeigen Sie, dass die R-Moduln Hom R (R, M) und M isomorph sind.
 Sommersemester 2006 Übungsblatt 1 Abgabe: am Mi 26.04.2006 in der Vorlesung. Aufgabe 1: Sei k ein Körper, sei R der Ring M n (k), und sei M der R-Modul k n mit der üblichen Modulstruktur. a) (3 P.) Sei
Sommersemester 2006 Übungsblatt 1 Abgabe: am Mi 26.04.2006 in der Vorlesung. Aufgabe 1: Sei k ein Körper, sei R der Ring M n (k), und sei M der R-Modul k n mit der üblichen Modulstruktur. a) (3 P.) Sei
Seminar über Darstellungstheorie endlicher Gruppen: Lemma von Schur, Darstellungen abelscher Gruppen, Räume von Darstellungshomomorphismen
 Seminar über Darstellungstheorie endlicher Gruppen: Lemma von Schur, Darstellungen abelscher Gruppen, Räume von Darstellungshomomorphismen Aline Kaszuba, Lukas Böke 15. März 2016 Die folgende Diskussion
Seminar über Darstellungstheorie endlicher Gruppen: Lemma von Schur, Darstellungen abelscher Gruppen, Räume von Darstellungshomomorphismen Aline Kaszuba, Lukas Böke 15. März 2016 Die folgende Diskussion
Testklausur II mit Lösungen
 Fachbereich Mathematik/Informatik 2. Juli 2011 Prof. Dr. H. Brenner Körper- und Galoistheorie Testklausur II mit en Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben
Fachbereich Mathematik/Informatik 2. Juli 2011 Prof. Dr. H. Brenner Körper- und Galoistheorie Testklausur II mit en Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben
Seminar zur Darstellungstheorie endlicher Gruppen
 Seminar zur Darstellungstheorie endlicher Gruppen Prof. Dr. Gebhard Böckle und Yujia Qiu Sommersemester 15, dienstags 16:15 17:45, Raum 248/INF 368. Beginn: 21.04.2015 Motivation und Ziele des Seminars
Seminar zur Darstellungstheorie endlicher Gruppen Prof. Dr. Gebhard Böckle und Yujia Qiu Sommersemester 15, dienstags 16:15 17:45, Raum 248/INF 368. Beginn: 21.04.2015 Motivation und Ziele des Seminars
Übungen zu Algebra 2
 Friedrich-Schiller-Universität Jena Mathematisches Institut M.Sc.Mikael Johansson Übungen zu Algebra 2 Sommersemester 2006 Lösungen zu Übungsblatt 4 Aufgabe 1: (4 P.) Die abelsche Gruppe G wird von den
Friedrich-Schiller-Universität Jena Mathematisches Institut M.Sc.Mikael Johansson Übungen zu Algebra 2 Sommersemester 2006 Lösungen zu Übungsblatt 4 Aufgabe 1: (4 P.) Die abelsche Gruppe G wird von den
UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN
 UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN VORLESUNG KOMMUTATIVE ALGEBRA, SOMMERSEMESTER 2007 1. Definitionen Ein kommutativer Ring mit Eins R ist ein Integritätsbereich, wenn er zumindest zwei
UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN VORLESUNG KOMMUTATIVE ALGEBRA, SOMMERSEMESTER 2007 1. Definitionen Ein kommutativer Ring mit Eins R ist ein Integritätsbereich, wenn er zumindest zwei
Die Klassifikation der sieben Friesgruppen
 Mathematisches Institut Heinrich-Heine Universität Düsseldorf Dr. Steffen Kionke Proseminar: Kristallographische Gruppen WS 2014/15 Die Klassifikation der sieben Friesgruppen Dieser Text behandelt die
Mathematisches Institut Heinrich-Heine Universität Düsseldorf Dr. Steffen Kionke Proseminar: Kristallographische Gruppen WS 2014/15 Die Klassifikation der sieben Friesgruppen Dieser Text behandelt die
Karlsruher Institut für Technologie Institut für Algebra und Geometrie
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. Jochen Schröder Einführung in Algebra und Zahlentheorie Übungsblatt 3 Aufgabe (4 Punkte ( 3 7 Gegeben
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. Jochen Schröder Einführung in Algebra und Zahlentheorie Übungsblatt 3 Aufgabe (4 Punkte ( 3 7 Gegeben
Der Beweis des Ergodizitätssatzes von Moore
 Der Beweis des Ergodizitätssatzes von Moore Markus Schwagenscheidt Forschungsseminar Darmstadt-Frankfurt am 23.05.2013 Moores Theorem Theorem (Moore) Sei G = G i endliches Produkt zusammenhängender nicht-kompakter
Der Beweis des Ergodizitätssatzes von Moore Markus Schwagenscheidt Forschungsseminar Darmstadt-Frankfurt am 23.05.2013 Moores Theorem Theorem (Moore) Sei G = G i endliches Produkt zusammenhängender nicht-kompakter
Körper- und Galoistheorie. Nachklausur mit Lösungen
 Fachbereich Mathematik/Informatik 14. Januar 2012 Prof. Dr. H. Brenner Körper- und Galoistheorie Nachklausur mit en Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben
Fachbereich Mathematik/Informatik 14. Januar 2012 Prof. Dr. H. Brenner Körper- und Galoistheorie Nachklausur mit en Dauer: Zwei volle Stunden + 10 Minuten Orientierung, in denen noch nicht geschrieben
Lösungen zur Klausur über Lie-Algebren
 Universität zu Köln Sommersemester 2017 Mathematisches Institut 19. Juli 2017 Prof. Dr. P. Littelmann Lösungen zur Klausur über Lie-Algebren Dies ist keine Muster -Lösung, sondern eine Hilfe um die Lösung
Universität zu Köln Sommersemester 2017 Mathematisches Institut 19. Juli 2017 Prof. Dr. P. Littelmann Lösungen zur Klausur über Lie-Algebren Dies ist keine Muster -Lösung, sondern eine Hilfe um die Lösung
Chr.Nelius: Grundzüge der Algebra (WS2005/06) 1. (14.1) DEF: Ein kommutativer Ring (K, +, ) heißt ein Körper, wenn gilt: 1) 1 K 0 K 2) K = K \ {0 K }
 Chr.Nelius: Grundzüge der Algebra (WS2005/06) 1 14 Körper (14.1) DEF: Ein kommutativer Ring (K, +, ) heißt ein Körper, wenn gilt: 1) 1 K 0 K 2) K = K \ {0 K } (14.2) BEM: a) Ist K ein Körper, so ist (K
Chr.Nelius: Grundzüge der Algebra (WS2005/06) 1 14 Körper (14.1) DEF: Ein kommutativer Ring (K, +, ) heißt ein Körper, wenn gilt: 1) 1 K 0 K 2) K = K \ {0 K } (14.2) BEM: a) Ist K ein Körper, so ist (K
Einführung in die Artinschen Zopfgruppen
 Universität Duisburg-Essen - Campus Duisburg - Fakultät für Mathematik W. Hümbs Einführung in die Artinschen Zopfgruppen In den Aufgaben 1-6 sollen Sie Erzeugendensysteme und das Rechnen mit Generatoren
Universität Duisburg-Essen - Campus Duisburg - Fakultät für Mathematik W. Hümbs Einführung in die Artinschen Zopfgruppen In den Aufgaben 1-6 sollen Sie Erzeugendensysteme und das Rechnen mit Generatoren
Klausur. Algebra SS Bearbeitungszeit: 120 Minuten
 Prof. Dr. Bernd Siebert Klausur Algebra SS 2014 Bearbeitungszeit: 120 Minuten Nachname: Vorname: Matrikelnr: Es dürfen alle Vorlesungsunterlagen inklusive Übungsaufgaben und Lösungen verwendet werden.
Prof. Dr. Bernd Siebert Klausur Algebra SS 2014 Bearbeitungszeit: 120 Minuten Nachname: Vorname: Matrikelnr: Es dürfen alle Vorlesungsunterlagen inklusive Übungsaufgaben und Lösungen verwendet werden.
Klausur zur Algebra und Zahlentheorie für Lehramt Gymnasium
 Technische Universität Dortmund Sommersemester 2012 Fakultät für Mathematik 23.07.2012 Klausur zur Algebra und Zahlentheorie für Lehramt Gymnasium Name: Vorname: Matrikelnummer: Studiengang: Wichtige Informationen:
Technische Universität Dortmund Sommersemester 2012 Fakultät für Mathematik 23.07.2012 Klausur zur Algebra und Zahlentheorie für Lehramt Gymnasium Name: Vorname: Matrikelnummer: Studiengang: Wichtige Informationen:
Musterlösung zur Probeklausur
 Musterlösung zur Probeklausur Markus Severitt 26. Juni 2006 Aufgabe 1. Sei G eine Gruppe mit g 2 = e für alle g G. Zeigen Sie, dass G abelsch ist. Lösung. g 2 = e für alle g G heißt gerade, dass alle Elemente
Musterlösung zur Probeklausur Markus Severitt 26. Juni 2006 Aufgabe 1. Sei G eine Gruppe mit g 2 = e für alle g G. Zeigen Sie, dass G abelsch ist. Lösung. g 2 = e für alle g G heißt gerade, dass alle Elemente
Universität Bielefeld Sommersemester Lineare Algebra 2 Übungsblatt 1
 Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
Übungsblatt 1 Abgabe bis 10:00 Uhr am Donnerstag, den 19. April 2018, im Postfach Ihrer Tutorin bzw. Ihres Tutors. Es sei K ein beliebiger Körper. Seien V und W endlich-dimensionale K-Vektorräume, mit
Lineare Algebra I. Prof. Dr. M. Rost. Übungen Blatt 2 (WS 2010/2011) Abgabetermin: Donnerstag, 28. Oktober.
 Lineare Algebra I Prof. Dr. M. Rost Übungen Blatt 2 (WS 2010/2011) Abgabetermin: Donnerstag, 28. Oktober http://www.math.uni-bielefeld.de/~rost/la1 Erinnerungen und Ergänzungen zur Vorlesung: Im Folgenden
Lineare Algebra I Prof. Dr. M. Rost Übungen Blatt 2 (WS 2010/2011) Abgabetermin: Donnerstag, 28. Oktober http://www.math.uni-bielefeld.de/~rost/la1 Erinnerungen und Ergänzungen zur Vorlesung: Im Folgenden
6. Vortrag - Das Kernstück der Galoistheorie
 Proseminar Körpertheorie 6. Vortrag - Das Kernstück der Galoistheorie Von: Nguyen Hoai Viet Dang 06.06.2013 Prof. K. Wingberg, K. Hübner 1. Hauptsatz Galois-Korrespondenz Satz 1.1: Sei (i) (ii) K L eine
Proseminar Körpertheorie 6. Vortrag - Das Kernstück der Galoistheorie Von: Nguyen Hoai Viet Dang 06.06.2013 Prof. K. Wingberg, K. Hübner 1. Hauptsatz Galois-Korrespondenz Satz 1.1: Sei (i) (ii) K L eine
Übungen zur Diskreten Mathematik I Blatt 6
 1 Blatt 6 Aufgabe 19 Es sei M := {n N : n 2} und R := {(n, m) M M : n teilt m}. a) Zeigen Sie, dass R eine Ordnungsrelation auf M ist. b) Überprüfen Sie, ob R eine totale Ordnung auf M ist. c) Zeigen Sie,
1 Blatt 6 Aufgabe 19 Es sei M := {n N : n 2} und R := {(n, m) M M : n teilt m}. a) Zeigen Sie, dass R eine Ordnungsrelation auf M ist. b) Überprüfen Sie, ob R eine totale Ordnung auf M ist. c) Zeigen Sie,
6.1 Präsentationen von Gruppen
 244 6.1 Präsentationen von Gruppen Es geht jetzt um die Beschreibung von Gruppen durch Erzeugende und Relationen, also z. B. um die genaue Beschreibung dessen, was Zeilen wie die folgende bedeuten: G :=
244 6.1 Präsentationen von Gruppen Es geht jetzt um die Beschreibung von Gruppen durch Erzeugende und Relationen, also z. B. um die genaue Beschreibung dessen, was Zeilen wie die folgende bedeuten: G :=
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Lösung zur Klausur Algebra und Zahlentheorie I im WS03/04 von Stephan Schmitz
 Lösung zur Klausur Algebra und Zahlentheorie I im WS03/04 von Stephan Schmitz Die folgenden Lösungen der Klausuraufgaben verwenden zumeist nicht den kürzesten oder elegantesten Lösungsweg, sondern den,
Lösung zur Klausur Algebra und Zahlentheorie I im WS03/04 von Stephan Schmitz Die folgenden Lösungen der Klausuraufgaben verwenden zumeist nicht den kürzesten oder elegantesten Lösungsweg, sondern den,
Lineare Algebra I Zusammenfassung
 Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
1. Symmetrische Gruppen
 http://wwwmathematikuni-bielefeldde/birep/alg/ 1 Symmetrische Gruppen 1 Bestimme alle Untergruppen der symmetrischen Gruppe S 4 Zeichne den entsprechenden Untergruppen-Verband 2 (a) Die Gruppe S n wird
http://wwwmathematikuni-bielefeldde/birep/alg/ 1 Symmetrische Gruppen 1 Bestimme alle Untergruppen der symmetrischen Gruppe S 4 Zeichne den entsprechenden Untergruppen-Verband 2 (a) Die Gruppe S n wird
1. Übungsblatt: Lineare Algebra I Abgabe: 1. November 2001 in den Übungsgruppen
 Hannover, den 25. Oktober 200. Übungsblatt: Lineare Algebra I Abgabe:. November 200 in den Übungsgruppen (je 3 Punkte) Beweisen oder widerlegen Sie die folgenden Aussagen über Mengen. a) A (B C) = (A B)
Hannover, den 25. Oktober 200. Übungsblatt: Lineare Algebra I Abgabe:. November 200 in den Übungsgruppen (je 3 Punkte) Beweisen oder widerlegen Sie die folgenden Aussagen über Mengen. a) A (B C) = (A B)
Algebra II, SS 2009 Montag $Id: endlich.tex,v /04/27 13:49:37 hk Exp $ GF(q) := {x A p x q = x}
 $Id: endlich.tex,v 1.4 2009/04/27 13:49:37 hk Exp $ 3 Endliche Körper Wir waren gerade mit dem Beweis von Satz 1 beschäftigt, und hatten die Existenzteile des Satzes bereits eingesehen. Satz 3.1 (Klassifikation
$Id: endlich.tex,v 1.4 2009/04/27 13:49:37 hk Exp $ 3 Endliche Körper Wir waren gerade mit dem Beweis von Satz 1 beschäftigt, und hatten die Existenzteile des Satzes bereits eingesehen. Satz 3.1 (Klassifikation
2.6 Ergänzungen und Beispiele: Semidirekte Produkte
 Algebra I 15. Oktober 2007 c Rudolf Scharlau, 2002 2007 66 2.6 Ergänzungen und Beispiele: Semidirekte Produkte Wir befassen uns mit der Zerlegung von Gruppen in kleinere Gruppen, bzw. der Konstruktion
Algebra I 15. Oktober 2007 c Rudolf Scharlau, 2002 2007 66 2.6 Ergänzungen und Beispiele: Semidirekte Produkte Wir befassen uns mit der Zerlegung von Gruppen in kleinere Gruppen, bzw. der Konstruktion
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 22 Algebraische Körpererweiterung Satz 1. Sei K L eine Körpererweiterung und sei f L ein Element. Dann sind folgende Aussagen
Algebra II. Prof. Dr. M. Rost. Übungen Blatt 3 (SS 2016) 1. Abgabetermin: Freitag, 6. Mai.
 Algebra II Prof. Dr. M. Rost Übungen Blatt 3 (SS 2016) 1 Abgabetermin: Freitag, 6. Mai http://www.math.uni-bielefeld.de/~rost/a2 Erinnerungen an die Vorlesung: Im Folgenden werden manchmal einige Definitionen
Algebra II Prof. Dr. M. Rost Übungen Blatt 3 (SS 2016) 1 Abgabetermin: Freitag, 6. Mai http://www.math.uni-bielefeld.de/~rost/a2 Erinnerungen an die Vorlesung: Im Folgenden werden manchmal einige Definitionen
Drei Beispiele zum Hauptsatz der GALOIS Theorie
 Chr.Nelius: Algebra (SS 2006) 6 Drei Beispiele zum Hauptsatz der GALOIS Theorie (12.8) BEISPIEL: Seien α := e 2πi 5 und L := (α). Die Galois Gruppe G := Gal(L : ) wird in Aufgabe 38a berechnet. f := T
Chr.Nelius: Algebra (SS 2006) 6 Drei Beispiele zum Hauptsatz der GALOIS Theorie (12.8) BEISPIEL: Seien α := e 2πi 5 und L := (α). Die Galois Gruppe G := Gal(L : ) wird in Aufgabe 38a berechnet. f := T
Klausur zur Einführung in die Algebra. Fasse den Klausurbogen nicht an, bevor die Klausur eröffnet wird!
 Christoph Hanselka Markus Schweighofer 16. März 2015 Wintersemester 2014/2015 Klausur zur Einführung in die Algebra Familienname: Matrikelnummer: Vorname: Übungsgruppenleiter: Aufgabe 1 2 3 4 5 6 7 erreichte
Christoph Hanselka Markus Schweighofer 16. März 2015 Wintersemester 2014/2015 Klausur zur Einführung in die Algebra Familienname: Matrikelnummer: Vorname: Übungsgruppenleiter: Aufgabe 1 2 3 4 5 6 7 erreichte
Themen und Übungen zum Lehrerweiterbildungskurs Wiederholung und Vertiefung Lineare Algebra/Analytische Geometrie I WiSe 2013/2014
 Themen und Übungen zum Lehrerweiterbildungskurs Wiederholung und Vertiefung Lineare Algebra/Analytische Geometrie I WiSe 2013/2014 [Sch]: R.-H.Schulz:Repetitorium Bachelor Mathematik [Sch-LAI] R.-H.Schulz:
Themen und Übungen zum Lehrerweiterbildungskurs Wiederholung und Vertiefung Lineare Algebra/Analytische Geometrie I WiSe 2013/2014 [Sch]: R.-H.Schulz:Repetitorium Bachelor Mathematik [Sch-LAI] R.-H.Schulz:
Die Konstruktion des regelmäÿigen n-ecks mit Zirkel und Lineal
 Die Konstruktion des regelmäÿigen n-ecks mit Zirkel und Lineal Für welche natürliche Zahlen n 3 kann man das regelmäÿige n-eck mit Zirkel und Lineal konstruieren? Wir haben in der Vorlesung gesehen, dass
Die Konstruktion des regelmäÿigen n-ecks mit Zirkel und Lineal Für welche natürliche Zahlen n 3 kann man das regelmäÿige n-eck mit Zirkel und Lineal konstruieren? Wir haben in der Vorlesung gesehen, dass
Lösung zu Serie 10. Lineare Algebra D-MATH, HS Prof. Richard Pink
 Lineare Algebra D-MATH, HS 2014 Prof. Richard Pink Lösung zu Serie 10 1. [Aufgabe] a) Sei V ein Unterraum eines K-Vektorraums V. Zeige, dass jede Linearform auf V eine Fortsetzung zu einer Linearform auf
Lineare Algebra D-MATH, HS 2014 Prof. Richard Pink Lösung zu Serie 10 1. [Aufgabe] a) Sei V ein Unterraum eines K-Vektorraums V. Zeige, dass jede Linearform auf V eine Fortsetzung zu einer Linearform auf
Klassische Algebra. Gesucht sind die Lösungsmengen der folgenden Gleichungen: x n + a n 1 x n a 1 x + a 0 = 0 (a 0,...
 Klassische Algebra Gesucht sind die Lösungsmengen der folgenden Gleichungen: x n + a n 1 x n 1 + + a 1 x + a 0 = 0 (a 0,..., a n 1 Q) Formeln für n {1, 2, 3, 4} sind bekannt. Abel, Galois: Für n N mit
Klassische Algebra Gesucht sind die Lösungsmengen der folgenden Gleichungen: x n + a n 1 x n 1 + + a 1 x + a 0 = 0 (a 0,..., a n 1 Q) Formeln für n {1, 2, 3, 4} sind bekannt. Abel, Galois: Für n N mit
Übungsaufgaben und Musterlösungen zur Einführung in die Algebra im Sommersemester 2004
 Übungsaufgaben und Musterlösungen zur Einführung in die Algebra im Sommersemester 2004 Aufgabe (1). Sei D eine nichtleere Menge und M := Abb(D D). (a) Zeigen Sie: M ist bzgl. der Hintereinanderausführung
Übungsaufgaben und Musterlösungen zur Einführung in die Algebra im Sommersemester 2004 Aufgabe (1). Sei D eine nichtleere Menge und M := Abb(D D). (a) Zeigen Sie: M ist bzgl. der Hintereinanderausführung
Sylow Sätze und Anwendungen
 KAPITEL 11 Sylow Sätze und Anwendungen 11A. Einführung und Überblick In diesem Kapitel widmen wir uns ausschließlich endlichen Gruppen. Der Satz von Lagrange besagt, das für jede Untergruppe H < G die
KAPITEL 11 Sylow Sätze und Anwendungen 11A. Einführung und Überblick In diesem Kapitel widmen wir uns ausschließlich endlichen Gruppen. Der Satz von Lagrange besagt, das für jede Untergruppe H < G die
2.7. RINGDIREKTE SUMME, SIMULTANE KONGRUENZEN 89
 2.7. RINGDIREKTE SUMME, SIMULTANE KONGRUENZEN 89 Beweis. 1.) ϕ : Z K : 1 1 definiert einen Homomorphismus. Da Bild ϕ endlich ist, ist Z/ Kern ϕ endlich und man sieht leicht Kern ϕ = pz für eine Primzahl
2.7. RINGDIREKTE SUMME, SIMULTANE KONGRUENZEN 89 Beweis. 1.) ϕ : Z K : 1 1 definiert einen Homomorphismus. Da Bild ϕ endlich ist, ist Z/ Kern ϕ endlich und man sieht leicht Kern ϕ = pz für eine Primzahl
