Einführung in die multiple Regression
|
|
|
- Lorenz Weiß
- vor 7 Jahren
- Abrufe
Transkript
1 Einführung in die multiple Regression Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg Bachelor S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 1 / 103
2 Agenda Multiple Regression Datenbeispiel Inferenzstatistische Absicherung des Regressionsmodells Gütekriterien der Regression Konfidenzintervalle Standardisierte Koeffizienten Nominale Variablen S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 2 / 103
3 Agenda (Forts. 2) Dummy und numerische Variablen Interaktion bzw. Moderation Nominale Variablen mit mehr als zwei Stufen Bericht der Ergebnisse S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 3 / 103
4 Multiple Regression Outline Multiple Regression Multiple Regression Gleichungen der multiplen Regression Notation Schätzung der Koeffizienten Zusammenhang mit Korrelation S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 4 / 103
5 Multiple Regression Multiple Regression Multiple Regression Multiple Regression meint eine Regression mit mehr als einer unabhängigen Variablen. Das Skalenniveau der unabhängigen Variablen ist beliebig. Der Methode der Parameterschätzung bleibt aber gleich: OLS (oridnary least square), Methode der kleinsten Quadrate. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 5 / 103
6 Multiple Regression Gleichungen der multiplen Regression Gleichungen der multiplen Regression Die Modellgleichung lautet: Modellgleichung y i = β 0 + β 1 x i β q x iq + ϵ i (1) mit yi x iq ϵ i ite Beobachtung der abhängigen Variable der i-ten Person Beobachtungen der iten-person bei insegsamt q unabhängigen Variablen mit i = 1,..., n Personen. Fehler bzw. Residuum der iten Beobachtung S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 6 / 103
7 Multiple Regression Gleichungen der multiplen Regression Zielfunktion der multiplen Regression Auch in der multiplen Regression wird die Summe der quadrierten Residuen e minimiert: Zielfunktion ŷ i = β 0 + β 1 x i β q x iq, wobei n n e 2 i = [y i ŷ i ] 2 min i=1 i=1 mit e i Fehler bzw. Residuum der iten Beobachtung S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 7 / 103
8 Multiple Regression Notation Notation Notation folgt Everitt und Hothorn (2006): n Anzahl der Messungen, q Anzahl der Koeffizienten ohne Interzept. In Matrixschreibweise ist y n = β 0 + β 1 x n β q x nq + ϵ n : y = βx + ϵ. AV y = (y 1,..., y n ), Koeffizienten β = (β 0, β 1,..., β q ), und ϵ = (ϵ 1,..., ϵ n ). Die Datenmatrix X lautet: 1 x 11 x x 1q 1 x 21 x x 2q X = x n1 x n2... x nq Diese Matrix nennt man auch Designmatrix. Die Einsen in der ersten Spalte von X repräsentieren den Interzept. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 8 / 103
9 Multiple Regression Schätzung der Koeffizienten Schätzung der Koeffizienten β Wie bei er OLS Regression werden die Koeffizienten nach der Methode der kleinsten Quadrate geschätzt: e 2 i = min. Eine unvollständige Herleitung findet sich bei Bortz und Schuster (2010, S. 360), mehr Hintergründe zeigt Fox (2008, S. 152ff). Schätzung der ˆβ Die geschätzten Koeffizienten ˆβ werden wie folgt berechnet: ˆβ = (X X) 1 X y (2) S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 9 / 103
10 Multiple Regression Zusammenhang mit Korrelation Zusammenhang mit Korrelation Die Regressionsgewichte β i können auch über Korrelationen geschätzt werden. So gilt für den Fall von zwei numerischen Prädiktorvariablen x 1 und x 2 : β 1 = r y1 r y 2 r 12 1 r 2 12 β 2 = r y 2 r y1 r 12 1 r 2 12 sy s 1 sy s 2 β 0 = ȳ β 1 x 1 β 2 x 2 mit r y1 Korrelation zwischen y mit x 1 etc. Die Korelationen sind um die Effekte der anderen Koeffizienten bereinigt. Dieser Ansatz kann auf eine beliebige Anzahl von Prädiktorvariablen erweitert werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 10 / 103
11 Datenbeispiel Outline Datenbeispiel Datenbeispiel Dotplot Datenmatrix / Vektoren Berechnung der Koeffizienten Visualisierung S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 11 / 103
12 Datenbeispiel Datenbeispiel Datenbeispiel Die Daten sind aus Budischewski (2008). Datentabelle: VP Sympathie Redefluss Attraktivität Wie hängt Sympathie mit dem Redefluss und der Attraktivität zusammen? S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 12 / 103
13 Datenbeispiel Dotplot Dotplot der Daten Redefluss Attraktivität Sympathie Redefluss + Attraktivität S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 13 / 103
14 Datenbeispiel Datenmatrix / Vektoren Datenmatrix / Vektoren Die Datentabelle in Vektoren und Matrixschreibweise: y = 13 12, X = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 14 / 103
15 Datenbeispiel Berechnung der Koeffizienten Berechnung der Koeffizienten ˆβ 1 Berechnung der Koeffizienten: ˆβ = (X X) 1 X y. 2 Damit: ˆβ = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 15 / 103
16 Datenbeispiel Berechnung der Koeffizienten Berechnung der Koeffizienten ˆβ (Forts. 2) 3 Die Matrix X X: X X = = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 16 / 103
17 Datenbeispiel Berechnung der Koeffizienten Berechnung der Koeffizienten ˆβ (Forts. 3) 4 Die Inverse ist: (X X) 1 = = Wichtig: Rundungsfehler wirken sich ernorm aus! Wird (X X) 1 z. B. auf 3 Nachkommestellen greundet, ergeben sich andere Koeffizienten. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 17 / 103
18 Datenbeispiel Berechnung der Koeffizienten Berechnung der Koeffizienten ˆβ (Forts. 4) 6 Der Ausdruck X y: X y = = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 18 / 103
19 Datenbeispiel Berechnung der Koeffizienten Berechnung der Koeffizienten ˆβ (Forts. 5) 7 Die Koeffizienten ˆβ = (X X) 1 X y ergeben sich damit zu: ˆβ = β = β 1 = β Die Regressiongleichung lautet somit: ŷ = x Redefluss x Attraktivität. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 19 / 103
20 Datenbeispiel Visualisierung Visualisierung 3D Scatterplot Sympathie Attraktivität Redefluss S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 20 / 103
21 Datenbeispiel Visualisierung Visualisierung 3D Scatterplot Sympathie Attraktivität Redefluss S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 21 / 103
22 Datenbeispiel Visualisierung Berechnung über Korrelationen Die Koeffizienten können auch über Korrelationen hergeleitet werden: β 1 = r y1 r y 2 r 12 1 r 2 12 β 2 = r y 2 r y1 r 12 1 r 2 12 sy s 1 sy s 2 β 0 = ȳ β 1 x 1 β 2 x 2 wobei die Produkt-Moment-Korrelation über: n n i=1 r PM = (x i y i ) ( n i=1 x ( i) n i=1 y ) i [ n n i=1 x2 i ( n i=1 x ) ] [ 2 i n n i=1 y2 i ( n i=1 y ) ] 2 i S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 22 / 103
23 Datenbeispiel Visualisierung Berechnung über Korrelationen (Forts. 2) und die Streuung mit: ( n ) s = 1 x 2 i ( n i=1 x i) 2 n 1 n bestimmt werden kann. i=1 Die Korrelationen und Streuungen sind dann: r y1 = r y 2 = r 12 = s y = s 1 = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 23 / 103
24 Datenbeispiel Visualisierung Berechnung über Korrelationen (Forts. 3) Für β 1 ergibt sich so: β 1 = r y1 r y 2 r 12 1 r 2 sy 12 s = = Äquivalent kann β 2 und daraufhin β 0 berechnet werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 24 / 103
25 Inferenzstatistische Absicherung des Regressionsmodells Outline Inferenzstatistische Absicherung des Regressionsmodells Statistische Überprüfung der Koeffizienten Berechnung der Standardfehler Beispielrechnung Berechnung der Varianz Berechnung der Standardfehler Berechnung der t-werte Ausgabe mit R und PSPP Interpretation F-Tests Varianztabelle der multiplen Regression S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 25 / 103
26 Inferenzstatistische Absicherung des Regressionsmodells Statistische Überprüfung der Koeffizienten Statistische Überprüfung der Koeffizienten Die Koeffizienten werden auf statistische Signifikanz geprüft. Hypothesen: H 0 : β q = 0 H 1 : β q 0 Hierzu wird der Koeffizient durch seinen Standardfehler dividiert: ˆβ q s.e.( ˆβ t(df = n q 1) (3) q ) Diese Größe ist t-verteilt mit n q 1 Freiheitsgraden. Hinweis: Es gibt weitere Verfahren, einen bzw. mehrere Koeffizienten auf statistische Bedeutsamkeit zu prüfen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 26 / 103
27 Inferenzstatistische Absicherung des Regressionsmodells Berechnung der Standardfehler Berechnung der Standardfehler Die Kovarianzmatrix Var( ˆβ) der Koeffizienten lautet σ 2 (X X) 1. Mit ˆσ 2 = 1 n q 1 n i=1 (y i ŷ i ) 2. Die Wurzel aus den Diagonalelementen von Var( ˆβ) liefert die Standardfehler der geschätzten Koeffizienten ˆβ. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 27 / 103
28 Inferenzstatistische Absicherung des Regressionsmodells Beispielrechnung Beispielrechnung Im folgenden werden die Rechengänge am Beispiel gezeigt: 1 Zunächst wird die Varianz ˆσ 2 berechnet. 2 Die Inverse (X X) 1 ist bereits bekannt. 3 Zur Berechnung von Var( ˆβ) muss noch das Produkt ˆσ 2 (X X) 1 berechnet werden. 4 Die Standardfehler sind die Wurzel aus den Diagonalelementen von Var( ˆβ). 5 Sind die Standardfehler berechnet, können die t-tests bestimmt werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 28 / 103
29 Inferenzstatistische Absicherung des Regressionsmodells Berechnung der Varianz Berechnung von ˆσ 2 Gleichung: ŷ = x Redefluss x Attraktivität Sympathie Redefluss Attraktivität ŷ i (y i ŷ) (y i ŷ) = 0.94 ˆσ 2 = 1 n n q 1 i=1 (y i ŷ i ) 2 1 = = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 29 / 103
30 Inferenzstatistische Absicherung des Regressionsmodells Berechnung der Standardfehler Berechnung der Standardfehler Berechnung von Var( ˆβ): σ 2 (X X) 1 = = Die Standardfehler sind diag(σ 2 (X X) 1 ): s.e.( ˆβ 0 ) = , s.e( ˆβ 1 ) = , s.e.( ˆβ 2 ) = und damit sind die Standardfehler: s.e.( ˆβ 0 ) = , s.e.( ˆβ 1 ) = , s.e.( ˆβ 2 ) = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 30 / 103
31 Inferenzstatistische Absicherung des Regressionsmodells Berechnung der t-werte Berechnung der t-werte Die t-werte ergeben sich zu: ˆβ q /s.e.( ˆβ q ) mit df = n q 1 = = 7. Damit: Interzept: β 0 /s.e.(β 0 ) = / = Redefluss: β 1 /s.e.(β 1 ) = / = Attraktivität: β 2 /s.e.(β 2 ) = / = Sind diese t-werte signifkant auf dem 5% Niveau? S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 31 / 103
32 Inferenzstatistische Absicherung des Regressionsmodells Ausgabe mit R und PSPP Ausgabe mit > fit <- lm(sympathie ~ Redefluss + Attraktivität, data = bsp) > summary(fit) Call: lm(formula = Sympathie ~ Redefluss + Attraktivität, data = bsp) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) Redefluss e-05 *** Attraktivität Signif. codes: 0 *** ** 0.01 * Residual standard error: on 7 degrees of freedom Multiple R-squared: ,^^IAdjusted R-squared: F-statistic: on 2 and 7 DF, p-value: 6.472e-06 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 32 / 103
33 Inferenzstatistische Absicherung des Regressionsmodells Ausgabe mit R und PSPP Ausgabe mit S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 33 / 103
34 Inferenzstatistische Absicherung des Regressionsmodells Interpretation Interpretation Nur der Koeffizient für den Redefluss ist signifikant. Die positive Steigung von 0.42 für Redefluss bedeutet, dass die wahrgenommene Sympathie, bei gleichem Wert für Attraktivität, pro weiteren Punkt Redefluss um 0.42 steigt. Wahrgenommene Attraktivität steuert offensichtlich keinen signifikanten Beitrag zur Vorhersage bei, kann damit weggelassen werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 34 / 103
35 Inferenzstatistische Absicherung des Regressionsmodells F-Tests F-Tests Die Koeffizienten eines Regressionsmodells werden mittels t-test auf statistische Signifikanz geprüft. Es wird dabei immer ein Koeffizient auf statistische Bedeutsamkeit geprüft. Man kann Koeffizienten zusammenfassen und mittels F-Test auf statistische Signifikanz überprüfen ANOVA. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 35 / 103
36 Inferenzstatistische Absicherung des Regressionsmodells Varianztabelle der multiplen Regression Varianztabelle der multiplen Regression Die Ergebnisse der multiplen Regression können auch in einer Varianztabelle zusammengefasst werden: Q.d.V. QS df Regression n i=1 (ŷ i ȳ) 2 q Residual n i=1 (ŷ i y i ) 2 n q 1 Total n i=1 (y i ȳ) 2 n 1 Mit einem F-Test kann die Hypothese H 0 : β 1 =... = β q = 0 geprüft werden: F = n i=1 (ŷ i ȳ) 2 /q n i=1 (y i ŷ i ) 2 /n q 1 (4) mit q und n q 1 Freiheitsgraden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 36 / 103
37 Inferenzstatistische Absicherung des Regressionsmodells Varianztabelle der multiplen Regression Varianztabelle im Beispiel Regressionsgleichung: ŷ = x Redefluss x Attraktivität S R A ŷ i (y i ŷ i ) (y i ŷ i ) 2 (ŷ i ȳ) (ŷ i ȳ) = 101 Residual Regression ȳ = 10.1 = 0.94 = S = Sympathie; R = Redefluss; A = Attraktivität S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 37 / 103
38 Inferenzstatistische Absicherung des Regressionsmodells Varianztabelle der multiplen Regression Varianztabelle im Beispiel (Forts. 2) F-Wert: F emp = = n i=1 (ŷ i ȳ) 2 /q n i=1 (ŷ i y i ) 2 /n q /2 0.95/(10 2 1) = Kritischer F-Wert bei α = 0.05: F [2,7] = Damit F emp > F krit H 1 Schlussatz: Mit einer Irrtumswahrscheinlichkeit von 5% ist mindestens ein Koeffizient verschieden von Null und hat einen statistisch bedeutsamen Einfluss auf die wahrgenommene Sympathie. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 38 / 103
39 Inferenzstatistische Absicherung des Regressionsmodells Varianztabelle der multiplen Regression Zum vergleich: PSPP S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 39 / 103
40 Gütekriterien der Regression Outline Gütekriterien der Regression Gütekriterien der Regression Bestimmtheitsmaß R Quadrat Interpratation von R-Quadrat Adjustiertes R-Quadrat Adjustiertes R-Quadrat im Beispiel S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 40 / 103
41 Gütekriterien der Regression Gütekriterien der Regression Gütekriterium der Regression Die statistische Absicherung der Koeffizienten sagt wenig über die Güte der Regressionslösung aus. Eine Möglichkeit die Güte einer Regression zu beurteilen, liegt darin die Residuen in ein Verhältnis zur Gesamtvarianz zu setzen. Idee: Je geringer die Residuen, desto genauer das Regressionsmodell. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 41 / 103
42 Gütekriterien der Regression Bestimmtheitsmaß R Quadrat Bestimmtheitsmaß R 2 Berechnung von R 2 R 2 = QS n Regression i=1 = (ŷ i ȳ) 2 QS n Total i=1 (y i ȳ) 2 = β X y nȳ 2 y y nȳ 2 (5) Bestimmheitsmaß R 2, R square oder multiple R 2. QS Regression wird auch als QS det bezeichnet. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 42 / 103
43 Gütekriterien der Regression Bestimmtheitsmaß R Quadrat Berechnung von R 2 Über Quadratsummen: QS Regression = Über Matrizen: n (ŷ i ȳ) 2 i=1 = ( ) 2 + ( ) ( ) 2 = n QS Total = (y i ȳ) 2 i=1 = ( ) 2 + (8 10.1) ( ) 2 = 28.9 R 2 = /28.9 = β X y nȳ 2 y y nȳ 2 =... = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 43 / 103
44 Gütekriterien der Regression Interpratation von R-Quadrat Interpratation von R 2 R 2 kann zwischen 0 und 1 liegen. Je größer R 2, desto besser. Ein R 2 von 0.97 ist also sehr gut. Es treten damit fasst keine Schätzfehler auf - der Sympathie-Wert kann damit fasst fehlerfrei auf Basis des Redeflusses und der Attraktivität vorhergesagt werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 44 / 103
45 Gütekriterien der Regression Adjustiertes R-Quadrat Adjustiertes R 2 R 2 wird größer, je mehr Terme in das Modell aufgenommen werden Überschätzung der Modellgüte. Daher wird R 2 nicht zur Modellselektion empfohlen, z. B. Fahrmeir, Kneib und Lang (2009). Ein Versuch diesen Umstand zu korrigieren, ist das adjustierte R 2, auch als R 2 bezeichnet. R2 entspricht einem an der Anzahl der Prädiktoren (Terme) und der Stichprobengröße relativiertem R 2. R2 ist nicht in gleicher Weise zu interpretieren wie R 2, sondern eher in der Art einer Schrumpfungskorrektur (engl: shrinkage estimator) und daher besser zur Modellselektion geeignet (engl. Feature selection). S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 45 / 103
46 Gütekriterien der Regression Adjustiertes R-Quadrat Adjustiertes R 2 Adjustiertes R 2 Das adjustierte R 2 kann folgendermaßen berechnet werden: R 2 = 1 (1 R 2 ) n 1 n q 1 = 1 QS Residual df Total (6) QS Total df Residual mit: R 2 Determinationskoeffizient n, q Stichprobengröße, Anzahl der Prädiktoren ohne Interzept QS Quadratsumme S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 46 / 103
47 Gütekriterien der Regression Adjustiertes R-Quadrat im Beispiel R 2 im Beispiel R 2 = Damit: R 2 = 1 (1 R 2 n 1 ) n q = 1 ( ) = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 47 / 103
48 Gütekriterien der Regression Adjustiertes R-Quadrat im Beispiel Zum Vergleich: PSPP Ausgabe S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 48 / 103
49 Konfidenzintervalle Outline Konfidenzintervalle Konfidenzintervalle für vorhergesagte Werte KI für vorhergesagten Wert Beispiel Berechnung CI Allgemeine Berechnung CIs S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 49 / 103
50 Konfidenzintervalle Konfidenzintervalle für vorhergesagte Werte Konfidenzintervalle für vorhergesagte Werte Auch in der multiplen Regression können Konfidenzintervalle für vorhergesagte Werte berechnet werden. Je besser der Zusammenhang zwischen AV und UVen, desto kleiner ist dieses Konfidenzintervall und vice versa. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 50 / 103
51 Konfidenzintervalle KI für vorhergesagten Wert KI für vorhergesagten Wert Konfidenzintervalle für vorhergesagte Werte KIs für vorhergesagte Werte werden in der multiplen Regression wie folgt berechnet: QS Residual ŷ i ± t (α/2,df=n q 1) df Residual wobei QSResidual df Residual berechnet werden: der Standardschätzfehler s e ist. Dieser kann wie folgt s e = n QS Residual i=1 = (ŷ i y i ) 2 df Residual n q 1 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 51 / 103
52 Konfidenzintervalle Beispiel Berechnung CI Beispiel Berechnung CI 1 Geschätzter Sympathie Wert ist ŷ = 10. Wie lautet das 95% KI? 2 Berechnung von QS Residual : QS Total = QS Regression + QS Residual QS Residual = QS Total QS Regression = = Freiheitsgrade: df Residual = n q 1 = = 7. 4 Damit: s e = QS Residual 0.95 = = df Residual 7 5 t-wert: t(α = 0.05, df = 7, zweiseitig) = 2.365; df = n q 1. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 52 / 103
53 Konfidenzintervalle Beispiel Berechnung CI Beispiel Berechnung CI (Forts. 2) 6 Die Grenzen sind damit: Obergrenze : ŷ i + t (α/2,df=n q 1) QS Residual df Residual = = QS Residual Untergrenze : ŷ i t (α/2,df=n q 1) df Residual = = Schlusssatz: Mit 95% Wahrscheinlichkeit befindet sich der Wert der Person innerhalb des Bereiches von 9.13 bis S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 53 / 103
54 Konfidenzintervalle Allgemeine Berechnung CIs Allgemeine Berechnung von CIs Es sei x 0 = x 01, x 02,..., x 0q ein Vektor mit Prädiktorvariablen. x 0 ist folgendermaßen definiert: 1 x 01 x 0 = x 02. x 0q Der gefittete Wert ŷ 0 an dieser Stelle ist: ŷ 0 = x 0 ˆβ. Ein 100(1 α)% KI kann für alle vorhergesagten Werte ŷ bei den Ausprägungen x 0 = x 01, x 02,..., x 0q konstruiert werden über: ŷ 0 ± t n q 1,α/2 ˆσ 2 x 0 (X X) 1 x 0 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 54 / 103
55 Standardisierte Koeffizienten Outline Standardisierte Koeffizienten Standardisierte Koeffizienten Berechnung der standardisierten β-gewichte Standardisierte Koeffizienten im Beispiel S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 55 / 103
56 Standardisierte Koeffizienten Standardisierte Koeffizienten Standardisierte Koeffizienten Die bisher berechneten β-gewichte sind nicht direkt miteinander vergleichbar. Sie beinhalten noch ihre ursprünglichen Einheiten, in denen sie gemessen wurden. Um die β-gewichte vergleichbar zu machen, müssen diese Einheiten entfernt werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 56 / 103
57 Standardisierte Koeffizienten Berechnung der standardisierten β-gewichte Grundgleichung Die Variablen werden einer z-transformation unterzogen z i = x i x σ. Damit: Mittelwert gleich Null und Varianz gleich Eins. Gleichung: Ẑ iy = B 0 + B 1 z i B q z iq Mit den transformierten Variablen wird eine multiple Regression gerechnet. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 57 / 103
58 Standardisierte Koeffizienten Berechnung der standardisierten β-gewichte Im Fall von zwei Prädiktoren Da für standardisierte Variablen s = 1 gilt, vereinfacht sich die Berechnung für zwei Prädiktoren zu: B 1 = r y1 r y 2 r 12 1 r 2 12 B 2 = r y 2 r y1 r 12 1 r 2 12 Nun gilt: β 1 = r y1 r y 2 r 12 1 r 2 12 β 2 = r y 2 r y1 r 12 1 r 2 12 sy s 1 sy s 2 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 58 / 103
59 Standardisierte Koeffizienten Berechnung der standardisierten β-gewichte Im Fall von zwei Prädiktoren (Forts. 2) Daher können die standardisierten Koeffizienten B i aus den Koeffizienten β i folgendermaßen gerechnet werden: B 1 = β 1 s1 s y B 2 = β 2 s2 s y Es gilt immer: β 0 = 0 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 59 / 103
60 Standardisierte Koeffizienten Berechnung der standardisierten β-gewichte Berechnung der standardisierten β-gewichte Zur Berechnung der standardisierten Koeffizienten wird die Streuung (Standardabweichung) der Prädiktor- und Kriteriumsvariablen benötigt. Standardisierte Koeffizienten wobei ˆσ = Es gilt immer β 0 = 0. B i =β i ˆσ x i, ˆσ y n i=1 (x i x) 2 n 1 = n i=1 x2 i ( n i=1 x i) 2 n n 1 (7) S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 60 / 103
61 Standardisierte Koeffizienten Standardisierte Koeffizienten im Beispiel Standardisierte Koeffizienten im Beispiel Zunächst müssen für Sympathie, Redefluss und Attraktivität die Streuungen s berechnet werden. Für Redefluss: Erstes Teilstück: s Redefluss = n i=1 x2 i ( n i=1 x i) 2 n n 1 n x 2 i = i= = 4222 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 61 / 103
62 Standardisierte Koeffizienten Standardisierte Koeffizienten im Beispiel Standardisierte Koeffizienten im Beispiel (Forts. 2) Zweites Teilstück: ( n ) 2 x i = ( i= ) 2 = = Damit s Redefluss = 10 1 = bzw. s Redefluss = = 3.97 Für Sympathie und Attraktivität wird äquivalent Verfahren. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 62 / 103
63 Standardisierte Koeffizienten Standardisierte Koeffizienten im Beispiel Standardisierte Koeffizienten im Beispiel (Forts. 3) Streuungen: s Redefluss = 3.97 s Attraktivität = 2.41 s Sympathie = 1.79 Die standardisierten Koeffizienten für Redefluss und Attraktivität lauten damit: Redefluss: β j sxj s y = = 0.93 Attraktivität: = 0.08 Interpretation: Der standardisierte Koeffizient von Redefluss ist knapp 12 mal so groß wie der der Attraktivität. Redefluss hat damit einen wesentlich bedeutsameren Einfluss auf die wahrgenommene Sympathie als Attraktivität. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 63 / 103
64 Nominale Variablen Outline Nominale Variablen Nominale Variablen in der multiplen Regression Modellgleichung mit Dummy-Codierung Berechnung mit Dummy-Codierung S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 64 / 103
65 Nominale Variablen Nominale Variablen in der multiplen Regression Nominale Variablen in der multiplen Regression Bisher haben wir nur numerische Variablen behandelt. Nominale Variablen können aber problemlos in der multiplen Regression verwendet werden. Dazu werden die nominalen Variablen einer Dummy Codierung bzw. Dummy Regressor, Indikator Variable unterzogen. Dies bedeutet, dass die Stufen der nominalen Variablen in einer Matrix re-kodiert werden. Es gibt verschiedene Möglichkeiten, diese Kodierung vorzunehmen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 65 / 103
66 Nominale Variablen Nominale Variablen in der multiplen Regression Beispiel einer Codierung Nehmen wir an, wir wollen unserem Datensatz die Variable Geschlecht hinzufügen (männlich / weiblich). Uns interessiert zunächst nur, ob sich die Sympathiewerte zwischen den Geschlechtern unterscheidet. Wir benötigen dann eine Spalte, in der kodiert ist, ob es sich bei einem Beobachtungsfall um eine Frau oder einen Mann handelt. Diese Spalte besteht aus einer 0 oder einer 1 je nachdem ob es sich um eine Frau oder einen Mann handelt. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 66 / 103
67 Nominale Variablen Nominale Variablen in der multiplen Regression Datensatz Sympathie Geschlecht Dummy Codierung 10 m 0 8 m 0 11 m 0 7 m 0 13 m 0 12 w 1 10 w 1 9 w 1 11 w 1 10 w 1 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 67 / 103
68 Nominale Variablen Nominale Variablen in der multiplen Regression Dummy-Codierung und Matrizen Grundsätzlich ändert sich an den Berechnungen nichts. Die Design Matrix: (Intercept) Geschlechtw Nun kann mit der bekannten Methodik weitergerechnet werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 68 / 103
69 Nominale Variablen Modellgleichung mit Dummy-Codierung Modellgleichung mit Dummy-Codierung Die Modellgleichung mit Dummy-Variablen sieht nun so aus: Y i = β 0 + β 1 D i + ϵ i mit Spaltenvektor D als Dummy (0 = m, 1 = w). Für Männer (D i = 0): Für Frauen (D i = 1): Y i = β 0 + β ϵ i = β 0 + ϵ i Y i = β 0 + β ϵ i = (β 0 + β 1 ) + ϵ i β 1 spiegelt damit den Unterschied zwischen den Stufen von D, hier Geschlecht, wieder. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 69 / 103
70 Nominale Variablen Berechnung mit Dummy-Codierung Berechnung mit Dummy-Codierung 1 Modelmatrix und Response Spaltenmatrix y: X = , y = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 70 / 103
71 Nominale Variablen Berechnung mit Dummy-Codierung Berechnung mit Dummy-Codierung (Forts. 2) 2 Das Produkt X X: [ ] X X = [ ] 10 5 = 5 5 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 71 / 103
72 Nominale Variablen Berechnung mit Dummy-Codierung Berechnung mit Dummy-Codierung (Forts. 3) 3 Die Inverse (X X) 1 : (X X) 1 = [ ] = 5 5 [ 0.20 ] S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 72 / 103
73 Nominale Variablen Berechnung mit Dummy-Codierung Berechnung mit Dummy-Codierung (Forts. 4) 4 Das Produkt X y: [ ] X y = [ ] 101 = 52 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 73 / 103
74 Nominale Variablen Berechnung mit Dummy-Codierung Berechnung mit Dummy-Codierung (Forts. 5) 5 Die Koeffizienten: [ ] [ ] (X X) X y = [ ] 9.8 = Die Berechnung der Standardfehler, t-tests etc. verläuft analog zu den bisher besprochenen Themen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 74 / 103
75 Nominale Variablen Berechnung mit Dummy-Codierung Ausgabe mit einem Statistikprogramm Call: lm(formula = Sympathie ~ Geschlecht, data = bsp2) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) e-06 *** Geschlechtw Signif. codes: 0 *** ** 0.01 * Residual standard error: on 8 degrees of freedom Multiple R-squared: ,^^IAdjusted R-squared: F-statistic: on 1 and 8 DF, p-value: S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 75 / 103
76 Nominale Variablen Berechnung mit Dummy-Codierung Interpretation Der Interzept 9.8 gibt den Mittelwert für die Gruppe Männer an (D i = 0). Dieser ist statistisch signifikant von Null verschieden. Der Koeffizient Geschlechtw von 0.6 bedeutet die Veränderung im Vergleich zu den Männern, wenn nun nur Frauen betrachtet werden. Dies ist statistisch nicht signifikant. Damit existiert kein Unterschied hinsichtlich der wahrgenommenen Sympathie von Frauen und Männern. Vergleiche: Mittelwert Männer = 9.8, Mittelwert Frauen = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 76 / 103
77 Dummy und numerische Variablen Outline Dummy und numerische Variablen Dummy und numerische Variablen Designmatrix Ergebnis Interpretation S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 77 / 103
78 Dummy und numerische Variablen Dummy und numerische Variablen Dummy und numerische Variablen Werden numerische und nominale Variablen gemeinsam verwendet, ändert sich an den zugrundeliegenden Berechnungen nichts. Beispiel: AV, Sympathie, UV: Geschlecht und Redefluss: Sympathie Redefluss Geschlecht m 8 16 m m 7 13 m m w w 9 18 w w w S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 78 / 103
79 Dummy und numerische Variablen Designmatrix Design Matrix X (Intercept) Redefluss Geschlechtw S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 79 / 103
80 Dummy und numerische Variablen Ergebnis Ergebnis Call: lm(formula = Sympathie ~ Redefluss + Geschlecht, data = bsp2) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) Redefluss e-06 *** Geschlechtw Signif. codes: 0 *** ** 0.01 * Residual standard error: on 7 degrees of freedom Multiple R-squared: 0.969,^^IAdjusted R-squared: F-statistic: on 2 and 7 DF, p-value: 5.247e-06 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 80 / 103
81 Dummy und numerische Variablen Interpretation Interpretation Die Variable Redefluss ist signifikant: je höher der Redefluss, als desto sympathischer wird eine Person empfunden. Die Koeffizient Geschlechtw (Frauen) spiegelt den Unterschied im Interzept zur Baseline Männer wieder: = Dieser Unterschied von 0.25 ist nicht signifikant, es gibt keinen statistisch Unterschied zwischen Männern und Frauen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 81 / 103
82 Interaktion bzw. Moderation Outline Interaktion bzw. Moderation Interaktion bzw. Moderation Interaktion bzw. Moderation Dummy und Interaktion mit numerischer Variablen Modellgleichung Designmatrix Ergebnis Interpretation S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 82 / 103
83 Interaktion bzw. Moderation Interaktion bzw. Moderation Interaktion bzw. Moderation Therapierfolg Frauen Männer Motivation S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 83 / 103
84 Interaktion bzw. Moderation Interaktion bzw. Moderation Erläuterungen Offensichtlich hat die gleiche Ausprägung der Motivation einen unterschiedlichen Einfluss auf den Therapieerfolg in Abhängigkeit vom Geschlecht. Männer profitieren, unabhängig von ihrer Motivation, nicht von der Therapie. Der Therapierfolg der Frauen hängt aber maßgeblich mit deren Motivation zusammen: je höher die Motivation, desto höher der Erfolg. Wir haben hier also eine Interaktion zwischen einer nominalen und einer numerischen Variablen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 84 / 103
85 Interaktion bzw. Moderation Interaktion bzw. Moderation Interaktion bzw. Moderation Interaktion wird auch als Moderation oder Wechselwirkung bezeichnet. Definition: Ein Effekt, der auf der Kombination zweier oder mehr Variablen beruht, z. B. eine UV, ein Moderator: Moderator x y Gibt es einen Moderator, sind die einzelnen UV und der Moderator typischerweise nicht mehr einzeln interpretierbar. Es sind auch höhere Interaktionen, z. B. zwischen drei Variablen, möglich. Die Interaktion zwischen Variablen entspricht algebraisch dem Produkt dieser Variablen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 85 / 103
86 Interaktion bzw. Moderation Dummy und Interaktion mit numerischer Variablen Dummy und Interaktion mit numerischer Variablen Nun soll der Frage nachgegangen werden, ob sich der Redefluss bei Frauen und Männern bezüglich der wahrgenommenen Sympathie unterschiedlich ausprägt. Man kann auch fragen: Moderiert das Geschlecht den Effekt des Redeflusses auf die wahrgenommene Sympathie? In der Regressionsanalyse entspricht dies der Fragestellung, ob sich die Steigung für den Redefluss zwischen Frauen und Männern unterscheidet Interaktion zwischen Geschlecht und Redefluss. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 86 / 103
87 Interaktion bzw. Moderation Modellgleichung Modellgleichung Die allgemeine Modellgleichung für eine numerische Variable X und eine nominale Variable D mit Interaktion lautet: Für Männer mit D i = 0: Y i = β 0 + β 1 X i + β 2 D i + β 3 (X i D i ) + ϵ i Y i =β 0 + β 1 X i + β β 3 (X i 0) + ϵ i =β 0 + β 1 X i + ϵ i S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 87 / 103
88 Interaktion bzw. Moderation Modellgleichung Modellgleichung (Forts. 2) Für Frauen mit D i = 1: Y i =β 0 + β 1 X i + β β 3 (X i 1) + ϵ i =(β 0 + β 2 ) + (β 1 + β 3 ) X i + ϵ i Der Koeffizient β 2 entspricht damit wieder dem Unterschied im Interzept zwischen den beiden Stufen von D. Der Koeffizient β 3 entspricht dem Unterschied in der Steigung zwischen den beiden Stufen von D. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 88 / 103
89 Interaktion bzw. Moderation Designmatrix Designmatrix Intercept β 0 Redefluss β 1 Geschlechtw β 2 Redefluss:Geschlechtw β S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 89 / 103
90 Interaktion bzw. Moderation Ergebnis Ergebnis Call: lm(formula = Sympathie ~ Redefluss * Geschlecht, data = bsp2) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) Redefluss e-05 *** Geschlechtw Redefluss:Geschlechtw Signif. codes: 0 *** ** 0.01 * Residual standard error: on 6 degrees of freedom Multiple R-squared: ,^^IAdjusted R-squared: F-statistic: on 3 and 6 DF, p-value: 6.18e-05 S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 90 / 103
91 Interaktion bzw. Moderation Interpretation Interpretation Für die Baseline Geschlecht=Männer: Interzept ist 1.17 (n.s.), und die Steigung für Redefluss ist 0.44 (signifikant). Für die Frauen (Geschlechtw) ist der Interzept = Diese Veränderung ist nicht signifikant. Die Steigung (Redefluss für die Männer) ist Dieser Koeffizient ist statistisch bedeutsam. Die Steigung Redefluss für die Frauen (Redefluss:Geschlechtw) ist = Diese Veränderung ist nicht signifikant. Damit ist der Koeffizient Redefluss aus statistischer Sicht für Frauen und Männer gleich. Zusammenfassung: Redefluss beeinflusst statistisch bedeutsam die wahrgenommene Sympathie. Es gibt keinen signifikanten Effekt für das Geschlecht und die Interaktion. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 91 / 103
92 Nominale Variablen mit mehr als zwei Stufen Outline Nominale Variablen mit mehr als zwei Stufen Datenbeispiel mit 3 Stufen Design Matrix Zu lösendes Gleichungssystem Ergebnis S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 92 / 103
93 Nominale Variablen mit mehr als zwei Stufen Nominale Variablen mit mehr als zwei Stufen Nominale Variablen können eine beliebige Anzahl an Stufen haben. Zur Kodierung reicht dann ein Vektor nicht mehr aus, es wird eine Matrix zur Kodierung benötigt. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 93 / 103
94 Nominale Variablen mit mehr als zwei Stufen Datenbeispiel mit 3 Stufen Datenbeispiel mit 3 Stufen Gehobene Stimmung soll in drei Kursen mit jeweils 3 Personen verglichen werden. AV: Gehobene Stimmung, Faktor: Kurs, 3-sttufig. Rohdaten: Kurs A B C S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 94 / 103
95 Nominale Variablen mit mehr als zwei Stufen Design Matrix Design Matrix (Intercept) KursB KursC S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 95 / 103
96 Nominale Variablen mit mehr als zwei Stufen Zu lösendes Gleichungssystem Zu lösendes Gleichungssystem Matrizen: X = 1 1 0, y = S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 96 / 103
97 Nominale Variablen mit mehr als zwei Stufen Zu lösendes Gleichungssystem Zu lösendes Gleichungssystem (Forts. 2) Gleichungssystem: ˆβ = (X X) 1 X y = Die Berechnung der Standardfehler, t-werte etc. erfolgt wie bisher besprochen. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 97 / 103
98 Nominale Variablen mit mehr als zwei Stufen Ergebnis Ergebnis Call: lm(formula = Stimmung ~ Kurs, data = bsp.3nom) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std. Error t value Pr(> t ) (Intercept) * KursB KursC * --- Signif. codes: 0 *** ** 0.01 * Residual standard error: 1 on 6 degrees of freedom Multiple R-squared: 0.5,^^IAdjusted R-squared: F-statistic: 3 on 2 and 6 DF, p-value: S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 98 / 103
99 Nominale Variablen mit mehr als zwei Stufen Ergebnis Mittelwerte Kurs effect plot 5 4 Stimmung A B C Kurs S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 99 / 103
100 Nominale Variablen mit mehr als zwei Stufen Ergebnis Interpretation Als Baseline wird Kurs A genommen. Der Interzept entspricht dem Gruppenmittelwert von Kurs A, dieser ist statistisch signifikant von Null verschieden. Kurs B hat einen Mittelwert von = 3, die Veränderung von 1 gegenüber Kurs A ist statistisch nicht bedeutsam. Kurs C hat einen Mittelwert von = 4, die Veränderung von 2 gegenüber Kurs A ist statistisch bedeutsam. Die F-Statistik ist äquivalent zum Omnibustest der einfaktoriellen Varianzanalyse. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 100 / 103
101 Bericht der Ergebnisse Outline Bericht der Ergebnisse S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 101 / 103
102 Bericht der Ergebnisse Bericht der Ergebnisse Typischerweise werden die Koeffizienten, Standardfehler, t-werte und p-werte als Tabelle dargestellt. Wenn standardisierte Koeffizienten von Interesse sind, werden diese ebenfalls in die Tabelle aufgenommen. Gütemaße wie R 2 und das adjustierte R 2 werden in die Tabellenüberschrift, als Anmerkung unter die Tabelle und / oder im Text des Ergebnisteils berichtet. Es gibt noch weitere Gütemaße, die berichtet werden können, aber nicht im Bachelor gelehrt werden. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 102 / 103
103 Bericht der Ergebnisse Literaturverzeichnis Bortz, J. & Schuster, C. (2010). Statistik für Human- und Sozialwissenschaftler (7.). Berlin: Springer. Budischewski, K. (2008). Zwei mal Drei macht Vier... Praktische Statistik. Skript Einführung in Statistik. Everitt, B. S. & Hothorn, T. (2006). A Handbook of Statistical Analyses Using R. Crc Pr Inc. Fahrmeir, L., Kneib, T. & Lang, S. (2009). Regression: Modelle, Methoden und Anwendungen (2.). Springer Berlin Heidelberg. Fox, J. (2008). A Mathematical Primer for Social Statistics (1. Aufl.). Sage Pubn Inc. S. Garbade (SRH Heidelberg) Multiple Regression Bachelor 103 / 103
Formelsammlung für das Modul. Statistik 2. Bachelor. Sven Garbade
 Version 2015 Formelsammlung für das Modul Statistik 2 Bachelor Sven Garbade Prof. Dr. phil. Dipl.-Psych. Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de
Version 2015 Formelsammlung für das Modul Statistik 2 Bachelor Sven Garbade Prof. Dr. phil. Dipl.-Psych. Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de
Prognoseintervalle für y 0 gegeben x 0
 10 Lineare Regression Punkt- und Intervallprognosen 10.5 Prognoseintervalle für y 0 gegeben x 0 Intervallprognosen für y 0 zur Vertrauenswahrscheinlichkeit 1 α erhält man also analog zu den Intervallprognosen
10 Lineare Regression Punkt- und Intervallprognosen 10.5 Prognoseintervalle für y 0 gegeben x 0 Intervallprognosen für y 0 zur Vertrauenswahrscheinlichkeit 1 α erhält man also analog zu den Intervallprognosen
Biostatistik 101 Korrelation - Regressionsanalysen
 Good Data don't need statistics Biostatistik 101 Korrelation - Regressionsanalysen Carl Herrmann IPMB Uni Heidelberg & DKFZ B080 carl.herrmann@uni-heidelberg.de Korrelation Sind Alter und Blutdruck miteinander
Good Data don't need statistics Biostatistik 101 Korrelation - Regressionsanalysen Carl Herrmann IPMB Uni Heidelberg & DKFZ B080 carl.herrmann@uni-heidelberg.de Korrelation Sind Alter und Blutdruck miteinander
Teil XIII. Multiple lineare Regression. Woche 11: Multiple lineare Regression. Zusammenfassung Einfache lineare Regression.
 Woche 11: Multiple lineare Regression Patric Müller Teil XIII Multiple lineare Regression ETHZ WBL 17/19, 10.07.017 Wahrscheinlichkeit und Statistik Patric Müller WBL
Woche 11: Multiple lineare Regression Patric Müller Teil XIII Multiple lineare Regression ETHZ WBL 17/19, 10.07.017 Wahrscheinlichkeit und Statistik Patric Müller WBL
7.1 Korrelationsanalyse. Statistik. Kovarianz. Pearson-Korrelation. Institut für angewandte Statistik & EDV Universität für Bodenkultur Wien
 Statistik 7.1 Korrelationsanalyse Institut für angewandte Statistik & EDV Universität für Bodenkultur Wien Sommersemester 2012 7 Regressions- und Korrelationsanalyse Kovarianz Pearson-Korrelation Der (lineare)
Statistik 7.1 Korrelationsanalyse Institut für angewandte Statistik & EDV Universität für Bodenkultur Wien Sommersemester 2012 7 Regressions- und Korrelationsanalyse Kovarianz Pearson-Korrelation Der (lineare)
Einführung in die Korrelationsrechnung
 Einführung in die Korrelationsrechnung Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) Korrelationsrechnung
Einführung in die Korrelationsrechnung Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) Korrelationsrechnung
1 Einfachregression 1.1In 10 Haushalten wurden Einkommen und Ausgaben für Luxusgüter erfragt:
 Beispiele zum Üben und Wiederholen zu Wirtschaftsstatistik 2 (Kurs 3) 1 Einfachregression 1.1In 10 Haushalten wurden Einkommen und Ausgaben für Luxusgüter erfragt: Haushaltseinkommen 12 24 30 40 80 60
Beispiele zum Üben und Wiederholen zu Wirtschaftsstatistik 2 (Kurs 3) 1 Einfachregression 1.1In 10 Haushalten wurden Einkommen und Ausgaben für Luxusgüter erfragt: Haushaltseinkommen 12 24 30 40 80 60
Tutorial: Regression Output von R
 Tutorial: Regression Output von R Eine Firma erzeugt Autositze. Ihr Chef ist besorgt über die Anzahl und die Kosten von Maschinenausfällen. Das Problem ist, dass die Maschinen schon alt sind und deswegen
Tutorial: Regression Output von R Eine Firma erzeugt Autositze. Ihr Chef ist besorgt über die Anzahl und die Kosten von Maschinenausfällen. Das Problem ist, dass die Maschinen schon alt sind und deswegen
Vorlesung: Statistik II für Wirtschaftswissenschaft
 Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 6 Genzwertsätze Einführung 1 Wahrscheinlichkeit: Definition und Interpretation
Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 6 Genzwertsätze Einführung 1 Wahrscheinlichkeit: Definition und Interpretation
Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen)
 3 Einfache lineare Regression Einfache lineare Modelle mit R 36 Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen) > summary(lm(y~x)) Call: lm(formula =
3 Einfache lineare Regression Einfache lineare Modelle mit R 36 Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen) > summary(lm(y~x)) Call: lm(formula =
Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen)
 3 Einfache lineare Regression Einfache lineare Modelle mit R 3.6 Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen) > summary(lm(y~x)) Call: lm(formula
3 Einfache lineare Regression Einfache lineare Modelle mit R 3.6 Einfache lineare Modelle mit Statistik-Software R Beispiel (Ausgaben in Abhängigkeit vom Einkommen) > summary(lm(y~x)) Call: lm(formula
Stochastik Praktikum Lineare Modelle
 Stochastik Praktikum Lineare Modelle Thorsten Dickhaus Humboldt-Universität zu Berlin 06.10.2010 Übersicht 1 Einfache lineare Regression 2 Multiple lineare Regression 3 Varianzanalyse 4 Verallgemeinerte
Stochastik Praktikum Lineare Modelle Thorsten Dickhaus Humboldt-Universität zu Berlin 06.10.2010 Übersicht 1 Einfache lineare Regression 2 Multiple lineare Regression 3 Varianzanalyse 4 Verallgemeinerte
Übung zur Empirischen Wirtschaftsforschung V. Das Lineare Regressionsmodell
 Universität Ulm 89069 Ulm Germany Dipl.-WiWi Christian Peukert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2010
Universität Ulm 89069 Ulm Germany Dipl.-WiWi Christian Peukert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2010
1 Beispiel zur Methode der kleinsten Quadrate
 1 Beispiel zur Methode der kleinsten Quadrate 1.1 Daten des Beispiels t x y x*y x 2 ŷ ˆɛ ˆɛ 2 1 1 3 3 1 2 1 1 2 2 3 6 4 3.5-0.5 0.25 3 3 4 12 9 5-1 1 4 4 6 24 16 6.5-0.5 0.25 5 5 9 45 25 8 1 1 Σ 15 25
1 Beispiel zur Methode der kleinsten Quadrate 1.1 Daten des Beispiels t x y x*y x 2 ŷ ˆɛ ˆɛ 2 1 1 3 3 1 2 1 1 2 2 3 6 4 3.5-0.5 0.25 3 3 4 12 9 5-1 1 4 4 6 24 16 6.5-0.5 0.25 5 5 9 45 25 8 1 1 Σ 15 25
Beispiel: Multiples Modell/Omitted Variable Bias I
 4 Multiple lineare Regression Konfidenzintervalle und Tests 4.3 Beispiel: Multiples Modell/Omitted Variable Bias I Beispieldatensatz mit Daten zur Lohnhöhe (y i ), zu den Ausbildungsjahren über den Hauptschulabschluss
4 Multiple lineare Regression Konfidenzintervalle und Tests 4.3 Beispiel: Multiples Modell/Omitted Variable Bias I Beispieldatensatz mit Daten zur Lohnhöhe (y i ), zu den Ausbildungsjahren über den Hauptschulabschluss
Interaktion unter Berücksichtigung des Skalenniveaus der Prädiktoren Dr. Markus Stöcklin, Universität Basel, Fakultät für Psychologie
 Interaktion unter Berücksichtigung des Skalenniveaus der Prädiktoren Dr. Markus Stöcklin, Universität Basel, Fakultät für Psychologie 1 Einleitung 3 2 Modell mit 0-1 kodierten nominalen Prädiktoren X 1
Interaktion unter Berücksichtigung des Skalenniveaus der Prädiktoren Dr. Markus Stöcklin, Universität Basel, Fakultät für Psychologie 1 Einleitung 3 2 Modell mit 0-1 kodierten nominalen Prädiktoren X 1
Übung V Lineares Regressionsmodell
 Universität Ulm 89069 Ulm Germany Dipl.-WiWi Michael Alpert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2007 Übung
Universität Ulm 89069 Ulm Germany Dipl.-WiWi Michael Alpert Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2007 Übung
Beispiel: Multiples Modell/Omitted Variable Bias I
 4 Multiple lineare Regression Konfidenzintervalle und Tests 4.3 Beispiel: Multiples Modell/Omitted Variable Bias I Beispieldatensatz mit Daten zur Lohnhöhe (y i ), zu den Ausbildungsjahren über den Hauptschulabschluss
4 Multiple lineare Regression Konfidenzintervalle und Tests 4.3 Beispiel: Multiples Modell/Omitted Variable Bias I Beispieldatensatz mit Daten zur Lohnhöhe (y i ), zu den Ausbildungsjahren über den Hauptschulabschluss
Biostatistik 101 Korrelation - Regressionsanalysen
 Good Data don't need statistics Biostatistik 101 Korrelation - Regressionsanalysen Carl Herrmann IPMB Uni Heidelberg & DKFZ B080 carl.herrmann@uni-heidelberg.de Korrelation Sind Alter und Blutdruck miteinander
Good Data don't need statistics Biostatistik 101 Korrelation - Regressionsanalysen Carl Herrmann IPMB Uni Heidelberg & DKFZ B080 carl.herrmann@uni-heidelberg.de Korrelation Sind Alter und Blutdruck miteinander
1 Wahrscheinlichkeitsrechnung. 2 Zufallsvariablen und ihre Verteilung. 3 Statistische Inferenz. 4 Intervallschätzung. 5 Hypothesentests.
 0 Einführung 1 Wahrscheinlichkeitsrechnung 2 Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung 5 Hypothesentests 6 Regression Lineare Regressionsmodelle Deskriptive Statistik:
0 Einführung 1 Wahrscheinlichkeitsrechnung 2 Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung 5 Hypothesentests 6 Regression Lineare Regressionsmodelle Deskriptive Statistik:
Vorlesung Wirtschaftsstatistik 2 (FK 040637) Multiple lineare Regression. Dipl.-Ing. Robin Ristl Wintersemester 2012/13
 Vorlesung Wirtschaftsstatistik 2 (FK 040637) Multiple lineare Regression Dipl.-Ing. Robin Ristl Wintersemester 2012/13 1 Grundidee: Eine abhängige Variable soll als Linearkombination mehrerer unabhängiger
Vorlesung Wirtschaftsstatistik 2 (FK 040637) Multiple lineare Regression Dipl.-Ing. Robin Ristl Wintersemester 2012/13 1 Grundidee: Eine abhängige Variable soll als Linearkombination mehrerer unabhängiger
Kapitel 8. Einfache Regression. Anpassen des linearen Regressionsmodells, OLS. Eigenschaften der Schätzer für das Modell
 Kapitel 8 Einfache Regression Josef Leydold c 2006 Mathematische Methoden VIII Einfache Regression 1 / 21 Lernziele Lineares Regressionsmodell Anpassen des linearen Regressionsmodells, OLS Eigenschaften
Kapitel 8 Einfache Regression Josef Leydold c 2006 Mathematische Methoden VIII Einfache Regression 1 / 21 Lernziele Lineares Regressionsmodell Anpassen des linearen Regressionsmodells, OLS Eigenschaften
Teil XII. Einfache Lineare Regression. Woche 10: Lineare Regression. Lernziele. Zusammenfassung. Patric Müller
 Woche 10: Lineare Regression Patric Müller Teil XII Einfache Lineare Regression ETHZ WBL 17/19, 03.07.2017 Wahrscheinlichkeit und Statistik Patric Müller WBL 2017 Wahrscheinlichkeit
Woche 10: Lineare Regression Patric Müller Teil XII Einfache Lineare Regression ETHZ WBL 17/19, 03.07.2017 Wahrscheinlichkeit und Statistik Patric Müller WBL 2017 Wahrscheinlichkeit
Aufgabensammlung (Nicht-MC-Aufgaben) Klausur Ökonometrie WS 2014/15. ( = 57 Punkte)
 Aufgabe 3 (6 + 4 + 8 + 4 + 10 + 4 + 9 + 4 + 8 = 57 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Mit Hilfe eines multiplen linearen Regressionsmodells soll auf
Aufgabe 3 (6 + 4 + 8 + 4 + 10 + 4 + 9 + 4 + 8 = 57 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Mit Hilfe eines multiplen linearen Regressionsmodells soll auf
Übungsklausur Lineare Modelle. Prof. Dr. H. Toutenburg
 Übungsklausur Lineare le Prof. Dr. H. Toutenburg Aufgabe Ein lineares Regressionsmodell mit der abhängigen Variablen Körpergröße und der unabhängigen Variablen Geschlecht wurde einmal mit der dummykodierten
Übungsklausur Lineare le Prof. Dr. H. Toutenburg Aufgabe Ein lineares Regressionsmodell mit der abhängigen Variablen Körpergröße und der unabhängigen Variablen Geschlecht wurde einmal mit der dummykodierten
Breusch-Pagan-Test I auf Heteroskedastie in den Störgrößen
 Breusch-Pagan-Test I Ein weiterer Test ist der Breusch-Pagan-Test. Im Gegensatz zum Goldfeld-Quandt-Test ist es nicht erforderlich, eine (einzelne) Quelle der Heteroskedastizität anzugeben bzw. zu vermuten.
Breusch-Pagan-Test I Ein weiterer Test ist der Breusch-Pagan-Test. Im Gegensatz zum Goldfeld-Quandt-Test ist es nicht erforderlich, eine (einzelne) Quelle der Heteroskedastizität anzugeben bzw. zu vermuten.
4 Multiple lineare Regression Multikollinearität 4.9
 Multikollinearität Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren (einschließlich des Absolutglieds
Multikollinearität Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren (einschließlich des Absolutglieds
4 Multiple lineare Regression Multikollinearität 4.9
 Multikollinearität Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren (einschließlich des Absolutglieds
Multikollinearität Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren (einschließlich des Absolutglieds
1 Kodierung kategorialer Einflussgrößen
 Übung zur Vorlesung Generalisierte Regressionsmodelle Blatt 1 Christiane Fuchs, Moritz Berger, Micha Schneider WiSe 16/17 1 Kodierung kategorialer Einflussgrößen Lösung zu Aufgabe 3 Einlesen der Daten:
Übung zur Vorlesung Generalisierte Regressionsmodelle Blatt 1 Christiane Fuchs, Moritz Berger, Micha Schneider WiSe 16/17 1 Kodierung kategorialer Einflussgrößen Lösung zu Aufgabe 3 Einlesen der Daten:
Lösungen zur Prüfung Angewandte Statistische Methoden in den Nutzierwissenschaften FS 2016
 ETH Zürich D-USYS Institut für Agrarwissenschaften Lösungen zur Prüfung Angewandte Statistische Methoden in den Nutzierwissenschaften FS 2016 Peter von Rohr Datum 30. Mai 2016 Beginn 08:00 Uhr Ende 08:45
ETH Zürich D-USYS Institut für Agrarwissenschaften Lösungen zur Prüfung Angewandte Statistische Methoden in den Nutzierwissenschaften FS 2016 Peter von Rohr Datum 30. Mai 2016 Beginn 08:00 Uhr Ende 08:45
Vorlesung: Statistik I für Studierende der Statistik, Mathematik & Informatik. Regression. Einfache lineare Regression
 Vorlesung: Statistik I für Studierende der Statistik, Mathematik & Informatik Regression Dozent: Fabian Scheipl Material: H. Küchenhoff LMU München 39 Einfache lineare Regression Bestimmung der Regressionsgerade
Vorlesung: Statistik I für Studierende der Statistik, Mathematik & Informatik Regression Dozent: Fabian Scheipl Material: H. Küchenhoff LMU München 39 Einfache lineare Regression Bestimmung der Regressionsgerade
Lineare Modelle in R: Klassische lineare Regression
 Lineare Modelle in R: Klassische lineare Regression Achim Zeileis 2009-02-20 1 Das Modell Das klassische lineare Regressionsmodell versucht den Zusammenhang zwischen einer abhängigen Variablen (oder Responsevariablen)
Lineare Modelle in R: Klassische lineare Regression Achim Zeileis 2009-02-20 1 Das Modell Das klassische lineare Regressionsmodell versucht den Zusammenhang zwischen einer abhängigen Variablen (oder Responsevariablen)
Statistik. R. Frühwirth. Statistik. VO Februar R. Frühwirth Statistik 1/536
 fru@hephy.oeaw.ac.at VO 142.090 http://tinyurl.com/tu142090 Februar 2010 1/536 Übersicht über die Vorlesung Teil 1: Deskriptive Teil 2: Wahrscheinlichkeitsrechnung Teil 3: Zufallsvariable Teil 4: Parameterschätzung
fru@hephy.oeaw.ac.at VO 142.090 http://tinyurl.com/tu142090 Februar 2010 1/536 Übersicht über die Vorlesung Teil 1: Deskriptive Teil 2: Wahrscheinlichkeitsrechnung Teil 3: Zufallsvariable Teil 4: Parameterschätzung
Prüfen von Unterschiedshypothesen für ordinale Variablen: Mann-Whitney Test und Ko
 Prüfen von Unterschiedshypothesen für ordinale Variablen: Mann-Whitney Test und Ko Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik
Prüfen von Unterschiedshypothesen für ordinale Variablen: Mann-Whitney Test und Ko Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik
Musterlösung. Modulklausur Multivariate Verfahren
 Musterlösung Modulklausur 31821 Multivariate Verfahren 25. September 2015 Aufgabe 1 (15 Punkte) Kennzeichnen Sie die folgenden Aussagen zur Regressionsanalyse mit R für richtig oder F für falsch. F Wenn
Musterlösung Modulklausur 31821 Multivariate Verfahren 25. September 2015 Aufgabe 1 (15 Punkte) Kennzeichnen Sie die folgenden Aussagen zur Regressionsanalyse mit R für richtig oder F für falsch. F Wenn
Multiple Regression III
 Multiple Regression III Werner Brannath VO Biostatistik im WS 2006/2007 Inhalt Überprüfung der Modellannahmen Residuen-Plot Normal-Q-Q-Plot Cook s Distanz-Plot Maßnahmen bei Abweichungen von Modellannahmen
Multiple Regression III Werner Brannath VO Biostatistik im WS 2006/2007 Inhalt Überprüfung der Modellannahmen Residuen-Plot Normal-Q-Q-Plot Cook s Distanz-Plot Maßnahmen bei Abweichungen von Modellannahmen
Multivariate Verfahren
 Selbstkontrollarbeit 1 Multivariate Verfahren Musterlösung Aufgabe 1 (40 Punkte) Auf der dem Kurs beigelegten CD finden Sie im Unterverzeichnis Daten/Excel/ die Datei zahlen.xlsx. Alternativ können Sie
Selbstkontrollarbeit 1 Multivariate Verfahren Musterlösung Aufgabe 1 (40 Punkte) Auf der dem Kurs beigelegten CD finden Sie im Unterverzeichnis Daten/Excel/ die Datei zahlen.xlsx. Alternativ können Sie
4.1. Verteilungsannahmen des Fehlers. 4. Statistik im multiplen Regressionsmodell Verteilungsannahmen des Fehlers
 4. Statistik im multiplen Regressionsmodell In diesem Kapitel wird im Abschnitt 4.1 zusätzlich zu den schon bekannten Standardannahmen noch die Annahme von normalverteilten Residuen hinzugefügt. Auf Basis
4. Statistik im multiplen Regressionsmodell In diesem Kapitel wird im Abschnitt 4.1 zusätzlich zu den schon bekannten Standardannahmen noch die Annahme von normalverteilten Residuen hinzugefügt. Auf Basis
Aufgabensammlung (Nicht-MC-Aufgaben) Klausur Ökonometrie WS 2017/18. ( = 58 Punkte)
 Aufgabe 3 (14 + 2 + 7 + 7 + 3 + 5 + 9 + 11 = 58 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Mit Hilfe der Statistiksoftware R soll der Datensatz HousePrices aus
Aufgabe 3 (14 + 2 + 7 + 7 + 3 + 5 + 9 + 11 = 58 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Mit Hilfe der Statistiksoftware R soll der Datensatz HousePrices aus
Dr. Maike M. Burda. Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp
 Dr. Maike M. Burda Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 8.-10. Januar 2010 BOOTDATA.GDT: 250 Beobachtungen für die Variablen... cm:
Dr. Maike M. Burda Welchen Einfluss hat die Körperhöhe auf das Körpergewicht? Eine Regressionsanalyse. HU Berlin, Econ Bootcamp 8.-10. Januar 2010 BOOTDATA.GDT: 250 Beobachtungen für die Variablen... cm:
Konfidenz-, Prognoseintervalle und Hypothesentests IV im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen
 4 Multiple lineare Regression Heteroskedastische Störgrößen 4.10 Konfidenz-, Prognoseintervalle und Hypothesentests IV im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen Ein approximatives
4 Multiple lineare Regression Heteroskedastische Störgrößen 4.10 Konfidenz-, Prognoseintervalle und Hypothesentests IV im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen Ein approximatives
Lineare Regression in R, Teil 1
 Lineare Regression in R, Teil 1 Christian Kleiber Abt. Quantitative Methoden, WWZ, Universität Basel October 6, 2009 1 Vorbereitungen Zur Illustration betrachten wir wieder den Datensatz CASchools aus
Lineare Regression in R, Teil 1 Christian Kleiber Abt. Quantitative Methoden, WWZ, Universität Basel October 6, 2009 1 Vorbereitungen Zur Illustration betrachten wir wieder den Datensatz CASchools aus
Sozialwissenschaftliche Fakultät der Universität Göttingen. Sommersemester Statistik mit SPSS
 Sommersemester 2009 Statistik mit SPSS 15. Mai 2009 15. Mai 2009 Statistik Dozentin: mit Esther SPSSOchoa Fernández 1 Überblick 1. Korrelation vs. Regression 2. Ziele der Regressionsanalyse 3. Syntax für
Sommersemester 2009 Statistik mit SPSS 15. Mai 2009 15. Mai 2009 Statistik Dozentin: mit Esther SPSSOchoa Fernández 1 Überblick 1. Korrelation vs. Regression 2. Ziele der Regressionsanalyse 3. Syntax für
2.5 Lineare Regressionsmodelle
 2.5.1 Wiederholung aus Statistik I Gegeben Datenpunkte (Y i, X i ) schätze die beste Gerade Y i = β 0 + β 1 X i, i = 1,..., n. 2 Induktive Statistik 409 Bsp. 2.30. [Kaffeeverkauf auf drei Flohmärkten]
2.5.1 Wiederholung aus Statistik I Gegeben Datenpunkte (Y i, X i ) schätze die beste Gerade Y i = β 0 + β 1 X i, i = 1,..., n. 2 Induktive Statistik 409 Bsp. 2.30. [Kaffeeverkauf auf drei Flohmärkten]
Perfekte Multikollinearität III. Multikollinearität
 Multikollinearität Perfekte Multikollinearität I Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren
Multikollinearität Perfekte Multikollinearität I Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren
Einleitung. Statistik. Bsp: Ertrag Weizen. 6.1 Einfache Varianzanalyse
 Einleitung Statistik Institut für angewandte Statistik & EDV Universität für Bodenkultur Wien Der Begriff Varianzanalyse (analysis of variance, ANOVA) taucht an vielen Stellen in der Statistik mit unterschiedlichen
Einleitung Statistik Institut für angewandte Statistik & EDV Universität für Bodenkultur Wien Der Begriff Varianzanalyse (analysis of variance, ANOVA) taucht an vielen Stellen in der Statistik mit unterschiedlichen
Statistik III Regressionsanalyse, Varianzanalyse und Verfahren bei Messwiederholung mit SPSS
 Statistik III Regressionsanalyse, Varianzanalyse und Verfahren bei Messwiederholung mit SPSS Verena Hofmann Dr. phil. des. Departement für Sonderpädagogik Universität Freiburg Petrus-Kanisius-Gasse 21
Statistik III Regressionsanalyse, Varianzanalyse und Verfahren bei Messwiederholung mit SPSS Verena Hofmann Dr. phil. des. Departement für Sonderpädagogik Universität Freiburg Petrus-Kanisius-Gasse 21
Aufgabensammlung (Nicht-MC-Aufgaben) Klausur Ökonometrie SS 2018
 Aufgabe 3 (15 + 1 + 7 + 7 + 7 + 5 = 42 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Mit Hilfe der Statistiksoftware R soll der Datensatz HousePrices aus dem Paket
Aufgabe 3 (15 + 1 + 7 + 7 + 7 + 5 = 42 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Mit Hilfe der Statistiksoftware R soll der Datensatz HousePrices aus dem Paket
Schätzung im multiplen linearen Modell VI
 Schätzung im multiplen linearen Modell VI Wie im einfachen linearen Regressionsmodell definiert man zu den KQ/OLS-geschätzten Parametern β = ( β 0, β 1,..., β K ) mit ŷ i := β 0 + β 1 x 1i +... β K x Ki,
Schätzung im multiplen linearen Modell VI Wie im einfachen linearen Regressionsmodell definiert man zu den KQ/OLS-geschätzten Parametern β = ( β 0, β 1,..., β K ) mit ŷ i := β 0 + β 1 x 1i +... β K x Ki,
Schweizer Statistiktage, Aarau, 18. Nov. 2004
 Schweizer Statistiktage, Aarau, 18. Nov. 2004 Qualitative Überprüfung der Modellannahmen in der linearen Regressionsrechnung am Beispiel der Untersuchung der Alterssterblichkeit bei Hitzeperioden in der
Schweizer Statistiktage, Aarau, 18. Nov. 2004 Qualitative Überprüfung der Modellannahmen in der linearen Regressionsrechnung am Beispiel der Untersuchung der Alterssterblichkeit bei Hitzeperioden in der
VS PLUS
 VS PLUS Zusatzinformationen zu Medien des VS Verlags Statistik II Inferenzstatistik 2010 Übungsaufgaben und Lösungen Inferenzstatistik 2 [Übungsaufgaben und Lösungenn - Inferenzstatistik 2] ÜBUNGSAUFGABEN
VS PLUS Zusatzinformationen zu Medien des VS Verlags Statistik II Inferenzstatistik 2010 Übungsaufgaben und Lösungen Inferenzstatistik 2 [Übungsaufgaben und Lösungenn - Inferenzstatistik 2] ÜBUNGSAUFGABEN
Das (multiple) Bestimmtheitsmaß R 2. Beispiel: Ausgaben in Abhängigkeit vom Einkommen (I) Parameterschätzer im einfachen linearen Regressionsmodell
 1 Lineare Regression Parameterschätzung 13 Im einfachen linearen Regressionsmodell sind also neben σ ) insbesondere β 1 und β Parameter, deren Schätzung für die Quantifizierung des linearen Zusammenhangs
1 Lineare Regression Parameterschätzung 13 Im einfachen linearen Regressionsmodell sind also neben σ ) insbesondere β 1 und β Parameter, deren Schätzung für die Quantifizierung des linearen Zusammenhangs
Fragen. Einführung in die induktive Statistik. Übersicht. Lineare Einfachregression
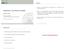 Fragen Welche Unsicherheitsfaktoren beeinflussen die Schätzung einer Regressionsgeraden? Einführung in die induktive Statistik Friedrich Leisch Institut für Statistik Ludwig-Maximilians-Universität München
Fragen Welche Unsicherheitsfaktoren beeinflussen die Schätzung einer Regressionsgeraden? Einführung in die induktive Statistik Friedrich Leisch Institut für Statistik Ludwig-Maximilians-Universität München
Einführung in die Induktive Statistik: Regressionsanalyse
 Einführung in die Induktive Statistik: Regressionsanalyse Jan Gertheiss LMU München Sommersemester 2011 Vielen Dank an Christian Heumann für das Überlassen von TEX-Code! Regressionsanalyse Ziel: Analyse
Einführung in die Induktive Statistik: Regressionsanalyse Jan Gertheiss LMU München Sommersemester 2011 Vielen Dank an Christian Heumann für das Überlassen von TEX-Code! Regressionsanalyse Ziel: Analyse
Multiple Regressionsanalyse - Kurzabriss
 Multiple Regressionsanalyse - Kurzabriss Ziele: Schätzung eines Kriteriums aus einer Linearkombination von Prädiktoren Meist zu Screening-Untersuchungen, um den Einfluß von vermuteten Ursachenvariablen
Multiple Regressionsanalyse - Kurzabriss Ziele: Schätzung eines Kriteriums aus einer Linearkombination von Prädiktoren Meist zu Screening-Untersuchungen, um den Einfluß von vermuteten Ursachenvariablen
V. Das lineare Regressionsmodell
 Universität Ulm 89069 Ulm Germany Tino Conrad, M.Sc. Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2016 Übung zur
Universität Ulm 89069 Ulm Germany Tino Conrad, M.Sc. Institut für Wirtschaftspolitik Fakultät für Mathematik und Wirtschaftswissenschaften Ludwig-Erhard-Stiftungsprofessur Sommersemester 2016 Übung zur
Instrument zur Untersuchung eines linearen Zusammenhangs zwischen zwei (oder mehr) Merkmalen.
 Gliederung Grundidee Einfaches lineares Modell KQ-Methode (Suche nach der besten Geraden) Einfluss von Ausreißern Güte des Modells (Bestimmtheitsmaß R²) Multiple Regression Noch Fragen? Lineare Regression
Gliederung Grundidee Einfaches lineares Modell KQ-Methode (Suche nach der besten Geraden) Einfluss von Ausreißern Güte des Modells (Bestimmtheitsmaß R²) Multiple Regression Noch Fragen? Lineare Regression
Schätzen und Testen von Populationsparametern im linearen Regressionsmodell PE ΣO
 Schätzen und Testen von Populationsparametern im linearen Regressionsmodell PE ΣO 4. Dezember 2001 Generalisierung der aus Stichprobendaten berechneten Regressionsgeraden Voraussetzungen für die Generalisierung
Schätzen und Testen von Populationsparametern im linearen Regressionsmodell PE ΣO 4. Dezember 2001 Generalisierung der aus Stichprobendaten berechneten Regressionsgeraden Voraussetzungen für die Generalisierung
Statistik II für Betriebswirte Vorlesung 8
 Statistik II für Betriebswirte Vorlesung 8 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 3. Dezember 2018 Dr. Andreas Wünsche Statistik II für Betriebswirte Vorlesung 8 Version:
Statistik II für Betriebswirte Vorlesung 8 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 3. Dezember 2018 Dr. Andreas Wünsche Statistik II für Betriebswirte Vorlesung 8 Version:
Konfidenz-, Prognoseintervalle und Hypothesentests II bei heteroskedastischen Störgrößen
 Konfidenz-, Prognoseintervalle und Hypothesentests II bei heteroskedastischen Störgrößen Achtung! Bei der Verwendung von heteroskedastie-konsistenten Schätzern für V( β) muss unbedingt darauf geachtet
Konfidenz-, Prognoseintervalle und Hypothesentests II bei heteroskedastischen Störgrößen Achtung! Bei der Verwendung von heteroskedastie-konsistenten Schätzern für V( β) muss unbedingt darauf geachtet
Empirische Wirtschaftsforschung in R
 Empirische Wirtschaftsforschung in R Schätzung der keynesianischen Geldnachfragefunktion auf Basis von Daten der dänischen Volkswirtschaft Jonas Richter-Dumke Universität Rostock, Institut für Volkswirtschaftslehre
Empirische Wirtschaftsforschung in R Schätzung der keynesianischen Geldnachfragefunktion auf Basis von Daten der dänischen Volkswirtschaft Jonas Richter-Dumke Universität Rostock, Institut für Volkswirtschaftslehre
Lineare Regressionen mit R (Ökonometrie SS 2014 an der UdS)
 Lineare Regressionen mit R (Ökonometrie SS 2014 an der UdS) Es soll untersucht werden, ob und wie sich Rauchen während der Schwangerschaft auf den Gesundheitszustand des Neugeborenen auswirkt. Hierzu werden
Lineare Regressionen mit R (Ökonometrie SS 2014 an der UdS) Es soll untersucht werden, ob und wie sich Rauchen während der Schwangerschaft auf den Gesundheitszustand des Neugeborenen auswirkt. Hierzu werden
Prüfungsliteratur: Rudolf & Müller S
 1 Beispiele zur univariaten Varianzanalyse Einfaktorielle Varianzanalyse (Wiederholung!) 3 Allgemeines lineares Modell 4 Zweifaktorielle Varianzanalyse 5 Multivariate Varianzanalyse 6 Varianzanalyse mit
1 Beispiele zur univariaten Varianzanalyse Einfaktorielle Varianzanalyse (Wiederholung!) 3 Allgemeines lineares Modell 4 Zweifaktorielle Varianzanalyse 5 Multivariate Varianzanalyse 6 Varianzanalyse mit
Statistik II. II. Univariates lineares Regressionsmodell. Martin Huber 1 / 20
 Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 20 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 20 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Statistik II. IV. Hypothesentests. Martin Huber
 Statistik II IV. Hypothesentests Martin Huber 1 / 41 Übersicht Struktur eines Hypothesentests Stichprobenverteilung t-test: Einzelner-Parameter-Test F-Test: Multiple lineare Restriktionen 2 / 41 Struktur
Statistik II IV. Hypothesentests Martin Huber 1 / 41 Übersicht Struktur eines Hypothesentests Stichprobenverteilung t-test: Einzelner-Parameter-Test F-Test: Multiple lineare Restriktionen 2 / 41 Struktur
Lean Body Mass [kg] Estimate Std. Error t value Pr(> t ) (Intercept) ??? lbm <2e-16 ***
![Lean Body Mass [kg] Estimate Std. Error t value Pr(> t ) (Intercept) ??? lbm <2e-16 *** Lean Body Mass [kg] Estimate Std. Error t value Pr(> t ) (Intercept) ??? lbm <2e-16 ***](/thumbs/76/73817896.jpg) Körperkraft [Nm] 0 50 100 150 200 250 0 20 40 60 80 Lean Body Mass [kg] Dieses Quiz soll Ihnen helfen, den R Output einer einfachen linearen Regression besser zu verstehen (s. Kapitel 5.4.1) Es wurden
Körperkraft [Nm] 0 50 100 150 200 250 0 20 40 60 80 Lean Body Mass [kg] Dieses Quiz soll Ihnen helfen, den R Output einer einfachen linearen Regression besser zu verstehen (s. Kapitel 5.4.1) Es wurden
Hypothesentests mit SPSS
 Beispiel für eine einfache Regressionsanalyse (mit Überprüfung der Voraussetzungen) Daten: bedrohfb_v07.sav Hypothese: Die Skalenwerte auf der ATB-Skala (Skala zur Erfassung der Angst vor terroristischen
Beispiel für eine einfache Regressionsanalyse (mit Überprüfung der Voraussetzungen) Daten: bedrohfb_v07.sav Hypothese: Die Skalenwerte auf der ATB-Skala (Skala zur Erfassung der Angst vor terroristischen
Vorlesung: Multivariate Statistik für Psychologen
 Vorlesung: Multivariate Statistik für Psychologen 7. Vorlesung: 05.05.2003 Agenda 2. Multiple Regression i. Grundlagen ii. iii. iv. Statistisches Modell Verallgemeinerung des Stichprobenmodells auf Populationsebene
Vorlesung: Multivariate Statistik für Psychologen 7. Vorlesung: 05.05.2003 Agenda 2. Multiple Regression i. Grundlagen ii. iii. iv. Statistisches Modell Verallgemeinerung des Stichprobenmodells auf Populationsebene
Kapitel 3 Schließende lineare Regression Einführung. induktiv. Fragestellungen. Modell. Matrixschreibweise. Annahmen.
 Kapitel 3 Schließende lineare Regression 3.1. Einführung induktiv Fragestellungen Modell Statistisch bewerten, der vorher beschriebenen Zusammenhänge auf der Basis vorliegender Daten, ob die ermittelte
Kapitel 3 Schließende lineare Regression 3.1. Einführung induktiv Fragestellungen Modell Statistisch bewerten, der vorher beschriebenen Zusammenhänge auf der Basis vorliegender Daten, ob die ermittelte
6.2 Lineare Regression
 6.2 Lineare Regression Einfache lineare Regression (vgl. Kap. 4.7) Y i = θ 0 + θ 1 X i + ǫ i ǫ i (0, σ 2 ) ˆθ 1 ˆθ 0 = S XY S 2 X = 1 ( Yi n ˆθ ) 1 Xi als Lösung der Minimumaufgabe n (Y i θ 1 X 1 θ 0 )
6.2 Lineare Regression Einfache lineare Regression (vgl. Kap. 4.7) Y i = θ 0 + θ 1 X i + ǫ i ǫ i (0, σ 2 ) ˆθ 1 ˆθ 0 = S XY S 2 X = 1 ( Yi n ˆθ ) 1 Xi als Lösung der Minimumaufgabe n (Y i θ 1 X 1 θ 0 )
Musterlösung zu Serie 1
 Prof. Dr. W. Stahel Regression HS 2015 Musterlösung zu Serie 1 1. a) > d.bv plot(blei ~ verkehr, data = d.bv, main
Prof. Dr. W. Stahel Regression HS 2015 Musterlösung zu Serie 1 1. a) > d.bv plot(blei ~ verkehr, data = d.bv, main
3.3 Das allgemeine lineare Modell (ALM), Methode der kleinsten Quadrate
 31 und 31 und (), Methode der 33 Das allgemeine (), Methode der kleinsten Quadrate 36 Kovarianzanalyse 37 Modelle mit Messwiederholungen 1 / 85 Eine grundsätzliche Bemerkung zu Beginn Es bestehen viele
31 und 31 und (), Methode der 33 Das allgemeine (), Methode der kleinsten Quadrate 36 Kovarianzanalyse 37 Modelle mit Messwiederholungen 1 / 85 Eine grundsätzliche Bemerkung zu Beginn Es bestehen viele
Kovarianzanalyse. Truthahngewicht. Truthahngewicht. Methoden empirischer Sozialforschung. 1 metrische und mehrere metrische und kategoriale Variablen
 Kovarianzanalyse 1 metrische und mehrere metrische und kategoriale Variablen Methoden empirischer Sozialforschung Lineare Modelle (2. Teil) Wie läßt sich die Abhängigkeit einer metrischen Variablen von
Kovarianzanalyse 1 metrische und mehrere metrische und kategoriale Variablen Methoden empirischer Sozialforschung Lineare Modelle (2. Teil) Wie läßt sich die Abhängigkeit einer metrischen Variablen von
Multiple lineare Regression
 Multiple lineare Regression Bisher eine Einflußgröße X 1 (und der Achsenabschnitt). Dagegen das Modell der multiplen Regression Y = β 0 X 0 + β 1 X 1 +... + β p X p + ε mit p Einflußgrößen und dem Achsenabschnitt.
Multiple lineare Regression Bisher eine Einflußgröße X 1 (und der Achsenabschnitt). Dagegen das Modell der multiplen Regression Y = β 0 X 0 + β 1 X 1 +... + β p X p + ε mit p Einflußgrößen und dem Achsenabschnitt.
Empirische Analysen mit dem SOEP
 Empirische Analysen mit dem SOEP Methodisches Lineare Regressionsanalyse & Logit/Probit Modelle Kurs im Wintersemester 2007/08 Dipl.-Volksw. Paul Böhm Dipl.-Volksw. Dominik Hanglberger Dipl.-Volksw. Rafael
Empirische Analysen mit dem SOEP Methodisches Lineare Regressionsanalyse & Logit/Probit Modelle Kurs im Wintersemester 2007/08 Dipl.-Volksw. Paul Böhm Dipl.-Volksw. Dominik Hanglberger Dipl.-Volksw. Rafael
Schriftliche Prüfung (90 Minuten)
 Dr. M. Kalisch Prüfung Statistik I Winter 2016 Schriftliche Prüfung (90 Minuten) Bemerkungen: Erlaubte Hilfsmittel: 10 hand- oder maschinengeschriebene A4 Seiten (=5 Blätter). Taschenrechner ohne Kommunikationsmöglichkeit.
Dr. M. Kalisch Prüfung Statistik I Winter 2016 Schriftliche Prüfung (90 Minuten) Bemerkungen: Erlaubte Hilfsmittel: 10 hand- oder maschinengeschriebene A4 Seiten (=5 Blätter). Taschenrechner ohne Kommunikationsmöglichkeit.
Versuchsplanung SoSe 2015 R - Lösung zu Übung 1 am 24.04.2015 Autor: Ludwig Bothmann
 Versuchsplanung SoSe 2015 R - Lösung zu Übung 1 am 24.04.2015 Autor: Ludwig Bothmann Contents Aufgabe 1 1 b) Schätzer................................................. 3 c) Residuenquadratsummen........................................
Versuchsplanung SoSe 2015 R - Lösung zu Übung 1 am 24.04.2015 Autor: Ludwig Bothmann Contents Aufgabe 1 1 b) Schätzer................................................. 3 c) Residuenquadratsummen........................................
D-CHAB Frühlingssemester 2017 T =
 D-CHAB Frühlingssemester 17 Grundlagen der Mathematik II Dr Marcel Dettling Lösung 13 1) Die relevanten Parameter sind n = 3, x = 1867, σ x = und µ = 18 (a) Die Teststatistik T = X µ Σ x / n ist nach Annahme
D-CHAB Frühlingssemester 17 Grundlagen der Mathematik II Dr Marcel Dettling Lösung 13 1) Die relevanten Parameter sind n = 3, x = 1867, σ x = und µ = 18 (a) Die Teststatistik T = X µ Σ x / n ist nach Annahme
Diagnostik von Regressionsmodellen (1)
 Diagnostik von Regressionsmodellen (1) Bei Regressionsanalysen sollte immer geprüft werden, ob das Modell angemessen ist und ob die Voraussetzungen eines Regressionsmodells erfüllt sind. Das Modell einer
Diagnostik von Regressionsmodellen (1) Bei Regressionsanalysen sollte immer geprüft werden, ob das Modell angemessen ist und ob die Voraussetzungen eines Regressionsmodells erfüllt sind. Das Modell einer
Perfekte Multikollinearität III. Multikollinearität
 Multikollinearität Perfekte Multikollinearität I Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren
Multikollinearität Perfekte Multikollinearität I Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den Regressoren
Übungsblatt 10: Lineare Regression (Sitzung 11)
 1 Übungsblatt 10: Lineare Regression (Sitzung 11) Aufgabe 1 a) Nach welchem Kriterium wird die Regressionsgerade zur Vorhersage von Y-Werten festgelegt? b) Was sind die Gemeinsamkeiten und Unterschiede
1 Übungsblatt 10: Lineare Regression (Sitzung 11) Aufgabe 1 a) Nach welchem Kriterium wird die Regressionsgerade zur Vorhersage von Y-Werten festgelegt? b) Was sind die Gemeinsamkeiten und Unterschiede
Auswertung und Lösung
 Körperkraft [Nm] 0 50 100 150 200 250 0 20 40 60 80 Lean Body Mass [kg] Dieses Quiz soll Ihnen helfen, den R Output einer einfachen linearen Regression besser zu verstehen (s. Kapitel 5.4.1) Es wurden
Körperkraft [Nm] 0 50 100 150 200 250 0 20 40 60 80 Lean Body Mass [kg] Dieses Quiz soll Ihnen helfen, den R Output einer einfachen linearen Regression besser zu verstehen (s. Kapitel 5.4.1) Es wurden
Korrelation - Regression. Berghold, IMI
 Korrelation - Regression Zusammenhang zwischen Variablen Bivariate Datenanalyse - Zusammenhang zwischen 2 stetigen Variablen Korrelation Einfaches lineares Regressionsmodell 1. Schritt: Erstellung eines
Korrelation - Regression Zusammenhang zwischen Variablen Bivariate Datenanalyse - Zusammenhang zwischen 2 stetigen Variablen Korrelation Einfaches lineares Regressionsmodell 1. Schritt: Erstellung eines
Teil: lineare Regression
 Teil: lineare Regression 1 Einführung 2 Prüfung der Regressionsfunktion 3 Die Modellannahmen zur Durchführung einer linearen Regression 4 Dummyvariablen 1 Einführung o Eine statistische Methode um Zusammenhänge
Teil: lineare Regression 1 Einführung 2 Prüfung der Regressionsfunktion 3 Die Modellannahmen zur Durchführung einer linearen Regression 4 Dummyvariablen 1 Einführung o Eine statistische Methode um Zusammenhänge
> r.lm < lm(log10(ersch) log10(dist), > summary(r.lm) > r.lms < summary(r.lm) R-Funktionen zur linearen Regression. data = d.
 3.4 S-Funktionen 75 R-Funktionen zur linearen Regression a Im package stat (immer vorhanden): lm > r.lm < lm(log10(ersch) log10(dist), data = d.spreng) b Funktion summary produziert Resultate, die man
3.4 S-Funktionen 75 R-Funktionen zur linearen Regression a Im package stat (immer vorhanden): lm > r.lm < lm(log10(ersch) log10(dist), data = d.spreng) b Funktion summary produziert Resultate, die man
Varianzkomponentenschätzung
 Qualitas AG Varianzkomponentenschätzung Peter von Rohr Qualitas AG Peter von Rohr Folien ZL I+II LFW C11 October 29, 2015 2 / 23 Multiple Lineare Regression Annahmen Modell y = Xb + e Varianz der Fehler
Qualitas AG Varianzkomponentenschätzung Peter von Rohr Qualitas AG Peter von Rohr Folien ZL I+II LFW C11 October 29, 2015 2 / 23 Multiple Lineare Regression Annahmen Modell y = Xb + e Varianz der Fehler
Einführung in die Varianzanalyse
 Einführung in die Varianzanalyse Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Modul Statistik 2 S. Garbade (SRH Heidelberg) ANOVA Modul
Einführung in die Varianzanalyse Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Modul Statistik 2 S. Garbade (SRH Heidelberg) ANOVA Modul
Lineare Regression II
 Lineare Regression II Varianzanalyse als multiple Regession auf Designvariablen Das lineare Regressionsmodell setzt implizit voraus, dass nicht nur die abhängige, sondern auch die erklärenden Variablen
Lineare Regression II Varianzanalyse als multiple Regession auf Designvariablen Das lineare Regressionsmodell setzt implizit voraus, dass nicht nur die abhängige, sondern auch die erklärenden Variablen
X =, y In welcher Annahme unterscheidet sich die einfache KQ Methode von der ML Methode?
 Aufgabe 1 (25 Punkte) Zur Schätzung der Produktionsfunktion des Unternehmens WV wird ein lineares Regressionsmodell der Form angenommen. Dabei ist y t = β 1 + x t2 β 2 + e t, t = 1,..., T (1) y t : x t2
Aufgabe 1 (25 Punkte) Zur Schätzung der Produktionsfunktion des Unternehmens WV wird ein lineares Regressionsmodell der Form angenommen. Dabei ist y t = β 1 + x t2 β 2 + e t, t = 1,..., T (1) y t : x t2
Statistische Eigenschaften der OLS-Schätzer, Residuen,
 Statistische Eigenschaften der OLS-Schätzer, Residuen, Bestimmtheitsmaß Stichwörter: Interpretation des OLS-Schätzers Momente des OLS-Schätzers Gauss-Markov Theorem Residuen Schätzung von σ 2 Bestimmtheitsmaß
Statistische Eigenschaften der OLS-Schätzer, Residuen, Bestimmtheitsmaß Stichwörter: Interpretation des OLS-Schätzers Momente des OLS-Schätzers Gauss-Markov Theorem Residuen Schätzung von σ 2 Bestimmtheitsmaß
Statistikpraktikum. Carsten Rezny. Sommersemester Institut für angewandte Mathematik Universität Bonn
 Statistikpraktikum Carsten Rezny Institut für angewandte Mathematik Universität Bonn Sommersemester 2014 Mehrdimensionale Datensätze: Multivariate Statistik Multivariate Statistik Mehrdimensionale Datensätze:
Statistikpraktikum Carsten Rezny Institut für angewandte Mathematik Universität Bonn Sommersemester 2014 Mehrdimensionale Datensätze: Multivariate Statistik Multivariate Statistik Mehrdimensionale Datensätze:
Dr. M. Kalisch. Statistik (für Biol./Pharm. Wiss.) Winter Musterlösung
 Dr. M. Kalisch. Statistik (für Biol./Pharm. Wiss.) Winter 2014 Musterlösung 1. (11 Punkte) a) Für welchen Parameter ist X ein geeigneter Schätzer? X ist ein geeigneter Schätzer für den Erwartungswert µ
Dr. M. Kalisch. Statistik (für Biol./Pharm. Wiss.) Winter 2014 Musterlösung 1. (11 Punkte) a) Für welchen Parameter ist X ein geeigneter Schätzer? X ist ein geeigneter Schätzer für den Erwartungswert µ
Aufgabensammlung (Nicht-MC-Aufgaben) Klausur Ökonometrie SS ( = 57 Punkte)
 Aufgabe 3 (9 + 5 + 7 + 7 + 3 + 9 + 7 + 10 = 57 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Zu Beginn der Studienjahre 2011 und 2012 wurden Studienanfänger an
Aufgabe 3 (9 + 5 + 7 + 7 + 3 + 9 + 7 + 10 = 57 Punkte) Hinweis: Beachten Sie die Tabellen mit Quantilen am Ende der Aufgabenstellung! Zu Beginn der Studienjahre 2011 und 2012 wurden Studienanfänger an
Kapitel 10. Multikollinearität. Exakte Multikollinearität Beinahe Multikollinearität
 Kapitel 0 Multikollinearität Exakte Multikollinearität Beinahe Multikollinearität Exakte Multikollinearität Unser Modell lautet y = Xb + u, Dimension von X: n x k Annahme : rg(x) = k Wenn sich eine oder
Kapitel 0 Multikollinearität Exakte Multikollinearität Beinahe Multikollinearität Exakte Multikollinearität Unser Modell lautet y = Xb + u, Dimension von X: n x k Annahme : rg(x) = k Wenn sich eine oder
Statistische Datenanalyse mit R, Korrelation und Regression. Dr. Andrea Denecke Leibniz Universität IT-Services
 Statistische Datenanalyse mit R, Korrelation und Regression Dr. Andrea Denecke Leibniz Universität IT-Services Korrelationsanalyse Eine Korrelationsanalyse soll herausfinden Ob ein linearer Zusammenhang
Statistische Datenanalyse mit R, Korrelation und Regression Dr. Andrea Denecke Leibniz Universität IT-Services Korrelationsanalyse Eine Korrelationsanalyse soll herausfinden Ob ein linearer Zusammenhang
Statistik II. II. Univariates lineares Regressionsmodell. Martin Huber 1 / 27
 Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 27 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
Statistik II II. Univariates lineares Regressionsmodell Martin Huber 1 / 27 Übersicht Definitionen (Wooldridge 2.1) Schätzmethode - Kleinste Quadrate Schätzer / Ordinary Least Squares (Wooldridge 2.2)
11. Übungsblatt zur Vorlesung Ökonometrie SS 2014
 Universität des Saarlandes Lehrstab Statistik Dr. Martin Becker Dipl.-Kfm. Andreas Recktenwald 11. Übungsblatt zur Vorlesung Ökonometrie SS 2014 Aufgabe 45 Die in Aufgabe 43 getroffene Annahme heteroskedastischer
Universität des Saarlandes Lehrstab Statistik Dr. Martin Becker Dipl.-Kfm. Andreas Recktenwald 11. Übungsblatt zur Vorlesung Ökonometrie SS 2014 Aufgabe 45 Die in Aufgabe 43 getroffene Annahme heteroskedastischer
